Open Access Article
Open Access ArticleCooperative aggregation of gold nanoparticles on phospholipid vesicles is electrostatically driven†
Helena
Mateos
 *a,
Antonia
Mallardi
b,
Miquel
Oliver
c,
Marcella
Dell’Aglio
*a,
Antonia
Mallardi
b,
Miquel
Oliver
c,
Marcella
Dell’Aglio
 d,
Pamela
Giannone
a and
Gerardo
Palazzo
d,
Pamela
Giannone
a and
Gerardo
Palazzo
 a
a
aDipartimento di Chimica and CSGI (Center for Colloid and Surface Science), Università degli Studi di Bari “Aldo Moro”, via Orabona n. 4, 70125 Bari, Italy. E-mail: helena.mateos@uniba.it
bCNR-IPCF, Institute for Chemical-Physical Processes, c/o Chemistry Department, University of Bari, Via Orabona 4, 70125 Bari, Italy
cFI-TRACE Group, Department of Chemistry, University of the Balearic Islands, Carretera de Valldemossa km 7.5, E-07122 Palma de Mallorca, Spain
dCNR-IFN (National Research Council – Institute for Photonics and Nanotechnologies), c/o Physics Department, University of Bari, Via Amendola 173, 70126 Bari, Italy
First published on 15th August 2024
Abstract
Gold nanoparticles (AuNP) are known to aggregate on the surface of lipid vesicles, yet the molecular mechanism behind this phenomenom remains unclear. In this work, we have investigated the binding behaviour of AuNPs, synthesized with pulsed laser ablation, to phospholipid vesicles under varying conditions of ionic strength (KCl concentration) and NP to vesicle ratios. Our observations reveal a strong influence of electrolyte concentration on AuNP aggregation mediated by vesicles. Notably, cluster formation is observed even at less than one AuNP per vesicle ratio at low enough ionic strengths. These results evidence a binding mechanism governed by electrostatic attraction with a distinct cooperative behaviour at very low salt concentrations, resulting in a significant increase in nanoparticle clustering. This behaviour is quantitatively analysed through a model that incorporates the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory, considering the electrical double layer attraction between dissimilar, non-oppositely charged objects. This study not only provides insight into the fundamental understanding of nanoparticle–vesicle interactions but also suggests potential strategies for controlling nanoparticle assembly in biological and synthetic systems by tuning the ionic strength.
Introduction
Metallic nanoparticles are an extremely versatile material, employed in a wide range of applications due to their unique physicochemical, optoelectronic, and catalytic properties.1,2 Their surface chemistry can be easily modified, and precise synthesis methods allow for the production of particles with well-defined sizes and shapes, good dispersion, and tailored properties for diverse application needs.3–5Among these, gold nanoparticles (AuNPs) stand out for their surface plasmon resonance (SPR), which arises from the collective oscillation of conduction band electrons. This phenomenon depends on the particle size and shape, resulting in visible color changes that indicate variations in their environment. These properties, combined with the biocompatibility and low toxicity of AuNPs, have led to their widespread investigation for a series of biomedical applications.6–9
Traditional synthesis of metallic nanoparticles relies on the chemical reduction of the corresponding oxidized cations with reagents that act as both reducers and stabilizers. The presence of a stabilizing layer on the nanoparticle is essential to prevent infinite growth, aggregation, and precipitation.10 However, this often complicates the study of processes involving interactions between NPs and other molecules or surfaces, as the reactivity of a given type of metallic NP strongly depends on the nature of the ligand used as a stabilizer.
AuNPs prepared by the Turkevich method, stabilized by a layer of citrate anions, are one of the most studied and characterized types of nanoparticles for biomedical applications.6 However, it becomes difficult to discriminate the contribution of the interactions between the NPs metal core and biological systems from those related to the capping agents and the system's ionic strength due to the presence of citrate.
Despite being the most extensively studied metallic nanoparticles in biomedical settings, our understanding of AuNP interactions within biological systems, especially at the nano-bio interface, remains incomplete.11–13 These interactions are crucial for determining the fate of nanostructured materials in living systems and are influenced by factors such as nanoparticle size, membrane composition, electrostatics, and environmental conditions such as ionic strength and temperature. Several studies, mainly focused on citrate-capped AuNPs, have only recently begun to investigate their aggregation behaviour on membranes made of zwitterionic but slightly negatively charged phosphatidylcholine (PC) lipids. In particular, the aggregation of AuNP on the surface of PC vesicles has been the subject of extensive investigations using the colour change associated with the AuNP cluster formation.
Positively charged AuNPs, like those capped with cetyltrimethylammonium bromide (CTAB), interact differently with lipid membranes compared to negatively charged citrate capped NPs. Sheridan et al.14 have shown that these cationic NPs can significantly disrupt cell membranes, especially those composed of anionic lipids. The strong electrostatic attraction between the positively charged NPs and the negatively charged lipid head groups leads to increased inclusion of the NPs into the lipid monolayer. Additionally, coarse-grained molecular dynamics (CGMD) simulations reveal that AuNPs with different surface ligands either adhere to the membrane surface or integrate into the bilayer. Cationic AuNPs can penetrate vesicle membranes more easily than planar lipid bilayers, with interactions influenced by surface charge density.15
Several researchers indicate that AuNP clustering on lipid membranes is highly dependent on the ratio of AuNPs to phospholipid vesicles. Wang et al.16 followed the citrate-capped AuNPs aggregation on phosphocholine lipid vesicles at different ratios and low ionic strength. They found that AuNPs were not uniformly distributed on the vesicle surface and that even at low AuNP to vesicle ratios, clusters were still present. The observed AuNPs cluster formation depends on the nature of the capping agent and was explained by the strong inter-AuNP van der Waals force among single AuNPs adsorbed on the same vesicle's surface. The same group also showed that AuNPs adsorption on fluid DOPC vesicles could induce local lipid gelation, forming AuNP/lipid complexes that diffuse in the low-viscosity surrounding lipids and merge into clusters.17
Sugikawa et al.18 observed that lower amounts of lipid vesicles relative to AuNPs lead to increased clustering of nanoparticles on the vesicle's surface at ionic strengths where the NPs alone do not aggregate. Similar interactions were also investigated under conditions of high ionic strength, where AuNPs alone would typically aggregate.19,20 These studies demonstrate that in the presence of vesicles, 3-D aggregation of AuNPs in bulk solution is prevented, with AuNPs preferring to adsorb on vesicles. When the AuNP/vesicles ratio is high, a colour change indicates cluster formation on the vesicle's surface. However, increasing the concentration of lipid vesicles prevents this aggregation. This is probably because, at low AuNP/vesicle and high salt concentrations, most of vesicles are decorated by one or fewer AuNPs.
Although several studies have investigated the binding and aggregation of AuNPs on vesicle surfaces, the detailed driving forces behind these processes have not been comprehensively explored. Interestingly, cluster formation mediated through the lipid membrane has been reported even at very low ionic strengths and at ratios of less than 1 AuNP/vesicle, where longer Debye screening lengths should enhance the repulsive forces and prevent interaction.21 The observed uneven distribution of AuNPs on vesicles under these conditions has been explained suggesting a cooperative mechanism that favours the binding of subsequent AuNPs after the adsorption of the first AuNP on the vesicle. To rationalize the cooperativity of the aggregation, the authors proposed that citrate release from the NP upon adsorption on the lipid membrane results in a transient increase in the local ionic strength, promoting further nanoparticle adhesion.21
In this study, to avoid the typical disadvantages associated with citrate-capped AuNPs, such as distinguishing the effects of the metal core's interactions with biological systems from those related to the capping agents and addressing issues arising from the system's ionic strength due to citrate presence, we used AuNPs produced by pulsed laser ablation in liquid (PLAL) without the use of any capping agents. We followed the interaction between these PLAL-AuNPs and synthetic vesicles consisting of phosphatidylcholine, focusing on experiments conducted at various controlled ionic strengths (in a low range of values) and different AuNP to vesicle ratios. Our goal is to delineate the role of ionic strength in modulating the adsorption of strongly negatively charged AuNPs on the surface of weakly negatively charged vesicles and the subsequent formation of AuNP clusters.
Results and discussion
The role of ion release in cooperative binding
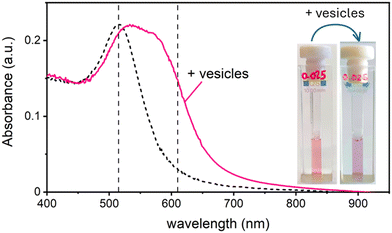
In this work, we study the interaction between AuNPs synthesized by PLAL with an average diameter of around 15 nm and a zeta potential (ζ) ranging from −40 mV to −50 mV, and phosphatidylcholine vesicles with a diameter of around 120 nm and a ζ = −6 mV. These “naked” AuNPs are synthesized in 100 μM KCl solution. Their colloidal stability is attributed to the presence of negative charges on their surface, which are commonly explained by a combination of adsorption of anions22 and an excess of electrons formed within the plasma phase of nanoparticle production.23In a first set of experiments, we followed their interaction with vesicle, leaving the ionic strength constant to match the synthesis medium of the nanoparticles (100 μM KCl). In the absence of vesicles, these AuNPs are well dispersed in solution, displaying a pink colour and exhibiting an SPR in the visible wavelength range centred at 515 nm. Upon mixing the AuNP with the vesicles at a ratio of 1 nanoparticle for every 2 vesicles, the solution undergoes a rapid colour change from pink to blue. This transformation is marked by the appearance of a new absorption band around 610 nm and a slight red shift of the SPR peak. Fig. 1 shows both the visible spectra of AuNPs and the respective photographs of the samples before and after the addition of the lipid vesicles. Given the ratio of less than 1 NP per vesicle, this colour change demonstrates that the AuNPs are adsorbing and clustering on the vesicle's lipid membranes unevenly. Consequently, most vesicles remain free of nanoparticles, while just a smaller subset carries aggregates of more than one AuNP.
Similar phenomena have been described by Montis et al.,21 in the presence of citrate-capped gold nanoparticles. The cooperative aggregation was explained by the sudden release of citrate ions, leading to a localized increase in ionic strength near the adhesion point of a AuNP on the lipid membrane, which in turn increases the probability of the adhesion of another AuNP onto the same vesicle. Although our system uses PLAL-AuNPs, which lack citrate, we can speculate that chlorine ions adsorbed on their surface might play a similar role to that postulated for citrate. If this hypothesis is correct, then calculating the local increase in ionic strength caused by the release of chlorine ions after the adsorption of the first NP, along with the diffusion times for both the second NP and the released ions, should provide evidence supporting this theory.
Let's go first with the calculation of the diffusion times. Consider a solution with a number density of vesicles [Vestot] (expressed in m−3). The average volume around a single vesicle can be described as [Vestot]−1. Within this volume, the number of AuNPs (G) is given by 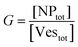 , where [NPtot] represents the number density of AuNPs. Each object within [Vestot]−1 occupies a volume
, where [NPtot] represents the number density of AuNPs. Each object within [Vestot]−1 occupies a volume 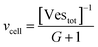 , where G + 1 is the total number of particles (G AuNP + 1 vesicle). This volume calculation is crucial as it is used to evaluate the effects of ions released by each AuNP in the vicinity of the vesicle. Within the range of conditions explored in this work, the smallest volume per particle is vcell = 3 × 108 nm3, which corresponds to the highest vesicle concentration of 3.3 nM. This volume can be visualized as a cube with an edge length
, where G + 1 is the total number of particles (G AuNP + 1 vesicle). This volume calculation is crucial as it is used to evaluate the effects of ions released by each AuNP in the vicinity of the vesicle. Within the range of conditions explored in this work, the smallest volume per particle is vcell = 3 × 108 nm3, which corresponds to the highest vesicle concentration of 3.3 nM. This volume can be visualized as a cube with an edge length 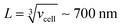 . Given the diffusivity D ∼ 2 × 10−9 m2 s−1 for small ions, the time to cover this distance is calculated as
. Given the diffusivity D ∼ 2 × 10−9 m2 s−1 for small ions, the time to cover this distance is calculated as 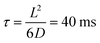 . During the same time, the nearest AuNP, with a diffusivity DNP ∼ 2 × 10−11 m2 s−1 explores only about 70 nm
. During the same time, the nearest AuNP, with a diffusivity DNP ∼ 2 × 10−11 m2 s−1 explores only about 70 nm 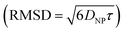 . Consequently, the AuNP cannot migrate quickly enough to exploit the concentration gradient created by the dispersing ions, and as a result, the ions achieve a uniform concentration across the space between the nanoparticle and the nearby vesicle before any significant movement of the AuNP occurs.
. Consequently, the AuNP cannot migrate quickly enough to exploit the concentration gradient created by the dispersing ions, and as a result, the ions achieve a uniform concentration across the space between the nanoparticle and the nearby vesicle before any significant movement of the AuNP occurs.
Having evaluated the diffusion times, we can calculate the local increase in ionic strength associated to the release of chlorine ions upon the adsorption of the first nanoparticle on the vesicle's membrane. In this calculation, we assume that the negative charge on the AuNP is entirely due to adsorbed anions. While this assumption is accurate for citrate capped AuNPs, it is questionable for the PLAL-AuNPs in the present investigation. The negative charge observed for PLAL-AuNPs is commonly attributed to a combination of anion adsorption and excess electrons formed within the plasma phase of nanoparticle production.23 Therefore, the result of the following calculation should be considered as the upper limit of the potential increase in ionic strength due to the binding of AuNP to a vesicle. With the simultaneous knowledge of both the AuNP zeta-potential (ζ, shown in Fig. S1A in the ESI†) and the exact ionic composition of the solution, we can assess the change in ionic strength associated with the release of adsorbed ions. According to the Grahame equation, the following relationship exists between the surface charge density (σ) and the zeta-potential of a planar surface:
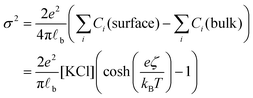 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b the Bjerrum's length, which is the distance at which the electrostatic interaction between two elementary charges equals the thermal energy kBT that in water is 0.7 nm. For spherical surfaces, there is no equivalent analytical solution to the problem. However, Hunter, in his classical book on zeta potential, suggested the following relation as an accurate approximation for the relationship between the charge on a sphere and the potential for a univalent symmetrical electrolyte:24
b the Bjerrum's length, which is the distance at which the electrostatic interaction between two elementary charges equals the thermal energy kBT that in water is 0.7 nm. For spherical surfaces, there is no equivalent analytical solution to the problem. However, Hunter, in his classical book on zeta potential, suggested the following relation as an accurate approximation for the relationship between the charge on a sphere and the potential for a univalent symmetrical electrolyte:24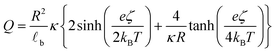 | (2) |
The nature of the interactions inducing AuNP clustering on the vesicle surface is electrostatic
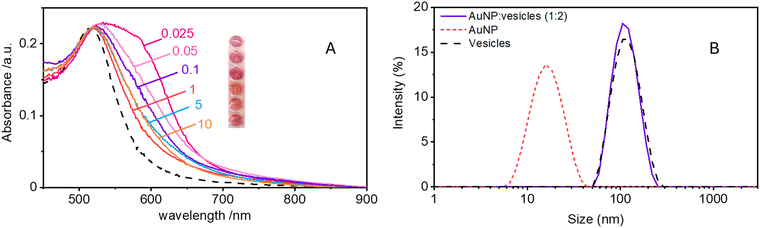
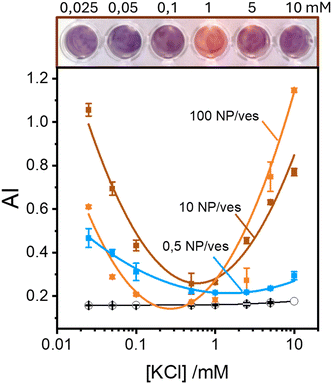
Maintaining the ratio of 1 NP to every 2 vesicles, the samples were further analysed at varying ionic strengths. The AuNPs spectra, shown in Fig. 2A, reveals how at low ionic strength the formation of a shoulder at 610 nm is more pronounced. This is an indication of AuNP aggregation that takes places on the surface of vesicles as demonstrated by the DLS results shown in Fig. 2B. Fig. 2B shows the size distribution of AuNPs in absence and in presence of vesicles and of vesicles alone. Given the higher refractive index of gold compared to that of the vesicles, for the AuNP–vesicle mixture we expect the DLS signal to be dominated by the stronger scattering from the AuNPs. As shown in Fig. 2B, the size-distribution peak corresponding to the AuNP–vesicle mixture shifts from that attributed solely to the AuNPs towards values corresponding to vesicles alone. We ascribe this effect to the strong interaction between the smaller AuNPs and the vesicles, indicating that all the AuNPs are bound to, and diffuse with, the vesicles. This behaviour is observed at all the explored KCl concentrations, as shown in Fig. S2 of ESI.† Such evidence demonstrates that even at high ionic strength, where the AuNP SPR indicates a low aggregation, all the nanoparticles are bound to the vesicles.The aggregation of AuNPs was quantified using UV-vis absorbance, specifically by calculating the so called “aggregation index” (AI), which is defined as the ratio of the absorbance value at 610 nm (reflecting mainly aggregated AuNPs) to the absorbance at 515 nm (reflecting monomeric AuNPs), as seen in Fig. 1.19,20 The AI values obtained from the spectra in Fig. 2A are plotted as a function of [KCl] in Fig. 3 in light blue. The aggregation is consistent at 0.025 mM but decreases upon increasing the salt concentration, becoming barely discernible for [KCl] > 1 mM. The clear influence of the salt concentration on the clustering of nanoparticles on the surface of the vesicles, particularly the enhanced aggregation observed at low ionic strength, strongly suggests that such a phenomenon is driven by electrostatic attractive interactions. This is a novel outcome since all previous interpretations assumed that the attraction between vesicles and the first interacting AuNP was solely driven by van der Waals forces.
These findings indicate that AuNP aggregation increases as the ionic strength decreases. This observation might appear counterintuitive in terms of classical DLVO theory, where repulsive interactions are expected to dominate between like-charged particles, such as the negatively charged AuNPs (around −45 mV) and the vesicles (around −6 mV, which is nearly neutral but still negative). Typically, lower ionic strengths enhance repulsive interactions due to reduced screening of charges. However, the vesicle surface represents a peculiar interface due to the orientational degrees of freedom of the phospholipids headgroups. Previous theoretical investigations suggest that short-range attractive interactions between negatively charged macroions and phospholipid surfaces can occur, but these are only effective at very short distance (<2 nm).25 Additionally, density functional theory (DFT) and Monte Carlo (MC) simulations foretell that the presence of counterions with an internal distribution of charges can induce the coagulation of equally charged particles.26,27 This mechanism could explain the coagulation induced by certain antibodies in negatively charged vesicles27 and AuNPs.28 However, in our study, the only cation present is the K+ that cannot play a similar role. Thus, the observed increase in aggregation likely points to a more complex mechanism that deserves a deeper study exploring other NP/vesicles ratios.
Surprisingly, these findings indicate that AuNP aggregation increases as the ionic strength decreases, which is counterintuitive given the negative zeta potential on both the AuNPs (around −45 mV) and the vesicles (around −6 mV, which is nearly neutral but still negative). Typically, lower ionic strengths would enhance repulsive interactions due to reduced screening of charges. However, the observed increase in aggregation points towards a more complex mechanism that deserves a deeper study exploring other NP/vesicles ratios.
Fig. 3 also shows the AI values calculated from spectra recorded in excess of AuNPs at ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 100
1 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AuNP/vesicle (brown and orange solid lines, respectively). In these cases, the pattern of AuNPs aggregation as a function of KCl concentration is clearly non-monotonic. Specifically, aggregation is high at both low (25 μM) and high (10 mM) ionic strengths, with a minimal value in the range 0.1–1 mM.
1 AuNP/vesicle (brown and orange solid lines, respectively). In these cases, the pattern of AuNPs aggregation as a function of KCl concentration is clearly non-monotonic. Specifically, aggregation is high at both low (25 μM) and high (10 mM) ionic strengths, with a minimal value in the range 0.1–1 mM.
Our findings, as seen in Fig. 3, reveal the critical importance of ionic strength in the quantification of lipid vesicles using AuNPs. When examining the data in Fig. 3 at a fixed ionic strength of, for example 10 mM KCl, we observe that the extent of aggregation increases with the number of nanoparticles per vesicle. This phenomenon has been used by several authors19,20,29 as a tool to quantify lipid vesicles, and ultimately, extracellular vesicles. According to Fig. 3, a reliable vesicle quantification using AuNPs is only feasible at suitable ionic strengths. As we approach the range 0.1–1 mM of electrolyte concentration, the relationship between vesicle concentration and NP aggregation vanishes. Therefore, to ensure accurate vesicle quantification in systems using AuNPs, it is crucial to maintain the ionic strength well above 1 mM to avoid misleading results.
At this point, it is evident that the aggregation of AuNPs in the presence of phospholipid membranes is a complex mechanism that depends both on the AuNP/vesicle ratio and the ionic strength of the system. In the following sections we will attempt to explain this complex behaviour by recognizing three important scenarios: (1) the binding of the first NP to a vesicle (2) the binding of a subsequent NP, and, therefore, the formation of a AuNP aggregate on the lipid membrane, and (3) the kinetics of these encounters.
Electrostatic attraction between dissimilar objects:30 the AuNP–vesicle first binding
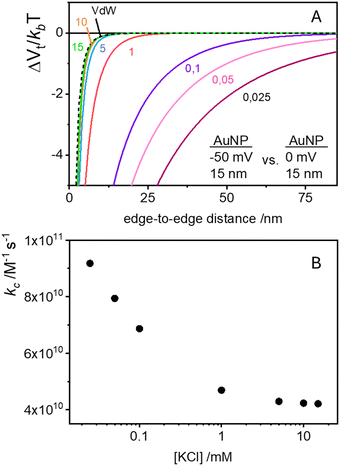
Traditional van der Waals (vdW) models fall short when applied to the interaction between nanoparticles and vesicles due to their substantial difference in size and charge. Considering that the vesicles are much larger than the NPs, their mutual van der Waals attraction is best described as the interactions between a flat wall of thickness t and a sphere of radius rNP placed at an end-to-end distance d (Tadmor2001):31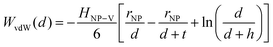 | (3) |
The EDL interactions depend on the surface charges of the vesicles and AuNPs, which can be modelled as spheres with surface potentials ζV and ζNP, respectively. The dissimilarity in charge magnitudes, with ζV = −6 mV and ζNP = −50 mV, suggest unique interactions that differ significantly from the familiar homo-coagulation between equally charged identical particles. The EDL interactions between dissimilar spherical particles have been previously evaluated under the Derjaguin approximation and different boundary conditions, like constant charge (CC) and constant potential (CP).32–34
In a scenario where the charge density remains unchanged upon approach (CC), charge repulsion typically occurs between objects bearing charges of the same sign, even when one is nearly neutral. According to the CC model, the van der Waals attraction between a nanoparticle and a vesicle is negligible for distances above 15 nm (eqn (3)), and therefore, this model fails to explain the observed attraction of a negative AuNP to a weakly negative vesicle. On the other hand, when the surface potential remains unchanged upon approach (CP), the interactions align more closely with the observed phenomena, as seen by the eqn (4) describing the EDL interaction potential in the CP case:35,36
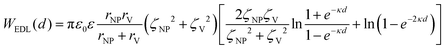 | (4) |
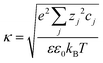 is the Debye–Hückel parameter, which is the reciprocal of the Debye length. Inspection of eqn (4) reveals that for equal potentials (ζV = ζNP), the first term in the brackets is large and positive, leading to a repulsion between the objects. But when one of the potentials is very small, this term becomes negligible. In the limiting case where the vesicles are effectively neutral (zV = 0), the first term in the brackets vanishes and the remaining term, ln(1 − e−2κd), is always negative, leading to an effective attraction between a AuNP and a vesicle. A peculiar feature of such an EDL attraction between non oppositely charged bodies is that it becomes stronger as the ionic strength decreases (i.e. when k decreases). According to the DLVO model, we have calculated the total interaction potential between a vesicle and a AuNP as the sum of the vdW (eqn (3)) and the EDL interactions (eqn (4)):
is the Debye–Hückel parameter, which is the reciprocal of the Debye length. Inspection of eqn (4) reveals that for equal potentials (ζV = ζNP), the first term in the brackets is large and positive, leading to a repulsion between the objects. But when one of the potentials is very small, this term becomes negligible. In the limiting case where the vesicles are effectively neutral (zV = 0), the first term in the brackets vanishes and the remaining term, ln(1 − e−2κd), is always negative, leading to an effective attraction between a AuNP and a vesicle. A peculiar feature of such an EDL attraction between non oppositely charged bodies is that it becomes stronger as the ionic strength decreases (i.e. when k decreases). According to the DLVO model, we have calculated the total interaction potential between a vesicle and a AuNP as the sum of the vdW (eqn (3)) and the EDL interactions (eqn (4)):| Wtot(d) = WvdW(d) + WEDL(d) | (5) |
These plots resemble the energy profiles found in chemical kinetics, but there is a profound difference. In chemical kinetics, as molecules move toward the origin along an energy profile, they navigate along a frictionless reaction coordinate path and, if they possess an energy larger than the energy barrier, the reaction becomes possible. In the case of aggregation kinetics, such movement describes a true interparticle distance filled by solvent.
As Verwey and Overbeek pointed out, the viscous friction will dissipate all the particles’ kinetic energy.37 Therefore, DLVO potential–distance curves should not be interpreted as mere potential barriers but rather as modulators of the probability that Brownian motion will bring particles closer or drive them apart. To quantify these interactions, the total potential Wtot is incorporated into the chemical potential used in Fick's first law.38 Solving it under the constraint of null velocity when two particles are in contact leads to the definition of the so-called stability ratio ω:30,38
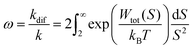 | (6) |
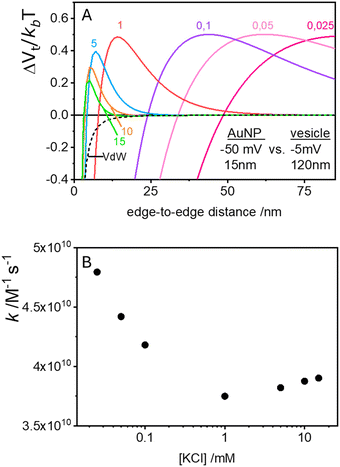
In the case of null potential (hard spheres), the integral is ½, resulting in a stability ratio of ω = 1. In the familiar case of interaction between equally charged particles, a large energy barrier (Wtot ≫ 0) dominates the integral in eqn (6) resulting in a repulsion characterized by ω > 1. Conversely, Fig. 4A shows the interaction between dissimilarly charged particles of the same sign. The barrier height is below 1kT and, more importantly, the region where Wtot < 0 extends to large distances when the salt concentration is low. Since this negative interaction potential serves as the argument of an exponential in eqn (6), it contributes a factor that is less than 1, thus resulting in ω < 1. In other words, the aggregation rate constant at low ionic strength is larger than the value obtained under diffusive control (k = kdif/ω) because of the additional attractive EDL interactions.
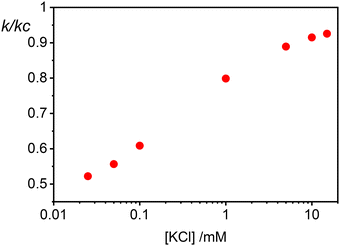
The rate constants for the first encounter between a AuNP and a vesicle have been evaluated at different KCl concentrations by means of the numerical integration of eqn (6) using the Wtot values shown in Fig. 4B. The numerical values of ω were then used to evaluate k = kdif/ω, where kdif = 1.8 × 1010 M−1 s−1 = 4π(rNP + rV)(DNP + DV), with DNP and DV being the diffusivities of NP and vesicles, respectively.39 The results, shown in Fig. 4B indicate that the process is fast at low [KCl] and the rate constants decline with increasing [KCl], finally attaining an almost constant value at [KCl] ≥ 1 mM.
These results are significant because they rationalize the strong affinity of AuNP for nearly neutral vesicles in terms of an EDL attraction that becomes stronger at low ionic strength.
Electrostatic attraction between dissimilar objects: the AuNP cooperative coagulation on the vesicle surface
The process of aggregation of AuNPs on vesicle surfaces is marked by two distinct steps. The initial attachment of a single AuNP to the vesicle surface and the subsequent binding of additional AuNPs to the same vesicle, which, due to the observed cooperativity, should be significantly faster and more favourable than binding to other pristine vesicles.According to the previous section, the initial binding of a AuNP to a vesicle is driven primarily by EDL attraction between dissimilarly charged bodies. To rationalize the cooperativity of the subsequent binding events, we follow the suggestion by Montis et al., who proposes a substantial loss of charges on the particles after adsorption on the vesicle.21 Instead of focusing on the negligible change in ionic strength, we note that this charge reduction changes the nature of the interaction between the bound AuNP and subsequent AuNPs in solution. With reduced charges on one NP, the EDL term becomes essentially attractive, and the large Hamaker constant of AuNP–AuNP interactions leads to a strong and long-range overall attraction that greatly favours further AuNP attachment. The exact mechanism of this potential reduction is not critical to the discussion. In this case, it could involve a combination of anion release and the distribution of excess electrons across the extensive surface of the vesicles.
To model the system, we consider that the Hamaker constant for the interaction between a AuNP and a vesicle is negligible in comparison with the AuNP–AuNP interactions. Accordingly, even though we are now considering the interaction between a free AuNP in solution and another AuNP that is anchored to a vesicle, we approximate the vdW contributions using the Hamaker equation for two identical spheres (expressed in terms of edge-to-edge distance as in ref. 31)
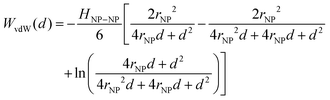 | (7) |
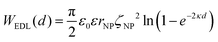 | (8) |
The corresponding stability ratio ω can be evaluated using the integral in eqn (6) to calculate the rate constant for the cooperative step as kc = kdif/ω, where kdif remains the same (1.8 × 1010 M−1 s−1) since the diffusivity and cross-sectional area of a NP anchored to a vesicle are similar to those of the vesicle alone. Indeed, if a vesicle binds a second AuNP at a distance from the first AuNP we expect a fast aggregation with the first AuNP, driven not only by electrostatic interactions but also by a combination of non-specific (and non-electrostatic) attractive nearest-neighbour direct interactions. The origin of these forces could include dipolar interactions18 lipid-mediated depletion and fluctuation-forces,40 and hydrophobic mismatch between NPs and lipids.41
The cooperative step rate constants (kc) at different KCl concentrations are plotted in Fig. 5B. The results show that at low salinity, kc is almost twice the rate constant k of the first binding event (see Fig. 4B). This suggests that, at low salinity, the initial binding of a AuNP to the vesicle is less probable than the subsequent binding events. Once a vesicle has bound the first AuNP, other NPs are very likely to aggregate with the first, leading to the formation of clusters on a few vesicles, even when the NP/vesicle ratio is less than one.
As the KCl concentration increases, kc decreases and approaches the value of k. In other words, at high ionic strength, both the first and subsequent binding events are equally probable, resulting in a random AuNPs binding to vesicles.
This model successfully reproduces the dependence of gold nanoparticle coagulation on vesicles as a function of [KCl] at low NP/vesicle ratios.
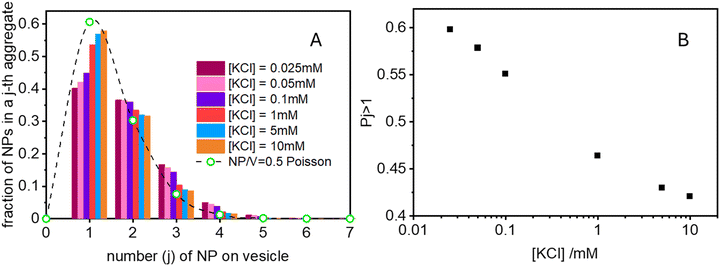
Finally in Fig. 6 we show the calculated ratio between the rate constants for the first binding (k) and the subsequent cooperative binding (kc) for all explored KCl concentrations. All the calculated values are lower than 1, which implies that kc > k, and therefore cooperativity. If for example k/kc is 0.5, it suggests that subsequent NP bindings occur at twice the rate of initial bindings. However, at values closer to 0.9, the initial binding is almost as frequent as subsequent bindings, reducing the cooperative binding advantage. Accordingly, at a NP/vesicle ratio of 0.5, increasing the KCl concentration above 1 mM, the AuNP still adsorb on the vesicles (as demonstrated by the DLS results in Fig. S2, ESI†) but do not from clusters because they are mainly distributed among vesicles as one NP per vesicle.
A minimal kinetic model
According to the data of Fig. 3, for NP to vesicle ratios larger than 1, there is a range of salinity where aggregation increases with electrolyte concentration. To understand the interplay between the NP/vesicle ratio and the binding rates of the first and subsequent NPs to the vesicles, a minimal kinetic model can be very useful.The aggregation of n nanoparticles on vesicle surfaces can be described as a series of sequential binding events, each leading to an increase in the number of NPs on a vesicle. Like so, first a NP binds to an unoccupied vesicle (Ves0) to form a single-particle vesicle (Ves1), and subsequent NPs can continue to bind forming (Ves2) from (Ves1), and so forth up to Vesj from Vesj−1:
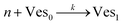 | (a) |
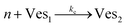 | (b) |
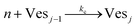 | (c) |
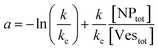 | (9) |
(i) NP/vesicles ratio: the higher the [NPtot]/[Vestot] ratio, the larger is the probability that several NPs are on the same vesicle.
(ii) Ratio k/kc: this ratio increases with salt concentration, as shown in Fig. 6, influencing the degree of cooperativity in binding. The smaller this ratio the higher the cooperativity, suggesting more clustered binding under lower salt concentrations. In the case of k/kc = 1, a will tend to [NPtot]/[Vestot].
At low [NPtot]/[Vestot] ratios (0.5 in Fig. 7) the excess of vesicles tends to favour individual nanoparticles binding to separate vesicles rather than forming large clusters, except under highly cooperative conditions induced by very low k/kc, which are found at low salt concentrations. Conversely, at high [NPtot]/[Vestot] ratios, there's a sufficient number of nanoparticles to ensure that a non-cooperative binding leads to several particles on all the vesicles. In this case, a moderately cooperative binding, leading to larger clusters on a few vesicles and leaving others empty, can reduce the mean occupancy of the vesicles. For strongly cooperative binding, the presence of large enough AuNP clusters on a few vesicles raises the mean occupancy of vesicles again, resulting in a parabolic trend of the occupancy as function of the cooperativity (k/kc).
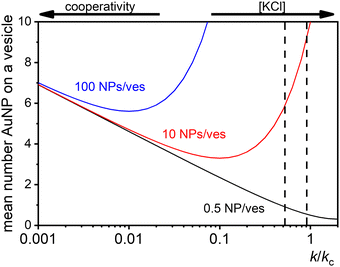 | ||
| Fig. 7 Theoretical predictions of the expected number of NPs per vesicle (a in eqn (9)) across a wide range of k/kc ratios from 0.001 to 10 for three different ratios of NPs to vesicles: 0.5 (black line), 10 (red line), and 100 (blue line). The two vertical dashed lines indicate the range of KCl concentrations explored in the study, with the left line at 0.025 mM and the right line at 10 mM. | ||
These dynamics are depicted in Fig. 7 for [NPtot]/[Vestot] = 10 and 100, and qualitatively align with experimental observations of NP aggregation on vesicles across varying salt concentrations as shown in Fig. 3.
The agreement between our model and experimental data is fundamentally qualitative. The AI measured in this study is a limited descriptor because it does not provide detailed information about the size of the clusters or the mean occupancy of the vesicles by nanoparticles. Comparing the experimental data (Fig. 3) and the outcome of our kinetic model (Fig. 7), it is evident that the main discrepancy relates to the range of k/kc. As seen in Fig. 6, the kinetic model predicts a broad parabolic behaviour extending from k/kc = 0.001 to 1. However, our experimental data exhibit this parabolic trend within a much narrower range, specifically from k/kc = 0.5 to 0.9 (corresponding to a [KCl] range from 0.025 mM to 10 mM), as indicated by the two dotted vertical lines in Fig. 7.
This narrow experimental range suggests a fundamental issue in how kc is calculated, particularly the assumption that the rate constants for the formation of clusters (j-mers) are the same as those for dimerization, shown in Fig. 5B. Given that van der Waals (vdW) attractions typically increase with the mass of interacting bodies, we expect that interactions involving a dimer and a free AuNP would be significantly stronger than those between a single AuNP on a vesicle and another free AuNP. If we could more accurately calculate kc, taking into account the enhanced vdW attractions for larger clusters, we might find that the lower range of our observed [KCl] concentration, specifically at 0.025 mM corresponding to k/kc = 0.5, would shift to a considerably lower value. Such a correction would potentially improve the alignment between the observed experimental trends and our theoretical predictions, showing a broader agreement across the examined KCl concentrations. Unfortunately, this increased complexity in the interactions leads to a kinetic model that is not analytically tractable, pointing to the need for computational simulations to better handle these dynamics.
The scenario with a low ratio [NPtot]/[Vestot] = 0.5 is the best matching between model and the experimental observations. This is likely because, at such a low NP to vesicle ratio, the aggregation is limited to small clusters (mainly dimers). Knowing the [Vesj] distribution (eqn (S7) in the ESI†) and the expected occupancy value (eqn (9)), it is possible to evaluate the fraction of NP forming clusters of j-NPs per vesicle as:
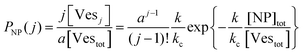 | (10) |
Conclusions
Gold nanoparticles prepared by PLAL without organic capping agents spontaneously adsorb to phospholipid vesicles. At low ionic strength, this adsorption leads to the cooperative aggregation on AuNPs on the vesicle surface. This means that the binding of a AuNP to a vesicle is favoured when another AuNP is already bound, resulting in a faster aggregation compared to binding to an unoccupied vesicle.When the NP to vesicle ratio is <1, AuNP aggregation is observed only at low ionic strength (below 1 mM). However, for ratios NP/vesicles ≫1, aggregation is evident at both low and high electrolyte concentration but is minimal at intermediate concentrations (0.1–1 mM). Under all these conditions, the AuNPs do not aggregate in absence of vesicles.
This behaviour is quantitatively explained using a model that incorporates the DLVO theory, considering the EDL attraction between objects with the same sign of the electrostatic potential but very different magnitudes. The significant mismatch between the experimental values of the zeta potentials of the vesicles (ζV = −6 mV) and the AuNPs (ζNP = −50 mV) induces a net attraction, facilitating the first binding of AuNPs on the vesicle surface.
Moreover, the thermodynamic aspect of AuNP aggregation on lipid vesicles is primarily governed by EDL interactions, which are largely entropic (osmotic) in nature. To explain the cooperativity in subsequent binding events, we propose that upon binding to the vesicle bilayer, the AuNP releases most of its adsorbed anions, reducing its negative potential. This results in an almost neutral AuNP on the vesicle surface, which interacts attractively with the negatively charged AuNPs in solution through EDL interactions. However, once the first NP is attached to the vesicle and has partially lost its charge, the van der Waals component of the DLVO theory, which is inherently enthalpic, becomes more significant, making the process an interplay between EDL (entropic) and van der Waals (enthalpic) interactions. The Hamaker constant for gold–gold interactions is much larger than for phospholipid–gold interactions, making the attraction leading to AuNPs dimer formation on the vesicle surface much stronger than the initial binding. Consequently, the rate constant for AuNP dimerization (kc) on the vesicle surface is larger than that for the initial binding (k). This disparity increases with decreasing ionic strength, justifying the observed cooperativity of AuNP aggregation at low electrolyte concentrations.
These results can be introduced in a minimal kinetic model that accurately describes the results obtained for AuNP/vesicles ratios <1, where dimers are the main aggregate species. For larger ratios the model provides only qualitative agreement.
Our results not only advance the fundamental understanding of nanoparticle–vesicle interactions but also highlight the significance of electrostatic interactions in biological systems, particularly where one surface is charged, and the other is nearly neutral. This physics, previously developed for studying heteroaggregation and deposition rates involving asymmetrically charged particles and surfaces, has been underexplored in biological contexts.
Several biological systems, such as the initial binding of negatively charged bacteria to negatively charged surfaces in biofilm formation, could exhibit similar attractions between like-charged objects. Our investigation suggests further strategies for controlling nanoparticle assembly in both biological and synthetic systems by manipulating ionic strength.
Materials and methods
Synthesis of PLAL AuNPs
The AuNPs were produced by PLAL as described in detail in ref. 42 using a gold target (99.999%, Kurt J. Lesker Company) immersed in ultrapure water (HPLC Plus water) containing KCl 100 μmol L−1. The laser, with a nominal pulse duration of 8 ns, operated with a 1064 nm laser wavelength, with a fluence of 64 J cm−2 and a laser frequency of 10 Hz. After synthesis, AuNPs solution shows also the presence of small aggregates with a fractal structure stabilized by strong long-range repulsive interactions.43 To remove these structures, we perform a centrifugation step of the solution obtained from ablation (10 min at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm in a bench-top Eppendorf centrifuge), which allows separation in the pellet of the aggregates leaving monodispersed AuNPs in solution.
000 rpm in a bench-top Eppendorf centrifuge), which allows separation in the pellet of the aggregates leaving monodispersed AuNPs in solution.
AuNPs concentration was evaluated from the SPR spectrum as described by Haiss et al.44
Vesicles preparation
Vesicles were prepared using the lipid film hydration method described elsewhere45 with slight modifications.200 μL of a 50 mM soybean phosphatidylcholine (PC) solution (in a mixture of chloroform/methanol in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio) were withdrawn, diluted to 3 ml with the same organic mixture and deposited into a 25 mL round-bottom flask. The lipids were dried in a rotavapor for 4 hours at 30 °C. Hydration of the dry lipid film was achieved by adding 1 mL of filtered (with 0.22 μm cellulose acetate) HPLC water to obtain a final concentration of 10 mM PC. The mixture was vortexed for 1 minute every 5 minutes over the course of 1 hour to facilitate swelling and complete resuspension of PC from the flask wall, resulting in the formation of multilamellar vesicles. The vesicles suspension was left refrigerated overnight for stabilization and finally extruded 30 times through a 100 nm pore size membrane filter using an Avanti Polar mini extruder. This procedure allowed the formation of unilamellar vesicles with a diameter of about 120 nm.
1 ratio) were withdrawn, diluted to 3 ml with the same organic mixture and deposited into a 25 mL round-bottom flask. The lipids were dried in a rotavapor for 4 hours at 30 °C. Hydration of the dry lipid film was achieved by adding 1 mL of filtered (with 0.22 μm cellulose acetate) HPLC water to obtain a final concentration of 10 mM PC. The mixture was vortexed for 1 minute every 5 minutes over the course of 1 hour to facilitate swelling and complete resuspension of PC from the flask wall, resulting in the formation of multilamellar vesicles. The vesicles suspension was left refrigerated overnight for stabilization and finally extruded 30 times through a 100 nm pore size membrane filter using an Avanti Polar mini extruder. This procedure allowed the formation of unilamellar vesicles with a diameter of about 120 nm.
Liposome–NP mixtures
The experimental setup was designed to explore the interactions between the vesicles and AuNPs at different NP to vesicles ratios and varying concentrations of KCl, starting from 0.025 mM. The samples were organized into three distinct series, each defined by a constant but different ratio of NP/vesicles (0.5, 10 and 100). Each sample was prepared by a first addition of KCl to the water, in order to vary the final KCl concentration from 0.025 to 10 mM. Subsequently, vesicles were added to the KCl solutions. The concentration of the vesicles differed depending on the NP/vesicles ratio:• For a ratio of 0.5 NP/vesicles: [lipids] = 400 μM
• For a ratio of 10 NP/vesicles: [lipids] = 20 μM
• For a ratio of 100 NP/vesicles: [lipids] = 2 μM
The final step was the addition of AuNPs to the mixtures, which was consistently maintained at 2 nM across all series. The complete mixtures were prepared in 96 wells microplates with a final volume of 300 μL. All samples were prepared in quintuplicates to ensure statistical reliability and reproducibility of the results. Alongside the experimental samples, a blank series was also prepared for each salt concentration to confirm that any observed aggregation was due to the presence of the liposomes and not merely a consequence of the presence of KCl.
The visible spectrum of the SPR of AuNPs was registered in cuvettes using an Agilent 8453 UV-Visible spectrophotometer or using spetraMax iD5 Microplate Reader from Molecular Devices. Dynamic light scattering (DLS) and by laser Doppler electrophoresis (LDE) measurements have been performed using a Zetasizer-Nano ZS from Malvern Instruments. The zeta-potential was subsequently evaluated from the electrophoretic mobility measured by LDE according to the Hückel approximation.
Author contributions
Helena Mateos: conceptualization, investigation, methodology, formal analysis, writing – original draft, writing – review & editing, supervision. Antonia Mallardi: methodology, investigation, writing – review & editing. Miquel Oliver, Marcella Dell’Aglio, Pamela Giannone: methodology, investigation, Gerardo Palazzo: conceptualization, methodology, formal analysis, writing – original draft, writing – review & editing.Data availability
The experimental data and the theoretical calculations supporting this article are included in the figures of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Italian Ministry of University and Research (MUR) under the program Progetti di Rilevante Interesse Nazionale and by European Union—Next Generation EU (PRIN 2022 PNRR) grant number P2022ZAHJY. H. M. was funded by MUR PNRR Extended Partnership initiative on Emerging Infectious Diseases – project no. PE00000007, INF-ACT and by University of Bari under the program ERC SEEDS UNIBA” – grant number 2023-UNBACLE-0243485. M. O. is grateful to the Spanish Ministry of Universities and the European Union (NextGenerationEU) for granting a “Margarita Salas” post-doctoral position in the framework of the Recovery, Transformation and Resilience Plan.Notes and references
- N. T. Dung, N. T. Linh, D. L. Chi, N. T. H. Hoa, N. P. Hung, N. T. Ha, P. H. Nam, N. X. Phuc, L. T. Tam and L. T. Lu, Optical properties and stability of small hollow gold nanoparticles, RSC Adv., 2021, 11, 13458–13465 RSC.
- E. Rebollar, M. Sanz, S. Pérez, M. Hernández, I. Martín-Fabiani, D. R. Rueda, T. A. Ezquerra, C. Domingo and M. Castillejo, Gold coatings on polymer laser induced periodic surface structures: assessment as substrates for surface-enhanced Raman scattering, Phys. Chem. Chem. Phys., 2012, 14, 15699–15705 RSC.
- T. Patil, R. Gambhir, A. Vibhute and A. P. Tiwari, Gold Nanoparticles: Synthesis Methods, Functionalization and Biological Applications, J. Cluster Sci., 2023, 34, 705–725 CrossRef CAS.
- A. Yañez-Aulestia, N. K. Gupta, M. Hernández, G. Osorio-Toribio, E. Sánchez-González, A. Guzmán-Vargas, J. L. Rivera, I. A. Ibarra and E. Lima, Gold nanoparticles: current and upcoming biomedical applications in sensing, drug, and gene delivery, Chem. Commun., 2022, 58, 10886 RSC.
- K. Roger and N. El Amri, Controlling nanoparticle formation from the onset of nucleation through a multi-step continuous flow approach, J. Colloid Interface Sci., 2022, 608, 1750–1757 CrossRef CAS PubMed.
- I. Ielo, G. Rando, F. Giacobello, S. Sfameni, A. Castellano, M. Galletta, D. Drommi, G. Rosace and M. R. Plutino, Synthesis, Chemical–Physical Characterization, and Biomedical Applications of Functional Gold Nanoparticles: A Review, Molecules, 2021, 26, 5823 CrossRef CAS PubMed.
- W. Zhou, X. Gao, D. Liu and X. Chen, Gold Nanoparticles for In Vitro Diagnostics, Chem. Rev., 2015, 115, 10575–10636 CrossRef CAS PubMed.
- A. Balestri, J. Cardellini and D. Berti, Gold and silver nanoparticles as tools to combat multidrug-resistant pathogens, Curr. Opin. Colloids Interface Sci., 2023, 66, 101710 CrossRef CAS.
- C. Arnau del Valle, P. Thomas, F. Galindo, M. Paz Munoz and M. J. Marın, Gold nanoparticle-based two-photon fluorescent nanoprobe for monitoring intracellular nitric oxide levels, J. Mater. Chem. B, 2023, 11, 3387 RSC.
- K. Hamad-Schifferly, Stability of dispersions and interactions, in Colloidal foundations of Nanoscience, ed. D. Berti and G. Palazzo, Elsevier, Amsterdam, 2014, pp. 33–46 Search PubMed.
- F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, Monolayer-Protected Anionic Au Nanoparticles Walk into Lipid Membranes Step by Step, J. Phys. Chem. Lett., 2015, 6, 3175–3179 CrossRef CAS.
- C. F. Su, H. Merlitz, H. Rabbel and J. U. Sommer, Nanoparticles of Various Degrees of Hydrophobicity Interacting with Lipid Membranes, J. Phys. Chem. Lett., 2017, 8, 4069–4076 CrossRef CAS PubMed.
- P. Gkeka, L. Sarkisov and P. Angelikopoulos, Homogeneous Hydrophobic-Hydrophilic Surface Patterns Enhanced Permeation of Nanoparticles through Lipid Membranes, J. Phys. Chem. Lett., 2013, 4, 1907–1912 CrossRef CAS PubMed.
- A. J. Sheridan, K. C. Thompson and J. M. Slater, Interaction of negatively and positively capped gold nanoparticle with different lipid model membranes, Biophys. Chem., 2022, 290, 106896 CrossRef CAS PubMed.
- X. Quan, D. Zhao and J. Zhou, The interplay between surface-functionalized gold nanoparticles and negatively charged lipid vesicles, Phys. Chem. Chem. Phys., 2021, 23, 23526–23536 RSC.
- F. Wang and J. Liu, Self-healable and reversible liposome leakage by citrate-capped gold nanoparticles: probing the initial adsorption/desorption induced lipid phase Transition, Nanoscale, 2015, 7, 15599 RSC.
- F. Wang, D. E. Curry and J. Liu, Driving Adsorbed Gold Nanoparticle Assembly by Merging Lipid Gel/Fluid Interfaces, Langmuir, 2015, 31, 13271–13274 CrossRef CAS PubMed.
- K. Sugikawa, T. Kadota, K. Yasuhara and A. Ikeda, Anisotropic Self-Assembly of Citrate-Coated Gold Nanoparticles on Fluidic Liposomes, Angew. Chem., Int. Ed., 2016, 55, 4059–4063 CrossRef CAS PubMed.
- A. Mallardi, N. Nuzziello, M. Liguori, C. Avolio and G. Palazzo, Counting of peripheral extracellular vesicles in Multiple Sclerosis patients by an improved nanoplasmonic assay and dynamic light scattering, Colloids Surf., B, 2018, 168, 134–142 CrossRef CAS PubMed.
- A. Zendrini, L. Paolini, S. Busatto, A. Radeghieri, M. Romano, M. H. M. Wauben, M. J. C. van Herwijnen, P. Nejsum, A. Borup, A. Ridolfi, C. Montis and P. Bergese, Augmented COlorimetric NANoplasmonic (CONAN) Method for Grading Purity and Determine Concentration of EV Microliter Volume Solutions, Front. Bioeng. Biotechnol., 2020, 7, 452 CrossRef PubMed.
- C. Montis, L. Caselli, F. Valle, A. Zendrini, F. Carlà, R. Schweins, M. Maccarini, P. Bergese and D. Berti, Shedding light on membrane-templated clustering of gold nanoparticles, J. Colloid Interface Sci., 2020, 573, 204–214 CrossRef CAS PubMed.
- L. Gentile, H. Mateos, A. Mallardi, M. Dell’Aglio, A. De Giacomo, N. Cioffi and G. Palazzo, Gold nanoparticles obtained by ns-pulsed laser ablation in liquids (ns-PLAL) are arranged in the form of fractal clusters, J. Nanopart. Res., 2021, 23, 35 CrossRef CAS.
- G. Palazzo, G. Valenza, M. Dell'Aglio and A. De Giacomo, On the stability of gold nanoparticles synthesized by laser ablation in liquids, J. Colloid Interface Sci., 2017, 489, 47–56 CrossRef CAS PubMed.
- R. J. Hunter, Zeta potential in colloidal science, Academic Press, 1st edn, 1981 Search PubMed.
- E. Gongadze, A. Velikonja, S. Perutkova, P. Kramar, A. Macek-Lebar, V. Kralj-Iglic and A. Iglic, Ions and water molecules in an electrolyte solution in contact with charged and dipolar surfaces, Electrochim. Acta, 2014, 126, 42–60 CrossRef CAS.
- J. Zelko, A. Iglič, V. Kralj-Iglič and B. Sunil Kumar, Effects of counterion size on the attraction between similarly charged surfaces, J. Chem. Phys., 2010, 133, 204901 CrossRef PubMed.
- J. Urbanija, K. Bohinc, A. Bellen, S. Maset, A. Iglič, V. Kralj-Iglič and P. B. Sunil Kumar, Attraction between negatively charged surfaces mediated by spherical counterions with quadrupolar charge distribution, J. Chem. Phys., 2008, 129, 105101 CrossRef PubMed.
- H. Mateos, A. Mallardi, E. Serrano-Pertierra, M. C. Blanco-Lopez, M. Izzi, N. Cioffi and G. Palazzo, Unusual gold nanoparticle-antibody interactions, JCIS Open, 2023, 11, 100089 CrossRef.
- D. Maiolo, L. Paolini, G. Di Noto, A. Zendrini, D. Berti, P. Bergese and D. Ricotta, Colorimetric Nanoplasmonic Assay To Determine Purity and Titrate Extracellular Vesicles, Anal. Chem., 2015, 87, 4168–4176 CrossRef CAS PubMed.
- R. J. Hunter, Foundations of Colloid Science, Oxford University Press, 1989 Search PubMed.
- R. Tadmor, The London–van der Waals interaction energy between objects of various geometries, J. Phys.: Condens.Matter, 2001, 13, L195–L202 CrossRef CAS.
- J. W. Goodwin, Colloids and Interfaces with Surfactants and Polymers – An Introduction, John Wiley & Sons, Ltd, 2004 Search PubMed.
- G. Trefalt, F. J. Montes Ruiz-Cabello and M. Borkovec, Interaction Forces, Heteroaggregation, and Deposition Involving Charged Colloidal Particles, J. Phys. Chem. B, 2014, 118, 6346–6355 CrossRef CAS PubMed.
- G. Trefalt, S. H. Behrens and M. Borkovec, Charge Regulation in the Electrical Double Layer: Ion Adsorption and Surface Interactions, Langmuir, 2016, 32, 380–400 CrossRef CAS PubMed.
- R. Hogg, T. W. Healy and D. W. Fuerstenau, Mutual Coagulation of Colloidal Dispersions, Trans. Faraday Soc., 1966, 62, 1638–1651 RSC.
- H. Mateos and G. Palazzo, Colloidal stability, in Colloidal Foundation of Nanoscience, ed. D. Berti and G. Palazzo, Elsevier, Amsterdam, 2nd edn, 2022, 57–83 Search PubMed.
- E. J. W. Verwey and J. Th. G. Overbeek, Theory of the stability of lyophobic colloids, Elsevier, Amsterdam, 1948, Reprinted in 1999 by Dover Publications, Mineola, N.Y Search PubMed.
- F. Evans and H. Wennerstrom, The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, Wiley-VCH, 2nd edn, 1999 Search PubMed.
- G. Palazzo, H. Mateos and D. Berti, Diffusion, aggregation and electrokinetics, Colloidal Foundation of Nanoscience, Elsevier, Amsterdam, 2nd edn, 2022, pp. 201–225 Search PubMed.
- T. Sintes and A. Baumgartner, Protein Attraction in Membranes Induced by Lipid Fluctuations, Biophys. J., 1997, 73, 2251–2259 CrossRef CAS PubMed.
- K. Bohinc, V. Kralj-Iglič and S. May, Interaction between two cylindrical inclusions in a symmetric lipid bilayer, J. Chem. Phys., 2003, 119, 7435–7444 CrossRef CAS.
- M. Dell’Aglio, V. Mangini, G. Valenza, O. De Pascale, A. De Stradis, G. Natile, F. Arnesano and A. De Giacomo, Silver and gold nanoparticles produced by pulsed laser ablation in liquid to investigate their interaction with Ubiquitin, Appl. Surf. Sci., 2016, 374, 297–304 CrossRef.
- L. Gentile, H. Mateos, A. Mallardi, M. Dell’Aglio, A. De Giacomo, N. Cioffi and G. Palazzo, Gold nanoparticles obtained by ns-pulsed laser ablation in liquids (ns-PLAL) are arranged in the form of fractal clusters, J. Nanopart. Res., 2021, 23, 35 CrossRef CAS.
- W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Determination of Size and Concentration of Gold Nanoparticles from UV-Vis Spectra, Anal. Chem., 2007, 79, 4215–4221 CrossRef CAS PubMed.
- A. D. Bangham, J. De Gier and G. D. Greville, Osmotic properties and water permeability of phospholipid liquid crystals, Chem. Phys. Lipids, 1967, 1, 225–246 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02060j |
| This journal is © the Owner Societies 2024 |