Open Access Article
Open Access ArticleDeconvolution of the X-ray absorption spectrum of trans-1,3-butadiene with resonant Auger spectroscopy†
David M. P.
Holland
 a,
Jiří
Suchan
a,
Jiří
Suchan
 b,
Jiří
Janoš
b,
Jiří
Janoš
 c,
Camila
Bacellar
d,
Ludmila
Leroy
d,
Thomas R.
Barillot
d,
Luca
Longetti
c,
Camila
Bacellar
d,
Ludmila
Leroy
d,
Thomas R.
Barillot
d,
Luca
Longetti
 d,
Marcello
Coreno
e,
Monica
de Simone
d,
Marcello
Coreno
e,
Monica
de Simone
 f,
Cesare
Grazioli
f,
Cesare
Grazioli
 f,
Majed
Chergui
f,
Majed
Chergui
 dg,
Eva
Muchová
*c and
Rebecca A.
Ingle
dg,
Eva
Muchová
*c and
Rebecca A.
Ingle
 *h
*h
aSTFC, Daresbury Laboratory, Daresbury, Warrington, Cheshire WA4 4AD, UK
bInstitute for Advanced Computational Science, Stony Brook University, Stony Brook, New York 11794-5250, USA
cDepartment of Physical Chemistry, University of Chemistry and Technology, Technická 5, 166 28 Prague, Czech Republic. E-mail: eva.muchova@vscht.cz
dLaboratoire de Spectroscopie Ultrarapide, Ecole Polytechnique Fédérale de Lausanne, ISIC, FSB, CH-1015 Lausanne, Switzerland
eISM-CNR, Istituto di Struttura dei Materiali, LD2 Unit, 34149 Trieste, Italy
fIOM-CNR, Istituto Officina dei Materiali, 34149 Trieste, Italy
gElettra-Sincrotrone Trieste S.C.p.A., S.S. 14 km 163,5 in Area Science Park, I-34012 Basovizza, Trieste, Italy
hDepartment of Chemistry, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: r.ingle@ucl.ac.uk
First published on 25th March 2024
Abstract
High-resolution carbon K-edge X-ray photoelectron, X-ray absorption, non-resonant and resonant Auger spectra are presented of gas phase trans-1,3-butadiene alongside a detailed theoretical analysis utilising nuclear ensemble approaches and vibronic models to simulate the spectroscopic observables. The resonant Auger spectra recorded across the first pre-edge band reveal a complex evolution of different electronic states which remain relatively well-localised on the edge or central carbon sites. The results demonstrate the sensitivity of the resonant Auger observables to the weighted contributions from multiple electronic states. The gradually evolving spectral features can be accurately and feasibly simulated within nuclear ensemble methods and interpreted with the population analysis.
1 Introduction
A major challenge in the spectroscopic study of complex molecules is the issue of spectral congestion. The high densities of vibrational and electronic states result in a large number of possible spectroscopic transitions that are closely spaced in energy. Thus there is a high probability that the corresponding spectral features will overlap. For X-ray spectroscopies, where the lineshape broadening originating from the short core-hole lifetimes is far from insignificant, the problem of spectral congestion is further exacerbated.1 Resonant X-ray techniques, such as resonant Auger and resonant inelastic X-ray scattering (RIXS), offer an experimental approach to the deconvolution of heavily congested absorption spectra and to the recovery of information on the electronic and vibrational structure of the molecule of interest.2 By restricting the incident photon bandwidth to less than the lifetime broadening of the spectral feature, a small subset of transitions or a single transition can be selectively excited, constraining the information present in the final resonant spectrum.Though RIXS with broadband SASE pulses has been recently demonstrated,3,4 the more traditional approach to performing resonant experiments is to use energetically tuneable, monochromatised radiation, for which synchrotron radiation sources are very well-suited.2 Selective probing of specific transitions offers not only the ability to deconvolute complex spectra but also the possibility for driving site-specific chemical dynamics5 (and references therein). In molecular systems, following the localised core excitation process, there is a competing cascade of processes which include the Auger cascade and charge reorganisation or delocalisation. If the subsequently formed valence hole remains sufficiently localised in the proximity of the core hole, site-selective chemical dynamics can occur. Such phenomena have been observed experimentally for a number of photofragmentation processes6–10 and predicted theoretically for non-dissociative processes such as photoisomerisation.11
While resonant spectroscopies such as resonant Auger offer a highly selective, information-rich approach to induce and probe site-specific chemical dynamics, for polyatomic systems there are still a number of key challenges for the accurate modelling and interpretation. A significant part of this challenge concerns the inclusion of the nuclear dynamics that can occur alongside the charge redistribution and Auger decay processes, and which have a profound effect on the final observed spectra.2,12–14 With improvements in experimental technologies making it possible to record vibrationally-resolved resonant Auger spectra for polyatomics, there is now an interesting opportunity to explore how the greater number of degrees of freedom in larger molecular systems influence the Auger spectra, both in terms of the vibrational populations and their relative cross sections. The final ionic states that may be formed through autoionisation of the core-excited neutral state are the same as those formed through direct photoionisation. However, autoionisation may result in electronic state intensity ratios and vibrational level populations that differ from those due to direct ionisation.15 The Auger spectra and cross sections are greatly influenced by the nuclear dynamics in both the intermediate decaying and final states.16 If the intermediate core-excited state is long lived, then the decay process is typically controlled by the Franck–Condon principle. In contrast, a short lifetime causes each energy level to be broadened, and neighbouring vibrational levels may overlap if the lifetime width is similar to the vibrational spacing. Since these levels may decay to the same final vibronic states, interference may occur from the coherently excited levels. Such effects have been investigated in several diatomic molecules (CO, NO etc.17,18) and interpreted within the Condon approximation.
For polyatomics, the additional degrees of freedom make the determination of accurate cross sections prohibitively difficult but the vibrational fingerprints in the intermediate and final states can still be investigated separately. In this work, we investigate how the vibrational fingerprints in the intermediate and final steps in the resonant Auger process manifest for a conjugated polyatomic, namely trans-1,3-butadiene (C4H6). Butadiene, sometimes considered a classic case of π delocalisation, poses some particular challenges in its experimental and theoretical study owing to the complexity of the structural conformers and their ionisation dynamics19 and to the high symmetry and core-hole localisation processes.20,21 While there is also some experimental ambiguity22 surrounding the expected structural adjustments associated with the π delocalisation, with a lengthening of the formal double bonds and a shortening of the formal single bond in comparison with standard lengths for corresponding localised bonds,23 previous X-ray absorption and photoelectron studies show clear evidence of two distinct carbon sites, each with distinct fragmentation dynamics.20–22
This work presents a series of valence band photoelectron spectra, high-resolution absorption spectra (XAS), X-ray photoelectron spectra (XPS), and resonant and non-resonant Auger measurements of trans-1,3-butadiene in combination with novel theoretical approaches. The experimental results are in excellent agreement with previously published data,20,24,25 and confirm the presence of vibrational structure in the resonant Auger spectra across the energy region encompassing excitation of the 1s → π* bands. With a combination of nuclear ensemble approaches (NEA) and vibronically-resolved calculations, it is possible to understand the multiple electronic states and vibrational progressions that contribute to the XAS spectrum. These, in turn, have been used to interpret the experimentally observed and theoretically predicted energy-dependent trends in the resonant Auger spectra.
2 Methods
2.1 Experimental methods
All experimental measurements were performed at the GasPhase endstation at the Elettra Synchrotron radiation facility.26 1,3-butadiene (≥99.6%, Sigma Aldrich, CAS: 106-99-0) was used without further purification and is assumed to be exclusively of the s-trans form.27 This assumption is supported by theoretical calculations which show that, at room temperature, the gauche conformer has an approximate molar fraction of 5% only.28 This prediction is further supported by assignments of the photoelectron spectra which show no evidence of the other conformer.29 An effusive gas jet was used to introduce ∼5 mbar of butadiene to the interaction region. An ion yield was recorded with a charged particle detector close to the interaction region, and it is assumed that this yield resembles the XAS spectrum. The present spectrum is in accord with previous measurements20,24,25 using electron detection but differs from an earlier ion yield measurement recorded using electron–ion coincidences.21 For the high-resolution XAS measurements, a monochromatised beam with approximately 40 meV bandwidth was scanned in steps of 10 meV. All the core-level spectra energy calibrations were performed relative to carbon dioxide.30A Scienta SES-200 hemispherical analyser mounted at the magic angle (57.4°) to the electric vector of the incident light was used for all of the photoelectron measurements, including the normal and resonant Auger spectra. For the XPS measurements, an analyser pass energy of 20 eV with an entrance slit width of 0.8 mm were used to give a theoretical spectrometer resolution of 40 meV. For the normal and resonant Auger measurements, a 20 eV pass energy and spectrometer entrance slit width of 2.5 mm were used to give a theoretical spectrometer resolution of 125 meV. An incident photon bandwidth of ∼65 meV was used for the resonant measurements. The valence band photoelectron measurements were calibrated with the argon 3s and 3p lines.31,32 Carbon dioxide was used to calibrate the C 1s binding energies.33
2.2 Theoretical methods
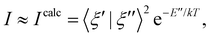 where ξ are vibrational wave functions for the initial and final states, using the ezFCF v.1.1 code.35 This approach was used for the valence band spectra, core-ionised spectra and core-excited spectra modelling. Each of these spectra typically requires a different strategy in electronic structure calculations. We, however, adopted a suitable approach for either the core or the valence region – the maximum overlap method (MOM). This approach was used with the B3LYP functional and the cc-pVTZ basis sets on the hydrogen atoms and the cc-pCVTZ basis sets on the carbon atoms (hereafter referred to as cc-pVTZ+cc-pCVTZ). See details in the ESI,† Section 1. (b) If the full characterisation of the potential energy surface is out of reach or unreliable, practical approaches based on harmonic models are convenient. In this work, we used the vertical Hessian approach (VH).36 In this case, the final electronic state potential energy surface is not optimised and ground electronic state gradient and Hessian are used instead.37 The overlaps are calculated as in the double-harmonic approximation. This approach was used for core-excited spectra modelling using the FCclasses3 code.37 (c) We also used an approach which goes beyond the harmonic approximation. The potential energy surfaces of the ground and the lowest core-excited states were represented on one-dimensional grids along the ground-state normal modes. Using the imaginary-time propagation, the lowest energy vibrational states were optimised for each electronic state and normal mode, and their overlaps were integrated numerically. More details are provided in the ESI,† Section 1. This approach was used for core-excited spectra modelling.
where ξ are vibrational wave functions for the initial and final states, using the ezFCF v.1.1 code.35 This approach was used for the valence band spectra, core-ionised spectra and core-excited spectra modelling. Each of these spectra typically requires a different strategy in electronic structure calculations. We, however, adopted a suitable approach for either the core or the valence region – the maximum overlap method (MOM). This approach was used with the B3LYP functional and the cc-pVTZ basis sets on the hydrogen atoms and the cc-pCVTZ basis sets on the carbon atoms (hereafter referred to as cc-pVTZ+cc-pCVTZ). See details in the ESI,† Section 1. (b) If the full characterisation of the potential energy surface is out of reach or unreliable, practical approaches based on harmonic models are convenient. In this work, we used the vertical Hessian approach (VH).36 In this case, the final electronic state potential energy surface is not optimised and ground electronic state gradient and Hessian are used instead.37 The overlaps are calculated as in the double-harmonic approximation. This approach was used for core-excited spectra modelling using the FCclasses3 code.37 (c) We also used an approach which goes beyond the harmonic approximation. The potential energy surfaces of the ground and the lowest core-excited states were represented on one-dimensional grids along the ground-state normal modes. Using the imaginary-time propagation, the lowest energy vibrational states were optimised for each electronic state and normal mode, and their overlaps were integrated numerically. More details are provided in the ESI,† Section 1. This approach was used for core-excited spectra modelling.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg state, with both the ground electronic state and the ionised
2Bg state, with both the ground electronic state and the ionised ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg state being optimised at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level. The vibrationally resolved core-level photoelectron spectrum for butadiene was calculated at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level. The core ionisation energies were benchmarked by a plethora of methods including CVS-EOM-IP-CCSD (core valence separation scheme, CVS) with cc-pVXZ+cc-pCVXZ (X = D,T,Q) or aug-cc-pVDZ basis sets, MOM/CCSD(T)/cc-pCVTZ. The calculations were performed in Q-Chem 6.0.49 The core-excitation energies were benchmarked at the following levels of theory – MOM/CCSD(T), CVS-ADC(2)-X/cc-pVTZ, SRC1-r150,51 with cc-pVXZ+cc-pCVXZ (X = D,T,Q) basis sets and aug-cc-pVTZ within the LR-TDDFT approach, or at the CVS-EOM-EE-CCSD level with cc-pVXZ+cc-pCVXZ basis sets (X = D,T,Q). It has been suggested recently that these basis sets work accurately especially for core-level spectroscopy due to the uncontracted additional polarisation functions.52 The spectra simulated within NEA were calculated for a set of 50 geometries at the CVS-EOM-EE-CCSD/cc-pVTZ+cc-pCVTZ level and for a set of 400 geometries using the tailored SRC1-r1 functional. To understand the character of the potential energy surfaces along all vibrational modes, the profiles of the potential energy surfaces and the oscillator strengths were calculated for the four lowest energy core-excited states along the ground electronic state vibrational modes. The calculations were performed in ORCA v4.2.053 and Q-Chem 6.049 at the SRC1-r1/cc-pVTZ+cc-pCVTZ level. The vibrationally resolved spectra were calculated with the three aformentioned approaches – (a) within the double-harmonic approximation at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level, (b) within the vertical Hessian approach at the SRC1-r1/cc-pVTZ level on a slightly distorted geometry (a cumulative total displacement of 0.22 Å on all carbon atoms was used) in order to break the symmetry and allow the optically dark (S1 and S3) states to become bright. We assume a constant transition dipole moment (TDM, within the Franck–Condon approximation) which bridges the zero value discontinuity at the actual Franck–Condon point. All imaginary modes on the excited states being removed. (c) Using the imaginary-time propagation for the four lowest energy vibrational states. The SRC1-r1 potential energy surfaces of the ground and four lowest core-excited states were used, the calculation does not include the TDM and was performed at 0 K. Auger spectra modelling. The Auger spectra were modelled within the classical two-step model using the Feschbach-Fano approach introduced by W. Skomorowski and A. I. Krylov54,55 in Q-Chem 6.0.49 For the resonant Auger spectra, the core-level state was modelled at the CVS-EOM-EE-CCSD/cc-pVTZ+cc-pCVTZ level, and the final state was modelled at the EOM-IP-CCSD/cc-pVTZ+cc-pCVTZ level. For non-resonant Auger decay, the initial states were computed by the EOM-IP-CCSD method and the final states were described by the EOM-DIP-CCSD variant with the same basis sets as in previous calculations. The continuum orbital was treated as the plane wave, which is computationally more practical compared to a Coulomb wave orbital.55 In our study, we focused mainly on the resonant spectra and principally on the participator decay processes which are the dominant channels in the electron kinetic energy range of 265–280 eV. The theoretical spectra were modelled as 2D maps via NEA for the set of 50 geometries at the EOM-CCSD/cc-pVTZ+cc-pCVTZ level and for the set of 400 geometries at the EOM-CCSD/cc-pVDZ+cc-pCVDZ level. In the experiment, the incident photon energies were selected to map the maxima in the vibrationally resolved XAS; however, NEA provides different information on XAS. Specifically, for a set of geometries sampling the ground electronic state, NEA evaluates both the overlap between the wave functions representing the ground and various excited electronic states, and also the changes in the TDMs. This means that the simulated data capture the changes in the electronic structure and no information on vibrations is provided. The simulated spectra were calculated for 9 equally energetically spaced intervals spanning the pre-edge XAS region. The Löwdin population analysis was performed for a set of 50 geometries at the B3LYP/cc-pVTZ level in ORCA v4.2.0.53
2Bg state being optimised at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level. The vibrationally resolved core-level photoelectron spectrum for butadiene was calculated at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level. The core ionisation energies were benchmarked by a plethora of methods including CVS-EOM-IP-CCSD (core valence separation scheme, CVS) with cc-pVXZ+cc-pCVXZ (X = D,T,Q) or aug-cc-pVDZ basis sets, MOM/CCSD(T)/cc-pCVTZ. The calculations were performed in Q-Chem 6.0.49 The core-excitation energies were benchmarked at the following levels of theory – MOM/CCSD(T), CVS-ADC(2)-X/cc-pVTZ, SRC1-r150,51 with cc-pVXZ+cc-pCVXZ (X = D,T,Q) basis sets and aug-cc-pVTZ within the LR-TDDFT approach, or at the CVS-EOM-EE-CCSD level with cc-pVXZ+cc-pCVXZ basis sets (X = D,T,Q). It has been suggested recently that these basis sets work accurately especially for core-level spectroscopy due to the uncontracted additional polarisation functions.52 The spectra simulated within NEA were calculated for a set of 50 geometries at the CVS-EOM-EE-CCSD/cc-pVTZ+cc-pCVTZ level and for a set of 400 geometries using the tailored SRC1-r1 functional. To understand the character of the potential energy surfaces along all vibrational modes, the profiles of the potential energy surfaces and the oscillator strengths were calculated for the four lowest energy core-excited states along the ground electronic state vibrational modes. The calculations were performed in ORCA v4.2.053 and Q-Chem 6.049 at the SRC1-r1/cc-pVTZ+cc-pCVTZ level. The vibrationally resolved spectra were calculated with the three aformentioned approaches – (a) within the double-harmonic approximation at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level, (b) within the vertical Hessian approach at the SRC1-r1/cc-pVTZ level on a slightly distorted geometry (a cumulative total displacement of 0.22 Å on all carbon atoms was used) in order to break the symmetry and allow the optically dark (S1 and S3) states to become bright. We assume a constant transition dipole moment (TDM, within the Franck–Condon approximation) which bridges the zero value discontinuity at the actual Franck–Condon point. All imaginary modes on the excited states being removed. (c) Using the imaginary-time propagation for the four lowest energy vibrational states. The SRC1-r1 potential energy surfaces of the ground and four lowest core-excited states were used, the calculation does not include the TDM and was performed at 0 K. Auger spectra modelling. The Auger spectra were modelled within the classical two-step model using the Feschbach-Fano approach introduced by W. Skomorowski and A. I. Krylov54,55 in Q-Chem 6.0.49 For the resonant Auger spectra, the core-level state was modelled at the CVS-EOM-EE-CCSD/cc-pVTZ+cc-pCVTZ level, and the final state was modelled at the EOM-IP-CCSD/cc-pVTZ+cc-pCVTZ level. For non-resonant Auger decay, the initial states were computed by the EOM-IP-CCSD method and the final states were described by the EOM-DIP-CCSD variant with the same basis sets as in previous calculations. The continuum orbital was treated as the plane wave, which is computationally more practical compared to a Coulomb wave orbital.55 In our study, we focused mainly on the resonant spectra and principally on the participator decay processes which are the dominant channels in the electron kinetic energy range of 265–280 eV. The theoretical spectra were modelled as 2D maps via NEA for the set of 50 geometries at the EOM-CCSD/cc-pVTZ+cc-pCVTZ level and for the set of 400 geometries at the EOM-CCSD/cc-pVDZ+cc-pCVDZ level. In the experiment, the incident photon energies were selected to map the maxima in the vibrationally resolved XAS; however, NEA provides different information on XAS. Specifically, for a set of geometries sampling the ground electronic state, NEA evaluates both the overlap between the wave functions representing the ground and various excited electronic states, and also the changes in the TDMs. This means that the simulated data capture the changes in the electronic structure and no information on vibrations is provided. The simulated spectra were calculated for 9 equally energetically spaced intervals spanning the pre-edge XAS region. The Löwdin population analysis was performed for a set of 50 geometries at the B3LYP/cc-pVTZ level in ORCA v4.2.0.53
3 Results and discussion
Interpretation of resonant Auger spectra requires an understanding of all the states involved in the Auger process – initial, intermediate and final states. As the resonant Auger spectra contain information on the valence electronic structure, we start with a discussion of the valence band photoelectron spectra, before progressing to the core-ionised and core-excited states.3.1 Valence band photoelectron spectra
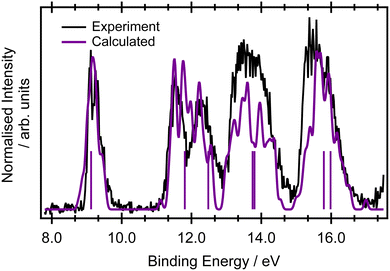
Only a limited discussion of the valence band photoelectron spectra will be presented here, as the measured and calculated results are in good agreement with previous higher resolution measurements56 and calculations at the ADC(3)/aug-ANO level of theory.29 The calculated lowest ionisation energies are presented in the ESI,† in Table S2.The ground state valence shell electronic configuration of butadiene, assuming C2h symmetry, is given as (3ag)2 (3bu)2 (4ag)2 (4bu)2 (5bu)2 (5ag)2 (6ag)2 (6bu)2 (7ag)2 (1au)2 (1bg)2. The onset of the photoelectron spectrum at 8.9 eV corresponds to the first ionised ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg state (Fig. 1) which shows a significant degree of vibrational structure. A comparison between the EOM-IP-CCSD/cc-pVTZ+cc-pCVTZ results simulated within the NEA approach (Fig. 1) and the experimental values shows good agreement for the vertical ionisation energies and peak widths, as well as being within a few tenths of an eV of the most accurate ADC(3)/aug-ANO calculations.29 This good agreement indicates that the final states in the resonant Auger spectrum are described properly at this level. A more detailed analysis of the vibrational structure on the
2Bg state (Fig. 1) which shows a significant degree of vibrational structure. A comparison between the EOM-IP-CCSD/cc-pVTZ+cc-pCVTZ results simulated within the NEA approach (Fig. 1) and the experimental values shows good agreement for the vertical ionisation energies and peak widths, as well as being within a few tenths of an eV of the most accurate ADC(3)/aug-ANO calculations.29 This good agreement indicates that the final states in the resonant Auger spectrum are described properly at this level. A more detailed analysis of the vibrational structure on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg band is included in the ESI,† in Fig. S2 and the corresponding assignments are given in Table S3 (ESI†). The calculated geometries and vibrational frequencies of the initial and ionised states are listed in Tables S4 and S5 (ESI†), respectively. The key findings from the vibrational analysis are that the peaks due to transitions into vibrationally excited levels of the ion are predicted in the energy region within several tenths of an eV above the peak due to the 0-0 transition at 9.011 eV.56 The most intense of these predicted transitions are due to the excitation of vibrational modes ν6 (CH2 rocking), ν12 (C–C stretching), ν18 (C
2Bg band is included in the ESI,† in Fig. S2 and the corresponding assignments are given in Table S3 (ESI†). The calculated geometries and vibrational frequencies of the initial and ionised states are listed in Tables S4 and S5 (ESI†), respectively. The key findings from the vibrational analysis are that the peaks due to transitions into vibrationally excited levels of the ion are predicted in the energy region within several tenths of an eV above the peak due to the 0-0 transition at 9.011 eV.56 The most intense of these predicted transitions are due to the excitation of vibrational modes ν6 (CH2 rocking), ν12 (C–C stretching), ν18 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching), ν20 (CH2 symmetric stretching), and ν22 (CH stretching).
C stretching), ν20 (CH2 symmetric stretching), and ν22 (CH stretching).
3.2 Core level photoelectron spectra
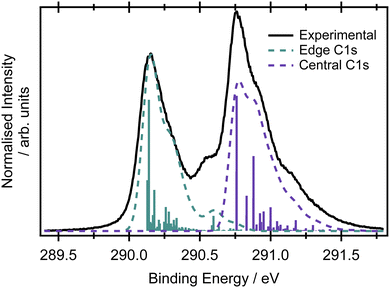
Assuming the geometry of butadiene is well-described by the C2h point group and has complete delocalisation of the π framework,23 there should be two inequivalent carbon environments and therefore two main peaks in the X-ray photoelectron spectrum. The two most intense features in the XPS spectrum of butadiene are separated by 0.62 eV (Fig. 2). The peaks are centred at 290.14 ± 0.01 and 290.76 ± 0.01 eV and both exhibit asymmetry to the high binding energy side. Within the experimental uncertainty, these binding energies are consistent with those reported by Thomas et al.57 in a recent high-resolution study. An additional feature is observed in the present spectrum at 290.56 eV which appears to be reasonably well separated from the peak at 290.14 eV and potentially belongs to the same vibronic progression that contributes to the asymmetry of the peak. Given the experimental conditions used to record the spectrum in Fig. 2, it would be expected that the core hole lifetime broadening (∼80 meV for most compounds1,58,59) would be the dominant contribution to the observed lineshapes, as opposed to any instrumental contributions.The large amount of structure and spectral congestion on the XPS spectrum makes a definitive assignment of the vibrational progressions from the experiment alone somewhat challenging. From an electronic structure and basis set benchmark of the vertical core-ionisation energies (Table 1), the two inequivalent carbon sites are energetically well separated independent of the method/basis set used. The absolute energetic values for the core-ionisation energies agree very well with experiment for the CVS-EOM-IP-CCSD methods, especially when extended basis sets are employed. The energy difference between ionisation from the central and edge carbons is, however, systematically underestimated by all employed methods and ranges from 0.3–0.4 eV compared to 0.62 eV in the experiment. This leads to a significant overlap of the peaks corresponding to ionisation from the central and edge carbon atoms in the core-ionised spectra if modelled within the NEA approach, see Fig. S3 in the ESI.† A full assignment of the vibrational structure in the core-level ionisation spectrum is included in Table S6 in the ESI,† for structures optimised at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level within the double-harmonic approximation; the optimised structures are provided in Table S4 (ESI†). On an important note, due to the hole localisation problem in symmetric molecules,60–63 non-totally symmetric vibrational modes can also be excited. The MOM calculations reveal that the vibrational progression for the central carbons is different to that for the edge carbons; differences can be observed also for the optimised structures with ionisation from the edge carbons leading to a greater degree of inequivalence in the C–C bond lengths than for ionisation from a central carbon, where the molecule remains largely symmetric (see Tables S4–S6 in the ESI†). A similar effect has been observed for ethene, where ionisation from the edge carbon leads to hole-localisation.20 The dominant progression in the spectrum upon ionisation from either of the carbon sites involves the CH2 rocking modes, but this progression is relatively more intense on ionisation from the central carbons. The progression at 290.56 eV corresponds mainly to the CH stretching mode. The results at the MOM level suggest planar structures for both core-ionised states, which result in a smaller role for the C–C stretching modes in the observed XPS spectrum than previously thought. Clearly, the asymmetries introduced by the core-hole localisation have a pronounced effect on the intensities and profiles of the vibronic structure.21
| Method | Edge carbon | Central carbon |
|---|---|---|
| a The employed basis set was cc-pVXZ on the hydrogen atoms and cc-pCVXZ on the carbon atoms. | ||
| Exp. | 290.14 | 290.76 |
| MOM/CCSD(T)/cc-pCVTZ | 290.7 | 291.2 |
| MOM/B3LYP/cc-pCVTZ | 285.7 | 285.9 |
| MOM/B3LYP/aug-cc-pCVTZ | 285.7 | 286.0 |
| CVS-EOM-IP-CCSD/cc-pCVDZa | 292.1 | 292.4 |
| CVS-EOM-IP-CCSD/cc-pCVTZa | 290.7 | 291.0 |
| CVS-EOM-IP-CCSD/cc-pCVQZa | 290.6 | 291.0 |
| CVS-EOM-IP-CCSD/aug-cc-pCVTZ | 290.8 | 291.1 |
3.3 X-ray absorption spectra
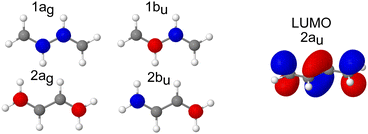
The pre-edge region in the X-ray absorption spectrum of butadiene shows a striking degree of complexity for a reasonably small, high symmetry system (Fig. 3 – the spectrum over an extended energy range is included in the ESI,† as Fig. S3). The structure in the spectrum has been attributed to vibronic progressions associated with two electronic transitions originating at 284.0 and 284.6 eV respectively,20,25,64 both C 1s → π* excitations, with a series of transitions to Rydberg states appearing between 286.5–290.0 eV. Assuming C2h symmetry, the electronic configuration of the four core orbitals is (1ag)2 (1bu)2 (2ag)2 (2bu)2 (Fig. 4). The two lowest-energy unoccupied orbitals (2au and 2bg) are both of π* character with a large (≈1.31 eV at the EOM-CCSD/cc-pVTZ+cc-pCVTZ level of theory) energy splitting between them – significantly greater than the 0.6 eV splitting between the ionisation energies of the central and edge carbons measured from the XPS, e.g. the lowest energy transitions are to the lowest unoccupied orbital (2au).First, we will consider the purely electronic contributions to the XAS spectrum. A benchmark of the computational methods used for calculation of the XAS observables is included in the ESI,† (Fig. S10 and Table 2). As with the XPS, the calculated XAS spectra show that the lower energy region corresponds to transitions with an initial orbital localised on the edge carbons, whereas the higher energy region corresponds to transitions from the central carbons (Fig. 3). The calculated difference between the excitation energies from the edge and central carbon atoms is 0.3–0.4 eV for the more accurate CVS-EOM-EE-CCSD and CVS-ADC(2)-X methods while the TDDFT method with tailored SRC1-r1 functional provides a consistently larger energy difference (0.6 eV) for all employed basis sets.
| Method | Edge carbons | Central carbons |
|---|---|---|
| (S1, S2) | (S3, S4) | |
| a The employed basis set was cc-pVXZ on the hydrogen atoms and cc-pCVXZ on the carbon atoms. | ||
| MOM/CCSD(T)/cc-pCVTZ | 284.9 | 285.6 |
| MOM/B3LYP/cc-pCVTZ | 279.8 | 280.4 |
| MOM/B3LYP/aug-cc-pCVTZ | 279.8 | 280.4 |
| SRC1-r1/aug-cc-pCVTZ | 284.7 | 285.3 |
| SRC1-r1/cc-pCVDZ | 285.1 | 285.7 |
| SRC1-r1/cc-pCVTZ | 284.8 | 285.4 |
| SRC1-r1/cc-pCVQZ | 284.7 | 285.3 |
| SRC1-r1/aug-cc-pCVTZ | 284.7 | 285.3 |
| CVS-EOM-EE-CCSD/cc-pCVDZa | 286.4 | 286.8 |
| CVS-EOM-EE-CCSD/cc-pCVTZa | 284.7 | 285.1 |
| CVS-ADC(2)-X/cc-pVTZ | 284.3 | 284.6 |
When the symmetry-adapted molecular orbitals are used (Fig. 4), at the Franck–Condon point, four low lying states can be identified – S1 and S2 correspond to the transitions from the edge carbons and S3 and S4 to transitions from the central carbons. Two of the states are bright (S2 and S4) corresponding to 2ag → 2au and 1ag → 2au, and two are dark (S1 and S3) corresponding to 2bu → 2au and 1bu → 2au, due to the selection rules dictated by the symmetry. However, while the calculated energies of the vertical excitations are in good agreement with the experimental spectrum, it is clear that calculating purely electronic transitions for this geometry provide an incomplete picture, and it is necessary to include vibronic effects.
The high-level accurate simulation of a vibrationally resolved spectrum of butadiene is non-trivial. While a single point calculation predicts two bright (S2 and S4) and two dark (S1 and S3) states, non-symmetric vibrational motions lead to hole localisation and non-zero values of the TDM for the dark states. The effect of the core-hole localisation can be clearly seen from the potential energy curves of the four low energy core excited states (Fig. S5 and S6 in the ESI†) and oscillator strengths (Fig. S7 and S8 in the ESI†) along the vibrational coordinates. Along several vibrational modes, the potential energy curves show double minima profiles for the first pair of electronic states (S1 and S2, transitions from the edge carbons) as well as for the second pair (S3 and S4, transitions from the central carbons); see, for example ν19 or ν21 in Fig. S6 in the ESI.† We can either employ the double-harmonic approximation, which in many cases yields well-resolved spectra while, at the same time, producing diabatic curves in the manifold of states, or we can concentrate on the fully adiabatic picture without the harmonic approximation.
For the double-harmonic approximation, the vibrational frequencies were calculated for the optimised geometries of the two lowest energy core-excited states at the MOM/B3LYP/cc-pVTZ+cc-pCVTZ level of theory (Table S7 and Fig. S9 in the ESI†). Optimisation of the core-excited states with transitions from the central carbon atoms (S4) is especially tedious because of the flat double well potential energy profiles which prefer a symmetric structure (with two negative low-frequency modes <100 cm−1). This approach neglects the dependence of the TDM on the coordinates and only provides information on the overlap of the ground state wave function with the core-excited wave functions of S2 and S4. For the S2 state, the highest intensity is observed for the ν21 mode (CH2 symmetric stretching mode), while for the S4 state, the highest intensity is observed for the ν17 and ν20 modes (C–C stretching and CH2 stretching modes, respectively).
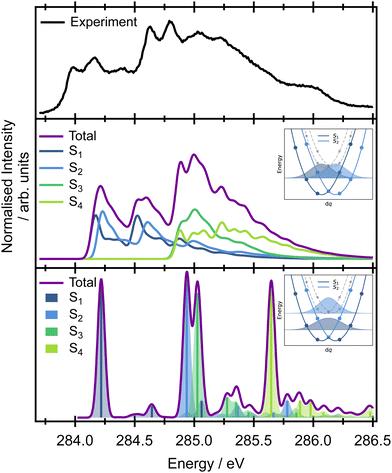
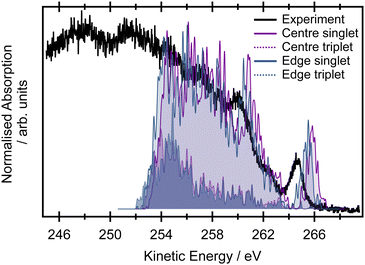
The vertical Hessian approximation, still within the harmonic approximation, is challenging at the Frank–Condon point due to the singularity of the TDM. The calculations were performed for a very slightly distorted geometry and a fixed value of the TDM (Fig. 3). Overall, the total calculated XAS spectrum with this approach shows reasonable energetic agreement with the experimental spectrum, and good agreement with the overall spectral linewidth and the presence of three broad spectral features that contribute to the overall observed lineshape. However, the harmonic approach cannot describe the true adiabatic surfaces resulting in degenerate states and the interpretation needs to be checked within fully adiabatic calculations. Of key importance to the later interpretation of the resonant Auger spectra is that the decomposition of the calculated spectrum into the contributions from individual electronic transitions reveals that the majority of the intensity below 284.5 eV in the experimental spectrum can be assigned to transitions to the S1 and S2 states, corresponding to excitation originating on the edge C 1s orbitals. The second broad feature predominantly arises from transitions to the S3 and S4 states from the central C 1s orbitals, though there is some overlap and intensity contribution from the lower energy features. Unfortunately, this approach is again lacking the complex TDM dependence on the molecular displacement which modifies the intensities corresponding to excitation of particular vibrational modes. Thus the spectra are not quantitatively represented.
Further insight on the vibronic XAS spectrum, beyond the harmonic approximation, is based on the precomputed 1D adiabatic curves. Full details of the procedure, involving integration of the exact 1D vibrational wave function for calculations of the XAS, are included in the ESI,† Section 1. Excitation energies and the corresponding wave function overlaps are shown in the bottom panel of Fig. 3. The results obtained using this approach show a qualitative difference from the previous data based on diabatic curves. While the S1/S2 and S3/S4 states are degenerate within the harmonic approximation, an ∼0.6 eV splitting emerges between the pairs of electronic states from the exact treatment of the normal modes. The discrepancy stems from a strong anharmonicity of the three vibrational modes – ν17, ν19, and ν21. Along these modes, the S1/S2 and S3/S4 state degeneracy is lifted and the lowest vibronic energies split. This splitting is not seen in the harmonic approximation (inset in Fig. 3). The fully adiabatic approach therefore suggests that the onset of the pre-edge XAS feature corresponds to the excitation to S1 only, while both the S2 and S3 states contribute to the band with an onset at 284.75 eV in the experimental spectrum. The S4 state lies above all of these features in the high energy part of the spectrum. The intensities in Fig. 3 correspond to only the overlaps between the states. To obtain the correct intensities of the current peaks, full integration of the TDM would be necessary. This is, however, non-trivial due to arbitrary changes in the sign of the TDMs in the electronic structure calculations. There are two more aspects that one needs to bear in mind while comparing the calculated spectra with the experiment. The calculations are based on the SRC1-r1 potential energy curves which exhibit a higher energy difference between the transitions from the edge (S1 and S2 states) and central carbon sites (S3 and S4 states) than do the CVS-EOM-CCSD or ADC-(2)-X methods, and this may be artificial. The second drawback is that the fully adiabatic calculation with our in-house code corresponds to 0 K, and this may alter the intensity of some of the vibrational modes; however, it should not alter the splitting of the states observed or invalidate the presented view of the spectra.
The non-trivial picture of X-ray absorption has further implications for the vibrationally resolved resonant Auger spectra simulations. Because none of the employed approximations provide the quantitative XAS spectra, we cannot apply the step model in which we would assume a coherent excitation of various stationary vibrational states in the intermediate state and we cannot calculate the amplitudes as the Franck–Condon factors between the vibrational functions of the ground and intermediate state and similarly between the intermediate and final state as:15,17,63,65
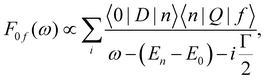 | (1) |
Calculation of the XAS spectrum is a key step for the simulations of the resonant Auger spectra that will be presented later. However, as we stated previously, the unambiguous identification of all the peaks in the high resolution XAS spectrum is not trivial. Therefore we pragmatically opt for using the “vibration-free” approach based on the NEA. The spectra are shown in the right panel in Fig. 6 at the CVS-EOM-EE-CCSD/cc-pVTZ+cc-PCVTZ level; the comparison for several methods is provided in Fig. S10 in the ESI.† The results for all tested methods (TDDFT/SRC1-r1/cc-pVTZ, CVS-EOM-EE-CCSD/cc-pVDZ+cc-PCVDZ and CVS-EOM-EE-CCSD/cc-pVTZ+cc-pCVTZ) show that the first peak corresponds exclusively to the excitation from the edge C 1s → π*. The second resolved peak in the XAS spectrum corresponds to the combination of edge C 1s → π* and central C 1s → π* excitations, which is in qualitative agreement with previous calculations. We can thus expect that in the resonant Auger spectra we will not see a rapidly changing signal, but gradually evolving features. The NEA calculations do not include any vibrational resolution, but they provide a description of the core-excited initial states prepared in the resonant Auger excitation process. They also provide information of the way in which these intermediate states influence the final observed Auger spectra.
3.4 Non-resonant Auger spectra
The non-resonant Auger spectrum of butadiene recorded at an incident photon energy of 395 eV is shown in Fig. 5. The spectrum displays one intense feature at a high kinetic energy of ∼264.6 eV and several overlapping features towards lower kinetic energies superimposed upon a large background. For comparison, the simulated non-resonant Auger spectra at the EOM-CCSD level within the NEA approach are shown decomposed into contributions arising from ionisation of the edge and central carbon atoms (and into contributions due to the different multiplicities of the final states involved in the Auger process). The theoretical spectrum was modelled for 25 final dicationic (2h) states and captures adequately the high kinetic energy range features. Across the entire kinetic energy range, the contributions from processes involving the central or edge carbons are very heavily overlapped. The small energetic pedestal on the high kinetic energy side of the feature at 265.5 eV in the calculated spectrum is potentially exclusively attributable to processes from the central carbon. The small energetic shift (∼0.4 eV) between the Auger spectra arising from ionisation of the central and edge carbon atoms reflects the energy difference between the respective core-ionised states.The calculated double ionisation potentials of the 25 final dicationic (2h) states are listed in Table S8 in the ESI.† These predicted energies allow the peak observed at a kinetic energy of 264.6 eV in the experimental spectrum to be attributed to the (1bg)−2 configuration. The more severely overlapped peaks observed towards lower kinetic energies correspond to the various final states involving the more tightly bound valence orbitals. The non-resonant Auger spectrum is heavily congested because it not only involves contributions from multiple core-hole initial states but also a large number of final states with different multiplicities. These complications provide a strong motivation for performing resonantly excited measurements on this system.
3.5 Resonant Auger spectra
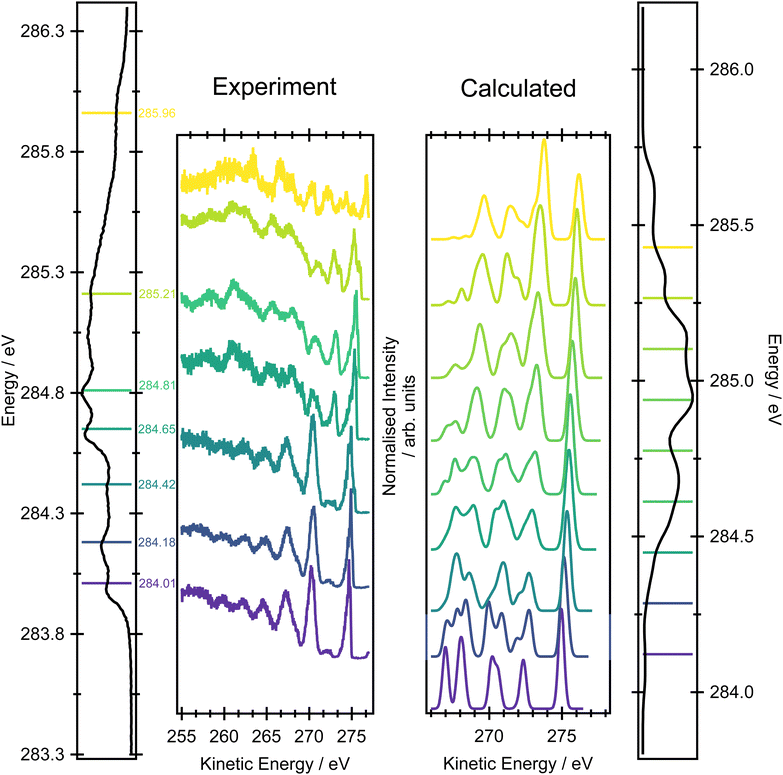
Fig. 6 shows a comparison between the experimental resonant Auger spectra recorded at a series of incident photon energies and the calculated Auger spectra within the NEA approach for a set of 50 geometries at the EOM-CCSD/cc-pVTZ+cc-pCVTZ level. Spectra calculated with the smaller cc-pVDZ+cc-pCVDZ basis set for a set of 400 geometries are provided in Fig. S15 in the ESI.† In the experiment, the incident photon energies were selected according to the local maxima of the vibrationally resolved XAS spectrum (the left-most panel of Fig. 6). However, within the NEA approach, the spectra are “vibration-free” so there are no local maxima corresponding to the excitation of the selected vibrational modes (the right-most panel of Fig. 6). The resonant Auger spectra were therefore constructed slightly differently. The X-ray absorption energies, Auger widths and Auger electron kinetic energies were calculated for all 50 geometries; these values can be plotted in the form of 2D histogram graph (see Fig. 7). This 2D map can then be filtered for an arbitrary excitation energy and width, e.g. the theoretical data can be more finely “sliced” in excitation energy than the corresponding experiment, thereby facilitating the visualisation and evaluating the changes in the resonant Auger spectra as the underlying electronic character changes across the XAS features.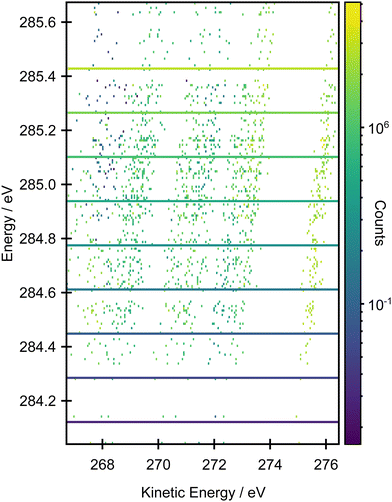 | ||
| Fig. 7 2D histogram plot of the resonant Auger spectrum calculated at the EOM-CCSD/cc-pVTZ+cc-pCVTZ level within the NEA approach for a set of 50 geometries. | ||
The resonant Auger spectrum recorded at an incident photon energy of 284.01 eV displays two intense features at kinetic energies of 270.27 eV and 274.69 eV (Fig. 6). The latter of these features shows a distinct asymmetry in the peak shape towards lower kinetic energies, together with a shoulder on the high kinetic energy side. A magnified version of this region of the spectrum is available in Fig. S16 in the ESI.† The feature with the highest kinetic energy is intense at all the photon energies used in the present study but its vibrational envelope exhibits pronounced changes as a function of photon energy. The feature at a kinetic energy of 270.27 eV is also intense in the spectra recorded at photon energies of 284.01, 284.18 and 284.42 eV, but at higher photon energies its intensity rapidly diminishes, and this reduction is correlated with the growth of a feature with a kinetic energy around 272.5 eV. At an excitation energy of 285.21 eV, and at higher excitation energies, the Auger spectra begin to show more significant changes which correlate with excitation into the tail of the broad 1s → π* features in the XAS and, for the Auger spectrum recorded at 285.96 eV, excitation into core-excited states of a different electronic character. Comparisons of the resonant Auger spectra to the valence band and the non-resonant Auger spectra are included in Fig. S12–S14 in the ESI.† The comparison to the valence band photoelectron spectrum demonstrates that the feature with the highest kinetic energy is due to participator decay into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg final state, where the hole is localised in the HOMO. Valence shell photoelectron spectra due to direct ionisation show that the
2Bg final state, where the hole is localised in the HOMO. Valence shell photoelectron spectra due to direct ionisation show that the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg state band exhibits significant vibrational structure.56 This structure shows some similarities with the vibrational envelope associated with the Auger peak at 274.69 eV but it is evident that autoionisation from the core-excited state leads to the population of high vibrational levels that are not populated in direct ionisation. The other main feature, at a kinetic energy of 270.27 eV, arises from participator decay into the
2Bg state band exhibits significant vibrational structure.56 This structure shows some similarities with the vibrational envelope associated with the Auger peak at 274.69 eV but it is evident that autoionisation from the core-excited state leads to the population of high vibrational levels that are not populated in direct ionisation. The other main feature, at a kinetic energy of 270.27 eV, arises from participator decay into the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Bu and
2Bu and ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) 2Ag states. Again, however, the overall shape of the Auger peak differs from that due to direct ionisation into these two states56 as a consequence of autoionisation.
2Ag states. Again, however, the overall shape of the Auger peak differs from that due to direct ionisation into these two states56 as a consequence of autoionisation.
Overall, the agreement between the calculated resonant Auger spectra and the experimental spectra is excellent because the main trends in peak positions and intensities are well reproduced. The subtle evolution, as a function of incident photon energy, in the relative intensities of the Auger peaks at 270.27, 272.0 and 274.69 eV is well-produced in the calculations (the two theoretical Auger spectra corresponding to the lowest incident photon energies are not accurate due to a limited number of sample geometries). The first significant change in the overall Auger spectrum, and the appearance of the features due to participator decay into the à 2Au and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Ag states, at excitation energies of 284.65 eV and above, corresponds to the underlying change in the electronic character of the core-excited state. From the analysis of the XAS spectrum, this overall change in the intensity profiles of the first three Auger bands matches the change in excitation of the 1s transitions located on the edge carbons to those localised on the central carbon atoms.
2Ag states, at excitation energies of 284.65 eV and above, corresponds to the underlying change in the electronic character of the core-excited state. From the analysis of the XAS spectrum, this overall change in the intensity profiles of the first three Auger bands matches the change in excitation of the 1s transitions located on the edge carbons to those localised on the central carbon atoms.
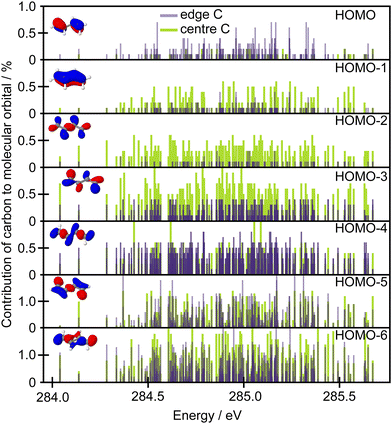
Further qualitative insight into the observed intensity changes can be based on discussing an overlap between the core orbitals localised on the edge or central carbons with the frontier molecular orbitals in terms of population analysis. Löwdin population analysis is particularly useful in this respect. The data in Fig. 8 show the contributions of the edge 1s carbon orbitals and the central 1s carbon orbitals to the frontier molecular orbitals. The population analysis was calculated for a set of 50 geometries and the contributions are shown with respect to the excitation energies calculated for each structure at the CVS-EOM-EE-CCSD/cc-pVTZ+cc-pCVTZ level. As can be seen from the figure, while the contribution to the HOMO is much higher for the edge carbons, for the HOMO−1 and HOMO−2 the situation is reversed. Thus, when the edge carbons are core excited, a higher intensity can be expected for the Auger peak with the highest kinetic energy, corresponding to participator decay leading to a hole in the HOMO, than if the central carbons are core excited. This is clearly in agreement with the experiment. The opposite trend is predicted for the second Auger peak which corresponds to the final states involving holes in the HOMO−1 and HOMO−2 orbitals (Ã 2Au and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Ag). The change in intensity is not so convincingly predicted for the final ionic states involving HOMO−3 and HOMO−4 (
2Ag). The change in intensity is not so convincingly predicted for the final ionic states involving HOMO−3 and HOMO−4 (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Bu and
2Bu and ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) 2Ag).
2Ag).
4 Conclusions
Despite its relatively small size, butadiene is an excellent example of a molecule which suffers from significant spectral congestion in the pre-edge region of the XAS spectrum, owing to contributions from multiple electronic and vibrational states which can be disentangled using the resonant Auger spectra. The high symmetry of butadiene, its reasonably rigid structure and the presence of core-hole localisation effects make it a highly challenging system to describe theoretically. We have tested the performance of several theoretical approaches, in particular the NEA approach and detailed calculations within the harmonic approximation or with full adiabatic vibronic calculations, for disentangling the XAS and resonant Auger spectra. The overall agreement of the positions of the two main 1s → π* transitions in the XAS spectra are in excellent agreement with fits of the linear-coupling models to the experimental data.20 A more comprehensive picture reveals the more subtle contributions from four electronic states due to the symmetry breaking connected to the hole-localisation and due to the different vibrational progressions associated with each electronic state. The comparison of the NEA approach with vibronic calculations demonstrates that a full description of the XAS requires consideration of both ensemble and vibronic effects. However, a simplified, “vibration-free” approach within NEA is largely sufficient for the calculations of the main trends in the resonant Auger observables while providing a very practical and feasible approach. Moreover, the NEA approach provides a straightforward way for plotting the resonant Auger spectra in the form of the 2D histogram. This allows the spectral manifestations of the subtle changes in the electronic structure to be captured effectively.For butadiene, the resonant Auger spectra offer a rich insight into the complexity that is somewhat obscured in the XAS spectra alone. The resonant Auger spectra and their theoretical interpretation show that excitation of different carbon environments is responsible for the observed variation in the intensities of the high kinetic energy spectral features. Specifically, if the edge carbons are core excited, a higher intensity is expected for the higher kinetic energy Auger (participator decay with a hole in the HOMO) and a very small intensity is expected for the second highest kinetic energy peak (participator decay with a hole in the HOMO−1 and HOMO−2). If the central carbons are core excited, the opposite trend occurs. The underlying reason can be understood in terms of the overlap between the core orbital and the HOMO conveniently modelled by the Löwdin population analysis. These observations demonstrate the advantages of utilising resonant Auger spectroscopy to distinguish between different electronic excitations and site-specific dynamics. Here, the Auger process projects overlapping complex core-excited states on more ‘interpretable’ final valence-ionised states and serves as a unique tool to identify the character of the electronic states involved in core-excitations. In another words, it is possible to disentangle energetically overlapping transitions and to understand the underlying electronic structure in polyatomic systems.
Interestingly, the reported high-resolution resonant Auger spectra demonstrate vibrational progressions. Higher-resolution, polarisation-dependent measurements would be beneficial for a better understanding of the vibrational contributions to the Auger spectra as it is clear from an analysis of the peaks corresponding to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Bg, Ã 2Au,
2Bg, Ã 2Au, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Ag,
2Ag, ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Bu and
2Bu and ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) 2Ag bands that the vibrational progressions observed do not reflect those in the valence band. Within the two-step model, the question then arises from which of the states (intermediate or final states) the vibrational information contained in the Auger spectrum arises and whether this information can be used not just to evaluate the relative character and weights of different contributions in complex absorption spectra but also to obtain more subtle information on the involvement of the nuclear dynamics in the Auger process itself and chemical insights into site selective dynamical processes.21 None of this information, however, can be inferred from the NEA approach. A full reconstruction of the time-dependent process of autoionisation would require an extension of the Fano theory.68
2Ag bands that the vibrational progressions observed do not reflect those in the valence band. Within the two-step model, the question then arises from which of the states (intermediate or final states) the vibrational information contained in the Auger spectrum arises and whether this information can be used not just to evaluate the relative character and weights of different contributions in complex absorption spectra but also to obtain more subtle information on the involvement of the nuclear dynamics in the Auger process itself and chemical insights into site selective dynamical processes.21 None of this information, however, can be inferred from the NEA approach. A full reconstruction of the time-dependent process of autoionisation would require an extension of the Fano theory.68
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank C. Puglia (Uppsala University, Sweden) and the Carl Tygger Foundation for making available the SES-200 photoelectron analyser at the Gas Phase beamline, Elettra, Italy. The research leading to this result has been supported by the project CALIPSOplus under Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. E. M. and J. J. thank the Czech Science Foundation for the support via project number 21-26601X (EXPRO project). This work was supported from the grant of Specific university research – grant No. A2_FCHI_2023_048. J. S. gratefully acknowledges support from the Institute for Advanced Computational Science Postdoctoral Fellowship program. D. M. P. H. is grateful to the Science and Technology Facilities Council (United Kingdom) for financial support.Notes and references
- C. Nicolas and C. Miron, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 267–272 CrossRef CAS.
- F. Gel'mukhanov, M. Odelius, S. P. Polyutov, A. Föhlisch and V. Kimberg, Rev. Mod. Phys., 2021, 93, 35001 CrossRef.
- F. D. Fuller, A. Loukianov, T. Takanashi, D. You, Y. W. Li, K. Ueda, T. Fransson, M. Yabashi, T. Katayama, T. C. Weng, R. Alonso-Mori, U. Bergmann, J. Kern, V. K. Yachandra, P. Wernet and J. Yano, Commun. Chem., 2021, 4, 84 CrossRef CAS PubMed.
- W. Błachucki, Y. Kayser, A. Wach, R. Fanselow, C. Milne, J. Sá and J. Szlachetko, Appl. Sci., 2021, 11, 8775 CrossRef.
- L. Inhester, B. Oostenrijk, M. Patanen, E. Kokkonen, S. H. Southworth, C. H. Bostedt, O. Travnikova, T. Marchenko, S. K. Son, R. Santra, M. Simon, L. Young and S. L. Sorensen, J. Phys. Chem. Lett., 2018, 9, 1156–1163 CrossRef CAS PubMed.
- H. Levola, E. Itälä, K. Schlesier, K. Kooser, S. Laine, J. Laksman, D. T. Ha, E. Rachlew, M. Tarkanovskaja, K. Tanzer and E. Kukk, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 063409 CrossRef.
- M. F. Erben, M. Geronés, R. M. Romano and C. O. Della Védova, J. Phys. Chem. A, 2006, 110, 875–883 CrossRef CAS PubMed.
- E. Itälä, D. T. Ha, K. Kooser, M. A. Huels, E. Rachlew, E. Nõmmiste, U. Joost and E. Kukk, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 119–124 CrossRef.
- S. Zagorodskikh, J. H. D. Eland, V. Zhaunerchyk, M. Mucke, R. J. Squibb, P. Linusson and R. Feifel, J. Chem. Phys., 2016, 145, 124302 CrossRef PubMed.
- P. Salén, L. Schio, R. Richter, M. Alagia, S. Stranges, S. Falcinelli and V. Zhaunerchyk, J. Chem. Phys., 2022, 157, 124306 CrossRef PubMed.
- S. Oberli, J. González-Vázquez, E. Rodríguez-Perelló, M. Sodupe, F. Martín and A. Picón, Phys. Chem. Chem. Phys., 2019, 21, 25626–25634 RSC.
- M. Eroms, O. Vendrell, M. Jungen, H. D. Meyer and L. S. Cederbaum, J. Chem. Phys., 2009, 130, 154307 CrossRef PubMed.
- G. Goldsztejn, R. Guillemin, T. Marchenko, O. Travnikova, D. Céolin, L. Journel, M. Simon, M. N. Piancastelli and R. Püttner, Phys. Chem. Chem. Phys., 2022, 24, 6590–6604 RSC.
- R. C. Couto, V. V. Cruz, E. Ertan, S. Eckert, M. Fondell, M. Dantz, B. Kennedy, T. Schmitt, A. Pietzsch, F. F. Guimarães, H. Ågren, F. Gel'mukhanov, M. Odelius, V. Kimberg and A. Föhlisch, Nat. Commun., 2017, 8, 14165 CrossRef CAS PubMed.
- M. N. Piancastelli, J. Electron Spectrosc. Relat. Phenom., 2000, 107, 1–26 CrossRef CAS.
- L. S. Cederbaum and F. Tarantelli, J. Chem. Phys., 1993, 98, 9691–9706 CrossRef CAS.
- M. Neeb, J.-E. Rubensson, M. Biermann and W. Eberhardt, J. Electron Spectrosc. Relat. Phenom., 1994, 67, 261–274 CrossRef CAS.
- M. N. Piancastelli, M. Neeb, A. Kivimäki, B. Kempgens, H. M. Köppe, K. Maier and A. M. Bradshaw, Phys. Rev. Lett., 1996, 77, 4302–4305 CrossRef CAS PubMed.
- M. A. Martin-Drumel, J. P. Porterfield, M. Goubet, P. Asselin, R. Georges, P. Soulard, M. Nava, P. B. Changala, B. Billinghurst, O. Pirali, M. C. McCarthy and J. H. Baraban, J. Phys. Chem. A, 2020, 124, 2427–2435 CrossRef CAS PubMed.
- S. L. Sorensen, S. J. Osborne, A. Ausmees, A. Kikas, N. Correia, S. Svensson, A. Naves de Brito, P. Persson and S. Lunell, J. Chem. Phys., 1996, 105, 10719–10724 CrossRef CAS.
- S. Oghbaiee, M. Gisselbrecht, N. Walsh, B. Oostenrijk, J. Laksman, E. P. Månsson, A. Sankari, J. H. D. Eland and S. L. Sorensen, Phys. Chem. Chem. Phys., 2022, 24, 28825–28830 RSC.
- A. P. Hitchcock, S. Beaulieu, T. Steel, J. Stöhr and F. Sette, J. Chem. Phys., 1984, 80, 3927–3935 CrossRef CAS.
- N. C. Craig, P. Groner and D. C. McKean, J. Phys. Chem. A, 2006, 110, 7461–7469 CrossRef CAS PubMed.
- R. N. Sodhi and C. E. Brion, J. Electron Spectrosc. Relat. Phenom., 1985, 37, 1–21 CrossRef CAS.
- A. Naves de Brito, S. Svensson, N. Correia, M. P. Keane, H. Ågren, O.-P. Sairanen, A. Kivimäki and S. Aksela, J. Electron Spectrosc. Relat. Phenom., 1992, 59, 293–305 CrossRef CAS.
- R. R. Blyth, R. Delaunay, M. Zitnik, J. Krempasky, R. Krempaska, J. Slezak, K. C. Prince, R. Richter, M. Vondracek, R. Camilloni, L. Avaldi, M. Coreno, G. Stefani, C. Furlani, M. de Simone, S. Stranges and M. Y. Adam, J. Electron Spectrosc. Relat. Phenom., 1999, 101, 959–964 CrossRef.
- D. Feller and N. C. Craig, J. Phys. Chem. A, 2009, 113, 1601–1607 CrossRef CAS PubMed.
- J. Saltiel, D. F. Sears and A. M. Turek, J. Phys. Chem. A, 2001, 105, 7569–7578 CrossRef CAS.
- M. Deleuze and S. Knippenberg, J. Chem. Phys., 2006, 125, 104309 CrossRef CAS PubMed.
- M. Tronc, G. C. King and F. H. Read, J. Phys. B: At. Mol. Phys., 1979, 12, 137–157 CrossRef CAS.
- C. E. Moore, Atomic Energy Levels as Derived from the Analyses of Optical Spectra, US Govt. Printing Office, Washington DC, 1971 Search PubMed.
- D. W. Turner, Molecular photoelectron spectroscopy: A handbook of He 584 Å spectra, Wiley Interscience, London, 1970 Search PubMed.
- V. Myrseth, J. D. Bozek, E. Kukk, L. J. Sæthre and T. D. Thomas, J. Electron Spectrosc. Relat. Phenom., 2002, 122, 57–63 CrossRef CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. Janesko, R. Gomperts, B. Mennucci, H. Hratchian, J. Ortiz, A. Izmaylov, J. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. Montgomery, J. Peralta, F. Ogliaro, M. Bearpark, J. Heyd, E. Brothers, K. Kudin, V. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. Burant, S. Iyengar, J. Tomasi, M. Cossi, J. Millam, M. Klene, C. Adamo, R. Cammi, J. Ochterski, R. Martin, K. Morokuma, O. Farkas, J. Foresman and D. Fox, Gaussian 09, Revision A.02, 2016 Search PubMed.
- S. Gozem and A. I. Krylov, The ezSpectra suite: An easy-to-use toolkit for spectroscopy modeling, 2021, https://iopenshell.usc.edu/downloads.
- A. Ferrer, F. José and F. Santoro, Phys. Chem. Chem. Phys., 2012, 14, 13549–13563 RSC.
- J. Cerezo and F. Santoro, J. Comput. Chem., 2023, 44, 626–643 CrossRef CAS PubMed.
- R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1237 Search PubMed.
- F. Della Sala, R. Rousseau, A. Görling and D. Marx, Phys. Rev. Lett., 2004, 92, 183401 CrossRef PubMed.
- D. Hollas, E. Muchová and P. Slavíček, J. Chem. Theory Comput., 2016, 12, 5009–5017 CrossRef CAS PubMed.
- M. Ončák, L. Šištík and P. Slavíček, J. Chem. Phys., 2010, 133, 174303 CrossRef PubMed.
- A. Prlj, E. Marsili, L. Hutton, D. Hollas, D. Shchepanovska, D. R. Glowacki, P. Slavíček and B. F. E. Curchod, ACS Earth Space Chem., 2022, 6, 207–217 CrossRef CAS PubMed.
- Š. Sršeň, J. Sita, P. Slavíček, V. Ladányi and D. Heger, J. Chem. Theory Comput., 2020, 16, 6428–6438 CrossRef PubMed.
- P. C. do Couto, D. Hollas and P. Slavíček, J. Chem. Theory Comput., 2015, 11, 3234–3244 CrossRef PubMed.
- E. Muchová, D. Hollas, D. M. P. Holland, C. Bacellar, L. Leroy, T. R. Barillot, L. Longetti, M. Coreno, M. de Simone, C. Grazioli, M. Chergui and R. A. Ingle, Phys. Chem. Chem. Phys., 2023, 25, 6733–6745 RSC.
- A. Prlj, D. Hollas and B. F. E. Curchod, J. Phys. Chem. A, 2023, 127, 7400–7409 CrossRef CAS PubMed.
- M. Ceriotti, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2009, 103, 030603 CrossRef PubMed.
- M. Ceriotti, G. Bussi and M. Parrinello, J. Chem. Theory Comput., 2010, 6, 1170–1180 CrossRef CAS.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z. Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. D. Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P. T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. Hanson-Heine, P. H. Harbach, A. Hauser, M. F. Herbst, M. H. Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y. P. Li, J. Liang, M. Liebenthal, H. H. Lin, Y. S. Lin, F. Liu, K. Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S. P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. Menger, J. M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y. C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J. D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. Deprince, R. A. Distasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C. P. Hsu, T. C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. Thom, A. Tkatchenko, D. G. Truhlar, T. V. Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- N. A. Besley, M. J. G. Peach and D. J. Tozer, Phys. Chem. Chem. Phys., 2009, 11, 10350–10358 RSC.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- M. A. Ambroise and F. Jensen, J. Chem. Theory Comput., 2019, 15, 325–337 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084124 CrossRef CAS PubMed.
- W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084125 CrossRef CAS PubMed.
- D. M. P. Holland, M. A. MacDonald, M. A. Hayes, P. Baltzer, B. Wannberg, M. Lundqvist, L. Karlsson and W. von Niessen, J. Phys. B: At. Mol. Phys., 1996, 29, 3091–3107 CrossRef CAS.
- T. D. Thomas, L. J. Sæthre, K. J. Børve, M. Gundersen and E. Kukk, J. Phys. Chem. A, 2005, 109, 5085–5092 CrossRef CAS PubMed.
- T. X. Carroll, J. Hahne, T. D. Thomas, L. J. Sæthre, N. Berrah, J. Bozek and E. Kukk, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 042503 CrossRef.
- R. Forbes, S. T. Pratt, A. De Fanis, A. R. Milosavljević, C. Nicolas, J. D. Bozek, N. A. Besley and D. M. P. Holland, Phys. Rev. A, 2020, 101, 023408 CrossRef CAS.
- L. S. Cederbaum and W. Domcke, J. Chem. Phys., 1977, 66, 5084–5086 CrossRef.
- H. Köppel, F. X. Gadea, G. Klatt, J. Schirmer and L. S. Cederbaum, J. Chem. Phys., 1997, 106, 4415–4429 CrossRef.
- A. Kivimäki, B. Kempgens, K. Maier, H. M. Köppe, M. N. Piancastelli, M. Neeb and A. M. Bradshaw, Phys. Rev. Lett., 1997, 79, 998–1001 CrossRef.
- M. Neeb, B. Kempgens, A. Kivimäki, H. M. Köppe, K. Maier, U. Hergenhahn, M. N. Piancastelli, A. Rüdel and A. Bradshaw, J. Electron Spectrosc. Relat. Phenom., 1998, 88–91, 19–27 CrossRef CAS.
- M. P. De Miranda, J. A. Beswick, P. Parent, C. Laffon, G. Tourillon, A. Cassuto, G. Nicolas and F. X. Gadea, J. Chem. Phys., 1994, 101, 5500–5514 CrossRef CAS.
- R. Flammini, M. Satta, P. O'Keeffe, M. Coreno, A. Kivimäki, M. de Simone, M. Carbone, V. Feyer, K. C. Prince and L. Avaldi, New J. Phys., 2014, 16, 073022 CrossRef CAS.
- L. S. Cederbaum and F. Tarantelli, J. Chem. Phys., 1993, 99, 5871–5884 CrossRef CAS.
- N. Sisourat, J. Chem. Phys., 2013, 139, 074111 CrossRef CAS PubMed.
- R. Y. Bello, S. E. Canton, D. Jelovina, J. D. Bozek, B. Rude, O. Smirnova, M. Y. Ivanov, A. Palacios and F. Martín, Sci. Adv., 2018, 4, eaat3962 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Optimised geometries, vibrationally-resolved valence band, core-ionised and core-excited spectra, details on adiabatic calculations, energy and transition dipole moments profiles along vibrational coordinates, resonant Auger spectra. See DOI: https://doi.org/10.1039/d4cp00053f |
| This journal is © the Owner Societies 2024 |