Open Access Article
Open Access ArticleExploring mechanochemistry of pharmaceutical cocrystals: effect of incident angle on molecular mixing during simulated indentations of two organic solids†
Michael
Ferguson
 * and
Tomislav
Friščić
* and
Tomislav
Friščić
 *
*
School of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK. E-mail: m.ferguson.5@bham.ac.uk; t.friscic@bham.ac.uk
First published on 21st February 2024
Abstract
The solid-state reaction of the active pharmaceutical ingredient theophylline with citric acid is a well-established example of a mechanochemical reaction, leading to a model pharmaceutical cocrystal. Here, classical force field molecular dynamics was employed to investigate the molecular mixing and structural distortion that take place on the mechanically driven indentation of a citric acid nanoparticle on a slab of crystalline theophylline. Through non-equilibrium molecular dynamics simulations, a 6 nm diameter nanoparticle of citric acid was introduced onto an open (001) surface of a theophylline crystal, varying both the angle of incidence of the nanoparticle between 15° and 90° and the indentation speed between 1 m s−1 and 16 m s−1. This theoretical study enabled the evaluation of how these two parameters promote molecular mixing and overall structural deformation upon the mechanical contraction of theophylline and citric acid, both of which are important parameters underlying mechanochemical cocrystallisation. The results show that the angle of incidence plays a key role in the molecular transfer ability between the two species and in the structural disruption of the initially spherical nanoparticles. Changing the indentation speed, however, did not lead to a discernible trend in molecular mixing, highlighting the importance of the incident angle in mechanochemical events in the context of supramolecular chemistry, such as the disruption of the crystal structure and molecular transfer between molecular crystals.
Introduction
Mechanochemical strategies, where mechanical energy is used to induce or promote chemical transformations, are one of the most attractive routes for cleaner, more efficient and sustainable synthesis of various molecular targets and functional materials.1 Mechanochemistry has been demonstrated to provide access to improved reaction yields, reduced reaction times, and vast reductions in solvent use,1 while also providing pathways for reactions between poorly soluble compounds2 and even access to products that are otherwise unobtainable.3 Mechanochemical reactions are most commonly performed in small batches using ball mills,1a but recent reports have also engaged resonant acoustic mixing4 (RAM) and twin-screw extrusion5 (TSE), opening the door to establishing highly scalable approaches to mechanochemistry. A wide range of mechanochemical techniques, including ball milling,6 TSE,7 and RAM,8 as well as mechanically activated approaches, such as accelerated aging (also known as vapour digestion)9 and vapour-assisted tumbling (VAT),10 have attracted particular attention in the context of the discovery and synthesis of pharmaceutical materials, such as polymorphs or cocrystals. Processes of relevance in mechanochemical cocrystallisation of pharmaceutical solids, as well as other types of organic and metal–organic materials, are likely to be the distortion or disruption of the crystal structure (e.g. amorphisation), formation of defects (polymorphic transformations), and molecular mixing (mass transfer). Importantly, mechanochemical processes leading to pharmaceutical cocrystals generally do not involve the cleavage of strong covalent bonds, but rather changes in molecular assembly in the solid state and surfaces, which is based on supramolecular transformations like in the recently discussed term of soft mechanochemistry.11,12Significant attention has been directed to developing a fundamental understanding of how diverse chemical and materials transformations, including cocrystal formation, proceed under mechanochemical conditions,13 with notable mechanistic knowledge acquired following the introduction of real-time in situ monitoring techniques by synchrotron powder X-ray diffraction,14 Raman spectroscopy,15,16 X-ray absorption spectroscopy,17 tandem Raman and fluorescence spectroscopies,18 nuclear magnetic resonance (NMR) spectroscopy,19 and acoustic spectroscopy.20 These techniques are now set to provide a wealth of information on mechanochemical reactivity in the bulk regime but cannot yet provide insights into underlying atomic and molecular processes that drive the reactions. Indeed, studies of mechanochemical reactions of molecular materials are in many ways additionally challenging compared to transformations of ionic solids, as intermediate and/or amorphous phases are very likely to rapidly relax before or during analysis.13
Theoretical techniques provide a wide range of strategies for probing the molecular-level mechanisms of mechanochemical processes that cannot be obtained experimentally. For example, discrete element modelling has been performed to understand how the motion of the grinding media (i.e., balls or screws used to transmit mechanical energy during milling or extrusion processes, respectively)21 or the shape of the mechanochemical reaction vessel22 affects the delivery of mechanical energy to the reaction system. Phase-field crystal theory has been utilised to investigate how mechanical energy input can reduce the energy barrier for the nucleation of nanoparticles from a homogenous solid matrix,23 while analytical models have been employed to model mechanochemical reaction kinetics24 and understand how ball impacts promote bulk changes in solids.25Ab initio methods have been employed to probe how mechanical stress leads to covalent bond cleavage.26,27 Additionally, ab initio calculations have shown how mechanical stress alters lattice vibrations in metal azides, which subsequently induce chemical reactions.28 These techniques have generated a greater understanding of mechanochemistry but generally need to sacrifice molecular-level details to study more global effects, which are more easily transferable to experimental results or dynamic information to study energetics at the atomic level. Force field molecular dynamics (MD) allows studying the molecular level processes that occur over short time periods (ns–μs) and, in the context of mechanochemistry, has already been employed to study the effects of shear stress on various tribochemical (i.e., friction-induced) transformations29 as well as for exploring molecular transfer processes between crystalline organic solids upon organic particle collisions.30 Such studies are performed using a direct indentation strategy, which involves using molecular walls to push two particles together until a predefined point of maximum indentation that is followed by pulling the particles apart to facilitate the analysis of molecular transfer between the species involved.
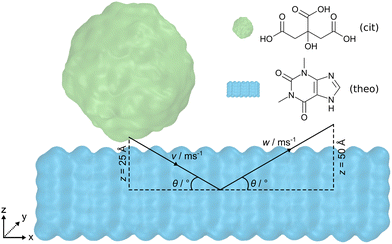
Here, we present the use of force field MD simulations to investigate the processes taking place upon the impact of an organic crystalline nanoparticle on the surface of an organic solid. Specifically, by varying the incident angle of the crystalline nanoparticle, as well as the incident speed of the nanoparticle, it was possible to observe different levels of particle distortion and molecular mixing – phenomena of critical importance for subsequent cocrystallisation. As model crystalline materials for our study, we chose citric acid (cit) and the active pharmaceutical ingredient (API) theophylline (theo), which provide relevance in the context of pharmaceutical materials science. Importantly, cocrystallisation of theo and cit acid through mechanochemical techniques has been reported by several groups, providing a model of broad significance.31 In contrast to previous work where two nanoparticles were indented upon one another,30 the current investigation focuses on the indentation of a spherical cit nanoparticle onto a flat theophylline surface (Fig. 1). By systematically reducing the incident angle from 90° to 15°, we gain insights into both the molecular transfer process and the structural deformation of the particles. Lower incident angles (15° and 30°) lead to a significant increase in the number of molecules exchanged between cit and theo, and a noticeable decrease in the sphericity of the originally spherical nanoparticles of cit. Additionally, the simulations reveal that the effects of the angle of incidence overshadow those of the incident speed during the presented indentations.
Computational methods
The molecular dynamics (MD) engine LAMMPS,32 v29Oct2020, was employed to simulate indentations of a cit nanoparticle on an open surface of a theo slab at various incident speeds along the vector v and angles θ, as shown in Fig. 1. Upon reaching the desired indentation point, the cit nanoparticle was retracted from the theo slab along the vector w, at the same speed as the indentation. Interatomic interactions were described by the OPLS-AA force field33 with non-bonded interactions modelled using Lennard-Jones34 potentials truncated at 12 Å. Hydrogen bonding interactions were incorporated by overlaying the Lennard-Jones potentials with the angle-dependent 12-10 form, as described in the DREIDING force field.35 Electrostatic interactions were calculated using the particle–particle particle–mesh (PPPM) solver36 with atomic charges that were obtained from Hirshfeld charge analysis performed using the periodic density functional theory (DFT) code CASTEP, v22.11.37 Crystal structures used to model cit and theo were obtained from the Cambridge Structural Database38 (CSD) with the reference codes CITRAC1039 and BAPLOT01,40 respectively. Full details of the DFT calculation parameters and sample input files for the MD simulations with LAMMPS can be found in the ESI.†To obtain a size comparable to previous work36 (diameter = ≈6 nm), a spherical region (radius = 30 Å) of molecules was extracted from a 12 × 30 × 15 supercell of the cit crystal structure. If any atom of a molecule falls within the radius, then that molecule was included as part of the nanoparticle, resulting in a final nanoparticle radius of 31.5 Å. The slab geometry for theo was generated by creating a 7 × 28 × 5 supercell of the pure crystal and then extending the z-axis by 130 Å. This allowed the cit nanoparticle to be positioned above the slab surface, while ensuring that there would be no interactions between the cit and the theo slab through the periodic boundary conditions. The nanoparticle and the slab were equilibrated separately for 1 ns at 300 K in the NVT ensemble and subsequently combined to produce a 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atom system ready for simulated indentations. Following previous studies,30,41 the motion of the objects in the presented simulations was controlled by fixing the trajectories of a small section of the molecules of each material. For theo, 392 molecules that formed the bottom layer of the slab were selected and their velocities were set to zero, to fix the slab in place. For cit, 115 molecules contained within the uppermost 15 Å of the particle were selected and used to move the nanoparticle at a given speed along v and w (Fig. S1, ESI†). Based on estimated ball speeds in a ball mills42,43 of 8 m s−1 and 1 m s−1, we decided on the set of speeds, 1, 4, 8, and 16 m s−1, where 16 m s−1 was chosen to overestimate the ferocity of the indentation. For the incident angle of the particle, we chose a range of θ = 15° to 90° with increments of 15°. In the case where θ = 90°, the cit nanoparticle was positioned so that its geometrical centre was directly above the centre of the xy centre of the theo slab and with a 5 Å separation in z between the two structures. The depth of the indentation in z of the cit nanoparticle to the slab was set at 20 Å; therefore, the nanoparticle will travel 25 Å in z to reach this point of maximum indentation. For indentations where θ ≠ 90°, the cit particle was displaced negatively along the x-axis, as calculated using simple trigonometry (Section S1.1, ESI†). This ensured that the position of the cit particles relative to the theo slab at the maximum indentation was identical for each simulated indentation. Upon reaching the maximum indentation, the cit particle was retracted from the theo slab to facilitate the analysis. The nanoparticle was retracted along w at the same speed and retracted over a distance of 50 Å to guarantee a final configuration comprising two contiguous objects.
000 atom system ready for simulated indentations. Following previous studies,30,41 the motion of the objects in the presented simulations was controlled by fixing the trajectories of a small section of the molecules of each material. For theo, 392 molecules that formed the bottom layer of the slab were selected and their velocities were set to zero, to fix the slab in place. For cit, 115 molecules contained within the uppermost 15 Å of the particle were selected and used to move the nanoparticle at a given speed along v and w (Fig. S1, ESI†). Based on estimated ball speeds in a ball mills42,43 of 8 m s−1 and 1 m s−1, we decided on the set of speeds, 1, 4, 8, and 16 m s−1, where 16 m s−1 was chosen to overestimate the ferocity of the indentation. For the incident angle of the particle, we chose a range of θ = 15° to 90° with increments of 15°. In the case where θ = 90°, the cit nanoparticle was positioned so that its geometrical centre was directly above the centre of the xy centre of the theo slab and with a 5 Å separation in z between the two structures. The depth of the indentation in z of the cit nanoparticle to the slab was set at 20 Å; therefore, the nanoparticle will travel 25 Å in z to reach this point of maximum indentation. For indentations where θ ≠ 90°, the cit particle was displaced negatively along the x-axis, as calculated using simple trigonometry (Section S1.1, ESI†). This ensured that the position of the cit particles relative to the theo slab at the maximum indentation was identical for each simulated indentation. Upon reaching the maximum indentation, the cit particle was retracted from the theo slab to facilitate the analysis. The nanoparticle was retracted along w at the same speed and retracted over a distance of 50 Å to guarantee a final configuration comprising two contiguous objects.
Results and discussion
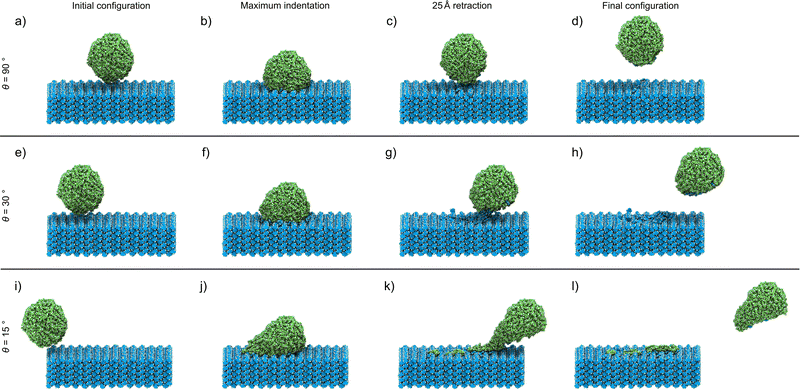
The analyses of the effect of the speed and incident angle are presented (Fig. 2 and 3) in a previously introduced format,30 whereby visual inspection of simulation trajectories is accompanied by molecular distribution histograms to understand mixing, force development curves in the direction of the indentation, and measurements of the length of the connective neck formed between the two objects. This study also incorporates an analysis of the structural deformation suffered by the nanoparticle by determining the changes in sphericity. In this study, we started with the simulation of direct indentations, where θ = 90°. Visual inspection allows us to observe the key points of the indentation process (Fig. 2(a)–(d)), with the indentation speed set at 8 m s−1 in this case. The simulation process is best described through forward indentation and subsequent retraction stages, corresponding to the processes in which the cit nanoparticle impacts and disrupts the theo surface, and processes in which the nanoparticle is being dragged out of the theo surface, respectively. These are illustrated by visual inspection of several key points of the experiment at which θ = 90° and the speed along v is 8 m s−1 (Fig. 2(a)–(d)).‡ The first key point corresponds to the starting configuration, in which the cit particle (green) is situated 5 Å above the centre of the theo (001) slab surface (blue) (Fig. 2(a)). The next key point (Fig. 2(b)) corresponds to the configuration at the maximum indentation of the cit particle into the surface, when the nanoparticle is indented on the surface by 20 Å. In the retraction stage, the key points for analysis are when cit has been retracted by 25 Å (Fig. 2(c)), i.e. when the molecules with fixed trajectories have the same separation from the slab in z as found in the starting position, and the final point of the simulation where the cit nanoparticle has been retracted by a total of 50 Å (Fig. 2(d)). While visually there does not appear to have been any transfer of molecules between the two materials, there is, in fact, a small number (13) of theo molecules that have been abstracted from the slab by the nanoparticle. This represents approximately 0.3% of the 4098 molecules, of both cit and theo, that were free to move in the simulation.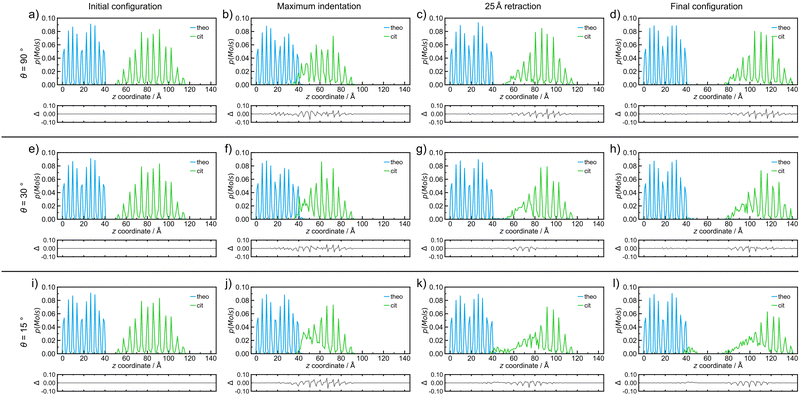 | ||
| Fig. 3 Probability density distributions of molecules of each species, theo (blue) and cit (green), for simulated indentations where the nanoparticle travels at 8 m s−1 and incident angles of (a–d) 90°, (e–h) 30°, and (i–l) 15°. The plot distributions when at (a, e and i) the initial configuration, (b, f and j) the point of maximum indentation, (c, g and k) after retraction of the nanoparticle by 25 Å, and (d, h and l) the final configuration after retraction of 50 Å for each simulated indentation process. The probability density distributions in this figure correspond directly to the simulation snapshots shown in Fig. 2. Below each distribution, a difference curve is given, which highlights the changes relative to the initial configuration. | ||
Since molecular mixing, especially if low fractions of molecules are involved, might be difficult to detect and quantify by visual inspection, the analysis of molecular mixing and transfer is best performed by tracking the centre of mass for all molecules in the system, followed by determining the number of molecules of theo and cit, whose z-coordinates were above and below 55 Å in the final configuration, respectively. The corresponding histogram plots of the molecular distributions along the z-axis (Fig. 3(a)–(d)) show two well-defined regions of the population with regularly spaced maxima for the initial configuration (Fig. 3(a)), which is expected due to the regular packing of molecules in the parent crystal structures. At the point of maximum indentation, the histogram corresponding to cit (green) exhibits a small amount of compression of ≈5 Å (Fig. 3(b)), which is a result of the nanoparticle being distorted upon being pressed into the theo slab. In the middle of the retraction step, a trace of theo (blue) can be observed occupying the same region as the cit, demonstrating molecular mixing. The lack of a probability density for either species in the range of 45 Å to 50 Å at this stage signifies that the two objects have been separated. The probability density histograms for the final configuration (Fig. 3(d)) are very similar to those of the previous stage, with the only perceivable difference being the larger separation between the two objects. The molecular transfer values were consistently low for all four of the indentation speeds investigated in this work and were almost 30 times lower than those observed for indentations between two nanoparticles in 2019.30 This is caused by two factors: (I) the surface of the pristine is free of defects and, consequently, molecules at the surface will be less mobile than those at a high curvature surface, such as the surface of previously studied nanoparticles,30 and (II) the large size of the theo slab, required for the simulations, results in large regions of theo molecules that are not involved in the indentation process, reducing the transfer percentage significantly. It was previously established that the interaction of organic nanoparticles, with or without the presence of liquid additives, leads to the formation of a connective neck, which is a small region of particles that maintains all of the particles in the simulation as a single object when the retraction process exceeds 20 Å (where the surface of theo terminates). The formation of a connective neck, which enables extensive intermolecular mixing, is likely to be a critical aspect of mechanochemical cocrystallisation and reactions of molecular materials. In this case (θ = 90°, speed along v was 8 m s−1), there was no evidence of connective neck formation (Fig. 2(c) and 3(c)), which is suggested to play a role in the molecular transfer process in mechanochemical indentations.36 However, at indentation speeds of 4 m s−1 to 1 m s−1, small short-lived connective necks were observed (Fig. S4 and S5 (ESI†), respectively), further suggesting that surface molecules on the theo surface are less prone to leaving the surface than were observed for indentations of two nanoparticles.36 Full details on the tracking and evaluations of molecular transfer and connective neck analyses are provided in Sections S2 and S3 (ESI†). Additionally, the results described here are clearly shown in the renders of the simulation trajectories supplied in the ESI.†
Reducing the incident angle θ to 75° leads to the formation of small 0.8 nm to 2.0 nm, short-lived (0.05 ns to 2.05 ns) connective necks between the nanoparticle and the slab during the retraction stage (Fig. S6–S9, ESI†). In this case, a connective neck was observed and measured (Table S4, ESI†) for each of the four speeds investigated, which is believed to be a key feature that facilitates molecular transfer during simulated indentations.36 However, the percentage of molecules transferred during the indentation remained comparable to indentations with θ = 90°, suggesting that the formation of a connective neck is not the sole indicator of improved transfer between molecular species. Additionally, there again appears to be little or no disruption to the geometry of the nanoparticle. Further decreasing θ, i.e. when the indentation becomes increasingly indirect, results in a much more pronounced formation of connective necks between the two indenting objects. Additionally, the simulation also reveals a greater degree of disruption to both the theo surface and the cit nanoparticle. This is most evident for indentations conducted at the lowest θ values used in this work (30° and 15°). Snapshots of an indentation with an indentation speed of 8 m s−1 and θ = 30° (Fig. 3(e)–(h))and θ = 15° (Fig. 3(i)–(l)) show the extent of the changes to the simulated indentation process. First, the extent of displacement x applied to the cit nanoparticle is observed to create the initial configurations (Fig. 3(e) and (i)). Again, at the point of maximum indentation, there is a noticeable compression in the distribution of cit molecules (Fig. 3(b) and (f)). In fact, for indentations where θ = 15°, the distribution is compressed by a further ≈5 Å when compared to indentations at 90°. This change is not caused by the increased force during indentation, as the force development analysis reveals a decrease in the maximum force experienced as θ decreases (Section S5, ESI†). Instead, this is due to the cit molecules being dragged across the surface of the slab; therefore, the molecules are being spread out in the xy plane, which can be seen in Fig. 2(j). After being retracted by 25 Å (Fig. 3(g) and (k)), a significant connective neck formed between the two materials in both cases. When θ = 30 Å, the connective neck appears to be formed predominantly by theo molecules (Fig. 2(g)), which is confirmed by molecular distribution analysis (Fig. 3(g)). However, when θ is reduced to 15 Å, the connective neck consists of predominantly cit molecules (Fig. 2 and 3(k)). This change in composition is likely not dependent on the angle and is more likely to be an effect of the initial conditions of each simulation. The transfer of cit molecules (green) to the theo surface (blue) is also visible when θ = 15° (Fig. 3(k)), with molecules of cit deposited upon the theo slab evident upon the separation of the objects (Fig. 3(l)). For the indentation where θ = 30°, a small number of theo and cit molecules were transferred between the two objects (Fig. 3(h)). In the case when θ = 15°, a clear number of cit molecules were deposited on the theo surface. In this case, a total of 45 molecules were transferred during the indentation. While still a low percentage of free molecules (≈1.0%), this is a three-fold increase in molecular transfer when compared to a direct collision. The values of molecular transfer for all simulated indentations (Table 1) show that the number of molecules transferred during indentations between cit and theo is generally low. However, the numbers suggest that decreasing θ improves the transfer process between the particles. Generally, θ values of 15° or 30° result in a greater amount of molecules being transferred during indentation. A more in-depth analysis of the trends in molecular transfer would require multiple, different initial configurations for the cit nanoparticle for each indentation trajectory, i.e. for all indentation speeds and θ, which is beyond the scope of the current work.
| Speed/m s−1 | θ/° | |||||
|---|---|---|---|---|---|---|
| 90 | 75 | 60 | 45 | 30 | 15 | |
| Molecules transferred | ||||||
| 16 | 6 | 8 | 9 | 3 | 12 | 28 |
| 8 | 13 | 3 | 7 | 12 | 18 | 45 |
| 4 | 5 | 1 | 9 | 8 | 14 | 12 |
| 1 | 4 | 8 | 5 | 3 | 4 | 53 |
More noticeable than the cit molecules on the theo surface (Fig. 3(d)), is the significant disruption of the cit nanoparticle as a result of the indentation, which in this case resembles an irregular ovoid rather than a sphere. To measure this disruption, we calculated the change in the sphericity of the particles for each simulated indentation. Sphericity was calculated using Waddel's sphericity index46 (Ψ),
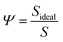 | (1) |
| Speed/m s−1 | θ/° | |||||
|---|---|---|---|---|---|---|
| 90 | 75 | 60 | 45 | 30 | 15 | |
| Δ%Ψ/% | ||||||
| 16 | −1.3 | −1.4 | −1.2 | −1.6 | −3.6 | −4.7 |
| 8 | −1.1 | −1.7 | −1.9 | −2.4 | −2.8 | −5.9 |
| 4 | −2.2 | −1.5 | −2.5 | −1.8 | −4.3 | −3.8 |
| 1 | −1.4 | −0.9 | −4.8 | −1.9 | −3.2 | −8.4 |
Conclusions
This study has focused on the use of theoretical methods to understand the effects of mechanical interactions on the structural disruption and transfer of molecules between organic molecular solids that are known to form a cocrystal by ball milling.31 Classical force field MD was employed to investigate how the angle of incidence and indentation speed play important roles in simulated mechanochemical indentations of a nanoparticle of citric acid on a slab of theophylline, two crystalline molecular solids of pharmaceutical interest. The results indicate that the angle of incidence, ranging from 90° or 75° for more direct indentations to 30° or 15° for more grazing indentations, has a significant and profound effect on the indentation outcome. First, the amount of material transferred between the two materials significantly increased at a lower value of θ. This occurs because a larger number of molecules are in contact with each other for a greater amount of time, increasing the chances of transfer occurring upon retraction. Second, the degree of disruption to the initially spherical nanoparticle is up to four times greater for more grazing angles of incidence when compared to more direct indentations. Reducing the speed of the incident nanoparticles promotes the formation of connective necks between citric acid and theophylline, which elongate as the speed is further reduced. However, this effect did not directly translate into a discernible trend in either molecular transfer or disruption of the nanoparticles. Although experimentally reactions do not necessarily occur at specified angles or speeds, this work suggests that lower angles of incidence between two particles are the most effective in the early stages of a mechanochemical reaction, regardless of their incident speeds. While considerable effort has been focused on the theoretical modelling of mechanochemistry in the context of rearrangements of covalent bonds,26–28 less attention has been dedicated to another aspect of mechanochemistry that typically precedes covalent transformations in organic solids: the mechanically induced rearrangement of molecules and the disruption of the supramolecular structure. We hope that the work presented herein will inspire future studies in this direction, aiming towards an integrated understanding of mechanochemical processes at the molecular and supramolecular levels.Author contributions
M. F.: (invited) conceptualization, investigation, data curation, formal analysis, visualization, writing – original draft, review & editing; T. F.: conceptualization, supervision, resources, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank support from the Leverhulme International Professorship (TF) and the University of Birmingham. Calculations were performed using the University of Birmingham's BlueBEAR HPC service and the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick. Sulis is funded by EPSRC grant EP/T022108/1 and the HPC Midlands+ consortium. We also thank Prof. A. J. Morris for fruitful discussions during the development of this work.Notes and references
-
(a) S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC
; (b) T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., Int. Ed., 2020, 59, 1018–1029 CrossRef PubMed
; (c) A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Front. Chem., 2021, 9, 685789 CrossRef CAS PubMed
.
- T. Seo, N. Toyoshima, K. Kubota and H. Ito, J. Am. Chem. Soc., 2021, 143, 6165–6175 CrossRef CAS PubMed
.
- Y. X. Shi, K. Xu, J. K. Clegg, R. Ganguly, H. Hirao, T. Friščić and F. García, Angew. Chem., Int. Ed., 2016, 55, 12736–12740 CrossRef CAS PubMed
.
-
(a) H. M. Titi, J.-L. Do, A. J. Howarth, K. Nagapudi and T. Friščić, Chem. Sci., 2020, 11, 7578–7584 RSC
; (b) L. Gonnet, C. B. Lennox, J.-L. Do, I. Malvestiti, S. G. Koenig, K. Nagapudi and T. Friščić, Angew. Chem., Int. Ed., 2022, 61, e202115030 CrossRef CAS
.
- D. E. Crawford and J. Casaban, Adv. Mater., 2016, 28, 5747–5754 CrossRef CAS
.
- D. Hasa and W. Jones, Adv. Drug Delivery Rev., 2017, 117, 147–161 CrossRef CAS PubMed
.
- C. Medina, D. Daurio, K. Nagapudi and F. Alvarez-Nunez, J. Pharm. Sci., 2010, 99, 1693–1696 CrossRef CAS PubMed
.
- K. Nagapudi, E. Y. Umanzor and C. Masui, Int. J. Pharm., 2017, 521, 337–345 CrossRef CAS PubMed
.
-
(a) D. Braga, S. L. Giaffreda, F. Grepioni, M. R. Chierotti, R. Gobetto, G. Palladino and M. Polito, CrystEngComm, 2007, 9, 879–881 RSC
; (b) D. Braga, F. Grepioni, L. Maini, S. Prosperi, R. Gobetto and M. R. Chierotti, Chem. Commun., 2010, 46, 7715–7717 RSC
; (c) M. J. Cliffe, C. Mottillo, R. S. Stein, D.-K. Bučar and T. Friščić, Chem. Sci., 2012, 3, 2495–2500 RSC
.
- A. J. Stirk, F. E. S. Souza, J. Gerster, F. M. Mir, A. Karadeolian and A. W. Rey, Green Chem., 2022, 24, 1505–1514 RSC
.
- P. Lavalle, F. Boulmedais, P. Schaaf and L. Jierry, Langmuir, 2016, 32, 7265–7276 CrossRef CAS PubMed
.
- J. B. Kelber, A. Bensalah-Ledoux, S. Zahouani, B. Baguenard, P. Schaaf, A. Chaumont, S. Guy and L. Jierry, Angew. Chem., Int. Ed., 2020, 59, 23283–23290 CrossRef CAS PubMed
.
-
A. A. L. Michalchuk, in Mechanochemistry and emerging technologies for sustainable chemical manufacturing, ed. E. Colacino and F. Garcia, CRC Press, London, England, 2023, ch. 3, pp. 60–83 Search PubMed
.
- I. Halasz, S. A. J. Kimber, P. J. Beldon, A. M. Belenguer, F. Adams, V. Honkimäki, R. C. Nightingale, R. E. Dinnebier and T. Friščić, Nat. Protoc., 2013, 8, 1718–1729 CrossRef PubMed
.
- D. Gracin, V. Štrukil, T. Friščić, I. Halasz and K. Užarević, Angew. Chem., Int. Ed., 2014, 53, 6193–6197 CrossRef CAS
.
- L. Batzdorf, F. Fischer, M. Wilke, K.-J. Wenzel and F. Emmerling, Angew. Chem., Int. Ed., 2015, 54, 1799–1802 CrossRef CAS PubMed
.
- P. F. M. de Oliveira, A. A. L. Michalchuk, A. G. Buzanich, R. Bienert, R. M. Torresi, P. H. C. Camargo and F. Emmerling, Chem. Commun., 2020, 56, 10329–10332 RSC
.
- P. A. Julien, M. Arhangelskis, L. S. Germann, M. Etter, R. E. Dinnebier, A. J. Morris and T. Friščić, Chem. Sci., 2023, 14, 12121–12132 RSC
.
- J. G. Schiffmann, F. Emmerling, I. C. Martins and L. Van Wüllen, Solid State Nucl. Magn. Reson., 2020, 109, 101687 CrossRef CAS PubMed
.
- C. Leroy, S. Mittelette, G. Félix, N. Fabregue, J. Špačková, P. Gaveau, T.-X. Métro and D. Laurencin, Chem. Sci., 2022, 13, 6328–6334 RSC
.
- P. Chattopadhyay, I. Manna, S. Talapatra and S. Pabi, Mater. Chem. Phys., 2001, 68, 85–94 CrossRef CAS
.
- M. Broseghini, M. D'Incau, L. Gelisio, N. Pugno and P. Scardi, Mater. Des., 2016, 110, 365–374 CrossRef CAS
.
- L. Yang, A. Moores, T. Friščić and N. Provatas, ACS Appl. Nano Mater., 2021, 4, 1886–1897 CrossRef CAS
.
- M. Carta, F. Delogu and A. Porcheddu, Phys. Chem. Chem. Phys., 2021, 23, 14178–14194 RSC
.
- M. Carta, L. Vugrin, G. Miletić, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Angew. Chem., Int. Ed., 2023, 62, e202308046 CrossRef CAS PubMed
.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed
.
- Y. S. Zholdassov, L. Yuan, S. R. Garcia, R. W. Kwok, A. Boscoboinik, D. J. Valles, M. Marianski, A. Martini, R. W. Carpick and A. B. Braunschweig, Science, 2023, 380, 1053–1058 CrossRef CAS PubMed
.
- A. A. L. Michalchuk, Faraday Discuss., 2023, 241, 230–249 RSC
.
-
(a) K. Mohammadtabar, S. J. Eder, N. Dörr and A. Martini, Tribol. Int., 2022, 176, 107922 CrossRef CAS
; (b) F. H. Bhuiyan, S. H. Kim and A. Martini, Appl. Surf. Sci., 2022, 591, 153209 CrossRef CAS
.
- M. Ferguson, M. S. Moyano, G. A. Tribello, D. E. Crawford, E. M. Bringa, S. L. James, J. Kohanoff and M. G. Del Pópolo, Chem. Sci., 2019, 10, 2924–2929 RSC
.
- S. Karki, T. Friščić, W. Jones and W. D. S. Motherwell, Mol. Pharmaceutics, 2007, 4, 347–354 CrossRef CAS PubMed
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
-
(a) W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed
; (b) W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS
.
- J. E. Lennard-Jones, Proc. Phys. Soc., 1931, 43, 461 CrossRef CAS
.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS
.
-
R. Hockney and J. Eastwood, Computer Simulation Using Particles, Taylor & Francis, New York, 1998 Search PubMed
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 CrossRef CAS
.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed
.
- J. P. Glusker, J. A. Minkin and A. L. Patterson, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 1969, 25, 1066–1072 CrossRef CAS PubMed
.
- Y. Ebisuzaki, P. D. Boyle and J. A. Smith, Acta Crystallogr., Sect. C: Struct., Chem., 1997, 53, 777–779 CrossRef
.
- U. Landman, W. Luedtke and E. M. Ringer, Wear, 1992, 153, 3–30 CrossRef CAS
.
- F. Delogu, M. Monagheddu, G. Mulas, L. Schiffini and G. Cocco, J. Non-Cryst. Solids, 1998, 232–234, 383–389 CrossRef CAS
.
- K. Linberg, P. Szymoniak, A. Schönhals, F. Emmerling and A. A. L. Michalchuk, Chem. – Eur. J., 2023, e202302150 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed
.
-
J. E. Stone, MSc thesis, University of Missouri-Rolla, MO, USA, 1996
.
- H. Wadell, J. Geol., 1932, 40, 443–451 CrossRef
.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of computational strategies, molecular transfer, connective neck, sphericity, and force development analyses. Additionally, 24 movies are supplied, one for each of the simulated indentations presented herein as well as sample input files to run a LAMMPS simulation of the system. See DOI: https://doi.org/10.1039/d3cp05475f |
| ‡ All simulation snapshots presented herein were visualised with VMD v1.9.4a5544 and rendered with Tachyon, v0.99.45 All atomic positions have been unwrapped from the periodic boundary conditions, and hydrogen atoms are rendered in white throughout for visualisation purposes. |
| This journal is © the Owner Societies 2024 |