Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling the activity trend of the hydrogen oxidation reaction under constant potential conditions†
Wenhui
Ling
,
Jian
Liu
 and
Bo
Yang
and
Bo
Yang
 *
*
School of Physical Science and Technology, ShanghaiTech University, 393 Middle Huaxia Road, Shanghai 201210, China. E-mail: yangbo1@shanghaitech.edu.cn
First published on 13th August 2024
Abstract
A microkinetic model is constructed for the electrocatalytic alkaline hydrogen oxidation reaction based on grand canonical density functional theory calculations and linear relationships with the adsorption energies of hydrogen and hydroxide as descriptors. Using this model, the activity trend suitable for efficient catalyst screening has been identified.
The continuous combustion of fossil fuels has led to significant detrimental impacts on the environment, encompassing the release of greenhouse gases and the exacerbation of air pollution. Consequently, there has been a pressing need for humanity to actively seek cleaner and more efficient methods for energy conversion.1 In this context, hydrogen fuel cell technology has emerged as a highly promising solution for the generation of clean and renewable energy.2–4 Within this field, alkaline polymer electrolyte fuel cells have gained considerable prominence owing to their capacity for economically viable operation under mild alkaline conditions, thereby propelling the advancement of clean energy production.5–7
Notwithstanding the considerable potential of hydrogen fuel cell technology, it continues to confront a range of obstacles in its advancement. Of particular significance is the hydrogen oxidation reaction (HOR), which serves as the pivotal anodic reaction, exerting a substantial influence on the effectiveness and sustainability of energy conversion. However, when operating under alkaline conditions, the kinetics of the HOR becomes considerably constrained at the anode interface.6,8,9 Consequently, acquiring a more profound comprehension of the kinetic characteristics of the alkaline HOR and establishing appropriate catalyst design strategies assume utmost importance in advancing the practical applications of this technology.
At present, there exist several perspectives regarding the pH-dependent nature of the HOR,10–14 but achieving a consensus remains challenging. Early studies suggested a correlation between the activity and hydrogen binding energy (HBE) over the catalysts under acidic conditions.15–18 Certain researchers have put forth a volcano-shaped relationship between exchange current density and HBE,19,20 positing HBE as the exclusive descriptor for catalytic activity in both the hydrogen evolution reaction (HER) and the HOR under acidic conditions.
Recent studies increasingly suggested that catalyst surfaces may not only host hydrogen adsorption but also hydroxyl adsorption.17,21–23 For instance, Koper and co-workers22 elucidated the presence of adsorbed hydroxide ions (OH*) within the conventional hydrogen underpotential deposition (HUPD) desorption potential range by quantifying the charge transfer per Pt atom on Pt(110) and assessing the onset potential for CO detachment from Pt(776). Consequently, hydroxyl binding energy (OHBE) is also considered as a descriptor for describing the kinetics of alkaline HER/HOR.
In light of the above, we employed the grand canonical density functional theory (GC-DFT) ensemble to simulate the reactions under constant potentials and established a microkinetic model that could be used for calculating reaction rates of the HOR. By employing this approach, a three-dimensional activity map can be constructed, correlating catalytic activity with descriptors, i.e., HBE and OHBE.
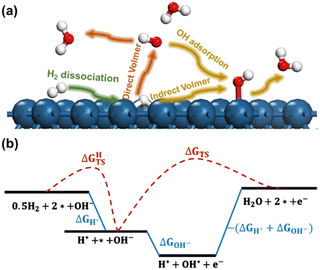
The reaction processes considered in the current work are presented in Fig. 1a. In the initial stage, known as the Tafel step, molecular hydrogen undergoes dissociation over the metal electrodes, leading to the formation of adsorbed hydrogen atoms (H*). We considered that the subsequent Volmer step involves two distinct reaction pathways. The first pathway is referred to as the Direct Volmer step, where H* reacts directly with hydroxyl ions in the solution (OH−). The second pathway is the Indirect Volmer step, in which OH− firstly adsorbs onto the surface forming the adsorbed OH* species, then the H* and OH* species on the surface combine to produce water molecules. This delineates the reaction process into two distinct pathways: Tafel-Direct Volmer and Tafel-Indirect Volmer. These steps are summarized as follows:
(i) Tafel: H2 dissociation.
| 0.5H2 + * → H* |
| H* + OH− → H2O + e− + * |
| H* + OH* → H2O + 2* |
A schematic free energy diagram depicting the above three steps is illustrated in Fig. 1b. The activation free energy and reaction free energy of the Tafel step are represented as ΔGHTS and ΔGH*, respectively. Then the activation free energy of the Direct Volmer process is denoted as ΔGTS. The adsorption free energy of OH− in the Indirect Volmer process is expressed as ΔGOH−. The activation free energy of the subsequent formation of H2O in the Indirect Volmer process is approximated as −(ΔGH* + ΔGOH−), as suggested in the literature.24
It should be noted that the Direct Volmer step involves electron transfer, indicating that its activation energy is associated with the electrode potential. Therefore, calculation of the activation energy for the Volmer process at acceptable computational efficiencies poses significant challenges. To address this issue, the GC-DFT method was employed through dynamically adjusting the electron numbers of the reacting system, allowing for the maintenance of a constant electrochemical potential throughout the simulations.
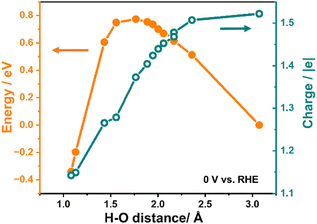
Fig. 2 illustrates the variation in system energy and the relative charge during the simulation of the Direct Volmer step on Pt(111) as an example, under the condition of a constant electrode potential of 0 V relative to the reversible hydrogen electrode (RHE). The initial state of the reaction involves H* and OH− in the solution, with an approximate H–O distance of 3 Å, while the final state depicts the formation of water molecules, with the H–O distance reduced to approximately 1 Å.
As presented in Fig. 2, it is evident that the energy of the system experiences an initial increase followed by a decrease while shortening the H–O distance, where H represents the adsorbed hydrogen atom, and O represents the oxygen atom in OH−, giving rise to an energy barrier of 0.77 eV for the Direct Volmer step over Pt(111). Throughout this process, the system is charged during simulations to maintain the electrode potential. The variation in the charge number of this system is also presented in Fig. 2. A notable observation in this figure is the continuous decrease in the charge number throughout the entire reaction process. This suggests that, as the reaction progresses, the electrode potential can remain constant without the addition of the same quantity of electrons as in the initial state, indicating the migration of electrons from OH− to the surface. This change in the charge number is essential to maintain a constant electrode potential until the reaction is complete. It is also noteworthy that at the transition state of this step (at a H–O distance of approximately 1.77 Å), the change in the charge number is around 0.15 |e| compared to the initial state, constituting 0.4 of the change in the charge number for the entire process from the initial state to the final state. This observation reveals dynamic changes in electron transfer during the Direct Volmer step, providing substantial insights into understanding the reaction mechanism.
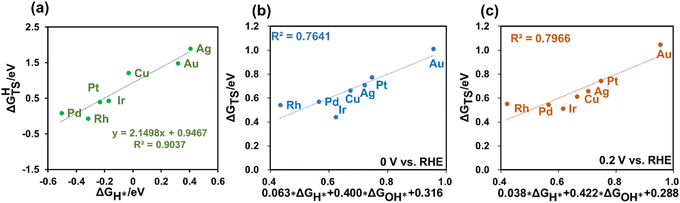
Given that H2 dissociation is a non-electrochemical step, DFT calculations were employed to calculate ΔGHTS and ΔGH*. Furthermore, our findings revealed a linear relationship between ΔGHTS and ΔGH* on different metals, as depicted in Fig. 3(a). This suggests the potential to express the barriers for H2 dissociation as a function of HBE, enabling the fast prediction of H2 dissociation barriers over diverse metal surfaces.
Using the GC-DFT method, we calculated the activation energies for the Direct Volmer step (ΔGTS) over Cu(111), Ag(111), Au(111) Pt(111), Ir(111), Pd(111) and Rh(111) at 0 V and 0.2 V vs. RHE. We employed the equation H2O + * → OH* + 0.5H2 to calculate OH adsorption energy (ΔGOH*), which is independent of the electrode potential. Furthermore, we established a relationship between ΔGOH* and ΔGOH− as introduced in the ESI.†Fig. 3(b and c) also revealed linear relationships between the activation free energies and H adsorption energies as well as OH adsorption energies at these two electrode potentials of interest. This outcome holds great promise, as it eliminates the need to calculate the activation energies for the Direct Volmer step on each catalyst surface at every electrode potential. Instead, by establishing a linear relationship, predictions for the activation energies can be made, significantly improving the computational efficiency.
When each of the three different elementary steps is considered as the rate-determining step (RDS), it leads to the derivation of three distinct rate equations, assuming that the other reactions in the process are quasi-equilibrated. Subsequently, the true reaction rate can be estimated with min(ri, max(rii, riii)), considering that the second and third steps are competing in the system. Similar methods have been introduced in our recent studies.25–28 For further details, please refer to the ESI.†
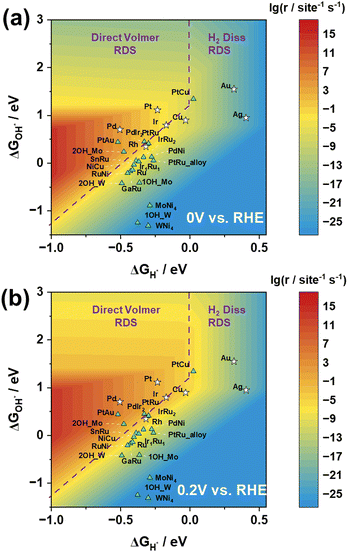
Based on the reaction rate expressions, we have successfully established a functional relationship between the reaction rate of the HOR and the adsorption energies of H and OH. As shown in Fig. 4(a), the logarithmic values of the reaction rate at 0 V vs. RHE exhibit a prominent volcano-shaped relationship with H adsorption energy and OH adsorption energy.
In the three-dimensional activity map, the activity characteristics of all pure metals, with the exception of Pd, correspond to experimental measurements, in the order of Pt > Ir > Cu and Au > Ag.29 However, it is important to note that experimental reports have indicated that metal Pd has the ability to store lattice hydrogen.30–33 Researchers believe that its reaction mechanism is not simply based on surface hydrogen and hydroxyl species, but involves H migration into the Pd lattice, followed by detachment from the lattice to react on the surface.30 This may explain why, in the experimental observations, the surface activity of Pd is inferior to that of Pt, but in the graph, Pd exhibits the best activity performance.
Moreover, as depicted in Fig. 4, the positioning of the catalysts in the three-dimensional volcano activity plot yields valuable insights into the RDS for different catalysts. The relationship between the reaction rate and H adsorption energy, along with its reliance on OH adsorption energy, naturally delineates distinct regions, each corresponding to a different RDS. Notably, our analysis of the location of Pt suggests that the Direct Volmer step governs the RDS in the HOR, which is consistent with previous research results.18
In order to validate the applicability of the three-dimensional volcano plot for screening other catalysts, we conducted calculations on the H and OH adsorption energies of 15 alloy catalysts. Our analysis distinctly reveals that by adjusting the types and proportions of catalysts, and subsequently fine-tuning the H adsorption energy and OH adsorption energy, the catalytic performance can be progressively enhanced, leading to discernible catalyst screening effects. This approach offers robust support for achieving superior catalytic performance through the careful selection of catalyst types and proportions. Fig. 4 potentially illustrates the trends in catalytic performance variations among different alloy catalysts.
The computational results for the MoNi4 and WNi4 catalysts may not be optimal, as they fail to reach the high-activity region despite demonstrating excellent catalytic performance in experiments. However, upon closer examination of the results for MoNi4 and WNi4, it was observed that the Mo and W sites on these catalysts exhibit significantly strong OH adsorption energies. In essence, during reactions with clean Mo/WNi4 catalysts, OH strongly adsorbs to the Mo/W sites, leading to an excessively high overall OH adsorption energy, making the desorption difficult and positioning them below the three-dimensional volcano activity plot. Nonetheless, when occupying a single Mo/W site, the OH adsorption energy weakens, resulting in an overall upward shift. Furthermore, when both Mo/W sites on the surface are occupied by OH, causing the reaction to occur only at other Ni sites, they demonstrate an appropriate OH adsorption energy, thus approaching the high-activity region more closely (Fig. S3, ESI†). Similarly, PtRu is also the case.
When considering the impact of electrode potential on the active region, Fig. 4(b) illustrates the volcano plot at 0.2 V vs. RHE. Notably, under the 0.2 V vs. RHE condition, the reaction rate is significantly higher than that under the 0 V vs. RHE condition, as observed by enlarging the red region in the graph. Despite certain variations in the active region under these two electrode potential conditions, the positions of the activity trends for both pure metal and alloy catalysts consistently align with experimental observations. This suggests that the transition from 0 V to 0.2 V (vs. RHE) in electrode potential does not result in a significant change in the RDS, validating the notion that an increase in potential leads to an elevation in reaction rates. This outcome underscores the influence of electrode potential modulation on catalytic activity, providing crucial experimental support for theoretical investigations.
In summary, through microkinetic simulations of the HOR pathway under alkaline conditions, we initially established two fundamental descriptors, the adsorption energy of H and OH. Subsequently, by establishing linear relationships between the activation energy of the primary reaction steps and these descriptors, we predicted the activation energy barriers. The construction of a three-dimensional volcano plot using microkinetic rate equations vividly illustrates the activity trends of pure metals and alloy catalysts. This enables the efficient screening of highly active catalysts for alkaline hydrogen oxidation, not only enhancing computational efficiency but also conserving computational resources.
This work was financially supported by the National Natural Science Foundation of China (21991152, 21991150, 22322302) and the National Key Research and Development Program of China (2022YFA1503804). We thank the HPC Platform of ShanghaiTech University for computing time.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Notes and references
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- L. Zhang, Q. Chang, H. Chen and M. Shao, Nano Energy, 2016, 29, 198–219 CrossRef CAS.
- S. Fukuzumi, Joule, 2017, 1, 689–738 CrossRef CAS.
- P. Wang, Q. Shao and X. Huang, Joule, 2018, 2, 2514–2516 CrossRef.
- S. Guo and E. Wang, Nano Today, 2011, 6, 240–264 CrossRef CAS.
- M. Zhou, H.-L. Wang and S. Guo, Chem. Soc. Rev., 2016, 45, 1273–1307 RSC.
- H. A. Miller, A. Lavacchi, F. Vizza, M. Marelli, F. Di Benedetto, F. D'Acapito, Y. Paska, M. Page and D. R. Dekel, Angew. Chem., Int. Ed., 2016, 55, 6004–6007 CrossRef CAS PubMed.
- J. Durst, A. Siebel, C. Simon, F. Hasché, J. Herranz and H. A. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260 RSC.
- K. Elbert, J. Hu, Z. Ma, Y. Zhang, G. Chen, W. An, P. Liu, H. S. Isaacs, R. R. Adzic and J. X. Wang, ACS Catal., 2015, 5, 6764–6772 CrossRef CAS.
- K. Zhao, X. Chang, H.-S. Su, Y. Nie, Q. Lu and B. Xu, Angew. Chem., Int. Ed., 2022, 61, e202207197 CrossRef CAS PubMed.
- S. Trasatti, J. Electroanal. Chem. Inter. Electrochem., 1972, 39, 163–184 CrossRef CAS.
- G. Wang, J. Parrondo, C. He, Y. Li and V. Ramani, J. Electrochem. Soc., 2017, 164, F1307 CrossRef CAS.
- P. Li, Y. Jiang, Y. Hu, Y. Men, Y. Liu, W. Cai and S. Chen, Nat. Catal., 2022, 5, 900–911 CrossRef CAS.
- L. Su, J. Chen, F. Yang, P. Li, Y. Jin, W. Luo and S. Chen, J. Am. Chem. Soc., 2023, 145, 12051–12058 CrossRef CAS PubMed.
- Z. Feng, L. Li, X. Zheng, J. Li, N. Yang, W. Ding and Z. Wei, J. Phys. Chem. C, 2019, 123, 23931–23939 CrossRef CAS.
- G. Zhao, L. Xia, P. Cui, Y. Qian, Y. Jiang, Y. Zhao, H. Pan, S. X. Dou and W. Sun, Nano Lett., 2021, 21, 4845–4852 CrossRef CAS PubMed.
- J. Li, S. Ghoshal, M. K. Bates, T. E. Miller, V. Davies, E. Stavitski, K. Attenkofer, S. Mukerjee, Z.-F. Ma and Q. Jia, Angew. Chem., Int. Ed., 2017, 56, 15594–15598 CrossRef CAS PubMed.
- L. Liu, Y. Liu and C. Liu, J. Am. Chem. Soc., 2020, 142, 4985–4989 CrossRef CAS PubMed.
- W. Sheng, M. Myint, J. G. Chen and Y. Yan, Energy Environ. Sci., 2013, 6, 1509–1512 RSC.
- T. T. Yang, R. B. Patil, J. R. McKone and W. A. Saidi, Catal. Sci. Technol., 2021, 11, 6832–6838 RSC.
- M. J. S. Farias, C. Busó-Rogero, R. Gisbert, E. Herrero and J. M. Feliu, J. Phys. Chem. C, 2014, 118, 1925–1934 CrossRef CAS.
- M. J. T. C. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. M. Koper, Catal. Today, 2013, 202, 105–113 CrossRef CAS.
- D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. van der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2013, 5, 300–306 CrossRef CAS PubMed.
- I. T. McCrum and M. T. M. Koper, Nat. Energy, 2020, 5, 891–899 CrossRef CAS.
- H. Liu, J. Liu and B. Yang, Phys. Chem. Chem. Phys., 2019, 21, 9876–9882 RSC.
- H. Liu, J. Liu and B. Yang, Phys. Chem. Chem. Phys., 2020, 22, 9600–9606 RSC.
- H. Liu and B. Yang, Chem. Commun., 2022, 58, 709–712 RSC.
- J. Li, H. Liu, J. Liu and B. Yang, Mater. Today Chem., 2023, 29, 101461 CrossRef CAS.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdóttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 22374 CrossRef.
- X. Song, X.-G. Zhang, Y.-L. Deng, Z.-A. Nan, W. Song, Y. Wang, L. Lü, Q. Jiang, X. Jin, Y. Zheng, M. Chen, Z. Xie, J.-F. Li, Z.-Q. Tian and F. R. Fan, J. Am. Chem. Soc., 2023, 145, 12717–12725 CrossRef CAS PubMed.
- G. Liu, W. Zhou, Y. Ji, B. Chen, G. Fu, Q. Yun, S. Chen, Y. Lin, P.-F. Yin, X. Cui, J. Liu, F. Meng, Q. Zhang, L. Song, L. Gu and H. Zhang, J. Am. Chem. Soc., 2021, 143, 11262–11270 CrossRef CAS PubMed.
- N. J. J. Johnson, B. Lam, B. P. MacLeod, R. S. Sherbo, M. Moreno-Gonzalez, D. K. Fork and C. P. Berlinguette, Nat. Mater., 2019, 18, 454–458 CrossRef CAS PubMed.
- T. Zhao, M. Li, D. Xiao, X. Yang, L. An, Z. Deng, T. Shen, M. Gong, Y. Chen, H. Liu, L. Feng, X. Yang, L. Li and D. Wang, Angew. Chem., Int. Ed., 2024, 63, e202315148 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc01825g |
| This journal is © The Royal Society of Chemistry 2024 |