Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular properties controlling chirality transfer to halide perovskite: computational insights†
Aaron
Forde
 *ab,
Amanda C.
Evans
*ab,
Amanda C.
Evans
 c,
Wanyi
Nie
c,
Wanyi
Nie
 d,
Sergei
Tretiak
d,
Sergei
Tretiak
 ad and
Amanda J.
Neukirch
ad and
Amanda J.
Neukirch
 *a
*a
aTheoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: aforde@lanl.gov; ajneukirch@lanl.gov
bCenter for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
cMaterials Science and Technology Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
dCenter for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
First published on 22nd August 2023
Abstract
Interfacing chiral molecules with achiral semiconductor nanomaterials has been shown to induce chiroptical (i.e., preferential absorption of circularly polarized light) signatures. This chirality transfer phenomena is attractive for enhancing the functionality of nanomaterials by making them sensitive to the circular polarization states of photons, and attractive for selective optical sensing applications. Chirality transfer via interfacing chiral molecules with nanomaterial surfaces generally gives small sensitivities as determined by anisotropy factors, the ratio of polarized and linear absorption. Here we use atomistic time-dependent density functional theory simulations to investigate the molecular properties which influence the chiroptical signatures of a lead-halide perovskite cluster. First, we find that for chiral molecules that contain aryl groups, such as (R/S)-methylbenzylamine and (R/S)-methylphenyl acetic acid, modulating their molecular dipole via meso functionalization with strong withdrawing groups, such as NO2, can enhance intensities of chiroptical signatures. Second, using the lactic acid series ((S)-lactic, (S)-malic, and (S,S) tartaric acid) we average over conformations of these molecules on the cluster surface. We find that limited conformational flexibility of lactic acid provides the largest chiroptical intensities while signal from tartaric acid quenches after conformational average. These results demonstrate an importance of chemical functionalization leading to a polarized chiral system. Altogether, either through acid–base equilibrium or strategic functionalization, and limited conformationally degrees of freedom are important for obtaining high-intensity nanomaterial chiroptical signatures through chirality transfer.
Introduction
Chiroptical signatures have fundamental and applied applications. This is realized for small molecules where spectroscopy methods, such as electronic and vibronic circular dichroism, can be used to assign absolute molecular configurations. Crystalline materials show chiroptical signatures when crystallizing in symmetry breaking crystal groups1,2 or when the chirality is induced (i.e., chirality transfer) from the semiconductors environment.3,4 Chiroptical signatures can also emerge when an achiral material is placed within an applied magnetic field5 or under applied stress.6 For applications related to optical sensing an important device parameter is the so-called anisotropy factor which is the ratio of circularly polarized absorption and linear absorption. The anisotropy factor sets the upper-bound on the ability for a material to reliably distinguish between circular polarization states of photons in linear spectroscopy.An attractive strategy for inducing chiroptical signatures into semiconductor nanomaterials is using chiral organic molecules as surface passivation ligands on semiconductor nanomaterial surfaces.3,7–10 The field of surface chemistry, specifically regarding colloidal stability11–13 and surface composition14,15 has undergone significant advancements and is now highly developed. Using chiral molecules would allow new materials to be synthesized and processed using established methods, but they are expected to provide enhanced optical functionality. An example of this is using the nanomaterials sensitivity of photon circular polarization to construct a quantum dot based spin bit device.16 Many studies focused primarily on binding chiral amino acids to semiconductor nanomaterials, such as (X)- penicillamine,7 (X)-cystine8,17–19 and (X)-glutathione,3 or other types of amines or ammoniums, such as (X,X), diaminocyclohexane,20 (X)-methylbenzylammonium,10 and (X)-octylbutylammonium where X = R,S denoting molecular chirality.10 Chiral carboxylic acids have been also been explored with quantum dots that exhibit excess metal on the surface that their conjugate bases, such as lactate, malate, and tartartate, can bind to.21 For chirality induction through chiral molecules on 0D quantum dot/nanocrystal surfaces the reported anisotropy factors are relatively low, on the order of 10−5–10−3.21 This motivates the exploration of design principles for how to enhance anisotropy spectra in semiconductor quantum dot systems.
There have been three conjectures as to the mechanism of chirality transfer between a semiconductor nanomaterial and a chiral molecule. One possible explanation is that templating a surface with chiral molecules introduces forces which coherently alter the structures.22,23 Charge transfer excitations have also been observed to result in emergent CD spectra between molecular dimers, so that hybridized semiconductor – chiral molecule excitations are also possible.24 Dipole interactions between semiconductor and chiral molecules has also been shown to result in emergent CD spectra with the orientation of the dipole field dictating preference of polarization in optical absorption.25 Our previous work has shown the chirality transfer mechanism is primarily due to the dipole interaction26 which has also been used to explain emergent circular dichroism in polymer blends.27 This motivates the investigation of structure–property relationships for these chiral molecular dipole induced chiroptical signatures. The contribution and manipulation of surface chemistry in relation to the impact of chirality-transfer induced circular dichroism is an aspect that has not been thoroughly explored.
Chemical modifications of the molecular ligand can enhance the optical properties of the quantum dot. Functionalizing with withdrawing groups is expected to increase the molecular dipole which can couple to the quantum dot and enhance optical features.28 Another aspect that has not appeared to be explored is the role of molecular conformations on the surface of the nanomaterial. For isolated molecules, such as in dilute solutions, it is well established that the circular dichroism is sensitive to changes in conformations and an averaging procedure is needed to accurately predict circular dichroism spectra from ab initio methods.29 Previous studies have noticed a binding configuration effect where there was a noticeable distinction between semiconductor CD when the molecule is in a different absolute configuration.17,26
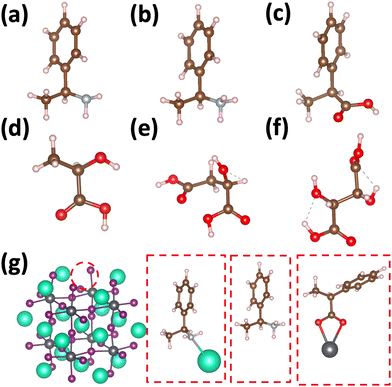
Using atomistic time-dependent density functional theory (TD-DFT) simulations, here we set out to explore two scenarios: (i) how chemical modifications and (ii) molecular conformations of the chiral molecule on the surface of a nanomaterial impact the resultant circular dichroism and anisotropy spectra from a halide perovskite nanomaterial (i.e. chirality transfer). For (i) chemical modification we initially explore a chiral methyl-aryl tetrahedrally coordinated carbon with either amine, ammonium and carboxylic acid functional groups. Here we provide a comment on chemical notation. To highlight the charge of the chemical species bound to the perovskite cluster we explicitly place a charged symbol on cation and anion moieties. When discussing the role of aryl functionalization at the meso location on increasing the polarization of the chiral molecule we will refer to as an added character to the end of the common molecular name, so instead of using the cumbersome (R)-4-chloro-methylbenylammonium naming convention we use (R)-MBAmm+-Cl. In Fig. 1 we show (a) (R)-methylbenzyl amine (MBA-H), (b) (R)-methylbenzyl ammonium (MBAmm+-H) cation, and (c) (R)-methylphenyl acetate (MPAc−-H) anion, to bind to the perovskite surface. We then test how substituting the meso position of the aryl groups with electron donating and withdrawing groups, such as hydroxy (OH) and nitro (NO2) groups, alter the chirality induction effect with the expectation that the stronger ground-state dipole of electron withdrawing groups induces higher intensity CD peaks. We find that when comparing the chirality transfer induced circular dichroism of (R)-MBA-H, (R)-MBAmm+-H, and (R)-MPAc−-H to a CsPbI3 cluster that (R)-MPAc−-H gives the largest CD peaks and anisotropy intensities. Modifying the meso position of the aryl groups for this set of chiral molecules with electron donating OH or electron withdrawing Cl ions, the circular dichroism remains unchanged. In contrast, functionalizing with NO2 results in larger CD intensities for all models, particularly most pronounced for (R)-MBA-NO2. We interpret this as a trade-off between charged molecules and their polarizability. The charged anionic (R)-MPAc−-H and (R)-MBAmm+-H surface ligand provides greater polarization of the perovskite cluster compared to the neutral (R)-MBA-H. However, the (R)-MBA-H molecule is more polarizable than (R)-MPAc−-Hand (R)-MBAmm+-H and, consequently, shows greater enhancement in CD peak intensities with aryl substitution of withdrawing NO2 groups.
To address (ii) exploring the influence of conformational degrees of freedom of chiral molecules on the surface, we use the molecules from the lactic acid series Fig. 1(d) (S)-lactic, (e) (S)-malic, and (f) (S,S) tartaric acids. Experimentally, it is observed that these molecules show relatively large anisotropies for their lowest optical band at approximately 10−2.30 An increase of molecular size lead to a concomitant increase of molecular conformational degrees of freedom. As such, (S)-malic and (S,S)-tartaric ligands adapt three principle conformations of trans, gaunche(−), and gaunche(+). When averaging over conformations of these molecules on the surface, we find (L)-lactic acid provides comparable circular dichroism and anisotropy intensities as (R)-MPAc−, while the effect drastically decreases when going to (S)-malic and (S,S) tartaric acids. We attribute this to chiroptically ‘dark’ conformers which are stabilized by the surface. Overall, this work provides modeling insight into molecular properties and degrees of freedom which impact the intensity of emergent CD from the perovskite quantum dots through chirality transfer. Namely, charged and polarizable molecular ligands provide enhanced chirality transfer and conformationally simple molecules are likely to provide more stable CD spectra due to the limited influence of chiroptically ‘dark’ conformations, which can be stabilized by the surface.
Results
(i) Considered structures
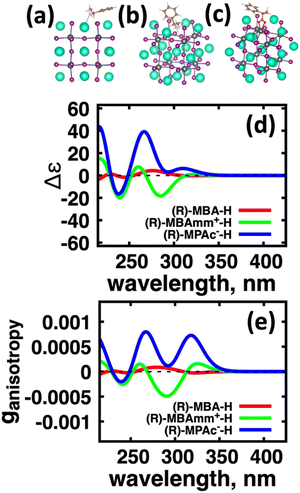
Fig. 1 shows the structures of the chiral molecules (a) (R)-methylbenzylamine ((R)-MBA-H), (b) (R)-methylbenzylammonium ((R)-MBAmm+), (c) (R)-methylphenyl acetic acid ((R)-MPAc−-H), (d) (S)-lactic acid, (e) (S)-malic acid, and (f) (S,S)-tartaric acid are taken from PubMed databases. The CsPbI3 perovskite models are generated by carving clusters from cubic bulk crystal. The most minimalistic symmetric cluster gives a Cs–I terminated (100) surface with stoichiometry of Cs19Pb8I36 and an overall charge of −1. Fig. 1(g) illustrates the binding site of chiral molecules to the perovskite surface. The chiral molecules are bound to the surface as a chemical moiety that has overall +1 charge, as either neutral (R)-MBA-H bound to Cs+, a ammonium cation (R)-MBAmm+-H, or a Pb2+(COOR)− compound which corresponds to a deprotonated (R)-MPAc−, (S)-lactate, (S)-malate, or (S,S)-tartate. We explore excess Pb2+ on the surface of LHP nanocrystals as it has been shown to be a prevalent defect for as-synthesized31 LHP nanocrystals which introduces shallow-defect states.32,33When binding (R)-MBA-H, (R)-MBAmm+-H, and (R)-MPAc−-H we neglect conformer averaging due to the conformation simplicity of these molecules, noting that (R)-MBAmm+-H shows no change in CD spectra when rotated on the cluster surface (as discussed later in text). From the optimized structures we substitute electron withdrawing groups, such as NO2 and Cl, and donating groups OH at the meso position of the aryl group and keep the nuclear coordinates frozen, but allowing the donating/withdrawing groups to optimize.
When binding the lactic acid series to the perovskite cluster surface we account for a distribution of initial conditions based on the trans, gaunche(−), and gaunche(+) conformers for (S)-malic and (S,S)-tartaric acid. For (S)-malic acid we consider six distinct initial conditions while for (S,S)-tartaric acid we model 3 distinct initial conditions. For the conformationally simpler (S)-lactic acid we consider 3 various initial conditions based on rotation about the chiral center. The optimized structures do not necessarily reflect the initial conditions and are characterized by the dihedral angle between the carboxylic acid groups.
(ii) Chemical modifications
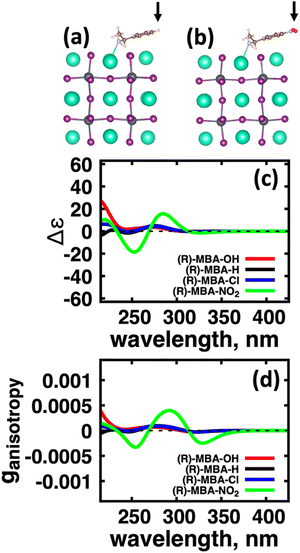
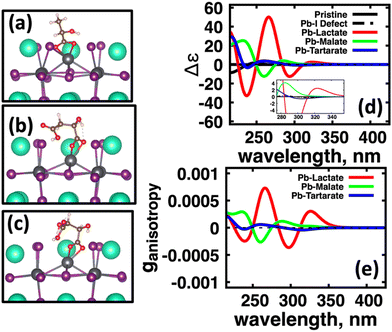
We first explore the chirality transfer properties based on binding different functional groups to a CsPbI3 halide perovskite cluster. Halide perovskite nanocrystals have a diverse surface chemistry due to the binary cationic–anionic surface termination of (100) crystal planes, as illustrated in Fig. 1(g). This allows for a variety of functional groups to bind to the surface, such as alkylamines,34 alkylammoniums,12,35–37 alkylcarboxylates38,39 and alkylphosphates.40,41Fig. 2(a)–(c) illustrate how we bind (a) the (R)-MBA-H to a surface Cs+ ion, (b) (R)-MBAmm+-H substitutionally replaces a Cs+ ion and hydrogen-bonds to surface I− ions, and (c) (R)-MPAc−-H anion coordinated to a surface Pb2+ ion that substitutionally replaces a surface Cs+ ion. Further details about model construction are provided in Methods section. From the geometry optimized structures we compute the chirality transfer induced CD spectrum shown in Fig. 2(d) for (a) (R)-MBA-H (red), (b) (R)-MBAmm+-H (green), and (c) (R)-MPAc−-H (blue) coordinated to the halide perovskite surface. Even though the chiral centers of the molecules are the same, we can see that the functional group and binding mode to the surface have a large impact on the CD spectrum with (R)-MPAc−-H providing an order of magnitude larger response compared to that of (R)-MBA and multiples larger than (R)-MBAmm+-H. This trend is also demonstrated in the anisotropy spectra, Fig. 2(e), with the two lowest energy CD peaks providing the largest anisotropy maxima.From the optimized structures, we further explore functionalizing the meso positions of the aryl group with electron donating (withdrawing) OH (Cl,NO2) groups. This is done to modulate the molecular dipole of the chiral molecule, which we hypothesize can enhance the intensity of chiroptical signatures due to their dependence on the magnitude of transition dipoles, see eqn (4) in Methods. To illustrate the effect of chemical functionalization on tuning the molecular dipole we first inspect the isolated molecules. Specifically, we examine the change in molecular polarization by functionalizing the meso position of the aryl group for the neutral molecules (R)-MBA-H and (R)-MPAc-H and the molecular complex (R)-MBAmm+-I. When functionalizing the chiral molecules (R)-MBA-H and (R)-MPAc-H with withdrawing and donating groups, shown in ESI,† Fig. S1, we observe that the ground-state dipole can be tuned from approximately 1 Debye up to 7 Debye, shown in Table S1 (ESI†). While for the ionic complex (R)-MBAmm-I we observe that the dipole magnitude increases significantly, the meso functionalization provides a narrower range of enhancement from 11.55 to 14.01 Debye.
When the functionalized chiral molecules are bound to the halide perovskite cluster surface, shown in ESI,† Fig. S2, the OH and Cl functionalization's provide a small change to the overall dipole moment, but NO2 can provide 1.5–2 times increased dipole moment, as shown in Table S1 (ESI†). For (R)-MBA-H, we observe a significant enhancement of the CD peak intensities with NO2 functionalization to (R)-MBA-NO2, while OH and Cl functionalizations (R)-MBA-OH and (R)-MBA-Cl provide almost identical CD spectra to the pristine models, as shown in Fig. 3. We note that the same trend emerges for functionalized (R)-MBAmm+-H and (R)-MPAc−-H, shown in ESI,† Fig. S3 and S4 (ESI†), respectively, but with NO2 functionalized (R)-MBAmm+-NO2 and (R)-MPAc−-NO2 providing less pronounced increase in CD peak intensities. This is attributed to the trend observed for the chiral molecules that (R)-MBA-H as a neutral species is more polarizable while the cation (R)-MBAmm+-H and anion (R)-MPAc−-H are less polarizable species.
To confirm that the observed chiroptical signatures of the molecule–cluster system originate from the halide perovskite cluster, we overlay the CD and absorption spectra of the isolated cluster, isolated molecule and the combined system for (R)-MBA-H, (R)-MBAmm+-H, and for (R)-MPAc−-H in ESI,† Fig. S5–S7, respectively. These plots show that the absorption spectra of the combined system are identical to the isolated cluster and that CD signals emerge below the optical gap of the isolated chiral molecule. For the NO2 functionalized models, we do detect a spectral feature below the optical gap of the isolated cluster, as shown in Table S1 (ESI†) the optical gap of the combined system shows a smaller optical gap compared to the unfunctionalized models. This feature is attributed to a partial intra-molecular charge transfer transition due to the strong electron-withdrawing nature of the NO2 group, see ESI,† Fig. S8.
An interesting observation is that for the neutral (R)-MBA-H molecule introducing an electron-withdrawing group NO2 through aryl substitution of the meso-position giving (R)-MBA-NO2, increases the maximum |ganisotropy| by a factor of 5. One possible explanation for this is due to the increased polarization at the bonding interface. This would consequently polarize the molecular orbitals and increase the magnetic dipole response. To investigate this trend, we analyze the charge distribution using Bader charge analysis and compare the charge associated to the cluster–ligand interface, illustrated in ESI,† Fig. S9. From comparing the Bader charges, shown in ESI,† Table S4, we find there is a negligible change in charge associated with atoms associated with the molecular–cluster bond. Thus, bond polarization does not contribute to the changes in the chiroptical response with a polar group functionalization.
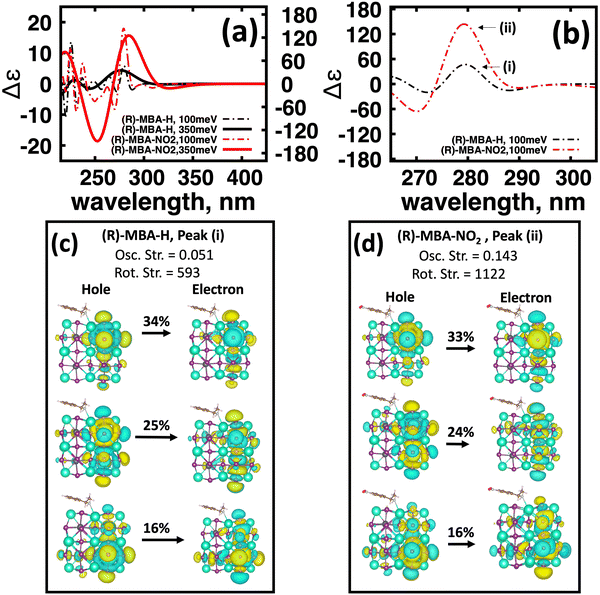
To further investigate the origin of CD intensity enhancement for a functionalized (R)-MBA-H system, we inspect the CD spectra calculated with a narrow linewidth of 100 meV. This allows us to examine contributions of specific electronic transitions. In Fig. 4(a) we overlay the CD spectra broadened by 350 meV with the narrower broadening of 100 meV for (R)-MBA-H and (R)-MBA-NO2. From this comparison, we observe that the increase in the |ganisotropy| is attributable to a significant increase in intensity between 270 nm and 290 nm, as seen in Fig. 4(a), which is identified as peak (i) and peak (ii) for (R)-MBA-H and (R)-MBA-NO2, respectively, in Fig. 4(b). For this CD peak, we further single out the most intense rotatory strengths and analyze the NTOs, shown in Fig. 4(c) and (d). We observe that the transitions are identical in terms of orbital density distribution. Upon further investigation we find that the enhancement is attributable to an increase of the transition electric dipole, as evident by the increased oscillator strength in ESI,† Table S3, while the transition magnetic dipole remains largely unchanged. This is an illustration of the concept of tuning the electronic polarization of the molecule to enhance the magnitude of chirality transfer driven by dipole coupling.
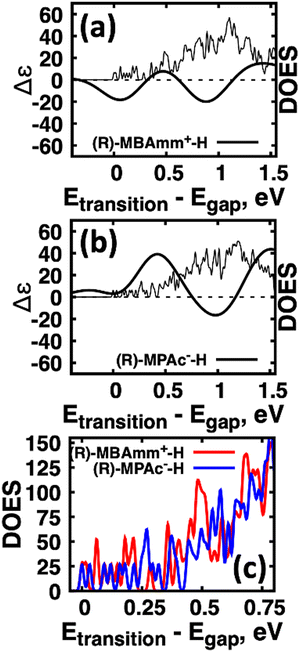
Another interesting observation is that the anionic (R)-MPAc−-H bound to the surface gives larger CD and |ganisotropy| intensities compared to that of cationic (R)-MBAmm+-H. Computing the root-mean-square for the rotatory strengths up to 5 eV for (R)-MBAmm+-H (N = 68) and (R)-MPAc−-H (N = 68) gives values of 440 and 480, respectively. This indicates that, on average, it would be expected the CD and |ganisotropy| maxima should be 10% larger for (R)-MPAc−-H compared to (R)-MBAmm+-H. The values in Table 1 show the first band and maximum band intensities increase by 910% and 62%, respectively. We find that the main differences in the CD spectra arise from the change in density of excited-states (DOES), as shown in Fig. 5. To directly compare the CD spectrum of these models we plot the spectrum normalized to the optical gap. Fig. 5 shows the bandgap normalized CD spectrum overlayed with their DOES for (a) (R)-MBAmm+-H and (b) (R)-MPAc−-H. Their EDOS are overlayed in Fig. 5(c). Comparing their DOES shows greater splitting of the lower energy transitions (below 0.25 eV) for (R)-MPAc−-H than that for (R)-MBAmm+-H. Thus the greater splitting between excited-states underpins the larger intensity CD spectra in (R)-MPAc−-H than (R)-MBAmm+-H due to reduced overlap between positive and negative contributions to the thermally broadened CD spectrum. This illustrates that not only the magnitude of chiroptical signatures matter, but the distribution of excited states, which contribute to chiroptical activity, have to be considered for trying to maximize the anisotropy signal.
| Chiral molecules + CsPbI3 cluster | 1st Band (nm) | |ganisotropy| | Max band, nm | |ganisotropy| |
|---|---|---|---|---|
| (R)-MBA-OH | 320 | 2.73 × 10−5 | 270 | 7.00 × 10−5 |
| (R)-MBA-H | 322 | 2.70 × 10−5 | 279 | 8.70 × 10−5 |
| (R)-MBA-Cl | 322 | 2.60 × 10−5 | 279 | 9.66 × 10−5 |
| (R)-MBA-NO2 | 328 | 2.49 × 10−4 | 292 | 3.98 × 10−4 |
| (R)-MBAmm+-H | 325 | 1.61 × 10−4 | 290 | 4.93 × 10−4 |
| (R)-MBAmm+-NO2 | 302 | 7.67 × 10−4 | 302 | 7.67 × 10−4 |
| (R)-,MPAc−-H | 318 | 7.26 × 10−4 | 267 | 7.97 × 10−4 |
| (R)-,MPAc−-NO2 | 316 | 1.14 × 10−3 | 316 | 1.14 × 10−3 |
| (S) Lactate | 326 | 3.03 × 10−4 | 266 | 7.31 × 10−4 |
| (S) Malate | 325 | 3.07 × 10−5 | 235 | 2.94 × 10−4 |
| (S,S) Tartartate | 315 | 4.08 × 10−5 | 260 | 4.08 × 10−5 |
We note that for these chiral aryl molecules we neglect conformational averaging on the surface. This is due to their inherent lack of conformational degrees of freedom aside from rotation of the functional groups around the chiral center. As a test, we explored various rotations of the (R)-MBAmm+-H molecule on the CsPbI3 cluster surface and find that the CD signal remains virtually unchanged, as shown in ESI,† Fig. S10.
(iii) Molecular conformations
Motivated by the observation that (R)-MPAc−-H provides the highest intensity CD peaks and most resolvable anisotropy peaks, see Fig. 2, we next explore the lactic acid series, i.e., (S)-lactic, (S)-malic, and (S,S) tartaric acids. The chiroptical signatures of these molecules have been explored recently, which shows that in aqueous solutions tartaric acid provides 4 times the CD intensity enhancements compared to Lactic and Malic Acids along with each of them showing |ganisotropy| maxima greater than 0.01 which is large for organic molecules.42 We hypothesize that these desirable chiroptical features can be transferred to the perovskite cluster. Similar to (R)-MPAc−-H these molecules are bound to the cluster in the de-protonated anion form of (S)-lactate, (S)-malate, and (S,S)-tartarate.(S)-Malate and (S,S) Tartarate can have three possible molecular conformations as characterized by dihedral angle between the four central carbon atoms: trans (θ = 0), gaunche− (θ = 120), and gaunche+ (θ = 300). For initial conditions, the molecules are placed in either trans (1-M,2-M,1-T), gaunche− (3-M,4-M,2-T), or gaunche+ (5-M,6-M,3-T) conformations on the surface of the halide perovskite cluster (for Lactate models 1-L, 2-L, and 3-L, we use various rotations about the chiral center). When geometry is optimized, as shown in ESI,† Fig. S11–S13, the trans and gaunche+ conformers remain in these conformers, while the gaunche− conformers are optimized into a structure in between trans and gaunche− with dihedrals ranging between 24 and 28 degrees, as seen in ESI,† Table S4.
We further compute Boltzmann weights and thermal average for each system with the values shown in Table S5 (ESI†). These thermal averages are then used to calculate the conformationally averaged CD spectra for models, which are shown in Fig. 6(a). For (S,S) Tartaric Acid, the gaunche(+) conformers are the most energetically favorable, in contrast to the solution phase where trans structure is typically observed.43,44 This is attributed to the ability for gaunche(+) to form additional hydrogen bonds between the carboxylic group and surface halides as well as hydroxyl groups forming coordination with surface Cs+ cations.
In Fig. 6(a) we observe that with (S)-lactate (red, solid) bound to the surface, the induced CD spectra from the perovskite cluster has much more intensity compared to the CD spectra induced by (S)-malate (green, solid) and (S,S)-tartartate (blue, solid). Fig. 4(b) shows computed the anisotropy factors for the conformationally averaged systems. Here we find a similar trend: Pb(lactate) (red, solid) bound to the surface has higher maximum intensity peaks than the induced by (S)-malate (green, solid) and (S,S)-tartartate (blue, solid) spectra. Overall, the molecules which have conformational flexibility, effectively ‘quench’ the CD signal from the CsPbI3 perovskite cluster.
This trend could have two possible origins. On one hand, each conformer could have ‘mirrored’ CD spectra and similar Boltzman weights. Hence, the signal would be quenched after averaging. On the other hand, there could be conformers that provide ‘bright’ and ‘dark’ chirality transfer with the nanomaterial surface stabilizing a ‘dark’ conformer. From the Boltzmann weights shown in ESI,† Table S5, we find that the gaunche(+) conformers of (S)-Malate and (S,S) Tartarate provide greater than 90% weight. Further, when examining the computed CD for 1, gaunche(+) for both molecules, as shown in ESI,† Fig. S14, it can be seen that these conformers induce ‘dark’ CD into the CsPbI3 perovskite cluster. In contrast, trans and gaunche(−) conformers of (S)-malate and (S,S)-tartartate on the surface can induce ‘bright’ chiroptical signatures comparable to intensity similar to (S)-lactate. Thus, we observe that simply binding chiral molecules to a nanomaterial surface does not guarantee ‘bright’ induced chirality transfer. Conformations of the chiral molecule greatly impact the induced nanomaterial's CD. Conformational effects have also shown to be important in determining tthe metal cluster circular dichroism spectrum as well.45
To explain the conformational dependence of chirality transfer and induced CD, we borrow ideas from literature. In a recent paper a curious correlation was found between the intensity of circular dichroism of the material and degree of spin-polarization of charge-carriers through the chirality induced spin selectivity (CISS).46 In the same spirit, we try to identify a mechanism for the observed quenching of circular dichroism spectra for perovskite clusters with gaunche(+) conformers on their surface based on CD spectra from the isolated molecule (i.e. correlation between isolated molecule CD intensity and CD induced by chirality transfer). ESI,† Table S6 shows the rotatory strength for the lowest energy S1 excited-state for the anionic molecule, the Root-Mean-Square (RMS) of the rotatory strength for all computed excited-states (N = 20), and the RMS for all computed excited-states for the joint cluster/molecule system (N = 300). In short, there is no clear correlation between isolated molecule conformation and the chirality transfer strength into the perovskite cluster. One observation is that the gaunche(+) conformers (5-M, 6-M, 3-T) and other chiroptically ‘dark’ models (4-M) have negative RS1 values. In contrast, for chiroptically active models, the isolated molecules have positive RS1 value. The exact coupling mechanism describing conformer's dependence is difficult to determine. Analysis such as non-degenerate coupled oscillator19 or machine learning of molecular descriptors47 are tools to be used to gain more insight.
Finally, we remark on a trend related to molecules giving the largest chiroptical intensities. The largest computed anisotropies are summarized in Table 1. Within the lactic acid series, we find that (L)-Lactate acid provides the largest anisotropy intensities. The other molecular systems, which gave consistently large anisotropy intensities include (R)-MPAc−-H and (R)-MBAmm+-H with (R)-MPAc-NO2 providing the largest anisotropy across all models investigated. All these molecules are conformationally limited, as they have one chiral center and are composed of a single central carbon atom. This indicates that conformational rigidity is important for inducing large chiroptical signatures via chirality transfer.
Conclusion
Using chiral molecules to induce chiroptical signatures into semiconductor nanomaterials (via chirality transfer) is an attractive prospect as it allows to leverage developments in colloidal surface chemistry to introduce enhanced functionality for opto-electronic applications, such as polarized photo-detectors. Such applications require high fidelity to distinguish between binary circularly polarized states, as characterized by anisotropy spectra. Typically for colloidal semiconductor quantum dots the maximum anisotropy value is in the range of 10−5–10−3. Here we use time-dependent density functional theory calculations to investigate molecular properties, such as charge state and conformational flexibility, which influence the chirality transfer between a chiral molecule (ligand) bound to an achiral lead halide perovskite cluster.First, we find that for chiral molecules that contain aryl groups, such as (R/S)-methylbenzylamine and (R/S)-methylphenyl acetic acid, modulating their molecule dipole via meso functionalization with strong withdrawing groups, such as NO2, can significantly enhance intensities of chiroptical signatures. Along the same line of thought, modulating the acid–base equilibrium of the chiral molecular to charged species, which binds to the nanomaterial surface, also increases the chirality transfer effect. Second, using the lactic acid series ((S)-lactic, (S)-malic, and (S,S) tartaric acids) we explore conformational ensemble average of these molecules on the cluster surface. With increasing molecular size and functionalization, there are also increasing number of chiral centers, which could contribute to enhancement of chiroptical signal. We find that limited conformational flexibility of lactic acid provides the largest chiroptical intensities while (S,S) tartaric acid effectively quenches them. Overall, these results demonstrate that chemical modification emphasizing a polarized chiral molecule, either through acid–base equilibrium or strategic functionalization, and limited conformationally degrees of freedom, are important for obtaining high-intensity nanomaterial chiroptical signatures featuring enhanced chirality transfer.
Methods
Ground-state geometry and electronic structure are found from the self-consistent DFT equations which minimizes total energies Ek for each conformer k. Excited-electronic states are found using time-dependent density functional theory (TDDFT) by solving the Casida equations. Briefly, the solutions of the Casida equation produce eigenvectors Xn and Yn, which represent transition densities, with eigenvalues Ωn which represent the transition frequencies. For chiroptical activity the optical transitions of interest are the electronic transition dipole, eqn (1) and magnetic transition dipole, eqn (2). These transition dipoles are represented as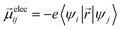 | (1) |
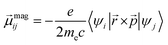 | (2) |
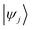 and
and 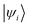 are Kohn–Sham wavefunctions of occupied and virtual electronic states, respectively, e represents the fundamental charge, me is electron mass, and c is the speed of light. Within TDDFT framework, these dipole moments are found from expectation values of the transition densities48
are Kohn–Sham wavefunctions of occupied and virtual electronic states, respectively, e represents the fundamental charge, me is electron mass, and c is the speed of light. Within TDDFT framework, these dipole moments are found from expectation values of the transition densities48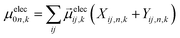 | (3) |
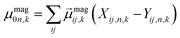 | (4) |
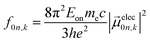 | (5) |
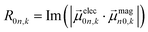 | (6) |
The extinction coefficient ε and differential extinction coefficient Δε, describing circular dichroism, for each conformer k are then generated with eqn (7) and (8), respectively
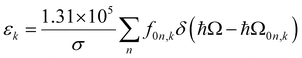 | (7) |
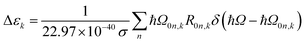 | (8) |
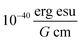 . The conformer averaged absorption and circular dichroism spectra are then obtained by weighting each conformer by thermal Boltzmann distribution
. The conformer averaged absorption and circular dichroism spectra are then obtained by weighting each conformer by thermal Boltzmann distribution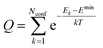 | (9) |
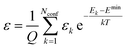 | (10) |
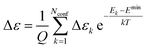 | (11) |
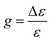 | (12) |
All calculations are done using Gaussian 16 package.50 For chiral molecules the structures are optimized with dispersion corrected ωb97xd functional and a 6-311++g** basis set. Both nuclear coordinates of the perovskite cluster and chiral molecule are allowed to relax during optimization. For the pristine perovskite cluster the stoichiometry Cs19Pb8I36 was chosen giving a total charge of −1. This structure was chosen to minimize any asymmetry induced circular dichroism signal. When adding molecules to the cluster surface the charge is kept at −1. TDDFT calculations for 20 excited states are then done using the same model chemistry combined with a polarized continuum model (PCM) to account for solvent effects, namely a conductor-like PCM (CPCM) formalism51,52 is used with solvent dielectric constant corresponding to toluene (ε = 2.37). For geometry optimization of the combined perovskite cluster/chiral molecule models ωb97xd functional and a split basis set is used with heavy elements {[Cs, Pb, I]} being treated with LANL2DZ effective core potentials53 while light elements [C,H,O,N,Cl] being treated with 6-311++g(d,p) basis set.54 300 electronic excited-states are then computed for each structure using TDDFT formalism and C-PCM solvent model corresponding to toluene dielectric constant. To visualize the distribution of the computed transition density we used the concept of natural transition orbitals55 (NTOs). When computing spectra for the isolated molecules, as shown in ESI,† 20 states are calculated. When computing the perovskite cluster with chiral molecules on the surface we compute 300 states for the shown circular dichroism spectra.
To ensure that the anisotropy factor ‘behaves nicely’ near the absorption onset transition energy, we add a constant number to the absorption spectra to avoid divergences for the singular denominator in the regions of band absorption onsets. For consistency the constant is chosen to be 10% of the first absorption peak intensity for each conformer averaged system. Bader charge analysis is done with the charge densities computed from the pseudo-potential56,57 plane-wave based Vienna ab Initio Software Program (VASP).58 A plane-wave basis set with a cut-off of 500 eV is used in a simulation cell with 11 A of vacuum in each cardinal direction. The Bader charges59 where determined using the Bader Charge Analysis program.60
Author contributions
All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work at Los Alamos National Laboratory (LANL) was supported by the LANL LDRD program (A. F., A. C. E., A. J. N.) and was done in part at Center for Nonlinear Studies (CNLS). This research used resources provided by the LANL Institutional Computing Program. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy under contract no. 89233218NCA000001. This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. Los Alamos National Laboratory, an affirmative action-equal opportunity employer, is managed by Triad National Security, LLC for the U.S. Department of Energy's NNSA, under contract 89233218CNA000001.References
- A. Ben-Moshe, A. da Silva, A. Müller, A. Abu-Odeh, P. Harrison, J. Waelder, F. Niroui, C. Ophus, A. M. Minor, M. Asta, W. Theis, P. Ercius and A. P. Alivisatos, Science, 2021, 372, 729–733 CrossRef CAS PubMed.
- T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887 CrossRef PubMed.
- Y. Zhou, Z. Zhu, W. Huang, W. Liu, S. Wu, X. Liu, Y. Gao, W. Zhang and Z. Tang, Angew. Chem., Int. Ed., 2011, 50, 11456–11459 CrossRef CAS PubMed.
- X. Gao, B. Han, X. Yang and Z. Tang, J. Am. Chem. Soc., 2019, 141, 13700–13707 CrossRef CAS PubMed.
- H. Htoon, S. A. Crooker, M. Furis, S. Jeong, A. L. Efros and V. I. Klimov, Phys. Rev. Lett., 2009, 102, 017402 CrossRef CAS PubMed.
- X. Li, A. C. Jones, J. Choi, H. Zhao, V. Chandrasekaran, M. T. Pettes, A. Piryatinski, N. Sinitsyn, S. A. Crooker and H. Htoon, arXiv, arXiv:2203.00797, 2022 DOI:10.48550/arXiv.2203.00797, e-prints.
- M. P. Moloney, Y. K. Gun'ko and J. M. Kelly, Chem. Commun., 2007, 3900–3902, 10.1039/B704636G.
- A. Ben-Moshe, A. Teitelboim, D. Oron and G. Markovich, Nano Lett., 2016, 16, 7467–7473 CrossRef CAS PubMed.
- G. Long, C. Jiang, R. Sabatini, Z. Yang, M. Wei, L. N. Quan, Q. Liang, A. Rasmita, M. Askerka, G. Walters, X. Gong, J. Xing, X. Wen, R. Quintero-Bermudez, H. Yuan, G. Xing, X. R. Wang, D. Song, O. Voznyy, M. Zhang, S. Hoogland, W. Gao, Q. Xiong and E. H. Sargent, Nat. Photonics, 2018, 12, 528–533 CrossRef CAS.
- Y.-H. Kim, Y. Zhai, E. A. Gaulding, S. N. Habisreutinger, T. Moot, B. A. Rosales, H. Lu, A. Hazarika, R. Brunecky, L. M. Wheeler, J. J. Berry, M. C. Beard and J. M. Luther, ACS Nano, 2020, 14, 8816–8825 CrossRef CAS PubMed.
- G. Almeida, L. Goldoni, Q. Akkerman, Z. Dang, A. H. Khan, S. Marras, I. Moreels and L. Manna, ACS Nano, 2018, 12, 1704–1711 CrossRef CAS PubMed.
- M. I. Bodnarchuk, S. C. Boehme, S. ten Brinck, C. Bernasconi, Y. Shynkarenko, F. Krieg, R. Widmer, B. Aeschlimann, D. Günther, M. V. Kovalenko and I. Infante, ACS Energy Lett., 2019, 4, 63–74 CrossRef CAS PubMed.
- A. Forde, J. A. Fagan, R. D. Schaller, S. A. Thomas, S. L. Brown, M. B. Kurtti, R. J. Petersen, D. S. Kilin and E. K. Hobbie, J. Phys. Chem. Lett., 2020, 11, 7133–7140 CrossRef CAS PubMed.
- D. Zherebetskyy, M. Scheele, Y. Zhang, N. Bronstein, C. Thompson, D. Britt, M. Salmeron, P. Alivisatos and L.-W. Wang, Science, 2014, 344, 1380–1384 CrossRef CAS PubMed.
- N. C. Anderson, M. P. Hendricks, J. J. Choi and J. S. Owen, J. Am. Chem. Soc., 2013, 135, 18536–18548 CrossRef CAS PubMed.
- H. Al-Bustami, B. P. Bloom, A. Ziv, S. Goldring, S. Yochelis, R. Naaman, D. H. Waldeck and Y. Paltiel, Nano Lett., 2020, 20, 8675–8681 CrossRef CAS PubMed.
- J. K. Choi, B. E. Haynie, U. Tohgha, L. Pap, K. W. Elliott, B. M. Leonard, S. V. Dzyuba, K. Varga, J. Kubelka and M. Balaz, ACS Nano, 2016, 10, 3809–3815 CrossRef CAS PubMed.
- F. Purcell-Milton, A. K. Visheratina, V. A. Kuznetsova, A. Ryan, A. O. Orlova and Y. K. Gun’ko, ACS Nano, 2017, 11, 9207–9214 CrossRef CAS PubMed.
- X. Gao, X. Zhang, K. Deng, B. Han, L. Zhao, M. Wu, L. Shi, J. Lv and Z. Tang, J. Am. Chem. Soc., 2017, 139, 8734–8739 CrossRef CAS PubMed.
- T. He, J. Li, X. Li, C. Ren, Y. Luo, F. Zhao, R. Chen, X. Lin and J. Zhang, Appl. Phys. Lett., 2017, 111, 151102 CrossRef.
- M. Puri and V. E. Ferry, ACS Nano, 2017, 11, 12240–12246 CrossRef CAS PubMed.
- S. D. Elliott, M. P. Moloney and Y. K. Gun’ko, Nano Lett., 2008, 8, 2452–2457 CrossRef CAS PubMed.
- Y.-H. Kim, R. Song, J. Hao, Y. Zhai, L. Yan, T. Moot, A. F. Palmstrom, R. Brunecky, W. You, J. J. Berry, J. L. Blackburn, M. C. Beard, V. Blum and J. M. Luther, Adv. Funct. Mater., 2022, 32, 2200454 CrossRef CAS.
- J.-i Fujisawa, N. Kaneko, T. Eda and M. Hanaya, Chem. Commun., 2018, 54, 8490–8493 RSC.
- T. A. R. Purcell and T. Seideman, ACS Photonics, 2018, 5, 4801–4809 CrossRef CAS.
- A. Forde, D. Ghosh, D. Kilin, A. C. Evans, S. Tretiak and A. J. Neukirch, J. Phys. Chem. Lett., 2022, 13, 686–693 CrossRef CAS PubMed.
- L. Wan, R. Zhang, E. Cho, H. Li, V. Coropceanu, J.-L. Brédas and F. Gao, Nat. Photonics, 2023, 17, 649–655 CrossRef CAS.
- D. M. Kroupa, M. Vörös, N. P. Brawand, N. Bronstein, B. W. McNichols, C. V. Castaneda, A. J. Nozik, A. Sellinger, G. Galli and M. C. Beard, J. Phys. Chem. Lett., 2018, 9, 3425–3433 CrossRef CAS PubMed.
- A. C. Evans, A. S. Petit, S. G. Guillen, A. J. Neukirch, S. V. Hoffmann and N. C. Jones, RSC Adv., 2021, 11, 1635–1643 RSC.
- J. Bockova, N. C. Jones, U. J. Meierhenrich, S. V. Hoffmann and C. Meinert, Commun. Chem., 2021, 4, 86 CrossRef CAS PubMed.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- B. A. Koscher, J. K. Swabeck, N. D. Bronstein and A. P. Alivisatos, J. Am. Chem. Soc., 2017, 139, 6566–6569 CrossRef CAS PubMed.
- A. Forde, E. Hobbie and D. Kilin, MRS Adv., 2019, 4, 1981–1988 CrossRef CAS.
- D. Quarta, M. Imran, A.-L. Capodilupo, U. Petralanda, B. van Beek, F. De Angelis, L. Manna, I. Infante, L. De Trizio and C. Giansante, J. Phys. Chem. Lett., 2019, 10, 3715–3726 CrossRef CAS PubMed.
- Y. Chen, S. R. Smock, A. H. Flintgruber, F. A. Perras, R. L. Brutchey and A. J. Rossini, J. Am. Chem. Soc., 2020, 142, 6117–6127 CrossRef CAS PubMed.
- A. Forde, T. Inerbaev and D. Kilin, MRS Adv., 2018, 1–7, DOI:10.1557/adv.2018.552.
- A. Forde and D. Kilin, J. Chem. Theory Comput., 2021, 17, 7224–7236 CrossRef CAS PubMed.
- S. R. Smock, T. J. Williams and R. L. Brutchey, Angew. Chem., Int. Ed., 2018, 57, 11711–11715 CrossRef CAS PubMed.
- A. Forde, T. Inerbaev, E. K. Hobbie and D. S. Kilin, J. Am. Chem. Soc., 2019, 141, 4388–4397 CrossRef CAS PubMed.
- B. Zhang, L. Goldoni, C. Lambruschini, L. Moni, M. Imran, A. Pianetti, V. Pinchetti, S. Brovelli, L. De Trizio and L. Manna, Nano Lett., 2020, 20, 8847–8853 CrossRef CAS PubMed.
- T. K. T. Tran, J. A. Adewuyi, Y. Wang, M. D. Morales-Acosta, T. Mani, G. Ung and J. Zhao, Chem. Commun., 2023, 59, 1485–1488 RSC.
- J. Bocková, N. C. Jones, U. J. Meierhenrich, S. V. Hoffmann and C. Meinert, Commun. Chem., 2021, 4, 86 CrossRef PubMed.
- J. Gawroński, K. Gawrońska, P. Skowronek, U. Rychlewska, B. Warżajtis, J. Rychlewski, M. Hoffmann and A. Szarecka, Tetrahedron, 1997, 53, 6113–6144 CrossRef.
- J. Gawroński and J. Grajewski, Org. Lett., 2003, 5, 3301–3303 CrossRef PubMed.
- M. Monti, G. Brancolini, E. Coccia, D. Toffoli, A. Fortunelli, S. Corni, M. Aschi and M. Stener, J. Phys. Chem. Lett., 2023, 14, 1941–1948 CrossRef CAS PubMed.
- A. K. Mondal, M. D. Preuss, M. L. Ślęczkowski, T. K. Das, G. Vantomme, E. W. Meijer and R. Naaman, J. Am. Chem. Soc., 2021, 143, 7189–7195 CrossRef CAS PubMed.
- T. Vermeyen, J. Brence, R. Van Echelpoel, R. Aerts, G. Acke, P. Bultinck and W. Herrebout, Phys. Chem. Chem. Phys., 2021, 23, 19781–19789 RSC.
- J. Autschbach, T. Ziegler, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 116, 6930–6940 CrossRef CAS.
- B. Han, Z. Zhu, Z. Li, W. Zhang and Z. Tang, J. Am. Chem. Soc., 2014, 136, 16104–16107 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805 RSC.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc02248j |
| This journal is © The Royal Society of Chemistry 2023 |