Open Access Article
Open Access ArticleMagnetic hysteresis and large coercivity in bisbenzimidazole radical-bridged dilanthanide complexes†
Florian
Benner
 a,
Léo
La Droitte
b,
Olivier
Cador
a,
Léo
La Droitte
b,
Olivier
Cador
 b,
Boris
Le Guennic
b,
Boris
Le Guennic
 b and
Selvan
Demir
b and
Selvan
Demir
 *a
*a
aDepartment of Chemistry, Michigan State University, 578 South Shaw Lane, East Lansing, Michigan 48824, USA. E-mail: sdemir@chemistry.msu.edu
bUniv Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes) – UMR 6226, F-35000 Rennes, France
First published on 3rd May 2023
Abstract
A judicious combination of radical ligands innate to diffuse spin orbitals with paramagnetic metal ions elicits strong magnetic exchange coupling which leads to properties important for future technologies. This metal-radical approach aids in effective magnetic communication of especially lanthanide ions as their 4f orbitals are contracted and not readily accessible. Notably, a high spin density on the donor atoms of the radical is required for strong coupling. Such molecules are extremely rare owing to high reactivity rendering their isolation challenging. Herein, we present two unprecedented series of bisbenzimidazole-based dilanthanide complexes [(Cp*2Ln)2(μ-Bbim)] (1-Ln = Gd, Tb, Dy, Bbim = 2,2′-bisbenzimidazole) and [K(crypt-222)][(Cp*2Ln)2(μ-Bbim˙)] −(2-Ln = Gd, Tb, Dy), where the latter contains the first Bbim3−˙ radical matched with any paramagnetic metal ion. The magnetic exchange constant for 2-Gd of J = −1.96(2) cm−1 suggests strong antiferromagnetic Gd-radical coupling, whereas the lanthanides in 1-Gd are essentially uncoupled. Ab initio calculations on 2-Tb and 2-Dy uncovered coupling strengths of −4.8 and −1.8 cm−1. 1-Dy features open hysteresis loops with a coercive field of Hc of 0.11 T where the single-molecule magnetism can be attributed to the single-ion effect due to lack of coupling. Excitingly, pairing the effective magnetic coupling with the strong magnetic anisotropy of Dy results in magnetic hysteresis with a blocking temperature TB of 5.5 K and coercive field HC of 0.54 T, ranking 2-Dy as the second best dinuclear single-molecule magnet containing an organic radical bridge. A Bbim4− species is formed electrochemically hinting at the accessibility of Bbim-based redox-active materials.
Introduction
Organic radicals, or organic compounds containing unpaired electrons, have been historically difficult to isolate due to their intrinsic instability and high reactivity. Despite the intricate handling, their unique electronic structure renders them valuable building blocks for next generation magnetic and electronic materials.1,2 Importantly, the combination of ligands containing unpaired electrons with metal ions gave rise to impressive advances in the fields of single-molecule magnets (SMMs) and molecular spintronics.3–7SMMs are molecules that show an energy barrier (Ueff) to magnetic relaxation which allows a retention of their magnetization orientation after removing an applied external magnetic field. These bulk magnetic-like features innate to SMMs are detectable by field-dependent magnetization experiments giving rise to open magnetic hysteresis loops. Metrics to best capture the properties of a magnetic hysteresis loop are the blocking temperature, TB, equalling to the temperature at which magnetic information is lost within a specific time frame, and the coercive field, HC, corresponding to the prerequisite magnetic field to counteract remnant magnetization. Such molecules have garnered immense interest owing to the impactful potential applications in high-density information storage, molecular spintronics, and quantum computing.8–13 To realize these applications, the key performance characteristics Ueff, TB and HC need to be augmented ideally up to room temperature.
One auspicious route to fulfil this goal is the generation of multinuclear SMMs to yield a large overall ground state concomitant with an attenuation of quantum tunnelling and an increase in relaxation times. Among all metals, lanthanides constitute ideal candidates for SMM design owing to their large magnetic anisotropy stemming from large unquenched orbital momentum and strong spin–orbit coupling. Over the course of the past decade, the implementation of radical bridging ligands has been extremely rewarding to construct polynuclear lanthanide SMMs, as radicals engendered strong magnetic coupling between otherwise isolated magnetic moments of the lanthanide ions.14–16 This metal-radical approach is an important concept since the use of diamagnetic ligands where typical donor atoms are oxygen or nitrogen usually hampers the magnetic communication between the lanthanide ions due to their contracted 4f-orbitals which prevent substantial involvement in chemical bonding and therefore, cannot transfer spin density onto the ligand system.17
An alternative, yet extremely rare, path explores the use of donor atoms comprising heavy p-block elements innate to expanded p-orbitals as those enable superexchange coupling pathways originating from an effective orbital overlap.18–20 Although exciting approach, such molecules are extremely scarce, possibly due to the added synthetic challenge compared to lighter p-block elements. By exploiting the more diffuse orbitals of radicals, this effect is substantially amplified and allows for direct exchange coupling between the radical and magnetic moments of the metals. Considering all metrics, the current best radical-bridged SMM constitutes the organometallic terbium complex [K(crypt-222)][(Cp*2Tb)2(μ-N2˙)] (where crypt-222 = 2.2.2-cryptand, Cp* = pentamethylcyclopentadienyl), where the coupling of two highly anisotropic terbium(III) ions via a dinitrogen radical N23−˙ engenders magnetic blocking and open hysteresis loops up to 30 K and a colossal coercive field of HC = 7.9 K.21 The magnitude of coercive field is only surpassed by a recently discovered mixed-valent lanthanide metal–metal-bonded system which is so far an impressive and sole example of this kind and thus, the accessibility of akin LnII–LnIII compounds need to be probed.22 Although the magnetism of the terbium N23−˙ molecule is impressive, relative to organic radical-bridged complexes, this temperature is low to allow for applications in consumer technology, for which the operating temperature has to approach ideally room temperature. Strategies to boost the operating temperatures of N23−˙ radical-bridged SMMs, by increasing the magnetic coupling strength through appropriate chemical substitution on the radical or successfully implementing the N23−˙ radical into higher-nuclearity clusters are promising yet hitherto unknown owing to the immense synthetic challenge.
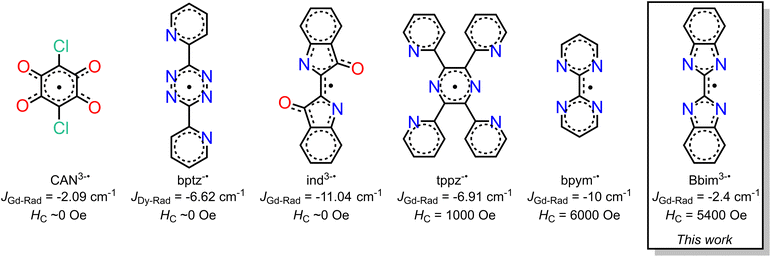
Organic radicals bear a huge advantage over N23−˙ radicals as they provide the prospect of being employed for the controlled synthesis of larger molecular clusters or extended solids. Key is to use suitable radical ligands with large spin densities on the donor atoms, which precludes the class of nitronyl nitroxide radicals as those feature low spin densities. Canvassing the literature, it is apparent that only a handful of radical ligands were effectively combined with anisotropic late lanthanides, Scheme 1.18–20,23–26 Those tetradentate bridges are particularly relevant for the prolific formation of multinuclear entities spanning from zero-dimensional to three-dimensional materials (i.e. clusters, chains, etc). Among those, only tetrapyridylpyrazine (tppz) and bipyrimidyl (bpym) radicals have led to open hysteresis loops, where the latter has also been probed regarding substitution effects on the radical.25,26 The scarcity of lanthanide-radical compounds highlights the necessity of generating new radical bridging ligands with the goal to reach higher blocking temperatures than currently accessible, and the challenge of devising successful synthetic routes that enable isolation.
We recognized 2,2′-bisbenzimidazole (Bbim) for its ability to form bridges in the dianionic state and robustness, and notably the possibility to construct higher nuclearity compounds.27,28 Although promising, radical states of Bbim were unknown yet even redox inactivity of that ligand was highlighted when unified with heavier d-block metals. Recently, we demonstrated the successful isolation of the first instance of a crystallographically characterised bisbenzimidazole radical anion Bbim3−˙ in the form of a dinuclear yttrium complex.29 The diamagnetic nature of yttrium(III) allowed an in-depth analysis involving NMR and EPR spectroscopy, as well as DFT studies. We concluded the Bbim radical to be an ideal candidate for SMM design due to the delocalized high spin density. Herein, we describe the synthesis, structural characterisation, and spectroscopic properties of the first organometallic bisbenzimidazole lanthanide complexes [(Cp*2Ln)2(μ-Bbim)] (1-Ln = Gd, Tb, Dy) which upon chemical reduction with KC8 in the presence of crypt-222 gave [K(crypt-222)][(Cp*2Ln)2(μ-Bbim˙)] (2-Ln = Gd, Tb, Dy), representing the first bisbenzimidazole radical-bridged compounds that contain paramagnetic metal ions. The complexes 1-Ln and 2-Ln were subjected to in-depth structural, spectroscopic, and magnetic analysis. The dynamic magnetization measurements uncovered substantial coercivity and magnetic blocking for 2-Dy placing it among the small set of radical-bridged SMMs displaying memory effect. 1-Dy was also subjected to variable-field magnetization measurements revealing open hysteresis loops of up to 5 K. Notably, the radical-bridge elicits a fivefold increase in coercive field height moving from 1-Dy to 2-Dy. Furthermore, 1-Dy and 2-Dy constitute the first single-molecule magnets that contain a bisbenzimidazole ligand in any oxidation state. The exchange coupling constant J was experimentally determined from fitting zero-field-cooled (zfc) DC magnetic data of 2-Gd and range among the highest determined values for radical-bridged lanthanide complexes. The electronic structures for 2-Ln (Ln = Tb, Dy) and 1-Dy were investigated via ab initio calculations using the State-Averaged Complete Active Space Self-Consistent Field approach with Restricted-Active-Space-State-Interaction method (SA-CASSCF/RASSI-SO). Magnetic blocking in 1-Dy and 2-Dy and the absence of blocking in 2-Tb were reproduced well from these calculations and suggest considerably different ligand field effects in comparison to bpym radical-bridged complexes. This insight is transformative and will guide towards the design of higher blocking SMMs. The accessibility of the tetraanionic state of 2-Dy was proven by electrochemical methods and will additionally allow access to new materials.
Experimental methods
General information
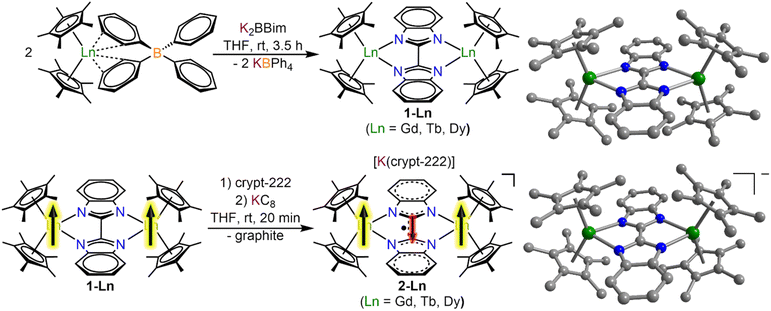
All manipulations were performed under inert conditions using either standard Schlenk techniques or argon-filled glovebox. nHexane, toluene and THF were purified by refluxing over potassium using benzophenone as an indicator and distilled prior to use. The chemicals pentamethylcyclopentadiene (Cp*H), allylmagnesium chloride (2.0 M in THF), potassium bistrimethylsilylamide (KN(Si(CH3)3)2) anhydrous LnCl3 (Ln = Gd, Tb, Dy), Celite, and 2.2.2-cryptand (crypt-222) were purchased from Sigma Aldrich. Crypt-222 was recrystallized from nhexane prior to use. KCp*,30 (HNEt3)(BPh4),31 Cp*2Ln(BPh4),26 H2Bbim,32 KC8 (ref. 33) and K2Bbim29 were synthesized according to literature procedures.Synthesis of [(Cp*2Ln)2(μ-Bbim)], 1-Ln = Gd, Tb, Dy
To THF solutions of the metal tetraphenylborate complexes Cp*2Ln(BPh4) (Ln = Gd, Tb, Dy) (2 equiv., ∼10 mL THF) the off-white deprotonated bisbenzimidazole ligand K2Bbim was added as a solid. An immediate colour change to yellow and the formation of a fine, colourless solid could be observed. The mixture was stirred for 3.5 h, briefly left standing for the solids to settle, and filtered through a Celite plug. The clear yellow solutions were evaporated to dryness to afford yellow and colourless solids which were extracted three times with toluene. Colourless insoluble solids were removed through filtration through Celite to afford a clear, yellow filtrate which was evaporated to dryness. The resulting yellow solids were redissolved in a minimum amount of toluene and stored at −30 °C for crystallization. Pale green block-shaped crystals of 1-Ln were grown over the course of 3 days.Synthesis of [K(crypt-222)][(Cp*2Ln)2(μ-Bbim˙)], 2-Ln = Gd, Tb, Dy
To a THF (8–10 mL) solution of the metal complexes, 1-Ln, 2.2.2-cryptand (1 equiv., 1 mL THF) was added and stirred for 5 min. Addition of solid KC8 (1 equiv.) resulted in an immediate colour change to dark green and the formation of an insoluble gray material, presumably graphite. After stirring for 20 min, the mixture was filtered to remove the insoluble solids and the clear, dark green filtrate was stored at −30 °C for crystallization. Dark green block-shaped crystals of 2-Ln were grown over the course of 3–5 days.IR spectroscopy
IR spectra were recorded with an Agilent Cary 630 ATR spectrometer in an argon-filled glovebox.UV/vis spectroscopy
UV/vis spectra were recorded in an argon-filled glovebox with an Agilent Cary 60 spectrometer, equipped with QP600-1-SR fiber optics and a Square One cuvette holder from Ocean Insight.SQUID magnetometry
Magnetic data were collected with a Quantum Design MPMPS3 SQUID magnetometer. Crystalline materials of 1-Ln and 2-Ln were washed with cold toluene or THF, respectively, and dried under vacuum for 1 h prior to sample preparation. Molten eicosane was added at 60 °C to the sample to immobilize the crystallites and to ensure good thermal contact between sample and the bath. The samples were sealed airtight and transferred to the SQUID magnetometer. All data were corrected for diamagnetic contributions from the eicosane and core diamagnetism estimated using Pascal's constants.34Cyclic voltammetry measurements
All cyclic voltammetry experiments were conducted under inert atmosphere in an argon-filled glovebox. Complex 2-Dy was measured using a PGSTAT204 from Metrohm with 1.3 mmol L−1 sample solution in THF with (nBu4N)(PF6) as supporting electrolyte (0.25 mol L−1) in conjunction with a glassy carbon working electrode, a Pt spring counter electrode and a Pt wire pseudo reference electrode. All voltammograms were externally referenced to a ferrocene solution with identical supporting electrolyte concentration.Elemental analysis
Elemental analyses were obtained at Michigan State University. In an argon-filled glovebox, solid samples (∼1–3 mg) were weighed into tin sample holders and folded multiple times to ensure proper sealing from surrounding atmosphere. Samples were transferred to the instrument under exclusion of air.Single crystal X-ray diffraction
Data of complex 1-Dy and 2-Dy were collected on a Bruker CCD (charge coupled device) based diffractometer using MoKα radiation. The instrument was equipped with an Oxford Cryostream low-temperature apparatus operating at 173 K. Data were measured using omega and phi scans of 1.0° per frame for 30 s. The total number of images was based on results from the program COSMO35 where redundancy was expected to be 4.0 and completeness of 100% out to 0.83 Å. Cell parameters were retrieved using APEX II software36 and refined using SAINT on all observed reflections. Data reduction was performed using the SAINT software37 which corrects for Lp. Scaling and absorption corrections were applied using SADABS38 multi-scan technique.Data on 1-Ln and 2-Ln (Ln = Gd, Tb) were collected on a XtaLAB Synergy DualflexHyPix four-circle diffractometer, equipped with a HyPix Hybrid Pixel Array Detector. The crystals were kept at 100 K during data collection. Data were measured using CuKα (1-Gd and 1-Tb) and MoKα (2-Gd and 2-Tb) radiation. The maximum resolution that was achieved was Θ = 71.296° (0.81 Å). The CrysAlisPro software package39 was used to retrieve and refine the cell parameters, as well as for data reduction. Correction for absorption effects was done using a numerical correction based on gaussian integration over a multifaceted crystal model and an empirical correction using spherical harmonics, implemented in SCALE3 ABSPACK40 scaling algorithm (spherical harmonics and frame scaling).
Using Olex2,41 the structures were solved with the ShelXT42 structure solution program using intrinsic phasing and refined with version 2018/3 of ShelXL43 using least squares minimization. All non-hydrogen atoms expect for the atoms belonging to disordered THF molecules in 2-Ln were refined anisotropically. Hydrogen atoms were calculated by geometrical methods and refined as a riding model. The crystals used for the diffraction study showed no decomposition during data collection. Crystal data and structure refinement for all compounds are shown in Tables S1 and S2.†
Calculations
Atomic positions were extracted from the crystal X-ray diffraction structures. Only the positions of the hydrogen atoms were optimized at the DFT level using the 2017 release of the ADF package,44–46 while other atom positions were kept frozen. The revPBE functional,47,48 the TZP basis set and the SR-ZORA Hamiltonian49 were used in the unrestricted formalism by considering an open-shell octet spin state for 2-Tb and an open-shell septet spin state for 1-Dy and 2-Dy.Complexes 2-Tb, 2-Dy and 1-Dy are not centrosymmetric. Thus, calculations were first performed on each LnIII centre, with the second LnIII centre replaced by the closed-shell YIII ion. In order to take into account the radical character of the Bbim ligand, point charges of −0.25e were placed on each nitrogen atom position during these calculations. Calculations were performed using the SA-CASSCF/RASSI-SO method, as implemented in the OpenMolcas package (version 19.11).50 All atoms were described by ANO-RCC basis set.51,52 The following contractions were used: [8s7p5d3f2g1h] for the Tb and the Dy atoms, [7s6p4d2f1g] for the Y atoms, [4s3p1d] for the N and the C atoms, [3s2p] for the C atoms of the methyl groups, and [2s] for the H atoms. Cholesky decomposition of the bielectronic integrals was employed to save disk space and to speed up the calculations.53
In a first approach, the active space consisted of the 4f electrons of the LnIII ions (eight for TbIII and nine for DyIII) spanning the seven 4f orbitals; CAS(8,7)SCF for 2-Tb and CAS(9,7)SCF for 2-Dy and 1-Dy. In RASSI-SO, 7 septets, 140 quartets, 91 triplets and 77 singlets for the TbIII ion, and 21 sextets, 224 quartets and 224 doublets for the DyIII ion, were mixed through spin–orbit coupling. The resulting spin–orbit wave functions and energies were used to compute the local magnetic properties using the SINGLE_ANISO routine. Then, dipole–dipole magnetic couplings between the LnIII centres were obtained using the POLY_ANISO routine.54,55 Exchange interactions were estimated within the Lines model, using computed values by POLY_ANISO and a homemade procedure to fit the exchange parameter by comparing the computed susceptibility curves and the experimental ones.56
In a second approach, the isotropic magnetic coupling between the LnIII ion and the radical ligand is computed at the CASSCF level without considering spin–orbit effects. For 2-Gd, the active space consisted of the seven 4f orbitals of the GdIII ion plus the singly occupied antibonding π* orbital of the radical ligand: eight electrons in eight orbitals, CAS(8,8). In a similar manner, the active spaces for 2-Tb and 2-Dy are CAS(9,8) and CAS(10,8), respectively. The energy of the lowest nonuplet and septet states was computed based on the set of molecular orbitals (MOs) of the septet state for 2-Gd. For 2-Tb, the energy of the lowest octet and sextet states was computed based on the set of MOs of the sextet state, and for 2-Dy, the energy of the lowest septet and quintet states was computed based on the set of MOs of the quintet state. Using these energies, exchange coupling constants were computed within Heisenberg model.
Results and discussion
Synthesis, structural and spectroscopic characterisation
The salt metathesis of Cp*2Ln(BPh4) with K2Bbim afforded the dinuclear lanthanide complexes [(Cp*2Ln)2(μ-Bbim)] (1-Ln), featuring a diamagnetic Bbim2− bridging ligand in yields ranging from 59% (1-Gd), 68% (1-Tb), to 73% (1-Dy). 1-Ln were crystallized by cooling concentrated toluene solutions to −30 °C, where 1-Dy crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , while 1-Gd and 1-Tb crystallized in the monoclinic space groups C2/m. For 1-Gd and 1-Tb, the asymmetric unit contains half a Bbim2− ligand and a disordered Cp*Ln unit, hence no torsion along the Tb1–N1–N2–Tb2 atoms is found (Fig. 1, S1 and S2, Tables 1 and S1†). Subsequent reduction of crystalline 1-Ln dissolved in THF with KC8 in the presence of crypt-222 yielded [K(crypt-222)][(Cp*2Ln)2(μ-Bbim˙)], 2-Ln, containing the Bbim3−˙ radical anion. Dark green single crystals of 2-Ln suitable for X-ray analysis were obtained by cooling a concentrated solution to −35 °C for several days in yields of 33% (2-Gd), 35% (2-Tb) and 28% (2-Dy). 2-Ln crystallize in the space group P
, while 1-Gd and 1-Tb crystallized in the monoclinic space groups C2/m. For 1-Gd and 1-Tb, the asymmetric unit contains half a Bbim2− ligand and a disordered Cp*Ln unit, hence no torsion along the Tb1–N1–N2–Tb2 atoms is found (Fig. 1, S1 and S2, Tables 1 and S1†). Subsequent reduction of crystalline 1-Ln dissolved in THF with KC8 in the presence of crypt-222 yielded [K(crypt-222)][(Cp*2Ln)2(μ-Bbim˙)], 2-Ln, containing the Bbim3−˙ radical anion. Dark green single crystals of 2-Ln suitable for X-ray analysis were obtained by cooling a concentrated solution to −35 °C for several days in yields of 33% (2-Gd), 35% (2-Tb) and 28% (2-Dy). 2-Ln crystallize in the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and are isostructural to the yttrium congener (Fig. 1, S3 and S4, Tables 2 and S2†).29 In this series of complexes, the coordination sphere of the lanthanide ions constitutes of two η5-coordinated Cp* rings and two bonding nitrogen atoms of the Bbim ligand, forming a bridge between the two metal ions. In addition, a [K(crypt-222)]+ counterion is apparent in the asymmetric unit accompanied by three THF molecules. Inspection of the structural parameters obtained for 2-Ln show that the chemical reduction of the BBim2− bridge is accompanied by significant contraction in the C–C bond connecting the two benzimidazole moieties of (−0.046 Å (Gd); −0.037 Å (Tb); −0.052 Å (Dy)), which can be attributed to the population of the ligand-cantered lowest unoccupied molecular orbital (LUMO), that exhibits a bonding region between the C2 and C2′ atoms.29 Within the series of heavy lanthanide complexes this bond distance seems to be largely indifferent to the metal ion. However, the reduction of the Bbim2− ligand induces a slight asymmetry within the Dy–N bonding, which is reflected in asymmetric Ln–N–N–Ln angles (21.7(4)/29.1(4)° (Gd); 18.5(5)/26.3(5)° (Tb); 15.5(5)/22.8(5)° (Dy)). In addition, the reduction of the Bbim ligand results in a shortened Ln–Ln distance (difference between 1-Ln and 2-Ln: −0.139 Å (Gd); −0.125 Å (Tb); −0.143 Å (Dy)), which also results in a slightly widened bite angle of the ligand (difference between 1-Ln and 2-Ln: 2.8° (Gd); 2.3° (Tb); 3.2° (Dy)). Such deformations are in accordance with the decrease in ionic radii within the lanthanide series. Strikingly, the reduction induces a slight decrease in the bending angle of the Cp moieties, as can be seen by the Cpcent–Ln–Cpcent angles (−2.2° (Gd); −2.2° (Tb); −3.5° (Dy)). The closest intermolecular Ln–Ln distance in 2-Ln (8.930(1) Å (Gd); 8.947(1) Å (Tb); 8.955(1) Å (Dy)) are significantly longer than the intramolecular Ln–Ln distances, hence rendering intermolecular dipolar coupling unlikely (Fig. S5–S7†).
and are isostructural to the yttrium congener (Fig. 1, S3 and S4, Tables 2 and S2†).29 In this series of complexes, the coordination sphere of the lanthanide ions constitutes of two η5-coordinated Cp* rings and two bonding nitrogen atoms of the Bbim ligand, forming a bridge between the two metal ions. In addition, a [K(crypt-222)]+ counterion is apparent in the asymmetric unit accompanied by three THF molecules. Inspection of the structural parameters obtained for 2-Ln show that the chemical reduction of the BBim2− bridge is accompanied by significant contraction in the C–C bond connecting the two benzimidazole moieties of (−0.046 Å (Gd); −0.037 Å (Tb); −0.052 Å (Dy)), which can be attributed to the population of the ligand-cantered lowest unoccupied molecular orbital (LUMO), that exhibits a bonding region between the C2 and C2′ atoms.29 Within the series of heavy lanthanide complexes this bond distance seems to be largely indifferent to the metal ion. However, the reduction of the Bbim2− ligand induces a slight asymmetry within the Dy–N bonding, which is reflected in asymmetric Ln–N–N–Ln angles (21.7(4)/29.1(4)° (Gd); 18.5(5)/26.3(5)° (Tb); 15.5(5)/22.8(5)° (Dy)). In addition, the reduction of the Bbim ligand results in a shortened Ln–Ln distance (difference between 1-Ln and 2-Ln: −0.139 Å (Gd); −0.125 Å (Tb); −0.143 Å (Dy)), which also results in a slightly widened bite angle of the ligand (difference between 1-Ln and 2-Ln: 2.8° (Gd); 2.3° (Tb); 3.2° (Dy)). Such deformations are in accordance with the decrease in ionic radii within the lanthanide series. Strikingly, the reduction induces a slight decrease in the bending angle of the Cp moieties, as can be seen by the Cpcent–Ln–Cpcent angles (−2.2° (Gd); −2.2° (Tb); −3.5° (Dy)). The closest intermolecular Ln–Ln distance in 2-Ln (8.930(1) Å (Gd); 8.947(1) Å (Tb); 8.955(1) Å (Dy)) are significantly longer than the intramolecular Ln–Ln distances, hence rendering intermolecular dipolar coupling unlikely (Fig. S5–S7†).
| 1-Ln | Gd | Tb | Dy |
|---|---|---|---|
| a Cnt = centroid of the pentamethylcyclopentadienyl ring. | |||
| C2–C2′ | 1.454(5) | 1.447(3) | 1.455(4) |
| Av. Ln–N | 2.440(4) | 2.428(3) | 2.423(2) |
| Ln–Ln | 6.239(1) | 6.215(1) | 6.203(3) |
| Cnt–Ln–Cnt | 138.0(1) | 138.0(1) | 138.8(1) |
| Ln1–N1–N2–Ln2 | 0.1(1) | 0.1(1) | 11.8(3)° |
| N1–Ln–N1′ | 72.0(1) | 72.4(1) | 72.3(1) |
| 2-Ln | Gd | Tb | Dy |
|---|---|---|---|
| a Cnt = centroid of the pentamethylcyclopentadienyl ring. | |||
| C2–C2′ | 1.408(4) | 1.410(6) | 1.403(7) |
| Av. Ln–N | 2.390(3) | 2.383(4) | 2.369(4) |
| Ln–Ln | 6.100(1) | 6.096(1) | 6.060(1) |
| Av. Cnt–Ln–Cnt | 135.8(2) | 135.8(2) | 135.3(2) |
| Ln1–N1–N2–Ln2 | 21.7(4)/29.1(4) | 18.5(5)/26.3(5) | 15.5(5)/22.8(5) |
| N1–Ln–N1′ | 74.3(1)/75.3(1) | 74.1(1)/75.2(1) | 75.4(1)/75.6(1) |
These structural changes upon reduction of 1-Ln are accompanied by pronounced changes of the IR spectra (Fig. S8–S12†), which is apparent by the emergence of additional signals around 1550 and 1100 cm−1. Such changes are indicative of a variation in metal–ligand interaction, which has been previously associated with increased ligand nucleophilicity and reduced π donation, traversing from neutral to radical anionic ligands.57
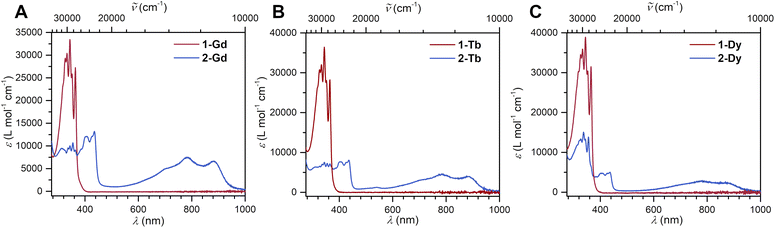
The reduction of 1-Ln results in drastic changes of the UV-vis spectra for 2-Ln: while 1-Ln show no absorption signals above 380 nm, 2-Ln exhibit multiple absorption bands between 380 and 450 nm, and three broad absorptions at 696 nm, 781 and 882 nm (Fig. 2 and S13–S15†). The additional absorptions in the visible region are ascribed to π → π* transitions from the SOMO to the vacant LUMO+1 orbital. This assignment is inspired by the spectroscopic results obtained for a trans-indigo (Ind−˙) radical and the radical-bridged complex meso-[(Ru(bpy)2)2(μ-Ind˙)](ClO4)3 (where Ind = Indigo).58,59
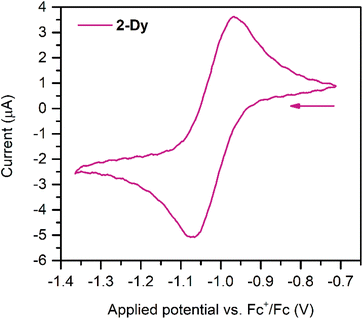
Cyclic voltammetry measurements were carried out on 2-Dy (Fig. 3) to gain insight into the electronic structure of the complex. Here, one quasi reversible feature was observed at −1.02(8) V, which is slightly anodically shifted compared to −1.29(8) V for 2-Y. This feature suggests that further ligand-based reduction to a diamagnetic Bbim4− species and reoxidation to Bbim3−˙ is feasible on the timescale of the electrochemical experiment. Following repeated scans an irreversible oxidation feature at +0.25(8) V appeared, which remained unchanged upon further cycles (Fig. S16†). This feature can potentially be attributed to the oxidation of decomposition products that may arise from scanning towards very negative potentials. Indeed, the analyte proved to gradually decompose over the course of the experiment as indicated through a gradual loss of the intense green colour associated with the Bbim3−˙ radical.
Static magnetic susceptibility behaviour
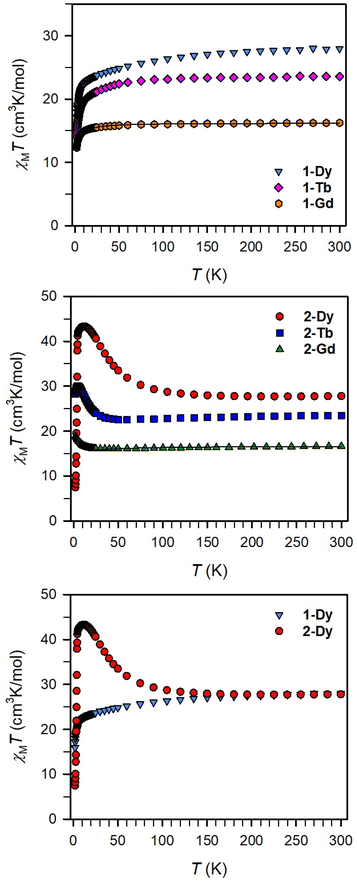
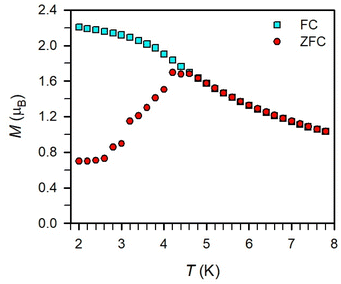
Magnetic exchange coupling in 2-Ln was initially investigated through measurement of the product of magnetic susceptibility and temperature, χMT, Fig. 4 and S17–S24† (ESI contains studies under various fields). Complexes 2-Gd, 2-Tb, and 2-Dy show under a 0.1 T applied dc field a room-temperature χMT values of 16.63, 23.50, and 27.80 cm3 K mol−1 which agree well with the values of 16.13, 24.00, and 28.71 cm3 K mol−1 for two magnetically isolated LnIII (S = 7/2 and g = 2.00 for GdIII, J = 6 and gJ = 3/2 for TbIII, J = 15/2 and gJ = 4/3 for DyIII) and one isolated S = ½ with g = 2.00 radical spin centre. As the temperature is lowered, a rise in χMT is apparent, indicative of a “giant spin” ground state arising from antiferromagnetic exchange coupling between the lanthanide ions and the bisbenzimidazole radical bridge. For 2-Dy, the maximum χMT value of 45.41 cm3 K mol−1 under a 0.1 T applied dc field is the largest found for an organic radical-bridged dinuclear dysprosium compound when compared to values of 32.3–37.1 cm3 K mol−1 and 36.32 cm3 K mol−1 for dysprosium molecules containing radical bridges of bipyrimidine derivatives and tetrapyridylpyrazine, respectively. This large χMT value signifies that both Dy ions in 2-Dy are effectively coupled through the Bbim3−˙ bridge. The peak in χMT is followed by a steep drop to a minimum value of 7.79 cm3 K mol−1 at 2 K. Notably, such precipitous drop is an indication of magnetic blocking which is affirmed by the sharp divergence of field- and zero-field-cooled magnetic susceptibility data at 4.6 K, Fig. 5. For 2-Tb, upon lowering the temperature a rise in χMT is observed first, akin to 2-Dy, however, at the lowest temperatures χMT declines gradually, as opposed to the precipitous drop seen for 2-Dy. This hints at the absence of magnetic blocking for 2-Tb expected on the timescale of this experiment. By contrast, for 2-Gd, an increase of the χMT product is observed at much lower temperature which culminates in a value of 18.83 cm3 K mol−1. At the lowest temperatures, a gradual downturn in χMT is only observed in the dc magnetic susceptibility data collected at 1 T, Fig. S17.†The intricate electronic structures of the paramagnetic lanthanide ions prevent an exact determination of the value and sign of the magnetic exchange coupling constant J for the vast majority of multinuclear lanthanide molecules. GdIII complexes inherent to a half-filled f-electron valence shell render them well-suited for a reliable exchange coupling quantification owing to their spin-only behaviour that is untainted by the effects of spin–orbit coupling. Thus, the dc magnetic susceptibility data were fit to a spin-only Hamiltonian Ĥ = –2JGd-radŜrad·(ŜGd(1) + ŜGd(2)), where JGd-rad accounts for the exchange constant ascribed to the intramolecular GdIII-Bbim3−˙ coupling, Ŝrad is the spin operator for the Bbim3−˙ radical, and ŜGd(n) is the spin operator for each GdIII ion (Fig. 4, and S18–S20†). A decline in χMT at the lowest temperatures at 0.5 and 1 T (Fig. 4 and S19–S21†) is observed and attributed to the Zeeman effect in lieu of long-range antiferromagnetic interactions as verified from variable-field variable-temperature magnetic susceptibility data (Fig. S21†). This effect is only consequential at the lowest temperatures and therefore, a fit to the data excluding the lowest temperature points is considered. Fitting the data at 0.1 T from 5.2 K to 300 K yielded a JGd-rad value of −1.96(2) cm−1, suggestive of strong antiferromagnetic coupling between the GdIII ions and the bridging Bbim3−˙ radical anion to afford a S = 13/2 ground state (Fig. 4). The value of JGd-rad is among the largest quantified for radical-bridged gadolinium complexes. But it is smaller than the coupling constants determined for bipyrimidyl radical- and tetra-2-pyridinylpyrazine radical-containing digadolinium complexes.
Although the anisotropic nature of the dysprosium ions precludes an accurate determination of the magnitude of exchange coupling in 2-Dy, the trend of the temperature dependence of the χMT data is not only similar but in fact much more pronounced in terms of both occurrence of the χMT peak maximum and the shallow minimum, suggesting strong antiferromagnetic dysprosium-radical coupling. In principle, the conceivable exchange coupling mechanism in 2-Ln are a spin polarization involving the empty LnIII 5d orbitals or a direct exchange between the Bbim3−˙ radical and the LnIII 4f orbitals.
To demonstrate the impact of the radical-bridge on the static magnetic susceptibility behavior of 2-Ln, dc magnetic susceptibility data were also collected on polycrystalline samples of 1-Ln in an applied magnetic field of 0.1 T from 2 to 300 K, Fig. 4 and S25–S40† (ESI contains studies under various fields). At 300 K, 1-Gd, 1-Tb, and 1-Dy show under 0.1 T dc field χMT values of 16.24, 23.55, and 27.96 cm3 K mol−1 which are in line with the expected values of 15.76, 23.62, and 28.34 cm3 K mol−1 for two non-interacting LnIII ions. In general, for all 1-Ln, with decreasing temperatures, the χMT values shrink progressively, whereby the decline is much more distinct at the lowest temperatures. Specifically: for 1-Gd, the χMT value remains almost invariant until 20 K (15.49 cm3 K mol−1) after which a more pronounced decline occurs to 9.88 cm3 K mol−1 at 2 K; for 1-Tb, a steady drop in χMT to 20.13 cm3 K mol−1 at 13 K is observed before declining more rapidly to 14.00 cm3 K mol−1 at 2 K; for 1-Dy, a steady decrease in χMT to 22.79 cm3 K mol−1 at 13 K occurs followed by a more rapid decline to 15.93 cm3 K mol−1 at 2 K. This χMT behaviour is ascribed to depopulation of low-lying excited states. Fitting the χMT (T) data for 1-Gd to the spin Hamiltonian Ĥ = −2JŜGdŜGd resulted in a small J value of −0.064(2) cm−1 (with g = 2.029(1)) which confirms that the two metals ions are noninteracting. Notably, placing an additional spin on the bridge increases the strength of magnetic exchange by two orders of magnitude (compare 1-Gdvs.2-Gd). Relative to 2-Ln and expectedly, there is no upturn of χMT observed as this would be indictive of lanthanide-radical coupling (Fig. 4 bottom).
Dynamic magnetic properties
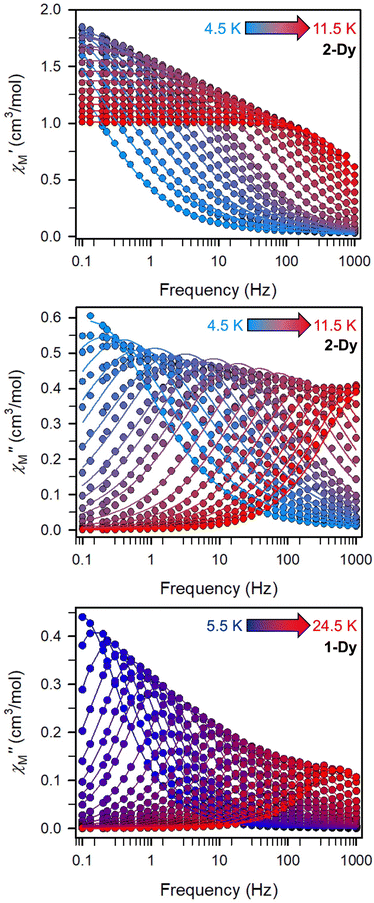
The precipitous drop at low temperatures in the static magnetic susceptibility data hints at magnetic blocking, and thus ac magnetic susceptibility measurements were performed to explore whether slow magnetic relaxation is occurring in each complex 2-Ln (Ln = Tb and Dy). Ac data collected for 2-Dy indeed shows frequency and temperature-dependent out-of-phase susceptibility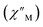 signals that suggest long relaxation times. When exposed to an ac magnetic field of 0.1–1000 Hz at temperatures between 4.5 and 11.5 K under zero dc field, 2-Dy exhibits a single
signals that suggest long relaxation times. When exposed to an ac magnetic field of 0.1–1000 Hz at temperatures between 4.5 and 11.5 K under zero dc field, 2-Dy exhibits a single 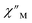 peak which maximum shifts over the whole investigated temperature domain, Fig. 6 and S41–S45†.
peak which maximum shifts over the whole investigated temperature domain, Fig. 6 and S41–S45†.
Magnetic relaxation times, τ, were extracted from fitting plots of 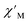 versus
versus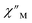 (Cole–Cole plots) to a generalized Debye model, Fig. S42.† The magnitude of τ as function of temperature gives an invaluable insight into the operative magnetic relaxation processes at specific temperatures for a respective system. Especially, in the event of a barrier to spin-reversal, an energy exchange of the system with the lattice via phonons is required to crest the top of the barrier after which magnetic relaxation can take place. This relaxation mechanism, referred to as Orbach process, affords relaxation times τ with an exponential dependence on temperature: τ = τ0
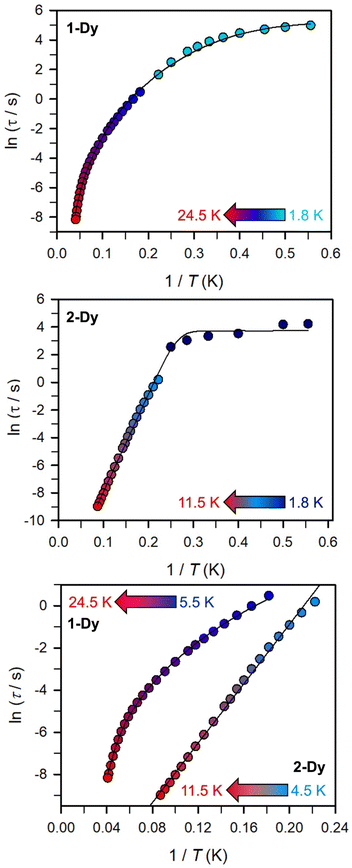
(Cole–Cole plots) to a generalized Debye model, Fig. S42.† The magnitude of τ as function of temperature gives an invaluable insight into the operative magnetic relaxation processes at specific temperatures for a respective system. Especially, in the event of a barrier to spin-reversal, an energy exchange of the system with the lattice via phonons is required to crest the top of the barrier after which magnetic relaxation can take place. This relaxation mechanism, referred to as Orbach process, affords relaxation times τ with an exponential dependence on temperature: τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT), where τ0 is the pre-exponential factor, Ueff is the effective spin-reversal barrier, and kB is the Boltzmann constant. Therefore, the extracted relaxation times were employed for the generation of Arrhenius plots to identify the key parameters Ueff and τ0, Fig. 6. For 2-Dy, the relaxation times τ are entirely temperature-dependent, implying that an Orbach relaxation process is in place over the total probed temperature and frequency range. A fit to the Arrhenius expression yields a barrier to spin relaxation of Ueff = 48.9(1) cm−1 with τ0 = 3.2(1) × 10−7 s. Notably, a slight deviation from linearity is detected at the lowest temperatures which potentially indicates other relaxation processes occurring within 4.5 and 5.25 K, Fig. 7 and S43.† Fitting the data points above 5.25 K afforded approximately constant values for barrier heights indicating the presence of true thermally activated relaxation, Fig. S44 and S45.† For instance, a fit to the Arrhenius equation between 5.5 and 11.5 K affords a slightly higher barrier Ueff = 51.9(1) cm−1 and τ0 = 1.91(1) × 10−7 s, Fig. S45.† In addition, dc relaxation experiments were pursued that can give information in terms of operative relaxation processes below the accessible temperatures through ac magnetic susceptibility techniques, Fig. S50–S56 and Table S3.† In this technique, at a given temperature, first, a large magnetic field is applied to the sample to reach magnetic saturation, second, the dc field is quickly removed, and then the relaxation recorded which follows an exponential dependence. Hence, relaxation times τ between 1.8 and 4 K were extracted from dc relaxation measurements, Table S3.† A successful modelling of the resulting Arrhenius plot required both a quantum tunnelling and Orbach term affording a Ueff = 49.2(1) cm−1 and τ0 = 3.1(1) × 10−7 s, Fig. 7 and S57, Table S4.† The inclusion of a Raman process did not improve the quality of the fit and yielded similar values, Fig. S58.† A fit to only Raman and Orbach processes did not provide meaningful results.
exp(Ueff/kBT), where τ0 is the pre-exponential factor, Ueff is the effective spin-reversal barrier, and kB is the Boltzmann constant. Therefore, the extracted relaxation times were employed for the generation of Arrhenius plots to identify the key parameters Ueff and τ0, Fig. 6. For 2-Dy, the relaxation times τ are entirely temperature-dependent, implying that an Orbach relaxation process is in place over the total probed temperature and frequency range. A fit to the Arrhenius expression yields a barrier to spin relaxation of Ueff = 48.9(1) cm−1 with τ0 = 3.2(1) × 10−7 s. Notably, a slight deviation from linearity is detected at the lowest temperatures which potentially indicates other relaxation processes occurring within 4.5 and 5.25 K, Fig. 7 and S43.† Fitting the data points above 5.25 K afforded approximately constant values for barrier heights indicating the presence of true thermally activated relaxation, Fig. S44 and S45.† For instance, a fit to the Arrhenius equation between 5.5 and 11.5 K affords a slightly higher barrier Ueff = 51.9(1) cm−1 and τ0 = 1.91(1) × 10−7 s, Fig. S45.† In addition, dc relaxation experiments were pursued that can give information in terms of operative relaxation processes below the accessible temperatures through ac magnetic susceptibility techniques, Fig. S50–S56 and Table S3.† In this technique, at a given temperature, first, a large magnetic field is applied to the sample to reach magnetic saturation, second, the dc field is quickly removed, and then the relaxation recorded which follows an exponential dependence. Hence, relaxation times τ between 1.8 and 4 K were extracted from dc relaxation measurements, Table S3.† A successful modelling of the resulting Arrhenius plot required both a quantum tunnelling and Orbach term affording a Ueff = 49.2(1) cm−1 and τ0 = 3.1(1) × 10−7 s, Fig. 7 and S57, Table S4.† The inclusion of a Raman process did not improve the quality of the fit and yielded similar values, Fig. S58.† A fit to only Raman and Orbach processes did not provide meaningful results.
The large magnetic anisotropy associated with the oblate-shaped DyIII ion may engender slow magnetic relaxation, especially if placed in an axial coordination environment. In particular, tailored bis-Cp scaffolds have been shown to boost its single-ion anisotropy.17,60–62 Thus, in light of the local environment of the metal ions in 1-Dy, the occurrence of single-molecule magnet behaviour was examined. When subjected to an ac magnetic field of 0.1–1000 Hz at temperatures between 5.5 and 24.5 K, 1-Dy features a single out-of-phase (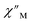 ) signal which maximum shifts over the entire probed temperature range, Fig. 6, S46 and S47.† The relaxation times τ are temperature-dependent but show a substantial curvature implying that 1-Dy has access to multiple pathways for spin relaxation with differing temperature-dependences, Fig. S48.† The best fit required the inclusion of a Raman and an Orbach relaxation process affording Ueff = 185.0(1) cm−1 with τ0 = 1.0(1) × 10−8 s, Fig. S49 and Table S6.† Dc relaxation experiments were conducted from 1.8 to 4.5 K and the relaxation times extracted, Fig. S59–S69 and Table S5.† A satisfactory fit to all relaxation times derived from ac measurements and dc relaxation experiments was achieved by considering quantum tunnelling, Raman and Orbach relaxation processes leading to Ueff = 182.1(1) cm−1 and τ0 = 3.0(1) × 10−8 s, Fig. 7 and S70, Table S6.†
) signal which maximum shifts over the entire probed temperature range, Fig. 6, S46 and S47.† The relaxation times τ are temperature-dependent but show a substantial curvature implying that 1-Dy has access to multiple pathways for spin relaxation with differing temperature-dependences, Fig. S48.† The best fit required the inclusion of a Raman and an Orbach relaxation process affording Ueff = 185.0(1) cm−1 with τ0 = 1.0(1) × 10−8 s, Fig. S49 and Table S6.† Dc relaxation experiments were conducted from 1.8 to 4.5 K and the relaxation times extracted, Fig. S59–S69 and Table S5.† A satisfactory fit to all relaxation times derived from ac measurements and dc relaxation experiments was achieved by considering quantum tunnelling, Raman and Orbach relaxation processes leading to Ueff = 182.1(1) cm−1 and τ0 = 3.0(1) × 10−8 s, Fig. 7 and S70, Table S6.†
1-Tb lacked single-molecule magnet behaviour under zero and applied dc fields which can be attributed to the non-Kramer's nature of TbIII ions alongside the non-ideal coordination environment for the metal centres.
The presence of single-molecule magnetism in 1-Dy can be solely ascribed to the single-ion effect as the metal ions are effectively uncoupled. The determined spin-reversal barrier is comparable to dysprosium metallocenes that feature two axially coordinating Cp ligands and an equatorially binding ligand. The latter induces transverse anisotropies that mix the levels of the ground ± MJ doublet.63 By comparison, the barrier height for 1-Dy is three times larger than for 2-Dy where the latter exhibits only one operative relaxation mechanism at the time scale of the ac measurements. Thus, the radical-bridge is reducing the number of possible relaxation pathways for spin-reversal in 2-Dy, and in this instance was able to suppress the Raman process.
Ab Initio calculations
To give more insight to the magnetic properties of 2-Dy and 2-Tb, ab initio calculations were performed at the SA-CASSCF/RASSI-SO level for each individual LnIII ion in both compounds (see computational details in experimental section). TbIII is a non-Kramers ion and therefore the ground states of both sites in 2-Tb are non-degenerate with essentially planar type anisotropy (Tables S7 and S8†) precluding any SMM behaviour in zero applied dc field. Calculated DyIII ions from 2-Dy present slightly mixed MJ = ±15/2 (∼76%) ground Kramers doublet with gz = 18.5 within the effective spin 1/2 Hamiltonian, and the first excited state calculated at ∼72 cm−1 above (Tables S10 and S11†).As shown earlier, the closest intermolecular Ln–Ln distance of 8.947 Å for 2-Tb and 8.956 Å for 2-Dy are large enough to consider intermolecular dipolar coupling neglectable. In the opposite, the relatively shorter intramolecular Ln–Ln distance of 6.096 Å for 2-Tb and 6.060 Å for 2-Dy makes the presence of an intramolecular Ln–Ln dipolar coupling possible. Using the previously computed individual Ln centres energies and wavefunctions in the POLY_ANISO routine, the intramolecular dipolar interactions are calculated by the following equation (eqn 1):
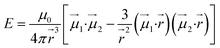 | (1) |
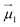 and
and 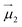 the magnetic moment vectors of the two LnIII centres. Within the same POLYANISO procedure, the exchange interactions (Jfitex) in 2-Tb and 2-Dy between the lanthanide centres and radical bridging ligand are then evaluated by fitting the experimental magnetic susceptibility data (Fig. S72 and S75†) varying the Jfitex in the following Hamiltonian (eqn (2)) with Jcalcdip obtained on the basis of eqn (1):21
the magnetic moment vectors of the two LnIII centres. Within the same POLYANISO procedure, the exchange interactions (Jfitex) in 2-Tb and 2-Dy between the lanthanide centres and radical bridging ligand are then evaluated by fitting the experimental magnetic susceptibility data (Fig. S72 and S75†) varying the Jfitex in the following Hamiltonian (eqn (2)) with Jcalcdip obtained on the basis of eqn (1):21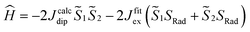 | (2) |
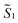 and
and 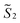 the pseudospin
the pseudospin 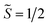 operators at both lanthanide sites, and SRad the spin 1/2 operator at the barycenter of the four nitrogen atoms of the radical bridging ligand. The calculated magnetic susceptibility curves reproduce fairly well the experiment with Jfitex = −0.9 cm−1 for 2-Tb (Fig. S73†) and −3.5 cm−1 for 2-Dy (Fig. S76†). As expected, the Ln–Ln dipolar couplings are very weak (∼−0.05 cm−1) in both compounds and do not play a significant role in the magnetism. The low-lying exchange states are presented in Tables S9 and S12,† and the anisotropy barrier for 2-Tb and 2-Dy are shown in Fig. 8, S78 and S82.† A significantly large tunnel splitting (0.8 × 10−2 cm−1) is observed between degenerate exchange ground states for 2-Tb. This suggests that fast relaxation occurs between these two states in agreement with the absence of relaxation. For 2-Dy, the relaxation is most likely to happen through the first excited state, with a computed Ueff value of 72.5 cm−1. The experimental and calculated Ueff values (49.2 cm−1vs. 72.5 cm−1) are slightly different but demonstrate that exchange coupling governs the relaxation.
operators at both lanthanide sites, and SRad the spin 1/2 operator at the barycenter of the four nitrogen atoms of the radical bridging ligand. The calculated magnetic susceptibility curves reproduce fairly well the experiment with Jfitex = −0.9 cm−1 for 2-Tb (Fig. S73†) and −3.5 cm−1 for 2-Dy (Fig. S76†). As expected, the Ln–Ln dipolar couplings are very weak (∼−0.05 cm−1) in both compounds and do not play a significant role in the magnetism. The low-lying exchange states are presented in Tables S9 and S12,† and the anisotropy barrier for 2-Tb and 2-Dy are shown in Fig. 8, S78 and S82.† A significantly large tunnel splitting (0.8 × 10−2 cm−1) is observed between degenerate exchange ground states for 2-Tb. This suggests that fast relaxation occurs between these two states in agreement with the absence of relaxation. For 2-Dy, the relaxation is most likely to happen through the first excited state, with a computed Ueff value of 72.5 cm−1. The experimental and calculated Ueff values (49.2 cm−1vs. 72.5 cm−1) are slightly different but demonstrate that exchange coupling governs the relaxation.
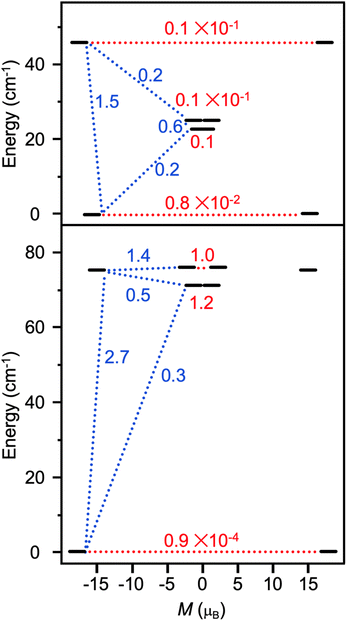 | ||
| Fig. 8 Low-lying exchange spectra calculated in 2-Tb (top) and 2-Dy (bottom) according to Tables S9 and S12,† respectively. Energies of the exchange states (in cm−1) in function of their magnetic moments (in μB) are in bold black lines. The red dotted lines correspond to the tunnelling pathways and the blue dotted lines correspond to Orbach/Raman possible relaxation pathways. Values are the largest matrix elements connecting each exchange doublet. | ||
In order to rationalize the impact of the radical-bridged ligand on the magnetic properties of 2-Dy, the same calculation procedure was applied to 1-Dy. Calculations at the SA-CASSCF/RASSI-SO level for each individual DyIII ion shows purer ground Kramers doublet than for 2-Dy, with MJ = ±15/2 (∼91%) and gz = 19.5 within the effective spin 1/2 Hamiltonian, which indicate a stronger Ising character (Tables S14 and S15†). The first excited state calculated at ∼160 cm−1 above the ground state is also purer than for 2-Dy, and significantly higher in energy. These differences are mostly explained by the absence of charge on the bridging ligand.
In the same way as for 2-Dy, the POLY_ANISO routine was employed to compute the dipolar coupling Jcalcdip (eqn (1) and eqn (2)) found at 0.05 cm−1. This small value confirms the two magnetic centres are not interacting (Fig. S81†).
In parallel, the exchange coupling between the lanthanide centre and the organic radical can be calculated at the CASSCF level for radical-based complexes. Calculations were carried out on the low spin configuration (septet for 2-Gd, sextet for 2-Tb and quintet for 2-Dy) set of molecular orbitals for the hypothetical YIII-Bbim˙-LnIII moieties (Fig. S74, S77 and S79†) at CAS(8,8)SCF, CAS(9,8)SCF and CAS(10,8)SCF level for Ln = Tb, Dy and Gd respectively (see computational details). Using the energy difference between the high spin states and low spin states, Jcalcex is calculated on the basis of the following Heisenberg Hamiltonian model (eqn (3)):
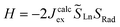 | (3) |
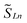 the spin operators of the lanthanide centers and SRad the spin operator of the radical ligand. Jcalcex is equal to −8.9 cm−1, −4.8 cm−1 and −1.8 cm−1 for 2-Gd, 2-Tb and 2-Dy, respectively (Tables 3 and S13†).
the spin operators of the lanthanide centers and SRad the spin operator of the radical ligand. Jcalcex is equal to −8.9 cm−1, −4.8 cm−1 and −1.8 cm−1 for 2-Gd, 2-Tb and 2-Dy, respectively (Tables 3 and S13†).
| Complex | J fitex | J calcex |
|---|---|---|
| 2-Gd | — | −8.9 |
| 2-Tb | −0.9 | −4.8 |
| 2-Dy | −3.5 | −1.8 |
Magnetic hysteresis
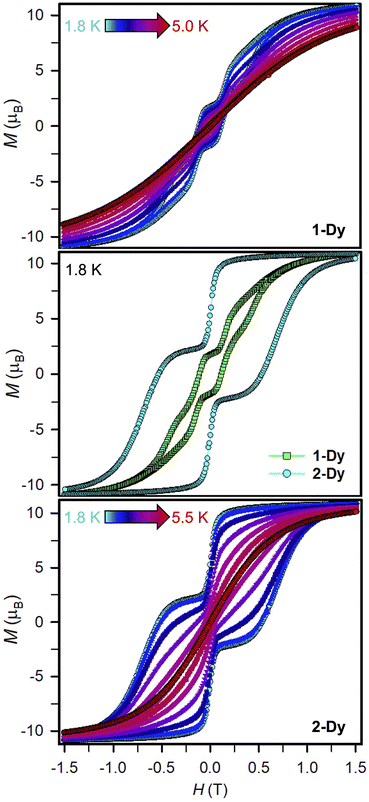
Variable-field magnetization data were collected for polycrystalline samples of 1-Dy and 2-Dy between ±7 T using an average sweep rate of 0.01 T s−1 (Fig. 9, S83, S84, and S89–S91†). The hysteresis loops measured for 1-Dy are open at zero field below 5 K, Fig. 9 top. The coercive field of HC = 0.11 T at 1.8 K steadily decreases as the temperature is raised. By contrast, the hysteresis loops collected for 2-Dy are open at zero field at temperatures below 5.5 K (Fig. 9). At 1.8 K, the coercive field is HC = 0.54 T which is among the largest found for organic radical-bridged SMMs (Fig. 10). The HC preserves its maximum up to approximately 2.5 K followed by a gradual decrease as the temperature is raised, and finally yields a closed hysteresis loop at 5.5 K (HC = 0.001 T, Fig. S83 and S84†). Accordingly, the magnetic hysteretic data are in good agreement with the relaxation times extracted from ac magnetic susceptibility measurements. Notably, the hysteresis loops feature a pronounced step at HC = 0 which points at the presence of quantum tunnelling pathways in 2-Dy. Such temperature-independent relaxation through QTM was not observed through the ac magnetic susceptibility measurements as those are conducted under considerably faster time scale. Remarkably, taking into account akin sweep rates, 2-Dy exhibits the second highest maximum temperature for magnetic hysteresis for organic radical-bridged dinuclear SMMs, surpassing those for tppz3−˙ and HAN3−˙ radical-bridged SMMs and being superseded by magnetic hysteresis temperatures of bpym−˙ radical-bridged SMMs.64,65 Notably, the radical-bridge causes a dramatic change of the shape of the magnetic hysteresis loop where Hc is quintupled in 2-Dy relative to 1-Dy which equals to enhanced suppression of quantum tunneling of the magnetization, Fig. 9 middle.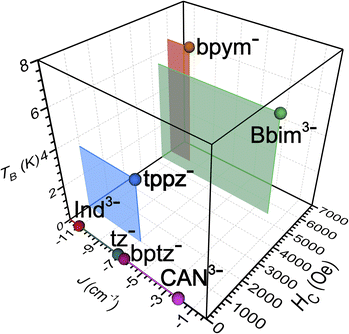 | ||
| Fig. 10 Plot of the exchange coupling constant J against the coercive field Hc and blocking temperature TB of the small set of known radical-bridged dinuclear lanthanide complexes. The J values were determined for Gd compounds except for bptz− which was quantified for the respective Dy complex. The Hc values were taken at 2 K and together with the TB values were derived from Dy compounds. Abbreviations correspond to the radical anions of indigo (Ind3−), 1,2,4,5-tetrazine (tz−), tetrapyridylpyrazine (tppz−), 3,6-bis(2-pyridyl)-1,2,4,5-tetrazine (bptz−), chloroanilate (CAN3−), and 2,2′-bipyrimidine (bpym), respectively.18–20,23–26,66 | ||
Field-dependent magnetization measurements on 1-Ln and 2-Ln were performed between 0–7 T and 2 and 10 K (Fig. S85–S87 and S92–S94†). At 2 K and low fields, the magnetization curve of 2-Dy exhibits at first a steep rise, then a dip at ∼0.1 T, followed by a less pronounced incline to ∼0.28 T, and subsequently goes into a steep ascent to 1 T. Such dip is not detected at higher temperatures and all curves surge to 1.0, 1.10, 1.25 and 1.5 T (4, 6, 8 and 10 K), respectively, before gradually plateauing. Such a nonlinear curve shape is associated with magnetic blocking, which is line with magnetization retention in hysteresis experiments below 5.5 K. The variable-temperature M(H) curve for 1-Dy at 2 K is reminiscent to 2-Dy where a dip at 0.1 T after the initial rise occurs, followed by a less distinct growth until ∼0.16 T, which transitions into a steep surge to 1 T, and gradually increases to a value of 11.70 μB at 7 T. Similarly to 2-Dy, signs for dips are lacking at higher temperatures for 1-Dy and all curves exhibit a gradual increase. By contrast, features indicative of magnetic blocking are not monitored for all magnetization measurements of 1-Gd, 1-Tb, 2-Gd and 2-Tb. All 1-Ln approach a saturation magnetization with values of 15.77 μB for 1-Gd, 10.35 μB for 1-Tb, and 11.70 μB for 1-Dy. By contrast, 2-Gd and 2-Dy approach a saturation magnetization of 14.47 μB and 11.25 μB at 2 K, whereas for 2-Tb a steady increase to a maximum of 11.29 μB is observed without reaching full magnetic saturation. Similar values have been documented for other radical-bridged dilanthanide complexes such as [K(THF)6][(Cp*2Ln)2(μ-Ind˙)] (Ln = Gd, Dy).24
The occurrence of such large magnetic hysteresis and coercivity in 2-Dy has huge ramifications for the SMM field: Although the determined coupling constant is moderate for a radical-bridged lanthanide system (Scheme 1 and Fig. 10) the generated coupling is evidently strong enough to suppress QTM. When compared to 1-Dy, the magnetic coupling is indeed strong enough to also suppress the Raman relaxation process. In fact, the coupling through the Bbim radical is much more efficient than through a chloroanilate radical which has been demonstrated to give a similar coupling strength in [CoCp2][(HBpz3)2Ln)2(μ-CAN˙)] (HBpz3− = hydrotris(pyrazol-1-yl)borate, CAN3−˙ = chloroanilate).18 Notably, HC of 2-Dy is with 5400 Oe huge and only surpassed by 6000 Oe detected for the currently best performing dinuclear organic radical-bridged SMM, [(Cp*2Ln)2(μ-bpym˙)]BPh4, where JGd–Rad approaches a value of −10 cm−1. Such deviations may be rationalized by considering magnetostructural correlations on each of these compounds and a thorough inspection of their crystallographic parameters (Table S16†): While the inner-ligand distances, especially of the ring-connecting C–C bonds, are essentially identical in both complexes (<0.01 Å), the Dy–N and Dy–Dy distances in 2-Dy are significantly shortened by 0.051 Å and 0.365 Å, respectively. Moreover, the bite angle of the N–Dy–N moiety for the Bbim radical ligand is found to be significantly widened by 7.1° for 2-Dy. This may be a first indication for alterations in the charge density around the lanthanide ions. In general, the coercivity Hc raises as J increases since for exchange-coupled systems, the separation between the ground and first excited state is given by |15JDy−Rad| and therefore directly proportional to the exchange coupling strength.21,25 Accordingly, the smaller magnetic coupling in 2-Dy is expected to afford a smaller spin-reversal barrier and indeed, this is in accordance with the acquired experimental data (compare Ueff = 49.2(1) cm−1vs. Ueff = 87.8(3) cm−1). In addition, a larger separation between those states is anticipated to give a reduced mixing of the mj states. The ground state Kramer's doublet in 2-Dy comprises a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of the MJ = ±15/2 and ±11/2 states, though the unknown composition of the ground state Kramer's doublet in [(Cp*2Ln)2(μ-bpym˙)]BPh4 precludes a direct comparison. However, theoretical analysis exists on structurally related methyl-substituted bpym˙ radical-bridged complex, [(Cp*2Ln)2(μ-bpym-Me2˙)]BPh4, featuring JGd–Rad = −9.54 cm−1, Ueff = 82 cm−1, and THyst = 6.5 K. Intriguingly, the calculated separation between ground state and first excited Kramer doublet was found to be 72.51 cm−1, which coincides excellently with the separation calculated for 2-Dy (73.4/71.5 cm−1). The calculations reveal that the ground state g-tensor components in 2-Dy possesses considerably larger equatorial contributions (0.0 (gx) 0.1 (gy) 18.6 (gz) (2-Dy)) relative to the bpym-Me2 bridged complex (0.00757 (gx) 0.0152 (gy) 19.604 (gz)). Moreover, the principal axes of the ground state g-tensors were found to lie perpendicular to the Bbim plane, following the Cnt–Dy–Cnt (where Cnt = centroid of the pentamethylcyclopentadienyl ring) axis (Fig. S80†), which is similar to the bpym-Me2-bridged complex, where the Cp*2 ligands are dominating the orientation of the magnetic moments. Notably, the orientation in the CAN3−˙ bridged complex is within the ligand plane, but the axes are pointing towards the ligand.18 Since the auxiliary ligand framework is identical for both 2-Dy and the bpym-Me2-bridged complexes, the differences likely originate from the bridging Bbim radical ligand. Taking into account the spin density distribution probed on the yttrium Bbim radical analogue, large spin density is expected to be also on the nitrogen donor atoms in 2-Dy.29 These observations could hint at the Bbim providing a somewhat equatorial ligand field and thus, matching Bbim radicals with prolate ions such as ErIII innate to an axially elongated electron cloud has the potential to lead to even better performing radical-bridged SMMs.
1 mixture of the MJ = ±15/2 and ±11/2 states, though the unknown composition of the ground state Kramer's doublet in [(Cp*2Ln)2(μ-bpym˙)]BPh4 precludes a direct comparison. However, theoretical analysis exists on structurally related methyl-substituted bpym˙ radical-bridged complex, [(Cp*2Ln)2(μ-bpym-Me2˙)]BPh4, featuring JGd–Rad = −9.54 cm−1, Ueff = 82 cm−1, and THyst = 6.5 K. Intriguingly, the calculated separation between ground state and first excited Kramer doublet was found to be 72.51 cm−1, which coincides excellently with the separation calculated for 2-Dy (73.4/71.5 cm−1). The calculations reveal that the ground state g-tensor components in 2-Dy possesses considerably larger equatorial contributions (0.0 (gx) 0.1 (gy) 18.6 (gz) (2-Dy)) relative to the bpym-Me2 bridged complex (0.00757 (gx) 0.0152 (gy) 19.604 (gz)). Moreover, the principal axes of the ground state g-tensors were found to lie perpendicular to the Bbim plane, following the Cnt–Dy–Cnt (where Cnt = centroid of the pentamethylcyclopentadienyl ring) axis (Fig. S80†), which is similar to the bpym-Me2-bridged complex, where the Cp*2 ligands are dominating the orientation of the magnetic moments. Notably, the orientation in the CAN3−˙ bridged complex is within the ligand plane, but the axes are pointing towards the ligand.18 Since the auxiliary ligand framework is identical for both 2-Dy and the bpym-Me2-bridged complexes, the differences likely originate from the bridging Bbim radical ligand. Taking into account the spin density distribution probed on the yttrium Bbim radical analogue, large spin density is expected to be also on the nitrogen donor atoms in 2-Dy.29 These observations could hint at the Bbim providing a somewhat equatorial ligand field and thus, matching Bbim radicals with prolate ions such as ErIII innate to an axially elongated electron cloud has the potential to lead to even better performing radical-bridged SMMs.
Taken together, it becomes apparent that the correlation between magnetic anisotropy, magnetic coupling, energy barrier, relaxation processes, open hysteresis loops and coercivity are still poorly understood and require further research in order to boost blocking temperatures towards room temperature for polynuclear complexes containing organic radical linkers.
Conclusion
The bridging dianion of 2,2′-bisbenzimidazole was employed to generate the first series of dinuclear lanthanide complexes containing Bbim2−. These molecules were further reduced to a second series of lanthanide complexes that consist of the radical bridging ligand, Bbim3−˙, representing the first compounds with this radical paired with any paramagnetic metal ion. The two series of molecules represent a rare study of the magnitude of exchange coupling and how that impacts the dynamic magnetic properties. The foregoing magnetic results demonstrate that the Bbim3−˙ engenders strong antiferromagnetic magnetic exchange coupling when paired with the mid-sized paramagnetic lanthanide ions Gd, Tb and Dy, giving rise to a “giant spin”. Remarkably, the coupling in 1-Gd is negligible and in fact, placing an additional spin on the bridge in 2-Gd increases the strength of magnetic exchange by two orders of magnitude. The strong coupling leads then to extraordinary single molecule magnet behaviour for the Dy congener, 2-Dy, which exhibits a spin reversal barrier of 49.2(1) cm−1 and magnetic blocking below 5.5 K. Notably, the strong magnetic exchange in 2-Dy suppresses quantum tunnelling of the magnetization effectively, affording the second highest coercive field for any dinuclear organic radical-bridged complex. Intriguingly, 1-Dy shows open hysteresis loops up to 5 K, where the single-molecule magnet behaviour originates from single-ion effect. In contrast to 2-Dy, there are several pathways to spin-reversal operative in 1-Dy one of which is the Raman relaxation process. Indeed, the relaxation times derived from ac magnetic measurements revealed that the strong coupling in 2-Dy is able to suppress both quantum tunnelling of the magnetisation and the Raman relaxation. Moreover, elaborate electronic structure calculations at the CASSCF level were employed to gain insight into the electronic structure and relaxation mechanism in this series of complexes. Calculations allowed a semi-quantitative assessment of the LnIII–Bbim3−˙ radical coupling where this antiferromagnetic interaction governs the relaxation of the magnetic moment. An additional feature of the 2-Dy complex is its accessible 4− oxidation state for the Bbim bridge on the time scale of the electrochemical experiment. Taken together, the Bbim3−˙ radicals produce powerful dinuclear molecular magnets and constitute an appealing path forward towards high-performing SMMs of higher nuclearity such as of tetra- or octanuclear nature. Notably, the systematic access to Bbim-bridged complexes allows for the synthesis of molecules containing functionalized Bbim ligands with substituents on the phenyl positions where the effects of electron withdrawing or donating groups on the strength of magnetic exchange concomitant with the arising magnetization dynamics can be probed. The high tunability of the Bbim ligand as well as controlled access of multiple oxidation states also enables the pursuit of two- and three-dimensional magnetic systems, such as magnetic MOFs, and conductive materials. Finally, the access of many other bisimidazole-based radicals can be envisioned, albeit yet unknown, and clearly in need of exploration for the development of new powerful magnets.Data availability
All computational data, spectroscopic data, supplementary figures and tables, and detailed crystallographic information can be found in the ESI.† Crystallographic data are available via the Cambridge Crystallographic Data Centre (CCDC): 2172767 (1-Gd), 2172768 (1-Tb), 2172769 (1-Dy), 2172770 (2-Gd), 2176480 (2-Tb) and 1997167 (2-Dy).Author contributions
F. B. prepared and characterised the compounds via crystallography, spectroscopy, electrochemistry, and magnetometry. L. La Droitte, O. Cador, B. Le Guennic performed CASSCF-SO calculations. S. D. assisted with data analysis, formulated, and directed the research, and wrote the manuscript with input from all authors.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
S. D. is grateful to the Department of Chemistry at Michigan State University (MSU) for generous start-up funds. We are grateful to Dr Rui Huang (MSU) for assistance with CHN analyses. Funding for the Single Crystal X-ray diffractometer was provided by the MRI program by the National Science Foundation under Grant No. CHE-1919565. L. L. D. and B. L. G. thanks the French GENCI/IDRIS-CINES centers for high-performance computing resources. L. L. D. acknowledges the ANR (French National Research Agency) under project number ANR-19-CE07-0019- 1 for PhD financial support.Notes and references
- L. Ji, J. Shi, J. Wei, T. Yu and W. Huang, Air-Stable Organic Radicals: New-Generation Materials for Flexible Electronics?, Adv. Mater., 2020, 32, 1908015 Search PubMed.
- Z. X. Chen, Y. Li and F. Huang, Persistent and Stable Organic Radicals: Design, Synthesis, and Applications, Chem, 2021, 7, 288–332 CAS.
- J. McGuire, H. N. Miras, J. P. Donahue, E. Richards and S. Sproules, Ligand Radicals as Modular Organic Electron Spin Qubits, Chem. – Eur. J., 2018, 24, 17598–17605 CrossRef CAS PubMed.
- J. McGuire, H. N. Miras, E. Richards and S. Sproules, Enabling Single Qubit Addressability in a Molecular Semiconductor Comprising Gold-Supported Organic Radicals, Chem. Sci., 2019, 10, 1483–1491 RSC.
- M. A. Lemes, G. Brunet, A. Pialat, L. Ungur, I. Korobkov and M. Murugesu, Strong Ferromagnetic Exchange Coupling in a {NiII4} Cluster Mediated through an Air-Stable Tetrazine-Based Radical Anion, Chem. Commun., 2017, 53, 8660–8663 RSC.
- X. Ma, E. A. Suturina, M. Rouzières, M. Platunov, F. Wilhelm, A. Rogalev, R. Clérac and P. Dechambenoit, Using Redox-Active π Bridging Ligand as a Control Switch of Intramolecular Magnetic Interactions, J. Am. Chem. Soc., 2019, 141, 7721–7725 CrossRef CAS PubMed.
- X. Ma, E. A. Suturina, S. De, P. Négrier, M. Rouzières, R. Clérac and P. Dechambenoit, A Redox-Active Bridging Ligand as a Tool to Promote Spin Delocalization, High Spin Complexes and Magnetic Multi-Switchability, Angew. Chem., Int. Ed., 2018, 57, 7841–7845 CrossRef CAS PubMed.
- M. N. Leuenberger and D. Loss, Quantum Computing in Molecular Magnets, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- D. Gatteschi and R. Sessoli, Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Magnetic Memory of a Single-Molecule Quantum Magnet Wired to a Gold Surface, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Molecular Spintronics Using Single-Molecule Magnets, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- S. Sanvito, Molecular spintronics. Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, Magnetic Interaction between a Radical Spin and a Single-Molecule Magnet in a Molecular Spin-Valve, ACS Nano, 2015, 9, 4458–4464 CrossRef CAS PubMed.
- S. Demir, I. R. Jeon, J. R. Long and T. D. Harris, Radical Ligand-Containing Single-Molecule Magnets, Coord. Chem. Rev., 2015, 289–290, 149–176 Search PubMed.
- C. Benelli and D. Gatteschi, Magnetism of Lanthanides in Molecular Materials with Transition-Metal Ions and Organic Radicals, Chem. Rev., 2002, 102, 2369–2387 CrossRef CAS PubMed.
- S. T. Liddle and J. Van Slageren, Improving f-Element Single Molecule Magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- J. D. Rinehart and J. R. Long, Exploiting Single-Ion Anisotropy in the Design of f-Element Single-Molecule Magnets, Chem. Sci., 2011, 2, 2078–2085 RSC.
- P. Zhang, F. Benner, N. F. Chilton and S. Demir, Organometallic Lanthanide Bismuth Cluster Single-Molecule Magnets, Chem, 2022, 8, 717–730 CAS.
- T. Pugh, V. Vieru, L. F. Chibotaru and R. A. Layfield, Magneto-Structural Correlations in Arsenic- and Selenium-Ligated Dysprosium Single-Molecule Magnets, Chem. Sci., 2016, 7, 2128–2137 RSC.
- T. Pugh, N. F. Chilton and R. A. Layfield, Antimony-Ligated Dysprosium Single-Molecule Magnets as Catalysts for Stibine Dehydrocoupling, Chem. Sci., 2017, 8, 2073–2080 RSC.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant Coercivity and High Magnetic Blocking Temperatures for N23− Radical-Bridged Dilanthanide Complexes upon Ligand Dissociation, Nat. Commun., 2017, 8, 2144 Search PubMed.
- C. A. Gould, K. R. Mcclain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Ultrahard Magnetism from Mixed-Valence Dilanthanide Complexes with Metal–Metal Bonding, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- B. S. Dolinar, D. I. Alexandropoulos, K. R. Vignesh, T. James and K. R. Dunbar, Lanthanide triangles supported by radical bridging ligands, J. Am. Chem. Soc., 2018, 140, 908–911 CrossRef CAS PubMed.
- F.-S. Guo and R. A. Layfield, Strong direct exchange coupling and single-molecule magnetism in indigo-bridged lanthanide dimers, Chem. Commun., 2017, 53, 3130–3133 Search PubMed.
- C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, Substituent Effects on Exchange Coupling and Magnetic Relaxation in 2,2'-Bipyrimidine Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2020, 142, 21197–21209 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, Exchange Coupling and Magnetic Blocking in Bipyrimidyl Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2012, 134, 18546–18549 CrossRef CAS PubMed.
- P. H. Dinolfo, M. E. Williams, C. L. Stern and J. T. Hupp, Rhenium-based Molecular Rectangles as Frameworks for Ligand-centered Mixed Valency and Optical Electron Transfer, J. Am. Chem. Soc., 2004, 126, 12989–13001 Search PubMed.
- T. Wu, Y. J. Lin and G. X. Jin, Design and Self-Assembly of Variform Organometallic Macrocycle with Terminal Imidazole-Based Bridging Ligands Utilizing Joints Twist and Rotation, Dalton Trans., 2014, 43, 2356–2360 RSC.
- F. Benner and S. Demir, Isolation of the Elusive Bisbenzimidazole Bbim3–• Radical Anion and Its Employment in a Metal Complex, Chem. Sci., 2022, 13, 5818–5829 RSC.
- W. J. Evans, S. A. Kozimor, J. W. Ziller and N. Kaltsoyannis, Reactivity, and Density Functional Theory Analysis of the Six-Electron Reductant, [(C5Me5)2U]2(μ-η6:η6-C6H6), Synthesized via a New Mode of (C5Me5)3M Reactivity, J. Am. Chem. Soc., 2004, 126, 14533–14547 CrossRef CAS PubMed.
- B. J. Barker and P. G. Sears, Conductance Behaviour of Some Ammonium and Partially Substituted Ammonium Tetraphenylborates in Oxazolidones, J. Phys. Chem., 1974, 78, 2687–2688 CrossRef CAS.
- A. F. Henwood, D. Antón-García, M. Morin, D. Rota Martir, D. B. Cordes, C. Casey, A. M. Z. Slawin, T. Lebl, M. Bühl and E. Zysman-Colman, Conjugated, Rigidified Bibenzimidazole Ancillary Ligands for Enhanced Photoluminescence Quantum Yields of Orange/Red-Emitting Iridium(III) Complexes, Dalton Trans., 2019, 48, 9639–9653 Search PubMed.
- D. E. Bergbreiter and J. M. Killough, Reactions of Potassium-Graphite, J. Am. Chem. Soc., 1978, 100, 2126–2134 CrossRef CAS.
- G. A. Bain and J. F. Berry, Diamagnetic Corrections and Pascal's Constants, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
- COSMO V1.61, Software for the CCD Detector Systems for Determining Data Collection Parameters, Bruker Analytical X-ray Systems, Madison, WI, 2009 Search PubMed.
- APEX2 V2010.11-3, Software for the CCD Detector System, Bruker Analytical X-ray Systems, Madison, WI, 2010 Search PubMed.
- R. H. Blessing, SAINT V 7.68a, Software for the Integration of CCD Detector System, Bruker Analytical X-ray Systems, Madison, WI, 2010 Search PubMed.
- R. H. Blessing, SADABS V2.008/2, Program for Absorption Corrections using Bruker-AXS CCD Based on the Method of Robert Blessing, Acta Crystallogr., 1995, A51, 33–38 CrossRef CAS PubMed.
- CrysAlisPro Software System, Rigaku Corporation, Oxford, 2020 Search PubMed.
- SCALE3 ABSPACK Empirical Absorption Correction, CrysAlis Pro – Software Package, Rigaku Corporation, Oxford, 2020 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: A Complete Structure Solution, Refinement and Analysis Program, J. Appl. Crystallogr., 2009, 42, 339–341 Search PubMed.
- G. M. Sheldrick, SHELXT – Integrated Space-Group and Crystal-Structure Determination, Acta Crystallogr., 2015, A71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Crystal Structure Refinement with SHELXL, Acta Crystallogr., 2015, C71, 3–8 CrossRef PubMed.
- G. T. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. T. te Velde and E. J. Baerends, Towards an Order-N DFT Method, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- Amsterdam Density Functional (ADF), SCM Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2017, http://www.scm.com Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic Regular Two-Component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS PubMed.
- F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, Cholesky Decomposition-Based Multiconfiguration Second-Order Perturbation Theory (CD-CASPT2): Application to the Spin-State Energetics of CoIII(diiminato)(NPh), J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur and A. Soncini, The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment, Angew. Chem., Int. Ed., 2008, 120, 4194–4197 CrossRef.
- L. Ungur, W. V. den Heuvel and L. F. Chibotaru, Ab initio Investigation of the Non-collinear Magnetic Structure and the Lowest Magnetic Excitations in Dysprosium Triangles, New J. Chem., 2009, 33, 1224–1230 RSC.
- M. E. Lines, Orbital Angular Momentum in the Theory of Paramagnetic Clusters, J. Chem. Phys., 1971, 55, 2977–2984 Search PubMed.
- W. Kaim, The Transition Metal Coordination Chemistry of Anion Radicals, Coord. Chem. Rev., 1987, 76, 187–235 CrossRef CAS.
- D. V. Konarev, L. V. Zorina, M. S. Batov, S. S. Khasanov, A. Otsuka, H. Yamochi, H. Kitagawa and R. N. Lyubovskaya, Optical and Magnetic Properties of Trans-Indigo˙− Radical Anions. Magnetic Coupling between Trans-Indigo˙− (S = 1/2) Mediated by Intermolecular Hydrogen N-H⋯O=C Bonds, New J. Chem., 2019, 43, 7350–7354 RSC.
- M. Chatterjee, P. Mondal, K. Beyer, A. Paretzki, W. Kaim and G. K. Lahiri, A Structurally Characterised Redox Pair Involving an Indigo Radical: Indigo Based Redox Activity in Complexes with One or Two [Ru(Bpy)2] Fragments, Dalton Trans., 2017, 46, 5091–5102 RSC.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- F. Guo, B. M. Day, Y. Chen, M. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic Hysteresis up to 80 Kelvin in a Dysprosium Metallocene Single-Molecule Magnet, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular Magnetic Hysteresis at 60 Kelvin in Dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- A. Swain, T. Sharma and G. Rajaraman, Strategies to Quench Quantum Tunneling of Magnetization in Lanthanide Single Molecule Magnets, Chem. Commun., 2023, 59, 3206–3228 RSC.
- C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, A Trinuclear Radical-Bridged Lanthanide Single-Molecule Magnet, Angew. Chem., Int. Ed., 2017, 56, 10103–10107 CrossRef CAS PubMed.
- S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Exchange Coupling and Magnetic Blocking in Dilanthanide Complexes Bridged by the Multi-Electron Redox-Active Ligand 2,3,5,6-tetra(2-pyridyl)pyrazine, Chem. Sci., 2014, 5, 4701–4711 Search PubMed.
- N. Mavragani, A. A. Kitos, A. Mansikkamäki and M. Murugesu, New Members of Radical Bridged Ln2 Metallocene Single-Molecule Magnets Based on the Unsubstituted 1,2,4,5-tetrazine Ligand, Inorg. Chem. Front., 2023, 10, 259–266 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2172767 (1-Gd), 2172768 (1-Tb), 2172769 (1-Dy), 2172770 (2-Gd), 2176480 (2-Tb) and 1997167 (2-Dy). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01562a |
| This journal is © The Royal Society of Chemistry 2023 |