Open Access Article
Open Access ArticlePET recycling under mild conditions via substituent-modulated intramolecular hydrolysis†
Shengbo
Zhang‡
a,
Yingying
Xue‡
b,
Yanfen
Wu‡
a,
Yu-Xiao
Zhang
 a,
Ting
Tan
*b and
Zhiqiang
Niu
a,
Ting
Tan
*b and
Zhiqiang
Niu
 *a
*a
aDepartment State Key Laboratory of Chemical Engineering, Department of Chemical Engineering, Tsinghua University, Beijing 100084, China. E-mail: niuzq@tsinghua.edu.cn
bLaboratory of Theoretical and Computational Nanoscience, CAS Key Laboratory of Nanophotonic Materials and Devices, National Center for Nanoscience and Technology, Chinese Academy of Sciences, Beijing 100190, China. E-mail: tant@nanoctr.cn
First published on 25th May 2023
Abstract
Catalytic depolymerization represents a promising approach for the closed-loop recycling of plastic wastes. Here, we report a knowledge-driven catalyst development for poly(ethylene terephthalate) (PET) recycling, which not only achieves more than 23-fold enhancement in specific activity but also reduces the alkali concentration by an order of magnitude compared with the conventional hydrolysis. Substituted binuclear zinc catalysts are developed to regulate biomimetic intramolecular PET hydrolysis. Hammett studies and density functional theory (DFT) calculations indicate that the substituents modify the charge densities of the active centers, and an optimal substituent should slightly increase the electron richness of the zinc sites to facilitate the formation of a six-membered ring intermediate. The understanding of the structure–activity relationship leads to an advanced catalyst with a specific activity of 778 ± 40 gPET h−1 gcatal−1 in 0.1 M NaOH, far outcompeting the conventional hydrolysis using caustic bases (<33.3 gPET h−1 gcatal−1 in 1–5 M NaOH). This work opens new avenues for environmentally benign PET recycling.
Introduction
The global plastic production reached 359 million tons in 2018, and the production rate is projected to keep growing rapidly.1–3 Although plastics are indispensable to modern society, they are generating more than 200 million tons of waste annually. The mismanaged plastic debris ends up in soils, freshwater, and ocean, posing severe threats to ecosystems. PET is the most abundantly manufactured polyester, with a volume of production over 70 million tons in 2020.1,4,5 It is widely used in synthetic fibers and beverage bottles due to its high chemical and thermal resistance, low permeability, and high strength-to-weight ratio.2 As PET accounts for 12% of global solid waste,6–8 there is a growing impetus to increase its recycling levels. The majority of post-consumer PET products are processed by mechanical recycling. But this method negatively affects the mechanical properties of the material, and the reclaimed PET (r-PET) can only be used in low-quality downstream products.9,10 Alternatively, chemical recycling depolymerizes PET waste into its original monomers and thus holds great promise for bottle-to-bottle recycling.11Catalysis has considerable potential to accelerate the reaction rate of chemical recycling processes. Several catalysts have been developed for PET depolymerization, including Zn(OAc)2, ZnO nanoparticles, tetrabutyl ammonium iodide (TBAI), ionic liquids, and so on. Compared with them, transition metal complexes have shown advantages due to their structure tunability.12–17 For instance, Zn(II)- and Mg(II)-complexes with various ligand structures can facilitate the glycolysis of PET.12–14 Ru(II)-complexes catalyze the hydrogenolysis of PET with high tolerance to impurities.15,16 However, due to the chemical inertness of PET, the current strategies for PET depolymerization are usually driven by high temperatures (150–200 °C), high pressure (20–40 atm), or high concentrations of bases or acids. More environmentally benign PET recycling approaches are needed to reduce the carbon footprint and bring about energy savings for plastic circularity. This goal relies on our understanding of the relationship between the catalyst structure and its catalytic activity.
Alkaline hydrolysis is a promising approach for PET recycling. Compared with other methods, the products from hydrolysis are easy to separate and the as-obtained terephthalic acid (TPA) is of high purity.18,19 These advantages make the hydrolysis method more suitable for bottle-to-bottle recycling. Nevertheless, it is performed in concentrated alkaline solution (1–5 M NaOH, Table S1†), and the product separation consumes a large volume of acid for neutralization to make TPA precipitate out of solution. Thus, reducing the alkali concentration is of great significance for environmental benignity and cost reduction. PET hydrolysis typically follows an intermolecular pathway (Fig. 1a), and the reaction rate would be largely reduced with the reduction of alkali concentration. Transforming the hydrolysis into an intramolecular pathway can achieve rate enhancement via the proximity effect (Fig. 1b). We recently have demonstrated this strategy using a binuclear zinc catalyst to bring the reactants in close vicinity.20 This is equivalent to increasing the local concentration of alkali and therefore achieves efficient PET depolymerization in dilute alkaline solution (0.1 M NaOH, Fig. 1b). Despite this, regulating the reactivity of the dizinc sites remains an open challenge.
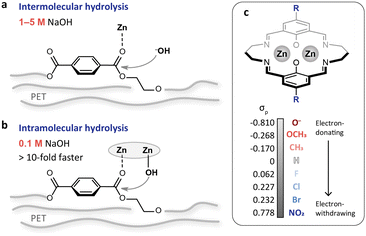 | ||
| Fig. 1 (a and b) Schematic illustrations of the intermolecular (a) and intramolecular (b) PET hydrolysis. The intramolecular pathway accelerates PET hydrolysis through the proximity effect, achieving more than 10-fold activity enhancement even when the NaOH concentration is reduced from 1–5 M to 0.1 M. (c) Binuclear zinc catalyst with para-substituents of different electron-donating and withdrawing capacities. The Hammett σp values are adapted from previous work by Hansch et al.21 | ||
In this regard, herein we investigate the structure–activity relationship for intramolecular PET hydrolysis and develop a more efficient catalyst on this basis. A series of para-substituted binuclear zinc complexes (Zn2L-R: R = –OH, –OCH3, –CH3, –H, –F, –Cl, –Br, and –NO2) are prepared. These substituents are similar in steric demand but different in electronic effects (Fig. 1c). Hammett reactivity studies reveal a volcano-shaped correlation between the reaction rate and the Hammett constant for different substituents. Mechanistic studies indicate that the electronic structure of the zinc site is modulated by the substituents and thus affects the potential-determining step (PDS). The activity “volcano” plot further guides us to identify a more efficient PET-degrading catalyst with more than 23-fold enhancement in specific activity under much less caustic conditions compared with the conventional hydrolysis.
Results and discussion
Hammett relation for substituted binuclear zinc catalysts
The substituted binuclear zinc catalysts were synthesized via a Schiff base reaction according to a previously reported method with minor modifications.22–24 Single-crystal X-ray diffraction (SCXRD), powder X-ray diffraction (XRD), proton nuclear magnetic resonance (1H NMR), and elemental analysis confirmed that these binuclear catalysts possess μ2-O bridged Zn–Zn sites (Fig. S1 and Table S2†). The para-positioned substituents in the phenyl ring of the macrocycle (Zn2L-R: R = –OH, –OCH3, –CH3, –H, –F, –Cl, –Br, and –NO2) present similar steric demand but very different electronic effects. We hypothesize that the binding strengths of the reactants on zinc sites (Fig. 1b) are related to the electron richness/poorness of the active centers. In other words, the substituents in the para position may modify the PET hydrolysis rate via electronic effects.To test this hypothesis, the PET hydrolysis was performed in 0.1 M NaOH aqueous solution at 60 °C. These reaction conditions are relatively mild compared with previously reported hydrolysis in terms of alkali concentration (0.1 M versus 1–5 M) and reaction temperature (60 °C versus 80–150 °C), but they deliver a comparable space-time-yield (STY) and specific activity (Table S1†), manifesting the advantage of the binuclear zinc complex in depolymerizing PET. To exclude the effect of mass transfer on the reaction rate, we examined the hydrolysis at different stirring speeds (0–800 rpm). It shows that a stirring speed of 400 rpm can effectively rule out the diffusion limitation (Fig. S2a†). The absence of the mass transfer effect was further confirmed by the Madon–Boudart test (Fig. S2b†),25 wherein the depolymerization rate of PET increased linearly with the concentration of the binuclear zinc catalyst.
The subsequent kinetic study suggests that PET hydrolysis follows a shrinking core model (Fig. 2a and S3a†). We first investigated the change of the particle size of PET during the reaction using a laser particle size analyzer (Fig. S3b†). The average particle size decreased from the initial 120–250 μm to 100–220 μm when the PET conversion was 28% and further reduced to 70–150 μm when the conversion reached 65%. XRD and differential scanning calorimetry (DSC) analysis of the fresh and the residual unreacted PET particles indicates that the crystallinity of PET doesn't change (38%, 38%, and 37% for the conversions of 0%, 28%, and 65%, respectively) during the hydrolysis (Fig. S3c and d†). These results imply that the hydrolysis may proceed on the surface of PET particles (Fig. S3a†). We then changed the particle size of raw PET in the range 20–120 mesh and investigated the variation of the reaction rate. It turns out that the hydrolysis rate is inversely proportional to the particle size of raw PET (Fig. S3e†), presenting a further hint of surface reactions.26–30 The shrinking core model is commonly used to describe reactions that take place on the solid surface.29,30 Therefore, we applied it here for kinetic modelling. As shown in Fig. 2a, the PET hydrolysis kinetics over the methyl-substituted Zn2L complex presents a good linear relationship (R2 > 0.99) based on the shrinking core model (Methods in the ESI†). Apart from this, all other binuclear zinc complexes exhibit similar linear dependence at different hydrolysis temperatures (Fig. S4†), further corroborating the validity of the shrinking core model for PET hydrolysis.
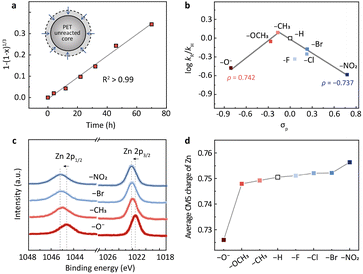 | ||
| Fig. 2 (a) The hydrolysis kinetics of PET based on the shrinking core model (inset). (b) The volcano-shaped correlation between the reaction rates and the Hammett constants (σp) for different substituents. The σp values are from previous work by Hansch et al.21 It should be noted that the –OH will convert into –O− due to the alkaline conditions. (c) XPS of Zn 2p spectra for binuclear zinc catalysts with different para-substituents (R = –O−, –CH3, –Br and –NO2). (d) The average CM5 charge of Zn with different substituents determined by DFT calculations. | ||
With the shrinking core model, we determined the PET hydrolysis rates and constructed a Hammett plot to evaluate the electronic effects of substituents on the rates (Fig. 2b). Hammett constants (σp) are commonly used to quantify the electron-withdrawing or electron-donating strength of the substituents in para positions.21,31–34Fig. 2b depicts the correlation between the Hammett constants (σp) and the PET hydrolysis rates (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kR/kH) over Zn2L-R catalysts, where kR/kH is the rate constant of the R-substituted Zn2L complex relative to the H-substituted. A volcano-shaped plot was identified from the correlation (Fig. 2b), wherein the small deviation observed for –F may arise from hydrogen bonding.35,36 Previous studies have pointed out that the volcano shape is indicative of a change in the rate-determining step (RDS),37–39 which will be elaborated later by DFT calculation. The volcano plot consists of two linear relationships with slopes (ρ) of 0.742 and −0.737, respectively. Generally, the value of the slope is related to the charge accumulation in the RDS.31,40–46 The negative slope (ρ = −0.737) from –CH3 to –NO2 indicates that a partial positive charge state is developed during the RDS, and thus the more electron-donating –CH3 facilitates the reaction. In contrast, the positive slope (ρ = 0.742) from –O− to –CH3 suggests the opposite: the more electron-withdrawing group (–CH3) would stabilize the developing negative charge in the transition state of the RDS and promote the reaction.
kR/kH) over Zn2L-R catalysts, where kR/kH is the rate constant of the R-substituted Zn2L complex relative to the H-substituted. A volcano-shaped plot was identified from the correlation (Fig. 2b), wherein the small deviation observed for –F may arise from hydrogen bonding.35,36 Previous studies have pointed out that the volcano shape is indicative of a change in the rate-determining step (RDS),37–39 which will be elaborated later by DFT calculation. The volcano plot consists of two linear relationships with slopes (ρ) of 0.742 and −0.737, respectively. Generally, the value of the slope is related to the charge accumulation in the RDS.31,40–46 The negative slope (ρ = −0.737) from –CH3 to –NO2 indicates that a partial positive charge state is developed during the RDS, and thus the more electron-donating –CH3 facilitates the reaction. In contrast, the positive slope (ρ = 0.742) from –O− to –CH3 suggests the opposite: the more electron-withdrawing group (–CH3) would stabilize the developing negative charge in the transition state of the RDS and promote the reaction.
Correlation of the Hammett relationship with the electronic structures of the active sites
We then investigated the charge densities of the active sites with different substituents and tried to correlate the information with the Hammett relation. X-ray absorption near-edge spectroscopy (XANES) reveals that the Zn K-edge shifted to higher energy as the substituent varied from –O− to –NO2 (Fig. S5a†). This trend is consistent with the X-ray photoelectron spectroscopy (XPS) results, where the binding energy of Zn 2p3/2 shifted from 1021.4 eV of –O− to 1022.2 eV of –NO2 (Fig. 2c). These observations indicate that the oxidation state of Zn increases with the electron-withdrawing strength. We then calculated the average CM5 charge on Zn using DFT. The results confirm the increased electron poorness with more electron-withdrawing groups (Fig. 2d). We reasoned that this variation trend of the charge density at the active sites could be correlated with the volcano-shaped Hammett relation through the Sabatier principle. The interaction between the active sites and the substrates can undergo a transition from too weak to too strong during the monotonic decrease of the electron richness of the Zn.Following this line of reasoning, we characterized the adsorption strength of ester at the zinc sites using diffuse reflection infrared Fourier transform spectroscopy (DRIFTS). We chose ethyl benzoate (EB) as a probe molecule, because it is a structural analog to PET but with a low boiling point.20 The free EB exhibits a broad band around 1719 cm−1 (Fig. S5b†), which can be assigned to the stretching vibration of the carbonyl group. In the presence of Zn2L–CH3, the peak of ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) in EB presents a redshift from 1719 to 1704 cm−1 upon O atom coordination to Zn. This redshift is more pronounced for –Br and –NO2 (Fig. S5b†), suggesting a stronger interaction between EB and the Zn sites with higher positive charge.47–50 This stronger adsorption of the carbonyl group could be detrimental to the desorption of the product and thus impair the catalytic activity. In contrast, with the –O− substituted catalyst, the ν(C
O) in EB presents a redshift from 1719 to 1704 cm−1 upon O atom coordination to Zn. This redshift is more pronounced for –Br and –NO2 (Fig. S5b†), suggesting a stronger interaction between EB and the Zn sites with higher positive charge.47–50 This stronger adsorption of the carbonyl group could be detrimental to the desorption of the product and thus impair the catalytic activity. In contrast, with the –O− substituted catalyst, the ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) peak is almost identical to that of free EB, indicating very weak or even negligible adsorption of EB on the catalyst relative to other substituted catalysts.41,51,52 This observation reflects that the more electron-donating group weakens the interaction between the carbonyl group of the ester and the zinc sites, and thus the reaction would hardly take place. These DRIFTS results support that the binding strength of C
O) peak is almost identical to that of free EB, indicating very weak or even negligible adsorption of EB on the catalyst relative to other substituted catalysts.41,51,52 This observation reflects that the more electron-donating group weakens the interaction between the carbonyl group of the ester and the zinc sites, and thus the reaction would hardly take place. These DRIFTS results support that the binding strength of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Zn increases with the electron poorness of the zinc sites, and –CH3 exerts a “just right” electronic effect on the active center.
O⋯Zn increases with the electron poorness of the zinc sites, and –CH3 exerts a “just right” electronic effect on the active center.
Mechanistic insights into the substituent effects from DFT calculations
To provide further insights into the substituent effects, DFT calculations were performed using ethylene glycol dibenzoate (EGD) as a model compound. The potential energy surfaces (PESs) of representative substituents, i.e., –O−, –CH3 and –NO2, are shown in Fig. 3a, while the others are provided in Fig. S6.† The catalytic cycle consists of five steps (Fig. 3a and S7†). In the first step, the reactant EGD adsorbs on Zn2L-R through Zn–O interaction, and this step is exothermic for all substituents. It should be noted that the EB employed in the DRIFTS study has only one carbonyl group while the EGD has two that could bind to the zinc sites. Therefore, the adsorption of EGD is exothermic for the –O− substituted catalyst. The second step leads to a stable six-membered ring acetyl-enzyme intermediate (Zn–O–C–O–Zn–μ2-O) through the nucleophilic attack of the oxygen atom on the hydroxyl group of Zn2L-R to the carbonyl carbon of EGD. For the third step, the absorbed ethylene glycol monobenzoate (EGM) is formed by an exothermic proton transfer process. Then in the fourth step, the leaving group (a molecule of EGM) is removed from Zn2L-R. Finally, the second product (benzoate, BzO) is released, and the remaining substrate returns to its initial state under alkaline hydrolysis conditions.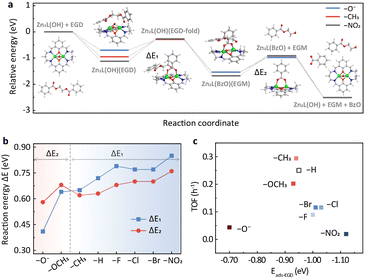 | ||
| Fig. 3 (a) Potential energy profile of EGD decomposition on the Zn2L-R compound (R = –NO2, –CH3, and –O−) computed at the M06-L/def2-TZVP//M06-L/6-31G(d)+LANL2DZ level. The inset shows the DFT-optimized geometries (R = –H) for reactants and intermediates. Green: Zn; blue: N; red: O; gray: C; white: H. (b) Reaction energies for the two key energy-consuming steps in (a) and Fig. S6† over Zn2L-R catalysts. (c) The effect of ester adsorption strength of different catalysts on catalytic activity based on the DFT results. | ||
DFT calculations suggest that the second and the fourth steps are the most endothermic processes with the reaction energies of ΔE1 and ΔE2, respectively (Fig. 3a). For –CH3, –H, –F, –Cl, –Br and –NO2, ΔE1 is larger than ΔE2, indicating that the formation of the six-membered ring is their PDS (Fig. 3b). In contrast, the opposite is observed for –OCH3 and –O−, suggesting that the PDS is the desorption of EGM (Fig. 3b). The change of PDS with different substituents is consistent with the nonlinear relationship of Hammett reactivity (Fig. 2b). Furthermore, the adsorption energy of EGD on the metal sites plays an important role in determining the turnover frequency (TOF) of the catalyst. As shown in Fig. 3c, relatively weaker (–O−) or stronger (e.g., –NO2) adsorption slows down the reaction rate, which is in line with the DRIFTS results (Fig. S5b†).
DFT calculations also reveal the charge development of these two endothermic processes. The second step is a process of positive charge accumulation due to the nucleophilic attack (Table S3†). This agrees with the negative slope (ρ = −0.737) of the Hammett plot from –CH3 to –NO2. In this case, the more electron-donating group weakens the Zn–OH bonding and therefore facilitates the nucleophilic attack. In contrast, negative charge develops accompanying the EGM leaving in the fourth step (Table S3†), in accordance with the positive slope (ρ = 0.742) of the Hammett plot from –O− to –CH3. The more electron-withdrawing group would be more conducive to stabilizing the transition state intermediate (Zn2L(BzO)) and thus promote the reaction.
Development of a more efficient catalyst based on the structure–activity relationship
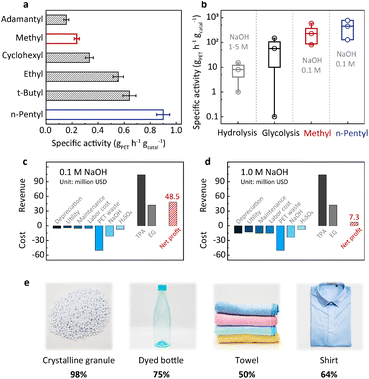
The above understanding of the structure–activity relationship encourages us to seek more efficient PET hydrolysis catalysts. The Hammett relation revealed in Fig. 2b signals that methyl is close to the top of the volcano. Therefore, further catalyst screening should focus on the substituents with a Hammett constant (σp) around the value of methyl (−0.17). In this regard, we synthesized a series of alkyl-substituted binuclear zinc complexes, including –ethyl, –tert-butyl, –n-pentyl, –cyclohexyl, and –adamantyl. Their Hammett constants are in the range of −0.01 to −0.20. DFT calculations suggest that these alkyl groups have little steric hindrance around the Zn–Zn centers (Fig. S8†). We then performed PET hydrolysis using these new catalysts. The comparison of their hydrolysis rates was complicated by their poor solubilities in water (Fig. S9a†). We therefore introduced methanol (20%) as a co-solvent (Fig. S9b†) to eliminate this influence. Consequently, PET hydrolysis kinetics reveal that ethyl, tert-butyl, n-pentyl, and cyclohexyl all exhibit improved catalytic activity compared with methyl (Fig. S10†). Particularly, the specific activity of the n-pentyl-substituted binuclear zinc complex is four times higher than that of the original methyl-substituted in 0.1 M NaOH at 60 °C (Fig. 4a).20With the optimized catalyst in hand, we set out to evaluate its efficiency under different hydrolysis conditions and test its robustness using real-world PET products. Temperature-dependent experiments indicate that the catalytic activity increases significantly with the increase of temperature (Fig. S4†). In order to enhance the PET processing capacity to an industrially relevant level, PET hydrolysis is performed under optimized conditions (pH 13 and 90 °C, 50 g PET, solid content of 100%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w/v, and 0.1–0.01 wt% catalyst). As shown in Fig. S11 and Table S1,† the specific activity of the n-pentyl-substituted catalyst is between 129 and 778 gPET h−1 gcatal−1, while its STY is in the range of 67–111 gTPA L−1 h−1, both higher than our previously reported values.20 This comparison shows that the n-pentyl-substituted catalyst has higher PET processing capacity, which could bring about a considerable profit increase as will be discussed later. As shown in Fig. 4b, the specific activity of this catalyst is at least one order of magnitude higher than that of the conventional alkaline hydrolysis (<33.3 gPET h−1 gcatal−1). More strikingly, such an enormous enhancement was achieved at an alkali concentration one order of magnitude lower than the previous methods (0.1 M versus 1–5 M, Table S1†). Techno-economic analysis indicates that our approach (0.1 M NaOH) would bring about a revenue increase of about 40 million USD compared with conventional alkaline hydrolysis (1.0 M NaOH) based on a capacity of 150 thousand tons of PET waste per year (Fig. 4c, d, Tables S4 and S5†). In addition, the net profit for hydrolysis conducted in 5.0 M NaOH would be negative (Fig. S12 and Table S6†). The n-pentyl-substituted binuclear catalyst was supported on carbon and subjected to recycling. There is 12% performance loss after 10 cycles of reuse, and the spent catalyst retained its pristine structure as demonstrated by NMR and XRD (Fig. S13†). It is worth mentioning that the n-pentyl-substituted exhibits lower Zn loss (0.5%) compared to the methyl-substituted catalyst (4.6%) in the first cycle of reuse, manifesting another merit of the n-pentyl-substituted catalyst.20 Table S8† systematically compares this new catalyst with a previously reported one and its advantages are summarized in the additional notes. We further examined the versatility of the n-pentyl-substituted catalyst using different PET feedstocks. Dyed bottles, towels, and shirts are daily-use products and are manufactured in mass every year. The n-pentyl-substituted binuclear zinc complex shows considerable TPA yields for these different PET sources (Fig. 4e). These results suggest that this catalyst is capable of handling real-life PET wastes.
w/v, and 0.1–0.01 wt% catalyst). As shown in Fig. S11 and Table S1,† the specific activity of the n-pentyl-substituted catalyst is between 129 and 778 gPET h−1 gcatal−1, while its STY is in the range of 67–111 gTPA L−1 h−1, both higher than our previously reported values.20 This comparison shows that the n-pentyl-substituted catalyst has higher PET processing capacity, which could bring about a considerable profit increase as will be discussed later. As shown in Fig. 4b, the specific activity of this catalyst is at least one order of magnitude higher than that of the conventional alkaline hydrolysis (<33.3 gPET h−1 gcatal−1). More strikingly, such an enormous enhancement was achieved at an alkali concentration one order of magnitude lower than the previous methods (0.1 M versus 1–5 M, Table S1†). Techno-economic analysis indicates that our approach (0.1 M NaOH) would bring about a revenue increase of about 40 million USD compared with conventional alkaline hydrolysis (1.0 M NaOH) based on a capacity of 150 thousand tons of PET waste per year (Fig. 4c, d, Tables S4 and S5†). In addition, the net profit for hydrolysis conducted in 5.0 M NaOH would be negative (Fig. S12 and Table S6†). The n-pentyl-substituted binuclear catalyst was supported on carbon and subjected to recycling. There is 12% performance loss after 10 cycles of reuse, and the spent catalyst retained its pristine structure as demonstrated by NMR and XRD (Fig. S13†). It is worth mentioning that the n-pentyl-substituted exhibits lower Zn loss (0.5%) compared to the methyl-substituted catalyst (4.6%) in the first cycle of reuse, manifesting another merit of the n-pentyl-substituted catalyst.20 Table S8† systematically compares this new catalyst with a previously reported one and its advantages are summarized in the additional notes. We further examined the versatility of the n-pentyl-substituted catalyst using different PET feedstocks. Dyed bottles, towels, and shirts are daily-use products and are manufactured in mass every year. The n-pentyl-substituted binuclear zinc complex shows considerable TPA yields for these different PET sources (Fig. 4e). These results suggest that this catalyst is capable of handling real-life PET wastes.
Conclusions
In summary, kinetic studies combined with DFT calculations reveal that the RDS of PET hydrolysis depends on the nature of the substituents of a binuclear zinc complex. The electron-donating substituents weaken the adsorption of carbonyl oxygen at the zinc sites and the cleavage of the ester C(sp3)–O bond has the highest energy barrier, while the electron-withdrawing groups lead to strong adsorption and enlarge the energy barrier for nucleophilic attack. The change in the RDS is supported by the volcano-shaped Hammett relation, wherein two linear relationships are established with –CH3 near the top of the “volcano”. This structure–activity relationship suggests that the substituents that most efficiently accelerate PET hydrolysis are those that slightly increase the electron richness of the active centers. This insight led us to discover a better catalyst with n-pentyl groups which has a four-fold rate enhancement compared with the methyl-substituted one. The effectiveness of this new catalyst is further reflected in its high specific activity (up to 778 ± 40 gPET h−1 gcatal−1 in 0.1 M NaOH), orders of magnitude higher than the conventional alkaline hydrolysis (less than 33.3 gPET h−1 gcatal−1 in 1–5 M NaOH). The strategy presented herein makes a step forward for PET recycling under mild conditions.Data availability
The data that support the findings of this study are available within the article and ESI.† Crystallographic data for the structures reported in this article have been deposited at the Cambridge Crystallographic Data Centre, under deposition no. CCDC 2205612 (Zn2L-OH(NO3)2), 2082453 (Zn2L-OCH3(NO3)2), 2082457 (Zn2L-CH3(NO3)2), 2205615 (Zn2L-H(NO3)2), 2205624 (Zn2L-F(NO3)2), 2205619 (Zn2L-Cl(NO3)2), 2205618 (Zn2L-Br(NO3)2), and 2205623 (Zn2L-NO2(NO3)2).†Author contributions
Z. N. conceptualized and guided this work. Z. N. and S. Z. designed the experiments. S. Z., Y. W., and Y.-X. Z. performed the experiments. Y. X. and T. T. performed the DFT calculations. Z. N., S. Z., Y. X., Y. W., and T. T. wrote the paper. All the authors participated in the data analysis and commented on the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the National Key R&D Program of China (2019YFA0709200), National Natural Science Foundation of China (22075162), Tsinghua University Initiative Scientific Research Program (20221080067), and China Post-doctoral Science Foundation (2021M691754). We acknowledge the BL14W1 station at the Shanghai Synchrotron Radiation Facility (SSRF) and 4B9A station at the Beijing Synchrotron Radiation Facility (BSRF) for the collection of XAFS data.References
- Plastics Europe, Plastics—The facts 2019. An analysis of European plastics production, demand and waste data. https://www.plasticseurope.org/application/files/1115/7236/4388/FINAL_web_version_Plastics_the_facts2019_14102019.pdf Search PubMed.
- R. Geyer, J. R. Jambeck and K. L. Law, Sci. Adv., 2017, 3, e1700782 CrossRef PubMed.
- L. T. J. Korley, T. H. Epps, B. A. Helms and A. J. Ryan, Science, 2021, 373, 66–69 CrossRef CAS PubMed.
- PET Polymer: Chemical Economics Handbook, IHS Markit, https://ihsmarkit.com/products/pet-polymer-chemical-economics-handbook.html Search PubMed.
- J. Diao, Y. Hu, Y. Tian, R. Carr and T. S. Moon, Cell Rep., 2023, 42, 111908–111923 CrossRef CAS PubMed.
- P. Benyathiar, P. Kumar, G. Carpenter, J. Brace and D. K. Mishra, Polymers, 2022, 14, 2366–2395 CrossRef CAS PubMed.
- N. George and T. Kurian, Ind. Eng. Chem. Res., 2014, 53, 14185–14198 CrossRef CAS.
- A. Stubbins, K. L. Law, S. E. Muñoz, T. S. Bianchi and L. Zhu, Science, 2021, 373, 51–55 CrossRef CAS.
- K. Ragaert, L. Delva and K. Van Geem, Waste Manag., 2017, 69, 24–58 CrossRef CAS.
- A. Rahimi and J. García, Nat. Rev. Chem., 2017, 1, 0046 CrossRef.
- J. M. Garcia and M. L. Robertson, Science, 2017, 358, 870–872 CrossRef CAS PubMed.
- J. M. Payne, G. Kociok-Köhn, E. A. Emanuelsson and M. D. Jones, Macromolecules, 2021, 54, 8453–8469 CrossRef CAS.
- C. Fliedel, D. Vila-Viçosa, M. J. Calhorda, S. Dagorne and T. Avilés, ChemCatChem, 2014, 6, 1357–1367 CrossRef CAS.
- J. Payne, P. McKeown, O. Driscoll, G. Kociok-Köhn, E. A. Emanuelsson and M. D. Jones, Polym. Chem., 2021, 12, 1086–1096 RSC.
- E. M. Krall, T. W. Klein, R. J. Andersen, A. J. Nett, R. W. Glasgow, D. S. Reader, B. C. Dauphinais, S. P. Mc Ilrath, A. A. Fischer, M. J. Carney, D. J. Hudsona and N. J. Robertson, Chem. Commun., 2014, 50, 4884–4887 RSC.
- S. Westhues, J. Idel and J. Klankermayer, Sci. Adv., 2018, 4, eaat9669 CrossRef CAS PubMed.
- X. Liao, Y. Su and X. Tang, Sci. China: Chem., 2022, 1–26 CAS.
- D. Paszun and T. Spychaj, Ind. Eng. Chem. Res., 1997, 36, 1373–1383 CrossRef CAS.
- G. P. Karayannidis, A. P. Chatziavgoustis and D. S. Achilias, Adv. Polym. Technol., 2002, 21, 250–259 CrossRef CAS.
- S. Zhang, Q. Hu, Y.-X. Zhang, H. Guo, Y. Wu, M. Sun, X. Zhu, J. Zhang, S. Gong, P. Liu and Z. Niu, Nat. Sustain., 2023 DOI:10.1038/s41893-023-01118-4 in press.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- N. H. Pilkinqton and R. Robson, Aust. J. Chem., 1970, 23, 2225–2236 Search PubMed.
- B. Dutta, P. Bag, U. Flolrke and K. Nag, Inorg. Chem., 2005, 44, 147–157 CrossRef CAS PubMed.
- B. F. Hoskins, R. Robson and G. A. Williams, Inorg. Chim. Acta, 1976, 19, 121–133 CrossRef.
- R. J. Madon and M. Boudart, Ind. Eng. Chem. Res., 1982, 21, 438–447 CAS.
- B. Liu, X. Lu, Z. Ju, P. Sun, J. Xin, X. Yao, Q. Zhou and S. Zhang, Ind. Eng. Chem. Res., 2018, 57, 16239–16245 CrossRef CAS.
- T. Yoshioka, N. Okayama and A. Okuwaki, Ind. Eng. Chem. Res., 1998, 37, 336–340 CrossRef CAS.
- R. López-Fonseca, M. P. González-Marcos, J. R. González-Velasco and J. I. Gutiérrez-Ortiz, J. Chem. Technol. Biotechnol., 2009, 84, 92–99 CrossRef.
- O. Levenspiel, Chemical Reaction Engineering; Wiley, New York, 2000, ch. 25 Search PubMed.
- R. López-Fonseca, J. R. González-Velasco and J. I. Gutiérrez-Ortiz, Chem. Eng. J., 2009, 146, 287–294 CrossRef.
- G. Kumar, L. Tibbitts, J. Newell, B. Panthi, A. Mukhopadhyay, R. M. Rioux, C. J. Pursell, M. Janik and B. D. Chandler, Nat. Chem., 2018, 10, 268–274 CrossRef CAS PubMed.
- M. H. Barbee, T. Kouznetsova, S. L. Barrett, G. R. Gossweiler, Y. Lin, S. K. Rastogi, W. J. Brittain and S. L. Craig, J. Am. Chem. Soc., 2018, 140, 12746–12750 CrossRef CAS PubMed.
- R. J. Burns, I. K. Mati, K. B. Muchowska, C. Adam and S. L. Cockroft, Angew. Chem., Int. Ed., 2020, 132, 16860–16867 CrossRef.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- P. I. Nagy, J. Phys. Chem. A, 2013, 117, 2812–2826 CrossRef CAS.
- S. Chakraborty and G. R. Desiraju, Cryst. Growth Des., 2018, 18, 3607–3615 CrossRef CAS.
- H. Hart and E. A. Sedor, J. Am. Chem. Soc., 1967, 89, 2342–2347 CrossRef CAS.
- I.-H. Um, L.-R. Im, E.-H. Kim and J. H. Shin, Org. Biomol. Chem., 2010, 8, 3801–3806 RSC.
- J. E. Leffler and E. Grunwald, Rates and equilibria of organic reactions: as treated by statistical, thermodynamic and extrathermodynamic methods, Courier Corporation, 2013 Search PubMed.
- J. Wu, Z. Wang, X. Jin, S. Zhang, T. Li, Y. Zhang, H. Xing, Y. Yu, H. Zhang, X. Gao and H. Wei, Adv. Mater., 2021, 33, 2005024 CrossRef CAS PubMed.
- J. Liu, Z. Li, X. Zhang, K.-i. Otake, L. Zhang, A. W. Peters, M. J. Young, N. M. Bedford, S. P. Letourneau, D. J. Mandia, J. W. Elam, O. K. Farha and J. T. Hupp, ACS Catal., 2019, 9, 3198–3207 CrossRef CAS.
- M. J. Zdilla, J. L. Dexheimer and M. M. Abu-Omar, J. Am. Chem. Soc., 2007, 129, 11505–11511 CrossRef CAS PubMed.
- D. R. Edwards, Y. B. Hleba, C. J. Lata, L. A. Calhoun and C. M. Crudden, Angew. Chem., Int. Ed., 2007, 119, 7945–7948 CrossRef.
- M. M. Konnick, N. Decharin, B. V. Popp and S. S. Stahl, Chem. Sci., 2011, 2, 326–330 RSC.
- R. Fuchs and D. M. Carlton, J. Am. Chem. Soc., 1963, 85, 104–107 CrossRef CAS.
- B. J. Stokes, K. J. Richert and T. G. Driver, J. Org. Chem., 2009, 74, 6442–6451 CrossRef CAS PubMed.
- Y. Wang, Y. Zhang, H. Song, Y. Wang, T. Deng and X. Hou, J. Cleaner Prod., 2019, 208, 1469–1475 CrossRef CAS.
- C. Sammon, J. Yarwood and N. Everall, Polym. Degrad. Stab., 2000, 67, 149–158 CrossRef CAS.
- J. Sun, D. Liu, R. P. Young, A. G. Cruz, N. G. Isern, T. Schuerg, J. R. Cort, B. A. Simmons and S. Singh, ChemSusChem, 2018, 11, 781–792 CrossRef CAS.
- X. Meng, L. Wang, L. Chen, M. Xu, N. Liu, J. Zhang, Y. Yang and M. Wei, J. Catal., 2020, 392, 69–79 CrossRef CAS.
- T. Szilágyi, J. Catal., 1990, 121, 223–227 CrossRef.
- A. Schranck, R. Marks, E. Yates and K. Doudrick, Environ. Sci. Technol., 2018, 52, 8638–8648 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, material characterization data, and catalytic measurement details. CCDC 2205612, 2082453, 2082457, 2205615, 2205624, 2205619, 2205618, and 2205623. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01161e |
| ‡ These authors contributed equally: Shengbo Zhang, Yingying Xue, and Yanfen Wu. |
| This journal is © The Royal Society of Chemistry 2023 |