Open Access Article
Open Access ArticleMaximized axial helicity in a Pd2L4 cage: inverse guest size-dependent compression and mesocate isomerism†‡
Witold M.
Bloch
 *ab,
Shinnosuke
Horiuchi
*ab,
Shinnosuke
Horiuchi
 ac,
Julian J.
Holstein
ac,
Julian J.
Holstein
 a,
Christoph
Drechsler
a,
Axel
Wuttke
d,
Wolf
Hiller
a,
Christoph
Drechsler
a,
Axel
Wuttke
d,
Wolf
Hiller
 a,
Ricardo A.
Mata
a,
Ricardo A.
Mata
 d and
Guido H.
Clever
d and
Guido H.
Clever
 *a
*a
aDepartment of Chemistry and Chemical Biology, TU Dortmund University, Otto-Hahn-Straße 6, 44227 Dortmund, Germany. E-mail: guido.clever@tu-dortmund.de
bInstitute for Nanoscale Science and Technology, College of Science and Engineering, Flinders University, Adelaide, South Australia 5042, Australia. E-mail: witold.bloch@flinders.edu.au
cDivision of Chemistry and Materials Science, Graduate School of Engineering, Nagasaki University, Bunkyo-machi, Nagasaki, 852-8521, Japan
dInstitute of Physical Chemistry, Georg-August University Göttingen, Tammannstraße 6, 37077 Göttingen, Germany
First published on 19th January 2023
Abstract
Helicity is an archetypal structural motif of many biological systems and provides a basis for molecular recognition in DNA. Whilst artificial supramolecular hosts are often helical, the relationship between helicity and guest encapsulation is not well understood. We report a detailed study on a significantly coiled-up Pd2L4 metallohelicate with an unusually wide azimuthal angle (∼176°). Through a combination of NMR spectroscopy, single-crystal X-ray diffraction, trapped ion mobility mass spectrometry and isothermal titration calorimetry we show that the coiled-up cage exhibits extremely tight anion binding (K of up to 106 M−1) by virtue of a pronounced oblate/prolate cavity expansion, whereby the Pd–Pd separation decreases for mono-anionic guests of increasing size. Electronic structure calculations point toward strong dispersion forces contributing to these host–guest interactions. In the absence of a suitable guest, the helical cage exists in equilibrium with a well-defined mesocate isomer that possesses a distinct cavity environment afforded by a doubled Pd–Pd separation distance.
Introduction
The prevalence of structural helicity in biological systems exemplifies its fundamental importance for complex functions. For example, the helical structure of DNA provides a chiral surface for recognition and facilitates tight packing of genetic information.1 Coiled motifs in peptide chains, such as α-helices, experience strong structural reinforcement through cooperative non-covalent interactions, giving rise to a stiff secondary structure. Clearly, helicity is important for defining the tertiary structure and biological function of proteins and other biomacromolecules.2These findings have inspired chemists to prepare artificial assemblies with structural helicity as the blueprint, such as helical molecules,3,4 foldamers5,6 and polymer aggregates.7 Many of these helical assemblies find strong applications in various areas, including asymmetric catalysis8 and biomedicine.9 For example, dinuclear metallohelicates composed of two or three twisted ligand strands have been shown to inhibit malignant cell growth by binding the major groove of DNA.10–12
The family of quadruple-stranded metallohelicates intersects with the compound class of M2L4 coordination cages, the former defined by a helical twist, the latter by an accessible cavity.13,14 The degree of axial helicity for M2L4 lantern-shaped cages can be defined by the azimuthal angle, α, which is the angular projection of the bridging ligand respective to the metal–metal axis (Fig. 1a).15 Many non-helical M2L4 cages (Fig. 1b) have shown promising functions for molecular separation,16,17 anion sequestration,18,19 catalysis20,21 and drug delivery.22–24 Despite helicity being a functional motif in nature, efforts to augment the host–guest chemistry of M2L4 cages have mainly focused on increasing their structural complexity.25 The incorporation of functional ligands (chiral, photo-switchable, redox-active, etc.) into such cage architectures offers the prospect of multi-functionalisation through heteroleptic, heterometallic or other low-symmetry assembly approaches.25–34 Moreover, structural motifs such as skewed geometry and double-cage interpenetration have been shown to give rise to phenomena such as shape recognition, allosteric binding and stimuli responsiveness.35–38
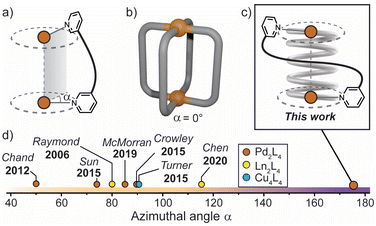 | ||
| Fig. 1 (a) Azimuthal angle (α) for a M2L4 helicate; (b) general structure of a non-helical M2L4 cage, where α = 0°; (c) this work: a tightly-wrapped Pd2L4 helicate that behaves as a supramolecular spring; (d) azimuthal angles (extracted from X-ray diffraction data) of selected quadruple-stranded metallohelicates, shown for comparison.15,39,42–46 | ||
The relationship between axial helicity and the guest binding properties of M2L4 coordination cages is somewhat ill-defined.19 McMorran and Steel demonstrated that a helical Pd2L4 cage assembled from flexible 4-bis(3-pyridyloxy)benzene ligands undergoes cavity adaptation by increasing its Pd–Pd separation and helical pitch upon binding anionic guests of increasing size.13,39 Jung and Lee demonstrated that a non-helical Pd2L4 cage assembled from alkyl-derived ligands behaves in a similar fashion, whereby an increase in the Pd–Pd separation is observed when the cage binds anions of increasing size.40 It is therefore unclear whether axial helicity or ligand flexibility is primarily responsible for mediating cavity expansion in M2L4 coordination cages.
In these and related M2L4 cages, the equilibrium constant for anion binding in polar solvents is rather low (<103 M−1) leading to the necessity of utilising non-polar solvents to achieve stronger host–guest interactions.41 Moreover, the azimuthal angle (α) of so far reported helical M2L4 cages (M = PdII, PtII or lanthanides) has been largely limited to ≤90° (Fig. 1d); increasing α beyond this limit represents uncharted territory for M2L4 cages. We postulated that maximising the axial helicity of M2L4 cages will lead to enhanced guest binding properties (compared to cages where α ≤ 90°) as the tightly-wrapped ligands should provide a large internal surface area and disfavour guest unbinding.
Herein, we report a Pd2L4 helical cage (1) with azimuthal angles ranging between 171–176° (Fig. 1c and d), representing the most axially-twisted M2L4 coordination cage reported so far. We closely examine the cage's unique structural changes associated with the binding of mono-anions through extensive X-ray crystallographic, NMR, MS and ITC analyses, as well as electronic structure calculations. Together, these experiments provide intimate structural details on the pronounced host–guest adaptability of 1, facilitated by its significantly twisted, spring-like architecture. In addition, we probe the anion-dependent equilibrium between the coiled-up metallohelicate and its elongated mesocate isomer, which is a unique feature of this system. Together, these findings provide new detailed insights into the relationship between axial helicity, structural adaptability and guest-binding phenomena of artificial host assemblies.
Results and discussion
Ligand design
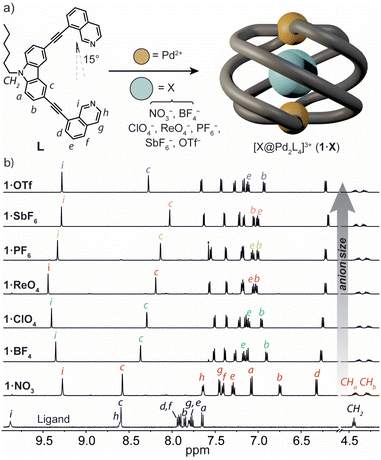
To prepare a coordination cage with an azimuthal angle of >90°, we designed a bis-monodentate ligand with a carbazole backbone and two inward-pointing 8-substituted isoquinoline donors (L).35 This pincer-shaped ligand has a theoretical ligand bite angle of 15° (Fig. 2a) as defined by the intersection of a vertical vector along the ligand backbone and one running parallel to the N-donor.47 Given the rigidity of L and the necessity of adopting a bite angle of ∼90° for lantern-shaped M2L4 coordination cages (particularly with square-planar PdII), we anticipated that the isoquinoline donors of L would need to undergo severe twisting to bridge two PdII ions. L was synthesized through a Sonogashira cross-coupling between 3,6-dibromo-9-hexyl-9H-carbazole and 8-ethynylisoquinoline in 53% yield (ESI†).Synthesis and solution-state analysis of 1·X
Heating a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of L with [Pd(CH3CN)4](BF4)2 at 70 °C in CD3CN resulted in the assembly of the coordination cage [BF4@Pd2L4](BF4)3 (herein denoted as 1·BF4) as revealed by 1H NMR spectroscopy and electrospray ionisation mass spectrometry (ESI-MS). In the 1H NMR spectrum, the proton resonances of the cage are significantly upfield-shifted relative to L (Fig. 2b), consistent with the presence of π-stacking interactions between neighbouring ligands in the cage assembly. The characteristic splitting of the diastereotopic N-hexyl CH2 resonances (CHa, CHb, 4.18–4.48 ppm at 298 K) provides direct evidence for axial helicity, and the P and M enantiomers of the Pd2L4 cage are in slow exchange relative to the 1H NMR time scale. The encapsulation of a BF4− anion within 1 was confirmed by 19F NMR spectroscopy, which revealed two resonances at −151.8 ppm and −149.4 ppm (Fig. S10†). These are assigned to the free and tightly encapsulated BF4− anion, respectively, and 19F exchange spectroscopy (EXSY) confirmed their exchange at 25 °C (Fig. S15†).
1 mixture of L with [Pd(CH3CN)4](BF4)2 at 70 °C in CD3CN resulted in the assembly of the coordination cage [BF4@Pd2L4](BF4)3 (herein denoted as 1·BF4) as revealed by 1H NMR spectroscopy and electrospray ionisation mass spectrometry (ESI-MS). In the 1H NMR spectrum, the proton resonances of the cage are significantly upfield-shifted relative to L (Fig. 2b), consistent with the presence of π-stacking interactions between neighbouring ligands in the cage assembly. The characteristic splitting of the diastereotopic N-hexyl CH2 resonances (CHa, CHb, 4.18–4.48 ppm at 298 K) provides direct evidence for axial helicity, and the P and M enantiomers of the Pd2L4 cage are in slow exchange relative to the 1H NMR time scale. The encapsulation of a BF4− anion within 1 was confirmed by 19F NMR spectroscopy, which revealed two resonances at −151.8 ppm and −149.4 ppm (Fig. S10†). These are assigned to the free and tightly encapsulated BF4− anion, respectively, and 19F exchange spectroscopy (EXSY) confirmed their exchange at 25 °C (Fig. S15†).
Next, we examined the self-assembly of 1 in the presence of anionic guests of different size and shape. We prepared a series of cage analogues (1·X), either from the respective PdII salt (X = NO3−, ClO4−, PF6−, SbF6− and OTf−), or by anion exchange (X = ReO4−). ESI-MS confirmed the Pd2L4 assembly for each counter-ion by prominent signals corresponding to [Pd2L4 + nX](4−n)+ cations; n = 1 and 2 (ESI†). When comparing their 1H NMR spectra, the hydrogens that point directly into the cage cavity appear at distinct chemical shifts (see resonances c and i, Fig. 2b). As for 1·BF4, also for 1·PF6 and 1·OTf, 19F NMR spectroscopy confirmed anion encapsulation, indicating that the cage cavity can accommodate anions of greatly different size and shape. In contrast to 1·BF4, 19F EXSY revealed that neither the larger PF6− nor OTf− encapsulated anion exchanges with solvated anions under the conditions of the NMR measurement (Fig. S27 and S34†). In addition to the resonances that are directly sensitive to the bound guest (c and i), those corresponding to hydrogens that point outside of the cage cavity (e and b) also undergo notable changes in chemical shift across the host–guest complexes of 1·X (Fig. 2b). Based on the data we discuss below, we interpret this as an anion-dependent ‘uncoiling/coiling-up’ behaviour.39 This is further supported by the tendency of non-encapsulated anions to influence the chemical shift of proton resonances directly adjacent to the metal centre (in this case, h and g).19,48
In order to gain further insight into the solution-state structure of 1·X, we examined the host–guest complexes by 1H–1H NOESY. These analyses revealed several intramolecular contacts diagnostic of axial helicity, including a strong inter-ligand correlation between protons f and a (e.g., Fig. S20†). Cage complexes of larger anions (e.g., SbF6−) display an additional NOE contact between protons i and f of neighbouring ligands (Fig. S39†). The former contact (f⋯a), in particular, confirms that the isoquinoline moiety of L is closely stacked on top of a neighbouring carbazole ligand backbone – a conformation that could only be afforded by a significantly twisted helical architecture.
The helical structure of 1·X (X = NO3−, ClO4−, ReO4−, PF6−, SbF6− and OTf−) was also examined by Ion-Mobility Mass Spectrometry (IM-MS). The experimental collisional cross section (CCS) values for the [X@Pd2L4]3+ species were found to range between 560 ± 10 (1·BF4) and 563 ± 17 Å2 (1·OTf) which correlates well to the calculated CCS obtained from their X-ray structures (Table S5.1† and vide infra). These CCS values indicate that the cage host maintains its compact helical structure in the solution and gas phase, even when encapsulating anions of notably different size and shape.
Solid-state analysis of 1·X
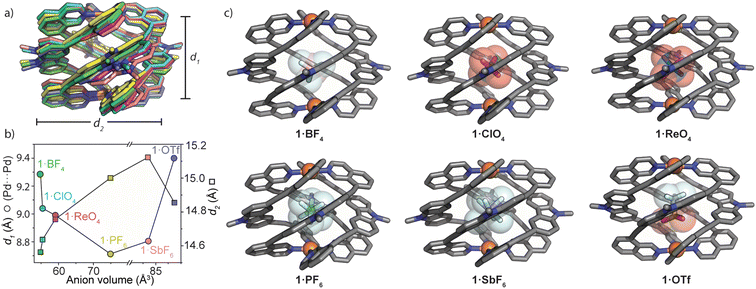
With MeCN solutions of 1·X in hand, we grew X-ray quality crystals of each sample (with the exception of 1·NO3) by slow-vapour diffusion with diisopropyl ether as the antisolvent. 1·BF4, 1·ClO4 and 1·ReO4 (anions with Td symmetry) crystallized in the tetragonal space group P42bc, whilst 1·PF6, 1·SbF6 and 1·OTf (Oh and C3v anion symmetry, respectively) crystallized in the monoclinic space group P21/n. For each structure, the asymmetric unit was occupied by one full molecule of the Pd2L4 cage with its respective counter ions and a variable number of solvent molecules. All forms of 1 are stabilised by strong π-stacking interactions between neighbouring ligands and these account for the upfield chemical shift of ligand resonances in the 1H NMR spectra of 1·X (Fig. 2b). Further inspection of the structures revealed that the azimuthal angle of the cage increases for larger anion guests (e.g., 171.6° and 176.2° for 1·BF4 and 1·SbF6, respectively – Table ESI 4.3†). This represents the largest axial twist for a M2L4 quadruple-stranded metallohelicate reported to date.For all solid-state structures of 1·X, one disordered anion was located inside the cage cavity (Fig. 3c), and additional anions sit in close proximity to the PdII centres. The encapsulated anions are stabilised by multiple weak hydrogen bonds (C–H⋯X = 2.2–2.5 Å) arising from the carbazole hydrogens that point directly inside the cavity of 1. For 1·PF6 and 1·SbF6, the bound anion is tilted by ca. 50° with respect to the longest anion axis and Pd(isoquinoline)4 plane, which contrasts with the vertical orientation of PF6− in other Pd2L4 cages38 as well as the bound OTf− in 1·OTf. The tilted orientation of PF6− and SbF6− presumably maximises host–guest interactions by orienting the fluoride substituents toward the surrounding hydrogen atoms of the host (also the case for the vertically oriented OTf− anion).
M2L4 cages typically accommodate guests of increasing size by increasing the separation between the metal centres.39,40,49 In analysing the solid-state structures of 1·X, we found the opposite trend for the Pd⋯Pd separation (d1) with respect to the size and shape of the encapsulated anion. Fig. 3a and b depict how 1 adapts to anions of increasing size. Counter-intuitively, the cage compresses along the Pd–Pd axis for larger anions; d1 (Pd⋯Pd distance) = 9.29 Å for 1·BF4 and 8.99 Å for 1·ReO4. A further decrease of d1 is observed for 1·PF6 (d1 = 8.71 Å) followed by a small increase for 1·SbF6 and a much larger increase for the non-globular OTf− guest (1·OTfd1 = 9.40 Å). Simultaneously, d2 (average distance between the opposing carbazole N atoms) increases incrementally from 1·BF4 (d2 = 14.56 Å) to 1·SbF6 (d2 = 15.12 Fig. 3b). It is worth noting that despite the similar molecular volumes of SbF6− and OTf− (84.9 and 85.4 Å3 respectively; RB3LYP/6-31g(d), LANL2DZ) 1 closely adapts to their different shape. This is reflected by large differences in d1 and d2 when comparing 1·OTf to 1·SbF6 (+0.59 Å and −0.27 Å, for d1 and d2, respectively; Fig. 3b). Combined, this shows that the wide azimuthal angle (or strong helical pitch) of 1 affords size and shape adaptability in guest binding, where the cavity trends from a prolate to an oblate shape; as d1 decreases, d2 increases. This behaviour enables 1 to alter its cavity volume by up to 18%; for example, the cavity volumes of 1·BF4 and 1·SbF6 are 119 Å3 and 140 Å3 respectively, as determined by VOIDOO50 calculations. These adaptations enable host–guest complexes of 1 to maintain a favourable packing coefficient of 0.55 ± 0.09.51
Anion exchange experiments
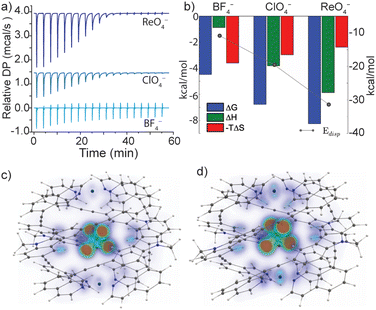
The versatile anion encapsulation properties of 1 motivated us to investigate anion exchange experiments in CD3CN solution. A fresh sample of 1·NO3 was titrated with tetrabutylammonium salts of BF4−, ClO4−, ReO4−, PF6−, SbF6− and OTf−. In the 1H NMR spectrum of these samples, slow exchange relative to the NMR timescale was observed in each case. Initial calculations revealed that for BF4−, K ≈ 103 M−1 whilst for the remaining anions, K was estimated to be >105 M−1, thus approaching the accuracy limit of K determination by 1H NMR spectroscopy.§To examine anion exchange more accurately, we turned to Isothermal Titration Calorimetry (ITC). Titrating 1·NO3 with tetrabutyl ammonium salts of BF4−, ClO4−, and ReO4− yielded titration curves consistent with the expected 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host–guest binding model (Fig. S52†). The equilibrium constants for anion exchange followed an anion size-dependent trend: K = 1.9 × 103 M−1 (BF4−), 9.2 × 104 M−1 (ClO4−) and 1.1 × 106 M−1 (ReO4−) (Fig. 4a and b and Table S3.1†). The thermodynamic data revealed that anion exchange of 1·NO3 with BF4− is entropically driven, whilst exchange with ClO4− and ReO4− is increasingly enthalpically driven (Fig. 4b). Given this, the encapsulated BF4− guest may be bound with more degrees of freedom compared to larger ClO4− and ReO4−. The high enthalpic contributions observed in the exchange of ClO4− and ReO4− with NO3− in 1 point towards a more optimized fit, which presumably maximizes the electrostatic and dispersive interactions in these host–guest complexes.
1 host–guest binding model (Fig. S52†). The equilibrium constants for anion exchange followed an anion size-dependent trend: K = 1.9 × 103 M−1 (BF4−), 9.2 × 104 M−1 (ClO4−) and 1.1 × 106 M−1 (ReO4−) (Fig. 4a and b and Table S3.1†). The thermodynamic data revealed that anion exchange of 1·NO3 with BF4− is entropically driven, whilst exchange with ClO4− and ReO4− is increasingly enthalpically driven (Fig. 4b). Given this, the encapsulated BF4− guest may be bound with more degrees of freedom compared to larger ClO4− and ReO4−. The high enthalpic contributions observed in the exchange of ClO4− and ReO4− with NO3− in 1 point towards a more optimized fit, which presumably maximizes the electrostatic and dispersive interactions in these host–guest complexes.
Monitoring anion exchange of 1·NO3 with PF6−, SbF6− and OTf− by ITC was uninformative due to the slow kinetics for the bimolecular exchange processes of these particular anions (e.g., complete exchange with SbF6− requires 1.5 h). Time-resolved 1H NMR array experiments revealed the rates of anion exchange to be OTf− > PF6− > SbF6−; 3.0 × 10−3 s−1, 2.3 × 10−3 s−1, 1.2 × 10−3 s−1 respectively (Fig. S53†). In contrast, ITC analysis indicated that anion exchange of 1·NO3 with BF4−, ClO4− or ReO4− is complete within seconds. It is worth noting that the K values for the exchange of nitrate in 1 with polyatomic anions are considerably high (≥105 M−1 for all anions except BF4−) compared to other M2L4 cages and related cage structures reported in the literature.19,52,53 For M2L4 cages (M = PdII or PtII), equilibrium exchange constants for monoanionic guests in polar solvent are usually in the order of <103 M−1,39,46 and non-polar solvents, large non-coordinating counter-ions or endohedral binding sites can be employed to further maximize host–guest interactions.41,54,55 Here, the exceptionally strong anion encapsulation properties of 1 can be credited to the large internal surface area of the tightly-wrapped cavity, which is afforded by the unusually wide azimuthal angles (171–176°).
To investigate the role of London dispersion interactions in the guest binding of 1, we performed electronic structure calculations on the host–guest complexes examined by ITC (i.e., 1·BF4, 1·ClO4 and 1·ReO4; all as 3+ cations with hexyl chains truncated to methyl substituents). All host–guest systems were optimized using the BP-86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56,57 functional with a def2-SVP58–61 basis and the D3-correction[D3] including three-body-terms.62,63 The optimised gas-phase structures were subjected to DF-SCS-LMP2/cc-pVTZ electronic structure calculations and the results were compared to the energies obtained from the corresponding solid-state geometries at the same level of theory.
56,57 functional with a def2-SVP58–61 basis and the D3-correction[D3] including three-body-terms.62,63 The optimised gas-phase structures were subjected to DF-SCS-LMP2/cc-pVTZ electronic structure calculations and the results were compared to the energies obtained from the corresponding solid-state geometries at the same level of theory.
Indeed, a strong correlation between the measured guest binding enthalpies and calculated dispersion contributions64–66 was found for both solid-state and gas-phase geometries, where 1 maintains a large contact surface to the bound guest (Fig. 4b–d, S71 and S72†). Additional calculations (DF-SCS-LMP2/VTZ level of theory) revealed that compression of the Pd⋯Pd axis of 1 is energetically demanding in the absence of a bound guest (Fig. S73†), which leads to the conclusion that dispersion interactions have a strong impact on the guest binding and corresponding structural adaptations of 1. The trend of increasing dispersion contributions for larger anions is consistent between the solid-state and gas-phase-optimised geometries (Table S5.3†), suggesting that the influence of crystal packing on the solid-state structure of 1 is minimal. This is supported by the fact that 1·BF4, 1·ClO4 and 1·ReO4 crystallise in the same tetragonal space group with almost identical unit cell dimensions (a, b = 30 Å, c = 29 Å, Table S4.2†).
Helicate/mesocate isomerism of 1
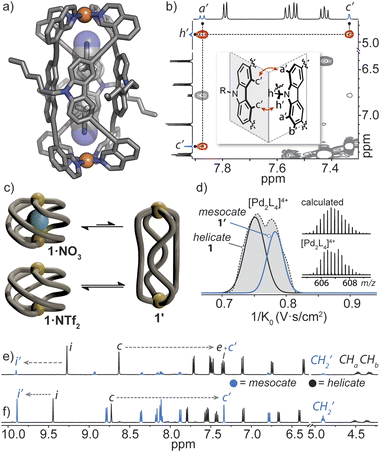
Helicate/mesocate isomerism is prevalent for double and triple-stranded metallohelicates, and control over their selective formation and isolation has been the subject of intense study.67–69 This in part is motivated by their respective properties; for example, triple-stranded di-ruthenium helicates exhibit selectivity toward certain cancer cells as compared to their mesocate counterparts.12 For these types of metallohelicates, ligand design (e.g., odd/even spacer length) or steric hindrance can lead to the formation of one isomer over the other.70,71 In many cases, both helicate and mesocate isomers can form from the same ligand and metal ion and exist either as separable static structures72 or in dynamic equilibrium;67,73 the latter is usually the case for helicates based on non-chelated coordination environments with high conformational flexibility (concerning the ligand–metal bonds). However, factors that drive the selective formation of helicates over mesocates remain ill-defined, especially for M2L4 quadruple-stranded metallohelicates. This may relate to their acute azimuthal angles (α < 90°), where only subtle structural distortions are required to invert helicity.74 This means that nearly all so far postulated M2L4 mesocates are transient species, rather than isolable ones.75,76In our attempts to grow single crystals of the helical cage 1·NO3, we were surprised to obtain crystals of a markedly different [Pd2L4]4+ cage complex (here denoted as 1′). X-ray analysis revealed that 1′ crystallizes in the orthorhombic space group Pccn with half of the Pd2L4 cage in the asymmetric unit. In the structure of 1′, the isoquinoline donors of L adopt a syn orientation and twist away from the carbazole backbone (giving individual ligands a Cs symmetry) – a conformation which gives rise to a mesocate (in contrast to the C2-symmetric ligand conformation in the helicates). In this elongated isomer, the Pd⋯Pd separation is 16.8 Å – which is almost double that of the most contracted form of helical 1·X. In contrast to the helicate, neighbouring carbazole backbones in mesocate 1′ participate in mutual edge-to-face π-stacking (closest C–H⋯π contact between two ligand backbones = 3.0 Å) and form the faces of the tubular, almost cuboid Pd2L4 structure. Instead of encapsulating a NO3− counterion, the C4h symmetric mesocate hosts two MeCN solvent molecules (Fig. 5a) that orient their nitrogen atoms toward the opposing PdII centres. This type of electrostatic interaction has been previously observed for other PdII-based cages77 and in the case of 1′, the MeCN guests are further stabilised by CH–π interactions (C–HMeCN⋯C-carbazole = 2.66 Å) inside the aromatic-rich cavity. Although we were not able to obtain an X-ray structure of the expected helical form of 1·NO3, the chemical shifts of inward-pointing protons i and c (Fig. 2a and 5e and f) are consistent with a helically-twisted cage encapsulating a NO3− guest.
To understand the helicate/mesocate isomerism of 1, we further examined the self-assembly process between L and Pd(NO3)2 in solution. As expected, the 1H NMR spectrum obtained minutes after combining L with Pd(NO3)2 clearly reflects the helical cage species, owing to the characteristic splitting pattern of the diastereotopic N–CH2 protons (CHa/CHb). However, when the CD3CN solution of 1·NO3 was allowed to equilibrate over two weeks at room temperature, another set of signals evolved which were assignable to a new PdII complex of L (Fig. 5e, ratio = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.15 in favour of 1·NO3). The chemical shifts of the newly evolved aromatic resonances appeared downfield compared to 1·NO3, with exception of c (denoted as c′), which appeared significantly upfield (−1.27 ppm). The significant shielding of proton c′ is in agreement with the X-ray structure of mesocate 1′ as this particular hydrogen points directly toward the π-system of an adjacent carbazole backbone in the mesocate (Fig. 5a and b).
0.15 in favour of 1·NO3). The chemical shifts of the newly evolved aromatic resonances appeared downfield compared to 1·NO3, with exception of c (denoted as c′), which appeared significantly upfield (−1.27 ppm). The significant shielding of proton c′ is in agreement with the X-ray structure of mesocate 1′ as this particular hydrogen points directly toward the π-system of an adjacent carbazole backbone in the mesocate (Fig. 5a and b).
The equilibrium between 1 and 1′ was further investigated by synthesizing 1·NTf2 (Fig. S42†). We chose NTf2− as a counter-ion because its volumetric size (157 Å3) is larger than the maximal cavity size of 1 (≤140 Å3). Thus, an ‘empty’ form of 1 was prepared by combining L with [Pd(CH3CN)4](NTf)2 at room temperature. Indeed, the absence of encapsulated NTf2− was confirmed by 19F NMR spectroscopy, which showed one isolated signal corresponding to free NTf2− present in solution (Fig. S43†). The 1H NMR spectrum of 1·NTf2 after 5 minutes of mixing the ligand and PdII salt revealed two sets of signals in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.24 ratio, with the helical, empty form of the cage predominating. After 2 weeks at room temperature, the sample equilibrated to a 1
0.24 ratio, with the helical, empty form of the cage predominating. After 2 weeks at room temperature, the sample equilibrated to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (Fig. 5f) of 1 and 1′. Importantly, 1H–1H NOESY unequivocally confirmed that the second set of signals corresponds to mesocate 1′. Two characteristic NOE contacts were observed: a′⋯c′ and c′⋯h′ (Fig. 5b and S46†). These contacts originate from the orthogonal relationship of neighbouring carbazole backbones (an arrangement only present in 1′) and are not observed in the NOESY spectrum of 1 or L. The difference in the equilibrium ratios of 1 and 1′ for 1·NO3 and 1·NTf2 reveals that the bound NO3− anion stabilizes the helicate 1 but is not necessarily required to template it (Fig. 5c). Mesocate 1′ was not observed to encapsulate anions, however, upon addition of a suitable guest (e.g., PF6−), the equilibrium shifts in favour of the metallohelicate 1 (Fig. S47†).
1 ratio (Fig. 5f) of 1 and 1′. Importantly, 1H–1H NOESY unequivocally confirmed that the second set of signals corresponds to mesocate 1′. Two characteristic NOE contacts were observed: a′⋯c′ and c′⋯h′ (Fig. 5b and S46†). These contacts originate from the orthogonal relationship of neighbouring carbazole backbones (an arrangement only present in 1′) and are not observed in the NOESY spectrum of 1 or L. The difference in the equilibrium ratios of 1 and 1′ for 1·NO3 and 1·NTf2 reveals that the bound NO3− anion stabilizes the helicate 1 but is not necessarily required to template it (Fig. 5c). Mesocate 1′ was not observed to encapsulate anions, however, upon addition of a suitable guest (e.g., PF6−), the equilibrium shifts in favour of the metallohelicate 1 (Fig. S47†).
Next, Trapped Ion Mobility (TIMS) ESI-MS analysis was carried out on an equilibrated sample of 1·NTf2 (containing both helicate 1 and mesocate 1′), in order to gain insight into the gas-phase behaviour of these isomeric structures. Based on previous studies examining structural variations in heteroleptic palladium cages,78 we anticipated that the drift times of the two isomers of 1 should be resolvable. Indeed, we observed two distinct mobilities corresponding to 4+ ions at 606.7 m/z (Fig. 5d and S69‡). Derivation of the experimental collisional cross sections (eCCS) for these mobilities revealed that the two 4+ species have an effective area of 605 Å2 and 631 Å2, which correspond well to the relative difference between the theoretically determined tCCS values of 1 and 1′ (568.6 Å2 and 578.9 Å2, respectively). Thus, the TIMS data confirms the helicate/mesocate pairs (i.e., isomers 1 and 1′) in the gas phase, suggesting that the MeCN solvent does not play a significant role in templating the formation of 1′. To investigate this hypothesis further, we examined the formation of 1·BF4 in DMSO by 1H NMR spectroscopy. In contrast to the exclusive formation of the helicate in MeCN, the 1H NMR spectrum of 1·BF4 in DMSO revealed the presence of both the helicate and mesocate in a ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, respectively. Thus, both anionic guests and solvent influence the equilibrium distribution of the helicate/mesocate pair.
1 ratio, respectively. Thus, both anionic guests and solvent influence the equilibrium distribution of the helicate/mesocate pair.
Conclusions
In summary, we have presented a comprehensive analysis of the solution state, solid state, and gaseous state structure and host–guest chemistry of the most axially twisted Pd2L4 cage reported to date. Through careful ligand design, the helical twist of this Pd2L4 cage (azimuthal angle of up to ∼176°) results in exceptionally tight anion binding which is mediated by prolate/oblate cavity size and shape adaptability. Notably, a comparison of six X-ray crystal structures of 1·X (X = BF4−, ClO4−, ReO4−, PF6−, SbF6− and OTf−) provided detailed insights on the compression/decompression of the Pd–Pd distance (d1), whereby d1 decreases when larger anions are bound within the cage cavity (with the exception of the non-globular OTf− guest). In the binding of anions of increasing size, we also observed a subtle increase in the azimuthal angle of the cage host. 1H NMR and ITC analysis revealed the benefit of large axial helicity for 1 by K values as high as 106 M−1 (ReO4−) for the bimolecular exchange of NO3− with larger anions. This can be attributed to the tightly-wrapped helical cage, which provides a large contact surface that facilitates strong dispersion forces toward the bound anion. In the absence of a suitable guest, 2D NMR, X-ray diffraction and TIM-MS revealed that 1 exists in a well-defined helicate/mesocate equilibrium, and convergence to the helicate is observed in the presence of an appropriate guest.Although factors such as cavity volume,79,80 ligand–guest interactions,55 host asymmetry35 and metal–metal distance19 all play a role in the host–guest chemistry of M2L4 coordination cages, our work exemplifies how maximising their axial helicity correlates with an exceptionally tight and adaptable binding pocket with a strong affinity toward a range of anionic guests. We anticipate this work will inspire further research into guest recognition/separation by tightly-wrapped helical cage compounds.
Data availability
The synthetic procedures, characterization, spectral data, and additional computational and crystallographic details are available in the ESI.‡ CCDC 1851098–1851104 contain the supplementary crystallographic data for this paper. Additional data is available from the authors upon request.Author contributions
W. M. B. and G. H. C. conceived the idea. W. M. B. conducted most of the synthesis, characterization, and analysis, and wrote the manuscript. S. H. and C. D. acquired and analysed the IM-MS data. J. J. H. and S. H. solved and refined the X-ray structures. R. A. M. and A. W. performed electronic structure calculations. W. H. performed 2D NMR measurements. G. H. C. managed the project, aided in experimental design, and reviewed the manuscript. All authors provided comments and approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Andreas Brockmeyer and Dr Petra Janning (Max-Planck Institute for Molecular Physiology, Dortmund) and Dr Holm Frauendorf (Georg-August University Göttingen) for mass spectra measurements. Dyanne Cruickshank from Rigaku Oxford diffraction is thanked for assistance in collecting X-ray data of 1·ReO4. W. M. B thanks the Alexander von Humboldt Foundation for a postdoctoral fellowship. S. H. thanks the JSPS Program for Advancing Strategic International Networks to Accelerate the Circulation on Talented Researchers. This work has been supported by the Deutsche Forschungsgemeinschaft under priority program SPP 1807 (Control of London Dispersion Interactions in Molecular Chemistry; CL489/3-2 and MA5063/3-2). The European Research Council (ERC Consolidator grant 683083, RAMSES) is also acknowledged for their support. Diffraction data 1·NO3, 1·PF6, 1·SbF6, and 1·OTf were collected at PETRA III at DESY, a member of the Helmholtz Association (HGF). We thank Anja Burkhardt for assistance at synchrotron beamline P11 (I-20160736).Notes and references
- P. B. Dervan, Bioorg. Med. Chem., 2001, 9, 2215–2235 CrossRef CAS PubMed
.
- A. A. Kornyshev, D. J. Lee, S. Leikin and A. Wynveen, Rev. Mod. Phys., 2007, 79, 943–996 CrossRef CAS
.
- C. Schmuck, Angew. Chem., Int. Ed., 2003, 42, 2448–2452 CrossRef CAS PubMed
.
- H. Song, M. Postings, P. Scott and N. J. Rogers, Chem. Sci., 2021, 12, 1620–1631 RSC
.
- D. Preston, Angew. Chem., Int. Ed., 2021, 60, 20027–20035 CrossRef CAS PubMed
.
- Y. Ferrand and I. Huc, Acc. Chem. Res., 2018, 51, 970–977 CrossRef CAS PubMed
.
- C. C. Lee, C. Grenier, E. W. Meijer and A. P. H. J. Schenning, Chem. Soc. Rev., 2009, 38, 671–683 RSC
.
- R. P. Megens and G. Roelfes, Chem.–Eur. J., 2011, 17, 8514–8523 CrossRef CAS PubMed
.
- E. Yashima, N. Ousaka, D. Taura, K. Shimomura, T. Ikai and K. Maeda, Chem. Rev., 2016, 116, 13752–13990 CrossRef CAS PubMed
.
- A. C. G. Hotze, B. M. Kariuki and M. J. Hannon, Angew. Chem., Int. Ed., 2006, 45, 4839–4842 CrossRef PubMed
.
- A. D. Richards and A. Rodger, Chem. Soc. Rev., 2007, 36, 471–483 RSC
.
- S. J. Allison, D. Cooke, F. S. Davidson, P. I. P. Elliott, R. A. Faulkner, H. B. S. Griffiths, O. J. Harper, O. Hussain, P. J. Owen-Lynch, R. M. Phillips, C. R. Rice, S. L. Shepherd and R. T. Wheelhouse, Angew. Chem., Int. Ed., 2018, 57, 9799–9804 CrossRef CAS PubMed
.
- D. A. McMorran and P. J. Steel, Angew. Chem., Int. Ed., 1998, 37, 3295–3297 CrossRef CAS PubMed
.
- M. Han, D. M. Engelhard and G. H. Clever, Chem. Soc. Rev., 2014, 43, 1848–1860 RSC
.
- D. Tripathy, A. K. Pal, G. S. Hanan and D. K. Chand, Dalton Trans., 2012, 41, 11273–11275 RSC
.
- M. Yamashina, M. Akita, T. Hasegawa, S. Hayashi and M. Yoshizawa, Sci. Adv., 2022, 3, e1701126 CrossRef PubMed
.
- D. Zhang, T. K. Ronson, Y.-Q. Zou and J. R. Nitschke, Nat. Rev. Chem., 2021, 5, 168–182 CrossRef CAS
.
- P. J. Steel and D. A. McMorran, Chem.–Asian J., 2019, 14, 1098–1101 CrossRef CAS PubMed
.
- G. H. Clever and P. Punt, Acc. Chem. Res., 2017, 50, 2233–2243 CrossRef CAS PubMed
.
- J. Wang, T. A. Young, F. Duarte and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 17743–17750 CrossRef CAS PubMed
.
- R. L. Spicer, A. D. Stergiou, T. A. Young, F. Duarte, M. D. Symes and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 2134–2139 CrossRef CAS PubMed
.
- J. E. M. Lewis, E. L. Gavey, S. A. Cameron and J. D. Crowley, Chem. Sci., 2012, 3, 778–784 RSC
.
- B. Woods, R. D. M. Silva, C. Schmidt, D. Wragg, M. Cavaco, V. Neves, V. F. C. Ferreira, L. Gano, T. S. Morais, F. Mendes, J. D. G. Correia and A. Casini, Bioconjugate Chem., 2021, 32, 1399–1408 CrossRef CAS PubMed
.
- A. Schmidt, V. Molano, M. Hollering, A. Pöthig, A. Casini and F. E. Kühn, Chem.–Eur. J., 2016, 22, 2253–2256 CrossRef CAS PubMed
.
- S. Pullen, J. Tessarolo and G. H. Clever, Chem. Sci., 2021, 12, 7269–7293 RSC
.
- W. M. Bloch and G. H. Clever, Chem. Commun., 2017, 53, 8506–8516 RSC
.
- X. Jing, C. He, L. Zhao and C. Duan, Acc. Chem. Res., 2019, 52, 100–109 CrossRef CAS PubMed
.
- V. Croué, S. Goeb and M. Sallé, Chem. Commun., 2015, 51, 7275–7289 RSC
.
- J. E. M. Lewis, A. Tarzia, A. J. P. White and K. E. Jelfs, Chem. Sci., 2020, 11, 677–683 RSC
.
- D. Ogata and J. Yuasa, Angew. Chem., Int. Ed., 2019, 58, 18424–18428 CrossRef CAS PubMed
.
- A. Tarzia, J. E. M. Lewis and K. E. Jelfs, Angew. Chem., Int. Ed., 2021, 60, 20879–20887 CrossRef CAS PubMed
.
- H. Yu, J. Li, C. Shan, T. Lu, X. Jiang, J. Shi, L. Wojtas, H. Zhang and M. Wang, Angew. Chem., Int. Ed., 2021, 60, 26523–26527 CrossRef CAS PubMed
.
- L. S. Lisboa, J. A. Findlay, L. J. Wright, C. G. Hartinger and J. D. Crowley, Angew. Chem., Int. Ed., 2020, 59, 11101–11107 CrossRef CAS PubMed
.
- M. T. Yong, O. M. Linder-Patton and W. M. Bloch, Inorg. Chem., 2022, 61, 12863–12869 CrossRef CAS PubMed
.
- W. M. Bloch, Y. Abe, J. J. Holstein, C. M. Wandtke, B. Dittrich and G. H. Clever, J. Am. Chem. Soc., 2016, 138, 13750–13755 CrossRef CAS PubMed
.
- S. Löffler, J. Lübben, L. Krause, D. Stalke, B. Dittrich and G. H. Clever, J. Am. Chem. Soc., 2015, 137, 1060–1063 CrossRef PubMed
.
- S. Freye, J. Hey, A. Torras-Galán, D. Stalke, R. Herbst-Irmer, M. John and G. H. Clever, Angew. Chem., Int. Ed., 2012, 51, 2191–2194 CrossRef CAS PubMed
.
- M. Frank, M. D. Johnstone and G. H. Clever, Chem.–Eur. J., 2016, 22, 14104–14125 CrossRef CAS PubMed
.
- P. J. Steel and D. A. McMorran, Chem.–Asian J., 2019, 14, 1098–1101 CrossRef CAS PubMed
.
- J. Lee, S. Lim, D. Kim, O.-S. Jung and Y.-A. Lee, Dalton Trans., 2020, 49, 15002–15008 RSC
.
- D. P. August, G. S. Nichol and P. J. Lusby, Angew. Chem., Int. Ed., 2016, 55, 15022–15026 CrossRef CAS PubMed
.
- J. Xu and K. N. Raymond, Angew. Chem., Int. Ed., 2006, 45, 6480–6485 CrossRef CAS PubMed
.
- S. M. McNeill, D. Preston, J. E. M. Lewis, A. Robert, K. Knerr-Rupp, D. O. Graham, J. R. Wright, G. I. Giles and J. D. Crowley, Dalton Trans., 2015, 44, 11129–11136 RSC
.
- X. Gao, L. Li, W. Sun and P. Chen, Dalton Trans., 2020, 49, 2843–2849 RSC
.
- S. A. Boer and D. R. Turner, Chem. Commun., 2015, 51, 17375–17378 RSC
.
- L.-P. Zhou and Q.-F. Sun, Chem. Commun., 2015, 51, 16767–16770 RSC
.
- W. M. Bloch, J. J. Holstein, W. Hiller and G. H. Clever, Angew. Chem., Int. Ed., 2017, 56, 8285–8289 CrossRef CAS PubMed
.
- J. E. M. Lewis and J. D. Crowley, Supramol. Chem., 2014, 26, 173–181 CrossRef CAS
.
- J.-Y. Wu, M.-S. Zhong and M.-H. Chiang, Chem.–Eur. J., 2017, 23, 15957–15965 CrossRef CAS PubMed
.
- G. J. Kleywegt and T. A. Jones, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, 50, 178–185 CrossRef CAS PubMed
.
- M. Sandro and J. J. Rebek, Chem.–Eur. J., 1998, 4, 1016–1022 CrossRef
.
- D. Preston, K. M. Patil, A. T. O'Neil, R. A. S. Vasdev, J. A. Kitchen and P. E. Kruger, Inorg. Chem. Front., 2020, 7, 2990–3001 RSC
.
- A. E. Martín Díaz and J. E. M. Lewis, Front. Chem., 2021, 9, 706462 CrossRef PubMed
.
- B. J. J. Timmer and T. J. Mooibroek, Chem. Commun., 2021, 57, 7184–7187 RSC
.
- A. Platzek, S. Juber, C. Yurtseven, S. Hasegawa, L. Schneider, C. Drechsler, K. E. Ebbert, R. Rudolf, Q.-Q. Yan, J. J. Holstein, L. V Schäfer and G. H. Clever, Angew. Chem., Int. Ed., 2022, 61, e202209305 CrossRef CAS PubMed
.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed
.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed
.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
- A. Tkatchenko, D. Alfè and K. S. Kim, J. Chem. Theory Comput., 2012, 8, 4317–4322 CrossRef CAS PubMed
.
- S. Löffler, A. Wuttke, B. Zhang, J. J. Holstein, R. A. Mata and G. H. Clever, Chem. Commun., 2017, 53, 11933–11936 RSC
.
- A. Wuttke and R. A. Mata, J. Comput. Chem., 2017, 38, 15–23 CrossRef CAS PubMed
.
- X. Aniban, B. Hartwig, A. Wuttke and R. A. Mata, Phys. Chem. Chem. Phys., 2021, 23, 12093–12104 RSC
.
- S. Suárez-Pantiga, P. Redero, X. Aniban, M. Simon, C. Golz, R. A. Mata and M. Alcarazo, Chem.–Eur. J., 2021, 27, 13358–13366 CrossRef PubMed
.
- J. Xu, T. N. Parac and K. N. Raymond, Angew. Chem., Int. Ed., 1999, 38, 2878–2882 CrossRef CAS PubMed
.
- K. L. Flint, D. M. Huang, O. M. Linder-Patton, C. J. Sumby and F. R. Keene, Eur. J. Inorg. Chem., 2022, 2022, e202200225 CAS
.
- M. Albrecht, Chem. Rev., 2001, 101, 3457–3498 CrossRef CAS PubMed
.
- M. Albrecht, Chem.–Eur. J., 2000, 6, 3485–3489 CrossRef CAS PubMed
.
- D. J. Cooke, J. M. Cross, R. V Fennessy, L. P. Harding, C. R. Rice and C. Slater, Chem. Commun., 2013, 49, 7785–7787 RSC
.
- Z. Zhang and D. Dolphin, Chem. Commun., 2009, 6931–6933 RSC
.
- F. Cui, S. Li, C. Jia, J. S. Mathieson, L. Cronin, X.-J. Yang and B. Wu, Inorg. Chem., 2012, 51, 179–187 CrossRef CAS PubMed
.
- Q. Lin, L. Gao, B. Kauffmann, J. Zhang, C. Ma, D. Luo and Q. Gan, Chem. Commun., 2018, 54, 13447–13450 RSC
.
- S. Carlotto, L. Armelao and M. Rancan, Int. J. Mol. Sci., 2022, 23, 10619 CrossRef CAS PubMed
.
- M. Rancan, J. Tessarolo, A. Carlotto, S. Carlotto, M. Rando, L. Barchi, E. Bolognesi, R. Seraglia, G. Bottaro, M. Casarin, G. H. Clever and L. Armelao, Cell Rep. Phys. Sci., 2022, 3, 100692 CrossRef CAS
.
- L. Escobar, D. Villarón, E. C. Escudero-Adán and P. Ballester, Chem. Commun., 2019, 55, 604–607 RSC
.
- K. E. Ebbert, L. Schneider, A. Platzek, C. Drechsler, B. Chen, R. Rudolf and G. H. Clever, Dalton Trans., 2019, 48, 11070–11075 RSC
.
- A. P. Birvé, H. D. Patel, J. R. Price, W. M. Bloch and T. Fallon, Angew. Chem., Int. Ed., 2022, 61, e202115468 CrossRef PubMed
.
- J. E. M. Lewis, Chem. Commun., 2022, 58, 13873–13886 RSC
.
Footnotes |
| † Dedicated to Professor Peter Steel on the occasion of his 68th birthday. |
| ‡ Electronic supplementary information (ESI) available: Full experimental details and supporting analysis. CCDC 1851098–1851104. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc06629g |
| § Furthermore, attempts to obtain reliable values of K for 1·X by 1H NMR spectroscopy were convoluted by the presence of proton resonances of mesocate 1′ which arose in samples of 1·NO3 and 1·BF4 after long periods of equilibration. |
| This journal is © The Royal Society of Chemistry 2023 |