Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The first HyDRA challenge for computational vibrational spectroscopy†
Taija L.
Fischer
 a,
Margarethe
Bödecker
a,
Margarethe
Bödecker
 a,
Sophie M.
Schweer
a,
Sophie M.
Schweer
 a,
Jennifer
Dupont
b,
Valéria
Lepère
b,
Anne
Zehnacker-Rentien
a,
Jennifer
Dupont
b,
Valéria
Lepère
b,
Anne
Zehnacker-Rentien
 b,
Martin A.
Suhm
b,
Martin A.
Suhm
 a,
Benjamin
Schröder
a,
Benjamin
Schröder
 a,
Tobias
Henkes
a,
Tobias
Henkes
 c,
Diego M.
Andrada
c,
Diego M.
Andrada
 d,
Roman M.
Balabin
d,
Roman M.
Balabin
 e,
Haobam Kisan
Singh
e,
Haobam Kisan
Singh
 f,
Himangshu Pratim
Bhattacharyya
f,
Himangshu Pratim
Bhattacharyya
 f,
Manabendra
Sarma
f,
Manabendra
Sarma
 f,
Silvan
Käser
f,
Silvan
Käser
 g,
Kai
Töpfer
g,
Kai
Töpfer
 g,
Luis I.
Vazquez-Salazar
g,
Luis I.
Vazquez-Salazar
 g,
Eric D.
Boittier
g,
Eric D.
Boittier
 g,
Markus
Meuwly
g,
Markus
Meuwly
 g,
Giacomo
Mandelli
g,
Giacomo
Mandelli
 h,
Cecilia
Lanzi
h,
Cecilia
Lanzi
 h,
Riccardo
Conte
h,
Riccardo
Conte
 h,
Michele
Ceotto
h,
Michele
Ceotto
 h,
Fabian
Dietrich
h,
Fabian
Dietrich
 i,
Vicente
Cisternas
i,
Ramachandran
Gnanasekaran
i,
Vicente
Cisternas
i,
Ramachandran
Gnanasekaran
 j,
Michael
Hippler
j,
Michael
Hippler
 k,
Mahmoud
Jarraya
k,
Mahmoud
Jarraya
 l,
Majdi
Hochlaf
l,
Majdi
Hochlaf
 l,
Narasimhan
Viswanathan
l,
Narasimhan
Viswanathan
 m,
Thomas
Nevolianis
m,
Thomas
Nevolianis
 m,
Gabriel
Rath
m,
Gabriel
Rath
 m,
Wassja A.
Kopp
m,
Wassja A.
Kopp
 m,
Kai
Leonhard
m,
Kai
Leonhard
 m and
Ricardo A.
Mata
m and
Ricardo A.
Mata
 *a
*a
aInstitut für Physikalische Chemie, Universität Göttingen, Tammannstraße 6, Göttingen, Germany. E-mail: rmata@gwdg.de
bInstitut des Sciences Moléculaires dOrsay, Université Paris-Saclay, CNRS, 91405 Orsay, France
cDepartment of Physics and Materials Science, University of Luxembourg, L-1511 Luxembourg City, Luxembourg
dInstitute for Inorganic Chemistry, Saarland University, 66123 Saarbrücken, Germany
eBond Street Holdings, Long Point Road, KN-1002 Henville Building 9, Charlestown, KN10 Nevis, St. Kitts and Nevis
fDepartment of Chemistry, Indian Institute of Technology Guwahati, Assam-781039, India
gDepartment of Chemistry, University of Basel, Klingelbergstrasse 80, 4056 Basel, Switzerland
hDipartimento di Chimica, Università degli Studi di Milano, via C. Golgi 19, 20133 Milano, Italy
iDepartment of Physics Science, Universidad de La Frontera, Francisco Salazar 01145, Temuco, Chile
jVellore Institute of Technology, School of Advanced Sciences (SAS), ChemistryDivision, Chennai 600 027, India
kDepartment of Chemistry, University of Sheffield, Sheffield S3 7HF, UK
lU. Gustave Eiffel, COSYS/IMSE, 5 BD Descartes 77454, Champs-sur-Marne, France
mInstitute of Technical Thermodynamics, RWTH Aachen University, Schinkelstraße 8, D-52072 Aachen, Germany
First published on 3rd August 2023
Abstract
Vibrational spectroscopy in supersonic jet expansions is a powerful tool to assess molecular aggregates in close to ideal conditions for the benchmarking of quantum chemical approaches. The low temperatures achieved as well as the absence of environment effects allow for a direct comparison between computed and experimental spectra. This provides potential benchmarking data which can be revisited to hone different computational techniques, and it allows for the critical analysis of procedures under the setting of a blind challenge. In the latter case, the final result is unknown to modellers, providing an unbiased testing opportunity for quantum chemical models. In this work, we present the spectroscopic and computational results for the first HyDRA blind challenge. The latter deals with the prediction of water donor stretching vibrations in monohydrates of organic molecules. This edition features a test set of 10 systems. Experimental water donor OH vibrational wavenumbers for the vacuum-isolated monohydrates of formaldehyde, tetrahydrofuran, pyridine, tetrahydrothiophene, trifluoroethanol, methyl lactate, dimethylimidazolidinone, cyclooctanone, trifluoroacetophenone and 1-phenylcyclohexane-cis-1,2-diol are provided. The results of the challenge show promising predictive properties in both purely quantum mechanical approaches as well as regression and other machine learning strategies.
1 Introduction
The ‘Pauling point’ is a term which has slowly faded out of use through the years, but which should be as relevant today as when it was first introduced. Its origins are discussed, for example, in ref. 1, 2. It refers to the point in a project where the theoretical predictions exactly match the experimental observables, but if one were to proceed and further improve on the calculations (e.g., larger basis sets, remove approximations such as the harmonic approach, etc.…) such agreement would disappear. Whenever one resorts to numerical methods to solve a physical problem, it is often the case that there are enough buttons to push and knobs to turn in a way that a close to perfect cancellation of error arises. This can happen accidentally, but the ‘Pauling point’ is often times actively pursued when the target observables are known. So, instead of aiming for the most advanced description possible, one might use and/or recommend relatively low levels of theory which have shown promise in a known chemical subspace. However, the true test to quantum chemistry is its potential for prediction over a large chemical space. Aiming for cheaper solutions might be deterrent to this ultimate goal. This raises the question of how to foster better practices or discover computational protocols robust enough to be used for predictions in an unbiased way.Blind challenges in the field of computational chemistry have become more and more popular over the past years. Particularly noteworthy examples thereof are the Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) challenges initiatives3,4 and the Cambridge crystallographic database structure challenges.5,6 This is followed in smaller scale by individual groups initiatives,7,8 or even in structured round-robin tests.9 Whatever the case may be, these challenges provide unique opportunities to pit different methods to the same observable in a collegiate (optimally unbiased) fashion. A previous challenge8,10 promoted by some of the groups involved was the furan-methanol challenge, whereby the binding preferences of methanol and a series of modified furan molecules was under scope. The question posed to the theoretical groups was to identify the most stable binding motif, an OH⋯O or OH⋯π bound conformer. Although the experimental data for the challenge were jet-cooled vibrational spectra, the target quantities were energy differences. The latter were estimated from the relative heights of the observed absorption peaks for the different binding modes. Albeit this being an indirect measurement, conservative error estimates were still below 1 kJ mol−1, well beyond the error bar of commonly accepted theory benchmarks.11
In this new joint effort, the observable to be tested is no longer inferred from the spectra. The goal is to correctly predict the experimental red shift of the OH bond stretch in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monohydrate complexes relative to the free symmetric stretch. This builds a much more rigorous connection point between theory and experiment in the important field of microhydration,12,13 as a quantity that both sides of the table feel comfortable estimating with minimal modelling on the experimental side. With its sensitivity to both electronic structure and nuclear motion aspects,14 it promises interesting error cancellation and thus Pauling point situations. As monohydrates are vibrationally15 far less characterised than rotationally,16,17 the topic also leaves enough playground for blind testing. As the layout of this blind test has been described extensively before,18 we refrain from repeating the experimental tools19–21 and caveats.22
1 monohydrate complexes relative to the free symmetric stretch. This builds a much more rigorous connection point between theory and experiment in the important field of microhydration,12,13 as a quantity that both sides of the table feel comfortable estimating with minimal modelling on the experimental side. With its sensitivity to both electronic structure and nuclear motion aspects,14 it promises interesting error cancellation and thus Pauling point situations. As monohydrates are vibrationally15 far less characterised than rotationally,16,17 the topic also leaves enough playground for blind testing. As the layout of this blind test has been described extensively before,18 we refrain from repeating the experimental tools19–21 and caveats.22
As detailed in our first publication introducing the challenge,18 a set of 10 hydrate systems were selected as ‘training set’, in order for the participants to fine tune or validate beforehand their approaches. The latter consisted of: acetone (ACE), acetophenone (APH), 1,2,4,5-tetrafluorobenzene (TFB), 1-phenylethanol (POH), imidazole (IMZ), aniline (ANL), dibenzofuran (DBZ), di-tert-butyl nitroxide (DBN), o-cyanophenol (OCP) and cyclobutanone (CBU). Another set of 10 structures was chosen18 and presented as the target of the challenge – from now on referred to as ‘test set’. The latter consisted of: cyclooctanone (CON), 1,3-dimethyl-2-imidazolidinone (DMI), formaldehyde (FAH), methyl lactate (MLA), 1-phenylcyclohexane-cis-1,2-diol (PCD), pyridine (PYR), tetrahydrofuran (THF), tetrahydrothiophene (THT), 2,2,2-trifluoroacetophenone (TPH) and 2,2,2-trifluoroethan-1-ol (TFE), all previously uncharacterised in terms of the experimental water stretching vibrations in the vacuum-isolated complex. The participants were given 6 months between the test set reveal and a submission deadline. Following said deadline, any inconsistencies in the submissions were addressed. One issue we had to address was the use of different levels of theory within a single submission (i.e., higher levels of theory for the smaller systems, computationally cheaper approaches for the larger cases). Our solution was in general to ask the participants to split the data into different sets. This was done to increase the amount of information about the different levels of theory featured, while ensuring a strict unique procedure (level of theory) per computational data set. There were also some issues with the definition of the reference – the symmetric water OH stretch. This was the only value which we allowed to be revised. Otherwise, all of the data was kept as submitted, even including mistakes in the molecular structure. TFE and PCD values in submission PH1 were based on the wrong molecules, same as with DMI in PH4 and FA3. These issues are discussed in further detail later in the text.
As previously discussed,18 the training and test sets covered roughly the same range of wavenumber downshifts, from a very low (10 and 8 cm−1 for TFB and TFE respectively) to a rather high end (199 and 203 cm−1 for IMZ and PYR respectively). Fig. 1 provides the Lewis structure of the compounds selected for both sets, as well as the experimentally obtained absolute position of the water OH donor stretch bands.
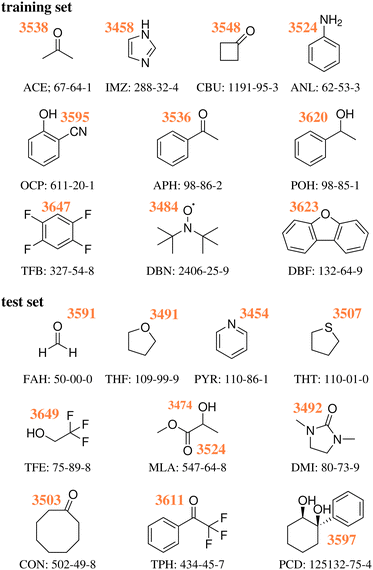 | ||
| Fig. 1 Experimental wavenumbers in cm−1 of the hydrogen-bonded OH stretching fundamentals of water in the monohydrates of the training18 and test23 systems without any anharmonic deperturbation attempt, together with their acronyms and CAS registry numbers, see also ESI.† | ||
2 List of submissions
In order to facilitate the discussion of the computational submissions, we established four categories, depending on the methods used to produce predictions.PH purely harmonic: results at any given level of theory which were directly obtained by diagonalisation of the mass-weighted Hessian matrix. In some cases, these were provided as extra data sets by the groups upon request of the organisers.
AC anharmonic corrected: results which are derived from the use of a nuclear Hamiltonian with a non-harmonic potential in one or more degrees of freedom involving the target OH stretch. The calculations are not fully-dimensional as in the following category.
FA fully anharmonic: results which are derived from a full anharmonic vibrational calculation of the monohydrate. This includes both molecular dynamics and static calculations with an appropriate nuclear wave function method, not necessarily using the same electronic structure method as for the harmonic part.
LS learning strategies: results which are obtained on the basis of regression techniques. We include in this category both least-squares fitting and more advanced machine learning approaches.
The naming of the data sets followed the above mentioned category acronyms, with numbers attached and incremental within each category. The order for the numbers is somewhat arbitrary, depending on the date of registration and when the final data was submitted. An overview of the participants is provided in Table 1, with a short summary of the techniques employed available in Table 2. It should be noted that in some cases the description is rather short and does not really do justice to the overall process. The readers should consult the ESI,† files for a full description and computational details.
| Participants | Submissions |
|---|---|
| Gnanasekaran | PH1 |
| Mandelli, Lanzi, Conte, Ceotto | FA1 |
| Dietrich, Cisternas | LS1 |
| Henkes, Andrada | AC1, PH3 |
| Töpfer, Boittier, Meuwly | AC2 |
| Vazquez-Salazar, Boittier, Meuwly | LS2 |
| Käser, Boittier, Meuwly | LS3 |
| Singh, Bhattacharyya, Sarma | PH4, FA3 |
| Hippler | PH5, AC4 |
| Viswanathan, Nevolianis, Rath, Kopp, Leonhard | AC3 |
| Balabin | LS4 |
| Jarraya, Hochlaf | PH2, PH6, PH7, |
| FA2, FA4, FA5 |
| Submission | Computational protocol |
|---|---|
| PH1 | B3LYP-D3(BJ)/def2-TZVPP harmonic values |
| PH2 | PBE0-D3/aug-cc-pVTZ harmonic values |
| PH3 | ωB97xD/def2-TZVP harmonic values |
| PH4 | B3LYP-D3(BJ)/def2-TZVP harmonic values |
| PH5 | MP2/6-31++G(2d,p) counterpoise-corrected harmonic values |
| PH6 | CCSD-F12/aug-cc-pVDZ harmonic values |
| PH7 | MP2-F12/aug-cc-pVDZ harmonic values |
| AC1 | ωB97xD/def2-TZVP with 1D numerical differences along the donor OH stretch normal mode |
| AC2 | Reproducing Kernel Hilbert Space+DVR3D based on B3LYP-D3(BJ)/aug-cc-pVTZ structures |
| AC3 | B2PLYP-D3(BJ)/aug-cc-pVTZ with selected anharmonic modes calculations |
| AC4 | MP2/6-311++G(d,p) counterpoise-corrected 2-D QFF cc-VSCF |
| FA1 | Quasi-classical B3LYP-D3/aug-cc-pVDZ trajectories |
| FA2 | VPT2 PBE0-D3(BJ)/aug-cc-pVTZ anharmonic values |
| FA3 | VPT2 B3LYP-D3(BJ)/def2-TZVP anharmonic values |
| FA4 | CCSD-F12/aug-cc-pVDZ harmonic+PBE0-D3(BJ)/aug-cc-pVTZ anharmonic corrections |
| FA5 | MP2-F12/aug-cc-VDZ harmonic+PBE0-D3/aug-cc-pVTZ anharmonic corrections |
| LS1 | PAW PBE-D3 adjusted with a 2-parameter linear regression function extracted from the training set values |
| LS2 | Kernel prediction of harmonic frequencies + delta learning correction with respect to the experiment |
| LS3 | Neural network on B3LYP-D3(BJ)/aug-cc-pVTZ structures + transfer Learning to experiment |
| LS4 | PBE0-D3(BJ)/may-cc-pVTZ|aug-cc-pVQZ adjusted with a 5-parameter linear regression function |
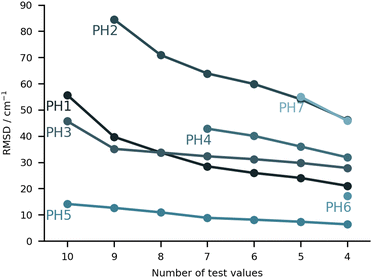
As clearly evidenced by Table 2 there is a wide variety of approaches to critically compare. There is no repetition of methods, although some entries do come close (e.g., PH1 and PH3 which only differ by the addition of extra polarisation functions in the atomic orbital set). In some cases (PH3, PH4, PH6 and PH7), we requested harmonic values to estimate the impact of the correction/regression approaches, although the original submission only featured anharmonic predictions.
3 Results and discussion
3.1 Reference experimental values
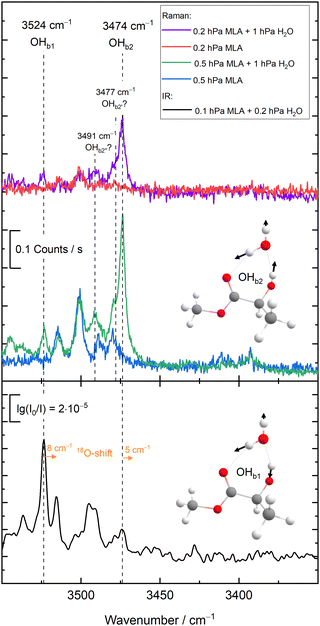
The new experimental data for the 10 members of the test set are detailed in the ESI,† as pre-published after the challenge submission deadline,23 together with the supersonic jet spectra and their assignments. They are listed in Fig. 1 together with the experimental values for the training set, which were discussed before.18In many cases, the assignments are straightforward and leave little room for interpretation, already based on infrared spectroscopy alone.19,21 In a few cases, complementary Raman spectroscopy20 was needed to safely identify the hydrogen-bonded OH stretch of the water unit in the monohydrate. Here, we only discuss some key results for the most complicated case of MLA, where there is evidence for mode mixing between the hydrogen-bonded OH groups of the two complexed molecules.
As illustrated in Fig. 2 and proven by rotational spectroscopy,24 the water molecule inserts into the intramolecular hydrogen bond between the α-hydroxy group and the carbonyl group of the ester, leading to a O–H⋯O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) chain of two coupled oscillators. The two top Raman spectra show the effect of adding water to a highly diluted MLA expansion. A strong band of the 1
chain of two coupled oscillators. The two top Raman spectra show the effect of adding water to a highly diluted MLA expansion. A strong band of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex emerges at 3474 cm−1. Minor satellite contributions near 3477 and 3491 cm−1 may be due to traces of larger complexes or due to dark overtone and combination states stealing some intensity from the OH stretching fundamental by perturbation. If the latter is true, the deperturbed (zeroth-order) state which should be compared to a harmonic or low-order anharmonic prediction is slightly higher than the peak wavenumber, perhaps around 3475–3478 cm−1. However, this is not so relevant, because the Raman spectrum is most sensitive for the in-phase stretching of the two OH oscillators. The out-of-phase stretching mode is better seen in the Raman spectra of the more concentrated expansions (central traces) at 3524 cm−1 and it is very prominent in the IR spectra (lowest spectrum in Fig. 2), because it involves a larger change of the dipole moment. As shown in the ESI,† it is the only strong transition attributable to the monohydrate in this spectral window and therefore corresponds to the requested wavenumber for the challenge. However,18 O-substitution in the water molecule demonstrates that both the out-of-phase and the in-phase OH stretching signals involve some water character, because they both downshift (see ESI†). As the downshift is more pronounced for the 3524 cm−1 band (8 vs. 5 cm−1), this is the band which should be compared to single theoretical predictions of the water OH stretch. Evidently, a comparison of both wavenumbers (listed in Fig. 1 for MLA) to their theoretical counterparts could be valuable as well in this particular case, but will be left for the future and the individual theory groups.
1 complex emerges at 3474 cm−1. Minor satellite contributions near 3477 and 3491 cm−1 may be due to traces of larger complexes or due to dark overtone and combination states stealing some intensity from the OH stretching fundamental by perturbation. If the latter is true, the deperturbed (zeroth-order) state which should be compared to a harmonic or low-order anharmonic prediction is slightly higher than the peak wavenumber, perhaps around 3475–3478 cm−1. However, this is not so relevant, because the Raman spectrum is most sensitive for the in-phase stretching of the two OH oscillators. The out-of-phase stretching mode is better seen in the Raman spectra of the more concentrated expansions (central traces) at 3524 cm−1 and it is very prominent in the IR spectra (lowest spectrum in Fig. 2), because it involves a larger change of the dipole moment. As shown in the ESI,† it is the only strong transition attributable to the monohydrate in this spectral window and therefore corresponds to the requested wavenumber for the challenge. However,18 O-substitution in the water molecule demonstrates that both the out-of-phase and the in-phase OH stretching signals involve some water character, because they both downshift (see ESI†). As the downshift is more pronounced for the 3524 cm−1 band (8 vs. 5 cm−1), this is the band which should be compared to single theoretical predictions of the water OH stretch. Evidently, a comparison of both wavenumbers (listed in Fig. 1 for MLA) to their theoretical counterparts could be valuable as well in this particular case, but will be left for the future and the individual theory groups.
The OH group contained in TFE might have caused a similar mode mixing problem,25 but here the coupling to the water OH is sufficiently weak for an unambiguous assignment. This is also the case for PCD,26 where the monohydrate features a network of three coupled OH oscillators but only one of them shows a strong isotope shift upon18 O substitution (ESI†).
The experimental downshifts from the symmetric water monomer stretch in the test set span a range of 8–203 cm−1 and thus exclude the more challenging strong hydrogen bonds, where the likelihood of anharmonic resonances increases substantially. None of the 10 test systems involves a proven b2lib resonance,22 where the water bending overtone (b2) and hydrogen bond libration (lib) ternary combination band steals intensity from the OH stretch fundamental. Therefore, the raw experimental data can be compared directly to the theoretical predictions, keeping in mind that there may be some mode mixing issue for the multi-chromophore systems MLA, TFA and PCD. Only in the MLA case is this mixing supported by experiment.
The experimental uncertainties of the OH stretches vary slightly. They only exceed ±2 cm−1 for the MLA case due to satellite bands close to the MLA-centered mode and for the PCD case due to the convolution between the rotational contour and the resolution of the laser used in the IR-UV experiments. Therefore, the individual experimental uncertainties of the test systems do not enter the following analysis.
3.2 Uncertainties in computed values
When formulating the challenge, uncertainty estimates were requested for all submissions. However, very few of the entries included such estimates, somewhat reflecting a common practice in the theoretical chemistry community. There is a heavy reliance on established methodologies, but little information on how the performance of the method can be derived from the previous works. The only submissions which provided error estimates were LS1, FA1 and LS4.Given that the training data was available for all the groups, any participant who also computed the training set (even if partially) would have been in a position to provide uncertainty estimates based on the performance of the method. Learning strategies heavily dependent on the latter would likely underestimate the uncertainty, but could provide this information nonetheless. LS1 provided a rather small uncertainty of 8 cm−1, similar to that of LS4 (7 cm−1). Both made use of linear fitting expressions, with comparable fitting quality for the test set. In the case of FA1, the only other submission with uncertainty quantification, the value was 16 cm−1, taken to be slightly above the mean average error of the training set quasi-classical simulation results.
Finally, one should note that one could make use of other deviation measures instead of relying on the root-mean-square deviation (RMSD).27 It is for example common to report the mean absolute error (MAE). However, the latter will give the smallest error estimates, as it tends to lessen the weight of outliers. Given that we are critically assessing the predictive power of computational protocols, a measure like RMSD seems a more natural choice. For fairness, we will also consider results when removing the largest outliers of each set, trying to set an equal footing for all submissions, whether complete or incomplete.
3.3 General performance
The full results are provided in the ESI,† as well as ref. 28. For the sake of clarity and ease of interpretation, most of our discussion will be based on general statistics and we will avoid as much as possible to focus on single instances. Often times, we will compare the results to a null hypothesis, which is constructed by taking the average of the training systems shifts. This requires no computation and provides a single estimate of 99.7 cm−1 for all test systems. The RMSD of the null hypothesis for the measured test values is 62.3 cm−1, which we will take as a general quality measure.A close inspection of the individual submissions showed that a few submissions made in fact use of the wrong organic molecule. We will mention this in the text. Of less concern was the computation of different minima. The most problematic system in this respect was PCD, with two alcohol groups. Otherwise, only small deviations were observed. It was commonly found in the TPH and FAH geometries that the water molecule was binding out of plane, breaking Cs symmetry. This seems to have a minimal impact on the predicted wavenumbers. Independent calculations were carried out at the CCSD(T)/aug-cc-pVTZ29–31 level of theory, confirming that the global minimum for both complexes should localise the water molecule in plane.
In order to give an overview of the submitted values, we provide in Fig. 3 the errors for each entry. For ease of visualisation, a kernel density estimator has been used, showing in bright yellow value ranges with a large number of submissions. The RMSD of the null hypothesis (±62.3 cm−1) is delimited by the dotted white lines. A few observations can be readily made. Most of the submitted values do outperform the null hypothesis. Although this is a low bar, it is not necessarily a given. If the quantity of interest had a low spread (small range of test values), the null hypothesis would be hard to compete with, as has been observed in other blind challenges (see for example ref. 32). Another observation to make is that there is no apparent systematic error (too small or too large shifts) with a fairly balanced distribution around 0. The density distribution readily highlights DMI, FAH and TFE as the systems with the best quality estimates, despite the fact that a few outliers (with errors beyond 62 cm−1) are observed. Rewardingly, these three systems span relatively strong, intermediate and very weak hydrogen bonding.
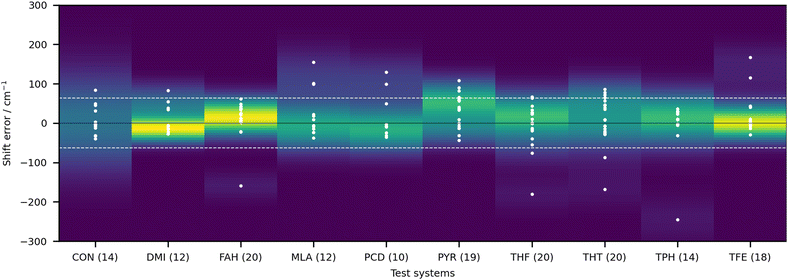 | ||
| Fig. 3 Deviations of the submitted OH stretch shifts relative to the measured experimental values (raw values) in cm−1 for the 10 test systems. A positive error means that the predicted wavenumber downshift from the monomer is too large. Each value is represented as a white dot (only one value is outside of the visualisation window, AC1 submission for CON, with an error of 460.5 cm−1). The color coding of the graph is provided by the probability density function of the error for each system. Yellow indicates larger density values, dark blue low density. The bandwidth selection has been made with Scott's rule.33 The dotted line delimits the RMSD range of the null hypothesis (62.3 cm−1), obtained as described in the text. | ||
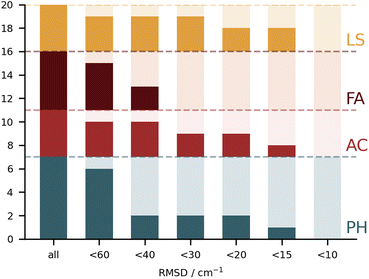
It is rather hard to analyse the results bundling all submissions together. In Fig. 4 an overview of the performance for all submissions is provided, taking the RMSD in the test set as a measure. This choice is not without bias, given that not all submissions included all 10 test systems. Nonetheless, it does allow for some first general considerations in regard to the different types of calculations. The best fully anharmonic submission (FA3) still exhibits a RMSD of 38.5 cm−1, a rather large value considering that the shifts only go up to 203 cm−1. It is in general the class with the lowest performance. Only 6 submissions are below the 30 cm−1 mark (PH5, AC2, AC4, LS1, LS3 and LS4) and 4 below 15 cm−1 (PH5, AC2, LS3 and LS4). Somewhat surprisingly, this shows that a similar accuracy can be reached with wildly varying approaches to the problem. Learning strategies do show some advantage, but the differences are not so significant that one would immediately exclude other approaches to the problem.
In the following text, we mention correct and incorrect structures based on the large agreement observed for the best submissions. These are considered as reference global minima and are then used to evaluate the other entries. The organisers of the challenge have not independently confirmed all of the minima for their stability.
3.4 Purely harmonic (PH) submissions
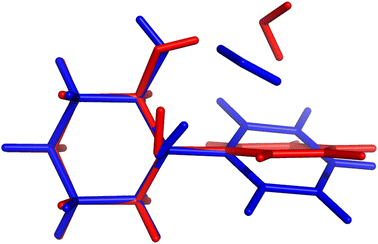
On paper, purely harmonic estimates should be the class of calculations with the least chance of success. They stand as the most accessible calculations, but will carry the full error of anharmonic effects. However, we have already observed in previous blind challenges8,10 that harmonic approaches can be surprisingly effective. In the furan-methanol challenge, the delicate energy balance between different conformers was critically dependent on the quality of the zero-point vibrational energy (ZPVE) estimates. However, the most successful entries in general only included harmonic estimates, while some anharmonic ZPVE corrections provided the wrong energetic ordering. It all boils down to the degree of error compensation in the model chemistry chosen. In the present case, most of the anharmonicity of an OH group is diagonal in nature and does not change much upon hydrogen bonding.34,35 By a quite significant margin, the best submission in this class was PH5, making use of MP2/6-31++G(2d,p)36,37 counterpoise-corrected harmonic values. The RMSD for all submissions in this class are depicted in Fig. 5. We provide values incrementally removing the worst prediction of each set, in order to compare in a more balanced way the different submissions. The largest deviations for PH1 and PH3 are due to wrong structures for the PCD minimum upon which the frequencies are based. In the case of PH1 the wrong organic molecule was used, 1-phenylcyclohexane-cis-2,5-diol instead of 1-phenylcyclohexane-cis-1,2-diol. In the case of PH3, a different minimum was found, leading to an error of 98.7 cm−1 for PCD. The water is correctly pointing to the ring system, but also is hydrogen bonding to one of the alcohols (in the accepted global minimum it should be accepting a bond from the alcohol). We provide the overlap of two selected PCD complex structures in Fig. 6. Both sets are of relatively similar quality, with B3LYP-D3(BJ)/def2-TZVPP38–44 (PH1) and ωB97xD/def2-TZVP45 (PH3) delivering the overall same level of accuracy. Once the outliers are removed, the RMSD is found to be below 40 cm−1 (Fig. 5).The PH2 submission worst value (for MLA, error of 155 cm−1) does not appear to be due to the minimum chosen, but solely the approach used. The PBE0-D3/aug-cc-pVTZ46 level of theory reveals large errors for the whole set, at least as submitted by the participating group. The only geometry which was not correctly predicted was for TPH. The water binds to the side of the trifluoro group, when it should be docking to the carbonyl group from the opposite end. Despite the wrong geometry, and through error compensation, the deviation is only 23 cm−1, the second best prediction in PH2. Curiously enough, despite the similarity in method between PH1 and PH4, the smaller basis set chosen in the latter submission seems to have a sizeable impact (an almost constant 15 cm−1 increase in RMSD). All structures of PH4 were in line with the best results, with the exception of DMI, where 2,5-dimethylpyrrole was wrongly used. Attempting to build a summary for this class of submissions, and removing the impact of wrong structure submissions, there was a decisive advantage in the use of the MP2 method and a small basis set. This could be due to the well documented fact that MP2 will overcorrect Hartree–Fock in predicting OH stretching hydrogen bond shifts (too large downshifts).34 By reducing the basis set, the amount of electron correlation described decreases, compensating the harmonic and method errors. This is partly confirmed in the harmonic estimates underlying the AC4 submission, where the basis was expanded to 6-311++G(d,p) and the results were overall worst (if no anharmonic corrections were included).
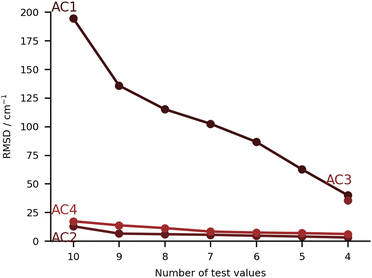
3.5 Anharmonic corrected (AC) submissions
In this class of submissions (Fig. 7), we have partly anharmonically corrected values for the bonding OH stretch. AC1 makes use of the wB97xD/def2-TZVP level of theory (the harmonic results built the PH4 set), and extends the prediction by including anharmonic corrections to the OH stretch mode. This was performed by computing numerical differences along the normal coordinates. The large errors found in this particular set are a direct consequence of the procedure used. When adding an anharmonic correction AC2 and AC4 are among the best submissions for this challenge. In the case of AC2, internal potentials for the water molecule in each monohydrated system were built from B3LYP-D3(BJ)/aug-cc-pVTZ calculations (a functional which was already confirmed to give good results in the PH category). The latter PESs were then used as reference to respectively fit three Morse potentials for the internal degrees of freedom of water adding a Reproducing Kernel Hilbert Space (RKHS) correction term47,48 which accounts for 2- and 3-mode coupling. The vibrational states are then computed with the Discrete Variable Representation Method (DVR) and the DVR3D program package,49,50 using the water molecule geometry as in the hydrated complex. This approach lays the focus on the treatment of the water internal potential, neglecting any coupling with the organic molecule vibrations. In case strong resonance effects or even harmonic mixing with alcohol groups would be present, this effect could not be captured, but this was not a point of concern for the set of molecules chosen in the challenge. It should be noted that the largest deviation in AC2 is found for the PYR system (36 cm−1 error), which is also where the largest experimental shift is observed. Close in performance, AC4 also focuses on the internal degrees of freedom in the water molecule, albeit with a different approach. The counterpoise corrected MP2/6-311++G(d,p) level of theory is used for both the optimisations and the potential energy calculations. Using the Quartic Force Field formulation of Yagi et al.,51 potential surfaces with up to 2-mode couplings were computed considering water displacements according to the normal modes computed for the complex (after identifying the modes of interest for the water). The structure of the pairing organic molecule was kept frozen. The final wavenumbers are computed from the correlation corrected VSCF method, which is described elsewhere.52,53 The agreement between AC2 and AC4 is striking, confirming the soundness of approximating the downshift by considering only the water internal degrees of freedom.The submission AC3 only included entries for FAH, THF, THT and TFE. The conformers of these four systems were found using CREST54 at GFN2-xTB55 level of theory. The resulting lowest-energy conformers were then optimized using the B2PLYP-D3(BJ)56,57 level of theory with an aug-cc-pVTZ basis set and harmonic vibrational frequency calculations were carried out. On paper, this was perhaps the highest-level method for the underlying PES. The same level of theory was then used for a VPT2 treatment of some selected modes that showed a significant contribution from the OH stretch. Preliminary calculations on the acetone-water test system showed significant improvement in the accuracy of the downshift (by 10 cm−1 with respect to experiments) when nine modes were selected instead of three. The previously mentioned modes were the ones that specifically involved the OH stretch. AC3 therefore chose an anharmonic treatment of nine selected vibrational modes throughout.
As one can extract from the discussion of the individual entries, the choice of dimensions used for the partial anharmonic corrections wildly varied. The water-benzene dimer (a system which was not featured in this challenge) was recently studied by Felker and Bačić.58 In their study they obtained a striking agreement between the symmetric OH shift calculated from an adapted PES considering only the water degrees of freedom and a larger 9 dimensional PES whereby coupling to large amplitude motions was included. However, the agreement is found to be precarious, as replacing one of the hydrogens by deuterium (HOD) shows. Deviations rise from under 1 cm−1 to an order of magnitude larger. A more systematic review of the systems featured in HyDRA could be warranted to observe how error compensation is at work from weakly to strongly interacting dimers.
3.6 Fully anharmonic (FA) submissions
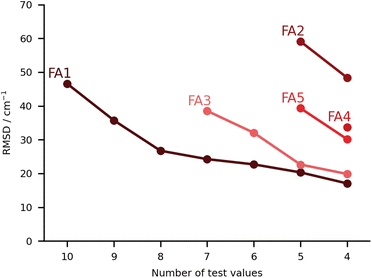
In this class we include submissions where fully anharmonic calculations (i.e., including all degrees of freedom in the cluster) were carried out. Interestingly, none of these submissions made its way into the top 5, meaning the submissions with the lowest RMSD. The worst performing submission under this category was FA2, with large deviations for the PYR and THT systems (90 and 86 cm−1 respectively), then abruptly falling below 40 cm−1 deviations. The values are estimated on the basis of VPT2,59 making use of the PBE0-D3(BJ)/aug-cc-pVTZ level of theory. We already noted that the PBE0 was the worst performing functional under the PH category (PH2). The anharmonic corrections have a relatively small impact, reducing the RMSD values by less than 10 cm−1. We observe no issues in the minima chosen for the calculations. The problems can be foremost linked to the choice of functional. The same authors submitted the dataset FA4, whereby the CCSD-F12/aug-cc-pVDZ60 harmonic values are corrected by the anharmonic difference estimated at the PBE0-D3(BJ)/aug-cc-pVTZ level (VPT2 vs. harmonic). The errors are greatly reduced in the latter variant. Comparison to FA2 on the basis of Fig. 8 should be careful. The FA2 set features the TFE value, which is an extremely small shift, while FA4 does not. Overall, the submissions which include TFE (with the right minimum) are somewhat favored by the metric we use, based on absolute errors, not relative. FA5 is also from the same group, with the same anharmonic corrections, but using MP2-F12/aug-cc-pVDZ61 harmonic values. The results are of comparable quality to those obtained with CCSD-F12 normal modes (FA4). The FA3 set consists of B3LYP-D3(BJ)/def2-TZVP VPT2 anharmonic frequencies. Again the largest deviations are found for the PYR and THT systems. Once these two are removed from the analysis, the RMSD falls below 30 cm−1. It could be of interest in a further publication to revisit these systems and understand in further depth the shortcomings of VPT2. We note in passing that the affordable combination of harmonic CCSD(T)-F12a/cc-pVTZ-F1260,62,63 with VPT2 at MP2/aug-cc-pVTZ level, which was explored for FAH when analysing the hydrate anharmonic resonance in ketone hydrates,22 made a blind prediction which now turns out to be within less than 10 cm−1 of experiment. This wave function based composite model belongs to the class of fully anharmonic methods and should be explored for the full test set in the future.Finally, we have the best set of values under this category, the FA1 submission. It falls close to FA3 for the best predictions, with the largest errors for MLA and THF, 101 and 76 cm−1 in absolute deviations. The total RMSD falls significantly once the two outliers are removed (RMSD of 27 cm−1). It is a unique set of calculations within the challenge. The authors carried out adiabatic ab initio molecular dynamics at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory. The fundamentals were taken from the power spectrum which is obtained by Fourier transform of the velocity autocorrelation function. Further details to the method are available in the corresponding FA1 ESI.† The single trajectories were started from optimised minima which fall in good agreement with the best predictions available, aside from a small difference in the conformation of the PCD hydrate. The source of the deviations should not be linked to the starting structures or the initial momenta. One should note that for this particular submission, the results for the training set were significantly better than for the test set, 18 vs. 47 cm−1. Most of this difference is due to the two aforementioned outliers, and which the authors anticipated as problematic. MLA and THF spectra were characterized by complex power spectra and more investigations should have been undertaken to best identify the target spectroscopic signal. Clearly this task is eased in the case of the training set.
3.7 Learning strategy (LS) submissions
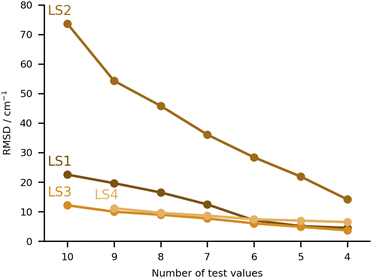
The final category of submissions were computational protocols which made use in one way or the other of learning strategies, either to correct computed harmonic frequencies, or to overall predict the position of the bands in the hydrate complexes. The worst performing set of values under this category was LS2 (see Fig. 9), with very large deviations for MLA, THT and TFE, 99, 88 and 166 cm−1 absolute errors respectively. We will discuss this set of values together with one of the best performing sets (LS3), since these originate from the same group and make use of the same training data. This consisted of the training and test set molecules, expanded by over 200 other organic molecules retrieved from the GDB11 dataset.64,65 The latter were chosen based on a similarity search, in an attempt to better cover the chemical space of the test set. For further details in the molecule selection, please consult the LS3 ESI.† The molecular geometries are available for download in https://github.com/MMunibas/Hydra/. The harmonic frequencies for the full set of hydrates were calculated at the B3LYP-D3(BJ)/aug-cc-pVTZ level of computation, which together with the measured hydrate frequencies (when available) served as data for both LS2 and LS3 learning approaches. In the case of LS2 (the worst performing submission in the LS category) a kernel was trained to reproduce the harmonic frequencies. The descriptors were generated from the Faber-Christensen-Huang-Lilienfeld (FCHL19) representation (total length 33 by 486).66 Using the same representation, the harmonic values were corrected to the known (experimental) training set values following the Δ-learning method.67 The two kernels were used in combination to arrive at the final predicted values, using the experimental OH symmetric stretch wavenumbers for water (3657 cm−1). In the case of LS3, the same underlying data was used, but this time a neural network was trained on the basis of the optimised geometries to provide the corresponding harmonic wavenumbers. The descriptors were also based upon FCHL19 (total length 193 after reduction by a principal component analysis, as described in the LS3 ESI†). The test set molecules were included in the training of the aforementioned neural network. Transfer learning was then used to replicate the experimental values for 9 hydrate complexes of the training set (the radical case was excluded). Further details on the architecture and algorithms used are provided in the respective ESI.† As one can observe comparing the LS2 and LS3 values, the transfer learning strategy was far more successful than the kernel approach. However, one should not necessarily pin this on the methods. After disclosing the results, a re-assessment of LS2 revealed that there was a mistake in the scaling of the standardised predictions. Instead of the anharmonic average and variance, the harmonic values were used, leading to an overestimation of the fundamentals values. With the correct procedure the root mean squared difference decreases from 74 to 54 cm−1. For further details, see “Re-evaluation of the Hydra results for Method LS2 (Δ-learning)” in the ESI.† It would be interesting to revisit both models with knowledge of the final target quantities.The other two submissions (LS1 and LS4) approached the problem making use of computed harmonic frequencies corrected by an empirical function. In the case of LS1, the base harmonic predictions were obtained at the PBE-D3 level of theory using the projector augmented wave approach (PAW). For calculation details please consult the corresponding ESI.† Eight complexes from the training set were used to fit a linear regression formula (two were excluded due to issues in the optimisation), the latter being applied to the harmonic predictions of the test set. The training and test sets roughly covered the same range of OH shifts, with similar types of interactions, providing a reasonable basis for the correction function. Albeit LS1 was not among the top group of submissions, the RMSD was still overall below 30 cm−1. Lastly, LS4 used a somewhat more complex linear correction function. The geometries and corresponding harmonic wavenumbers were obtained with the PBE0-D3(BJ) functional. The basis sets used were may-cc-pVTZ for the organic molecules, aug-cc-pVQZ for the water molecule in the complex. An empirical linear function was then used to correct the harmonic predictions to target experimental values. The training data consisted of 42 hydrate complexes with published spectroscopic data. The linear function included two parameters which were fitted to the aforementioned data, weighing in the OH bond elongation. Further details are provided in the LS4 ESI.† The performance of this approach was very similar to that of LS3 (Fig. 9).
4 Revisiting the training set
At this point it is worth revisiting the training set, both experimentally and in terms of theory performance. The latter is limited to those submissions which have provided training performance data. As the training set also included cases with a proven or speculated higher-order anharmonic resonance22 which shifts around the OH stretching energy levels by up to ±10 cm−1, one can now check whether submissions without regression step fit better the raw or the deperturbed experimental data, to learn more about the impact of this resonance. Finally, one can check whether a method performs better for the training set than for the test set or more or less equally well for both. Because the spread of wavenumber values turned out to be quite similar for the test and training data set, a balanced performance would not be too surprising.4.1 Reference experimental values and deperturbation
The case of ANL was experimentally revisited in the present work (see ESI,† and ref. 23 for details), because there was a hypothesis of an anharmonic perturbation in place.22 The size-selected literature spectrum of the monohydrate of ANL68 exhibits a very strong, partially saturated signal at 3524 cm−1 and a sharp satellite at 3547 cm−1 with unclear origin. To account for the possibility of an intensity stealing by this satellite, 3526 cm−1 with an uncertainty of ±3 cm−1 was proposed for the best deperturbed band position estimate.18 Comparison with the FTIR spectra in the present work confirms the main peak at 3525 cm−1, i.e. within 1 cm−1. It rules out a relative intensity of 10% or more for any weak satellite contribution near 3547 cm−1. Therefore, the resonance hypothesis can be dropped and the new best estimate is 3525 cm−1 with an uncertainty of ±1 cm−1, in line with the original raw result.68For all the other training set members, there is no new evidence which would cause a revision of the originally proposed fundamental wavenumbers, with or without deperturbation, although the DBN case is currently under reinvestigation. Hence, the following training set wavenumber alternatives remain, depending on whether raw results for the strongest signal or deperturbation for the high order anharmonic resonance22 is attempted. For ACE, the raw/deperturbed alternatives are 3538/3531 cm−1, for APH 3536/3530 cm−1, for DBN 3484/3487 cm−1. Note that Fig. 1 only lists the raw values. The methods shown in Fig. 10 would profit by at most 10% in their RMSD when switching to deperturbed reference values. Other deficiencies of the models clearly dominate. Still, it is rewarding to see that none of the discussed methods deteriorate with the deperturbation. On the other hand, none of the submissions has attempted to model the high-order resonance explicitly. Therefore, this subtle anharmonic aspect22 is left for future iterations of HyDRA, with better performing theoretical methods.
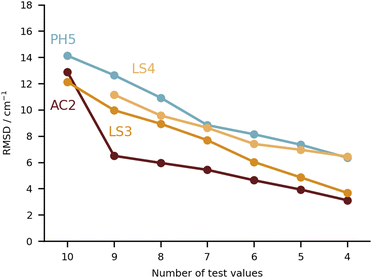
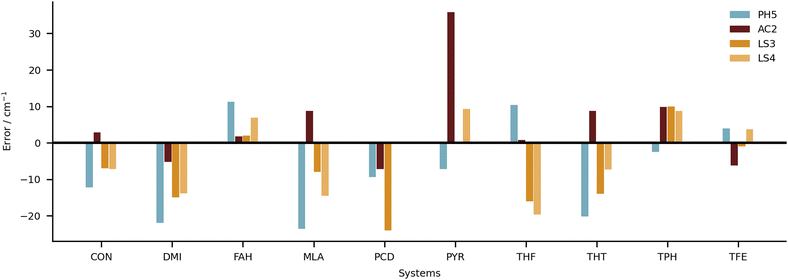
Keeping the discussion on the best performing methods, it is interesting to consider the individual errors plotted in Fig. 10. PH5, LS3 and LS4 predominantly underestimate the stretch frequencies shifts, whereas AC2 is more balanced in this regard. The major flaw in the AC2 prediction is PYR for which a large shift overestimation is found. The accumulated negative errors (underestimates) are −97.1, −18.6, −85.0 and −62.6 cm−1 compared with accumulated shift overestimates of 25.6, 68.6, 12.0 and 28.6 cm−1 for PH5, AC2, LS3 and LS4, respectively. For the case of AC2 it is interesting to note that PYR has the farthest red shift (i.e. strongest interaction between water and probe molecule) which is consistent with results on the training set (see AC2 ESI†) for which the bands shifted most to the red are typically captured least reliably. This points towards a genuine deficiency of B3LYP for the calculation of the PES, which is required in the DVR3D calculations.
4.2 Training set performance vs. test set performance
A global comparison of the training set performance is not straightforward, because the submitted methods differ widely in their system coverage. However, the group of methods which achieve a test set RMSD better than 15 cm−1 (PH5, AC2, LS3, LS4) overlaps well with the methods achieving a training performance better than 15 cm−1 (PH5, LS3, LS4). AC2, the only outlier in this correspondence, is unusual because it actually shows a 25% better performance for the (blind) test set than for the (known) training set. The other three methods perform better for the training set, which is expected for learning methods and for a purely harmonic approach (PH5) which has been manually tuned to achieve a good agreement with the training data.5 Future extensions
It will now be important to substantially and dynamically69 extend the HyDRA database in different directions such as larger downshifts, other compound classes, dihydrates, charged systems or spectral ranges, before another blind challenge might follow. Such a second generation blind challenge may decide more clearly between purely harmonic, anharmonically corrected, fully anharmonic and learning strategies. It may also reach a prediction quality which helps to better understand newly discovered anharmonic resonances in hydrate complexes.As an example for the power of this collaborative approach, we suggested to the authors of the best submissions to compute the results for the OH donor vibration in the water dimer, which has been a rather controversial observable over the last few years.22,70–73 A well-converged full-dimensional variational treatment of the donor OH stretch band origin on a high quality analytical potential energy hypersurface is now available74 yielding a value of 3599 cm−1. This calculation matches the experimental consensus of about 3601 cm−1 well within the ≈10 cm−1 spread due to quantum tunneling of indistinguishable nuclei present in this floppy dimer. It is of interest how close different local strategies without such tunneling contributions come to experiment. The results are summarised in Table 3. One can see that none of the predictions from this work supports the multiply refuted22,71–73 recent IR-VUV result and interpretation.70 AC2 comes closest but its focus on monomer anharmonicity is likely to perform poorly for the lightest, strongly librating hydrates, i.e. water dimer. All others consistently predict the water donor OH stretching downshift some 20 cm−1 above experiment and above the full-dimensional variational treatment, perhaps again a consequence of the particularly light and thus delocalised nature of the binding partner. This is also qualitatively true for the second-lightest case of formaldehyde (FAH, Fig. 11). It is encouraging that the three particularly successful independent approaches based on a harmonic reference are so consistent for such an extreme testing case.
 | ||
| Fig. 11 Individual errors in predicted shifts for the four submissions with the lowest RMSD overall (PH5, AC2, LS3 and LS4). | ||
6 Conclusions
Despite the manifold challenges posed to the participants, there are good reasons to be optimistic. We start with the positive points. In Fig. 10 and 11, a closer look is taken at the four submissions with the lowest RMSD overall (falling below 15 cm−1). The differences among these sets are statistically not significant and we see no point in crowning a unique winner. They show how quite different strategies can be across the board successful, with RMSDs reaching close to the 10 cm−1 value. This would be an interesting milestone for the future. If one would have to select winning categories, these would be perhaps the learning strategies (LS) and the anharmonic corrected (AC) submissions. These are the procedures which most strongly focus on the quantity of interest, and inherently carry an advantage for such a specific quantity. Nonetheless, as some results show, this is not at all a guarantee for success.The other side of the coin are the purely harmonic (PH) calculations, which heavily rely on error compensation. PH5 is built on a very conscious decision of using the ‘Pauling point’. Albeit calculations with larger basis sets were available (and provide the basis for AC4), cutting the number of functions leads to an improved error compensation. The robustness is impressive given the amount of approximations involved. We find two questions of interest for the future. The first one is whether this robustness will still hold when increasing the number or diversity of systems under study. This could be verified in future editions of the challenge or simply calculating some of the other systems which were suggested for the training set. The other question is whether this type of error cancellation can be found in other (relatively cheap) electronic structure methods, in particular DFT functionals. The three models used in this category (B3LYP, PBE0 and ωB97xD) seem to not hold to the task. However, the PH data sets are mostly subproducts of other computational protocols, and the ‘Pauling point’ was not being explicitly sought for. There could be alternatives.
The fully anharmonic submissions were perhaps the biggest upset overall. Some submissions were able to break below an RMSD of 40 cm−1, but they were far from reaching the top 4. One should say that this is partly due to the way the challenge was conceived. The test set consisted of both large and small systems, significantly limiting the level of theory that could be applied across all (or at the least the majority of) systems. It would have been perhaps of interest to have a few higher-level calculations for the smallest hydrates. This can be a task for future studies, although one will miss the blind character of the challenge. In future editions, one could also attempt to include more groups with a focus on ab initio vibrational spectroscopy which could potentially restrict themselves to the smallest systems featured. Another deciding factor was to estimate the shift in the OH frequency, i.e. to estimate a difference of frequencies instead of the absolute value. This decreases the importance of anharmonic effects and strongly favours methods which most heavily rely on error compensation (e.g., the PH submissions). The fully anharmonic (FA) methods have a much better comparative performance when looking at absolute fundamental band positions.
Finally, one should note that the conditions were not the best for machine learning approaches. Only a very small training set was made available. All LS submissions (with the exception of LS1) compensated for this fact by performing additional calculations on molecular datasets. Moving forward, it would be well-advised to combine the experimental information (e.g., for the 20 systems featured in this challenge) and libraries of computed vibrational spectra, even if just under the harmonic approximation. The curated data should reduce the overhead in building such models, besides significantly improving their accuracy.
Author contributions
Taija L. Fischer: conceptualization, data curation, formal analysis, investigation, validation, visualization, writing – review & editing. Margarethe Bödecker: data curation, formal analysis, investigation, validation, visualization, writing – review & editing. Sophie M. Schweer: investigation, validation, visualization, writing – review & editing. Jennifer Dupont: investigation, data curation, formal analysis, validation, visualization. Valéria Lepère: investigation, visualization, validation. Anne Zehnacker-Rentien: conceptualization, formal analysis, investigation, supervision, validation, writing – review & editing. Martin A. Suhm: conceptualization, formal analysis, funding acquisition, project administration, supervision, validation, writing – review & editing. Benjamin Schröder: investigation, formal analysis, validation, writing – review & editing. Tobias Henkes: investigation, formal analysis. Diego M. Andrada: supervision, project administration, resources, writing – review & editing. Roman M. Balabin: investigation, formal analysis, project administration, resources, writing – review & editing. Haobam Kisan Singh: investigation, formal analysis. Himangshu Pratim Bhattacharyya: investigation, formal analysis. Manabendra Sarma: conceptualization, formal analysis. Silvan Käser: investigation, data curation. Kai Töpfer: investigation, data curation. Luis I. Vazquez-Salazar: investigation, data curation. Eric D. Boittier: investigation, data curation. Markus Meuwly: supervision, project administration. Giacomo Mandelli: investigation, data curation, writing, review and editing. Cecilia Lanzi: investigation, data curation, writing, review and editing. Riccardo Conte: supervision, project administration, resources, writing – review & editing. Michele Ceotto: supervision, project administration, resources, writing – review & editing. Fabian Dietrich: data curation, formal analysis, investigation, methodology. Vicente Cisternas: investigation, formal analysis. Ramachandran Gnanasekaran: investigation, formal analysis, project administration, resources, writing – review & editing. Michael Hippler: investigation, formal analysis, project administration, resources, writing – review & editing. Mahmoud Jarraya: investigation, formal analysis. Majdi Hochlaf: supervision, project administration, resources, writing – review & editing. Narasimhan Viswanathan: investigation, formal analysis, writing – review & editing. Thomas Nevolianis: investigation, formal analysis. Gabriel Rath: investigation, formal analysis. Wassja A. Kopp: investigation, formal analysis. Kai Leonard: supervision, project administration, resources, writing – review & editing. Ricardo A. Mata: conceptualization, data curation, formal analysis, project administration, validation, visualization, writing – original draft, writing – review & editing.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
Simulations for submission AC3 were performed with computing resources granted by RWTH Aachen University under project rwth0821. WAK acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germanys Excellence Strategy – Cluster of Excellence 2186 “The Fuel Science Center” – ID: 390919832. NV acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for the project “Ab initio Thermochemistry and Kinetics of Molecules with Coupled Large-Amplitude Motions” – 403683184. RMB would like to thank E. M. Lichak for his technical assistance and fruitful discussions. FD thanks for the support by the ANID (Fondecyt Project 3200596) and the supercomputing infrastructure of the NLHPC (ECM-02). HKS acknowledges the financial support from the Ministry of Human Resource Development (MHRD), Government of India. HPB also thanks the Department of Science and Technology, GoI for the financial assistance through INSPIRE Fellowship (No. DST/INSPIRE Fellowship/2017/IF170899). MS, HKS and HPB thank Param-Ishan, IIT Guwahati supercomputing facilities and Department of Chemistry, IIT Guwahati. RG wishes to thank VIT-Chennai University and “VIT SEED GRANT” for providing the computing facilities to carry out the calculations. TLF, MB, SMS, MAS, BS and RAM acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455. MC and RC acknowledge financial support from the European Research Council (Grant Agreement No. 647107) SEMICOMPLEX ERC-2014-CoG under the European Union's Horizon 2020 research and innovation programme.Notes and references
- P.-O. Löwdin, Int. J. Quantum Chem., 1986, 28, 19–37 CrossRef.
- P.-O. Löwdin, Pure Appl. Chem., 1989, 61, 2185–2194 CrossRef.
- M. Amezcua, L. El Khoury and D. L. Mobley, J. Comput.-Aided Mol. Des., 2021, 35, 1–35 CrossRef CAS PubMed.
- M. Işık, A. S. Rustenburg, A. Rizzi, M. R. Gunner, D. L. Mobley and J. D. Chodera, J. Comput.-Aided Mol. Des., 2021, 35, 131–166 CrossRef PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. D. Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2011, 67, 535–551 CrossRef CAS PubMed.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H. Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef CAS PubMed.
- K. I. Assaf, M. Florea, J. Antony, N. M. Henriksen, J. Yin, A. Hansen, Z. Wang Qu, R. Sure, D. Klapstein, M. K. Gilson, S. Grimme and W. M. Nau, J. Phys. Chem. B, 2017, 121, 11144–11162 CrossRef CAS PubMed.
- H. C. Gottschalk, A. Poblotzki, M. A. Suhm, M. M. Al-Mogren, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, L. C. Kröger, K. Leonhard, H. Mouhib, F. Neese, M. N. Pereira, I. S. Ulusoy, A. Wuttke and R. A. Mata, J. Chem. Phys., 2018, 148, 014301 CrossRef PubMed.
- M. Schappals, A. Mecklenfeld, L. Kröger, V. Botan, A. Köster, S. Stephan, E. J. García, G. Rutkai, G. Raabe, P. Klein, K. Leonhard, C. W. Glass, J. Lenhard, J. Vrabec and H. Hasse, J. Chem. Theory Comput., 2017, 13, 4270–4280 CrossRef CAS PubMed.
- H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. Mogren Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, J. Chem. Phys., 2020, 152, 164303 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- P. M. Felker and A. H. Zewail, Chem. Phys. Lett., 1983, 94, 454–460 CrossRef CAS.
- R. Bombach, E. Honegger and S. Leutwyler, Chem. Phys. Lett., 1985, 118, 449–454 CrossRef CAS.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS PubMed.
- A. Potapov and P. Asselin, Int. Rev. Phys. Chem., 2014, 33, 275–300 Search PubMed.
- M. Becucci and S. Melandri, Chem. Rev., 2016, 116, 5014–5037 CrossRef CAS PubMed.
- S. E. Novick, Bibliography of rotational spectra of weakly bound complexes; https://wesfiles.wesleyan.edu/home/snovick/SN_webpage/vdw.pdf, 2019.
- T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454 RSC.
- K. Le Barbu, F. Lahmani, M. Mons, M. Broquier and A. Zehnacker, Phys. Chem. Chem. Phys., 2001, 3, 4684–4688 RSC.
- M. Nedić, T. N. Wassermann, R. W. Larsen and M. A. Suhm, Phys. Chem. Chem. Phys., 2011, 13, 14050–14063 RSC.
- M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721 RSC.
- T. L. Fischer, T. Wagner, H. C. Gottschalk, A. Nejad and M. A. Suhm, J. Phys. Chem. Lett., 2021, 12, 138–144 CrossRef CAS PubMed.
- M. A. Suhm, A. Zehnacker-Rentien, V. Lepère, J. Dupont, S. M. Schweer, M. Bödecker and T. L. Fischer, Experimental Supplement to the HyDRA blind challenge, GRO.data, Göttingen Research Online, 2023 DOI:10.25625/FLGZYE.
- J. Thomas and Y. Xu, J. Chem. Phys., 2014, 140, 234307 CrossRef PubMed.
- M. Heger, T. Scharge and M. A. Suhm, Phys. Chem. Chem. Phys., 2013, 15, 16065–16073 RSC.
- E. Galántay, Tetrahedron, 1963, 19, 319–321 CrossRef.
- T. Chai and R. R. Draxler, Geosci. Model Dev., 2014, 7, 1247–1250 CrossRef.
- R. A. Mata, Submitted data to the first HyDRA blind challenge, GRO.data, Göttingen Research Online, 2023 DOI:10.25625/F5C8IO.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- C. C. Bannan, K. H. Burley, M. Chiu, M. R. Shirts, M. K. Gilson and D. L. Mobley, J. Comput.-Aided Mol. Des., 2016, 30, 927–944 CrossRef CAS PubMed.
- D. W. Scott, Multivariate Density Estimation, Wiley, 1992 Search PubMed.
- M. Heger, M. A. Suhm and R. A. Mata, J. Chem. Phys., 2014, 141, 101105 CrossRef PubMed.
- F. Kollipost, K. Papendorf, Y.-F. Lee, Y.-P. Lee and M. A. Suhm, Phys. Chem. Chem. Phys., 2014, 16, 15948–15956 RSC.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- T.-S. Ho and H. Rabitz, J. Chem. Phys., 1996, 104, 2584–2597 CrossRef CAS.
- O. T. Unke and M. Meuwly, J. Chem. Inf. Model., 2017, 57, 1923–1931 CrossRef CAS PubMed.
- D. O. Harris, G. G. Engerholm and W. D. Gwinn, J. Chem. Phys., 1965, 43, 1515–1517 CrossRef.
- J. Tennyson, M. A. Kostin, P. Barletta, G. J. Harris, O. L. Polyansky, J. Ramanlal and N. F. Zobov, Comput. Phys. Commun., 2004, 163, 85–116 CrossRef.
- K. Yagi, K. Hirao, T. Taketsugu, M. W. Schmidt and M. S. Gordon, J. Chem. Phys., 2004, 121, 1383–1389 CrossRef CAS PubMed.
- G. M. Chaban, J. O. Jung and R. B. Gerber, J. Chem. Phys., 1999, 111, 1823–1829 CrossRef CAS.
- N. Matsunaga, G. M. Chaban and R. B. Gerber, J. Chem. Phys., 2002, 117, 3541–3547 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- F. Neese, T. Schwabe and S. Grimme, J. Chem. Phys., 2007, 126, 124115 CrossRef PubMed.
- P. M. Felker and Z. Bačić, J. Chem. Phys., 2020, 152, 124103 CrossRef CAS PubMed.
- V. Barone, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- H.-J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126, 164102 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108 CrossRef PubMed.
- T. Fink, H. Bruggesser and J.-L. Reymond, Angew. Chem., Int. Ed., 2005, 44, 1504–1508 CrossRef CAS PubMed.
- T. Fink and J.-L. Reymond, J. Chem. Inf. Model., 2007, 47, 342–353 CrossRef CAS PubMed.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. A. von Lilienfeld, J. Chem. Phys., 2020, 152, 044107 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- I. León, P. F. Arnáiz, I. Usabiaga and J. A. Fernández, Phys. Chem. Chem. Phys., 2016, 18, 27336–27341 RSC.
- T. Weymuth and M. Reiher, Phys. Chem. Chem. Phys., 2022, 24, 14692–14698 RSC.
- B. Zhang, Y. Yu, Z. Zhang, Y.-Y. Zhang, S. Jiang, Q. Li, S. Yang, H.-S. Hu, W. Zhang, D. Dai, G. Wu, J. Li, D. H. Zhang, X. Yang and L. Jiang, J. Phys. Chem. Lett., 2020, 11, 851–855 CrossRef CAS PubMed.
- H. C. Gottschalk, T. L. Fischer, V. Meyer, R. Hildebrandt, U. Schmitt and M. A. Suhm, Instruments, 2021, 5, 12 CrossRef CAS.
- I. León, R. Montero, A. Longarte and J. A. Fernández, J. Phys. Chem. Lett., 2021, 12, 1316–1320 CrossRef PubMed.
- E. Vogt and H. G. Kjaergaard, Annu. Rev. Phys. Chem., 2022, 73, 209–231 CrossRef PubMed.
- X.-G. Wang and T. Carrington, J. Chem. Phys., 2023, 158, 084107 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental data for test set members, detailed analysis of the theoretical submissions and computational details for individual submissions. See DOI: https://doi.org/10.1039/d3cp01216f |
| This journal is © the Owner Societies 2023 |