 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular modelling of the thermophysical properties of fluids: expectations, limitations, gaps and opportunities†
Marcus J.
Tillotson
 a,
Nikolaos I.
Diamantonis
a,
Nikolaos I.
Diamantonis
 b,
Corneliu
Buda
c,
Leslie W.
Bolton
b,
Corneliu
Buda
c,
Leslie W.
Bolton
 d and
Erich A.
Müller
d and
Erich A.
Müller
 *a
*a
aDepartment of Chemical Engineering, Imperial College London, London, UK. E-mail: e.muller@imperial.ac.uk
bbp, Innovation and Engineering, Sunbury, UK
cbp, Innovation and Engineering, Naperville, USA
dIndependent Consultant, Fleet, UK
First published on 28th April 2023
Abstract
This manuscript provides an overview of the current state of the art in terms of the molecular modelling of the thermophysical properties of fluids. It is intended to manage the expectations and serve as guidance to practising physical chemists, chemical physicists and engineers in terms of the scope and accuracy of the more commonly available intermolecular potentials along with the peculiarities of the software and methods employed in molecular simulations while providing insights on the gaps and opportunities available in this field. The discussion is focused around case studies which showcase both the precision and the limitations of frequently used workflows.
1. Introduction
Physical property data is at the heart of all chemical, biological and physical manufacturing processes.1,2 Uncertainty and/or sheer lack of data has a direct impact on the deployment of efficient processes and is one of the most salient stumbling blocks in process design.3 Without suitable data, the process engineer cannot rationally evaluate the appropriate extent of overdesign and more crucially assess the risk of process failure.4 This is particularly true of processes with many stages, such as distillation, absorption, trains of batch reactors, etc. Even small uncertainties in a few key thermophysical properties can skew the design by large amounts5 (see Fig. 1).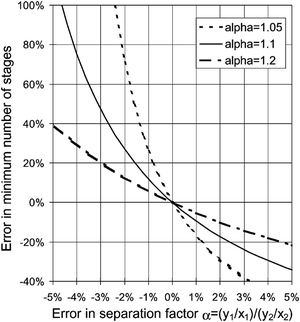 | ||
| Fig. 1 Influence of the errors in the determination of the separation factor, α (the ratio of vapour mole fraction to liquid mole fraction between two components), on the minimum number of theoretical stages in a typical distillation column. For “difficult” separations (α close to 1), one needs many theoretical stages, e.g. between 100 and 200 stages, and high investment costs. An uncertainty of the order of a few percent can cause deviations which are larger than 100%. Taken with permission from ref. 5. Copyright 2002 Elsevier. | ||
Physical properties of fluids can be, and have been measured experimentally since the dawn of modern science. Densities, vapour pressures, critical point data, viscosities, solubilities, surface tensions, thermal conductivities, etc. are all routinely measured and collated in existing open-access6 and proprietary databanks. Pure compound data is presently available for several thousand to tens of thousands chemical compounds of interest (depending on the data-bank), a number which pales against the over 120 million chemical structures identified to date.7 When one considers mixtures, a much smaller (relative) number of systems has been explored (e.g. DECHEMA claims to have data for roughly 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 systems from 80
000 systems from 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 constituent pure fluids). Databases themselves grow at a slow pace, to the order of a million data points per year. Entire scientific journals8 devoted to this pursuit give evidence that the progress is very incremental, at the most. This level of “data ignorance” is problematic, and no practical increase in the level of experimentation will allow us to explore this universe in any meaningful way. The implications of this void are vast and not limited to chemical processes: the plight of the pharma industry to discover new drugs is a clear consequence of the asymmetry between our existing physical property knowledge and the phase space that could be potentially searched.9
000 constituent pure fluids). Databases themselves grow at a slow pace, to the order of a million data points per year. Entire scientific journals8 devoted to this pursuit give evidence that the progress is very incremental, at the most. This level of “data ignorance” is problematic, and no practical increase in the level of experimentation will allow us to explore this universe in any meaningful way. The implications of this void are vast and not limited to chemical processes: the plight of the pharma industry to discover new drugs is a clear consequence of the asymmetry between our existing physical property knowledge and the phase space that could be potentially searched.9
Notwithstanding their immense value, the slow pace of acquisition (and high cost) of experimental data needs requires them to be extended and supported by theories and numerical models. The appreciation of the impact that models that help correlate and predict physical properties have on the scientific community can be summarized by two Nobel prizes awarded almost a century apart. The 1910 physics Nobel prize was awarded to J. D. van der Waals, for the recognition that analytical (mathematical) models were capable of modelling vapour–liquid equilibria, including the unique phenomenon of the appearance of a critical point. Today, successors of these expressions, better known as cubic Equations of State (EoS) are a staple of engineering design. The van der Waals equation kick-started a century of research into the link between the different macroscopic thermodynamic properties, at the time when science was assessing and understanding the atomic nature of matter. Statistical mechanics ultimately provided the link between the intermolecular forces amongst molecules and the integrated macroscopic observable product of the collective behaviour of ensembles of molecules.10,11 While elegant and self-consistent, the expressions provided by statistical mechanics are only solvable for a handful of ideal cases. Our understanding of the nature of intermolecular forces provided yet another path to the description of the molecular interactions through the solution of Schrödinger's equations. Referring to this, Dirac suggested almost a century ago12 that “the underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are … completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble”. The combination of quantum mechanical calculations and highly sophisticated numerical tools provides the promise of an avenue to process and correlate the available experimental data. This, in its own right, is a striving area of research, particularly with the use of group contribution approaches,13,14 but its practical usefulness is limited by the requirements of large computational resources and the availability of experimental data to validate the results.
A more recent chemistry Nobel prize award was presented in 2013 to Martin Karplus, Michael Levitt and Arieh Warshel acknowledging that atomistically-detailed force fields based on information taken from quantum mechanical calculations represented a game-changing approach allowing the computer-based prediction of physical properties. Indeed, in the past 50 years we have experienced an unexpected and unparalleled change in the way scientists view physical property prediction.15 Within the lifetime of many (and in particular of the more senior) industrialists and academics, computational power has progressed immensely on the back of the shade provided by Moore's Law (the empirical observation/prediction that computer hardware speed doubles every two years).16 Digital computers, which started becoming available to mainstream scientists as early as the 1950's, were initially employed for supporting the development of statistical mechanical theories.17,18 Seminal papers describing molecular dynamics19,20 and Monte Carlo21,22 simulations appeared in the literature at this time and garnered the attention of science-driven engineers and companies who saw them as platforms for the calculations of properties of real substances.23 Today, those “heroic” simulations of the past century are dwarfed by equivalent (or much larger) ones performed routinely even as undergraduate-level coursework.24,25 The reader is referred to some of the review papers on the history of molecular modelling and on the overview of its implementation in the physical and chemical sciences26–28 for a detailed chronicle.
The level of molecular modelling described in the preceding paragraph is orders of magnitude less demanding than the full quantum calculations which it tries to emulate and matches well the current availability of rather inexpensive and relatively powerful hardware. This, alongside the accessibility of dedicated software prompts the use of these molecular modelling tools to predict the physical properties of fluids.29,30 The rationale behind this is self-evident. Simulations have the potential to provide for exact solutions of the statistical mechanical expressions that govern the macroscopic behaviour of matter. They provide so within a reasonably inexpensive framework and are able to access regions of phase space inaccessible to experiments because of practical constraints such as toxicity,31 extreme conditions,32 and ocassionally low (or unknown) purity of materials. Furthermore, molecular simulations are in principle able to predict the behaviour and properties of new materials and molecules prior to their synthesis, a key driving tool for innovation in the pharmaceutical and material science industries. Unfortunately, one of the largest challenges faced by molecular simulation is the “hype” or over-selling of the techniques implied by this last sentence. This has led to unrealistic expectations among those seeking to use them to supplement, or even to replace the experimental measurements. A method of modelling all entities and properties of a system with a low degree of uncertainty is certainly the ultimate goal, however such predictive method remains far from being realised. In practice, some degree of judgement is needed to select simplifications which make solution tractable yet do not compromise accuracy. Reasonable expectations must always be borne in mind and only in very few spaces can one find information on the myths and misconceptions of computer modeling.33
Two decades ago, a multidisciplinary panel reviewed the development and applications of molecular and materials modelling across the globe, with particular focus on the deployment within industrial companies.34 The report and the interviews with the leaders and practicing engineers and scientists, reflect the mindset of the time – that molecular modelling was for only very difficult ultra-high value problems, such as the discovery of a new catalyst (ostensibly because they were experimentally challenging), and pursuing the presumably simpler things, such as predicting fluid properties, was not so much a high priority – as measurement was often cheaper (and always more accurate!) than simulation. Nonetheless, the complexity of doing such “high value” calculations was consistently underestimated (e.g., it was not always obvious what to simulate) and the results were rather underwhelming. The report already highlighted the disproportionate hype and over-promising that affected the field, maybe just a manifestation of the excitement of the players at the opportunities that lay ahead. In fact, this report suggested that in the ten years following it, “molecular based modelling approaches (understood here as the collective of computational quantum chemistry, molecular simulations, mesoscale modelling, molecular-structure/macroscale property correlations and related information technologies) would profoundly affect how chemistry, biology, and materials physics are understood, communicated, and transformed to technology, both in intellectual and commercial applications”. It anticipated that in the near future (i.e., today) experimentalists and management would not only become used to accepting the use of molecular modelling, but they would expect it.3,35 But a decade past this deadline, has this prophesy been fulfilled? Where do we stand with respect to the balance between promise and delivery? This manuscript is focused on providing an objective assessment and a guide to manage these expectations and to understand both the opportunities and limitations of the molecular modelling36 from the viewpoint of a joint academic/industrial experience, complementing some of the previous guidance in the open literature.37,38
2. Scope of this manuscript
The terms simulation and molecular modelling are commonly used indistinctively but have diverse interpretations, depending on the interests and background of the user. Anything from the quantum mechanics calculations of a small set of atoms to the large-scale plant optimizations fall under the remit of “simulations”, although they refer to unrelated procedures, aims and results. Crucial to any modelling study, however, is the question of the scale which relates to the problem at hand. Different techniques will probe different length (and time) scales, in a sort of “ladder” that scales from the nm (fs) to the meter (day) range. The present manuscript deals with classical molecular simulations, understood to be the numerical solution of the statistical mechanics of molecules for small systems and/or the solution of Newton's equations of motion for classical forcefields. We are explicitly not covering the bottom end of the ladder: quantum mechanical and ab initio calculations, renormalization group theory, density functional theories and similar techniques aimed at providing numerical solution of the Schrödinger equation for the many-body wavefunction. At the other end of the spectrum, we will not include in the discussion non-particle coarse-gaining methods such as dissipative particle dynamics (DPD), Lattice Boltzmann nor computational fluid dynamics (CFD) modelling. Similarly, equations of state calculations will not be explicitly discussed. While the “holy grail” of the simulation community is to be able to use all different scales seamlessly, we presently struggle passing information up and down these different scales and again, this multi-scale approach is beyond the scope of the present discussion.39 The focus here will be on an arguably small, but relatively mature, sub-section of the simulation spectrum, concerned with the description of matter by means of discrete models which describe matter at the atomic level. Furthermore, although the atomistic (and related particle-based coarse-grained) methods described here are the same used in biomolecular computations, the onus of this contribution is to look at fluid mixtures of interest to the chemical, petrochemical, biochemical and similar industries, i.e. organic molecules of usually less than 1000 Da, including aqueous and ionic solutions.3. In silico veritas40 (In computation we trust)
Classical molecular modelling relies on the successful amalgamation of four factors: (1) appropriate computational power, expressed as the accessibility of suitable high-end hardware; (2) related software which can resolve, in a numerical fashion, the statistical mechanical equations that provide the configurational properties; (3) the force field or intermolecular potentials which describes the molecular properties; and last, but not least, (4) the human operator who not only processes the information and makes judgement as to what assumptions are reasonable and/or appropriate, but ultimately discerns and assesses the validity of the results. While all four elements are required, undoubtedly the latter is usually the limiting step, as it relies on both training and experience. We will briefly discuss these four elements in turn.3.1 Hardware
The current atomistic molecular dynamics “world record” for the largest simulation41 corresponds to a molecular dynamics (MD) simulation of 3.02. 1013 atoms. While an impressive feat, these types of simulations are one-off examples used to test the scalability of parallel programs and algorithms but are not intended as production runs. They are heroic feats, but are destined to be short-lived records,42 as the computing power available per unit of currency only increases with time. With another optic, these computations are dwarfed by the scale needed to model even just a few grams of a simple monoatomic substance (of the order of an Avogadro's number 6.02. 1023 atoms) and/or the scales needed to model complex biological systems. Thankfully, for the cases of interest here, the use of periodic boundary conditions (mimicking infinite systems) and simplification of the physics allow the simulation of a state point of a modest-size system O(105 atoms), enough for many practical applications, in a matter of wall-clock hours. As a typical case, consider the calculation of transport properties (self-diffusion coefficient and/or shear viscosity) of a 50/50 mixture of methanol/water. If one is to use 1000 atomically-detailed models of molecules and run for 1 ns of molecular time with current hardware (e.g. a 32-core processing unit, Intel Xeon Processor E5-2697A v4 @ 2.60 GHz), one would require 20 core hours per state point43 (less than 1 h of wall-clock time).44 A similar argument can be made with respect to the length of a typical molecular simulation. Several nanoseconds can be comfortably achieved with available hardware for modest systems, however, as an extreme example, microsecond runs, reflecting the motion on protein complexes, have been reported.45 The use of coarse-grained force-fields (discussed in the next section) relax the scale and time limitations of atomistic models, but even then, only the microscale (a few micrometers or microseconds: one usually precludes the other) can be comfortably explored.Specialized hardware has been designed for the unique task of performing MD simulations,46 which is capable of running a 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558-atom benchmark system at a rate of 85 μs day−1. More recently, the community has benefitted from advances derived from the gaming industry, for which graphical processing units (GPU's) were developed at relatively low cost. It was rather straightforward to adapt these game boards to molecular modelling software, as parallel algorithms are now the norm for MD simulations.47 The result was a noticeable increase in the available computational power and the possibility of having desktop units performing at the level of the supercomputers of a few decades ago (see for example the comments made during a recent Faraday Discussion on the topic48).
558-atom benchmark system at a rate of 85 μs day−1. More recently, the community has benefitted from advances derived from the gaming industry, for which graphical processing units (GPU's) were developed at relatively low cost. It was rather straightforward to adapt these game boards to molecular modelling software, as parallel algorithms are now the norm for MD simulations.47 The result was a noticeable increase in the available computational power and the possibility of having desktop units performing at the level of the supercomputers of a few decades ago (see for example the comments made during a recent Faraday Discussion on the topic48).
In summary, Moore's law16 has been a contributing factor to the explosion of capabilities in the field. However, no amount of computer power will ever suffice the researcher, who will always find a bigger and more complex system to study. Notwithstanding, the sustained increase in computer power (understood either as the increase in simulation speed per unit of currency, or the maximum speed, or the maximum floating point operations per seconds) with time clearly suggests that hardware is not the most relevant bottleneck of physical property predictions49 (or at least is not one we have control over). For more accurate and subtle overviews on the increase in computer power for simulations (and especially biomolecular simulations) the reader is referred to the discussions by Schlick et al.50,51
Quantum computers hold a significant promise in terms of propelling chemical computations (in particular, the solutions of Schrödinger's equations) into a new era, by providing several orders of magnitude of computational power above their digital counterparts. While the so-called “quantum supremacy” has already been hailed,52 it is unlikely that large-scale quantum computers will be commonly available in the near future. Certainly, there are already glimpses that they could provide for a transformative change in the way thermophysical properties are predicted.53 This is, however, a very long-term prediction which would be foolish to appraise.14
3.2 Software
Advances in software and algorithms seem to be shadowed by the fact that every year it is possible to run bigger, longer and more complex simulations with the same cost. As discussed above, the concept of parallel processing has been taken up within MD software suites, as the method is particularly suited for segmenting the problem into smaller fractions (e.g. by domain decomposition), allowing individual processors to resolve the equations of motion of the several groups of molecules independently.54 This has propelled the widespread use of MD software over other simulation strategies, notably Monte Carlo (MC) methods.In general, nowadays, software for running simulations is readily available, both in free open-access format and in commercial suites. Most of the “free” packages are maintained by, or have their roots, in collaborative academic programs.55 These codes are a compilation of many coder/years and as such are not simple for the novice to employ. It might take a typical graduate student a few months to be reasonably confident with the use of the programs, even when having had a previous knowledge of the theory behind modelling. The choice is bewildering and is commonly driven by familiarity rather than by performance. While some open-access programs have well-established user-manuals and a community of users willing to provide guidance, it is evident that there is a large entrance barrier to be able to use these codes efficiently. Even at this stage, the use of the programs is far from straightforward and much care need to be taken in running and interpreting the results. With each of the several steps associated with performing a molecular simulation (setup of the system and data files, production runs, data analysis and visualization), one encounters a large choice of stand-alone programs which may or may not be used in an integrated fashion. Commercial packages56 strive to bridge this gap, providing for graphical user interfaces (GUI), pre-packed force fields, and technical support, all for a significant price. The field is now being driven towards open-source suites which integrate different programs, e.g. the MoSDeF software stack.57
In our view, one of the hazards here (and not one which uniquely applies to molecular modelling) is that user-friendly GUI-based tools enable non-expert users to set-up and successfully run molecular simulations, but not necessarily the most “appropriate” ones. Here, the story of the “Sorcerer's Apprentice”,58 comes to mind.
3.3 Force fields
Within the specification of a molecular simulation, one of the key decisions to make refers to the description of the intermolecular forces. This is commonly done by stipulating a set of semi-empirical analytical expressions and corresponding parameter sets, collectively known as force fields, that describe the atom–atom (or particle–particle) potential energies. Force fields are the heart and soul of a molecular simulation. The other elements (hardware, software and humans) all work to extract the macroscopically observed properties which stem directly and exclusively from the intermolecular forces.Atomistically-detailed, also referred as all-atom (AA) analytical force fields (e.g. OPLS,59 AMBER,60 CHARMM,61 COMPASS62etc.) developed historically for biomolecular simulations are now extensively used in engineering and in the physical chemistry fields.63 The underlying functional form of these force field families are strikingly similar (cf.Fig. 2), with differences in the technical details and parametrization strategies. The original force-fields based on the general form shown in Fig. 2 (sometimes referred to Class I force fields) have been expanded by the inclusion of cross terms describing the coupling between stretching, bending, and torsion leading to a new category of force fields, referred to as Class II. The most important recent enhancement to the standard potential is the inclusion of polarization effects explicitly.64,65 In general, the force-field approach has proven extremely successful, however, a high accuracy in the results is closely correlated to the fact that the simulated system of interest is constructed from a set of similar previously parametrized chemical moieties. Force fields of this sort are empirically optimized to reproduce internal molecular degrees of freedom calculated through quantum mechanics (QM) and some limited experimental properties.66 This fitting process is difficult and cumbersome,67 and most often relies on reaching compromises amongst multi-objective functions and/or on employing ad hoc procedures. The consequence is that, in general, the force field will perform well for the description of the systems and properties which were used to parametrize it, but issues of representability, robustness and transferability68,69 will inevitably be present. There is no force field that can claim to be useful for all systems of interest and it is not uncommon to find that a force field of choice lacks parameters for certain atom groups. Consequently, the engineer must use his/her judgement and expertise to select from a library of force-fields each having some advantages and disadvantages. This choice can have a profound impact on the simulation results.
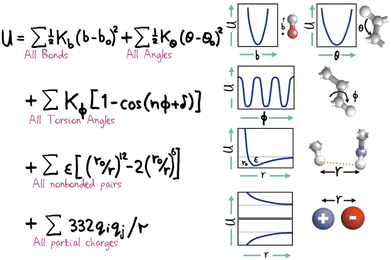 | ||
| Fig. 2 Hand-drawn representation of the total potential energy contributions of a molecule as the sum of simple analytical terms allowing for bond stretching, bond angle bending, bond twisting, van der Waals interactions and electrostatics, attributed to Shneior Lifson in the early 70's. Almost all force fields employed today still retain most of the elements shown above. Reprinted by permission from SpringerNature from a retrospective by Michael Levitt, ref. 70. | ||
Coarse graining (CG) is a term that refers to the use of simplified molecular models, where the atomistic detail is removed and substituted by the description of molecules in terms of “super-atoms” which represent, typically, a small number of heavy atoms. For example, the TraPPE71 force field, parametrized extensively toward liquid state and phase equilibrium properties of fluid systems widely encountered in chemical engineering, recognizes that the effect of explicitly considering the hydrogen atoms in organic molecules adds a substantial degree of complexity to the calculations which is not balanced by a corresponding additional degree of accuracy. Hence, in a first level of coarse graining, “united atoms” are considered, where the influence of associated hydrogen atoms are included in effective heavy atom beads. In a further degree of coarse graining, a propane molecule could be modelled as an isotropic spherical bead where all the electronic details, the intramolecular vibrations, bond fluctuations and molecular topology are incorporated within a point pair-wise interaction model. Further levels of integration (and corresponding lower fidelity coarse graining) for example, would be suitable for the description of entire polymer segments as single particles.72 One of the key issues in developing CG force fields is the methodology used to parameterize the intermolecular potential.73 Although not uniquely, most CG approaches start with an atomistically-detailed model and integrate out the degrees of freedom not deemed to be relevant.74 This procedure, by its own nature, removes information and the resulting force field is inherently deficient, especially in terms of transferability and robustness. Furthermore, it is driven by the judgement and expertise required to decide what is and is not “relevant” detail in a simulation problem. A fundamentally different “top-down” approach can be employed where the CG potential parameters are optimized to reproduce the macroscopically observed thermophysical properties (instead of integrating high fidelity atomistic models).75,76 With judicious choices, the resulting models and force fields have proved that they can be of equal or superior accuracy to the current state-of-the-art quantum and atomistic models77 while reducing the computational requirements by several orders of magnitude.
A new area of research has spawned in the quest of expanding the range of applications of accurate quantum calculations by correlating them with the aid of machine learning (ML) models78,79 (cf. Section 5.5). This approach, in principle, allows the production of force-fields with a high level of accuracy which could be embedded in classical MD simulations80 but at a significantly reduced computational overhead compared to the underlying quantum models.81 A particularly interesting feature of ML force fields is that they can be made to include many-body interactions in a natural fashion without having to pre-empt any particular mathematical closed form. Topical research in the field aims at the production of “universal” force fields, as for example the ANI-182 and GAP83 family of potentials. These workflows attempt to both generalize and extend the results obtained from quantum-based calculations (such as density functional theory). While useful for describing electronic structure prediction, reactions and solids, they struggle with the prediction of dispersion interactions, which, unfortunately, are key to most of the liquid and dense fluid properties84 as even the requirement of “quantum chemical accuracy” has proven to be woefully unsuitable for fluid-phase properties.85
3.4 The users, resources, tutorials, books and papers
Excellent textbooks86–93 and entry-level tutorial papers94–96 are available for both the novice and the experienced user which lucidly describe both the underlying statistical mechanics and theory behind the current modelling approaches and the practical implementations of modelling. Accounts of the intricate details of MC21,97 and MD codes98,99 are also available. While certainly the information is available in books and tutorials, there are very few dedicated college degrees focused on preparing individuals for the task of being “modellers”. The community is fuelled by graduates from chemistry, physics, engineering and similar disciplines who have pursued higher education in academic research groups with experience in these areas and who have taken relevant courses and/or workshops. An accompanying issue refers to individuals having a very high level of specialisation (in their PhDs and post docs) rather than a broad awareness across the entire field.For both the novice and for environments where dedicated resources are scarce, turn-key solutions are becoming available, which include a “black-box” equipment pre-loaded with the required software and databases, comprising the required force fields and GUIs that allow the rapid set-up and running of molecular simulations.100 This presents a key problem: the outcome of a molecular simulation is dependent on the expertise of the individual selecting and applying the force-field. It also supposes that a force-field capable of correctly describing all of the different molecules in the system exists, whereas in practice most force-fields are optimised for particular components or chemical families.
4. Case studies
It would be unrealistic to review the applicability and accuracy of all available force-fields and simulation strategies in an unabridged way. In this section we discuss some generalities that should be understood as guidelines for understanding the current state of the art in terms of molecular modelling of fluids. We aim to detail, without prejudice, case studies taken from the open literature which provide guidance and showcase the range and accuracy of the results expected for several of the most common thermophysical properties of fluids. Further selected examples are included in the ESI.†4.1 Density
Density calculations are possibly the most reliable properties that can be obtained from molecular simulations. In parallel, single-phase liquid density is one of the simplest thermophysical properties; it may be measured rather inexpensively and with very high precision employing vibrating tube densimeters.101 From the simulation standpoint, densities can be obtained rather straightforwardly from single phase isobaric–isothermal simulations, so naturally, these properties are commonly employed to either benchmark or refine force field parameters. Densities provide direct information useful to estimate the characteristic length in force fields (σ in most models) to a good degree of accuracy. Liquid phase densities under ambient conditions will usually be computed to within a few percent of the values reported in critically-evaluated data sources and are possibly the most reliable properties that can be obtained from molecular simulations.102 However, densities of most liquids of interest are always in the range 700–1150 kg m−3 (e.g., for paraffinic hydrocarbons, they are always in the range 750–850 kg m−3) so “a few percent” may actually represent a more significant error than that suggested by the statistics. For example, one would like to think that a better accuracy is achievable, which is not generally the case. Differences larger than a few percent usually trigger further investigations, including assessment of the experimental data and reported uncertainty, checking the software/computation for errors (such as incorrect atom type assignments, bugs, etc.), comparing optimized isolated molecule structures obtained using the force field and QM calculations etc.103 For pure substances, given the rather modest system sizes, density calculations can be performed almost “on-the-fly”, hence it is a good, but not ultimate, test of the overall capability of the force field.To clarify, consider an apparently simple task, such as determining the density of an unknown compound, 1-(2-hydroxyethyl)-2-imidazolidinone (HEIA), a compound of interest for capturing carbon dioxide from flue gas. No experimental data are (yet) available in the open literature. Correlations are not applicable and common equations of state and models fail as the molecule has unknown critical point and has peculiar non-idealities (a consequence of a significant dipole moment and the distortion of the electronic clouds due to the presence of the nitrogen centres). Fig. 3 shows the results of the density predictions of a well-developed force field (PCFF+)104 as tested against unknown and undisclosed data, along with the results of a similar molecule, 1,3-dimethyl-2-imidazolidinone, (DMIA) sharing the same atoms and functionalities, but for which there are published data. There is a clear discrepancy between the accuracy of the results for the two molecules, while for DMIA the simulation data fall within the spread of the experimental data, the results for the unknown HEIA show a systematic underestimation of the density by 2%. A more meaningful measure, however, is the proportion of the difference between the densities of the two species (i.e., more than 10%).
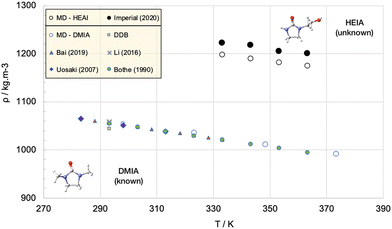 | ||
| Fig. 3 MD simulations with the PCFF+ force field are able to represent the properties of a known compound (DMIA – blue symbols) to which the force fields parameters are tuned, however it fails to accurately predict the properties of an “unknown” compound with similar morphology (HEIA). Open symbols are simulation data, closed symbols are experimental data.105–109 | ||
In general, the accuracy of molecular simulations to predict on liquid densities will be close to 2% for mono-functional molecules and 4% for multi-functional molecules. Exception is the region very close to the critical point, where in most cases, even the shape of the phase envelope is poorly captured. This is caused, amongst other factors, by the fact that the finite size of the simulations precludes the capturing of the large fluctuations and long correlations lengths (which rapidly exceed the dimensions of the simulation boxes). Notwithstanding, the main limitation here is most likely the adequacy of the force fields used.36Fig. 4 shows a further example where one can appreciate the extent to which the liquid density predictions for some cyclic and polycyclic compounds can be made with united atom models, with typical errors less than 1%.
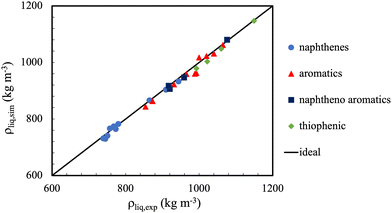 | ||
| Fig. 4 The TraPPE-UA potential, modified for ternary and quaternary carbons in naphthenes and aromatics, provides excellent liquid density predictions for a wide range of molecular conformations. Symbols represent predictions of the TraPPE-UA force fields compared to experimental liquid densities (straight line). There was no significant drift in observed deviation with regard to chemical family. Adapted with permission from ref. 110. Copyright 2019 Elsevier. | ||
4.2 Vapour pressure
Along with density, pure component vapour pressure is one of the most widely available experimental properties. For mixtures, the saturation (bubble point or dew point) pressure measurement presents some challenges. While it is relatively easy to synthesise a mixture and measure its saturation pressure, this procedure only provides the liquid composition and the corresponding pressure. For design of separations such as distillation, it is desirable also to measure the composition of the vapour, which is more difficult, costly, and potentially inaccurate as direct sampling perturbs the equilibrium.111From a simulation point of view, vapour pressure calculation requires a two-phase system, where the saturated phases coexist (in sufficient quantity). This can be particularly challenging for low vapour pressure compounds (e.g. molecules with a MW > 200 Da) where the statistics will be poor due to the constraints on system sizes (as the density of the vapour phase will be very low). Pressures are usually calculated in simulations relying on the evaluation of largely fluctuating quantities.112 The direct consequence of this is that an average error of 2–4% is generally expected for the normal boiling point for most small molecules, although the error in the vapour pressure (at other temperatures) is generally much larger. Fig. 5 shows a typical example which also highlights the effect of using different force fields.
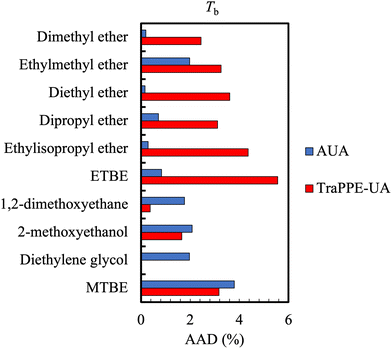 | ||
| Fig. 5 Comparison of the average absolute deviations of the AUA and TraPPE-UA force fields for the prediction of boiling point data for ethers and glycols. Boiling point calculations differed against DIPPR data by no more than 5% for TraPPE-UA and no more than 4% for AUA. Adapted with permission from ref. 113. Copyright 2013 Taylor & Francis. | ||
A closely-related property is the heat of vaporization, ΔHvap, which can be obtained from the slope of the vapour pressures curves on the P–T representation. The heat of vaporization can be obtained directly from GEMC, as it is obtained by assessing the configurational energy difference between the equilibrium vapour and liquid simulation boxes (plus the corresponding PΔv term). Furthermore, the calculation of a single value of ΔHvap and a point on the saturation line is enough to, in principle, calculate the whole saturation line via thermodynamic integration.114 In addition, the cohesive energy difference, and the related Hildebrand solubility parameter, can also be obtained directly from equilibrium simulations, (particulary GEMC), recording the energy difference amongst phases. It is obvious that the fidelity in describing the vapor pressure impinges on the accuracy of the prediction of the heats of vaporization (and the solubility parameter). Even for simple fluids (such as alkanes), they typical error is in the order of 10%.115 The agreements (or disagreements) show evidence of the quality of fit of the energy scales (or in essence the non-bonded interactions) of the force fields.116
4.3 Water and electrolyte solutions
Although water is a ubiquitous fluid, even after more than a century of research, it has been particularly challenging to obtain a force field that represents in an overall sense most (or even a few) of its fluid properties.117,118 This is an excellent example of a system for which there is a lack of representability, where there is no guarantee that a force field optimized for a given property will be expected to perform with the same level of accuracy for other properties. This lack of representability is evidence of fundamental flaws in the molecular models (although it is sometimes attributed to sub-optimal parametrizations) and is particularly aggravated in this case. Water potentials for simulations are typically fitted to liquid phase properties.119 The small size of the water molecule along with its very asymmetric charge distribution contribute to the molecule having an exceedingly large dipole moment, but more importantly, a large polarizability. In practice this means that the charge distribution calculated for the molecule in vacuum (as is commonly done when considering QM calculations) does not reflect the effects of the multi-body interactions seen in the liquid phase. For example, although the dipole moment in vacuo is of the order of 1.85 D, in the liquid it is estimated120–122 to be in the range of 2.5–3.1 D and somehow larger than the target values used in non-polarizable force fields (SPC/E employs a value of 2.35 D; TIP4P a value of 2.18 D). The simplifications of using a rigid non-polarizable model carry the consequence of a rather narrow region in which the fluid properties of water are well represented (see Table 1 for an abridged table of comparison for two popular models). Furthermore, the exclusion of polarizable effects neglects the dependence of the interactions on the local environment, making essentially impossible to correctly consider interfacial regions, such as the vapour–liquid interface. Not surprising then, the vapour pressures (and consequently interfacial tensions) are poorly represented with these models. For that reason, the original papers describing the development of the SPC/E and TIP4P/2005 models invoke a polarization correction term that changes the value of the enthalpy of vaporization. Furthermore, the melting point (not shown) is typically also off by a large margin, thus the low-temperature viscosity is also poorly represented. One can improve the results by further refining the models (e.g. focusing on the description of interfacial and solid regions) but usually at the expense of other properties. As an example, the success of the TIP4P/2005 model can be traced back to the consideration of solid phases in the parameterization. Water is a substance for which a significant body of research has been garnered to extract intermolecular potentials from ab initio methods123,124 with some success, however, the more “accurate” quantum models tend to be difficult to deploy for evaluating fluid phase properties. The reader is directed to the available reviews on the development of force fields for water with emphasis on quantum-level descriptions;125 classical atomistic models;126 polarisable models127,128 and coarse-grained representations.129| Property | Experimental value | SPC/E | TIP4P | ||
|---|---|---|---|---|---|
| Error (%) | Error (%) | ||||
| Heat of vaporization | |||||
| ΔHvap/kcal mol−1 | 10.52 | 11.79 | 12 | 10.65 | 1.2 |
| Vapour pressure | |||||
| Pv (350 K)/bar | 0.417 | 0.14 | −66 | 0.57 | 37 |
| Pv (450 K)/bar | 9.32 | 5.8 | −38 | 13.3 | 43 |
| Liquid density | |||||
| ρ (298 K)/kg m−3 | 997 | 994 | −0.3 | 988 | −0.9 |
| ρ (450 K)/kg m−3 | 890.3 | 860 | −3.4 | 823 | −7.6 |
| Shear viscosity | |||||
| η (298 K)/mPa s | 0.896 | 0.729 | −19 | 0.494 | −45 |
| η (373 K)/mPa s | 0.284 | 0.269 | −5.3 | 0.196 | −31 |
| Interfacial tension | |||||
| γ (300 K)/mN m−1 | 71.73 | 63.2 | −12 | 59 | −18 |
| γ (450 K)/mN m−1 | 42.88 | 36.7 | −14 | 27.5 | −36 |
While water itself is a fascinating fluid, it rarely exists in pure form. Many areas of interest exist for the study of electrolyte solutions, including biological, geological and industrial applications. The scope of properties of interest includes solubility, osmotic pressure, chemical potentials, activity and osmotic coefficients. To its merit, simulation has the potential to explore a diverse range of concentrations from the infinitely dilute up to the solubility limit and beyond into the thermodynamically metastable supersaturated regime. Central to the simulation of brines, polyelectrolytes, deep eutectic solvents131 and/or ionic liquids132 using classical force fields is the incorporation of many-body forces such as polarizability and charge transfer. Early on it was recognised that the use of fixed charges in the studies of ionic liquids leads to unsatisfactory prediction of transport properties (viscosity was overestimated and diffusivity underestimated with regard to experiment).133–135 Additionally, ions exhibited overly strong clustering resulting in too low solubility values as a result of the system phase separating into a salt rich phase and a salt poor phase.136–141 Unsurprisingly, the results for solubility improve if polarisable models are used.142,143 Examples of polarisable interaction charge models include fluctuating charge models,144 AMOEBA145 and models based on Drude oscillators.146Fig. 6 shows a typical example of the improvement that can be achieved in the description of the mean ionic activity of an electrolyte in water. However, incorporating polarizability in simulations is demanding and only partially captures the effect of charge transfer. A work-around involves utilizing charge scaling of ionic charge values122,147,148 Scaling the short-distance ion charge interaction improves the ion–water term and leads to more realistic ion pairing and clustering. Electronic polarizability depends on the density of the polarisable ions so unavoidably, the scaling factor will also depend on the density.
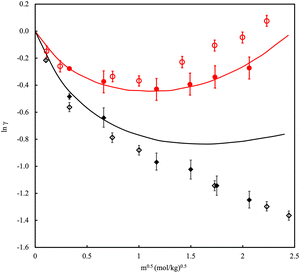 | ||
| Fig. 6 Mean ionic activity coefficient, γ, of NaCl in water at (red) 298.15 K and 1 bar and (black) 473.15 K and 15.5 bar versus molality, m. Solid lines are experimental data. Filled symbols are polarizable models, open symbols are fixed charge models. Adapted with permission from ref. 149. Copyright 2015 American Chemical Society. | ||
In summary, (i) predicting properties of pure water is a challenging activity on its own and we are still far from being able to champion a force field that is satisfactory for all properties, and (ii) predicting properties of mixtures involving water is likely to be highly prone to a high degree of error as models not only need to be good both for water and for the other molecules involved but require physically accurate description of the density dependent polarizability effects.
4.4 Viscosity
Models that provide for the correct density and are fitted to have the correct molecular geometry (through, for example, molecular mechanics) are presumed good candidates for the prediction of other related fluid phase properties, as in general, it is expected that force fields be representative (i.e., the accurate prediction of one property should lead to a similar accuracy in other quantities). Water is a good counterexample of the validity of the representability assumption. In a related fashion, since liquid phase viscosity is in principle linearly dependent on density, one would expect a good overall representation through standard modelling techniques. However, viscosity, being a transport property, is more challenging to determine than equilibrium counterparts (such as density and vapour pressures), as it requires the study of dynamic effects. Two general modelling strategies are employed, one based on exploring the velocity auto-correlation functions via the Green–Kubo formulations and another through the use of explicit shearing of the simulation boxes to induce a Couette flow and from there extracting the stress–strain relations. Excellent reviews on best practices for calculating transport properties are available.150,151Since the size, shape and flexibility of the molecule are key properties for the accurate description of transport properties, one would expect that all-atom models would excel in this regard, and progressively, as the refinement in the potentials decreases, that the quality of fit would decline. However, united-atom and even coarse-grained models can be successfully employed to describe transport properties.
An example is provided in Fig. 7 comparing the shear viscosity of three linear alkanes (n-decane, n-hexadecane and n-docosane) with different force fields. While one may improve the results with an appropriate choice of force field, the overall accuracy of viscosity calculations is low (with typical errors of 35%).
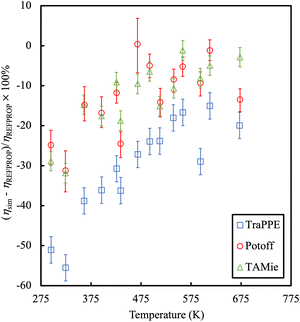 | ||
| Fig. 7 Percentage error in the calculation of shear viscosities as compared to experimental data for long chain alkanes. Colours refer to different force fields, blue symbols are TraPPE,67 green and red symbols are Mie-based potentials.152,153 Adapted with permission from ref. 154. Copyright 2019 Elsevier. | ||
A particular pitfall of molecular modelling of viscosity arises when one approaches relatively low temperatures, close to those where the melting (freezing) is expected to occur. In this region, the fluid viscosity typically increases exponentially, as the system becomes progressively arrested. This behaviour is rarely captured by common force fields for fluids as they seldomly reproduce accurately the correct solid (crystal) phase(s). The determination of the melting point of a compound depends crucially on the details of the potential but even more importantly, on the electronic structure and polarizability. Researchers in the area of crystal structure prediction routinely fit intermolecular force fields that capture the different polymorphs of rigid molecules using a combination of ab initio (quantum calculations) and empirical components,155 or by DFT calculations.156 While it would seem logical that said potentials would give accurate representations of melting points and/or be good choices to predict fluid phase behaviour, the practice suggests otherwise, and the potentials fit to the solid phases do not accurately reproduce the thermophysical properties of the corresponding liquids. In fact, it is rare to find molecular models that can be used for both solid and fluid phases.157 This apparent inconsistency points to some of the underlying limitations of the standard “Lennard–Jones plus point charge” models in current use for fluids and to the fact that some of the assumptions (such as the anisotropy of the atomic van der Waals radii, the neglect of multi-body effects and of polarizability or the non-spherical features of the atomic charge densities) might be important.158 Analogous arguments can be made with respect to the calculation of self-diffusion coefficients close to the melting point and of second order phase transitions (e.g., glass transition temperatures159) and related properties such pour point calculations and wax appearance temperatures.160
Although the calculation of viscosities at high pressures will inevitably explore very high molecule packings, it seemingly does not suffer from the limitations of an underlying solid phase, and one can confidently explore up to the GPa region161 in as long as the system retains fluidity and the molecular model retains semblance to the full atomic structure (CG models inevitably fail, as they are incapable of resolving the correct molecular packing162). A study by Ewen et al.163 compares the viscosity of hexadecane at ambient conditions to those at high pressures (and moderate increases in temperature) for a series of force fields. Although the density predictions are satisfactory (below 15% error) for all cases, the viscosity predictions were consistently under-predicted by UA force fields. Furthermore, for some AA force fields, viscosity predictions were two orders of magnitude higher than the experimental value due to crystallization. The predictions are poorer at higher pressures where the molecular 'roughness' has a greater impact on the viscosity prediction suggesting that the molecules move past each other more easily at low density conditions. Similar arguments come into play for very polar fluids and those where hydrogen bonding is relevant. The physical representation of hydrogen atoms may not be important at ambient conditions but become relevant at high pressures where the accurate description of the structure of the fluid becomes important. The use of UA force fields is likely to have a detrimental effect on the simulated friction coefficients for the interest of tribological situations. In spite of this, they continue to confer an advantage for capturing the trends in large, complex systems due to their relatively low computational expense.164 In a similar way, polymer structural properties such as glass transition temperatures, entanglement, relaxion times, can be confidently explored with AA and UA models, provided the systems are large enough to avoid finite-size effects.165
4.5 Diffusion coefficients
Self-diffusion is a measure of the inherent mobility of a species in solution as a result of random Brownian motion and is quantified by the self-diffusion coefficient, D. Its value is influenced by molecular properties, particularly relating to interactions with the surrounding environment. For example, the self-diffusion coefficient of ethanol is lower than suggested by its molecular mass, due to the “stickiness” of the hydrogen bond associations. As such, the self-diffusion coefficient can provide insight into molecular interactions as well as the aggregation behaviour of pure components and their mixtures. Self-diffusion coefficients can be calculated directly through Green–Kubo relationships or by tracking the mean-squared displacement of a particle over a certain time interval166 and can be directly measured in experiments.167 An important source of error in these calculations is the neglect in considering the unexpected effect of the simulation box size168 and the effect of periodic boundary conditions.169 A distinction must be made between this property and the transport diffusivity, the proportionality constant relating a mass flux to the gradient (pressure, chemical potential, concentration, etc.) that induces it. These latter transport quantities require more refined calculation methods and/or the use of non-equilibrium simulations.170In the study by Bellaire et al.,171 the self-diffusion values of binary mixtures in bulk were measured by 1H pulsed field gradient PFG-NMR spectroscopy. This is a method that enables the tracking of diffusive motion without perturbing the system. The D from MD simulation was acquired using rigid multi-centre Lennard–Jones (LJ) models with superimposed point dipoles and point quadrupoles. There was good agreement between the experimental data and the MD simulations for the D of simple organics (e.g. toluene/cyclohexane mixture). However, a challenge to the simulation is observed for the toluene/ethanol system (Fig. 8). The poor agreement with MD simulation is presumably a consequence of the effect of hydrogen bonding not being well described. This is a particularly common occurrence when dealing with mixtures in which the cross-interactions are of a different nature than those occurring in the pure components (e.g., water-alkanes; CO2-organics; ketones-alcohols, etc.).
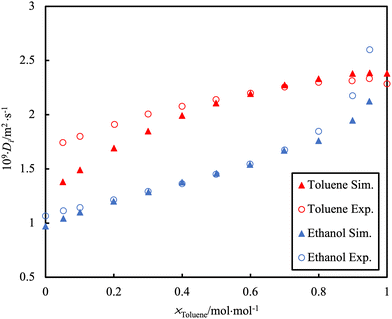 | ||
| Fig. 8 PFG-NMR data (open symbols) for the self-diffusion, D, of individual toluene or ethanol molecules in the binary mixture at 298.15 K and ambient pressure as compared to simulation data (filled symbols). Adapted with permission from ref. 171. Copyright 2018 Springer Nature. | ||
4.6 Interfacial tension
The interfacial tension has a crucial role in determining the free energy barrier for the nucleation of new phases, the mesoscale self-assembly of matter, and the transport and diffusion of molecules through fluid interfaces. It is a key property involved in the design of inhomogeneous fluid processes. Molecular modelling is ideally suited to explore and describe the behaviour of inhomogeneous fluid mixtures as it allows a unique perspective into the physics at the scale relevant to interfacial properties, filling the gaps between experimental determinations and theoretical predictions. In particular, the interfacial (surface) tension, which commonly refers to the liquid–liquid (vapour–liquid) interface can be naturally probed by molecular simulations.172 The main advantage of force field models for studying interfaces of fluids is that it allows the explicit representation of the molecules in an environment which is commensurate with the dimension of the interfacial region of fluids (of the order of 1–10 nm). The common practice is to consider explicitly the interfacial regions as they are characterized by sharp changes in densities and compositions,173 hence the overall system sizes, in terms of number of particles, can easily reach O(105), which is considerably more than what is typical in single phase studies. However, these system sizes are well within what can be now explored routinely.The prediction of interfacial and transport properties is a strenuous test for any force field within molecular models since most intermolecular potentials are fitted to a set of properties (e.g., densities, heats of vaporisation, radial distribution function) in the homogeneous fluid state. Therefore, the representation of other thermodynamic state points not involved in the original fitting can be employed as a gauge to the overall performance of the molecular model.
Fundamentally, the interfacial tension is directly related to components of the macroscopically observed pressure tensor, and to the vapour and liquid densities, hence the quality of the prediction depends crucially on these factors. Models such as those for water (see Section 4.3), which consistently provide for poor estimates of vapour pressure, provide equally poor predictions for the interfacial tension. For example, Underwood and Greenwell174 exemplify how the surface tension is underestimated by at least 15% by most water models, except TIP4P2005 which underestimated the value by 7%.1
An interesting comparison of models took place during the 9th industrial fluid properties simulation collective (IFPSC) competition.71 Liquid–liquid interfacial tensions were investigated for binary mixtures of dodecane + water, toluene + water and a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (wt%) mix of dodecane/toluene + water at 1.825 MPa (250 psig) and 110–170 °C. A wide range of models and techniques were tested (Fig. 9), which included atomistic models, semi-empirical theories and coarse-grained models. In most of these simulations interfacial tensions are calculated from an elongated simulation cell, sampled through either molecular dynamics or Monte Carlo methods where the global composition is predetermined.175 A consequence of this set-up is that the coexisting phase compositions can not be specified a priori, but result from the combination of the phase split and the (usually unknown) surface enrichment at the given pressure and temperature. The use of Gibbs Ensemble Monte Carlo simulations circumvent this latter problem.176 Binary interaction parameters describing the cross-interactions were obtained by fitting constituent binaries at lower temperatures and pressures, then taken as constants for all conditions and mixtures studied. The spread of the computed results was very high, with overpredictions of up to 10 mN m−1 although the trends with temperature were followed faithfully. Importantly, the two-phase simulations were able to shed light on the molecular detail of the interfaces (see Fig. 10).
50 (wt%) mix of dodecane/toluene + water at 1.825 MPa (250 psig) and 110–170 °C. A wide range of models and techniques were tested (Fig. 9), which included atomistic models, semi-empirical theories and coarse-grained models. In most of these simulations interfacial tensions are calculated from an elongated simulation cell, sampled through either molecular dynamics or Monte Carlo methods where the global composition is predetermined.175 A consequence of this set-up is that the coexisting phase compositions can not be specified a priori, but result from the combination of the phase split and the (usually unknown) surface enrichment at the given pressure and temperature. The use of Gibbs Ensemble Monte Carlo simulations circumvent this latter problem.176 Binary interaction parameters describing the cross-interactions were obtained by fitting constituent binaries at lower temperatures and pressures, then taken as constants for all conditions and mixtures studied. The spread of the computed results was very high, with overpredictions of up to 10 mN m−1 although the trends with temperature were followed faithfully. Importantly, the two-phase simulations were able to shed light on the molecular detail of the interfaces (see Fig. 10).
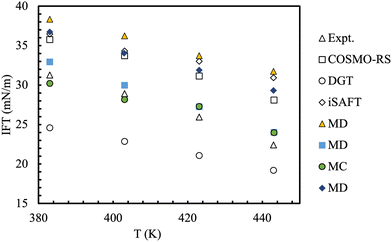 | ||
Fig. 9 Benchmark and predicted interfacial tensions for the water/50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 n-dodecane + toluene mixture. The uncertainty is of the order of 1 mN m−1 for the experimental data and aprox. 0.5–3 mN m−1 for the predictive methods. Adapted with permission from ref. 77. See original source for the full discussion of the methods and force-fields used. Copyright 2018 Elsevier. 50 n-dodecane + toluene mixture. The uncertainty is of the order of 1 mN m−1 for the experimental data and aprox. 0.5–3 mN m−1 for the predictive methods. Adapted with permission from ref. 77. See original source for the full discussion of the methods and force-fields used. Copyright 2018 Elsevier. | ||
 | ||
| Fig. 10 Snapshot of the liquid–liquid interface of an equilibrium configuration of the ternary mixture of water (blue) + toluene (red) + dodecane (green) at 130 °C from the winning entry of the 9th IFPSC challenge.177 The ternary mixture was overpredicted by an average of 1.3 mN m−1. It is seen that the liquid–liquid interface of the water–toluene–dodecane mixture is very diffuse, spanning about 3 nm. The aqueous phase is essentially pure water, whilst an appreciable amount of water is seen to diffuse into the organic phase. As the temperature increases the interface becomes wider, the toluene enrichment is less pronounced and the interfacial tension decreases. Taken with permission from ref. 177. Copyright 2018 Elsevier. | ||
4.7 Caloric and derivative properties
Most of the volumetric and transport properties discussed above can be calculated directly from rather standard molecular simulations. Nevertheless, there are other properties, whose inherent nature requires the assessment of the fluctuations that appear in these otherwise canonical simulations,178,179 or the computation through extended ensembles.180 These calculations are usually much more demanding, requiring either multiple simulations for each data point and/or long simulations to accurately capture the details in the fluctuations of the system.While there has been considerable attention placed on the prediction of volumetric properties, much less attention has been given to directly measurable caloric properties, exemplified by heat capacities, thermal conductivity and the coefficient of thermal expansion. In the particular case of heat capacities, classical simulations provide only the properties corresponding to the configurational contribution, (i.e., the contribution that stems from the intermolecular force field). However, the contributions stemming from the translational (and rotational) degrees of freedom need to be explicitly and independently taken into account. In the case of flexible molecules, the other further contributions arise from internal degrees of freedom and intramolecular potentials.181 The resulting value is a sum of terms which need to be calculated both from a pure fluid simulation and an additional single-molecule in vacuum calculation.182 The prerequisite of knowing the ideal gas contribution is by no means a constraint, as this quantity can be estimated by using well-established quantum mechanical techniques (or even by semi-empirical group contribution methods) with errors of a few percent.
The MD predicted heat capacity at constant pressure, Cp, is often overestimated183 indicating more energy is adsorbed (i.e., in molecular modes of vibration) for every degree of temperature rise. To this end, Fig. 11 showcases the calculation of the thermal conductivity of n-decane employing all-atom force fields.184 The thermal conductivity is found to be heavily overestimated, interestingly enough, the TraPPE-UA force field provided better performance in comparison to experimental data, presumably due to the removal of high-frequency degrees of freedom that act as quantum-mechanical oscillators and do not contribute to thermal conduction.
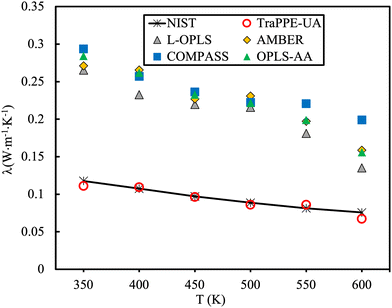 | ||
| Fig. 11 Comparison of the thermal conductivity of n-decane for different force fields at 3 MPa. Experimental data (solid line). Figure adapted with permission from ref. 184. Copyright 2021 Elsevier. | ||
Other properties which are influenced by the internal degrees of freedom require similar care in their calculation, such as bulk (not shear) viscosity, κ, is also known as the volume or dilation viscosity.185 Additionally, derivative properties, such as the Joule–Thomson coefficient, μJT, which are commonly used to validate both equations of state and force fields, can be calculated from intermolecular potentials.186,187
5. Final thoughts
5.1 Bugs, machines and humans
Today's “smart” hand-wrist watches have processors that are orders of magnitude more powerful than the supercomputers of the past century. Our amazement at the speed in which modern computers can process data often occludes the obvious fact that the results of a computer program are not moderated by intelligence (yet). The result of a simulation remains largely dictated by the choices made by the user. While it is generally always possible to obtain some sort of numerical result from a computer, it is imperative to understand the limits of those results, the plausibility of the answer and ultimately the implications that an erroneous result will have on the end use of the data. There is always a risk of GIGO (garbage in – garbage out), commonly a problem stemming from the selection of a model that does not reflect the physical reality, a poor choice of a force field, and/or an inadequate operation of the software.188 Notwithstanding these sources of errors, there might be sources of errors which are beyond the control of the user. Simulation codes are typically composed of many thousands of lines of code, contributed by disparate and distributed authors. Such collaboration inevitably brings in the possibility of making mistakes. The corresponding number of coding errors (bugs) in a modern molecular simulation code is estimated189 to be in the upper 100's, even after extensive testing. Many of these bugs will be inconsequential to a simulation, but some might eventually creep into the results. More frequently however, human errors and faulty implementations are the cause of fatal (or undetectable) errors.190 In the argot of computer science, these bugs (or the absence of them) could be resolved by what is called “formal verification”, essentially a mathematical proof of the correctness of properties of the code. This path is challenging as the proofs required are exceedingly complex and off-the-shelf tools for verifying code are not available at the level required. In either case, it is important to validate in detail191 an existing calculation to ensure reproducibility and to minimize the effect of bugs and humans.As an example of how the different implementations of a program can affect the ultimate result, consider the simulation of the density and vapour pressure of pure CO2. Details of the force field and computations are provided in ref. 142. A comparison is made between a small selection of available simulation packages (Table 2).
| T/K | DL_POLY | GROMACS | ms2 | GIBBS |
|---|---|---|---|---|
| Vapour pressure/MPa | ||||
| 220 | 0.496 | 0.652 | 0.636 | 0.629 |
| 240 | 1.211 | 1.343 | 1.264 | 1.284 |
| 260 | 2.416 | 2.483 | 2.412 | 2.422 |
| 280 | 4.24 | 4.19 | 4.07 | 4.08 |
| Saturated liquid density/kg m−3 | ||||
| 220 | 1144 | 1149 | 1151 | 1153 |
| 240 | 1067 | 1075 | 1077 | 1077 |
| 260 | 980 | 988 | 993 | 994 |
| 280 | 868 | 875 | 889 | 888 |
A further comparison with the expected theoretical results is provided in the ESI.† In any case, the important comparison is amongst the simulation results, as they should all reproduce the same values, within the simulation uncertainty. For most cases, this is true, although some values calculated with DL_POLY are seen to be outliers, particularly at low temperatures. It is for this analysis that the human element (sometimes driven by experience) is invaluable. In this particular case there is a cross-reference which serves to validate the results, but the bigger question is what happens when such a gauge does not exist. While this is by no means an exhaustive comparison,109 it does show that care has to be taken in both the selection of the program employed to resolve the molecular simulations and in the subsequent interpretation of the results.
On the other hand, simulations must be treated as if they were experiments performed in silico. They are subject to statistical uncertainty, due to the relatively small system sizes and configurations that are explored.196 They should be repeated or cross-checked if the data is to be used for sensitive calculations. As with the experiments they try to supplant, some types of calculations are prone to larger errors, e.g. the interfacial tension calculations depend on the monitoring of the difference between two large quantities (the normal and tangential elements of a pressure tensor), which themselves are subject to large fluctuations, while others, e.g. densities are relatively insensitive to the simulation parameters. The expected fluctuations and statistical uncertainty of the results should always be reported and taken into consideration.
5.2 Taking the correlation path
Currently, filling the gap for the absence of data is commonly done through empirical and semi-empirical models that strive to interpolate between the available data. Included in this genre are Quantitative Structure Property Relations (QSPR) methods. QSPR are based on interpreting and representing the chemical characteristics responsible for differences between diverse families of compounds.197–199 QSPRs rely on the generation of molecular descriptors and the analysis of the correlation of these to the expected properties.200 There is ample research in this area,201 and most of the success has been for pure component property prediction.5.3 When atomistic simulation is not enough
Although not apparent from the outset, atomistic molecular simulations have very strong constraints with respect to the size and complexity of the system that can be studied. This is directly correlated with the computational power available and it is obvious to whoever reviews the literature how the target systems (and the molecules studied) have become bigger with time. Three areas where this is particularly apparent are polymer sciences, the life-science and biochemistry areas and some material properties.For the case of polymers, the problem becomes apparent by the sheer nature of the molecular weight of single molecules. If one considers that even with state-of-the-art equipment, it is unrealistic to model more than a few million atoms at a time (cf. Section 3.1), it becomes apparent how futile it can be to attempt to model a realistic high molecular weight polymer blend or a complex biological system. However, another aspect of the problem is that of the time scale involved. Molecular dynamics can only “observe” events whose expectation times are typically in the order of nanoseconds and in the best of cases of the order of fractions of microseconds. However, it is very possible that the characteristic time of the systems easily exceed the simulation time. The long-standing scientific question of qualitatively predicting protein folding events is a particularly extreme example of a research question which surpasses the current and foreseeable capacity of atomistic modeling.202 However, more mundane problems, regarding the self-assembly of soft matter or the solidification of simple fluids will also encounter the same limitations. While in some cases the limitations are obvious, in others they are not – and therein lies the danger. Fig. 12 showcases the results of performing a reasonably large simulation of a system of 27 asphaltene-like molecules dissolved in a good (toluene) and a poor (heptane) poor solvent. Both simulations (Fig. 12 middle) appear to reach a plateau in terms of the average cluster size, suggesting that no further aggregation is expected after 80 ns of simulation time. It is only when looking at a simulation which is an order of magnitude longer does one perceive the actual physical behaviour which implies a rather complete clustering (precipitation) of the asphaltene in hexane.
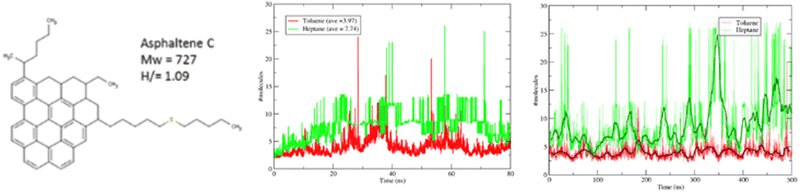 | ||
| Fig. 12 All-atom simulations of 27 asphaltene C molecules in 7% mass heptane (green) and toluene (red). The plots show the average number of asphaltene molecules in a cluster. Middle corresponds to an 80 ns simulation while right showcases the results of a 0.5 μs simulation. Taken with permission from ref. 203 and 204. Copyright 2017 American Chemical Society. | ||
In the cases where either the size complexity is unsurmountable and/or the disparity in the observed and inherent time scales becomes important, it might be necessary to consider coarse-grained (CG) models. A distinction is made here between the models focused on describing the general phenomenology and those models which are quantitatively accurate and can be used directly to estimate thermophysical properties.
Fig. 13 showcases the results of the simulation of a CG model of long chain complex models, namely atactic polystyrene (PS) in n-hexane solvent modelled using the SAFT-γ force field.70 The model is employed within large-scale simulations that emulate approximately one million atoms and serve to describe the temperature-composition fluid-phase behaviour of binary systems. A single temperature-independent unlike interaction energy parameter is employed to reproduce experimental solubility behaviour; this is sufficient for the quantitative prediction of both upper and lower critical solution points and the transition to the characteristic “hourglass” phase expected for these systems. Transferability was demonstrated through the ability to represent PS models of different molecular weight. Noticeably, the values of the diffusion coefficient were between 2 and 3 orders of magnitude higher than experiment, presumably due to the lack of friction from the coarser representation resulting in faster dynamics.
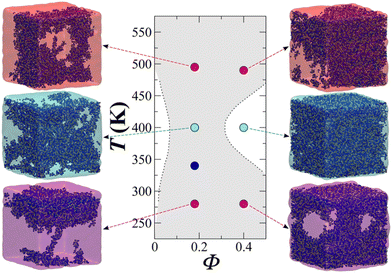 | ||
| Fig. 13 Temperature–volume fraction (Φ) phase diagram for polystyrene (MW = 4800) + n-hexane. The snapshots correspond to equilibrium configurations of the system at different temperatures. Greyed-out regions correspond to the two-phase regions. Dashed lines are smoothed experimental data. Taken with permission from ref. 205. Copyright 2017 American Chemical Society. | ||
5.4 Continuum solvation models (COSMO)
An interesting hybrid approach stems from the seminal continuum solvation model of Klamt and Schüürmann.206 It is a quantum chemistry-based method for determining the electrostatic interaction between a molecule and the surrounding solvent. In these approaches the solute molecules are represented as molecular cavities and the solvent is treated as a dielectric continuum with permittivity surrounding the solute.207,208 The polarisation charges of the solvent are caused by the polarity of the solute and are calculated from a scaled-conductor approximation. The polarisation charge density is used as a means of quantifying the interaction energy of pairwise interacting surface segments, in the framework of statistical thermodynamics. Fundamentally, these are not models based on rigid force fields that can be amenable to computer simulations, although they are frequently applied and compared to them.The method requires each molecule to be described by a quantum chemically generated charge density (σ) surface. The 3D distribution of the polarisation charges σ on the surface of each molecule X is converted into a surface composition function, pX(σ) (a histogram function called the σ profile). This describes the amount of surface with polarity σ for each molecule. The interactions between molecules are modelled by applying statistical mechanics on the interactions between surfaces. The properties of phase equilibria, solubility of solid solutes including polymers in different solvents, prediction of acid dissociation constants, partitioning in micellar systems and modelling of systems that contain isomers can be calculated from the σ potential of the mixture. The main advantage of quantum-chemically generated charge densities is that it enables the prediction of properties of molecules that include functional groups not available from traditional group contribution methods.
A popular implementation, known as COSMO-RS209 positions itself as an alternative predictive method to the rather empirical, structure-interpolating group contribution methods and the relatively longer time-consuming force field methods based on Monte Carlo and Molecular Dynamics simulation. As such, it has become one of the standard industrial tools for the simulation of fluid phase thermodynamics and especially for solvent and solute screening.210,211 COSMO-RS is implemented in the commercial software package COSMOtherm.212 Open-source implementations of a competing version (COSMO-SAC) are, however, available online.213
While COSMO models excel at calculating solvation properties (e.g., solubilities of small molecules in organic solvents, pKa, etc.) their performance in calculating fluid phase equilibria is comparable to the other force field methodologies, and to traditional excess Gibbs energy models (e.g., UNIFAC). A key area where COSMO models are a gold standard are for the prediction of ionic liquids mixtures.214–217
The 6th IFSPC challenge218 was set up to predict liquid–liquid equilibria (LLE) of a commercial dipropylene glycol dimethyl ether (DPGDME) isomeric mixture and water at ambient pressure and a range of temperatures. Modellers were provided with the results of the liquid–liquid equilibria at room temperature and asked to predict the temperature dependence of the mutual solubilities in the aqueous and ether-rich phases. The experimental data shows an inverse temperature dependence on solubility, i.e., increased solubility at lower temperatures, resulting from the interplay of hydrogen bonding and hydrophobic interactions. It represents a system consisting of interactions from a conformationally flexible and relatively large solvent molecule with the small, strongly hydrogen bonding solvent water molecules. This DPGDME/water LLE system is challenging to predict using molecular simulation for two reasons; (i) the DPGDME molecules are much too large to allow direct particle exchange in Gibbs ensemble Monte Carlo simulations and (ii) the DPGDME diffusion coefficients are extremely low making molecular dynamics simulations of phase transitions impractical. In addition, the DPGME molecules are amphiphilic due to a balance of hydrophilic and hydrophobic moieties and hence are likely to form complex aggregates in the aqueous phase. Fig. 14 shows the resulting predictions obtained by employing configurational bias Gibbs ensemble Monte Carlo simulations using the TraPPE-UA force field219 (along with the TIP4P water model). Alongside are the predictions employing two flavours of the COSMO models: COSMO-RS220 and COSMO-SAC.221 The predictions are of remarkable accuracy, especially at high temperatures. The industrial referees commented that “The molecular structures studied here are neither especially large nor exotic, yet predictions of their phase behaviour by molecular modelling represent a very significant challenge (especially in the absence of any experimental data)”.36 It is important, however, to note that the modellers were able to fine-tune the models (cf. red symbols in Fig. 14), as the predictions tended to degrade significantly without that “calibration”.
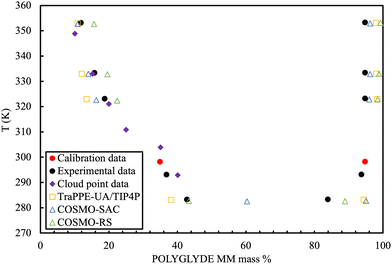 | ||
| Fig. 14 Liquid–liquid equilibrium of POLYGLYDE MM (a mixture of dipropylene glycol dimethyl ethers) in water. Experimental calibration points (red) were provided to fine-tune parameters for the models. Experimental results and cloud point data222 are compared against results from Gibbs ensemble Monte Carlo using the TraPPE-UA force field, and two versions of the COSMO approach. Adapted with permission from ref. 220. Copyright 2011 Elsevier. | ||
5.5 Machine learning for property prediction
The quest for employing machine learning in fluid phase property prediction is not new,223 but it has taken a new breath of air by the low-cost availability of hardware and user-friendly software (MATLAB,224 TensorFlow,225etc.).226 Most of the effort in the field has been focused on employing artificial neural networks (ANN), mostly due to the ease in which they can be deployed.227 ANNs have been used to selectively correlate a limited number of thermophysical properties of restricted families of compounds, for example alkanes,228,229 ionic liquids,230,231 refrigerants,232,233 components of biofuels,234 gases.235,236 Critical properties,237 interfacial properties,238 partition coefficients239,240 and self-diffusion coefficients241 have all been individually explored. In most of these examples, the requirement has been on the correlation of a selected and well-chosen sub-set of properties of a well-defined family of chemical compounds. The agreement has been shown to be good and the methodologies robust, but the crux of the matter is that regardless of how well the ANN fit the data, they cannot go beyond the data itself. ML models interpolate well but cannot be expected to extrapolate or predict in regions where they have not been “trained”.A path which is not currently mature, but is gaining considerable momentum, leads from the reasonably automated production of “pseudo-experimental” data from quantum-based simulations and other less refined scales of modelling to the full prediction of properties.72,242,243 The workflows to make these techniques available to the process industry and in particular within process simulators, as we currently do with classical theories and correlations, is still in its infancy.244–246 A key tool here will be the development and maturity of machine-learned potentials, capable of combining quantum ab initio accuracy with a much more manageable computational overhead. One can confidently foresee that data-driven research will be a key element of our toolbox in the future.
6. Conclusions
The current limits in the accuracy of the prediction of thermophysical properties through molecular simulations are outlined in this manuscript. The classical molecular simulation methodology (MD and/or MC) employing classical (non-quantum) force fields can be successful in correlating and predicting the equilibrium, transport and caloric properties of pure fluids and simple few-component mixtures. The case studies shown here are but a minute specimen of the available applications however they attempt to provide an overview of commonly encountered results. Obviously, there will be situations, systems and conditions where the heuristics given above will be flawed, and as such, the recommendations should be taken with care.The underlying question, however, is whether the current molecular modelling approaches have matured enough to become an infallible and universal tool to predict thermophysical properties of fluids and the immediate answer is probably negative. For the “simpler” properties discussed in this manuscript (densities, vapour pressures, viscosities, etc.) and “simple” organic fluids, the outlook is promising. However, the systems very rapidly become challenging (and the results unreliable) as the demand to incorporate complexity increases. Furthermore, molecular modelling is not simple to deploy in an industrial scenario, requiring specialized software used by experts with a broad knowledge of its pitfalls and limitations. More accurate computer modelling, in the realm of quantum mechanical calculations is even more difficult, less applicable to larger systems and complex molecules and even further away from practical deployment. On the other hand, experimental determination is time-consuming and requires specialist laboratories and personnel. The real “competition” comes from empirical correlations, including group contribution models.247,248 These models have been refined over many years, employing large amounts of data, and provide for a rather robust interpolation in the domains to which they have been fitted. Molecular modelling, however, has a significant advantage: once a potential has been validated (or fitted) to a particular state point, the extrapolation to other closely related conditions can be confidently made. Furthermore, although we have not dealt with it here, molecular modelling is capable of providing a wealth of additional information, which might be relevant to the user and would be challenging to obtain through either experimentation or correlation. We think here of molecular-level characterizations such as the distribution of molecules along interfaces and within clusters, incipient stages of phase separation, liquid crystal behaviour, etc. Similarly, related properties such as water–octanol partition coefficients,223,249 infinite-dilution activity coefficients, etc. are usually well-behaved extrapolations which build upon the underlying robustness of the physics behind the force fields. Notwithstanding, while we have high hopes for the digitalization of thermodynamics,250 the reality is that we are still far away from achieving success and substantial progress remains to be made. The sheer diversity and complexity of chemical systems continues to defy attempts to find a universally applicable, yet tractable, approach for accurate, reliable simulation. It remains necessary for modellers to apply deep insight and judgement to choose appropriate models and apply them effectively. This uncertainty in the accuracy of the prediction from simulations employing classical force fields has a critical impact on our ability to trust the results. A method of modelling all entities and properties of a system with a low degree of uncertainty is certainly the ultimate goal, however such a predictive method is far from being realised.
7. Epilogue
• In silico physical property prediction has become accepted as a mainstream tool, with very impressive prediction accuracy when used judiciously. On the other hand, the results are directly impacted by the applicability of the force field to the problem at hand and in some cases significantly handicapped by errors in the methods, software and even in the human implementation. We have not reached a state where we can confidently assume that molecular simulations using force fields provide unequivocal answers of experimental accuracy for all thermophysical properties of industrial fluids.• Never trust the results of a simulation on the basis that they come from a computer; the greatest strength of a computer is the speed of the computations, not its “intelligence”. There is still no substitute for the human intuition which ultimately has to decide the applicability of the results. The efforts to form researchers in this area lags behind the scale of the progress in software and hardware.
• The digitalization of thermodynamics has been advancing at a heightened pace in the last decade; advances in cheminformatics fuelled by enhanced hardware and machine learning algorithms are bringing in rapid changes to the way we look at physical property prediction.
Supplementary information
A collection of selected case studies which support the comments and appraisals provided in the main paper are presented in the ESI.† The emphasis of the selection has been placed on the assessment of the quality of the prediction and the limitations of the methods.Contents of the ESI†
• Prediction of viscosities and vapour–liquid equilibria for polyhydric alcohols.• Molecular dynamics simulation of pure n-alkanes and their mixtures at elevated temperatures.
• Molecular simulation of thermodynamic properties from models with internal degrees of freedom.
• The use of molecular dynamics to measure thermodynamic properties of n-alkanes – case study with GROMACS.
• Fluid-solid phase transition of n-alkane mixtures.
• Comparison of classical force-fields for Molecular Dynamics simulations of lubricants.
• Water-alkane interface at various NaCl salt concentrations.
• Molecular dynamics simulations of CO2 diffusivity in n-hexane, n-decane, n-hexadecane, cyclohexane and squalane.
• Self-diffusion coefficient and viscosity of propane.
• Self-diffusion coefficients – force field comparison and finite boundary effects in the simulation of methane/n-hexane mixtures at high pressures.
• Comparison of force fields with fixed bond lengths and flexible bond lengths.
• Thermal conductivity of n-decane at sub/supercritical pressure.
• Thermodynamic and transport properties of supercritical carbon dioxide and methane.
• Cyclic and polycyclic compounds.
• Enthalpy of mixing predicted using molecular dynamics.
• Phase equilibria applied to alkanes, perfluoroalkanes, alkenes and alcohols.
• VLE and interfacial properties of fatty acid methyl esters from molecular dynamics simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the funding and technical support from bp through the bp International Centre for Advanced Materials (bp-ICAM), project ICAM-65, which made this research possible. Enlightening discussions with P. R. Westmoreland are gratefully acknowledged.References
- R. Smith, Chemical Process Design and Integration, John Wiley & Sons, 2005 Search PubMed.
- R. Sinnott and G. Towler, Chemical Engineering Design, 6th edn, Elsevier, 2020 Search PubMed.
- G. M. Kontogeorgis, R. Dohrn, I. G. Economou, J. C. De Hemptinne, A. Kate, S. Kuitunen, M. Mooijer, L. F. Zilnik and V. Vesovic, Ind. Eng. Chem. Res., 2021, 60, 4987–5013 CrossRef CAS PubMed.
- W. B. Whiting, J. Chem. Eng. Data, 1996, 41, 935–941 CrossRef CAS.
- R. Dohrn and O. Pfohl, Fluid Phase Equilib., 2002, 194–197, 15–29 CrossRef CAS.
- An unprejudiced and incomplete list of examples include REFPROP NIST (https://www.nist.gov/srd/refprop), DETHERM DECHEMA https://dechema.de/en/detherm.html), DIPPR Project 801 (https://www.aiche.org/dippr), Dortmund Data Bank (http://www.ddbst.com/ddb-search.html).
- ChemSpider (Royal Society of Chemistry), http://www.chemspider.com, (accessed 15 March 2023).
- For example: J. Chem. Eng. Data, Fluid Phase Equilib., J. Molec. Fluids, Int. J. Thermophys Search PubMed.
- O. M. H. Salo-Ahen, I. Alanko, R. Bhadane, A. M. J. J. Bonvin, R. V. Honorato, S. Hossain, A. H. Juffer, A. Kabedev, M. Lahtela-Kakkonen, A. S. Larsen, E. Lescrinier, P. Marimuthu, M. U. Mirza, G. Mustafa, A. Nunes-Alves, T. Pantsar, A. Saadabadi, K. Singaravelu and M. Vanmeert, Processes., 2021, 9, 71 CrossRef CAS.
- I. Müller, A History of Thermodynamics: The Doctrine of Energy and Entropy, Springer, Berlin, Heidelberg, 2007 Search PubMed.
- J. S. Rowlinson, Cohesion: A Scientific History of Intermolecular Forces, Cambridge University Press, 2005 Search PubMed.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714–7333 CAS.
- V. Van Speybroeck, R. Gani and R. J. Meier, Chem. Soc. Rev., 2010, 39, 1764–1779 RSC.
- R. Gani, Curr. Opin. Chem. Eng., 2019, 23, 184–196 CrossRef.
- L. Brus, Nano Lett., 2020, 20, 801–802 CrossRef CAS PubMed.
- G. E. Moore, Electronics, 1965, 38, 114 Search PubMed . Retrieved from https://newsroom.intel.com/wp-content/uploads/sites/11/2018/05/moores-law-electronics.pdf(accessed 24th August 1991).
- W. W. Wood, Early history of computer simulation in statistical mechanics, in H. Schlacken, Molecular-dynamics simulation of statistical-mechanical systems. Proceedings of the Enrico Fermi International Summer School of Physics, ed. G. Ciccotti and W. G. Hoover, Elsevier Science, North-Holland, Amsterdam, 1986, Course 97, p. 3 Search PubMed.
- K. E. Gubbins, Fluid Phase Equilib., 2016, 416, 3–17 CrossRef CAS.
- B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1957, 27, 1208–1209 CrossRef CAS.
- B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1959, 31, 459–466 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- M. N. Rosenbluth and A. W. Rosenbluth, J. Chem. Phys., 1954, 22, 881–884 CrossRef CAS.
- A. B. Richon, Drug Discovery Today, 2008, 13, 659–664 CrossRef CAS PubMed.
- M. B. Jones, J. Chem. Educ., 2001, 78, 867 CrossRef CAS.
- D. V. Schroeder, Am. J. Phys., 2015, 83, 210–218 CrossRef CAS.
- A. B. Richon, Drug Discovery Today, 2008, 13, 659–664 CrossRef CAS PubMed.
- F. K. Brown, E. C. Sherer, S. A. Johnson, M. K. Holloway and B. S. Sherborne, J. Comput. Aid Mol. Des., 2017, 31, 255–266 CrossRef CAS PubMed.
- K. E. Gubbins and J. D. Moore, Ind. Eng. Chem. Res., 2010, 49, 3026–3046 CrossRef CAS.
- E. Maginn and J. R. Elliott, Ind. Eng. Chem. Res., 2010, 49, 3059–3307 CrossRef CAS.
- J. C. Palmer and P. G. Debenedetti, AIChE J., 2015, 61, 370–383 CrossRef CAS.
- A. Emelianova, E. A. Basharova, A. L. Kolesnikov, E. V. Arribas, E. V. Ivanova and G. Y. Gor, J. Phys. Chem. B, 2021, 125, 4086–4098 CrossRef CAS PubMed.
- J. P. Ewen, D. M. Heyes and D. Dini, Friction, 2018, 6, 349–386 CrossRef CAS.
- D. Frenkel, Eur. Phys. J. Plus, 2013, 128, 10 CrossRef.
- P. R. Westmoreland, P. A. Kollman, A. M. Chaka, P. T. Cummings, K. Morokuma, M. Neurock, E. B. Stechel and P. Vashishta, Applications of Molecular and Materials Modeling, International Technology Research Institute, Maryland, 2002, https://apps.dtic.mil/sti/pdfs/ADA467500.pdf, (accessed on 17th August 2021). See also P. R. Westmoreland, P. A. Kollman, A. M. Chaka, P. T. Cummings, K. Morokuma, M. Neurock, E. B. Stechel and P. Vashishta, Applying Molecular and Materials Modeling, Springer, Netherlands, 2002.
- R. H. DeVane, M. S. Wagner and B. P. Murch, in Materials Reseach for Manufactoring, ed. L. D. Madsen and E. B. Svedberg, Springer International Publishing, Cham, 2016, pp. 303–328 Search PubMed.
- P. Ungerer, C. Nieto-Draghi, B. Rousseau, G. Ahunbay and V. Lachet, J. Mol. Liq., 2007, 134, 71–897 CrossRef CAS.
- C. Nieto-Draghi, G. Fayet, B. Creton, X. Rozanska, P. Rotureau, J.-C. de Hemptinne, P. Ungerer, B. Rousseau and C. Adamo, Chem. Rev., 2015, 115, 13093–13164 CrossRef CAS PubMed.
- G. Guevara-Carrion, H. Hasse and J. Vrabec, in Multiscale Molecular Methods in Applied Chemistry, ed. B. Kirchner and J. Vrabec, Springer, Berlin, Heidelberg, 2012, pp. 201–249 Search PubMed.
- See for example A. G. Hoekstra, S. Portegies Zwart and P. V. Coveney, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 2019, 377, 20180355 CrossRef PubMed and the papers in this themed issue.
- A. S. Barnard, ACS Nano, 2014, 8, 6520–6525 CrossRef CAS PubMed.
- G. Chu, Y. Li, R. Zhao, S. Ren, W. Yang, X. He, C. Hu and J. Wang, Comput. Phys. Commun., 2021, 269, 108128 CrossRef CAS.
- N. Tchipev, S. Seckler, M. Heinen, J. Vrabec, F. Gratl, M. Horsch, M. Bernreuther, C. W. Glass, C. Niethammer, N. Hammer, B. Krischok, M. Resch, D. Kranzlmüller, H. Hasse, H.-J. Bungartz and P. Neumann, Int. J. High Perform. Comput. Appl., 2019, 33, 838–854 CrossRef.
- S. H. Jamali, L. Wolff, T. M. Becker, M. de Groen, M. Ramdin, R. Hartkamp, A. Bardow, T. J. H. Vlugt and O. A. Moultos, J. Chem. Inf. Model., 2019, 59, 1290–1294 CrossRef CAS PubMed.
- This number should be taken only as a gross estimate, as it will depend strongly on the hardware, software, and input/output lead times.
- A. C. Pan, D. Jacobson, K. Yatsenko, D. Sritharan, T. M. Weinreich and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4244–4249 CrossRef CAS PubMed.
- D. E. Shaw, et al., SC '14: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 2014, pp. 41–53 DOI:10.1109/SC.2014.9.
- J. C. Phillips, D. J. Hardy, J. D. C. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin, W. Jiang, R. McGreevy, M. C. R. Melo, B. K. Radak, R. D. Skeel, A. Singharoy, Y. Wang, B. Roux, A. Aksimentiev, Z. Luthey-Schulten, L. V. Kalé, K. Schulten, C. Chipot and E. Tajkhorshid, J. Chem. Phys., 2020, 153, 44130 CrossRef CAS PubMed.
- See the proceedings of the 169 Faraday Discussion Molecular Simulations and Visualization, J. D. Hirst, D. R. Glowacki and M. Baaden, Faraday Discuss., 2014, 169, 9–22 Search PubMed.
- C. E. Leiserson, N. C. Thompson, J. S. Emer, B. C. Kuszmaul, B. W. Lampson, D. Sanchez and T. B. Schardl, Science, 2020, 368, eaam9744 CrossRef CAS PubMed.
- T. Schlick, et al. , Annu. Rev. Biophys., 2021, 50, 1–35 CrossRef PubMed.
- T. Schlick and S. Portillo-Ledesma, Nat. Comput. Sci., 2021, 1, 321–331 CrossRef PubMed.
- F. Arute, et al. , Nature, 2019, 574, 505–510 CrossRef CAS PubMed.
- S. T. Stober, S. M. Harwood, D. Trenev, P. K. Barkoutsos, T. P. Gujarati and S. Mostame, Phys. Rev. A, 2022, 105, 12425 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- With no preferential order or prejudice, a shortlist of free programs include HOOMD (https://glotzerlab.engin.umich.edu/hoomd-blue/), GROMACS (https://www.gromacs.org), DL_POLY (https://www.scd.stfc.ac.uk/Pages/DL_POLY.aspx), LAMMPS (https://www.lammps.org), NAMD (https://www.ks.uiuc.edu/Research/namd/), Cassandra (https://cassandra.nd.edu/), ms2 (https://www.ms-2.de/home.html).
- With no preferential order or prejudice, a shortlist of commercial suites include MedeA Materials Design, http://materialsdesign.com, Schrödinger, https://www.schrodinger.com, Culgi, https://www.culgi.com, Scienomics, https://www.scienomics.com and BIOVIA Material Studio, https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio, (accessed 17 August 2021).
- P. T. Cummings, C. McCabe, C. R. Iacovella, A. Ledeczi, E. Jankowski, A. Jayaraman, J. C. Palmer, E. J. Maginn, S. C. Glotzer, J. A. Anderson, J. Ilja Siepmann, J. Potoff, R. A. Matsumoto, J. B. Gilmer, R. S. DeFever, R. Singh and B. Crawford, AIChE J., 2021, 67, 1–12 CrossRef . See also https://mosdef.org, (accessed June 2021).
- J. W. von Goethe, “Der Zauberlehrling”, 1797. A popular version was depicted in the movie “Fantasia”, Walt Disney Productions, 1940 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179 CrossRef CAS.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. J. Karplus, Comput. Chem., 1983, 4, 187 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- S. Riniker, J. Chem. Inf. Model., 2018, 58, 565–578 CrossRef CAS PubMed.
- A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045 CrossRef CAS PubMed.
- X. He, B. Walker, V. H. Man, P. Ren and J. Wang, Curr. Opin. Struct. Biol., 2022, 72, 187–193 CrossRef CAS PubMed.
- A. D. Mackerell Jr., J. Comput. Chem., 2004, 25, 1584–1604 CrossRef PubMed.
- B. J. Befort, R. S. DeFever, G. M. Tow, A. W. Dowling and E. J. Maginn, J. Chem. Inf. Model., 2021, 61, 4400–4414 CrossRef CAS PubMed.
- C. Avendaño, T. Lafitte, A. Galindo, C. S. Adjiman, G. Jackson and E. A. Müller, J. Phys. Chem. B, 2011, 115, 11154–11169 CrossRef PubMed.
- M. G. Guenza, M. Dinpajooh, J. McCarty and I. Y. Lyubimov, J. Phys. Chem. B, 2018, 122, 10257–10278 CrossRef CAS PubMed.
- M. Levitt, Nat. Struct. Biol., 2001, 8, 392–393 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- S. C. Glotzer and W. Paul, Annu. Rev. Mater. Res., 2002, 32, 401–436 CrossRef CAS.
- M. G. Guenza, M. Dinpajooh, J. McCarty and I. Y. Lyubimov, J. Phys. Chem. B, 2018, 122, 10257–10278 CrossRef CAS PubMed.
- M. G. Saunders and G. A. Voth, Annu. Rev. Biophys., 2013, 42, 73–93 CrossRef CAS PubMed.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed.
- E. A. Müller and G. Jackson, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 405–427 CrossRef PubMed.
- J. D. Moore, R. D. Mountain, R. B. Ross, V. K. Shen, D. W. Siderius and K. D. Smith, Fluid Phase Equilib., 2018, 476, 1–5 CrossRef CAS PubMed . See also http://fluidproperties.org/9th.
- O. A. von Lilienfeld and K. Burke, Nat. Commun., 2020, 11, 4895 CrossRef CAS PubMed.
- N. E. Jackson, A. S. Bowen, L. W. Antony, M. A. Webb, V. Vishwanath and J. J. de Pablo, Sci. Adv., 2022, 5, eaav1190 CrossRef PubMed.
- S. Doerr, M. Majewski, A. Pérez, A. Krämer, C. Clementi, F. Noe, T. Giorgino and G. De Fabritiis, J. Chem. Theory Comput., 2021, 17, 2355–2363 CrossRef CAS PubMed.
- Z. Guo, D. Lu, Y. Yan, S. Hu, R. Liu, G. Tan, N. Sun, W. Jiang, L. Liu, Y. Chen, L. Zhang, M. Chen, H. Wang and W. Jia, Proceedings of the 27th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Association for Computing Machinery, New York, USA, 2022, pp. 205–218 Search PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- See, for example M. J. McGrath, I.-F. W. Kuo, J. N. Ghogomu, C. J. Mundy and J. I. Siepmann, J. Phys. Chem. B, 2011, 115, 11688–11692 CrossRef CAS PubMed.
- “Quantum chemical accuracy” is defined as errors below 1 kcal mol−1, which if expressed in terms of boiling points, amounts to errors of ±500 K. see M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Nat. Commun., 2020, 11, 5223 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, OUP, Oxford, 2nd edn, 2017 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier Science, 2nd edn, 2002 Search PubMed.
- G. Raabe, Molecular Simulation studies on Thermophysical properties, Springer, 2017 Search PubMed.
- A. Satoh, Introduction to the practice of molecular simulation, Elsevier Science, 2011 Search PubMed.
- A. Leach, Molecular Modelling: Principles and Applications, Pearson Education Limited, 2nd edn, 2001 Search PubMed.
- P. Ungerer, B. Tavitian and A. Boutin, Applications of Molecular Simulation in the Oil and Gas Industry: Monte Carlo Methods, Editions Technip, 2005 Search PubMed.
- W. M. G. Hoover, Molecular Dynamics, Lecture notes in Physics 258, Spinger-Verlag, Berlin, 1986 Search PubMed.
- T. Schlick, Molecular Modelling and Simulation: An Interdisciplinary Guide, Springer, 2nd edn, 2010 Search PubMed.
- P. A. Bopp, E. Hawlicka and S. Fritzsche, ChemTexts, 2018, 4, 1–16 CrossRef.
- E. Braun, J. Gilmer, H. B. Mayes, D. L. Mobley, J. I. Monroe, S. Prasad and D. M. Zuckerman, Living J. Comput. Mol. Sci., 2019, 1, 5957 Search PubMed . See also the other papers in the Journal, in particular the “tutorial” sections.
- M. A. González, Collection SFN, 2011, 12, 169–200 CrossRef.
- D. Dubbeldam, A. Torres-Knoop and K. S. Walton, Mol. Simul., 2013, 39, 1253–1292 CrossRef CAS.
- D. C. Rapaport, The Art of Molecular Dynamics Simulation, Cambridge University Press, 2nd edn, 2004 Search PubMed.
- J. M. Haile, Molecular Dynamics Simulation. Elementary Methods, John Wiley & Sons, 1992 Search PubMed.
- Example is the MedeA Instrument, an 80+ core integrated platform capable of over 3 TFLOPS on a desktop. See https://www.materialsdesign.com/medea-instrument, (accessed 17th August 2021).
- E. F. May, W. J. Tay, M. Nania, A. Aleji, S. Al-Ghafri and J. P. Martin Trusler, Rev. Sci. Instrum., 2014, 85, 95111 CrossRef PubMed.
- M. G. Martin and A. P. Thompson, Fluid Phase Equilib., 2004, 217, 105–110 CrossRef CAS.
- M. Yiannourakou, Private Communication 2020.
- PCFF+ is an extention of the PCFF forcefield, included in the MedeA software. See also CrossRef CAS; H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS; J. R. Maple, M.-J. Hwang, T. P. Stockfisch, U. Dinur, M. Waldman, C. S. Ewig and A. T. Hagler, J. Comput. Chem., 1994, 15, 162–182 CrossRef; M. J. Hwang, T. P. Stockfisch and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2515–2525 CrossRef.
- X. Li, Y. Jiang, G. Han and D. Deng, J. Chem. Eng. Data, 2016, 61, 1254–1261 CrossRef CAS.
- L. Bai, S.-N. Li, Q.-G. Zhai, Y.-C. Jiang and M.-C. Hu, Chem. Eng. Commun., 2016, 203, 985–993 CrossRef CAS.
- Y. Uosaki, T. Motoki, T. Hamaguchi and T. Moriyoshi, J. Chem. Thermodyn., 2007, 39, 810–816 CrossRef CAS.
- A. Bothe, U. Nowaczyk and E. Schmidt, Studies on the thermal and mass transfer of new working pair components in absorption heat pumps, 1990, as cited within Detherm ref. DELI-042050.
- Data for HEAI was measured by Prof. J.P.M. Trusler; department of chemical engineering; Imperial College London. Unpublished data.
- M. Yiannourakou, P. Ungerer, V. Lachet, B. Rousseau and J. M. Teuler, Fluid Phase Equilib., 2019, 481, 28–43 CrossRef CAS.
- Indirect and non-invasive sampling, as for example the measurement of densities, refractive indexes, etc. can be used as surrogates of direct composition measurements, in particular for binary systems. See for example N. C. Rodewald, J. A. Davis and F. Kurata, AIChE J., 1964, 10, 937–943 CrossRef CAS.
- K. Shi, E. R. Smith, E. E. Santiso and K. E. Gubbins, J. Chem. Phys., 2023, 158, 040901 CrossRef CAS PubMed.
- M. Yiannourakou, P. Ungerer, B. Leblanc, N. Ferrando and J.-M. Teuler, Mol. Simul., 2013, 39, 1165–1211 CrossRef CAS.
- D. A. Kofke, J. Chem. Phys., 1993, 98, 4149–4162 CrossRef CAS.
- G. E. Lindberg, J. L. Baker, J. Hanley, W. M. Grundy and C. King, Liquids, 2021, 1, 47–59 CrossRef.
- J. Wang and T. Hou, J. Chem. Theory Comput., 2011, 7, 2151–2165 CrossRef CAS PubMed.
- A. Ben-naim, Molecular Theory Of Water And Aqueous Solutions - Part 1: Understanding Water, World Scientific Publishing Company, 2009 Search PubMed.
- J. S. Rowlinson, Cohesion: A Scientific History of Intermolecular Forces, Cambridge University Press, 2005 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS PubMed.
- T. Zhu and T. Van Voorhis, J. Phys. Chem. Lett., 2021, 12, 6–12 CrossRef CAS PubMed.
- I. Skarmoutsos, M. Masia and E. Guardia, Chem. Phys. Lett., 2016, 648, 102–108 CrossRef CAS.
- M. J. McGrath, J. I. Siepmann, L. F. Kuo and C. J. Mundy, Mol. Phys., 2007, 105, 1411–1417 CrossRef.
- K. Szalewicz, C. Leforestier and A. van der Avoird, Chem. Phys. Lett., 2009, 482, 1–14 CrossRef CAS.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901–130933 CrossRef PubMed.
- B. Santra, J. Klimes, A. Tkatchenko, D. Alfe, B. Slater, A. Michaelides, R. Car and M. Scheffler, J. Chem. Phys., 2013, 139, 154702 CrossRef PubMed.
- S. P. Kadaoluwa Pathirannahalage, N. Meftahi, A. Elbourne, A. C. G. Weiss, C. F. McConville, A. Padua, D. A. Winkler, M. Costa Gomes, T. L. Greaves, T. C. Le, Q. A. Besford and A. J. Christofferson, J. Chem. Inf. Model., 2021, 61, 4521–4536 CrossRef CAS PubMed.
- A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045 CrossRef CAS PubMed.
- O. Demerdash, E. H. Yap and T. Head-Gordon, Annu. Rev. Phys. Chem., 2014, 65, 149 CrossRef CAS PubMed.
- O. Lobanova, C. Avendaño, T. Lafitte, E. A. Müller and G. Jackson, Mol. Phys., 2015, 113, 1228–1249 CrossRef CAS.
- C. Vega and J. L. F. Abascal, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688 RSC.
- S. J. Rukmani, B. W. Doherty, O. Acevedo and C. M. Colina, in Reviews in Computational Chemistry, ed. A. L. Parrill and K. B. Lipkowitz, Wiley, 2022, vol. 32 Search PubMed.
- E. J. Maginn, J. Phys.: Condens. Matter, 2009, 37, 373101 CrossRef PubMed.
- Z. Hu and C. J. Margulis, Acc. Chem. Res., 2007, 40, 1097–1105 CrossRef CAS PubMed.
- B. L. Bhargava and S. Balasubramanian, J. Chem. Phys., 2005, 123, 144505 CrossRef CAS PubMed.
- J. Picálek and J. Kolafa, Mol. Simul., 2009, 35, 685–690 CrossRef.
- P. Auffinger, T. E. Cheatham III and A. C. Vaiana, J. Chem. Theory Comput., 2007, 3, 1851–1859 CrossRef CAS PubMed.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2009, 113, 13279–13290 CrossRef CAS PubMed.
- F. Moucka, I. Nezbeda and W. R. Smith, J. Chem. Phys., 2013, 138, 154102 CrossRef PubMed.
- P. E. Mason, C. E. Dempsey, G. W. Neilson and J. W. Brady, J. Phys. Chem. B, 2005, 109, 24185–24196 CrossRef CAS PubMed.
- A. A. Chialvo and J. M. Simonson, Collect. Czech. Chem. Commun., 2010, 75, 405–424 CrossRef CAS.
- H. Jiang, O. A. Moultos, I. G. Economou and A. Z. Panagiotopoulos, J. Phys. Chem. B, 2016, 120, 12358–12370 CrossRef CAS PubMed.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed.
- L. Olano and S. Rick, J. Comput. Chem., 2005, 26, 699–707 CrossRef CAS PubMed.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- G. Lamoureux, D. Allouche, M. Souaille and B. Roux, Biophys. J., 2000, 78, 330A–330A Search PubMed.
- J. Li and F. Wang, J. Chem. Phys., 2015, 143, 194505 CrossRef PubMed.
- A. L. Benavides, M. A. Portillo, V. C. Chamorro, J. R. Espinosa, J. L. F. Abascal and C. Vega, J. Chem. Phys., 2017, 147, 104501 CrossRef CAS PubMed.
- H. Jiang, Z. Mester, O. A. Moultos, I. G. Economou and A. Z. Panagiotopoulos, J. Chem. Theory Comput., 2015, 11, 3802–3810 CrossRef CAS PubMed.
- E. J. Maginn, R. A. Messerly, D. J. Carlson, D. R. Roe and J. R. Elliot, Living J. Comput. Mol. Sci., 2020, 2, 1–20 Search PubMed.
- P. Santak and G. Conduit, J. Chem. Phys., 2020, 153, 1–12 CrossRef PubMed.
- A. Hemmen and J. Gross, J. Phys. Chem. B, 2015, 119, 11695–11707 CrossRef CAS PubMed.
- J. J. Potoff and D. A. Bernard-Brunel, J. Phys. Chem. B, 2009, 113, 14725–14731 CrossRef CAS PubMed.
- R. A. Messerly, M. C. Anderson, S. M. Razavi and J. R. Elliott, Fluid Phase Equilib., 2019, 483, 101–115 CrossRef CAS.
- C. A. Gatsiou, C. S. Adjiman and C. C. Pantelides, Faraday Discuss., 2018, 211, 297 RSC.
- M. A. Neumann, J. Phys. Chem. B, 2008, 112, 9810–9829 CrossRef CAS PubMed.
- Counter-examples are the mononuclear atoms, (e.g. Argon). See Y. Zhang and E. J. Maginn, J. Chem. Phys., 2012, 136, 144116 CrossRef CAS PubMed ; the TIP4P/2005 water model; and the TraPPE model for hydrogen sulfide which considered unary and binary VLE, the triple point, self-diffusion, and relative permittivity, See M. S. Shah, M. Tsapatsis and J. I. Siepmann, J. Phys. Chem. B, 2015, 119, 7041–7052 CrossRef PubMed.
- M. J. Van Vleet, A. J. Misquitta and J. R. Schmidt, J. Chem. Theory Comput., 2018, 14, 739–758 CrossRef CAS PubMed.
- J. Gupta, C. Nunes and S. Jonnalagadda, Mol. Pharmaceut., 2013, 10, 4136–4145 CrossRef CAS PubMed.
- S. Shahruddin, G. Jiménez-Serratos, G. J. P. Britovsek, O. K. Matar and E. A. Müller, Sci. Rep., 2019, 9, 1–9 CrossRef CAS PubMed.
- M. A. Galvani Cunha and O. M. Robbins, Fluid Phase Equilib., 2019, 495, 28–32 CrossRef CAS.
- L. Zheng, J. P. M. Trusler, F. Bresme and E. A. Müller, Fluid Phase Equilib., 2019, 496, 1–6 CrossRef CAS.
- J. P. Ewen, C. Gattinoni, F. M. Thakkar, N. Morgan, H. A. Spikes and D. Dini, Mater., 2016, 9, 651 CrossRef PubMed.
- A. I. Vakis, V. A. Yastrebov, J. Scheibert, L. Nicola, D. Dini, C. Minfray, A. Almqvist, M. Paggi, S. Lee, G. Limbert, J. F. Molinari, G. Anciaux, R. Aghababaei, S. Echeverri Restrepo, A. Papangelo, A. Cammarata, P. Nicolini, C. Putignano, G. Carbone, S. Stupkiewicz, J. Lengiewicz, G. Costagliola, F. Bosia, R. Guarino, N. M. Pugno, M. H. Müser and M. Ciavarella, Tribol. Int., 2018, 125, 169–199 CrossRef.
- J. Ramos, J. F. Vega and J. Martínez-Salazar, Eur. Polym. J., 2018, 99, 298–331 CrossRef CAS.
- E. Maginn, R. Messerly, D. Carlson, D. Roe and R. Elliott, Living J. Comput. Mol. Sci., 2018, 1, 1–20 Search PubMed.
- H. Weingärtner, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 1994, 91, 37–69 RSC.
- T. J. P. dos Santos, C. R. A. Abreu, B. A. C. Horta and F. W. Tavares, J. Supercrit. Fluids, 2020, 155, 104639 CrossRef CAS.
- S. von Bülow, J. T. Bullerjahn and G. Hummer, J. Chem. Phys., 2020, 153, 021101 CrossRef PubMed.
- R. Krishna and J. A. Wesselingh, Chem. Eng. Sci., 1997, 52, 861–911 CrossRef CAS.
- D. Bellaire, H. Kiepfer, K. Münnemann and H. Hasse, J. Chem. Eng. Data, 2019, 65, 793–803 CrossRef.
- E. A. Müller, Å. Ervik and A. Mejía, Living J. Comput. Mol. Sci., 2021, 2, 1–27 Search PubMed.
- S. Stephan, H. Cárdenas, A. Mejía and E. A. Müller, Fluid Phase Equilib., 2022, 564, 113596 CrossRef.
- T. R. Underwood and H. C. Greenwell, Sci. Rep., 2017, 8, 1–11 Search PubMed.
- F. Martínez-Veracoechea and E. A. Müller, Mol Simulat, 2005, 31, 33–43 CrossRef.
- J. L. Chen, B. Xue, D. B. Harwood, Q. P. Chen, C. J. Peters and J. I. Siepmann, Fluid Phase Equilib., 2018, 476, 16–24 CrossRef CAS.
- C. Herdes, Å. Ervik, A. Mejía and E. A. Müller, Fluid Phase Equilib., 2018, 476, 9–15 CrossRef CAS.
- M. Lagache, P. Ungerer, A. Boutin and A. H. Fuchs, Phys. Chem. Chem. Phys., 2001, 3, 4333–4339 RSC.
- B. Cheng and D. Frenkel, Phys. Rev. Lett., 2020, 125, 130602 CrossRef CAS PubMed.
- F. A. Escobedo, J. Chem. Phys., 1998, 108, 8761–8772 CrossRef CAS.
- W. R. Smith, J. Jirsák, I. Nezbeda and W. Qi, J. Chem. Phys., 2017, 147, 34508 CrossRef PubMed.
- L. B. Stutzman, F. A. Escobedo and J. W. Tester, Mol. Simul., 2017, 44, 1–9 Search PubMed.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74 CrossRef CAS PubMed.
- X. Yang, Y. Gao, M. Zhang, W. Jiang and B. Cao, J. Mol. Liq., 2021, 342, 117478 CrossRef CAS.
- F. Jaeger, O. K. Matar and E. A. Müller, J. Chem. Phys., 2018, 148, 174504 CrossRef PubMed.
- A. Chacín, J. M. Vázquez and E. A. Müller, Fluid Phase Equilib., 1999, 165, 147–155 CrossRef.
- F. A. Escobedo and Z. Chen, Mol. Simul., 2001, 26, 395–416 CrossRef CAS.
- W. F. van Gunsteren and A. E. Mark, J. Chem. Phys., 1998, 108, 6109–6116 CrossRef CAS.
- M. Schappals, A. Mecklenfeld, L. Kröger, V. Botan, A. Köster, S. Stephan, E. J. García, G. Rutkai, G. Raabe, P. Klein, K. Leonhard, C. W. Glass, J. Lenhard, J. Vrabec and H. Hasse, J. Chem. Theory Comput., 2017, 13, 4270–4280 CrossRef CAS PubMed.
- J. Wong-ekkabut and M. Karttunen, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2529–2538 CrossRef CAS PubMed.
- P. T. Merz and M. R. Shirts, PLoS One, 2018, 13, e0202764 CrossRef PubMed.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- G. Rutkai, A. Köster, G. Guevara-Carrion, T. Janzen, M. Schappals, C. W. Glass, M. Bernreuther, A. Wafai, S. Stephan, M. Kohns, S. Reiser, S. Deublein, M. Horsch, H. Hasse and J. Vrabec, Comput. Phys. Commun., 2017, 221, 343–351 CrossRef CAS.
- M. Yiannourakou, P. Ungerer, B. Leblanc, N. Ferrando and J.-M. Teuler, Mol. Simul., 2013, 39, 1165–1211 CrossRef CAS.
- See also the issue of uncertainty quantification in molecular simulations: M. Vassaux, S. Wan, W. Edeling and P. V. Coveney, J. Chem. Theory Comput., 2021, 17, 5187–5197 CrossRef CAS PubMed.
- J. C. Dearden, Int. J. Quant. Struct. Prop. Relatsh., 2017, 2, 36–46 CAS.
- A. Cherkasov, E. N. Muratov, D. Fourches, A. Varnek, I. I. Baskin, M. Cronin, J. Dearden, P. Gramatica, Y. C. Martin, R. Todeschini, V. Consonni, V. E. Kuz’min, R. Cramer, R. Benigni, C. Yang, J. Rathman, L. Terfloth, J. Gasteiger, A. Richard and A. Tropsha, J. Med. Chem., 2014, 57, 4977–5010 CrossRef CAS PubMed.
- A. R. Katritzky, M. Kuanar, S. Slavov, C. D. Hall, M. Karelson, I. Kahn and D. A. Dobchev, Chem. Rev., 2010, 110, 5714–5789 CrossRef CAS PubMed.
- M. Karelson, V. S. Lobanov and A. R. Katritzky, Chem. Rev., 1996, 96, 1027–1044 CrossRef CAS PubMed.
- R. Gani, Curr. Opin. Chem. Eng., 2019, 23, 184–196 CrossRef.
- The problem has actually been “solved” by using machine learning. See for example J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- T. F. Headen, E. S. Boek and N. T. Skipper, Energy Fuels, 2009, 23(3), 1220–1229 CrossRef CAS.
- T. F. Headen, E. S. Boek, G. Jackson, T. S. Totton and E. A. Müller, Energy Fuels, 2017, 31, 1108–1125 CrossRef CAS.
- G. Jiménez-Serratos, C. Herdes, A. J. Haslam, G. Jackson and E. A. Müller, Macromolecules, 2017, 50, 4840–4853 CrossRef.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- C.-H. Hsieh, S. I. Sandler and S.-T. Lin, Fluid Phase Equilib., 2010, 297, 90–97 CrossRef CAS.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
- A. Klamt, F. Eckert and W. Arlt, Annu. Rev. Chem. Biomol., 2010, 1, 101–122 CrossRef CAS PubMed.
- A compilation of COSMO-RS papers can be found here http://www.cosmologic.de/theory/scientific-papers.html.
- https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/solvation-chemistry/ .
- See and the corresponding reference: I. H. Bell, E. Mickoleit, C.-M. Hsieh, S.-T. Lin, J. Vrabec, C. Breitkopf and A. Jäger, J. Chem. Theory Comput., 2020, 16, 2635–2646 CrossRef CAS PubMed.
- M. Diedenhofen and A. Klamt, Fluid Phase Equilib., 2010, 294, 31–38 CrossRef CAS.
- M. Ramdin, T. W. de Loos and T. J. H. Vlugt, Ind. Eng. Chem. Res., 2012, 51, 8149–8177 CrossRef CAS.
- B. S. Lee and S. T. Lin, AIChE J., 2017, 63, 3096–3104 CrossRef CAS.
- K. Paduszyński and M. Królikowska, Ind. Eng. Chem. Res., 2020, 59, 11851–11863 CrossRef.
- F. H. Case, A. Chaka, J. D. Moore, R. D. Mountain, R. B. Ross, V. K. Shen and E. A. Stahlberg, Fluid Phase Equilib., 2011, 310, 1–3 CrossRef CAS.
- P. Bai and J. I. Siepmann, Fluid Phase Equilib., 2011, 310, 11–18 CrossRef CAS.
- J. Reinisch, A. Klamt, F. Eckert and M. Diedenhofen, Fluid Phase Equilib., 2011, 310, 7–10 CrossRef CAS.
- S.-T. Lin, L.-H. Wang, W.-L. Chen, P.-K. Lai and C.-M. Hsieh, Fluid Phase Equilib., 2011, 310, 19–24 CrossRef CAS.
- F. A. Donate, K. Hasegawa and J. D. Moore, Fluid Phase Equilib., 2011, 310, 4–6 CrossRef CAS.
- D. M. Himmelblau, Ind. Eng. Chem. Res., 2008, 47, 5782–5796 CrossRef CAS.
- http://http:/www.mathworks.com/ .
- https://www.tensorflow.org/ .
- F. Jirasek and H. Hasse, Fluid Phase Equilib., 2021, 549, 113206 CrossRef CAS.
- L. Joss and E. A. Müller, J. Chem. Educ., 2019, 96, 697–703 CrossRef CAS.
- M. Pirdashti, K. Movagharnejad, P. Akbarpour, E. N. Dragoi and I. Khoiroh, Int. J. Thermophys., 2020, 41, 1–29 CrossRef.
- P. Santak and G. Conduit, Fluid Phase Equilib., 2019, 501, 112259 CrossRef CAS.
- K. Golzar, S. Amjad-Iranagh and H. Modarress, Ind. Eng. Chem. Res., 2014, 53, 7247–7262 CrossRef CAS.
- P. Dhakal and J. K. Shah, Fluid Phase Equilib., 2021, 549, 113208 CrossRef CAS.
- A. Åžencan, İ. İ. Köse and R. Selbaş, Energy Convers. Manage., 2011, 52, 958–974 CrossRef.
- A. Azari, S. Atashrouz and H. Mirshekar, ISRN Chem. Eng., 2013, 2013, 1–11 CrossRef.
- D. A. Saldana, L. Starck, P. Mougin, B. Rousseau, N. Ferrando and B. Creton, Energy Fuels, 2012, 26, 2416–2426 CrossRef CAS.
- G. Coccia, G. Di Nicola, S. Tomassetti, M. Pierantozzi and G. Passerini, Fluid Phase Equilib., 2019, 493, 36–42 CrossRef CAS.
- A. Bouzidi, S. Hanini, F. Souahi, B. Mohammedi and M. Touiza, J. Appl. Sci., 2007, 7, 2450–2455 CrossRef CAS.
- L. H. Hall and C. T. Story, J. Chem. Inf. Comput. Sci., 1996, 36, 1004–1014 CrossRef CAS.
- Y. Vasseghian, A. Bahadori, A. Khataee, E. N. Dragoi and M. Moradi, ACS Omega, 2020, 5, 781–790 CrossRef CAS PubMed.
- J. J. Huuskonen, D. J. Livingstone and I. V. Tetko, J. Chem. Inf. Comput. Sci., 2000, 40, 947–955 CrossRef CAS PubMed.
- E. W. Lowe, M. Butkiewicz, M. Spellings, A. Omlor and J. Meiler, 2011 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), 2011, pp. 1–6 Search PubMed.
- J. P. Allers, F. H. Garzon and T. M. Alam, Phys. Chem. Chem. Phys., 2021, 23, 4615–4623 RSC.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765 CrossRef CAS PubMed.
- G. M. Kontogeorgis and G. K. Folas, Thermodynamic Models for Industrial Applications: From Classical and Advanced Mixing Rules to Association Theories, John Wiley & Sons Ltd, 2010, pp. 41–77 Search PubMed.
- A. S. Alshehri, A. K. Tula, F. You and R. Gani, AIChE J., 2022, 68, e17469 CrossRef CAS.
- N. M. Garrido, I. G. Economou, A. J. Queimada, M. Jorge and E. A. Macedo, AIChE J., 2012, 58, 1929–1938 CrossRef CAS.
- E. Forte, F. Jirasek, M. Bortz, J. Burger, J. Vrabec and H. Hasse, Chem. Ing. Tech., 2019, 91, 201–214 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05423j |
| This journal is © the Owner Societies 2023 |
