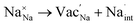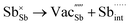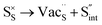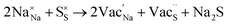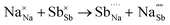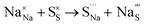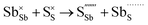Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical study on stability and ion transport property with halide doping of Na3SbS4 electrolyte for all-solid-state batteries†
Randy
Jalem
 *abc,
Bo
Gao
a,
Hong-Kang
Tian
ad and
Yoshitaka
Tateyama
*abc,
Bo
Gao
a,
Hong-Kang
Tian
ad and
Yoshitaka
Tateyama
 *ac
*ac
aCenter for Green Research on Energy and Environmental Materials (GREEN), National Institute for Materials Science (NIMS), Tsukuba, Japan. E-mail: JALEM.Randy@nims.go.jp
bPRESTO, Japan Science and Technology Agency (JST), Saitama, Japan
cElements Strategy Initiative for Catalysts & Batteries, Kyoto University, Kyoto, Japan
dDepartment of Chemical Engineering, National Cheng Kung University, 1 University Road, Tainan City 70101, Taiwan
First published on 1st December 2021
Abstract
All-solid-state Na ion battery (ASS-NIB) is a new class of battery which is a potential alternative to the conventional all-solid-state Li ion battery. Herein, we focused on Na3SbS4, a reported candidate solid electrolyte for ASS-NIB application, and performed a comprehensive theoretical study, primarily based on density functional theory calculations, to evaluate (electro)chemical stability, defect chemistry, and Na ion transport property. The calculated results reveal that when in contact with a layered cathode compound (e.g., NaCrO2), sulfur in Na3SbS4 tends to migrate across the interface, leading to interface atomic rearrangement, interface disordering and/or decomposition. The material is also predicted to decompose under reductive voltage conditions (0 V vs. Na+/Na), in agreement with experiment. Kinetic modeling for stresses and electron density distribution showed that the interface between Na3SbS4 and Na metal anode under typical electrodeposition surface roughness would lead to dendrite initiation and growth. Aside from controlling Na vacancy concentration, halide doping at the S site was predicted by DFT molecular dynamics (MD) calculations to directly affect the Na+ ion activation energy. This can be ascribed to the size modulation of the Na site-to-site pathway bottleneck. Cl and Br halide dopants are both determined to be promising for conductivity optimization, with low DFT-MD Na+ ion activation energy (∼0.1 eV at 4% Na vacancy). Thermodynamic analysis shows the possible factors that can influence the final conductivity of Na3SbS4: secondary phases and intrinsic defects. Overall, our findings offer valuable insights for the rational design of solid electrolytes.
Introduction
Due to cost and accessibility issues associated with Li and the ever increasing desire of the society to tap more into clean/renewable energy sources that have less carbon footprint, many research studies now focus on alternative technologies besides Li-ion rechargeable batteries, one being based on the highly abundant Na element.1–4 Na is especially appealing cost-wise such as in stationary applications wherein gravimetric and form factors are not as crucial (e.g., in back-up power systems, smart grids, etc.). Material components in Na and Li ion batteries share many similar chemistries. As a result, the former has benefited in terms of accelerated development cycles by leveraging on accumulated knowledge and expertise from the latter.5–22Similar to the Li ion battery, the increasing demand for high safety in electric/electronic applications has also motivated many to rethink the current design of a typical sodium ion battery (NIB). One approach that is seriously considered as a solution is the replacement of the combustible conventional organic-/liquid-based electrolyte with a solid electrolyte (SE), shifting the current paradigm towards an all-solid-state Na ion battery (ASS-NIB) concept. Some of the candidate SE materials that have been explored are Na-β′′-alumina,23 NASICON NaZr2(PO4)3 and Na3.4Sc0.4Zr1.6(SiO4)2(PO4),24,25 borohydride Na2B12H12,26 anti-perovskite Na3OBr,27 and sulfides such as Na11Sn2PS12,28 Na3PS4,29 Na3−xPS4−xClx,30 Na3PSe4 (ref. 31) and Na3SbS4.32–34 Specifically, Na3SbS4 (NSS), a recently reported one, has shown great promise in terms of ease in processing,33 ionic conductivity (i.e., order of 10−3 S cm−1),32,34 and material processing (i.e., less-intensive conditions are needed for high-elasticity sulfide-type SEs, as compared to stiff oxide-type SEs). The good interface mechanical behavior of NSS when in contact with a cathode (NaCrO2) under cycling operation has also been reported.33 NSS has also been found to be more chemically stable than a predecessor electrolyte Na3PS4, in particular against toxic H2S gas formation from H2O contact.29,32
NSS was noted to undergo chemical decomposition when in direct contact with a Na metal anode (without cell biasing), forming decomposition phases such as Na2S and Na3Sb based on XPS analysis.35 Such anode-side reactions can have profound impact on battery cell performance. Another issue that is yet to be studied is the electrodeposition stability with Na–SEs against initiation of dendrites on the anode surface.
In terms of ionic conductivity (σ), NSS was reported to vary by a factor of 1–2 between its two known phases, the low-temperature tetragonal (t-NSS) phase and the high-temperature cubic phase (c-NSS), with comparison being 1.77 × 10−3 S cm−1vs. 2.80 × 10−3 S cm−1, respectively.32–34,36 The ion conduction mechanism in both phases was presumed to be governed by Na vacancies. A DFT-based calculation using a dilute vacancy model with the single hopping mechanism has predicted an enormously low local energy barrier (<0.1 eV) along the Na diffusion channel.37 Since then, σ improvement has been attempted in several studies such as by applying pressure (1.00 × 10−3 S cm−1 at 0.9 GPa),38 isovalent substitution at the S2− site by Se2− (0.85 × 10−3 S cm−1),39 and aliovalent substitutions at the Sb5+ site by Sn4+ (0.50 × 10−3 S cm−1),40 W6+ (10−2 S cm−1),41,42 and Mo6+ (10−3 S cm−1).43 Meanwhile, aliovalently doping the S site with halide anions is another interesting strategy which can modulate the vacancy concentration and diffusion pathway. In particular, the ion conduction channel size can be largely affected by variation in the anion sublattice which largely determines the packing in crystalline solids. The remaining spaces excluding the anion sublattice are Na sites, non-Na cation sites (e.g., Sb5+ in NSS), and interstitial sites.
Given the high expectation for NSS as a key SE material for next-generation ASSBs, we thus aimed in this work to further investigate it on three key issues that are crucial for practical application: (i) compatibility with the cathode (i.e., crossing tendency of chemical species across the cathode–electrolyte interface that may lead to increased impedance), (ii) stability with the Na metal anode from the viewpoint of decomposition and Na dendrite growth, and (iii) ion transport with respect to halide anion substitution at the S site. Our results not only provide theoretically determined properties that can be compared directly with experimental values, but they can also be used when formulating possible material optimization strategies for solid electrolytes in general.
Computational details
Geometry optimization
DFT calculations were performed using the VASP code44,45 which implements the projector augmented wave (PAW) formalism for the ion–electron interactions.46–48 The generalized gradient approximation (GGA) as parameterized by Perdew, Burke, and Ernzerhof (PBE) was employed as the functional for the exchange–correlation energy.49,50 Except for the Na pseudopotential which includes semi-core p states as valence states, standard pseudopotentials were used for Sb, S, and dopant anions F, Cl, Br, and I. The cutoff for kinetic energy was set to 520 eV and a k-point mesh of at least 1000 was assigned with the Monkhorst–Pack grid scheme.51 All calculations were carried out under spin-polarized conditions. Initial structural data were taken from the Inorganic Crystal Structure Database (ICSD).52 The supercell cell size for Na3SbS4 was set to 2 × 2 × 2 (for the cubic phase, this results to ∼14 Å cell edge dimension in three crystallographic directions). Optimization convergence was set to <1 meV per atom in energy and <0.01 eV Å−1 in residual forces.Thermodynamics calculation
Competing phases were referred from the Materials Project database via its application programming interface which also provided tools in this work to aid in phase diagram construction and analysis.53,54 Na3SbS3, a compound which was separately reported in a previous work,37 was included in the list of compound entries (resulting in a total of 61 phases) for the phase diagram construction.The Gibbs free energy (G) at a given temperature (T) and pressure (P) was then calculated by:55
| G(T,P,NNa,NSb,NS) = H(T,P,NNa,NSb,NS) + PV(T,P,NNa,NSb,NS) − TS(T,P,NNa,NSb,NS), | (1) |
For (electro)chemical stability analysis, the grand potential phase diagram was formulated,55 identifying the phase equilibria with respect to open Na species (μNa). The applied electrostatic potential ϕ is defined as:
| μNa(ϕ) = μ0Na − eϕ. | (2) |
In here, the decomposition energy of NSS at a given ϕ (ΔEd(ϕ)) was determined using:54–56
| ΔEd(ϕ) = Eequil(Cequil([xNa,xSb,xS],ϕ)) − E(Na3SbS4) − ΔnNa × (μNa(ϕ)), | (3) |
Chemical stability analysis was also performed under “rich” and “poor” conditions of non-Na species in NSS, SE-related phases and possible cathode materials using the methodology in ref. 70. Chemical potentials for open Sb and open S species are referenced as well to μ0Sb and μ0S, respectively, which means that under Sb-rich (e.g., direct contact with Sb metal) and S-rich (e.g., direct contact with S solid) conditions, μSb = 0 and μS = 0, respectively. Going towards Sb-poor or S-poor conditions means μSb < 0 and μS < 0, respectively.
Elastic property calculation
Geometry optimizations were performed using stricter settings: kinetic energy cut-off of 700 eV, electronic self-consistency convergence of 10−7 eV, and at least 4 × 4 × 4 k-point. Optimized structures were used as initial cells to determine the elastic tensor. The symmetry-general least-squares extraction approach of elastic coefficients for strained materials was implemented, with elastic moduli including both contributions for distortions with rigid ions and from the ionic relaxations.57 The elastic tensor was determined by carrying out 6 finite lattice distortions, after which the elastic constants were calculated from the resulting strain–stress relationship. For the bcc Na metal, experimental elastic data were used.58Defect calculation
The NSS unit cell was expanded into a 2 × 2 × 2 supercell (128 atoms). The defect formation energy (Ef,d) was calculated using the expression: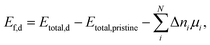 | (4) |
Molecular dynamics calculation
For molecular dynamics (MD) calculations, a 2 × 2 × 2 c-NSS supercell with ∼14 Å cell edges was used. A cutoff kinetic energy of 400 eV was set and the k-point grid was fixed to 1 × 1 × 1. A revised PBE-GGA functional for densely packed solids (PBEsol) was used to describe electron exchange–correlation energy.59Different supercells were constructed for both undoped and halide-doped systems. In the doped models, 2 dopant atoms are introduced homogeneously at 2 S sites (see Fig. S1†) with charge compensation by Na vacancy (∼4%).
A comparison of the energetic stability between the tetragonal and the cubic NSS phase was performed and it showed the increasing stability of the latter with increasing Na vacancy concentration and halide doping content (see Fig. S2†). In addition, it was determined both by the present DFT analysis that the tetragonality of the NSS structure weakens with increasing number of Na vacancies and the structure becomes more cubic, this is consistent with an experimental study.60 Specifically, there is a decrease in the ratio between the longer and the shorter lattice parameters of the tetragonal structure with Na vacancy introduction via halide doping (see Table S1†). Based on these results, the use of the cubic structure for the MD runs of halide-doped systems is reasonable and justified.
Standard pseudopotentials were employed for Na, Sb, S, F, Cl, Br, and I. The MD step size was set to 1 fs. Sampling temperatures were chosen in the range of 373–973 K, at every 100 K interval. To account for thermal expansion, an equilibration step was performed for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps using a Langevin thermostat (NPT ensemble).61 The last 3000 MD steps were used to estimate the average lattice constant of the cubic cell at every trajectory-sampling temperature with 100
000 MD steps using a Langevin thermostat (NPT ensemble).61 The last 3000 MD steps were used to estimate the average lattice constant of the cubic cell at every trajectory-sampling temperature with 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps for the production run. The latter procedure used a thermostat in the Nose–Hoover formalism (NVT ensemble).62
000 steps for the production run. The latter procedure used a thermostat in the Nose–Hoover formalism (NVT ensemble).62
To characterize the sampled trajectories, the mean square displacement (MSD) of the atoms was calculated:
MSD = 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t + τ) − (t + τ) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t)]2〉, (t)]2〉, | (5) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t), t and τ are the atom position, time and lag time, respectively. Diffusion coefficient (D) calculation was based on the Einstein–Smoluchowski equation:63
(t), t and τ are the atom position, time and lag time, respectively. Diffusion coefficient (D) calculation was based on the Einstein–Smoluchowski equation:63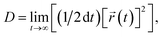 | (6) |
Results and discussion
Crystal structure and electronic properties
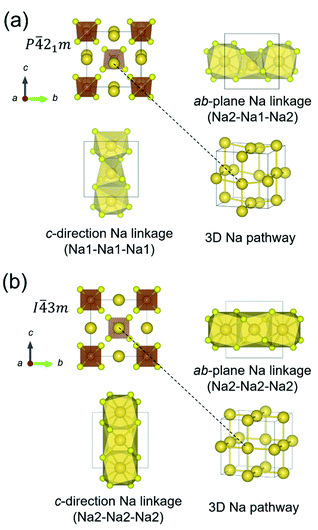
The crystal structures of t-NSS and c-NSS are shown in Fig. 1. In t-NSS, isolated SbS4 tetrahedral units (Wyckoff 2b Sb, 8e S) form a body-centered-type arrangement and 2 distinct Na sites (Na1: 4d, Na2: 2a) in distorted polyhedral units are positioned inside 6-S and 8-S cages. Two characteristic local pathway linkages form a contiguous 3D network for long range Na inter-diffusion: the ab-plane pathway with alternating Na1 and Na2 sites and the c-direction pathway which comprises only Na1 sites. In the case of c-NSS, only one Na Wyckoff site exists and the resulting pathway is 3D-symmetric.DFT-calculated lattice information for NSS is summarized in Table 1. Values are noted to be overestimated at most by 1.2% and 3.7% for the lattice parameters and volume, respectively, vs. experiment. Experimental bond distances are reproduced by DFT to within 2.3% (Table S2†). These discrepancies are error levels typical for the GGA-PBE functional.64 From DFT total energy comparison, t-NSS was predicted to be more stable than the c-NSS, this is also consistent with experiment. Halide anion addition into the c-NSS structure results in a slightly expanded lattice cell by about 0.43–0.87% relative to its undoped form. Overall, the lattice constant increases with increasing halide anion radius (see Table S3†).
| Phase | Lattice cell information | DFT total energy/eV per cell | |||
|---|---|---|---|---|---|
| a, b, c/Å | Δ/% | V/Å3 | Δ/% | ||
t-Na3SbS4 (P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c) 21c) |
7.23 (7.14), 7.23 (7.14), 7.37 (7.28) | 1.2, 1.2, 1.2 | 385.3 (371.5) | 3.7 | −61.4313 |
c-Na3SbS4 (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) 3m) |
7.25 (7.17), 7.25 (7.17), 7.25 (7.17) | 1.1, 1.1, 1.1 | 380.5 (368.6) | 3.2 | −61.3648 |
Based on the density of states (DOS) profile of t-NSS (Fig. S3†), the top of valence bands and the bottom of the conduction bands are found to comprise bonding and antibonding combinations of Sb and S, respectively. The bottom of the conduction band is split into: (i) S antibonding states and Sb 5s states for the lower band and (ii) S antibonding states and Sb 5p states for the upper band. The estimated GGA-PBE electronic band gap energy is 2.1 eV (we calculated at the HSE level a value of 3.1 eV), this is comparable with other sulfide-type SEs such as Li10GeP2S12 (3.6 eV).65 Usually, the band gap energy is used as a parameter for the SE electrochemical stability window (positive correlation) and electronic conductivity (negative correlation).
Thermodynamic phase stability, possible secondary phases
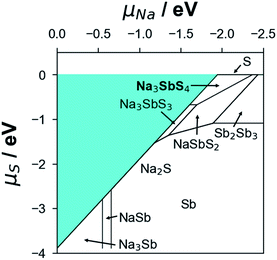
Using the formation energy data of competing phases in the Na–Sb–S system (see Table S4†), the convex hull results point to t-NSS as a ground-state phase (see Fig. S4†). Unless explicitly mentioned hereafter, thermodynamic-related analyses will be based on t-NSS. For (electro)chemical stability evaluation with cathode/anode contact and ion conduction property analysis, possible secondary/decomposition phases that may appear during material synthesis and battery cycling were also considered. This would enable the following: (i) the direct analysis of bulk-related properties and (ii) the qualitative analysis of inter-grain-related properties. During the material synthesis of NSS, chemical potentials of Na and S can be controlled (e.g., via Na2S loss at high temperature to achieve ‘Na-poor’ synthesis conditions, or by explicit addition of excess Na2S to realize ‘Na-rich’ conditions); this can lead to formation of other phases. Based on the Na–S grand potential phase diagram as shown in Fig. 2, possible secondary/decomposition phases were identified from the bounding phases of the NSS chemical potential stability region, these are Na3SbS3 (P213), NaSbS2 (C2/c), and Na2S (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).
m).
Cathode-side stability
Interface stability at the SE–cathode contact is an important issue that directly affects the cycling performance of solid-state batteries. It may be evaluated according to the thermodynamic tendencies of chemical species to migrate across the SE–cathode interface which could trigger the interface atomic rearrangement and/or interfacial decomposition, eventually leading to an increased interfacial resistance and poor capacity retention. Some reports have shown the formation of a reaction layer which may have been facilitated by species diffusion at the solid hetero-interface.66,67 Other studies depict an interface region based on the space-charge layer effect in the scale of few-to-several atomic layers.68 In here, the tendency for chemical species migration was qualitatively investigated using bulk chemical potential relationships to provide insight into the chemical driving forces that would cause the compositional change around the interface. For the cathode counterpart, the layered structures (Na[TM]O2, where TM = {V, Cr, Mn, Fe, Co, Ni}) were considered here as contact materials with the electrolyte. To identify the possible reactions, the chemical potentials of the different species from the cathode and SE component were determined from element stoichiometry and bulk Gibbs free energy of relevant phases.In the case of reductive and oxidative stability evaluation related to battery charge/discharge, it is noted that the local equilibrium of Na+, e−, and Na determines the electrode potential. It is assumed here that the local equilibrium may be established and the phase stability range of the SE compound can be defined (i.e., vs. Na+/Na).69 This can be extended as well to other chemical species in the system. The phase stability range ([μ1, μ2]) can be described with respect to a specified open chemical species, where μ1 and μ2 denote bounds towards “rich” and “poor” conditions, respectively.70–72 Outside [μ1, μ2], the equilibrium is pushed towards decomposition which forms the stable competing phases. When viewed at the cathode–SE contact, species migration is assumed to be likely if no common μ exists (for both the cathode and SE) that would allow for a possible equilibrium μ condition across the interface (i.e., checking if [μ1,μ2]cathode∪[μ1,μ2]SE = ∅). Otherwise, there would be no driving force for species migration (i.e., if [μ1,μ2]cathode∪[μ1,μ2]SE > ∅). For the cathode counterpart, experimentally confirmed compounds with layered structures were selected, such as NaCrO2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).73 Overall, 6 cathode compounds under pre-charged (i.e., full sodiation) and charged (i.e., full desodiation) conditions, as well as 4 SE/SE-related compounds (NSS, Na3SbS3, NaSbS2, Na2S) were investigated (total: 6 × 2 × 4 = 48 different interface–contact combinations).
m).73 Overall, 6 cathode compounds under pre-charged (i.e., full sodiation) and charged (i.e., full desodiation) conditions, as well as 4 SE/SE-related compounds (NSS, Na3SbS3, NaSbS2, Na2S) were investigated (total: 6 × 2 × 4 = 48 different interface–contact combinations).
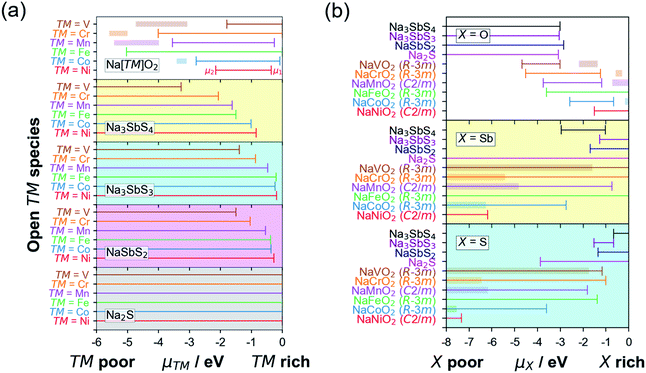
Fig. 3a shows the [μ1, μ2] relationship for various cathodes and SE/SE-related compound pairings. The horizontal axis represents μ of the open TM species while the vertical axis represents the index/label for various layered Na[TM]O2 cathode compounds. The horizontal lines for different compounds represent the [μ1, μ2] stability range. Additionally, for the different cathodes, the horizontal lines indicate the pre-charging condition (full Na content) while the corresponding horizontal bands are for the charging condition (full desodiation cases). An example for the assignment of μ1 and μ2 is shown in the top subplot for Ni species in NaNiO2 (in red). Meanwhile, actual [μ1, μ2] values for open V, Cr, Mn, Fe, Co, and Ni species in NaVO2, NaCrO2, NaMnO2, NaFeO2, NaCoO2, and NaNiO2, respectively, are determined to be [0 eV, −1.79 eV], [0 eV, −4.01 eV], [−0.25 eV, −3.55 eV], [0 eV, −5.03 eV], [−0.08 eV, −2.78 eV], and [−0.36 eV, −2.15 eV], respectively. For NSS, μ ranges for open V, Cr, Mn, Fe, Co, and Ni species are [−3.27 eV, −∞], [−2.06 eV, −∞], [−1.62 eV, −∞], [−1.50 eV, −∞], [−1.01 eV, −∞], and [−0.84 eV, −∞], respectively. Based on the (non-)overlap in the μ ranges between the cathodes and SE/SE-related phases, the tendency for TM cation migration across the interface under battery pre-charging (or simple contact) and charging conditions is predicted to be unlikely, except for TM = V. The schematic summary is shown in Fig. 4a and detailed reactions are summarized in Tables S5 and S6.†
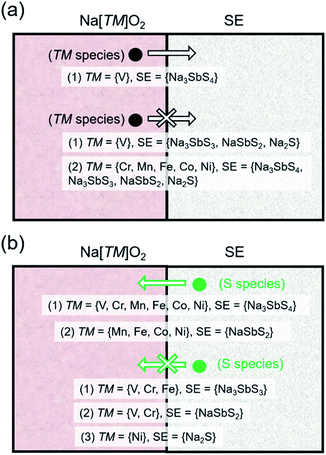 | ||
| Fig. 4 Schematic picture for (a) transition metal (TM) species and (b) S species tendency to migrate across the Na[TM]O2–SE interface based on the chemical potential relationship as shown in Fig. 3a and b, respectively. | ||
Fig. 3b shows the [μ1, μ2] relationship for open species X = {O, Sb, S}. For X = O, all 4 SE-related phases have common μ values with TM = {V, Cr, Mn, Fe} but not with TM = {Co, Ni} under the pre-charged cathode condition (i.e., full sodiation, horizontal lines in Fig. 3b). For X = Sb, overlap in [μ1, μ2] is noted for pairs NSS–TM = {V, Cr, Mn, Fe, Co}, SE = {Na3SbS3, NaSbS2} – TM = {V, Cr, Mn, Fe }, and Na2S–TM = {V, Cr, Mn, Fe, Co, Ni}. No common μ values appear for NSS–TM = Ni, and SE = {Na3SbS3, NaSbS2} TM = {Co, Ni}. For X = S, species migration is predicted to be favorable between NSS and all Na[TM]O2 compounds. Na3SbS3 has [μ1, μ2] overlap for TM = {V, Cr, Fe}, while for NaSbS2 only overlaps for TM = {V, Cr}. Na2S has overlap for TM = {V, Cr, Mn, Fe, Co}, but not for TM = Ni. These results are similar to the experimental observation for the Li-based cathode–SE interface, especially on S species migration tendency.66,67 A schematic picture is shown in Fig. 4b for S species (see Fig. S5 in the ESI† for X = {O, Sb}). Under charging conditions (i.e., full desodiation, horizontal bands in Fig. 3b), the [μ1, μ2] ranges for X = O for the cathodes become largely narrow, their overlap with the [μ1, μ2] ranges of NSS/SE-related phases disappear (such as for TM = {V, Cr, Mn, Fe}), suggesting the increased chemical driving force for O species migration from the charged cathode to the SE side. The same trends are observed for X = {Sb, S}. These findings highlight the reactive nature of the charged cathode which can facilitate crossing of species and reactions at the cathode–SE contact. Detailed reactions are listed in Tables S7 and S8.†
The above results for the pre-charged cathode are found to be consistent with a previous DFT study. The result indicates the less favorable displacement reaction of S2− by O2− for NSS and pre-charged layered-type cathodes.74 The contrast between NSS and the other electrolyte Na3PS4 was also confirmed, that is, the contact between Na3PS4 and layered-type cathodes highly favors PO4 formation.74 This difference between NSS and Na3PS4 may be further explained by the hard–soft acid–base theory, which emphasizes that Sb5+ (a soft acid) prefers to bind with S2− (a soft base) while P5+ (a hard acid) prefers to bind with O2− (a hard base).32
Anode-side stability
The (electro)chemical stability of NSS is evaluated here by simulating conditions at the low (reduction, high μNa) and high (oxidation, low μNa) voltage regimes of a typical battery cycling process. The evaluation is assumed to be closely linked to Na insertion/de-insertion into/from the SE structure. Two possible scenarios could occur: (i) no reductive/oxidative decomposition or zero Na net loss for SE (i.e., Na+ ions are simply being shuttled between the anode and the cathode) or (ii) non-zero Na net loss for SE which is associated with irreversible side reactions (i.e., Na+ ions are trapped inside decomposition phases and become excluded from the shuttling process between the anode and the cathode). Table 2 summarizes the competing phases that would likely form during electrochemical cycling. Overall, narrow voltage windows were found for NSS, Na3SbS3, and NaSbS2; calculated ranges are [1.60 V, 2.37 V], [1.18 V, 1.69 V], and [1.35 V, 2.43 V], respectively. These materials are predicted to react and decompose, both reductively (e.g., at <1 V) and oxidatively (e.g., at >2.5 V). Meanwhile, Na2S shows a window of [0 eV, 1.94 V] which indicates stability at the low voltage regime. If it forms after the first few cycling steps or it already exists in the pre-cycled SE powder/pellet, it can form a passivating phase (electronic insulator) that may prevent further SE decomposition at the anode side. It is noted that the change in volume between NSS and its decomposition products (at the reductive regime) can be significant enough to possibly result in stress build-up and eventually, cracking and contact loss around the interface region.74| Compound | Voltage/0 V vs. Na+/Na | Reaction product phases |
|---|---|---|
| Na3SbS4 | <1.60 | Na3Sb, NaSb, Sb, Na3SbS3, Na2S |
| >2.37 | NaSbS2, Sb2S3, S | |
| Na3SbS3 | <1.18 | Na3Sb, NaSb, Sb, Na2S |
| >1.69 | Na3SbS4, NaSbS2, Sb2S3, S | |
| NaSbS2 | <1.35 | Na3Sb, NaSb, Sb, Na2S |
| >2.43 | Sb2S3, S | |
| Na2S | >1.94 | S |
Anode-side dendrite formation tendency
Dendrite formation is another major hindrance towards developing batteries with metal anode design. In here, dendrite initiation/growth tendency on the Na metallic anode surface in contact with an SE material was evaluated using the Monroe–Newman 2D model.75,76 This model evaluates the effects of general stresses on current density distributions at roughening interfaces. Starting from the typical reduction and deposition of Na+ ion as given by the reaction:| Na+ + e− ⇌ Na, | (7) |
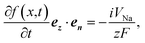 | (8) |
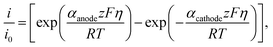 | (9) |
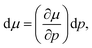 | (10) |
Taking the ratio between the deformed and ideal interface (using eqn (9)), the rate of change of the electron electrochemical potential (Δμe−) is derived as:75,76
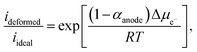 | (11) |
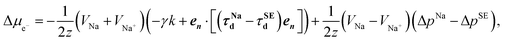 | (12) |
Δμe− = χRe{A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eikx}, eikx}, | (13) |
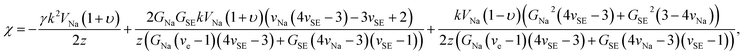 | (14) |
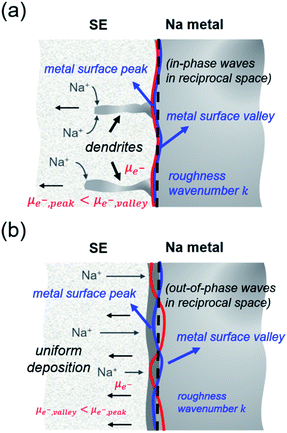
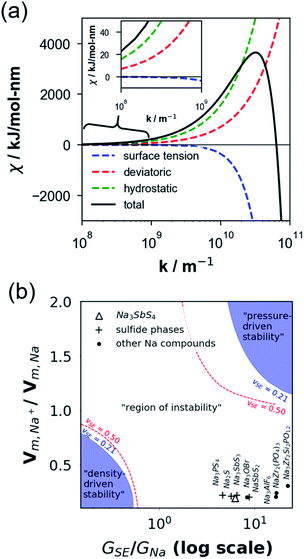
When χ > 0, electrodeposition becomes unstable (i.e., perturbation is in phase with current density), resulting in a faster deposition at the metal surface peaks rather than at the metal surface valleys (i.e., electron chemical potential is lower at the peaks than at the valleys) and thereby promoting Na dendrite formation (see Fig. 5a). When χ < 0, the reverse is true in which electrodeposition is predicted to be stable (i.e., perturbation is out of phase with current density), resulting in a faster deposition rate at the valleys than at the peaks of the deformed/rough Na metal surface (i.e., electron chemical potential is lower at the surface valleys than at the surface peaks), resulting in a more uniform deposition and no dendrite growth (see Fig. 5b). To determine χ, elastic data calculated by DFT and partial molar volumes of Na+ ion in the SE/SE-related compound structures from DFT-optimized structures are used.
Fig. 6a plots the contributions of the surface tension and general stresses to χ as a function of surface roughness k (in m−1) for the Na–NSS interface. It indicates a stabilizing effect for surface tension (χ < 0) while a destabilizing effect for deviatoric and hydrostatic stresses (χ > 0); this is consistent with calculations performed for metal–SE interfaces for Li-based solid-state batteries.76 Using the k value in a typical electrodeposition process (1 × 108 m−1),75 the contributions of surface tension, deviatoric stress, and hydrostatic stress with NSS are −0.04 kJ mol−1 nm−1, +7.09 kJ mol−1 nm−1, and +15.68 kJ mol−1 nm−1, respectively, leading to a χ value of +22.73 kJ mol−1 nm−1 (see k-axis intercept in Fig. 6a inset). This suggests that Na dendrite formation is likely to occur during Na plating/stripping with metallic Na. No dendrite suppression is expected as well for other SE-related phases (Na3SbS3: +21.41 kJ mol−1 nm−1, NaSbS2: +29.62 kJ mol−1 nm−1, Na2S: +24.77 kJ mol−1 nm−1). A stability map using the ratio of molar volume quantities (Vm,Na+/Vm,Na) and shear moduli parameters (GSE/GNa) is displayed in Fig. 6b for various Na-based SE compounds, including non-sulfide-type ones (e.g., NaZr2(PO4)3,24 Na3Zr2Si2PO12,77 Na3AlF6,78 Na3OBr27). There are 3 regions in the plot: (i) density-driven stability region in the lower left, (ii) “region of instability” in the middle, and (iii) pressure-driven stability region in the upper right. All the considered SE compounds lie in region (ii) (i.e., Vm,Na+/Vm,Na < 0 and GSE > GNa). Overall, none of the investigated compounds are predicted to be stable against dendrite growth. Meanwhile, along the log(GSE/GNa) axis, NSS is noted to be closer to the frontier of region (i) than the non-sulfide types.
Intrinsic bulk defects
Table 3 lists the various defect complexes (in the Kroger–Vink notation) for the NSS compound. The lowest defect energies were noted for S Frenkel (1.26 eV), Na–S antisite (1.01 eV), and Na2S Schottky (2.05 eV) (S Frenkel and Na–S antisite are visualized in Fig. 7). These values suggest that intrinsic disorder is maybe common in the material in its as-prepared form, in particular under the high-temperature synthesis condition.30 Meanwhile, the Na-Frenkel model showed a defect energy of 0.15 eV, but this defect configuration naturally relaxes back to the normal Na sites, that is, Na and defect species redistribute according to the reaction: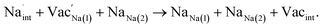 | (15) |
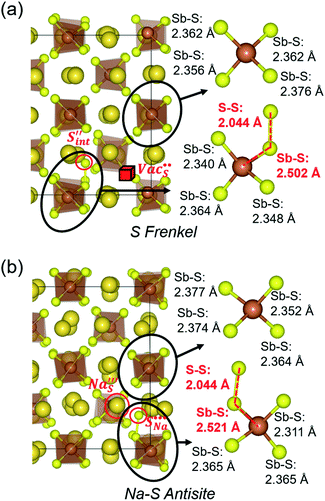 | ||
Fig. 7 Schematic illustration of (a) S Frenkel and (b) Na–S antisite from DFT-optimized supercells. Defect species such as 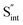 , , 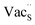 , , 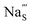 , and , and 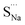 and defect-related bond lengths are shown in red. and defect-related bond lengths are shown in red. | ||
This is reflective of a Na pathway with energetically shallow local sites, favourable for fast Na diffusion. On the other hand, for S Frenkel and Na–S antisite, we found that after structural optimization the interstitial S 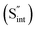 actually prefers to form a chemical bonding with a corner S (Scorner) of a neighboring SbS4 unit (see Fig. 7a and b) as evidenced by the shorter distance between Sint and Scorner (2.044 Å). Interatomic distance is also increased between Scorner and its center Sb (Sbcenter) of the same SbS4 unit (from 2.350 Å in the pristine model to ∼2.5 Å at post-relaxation), indicating Sb–S bond weakening due to Sint. The Sint–Scorner complex forms a basic bridging S unit which is similar to those observed in polysulfide compounds such as I
actually prefers to form a chemical bonding with a corner S (Scorner) of a neighboring SbS4 unit (see Fig. 7a and b) as evidenced by the shorter distance between Sint and Scorner (2.044 Å). Interatomic distance is also increased between Scorner and its center Sb (Sbcenter) of the same SbS4 unit (from 2.350 Å in the pristine model to ∼2.5 Å at post-relaxation), indicating Sb–S bond weakening due to Sint. The Sint–Scorner complex forms a basic bridging S unit which is similar to those observed in polysulfide compounds such as I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d NaS2 (in which the experimental S–S average bond length is 2.070 Å).79 It is pointed out here that S–S bonding formation may facilitate the stabilization of Na vacancy defects via the charge compensation mechanism. Previous characterization by Rietveld refinement for the undoped NSS phase has indicated the presence of 5% vacancies in one of the Na Wyckoff sites.32
2d NaS2 (in which the experimental S–S average bond length is 2.070 Å).79 It is pointed out here that S–S bonding formation may facilitate the stabilization of Na vacancy defects via the charge compensation mechanism. Previous characterization by Rietveld refinement for the undoped NSS phase has indicated the presence of 5% vacancies in one of the Na Wyckoff sites.32
Na ion transport property
For ground-state t-NSS, two distinct Na local pathways describe the 3D long-range inter-diffusion process (see Fig. 1a). Meanwhile, for metastable c-NSS which has a higher σ than t-NSS by a factor of ∼2, there is a 3D symmetric pathway of linked equivalent Wyckoff sites as shown by the DFT-MD 2D-projected trajectory in Fig. 8a. Similar to the strategy for other known metastable SE materials, c-NSS stabilization can also be realized via doping, for example by halide anions X (F, Cl, Br, I) at the S site. Similar to the intrinsic defect energies calculated for the undoped NSS phase, DFT doping energies for NSS by halide anions with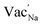 introduction were also estimated to be sufficiently low (0.95–1.11 eV f.u.−1) to be accessible during high-temperature synthesis.30,80 Thus, we focus hereafter on c-NSS and investigate σ and effects of halide doping on it. For this, the Arrhenius relationship was employed:81
introduction were also estimated to be sufficiently low (0.95–1.11 eV f.u.−1) to be accessible during high-temperature synthesis.30,80 Thus, we focus hereafter on c-NSS and investigate σ and effects of halide doping on it. For this, the Arrhenius relationship was employed:81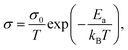 | (16) |
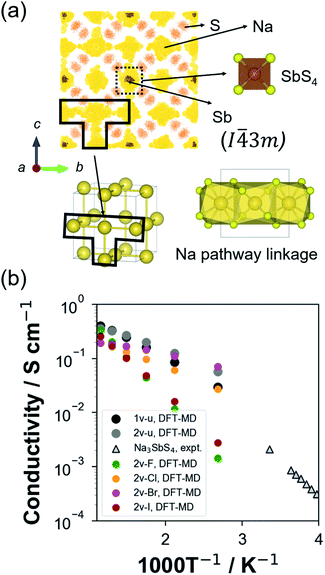 | ||
Fig. 8 (a) 2D-projected atom trajectory density from 100 ps NVT-MD calculation (473 K) of the 1-vacancy c-NSS (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) supercell model. (b) DFT-MD-derived Arrhenius plot for Na+ ionic conductivity at different temperatures of 1-vacancy undoped (1v-u), 2-vacancy undoped (2v-u), F-doped (2v-F), Cl-doped (2v-Cl), Br-doped (2v-Br), and I-doped (2v-I) supercell models. Experimental data for undoped Na3SbS4 are included for comparison.41 3m) supercell model. (b) DFT-MD-derived Arrhenius plot for Na+ ionic conductivity at different temperatures of 1-vacancy undoped (1v-u), 2-vacancy undoped (2v-u), F-doped (2v-F), Cl-doped (2v-Cl), Br-doped (2v-Br), and I-doped (2v-I) supercell models. Experimental data for undoped Na3SbS4 are included for comparison.41 | ||
Fig. 8b shows the Arrhenius plot derived from temperature-dependent MSD profiles (see Fig S6†). We note that, for example, in the 1v-u model which is the closest representative of the reported undoped phase, the same order of magnitudes was calculated for Ea and room-temperature σ (σRT) vs. experimental data. Thus, comparison can be reasonably and systematically carried out based on our calculation results. Without doping, such as in 1v-u and 2v-u models, an increase from a single vacancy (∼2%) to two vacancies (∼4%) resulted in a decrease in the logσ vs. 1000T−1 slope. The slope is directly correlated with Ea, the estimated values of 0.201 ± 0.042 eV to 0.159 ± 0.052 eV, respectively, reveal the importance of Na vacancies in activating the superionic conduction in NSS. Without vacancy, a negligible diffusivity was found as confirmed by a flat MSD trend (see Fig. S7†).
As previously pointed out, it is expected that Ea may be further modulated with respect to halide dopant type since the diffusion channel can be modified differently even at the same level of vacancy concentration, this is owing to the ionic size and electronegativity/ionicity difference among halide anions. To examine this, results for halide anion dopant radius rX,82Ea, and extrapolated σRT from DFT-MD runs were collected and summarized in Table 4 (experimental data included for comparison). The rX parameter was initially chosen to check whether it has a direct correlation with Ea and σRT, noting that it may be correlated with the variation in the anion sublattice packing and thus, the diffusion pathway.
| Composition | Dopant anion radius rXa/Å | DFT-MD Ea/eV (expt.) | DFT σRT/10−2 S cm−1 |
|---|---|---|---|
| a 6 nearest neighbors.81 b Nominal Na3SbS4.41 | |||
| Na2.9375SbS4 (2% vacancy, 1v-u) | — | 0.201 ± 0.042 (0.269)b | 0.828 (0.21)b |
| Na2.875SbS4 (4% vacancy, 2v-u) | — | 0.159 ± 0.052 (—) | 0.220 (—) |
| Na2.875SbS3.875F0.125 (4% vacancies, 2v-F) | 1.33 | 0.281 ± 0.078 (—) | 0.178 (—) |
| Na2.875SbS3.875Cl0.125 (4% vacancies, 2v-Cl) | 1.81 | 0.105 ± 0.017 (—) | 4.489 (—) |
| Na2.875SbS3.875Br0.125 (4% vacancies, 2v-Br) | 1.96 | 0.073 ± 0.007 (—) | 10.240 (—) |
| Na2.875SbS3.875I0.125 (4% vacancies, 2v-I) | 2.20 | 0.267 ± 0.029 (—) | 0.253 (—) |
DFT-MD Ea values reveal a concave up trend with increasing rX as follows: 0.281 ± 0.078 eV with F doping, 0.105 ± 0.017 eV with Cl doping, 0.073 ± 0.007 eV with Br-doping, and 0.267 ± 0.027 eV with I doping. Correspondingly, the σRT trend shows a concave down behaviour: 0.178 × 10−2 S cm−1, 4.489 × 10−2 S cm−1, 10.240 × 10−2 S cm−1, and 0.253 × 10−2 S cm−1, respectively. Overall, Cl and Br doping appears to be promising as dopants for σ optimization. To study how rX correlates with the changes in the diffusion channel, other physical parameters were also investigated such as Na site cage diameter (d0) and site-to-site bottleneck diameter (d1), as displayed in Fig. 9a. These parameters were determined by the Voronoi tessellation approach and using the DFT geometry-optimized structures.84Fig. 9b and c display the ranges for d0 and d1 which are 2.1–2.7 Å and 1.60–1.67 Å, respectively. The undoped models (1v-u, 2v-u) show the smallest d0 and largest d1 values. For the F-doped model (2v-F), both its d0 and Ea are the largest, but it has the smallest d1 values relative to other models. It can be interpreted as the path bottleneck becoming smaller and thus Ea becoming larger with F doping. It is apparent that there is a critical value for d1 (∼1.62 Å), below which Ea starts to increase significantly as shown in Fig. 9c (for 2v-F and 2v-I models). No monotonic decrease in Ea is determined with further increase beyond the noted critical value of d1 (for 1v-u and 2v-u models). Therefore, it can be argued that, aside from inducing ionic conduction via Na vacancy creation, the dopant halide anion type modulates the diffusion channel for the moving Na+ ion by changing the Na site-to-site bottleneck size.
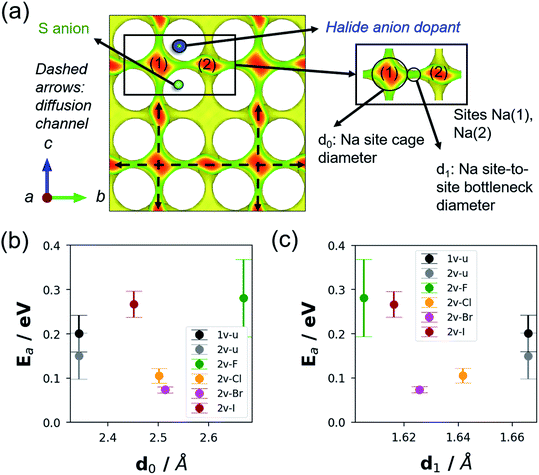 | ||
| Fig. 9 (a) Schematic illustration of the Na diffusion channel isosurface in NSS. The isosurface is generated by the bond valence sum (BVS) approach.83 Na sites labelled 1 and 2 are highlighted, with local pathway features described; d0: Na site cage diameter and d1: Na site-to-site bottleneck diameter. (b) DFT-Eavs. d0 plot and (c) DFT-Eavs. d1 plot for 1-vacancy undoped (1v-u), 2-vacancy undoped (2v-u), F-doped (2v-F), Cl-doped (2v-Cl), Br-doped (2v-Br), and I-doped (2v-I) supercell models. | ||
Discussion
Considering that there are only a few practical SE material choices so far for ASS-NIB application, NSS may be expected as one of the base SE materials which satisfy the high-σ requirement for actual application. When it is incorporated in the actual solid-state cell, further improvement (e.g., via morphology control and interface engineering) is still necessary to satisfy the other metrics such as chemical/electrochemical compatibility vs. electrode materials and stability vs. dendrite initiation/growth during the anode-side Na plating/stripping process.The tendency of S species in NSS to migrate across the interface with the cathode is predicted as one of the highly likely processes that would drive the chemical makeup variation and atomic rearrangement around the interface region. This predicted single-species-type migration may also form part as an elementary process of other experimentally suggested reactions such as mutual species exchange and defect-driven redistribution of chemical species across the cathode–SE contact.66,67 Usually, these reactions are linked to resistance increase around the cathode–SE interface region.85,86 One possible way to reduce this interfacial resistance is by introducing a thin oxide buffer layer which acts as a physical barrier that prevents interface reaction.70,87,88
Similarly, the insertion of a physical barrier between the anode and SE component is also a possible approach to prevent or limit SE decomposition. For instance, NaCl was found to be able to slow SE degradation kinetics in NSS.35 The formation of NaCl at the low-voltage regime (i.e., under high Na chemical potential) in Cl-doped NSS was verified to be energetically preferable in the present work according to DFT free-energy phase diagram calculations (see Table S9†). However, a trade-off with interface and grain boundary ion transport is to be expected, given the difference in σ of the inserted barrier compound. The use of an alloy metal anode may also address the aforementioned stability problem, since the chemical potential of Na in the alloy phase is relatively lower than in the pure Na metal phase. For example, instead of Na metal as the starting anode, Na3Sb and NaSb alloys may be used instead which are more stable phases under low voltage conditions. However, a possible drawback of this approach would be volume expansion/contraction, particularly at high current densities. This volume change can cause poor cycle performance due to eventual contact loss. To address this issue on volume change, porous morphology structures or porous supports have been tested.89 Meanwhile, to stop dendrite initiation at the Na metal anode surface, the electrodeposition stability map in Fig. 4b suggests two ways to achieve density-driven stability (i.e., region (i)): (i) make Na in the SE compound more densely packed than Na in the Na metal anode or (ii) appropriately pair the SE compound with an anode with lower effective molar volume for Na atom (e.g., alloy). In addition, intentionally increasing the Na metal surface roughness may also prevent dendrite formation, as shown in the total χ curve in Fig. 4 in which the value becomes negative at higher surface roughness k (e.g., at ∼6.41 × 1011 m−1). The density-driven stability (region (i)) may also be achieved via interface morphology control, by taking into account the anisotropy owing to the crystallographic orientation of Na metal and SE surfaces.90 The stress–strain condition and electron density distribution around the anode–SE interface may also be controlled by modulating the cell stack pressure.91
Na ion transport in NSS is determined to be assisted by 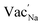 as revealed by DFT-MD results. The halide dopants modify the bulk σ value by: (i) controlling Na vacancy concentration and (ii) varying the size of the Na inter-site path bottleneck. An order of 10−2 S cm−1 is predicted to be accessible for Br-doped and Cl-doped NSS phases. A previous experimental report showed σ optimization by Cl doping in a material analogue Na3−δPS4−xClx (x = 0.2).92 Interestingly, the analysis indicated that this system is a case in which the Na vacancy is limited and Cl is abundant, rather than Na vacancy and Cl concentrations being equal (i.e., following a typical charge compensation for S2− substitution with Cl−). It was suggested that, for charge compensation, the P oxidation state was changed from 5+ to 4+ (based on solid-state NMR analysis). It is noted here that 4+ is an uncommon electronic configuration for the P element, instead it is 5+ which is the natural oxidation state. This is in contrast with the present DFT work, in which the Na vacancy concentration depends on halide content for charge neutrality and there is no change in the oxidation state of Sb (such as from 5+ to 4+). So far, we found no experimental report yet that suggests the possible oxidation state change of Sb from 5+ to 4+ in NSS. Meanwhile, experiments have demonstrated a room-temperature conductivity maximum by Cl doping, the values are 9.0 × 10−4 S cm−1 and 2.9 × 10−3 S cm−1 for xCl = 0.05 and xCl = 0.0625, respectively.60,93,94 These measurements are consistent with the present DFT-MD data for Cl doping, but the experimental doping concentrations are noted to be slightly lower. Although a higher conductivity is exhibited by our prediction, our simulated doping level (at xCl = 0.125) is apparently difficult to obtain experimentally because of decreased achievable SE pellet density.60 The formation of new structure and/or secondary phases (with inherently lower conductivity) could also play a role in the observed decrease in experimental conductivity.60
as revealed by DFT-MD results. The halide dopants modify the bulk σ value by: (i) controlling Na vacancy concentration and (ii) varying the size of the Na inter-site path bottleneck. An order of 10−2 S cm−1 is predicted to be accessible for Br-doped and Cl-doped NSS phases. A previous experimental report showed σ optimization by Cl doping in a material analogue Na3−δPS4−xClx (x = 0.2).92 Interestingly, the analysis indicated that this system is a case in which the Na vacancy is limited and Cl is abundant, rather than Na vacancy and Cl concentrations being equal (i.e., following a typical charge compensation for S2− substitution with Cl−). It was suggested that, for charge compensation, the P oxidation state was changed from 5+ to 4+ (based on solid-state NMR analysis). It is noted here that 4+ is an uncommon electronic configuration for the P element, instead it is 5+ which is the natural oxidation state. This is in contrast with the present DFT work, in which the Na vacancy concentration depends on halide content for charge neutrality and there is no change in the oxidation state of Sb (such as from 5+ to 4+). So far, we found no experimental report yet that suggests the possible oxidation state change of Sb from 5+ to 4+ in NSS. Meanwhile, experiments have demonstrated a room-temperature conductivity maximum by Cl doping, the values are 9.0 × 10−4 S cm−1 and 2.9 × 10−3 S cm−1 for xCl = 0.05 and xCl = 0.0625, respectively.60,93,94 These measurements are consistent with the present DFT-MD data for Cl doping, but the experimental doping concentrations are noted to be slightly lower. Although a higher conductivity is exhibited by our prediction, our simulated doping level (at xCl = 0.125) is apparently difficult to obtain experimentally because of decreased achievable SE pellet density.60 The formation of new structure and/or secondary phases (with inherently lower conductivity) could also play a role in the observed decrease in experimental conductivity.60
Out of all the bounding phases in the phase diagram for NSS, only Na2S may offer a favorable grain boundary pathway between particles, as suggested by its relatively low Na+ ion migration energy (see Fig. S8 and S9†). Thus, suppression of other secondary phases is crucial to achieve high σ. In addition, intrinsic defects such as S Frenkel and Na–S antisite are expected to also affect σ since they may alter a long-range inter-diffusion process in the bulk, possibly even blocking the Na pathway (see Fig. 7). Control of these intrinsic defects should thus be considered as well, particularly during the actual material synthesis of NSS.
Conclusions
A comprehensive theoretical study based on DFT and advanced kinetic modelling was carried out to investigate the phase stability, (electro)chemical stability, electrodeposition stability, defect chemistry, and Na ion transport property of NSS SEs for ASS-NIB application. In the cathode side (e.g., using NaCrO2), interface atomic rearrangement is highly likely to be facilitated by S chemical species diffusion. Meanwhile, NSS undergoes decomposition under the low voltage (Na insertion reaction) and high voltage (Na de-insertion reaction) conditions; the predicted electrochemical window is 1.60–2.37 V vs. Na+/Na. It was determined that Na dendrite formation is likely during the electrodeposition process on the Na metal anode surface with NSS as the contact SE material, highlighting the need for other strategies to be implemented such as control of morphology and cell stack pressure. Halide doping at the S site enables increasing the Na vacancy concentration and modulating the diffusion path bottleneck size to tune the conductivity and activation energy barrier. Among the dopants, Br− and Cl− anions are predicted to be the most promising ones, both with activation energies of about ∼0.1 eV at 4% Na vacancies. Secondary phases and intrinsic defects during NSS synthesis are possible hindrances for maximizing the conductivity. Na2S, a possible secondary phase that could either exist in the as-prepared sample or could form during battery charge–discharge operation, may aid in the inter-grain transport because of its low Na+ ion migration energy.Author contributions
R. J. and Y. T. conceived the study with the help of B. G., and H. K. T. Calculations were performed by R. J. Contributions were made by Y. T., B. G., and H. K. T. in relation to the analysis and discussion of thermodynamic reactions, chemical potential relationships, and ion transport. The manuscript was written by R. J., with input/comments/feedbacks from other authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. J. is thankful to the Japan Science and Technology Agency (JST) Precursory Research for Embryonic Science and Technology (PRESTO) program for the financial support. This research was also supported in part by JST through “Materials research by Information Integration” Initiative (MI2I)”, ALCA-SPRING Grant Number JPMJAL1301 and COI-NEXT Grant Number JPMJPF2016, by JSPS KAKENHI Grant Numbers JP19H05815 and JP21K14729, and by MEXT as Elements Strategy Initiative Grant Number JPMXP0112101003, Materials Processing Science project (“Materealize”) Grant Number JPMXP0219207397 and “Program for Promoting Researches on the Supercomputer Fugaku” Grant Number JPMXP1020200301. The calculations were performed on the supercomputers at NIMS (Numerical Materials Simulator), Nagoya University (CX400), Kyushu University (ITO) and the supercomputer Fugaku at the RIKEN through the HPCI System Research Project (project ID: hp210105). Visualization of crystal structures was made with the VESTA software.95 The molecular dynamics trajectory in Fig. 8a was visualized using the VMD software.96 Plots were generated using python Matplotlib.97Notes and references
- C. Delmas, Adv. Energy Mater., 2018, 8, 1703137 CrossRef
.
- K. Kubota, J. Electrochem. Soc., 2015, 162, A2538–A2550 CrossRef CAS
.
- S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2010, 2, 710–721 CrossRef
.
- Y. Yuan, K. Amine, J. Lu and R. Shahbazian-Yassar, Nat. Commun., 2017, 8, 15806 CrossRef CAS
.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS
.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS
.
- T. A. Hewston and B. L. Chamberland, J. Phys. Chem. Solids, 1987, 48, 97–108 CrossRef CAS
.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS
.
- S.-M. Oh, S.-T. Myung, J. Hassoun, B. Scrosati and Y.-K. Sun, Electrochem. Commun., 2012, 22, 149–152 CrossRef CAS
.
- M. Ati, B. C. Melot, J.-N. Chotard, G. Rousse, M. Reynaud and J.-M. Tarascon, Electrochem. Commun., 2011, 13, 1280–1283 CrossRef CAS
.
- R. Tripathi, T. N. Ramesh, B. L. Ellis and L. F. Nazar, Angew. Chem., Int. Ed., 2010, 49, 8738–8742 CrossRef CAS PubMed
.
- S. Nishimura, M. Nakamura, R. Natsui and A. Yamada, J. Am. Chem. Soc., 2010, 132, 13596–13597 CrossRef CAS PubMed
.
- P. Barpanda, G. Liu, C. D. Ling, M. Tamaru, M. Avdeev, S.-C. Chung, Y. Yamada and A. Yamada, Chem. Mater., 2013, 25, 3480–3487 CrossRef CAS
.
- K. Ozawa, Solid State Ionics, 1994, 69, 212–221 CrossRef CAS
.
- S. Komaba, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Adv. Funct. Mater., 2011, 21, 3859–3867 CrossRef CAS
.
- W. J. H. Borghols, D. Lützenkirchen-Hecht, U. Haake, W. Chan, U. Lafont, E. M. Kelder, E. R. H. van Eck, A. P. M. Kentgens, F. M. Mulder and M. Wagemaker, J. Electrochem. Soc., 2010, 157, A582–A588 CrossRef CAS
.
- H. Xiong, M. D. Slater, M. Balasubramanian, C. S. Johnson and T. Rajh, J. Phys. Chem. Lett., 2011, 2, 2560–2565 CrossRef CAS
.
- E. Ferg, R. J. Gummow, A. de Kock and M. M. Thackeray, J. Electrochem. Soc., 1994, 141, L147–L150 CrossRef CAS
.
- Y. Sun, L. Zhao, H. Pan, X. Lu, L. Gu, Y.-S. Hu and H. Li, Nat. Commun., 2013, 4, 1870 CrossRef
.
- Y. Wang, X. Yu, S. Xu, J. Bai, R. Xiao, Y.-S. Hu, H. Li, X.-Q. Yang, L. Chen and X. Huang, Nat. Commun., 2013, 4, 2365 CrossRef PubMed
.
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed
.
- H. Che, S. Chen, Y. Xie, H. Wang, K. Amine, X.-Z. Liao and Z.-F. Ma, Energy Environ. Sci., 2017, 10, 1075–1101 RSC
.
- F. G. Will and S. P. Mitoff, J. Electrochem. Soc., 1975, 122, 457–461 CrossRef CAS
.
- A. K. Ivanov-Schitz and A. B. Bykov, Solid State Ionics, 1997, 100, 153–155 CrossRef CAS
.
- Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Chem. Mater., 2016, 28, 4821–4828 CrossRef CAS
.
- T. J. Udovic, M. Matsuo, A. Unemoto, N. Verdal, V. Stavila, A. V. Skripov, J. J. Rush, H. Takamura and S. Orimo, Chem. Commun., 2014, 50, 3750–3752 RSC
.
- H. Nguyen, S. Hy, E. Wu, Z. Deng, M. Samiee, T. Yersak, J. Luo, S. P. Ong and Y. S. Meng, J. Electrochem. Soc., 2016, 163, A2165–A2171 CrossRef CAS
.
- Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93 RSC
.
- S. S. Berbano, I. Seo, C. M. Bischoff, K. E. Schuller and S. W. Martin, J. Non-Cryst. Solids, 2012, 358, 93–98 CrossRef CAS
.
- I.-H. Chu, C. S. Kompella, H. Nguyen, Z. Zhu, S. Hy, Z. Deng, Y. S. Meng and S. P. Ong, Sci. Rep., 2016, 6, 33733 CrossRef CAS PubMed
.
- L. Zhang, K. Yang, J. Mi, L. Lu, L. Zhao, L. Wang, Y. Li and H. Zeng, Adv. Energy Mater., 2015, 5, 1501294 CrossRef
.
- H. Wang, Y. Chen, Z. D. Hood, G. Sahu, A. S. Pandian, J. K. Keum, K. An and C. Liang, Angew. Chem., Int. Ed., 2016, 55, 8551–8555 CrossRef CAS
.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S.-T. Hong and Y. S. Jung, Angew. Chem., Int. Ed., 2016, 55, 9634–9638 CrossRef CAS
.
- L. Zhang, D. Zhang, K. Yang, X. Yan, L. Wang, J. Mi, B. Xu and Y. Li, Adv. Sci., 2016, 3, 1600089 CrossRef
.
- E. A. Wu, C. S. Kompella, Z. Zhu, J. Z. Lee, S. C. Lee, I.-H. Chu, H. Nguyen, S. P. Ong, A. Banerjee and Y. S. Meng, ACS Appl. Mater. Interfaces, 2018, 10, 10076–10086 CrossRef CAS
.
- D. Zhang, X. Cao, D. Xu, N. Wang, C. Yu, W. Hu, X. Yan, J. Mi, B. Wen, L. Wang and L. Zhang, Electrochim. Acta, 2018, 259, 100–109 CrossRef CAS
.
- L. E. Rush Jr, Z. D. Hood and N. A. W. Holzwarth, Phys. Rev. Mater., 2017, 1, 075405 CrossRef
.
- H. Wang, M. Yu, Y. Wang, Z. Feng, Y. Wang, X. Lü, J. Zhu, Y. Ren and C. Liang, J. Power Sources, 2018, 401, 111–116 CrossRef CAS
.
- S. Xiong, Z. Liu, H. Rong, H. Wang, M. McDaniel and H. Chen, Sci. Rep., 2018, 8, 9146 CrossRef PubMed
.
- J. W. Heo, A. Banerjee, K. H. Park, Y. S. Jung and S.-T. Hong, Adv. Energy Mater., 2018, 8, 1702716 CrossRef
.
- A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, Nat. Commun., 2019, 10, 5266 CrossRef CAS
.
- T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, ACS Energy Lett., 2020, 5, 146–151 CrossRef CAS
.
- F. Tsuji, N. Masuzawa, A. Sakuda, M. Tatsumisago and A. Hayashi, ACS Appl. Energy Mater., 2020, 3, 11706–11712 CrossRef CAS
.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
-
G. Bergerhoff and I. D. Brown, in Crystallographic Databases, F. H. Allenet al. (Hrsg.), International Union of Crystallography, Chester, 1987 Search PubMed
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef
.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS
.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, Chem. Mater., 2008, 20, 1798–1807 CrossRef CAS
.
- Y. L. Page, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef
.
-
G. Simmons and H. Wang, Single Crystal Elastic Constants and Cal-culated Aggregate Properties: A Handbook, Massachusetts Institute of Technology Press, Cambridge, 1971, p. 370 Search PubMed
.
- C. Monroe and J. Newman, J. Electrochem. Soc., 2004, 151, A880–A886 CrossRef CAS
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- F. Tsuji, S. Yubuchi, A. Sakuda, M. Tatsumisago and A. Hayashi, J. Ceram. Soc. Jpn., 2020, 128, 641–647 CrossRef CAS
.
- W. G. Hoover, A. J. C. Ladd and B. Moran, Phys. Rev. Lett., 1982, 48, 1818–1820 CrossRef CAS
.
- J. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
-
P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, Oxford, 2006 Search PubMed
.
- L. He, F. Liu, G. Hautier, M. J. T. Oliveira, M. A. L. Marques, F. D. Vila, J. J. Rehr, G.-M. Rignanese and A. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 064305 CrossRef
.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17 CrossRef CAS
.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Chem. Mater., 2010, 22, 949–956 CrossRef CAS
.
- R. Koerver, I. Aygün, T. Leichtweiß, C. Dietrich, W. Zhang, J. O. Binder, P. Hartmann, W. G. Zeier and J. Janek, Chem. Mater., 2017, 29, 5574–5582 CrossRef CAS
.
- K. Takada, N. Ohta, L. Zhang, K. Fukuda, I. Sakaguchi, R. Ma, M. Osada and T. Sasaki, Solid State Ionics, 2008, 179, 1333–1337 CrossRef CAS
.
- H. Yokokawa, Solid State Ionics, 2016, 285, 126–135 CrossRef CAS
.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS
.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS
.
- Y. Zhu, X. Hea and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC
.
- S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12, 355–358 CrossRef CAS
.
- H. Tang, Z. Deng, Z. Lin, Z. Wang, I. H. Chu, C. Chen, Z. Zhu, C. Zheng and S. P. Ong, Chem. Mater., 2018, 30(1), 163–173 CrossRef CAS
.
- C. Monroe and J. Newman, J. Electrochem. Soc., 2005, 152, A396–A404 CrossRef CAS
.
- Z. Ahmad and V. Viswanathan, Phys. Rev. Lett., 2017, 119, 056003 CrossRef
.
- C. L. Tsai and H. Y.-P. Hong, Mater. Res. Bull., 1983, 18, 1399–1407 CrossRef CAS
.
- M. Jansen, Angew. Chem., Int. Ed., 1991, 30, 1547–1558 CrossRef
.
- R. Tegman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1463–1469 CrossRef CAS
.
- L. J. Miara, W. D. Richards, Y. E. Wang and G. Ceder, Chem. Mater., 2015, 27, 4040–4047 CrossRef CAS
.
-
R. J. D. Tilley, Defects in Solids, Wiley VCH, Hoboken, NJ, 10th edn, 2008 Search PubMed
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
-
I. D. Brown, The Chemical Bond in Inorganic Chemistry - the Bond Valence Model, Oxford University Press, New York, 2002 Search PubMed
.
- C. H. Rycroft, Chaos, 2009, 19, 041111 CrossRef
.
- B. Gao, R. Jalem, Y. Ma and Y. Tateyama, Chem. Mater., 2020, 32, 85–96 CrossRef CAS
.
- H.-K. Tian, R. Jalem, B. Gao, Y. Yamamoto, S. Muto, M. Sakakura, Y. Iriyama and Y. Tateyama, ACS Appl. Mater. Interfaces, 2020, 12, 54752–54762 CrossRef CAS PubMed
.
- N. Ohta, K. Takada, L. Zhang, R. Ma, M. Osada and T. Sasaki, Adv. Mater., 2006, 18, 2226–2229 CrossRef CAS
.
- A. Sakuda, H. Kitaura, A. Hayashi, K. Tadanaga and M. Tatsumisago, J. Electrochem. Soc., 2009, 156, A27–A32 CrossRef CAS
.
- L. Cao, T. Huang, Q. Zhang, M. Cui, J. Xu and R. Xiao, ACS Appl. Mater. Interfaces, 2020, 12, 57071–57078 CrossRef CAS PubMed
.
- Z. Ahmad and V. Viswanathan, Phys. Rev. Mater., 2017, 1, 055403 CrossRef
.
- J.-M. Doux, H. Nguyen, D. H. S. Tan, A. Banerjee, X. Wang, E. A. Wu, C. Jo, H. Yang and Y. S. Meng, Adv. Energy Mater., 2020, 10, 1903253 CrossRef CAS
.
- X. Feng, P.-H. Chien, Z. Zhu, I.-H. Chu, P. Wang, M. Immediato-Scuotto, H. Arabzadeh, S. P. Ong and Y.-Y. Hu, Adv. Funct. Mater., 2019, 29, 1807951 CrossRef
.
- H. Cao, M. Yu, L. Zhang, Z. Zhang, X. Yan, P. Li and C. Yu, J. Mater. Sci. Technol., 2021, 70, 168–175 CrossRef
.
- H. Gamo, N. H. H. Phuc, H. Muto and A. Matsuda, ACS Appl. Energy Mater., 2021, 4, 6125–6134 CrossRef CAS
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta07292g |
| This journal is © The Royal Society of Chemistry 2022 |