Protagonists and spectators during photocatalytic solar water splitting with SrTaOxNy oxynitride†
Craig
Lawley
 ab,
Zahra Pourmand
Tehrani
ab,
Adam H.
Clark
ab,
Zahra Pourmand
Tehrani
ab,
Adam H.
Clark
 a,
Olga V.
Safonova
a,
Olga V.
Safonova
 a,
Max
Döbeli
c,
Vladimir N.
Strocov
a,
Thomas J.
Schmidt
a,
Max
Döbeli
c,
Vladimir N.
Strocov
a,
Thomas J.
Schmidt
 ad,
Thomas
Lippert
abe,
Maarten
Nachtegaal
*a and
Daniele
Pergolesi
ad,
Thomas
Lippert
abe,
Maarten
Nachtegaal
*a and
Daniele
Pergolesi
 *a
*a
aPaul Scherrer Institute (PSI), CH-5232 Villigen, Switzerland. E-mail: daniele.pergolesi@psi.ch; maarten.nachtegaal@psi.ch
bETH Zürich, Laboratory of Inorganic Chemistry, CH-8093 Zurich, Switzerland
cETH Zürich, Laboratory of Ion Beam Physics, CH-8093 Zurich, Switzerland
dETH Zürich, Laboratory of Physical Chemistry, CH-8093 Zurich, Switzerland
eInternational Institute for Carbon-Neutral Energy Research (I2CNER), Kyushu University, 744 Motooka, 819-0395 Fukuoka, Japan
First published on 21st September 2021
Abstract
Oxynitrides have been shown to be promising visible light water splitting photocatalysts, but rapidly degrade under operating conditions. With a custom designed photoelectrochemical cell, we perform operando grazing incidence X-ray absorption spectroscopy measurements on the oxynitride semiconductor SrTaOxNy during photocatalytic solar water splitting. We show that the nature of the A-site (Sr) and its evolution during operation have large impacts on the overall stability and catalytic activity of the material, leading to an enriched BO2 (Ta(OH)/TaO(OH)) like surface. However, this usually beneficial effect with respect to increased surface hydrophilicity has complications for the efficiency of the photocatalytic process, as the OH and O(OH) intermediates formed are in competition between O2 generation and NOx species formation in the initial stages of operation. Operando characterisation of the evolution of the electronic structure of the photocatalyst proves to be an invaluable tool for the rational design and discovery of new and better performing materials.
Introduction
Independence from the reliance on fossil and nuclear fuels requires the sustainable production of green energy and chemicals. As an alternative, utilisation of solar energy is possible by several means: solar thermal applications,1 the direct conversion to electricity (photovoltaic),2 or storage in the form of chemical energy as solar fuels.3 One promising clean energy carrier and renewable fuel source is hydrogen harvested from photoelectrochemical (PEC) water splitting.4–6PEC water splitting requires the use of semiconductor (SC) photocatalysts that utilise solar light energy to generate electron/hole pairs. After reaching the surface, in contact with water, these charge carriers can be used to dissociate water molecules directly into molecular hydrogen and oxygen.7 Perovskite oxynitrides are a promising class of SC materials for solar light driven water splitting. These materials have the general formula ABO3−xNx (where A can be La, Sr, Ba, Ca, etc., and the B site: Ti, Ta, or Nb for example). The substitution of N into the O site of the precursor oxides affect the energy position of the band edges, reducing the band gap down to the visible light energy range.8 Moreover, in this class of compounds, the photogenerated electrons and holes, both possess enough energy to promote the hydrogen and oxygen evolution reaction, respectively.
The majority of studies to date focus on the characterisation of the photocatalytic properties of these materials in the form of powders,9–11 since powder development and optimisation is the primary way to device design and engineering. However, with powder samples, probing specific material properties is challenging. For example, the polycrystalline oxynitride powders do not provide well-defined surfaces to allow detailed studies of the solid–liquid interface, where the electrochemical reactions take place. The understanding of the catalytic process at the solid–liquid interface of oxynitride materials is therefore limited, as a result. A way to circumvent this limitation is the growth of thin films. By physical or chemical vapour deposition methods, it is possible to fabricate thin films with well-defined and atomically flat surfaces, therefore representing ideal model systems that allow the investigation of the surface and interface properties.
In this work, we present an operando study of the evolution of the photocatalyst semiconductor/water interface during photoelectrochemical solar water splitting using SrTaOxNy (STON) thin films. Grazing incidence X-ray absorption spectroscopy (GIXAS) coupled with modulation excitation (ME)-XAS were used to increase the surface sensitivity, whilst probing epitaxially grown STON thin films with a custom designed operando reactor cell. This technique and experimental setup allow us to probe, during operation conditions, the changes of the local chemical and geometric environment surrounding the A- and B-cations of perovskite oxynitrides near and at the solid–liquid interface. Due to the attenuation of X-rays by the aqueous electrolyte, it is not feasible to extend this study to the O and N anions, since the O 1s and N 1s edges are too low in energy (543.1 eV and 409.9 eV, respectively). Therefore, complimentary ex situ X-ray photoelectron spectroscopy (XPS) has been included to observe all four elements (Sr, Ta, O, and N) in their initial and final states. STON was chosen as it has been reported to be a promising visible light responsive photocatalyst material.12 There are also reports that STON is a possible ferroelectric.13 Various studies have also shown that ferroelectric polling can increase the photocatalytic activity.14–16 Therefore, STON is a representative material to study several enhancement techniques with the aim to improve and design better performing materials. With this experimental strategy, we are able to show that it is possible to achieve a better understanding of the physicochemical processes occurring at the oxynitride–liquid interface, leading to a degradation of the photocatalytic activity. Our findings can be of great importance for the rational design of stable oxynitride SC's for solar water splitting.
Results and discussion
Photoelectrochemical water splitting
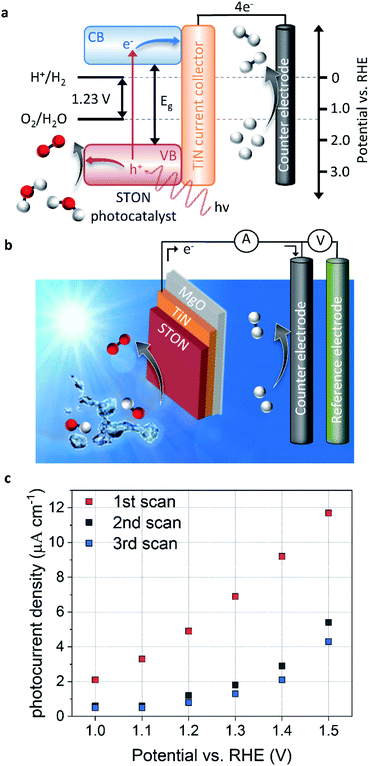
The splitting of water into molecular H2 and O2 is an energetically unfavourable reaction. It requires a standard Gibbs free energy change of +237.2 kJ mol−1, which also corresponds to a potential of 1.23 eV per electron. Moreover, for both half reactions of the solar water splitting process to proceed, that is the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER), first the kinetic overpotentials must be overcome. Therefore, a suitable SC material for visible light PEC water splitting should have (a) a band gap in the range of 1.6–2.4 eV to sufficiently utilise the solar spectrum and drive the reactions, and (b) energy position of the band edges appropriately aligned with respect to the HER and OER redox potentials.As mentioned above, a number of oxynitride perovskite materials possess these characteristics, making them ideal candidates for PEC solar water splitting.8,9,11,17,18 Thin films of these materials provide excellent model systems to probe the physical and chemical evolution of the surface of the SC, in contact with water. Fig. 1 shows the energy diagram schematic for PEC water splitting using a STON thin film as a light harvesting SC photocatalyst and TiN as the current collector. In Fig. 1a, we see that upon light irradiation with photons with an energy (hv) > 1.23 eV, the photon is absorbed promoting a photoexcited electron (e−) from the valence band (VB) to the conduction band (CB). The photoelectrons travel via a TiN current collector layer and external circuit where they are involved in the HER using a platinum counter electrode (cathode). The generation of a photoelectron leaves behind a photogenerated electron–hole (h+) which migrates towards the surface of the SC oxynitride where it is then involved in the OER.
Fig. 1b shows the three-electrode configuration used in this work, where the STON SC photocatalyst is used as a photoanode to study the OER, a platinum counter electrode used for the HER half reaction, and a Ag/AgCl reference electrode is used to control the applied potential on the working electrode. The electronic current between the working and counter electrodes is called the photocurrent and the photocurrent is proportional to the amount of molecular H2 and O2 produced.
The photocurrent is defined as the current response under light conditions minus the current response under dark conditions. More in-depth experimental details are included in the corresponding methods section. Fig. 1c shows the PEC performance of the STON oxynitride thins. For sake of clarity, the dark current has been subtracted (ESI Fig. 2†). The initial photocurrent reaches a photocurrent density of ca. 12 μA cm−1 at 1.5 V vs. reversible hydrogen electrode (RHE). This value is in line with previous reports on oxynitride thin films using the bare SC material without surface decoration with co-catalyst, which dramatically facilitate hole extraction. On the one hand, the N content of textured thin films is typically lower than the stoichiometric value that can be obtained with powder samples.12 This reduces the thin films photo-response to visible light illumination. On the other, the thin films possess atomically flat surfaces compared to the corresponding oxynitride powders. Therefore, the surface area is ca. 20 times smaller than it would be in their powder forms. It has been noted that direct comparison of the PEC performances favours the oxynitride powders due to their increased surface area.19 However, due to the better crystalline quality and the grain morphologies, the oxynitride thin films can show improved charge carrier separation and the subsequent migration to the surface to be consumed in the OER.
However, after successive measurements (potentiodynamic sweeps) the material shows significant degradation in its initial performance. The stabilised photocurrent density shows values ca. 40% of its initial value. The sudden and large degradation in performance is a huge hindrance for the application of a material that initially seems quite promising. Some studies have looked at ways of improving the performance and long-term stability of STON10,20,21 by doping constituent elements and/or decorating the surface with co-catalyst nanoparticles. However, probing the physicochemical evolution of the surface under operation conditions will provide insight into what physical and chemical processes occur at the surface during the OER and therefore, allow a rational design of stable STON.
Oxynitride thin films
The STON thin films were fabricated using a modified pulsed laser deposition technique described in previous works,22 followed by post annealing in NH3 for 1 hour. The epitaxial oxynitride STON films were deposited on titanium nitride (TiN) coated magnesium oxide single crystal substrates (001) oriented. Rutherford back scattering (RBS) and elastic recoil detection analysis (ERDA) determined the chemical compositions of the STON thin films as Sr0.94Ta1.06O2.80N0.31. The experimental uncertainties for Sr and Ta are ±2% (RBS) and ±7% for O and N (ERDA). The full results have been included in ESI Fig. 1 and ESI Table 1.† The O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio of ca. 10 is in line with previous examples of highly ordered oxynitride thin films, since there is a trade-off between overall nitrogen content and crystalline quality,23 where films with larger N contents tend to be more disordered. Atomic force microscopy and X-ray reflectivity measurements have been included in ESI Fig. 3.†
N ratio of ca. 10 is in line with previous examples of highly ordered oxynitride thin films, since there is a trade-off between overall nitrogen content and crystalline quality,23 where films with larger N contents tend to be more disordered. Atomic force microscopy and X-ray reflectivity measurements have been included in ESI Fig. 3.†
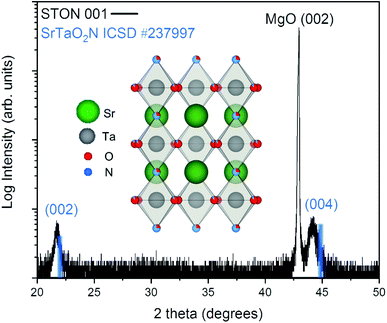
From Fig. 2 it can be seen that the TiN buffer layer grows (001) epitaxially oriented on the MgO substrate. The (002) reflex of TiN is visible as a shoulder on the left-hand side of the peak of the substrate (see ESI Fig. 4†). Fig. 2 also shows that STON grows epitaxially on the TiN buffer layer22 with the (hkl) reflexes (002) and (004) appearing at 2θ values of ca. 21.8° and 44.2°, respectively. The angular position of the (00l) reflexes of the perovskite SrTaO2N have been marked in blue as reference from the Inorganic Crystal Structure Database (ICSD).
There is very good crystallographic matching between the face centered cubic structure of MgO and TiN. The lattice parameters are ca. 4.21 and 4.24 Angstrom, respectively. In the pseudo-cubic approximation, the lattice parameter of SrTaO2N is about 4.03 Angstrom. There is a relatively large lattice mismatch of ca. 4.7%, however, the presence of interfacial misfit dislocations, the most common mechanism of stress relaxation in thin films, can easily account for the epitaxial growth of STON on TiN, by releasing part of the strain.
Both the 002 and 004 reflexes of the STON thin film are slightly shifted to lower 2θ values compared to the SrTaO2N reflexes. This is due to the combined effect of a difference in N content to the stoichiometric reference and the crystalline constrain (lattice mismatch between the substrate and film) induced by the TiN-coated MgO substrate. The perovskite structure of STON remains stable, within a large range of N content. However, the cell parameters can be significantly affected since the N content affects the Ta–O–Ta dihedral bond angle and ultimately, the overall distortion of the cell. To characterise how the OER modifies the physicochemical properties of the surface of our STON films, we first used XPS to compare changes of the oxidation state of all four elements before and after the photoelectrochemical reaction (PECR).
X-ray photoelectron spectroscopy
The XPS spectra for all four elements are shown in Fig. 3, for peak fitting analysis the reader can refer to ESI Fig. 5 and the ESI tables.†Fig. 3a shows the carbon signals that arise due to adventitious carbon, present during the ex situ transfer of the samples. After PEC, the intensity of the main peak reduces suggesting the oxidation/loss of the carbon-based surface contaminates after exposure to the electrolyte and/or X-ray beam. The shoulder features result from C–O and O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O like environments. Although, the intensities of the main peak reduce in intensity after PEC, suggesting that the total number of C based species are reduced after PEC, the peak fit suggest that the shoulder C–O contribution increases after PEC, likely due to oxidation during the PEC reaction. With respect to oxygen, after PEC, the O 1s spectra (Fig. 3b) exhibits a large increase in the intensity of the main peak and shoulder feature(s). The shoulder feature is observable on the high-energy side of the asymmetric O 1s lattice peak at ca. 531.5–534 eV. It is likely in reality that there exists a number of O based chemical environments (lattice O, SrO, C–O, OH and H2O). Trying to estimate these environments would produce a high degree of uncertainty in the peak fit models. However, peak fitting suggests a minimum of two chemical environments likely associated with chemisorbed OH and/or H2O species.
O like environments. Although, the intensities of the main peak reduce in intensity after PEC, suggesting that the total number of C based species are reduced after PEC, the peak fit suggest that the shoulder C–O contribution increases after PEC, likely due to oxidation during the PEC reaction. With respect to oxygen, after PEC, the O 1s spectra (Fig. 3b) exhibits a large increase in the intensity of the main peak and shoulder feature(s). The shoulder feature is observable on the high-energy side of the asymmetric O 1s lattice peak at ca. 531.5–534 eV. It is likely in reality that there exists a number of O based chemical environments (lattice O, SrO, C–O, OH and H2O). Trying to estimate these environments would produce a high degree of uncertainty in the peak fit models. However, peak fitting suggests a minimum of two chemical environments likely associated with chemisorbed OH and/or H2O species.
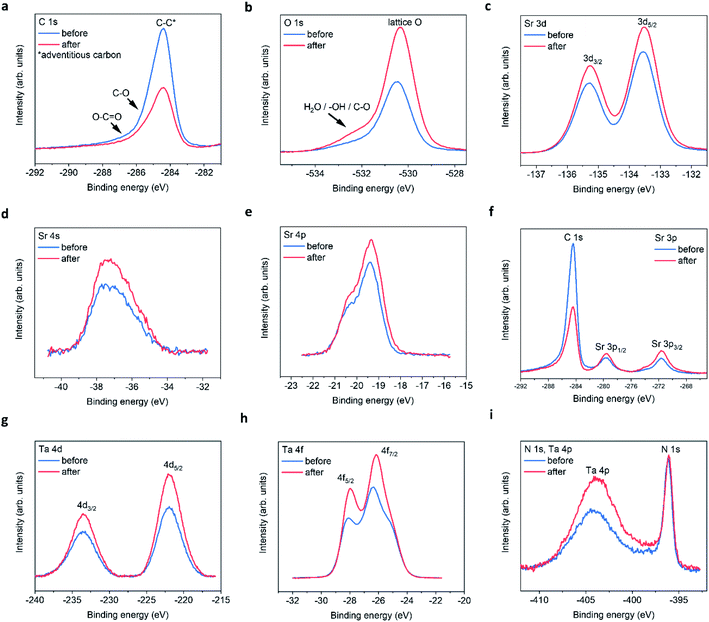 | ||
| Fig. 3 STON thin film XPS spectra before and after PEC. (a) C 1s, (b) O 1s, (c) Sr 3d, (d) Sr 4s, (e) Sr 4p, (f) Sr 3p, (g) Ta 4d, (h) Ta 4f, (i) N 1s and Ta 4p edges. | ||
In addition, after PEC the integrated area under of the shoulder increases, suggesting an increase in hydrophilicity of the surface. The increased O content suggests that any lattice vacancies generated at the surface/surface layers are self-healed under OER conditions by oxygen based species.24
For the Sr 3d spectra (Fig. 3c), peak fitting suggests that the epitaxial STON thin films as grown exhibit a preferential AO (SrO) termination, also noted for various perovskites using low energy ion scattering (LEIS)25–29 and XPS.29–31 Under ambient conditions/aqueous environment, Sr should be covered in OH adsorbates. After deprotonation (slow step) the OER would proceed, leaving vacant oxygen cavity on Sr, assuming the traditional 4-step mechanism for the OER.32 However, SrO is partially soluble in water to form ionic Sr2+ and 2OH−. Therefore, dissolution and leaching of Sr2+ into the electrolyte would be expected.33 Especially, in an alkaline medium such as NaOH/H2O with a pH of 13.
After PEC, the peak fitting suggests a large decrease in the SrO content at the surface and an overall increase in peak area and intensity for the remaining Sr XPS spectra (Fig. 3c–f). It has previously been shown, that an increase in XPS peak intensity can result from Sr segregation/accumulation34,35 as well as, with increased doping concentrations.36 Peak intensity/area increases are also observed due to Sr particle/Sr surface species formation.34,35 Therefore, the increase in Sr signal in this work is likely due to the loss of SrO and the apparent enrichment of the Sr lattice contribution.
Fig. 3g–i, include the Ta 4d, Ta 4f, and Ta 4p edges respectively. From peak fitting the Ta 4d spectra suggests one binding environment, which is the lattice Ta contribution. After the PECR, this intensity and area of the Ta 4d peak increases as seen for the lattice Sr contributions. This suggests that after the loss of SrO the underlying lattice Ta appears enriched by XPS. The Ta 4f spectra (Fig. 3h) exhibits two peaks due to the Ta 4f5/2 and 4f7/2 contributions. The peak fitting analysis suggests that there are two Ta binding environments for both the 5/2 and 7/2 peaks corresponding to TaOx and TaOxNy like environments (ESI Fig. 5†) which, after the PECR, the peak contributions of TaOxNy decrease and those of TaOx increase. Again, like the O 1s spectra, suggesting a slight loss of nitrogen and an increase in the overall oxygen content at the surface/surface layers of the thin film. The energy positions of the peaks suggest a slight reductive shift by ca. +0.15 eV. However, the Ta 4d spectra in Fig. 3d show an increase in the FWHM and peak intensities, but no shift in energy position or peak separation. The shift in the Ta 4f spectra may then also be related to the changing O/N, resulting in disorder and differences in the charge transfer between the Ta 4f final states and the O 2p/N 2p orbitals. This then shifts the mid gap f band higher towards the CB or above,37 leaving the 4d core states unchanged. The increase in intensity observed could be a result of apparent lattice Ta enrichment due to the O/N vacancy generation exposing the subsurface B sites.27 It could also be a result of SrO leaching, also exposing the subsurface Ta on average. Since Sr is more soluble than Ta and, it has been shown that Ta is passive in alkaline electrolytes with concentrations 2.5× stronger than used in this work.38
The electronic configuration of Ta0 is [Xe] 4f145d36s2 and that for Ta5+ should then consist of [Xe] 4f14+. This may then explain, the changes in charge transfer and hybridisation between the Ta 4f and O/N 2p atomic orbitals as observed in this work and suggested by the peak fitting analysis. This is also interesting as the f orbitals are typically ignored when considering the density of states (DOS) using density functional theory (DFT) calculations for materials due to the complexity, time and cost involved in the computation of the f states.
The Ta 4p3/2 is observed as a broad peak at ca. 404–405 eV (Fig. 3e). However, the Ta 4p3/2 spectrum overlaps with the N 1s signal in the energy region at ca. 402–408 eV which contains the N 1s information regarding interstitial and/or chemisorbed NO, NO2, NO3 and N2, making the peak analysis difficult. The N 1s Ta–N lattice signal can be seen as a sharp peak at ca. 396.1 eV. After the PECR, the broad peak in the region, which contains the convoluted N 1s and Ta 4p3/2 signals increases significantly suggesting an increase in the number of electronically decoupled N states. As well as, the apparent lattice Ta enrichment as seen previously.
At ca. 407.5 eV there is a small but obvious increase in intensity belonging to a different Ta/N binding state, which is likely a contribution due to chemisorbed NO3 according to literature reports (ESI Table 5†). It is therefore assumed that NO and NO2 would contribute to the overall increased intensity/peak area observed, where the O(OH) OER intermediate formed during the reaction likely oxidise the NOx species in competition with O2 evolution. This would reduce the overall efficiency of the material, and chemisorbed NOx species would occupy possible active sites. This, in conjunction with the surface reconstruction after the loss of SrO and the changing N/O content, could explain the large degradation in initial photocurrent observed. Likely hampered by side reactions and charge recombination.
Clearer evidence of NOx formation for the oxynitride LaTiOxNy where Ta does not convolute the N 1s signal can be seen by XPS (ESI Fig. 5†). We would like to focus our discussion on the PEC nitrogen evolution reactions at the surface of the oxynitride SC, since the literature on this topic is scarce. Although, this process seems to have important consequences on the oxygen and hydrogen evolution half reactions.
Photocatalytic nitrate formation on Ti dioxide surfaces irradiated by UV or sunlight irradiation under atmospheric N2 and O2 has been discussed by Yuan et al.39 Where the photogenerated holes on the Ti SC surface catalyse the intermediary NOx species according to the following reactions given by eqn (1) and (2):
| N2 + O2 → 2NO | (1) |
| N2 + 2H2O + 4h+ → 4H+ + 2NO | (2) |
Dai et al.40 recently looked at the nitrogen oxidation reaction (NOR) catalysed by Fe/Co spinel oxides in alkaline electrolyte. Where they show that adsorbed N2 is oxidised to intermediate NOx species by the adsorbed OH and the OER intermediate O(OOH) according to eqn (3) and (4):
| N2 + 2OH− → N* + NO + H2O + 2e− | (3) |
| N* + 2OH− → NO + H2O + 2e− | (4) |
| NO + 2OH− → NO2 + H2O + 2e− | (5) |
| NO2 + 2OH− → NO3− + H2O + e− | (6) |
With the aid of theoretical calculations, the authors note that Co shows increased hybridisation with the O 2p states, which aids in the stabilisation of OH− adsorption. This superficial CoO(OH) enriched surface layer has a beneficial effect on the OER for the oxides.40,41 However, in the presence of surface nitrogen based species, the stabilised CoO(OH) contribute to both the NOR and OER.40
Kato and Kudo42 looked at numerous tantalate oxide photocatalysts, and the authors observed nitrate reduction under UV irradiation in an aqueous environment. Where nitrate forms intermediate nitrite, dinitrogen and ammonia, even in the absence of a co-catalyst or reducing agents. The authors proposed the following mechanisms shown in eqn (7)–(10):
| NO3− + 2H+ + 2eCB− → NO2− + H2O | (7) |
| NO2− + 7H+ + 6eCB− → NH3 + 2H2O | (8) |
| 2NO3− → 2NO2− + O2 | (9) |
| 2NH3 + 6hVB+ → N2 + 6H+ | (10) |
Wei et al.43 recently reported increased photocatalytic activity for nitride reduction on Ni2P modified tantalum nitride and tantalum oxynitride (Ta3N5 and TaON, respectively). Where the photogenerated holes in the VB of the two materials are involved in the water oxidation reaction (eqn (12)) and, the photogenerated electrons in the CB transfer to the Ni2P states where they are involved in the photocatalytic reduction of NO3−. For a detailed overview on the role of N in electrocatalysis, the readers are directed to the work by Rosca et al.44
The photocurrent is proportional to stoichiometric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2/O2 generation, according to the two half reactions of the water splitting process on a SC photocatalyst (eqn (11) and (12)).
1 H2/O2 generation, according to the two half reactions of the water splitting process on a SC photocatalyst (eqn (11) and (12)).
| 4H+ + 4eCB− → 2H2 | (11) |
| 2H2O → 4hVB+ + O2 + 4H+ | (12) |
As the potential increases, the forward reactions for O2 generation dominate since the nitrogen content at the surface is limited, compared to the high OH− content in the alkaline electrolyte. Once the nitrogen species desorbs from the surface, the OER could proceed on the now vacant active site and/or the adsorbed intermediates would no longer contribute to N2/NOx formation in competition. As shown by the increase in photocurrent density as seen in Fig. 1c and 6b. However, the above-mentioned changes for STON result in a surface reconstruction during the initial stages of operation, reducing its long-term performance.
As previously discussed, the CB of STON is primarily comprised of Ta 5d states (no f state information). Considering the changes in the disorder, especially the local disorder surrounding the Ta cations, this would result in generation of defect Ta states at/near to the CB minimum or, even mid bandgap defect states. These defect states would trap the photogenerated electrons, leading not only to charge recombination, as previously discussed but also, contribute to the reduction of the generated nitrate species (eqn (7) and (8)) as suggested by the works by Kato and Kudo (2002),42 Wei et al. (2020)43 and the XPS analysis in this work.
The CB minimum and VB maximum of STON incorporate not only the redox potentials of the OER and HER, but also those for NO3−/NH4+ (0.88 V), NO3−/HNO2 (0.94 V) and NO3−/N2 (1.24 V) at pH = 0, vs. NHE.43 This implies that all photogenerated electrons consumed in these competing reactions would no longer contribute to the HER at the Pt counter electrode (Fig. 1a), reducing the potential magnitude of the photocurrent density. The photogenerated holes that do not recombine would then primarily contribute to water oxidation (eqn (12)).
The surface nitrogen that remains chemisorbed in the form of molecular N2/NOx would likely, (a) occupy possible O2 generation sites, effectively blocking the site until it desorbs or, (b) reduce or oxidise to form additional chemisorbed N2/NOx species as suggested by XPS. The apparent mechanism is likely then associated with one or more of the previously discussed eqn (1)–(10). Since the electron density surrounding Ta is conserved, the nitrogen vacancies generated are then likely healed by the OER intermediate adsorbates.24 The changing stoichiometry, tensile strain and changes in the charges of the surface layer result in a surface reconstruction that would affect the surface binding energies of the intermediate products produced during OER conditions (*OH, *O, *OOH). The intermediates that adsorb too weakly or too strongly will reduce the overall kinetics and, increase the overpotential of the OER.24,45
To conclude, OER and HER remain the dominant reactions, however the initial reconstruction and the following competitive reactions, limit the overall efficiency of STON compared to its initial performance. The XPS analysis of the initial and final state of the STON photocatalyst suggest that STON suffers from a surface degradation and reconstruction, which lead to a dramatic decrease in photocurrent (Fig. 1c). This process involves (a) loss of surface terminated SrO, (b) enrichment of lattice Sr and Ta, (c) change in hybridisation/charge transfer between the N and O 2p, (d) oxidation of NOx species in competition with O2 generation, and (e) increase in hydrophilicity (oxygen content at surface).
Next, we explore the effect of several external stimuli (applied potential and light) on the surface of the oxynitride SC under oxygen evolution reaction conditions by operando XAS in liquid phase.
Operando reactor cell
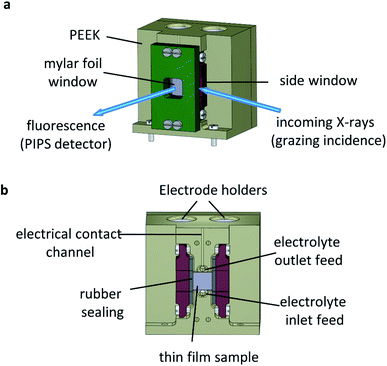
The operando XAS measurements were performed in a custom-built reactor cell designed and fabricated at the Paul Scherrer Institute for the specific purpose of operando GIXAS in aqueous electrolytes for thin films. The cell design is schematically depicted in Fig. 4.The cell is made of polyether ether ketone (PEEK), a thermoplastic with high mechanical and chemical stability, allowing the use of most common acidic/alkali based aqueous electrolytes. The X-ray beam illuminates the surface of the sample at grazing angle and the fluorescent signal is detected as a cone along the surface normal, as shown in Fig. 4a. The surface sensitivity that can be achieved in grazing angle geometries considering the incident energy of the X-rays is ca. 3 nm.46 The cell is designed to hold thin films grown onto standard substrate sizes. Typically, 10 × 5 mm or 10 × 10 mm with a substrate thickness of 0.5–1.0 mm. The window material used is an optically clear Mylar foil (t = 0.19 mm), which allows the transmission of visible light onto the sample whilst also allowing >90% X-ray transmission at the energy ranges used in this work (ESI Fig. 6†). The use of Mylar foil as a window provides flexibility in enabling visible light to shine onto the sample whilst detecting the fluorescence signal, as well as allowing grazing incidence angles of <1° onto the sample surface in an aqueous environment. Synthetic rubber pieces clamped into position seal the Mylar foil window to prevent leaks (Fig. 4b). On the backside (ESI Fig. 7†) are two threaded openings, allowing the use of an external electrolyte reservoir as well as connecting a peristaltic pump or a syringe pump system to circulate the electrolyte as required. Alternatively, the cell can use an internal electrolyte reservoir situated behind the sample. The cells' internal reservoir can house both the counter and reference electrodes.
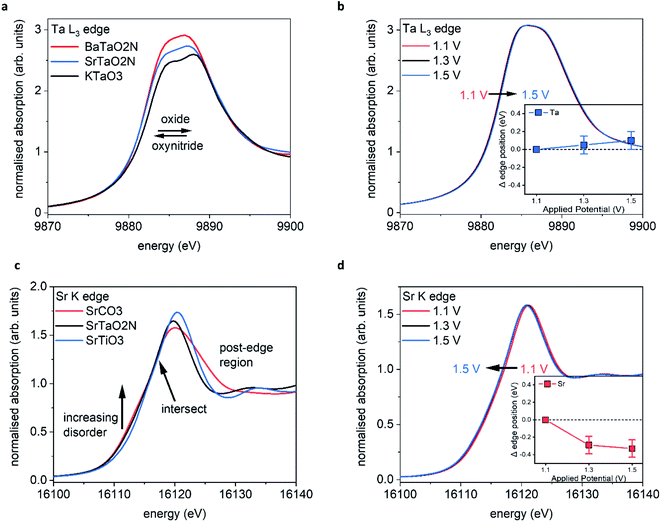
Tantalum L3 edge XANES
Fig. 5a shows the XANES spectra recorded ex situ at the Ta L3 edge (E0 = 9881 eV) for BaTaO2N (BTON), STON, and KTaO3 powder samples. These measurements are used as reference to understand the corresponding GIXAS measurements performed during OER using the STON thin films, as shown in Fig. 5b. We use KTaO3 as a reference for this work since the parent oxide of STON, which would be Sr2Ta2O7, possesses a different crystal structure, therefore, the electronic structure would differ significantly. KTaO3 has a cubic crystal structure like SrTaO2N and BaTaO2N. Moreover, in all three cases Ta exists in the 5+ oxidation state, therefore allowing a sensible comparison of their electronic structures (Fig. 5a). We can see that, compared to KTaO3, for the oxynitride powders there is a shift of the edge position (E0) to lower energies by ca. 0.5 eV ± 0.1. This shift of the absorption edge is not due to the reduction of Ta but rather due to the downward shifting of the CB minimum of STON and BTON compared to KTaO3. Since, the CB is comprised of Ta 5d orbitals for all three materials.47 The substitution of nitrogen into the oxygen sites affects the Ta–O/N–Ta dihedral bond angle and the overall electronegativity of the anions. Both these effects can explain the downward shift in energy of the CBM.48,49The increase in intensities for the XANES spectra most likely result from the nitrogen substitution. In the cubic perovskite oxide KTaO3, the Ta–O–Ta angle is 180°. In the orthorhombic oxynitride perovskites, the dihedral bond angle is distorted and its value depends on the total N content and the size of the A cation. Therefore, with the lowering of symmetry and increased p–d orbital mixing, the 2p–5d transition will be more favourable and reflected in the relative intensities of the peaks.
Fig. 5b shows the operando XANES measurements performed on STON thin films during the chronoamperometry measurements (measuring the photocurrent at a fixed applied potential over time). We can see that for all applied potentials, there is no significant change in the spectral shape or in the edge position, indicating no change in formal oxidation state. When inspecting the magnified inset, there are small shifts in the edge positions to higher energies when moving from 1.1 to 1.3 and 1.3 to 1.5 V vs. RHE, corresponding to ca. 0.05 and 0.1 eV respectively.
Baring in mind the experimental uncertainties with respect to the composition provided by RBS and ERDA (Sr0.94Ta1.06O2.80N0.31), Ta4+ defect centers should exist which are oxidised to Ta5+ during the OER. However, it has previously been shown that for various compounds which all contain formally Ta5+ species, the edge position can vary by ca. 1.4 eV (ref. 50) due to the variation of the electronic structure and the relative position of the Ta 5d states. Therefore, the small shifts seen in edge position for Ta are unlikely to be oxidation of Ta at the surface. Even though oxidation states are often valid interpretations due to the correlation between formal oxidation state and edge position,51–53 the changes shown here are first, within error and second, any small change is likely due to the slight loss of lattice nitrogen and/or the possible formation of NOx species at the surface of the STON thin film as suggested by the XPS analysis in this work. As previously discussed, upon partial N loss in the surface layer, it will also result in a local loss of hybridisation between the Ta 5d and the N 2p states at the VB maximum (Fig. 5c). As a result, a more ‘oxide-like’ electronic structure forms at the surface as the potential is increased.
It is reasonable to assume that Ta will tend to fulfil its full coordination sphere upon loss of N by replacing with O under OER conditions.24 This would also explain why there is no significant change in the spectral shape for Ta. There is instead, a slight shift to higher energy of the absorption edge. However, the replacement of N3− with O2− should see a reductive shift to lower energy for Ta. This again suggests that the charge around Ta is stabilised, like for Ti in LaTiOxNy,46 but due to slight changing O/N concentrations at the surface, the Ta octahedra undergo a slight disorder. Since the CBM is comprised of delocalised Ta 5d states in STON,54 the resulting changes in the O/N–Ta–O/N dihedral bond angle and degree of hybridisation, affect the conduction band minimum position.49
Strontium K edge XANES
Fig. 5c shows the XANES spectra measured at the Sr K edge (E0 = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 eV) for Sr containing oxide (SrTiO3), carbonate (SrCO3) and oxynitride (STON) powders. Small changes in the post edge region and in the intensities of the main peak (16
105 eV) for Sr containing oxide (SrTiO3), carbonate (SrCO3) and oxynitride (STON) powders. Small changes in the post edge region and in the intensities of the main peak (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120–16
120–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 eV) can be observed and are due to the differences in coordination environment surrounding the Sr cations.55 There are also changes of intensity of a broad shoulder in the pre-edge region at ca. 16
140 eV) can be observed and are due to the differences in coordination environment surrounding the Sr cations.55 There are also changes of intensity of a broad shoulder in the pre-edge region at ca. 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108–16
108–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 115 eV. Pre edge features relate to changes in the local geometry and degree of disorder surrounding the absorbing element of interest. Therefore, as one moves away from a perfect octahedral environment the pre-edge intensities increase56 and this is observed from the perfect octahedral environment surrounding Sr in SrTiO3, to the increasingly disordered octahedra in SrTaO2N and SrCO3, respectively.
115 eV. Pre edge features relate to changes in the local geometry and degree of disorder surrounding the absorbing element of interest. Therefore, as one moves away from a perfect octahedral environment the pre-edge intensities increase56 and this is observed from the perfect octahedral environment surrounding Sr in SrTiO3, to the increasingly disordered octahedra in SrTaO2N and SrCO3, respectively.
Fig. 5d shows the operando XANES measurements performed on the STON films during the chronoamperometry measurements as described previously. Unlike for the Ta B site, here we observe a more significant shift in the edge position due to an increase of electron density on Sr2+, with increasing the applied potential from 1.1 to 1.3 V vs. RHE. Increasing the potential further from 1.3 V to 1.5 V does not show any further significant modification of either the local coordination or electronic structures around the Sr cations. The observed shift in edge position with potential is not constant, unlike observed for Ta.
Many of these oxides and oxynitride perovskites tend to typically exhibit AO (SrO) surface terminations25,27,57 rather than BO2 (TaO2). As previously discussed, a Sr/SrOx surface initially covered by oxygen adsorbates, would then initially contribute to overall O2 generation.47 As the potential increases to 1.3 V, the Sr starts to reduce (Fig. 5d) likely associated with the decoupling of the OER intermediates leaving the adsorption site on Sr vacant47 before further adsorption.
However, the degradation in the initial performance of STON and the XPS and XAS results, suggests these changes on Sr are permanent and detrimental. When changing the applied potential from 1.3 to 1.5 V, we see no significant change, except an overall further reductive shift albeit, at a reduced magnitude (Fig. 5d inset) within error. This observation could be explained by the earlier discussion regarding the deprotonation of Sr as the overpotential determining step (ODS). As the potential increases the majority of the Sr species reduce, followed by Sr/SrO/SrOH leaching. This disorder would also lead to defect Ta 5d states near the CBM which will then trap electrons,58 leading to charge-recombination.59 This, in conjunction with changes seen for Sr and the generation of N species in competition with O2 generation, can explain why there is unusually large degradation in the initial photoelectrochemical performance of STON before the material stabilises.
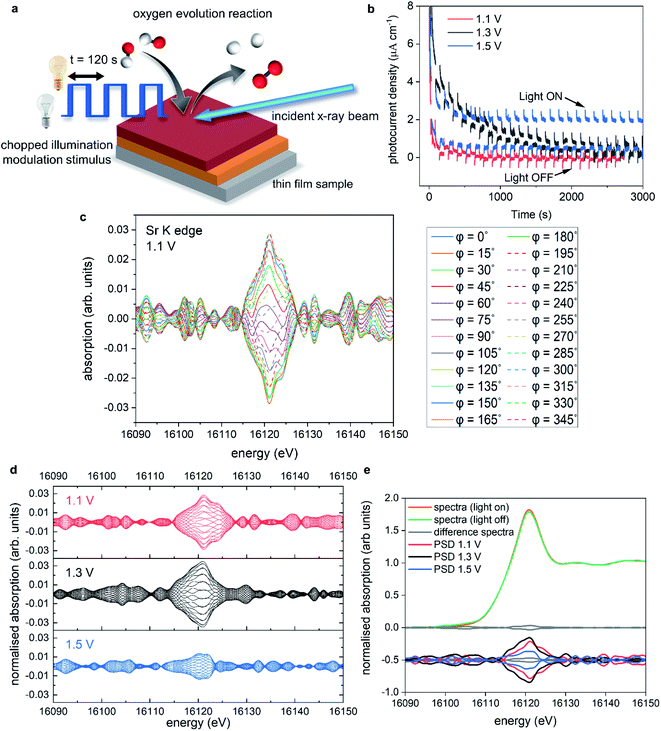
Modulation excitation X-ray absorption spectroscopy
In a different and complementary experimental strategy, we performed modulation excitation XAS (ME-XAS) to monitor the real time effects of the chemical modification of the surface using light as the external stimulus. The description of the experiment can be seen in Fig. 6a, where the thin film sample is stimulated by periodic modulation of light (chopped illumination) whilst time resolved XAS measurements are performed and data collected simultaneously during operation conditions at different, fixed potentials. Spectral changes induced by external stimuli (light in this case) are often small and/or prone to overshadowing by noise and background signals due to the experimental set-up.60 One can improve the signal-to-noise ratio by averaging data sets over several modulation periods. Furthermore, improvements in signal-to-noise ratio can be achieved through analysis of ME-XAS with phase sensitive detection (PSD).61–64 PSD converts time-resolved XAS data into a set of phase (φPSD) resolved data akin to a digital lock-in amplifier, enhancing the sensitivity of the ME-XAS experiment to spectral responses that match the frequency of the chopped light stimulus. More information on the PSD approach is included in the ESI Discussion.†Fig. 6b shows the chronoamperometry measurements at 1.1, 1.3, and 1.5 V vs. RHE where the incident light was modulated with 120 second periods (60 seconds on, 60 seconds off). Fig. 6b has been adapted for sake of clarity, where the photocurrent spikes (labelled light ON/OFF), are minimised. At 1.1 V, the photocurrent response is limited, but as the potential is increased further the photocurrent response also increases, as expected. However, at 1.3 V there is a large increase in the dark current response compared to 1.1 V. This increase degrades over time, before minimising after ca. 3000 s. When the potential is stepped to 1.5 V, there is an initial increase in the dark current response, which stabilises ca. 1/3 faster than at 1.3 V. There is also an overall increase in the stabilised dark current response compared to 1.1 and 1.3 V. These increases in the dark current at 1.3 V also coincide with the changes seen in the operando XAS data measured at 1.3 V, with the increase of electron density on Sr, resulting in increased overpotentials.
Fig. 6c shows, as an example, the PSD data analysis of data acquired at the Sr K edge for STON measured at 1.1 V. The benefit of PSD is the significantly enhanced signal-to-noise ratios, as it contains primarily only the signals from the changes due to the external light stimulus,65,66 while spurious effects from inactive species, spectators and noise are filtered out.
Fig. 6d includes the phase resolved spectra for Sr measured at 1.1, 1.3, and 1.5 V in red, black and blue, respectively. Not only can we see that there are small changes due to stimulus with light, but there is also a potential dependence. The spectra collected at 1.5 V show decreased sensitivity (smaller differences) due to the modulated light stimulus compared to 1.1 and 1.3 V. Fig. 6e shows an example of averaged spectra collected under illumination and dark conditions at one potential, along with the difference of the two plots shown as a solid grey line and the PSD spectra shown below.
Upon irradiation with light, photons with sufficient energy are absorbed; generating electrons and electron–hole pair charge carriers. The charge carriers are subsequently consumed in the water splitting process or recombine. The promotion of electrons from the valence band to the conduction band will induce small changes in the overall electronic system. This is reflected by the change in intensity of the Sr K-edge main peak under illumination (Fig. 6e).
We saw for the XANES (Fig. 5d) that when the Sr species reduce, there is a gain of electron density surrounding Sr with applied potential. The electronic configuration for Sr should reflect [Kr] 5s2 and that for oxidised Sr2+ represented by [Kr]. Therefore, as Sr reduces with applied potential, one would expect the lower lying energy 5s orbitals to be partially filled compared to the 4d states, according to Hund's rule. Typically, the intensity, especially in the case of L edges, is assumed to be related to holes in the d-band. Therefore, an oxidised species with electron–holes in the d-band would typically exhibit larger intensity of that of a more reduced species with a filled d band.67 The Sr K edge transition includes dipole s to p transitions like the L edges previously mentioned, however, it also includes quadrupole transitions s > d and p > f, complicating the interpretation further. Especially, as these quadrupole transitions should be forbidden due to selection rules. However, due to disorder and p–d orbital mixing, the forbidden s > d transitions are observable in the K edge spectra. According to p-DOS, the CB for STON is comprised of primarily Ta d states, but also Sr d states and with increasing energy, the Sr p and s states.54
This can be reflected visually in Fig. 5d with the pre-edge features of various Sr containing species with, the local coordination surrounding the absorbing Sr showing signs of disorder from the perfect octahedral. With increasing degrees of disorder and orbital mixing, the intensity of the pre-edge features increases, as the usually forbidden s > d transitions are now allowed. Therefore, the main peak intensity may not be solely related to oxidation state and holes in the d band, like for the L edges, but also to the effect of the Sr s and p states and, the local coordination surrounding Sr. As previously mentioned, due to the highly crystalline nature of the epitaxial films, diffraction renders the EXAFS data unreliable to investigate any changes in the local coordination environment of Sr. Future work will look at ways to circumvent this limitation.
As electron density on Sr increases, the reduced intensity of the PSD data at 1.5 V (Fig. 6d) may then be related to (a) reduced probability for an electron to promote to the Sr states in the CB, as they are now partially occupied and/or (b) increased recombination of electron–hole pairs due to the surface reconstruction and the proceeding of the forwards reaction of the OER.
The suggested changes to the surface stoichiometry would result in a surface reconstruction that affects the binding energies of the intermediate products (*OH, *O, *OOH) produced during OER conditions. The intermediates that adsorb too weakly or too strongly will reduce the overall kinetics and, increase the overpotential of the OER.24,45 At 1.5 V, the applied potential overcomes the increased overpotentials, reflected in the increased photocurrent response.
Both the A (Sr) and B (Ta) are both described as active sites for the OER mechanism to proceed on.47 With Sr covered in OH adsorbates contributing to O2 generation. Deprotonation was shown to be the ODS for STON,47 Therefore, upon deprotonation, most Sr species would exist as SrO which, as previously discussed, is partially soluble in the electrolyte. However, unlike Sr, the Ta PSD signals never increase above the level of noise (ESI Fig. 8†). This suggests either two things: (1) Ta is not responsive to the light and not involved in the photo absorption process, a hypothesis which would contradict available literature12,47,68 or, (2) the kinetics for Ta are faster than those for Sr47 therefore Ta evolves O2 at faster rates.
Conclusion
In this work, we employed operando grazing incidence and modulated excitation X-ray absorption spectroscopy to study the effect of several stimuli on STON oxynitride thin films during photoelectrochemical water splitting. A comparison with ex situ XPS of the samples in their initial and final states is also included. The XPS analysis suggests (a) partial dissolution of SrOx into the alkaline electrolyte, (b) an increase in electron density on Sr, (c) lattice Sr and Ta enrichment at the surface, (d) changes in hybridisation with the N 2p and O 2p states. (e) Increase in surface hydrophilicity, evidenced by the increased adsorbed OH/O(OH)/H2O content, (f) slight loss of N from the structure where N remains chemisorbed as N2/NOx species.Surface reconstruction under OER conditions has previously been discussed for Sr and Co containing perovskite oxide catalysts41,69–71 where, the OER proceeds under applied potential together with the lattice-oxygen evolution reaction.41,72 This has been shown to have a beneficial effect with respect to the OER due to the formation of an enriched BOH/BO(OH) surface, increased hydrophilicity and an increase in catalytic activity.41,73 For the oxynitride STON, we also observe surface enrichment of the B cation (Ta) and increased hydrophilicity. However, contrary to oxides, this superficial BOH/BO(OH) enriched surface layer may have complications for the oxynitrides. Since, the N 1s XPS analysis of LTON and STON oxynitride thin films before and after the PECR, evidence N2/NOx chemisorbed species. As discussed previously, likely formed in competitive reactions from the surface lattice N and the OER intermediates.
Operando GIXAS determined that the surface reconstruction occurs when the applied potential increases above 1.3 V vs. RHE. ME-XAS-PSD measurements with modulated light as an external stimulus. It was previously shown for LaTiOxNy that light and the electrolyte do not contribute to the degradation of the material.46 However, we observe small changes in the light response for Sr, with respect to its electronic structure and its evolution as a function of applied potential. Here we show that the nature of the A cation and the evolution of its electronic and geometric environment at the solid/liquid interface has large impacts on the overall stability and catalytic activity of the material during operation conditions.
We also note that nitrogen determines the bulk electronic structure of oxynitrides and in turn, the light absorption properties of the photocatalysts. However, at the surface, the nitrogen species take on a more apparent antagonistic role, competing with the OER. To improve the performance of semiconductor photocatalysts, it is important to understand on a fundamental level what is occurring at the photocatalyst surface during operation.
This study presents the first operando surface sensitive characterisation of the solid–liquid interface during the visible light driven oxygen evolution reaction. An important advance, for future work to explore in operando, the effect of applied potential and the synergistic effects first row transition metal-based co-catalysts have on the performance and stability of the oxynitride photocatalyst templates, where it has been shown that passivation layers and co-catalysts can prevent/minimise the detrimental surface reconstruction. Future experiments involve the screening of co-catalysts (material, deposition method, time, potential etc.) with respect to enhanced performance and stability. With the optimised SC and co-catalyst pairing, the ferroelectric polling enhancement method previously reported can be combined with comparing the 001, 011 and 111 (hkl) orientated STON films. The operando studies are not limited to the visible-light responsive oxynitrides thin film photocatalysts. Operando surface sensitive characterisations and comparisons can also be made with thin films representative UV-only responsive, wide band gap oxides.
Methods
Thin film deposition
Three sets of films used in this work were grown using pulsed laser deposition (PLD). A KrF excimer laser (Lambda Physik LPX 300, 30 ns pulse width, λ = 248 nm) was used to ablate a target of Sr2Ta2O7 fabricated in our laboratory. The target to substrate distance was set at 5 cm. The laser was focused on a spot of 1.1 mm2 with a laser fluence of ca. 3 J cm−2 and laser repetition rate of 10 Hz. Commercially available (001)-oriented MgO was used as a substrate (10 × 10 × 0.5 mm). Platinum paste was applied between the substrates and heating stage to provide good thermal conductivity. The substrate temperature of 750 °C was measured via a pyrometer. N2 background partial pressure of 8.0 × 10−4 mbar was set via a gas inlet line to the vacuum chamber. NH3 gas was injected through a nozzle near the laser spot at the target. The titanium nitride current collector layer was grown in situ, prior to the deposition of the oxynitride film, by conventional PLD using a commercially available TiN target under vacuum with a base pressure of ca. 5 × 10−6 mbar. The substrate to target distance, substrate temperature, laser repetition and fluence were the same as above. The TiN and STON layers were both ca. 100 nm thick (±5 nm).Photoelectrochemical characterisation
Photoelectrochemical (PEC) measurements were performed using a three-electrode configuration in the operando reactor cell described in Fig. 3. The working and counter electrode were the STON thin films and Pt wire respectively. A KCl saturated Ag/AgCl electrode was used as the reference. An aqueous solution of 0.5 molar NaOH (pH = 13) was used as an electrolyte. For the electrical contact of the STON films a wire was adhered to the TiN current collector to apply the electrical contact to the potentiostat (Metrohm Autolab). The electrically connected area was then insulated with epoxy and the sample then immersed into the electrolyte in the cell. The samples were illuminated with a 405 nm laser diode (Laser2000) which has a 5 mW power output and spot size of ca. 0.0308 cm2. The corresponding light intensity is ca. 130 mW cm−2. To measure the dark and light current the laser diode was modulated for 60 second periods (60 seconds on, 60 seconds off). The potentiodynamic measurements were performed at a scan rate of 10 mV s−1 under chopped illumination with 4 second periods.Chemical composition
Rutherford Backscattering (RBS) and Elastic Recoil Detection Analysis (ERDA) were employed to determine the chemical compositions of the STON thin films. RBS provides the metal ratios and oxygen content whereas, ERDA provides nitrogen-to-oxygen ratio. The RBS measurements were performed using a 2 MeV He beam and a silicon PIN diode detector. ERDA was carried out with a 13 MeV 127I beam and the combination of a time-of-flight spectrometer with a gas ionisation detector. RBS data was analysed using RUMP.74Crystalline properties
XRD measurements were performed using a Seifert X-ray Diffractometer with characteristic Cu Kα radiation 0.154 nm. Theta–2theta scans were performed to determine the out-of-plane orientations of the films.X-ray photoelectron spectroscopy
The XPS measurements were performed at the SX-ARPES endstation75 of the Advanced Resonant Spectroscopies (ADRESS) beamline76 situated at the Swiss Light Source, Paul Scherrer Institute, Switzerland. The photon flux was ca. 1013 photons per s and focused into a spot size of 30 × 75 μm2 on the sample surface at an X-ray grazing incidence angle of 20°. The energy resolution was set to 50 meV and the sample temperature was kept at 298 K. Spectra were calibrated using the C 1s signal due to adventitious carbon situated at 284.8 eV.X-ray absorption spectroscopy
The time resolved XAS were measured using the quickXAS method64 at the SuperXAS beamline at the SLS, Paul Scherrer Institut in Switzerland. The polychromatic beam of the 2.9 Tesla superbend was collimated by a Si-coated collimating mirror and subsequently monochromatised by a Si (111) channel-cut crystal of the quickXAS monochromator, which oscillated at 1 Hz frequency with an acquisition time of 500 milliseconds per spectrum. Energy calibration was performed using Pb (L1 edge E0 = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 eV) and Zn (K edge E0 = 9659 eV) thin foils for the Sr K (E0 = 16
861 eV) and Zn (K edge E0 = 9659 eV) thin foils for the Sr K (E0 = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 eV) and Ta L3 (E0 = 9881 eV) edges, respectively. A focused beam was used with a spot size of 100 × 100 μm2. The samples were fixed into the cell and the cell was mounted in grazing incidence to the incoming X-ray beam, with an incident angle between 0–1°. Data analysis was performed using the ProQEXAFS,77 Athena78 and Larch79 software packages.
105 eV) and Ta L3 (E0 = 9881 eV) edges, respectively. A focused beam was used with a spot size of 100 × 100 μm2. The samples were fixed into the cell and the cell was mounted in grazing incidence to the incoming X-ray beam, with an incident angle between 0–1°. Data analysis was performed using the ProQEXAFS,77 Athena78 and Larch79 software packages.
Author contributions
Conceptualisation, C. L., A. C., O. S., M. N., and D. P.; investigation, C. L., A. C., Z. P., O. S., V. S., M. D.; formal analysis, C. L., A. C., Z. P., V. S.; M. D.; writing – original draft, C. L. and D. P.; writing – review & editing, C. L., A. C., Z. P., O. S., M. N., V. S., M. D., T. S., D. P. and T. L.; funding acquisition, D. P., M. N., T. S., T. L.; supervision, V. S., M. N., D. P., and T. L.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Paul Scherrer Institute for financial support through a CROSS grant and the Swiss Light Source for the provision of beamtime at the SuperXAS beamline and to thanks Dr Nick Shepelin for his assistance with the AFM characterisation. TJS thanks Innosuisse and the Swiss Competence Center for Energy Research (SCCER) Heat & Electricity Storage for financial support.References
- Y. Tian and C. Y. Zhao, Appl. Energy, 2013, 104, 538–553 CrossRef CAS.
- B. Parida, S. Iniyan and R. Goic, Renewable Sustainable Energy Rev., 2011, 15, 1625–1636 CrossRef CAS.
- J. H. Montoya, L. C. Seitz, P. Chakthranont, A. Vojvodic, T. F. Jaramillo and J. K. Norskov, Nat. Mater., 2016, 16, 70–81 CrossRef PubMed.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef CAS.
- J. H. Kim, D. Hansora, P. Sharma, J. W. Jang and J. S. Lee, Chem. Soc. Rev., 2019, 48, 1908–1971 RSC.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 RSC.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535 RSC.
- T. Takata, C. Pan and K. Domen, Sci. Technol. Adv. Mater., 2015, 16, 033506 CrossRef PubMed.
- T. Takata and K. Domen, Dalton Trans., 2017, 46, 10529–10544 RSC.
- J. Seo, Y. Moriya, M. Kodera, T. Hisatomi, T. Minegishi, M. Katayama and K. Domen, Chem. Mater., 2016, 28, 6869–6876 CrossRef CAS.
- K. Maeda and K. Domen, MRS Bull., 2011, 36, 25–31 CrossRef CAS.
- Y. Zhong, Z. Li, X. Zhao, T. Fang, H. Huang, Q. Qian, X. Chang, P. Wang, S. Yan, Z. Yu and Z. Zou, Adv. Funct. Mater., 2016, 26, 7156–7163 CrossRef CAS.
- D. Oka, Y. Hirose, H. Kamisaka, T. Fukumura, K. Sasa, S. Ishii, H. Matsuzaki, Y. Sato, Y. Ikuhara and T. Hasegawa, Sci. Rep., 2014, 4, 4987 CrossRef CAS.
- J. Song, T. L. Kim, J. Lee, S. Y. Cho, J. Cha, S. Y. Jeong, H. An, W. S. Kim, Y.-S. Jung, J. Park, G. Y. Jung, D.-Y. Kim, J. Y. Jo, S. D. Bu, H. W. Jang and S. Lee, Nano Res., 2017, 11, 642–655 CrossRef.
- Y. Li, J. Li, W. Yang and X. Wang, Nanoscale Horiz., 2020, 5, 1174–1187 RSC.
- W. Ji, K. Yao, Y.-F. Lim, Y. C. Liang and A. Suwardi, Appl. Phys. Lett., 2013, 103, 062901 CrossRef.
- Y. Moriya, T. Takata and K. Domen, Coord. Chem. Rev., 2013, 257, 1957–1969 CrossRef CAS.
- R. M. Navarro Yerga, M. C. Alvarez Galvan, F. del Valle, J. A. Villoria de la Mano and J. L. Fierro, ChemSusChem, 2009, 2, 471–485 CrossRef CAS.
- F. Haydous, M. Döbeli, W. Si, F. Waag, F. Li, E. Pomjakushina, A. Wokaun, B. Gökce, D. Pergolesi and T. Lippert, ACS Appl. Energy Mater., 2019, 2, 754–763 CrossRef CAS.
- Y. Wang, S. Wei and X. Xu, Appl. Catal., B, 2020, 263, 118315 CrossRef CAS.
- K. Kawashima, M. Hojamberdiev, C. Stabler, D. Vrankovic, K. Yubuta, R. Riedel, K. Domen and K. Teshima, Mater. Renew. Sustain. Energy, 2017, 6, 10 CrossRef.
- M. Pichler, D. Pergolesi, S. Landsmann, V. Chawla, J. Michler, M. Döbeli, A. Wokaun and T. Lippert, Appl. Surf. Sci., 2016, 369, 67–75 CrossRef CAS.
- M. Pichler, W. P. Si, F. Haydous, H. Tellez, J. Druce, E. Fabbri, M. El Kazzi, M. Dobeli, S. Ninova, U. Aschauer, A. Wokaun, D. Pergolesi and T. Lippert, Adv. Funct. Mater., 2017, 27, 1605690 CrossRef.
- H. Ouhbi and U. Aschauer, ACS Mater. Lett., 2019, 1, 52–57 CrossRef CAS.
- J. Druce, H. Téllez, M. Burriel, M. D. Sharp, L. J. Fawcett, S. N. Cook, D. S. McPhail, T. Ishihara, H. H. Brongersma and J. A. Kilner, Energy Environ. Sci., 2014, 7, 3593–3599 RSC.
- A. Staykov, H. Téllez, T. Akbay, J. Druce, T. Ishihara and J. Kilner, Chem. Mater., 2015, 27, 8273–8281 CrossRef CAS.
- A. Staykov, H. Tellez, J. Druce, J. Wu, T. Ishihara and J. Kilner, Sci. Technol. Adv. Mater., 2018, 19, 221–230 CrossRef CAS PubMed.
- G. M. Rupp, H. Téllez, J. Druce, A. Limbeck, T. Ishihara, J. Kilner and J. Fleig, J. Mater. Chem. A, 2015, 3, 22759–22769 RSC.
- Y. Chen, H. Téllez, M. Burriel, F. Yang, N. Tsvetkov, Z. Cai, D. W. McComb, J. A. Kilner and B. Yildiz, Chem. Mater., 2015, 27, 5436–5450 CrossRef CAS.
- Z. Cai, M. Kubicek, J. Fleig and B. Yildiz, Chem. Mater., 2012, 24, 1116–1127 CrossRef CAS.
- E. Bucher, W. Sitte, F. Klauser and E. Bertel, Solid State Ionics, 2011, 191, 61–67 CrossRef CAS.
- F. Wang, T. A. Shifa, X. Zhan, Y. Huang, K. Liu, Z. Cheng, C. Jiang and J. He, Nanoscale, 2015, 7, 19764–19788 RSC.
- H. Wang, K. J. Yakal-Kremski, T. Yeh, G. M. Rupp, A. Limbeck, J. Fleig and S. A. Barnett, J. Electrochem. Soc., 2016, 163, F581–F585 CrossRef CAS.
- A. K. Opitz, C. Rameshan, M. Kubicek, G. M. Rupp, A. Nenning, T. Gotsch, R. Blume, M. Havecker, A. Knop-Gericke, G. Rupprechter, B. Klotzer and J. Fleig, Top. Catal., 2018, 61, 2129–2141 CrossRef CAS PubMed.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. Jung, Joule, 2018, 2, 1476–1499 CrossRef CAS.
- S. S. Pramana, A. Cavallaro, C. Li, A. D. Handoko, K. W. Chan, R. J. Walker, A. Regoutz, J. S. Herrin, B. S. Yeo, D. J. Payne, J. A. Kilner, M. P. Ryan and S. J. Skinner, J. Mater. Chem. A, 2018, 6, 5335–5345 RSC.
- D. F. Mullica, C. K. Lok, H. O. Perkins and V. V. Young, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 4039–4042 CrossRef CAS.
- A. Robin, J. Appl. Electrochem., 2003, 33, 37–42 CrossRef CAS.
- S. J. Yuan, J. J. Chen, Z. Q. Lin, W. W. Li, G. P. Sheng and H. Q. Yu, Nat. Commun., 2013, 4, 2249 CrossRef.
- C. Dai, Y. Sun, G. Chen, A. C. Fisher and Z. J. Xu, Angew. Chem., Int. Ed., 2020, 59, 9418–9422 CrossRef CAS PubMed.
- E. Fabbri, M. Nachtegaal, T. Binninger, X. Cheng, B. J. Kim, J. Durst, F. Bozza, T. Graule, R. Schaublin, L. Wiles, M. Pertoso, N. Danilovic, K. E. Ayers and T. J. Schmidt, Nat. Mater., 2017, 16, 925–931 CrossRef CAS PubMed.
- H. Kato and A. Kudo, Phys. Chem. Chem. Phys., 2002, 4, 2833–2838 RSC.
- L. Wei, M. A. S. Adamson and J. Vela, ChemNanoMat, 2020, 6, 1179–1185 CrossRef CAS.
- V. Rosca, M. Duca, M. T. de Groot and M. T. Koper, Chem. Rev., 2009, 109, 2209–2244 CrossRef CAS.
- E. Fabbri, A. Habereder, K. Waltar, R. Kötz and T. J. Schmidt, Catal. Sci. Technol., 2014, 4, 3800–3821 RSC.
- C. Lawley, M. Nachtegaal, J. Stahn, V. Roddatis, M. Döbeli, T. J. Schmidt, D. Pergolesi and T. Lippert, Nat. Commun., 2020, 11, 1178 CrossRef.
- H. Ouhbi and U. Aschauer, Surf. Sci., 2018, 677, 258–263 CrossRef CAS.
- M. Pichler, J. Szlachetko, I. E. Castelli, N. Marzari, M. Dobeli, A. Wokaun, D. Pergolesi and T. Lippert, ChemSusChem, 2017, 10, 2099–2106 CrossRef CAS PubMed.
- R. Aguiar, D. Logvinovich, A. Weidenkaff, A. Rachel, A. Reller and S. G. Ebbinghaus, Dyes Pigm., 2008, 76, 70–75 CrossRef.
- S.-M. Paek and Y.-I. Kim, J. Alloys Compd., 2014, 587, 251–254 CrossRef CAS.
- A. O. Ibidunni, R. L. Masaitis, R. L. Opila, A. J. Davenport, H. S. Isaacs and J. A. Taylor, Surf. Interface Anal., 1993, 20, 559–564 CrossRef CAS.
- T. S. Wu, Y. C. Chen, Y. F. Shiu, H. J. Peng, S. L. Chang, H. Y. Lee, P. P. Chu, C. W. Hsu, L. J. Chou, C. W. Pao, J. F. Lee, J. Kwo, M. Hong and Y. L. Soo, Appl. Phys. Lett., 2012, 101, 022408 CrossRef.
- X. Cheng, B. J. Kim, E. Fabbri and T. J. Schmidt, ACS Appl. Mater. Interfaces, 2019, 11, 34787–34795 CrossRef CAS.
- A. Mahmood, S. Azam, M. Irfan, M. A. Kamran, T. Alharbi, A. Majid, M. W. Iqbal, S. Muhammad, A. G. Al-Sehemi, S. A. Khan and S. Goumri-Said, Mater. Sci. Semicond. Process., 2020, 107, 104800 CrossRef CAS.
- R. B. Greegor, N. E. Pingitore Jr and F. W. Lytle, Science, 1997, 275, 1452–1454 CrossRef CAS PubMed.
- F. Farges, J. Non-Cryst. Solids, 1996, 204, 53–64 CrossRef CAS.
- A. Staykov, S. Fukumori, K. Yoshizawa, K. Sato, T. Ishihara and J. Kilner, J. Mater. Chem. A, 2018, 6, 22662–22672 RSC.
- J. Lee, W. D. Lu and E. Kioupakis, Nanoscale, 2017, 9, 1120–1127 RSC.
- X. Wen, Y. Feng, S. Huang, F. Huang, Y.-B. Cheng, M. Green and A. Ho-Baillie, J. Mater. Chem. C, 2016, 4, 793–800 RSC.
- H. Abe, G. Aquilanti, R. Boada, B. Bunker, P. Glatzel, M. Nachtegaal and S. Pascarelli, J. Synchrotron Radiat., 2018, 25, 972–980 CrossRef CAS PubMed.
- D. Ferri, M. A. Newton and M. Nachtegaal, Top. Catal., 2011, 54, 1070–1078 CrossRef CAS.
- G. L. Chiarello and D. Ferri, Phys. Chem. Chem. Phys., 2015, 17, 10579–10591 RSC.
- C. F. J. König, J. A. van Bokhoven, T. J. Schildhauer and M. Nachtegaal, J. Phys. Chem. C, 2012, 116, 19857–19866 CrossRef.
- M. Nachtegaal, O. Müller, C. König and R. Frahm, in X-Ray Absorption and X-Ray Emission Spectroscopy, ed. J. A. V. Bokhoven and C. Lamberti, John Wiley & Sons, 2016, ch. 7, pp. 155–183, DOI:10.1002/9781118844243.ch7.
- D. Baurecht and U. P. Fringeli, Rev. Sci. Instrum., 2001, 72, 3782–3792 CrossRef CAS.
- A. Urakawa, T. Bürgi and A. Baiker, Chem. Eng. Sci., 2008, 63, 4902–4909 CrossRef CAS.
- H. Yoshida, S. Nonoyama and Y. Y. T. Hattori, Phys. Scr., 2005, 115, 813–815 CrossRef.
- P. Zhang, J. Zhang and J. Gong, Chem. Soc. Rev., 2014, 43, 4395–4422 RSC.
- X. Deng and H. Tüysüz, ACS Catal., 2014, 4, 3701–3714 CrossRef CAS.
- K. J. May, C. E. Carlton, K. A. Stoerzinger, M. Risch, J. Suntivich, Y.-L. Lee, A. Grimaud and Y. Shao-Horn, J. Phys. Chem. Lett., 2012, 3, 3264–3270 CrossRef CAS.
- T. Das, J. D. Nicholas and Y. Qi, J. Mater. Chem. A, 2017, 5, 25031–25043 RSC.
- E. Fabbri and T. J. Schmidt, ACS Catal., 2018, 8, 9765–9774 CrossRef CAS.
- X. Sun, F. Wu, G. Liu and X. Xu, J. Mater. Chem. A, 2018, 6, 20760–20768 RSC.
- L. R. Doolittle, Nucl. Instrum. Methods Phys. Res., Sect. B, 1986, 15, 227–231 CrossRef.
- V. N. Strocov, X. Wang, M. Shi, M. Kobayashi, J. Krempasky, C. Hess, T. Schmitt and L. Patthey, J. Synchrotron Radiat., 2014, 21, 32–44 CrossRef CAS PubMed.
- V. N. Strocov, T. Schmitt, U. Flechsig, T. Schmidt, A. Imhof, Q. Chen, J. Raabe, R. Betemps, D. Zimoch, J. Krempasky, X. Wang, M. Grioni, A. Piazzalunga and L. Patthey, J. Synchrotron Radiat., 2010, 17, 631–643 CrossRef CAS PubMed.
- A. H. Clark, J. Imbao, R. Frahm and M. Nachtegaal, J. Synchrotron Radiat., 2020, 27, 551–557 CrossRef PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS.
- M. Newville, J. Phys.: Conf. Ser., 2013, 430, 012007 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta05052d |
| This journal is © The Royal Society of Chemistry 2022 |