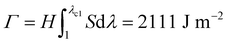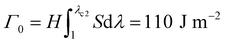Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An extreme toughening mechanism for soft materials†
Shaoting
Lin
 a,
Camilo Duque
Londono
a,
Camilo Duque
Londono
 a,
Dongchang
Zheng
a,
Dongchang
Zheng
 a and
Xuanhe
Zhao
a and
Xuanhe
Zhao
 *ab
*ab
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: zhaox@mit.edu
bDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 27th June 2022
Abstract
Soft yet tough materials are ubiquitous in nature and everyday life. The ratio between fracture toughness and intrinsic fracture energy of a soft material defines its toughness enhancement. Soft materials’ toughness enhancement has been long attributed to their bulk stress-stretch hysteresis induced by dissipation mechanisms such as Mullins effect and viscoelasticity. With a combination of experiments and theory, here we show that the bulk dissipation mechanisms significantly underestimate the toughness enhancement of soft tough materials. We propose a new mechanism and scaling law to account for extreme toughening of diverse soft materials. We show that the toughness enhancement of soft materials relies on both bulk hysteretic dissipation, and near-crack dissipation due to mechanisms such as polymer-chain entanglement. Unlike the bulk hysteretic dissipation, the near-crack dissipation does not necessarily induce large stress-stretch hysteresis of the bulk material. The extreme toughening mechanism can be potentially universally applied to various soft tough materials, ranging from double-network hydrogels, interpenetrating-network hydrogels, entangled-network hydrogels and slide-ring hydrogels, to unfilled and filled rubbers.
Introduction
Soft yet tough materials – mainly constituted of polymer networks – are ubiquitous in nature and everyday life, ranging from animal and plant tissues,1,2 to synthetic and natural elastomers,3,4 to recently developed tough hydrogels including double-network hydrogels,5,6 interpenetrating-network hydrogels,7 polyampholyte hydrogels,8 and slide-ring hydrogels.9 For instance, while the Young's moduli of natural muscles,10 triple-network elastomers,11 and interpenetrating-network hydrogels7 are below a few megapascals, their fracture toughness can reach up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2 – approximating that of tough steels.12 Such high fracture toughness of soft materials is crucial for their mechanical integrity and robustness in nature and in engineering applications.
000 J m−2 – approximating that of tough steels.12 Such high fracture toughness of soft materials is crucial for their mechanical integrity and robustness in nature and in engineering applications.
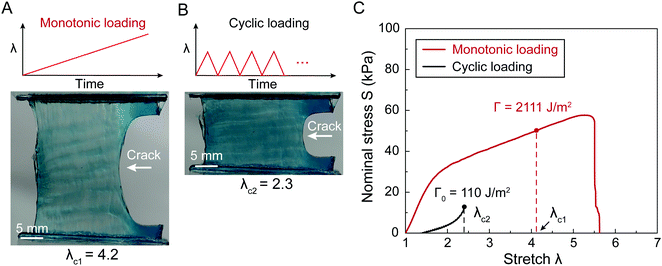
Fracture toughness of soft materials has been long attributed to two physical processes:13–15 (1) scission of a layer of polymer chains on the crack tip, and (2) hysteretic mechanical dissipation in the bulk material around the crack tip due to mechanisms such as Mullins effect and viscoelasticity. The first process defines the intrinsic fracture energy Γ0, and the second process gives the bulk hysteretic dissipation's contribution to fracture toughness ΓbulkD. Consequently, the total fracture toughness of the soft material Γ0 can be expressed as Γ = Γ0 + ΓbulkD, which is often named the bulk dissipation model.14,16–20 The fracture toughness Γ of a soft material can be measured as the critical energies required to propagate a crack by a unit area in a material under monotonic loading in a fracture test (Fig. 1(A) and (C)). The fatigue threshold Γ0 of a soft material can be measured as the critical energy required to propagate a crack by a unit area in a material under infinite cycles of loading in a fatigue test (Fig. 1(B) and (C)). Despite their high fracture toughness up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−2,3–8 the measured intrinsic fracture energy of soft materials is usually on the order of 10 to 100 J m−2.18,21 Soft materials’ toughness enhancement – defined as Γ/Γ0 – has been long attributed to the bulk dissipation mechanisms such as Mullins effect and viscoelasticity.13–15,17,19,20
000 J m−2,3–8 the measured intrinsic fracture energy of soft materials is usually on the order of 10 to 100 J m−2.18,21 Soft materials’ toughness enhancement – defined as Γ/Γ0 – has been long attributed to the bulk dissipation mechanisms such as Mullins effect and viscoelasticity.13–15,17,19,20
With a combination of experiments and theory, this work shows that the bulk dissipation mechanisms significantly underestimate the toughness enhancement of soft tough materials. We present a new model and scaling law to account for an extreme toughening mechanism in diverse soft tough materials, which relies on both bulk hysteretic dissipation, and near-crack dissipation due to mechanisms such as polymer-chain entanglement and strain-induced crystallization. Using polyacrylamide (PAAm)-alginate hydrogels as an example, we show that the bulk dissipation model underestimates the toughness enhancement of PAAm-alginate hydrogels up to 6.6 times. In contrast, our new model can quantitively predict the toughness enhancement of PAAm-alginate hydrogels across a wide range of bulk hysteresis. We further show that the extreme toughening mechanism can be potentially universally applied to various soft tough materials, ranging from interpenetrating-network hydrogels,7 double-network hydrogels,5,6 slide-ring gels,9 and entangled-network hydrogels,22,23 to unfilled and filled rubbers.24–27
Results and discussion
Extreme toughening model
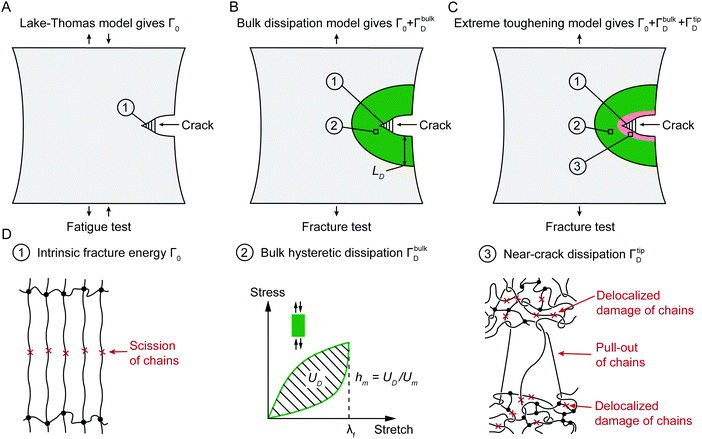
Fig. 2 schematically illustrates the physical picture of the extreme toughening model. Considering a notched soft material subject to a tensile load, crack propagation in the material first requires the scission of a single layer of polymer chains on the crack path. The required mechanical energy for chain scission divided by the area of crack surface at undeformed state gives the intrinsic fracture energy Γ0, following Lake–Thomas model (Fig. 2(A) and (D)).18 As the crack propagates, the material in a process zone around the crack path experiences a loading–unloading process, which dissipates mechanical energy due to bulk hysteresis, following the bulk dissipation model (Fig. 2(B) and (D)).14 The dissipated energy divided by the area of the crack surface at undeformed state contributes to the fracture toughness by ΓbulkD. In addition, if the material contains polymer-chain entanglements, the crack propagation also requires pulling out of chains and delocalized damage of chains adjacent to the crack path, which give the near-crack dissipation (Fig. 2(C) and (D)).22 The dissipated energy divided by the area of crack surface at undeformed state further contributes to the fracture toughness by ΓtipD. Therefore, the total fracture toughness of a soft material can be expressed as| Γ = Γ0 + ΓbulkD + ΓtipD | (1) |
The term ΓbulkD in eqn (1) can be estimated by
| ΓbulkD = UDLD | (2) |
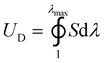 , where S and λ are stress and stretch of the material under monotonic loading, λmax is the maximum stretch at which the material fails under the pure-shear deformation. The effective size of the process zone LD can be estimated by the stress distribution profile around the crack tip. As material within the process zone experiences sufficiently high deformation for contributing to bulk hysteretic dissipation, the boundary of the process zone can be determined by identifying a critical length scale.
, where S and λ are stress and stretch of the material under monotonic loading, λmax is the maximum stretch at which the material fails under the pure-shear deformation. The effective size of the process zone LD can be estimated by the stress distribution profile around the crack tip. As material within the process zone experiences sufficiently high deformation for contributing to bulk hysteretic dissipation, the boundary of the process zone can be determined by identifying a critical length scale.
Without loss of generality, we take the soft material as a neo-Hookean solid. For a neo-Hookean solid under pure-shear fracture test (Fig. 1(A)), the leading order of the nominal stress at a point near the crack tip scales as 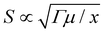 , where μ is the shear modulus of the materials and x is the distance from the point to the crack tip.14 Further, given the maximum nominal stress that the material can reach under the pure-shear deformation is Smax, we can estimate the size of the process zone as
, where μ is the shear modulus of the materials and x is the distance from the point to the crack tip.14 Further, given the maximum nominal stress that the material can reach under the pure-shear deformation is Smax, we can estimate the size of the process zone as
| LD ∝ Γμ/Smax2 ∝ Γ/Umax | (3) |
| ΓbulkD ∝ Γhm | (4) |
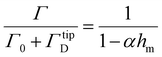 | (5) |
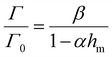 | (6) |
Experiments
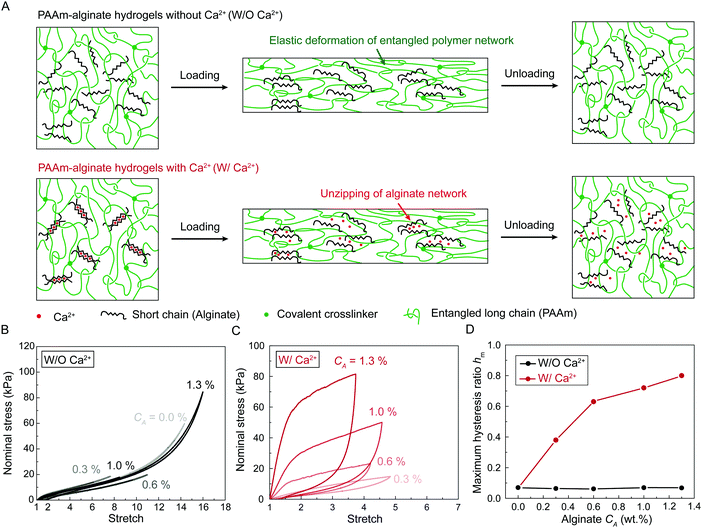
We chose polyacrylamide-alginate (PAAm-alginate) hydrogels as a model material to validate the model. Due to its extremely high fracture toughness, PAAm-alginate hydrogel has been intensively exploited as a key component for devices and machines with examples such as tough hydrogel bonding,29 soft robots,26 hydrogel bandage,30 acoustic metamaterials,31 ultrasound imaging,32 and living sensors.33 A PAAm-alginate hydrogel is made of two interpenetrating polymer networks: covalently crosslinked long-chain PAAm network, and ionically-crosslinked short-chain alginate network. The covalently crosslinked long-chain PAAm network provides the material's stretchable elasticity, and the ionically crosslinked short-chain alginate network dissociates as the material is highly deformed, giving the material's bulk hysteresis. In this work, we maintain the concentration and crosslinking density of PAAm network while varying the concentration and crosslinking density of alginate network, thereby tuning the bulk hysteresis of PAAm-alginate hydrogels.We synthesize two series of PAAm-alginate hydrogels (Fig. 3(A)). As schematically illustrated in Fig. 3(A), both series of PAAm-alginate hydrogels contain covalently crosslinked PAAm long-chain network. In our recent work, we varied the average number of monomers between neighboring crosslinkers by changing crosslinker densities while maintaining the polymer content in the polyacrylamide (PAAm) hydrogels to systematically control the level of chain entanglement. In this work, the average number of AAm monomers between neighboring crosslinkers in the as-prepared state is fixed as N = 2263, giving substantial chain entanglement according to our rheology characterization.22 In the first series of PAAm-alginate hydrogels, the sodium alginate polymers are uncrosslinked mobile chains. In the second series of PAAm-alginate hydrogels, the sodium alginate polymers are ionically crosslinked into polymer networks. Unless otherwise stated, we denote the first series of PAAm-alginate hydrogels as hydrogels without Ca2+ (i.e., W/O Ca2+), and denote second series of PAAm-alginate hydrogels as hydrogels with Ca2+ (i.e., W/Ca2+).
We first characterize the stress-stretch curves of the two series of PAAm-alginate hydrogels up to failure points under the pure-shear deformation. For hydrogels without Ca2+, the sodium alginate concentration CA has little effect on the nonlinear stress-stretch relationship (Fig. S1, ESI†), because the alginate chains are uncrosslinked mobile chains and do not contribute to the elasticity of the hydrogels. In contrast, for hydrogels with Ca2+, the sodium alginate concentration has significant impacts on stress-stretch curves (Fig. S1, ESI†). As the sodium alginate concentration CA increases, the nominal stress increases accordingly while the ultimate stretch remains constant. Compared to hydrogels without Ca2+, the ultimate stretches of hydrogels with Ca2+ decrease drastically, possibly because the ionically crosslinked alginate network suppresses the stretchablity of the polyacrylamide network.
We further characterize the stress-stretch hysteresis of the two series of PAAm-alginate hydrogels. Fig. S2 (ESI†) plots the stress-stretch curves under one cycle of loading at different stretch levels for hydrogels without Ca2+. The measured bulk hysteresis is consistently below 10% even when the maximum stretch approaches the failure points (Fig. 3(B) and (D)). This is because the uncrosslinked alginate polymers do not contribute to elasticity or hysteresis of the material and the entangled PAAm polymer network exhibits low bulk hysteresis.22 In contrast, since alginate polymers form the ionically crosslinked network in hydrogels with Ca2+, the alginate network unzips progressively when the material is highly deformed, which gives the huge bulk hysteresis (Fig. 3(A)). Fig. 3(C) and Fig. S3 (ESI†) plot the stress-stretch curves under one cycle of loading at different stretch levels for hydrogels with Ca2+. The bulk hysteresis of hydrogels with Ca2+ monotonically increases with the applied stretch and reaches a maximum plateau. We take the maximum plateau as the maximum bulk hysteresis hm. As summarized in Fig. 3(D), the maximum bulk hysteresis of hydrogels with Ca2+ increases with the alginate concentration CA. This further indicates the critical role of ionically crosslinked alginate network in promoting the bulk hysteresis.
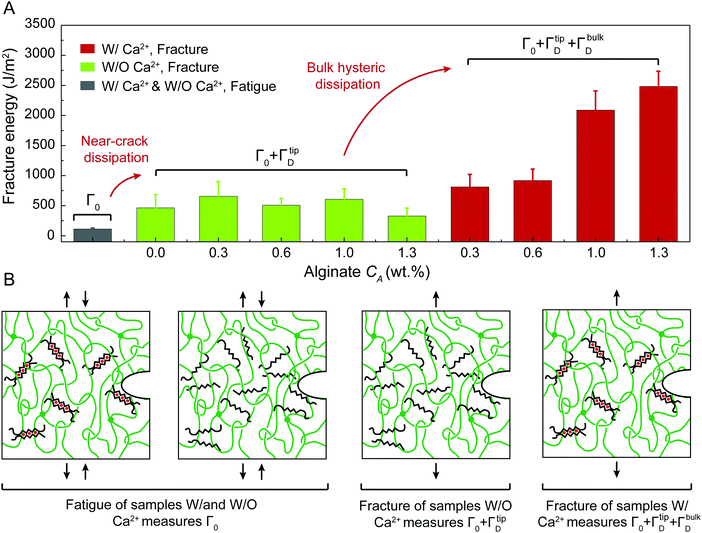
We next use fracture and fatigue tests to measure the fracture toughness Γ and fatigue threshold Γ0 of the two series of PAAm-alginate hydrogels. We first adopt both pure-shear and single-notch methods to measure their fatigue thresholds (Fig. S4–S6, ESI†), which give their intrinsic fracture energies Γ0. The measured fatigue thresholds of both series of hydrogels are consistently around 110 J m−2. (Unless otherwise stated, the reported values of fatigue threshold have been converted to the corresponding values in the as-prepared or reference state by accounting for swelling of the hydrogels. The swelling ratios in volume are summarized in Fig. S7, ESI.†) This indicates the presence of ionically crosslinked alginate network does not contribute to the fatigue threshold (Fig. 3(B)), because the resistance to fatigue crack propagation after prolonged cycles of loading is the energy required to fracture a layer of PAAm polymer chains (i.e., the intrinsic fracture energy), which is unaffected by the additional bulk dissipation mechanisms by unzipping the ionically crosslinked alginate network.34
We further use the pure-shear method to measure the fracture toughness of the two series of PAAm-alginate hydrogels. For hydrogels without Ca2+, the alginate concentration CA has little effect on the fracture toughness (Fig. S8, ESI†). Even though the bulk hysteretic dissipations in hydrogels without Ca2+ are negligible, the measured fracture toughness is still relatively high (480 J m−2), about 4.3 times of their fatigue threshold (i.e., 110 J m−2). This indicates that the difference between fracture toughness and fatigue threshold of hydrogels without Ca2+ is due to the near-crack dissipation, not the bulk dissipation.22 Therefore, the fracture toughness of hydrogels without Ca2+ measures Γ0 + ΓtipD (Fig. 3). Our recent work has systematically studied the presence of chain entanglement as a new toughening mechanism. Once a crack propagates in an entangled polymer network, the highly entangled polymer chains across the crack plane are pulled out, potentially dissipating substantial energy due to abundant intermolecular interactions between neighboring chains. In addition, once the entangled chains around the crack tip are highly stretched, scissions of chains can be delocalized to multiple adjacent layers around the crack plane, dissipating more energy than fracturing a single layer of chains.
For hydrogels with Ca2+, the alginate concentration CA significantly affects the fracture toughness (Fig. 4(A) and Fig. S8, ESI†). As CA increases, the fracture toughness of hydrogels with Ca2+ increases drastically from 500 to 2800 J m−2 (Fig. 4(A)). This enhancement of the fracture toughness is due to the bulk hysteretic dissipation by unzipping the ionically crosslinked alginate network; the level of bulk hysteretic dissipation is determined by the alginate concentration CA. Consequently, the fracture toughness of hydrogels with Ca2+ measures Γ0 + ΓbulkD + ΓtipD (Fig. 4).
Comparison between experiments and models
Given the measured maximum bulk hysteresis hm, fracture toughness Γ, and fatigue threshold Γ0 of the hydrogels with Ca2+, we summarize the measured toughness enhancement Γ/Γ0 as a function of the measured maximum bulk hysteresis hm in Fig. 5(A). When the maximum bulk hysteresis is small, the toughness enhancement can still achieve 4.3. As the maximum bulk hysteresis increases, the toughness enhancement increases accordingly. When the maximum bulk hysteresis reaches 80%, the toughness enhancement can be as high as 22.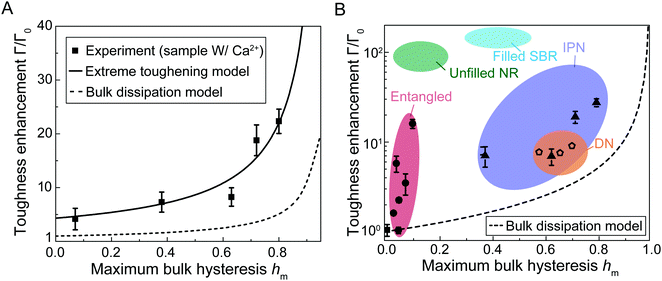 | ||
| Fig. 5 Comparisons between experiments and models for toughness enhancement versus maximum bulk hysteresis hm. (A) Comparisons of toughness enhancement Γ/Γ0versus maximum bulk hysteresis hm between the experimental results and the two models (extreme toughening model and bulk dissipation model). (B) Toughness enhancement Γ/Γ0 and maximum bulk hysteresis hm for various soft tough materials including interpenetrating-network (IPN) hydrogels,7,21 double-network (DN) hydrogels,5,35 entangled hydrogels,22 unfilled natural rubbers (NR),24,25 and filled styrene-butadiene rubbers (SBR).26,27 The bulk dissipation model consistently underestimates the toughness enhancement of these soft tough materials. | ||
We then use eqn (6) to calculate the relationship between fracture toughness enhancement Γ/Γ0 and maximum bulk hysteresis hm. The parameter β = (Γ0 + ΓtipD)/Γ0 is identified as 4.3 given the measured Γ0 + ΓtipD (i.e., 480 J m−2) and the measured Γ0 (i.e., 112 J m−2). The parameter α is taken as 1 since PAAm-alginate hydrogels are highly stretchable. Given the identified β and α, we can plot toughness enhancement Γ/Γ0 as a function of the maximum bulk hysteresis hm. As shown in Fig. 5(A), our extreme toughening model can quantitatively capture the toughness enhancement across a wide range of the maximum bulk hysteresis hm. In contrast, we also plot Γ/Γ0versus hm following the bulk dissipation model, and the predicted toughness enhancement is significantly lower than the experimental results.
We further summarize reported toughness enhancement and maximum bulk hysteresis of various soft tough materials, including interpenetrating-network hydrogels,7,21 double-network hydrogels,5,35 entangled-network hydrogels,22 slide-ring gels,9 unfilled natural rubbers,24,25 and filled styrene-butadiene rubbers.26,27 The predicted toughness enhancements following the bulk dissipation model are consistently lower than the measured values (Fig. 5(B)). For example, the toughness enhancement of the interpenetrating-network hydrogels7 with bulk hysteresis of around 80% should be around 5 following the bulk dissipation model, but the measured toughness enhancement is more than 20.21 The toughness enhancement of the double-network hydrogels5 with bulk hysteresis of around 70% should be around 3.3 following the bulk dissipation model, but the measured toughness enhancement is at least 8.35 The toughness enhancement of unfilled natural rubbers with bulk hysteresis of around 20% should be around 1.2 following the bulk dissipation model,25 but the measured toughness enhancement is as high as 100.24 We envision our extreme toughening model can quantitatively capture the toughness enhancements of various soft toughen materials, because nearly all these soft tough materials contain substantial near-crack dissipation due to mechanisms such as chain entanglements.
Discussion
Here, we use a combination of experiments and theory to show that the bulk dissipation mechanisms significantly underestimate the toughness enhancement of soft tough materials. We propose a new mechanism and scaling law to account for the extreme toughening of diverse soft tough materials. The extreme toughening relies on both bulk hysteretic dissipation and near-crack dissipation due to mechanisms such as polymer-chain entanglement and strain-induced crystallization. Using polyacrylamide (PAAm)-alginate hydrogels as an example, we show that the bulk dissipation model underestimates the toughness enhancement of PAAm-alginate hydrogels up to 6.6 times. In contrast, our new extreme toughening model can quantitively predict the toughness enhancement of PAAm-alginate hydrogels across a wide range of bulk hysteresis. We envision the extreme toughening mechanism can be potentially universally applied to various soft tough materials, ranging from double-network hydrogels, interpenetrating-network hydrogels, entangled-network hydrogels and slide-ring hydrogels, to unfilled and filled rubbers. Our study resolves a fundamental dilemma in toughening mechanisms of soft materials. It is hoped that this work can help the development of next-generation tough, fatigue-resistant, and resilient soft materials. One limitation of the current study is there is no quantitative differentiation of the process zone size for bulk hysteretic dissipation and the process zone size for near-crack dissipation. Future work will focus on new experimental tools to visualize and quantify the damage occurring in the process zones due to bulk hysteretic dissipation and near-crack dissipation.Author contributions
Shaoting Lin: conceptualization, methodology, data curation, formal analysis, investigation, writing – original draft, writing – review & editing. Camilo Duque Londono: data curation, formal analysis, writing – review & editing. Dongchang Zheng: data curation, formal analysis. Xuanhe Zhao: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review & editing.Conflicts of interest
The authors declare no competing interest.Acknowledgements
This work was supported by National Institutes of Health (No. 1R01HL153857-01), National Science Foundation (No. EFMA-1935291) and the U.S. Army Research Office through the Institute for Soldier Nanotechnologies at MIT (W911NF-13-D-0001).References
- M. A. Meyers, J. McKittrick and P.-Y. Chen, Structural biological materials: Critical mechanics-materials connections, Science, 2013, 339, 773–779 CrossRef CAS.
- W. Huang, et al., Multiscale toughening mechanisms in biological materials and bioinspired designs, Adv. Mater., 2019, 31, 1901561 CrossRef CAS.
- S. Toki and B. S. Hsiao, Nature of strain-induced structures in natural and synthetic rubbers under stretching, Macromolecules, 2003, 36, 5915–5917 CrossRef CAS.
- A. Gent, S. Kawahara and J. Zhao, Crystallization and strength of natural rubber and synthetic cis-1, 4-polyisoprene, Rubber Chem. Technol., 1998, 71, 668–678 CrossRef CAS.
- J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Double-network hydrogels with extremely high mechanical strength, Adv. Mater., 2003, 15, 1155–1158 CrossRef CAS.
- Q. Chen, L. Zhu, C. Zhao, Q. Wang and J. Zheng, A robust, one-pot synthesis of highly mechanical and recoverable double network hydrogels using thermoreversible sol–gel polysaccharide, Adv. Mater., 2013, 25, 4171–4176 CrossRef CAS.
- J.-Y. Sun, et al., Highly stretchable and tough hydrogels, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- T. L. Sun, et al., Physical hydrogels composed of polyampholytes demonstrate high toughness and viscoelasticity, Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- C. Liu, et al., Tough hydrogels with rapid self-reinforcement, Science, 2021, 372, 1078–1081 CrossRef CAS.
- D. Amiel, C. Frank, F. Harwood, J. Fronek and W. Akeson, Tendons and ligaments: A morphological and biochemical comparison, J. Orthop. Res., 1983, 1, 257–265 CrossRef.
- E. Ducrot, Y. Chen, M. Bulters, R. P. Sijbesma and C. Creton, Toughening elastomers with sacrificial bonds and watching them break, Science, 2014, 344, 186–189 CrossRef CAS.
- R. O. Ritchie, J. F. Knott and J. Rice, On the relationship between critical tensile stress and fracture toughness in mild steel, J. Mech. Phys. Solids, 1973, 21, 395–410 CrossRef CAS.
- X. Zhao, Multi-scale multi-mechanism design of tough hydrogels: Building dissipation into stretchy networks, Soft Matter, 2014, 10, 672–687 RSC.
- T. Zhang, S. Lin, H. Yuk and X. Zhao, Predicting fracture energies and crack-tip fields of soft tough materials, Extreme Mech. Lett., 2015, 4, 1–8 CrossRef.
- R. Long and C.-Y. Hui, Fracture toughness of hydrogels: Measurement and interpretation, Soft Matter, 2016, 12, 8069–8086 RSC.
- A. G. Evans, Perspective on the development of high-toughness ceramics, J. Am. Ceram. Soc., 1990, 73, 187–206 CrossRef CAS.
- R. McMeeking and A. Evans, Mechanics of transformation-toughening in brittle materials, J. Am. Ceram. Soc., 1982, 65, 242–246 CrossRef.
- G. Lake and A. Thomas, The strength of highly elastic materials, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CAS.
- J. Yang, R. Bai, B. Chen and Z. Suo, Hydrogel adhesion: A supramolecular synergy of chemistry, topology, and mechanics, Adv. Funct. Mater., 2020, 30, 1901693 CrossRef CAS.
- P.-G. de Gennes, Soft adhesives, Langmuir, 1996, 12, 4497–4500 CrossRef CAS.
- R. Bai, et al., Fatigue fracture of tough hydrogels, Extreme Mech. Lett., 2017, 15, 91–96 CrossRef.
- D. Zheng, S. Lin, J. Ni and X. Zhao, Fracture and fatigue of entangled and unentangled polymer networks, Extreme Mech. Lett., 2022, 51, 101608 CrossRef.
- C. Norioka, Y. Inamoto, C. Hajime, A. Kawamura and T. Miyata, A universal method to easily design tough and stretchable hydrogels, NPG Asia Mater., 2021, 13, 1–10 CrossRef.
- G. Lake and P. Lindley, The mechanical fatigue limit for rubber, J. Appl. Polym. Sci., 1965, 9, 1233–1251 CrossRef.
- Z. Wang, et al., Stretchable materials of high toughness and low hysteresis, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5967–5972 CrossRef CAS.
- H. Yuk, et al., Hydraulic hydrogel actuators and robots optically and sonically camouflaged in water, Nat. Commun., 2017, 8, 1–12 CrossRef.
- D. Roucou, J. Diani, M. Brieu and D. Colombo, Experimental identification of fracture toughness of a carbon black-filled styrene butadiene rubber undergoing energy dissipation by Mullins softening, Mech. Mater., 2020, 151, 103645 CrossRef.
- Y. Qi, J. Caillard and R. Long, Fracture toughness of soft materials with rate-independent hysteresis, J. Mech. Phys. Solids, 2018, 118, 341–364 CrossRef.
- H. Yuk, T. Zhang, S. Lin, G. A. Parada and X. Zhao, Tough bonding of hydrogels to diverse non-porous surfaces, Nat. Mater., 2016, 15, 190–196 CrossRef CAS.
- S. Lin, et al., Stretchable hydrogel electronics and devices, Adv. Mater., 2016, 28, 4497–4505 CrossRef CAS.
- K. Zhang, et al., Metagel with broadband tunable acoustic properties over air–water–solid ranges, Adv. Funct. Mater., 2019, 29, 1903699 CrossRef.
- L. Chen, et al., Soft elastic hydrogel couplants for ultrasonography, Mater. Sci. Eng., C, 2021, 119, 111609 CrossRef CAS.
- X. Liu, et al., Stretchable living materials and devices with hydrogel–elastomer hybrids hosting programmed cells, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2200–2205 CrossRef CAS.
- S. Lin, et al., Anti-fatigue-fracture hydrogels, Sci. Adv., 2019, 5, eaau8528 CrossRef PubMed.
- W. Zhang, et al., Fatigue of double-network hydrogels, Eng. Fract. Mech., 2018, 187, 74–93 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00609j |
| This journal is © The Royal Society of Chemistry 2022 |