Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase separation dynamics in deformable droplets†
Simon
Gsell
 ab and
Matthias
Merkel
ab and
Matthias
Merkel
 *a
*a
aAix Marseille Univ, Université de Toulon, CNRS, CPT (UMR 7332), Turing Centre for Living Systems, Marseille, France. E-mail: simon.gsell@univ-amu.fr; matthias.merkel@cnrs.fr
bAix Marseille Univ, CNRS, IBDM (UMR 7288), Turing Centre for Living Systems, Marseille, France
First published on 16th March 2022
Abstract
Phase separation can drive spatial organization of multicomponent mixtures. For instance in developing animal embryos, effective phase separation descriptions have been used to account for the spatial organization of different tissue types. Similarly, separation of different tissue types is also observed in stem cell aggregates, where the emergence of a polar organization can mimic early embryonic axis formation. Here, we describe such aggregates as deformable two-phase fluid droplets, which are suspended in a fluid environment (third phase). Using hybrid finite-volume Lattice-Boltzmann simulations, we numerically explore the out-of-equilibrium routes that can lead to the polar equilibrium state of such a droplet. We focus on the interplay between spinodal decomposition and advection with hydrodynamic flows driven by interface tensions, which we characterize by a Peclet number Pe. Consistent with previous work, for large Pe the coarsening process is generally accelerated. However, for intermediate Pe we observe long-lived, strongly elongated droplets, where both phases form an alternating stripe pattern. We show that these “croissant” states are close to mechanical equilibrium and coarsen only slowly through diffusive fluxes in an Ostwald-ripening-like process. Finally, we show that a surface tension asymmetry between both droplet phases leads to transient, rotationally symmetric states whose resolution leads to flows reminiscent of Marangoni flows. Our work highlights the importance of advection for the phase separation process in finite, deformable systems.
1 Introduction
Systems composed of two or more components can undergo phase separation.1–3 During this process, phase domains of different composition first emerge either through spinodal decomposition or nucleation, before these domains coarsen through diffusive processes such as Ostwald ripening. Coarsening is associated with a power-law growth of typical domain size λ, which scales as λ ∼ t1/3 with time t.1 In the case of fluid–fluid phase separation, coarsening can also occur through advection with hydrodynamic flows that are driven by the interface tension between adjacent domains. Such hydrodynamic flows can speed up domain coarsening, which can lead to e.g. a linear scaling λ ∼ t.1 However, the precise interplay between diffusive and hydrodynamic processes can be quite complex, leading to a rich phenomenology.4While phase separation has long been employed for industrial processes, it has also been identified as a key organizing mechanism in biological systems, from the sub-cellular5 to the ecological6 scale. For example, the interior of biological cells is organized in part through fluid compartments that can emerge from phase separation.5,7,8 Phase separation has moreover been used as effective model to describe the formation of multi-cellular aggregates.9 But it has also been used to describe separation of different types of biological tissues.10–13 This was motivated by experiments showing that different embryonic cell populations can unmix.14,15 Moreover, given that embryonic tissues and aggregates often behave like viscous liquids on long times,15–21 unmixing of cell populations could also be accelerated by long-range hydrodynamic flows.
Phase separation of biological tissues could also help to understand an important question in the field of developmental biology: How does the vertebrate axis form during animal development? To address this and related questions, experimentalists study aggregates of stem cells, called gastruloids, which have been shown to mimic vertebrate development (Fig. 1a and b).22–24 Such gastruloids initially consist of spherical aggregates of undifferentiated stem cells (Fig. 1a). Even under isotropic boundary conditions, these aggregates then reliably25 form polarized structures with different cell populations (Fig. 1b).26 This process has been related to the definition of the axis of the vertebral column in vivo.23,27 However, how exactly this axis initially emerges has remained unclear.
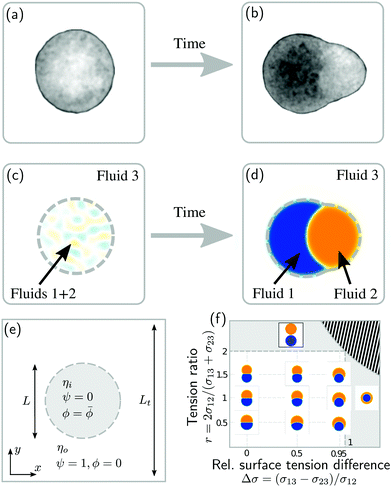 | ||
| Fig. 1 Phase separation and symmetry breaking in deformable multicomponent droplets. (a and b) Microscopy images of cell aggregates mimicking early vertebrate development, taken 1 day apart from each other. Brighter regions indicate the early mesoderm marker T/Brachyury (images taken from ref. 26). (c–e) Ternary fluid mixture model: a droplet, immersed in fluid 3 and initially composed of a mixture of fluids 1 and 2 (c), undergoes phase-separation until reaching the thermodynamic equilibrium state (d) characterized by a surface tension balance between all interfaces. (e) Schematic representation of the physical configuration. (f) Dependence of the thermodynamic equilibrium state on the inner-to-outer tension ratio r = 2σ12/(σ13 + σ23) and the relative surface tension difference Δσ = (σ13 − σ23)/σ12. The hatched region marks an unphysical regime, because at least one of the tensions σij would need to be negative there. | ||
As a first step towards building a better physical understanding of such cellular aggregates, we study here the passive dynamics of a ternary phase-separating system (Fig. 1c–e), where a droplet made out of two fluid phases (1 and 2) is suspended in a third fluid phase (3). There is a limited number of possibilities for the thermodynamic equilibrium state of such a ternary system, depending on the ratios of the interface tension σ12 to the surface tensions σ13 and σ23 (Fig. 1f). Here, we focus on the case where the equilibrium state is a Janus droplet (Fig. 1d), i.e. where σ12 < σ13 + σ23 and |σ13 − σ23| < σ12 (white region in Fig. 1f). While the equilibrium state is well known, we are interested in the dynamics that leads to this state, and how it depends on the interplay between diffusion and hydrodynamic flows. We start from an initial state where fluids 1 and 2 are almost homogeneously mixed inside of a spherical droplet (Fig. 1c). Thus, during the phase separation process, the system needs to spontaneously break rotational symmetry to reach the polarized equilibrium state (Fig. 1d).
Here, we numerically study the dynamics of this ternary system using 2D hybrid finite-volume Lattice-Boltzmann simulations of coupled Cahn-Hilliard and Stokes equations. We study the system's dynamics in terms of a Peclet number Pe that characterizes the magnitude of hydrodynamic advection as compared to diffusive effects. We find that while increasing Pe generally speeds up the phase separation process, intermediate Pe give rise to long-lived “croissant” states that slow down the relaxation to the final polarized state. When including an asymmetry between the surface tensions σ13 and σ23, transient polar Marangoni flows are created, but the overall Pe-dependency remains. Taken together, our work demonstrates the importance of hydrodynamic flows in deformable multi-phase droplets.
Note that our study does not constitute a complete description of the polarization of stem cell aggregates. Rather, we study the interaction of two effects that likely are important for this process: unmixing of cell populations and interface-tension-driven advection. This lays ground work for constructing effective physical descriptions for the collective cellular behavior in stem cell aggregates (see Section 5).
2 Model
2.1 Free energy
We describe a 2D ternary system where the three components have area fractions C1, C2, and C3, which sum up to one everywhere:| C1 + C2 + C3 = 1. | (1) |
 | (2) |
 ensure finite widths of all interfaces. For any binary interface between phases of dominating components j and k, i.e. where the third area fraction vanishes, interface width αjk and interface tension σjk take on the well-known values:28
ensure finite widths of all interfaces. For any binary interface between phases of dominating components j and k, i.e. where the third area fraction vanishes, interface width αjk and interface tension σjk take on the well-known values:28 | (3) |
2.2 Dynamic equations
To define the dynamics of the area fractions Cj such that eqn (1) remains fulfilled, we follow Semprebon et al.28 by introducing phase fields ϕ and ψ as| ϕ = C1 − C2 and ψ = C3. | (4) |
 | (5) |
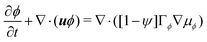 | (6a) |
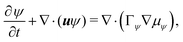 | (6b) |
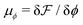 and
and 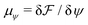 are the chemical potentials of ϕ and ψ, respectively. The factor [1 − ψ] in eqn (6a) ensures that fluids 1 and 2 do not diffuse across fluid 3. This is motivated by the biological background – we exclude any dissociation and re-association of cells (components 1 and 2) from/to the aggregate.
are the chemical potentials of ϕ and ψ, respectively. The factor [1 − ψ] in eqn (6a) ensures that fluids 1 and 2 do not diffuse across fluid 3. This is motivated by the biological background – we exclude any dissociation and re-association of cells (components 1 and 2) from/to the aggregate.
To account for hydrodynamic effects, we describe all phases of the system as incompressible Newtonian fluids, using the incompressible Stokes' equations:
| 0 = ∇·u | (7a) |
| 0 = −∇Π +∇·(2ηS) − ϕ∇μϕ − ψ∇μψ. | (7b) |
2.3 Initial and boundary conditions
We initialize the 2D system in a configuration schematized in Fig. 1c and e. The system initially consists of a circular droplet with diameter L, composed of a mixture of fluids 1 and 2 with ψ = 0, which is surrounded by fluid 3 with ψ = 1 and ϕ = 0. The inside of the droplet is initialized as ϕ =![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + ΔϕICξ, where
+ ΔϕICξ, where ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) and ΔϕIC are scalar parameters, and ξ is zero-mean, delta-correlated Gaussian white noise. The parameter
and ΔϕIC are scalar parameters, and ξ is zero-mean, delta-correlated Gaussian white noise. The parameter ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) corresponds to the conserved area average of ϕ, defined as
corresponds to the conserved area average of ϕ, defined as 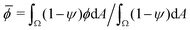 . We simulate the system in a squared periodic box with side length Lt. Parameter values are listed in Table 1.
. We simulate the system in a squared periodic box with side length Lt. Parameter values are listed in Table 1.
| Parameter |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif)
|
L/α | r | Peψ | η i/ηo | ΔϕIC | L t /L | Δx/α | Δt/(Δxηi/σ12) |
|---|---|---|---|---|---|---|---|---|---|
| Value | 0 | 64 | 1 | 15/32 | 20 | 0.01 | 2 | 1 | 1/640 |
2.4 Dimensionless parameters
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) in area fractions between fluids 1 and 2. Here we focus exclusively on the case
in area fractions between fluids 1 and 2. Here we focus exclusively on the case ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0, i.e. each fluid occupies half of the droplet area. Second, we set the ratio between droplet size L and interface width α to L/α = 64.
= 0, i.e. each fluid occupies half of the droplet area. Second, we set the ratio between droplet size L and interface width α to L/α = 64.
Finally, the equilibrium state also depends on the three tensions σjk, for which we choose the following two dimensionless ratios:
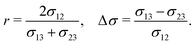 | (8) |
First, we define a Peclet number that compares advective fluxes due to hydrodynamic flows to the diffusive fluxes of the ϕ-field:
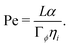 | (9) |
Second, we define a Peclet number with respect to the ψ field, and with respect to the interface width α, as Peψ = α2/(Γψηi). Here, we fix this number to a relatively small value of Peψ = 15/32 to ensure that the outer droplet interface remains stable during the simulations.
Third, we fix the viscosity ratio between droplet and the surrounding fluid to the value ηi/ηo = 20. We have checked that changes of this ratio do not strongly affect the simulation results as long as ηi/ηo ≳ 10.
2.5 Numerical implementation
We solve the dynamical equations (6a)–(7b) using a hybrid finite-volume Lattice Boltzmann approach. Similar methods have been used in earlier publications,30–32 which employed finite-difference schemes for the phase field dynamics. Here, we use a finite-volume scheme instead to ensure exact conservation of the scalar fields ϕ and ψ.33We discretize space using a Cartesian square grid with spacing Δx = α. For the advection terms in eqn (6a) and (6b), we use a first-order upwind scheme, and for the diffusive fluxes we use a central second-order scheme. We integrate over time using a first-order explicit Euler scheme. We solve the incompressible Stokes eqn (7a) and (7b) using a two-relaxation-time Lattice Boltzmann method.34 While the Lattice Boltzmann method actually solves the Navier–Stokes equations, which include inertia, we treat the Reynolds number (i.e. inertia) as a small numerical parameter here. The time step for both finite-volume and Lattice Boltzmann parts is Δt = (Δx/vf)/640 with the flow velocity scale vf = σ12/ηi. Details on the numerical method are provided in the ESI.†
3 Results
In the following, we examine how the droplet polarization dynamics depends (i) on the magnitude of advection as quantified by the Peclet number Pe (Sections 3.1 and 3.2) and (ii) on surface tension asymmetry, Δσ ≠ 0 (Section 3.3).3.1 Advection speeds up the polarization process
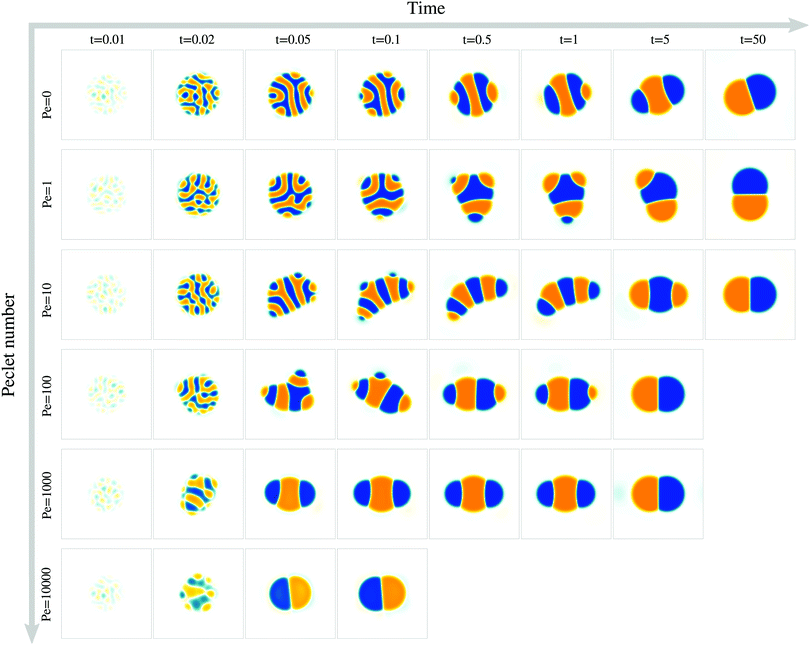
To study the role of advection for the phase separation process, we run simulations with symmetric surface tensions, Δσ = 0, and varying Peclet number Pe (Fig. 2, Movies S1–S3, ESI†). In all cases, the system reaches indeed the polar equilibrium state. Leading up to this equilibrium state, we find well-known features of spinodal decomposition, including an initial decomposition phase where |ϕ| generally grows until it saturates at ≈1, and a subsequent coarsening phase. However, Fig. 2 also suggests (1) that increasing the Peclet number speeds up the phase separation process (discussed below in this section),1 and (2) that intermediate Peclet numbers give rise to long-lived strongly elongated droplets (discussed in the next Section 3.2).To quantify in how far increasing the Peclet number speeds up the droplet polarization process, we measure the time evolution of a dipole moment, which we define as
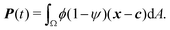 | (10) |
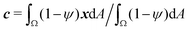 . We study the normalized magnitude p = |P|/P0, where P0 = L3/6 is a reference dipole moment, which corresponds to a circular droplet of diameter L split in two semi-circular regions with ϕ = 1 and ϕ = −1. We find that indeed, the dipole moment p grows faster for higher Peclet number (Fig. 3a). We moreover define a polarization time tp of the system as the time when the polarization first reaches p ≥ 0.9peq, where peq is the dipole moment of the equilibrium state. Consistent with known results from the literature,1 we find that advection speeds up the phase separation process (Fig. 3b). However, we note this effect only for Pe ≳ 100, while tp remains approximately constant for Peclet numbers below 100. To better understand this Pe dependence of the polarization process, we now discuss the different phases of the process separately.
. We study the normalized magnitude p = |P|/P0, where P0 = L3/6 is a reference dipole moment, which corresponds to a circular droplet of diameter L split in two semi-circular regions with ϕ = 1 and ϕ = −1. We find that indeed, the dipole moment p grows faster for higher Peclet number (Fig. 3a). We moreover define a polarization time tp of the system as the time when the polarization first reaches p ≥ 0.9peq, where peq is the dipole moment of the equilibrium state. Consistent with known results from the literature,1 we find that advection speeds up the phase separation process (Fig. 3b). However, we note this effect only for Pe ≳ 100, while tp remains approximately constant for Peclet numbers below 100. To better understand this Pe dependence of the polarization process, we now discuss the different phases of the process separately.
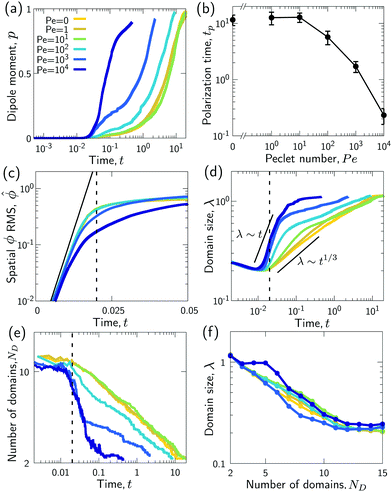 | ||
Fig. 3 Advection speeds up droplet polarization by accelerating the coarsening phase. (a) Dipole moment p depending on time for different Pe. (b) Polarization time tp as a function of the Peclet number; error bars indicate the standard error of the mean. (c) Spatial root-mean-square of ϕ depending on time. The black line shows the initial growth with rate ω predicted by linear stability analysis, 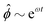 . (d) Domain size λ as defined in the ESI,† depending on time. (e) Number of phase domains ND depending on time. (f) Domain size λ as a function of the number of phase domains ND. Legends in panels c–f same as in panel a. In panels c–e, the vertical dashed line indicates the approximate end time td ≈ 0.02τD of the initial decomposition phase. The quantities on all ordinate axes are averaged over 25 simulation runs. . (d) Domain size λ as defined in the ESI,† depending on time. (e) Number of phase domains ND depending on time. (f) Domain size λ as a function of the number of phase domains ND. Legends in panels c–f same as in panel a. In panels c–e, the vertical dashed line indicates the approximate end time td ≈ 0.02τD of the initial decomposition phase. The quantities on all ordinate axes are averaged over 25 simulation runs. | ||
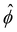 (RMS) of ϕ, defined as
(RMS) of ϕ, defined as 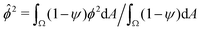 . Fig. 3c shows that
. Fig. 3c shows that 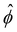 initially increases exponentially, and reaches a saturation at approximately td. Except for very large Pe, the behavior during this initial phase does not depend very strongly on the Peclet number.
initially increases exponentially, and reaches a saturation at approximately td. Except for very large Pe, the behavior during this initial phase does not depend very strongly on the Peclet number.
For very large Peclet number, Pe ≳ 103, we observe a coarsening exponent close to one (Fig. 3d), which corresponds to the expected result for advection-dominated coarsening. For such large Pe numbers, advection even induces noticeable coarsening already during the initial decomposition phase (Fig. 3d). This early coarsening is also the likely reason for the slowing down of the initial decomposition for very large Pe (Fig. 3c), since diffusive unmixing needs to act over larger length scales in this regime.
The difference in the coarsening behavior between small and large Peclet number is also apparent when studying the behavior of the number of phase domains ND (Fig. 3e). We computationally define a phase domain as a connected region with constant sign of ϕ. The number of domains ND decreases during the coarsening process until it reaches a minimum of two, which is attained in the equilibrium state. Indeed, ND decreases more rapidly for larger Peclet number (Fig. 3e). This confirms that advection speeds up the coarsening process, as ND and λ are strongly correlated (Fig. 3f).
For intermediate Peclet number, we initially observe a relatively fast coarsening (Fig. 3d). However, coarsening subsequently significantly slows down, which is also the reason why the polarization time tp decreases only for very large Pe (compare Fig. 3b and d). What could be responsible for this slow down?
3.2 Elongated, striped droplets at intermediate Pe
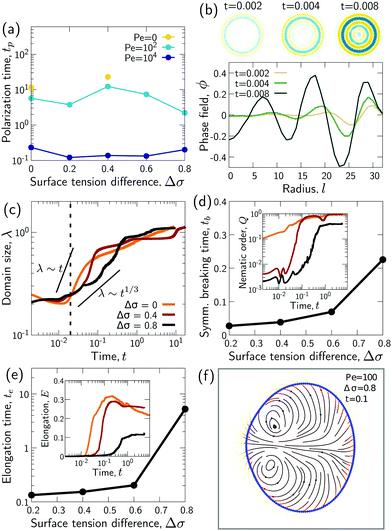
We wondered whether the elongated, striped droplets that emerge for intermediate Pe (Fig. 2) could be related to the slow down of the coarsening at intermediate Pe numbers. To test this hypothesis, we quantified the time evolution of droplet elongation E. We define E by expressing the droplet shape in polar coordinates and computing the second angular Fourier mode (Fig. 4a, details in ESI†). It is normalized such that E corresponds to the maximal radius variation of the second Fourier mode relative to the initial droplet radius r0 = L/2.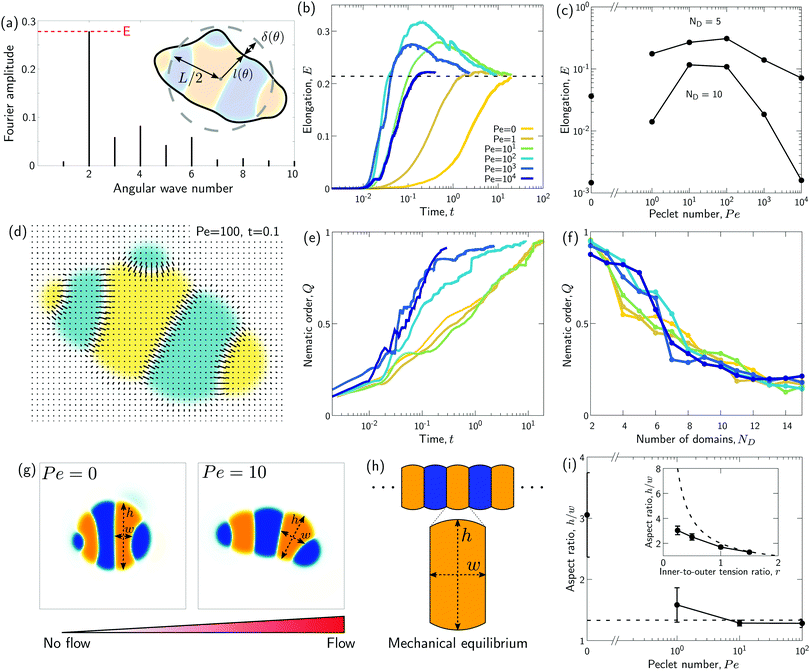 | ||
| Fig. 4 Transient “croissant” states, which are elongated and show a striped organization of the phase domains. (a) Illustrative example of droplet surface deformation, at Pe = 100 and t = 0.1, and resulting angular Fourier spectrum used to define the droplet elongation E. (b) Evolution of the droplet elongation as a function of time. (c) Transient droplet elongation as a function of the Peclet number at fixed numbers of phase domains, ND. (d) Illustrative nematic field based on the ϕ-field gradient, at Pe = 100 and t = 0.1. (e and f) Evolution of the global nematic order as a function of (e) time and (f) ND, for different Peclet numbers. (g) Comparison for two snapshots for Pe = 0 and Pe = 10 with ND = 5. (h) Limiting case of infinite chain of equally-sized phase domains in mechanical equilibrium, where h/w = 2/r (see ESI†). (i) Phase domain aspect ratio h/w as of function of Pe for r = 1.5. (i inset) Aspect ratio over inner-to-outer tension ratio r for Pe = 10. The aspect ratio is averaged over all domains having exactly two neighboring domains (i.e. all non-branching inner domains) for time points with ND = 5. The quantities in all panels are averaged over a series of 25 simulations. | ||
We find that for Pe = 0, where the droplet changes its shape through diffusive processes only, and very large Pe, where advection dominates, the droplet elongation E monotonically increases with time until E ≈ 0.2 (Fig. 4b), which corresponds to the elongation of the final equilibrium state. However, for intermediate Pe, droplet elongation first increases as high as E ≈ 0.3 before decreasing back to the final value of ≈0.2. Moreover, this regime of transient elongation is correlated in time to the phase of slow coarsening (compare Fig. 3d and 4b). This suggests that the elongated droplet structures could indeed be related to the observed coarsening slow down for intermediate Pe.
Because the temporal coarsening dynamics differs when varying the Pe number, we also plot the droplet elongation over the number of domains ND. This allows to compare droplet elongation E at similar “stages” of the coarsening process across different Pe numbers. We find that at the same ND, elongation can be up to two orders of magnitude larger for intermediate Pe (Fig. 4c).
We also observe in Fig. 2 that elongated droplets show striped domain patterns. Such a striped arrangement could indeed help to explain the observed coarsening slow down even for intermediate Pe. A striped pattern of domains could be close to a mechanical equilibrium where only little hydrodynamic flows occur. In this case, coarsening would occur almost entirely through diffusion in an Ostwald-ripening-like process: Due to an increased Laplace pressure in small stripes as compared to larger stripes of the same color, the larger domain would slowly grow at the expense of the smaller domain through diffusive fluxes across the domains of opposite color.
To test these ideas and to better understand how elongated droplet shapes emerge, we quantify the nematic order of inner domain boundaries (i.e. between droplet domains 1 and 2) by an order parameter Q (Fig. 4d). To this end, we first introduce a tensor field Aαβ that characterizes the local orientation of ϕ interfaces (Fig. 4d):
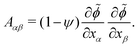 | (11) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = (C1 − C2)/(C1 + C2) = ϕ/(1 − ψ). We then introduce the tensor Qαβ as the spatially averaged, symmetric, traceless part of Aαβ:
= (C1 − C2)/(C1 + C2) = ϕ/(1 − ψ). We then introduce the tensor Qαβ as the spatially averaged, symmetric, traceless part of Aαβ: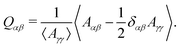 | (12) |
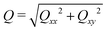 . When the domain interfaces are randomly oriented, nematic order vanishes, Q = 0, while when all domain interfaces are straight and perfectly aligned, Q = 1.
. When the domain interfaces are randomly oriented, nematic order vanishes, Q = 0, while when all domain interfaces are straight and perfectly aligned, Q = 1.
Generally, the nematic interface alignment Q increases over time, and it does so more quickly for large Pe numbers (Fig. 4e). Note that the final equilibrium state has Q ≈ 1, because it consists of a single straight internal interface. Notably, if we plot Q over ND, we find no strong difference across Pe numbers (Fig. 4f). Indeed, Fig. 2 also show striped domain patterns not only for intermediate Pe, but also for Pe = 0. But if the domain pattern is also striped for Pe = 0, then why do we find elongated droplets only for intermediate Pe (Fig. 4g)?
A possible reason for why Pe > 0 droplets are more elongated is that hydrodynamic flows would drive the system closer to mechanical equilibrium, where in mechanical equilibrium the droplets might be elongated. To test these ideas, we first analytically compute the mechanical equilibrium state for a striped droplet. For simplicity, we focus on the limiting case of an infinite chain of equally sized domains (Fig. 4h). In mechanical equilibrium with Δσ = 0, interfaces between phases 1 and 2 are parallel straight lines, and surfaces to the external fluid 3 are circular arcs. One can furthermore show that the aspect ratio of a single domain in mechanical equilibrium depends only on the inner-to-outer tension ratio r as h/w = 2/r (derivation in ESI†). Thus, in a crude approximation, a droplet with ND domains in mechanical equilibrium would have aspect ratio NDw/h = NDr/2.
To test whether droplets for intermediate Pe approach the mechanical equilibrium state, we quantified the domain aspect ratio h/w in our simulations (details in ESI†). We plot h/w for r = 1.5 depending on Pe in Fig. 4i and compare to the theoretical solution of the infinite chain (dashed line). Our results suggest that the droplets do indeed approach mechanical equilibrium as Pe increases.
To further test these ideas, we compared domain aspect ratios also across different values of the inner-to-outer tension ratio r (Fig. 4i inset). We found that for smaller r, the measured aspect ratio started to become smaller than the theoretical prediction. This makes sense since for smaller r, the overall droplet aspect ratio also becomes smaller and so the simulated droplets deviate more strongly from the theoretical picture of a chain of equally sized domains. Indeed, for r → 0, the infinite-chain prediction would be h/w = 2/r → ∞. However, in this limit, there is no inner interface tension, σ12 = 0, and the droplet shape is spherical. When dividing a spherical droplet into ND domains of equal width, the domain aspect ratio is h/w ≤ ND, which corresponds to an approximate upper bound for h/w.
Taken together, our results show that for intermediate Pe, transient droplet states form, which are striped and elongated. They are close to mechanical equilibrium and coarsen only through diffusive fluxes, which makes them long-lived.
3.3 Effect of a difference between the surface tensions of the two droplet phases
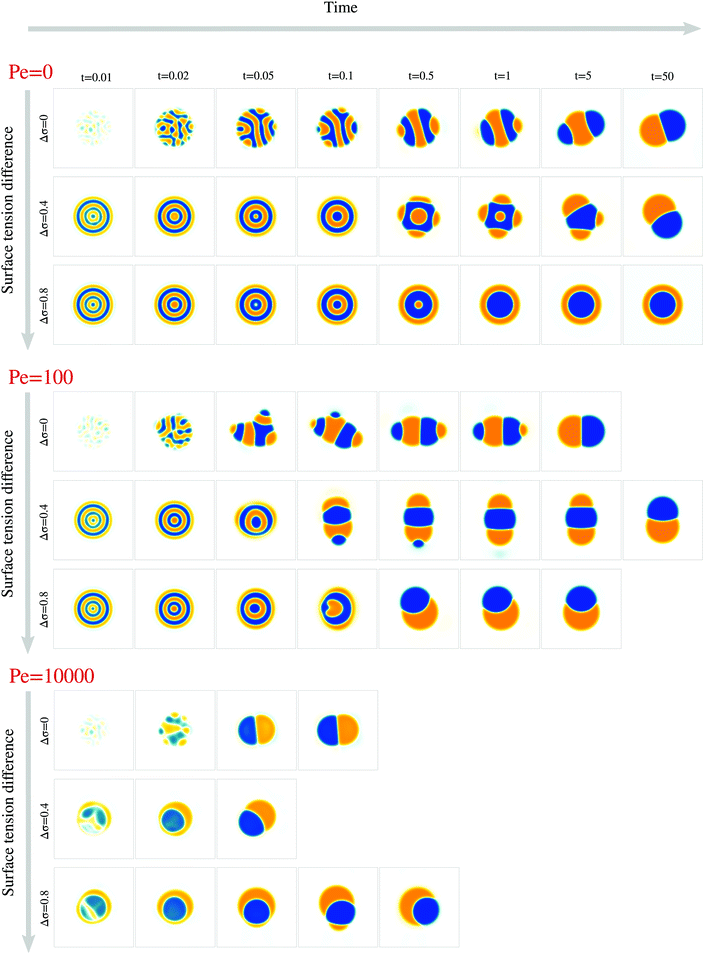
We next study the effect of different surface tensions between the two droplet phases, Δσ ≠ 0. To this end, we carried out simulations with varying 0 ≤ Δσ < 1 for the Peclet numbers 0, 100, and 104 (Fig. 5, Movies S1–S9, ESI†).We first examined how varying the surface tension difference Δσ would change the time tp required to reach the polarized equilibrium state (Fig. 6a). Although a Janus droplet is the equilibrium state for the chosen parameter regime, the system can exhibit very long-lived rotationally symmetric patterns. This is particularly true for Pe = 0, where only simulations with Δσ = 0 and Δσ = 0.4 reached the polar equilibrium state within the maximal simulation time of tmax = 50. For the two larger Pe values, the equilibrium state was always reached after a finite time tp, but no clear trend in the dependency on Δσ is apparent. To better understand these results, we again separately discuss several phases of the process.
Thus, while the time tp for the whole process varies non-monotonically with Δσ, the time te when the croissant state appears increases monotonically but is generally much smaller than tp (compare Fig. 6a and e). This means that the variation in tp is due to a variation in the life time of the croissant states. In the previous section, we concluded that for intermediate Pe, these states coarsen only due to an Ostwald-ripening-like process, where smaller domains shrink at the expense of larger ones. This suggests that the variation in tp may just be due to the way the two droplet phases happen to be distributed into different domains by the transient flows that follow the symmetry breaking. Indeed, we find for instance that for Pe = 100, the simulations with Δσ = 0.4 need longest to relax to the 2-domain equilibrium state (Fig. 6a), and these are also the simulations where two approximately equally-sized orange domains form (Fig. 5), leading to an initially slow diffusion between the two domains.
Finally, in simulations with Pe = 104, a first symmetry breaking event occurred at a time around 0.01. The ensuing transient flows often resulted in a second approximately rotationally symmetric state with 2 domains at a time around 0.02. This state only later resolved into the polar equilibrium state. We believe this second, 2-domain rotationally symmetric state forms in this case because the first breaking of rotational symmetry occurs before the initial decomposition is finished, i.e. when |ϕ| is significantly smaller than one within the domains. As a consequence, the interface tension between both domains, which scales as ∼ϕ2, is smaller, and thus the effective value of Δσ = (σ13 − σ23)/σ12 is larger than its nominal value. Hence, we believe that we find the rotationally symmetric 2-domain state as transient state, because the expected equilibrium state is the rotationally symmetric one as long as the effective Δσ is larger than one (Fig. 1f).
4 Discussion
In this article, we discussed phase separation in a two-phase deformable droplet. While the thermodynamic equilibrium state for such a system is well known, we studied the route to reach equilibrium. In particular, we focused on the interplay between spinodal decomposition and advection with hydrodynamic flows created by interface tensions. While this interplay has been studied before,4 it was unknown how it plays out in a finite, deformable system. We found that advection can speed up the coarsening process as reported earlier.1We moreover found that for intermediate Pe numbers, elongated, striped droplet states emerge, which we call “croissant” states. The stripes correspond to a nematic alignment of inner domain boundaries, which emerges for low and intermediate Pe. For intermediate Pe, the striped droplets elongate as they approach mechanical equilibrium. These states are long-lived, because they coarsen almost exclusively via diffusion, through an Ostwald-ripening-like process. We did not observe such “croissant” states for very large Pe numbers, where coarsening is entirely dominated by advection, which leads to coalescence of the phase domains before a striped pattern can develop (Movie S3, ESI†).
We also studied the effect of an asymmetry between the surface tensions of the two droplet phases, and we found that it changes in particular the beginning of the phase separation process. The emergence of composition waves initially creates a rotationally symmetric system, which then starts to coarsen diffusively. Breaking of this rotationally symmetric state triggers transient flows that are reminiscent of Marangoni flows in droplets.37,38 These transient flows typically gave rise to a long-lived croissant state. Taken together, our results demonstrate that advection can play an important role in the coarsening dynamics of deformable two-phase droplets.
The croissant states that we observe are reminiscent of past observations made in the field. First, similar observations have been made in ternary phase separation starting from homogeneous states, even for Pe = 0.28,39 However, with a circular droplet as initial state (Fig. 1c), the emergence of an elongated croissant requires large deformations, which are promoted by advective effects. Second, striped and elongated states can also be observed in vesicles on whose surface different phases coexist.40,41 However, while the croissant states in our study are created by the interface tensions between bulk phases, the vesicle shapes are affected by the constant surface area, line tensions between phases on the surface, and a phase-dependent free energy of the membrane curvature. Thus, the pattern- and shape-forming mechanisms in these two kinds of systems are likely quite different.
It would be interesting to test whether the croissant states can be reproduced experimentally. Indeed, e.g. multi-component emulsion droplets are receiving continuing attention42–44 given their applications in the food and pharmaceutical industries.45 The croissant states might open up new avenues in these areas.
5 Symmetry breaking in stem cell aggregates
This work has also important implications for the kinds of biological systems that originally motivated this study.22,23,26,27,46–48 Aggregates of stem cells that mimic early vertebrate axis formation are known to develop a polar structure (Fig. 1a and b),22 reminiscent of two-phase Janus droplets in thermodynamic equilibrium (Fig. 1d), where the different phases correspond to different cell types. While current studies of such stem cell colonies focus almost exclusively on the biochemical dynamics,49,50 tissue flow and advection likely play an important role as well. Indeed, recent experiments have identified significant large-scale tissue flows in stem cell aggregates.26As a first rough estimate, the Peclet number in mouse embryonic stem cell aggregates is of the order of Pe ∼ Lσ/Dη ∼ 200. This is based on an aggregate size of L ∼ 200 μm,26 a tension-to-viscosity ratio of σ /η ∼ 5 μm h−1,51 and a diffusion constant of order D ∼ 5 μm2 h−1 (unpublished preliminary data, lab of Pierre-François Lenne). In this Pe regime, we observe in our simulations the emergence of the croissant states. Indeed, these states appear visually reminiscent of somites, which have also been observed to form in gastruloids,27 while an interface tension has been reported at somite–somite boundaries in vivo.52 However, first, the mechanism of somite formation in vertebrates is generally believed to crucially involve the complex interplay of biochemical signals in a clock-and-wavefront model53 (even though purely mechanical models are discussed as well54). Second, different from our model, gastruloids exhibit a polar organization before somites form.27 This raises the question why in experiments there are usually no croissant states observed before polarization.
Stem cell cultures are of course much more complex than the model we studied here, and future refined studies should take additional effects into account. First, experiments indicate that the dynamics of some biological signaling molecules and transcription factors is non-conserving in these systems.26,49,50 To take this into account in our model, a source term needs to be added in the ϕ equation eqn (6a). Similarly, we studied here a droplet of constant volume, while the stem cell colonies are typically growing. To implement this, source terms need to be added to the ψ dynamics eqn (6b) and in the incompressibility condition eqn (7a).
Second, we focused here on a 2D model, while the stem cell systems motivating this study are 3D aggregates.22,26 While there are likely several commonalities between the 2D and 3D cases, we expect differences for instance due to Laplace pressure effects.36,55,56 Such effects arise only in 3D, where in tube-shaped phase domains, interface tension creates a Laplace pressure that depends on the tube radius. This pressure can lead to necking and breakup of connected domains in a Plateau-Rayleigh instability,55 but it can also lead to a pumping effect that makes the surface layer of the droplet grow more rapidly.36 It will be interesting to dissect the consequences of these effects for a deformable 3D droplet in future work.
Third, while we focused here on the case of a purely liquid aggregate, the rheology is very likely more complicated.16 Indeed, relatively young mouse stem cell aggregates have been described as visco-elastic solids before,51 and the buildup of elastic stresses would likely affect the aggregate behavior.
Fourth, the cell aggregates are active systems, and so activity may need to be included for an effective description of symmetry breaking in the aggregates.57,58
Fifth, additional hydrodynamic fields may be required to fully account for some features of the stem cell aggregate dynamics. In particular, the inclusion of more scalar fields in addition to ϕ may be required,49,50 or of a polar field as experiments on fish aggregates have pointed to a role of polarity proteins.59,60
Finally, the real system dynamics is likely influenced by several types of noise. Moreover, a ϕ-dependence of mechanical properties such as viscosity or local volume growth may be required to explain some of the experimental observations.61
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank Andrej Košmrlj, Pierre-François Lenne, and Sham Tlili for critical reading of the manuscript. We also thank Pierre-François Lenne and Sham Tlili for useful discussions and experimental data. The project leading to this publication has received funding from the “Investissements d'Avenir” French Government program managed by the French National Research Agency (ANR-16-CONV-0001) and from “Excellence Initiative of Aix-Marseille University – A*MIDEX”. The Centre de Calcul Intensif dAix-Marseille is acknowledged for granting access to its high performance computing resources. M. M. thanks the Centre Interdisciplinaire de Nanoscience de Marseille (CINaM) for office space.References
- A. J. Bray, Adv. Phys., 2002, 51, 481–587 CrossRef.
- S. Mao, D. Kuldinow, M. P. Haataja and A. Košmrlj, Soft Matter, 2019, 15, 1297–1311 RSC.
- S. Mao, M. S. Chakraverti-Wuerthwein, H. Gaudio and A. Košmrlj, Phys. Rev. Lett., 2020, 125, 218003 CrossRef CAS PubMed.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 1998, 81, 389–392 CrossRef CAS.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 CrossRef CAS PubMed.
- Q.-X. Liu, A. Doelman, V. Rottschäfer, M. de Jager, P. M. Herman, M. Rietkerk and J. van de Koppel, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11905–11910 CrossRef CAS PubMed.
- C. P. Brangwynne, J. Cell Biol., 2013, 203, 875–881 CrossRef CAS PubMed.
- R. J. Wheeler and A. A. Hyman, Philos. Trans. R. Soc., B, 2018, 373, 20170193 CrossRef PubMed.
- H.-S. Kuan, W. Pönisch, F. Jülicher and V. Zaburdaev, Phys. Rev. Lett., 2021, 126, 18102 CrossRef CAS PubMed.
- M. S. Steinberg, Science, 1963, 141, 401–408 CrossRef CAS PubMed.
- R. A. Foty and M. S. Steinberg, Dev. Biol., 2005, 278, 255–263 CrossRef CAS PubMed.
- E. Cachat, W. Liu, K. C. Martin, X. Yuan, H. Yin, P. Hohenstein and J. A. Davies, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed.
- J. D. Amack and M. L. Manning, Science, 2012, 338, 212–215 CrossRef CAS PubMed.
- P. L. Townes and J. Holtfreter, J. Exp. Zool., 1955, 128, 53–120 CrossRef.
- E.-M. Schötz, R. D. Burdine, F. Jülicher, M. S. Steinberg, C.-P. Heisenberg and R. A. Foty, HFSP J., 2008, 2, 42–56 CrossRef PubMed.
- P. Marmottant, A. Mgharbel, J. Kafer, B. Audren, J.-P. Rieu, J.-C. Vial, B. van der Sanden, A. F. M. Maree, F. Graner and H. Delanoe-Ayari, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17271–17275 CrossRef CAS PubMed.
- R. Etournay, M. Popović, M. Merkel, A. Nandi, C. Blasse, B. Aigouy, H. Brandl, G. Myers, G. Salbreux, F. Jülicher and S. Eaton, Elife, 2015, 4, e07090 CrossRef PubMed.
- H. Morita, S. Grigolon, M. Bock, S. F. Krens, G. Salbreux and C. P. Heisenberg, Dev. Cell, 2017, 40, 354–366.e4 CrossRef CAS PubMed.
- S. J. Streichan, M. Lefebvre, N. Noll, E. F. Wieschaus and B. I. Shraiman, Elife, 2018, 7, e27454 CrossRef PubMed.
- S. Münster, A. Jain, A. Mietke, A. Pavlopoulos, S. W. Grill and P. Tomancak, Nature, 2019, 568, 395–399 CrossRef PubMed.
- S. Grosser, J. Lippoldt, L. Oswald, M. Merkel, D. M. Sussman, F. Renner, P. Gottheil, E. W. Morawetz, T. Fuhs, X. Xie, S. Pawlizak, A. W. Fritsch, B. Wolf, L.-C. Horn, S. Briest, B. Aktas, M. L. Manning and J. A. Käs, Phys. Rev. X, 2021, 11, 011033 CAS.
- S. C. van den Brink, P. Baillie-Johnson, T. Balayo, A.-K. Hadjantonakis, S. Nowotschin, D. A. Turner and A. Martinez Arias, Development, 2014, 141, 4231–4242 CrossRef CAS PubMed.
- L. Beccari, N. Moris, M. Girgin, D. A. Turner, P. Baillie-Johnson, A.-C. Cossy, M. P. Lutolf, D. Duboule and A. M. Arias, Nature, 2018, 562, 272–276 CrossRef CAS PubMed.
- T. Fulton, V. Trivedi, A. Attardi, K. Anlas, C. Dingare, A. M. Arias and B. Steventon, Curr. Biol., 2020, 30, 2984–2994.e3 CrossRef CAS PubMed.
- F. Cermola, C. D'Aniello, R. Tatè, D. De Cesare, A. Martinez-Arias, G. Minchiotti and E. J. Patriarca, Stem Cell Reports, 2021, 16, 354–369 CrossRef CAS PubMed.
- A. Hashmi, S. Tlili, P. Perrin, A. Martinez-Arias and P. F. Lenne, bioRxiv, 2020 DOI:10.1101/2020.05.21.105551.
- S. C. van den Brink, A. Alemany, V. van Batenburg, N. Moris, M. Blotenburg, J. Vivié, P. Baillie-Johnson, J. Nichols, K. F. Sonnen, A. Martinez Arias and A. van Oudenaarden, Nature, 2020, 582, 405–409 CrossRef CAS PubMed.
- C. Semprebon, T. Krüger and H. Kusumaatmaja, Phys. Rev. E, 2016, 93, 033305 CrossRef PubMed.
- R. David, O. Luu, E. W. Damm, J. W. H. Wen, M. Nagel and R. Winklbauer, Development, 2014, 141, 3672–3682 CrossRef CAS PubMed.
- A. Tiribocchi, N. Stella, G. Gonnella and A. Lamura, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 026701 CrossRef CAS PubMed.
- M. L. Blow, S. P. Thampi and J. M. Yeomans, Phys. Rev. Lett., 2014, 113, 248303 CrossRef PubMed.
- A. Doostmohammadi, S. P. Thampi and J. M. Yeomans, Phys. Rev. Lett., 2016, 117, 048102 CrossRef PubMed.
- R. Eymard, T. Gallouët and R. Herbin, Handb. Numer. Anal., 2000, 7, 713–1018 Search PubMed.
- S. Gsell, U. D'Ortona and J. Favier, J. Comput. Phys., 2021, 429, 109943 CrossRef CAS.
- B. P. Lee, J. F. Douglas and S. C. Glotzer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 60, 5812 CrossRef CAS PubMed.
- H. Tanaka, J. Phys.: Condens. Matter, 2001, 13, 4637 CrossRef CAS.
- M. Schmitt and H. Stark, Phys. Fluids, 2016, 28, 012106 CrossRef.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193 CrossRef CAS.
- L.-Q. Chen, Acta Metall. Mater., 1994, 42, 3503–3513 CrossRef CAS.
- T. Taniguchi, Phys. Rev. Lett., 1996, 76, 4444 CrossRef CAS PubMed.
- M. Yanagisawa, M. Imai and T. Taniguchi, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- A. S. Utada, E. Lorenceau, D. R. Link, P. D. Kaplan, H. A. Stone and D. Weitz, Science, 2005, 308, 537–541 CrossRef CAS PubMed.
- T. Nisisako, Curr. Opin. Colloid Interface Sci., 2016, 25, 1–12 CrossRef CAS.
- N. Wang, C. Semprebon, H. Liu, C. Zhang and H. Kusumaatmaja, J. Fluid Mech., 2020, 895, A22 CrossRef CAS.
- M. Iqbal, N. Zafar, H. Fessi and A. Elaissari, Int. J. Pharmaceutics, 2015, 496, 173–190 CrossRef CAS PubMed.
- D. A. Turner, M. Girgin, L. Alonso-Crisostomo, V. Trivedi, P. Baillie-Johnson, C. R. Glodowski, P. C. Hayward, J. Collignon, C. Gustavsen and P. Serup, et al. , Development, 2017, 144, 3894–3906 CAS.
- N. Moris, K. Anlas, S. C. van den Brink, A. Alemany, J. Schröder, S. Ghimire, T. Balayo, A. van Oudenaarden and A. M. Arias, Nature, 2020, 582, 410–415 CrossRef CAS PubMed.
- K. Anlas, N. Gritti, D. Oriola, K. Arató, F. Nakaki, J. Le Lim, J. Sharpe and V. Trivedi, bioRxiv, 2021 DOI:10.1101/2021.02.24.432766.
- F. Etoc, J. Metzger, A. Ruzo, C. Kirst, A. Yoney, M. Z. Ozair, A. H. Brivanlou and E. D. Siggia, Dev. Cell, 2016, 39, 302–315 CrossRef CAS PubMed.
- S. Chhabra, L. Liu, R. Goh, X. Kong and A. Warmflash, PLOS Biol., 2019, 17, e3000498 CrossRef CAS PubMed.
- D. Oriola, M. Marin-Riera, G. Aalderink, K. Anlas, N. Gritti, J. Sharpe and V. Trivedi, 2020, arXiv:2012.01455.
- E. Shelton, S. Kim, B. Gross, R. Wu, M. Pochitaloff, I. Lim, E. Sletten and O. Campàs, bioRxiv, 2021 DOI:10.1101/2021.03.27.437325.
- A. C. Oates, L. G. Morelli and S. Ares, Development, 2012, 139, 625–639 CrossRef CAS PubMed.
- P. Adhyapok, A. M. Piatkowska, M. J. Norman, S. G. Clendenon, C. D. Stern, J. A. Glazier and J. M. Belmonte, iScience, 2021, 24, 102317 CrossRef CAS PubMed.
- E. D. Siggia, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 595–605 CrossRef CAS.
- M. S. Hutson, G. W. Brodland, J. Yang and D. Viens, Phys. Rev. Lett., 2008, 101, 148105 CrossRef PubMed.
- A. Tiribocchi, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 115, 1–5 CrossRef PubMed.
- C. A. Weber, D. Zwicker, F. Jülicher and C. F. Lee, Rep. Prog. Phys., 2019, 82, 064601 CrossRef CAS PubMed.
- M. L. Williams and L. Solnica-Krezel, Elife, 2020, 9, 1–25 Search PubMed.
- E. Tjhung, D. Marenduzzo and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12381–12386 CrossRef CAS PubMed.
- A. Mongera, P. Rowghanian, H. J. Gustafson, E. Shelton, D. A. Kealhofer, E. K. Carn, F. Serwane, A. A. Lucio, J. Giammona and O. Campàs, Nature, 2018, 561, 401–405 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01647d |
| This journal is © The Royal Society of Chemistry 2022 |