Single-molecule magnets beyond a single lanthanide ion: the art of coupling

Abstract

The promising future of storing and processing quantized information at the molecular level has been attracting the study of Single-Molecule Magnets (SMMs) for almost three decades. Although some recent breakthroughs are mainly about the SMMs containing only one lanthanide ion, we believe SMMs can tell a much deeper story than the single-ion anisotropy. Here in this Perspective, we will try to draw a unified picture of SMMs as a delicately coupled spin system between multiple spin centres. The hierarchical couplings will be presented step-by-step, from the intra-atomic hyperfine coupling, to the direct and indirect intra-molecular couplings with neighbouring spin centres, and all the way to the inter-molecular and spin–phonon couplings. Along with the discussions on their distinctive impacts on the energy level structures and thus magnetic behaviours, a promising big picture for further studies is proposed, encouraging the multifaceted developments of molecular magnetism and beyond.

---

Yan-Cong Chen

Yan-Cong Chen was born in Guangzhou, China in 1990. He obtained his BSc (Chemistry, 2012) and PhD degrees (Inorganic Chemistry, 2017) from Sun Yat-Sen University, under the supervision of Prof. Ming-Liang Tong. He worked as a postdoctoral fellow in the same laboratory supported by the National Postdoctoral Program for Innovative Talents until 2021, and has been continuing as an associated researcher until now. His research interests cover the design, synthesis and characterization of various aspects of molecule-based magnetic materials, as well as their devices.

Ming-Liang Tong

Ming-Liang Tong was born in Hubei, China, in 1967. He received his BSc in 1989 from Central China Normal University (P. R. China), MSc in 1996 and PhD in 1999 from Sun Yat-Sen University (P. R. China). Then he joined the faculty at Sun Yat-Sen University and was promoted to a Professor in 2004. He worked as a Japan Society for the Promotion of Science (JSPS) postdoctoral fellow at Kyoto University (Japan) from 2001 to 2003. His current interests focus upon the design and development of new synthetic methods towards molecular magnetic materials including single-molecule magnets, cryogenic molecular magnetic refrigerants, spin crossover, and multifunctional molecular materials.

---

1. Introduction

Single-Molecule Magnets (SMMs) have attracted unprecedented interest in recent years due to their ability to store and process quantized information at the molecular level.¹ In such a manner, they have become one of the most promising candidates for the next-generation non-volatile memory elements, quantum information processors and molecular spintronic devices.^2–6 Since the discovery of {Mn₁₂} as an SMM until now,⁷ almost three decades have passed and great progress has been made one after another.^8–11 Most recently, multiple breakthroughs have been made especially in monometallic SMMs, namely Single-Ion Magnets (SIMs). By understanding and optimizing the single-ion parameters such as the anisotropy and energy barrier, many high-performance lanthanide SIMs (Ln-SIMs) have been reported,^12–15 leading to milestones such as the open magnetic hysteresis above liquid-nitrogen temperature.¹⁵

Although a lot of relevant studies mainly focus on optimizing the single-ion properties, especially the energy barriers, we believe this should not be the whole story, nor is it the end of the story. Coupling high-performance SIMs into SMMs is a natural extension, which however requires rational design better than trial and error. At this stage, we feel it is necessary to take some lessons learnt from Ln-SIMs and draw a blueprint toward higher-order systems by delicate couplings, in the hope of fuelling the upcoming leaps in SMMs and thus molecular magnetism.

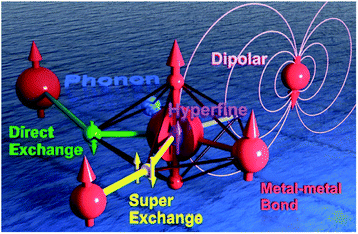
Here in this Perspective, we will look upon an SMM as a coupled multi-spin system between different spin centres (Fig. 1). We will present the hierarchical couplings from the hyperfine coupling with the nuclei, to the direct and indirect couplings with neighbouring spin centres, and all the way to the inter-molecular and spin–phonon couplings in the lattice. Meanwhile, a selected portion of related studies (rather than a complete collection) will also be discussed as characteristic examples. We hope that such insights can provide a deeper understanding of the fascinating behaviours of SMMs, inspire new ideas and research, and promote multifaceted developments of molecular magnetism as well as relevant fields in the near future.

Fig. 1 The schematic model of a Single-Ion Magnet building block (central red sphere) that is coupled to an intra-atomic nuclear spin through the hyperfine interactions (purple), to a radical-bridged spin centre through the direct exchange (green), to a nearby metal ion through a metal–metal bond (red), to a ligand-bridged spin centre through superexchange (yellow), to the dipolar field generated by a distant spin centre (pink), and to the lattice vibration/phonon (the blue ocean).

2. Lessons learnt from lanthanide single-ion magnets

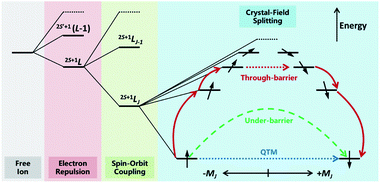
The discovery of double-decker phthalocyanine complexes (TBA)[Ln(Pc)₂] functioning as SMMs brought an exciting inspiration that even a single metal ion is capable of retaining its magnetic memory in a suitable coordination environment.^12,16–20 In the subsequent nearly two decades, more than a thousand SIMs have been reported,^21–24 which form a huge database for mining some of the fundamental knowledge towards high-performance SIMs and SMMs. In such a manner, the most important reason for studying SIMs may be their relatively simpler molecular structures and therefore clearer magneto–structural correlations. In particular, from the state-of-the-art ab initio calculation^25,26 to the intuitive and easy-to-use SIMPRE,²⁷ it is revealed that the magnetic properties of Ln-SIMs are dominated by the crystal field environments from an electrostatic point of view (Fig. 2). As a result, some optimization strategies toward high-performance Ln-SIMs have been put forward based on real-world successful examples combined with some basic principles of crystal field theory.^28–31

Fig. 2 The energy level splitting of a typical heavy Ln³⁺ ion placed in an axial electrostatic crystal field, as well as the possible relaxation pathways. Higher-energy spin states are abbreviated for clarity.

To put it in a nutshell, firstly a highly anisotropic crystal field environment that matches the electron density distribution of the central ion is crucial to creating a large energy splitting between different m_J states and stabilising the large ±m_J states as the ground states.²⁸ Moreover, the local symmetry of the coordination environment shall be intentionally controlled to minimize the transverse crystal fields, reduce the mixing between different m_J states and suppress the quantum tunnelling of magnetization (QTM).³¹ Indeed, the outstanding SIM properties are more frequently achieved in heavy lanthanides simultaneously possessing large S, L and J in ^2S+1L_J terms, namely Tb³⁺(⁷F₆),^12,16–20 Dy³⁺(⁶H_15/2),^{14,15,32–38} Ho³⁺(⁵I₈),^{17,33,39–41} and Er³⁺(⁴I_15/2),^13,42,43 with specific pseudo local symmetries such as D_4d,^12,16–20D_5h,^{34,35,38,39,44,45} and C_∞.^{13–15,37,42,43}

Such lessons learnt from Ln-SIMs not only fuelled their rapid progress in recent years, but also implicated the possibility of utilizing high-performance Ln-SIMs as building blocks for multi-spin SMMs. In such a way, magnetic couplings between multiple spin centres may give birth to even more interesting molecular/electronic structures and thus fascinating magnetic behaviours, as we will see below.

3. Single-molecule magnets beyond a single lanthanide ion

3.1 Intra-atomic hyperfine coupling

When we talk about Ln-SIMs, usually we are only focusing on the well-shielded 4f electronic spins. However, most lanthanides contain certain isotopes that have nuclear spins. Despite often being neglected, the hyperfine interactions are always there because the nuclear spins are always there. The hyperfine interaction couples the nuclear spin I with the electronic spin J into a multi-spin system, which from the magnetic point of view is better treated like an multinuclear SMM system even for a Ln-SIM.

The major difficulty in studying the hyperfine interactions in SMMs is that such an effect is quite weak (energy level splitting Δ = 10⁻¹–10⁰ cm⁻¹), so it is easily overwhelmed by large QTMs from dissatisfied coordination environments and/or other inter-metallic magnetic couplings.⁴⁶ Therefore until now, only a few well-defined SIMs can serve as suitable platforms to clarify the hyperfine interactions,^{4,5,16,17,39,41,47–52} which are usually further accompanied by diamagnetic dilution.

Here in a schematic representation (Fig. 3), the lowest ±m_J electronic spin states are coupled with all ± m_I nuclear spin in a Ĥ_hf = A_hfĴÎ manner for a typical ¹⁵⁹Tb³⁺ (I = 3/2) ion, where A_hf is the hyperfine-interaction parameter. In the pseudo D_4d local symmetry for [¹⁵⁹Tb(Pc)₂]⁻,¹⁶ the avoided level crossings that allow the QTM are only significant at four field positions (Fig. 3b), and some additional small steps are explained by the nuclear quadrupole interaction term. On the other hand, the common step at a zero field is absent, meaning that the QTM here is suppressed.

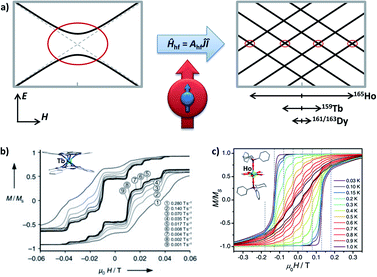Fig. 3 (a) The Zeeman diagrams of an electronic pseudo-spin J = 1/2 (red arrow) coupled to the intra-atomic nuclear spin I = 3/2 (blue arrow) by hyperfine interaction A_hf. The avoided level crossings for QTM are represented by red circles. E stands for energy, and H stands for the external magnetic field. The relative strengths of the hyperfine interactions for Ho³⁺, Tb³⁺, and Dy³⁺ are respectively shown, in an intuitive form of the typically affected field region. (b) Normalized magnetic hysteresis loops at 0.04 K for a single crystal of diluted [Tb(Pc)₂]⁻ measured at several field scan rates, along with the molecular structure in the inset. Adapted with permission from ref. 16; copyright: (2005) Wiley-VCH. (c) Normalized magnetic hysteresis loops for a single crystal of diluted [Ho(CyPh₂PO)₂(H₂O)₅]³⁺ at a field sweep rate of 0.07 T s⁻¹ and several temperatures, along with the molecular structure in the inset. Adapted with permission from ref. 39; copyright: (2017) Wiley-VCH.

For ¹⁶⁵Ho (I = 7/2), the situation is similar despite that a larger I number allows more field positions for QTM. Considering the isostructural [¹⁶⁵Ho(Pc)₂]⁻,¹⁷ taking local symmetry into account, as many as 15 field positions are proposed and categorized into three types based on their origins ranging from transverse crystal field terms or transverse magnetic fields. Furthermore, by stabilizing the largest and purer m_J = ±8 states as the ground states using a compressed pentagonal bipyramidal coordination environment,^39,41 the number of these QTM positions can be lowered to eight (Fig. 3c). Similarly, with the presence of the hyperfine interactions, the avoided level crossing at a zero field is absent. These results also can be understood by coupling the half-integer nuclear spins with the integer electronic spins for ¹⁵⁹Tb (J = 6) and ¹⁶⁵Ho (J = 8), which forms a Kramers system thus the degeneracy at a zero magnetic field is protected.

For Dy, unlike ¹⁵⁹Tb and ¹⁶⁵Ho that have only one natural nuclide, there are four major natural isotopes (^161–164Dy), each of which accounts for roughly a quarter. Among them, ¹⁶¹Dy and ¹⁶³Dy have an I = 5/2 nuclear spin while the others do not. Although some hyperfine features can be glimpsed for [Dy(Pc)₂]⁻,¹⁶ it is not until the isotopic enrichment studies^46–50 that the effect of the hyperfine interactions on Dy³⁺ is revealed for SMMs. In general, the nuclear-spin-free ¹⁶⁴Dy shows longer relaxation times than ¹⁶¹Dy and ¹⁶³Dy,^47,48 especially in the temperature-independent regime where QTM is dominant. In addition, different magnetic relaxation times were also observed between ¹⁶¹Dy and ¹⁶³Dy despite their same nuclear spin, which is attributed to the difference in A_hf.⁵⁰ Finally, wider magnetic hysteresis loops are also observed for ¹⁶⁴Dy, but sharp tunnelling, as well as short relaxation times at a zero field, is still present.⁴⁸ The relatively narrower “hyperfine region” (typically between ±200 Oe) for Dy³⁺ compared with Ho³⁺ (can be up to ±2000 Oe) is also an obstacle, so a highly diluted single-crystal characterization is usually required.

From our perspective, the isotopically enriched and magnetically isolated versions of some high-performance Dy SIMs¹⁵ would be nice platforms to further study and clarify the hyperfine interactions in an ^I≠0Dy SIM. In addition, some new techniques should be paid attention to, such as utilizing ¹⁶¹Dy for time-domain synchrotron Mössbauer spectroscopy⁵¹ and nuclear resonance vibrational spectroscopy⁵² to probe the influence of the coordinating ligands as well as the vibration. Moreover, some less-common lanthanide ions, such as ^171–174Yb,^53–55 could also be further studied with regard to the dependence of their magnetic behaviours on the hyperfine interactions. Taking back about ¹⁵⁹Tb and ¹⁶⁵Ho, the clearer hyperfine pictures make them more suitable candidates for molecular quantum bits for some quantum operations,^4,5 and the interplay between their hyperfine interactions with other factors such as inter-metallic couplings would be interesting topics.^56,57 We would also like to emphasize the importance of including the hyperfine interactions in the precise theoretical calculations, especially when dealing with energy state mixings and QTM for Dy³⁺, in order to get a closer reflection of reality.

3.2 Intra-molecular couplings in multimetallic SMMs

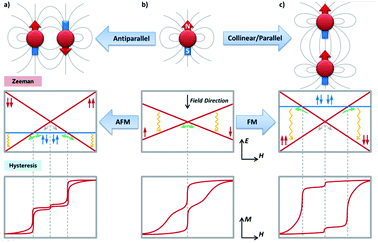
Now, we will move to intra-molecular magnetic couplings, which are the dominant interactions in the majority of multimetallic SMMs. First of all, let us look at the easiest f–f dipolar couplings as clever combination of single-ion anisotropy and molecular architecture. The extremely anisotropic f-block SIMs make them nice examples for through-space dipolar couplings, where a spin centre can be regarded as a small bar magnet generating a set of magnetic field lines (from the north pole to the south pole). As a result, the other spin centres at a distance will more or less sense an additional magnetic field (reduces with the inverse-cube of the distance), and the energy will be lower when the magnetic moment points in the same direction as the dipolar field. It is easy to infer that, for a simple dinuclear SMM (Fig. 4), placing the two anisotropic metal ions in a collinear/parallel way stabilizes the same orientation of their magnetic moments, or in other words, a ferromagnetic (FM) ground state (Fig. 4c). In contrast, an antiparallel placement results in an antiferromagnetic (AFM) ground state (Fig. 4a).

Fig. 4 The dipolar couplings between two neighbouring spin centres with strong axial anisotropy, showing the importance of the relative orientation of the magnetic moments with their spatial locations (top), from an independent spin center (b) to a ferromagnetic (c) or antiferromagnetic (a) dimer. The solid grey lines qualitatively represent the magnetic field lines generated by the spin centre treated as a small bar magnet. The corresponding Zeeman diagrams (middle) and the typical magnetic hysteresis loops (bottom, at a relatively low temperature) are also presented. Green/grey arrows indicate the possible positions for strong/weak avoided level crossings and thus fast/slow QTM, respectively. They are further linked with the steps on the magnetic hysteresis loops by the grey dashed lines. The one-way green arrows in the FM scenario should be particularly noted, which only happens in the demagnetization process. Field-enhanced relaxation process such as the direct process is mainly responsible for the closing of the hysteresis loops at higher fields, which is marked with yellow wavy arrows.

Interesting things happen when we look at their low-lying (Δ ≈ 10⁰ cm⁻¹) energy levels using Zeeman diagrams and the transitions between different states. For an uncoupled SIM (Fig. 4b), the only fast transition is near a zero field and it is mostly owing to QTM, which is often witnessed by a sharp drop of the magnetization in the magnetic hysteresis loop. For an FM coupled dimer (Fig. 4c and 5a),^58,59 the zero-field QTM is suppressed owing to the reduced tunnelling probability for the need to simultaneously flip two magnetic moments (grey arrows in Fig. 4c). As a result, the relaxation times near a zero field are increased, and the most effective transitions will only happen when the FM Zeeman line meets the diamagnetic one in the demagnetization process (one-way green arrows in Fig. 4c). As a result, a wide hysteresis loop with large remnant magnetization and coercive field is promoted.

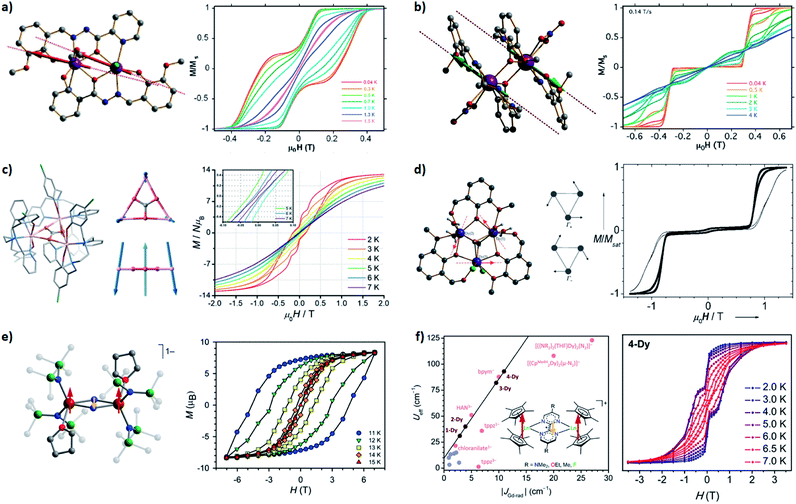Fig. 5 Selected SMMs with the dipolar couplings (a–d) and the direct couplings (e and f). Arrows represent the relative orientations of local magnetic moments at the ground state. (a) A ferromagnetic dimer: the molecular structure (left) and the normalized magnetic hysteresis loops (right) at 0.035 T s⁻¹ for a single crystal of [Dy₂(ovph)₂Cl₂(MeOH)₃]·MeCN. Adapted with permission from ref. 59; copyright: (2011) American Chemical Society. (b) An antiferromagnetic dimer: the molecular structure (left) and the normalized magnetic hysteresis loops (right) at 0.14 T s⁻¹ for a single crystal of [Dy₂(valdien)₂(NO₃)₂]. Adapted with permission from ref. 60; copyright: (2011) American Chemical Society. (c) A frustration-type triangle: the molecular structure (left), relative orientations of the magnetic moments at the ground state (middle), and the magnetic hysteresis loops (right) at 0.02 T s⁻¹ for the powder of [Dy₃(μ₃-CO₃)(Clbbpen)₃]⁺. Adapted with permission from ref. 63; copyright: (2020) Royal Society of Chemistry. (d) Single-Molecule Toroics: the molecular structure (left), orientations of the magnetic moments at the degenerate ground states (middle), and the normalized magnetic hysteresis loops (right) at 0.028 T s⁻¹ for a single crystal of [Dy₃(μ₃-OH)₂(o-vanillinato)₃Cl(H₂O)₅]³⁺. Adapted with permission from ref. 68 and 69; copyright: (2006, 2008) Wiley-VCH. (e) A strongly coupled Ln–rad–Ln trimer: the molecular structure (left) and the magnetic hysteresis loops (right) at 0.9 mT s⁻¹ for the powder of {[(Me₃Si)₂N]₂(THF)Ln}₂(μ-N₂)⁻. Adapted with permission from ref. 73; copyright: (2011) American Chemical Society. (f) Not-so-strongly coupled Ln–rad–Ln trimers: the correlations between U_eff and the coupling constants for a series of [(Cp*₂Ln)₂(μ-R₂bpym)]⁺ (left) and the magnetic hysteresis loops (right) for the powder of the (Ln = Dy, R = F) derivative. Adapted with permission from ref. 74; copyright: (2020) American Chemical Society.

On the other hand, for an AFM coupled dimer (Fig. 4a and 5b),^60,61 the ground state at a zero field is diamagnetic (the blue line in Fig. 4a). The magnetization will drop significantly prior to reaching a zero field, leaving a tiny (if any) hysteresis loop. Indeed, from the definition point of view, it ceases to be a magnet in the low-temperature, low-field regime. Nevertheless, at higher temperatures and/or higher fields, the AFM coupling is overwhelmed, thus a typical slow relaxation of magnetization can still be observed because of the increased population of its excited FM states.

It should be noted that sometimes the dipolar coupling can be enhanced/overcome by through-ligand superexchange couplings. For example, the dipolar coupling in triple-decker [Er₂(COT′′)₃] is FM,⁶² but the bridging ligand mediates a larger superexchange AFM coupling. Overall it is still an AFM dimer with a Δ_FM–AFM around 15 cm⁻¹. Interestingly, when there are multiple competing AFM couplings, like those observed in a perfect {Dy₃} triangle, a spin-frustration-type arrangement can be one of the solutions (Fig. 5c).⁶³ Finally, if the magnetic anisotropic axes of neighbouring spin centres are angled,^64–66 it cannot be described using such a simple FM/AFM terminology. Anisotropic couplings are expected and a significant transverse magnetic field will inevitably exist, which usually limits the SMM behaviours, especially at the quantum regime. A special case, however, is the Single-Molecule Toroics (SMT, Fig. 5d),^67–72 where the magnetic moments are arranged in a toroidal way at the ground state due to non-collinear Ising-type magnetic interactions. Although no conventional total magnetic moment is preserved, a net toroidal magnetic moment takes the place. On the other hand, at higher temperatures and/or higher fields, the thermally populated excited states allow similar magnetic behaviours like SMMs.

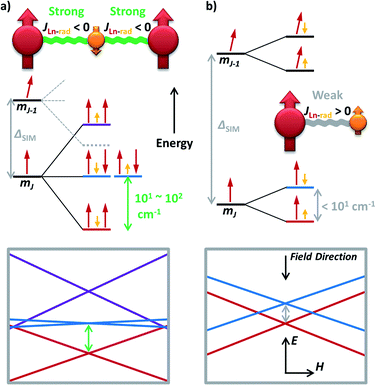
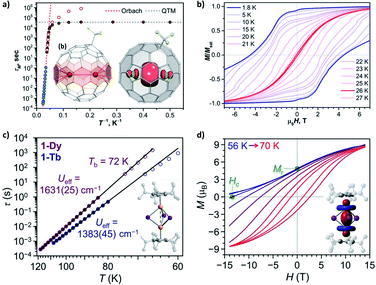
Now one may ask a question: what if the magnetic coupling between spin centres is exceptionally strong? That is just the case for some high-performance radical-bridged dilanthanide SMMs possessing strong direct exchange.^73–77 Although the J_Ln–rad is antiferromagnetic, such a Ln–rad–Ln pattern still results in ferrimagnetic ground states, which are separated from the excited states by a large Δ up to 10¹–10² cm⁻¹ (Fig. 6a, 5e and f). Such a Δ_exchange replaces the original Δ_SIM between different m_J states and acts as the new effective energy barrier. Like the situation for FM dimers, here the QTM between the ferrimagnetic ground states is largely suppressed. Moreover, a large Δ can also move the FM/AFM intersections far outside the experimental region. As a result, high-temperature magnetic blocking and giant coercivity are made possible despite their moderate U_eff (e.g. 227 cm⁻¹ for {Tb₂(N₂)}).^73,75,77

Fig. 6 The simplified energy level splitting of the low-lying states for (a) a lanthanide–radical–lanthanide (Ln–rad–Ln) spin system with strong antiferromagnetic Ln–rad coupling; and (b) a lanthanide–radical (Ln–rad) dimer with weak ferromagnetic coupling. Only the positive half (spin up) of the degenerated states are depicted for clarity, as the other half is simply with all opposite orientations. The corresponding Zeeman diagrams are also presented. The large difference of the final Δ (grey and green arrows, respectively) compared with the original single ion Δ_SIM should be particularly noted.

However, simply incorporating a radical ligand into an SMM does not automatically guarantee outstanding magnetic behaviours.⁷⁸ In fact, for these thermally activated magnetic relaxations, the excited states usually act as a ceiling, which can be as low as Δ < 10¹ cm⁻¹ in weakly coupled Ln–radical systems (Fig. 6b) and destroy the hope for magnetic blocking except at an extremely low temperature. In addition, a relatively large Δ_SIM is still required even in the strongly coupled scenario, as the large splitting makes the original ± m_J−1 states join the low-lying energy diagrams (Fig. 6a, grey dashed lines). Moreover, the mismatched orientations of the magnetic moments can still generate transverse magnetic couplings and facilitate QTM.⁷⁹ A feasible approach may be utilizing the redox properties of the ligand to probe the true impact of the radical by comparing the SMM properties between different oxidation states.^20,80 Nevertheless, the general recipe of combining strong axial single-ion magnetic anisotropy with strong magnetic exchange coupling still holds for high-performance radical-containing SMMs.

Furthermore, in a confined space where two magnetic metal ions are placed in close proximity to each other, a metal–metal bond could be created from the direct bonding between their atomic orbitals. In some endohedral metallofullerenes Ln₂@C₈₀–R (Fig. 7a)^81–83 and endohedral metalloazafullerenes Ln₂@C₇₉N,^84,85 the Ln⋯Ln distance can be as short as 3.7–3.9 Å. From the experimental and theoretical study, the presence of a single-electron Ln–Ln σ-bond of 6s orbital parentage has been verified. An exceptionally strong FM Ln^III⋯e⁻⋯Ln^III coupling is modelled, which generates the exchange states at Δ = 10²–10³ cm⁻¹ and acts as the U_eff. Therefore, magnetic blocking can be observed at relatively high temperatures (Fig. 7b).

Fig. 7 Selected SMMs with metal–metal bonds. (a) Magnetic relaxation times for Tb₂@C₈₀-CF₃ in a zero field and a 0.2 T dc field, along with the molecular structure and spin density (DFT-computed for the Y derivative) in the inset. (b) Magnetic hysteresis loops for Tb₂@C₈₀-CF₃. Adapted (a and b) with permission from ref. 83; copyright: (2021) American Chemical Society. (c) Magnetic relaxation times for [(Cp^iPr5)₂Ln₂I₃], along with the molecular structure in the inset. (d) Field-cooled demagnetization and magnetic hysteresis loops for [(Cp^iPr5)₂Dy₂I₃] at a field sweep rate of 0.01 T s⁻¹, along with the spin density (CASSCF-computed for the Gd derivative) in the inset. Adapted (c and d) with permission from ref. 86; copyright: (2022) The American Association for the Advancement of Science. The different shapes of the distributions of spin density (between a and d) should be particularly noted.

In a similar manner, the recently achieved mixed-valence (Ln^II–Ln^III) dilanthanide SMMs⁸⁶ adopt a single-electron Ln–Ln σ-bond of 5d_z² orbital parentage (Fig. 7c and d). The exchange constant for the FM coupling is more than doubled, thus a record Δ exceeding 10³ cm⁻¹ (forming U_eff) as well as an enormous coercive magnetic field even at 60 K is achieved. For comparison, its all-Dy^III analogue acts more like a conventional dinuclear SMM with weak dipolar/superexchange coupling, which highlights the decisive importance of the extra electron in the diffuse 5d orbitals. In addition, we would like to point out that the usually adopted Ln^III⋯e⁻⋯Ln^IIIversus Ln^II–Ln^III pictures for these two systems are intrinsically equivalent. Their atomic orbitals are highly combined into molecular orbitals, which can be regarded as a superatom. The electron in the singly occupied molecular orbital (SOMO) is completely delocalized, and so does the valence. Finally, on the other hand, bonding lanthanides with closed-shell diamagnetic main group metal ions such as Sb⁸⁷ and Bi⁸⁸ is more like bridging by a p-block organic ligand. Still, these heavy donors with more diffuse valence orbitals could mediate a stronger superexchange coupling (e.g. Δ ∼10 cm⁻¹ for [(Cp*)₂Dy₂Bi₆]²⁻)⁸⁸ than common ligands with lighter C/N/O/Cl donors.

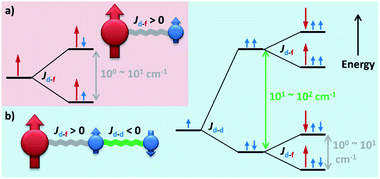
Moving forward, introducing a magnetic d-block ion near a lanthanide ion usually creates moderate (Δ = 10⁰–10¹ cm⁻¹) d–f couplings (Fig. 8a),^89–94 which are mostly due to the superexchange interactions mediated by the bridging ligand(s). Such a scenario is somewhat similar to a weakly coupled Ln–radical system (Fig. 6b), and so do their magnetic behaviours.⁹¹ On the other hand, a more strongly coupled f–d–f or f–d–d–f system⁹² can be similar to some moderate radical-bridged lanthanide complexes,⁷⁴ although the magnetic anisotropy of the d-block ions cannot be neglected.^93,94 Moreover, since J_d–d is larger than J_d–f (in an S = 1/2 pseudo-spin context), connecting multiple d-block ions may further generate greater Δ = 10¹–10² cm⁻¹ in f–d–d systems (Fig. 8b) and beyond.^89,90 The presence of these additional exchange excited states enables unusual two U_eff (e.g. for {Co₂Dy₂},⁸⁹Fig. 9a) or even three U_eff (e.g. for {DyCu₅},⁹⁰Fig. 9b) that corresponds to Δ_SIM, Δ_d–d, and Δ_d–f, respectively, to be observed.

Fig. 8 The simplified energy level splitting of the low-lying states for (a) a ferromagnetically coupled d–f dimer and (b) a three-body f–d–d spin system in which the d–f coupling is ferromagnetic while the d–d coupling is antiferromagnetic. Only half of the degenerated states are depicted for clarity.

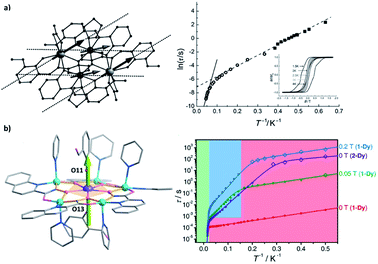Fig. 9 Selected SMMs with both d–f and d–d superexchange couplings. Arrows represent the directions of local magnetic moments at the ground state. (a) The molecular structure (left) and the two-U_eff Arrhenius plot (right) for {Co₂Dy₂}, along with the magnetic hysteresis loops in the inset. Adapted with permission from ref. 89; copyright: (2012) Wiley-VCH. (b) The molecular structure (left) and the three-U_eff Arrhenius plot (right) for {DyCu₅}. Adapted with permission from ref. 90; copyright: (2021) Wiley-VCH.

3.3 Inter-molecular couplings: SMMs in lattices

Until now, our discussions are mostly about “an ellipsoidal SMM in a vacuum”. In reality, the study of SMMs always takes place in a specific lattice, or at least, a specific environment. Unless there are other effective pathways to mediate strong magnetic couplings, usually the inter-molecular magnetic interactions are dominated by dipolar coupling. From a crystallographic point of view, the packing of neighbouring SMMs must follow the crystallographic symmetry, which limits the directions and distances between discrete molecules and thus affects the dipolar coupling. This is undoubtedly the playground for molecular engineering and crystal engineering.

In particular, a 1-dimensional column of collinear magnetic moments of [TbNcPc]⁺ promotes an inter-molecular ferromagnetic coupling,⁹⁵ which effectively suppresses QTM compared with the diluted sample (Fig. 10a). In addition, partial oxidation of the ligands can further introduce inter-molecular delocalized radicals through the column and thus electroconductivity.⁹⁷ The supramolecular dimer of an {Mn₄} SMM produces antiferromagnetic coupling through the C–H⋯Cl and Cl⋯Cl approach, which results in exchange-biased QTM (Fig. 10b).⁹⁶ It also implies that the magnetic behaviours observed on the as-synthesized crystalline samples might be a mixture of single-molecule properties and inter-molecular interactions. Therefore, diamagnetic dilution remains an effective tool to clarify whether there are significant inter-molecular contributions.⁶¹ Alternatively, loading SMMs inside the pores of metal–organic frameworks (MOFs) is a feasible way to not only weaken the inter-molecular couplings but also enable nanostructuring,^98,99 however strong solvent stability of the studied SMM is mandatory.

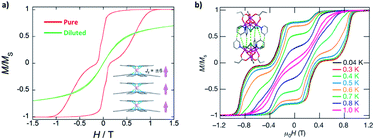Fig. 10 Selected assemblies of SMMs with clear supramolecular couplings. (a) Normalized magnetic hysteresis loops for a single crystal of [TbNcPc]⁺ compared with the diluted sample, along with the packing diagram in the inset. Adapted with permission from ref. 95; copyright: (2018) Wiley-VCH. (b) Normalized magnetic hysteresis loops for a single crystal of {Mn₄} dimer at a field sweep rate of 0.14 T s⁻¹ at different temperatures, along with the dimer structure in the inset. Adapted with permission from ref. 96; copyright: (2002) Springer Nature.

Last but not least, we would like to briefly mention the spin–phonon coupling that links the magnetic behaviours of SMMs with the lattice vibration.^100–105 Instead of a static picture, now the dynamic features are taken into account. In other words, the atoms are allowed to vibrate and rotate in the discussion and calculation, like what they actually do in reality. It is identified that, some “harmful” low-energy vibrational modes can produce large anisotropy tensor modulations and therefore facilitate magnetic relaxation. Several general strategies to suppress the spin–phonon coupling have been put forward, which include (but not limited to): (1) using structurally rigid ligands; (2) incorporating heavy substituting atoms; and (3) employing highly axial spin centres to reduce the QTM. Still, increasing the energy level splitting is helpful for moving the relaxations off-resonance with lattice vibration, due to the lack of such high-energy phonons at low temperatures. It is believed that vibration/phonon engineering can further tailor the spin–lattice relaxation in addition to the successful practices of spin engineering, as the icing on the cake.

4. The art of coupling: a big picture

4.1 From chasing energy barriers to reshaping magnetic dynamics

It should be noted that the idea of introducing coupling is not about simply achieving a large energy level splitting (Δ). In fact, the Δ is usually reduced compared with Δ_SIM due to an increased number of excited states (thus denser). However, by altering and recombining the components of the low-lying states of different spin centres, some under-barrier relaxations as well as QTM may be blocked. As a result, a larger U_eff and longer relaxation times can be obtained by relaxations through higher excited states. In such a manner, some moderate Ln-SIM may profit from these couplings, especially for some light lanthanide ions that usually have significant QTM in the single-ion form. On the other hand, purposely removing couplings (e.g. by dilution, by isotopic enrichment) from some coupled systems will be a credible way to clarify the important roles of different couplings, respectively.

Moreover, compared with the simple double-well model for a Ln-SIM, some low-lying exchange states can be formed via coupling multiple spin centres into an SMM, and therefore some interesting magnetic dynamics are also made possible. For example, AFM 3d clusters seem boring for an SMM, but adding a 4f ion (and therefore introducing Δ_SIM, and J_d–f) yields three-U_eff Arrhenius behaviours adopting different excited states (Fig. 9b).⁹⁰

4.2 From differences in mechanisms to similarities in energy level structures

Now we have witnessed the diversity of couplings in SMMs from the intra-atomic to the inter-molecular scale. Let us recall the highly different energy ranges that they usually affect (Fig. 11). Such a hierarchy is demonstrated from the weak hyperfine interactions with a Δ as small as 10⁻¹ cm⁻¹, to the dipolar couplings around 10⁰ cm⁻¹, to the ligand-bridged superexchange couplings exceeding 10¹ cm⁻¹, to the radical-bridged direct couplings creating a Δ over 10² cm⁻¹, and finally to the strong metal–metal bonds going beyond 10³ cm⁻¹. These differences are undoubtedly due to their distinct quantum mechanical origins.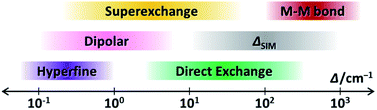

Fig. 11 The schematic representation of the energy ranges that the discussed magnetic couplings usually affect, along with the single-ion Δ_SIM, in a lanthanide-based SMM.

Even so, if we take a step back to look at their Zeeman diagrams and magnetic hysteresis loops, we can still discover some similarities under certain conditions. For example, the exchange-biased QTM produced by hyperfine interactions (Fig. 3b and c) and by intermolecular couplings (Fig. 10b) can have similar steps. The low-lying states in a weakly coupled Ln–radical system (Fig. 6b) and in a d–f dimer (Fig. 8a) can have similar energy level splitting. The ferromagnetic or ferrimagnetic couplings in an FM Ln₂ dimer (Fig. 4c), in a Ln–rad–Ln trimer (Fig. 5e), and in a mixed-valence (Ln^II–Ln^III) with metal–metal bonds (Fig. 7) can generate similar protected ground doublets and thus outstanding behaviours.

Such similarities are in fact reasonable, because their underlying coupling mechanisms are now affecting nearby energy ranges. Therefore, it is possible to obtain similar energy level structures despite their different origins. It is a natural way for human beings to understand the world with classification discussion, like we usually construct a series of different Hamiltonians (Ĥ = Ĥ_Single-ion + Ĥ_hf + Ĥ_J + Ĥ_zJ + …) to facilitate the discussion. However, the world itself is not split, and these Hamiltonians will finally be unified into a big energy matrix (a big picture). Figuratively speaking, if we put ourselves in the shoes of a Ln ion, some Hamiltonians such as Ĥ_hf = A_hfĴÎ and Ĥ_J = −2JŜ₁Ŝ₂ are not only formally similar, but also capable of yielding similar results. After all, Ĥψ = Eψ, it is the total energy (including its dependencies on temperature, field, etc.) that finally matters.

4.3 From the passive interpretation of coexisting couplings to the active introduction of favourable couplings

Passively, researchers have been devoting enormous effort to interpreting the role of each coupling in SMMs, by adding one Hamiltonian after another whenever it is needed. However, understanding the world is only the first step; transforming the world is what follows. From the discussions above, it is evidenced that some encouraging results have been obtained via actively introducing couplings into Ln-SIMs, forming Ln-based SMMs. We would like to emphasize again the importance of actively coupling high-performance Ln building blocks together via targeted design and directional assembly into strong, collinear, and ferromagnetic systems, rather than accidental coexistence.

In addition, although our discussions here are mostly based on Ln-SIMs, we must point out that this is mainly because they are simpler models. D-block SIMs^23,106 are relatively more complicated due to covalency, but they are still competing candidates when having an unquenched orbital angular momentum and a large (positive or negative) D, while the transverse anisotropy as well as its contribution to QTM is minimized (or in other words, a small E). Some representative examples include linear Fe(I, II)/Co(II),^107–109 tetrahedral Co(II) with 2-fold distortion,¹¹⁰ trigonal pyramidal Fe(II)^111,112 and trigonal prismatic Co(II).^113,114 We would like to further encourage the idea of purposely coupling the high-performance d-block and f-block SIMs together in a building block approach, while keeping their single-ion anisotropies intact or even improved. We can only imagine what fascinating behaviours it will bring.

4.4 From couplings to couplingⁿ: bigger than bigger

Furthermore, having multiple couplings together within a single molecule can lead to even more interesting behaviours. In fact, each additional coupling is not just adding a new variable, but adding a whole dimension from the mathematical point of view. For example, in a double-decker {Dy₂Cu₁₀} (or more clearly, {Cu₅Dy-DyCu₅}) metallacrown,⁹⁰ an additional axial FM f–f coupling further opens the magnetic hysteresis loops at a zero field compared with the butterfly-shaped ones for mono-decker {DyCu₅}. Also in a {HoNi₅} metallacrown,¹¹⁵ all hyperfine, d–d and d–f couplings jointly create a field-induced oscillation of relaxation mechanisms. Indeed, sometimes the difference between the coupling strengths in the order of magnitude is somehow advantageous for a clear distinction of their respective contributions to the magnetic dynamics, via the distinct dependencies on the temperature/field conditions.

Last but not least, it may be even more attractive to investigate how different couplings can be further coupled together, such as how the metal–metal bonding may affect the direct exchange if the ligands are radicals, or how lattice vibration may affect the dipolar coupling by altering the directions of magnetic moments. These open questions are surely waiting for constructive answers.

5. Concluding remarks

In conclusion, going beyond the single-ion anisotropy of Ln-SIMs, here we draw a unified picture of diverse magnetic couplings that shape and decorate the energy levels of SMMs in different energy scales. These couplings, alone or together, are the keys to understanding the fascinating and multifaceted behaviours of SMMs compared with their SIM components. We believe the essence and art of constructing multimetallic SMMs are the intended, directional and delicate couplings between spin centres, which makes it possible to create distinctive energy level structures that can never be obtained from a single magnetic ion. In addition to the above-mentioned art of coupling, it may be promising to develop even more new types of couplings and open up new dimensions for the endless development of molecular magnetism. Indeed, some of these efforts have already been producing exciting results, and we are encouraging the community to keep advancing forward. As the saying goes,¹¹⁶every era is a golden age, it's just a matter of perspective.

Author contributions

Y.-C. C. drafted the manuscript with inputs from M.-L. T., who led the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (2018YFA0306001), the NSFC (Grant nos 222131011, 21805313) and the Pearl River Talent Plan of Guangdong (2017BT01C161).

Notes and references

1. D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press, 2006.
2. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
3. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
4. S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138.
5. M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351.
6. E. Moreno-Pineda and W. Wernsdorfer, Nat. Rev. Phys., 2021, 3, 645–659.
7. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
8. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
9. R. A. Layfield, Organometallics, 2014, 33, 1084–1099.
10. M. Feng and M.-L. Tong, Chem.–Eur. J., 2018, 24, 7574–7594.
11. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984.
12. N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
13. K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957.
14. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
15. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
16. N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935.
17. N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651.
18. F. Branzoli, P. Carretta, M. Filibian, G. Zoppellaro, M. J. Graf, J. R. Galan-Mascaros, O. Fuhr, S. Brink and M. Ruben, J. Am. Chem. Soc., 2009, 131, 4387–4396.
19. M. Gonidec, F. Luis, À. Vílchez, J. Esquena, D. B. Amabilino and J. Veciana, Angew. Chem., Int. Ed., 2010, 49, 1623–1626.
20. M. Gonidec, E. S. Davies, J. McMaster, D. B. Amabilino and J. Veciana, J. Am. Chem. Soc., 2010, 132, 1756–1757.
21. Y. Duan, J. T. Coutinho, L. E. Rosaleny, S. Cardona-Serra, J. J. Baldoví and A. Gaita-Ariño, 2021, arXiv:2103.03199.
22. H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33.
23. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
24. V. S. Parmar, D. P. Mills and R. E. P. Winpenny, Chem.–Eur. J., 2021, 27, 7625–7645.
25. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
26. L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112.
27. J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2013, 34, 1961–1967.
28. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
29. D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770–13778.
30. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056.
31. J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453.
32. S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451.
33. S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, A. Camón, M. Evangelisti, F. Luis, M. J. Martínez-Pérez and J. Sesé, J. Am. Chem. Soc., 2012, 134, 14982–14990.
34. Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837.
35. Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074.
36. M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165.
37. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
38. K.-X. Yu, J. G. C. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. F. Chilton and Y.-Z. Zheng, Chem, 2020, 6, 1777–1793.
39. Y.-C. Chen, J.-L. Liu, W. Wernsdorfer, D. Liu, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2017, 56, 4996–5000.
40. Y. Ma, Y.-Q. Zhai, Y.-S. Ding, T. Han and Y.-Z. Zheng, Chem. Commun., 2020, 56, 3979–3982.
41. Y. Liu, L. T. A. Ho, G.-Z. Huang, Y.-C. Chen, L. Ungur, J.-L. Liu and M.-L. Tong, Angew. Chem., Int. Ed., 2021, 60, 27282–27287.
42. S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733.
43. L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417.
44. J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316.
45. M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875.
46. E. Moreno-Pineda, G. Taran, W. Wernsdorfer and M. Ruben, Chem. Sci., 2019, 10, 5138–5145.
47. F. Pointillart, K. Bernot, S. Golhen, B. Le Guennic, T. Guizouarn, L. Ouahab and O. Cador, Angew. Chem., Int. Ed., 2015, 54, 1504–1507.
48. E. Moreno-Pineda, M. Damjanović, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., Int. Ed., 2017, 56, 9915–9919.
49. L. Tesi, Z. Salman, I. Cimatti, F. Pointillart, K. Bernot, M. Mannini and R. Sessoli, Chem. Commun., 2018, 54, 7826–7829.
50. J. Flores Gonzalez, F. Pointillart and O. Cador, Inorg. Chem. Front., 2019, 6, 1081–1086.
51. L. Scherthan, S. F. M. Schmidt, H. Auerbach, T. Hochdörffer, J. A. Wolny, W. Bi, J. Zhao, M. Y. Hu, T. Toellner, E. E. Alp, D. E. Brown, C. E. Anson, A. K. Powell and V. Schünemann, Angew. Chem., Int. Ed., 2019, 58, 3444–3449.
52. L. Scherthan, R. F. Pfleger, H. Auerbach, T. Hochdörffer, J. A. Wolny, W. Bi, J. Zhao, M. Y. Hu, E. E. Alp, C. E. Anson, R. Diller, A. K. Powell and V. Schünemann, Angew. Chem., Int. Ed., 2020, 59, 8818–8822.
53. K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804.
54. R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818.
55. J. Flores Gonzalez, H. Douib, B. Le Guennic, F. Pointillart and O. Cador, Inorg. Chem., 2021, 60, 540–544.
56. T. Fukuda, K. Matsumura and N. Ishikawa, J. Phys. Chem. Lett., 2013, 117, 10447–10454.
57. Y. Horii, K. Katoh, K. Sugimoto, R. Nakanishi, B. K. Breedlove and M. Yamashita, Chem.–Eur. J., 2019, 25, 3098–3104.
58. N. Ishikawa, S. Otsuka and Y. Kaizu, Angew. Chem., Int. Ed., 2005, 44, 731–733.
59. Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951.
60. J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319–5328.
61. F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830–8833.
62. J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003–8010.
63. G. Lu, Y. Liu, W. Deng, G.-Z. Huang, Y.-C. Chen, J.-L. Liu, Z.-P. Ni, M. Giansiracusa, N. F. Chilton and M.-L. Tong, Inorg. Chem. Front., 2020, 7, 2941–2948.
64. R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678.
65. E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243.
66. M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren, S. Carretta, T. Guidi, E. J. L. McInnes, R. E. P. Winpenny and N. F. Chilton, J. Am. Chem. Soc., 2018, 140, 2504–2513.
67. L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905.
68. J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733.
69. L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129.
70. S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Angew. Chem., Int. Ed., 2012, 51, 12767–12771.
71. L. Ungur, S. K. Langley, T. N. Hooper, B. Moubaraki, E. K. Brechin, K. S. Murray and L. F. Chibotaru, J. Am. Chem. Soc., 2012, 134, 18554–18557.
72. G. Fernandez Garcia, D. Guettas, V. Montigaud, P. Larini, R. Sessoli, F. Totti, O. Cador, G. Pilet and B. Le Guennic, Angew. Chem., Int. Ed., 2018, 57, 17089–17093.
73. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239.
74. C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, J. Am. Chem. Soc., 2020, 142, 21197–21209.
75. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542.
76. S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549.
77. S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144.
78. S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176.
79. B. S. Dolinar, D. I. Alexandropoulos, K. R. Vignesh, T. A. James and K. R. Dunbar, J. Am. Chem. Soc., 2018, 140, 908–911.
80. F.-S. Guo and R. A. Layfield, Chem. Commun., 2017, 53, 3130–3133.
81. F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098.
82. F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz, S. Schiemenz, F. Ziegs, K. Nenkov, A. Kostanyan, T. Greber, A. U. B. Wolter, M. Richter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Nat. Commun., 2019, 10, 571.
83. Y. Wang, G. Velkos, N. J. Israel, M. Rosenkranz, B. Büchner, F. Liu and A. A. Popov, J. Am. Chem. Soc., 2021, 143, 18139–18149.
84. G. Velkos, D. S. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. M. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp, H. C. Dorn and A. A. Popov, Angew. Chem., Int. Ed., 2019, 58, 5891–5896.
85. Y. Wang, J. Xiong, J. Su, Z. Hu, F. Ma, R. Sun, X. Tan, H.-L. Sun, B.-W. Wang, Z. Shi and S. Gao, Nanoscale, 2020, 12, 11130–11135.
86. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
87. T. Pugh, N. F. Chilton and R. A. Layfield, Chem. Sci., 2017, 8, 2073–2080.
88. P. Zhang, F. Benner, N. F. Chilton and S. Demir, Chem, 2022, 8, 717–730.
89. K. C. Mondal, A. Sundt, Y. Lan, G. E. Kostakis, O. Waldmann, L. Ungur, L. F. Chibotaru, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2012, 51, 7550–7554.
90. J. Wang, Q.-W. Li, S.-G. Wu, Y.-C. Chen, R.-C. Wan, G.-Z. Huang, Y. Liu, J.-L. Liu, D. Reta, M. J. Giansiracusa, Z.-X. Wang, N. F. Chilton and M.-L. Tong, Angew. Chem., Int. Ed., 2021, 60, 5299–5306.
91. J.-L. Liu, J.-Y. Wu, Y.-C. Chen, V. Mereacre, A. K. Powell, L. Ungur, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2014, 53, 12966–12970.
92. S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed., 2013, 52, 12014–12019.
93. Y. Peng, M. K. Singh, V. Mereacre, C. E. Anson, G. Rajaraman and A. K. Powell, Chem. Sci., 2019, 10, 5528–5538.
94. L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337.
95. K. Katoh, S. Yamashita, N. Yasuda, Y. Kitagawa, B. K. Breedlove, Y. Nakazawa and M. Yamashita, Angew. Chem., Int. Ed., 2018, 57, 9262–9267.
96. W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406–409.
97. T. Sato, B. K. Breedlove, M. Yamashita and K. Katoh, Angew. Chem., Int. Ed., 2021, 60, 21179–21183.
98. D. Aulakh, J. B. Pyser, X. Zhang, A. A. Yakovenko, K. R. Dunbar and M. Wriedt, J. Am. Chem. Soc., 2015, 137, 9254–9257.
99. D. Aulakh, L. Liu, J. R. Varghese, H. Xie, T. Islamoglu, K. Duell, C.-W. Kung, C.-E. Hsiung, Y. Zhang, R. J. Drout, O. K. Farha, K. R. Dunbar, Y. Han and M. Wriedt, J. Am. Chem. Soc., 2019, 141, 2997–3005.
100. A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059.
101. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620.
102. L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275.
103. K. Irländer and J. Schnack, Phys. Rev. B, 2020, 102, 054407.
104. D. Reta, J. G. C. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950.
105. M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645.
106. S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018.
107. J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581.
108. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138.
109. P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. v. Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319.
110. J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734.
111. D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225.
112. W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126.
113. Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806.
114. V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795.
115. S.-G. Wu, Z.-Y. Ruan, G.-Z. Huang, J.-Y. Zheng, V. Vieru, G. Taran, J. Wang, Y.-C. Chen, J.-L. Liu, L. T. A. Ho, L. F. Chibotaru, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Chem, 2021, 7, 982–992.
116. H. Ford, Living in the age of airplanes, National Geographic, 2016.

---