Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring seebeck-coefficient fluctuations in endohedral-fullerene, single-molecule junctions†
Ali K.
Ismael‡
 *ab,
Laura
Rincón-García‡
*ab,
Laura
Rincón-García‡
 c,
Charalambos
Evangeli‡
d,
Panagiotis
Dallas‡
c,
Charalambos
Evangeli‡
d,
Panagiotis
Dallas‡
 ef,
Turki
Alotaibi‡
ag,
Alaa A.
Al-Jobory‡
ef,
Turki
Alotaibi‡
ag,
Alaa A.
Al-Jobory‡
 ah,
Gabino
Rubio-Bollinger
ci,
Kyriakos
Porfyrakis
ah,
Gabino
Rubio-Bollinger
ci,
Kyriakos
Porfyrakis
 fk,
Nicolás
Agraït
fk,
Nicolás
Agraït
 *cij and
Colin J.
Lambert
*cij and
Colin J.
Lambert
 *a
*a
aDepartment of Physics, Lancaster University, Lancaster, UK. E-mail: k.ismael@lancaster.ac.uk
bDepartment of Physics, College of Education for Pure Science, Tikrit University, Tikrit, Iraq
cDepartamento de Física de la Materia Condensada, Universidad Autónoma de Madrid, E-28049 Madrid, Spain
dDepartment of Materials, University of Oxford, Parks Road, OX1 3PH, Oxford, UK
eInstitute of Nanoscience and Nanotechnology, NCSR Demokritos, 15310 Athens, Greece
fDepartment of Materials, University of Oxford, OX1 3PH, UK
gDepartment of Physics, College of Science, Jouf University, Sakaka, Saudi Arabia
hDepartment of Physics, College of Science, University of Anbar, Anbar, Iraq
iCondensed Matter Physics Center (IFIMAC) and Instituto Universitario de Ciencia de Materiales “Nicolás Cabrera” (INC), Universidad Autónoma de Madrid, E-28049 Madrid, Spain
jFundación IMDEA Nanociencia, Calle Faraday 9, Campus Universitario de Cantoblanco, E-28049 Madrid, Spain
kFaculty of Engineering and Science, University of Greenwich, Central Avenue, Chatham Maritime, ME4 4TB, UK
First published on 19th April 2022
Abstract
For the purpose of creating single-molecule junctions, which can convert a temperature difference ΔT into a voltage ΔV via the Seebeck effect, it is of interest to screen molecules for their potential to deliver high values of the Seebeck coefficient S = −ΔV/ΔT. Here we demonstrate that insight into molecular-scale thermoelectricity can be obtained by examining the widths and extreme values of Seebeck histograms. Using a combination of experimental scanning-tunnelling-microscopy-based transport measurements and density-functional-theory-based transport calculations, we study the electrical conductance and Seebeck coefficient of three endohedral metallofullerenes (EMFs) Sc3N@C80, Sc3C2@C80, and Er3N@C80, which based on their structures, are selected to exhibit different degrees of charge inhomogeneity and geometrical disorder within a junction. We demonstrate that standard deviations in the Seebeck coefficient σS of EMF-based junctions are correlated with the geometric standard deviation σ and the charge inhomogeneity σq. We benchmark these molecules against C60 and demonstrate that both σq, σS are the largest for Sc3C2@C80, both are the smallest for C60 and for the other EMFs, they follow the order Sc3C2@C80 > Sc3N@C80 > Er3N@C80 > C60. A large value of σS is a sign that a molecule can exhibit a wide range of Seebeck coefficients, which means that if orientations corresponding to high values can be selected and controlled, then the molecule has the potential to exhibit high-performance thermoelectricity. For the EMFs studied here, large values of σS are associated with distributions of Seebeck coefficients containing both positive and negative signs, which reveals that all these EMFs are bi-thermoelectric materials.
New conceptsIf high-thermoelectric-performance molecules could be identified, then they could be used as building blocks for organic thin-film materials able to convert waste heat into electricity. A key parameter governing thermoelectric performance is the Seebeck coefficient S, which determines the voltage generated when a temperature difference is applies to a single-molecule junction. In the literature, ensemble averaged values of S are typically reported. Here we demonstrate that the search for high-performance molecules can be accelerated by focussing attention on fluctuations in S. We study the electrical conductance and Seebeck coefficient of three endohedral metallofullerenes (EMFs) Sc3N@C80, Sc3C2@C80, and Er3N@C80, which based on their structures, are selected to exhibit different degrees of charge inhomogeneity and geometrical disorder within a junction. These cause the molecules to exhibit a wide range of Seebeck coefficients, which means that if orientations corresponding to high values can be selected and controlled, then the molecules have the potential to exhibit high-performance thermoelectricity. Furthermore, the EMFs studied here exhibit distributions of Seebeck coefficients containing both positive and negative signs, which reveals that all these EMFs are bi-thermoelectric materials. The strategy of exploiting fluctuations is a new concept and will lead to new strategies for designing thermoelectric materials. |
Introduction
During recent years, the search for non-toxic and easily processable thermoelectric materials has led several groups to explore the potential of molecular-scale devices for converting waste heat into electricity.1–41 This is achieved via the Seebeck effect, which converts a temperature difference ΔT into a voltage ΔV = −SΔT, where the constant of proportionality is the Seebeck coefficient S. Measured values of S are currently too low to create an economically viable technology and therefore there is a need to develop strategies for rapidly assessing the ability of a given molecule to deliver high values of S. In the 1980s, studies of sample-to-sample variations in electrical conductance G of mesoscopic, phase-coherent solids led to remarkable discoveries such as universal conductance fluctuations (UCFs), in which the standard deviation σG in the conductance is σG = aG0, where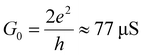 is the quantum of conductance.42,43 In this expression, a is a number of order unity, which is independent of the average value of G, and depends only on the presence of an applied magnetic field or spin–orbit scattering. Since that time, the field of single-molecule electronics has been established, in which the electrical conductor is a single molecule located between electrodes separated by a few nanometres. However, even though many experiments have confirmed that transport through single molecules is phase coherent,44–53 even at room temperature, information contained in fluctuations has been largely ignored. Here, our aim is to demonstrate that studies of fluctuations in single-molecule transport properties are of particular interest in the search for molecules with high thermoelectrical performance, because rare examples of junctions exhibiting extreme values of Seebeck coefficients are a proof of principle that such junctions can exhibit high thermopowers.
is the quantum of conductance.42,43 In this expression, a is a number of order unity, which is independent of the average value of G, and depends only on the presence of an applied magnetic field or spin–orbit scattering. Since that time, the field of single-molecule electronics has been established, in which the electrical conductor is a single molecule located between electrodes separated by a few nanometres. However, even though many experiments have confirmed that transport through single molecules is phase coherent,44–53 even at room temperature, information contained in fluctuations has been largely ignored. Here, our aim is to demonstrate that studies of fluctuations in single-molecule transport properties are of particular interest in the search for molecules with high thermoelectrical performance, because rare examples of junctions exhibiting extreme values of Seebeck coefficients are a proof of principle that such junctions can exhibit high thermopowers.
To demonstrate that fluctuations can be used to search for molecules with potential for high thermoelectric performance, we report a combined experimental and theoretical study of a family of endohedral metallofullerenes (EMFs), specifically chosen to exhibit large fluctuations. EMFs are chosen because they can form single-molecule junctions without the need for anchor groups, which in the literature, are often used to bind molecules to electrodes. Such anchor groups would restrict the number of binding configurations within a junction and reduce fluctuations, whereas in this study, we would like to explore the full phase space of molecular configurations within a junction.
EMFs represent a fascinating class of nanomaterials, whose optical,54 electrochemical55 or magnetic56 properties are controlled by the type of metal atom(s) encapsulated by the fullerene cage. For example, erbium containing EMFs possess a characteristic 1520 nm emission associated with the erbium ion, which is of fundamental importance for telecommunication applications and the fabrication of erbium doped amplifiers.57 Moreover, there is a broad spectrum of scandium-containing metallofullerenes, including the paramagnetic Sc@C82 and Sc3C2@C80, which can find applications as spin probes and quantum information processing components.58 The latter exhibits a unique diamond shaped EPR, with respect to the three equivalent scandium atoms (see Fig. S4, ESI†). For the purpose of probing fluctuations in transport properties, these molecules are attractive, because they not only bind to electrodes with a range of different orientations, but also by making different choices for the encapsulated moiety, they can possess highly inhomogeneous charge distributions (for example as in the case of Sc3C2@C80) or possess a relatively homogeneous charge distribution (as for C60). Therefore, a study of their transport properties is expected to reveal how charge distributions and geometry are correlated with fluctuations in their Seebeck coefficients and their ability to exhibit high values of S.
To investigate correlations between Seebeck coefficient, geometry and charge inhomogeneity, our aim is to compare transport properties of Sc3N@C80 and C60 (ref. 11), with those of two other trimetallic EMFs, namely, the paramagnetic Sc3C2@C80 (see Fig. S4, ESI†) and a rare-earth-based EMF, Er3N@C80. Like Sc3N@C80, these EMFs are formed with the fullerene cage Ih–C80, composed of 80 C atoms organised in an icosahedral structure (Ih symmetry also shared by C60) (see Fig. 1a)57–61 and their cages possess sizeable charge inhomogeneity. Our main result is that the standard deviations of Seebeck coefficients of these four molecules are strongly correlated with standard deviations in the charge distributions on their fullerene cages, thereby establishing a structure–function relationship between Seebeck fluctuations and charge inhomogeneity. Furthermore, molecules with high charge inhomogeneity exhibit rare examples of high thermopower, which means that if these rare junction configurations could be isolated and controlled, then such molecules have the potential to deliver high-performance thermoelectricity.
Results and discussion
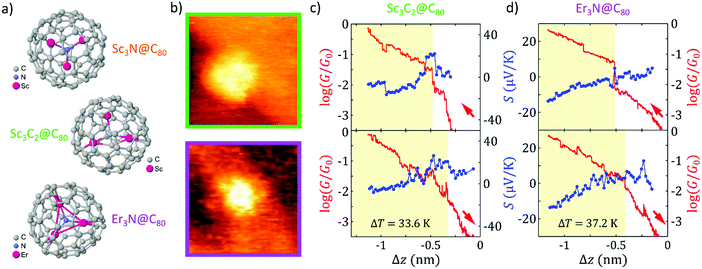
All molecules were deposited on gold (111) substrates by drop-casting from very dilute 1,2,4-trichlorobenzene (TCB) solutions of the corresponding EMF. The Au substrates were previously flame annealed to form atomically flat surfaces (see ESI† for more details on sample preparation). We perform our measurements in ambient conditions and at room temperature using a home-built scanning tunnelling microscope (STM) adapted to measure simultaneously the conductance G and Seebeck coefficient S of single-molecule junctions with our previously reported technique4,11 (see ESI† for more details).To localize individual molecules on the Au surface, we proceed by recording STM images of successively smaller areas.4,11 Two typical STM images of individual scandium carbide and erbium nitride EMFs can be seen in Fig. 1b and additional images can be found in the ESI.† To form the molecular junction, the tip is then placed on top of the fullerene and is approached until a certain conductance threshold is reached. As the tip approaches, its motion is stopped every few picometers and a small voltage ramp (±10 mV) is applied, recording I–V curves (measured current I vs. applied voltage V). When a temperature difference of ΔT = 34–42 K is established between the tip and the substrate, I–V curves show a ΔT-dependent voltage offset at zero current, which is identified with the thermovoltage Vth of the fullerene junction and this one with the Seebeck coefficient S = Vth/ΔT. Furthermore, from the slope of the I–V curves, we obtain simultaneously the electrical conductance, G = I/V (see ESI† for a detailed description of the technique).
Two examples of simultaneous conductance G and Seebeck coefficient S approach-retraction cycles, as a function of the tip displacement ΔZ, are shown in Fig. 1c and d for single-molecule junctions of the new EMFs studied As the tip approaches the molecule (top panels in Fig. 1c and d, ΔZ decreases from zero; G plotted in red; S, in blue), the logarithmic conductance of the junction increases linearly with the distance (in semilogarithmic scale) until a physical contact is made with the corresponding EMF and a sudden jump in the signal is measured. The tip moves towards the fullerene for a further ∼ 0.7 nm, to establish a better tip-molecule contact (the contact regime during the tip approach in Fig. 1c and d has been shaded yellow for clarity). Simultaneous thermovoltage measurements allow us to obtain the thermopower of each single-molecule junction as it is formed. Fig. 1c shows an example of a junction with an initially positive Seebeck coefficient, while the junction in Fig. 1d has an initially negative Seebeck coefficient. A jump in Seebeck coefficient is also typically observed when physical contact is established (see Fig. 1c). Additionally, in the curves shown in Fig. 1c and d, we observe a clear correlation between small jumps observed in the conductance and the simultaneous thermopower signals once the contact is formed, showing that both magnitudes are sensitive to small changes in the junction geometry, such as atomic rearrangements in the electrodes.62–64 During retraction, the curves remain almost the same, indicating that the junctions were unaltered (bottom panels in Fig. 1c and d). In particular, their conductance shows generally a change of the slope or a jump down, although some hysteresis is observed and the features of both G and S retraction traces are usually slightly shifted in ΔZ with respect to the approach curves, possibly due to elastic deformations of the Au atoms in the electrodes.62–64 Further examples of individual junctions (see the ESI†) show both signs of the Seebeck coefficient in the case of the two EMFs analysed, demonstrating their bi-thermoelectric nature, with either positive or negative values of S depending on the single molecule studied. This behaviour is similar to the reported bi-thermoelectricity of Sc3N@C80 junctions and is in clear contrast to the consistently negative Seebeck coefficient values obtained for the C60.11
The bi-thermoelectric response of the scandium nitride, scandium carbide and erbium nitride are compared with the more conventional C60 behaviour in Fig. 2a and b, which shows 2D histograms of the Seebeck coefficient S as a function of the conductance G (the data of C60 and Sc3N@C80 junctions are those previously reported in ref. 11). While the histograms in Fig. 2a are formed with all the experimental data obtained from the complete approach traces (i.e. the whole tip movement from tunnelling until the selected conductance threshold), for the histograms in Fig. 2b, only G and S values at first-contact between the tip and molecule are collected, i.e. values measured within 0.1 nm after the contact in the G(ΔZ) curve, where pressure from the tip does not appreciably deform the fullerene-electrodes junction. These histograms, and especially those of first-contact values, show that Sc3N@C80 and Er3N@C80 present smaller G values than Sc3C2@C80 and C60 systems. Furthermore, these two trinitrate molecules present both positive and negative Seebeck coefficients mostly centred at zero. In contrast, the Seebeck coefficient of Sc3C2@C80 junctions seems to be preferentially displaced towards negative values, despite also showing both signs and a considerable dispersion. C60 junctions, as previously reported,4,11 present only negative values of S.
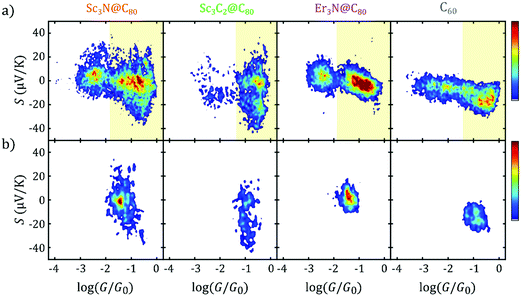 | ||
| Fig. 2 Conductance G and Seebeck coefficient S histograms of the monomers of EMFs and C60. (a) S vs. G 2D histograms built with all the data from the I–V curves measured during the complete approach of the tip, from the noise level until close to the metallic contact. The area shadowed in yellow corresponds approximately to the contact regime (highlighted also in yellow in Fig. 1c and d). (b) S vs. G 2D histograms built with first-contact values, i.e., within 0.1 nm right after junction formation. In a and b, each column corresponds to one molecule, as indicated on top; from left to right: Sc3N@C80, Sc3C2@C80, Er3N@C80 and the fullerene C60. The colour scale accounts for the number of points in each histogram. | ||
An additional striking feature of the histograms in Fig. 2b is the broad distribution of Seebeck coefficients obtained for Sc3C2@C80 and Sc3N@C80, compared with the narrower distributions obtained for Er3N@C80 and C60. This can be more easily observed in the 1D histograms of G and S shown in Fig. 3a and b for all four molecules. Fig. 3b and 2b show that all the EMFs present a bi-thermoelectric behaviour, signalled by the presence of both positive and negative values of S, in clear contrast with the empty fullerene C60 that exhibits only negative Seebeck coefficients. The mean Seebeck coefficients ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) of Sc3N@C80 and Er3N@C80 junctions are very small, while in the case of Sc3C2@C80 (in green in Fig. 3b), two peaks appear in the 1D histogram, centred at 0 μV K−1 and −20 μV K−1, which means that it is equally likely to connect a molecule with a small value of S close to zero or with a negative value similar to that of C60. Finally, Sc3N@C80 and Sc3C2@C80 have a larger dispersion of S values than Er3N@C80. The Seebeck coefficient measurements of the latter are spread only over a range of approximately −20 μV K−1 to +20 μV K−1, whereas the range of values of the EMFs with three scandium atoms is twice as wide. The standard deviation σS in the Seebeck coefficients obtained from Fig. 3b for all the compounds are shown in column 6 of Table 1, (Note that the error in the determination of the thermopower is less than 0.9 μV K−1).
of Sc3N@C80 and Er3N@C80 junctions are very small, while in the case of Sc3C2@C80 (in green in Fig. 3b), two peaks appear in the 1D histogram, centred at 0 μV K−1 and −20 μV K−1, which means that it is equally likely to connect a molecule with a small value of S close to zero or with a negative value similar to that of C60. Finally, Sc3N@C80 and Sc3C2@C80 have a larger dispersion of S values than Er3N@C80. The Seebeck coefficient measurements of the latter are spread only over a range of approximately −20 μV K−1 to +20 μV K−1, whereas the range of values of the EMFs with three scandium atoms is twice as wide. The standard deviation σS in the Seebeck coefficients obtained from Fig. 3b for all the compounds are shown in column 6 of Table 1, (Note that the error in the determination of the thermopower is less than 0.9 μV K−1).
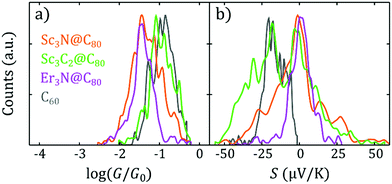 | ||
| Fig. 3 Experimental first-contact histograms of log (G/G0) and S. G (a) and S (b) 1D histograms for all the molecules, showing only the values right after junction formation (at first contact). The data shown in these 1D histograms is the same as in Fig. 2b. | ||
| Molecule | σ θ | σ Φ | σ q Hirshfeld | σ q Voronoi | σ S Exp. (μV K−1) | σ S Theor. (μV K−1) |
|---|---|---|---|---|---|---|
| Sc3C2@C80 | 1.47 | 1.09 | 113 × 10−4 | 133 × 10−4 | 19.2 | 36.0 |
| Sc3N@C80 | 1.43 | 0.95 | 109 × 10−4 | 119 × 10−4 | 17.6 | 29.4 |
| Er3N@C80 | 1.43 | 0.95 | 26 × 10−4 | 27 × 10−4 | 7.7 | == |
| C60 | == | == | 5.7 × 10−4 | 8.5 × 10−4 | 6.8 | 2.44 |
To understand the origin of these differences in Seebeck fluctuations, we used density functional theory (DFT) to examine the binding energies of these junctions under various rotations. The basic theoretical principles of the method can be found in ref. 65 and 66. There are an infinite number of inequivalent orientations of the metallic moieties relative to their fullerene cage. Here we consider a selection of rotations about high-symmetry axes. Fig. 4 shows four axes of rotation θ, Φ, α and β considered below, while Fig. 5 shows how these axes pass through the metallic moieties. For each of the four axes of rotation, we investigate how the total energy varies with angle of rotation, both in presence and absence of the gold substrate. For each of these four axes, we consider one mode of rotation in the gas phase and three modes of rotation on a substrate.
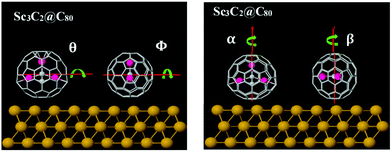 | ||
| Fig. 4 Illustration of the four rotation axes: θ and Φ are horizontal axes, α and β are vertical axes. This Figure shows how the axes pass through the Ih–C80 cage + metallic moiety. | ||
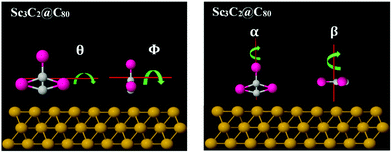 | ||
| Fig. 5 Illustration of how the four rotation axes θ, Φ, α and β, pass through the metallic moiety (in the absence of the cage). | ||
In the gas phase, we consider rotation of the metallic moiety relative to a fixed fullerene cage. For this rotational mode, rotations about the β and Φ axes are equivalent, so in the gas phase, rotations about 3 distinct axes are investigated. In the presence of the gold substrate, we consider three modes of rotation about each of the four axes: rotation of the bare metallic moiety (in the absence of the cage), rotation of the metallic moiety in the presence of a fixed cage, and rotation of both the metallic moiety and cage, such that their relative orientation is fixed. This means that in total, on a substrate, 12 distinct cases are considered (4 axes x 3 modes of rotation). For simplicity of notation, in what follows, the same symbol (e.g. θ) is used to label both the rotation axis and the angle of rotation about the axis.
To quantify geometrical variations under rotation, it is convenient to define the distance d to be the smallest vertical distance between the top-most plane of the Au-substrate and the closest metal atom of the encapsulated moiety. Fig. S12 (ESI†) shows the variation of d with rotations about the above axes, while Table 1 (colums 2 and 3) shows the standard deviations σθ, σΦ in d under rotations about the axes θ, Φ. By symmetry σα = σβ = 0 and therefore these follow the order σθ > σΦ > σα, σβ. Furthermore, the values of both σθ and σΦ associated with Sc3C2@C80 are higher than those associated with Sc3N@C80 and Er3N@C80 (for more detail see Table S2 in the ESI†).
To quantify the charge inhomogeneities associated with these molecules, we also computed the standard deviations σq of the charge distributions on their cages, using two different definitions of charge (Hirshfeld and Voronoi).67,68 If the charge on atom i of the cage is |e|ni|, then the standard deviation σq in the charge is defined by:
| σ2q = 〈< (ni − 〈ni〉)2〉 |
As a first step in the calculations leading to Table 1, energy barriers to rotation about the above axes were computed, to obtain the preferred angles of rotation, which minimise the total energy. σS was then obtained by computing Seebeck coefficients using an ensemble of angles and a distribution of Fermi energies EF, as described in sections 5.7 to 5.15 of the ESI.†Table 2 shows the computed gas-phase energy barriers ΔE(θ), ΔE(Φ), ΔE(α) associated with rotations about θ, Φ, α of Sc3C2, Sc3N and Sc3N within the fixed Ih–C80 cage, along with the preferred orientation angles for the three rotation axes (see Section 5.5 in the ESI†). This reveals that for all three axes, Sc3C2@C80 possesses the highest energy barriers to rotation, followed by Sc3N@C80, with Er3N@C80 possessing the lowest barriers. These correlate closely with their values of σ2q and furthermore, the highest energy barrier associated with Sc3C2@C80 correlates with the high value of the standard deviation in d.
| EMF | ΔE(θ) (meV) | Preferred orientations (θ) | ΔE(Φ) (meV) | Preferred orientations (Φ) | ΔE(α) (meV) | Preferred orientations (α) |
|---|---|---|---|---|---|---|
| Sc3C2@C80 | 400 | 0°, 190° and 360° | 350 | 0°, 110°, 180°, 210°, 270° and 360° | 300 | 0°, 75°, 160°, 240° and 320° |
| Sc3N@C80 | 300 | 0°, 190° and 360° | 250 | 10°, 95°, 200°, 280° and 340° | 150 | 0°, 75°, 100°, 150°, 200° 250°, 300° and 350° |
| Er3N@C80 | 130 | 0°, 190° and 360° | 100 | 0°, 120°, 250° and 350° | 60 | 0°, 80°, 150°, 225°, 320°and 360° |
Table 2 shows that for all EMFs, in the gas phase, the energy barriers to rotation follow the order ΔE(θ) > ΔE(Φ) > ΔE(α). Fig. S21 (ESI†) shows that on a gold surface, the binding energies are also higher for the θ and Φ axes and follow the order ΔE(θ)> ΔE(Φ)> ΔE(α) > ΔE(β). Furthermore the barriers are higher for Sc3C2@C80 and lower for Er3N@C80. On a gold substrate, the energy barriers significantly increase to approximately 0.6 eV for Sc3C2@C80, which means that the configurational degrees of freedom of the endofullerene relative to the electrode exhibit a small number of preferred orientations corresponding to minima in the total energy of the endofullerene/electrode complex as shown in Fig. S21 (ESI†) (for more detail see section 5.6 of the ESI†). The energy barrier for Sc3N@C80 is 0.3 eV and the lowest barrier of 0.1 eV is obtained for Er3N@C80 (see Fig. S18, ESI†). (Note: Fig. S21, ESI† shows the four rotation axes, while Fig. S18, ESI† shows only θ).
To obtain the theoretical values of σS in Table 1 from the above distribution of orientations, we used a combination of the quantum transport code Gollum75 and the density functional theory (DFT) code SIESTA,76 to calculate the transmission coefficient T(E) for electrons of energy E passing through the EMFs, when contacted to gold electrodes (a detailed description can be found in the ESI†). The energy dependence of transmissions curves for Sc3C2@C80, Sc3N@C80 and C60, and their Seebeck coefficients for all minimum-energy orientations, are shown in Fig. S23 to S44 (ESI†). Since the curves are rather smooth on the scale of kBT at room temperature, their electrical conductance G is approximated by G ≈ T (EF)G0, where G0 is the quantum of conductance, and 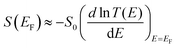 65 In the latter equation, if E is measured in units of electron volts, then S0 = αT, which at T = 300 K, takes the value S0 = 7.3 μV K−1. Fig. S23 to S44 (ESI†) clearly show that rotations about the θ axis cause much more severe fluctuations in the transmission functions than rotations about the other axes. By sampling the transmission curves over a range of Fermi energies and preferred orientations (as described in the ESI†), we obtain the theoretical 2D histograms shown in Fig. S45, (ESI†) from which the theoretical values of σS in Table 1 were obtained. In general, depending on the value of EF, the Seebeck coefficient can achieve high values when the distance d between the metallic moiety and the Au substrate is large (e.g., for θ = 90°, in Fig. S22, ESI†), whereas S tends to be lower when d is small (e.g., for θ = 0°, in Fig. S22, ESI†).
65 In the latter equation, if E is measured in units of electron volts, then S0 = αT, which at T = 300 K, takes the value S0 = 7.3 μV K−1. Fig. S23 to S44 (ESI†) clearly show that rotations about the θ axis cause much more severe fluctuations in the transmission functions than rotations about the other axes. By sampling the transmission curves over a range of Fermi energies and preferred orientations (as described in the ESI†), we obtain the theoretical 2D histograms shown in Fig. S45, (ESI†) from which the theoretical values of σS in Table 1 were obtained. In general, depending on the value of EF, the Seebeck coefficient can achieve high values when the distance d between the metallic moiety and the Au substrate is large (e.g., for θ = 90°, in Fig. S22, ESI†), whereas S tends to be lower when d is small (e.g., for θ = 0°, in Fig. S22, ESI†).
The high values of σS and the bi-thermoelectric response of these EMF junctions confirm our initial intuition that charge inhomogeneity leads to larger variability in the transport properties, compared with pristine C60. This interesting behaviour is also observed in ref. 77, where Gd@C82 and Ce@C82 and the empty C82 were reported to present mainly negative Seebeck coefficients, with occasional positive values that were attributed possibly to meta-stable configurations of the junctions. The values reported for the Seebeck coefficient show an enhancement in the endohedral fullerenes with respect to the C82. Compared to our investigated EMFs, the main difference with the systems studied in ref. 77 is the total number of metal atoms inside the fullerene cage, which in the case of ref. 77 is just one atom placed out of centre.
Of particular interest for quantifying the thermoelectric performance of molecular junctions is the power factor GS2. Fig. 6 shows a comparison between the experimental and theoretical power factor distributions. These possess comparable shapes and, in both cases, reveal that rare values corresponding to particular configurations of the junctions can lead to very high-power factors.
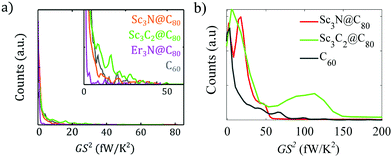 | ||
| Fig. 6 Power factor GS2 analysis. a) Experimental 1D histograms of power factor at first contact, built with the data in Fig. 3. The inset zooms into the details of the main panel. b). Theoretical 1D histograms of power factor obtained from Fig. S46 of the ESI.† | ||
Fig. 6 also shows that the high conductance and Seebeck coefficient values measured for the carbide EMF translate into quite high values of power factor GS2, with the highest power factor values of Sc3C2@C80 significantly exceeding those of C60, both in value and probability.
Lee et al77 noted that their EMF-based junctions possessed a high single molecule power factor of 16.2 fW K−2 for Gd@C82, which corresponds to around 4 × 10 μW K−2 m−1 for a thin-film device consisting of a monolayer of Gd@C82, which at the time of publication was the largest power factor obtained for a single molecule device. From the first-contact data in Fig. 3, we find even higher values up to 50 fW K−2 for Sc3N@C80 and Sc3C2@C80 junctions, and even two examples of values up to 70–80 fW K−2 (for these two EMFs). Statistically, we find larger values for the carbide compound (Sc3C2@C80 junctions). Furthermore, considering all the measured conductance and Seebeck coefficient values (Fig. S9, ESI†), the power factor can be statistically increased when the junction becomes slightly compressed, because under compression, G increases and S becomes more negative.
Conclusions
Through a combination of experimental STM-based transport measurements and DFT-based transport calculations, we have studied the electrical conductance and Seebeck coefficient of three endohedral metallofullerenes (EMFs) Sc3N@C80, Sc3C2@C80, and Er3N@C80, and found that all EMFs studied are bi-thermoelectric systems, exhibiting both positive and negative Seebeck coefficients, in contrast to the empty C60. To understand the origin of these fluctuations in thermoelectric properties, DFT simulations of a selection of orientations were carried out, that allowed us to answer the following questions:1) Can variations in the orientations of the fullerenes and their encapsulated moieties lead to fluctuations in Seebeck coefficients on the scale of those measured experimentally? DFT modelling shows that fluctuations on the scale of the measured values can indeed arise from variations in the orientations of the fullerenes and their encapsulated moieties and the degree of variation is characterised by the associated standard deviation σ, which is a purely geometric quantity. This is an important result, because it shows that such fluctuations are an intrinsic property of the junctions and not due to some unknown extrinsic effect.
2) Are there correlations between Seebeck fluctuations and the degree of charge inhomogeneity? To establish these correlations, in Fig. 4, 5 and Fig. S15, S21, Table S3, (ESI†) we explored a large number (360 × 3 axes in gas phase and 360 × 4 axes onto a gold surface) of different geometries and identified the most energetically favourable configurations, which are relevant experimentally. These calculations demonstrate a clear correlation between Seebeck fluctuations and the degree of charge inhomogeneity, which can be characterised by a standard deviation σq.
We found that standard deviations in the Seebeck coefficients σS of EMF-based junctions are correlated with the geometric standard deviation σ and the charge inhomogeneity σq. We benchmarked these molecules against C60 and found that all of σq,σS are the largest for Sc3C2@C80, all are the smallest for C60 and for the other EMFs, they follow the order Sc3C2@C80 >Sc3N@C80 > Er3N@C80 > C60. This means that external measurements of fluctuations in the Seebeck coefficient provide insight into the internal structure and charge distribution of endohedral metallofullerenes.
This points the way to designs of molecular switches and bi-thermoelectric materials, because molecules with large values of σq possess large values of σS; the former is a sign that a molecule can switch between orientation-dependent electrical conductances, whereas the latter indicates that a molecule can exhibit a wide range of Seebeck coefficients with both positive and negative signs. If the orientation and Fermi energy of such molecules can be controlled, then high thermoelectric performance is possible. On the other hand, if the aim is to minimise fluctuations, then our study suggests that molecules with low values of σ and σq should be selected.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. D. acknowledges support from the Hellenic Foundation for Research and Innovation (Grant number: 1468). A. K. I. acknowledges the Leverhulme Trust for Early Career Fellowship ECF-2020-638. A. K. I and A. A are also grateful for financial assistance from Tikrit and Anbar Universities (Iraq), and the Iraqi Ministry of Higher Education (SL-20). T. A. is grateful for financial assistance from Al-Jouf University (Saudi Arabia), and the Saudi Ministry of Education. A. K. I and C. J. L. acknowledge financial support from the UK EPSRC, through Grant no. EP/M014452/1, EP/P027156/1 and EP/N03337X/1. This work was additionally supported by the European Commission is provided by the FET Open project 767187–QuIET. N. A. and G. R.-B. acknowledge the Spanish MINECO (grants MAT2014-57915-R, MAT2017-88693-R, and MDM-2014-0377, and the María de Maeztu Programme for Units of Excellence in R&D MDM-2014-0377 and CEX2018-000805-M) and Comunidad de Madrid (grants NANOFRONTMAG-CM, S2013/MIT-2850, and NANOMAGCOST-CM, P2018/NMT-4321). L. R.-G. acknowledges financial support from the Spanish MECD (Grant no. FPU14/03368). N. A. and L. R.-G. are also grateful for financial support from the Education and Research Council of the Comunidad de Madrid and the European Social Fund (Ref. PEJD-2019-POST/IND-16353).References
- F. Pauly, J. K. Viljas and J. C. Cuevas, Length-dependent conductance and thermopower in single-molecule junctions of dithiolated oligophenylene derivatives: A density functional study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(3), 035315 CrossRef.
- D. Nozaki, H. Sevinçli, W. Li, R. Gutiérrez and G. Cuniberti, Engineering the figure of merit and thermopower in single-molecule devices connected to semiconducting electrodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(23), 235406 CrossRef.
- M. Bürkle, L. A. Zotti, J. K. Viljas, D. Vonlanthen, A. Mishchenko, T. Wandlowski, M. Mayor, G. Schön and F. Pauly, Ab initio study of the thermopower of biphenyl-based single-molecule junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(11), 115304 CrossRef.
- C. Evangeli, K. Gillemot, E. Leary, M. T. Gonzalez, G. Rubio-Bollinger, C. J. Lambert and N. Agrait, Engineering the thermopower of C60 molecular junctions, Nano Lett., 2013, 13(5), 2141–2145 CrossRef CAS PubMed.
- O. Karlström, M. Strange and G. C. Solomon, Understanding the length dependence of molecular junction thermopower, J. Chem. Phys., 2014, 140(4), 044315 CrossRef PubMed.
- C. G. Péterfalvi, I. Grace, D. Z. Manrique and C. J. Lambert, Thermoelectric performance of various benzo-difuran wires, J. Chem. Phys., 2014, 140(17), 174711 CrossRef PubMed.
- V. M. García-Suárez, C. J. Lambert, D. Z. Manrique and T. Wandlowski, Redox control of thermopower and figure of merit in phase-coherent molecular wires, Nanotechnology, 2014, 25(20), 205402 CrossRef PubMed.
- A. K. Ismael, I. Grace and C. J. Lambert, Increasing the thermopower of crown-ether-bridged anthraquinones, Nanoscale, 2015, 7(41), 17338–17342 RSC.
- H. Sadeghi, S. Sangtarash and C. J. Lambert, Oligoyne molecular junctions for efficient room temperature thermoelectric power generation, Nano Lett., 2015, 15(11), 7467–7472 CrossRef CAS PubMed.
- M. Bürkle, T. J. Hellmuth, F. Pauly and Y. Asai, First-principles calculation of the thermoelectric figure of merit for [2, 2] paracyclophane-based single-molecule junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(16), 165419 CrossRef.
- L. Rincón-García, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis, N. Agraït and C. J. Lambert, Molecular design and control of fullerene-based bi-thermoelectric materials, Nat. Mater., 2016, 15(3), 289–293 CrossRef PubMed.
- C. Perroni, D. Ninno and V. Cataudella, Thermoelectric efficiency of molecular junctions, J. Phys.: Condens. Matter, 2016, 28(37), 373001 CrossRef CAS PubMed.
- D. Z. Manrique, Q. Al-Galiby, W. Hong and C. J. Lambert, A new approach to materials discovery for electronic and thermoelectric properties of single-molecule junctions, Nano Lett., 2016, 16(2), 1308–1316 CrossRef CAS PubMed.
- L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Thermopower measurements in molecular junctions, Chem. Soc. Rev., 2016, 45(15), 4285–4306 RSC.
- C. J. Lambert, H. Sadeghi and Q. H. Al-Galiby, Quantum-interference-enhanced thermoelectricity in single molecules and molecular films, C. R. Phys., 2016, 17(10), 1084–1095 CrossRef CAS.
- Y. Li, L. Xiang, J. L. Palma, Y. Asai and N. Tao, Thermoelectric effect and its dependence on molecular length and sequence in single DNA molecules, Nat. Commun., 2016, 7(1), 1–8 Search PubMed.
- L. Cui, R. Miao, C. Jiang, E. Meyhofer and P. Reddy, Perspective: Thermal and thermoelectric transport in molecular junctions. The, J. Chem. Phys., 2017, 146(9), 092201 CrossRef.
- P. Gehring, A. Harzheim, J. Spiece, Y. Sheng, G. Rogers, C. Evangeli, A. Mishra, B. J. Robinson, K. Porfyrakis and J. H. Warner, Field-effect control of graphene–fullerene thermoelectric nanodevices, Nano Lett., 2017, 17(11), 7055–7061 CrossRef CAS PubMed.
- J.-C. Klöckner, R. Siebler, J. C. Cuevas and F. Pauly, Thermal conductance and thermoelectric figure of merit of C 60-based single-molecule junctions: electrons, phonons, and photons, Phys. Rev. B, 2017, 95(24), 245404 CrossRef.
- Q. H. Al-Galiby, H. Sadeghi, D. Z. Manrique and C. J. Lambert, Tuning the Seebeck coefficient of naphthalenediimide by electrochemical gating and doping, Nanoscale, 2017, 9(14), 4819–4825 RSC.
- X. Wang, T. L. Bennett, A. Ismael, L. A. Wilkinson, J. Hamill, A. J. White, I. M. Grace, O. V. Kolosov, T. Albrecht and B. J. Robinson, Scale-up of room-temperature constructive quantum interference from single molecules to self-assembled molecular-electronic films, J. Am. Chem. Soc., 2020, 142(19), 8555–8560 CrossRef CAS PubMed.
- A. Ismael, A. Al-Jobory, X. Wang, A. Alshehab, A. Almutlg, M. Alshammari, I. Grace, T. L. Benett, L. A. Wilkinson and B. J. Robinson, Molecular-scale thermoelectricity: as simple as ‘ABC’, Nanoscale Adv., 2020, 2(11), 5329–5334 RSC.
- A. Ismael, X. Wang, T. L. Bennett, L. A. Wilkinson, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, Tuning the thermoelectrical properties of anthracene-based self-assembled monolayers, Chem. Sci., 2020, 11(26), 6836–6841 RSC.
- X. Wang, A. Ismael, A. Almutlg, M. Alshammari, A. Al-Jobory, A. Alshehab, T. L. Bennett, L. A. Wilkinson, L. F. Cohen and N. J. Long, Optimised power harvesting by controlling the pressure applied to molecular junctions, Chem. Sci., 2021, 12(14), 5230–5235 RSC.
- A. Harzheim, Thermoelectricity in single-molecule devices, Mater. Sci. Technol., 2018, 34(11), 1275–1286 CrossRef CAS.
- L. Algharagholy, T. Pope and C. Lambert, Strain-induced bi-thermoelectricity in tapered carbon nanotubes, J. Phys.: Condens. Matter, 2018, 30(10), 105304 CrossRef CAS PubMed.
- G. Yzambart, L. Rincón-García, A. A. Al-Jobory, A. K. Ismael, G. Rubio-Bollinger, C. J. Lambert, N. Agraït and M. R. Bryce, Thermoelectric Properties of 2, 7-Dipyridylfluorene Derivatives in Single-Molecule Junctions. The, J. Phys. Chem. C, 2018, 122(48), 27198–27204 CrossRef CAS PubMed.
- R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark and E. Meyhofer, Influence of quantum interference on the thermoelectric properties of molecular junctions, Nano Lett., 2018, 18(9), 5666–5672 CrossRef CAS PubMed.
- M. K. Al-Khaykanee, A. K. Ismael, I. Grace and C. J. Lambert, Oscillating Seebeck coefficients in π-stacked molecular junctions, RSC Adv., 2018, 8(44), 24711–24715 RSC.
- L. Cui, R. Miao, K. Wang, D. Thompson, L. A. Zotti, J. C. Cuevas, E. Meyhofer and P. Reddy, Peltier cooling in molecular junctions, Nat. Nanotechnol., 2018, 13(2), 122–127 CrossRef CAS PubMed.
- M. Famili, I. M. Grace, Q. Al-Galiby, H. Sadeghi and C. J. Lambert, Toward high thermoelectric performance of thiophene and ethylenedioxythiophene (EDOT) molecular wires, Adv. Funct. Mater., 2018, 28(15), 1703135 CrossRef.
- H. Khalatbari, S. I. Vishkayi and H. R. Soleimani, Effect of dopant nitrogen on the thermoelectric properties of C20 and C60 fullerene in graphene nanoribbon junction, Phys. E, 2019, 108, 372–381 CrossRef CAS.
- H. Chen, S. Sangtarash, G. Li, M. Gantenbein, W. Cao, A. Alqorashi, J. Liu, C. Zhang, Y. Zhang and L. Chen, Exploring the thermoelectric properties of oligo (phenylene-ethynylene) derivatives, Nanoscale, 2020, 12(28), 15150–15156 RSC.
- A. K. Ismael and C. J. Lambert, Molecular-scale thermoelectricity: a worst-case scenario, Nanoscale Horiz., 2020, 5(7), 1073–1080 RSC.
- M. Noori, H. Sadeghi, Q. Al-Galiby, S. W. Bailey and C. J. Lambert, High cross-plane thermoelectric performance of metallo-porphyrin molecular junctions, Phys. Chem. Chem. Phys., 2017, 19(26), 17356–17359 RSC.
- S. Sangtarash, H. Sadeghi and C. J. Lambert, Connectivity-driven bi-thermoelectricity in heteroatom-substituted molecular junctions, Phys. Chem. Chem. Phys., 2018, 20(14), 9630–9637 RSC.
- S. Naghibi, A. K. Ismael, A. Vezzoli, M. K. Al-Khaykanee, X. Zheng, I. M. Grace, D. Bethell, S. J. Higgins, C. J. Lambert and R. J. Nichols, Synthetic Control of Quantum Interference by Regulating Charge on a Single Atom in Heteroaromatic Molecular Junctions, J. Phys. Chem. Lett., 2019, 10(20), 6419–6424 CrossRef CAS PubMed.
- H. Dekkiche, A. Gemma, F. Tabatabaei, A. S. Batsanov, T. Niehaus, B. Gotsmann and M. R. Bryce, Electronic conductance and thermopower of single-molecule junctions of oligo (phenyleneethynylene) derivatives, Nanoscale, 2020, 12(36), 18908–18917 RSC.
- P. Gehring, J. K. Sowa, C. Hsu, J. de Bruijckere, M. van der Star, J. J. Le Roy, L. Bogani, E. M. Gauger and H. S. van der Zant, Complete mapping of the thermoelectric properties of a single molecule, Nat. Nanotechnol., 2021, 16(4), 426–430 CrossRef CAS PubMed.
- K. Wang, E. Meyhofer and P. Reddy, Thermal and thermoelectric properties of molecular junctions, Adv. Funct. Mater., 2020, 30(8), 1904534 CrossRef CAS.
- S. Park, H. Kang and H. J. Yoon, Structure–thermopower relationships in molecular thermoelectrics, J. Mater. Chem. A, 2019, 7(24), 14419–14446 RSC.
- E. Akkermans and G. Montambaux, Mesoscopic physics of electrons and photons. Cambridge university press, 2007 Search PubMed.
- S. Datta, Electronic transport in mesoscopic systems. Cambridge university press, 1997 Search PubMed.
- W. Hong, H. Valkenier, G. Mészáros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. García, C. J. Lambert, J. C. Hummelen and T. Wandlowski, An MCBJ case study: The influence of π-conjugation on the single-molecule conductance at a solid/liquid interface, Beilstein J. Nanotechnol., 2011, 2(1), 699–713 CrossRef PubMed.
- G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott and N. Bennett, Long-range electron tunnelling in oligo-porphyrin molecular wires, Nat. Nanotechnol., 2011, 6(8), 517–523 CrossRef CAS PubMed.
- S. Ballmann, R. Härtle, P. B. Coto, M. Elbing, M. Mayor, M. R. Bryce, M. Thoss and H. B. Weber, Experimental evidence for quantum interference and vibrationally induced decoherence in single-molecule junctions, Phys. Rev. Lett., 2012, 109(5), 056801 CrossRef PubMed.
- V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, Correlations between molecular structure and single-junction conductance: a case study with oligo (phenylene-ethynylene)-type wires, J. Am. Chem. Soc., 2012, 134(11), 5262–5275 CrossRef CAS PubMed.
- J. Chaste, A. Eichler, J. Moser, G. Ceballos, R. Rurali and A. Bachtold, A nanomechanical mass sensor with yoctogram resolution, Nat. Nanotechnol., 2012, 7(5), 301–304 CrossRef CAS PubMed.
- H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. Hybertsen, Probing the conductance superposition law in single-molecule circuits with parallel paths, Nat. Nanotechnol., 2012, 7(10), 663–667 CrossRef CAS PubMed.
- W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, Single molecular conductance of tolanes: experimental and theoretical study on the junction evolution dependent on the anchoring group, J. Am. Chem. Soc., 2012, 134(4), 2292–2304 CrossRef CAS PubMed.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. Woerde, R. Eelkema, F. C. Grozema and H. S. Van Der Zant, Signatures of quantum interference effects on charge transport through a single benzene ring, Angew. Chem., Int. Ed., 2013, 52(11), 3152–3155 CrossRef CAS PubMed.
- Y. Geng, S. Sangtarash, C. Huang, H. Sadeghi, Y. Fu, W. Hong, T. Wandlowski, S. Decurtins, C. J. Lambert and S.-X. Liu, Magic ratios for connectivity-driven electrical conductance of graphene-like molecules, J. Am. Chem. Soc., 2015, 137(13), 4469–4476 CrossRef CAS PubMed.
- M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li and S. Xiao, Comprehensive suppression of single-molecule conductance using destructive σ-interference, Nature, 2018, 558(7710), 415–419 CrossRef CAS PubMed.
- Y. Ito, T. Okazaki, S. Okubo, M. Akachi, Y. Ohno, T. Mizutani, T. Nakamura, R. Kitaura, T. Sugai and H. Shinohara, Enhanced 1520 nm photoluminescence from Er3+ ions in di-erbium-carbide metallofullerenes (Er2C2)@ C82 (isomers I, II, and III), ACS Nano, 2007, 1(5), 456–462 CrossRef CAS PubMed.
- L. Dunsch and S. Yang, Metal nitride cluster fullerenes: their current state and future prospects, Small, 2007, 3(8), 1298–1320 CrossRef CAS PubMed.
- C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov and A. Kostanyan, Selective arc-discharge synthesis of Dy 2 S-clusterfullerenes and their isomer-dependent single molecule magnetism, Chem. Sci., 2017, 8(9), 6451–6465 RSC.
- C. D. Tran and G.-H. Gao, Characterization of an erbium-doped fiber amplifier as a light source and development of a near-infrared spectrophotometer based on the EDFA and an acoustooptic tunable filter, Anal. Chem., 1996, 68(13), 2264–2269 CrossRef CAS PubMed.
- M. Krause, M. Hulman, H. Kuzmany, O. Dubay, G. Kresse, K. Vietze, G. Seifert, C. Wang and H. Shinohara, Fullerene quantum gyroscope, Phys. Rev. Lett., 2004, 93(13), 137403 CrossRef CAS PubMed.
- A. Rodríguez-Fortea, A. L. Balch and J. M. Poblet, Endohedral metallofullerenes: a unique host–guest association, Chem. Soc. Rev., 2011, 40(7), 3551–3563 RSC.
- A. Rodríguez-Fortea, S. Irle and J. M. Poblet, Fullerenes: formation, stability, and reactivity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(3), 350–367 Search PubMed.
- X. Aparicio-Anglès, N. R. Alegret, A. Clotet, A. Rodríguez-Fortea and J. M. Poblet, Endohedral metallofullerenes containing lanthanides: a robust yet simple computational approach, J. Phys. Chem. C, 2013, 117(24), 12916–12921 CrossRef.
- N. Agrait, G. Rubio and S. Vieira, Plastic deformation of nanometer-scale gold connective necks, Phys. Rev. Lett., 1995, 74(20), 3995 CrossRef PubMed.
- N. Agrait, G. Rubio and S. Vieira, Plastic deformation in nanometer scale contacts, Langmuir, 1996, 12(19), 4505–4509 CrossRef.
- G. Rubio, N. Agrait and S. Vieira, Atomic-sized metallic contacts: mechanical properties and electronic transport, Phys. Rev. Lett., 1996, 76(13), 2302 CrossRef CAS PubMed.
- C. J. Lambert, Quantum Transport in Nanostructures and Molecules. IOP Publishing, 2021 Search PubMed.
- C. Lambert, Basic concepts of quantum interference and electron transport in single-molecule electronics, Chem. Soc. Rev., 2015, 44(4), 875–888 RSC.
- F. Bickelhaupt and N. van Hommes, Organometallics, 1996, 15, 2923 CrossRef CAS; C. Fonseca Guerra, J. W. Handgraaf, E. J. Baerends and F. Bickelhaupt, J. Comput. Chem., 2004, 25, 189 CrossRef PubMed.
- H. Hirshfeld, Synthesis, Crystal structure, and Hirshfeld Surface Analysis of a New Mixed Ligand Copper(II) Complex, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef.
- P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Thermoelectricity in molecular junctions, Science, 2007, 315(5818), 1568–1571 CrossRef CAS PubMed.
- J. A. Malen, P. Doak, K. Baheti, T. D. Tilley, R. A. Segalman and A. Majumdar, Identifying the length dependence of orbital alignment and contact coupling in molecular heterojunctions, Nano Lett., 2009, 9(3), 1164–1169 CrossRef CAS PubMed.
- S. Park, N. Cho and H. J. Yoon, Two Different Length-Dependent Regimes in Thermoelectric Large-Area Junctions of n-Alkanethiolates, Chem. Mater., 2019, 31(15), 5973–5980 CrossRef CAS.
- S. Park, J. Jang and H. J. Yoon, Validating the Mott Formula with Self-Assembled Monolayer (SAM)-Based Large-Area Junctions: Effect of Length, Backbone, Spacer, Substituent, and Electrode on the Thermopower of SAMs. The, J. Phys. Chem. C, 2021, 125(36), 20035–20047 CrossRef CAS.
- S. Park, S. Kang and H. J. Yoon, Power factor of one molecule thick films and length dependence, ACS Cent. Sci., 2019, 5(12), 1975–1982 CrossRef CAS PubMed.
- S. Park and H. J. Yoon, New Approach for large-area thermoelectric junctions with a liquid eutectic gallium–indium electrode, Nano Lett., 2018, 18(12), 7715–7718 CrossRef CAS PubMed.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. Bailey and K. Gillemot, GOLLUM: a next-generation simulation tool for electron, thermal and spin transport, New J. Phys., 2014, 16(9), 093029 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745 CrossRef CAS.
- S. K. Lee, M. Buerkle, R. Yamada, Y. Asai and H. Tada, Thermoelectricity at the molecular scale: a large Seebeck effect in endohedral metallofullerenes, Nanoscale, 2015, 7(48), 20497–20502 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, purification and MALDI-TOF data of the EMFs, HPLC graphs demonstrating the purification process for the Sc3N@C80; Tauc plots and UV-Visible spectra for Er3N@C80 and Sc3N@C80; EPR of the Sc3C2@C80; details on the experimental methods, further examples of individual measurements and complementary analysis of the results; details on the theoretical methods, and complementary results from the theoretical calculations are available free of charge via the internet. See DOI: https://doi.org/10.1039/d1nh00527h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |