Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards high-resolution X-ray scattering as a probe of electron correlation
Andrés
Moreno Carrascosa
 *ac,
Jeremy P.
Coe
*ac,
Jeremy P.
Coe
 b,
Mats
Simmermacher
b,
Mats
Simmermacher
 ac,
Martin J.
Paterson
ac,
Martin J.
Paterson
 b and
Adam
Kirrander
b and
Adam
Kirrander
 *ac
*ac
aEaStCHEM, School of Chemistry, University of Edinburgh, Edinburgh EH9 3FJ, UK. E-mail: andres.morenocarrascosa@chem.ox.ac.uk; adam.kirrander@chem.ox.ac.uk
bInstitute of Chemical Sciences, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh EH14 4AS, UK
cDepartment of Chemistry, Physical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford OX1 3QZ, UK
First published on 4th October 2022
Abstract
X-ray scattering cross sections are calculated using a range of increasingly correlated methods: Hartree–Fock (HF), complete active space self-consistent field (CASSCF), Monte Carlo configuration interaction (MCCI), and full configuration interaction (FCI). Even for the seemingly straightforward case of ground state Ne, the accuracy of the total scattering is significantly better with a more correlated wavefunction. Scanning the bond distance in ground state CO shows that the total scattering signal tracks the multireference character. We examine the convergence of the elastic, inelastic, and total scattering of O3. Overall, the inelastic and total components are found to be the most sensitive to the strength of correlation. Our results suggest that highly accurate measurement of X-ray scattering could provide a sensitive probe of pair-wise correlation between electrons.
1 Introduction
X-ray and electron scattering have had great impact on our understanding of the structure of matter.1–3 In X-ray crystallography, the relationship between the arrangement of the atoms in the unit cell and the elastic scattering measured in the Bragg peaks has enabled remarkable progress in structure determination.4–6 The corresponding measurements in the gas phase appeared early, with important contributions made by Debye and colleagues, who established the widely-used independent atom model (IAM).7,8 Electrons have larger cross sections compared to photons, which allowed gas-phase electron scattering to develop into an important technique for the structure determination of free molecules.9 Recently, the emergence of X-ray free-electron lasers (XFELs) has spurred a revival of gas-phase scattering using X-rays,10–13 not the least in the domain of ultrafast X-ray scattering.14–20 The high intensity and repetition rate at next-generation XFELs opens the prospect of accurate scattering measurements with excellent signal-to-noise on isolated and unperturbed targets in the gas phase.Experiments capable of probing quantitatively the intriguing relationship between total scattering and electron correlation, originally pointed out by Bartell and Gavin21,22 and illustrated in Fig. 1, may thus be approaching. It is therefore pertinent to develop the theoretical and computational tools to analyse such experimental data and to examine the relationship between electronic structure calculations and scattering signals, especially given the potential for new experimental benchmarks. Computational methods that calculate scattering cross sections from electronic wavefunctions can now efficiently provide elastic, inelastic, and total scattering cross sections for both electronic ground and excited states.23–36 Notably, the accuracy of the cross section depends crucially on the quality of the underlying electronic wavefunction and therefore on the electronic structure method from which it is derived.
In the following, we examine the effect of electron correlation on scattering cross sections and demonstrate that highly correlated methods are necessary to match the anticipated accuracy of future X-ray scattering experiments. One of the tools employed for this purpose is Monte Carlo configuration interaction (MCCI), which is capable of converging close to the benchmark of full configuration interaction (FCI), but with a much more compact expansion and at significantly lower computational cost.37,38 As a result, highly accurate total scattering cross sections can be obtained that more rigorously account for the effect of strong electron correlation in atoms and small molecules.
2 Theory
2.1 Scattering
The non-resonant scattering of hard X-rays by an atom or molecule can be described by first-order time-dependent perturbation theory and quantum electrodynamics.39,40 If the system is in the stationary electronic ground state, the expression for the experimentally observable differential X-ray scattering cross section, dσ/dΩ, derived within this framework reads,41,42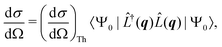 | (1) |
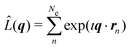 is the scattering operator with q = ks − k0 the momentum transfer vector where the wave vectors of the incident and scattered photons are k0 and ks, while rn is the coordinate of an electron with index n, and Ne is the number of electrons in the system. The matrix element in eqn (1) implies integration over all electronic coordinates and can be expressed as,
is the scattering operator with q = ks − k0 the momentum transfer vector where the wave vectors of the incident and scattered photons are k0 and ks, while rn is the coordinate of an electron with index n, and Ne is the number of electrons in the system. The matrix element in eqn (1) implies integration over all electronic coordinates and can be expressed as,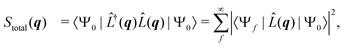 | (2) |
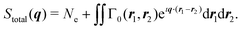 | (3) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) (q)|Ψ0〉|2 term in the sum in eqn (2), which corresponds to the absolute-squared Fourier transform of the ground-state one-electron density, ρ0(r),
(q)|Ψ0〉|2 term in the sum in eqn (2), which corresponds to the absolute-squared Fourier transform of the ground-state one-electron density, ρ0(r),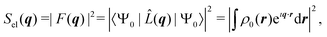 | (4) |
| Sinel(q) = Stotal(q) − Sel(q). | (5) |
As mentioned in the Introduction, a key difference between crystalline and gas-phase targets is the absence of a lattice that coherently amplifies the elastic signal in the latter. This has profound consequences. While elastic scattering in crystallography stems predominantly from the electron density of the target (eqn (4)), the total scattering measured in the gas phase with energy-integrating detectors is sensitive to static and dynamic correlation via the two-electron density (eqn (3)), which incorporates all electron–electron correlations of the system.
2.2 Multiconfigurational wavefunctions
Due to the above-mentioned importance of electron correlation, we anticipate that accurate scattering cross sections will require post Hartree–Fock (HF) methods. Multiconfigurational methods such as complete active space self-consistent field (CASSCF) are capable of capturing a large fraction of the electron correlation44 but fall short of full configuration interaction (FCI), which is exact within the limits of a given basis. In order to quantify the effect of electron correlation on gas-phase X-ray scattering, we compare HF and CASSCF with the highly correlated MCCI method. In each case, the results are benchmarked against truncated CI or, when possible, FCI. While MCCI, alongside FCI and multireference CI (MRCI), is able to capture a great portion of the static and dynamic correlation, methods such as CASSCF often include the latter to a smaller degree, with the quality of the results strongly dependent on the selected active space.All these methods construct the wavefunction as a linear combination of Slater determinants,
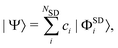 | (6) |
In contrast to single-reference methods such as HF, coupled cluster, or Møller–Plesset perturbation theory, FCI considers all possible determinants within a given basis to build the wavefunction. The number of Slater determinants therefore grows combinatorially with the size of the basis. Complete active space (CAS), restricted active space (RAS), and generalised active space (GAS) self-consistent field (SCF) circumvent this problem by restricting the number of occupied orbitals and therefore the number of Slater determinants. These methods are affordable for medium-sized systems, but the selection of a good active space requires experience and chemical intuition. In contrast, MCCI provides an automated, unbiased, and efficient truncation of the FCI expansion by stochastically selecting the smallest number of configurations needed to achieve the desired value of energy convergence and does not require extensive benchmarking to confirm that the active space produces reliable results. The number of configurations included in the MCCI expansion will depend on the cut-off value, which relates to the retention of configurations based on their coefficients. The smaller the cut-off, the more configurations are included, and the closer the result is to FCI. Overall, the flexibility, accuracy, and adaptability of MCCI permits the prediction of exceptionally accurate scattering cross sections.
2.3 One- and two-electron densities
Following eqn (3) and (4), the calculation of elastic and total scattering cross sections requires one- and two-electron densities. These can be calculated directly from the multiconfigurational wavefunction in eqn (6). The two-electron density required for the calculation of the total scattering in eqn (3) is,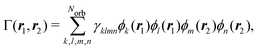 | (7) |
Analogously, the one-electron density required to calculate elastic scattering, eqn (4), can be constructed as,
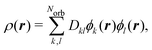 | (8) |
3 Results and discussion
To demonstrate the influence of the multireference character of the wavefunction on the scattering cross section, we consider three systems with increasing strength of correlation in their electronic ground state: Ne, CO, and O3. We use the 6-31G* basis set for Ne and the 6-31G basis set for CO and O3 throughout to ensure consistency across all methods, up to the computationally demanding FCI reference calculations. In each case, the active spaces for CASSCF and complete active space configuration interaction (CASCI) have been chosen to account for a full-valence description, closing the appropriate orbitals to match the FCI/CISDTQ references. The convergence of scattering cross sections with respect to the basis sets has been analysed elsewhere.28,30 As mentioned before, we do not consider nuclear motion42 and the nuclei are hence treated as frozen, with no integration over nuclear coordinates involved.29 Finally, the results are rotationally averaged, as appropriate when considering static ground-state scattering.In the following, the computational results are presented and analysed in terms of the percent difference scattering,
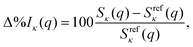 | (9) |
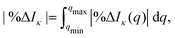 | (10) |
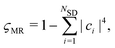 | (11) |
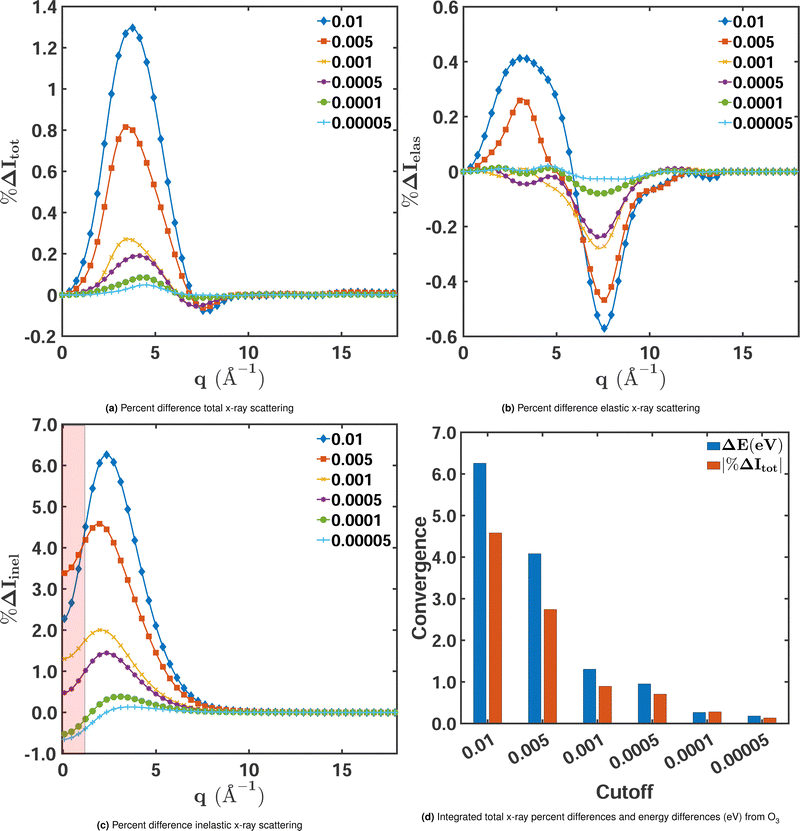
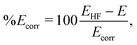 | (12) |
3.1 The Ne atom
We use the closed-shell ground state Ne atom to evaluate the effect of electron correlation on scattering for a system with small multireference character. Fig. 2a shows the percent difference |%ΔIκ| for the total X-ray scattering cross section calculated at different levels of theory, with FCI(1-Frozen)/6-31G* used as the reference. The maximum percent difference for HF/6-31G* and CASSCF(8,8)/6-31G* is ∼2.1%, while for MCCI(0.001)(1-Frozen)/6-31G*‡ it is one order of magnitude more accurate with ∼0.1%. This means that even for Ne, which has weak multireference character (ςMR = 0.08 for the FCI(1-Frozen)/6-31G* wavefunction), a highly correlated wavefunction makes a significant difference in the convergence of the total X-ray scattering cross section. We note that is also true if the coupled cluster singles and doubles (CCSD) two-electron density is used.49 This density can be calculated with the PySCF package,50 and has an error comparable to MCCI(0.001). The similar magnitude of the HF and CASSCF errors suggests that their deviation from the FCI reference stems primarily from their lack of dynamic correlation, well described by both CCSD and MCCI.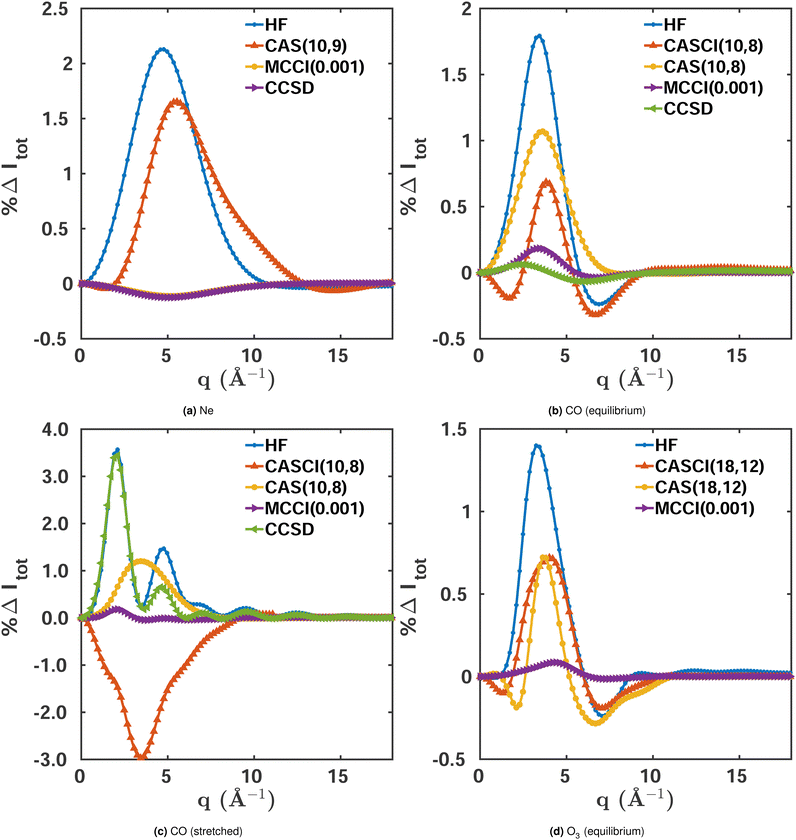 | ||
| Fig. 2 Percent differences for total scattering, Δ%Itot(q), calculated using eqn (9) for the following systems in their electronic ground states: (a) Ne, (b) CO (equilibrium geometry, Req = 2.13 a0), (c) CO (stretched geometry, R = 4 a0), (d) O3 (equilibrium geometry). FCI(1-Frozen)/6-31G* and FCI(2-Frozen)/6-31G are used as the references for Ne and CO, while for O3 we used CISDTQ(3-Frozen)/6-31G as the reference. Results are shown for HF, CASSCF, and MCCI(0.001)(1-2-3 Frozen). Further details are provided in the text. | ||
Integrated absolute percent differences, the percent recovered correlation energy, and the numbers of configurations included in each calculation are given in the first column of Table 1. The table shows a close relation between the quality of the results, as measured by the integrated |%ΔItot|, and the percent recovered correlation energy %Ecorr. The small number of Slater determinants included in the MCCI wavefunction (291) compared to FCI (>105), demonstrates the ability of MCCI to capture a significant part of the electron correlation with a compact expansion.
| Method | Ne | CO (R = 2.13 a0) | CO (R = 4.00 a0) | O3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |%ΔItot| | %Ecorr | N SD | |%ΔItot| | %Ecorr | N SD | |%ΔItot| | %Ecorr | N SD | |%ΔItot| | %Ecorr | N SD | |
| HF | 10.1 | 0 | 1 | 5.41 | 0 | 1 | 8.46 | 0 | 1 | 4.09 | 0 | 1 |
| CAS | 8.33 | 49 | 873(4900) | 3.54 | 65 | 1223(3136) | 4.18 | 69 | 1315(3136) | 2.08 | 53 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111(48 111(48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) 400) |
| CASCI | — | — | — | 2.42 | 32 | 1307(3136) | 11.6 | 53 | 1191(3136) | 2.40 | 54 | 6079(48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) 400) |
| MCCI(0.001) | 0.65 | 98 | 291 | 0.57 | 95 | 1757 | 0.46 | 96 | 3934 | 0.90 | 89 | 6160 |
| CCSD | 0.75 | 98 | — | 0.45 | 96 | — | 6.46 | 46 | — | — | — | — |
| FCI/CISDTQ | — | 100 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 861 |
— | 100 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 777![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
— | 100 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 777![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
— | 100 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 526 526![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 866 |
3.2 The CO molecule
Comparing the total scattering percent differences at Req with the FCI(2-Frozen)/6-31G reference, shown in Fig. 2b, we unsurprisingly see that the HF/6-31G calculation displays the largest maximum error at ∼1.9%. This is followed by CASSCF(10,8)/6-31G, which performs better with a maximum error of ∼1.1%, reflecting that the multiconfigurational CASSCF wavefunction recaptures a sizeable portion of the static correlation absent in the HF wavefunction. As for Ne, MCCI(0.001)(2-Frozen)/6-31G outperforms the other methods with a maximum error of ∼0.2%, getting quite close to the FCI reference with only a small fraction of the configurations of FCI (see Table 1). CCSD wavefunctions also perform well with a deviation comparable to the one seen in MCCI, reflecting the small multireference character of equilibrium CO.
Fig. 2b also includes a CASCI(10,8)/6-31G calculation where, in contrast to CASSCF, the HF orbitals have not been re-optimised. Possibly thanks to a larger number of significantly contributing Slater determinants, NSD = 1307 compared to NSD = 1223 for CASSCF, this calculation achieves better convergence of the scattering cross section, with a maximum error of ∼0.6%. It is notable that, although the cross section improves, the energy does not. This is to be expected, since it is the purpose of the orbital re-optimisation in CASSCF to aid the optimisation of the energy. The integrated absolute percent differences are listed in Table 1 alongside the percent recovered correlation energy and the number of Slater determinants.
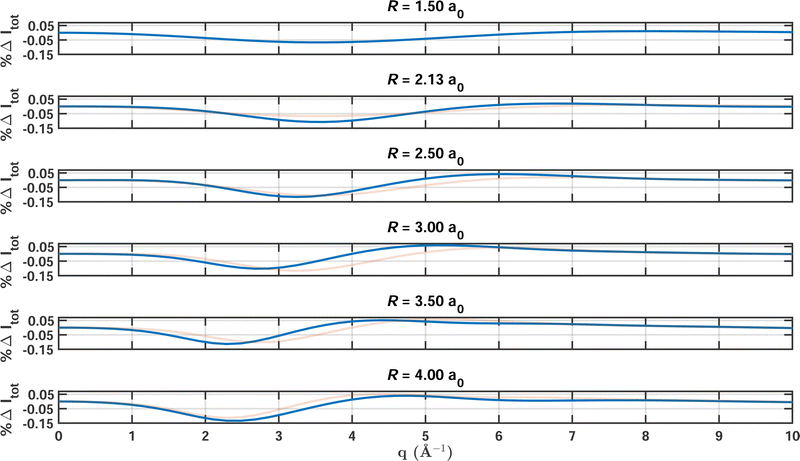
Examining stretched CO, shown in Fig. 2c, we see similar overall trends as for the molecule's equilibrium structure. However, in this case, CCSD fails to account for the stronger multireference character and its error is comparable to HF. Nevertheless, the comparison between CASSCF and CASCI displays an interesting difference. As before, the orbital-optimisation decreases the energy but the orbital-frozen calculation yields worse scattering cross sections compared to CASSCF. The cause of this discrepancy is most likely the smaller number of non-zero Slater determinants in the CASCI calculation (Table 1). However, one should be cautious not to draw too general conclusions about the link between the number of Slater determinants in the wavefunction and the convergence of the scattering cross section. The latter is clearly also a question of including the correct configurations, as illustrated by the fact that the MCCI calculations manage to capture a large portion of the electron correlation and converge the scattering cross sections close to the FCI reference with significantly more compact expansions.
| R (a0) | MCCI | HF | ||||
|---|---|---|---|---|---|---|
| N SD | ς MR | |%ΔItot| | max(|%ΔItot|) | |%ΔItot| | max(|%ΔItot|) | |
| 1.5 | 2398 | 0.09 | 0.14 | 0.07 | 2.63 | 1.32 |
| 2.13 | 3997 | 0.17 | 0.17 | 0.11 | 2.87 | 1.79 |
| 2.5 | 5418 | 0.25 | 0.18 | 0.12 | 3.11 | 2.11 |
| 3.0 | 6797 | 0.43 | 0.19 | 0.10 | 3.62 | 2.80 |
| 3.5 | 7967 | 0.85 | 0.20 | 0.12 | 3.77 | 3.81 |
| 4.0 | 8059 | 0.95 | 0.19 | 0.13 | 5.73 | 4.79 |
Fig. 3 shows the percent difference as a function of q with FCI/6-31G as the reference for a sequence of increasing bond lengths that correspond to the calculations featured in Table 2. Overall, the results at different bond lengths are quite similar, with the values oscillating between 0.02% and 0.12%. The maximum errors occur for values of q between 2.0 Å−1 and 4.0 Å−1, where the electron correlation manifests most strongly. In this region of q, the scattering is to a large part inelastic but has not yet reached the large-q limit, Sinel(∞) = Ne. We note that the reciprocal relationship between real and momentum space causes the maxima of the scattering signal to shift to smaller values of q with increasing bond length. Also, the second peak in the percent difference relates to the appearance of a second maximum in the scattering signal when the atoms are separated by more than R = 3 a0.
3.3 The O3 molecule
 | ||
| Fig. 4 Percent differences as a function of MCCI(3-Frozen) cut-offs for (a) total, (b) elastic, and (c) inelastic X-ray scattering cross sections for ground-state O3 in its equilibrium geometry. The percent differences Δ%Itot/elas/inel(q) are calculated using eqn (9) with CISDTQ(3-Frozen)/6-31G taken as the reference. The percent differences at q ∼ 0 Å−1 and q ∼ 15 Å−1 have been filtered out as they are highly sensitive to numerical errors. Also, the area between 0 < q < 0.5 Å−1 has been shaded to indicate that numerical instabilities are likely to occur in this region. Panel (d) shows the integrated absolute percent differences |%ΔItot| with the corresponding ΔE in electronvolts. | ||
We note, however, that the relative errors of the inelastic scattering cross sections at low values of q in Fig. 4c do not provide reliable information about the signal's convergence. These errors should be considered largely a numerical artefact that stems from the division by a small reference value since inelastic scattering is weak at low momentum transfer (at q = 0, it is exactly zero). This is different for elastic and total scattering, which are largest at q = 0. Nevertheless, even for elastic and total scattering, it is of limited use to evaluate the performance of an electronic structure method in the low momentum-transfer region. At q = 0, they are proportional to the squared number of the molecule's electrons, not affected by electron correlation, and thus, in principle, identical for all methods. To indicate that one should interpret the respective relative errors of the inelastic component with caution, the region of low q in Fig. 4c is shaded. The effect of electron correlation reliably manifests itself in the region of intermediate momentum transfer, roughly between 1.5 Å−1 and 6.0 Å−1.
| Cutoff | |%ΔItot| | |%ΔIelas| | |%ΔIinel| | %Ecorr | N SD |
|---|---|---|---|---|---|
| 0.01 | 1.00 | 0.44 | 0.63 | 50 | 215 |
| 0.005 | 0.57 | 0.20 | 0.45 | 90 | 786 |
| 0.001 | 0.16 | 0.05 | 0.19 | 92 | 6160 |
| 0.0005 | 0.13 | 0.05 | 0.14 | 98 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
| 0.0001 | 0.05 | 0.02 | 0.04 | 99 | 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 850 |
| 0.00005 | 0.02 | 0.01 | 0.02 | 100 | 393![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 620 |
| CISDTQ | — | — | — | 100 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 525![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 866 |
Finally, we examine the relationship between the convergence of the calculated energies and the scattering signals. Fig. 4d shows the integrated absolute percent differences for total X-ray scattering (red bars) alongside the corresponding correlation energies for the MCCI calculations (blue bars) for decreasing cut-offs. The convergence of the energy and the scattering cross sections follows the same trend, as seen previously. The rate of convergence is also similar, with both quantities converging at the same rate towards a negligible energy and scattering difference beyond the 0.001 cut-off.
3.4 Further examinations of MCCI
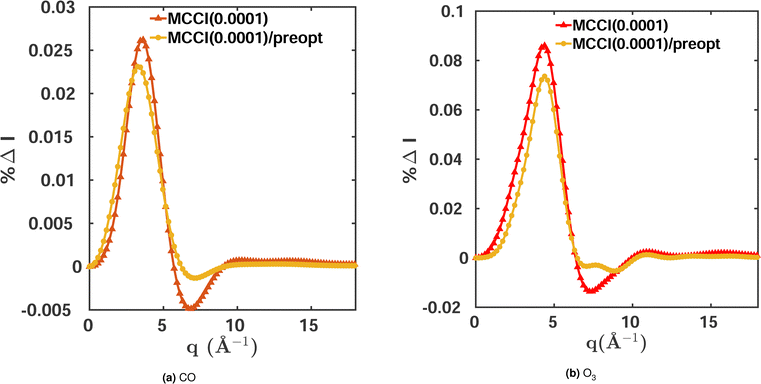
The orbital optimisation is performed within a given active space and for a chosen set of electronic states. Here, we use equilibrium-geometry CO and O3 in their electronic ground states to investigate the effect of orbital pre-optimisation on the scattering cross sections. We calculate the total scattering cross sections and compare them to FCI(3-Frozen)/6-31G and CISDTQ(3-Frozen)/6-31G references, respectively, using CAS(14,10) pre-optimised orbitals in each case. The results for a 0.0001 MCCI cut-off are shown in Fig. 5. A notable improvement is achieved in the cross sections when pre-optimised orbitals are used. The calculations of the two-electron density and of the cross sections are faster, since the pre-optimised orbital approach reduces the number of Slater determinants required. Likewise, the energies improve slightly when the pre-optimisation is used. The results are summarised in Table 4. We note, however, that this advantage is diminished by the additional computational overhead of the pre-optimisation.
| Method | CO | O3 | ||||
|---|---|---|---|---|---|---|
| |%ΔItot| | %Ecorr | N SD | |%ΔItot| | %Ecorr | N SD | |
| MCCI(0.0001) | 0.08 | 99.5 | 25960 | 0.28 | 98 | 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 850 |
| MCCI(0.0001)/preopt | 0.07 | 99.6 | 20495 | 0.20 | 99 | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
Fig. 6 shows the variability of the MCCI cross sections at different values of q. The standard error Est(q) is defined as,
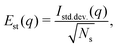 | (13) |
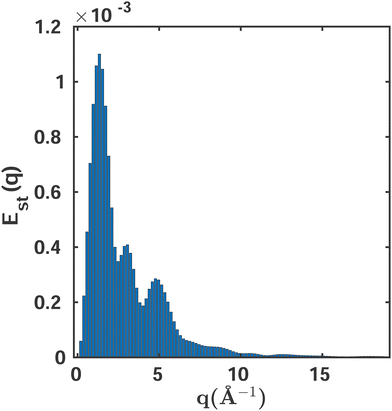 | ||
| Fig. 6 The standard error Est as a function of the momentum transfer vector q calculated using eqn (13). A sampling space of Ns = 10 MCCI(0.001)(3-Frozen)/6-31G calculations is used. | ||
4 Conclusion
We have demonstrated that electron–electron correlation influences X-ray scattering cross sections, with stronger effects seen in the inelastic and total components. In order to accurately converge the total scattering signal, correlation must be accounted for even in comparably simple systems such as the Ne atom. In this context, MCCI emerges as a powerful method, capable of reproducing FCI results at a fraction of their computational cost. Notably, MCCI delivers compact and highly correlated wavefunctions that yield accurate scattering cross sections even in challenging cases. Possible future work includes examining if there are general patterns in how the approximations involved in different ab initio methods translate into scattering signals for different values of the momentum transfer q and a detailed examination of basis set effects in MCCI. However, the present results clearly demonstrate that MCCI is a strong option for calculating highly accurate X-ray scattering cross sections.For elastic scattering, mean-field methods such as HF already offer a significant improvement over the independent atom model (IAM),26,28,54 quite possibly delivering all the accuracy needed to reproduce accurate measurements of the elastic signals in X-ray crystallography, as in the burgeoning field of quantum crystallography.55 Given that IAM form factors are occasionally used outside the realm of crystallography, one might consider updating tabulated non-relativistic IAM inelastic scattering functions56 using post-HF methods, which would constitute a potential extension of the work presented in this article.
Importantly, for gas-phase experiments that measure total rather than elastic scattering, electron correlation should ideally be included via methods such as for instance MCCI or density matrix renormalization group (DMRG).57,58 One context of growing importance is ultrafast X-ray scattering.42,46,59–64 As demonstrated recently, the accuracy achievable in gas-phase scattering is now sufficient to distinguish different electronic states.20 Considering the progress towards high-repetition rate and high-energy modes at the European XFEL and the next-generation LCLS-II, it is reasonable to anticipate that measurements on static molecules in the gas phase could achieve large values of qmax and experimental accuracy on the order of 0.1% or less. Such measurements would provide exciting opportunities to probe the electronic structure of atoms and molecules in a manner complementary to spectroscopy and with a direct link between the observable and the two-electron density. Conceivably, future experiments may achieve such measurements on rotationally aligned molecules, further increasing the amount of information available in the experimental data.10,65 The coming years are likely to see rapid progress towards an experimental-evidence based understanding of electron correlation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from the Engineering and Physical Sciences Research Council UK (EPSRC) is gratefully acknowledged: EP/V006819 (A. K. and A. M. C.), EP/V049240 (A. K. and M. S.), EP/V006746 (M. J. P. and J. P. C.), EP/P001459 (M. J. P.), and EP/T021675 (M. J. P.). M. J. P. and A. K. also acknowledge support from the Leverhulme Trust (RPG-2020-208). Finally, A. K. acknowledges a Fellowship at the Swedish Collegium for Advanced Studies supported by the Erling-Persson Family Foundation and the Knut and Alice Wallenberg Foundation, as well as support by the Department of Energy, Office of Science, Basic Energy Sciences, under award number DE-SC0020276.Notes and references
- M. V. Laue, Nobelprize.org, Nobel Media AB 2014, 1915 Search PubMed.
- W. H. Bragg and W. L. Bragg, Nature, 1913, 91, 557 CrossRef.
- M. H. Pirenne, The Diffraction of X-Rays and Electrons by Free Molecules, Cambridge University Press, London, 1946 Search PubMed.
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738 CrossRef CAS PubMed.
- M. Perutz, Proc. R. Soc. London, Ser. A, 1954, 225, 287 Search PubMed.
- D. C. Hodgkin, J. Kamper, M. Mackay, J. Pickworth, K. N. Trueblood and J. G. White, Nature, 1956, 178, 64 EP CrossRef.
- P. Debye, L. Bewilogua and F. Ehrhardt, Phys. Zeits., 1929, 30, 84 CAS.
- P. Debye, Phys. Zeits., 1930, 31, 419–428 CAS.
- I. Hargittai and M. Hargittai, Stereochemical applications of gas-phase electron diffraction: Part A The Electron Diffraction Technique, VCH, New York, 1st edn, 1988 Search PubMed.
- J. Küpper, S. Stern, L. Holmegaard, F. Filsinger, A. Rouzée, A. Rudenko, P. Johnsson, A. V. Martin, M. Adolph, A. Aquila, S. Bajt, A. Barty, C. Bostedt, J. Bozek, C. Caleman, R. Coffee, N. Coppola, T. Delmas, S. Epp, B. Erk, L. Foucar, T. Gorkhover, L. Gumprecht, A. Hartmann, R. Hartmann, G. Hauser, P. Holl, A. Hömke, N. Kimmel, F. Krasniqi, K.-U. Kühnel, J. Maurer, M. Messerschmidt, R. Moshammer, C. Reich, B. Rudek, R. Santra, I. Schlichting, C. Schmidt, S. Schorb, J. Schulz, H. Soltau, J. C. H. Spence, D. Starodub, L. Strüder, J. Thøgersen, M. J. J. Vrakking, G. Weidenspointner, T. A. White, C. Wunderer, G. Meijer, J. Ullrich, H. Stapelfeldt, D. Rolles and H. N. Chapman, Phys. Rev. Lett., 2014, 112, 083002 CrossRef.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. Robinson, T. J. Lane, D. Ratner, K. Saita, T. Northey, B. Stankus, V. Cofer-Shabica, J. Hastings and P. M. Weber, Faraday Discuss., 2014, 171, 81 RSC.
- M. Stefanou, K. Saita, D. V. Shalashilin and A. Kirrander, Chem. Phys. Lett., 2017, 683, 300–305 CrossRef CAS.
- L. Ma, H. Yong, J. D. Geiser, A. Moreno Carrascosa, N. Goff and P. M. Weber, Struct. Dyn., 2020, 7, 034102 CrossRef CAS.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. S. Robinson, D. Ratner, T. J. Lane, D. Zhu, J. M. Glownia, M. Kozina, H. T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J. B. Hastings and P. M. Weber, Phys. Rev. Lett., 2015, 114, 255501 CrossRef CAS.
- H. Yong, N. Zotev, B. Stankus, J. M. Ruddock, D. Bellshaw, S. Boutet, T. J. Lane, M. Liang, S. Carbajo, J. S. Robinson, W. Du, N. Goff, Y. Chang, J. E. Koglin, M. D. J. Waters, T. I. Sølling, M. P. Minitti, A. Kirrander and P. M. Weber, J. Phys. Chem. Lett., 2018, 9, 6556–6562 CrossRef CAS PubMed.
- B. Stankus, H. Yong, N. Zotev, J. M. Ruddock, D. Bellshaw, T. J. Lane, M. Liang, S. Boutet, S. Carbajo, J. S. Robinson, W. Du, N. Goff, Y. Chang, J. E. Koglin, M. P. Minitti, A. Kirrander and P. M. Weber, Nat. Chem., 2019, 11, 716–721 CrossRef CAS PubMed.
- J. M. Ruddock, N. Zotev, B. Stankus, H.-W. Yong, D. Bellshaw, S. Boutet, T. J. Lane, M. Liang, S. Carbajo, W. Du, A. Kirrander, M. P. Minitti and P. M. Weber, Angew. Chem., Int. Ed., 2019, 58, 6371–6375 CrossRef CAS.
- J. M. Ruddock, H. Yong, B. Stankus, W. Du, N. Goff, Y. Chang, A. Odate, A. M. Carrascosa, D. Bellshaw, N. Zotev, M. Liang, S. Carbajo, J. Koglin, J. S. Robinson, S. Boutet, A. Kirrander, M. P. Minitti and P. M. Weber, Sci. Adv., 2019, 5, eaax6625 CrossRef CAS PubMed.
- H. Yong, N. Zotev, J. M. Ruddock, B. Stankus, M. Simmermacher, A. M. Carrascosa, W. Du, N. Goff, Y. Chang, D. Bellshaw, M. Liang, S. Carbajo, J. E. Koglin, J. S. Robinson, S. Boutet, M. P. Minitti, A. Kirrander and P. M. Weber, Nat. Commun., 2020, 11, 2157 CrossRef CAS PubMed.
- H. Yong, S. M. Cavaletto and S. Mukamel, J. Phys. Chem. Lett., 2021, 12, 9800–9806 CrossRef CAS.
- L. Bartell and R. Gavin, J. Am. Chem. Soc., 1964, 86, 3493–3498 CrossRef CAS.
- L. Bartell and R. Gavin, J. Chem. Phys., 1965, 43, 856–861 CrossRef CAS.
- A. Debnarova and S. Techert, J. Chem. Phys., 2006, 125, 224101 CrossRef PubMed.
- A. Debnarova, S. Techert and S. Schmatz, J. Chem. Phys., 2010, 133, 124309 CrossRef PubMed.
- A. Debnarova, S. Techert and S. Schmatz, J. Chem. Phys., 2011, 134, 054302 CrossRef PubMed.
- T. Northey, N. Zotev and A. Kirrander, J. Chem. Theory Comput., 2014, 10, 4911–4920 CrossRef CAS PubMed.
- H. J. Suominen and A. Kirrander, Phys. Rev. Lett., 2014, 112, 043002 CrossRef PubMed.
- T. Northey, A. M. Carrascosa, S. Schäfer and A. Kirrander, J. Chem. Phys., 2016, 145, 154304 CrossRef PubMed.
- A. M. Carrascosa, T. Northey and A. Kirrander, Phys. Chem. Chem. Phys., 2017, 19, 7853–7863 RSC.
- A. M. Carrascosa and A. Kirrander, Phys. Chem. Chem. Phys., 2017, 19, 19545–19553 RSC.
- G. Hermann, V. Pohl, J. C. Tremblay, B. Paulus, H.-C. Hege and A. Schild, J. Comput. Chem., 2016, 37, 1511–1520 CrossRef CAS.
- V. Pohl, G. Hermann and J. C. Tremblay, J. Comput. Chem., 2017, 38, 1515–1527 CrossRef CAS PubMed.
- G. Hermann, V. Pohl and J. C. Tremblay, J. Comput. Chem., 2017, 38, 2378–2387 CrossRef CAS PubMed.
- R. M. Parrish and T. J. Martínez, J. Chem. Theory Comput., 2019, 15, 1523–1537 CrossRef CAS PubMed.
- A. M. Carrascosa, H. Yong, D. L. Crittenden, P. M. Weber and A. Kirrander, J. Chem. Theory Comput., 2019, 15, 2836–2846 CrossRef.
- N. Zotev, A. Moreno Carrascosa, M. Simmermacher and A. Kirrander, J. Chem. Theory Comput., 2020, 16, 2594–2605 CrossRef CAS PubMed.
- J. Greer, J. Comput. Phys., 1998, 146, 181–202 CrossRef.
- L. Tong, M. Nolan, T. Cheng and J. Greer, Comput. Phys. Commun., 2000, 131, 142–163 CrossRef CAS.
- N. E. Henriksen and K. B. Møller, J. Phys. Chem. B, 2008, 112, 558 CrossRef CAS PubMed.
- G. Dixit, O. Vendrell and R. Santra, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11636 CrossRef CAS PubMed.
- W. Schülke, Electron Dynamics by Inelastic X-Ray Scattering, Oxford Science Publications, 1st edn, 2007 Search PubMed.
- M. Simmermacher, A. Moreno Carrascosa, N. E. Henriksen, K. B. Møller and A. Kirrander, J. Chem. Phys., 2019, 151, 174302 CrossRef PubMed.
- R. A. Bonham and M. Fink, High Energy Electron Scattering, Van Nostrand Reinhold Company, ACS Monograph, 169 edn, 1974 Search PubMed.
- C. J. Stein, V. von Burg and M. Reiher, J. Chem. Theory Comput., 2016, 12, 3764–3773 CrossRef CAS PubMed.
- J. P. Coe, A. M. Carrascosa, M. Simmermacher, A. Kirrander and M. J. Paterson, J. Chem. Theory Comput., 2022 Search PubMed , submitted.
- M. Simmermacher, N. E. Henriksen, K. B. Møller, A. Moreno Carrascosa and A. Kirrander, Phys. Rev. Lett., 2019, 122, 073003 CrossRef CAS PubMed.
- J. P. Coe and M. J. Paterson, J. Chem. Theory Comput., 2015, 11, 4189–4196 CrossRef CAS PubMed.
- J. P. Coe and M. J. Paterson, J. Chem. Phys., 2014, 141, 124118 CrossRef CAS PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- S. Keller, K. Boguslawski, T. Janowski, M. Reiher and P. Pulay, J. Chem. Phys., 2015, 142, 244104 CrossRef PubMed.
- J. P. Coe and M. J. Paterson, Theor. Chem. Acc., 2015, 134, 58 Search PubMed.
- J. P. Coe, D. J. Taylor and M. J. Paterson, J. Chem. Phys., 2012, 137, 194111 CrossRef PubMed.
- T. Northey and A. Kirrander, J. Phys. Chem. A, 2019, 123, 3395–3406 CrossRef CAS PubMed.
- Modern Charge-Density Analysis, ed. C. Gatti and P. Macchi, Springer, Netherlands, 1st edn, 2012 Search PubMed.
- J. H. Hubbell, W. J. Veigele, E. A. Briggs, R. T. Brown, D. T. Cromer and R. J. Howerton, J. Phys. Chem. Ref. Data, 1975, 4, 471–538 CrossRef CAS.
- K. H. Marti and M. Reiher, Z. Phys. Chem., 2010, 224, 583–599 CrossRef CAS.
- S. Wouters and D. V. Neck, Eur. Phys. J. D, 2014, 68, 1–20 CrossRef CAS.
- J. M. Budarz, M. P. Minitti, D. V. Cofer-Shabica, B. Stankus, A. Kirrander, J. B. Hastings and P. M. Weber, J. Phys. B, 2016, 49, 034001 CrossRef.
- B. Stankus, H. Yong, J. Ruddock, L. Ma, A. Moreno Carrascosa, N. Goff, S. Boutet, X. Xu, N. Zotev, A. Kirrander, M. P. Minitti and P. M. Weber, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 234004 CrossRef.
- A. Odate, A. Kirrander, P. M. Weber and M. P. Minitti, Adv. Phys. X, 2022 Search PubMed , under submission.
- A. Kirrander, K. Saita and D. V. Shalashilin, J. Chem. Theory Comput., 2016, 12, 957–967 CrossRef CAS PubMed.
- A. Kirrander and P. M. Weber, Appl. Sci., 2017, 7, 534 CrossRef.
- M. Simmermacher, N. E. Henriksen and K. B. Møller, Phys. Chem. Chem. Phys., 2017, 19, 19740–19749 RSC.
- J. Yang, V. Makhija, V. Kumarappan and M. Centurion, Struct. Dyn., 2014, 1, 044101 CrossRef PubMed.
Footnotes |
| † For FCI the method dependence in the value of ςMR is removed. However, the value of ςMR may remain sensitive to the orbitals used. |
| ‡ MCCI(0.001) indicates that the MCCI cutoff is 0.001, while ‘(N-Frozen)’ indicates that the number of frozen orbitals is N. |
| This journal is © the Owner Societies 2022 |