Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Can domain-based local pair natural orbitals approaches accurately predict phosphorescence energies?†
Giovanna
Bruno
 a,
Bernardo
de Souza
b,
Frank
Neese
c and
Giovanni
Bistoni
a,
Bernardo
de Souza
b,
Frank
Neese
c and
Giovanni
Bistoni
 *cd
*cd
aDipartimento di Chimica, Università degli Studi di Milano, via Golgi 19, 20133 Milano, Italy
bFAccTs GmbH, Köln, Germany
cMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, D-45470 Mülheim an der Ruhr, Germany
dDipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, Perugia, Italy. E-mail: giovanni.bistoni@unipg.it
First published on 23rd May 2022
Abstract
Since the discovery of the peculiar conducting and optical properties of aromatics, many efforts have been made to characterize and predict their phosphorescence. This physical process is exploited in modern Organic Emitting Light Diodes (OLEDs), and it is also one of the processes decreasing the efficiency of Dye-sensitized solar cells (DSSCs). Herein, we propose a computational strategy for the accurate calculation of singlet–triplet gaps of aromatic compounds, which provides results that are in excellent agreement with available experimental data. Our approach relies on the domain-based local pair natural orbital (DLPNO) variant of the “gold standard” CCSD(T) method. The convergence of our results with respect to the key technical parameters of the calculation, such as the basis set used, the approximations employed in the perturbative triples correction, and the dimension of the PNOs space, was thoroughly discussed.
1 Introduction
Aromatic compounds constitute about 30% of all the known synthetic and natural organic compounds.1 Thanks to their peculiar thermodynamic stability, reactivity and physical–chemical properties, they are suitable materials for many industrial, medicinal and engineering applications.During the first half of the last century, scientists observed that aromatic molecules, either isolated or polymeric, exhibited interesting conducting and absorption properties, which could be exploited for the design of low-cost, easy to fabricate, flexible, green, electrical and emitting devices.2–5 The first purely organic semiconductor, the charge-transfer complex TTF–TCNQ, whose donor and acceptor moieties are both aromatic (tetrathiafulvalene (TTF) and tetracyano-p-quinodimethane (TCNQ)6), was proposed in 1973 by J. Ferraris et al.7 In such materials, conduction can be activated by applying a voltage across an electrochemical cell, by doping or by photoexcitation. The latter is also a fundamental step of the dye-sensitized solar cells work-flow,8 in which an organic or metalorganic dye, usually containing highly conjugated aromatic moieties,9–16 is excited to a low-lying excited state by absorbing UV-vis or NIR wavelenghts; then, through a relaxing non-radiative process, it injects electrons into the band gap of an inorganic semiconductor, initiating the current flux. Thus, in such a device, radiative relaxation processes, such as fluorescence or phosphorescence, could dramatically decrease the efficiency. In contrast, these radiative processes are the basis for the functioning of OLEDs (Organic Light Emitting Diodes),17 whose layers are usually made of aromatic polymers or molecules.18–20
The ubiquitous importance of aromatic compounds in chemistry stimulated many experimental and computational studies aimed at characterizing their ground state and excited states properties.21–26 In particular, the low-lying triplet states of aromatic compounds have always attracted the interest of the scientific community due to their unique photophysical and photochemical properties, so that the first extensive experimental work on the topic was carried out by Lewis and Kasha as early as 1944.27 Since the transition from the first excited triplet state (T1) to the singlet ground state (S0) is spin-forbidden, T1 states have longer lifetimes (up to seconds) than S1 states (around nanoseconds)16,21 implying that phosphorescence may persist much longer than fluorescence after excitation. Besides, the probability of formation of triplet excitons, pursuant to electrical excitation, is three times higher than that of singlet excitons,28,29 making phosphorescent OLEDs usually more efficient than fluorescent ones.30,31 In addition, although spin-orbit coupling is usually considered to be small in organic compounds, many studies have demonstrated that benzene derivatives and polycyclic aromatic hydrocarbons, conjugated or substituted by pnictogens or chalcogens, still exhibit ultrafast intersystem crossing.32–36 Triplet states of aromatic compounds can also promote reduction and addiction reactions which are usually highly endothermic in the ground state (S0).37–39 The reason of this behavior has been identified with the anti-aromaticity of triplet states.40–42
Computational protocols for the prediction of singlet–triplet gaps have been proposed since the end of 90s, based on a plethora of different electronic structure methods. Time-Dependent Density Functional Theory (TDDFT) is of course a popular approach in this context, as it allows the simulation of large molecules and macromolecules in their excited states.22,43 However, many benchmark studies on organic molecules (including acenes44) have emphasized the accuracy limits of popular exchange correlation functionals, especially in the calculation of triplet state energies.45–52 Thus, several attempts have been made over the years to overcome these limitations of DFT. In particular, double-hybrid functionals53 demonstrated remarkable accuracy for the calculation of singlet–triplet excitation energies of organic compounds,54,55 as well as of spin states energies of metalorganic complexes.56 In contrast, correlated wavefunction-based methods such as Full Configuration Interaction (FULL-CI)57 and Canonical Coupled Cluster with Single, Double and Perturbative Triple excitations (CCSD(T))58 have shown great accuracy for small model systems. Unfortunately, due to their steep scaling with the system size, applications of these approaches in their canonical implementation are still limited to small and medium-size molecules. Machine learning techniques, obviously affected by generality issues, have also been recently applied to large datasets59 of organic molecules to compute phosphorescence energy gaps, yielding errors comparable to DFT ones (∼0.1 eV).60,61
In this work, we explore the use of the Domain-Based Local Pair Natural Orbital CCSD(T) method62,63 (DLPNO-CCSD(T)) for the calculation of phosphorescence energies of aromatics. This method belongs to the family of Local Correlation CCSD(T) approaches,64–66 which exploit the short-range nature of electron correlation to increase the efficiency of post Hartree-Fock approaches. In particular, we propose two computational protocols based on the DLPNO-CCSD(T) methodology that differ in their accuracy and computational cost: (i) “Gold” settings are designed to provide results that are at convergence with respect to both the basis set size and the DLPNO thresholds used, and thus retain essentially canonical CCSD(T) accuracy; (ii) “Silver” settings provide the optimal balance between accuracy and computational cost for large systems, thus allowing the calculation phosphorescence energies for systems with potentially hundreds of atoms.
The manuscript is organized as follows. Computational details are given in Section 2.3. In Section 3.1, the convergence of the DLPNO-CCSD(T) energy of aromatic molecules in their singlet and triplet states with respect to the key technical parameters of the calculation is studied in detail. This information is then used for defining the Gold and Silver DLPNO-CCSD(T) settings. In Section 3.2, these settings are used to compute adiabatic singlet–triplet gaps of a series of aromatic molecules, and their accuracy is verified using experimental data as reference. In Section 3.3, our Silver methodology is used to compute the key photophysical properties of challenging carbazolyl dicyanobenzene (CDCB) compounds as an illustrative example of its potentially broad applicability.
2 Computational details
2.1 Experimental reference data
The reference experimental phosphorescence energies were mainly taken from the work by Lewis and Kasha27 and partly from the works by Siebrand67 and by Metcalfe et al.68 The entire set consists of about 100 aromatic compouds. Among those, we selected 18 compounds trying to maximize the sample's variance with respect to chemical structure. Therefore, our sample includes benzene derivatives (Group A), naphthalene derivatives (Group B), polycyclic aromatic hydrocarbons (Group C), a group named by us “complex conjugated compounds” (Group D), which are mainly biphenyl derivatives, and heterocycles (Group E) (Fig. 1).2.2 Methodological aspects
The theoretical phosphorescence energy, corresponding to the adiabatic singlet–triplet gap (ΔE00), was computed by adding the differential zero-point energy correction (ΔZPE) to the “well to well” singlet–triplet gap (ΔE) (eqn (1)) computed at various levels of electronic structure theory.| ΔE00 = ΔE + ΔZPE | (1) |
2.3 Computational details
Therefore, in our final computational protocols, we employ the B3LYP-D3 functional in conjuction with the def2-TZVPP basis set. The RI approximation for both Coulomb (J) and Exchange (K) integrals (RIJK option of ORCA 4.2.175)76,77 was used to speed up the calculations. Numerical frequencies at the same level of theory were computed to get the zero-point energy (ZPE) correction used in the calculation of the adiabatic phosphorescence gap (ΔE00). In all cases and for all molecules real vibrational frequencies were obtained, confirming that the B3LYP optimized geometries correspond to local minima.
With respect to the triples correction evaluation, the (T0) and (T1) corrections were tested in DLPNO calculations. The abbreviation (T0) denotes the traditional semi-canonical perturbative triples correction,65,82 while (T1) denotes the recently implemented iterative algorithm.83 The latter is computationally more demanding but returns more accurate results by iteratively calculating triples amplitudes.
In the basis set convergence study, the correlation-consistent basis sets of Dunning84 (i.e., cc-pVNZ) as well as their “augmented” counterparts (i.e., aug-cc-pVNZ) featuring additional diffuse functions85 were used. Thus, DLPNO-CCSD(T) single point calculations were performed by increasing the basis set cardinality (N = D, T, Q) of both the cc-pVNZ and aug-cc-pVNZ family. The extrapolation to the complete basis set (CBS) limit for each basis set class was carried out using a two-point extrapolation scheme for both the SCF and the correlation energy. For the SCF energy, the Karton and Martin's formula86 (eqn (2a)), also used by Zhong et al.,87 was used. For the correlation energy instead, Truhlar's version88 of the Helgaker formula89,90 (eqn (2b)) was employed.
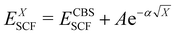 | (2a) |
| EXcorr = ECBScorr + AX−β | (2b) |
In particular, ECBSSCF and ECBScorr were obtained by using 3-ζ and 4-ζ basis sets in combination with α and β parameters calibrated by Neese and Valeev91 for the 3/4 extrapolation (α = 5.79, β = 3.05). In the following, cc-pVNZ basis sets (N = D, T, Q) are sometimes abbreviated as “NZ” for the sake of simplicity, while aug-cc-pVNZ basis sets are denoted as “aNZ”.
Related to the convergence of the DLPNO-CCSD(T) energies as a function of the DLPNO thresholds, two main parameters were considered: (i) TCutPNO, which determines the pair natural orbitals included in the virtual space of each electron pair while solving the coupled cluster equations (PNOs with occupation numbers lower than the set threshold are discarded); (ii) TCutPairs, which determines the electron pairs included in the coupled cluster treatment (only those whose MP2 correlation energy is higher than the set threshold are included in the Coupled Cluster calculation). In particular, two recent studies by Altun et al.92,93 on the GMTKN55 superset94 showed that DLPNO-CCSD(T) accuracy can be considerably improved by extrapolating to the complete PNOs space limit (CPS), using the simple two points extrapolation scheme reported in eqn (3):
| E = EX + F·(EY − EX) | (3) |
in which EX and EY represent the energies obtained at TCutPNO = 10−X and TCutPNO = 10−Y levels, respectively (Y = X + 1) and F is a parameter that minimizes the deviation from the canonical CCSD(T) energy. In particular, we followed the procedure proposed by Altun et al.92 by using the pair X = 6 and Y = 7 and the optimal value F = 1.5. This approach is denoted hereafter as CPS(6/7).
2.4 Phosphorescence spectra and rate constants
For the calculation of phosphorescence rates and spectra, the path integral approach implemented in the ORCA_ESD module was used.95,96 It relies on the harmonic approximation to propagate the time evolution of the systems analytically, but has the advantage to exactly include temperature effects and is able to also include vibronic coupling to the transition dipole moments, which is a key factor for organic molecules without heavy atoms. The method essentially needs the well to well singlet–triplet gap (T1 → S0) ΔE, obtained here from DLPNO-CCSD(T), to compute both the spectrum and the rate constant, together with the oscillator strengths, which were computed using SOC-TDDFT. We performed these excited state calculations using B3LYP with RIJCOSX97 in combination with def2-TZVPP basis set, LR-CPCM98 under equilibrium conditions to include the toluene solvation effects and the RI-SOMF(1X)99 method for the spin-orbit coupling related integrals. The temperature of the simulations was set to 77 K and we used the Silver DLPNO-CCSD(T) ΔE calculated prior to it.3 Results and discussion
3.1 The “Gold” and “Silver” DLPNO-CCSD(T) Settings
In Fig. 2, we report the basis set convergence plots for the S0 and T1 energies, alongside with that of ΔE (Eqn 1) for compound 3d. Analogous plots for compounds 1a and 6a are reported in Section S3 of ESI.† All the relevant energies are reported in Table 1.
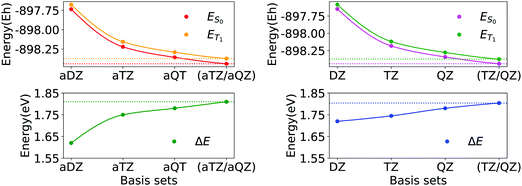 | ||
| Fig. 2 Basis set convergence of singlet state (ES0), triplet state (ET1) and ΔE gap of compound 3d (Fig. 1) for basis sets family aug-cc-pVNZ (N = D, T, Q) and for basis sets family cc-pVNZ (N = D, T, Q). Horizontal dotted lines represent energies extrapolated by means of eqn (2a) and (2b). | ||
| Compounds | Basis sets | ΔE |
|---|---|---|
| 1a | (aug)/cc-pVDZ | (3.38) 3.87 |
| (aug)/cc-pVTZ | (3.94) 3.95 | |
| (aug)/cc-pVQZ | (3.97) 3.96 | |
| (aug)/(TZ/QZ) | (3.99) 3.99 | |
| 6a | (aug)/cc-pVDZ | (3.29) 3.44 |
| (aug)/cc-pVTZ | (3.43) 3.46 | |
| (aug)/cc-pVQZ | (3.47) 3.48 | |
| (aug)/(TZ/QZ) | (3.50) 3.50 | |
| 3d | (aug)/cc-pVDZ | (1.62) 1.72 |
| (aug)/cc-pVTZ | (1.75) 1.75 | |
| (aug)/cc-pVQZ | (1.79) 1.78 | |
| (aug)/(TZ/QZ) | (1.81) 1.80 |
Interestingly, by increasing the dimension of the basis set, the singlet–triplet gap increases. Thus, improving the quality of the simulation returns a more endothermic description of the process. Remarkably enough, both the absolute energies and the gap smoothly converge to essentially the same values upon CBS extrapolation, irrespective of the basis set family used. In addition, the variance of the cc-pVNZ gap with respect to N is smaller than that associated with the aug-cc-pVNZ gap. Hence, in the case of cc-pVNZ basis set family, the increase of cardinality affects the gap to a lesser extent.
In order to select the best basis set for the Gold and the Silver protocols, we analysed both the accuracy and the computational cost associated with each basis set. We used the ΔE values extrapolated to the complete basis set limit of the aug-cc-pVNZ family (aTZ/aQZ) as reference to evaluate the error obtained with smaller basis sets. The corresponding energy differences are shown in Fig. 3.
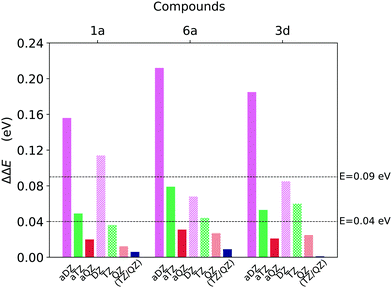 | ||
| Fig. 3 Basis set incompleteness error associated with DLPNO-CCSD(T) well to well singlet–triplet gap (T1 → S0) ΔE calculations for compounds 1a, 6a and 3d (Fig. 1), obtained for different basis sets and extrapolation schemes. The gap computed at the CBS(aTZ/aQZ) limit was used as reference. | ||
The accuracy of the aug-cc-pVDZ basis set is not satisfactory inasmuch as the deviation from the (aTZ/aQZ) limit ranges from around 0.15 eV to around 0.22 eV. The performances of the cc-pVDZ basis set are slightly better since the deviation remains below 0.09 eV for two of the three compounds analysed. On the contrary, the error associated with basis sets of cardinality N = T and N = Q is always smaller than 0.08 eV and 0.03 eV, respectively, for both the cc-pVNZ and aug-cc-pVNZ basis set families.
In terms of efficiency, the analysis of the computation time in terms of CPU hours (Fig. 4) revealed that, by increasing the cardinality from N = T to N = Q, the computational cost of the calculations increases by 3–4 times for all compounds.
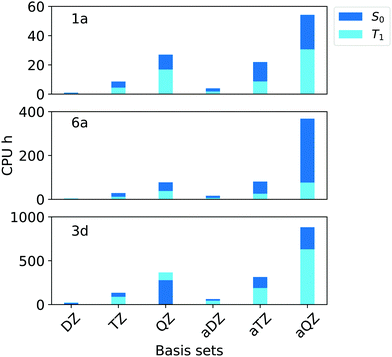 | ||
| Fig. 4 Computation times in CPU hours for the simulation of singlet (S0, blue bars) and triplet state (T1, light blue bars) of compounds 1a, 6a and 3d (Fig. 1) corresponding to aug-cc-pVNZ and cc-pVNZ basis sets family (N = D,T,Q) in combination with T1 and TightPNO options of ORCA 4.2.1. | ||
Importantly, the use of diffuse functions in the aug-cc-pVNZ increases dramatically the computational cost with respect to that obtained with the cc-pVNZ family. For example, the computational times associated with the aug-cc-pVQZ basis set are roughly twice the sum of that obtained with cc-pVTZ and cc-pVQZ basis sets. These results demonstrate that cc-pVTZ/cc-pVQZ extrapolation provides ΔE that are at convergence with the basis set size while being at the same time computationally affordable. Thus, this scheme was selected for our “Gold” protocol. For our “Silver” protocol, the cc-pVTZ was used. This basis set provides errors that are below our chosen threshold of 0.09 eV while reducing the the computation time by 55–75% with respect to the corresponing aug-cc-pVTZ basis set.
| Compounds | T CutPNO = 10−X | ΔE | ΔE(T0) | ΔE(T1) |
|---|---|---|---|---|
| 1a | X = 6 | 3.88 | 3.91 | 3.95 |
| X = 7 | 3.88 | 3.90 | 3.94 | |
| (6/7) | 3.88 | 3.89 | 3.93 | |
| 6a | X = 6 | 3.37 | 3.43 | 3.44 |
| X = 7 | 3.36 | 3.41 | 3.42 | |
| (6/7) | 3.35 | 3.40 | 3.41 | |
| 3d | X = 6 | 1.65 | 1.73 | 1.76 |
| X = 7 | 1.66 | 1.72 | 1.75 | |
| (6/7) | 1.67 | 1.72 | 1.75 |
For these systems, the triples contributions to the gap appear to be rather small. Regardless of the TCutPNO value used, the deviation between DLPNO-CCSD and DLPNO-CCSD(T0/T1) is always below 0.09 eV. Only for compound 3d the contribution of the triples becomes significant, reaching up to 0.11 eV. Hence, it is not surprising that the difference between the DLPNO-CCSD(T0) and the DLPNO-CCSD(T1) results is even smaller, remaining below 0.04 eV in all cases. Interestingly, a noteworthy difference exists between T0 and T1 triples algorithms in terms of efficiency, as shown in Fig. 5.
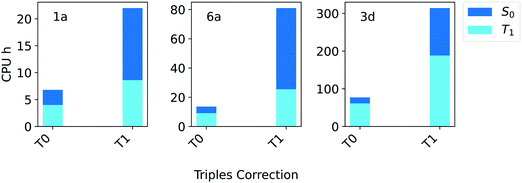 | ||
| Fig. 5 Computation times in CPU hours for DLPNO-CCSD(T) calculations of the singlet (S0, blue bars) and triplet state (T1, light blue bars) of compounds 1a, 6a and 3d (Fig. 1) corresponding to T0 and T1 triples corrections. In all cases, the aug-cc-pVTZ basis set and TightPNO settings were used. | ||
The computational cost of a DLPNO-CCSD(T0/T1) calculation for these systems increases by 3–5 times with T1. Based on these results, the T0 algorithm was selected for the Silver settings, while the more robust T1 triples correction is used in Gold settings.
In terms of efficiency, the computation times associated with TCutPNO = 10−6, TCutPNO = 10−7 and CPS(6/7) calculations are shown in Fig. 6.
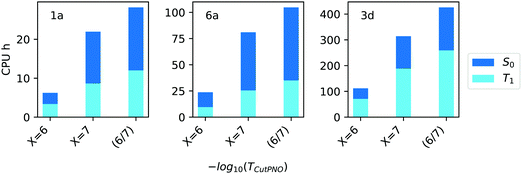 | ||
| Fig. 6 Computation times in CPU hours for the calculation of singlet (S0, blue bars) and triplet state (T1, light blue bars) of compound 1a, 6a and 3d (Fig. 1) with different TCutPNO = 10−X thresholds as well as with CPS(6/7) extrapolation. | ||
Interestingly, as TCutPNO = 10−6 calculations are extremely efficient, the overall computational cost of CPS(6/7) is only slightly higher than that associated with TCutPNO = 10−7. Based on these results, we decided to use the extrapolation technique for the treatment of PNOs virtual space in the Gold settings. For the Silver methodology, we decided to set TCutPNO to an intermediate value between 10−6 and 10−7, as both thresholds provided similar accuracy. Specifically, we set TCutPNO = 3.33 × 10−7, corresponding to the default value of DLPNO-CCSD(T) calculations.
Finally, we also investigated the convergence of the results with respect to the TCutPairs parameter. Three thresholds were tested: TCutPairs = 10−4, TCutPairs = 10−5 and TCutPairs = 10−6. In all cases, the aug-cc-pVTZ basis set was used in conjuction with the T1 triples correction and TCutPNO = 10−7. It was found that the results are weakly affected by the specific value used for TCutPairs parameter, with maximum deviations below 0.02 eV. The computational cost associated with the calculations is also comparable. For these reasons, we selected the TCutPairs = 10−4 threshold for the Silver settings, and the more conservative TCutPairs = 10−5 threshold for the Gold settings. These correspond to the default thresholds of NormalPNO and TightPNO calculations, respectively.
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) for both the methodologies are summarized in Table 3.
) for both the methodologies are summarized in Table 3.
| Method | Basis set | Triples correction | T CutPNO | T CutPairs | t |
|---|---|---|---|---|---|
| Gold DLPNO-CCSD(T) | CBS(TZ/QZ) | T1 | CPS(6/7) | 10−5 | 562 |
| Silver DLPNO-CCSD(T) | cc-pVTZ | T0 | 3.33 × 10−7 | 10−4 | 8 |
3.2 Computed vs experimental phosphorescence energies
In this section, we analyse the agreement between the experimental and theoretical phosphorescence gap for the compounds reported in Fig. 1.Table 4 reports the ΔE00 values computed using the Silver and the Gold DLPNO-CCSD(T) settings for the calculation of ΔE; it also reports the corresponding UHF and QRO energies (E(0), which is expected to be close to the corresponding Restricted Open Hartree-Fock (ROHF) energy), as well as the experimental phosphorescence gap and the differential zero-point energy correction (ΔZPE).
| Compounds | ΔE00 | |||||
|---|---|---|---|---|---|---|
| UHF | E(0) | DLPNO-CCSD | DLPNO-CCSD(T) | ΔZPE | E exp | |
| a Data taken from work by Siebrand.67 b Data taken from work by Metcalf et al.;68 all the other data are taken from work by Lewis and Kasha.27 To facilitate the discussion, we calculated the deviation between the computed and the experimental phosphorescence gap at various levels of theory (Fig. 7). | ||||||
| 1a | 2.51 (2.51) | 3.80 (3.81) | 3.70 (3.66) | 3.76 (3.69) | −0.22 | 3.66b |
| 2a | 2.44 (2.45) | 3.72 (3.72) | 3.61 (3.58) | 3.67 (3.61) | −0.20 | 3.58 |
| 3a | 2.54 (2.55) | 3.79 (3.80) | 3.70 (3.66) | 3.76 (3.70) | −0.21 | 3.65b |
| 4a | 1.70 (1.69) | 2.74 (2.74) | 3.18 (3.11) | 3.25 (3.15) | −0.10 | 3.30 |
| 5a | 2.38 (2.38) | 3.64 (3.65) | 3.53 (3.51) | 3.59 (3.53) | −0.18 | 3.52b |
| 6a | 5.25 (2.25) | 3.11 (3.13) | 3.32 (3.29) | 3.39 (3.35) | −0.10 | 3.62b |
| 7a | 1.39 (1.32) | 2.49 (2.40) | 2.88 (2.82) | 2.87 (2.84) | −0.11 | 2.65 |
| 1b | 2.04 (2.05) | 2.90 (2.90) | 2.73 (2.71) | 2.72 (2.67) | −0.14 | 2.64 |
| 2b | 0.59 (0.57) | 1.59 (1.56) | 2.79 (2.71) | 3.01 (2.88) | −0.08 | 2.69 |
| 3b | 1.82 (1.82) | 2.59 (2.59) | 2.54 (2.54) | 2.55 (2.54) | −0.20 | 2.49 |
| 4b | 1.99 (1.99) | 3.02 (3.03) | 2.74 (2.74) | 2.73 (2.71) | −0.14 | 2.60 |
| 5b | 1.84 (1.87) | 2.77 (2.79) | 2.44 (2.44) | 2.43 (2.40) | −0.15 | 2.37 |
| 1c | 2.05 (2.03) | 3.32 (3.49) | 3.00 (3.01) | 3.00 (2.99) | −0.13 | 2.81 |
| 2c | 1.24 (1.24) | 1.81 (1.81) | 1.93 (1.93) | 1.95 (1.95) | −0.10 | 1.85a |
| 1d | 2.04 (2.05) | 3.44 (3.45) | 3.08 (3.08) | 3.07 (3.07) | −0.14 | 2.86 |
| 2d | 1.68 (1.65) | 4.33 (4.43) | 3.03 (3.03) | 2.96 (2.97) | −0.11 | 2.65 |
| 3d | 0.24 (0.23) | 1.50 (1.49) | 1.67 (1.61) | 1.75 (1.68) | −0.05 | 1.86 |
| 1e | 1.73 (2.03) | 2.99 (2.99) | 2.81 (2.81) | 2.82 (2.79) | −0.14 | 2.69 |
The mean absolute error associated to the UHF and E(0) references is extremely high, though the transformation of the UHF canonical orbitals into quasi-restricted orbitals markedly improves the accuracy.
Remarkably enough, DLPNO-CCSD and the DLPNO-CCSD(T) perform equally well, with errors of the order of few tenths of eV. Importantly, the mean absolute error (MAE) of Gold DLPNO-CCSD(T) is the same of the canonical CCSD(T) one (0.14 eV) reported by Hajgató and co-workers.58 In addition, the accuracy of the Silver and Gold methodologies is comparable in all cases. The mean absolute error (MAE) is actually smaller for the Silver settings than for the Gold settings of about 0.02 eV, due to favorable error cancellation. It is also worth mentioning here that ΔZPE ranges from around −0.22 eV to −0.05 eV, and significantly affects the singlet–triplet gap, improving the overall agreement between theory and experiment.
Summarizing the results obtained so far, we can conclude that: (i) the use of the DLPNO approximation enables to simulate the phosphorescence gap of small and medium size aromatic compounds with the same accuracy of the canonical CCSD(T) at a relatively low computational cost, provided that enough care is made in the selection of the technical parameters of the calculation (Gold DLPNO-CCSD(T), Table 3). (ii) For these systems, the effect of the perturbative triples correction on the accuracy is extremely small; this indicates that popular approaches that do not explicitly include this term, such as EOM-CCSD, STEOM-CCSD etc., are expected to provide an adequately accurate description of analogous aromatic compounds in their excited states. (iii) Finally, in spite of the looser thresholds, the Silver methodology (Table 3) provides an accuracy that is comparable to that obtained using the much more conservative Gold settings. This suggests that, by employing the Silver procedure, one may obtain highly accurate results also for large aromatic molecules with a complex electronic structure, as discussed in the next section. It is worth pointing out that since DLPNO-CCSD(T) is a single reference method, it converges on a specific triplet state wave function in case of degenerate or nearly degenerate triplet states. Obviously, this would not affect the singlet–triplet energy gap but it may affect other physical observables.
3.3 The photophysical properties of CDCB compounds
To test the broad applicability of the Silver methodology (Section 2), we applied it to compute the phosphorescence gap of two challenging systems, namely the 4,5-bis(carbazol-9-yl)-1,2-dicyanobenzene (2CzPN) and 1,2,3,5-tetrakis(carbazol-9-yl)-4,6-dicyanobenzene (4CzIPN) (Fig. 8), belonging to carbazolyl dicyanobenzene (CDCB) family. Such systems are charge transfer compounds in which the dicyanobenzene acts as the electron-withdrawing group, while carbazolyl as the electron-donating one, and have found applications as thermally activated delayed fluorescence (TADF) emitters103–107 and photocatalysts.108,109 In particular, among the CDCB compounds, 2CzPN and 4CzIPN have drawn special attention since they represent a viable alternative to transition metal-based chromophores. In fact, they show high photoluminescence quantum yield at room temperature (around 74% for compound 4CzIPN and around 47% for compound 2CzPN).103 Therefore, they have been widely studied and characterized by both experimental techniques and simulations.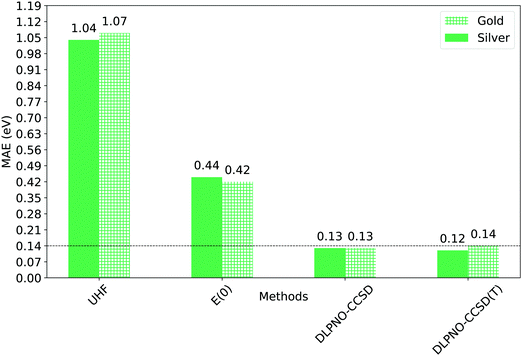 | ||
| Fig. 7 Mean absolute errors (MAEs) between experimental singlet–triplet gap and computed adiabatic one (ΔE00). ΔE00 was calculated using Gold and Silver settings for the dominant ΔE term (Table 3). The corresponding ZPE-corrected UHF and QRO energies (E(0)) are also shown for comparison. | ||
However, the large size of these molecules (54 atoms and 238e− for compound 2CzPN; 94 atoms and 410e− for compound 4CzIPN) considerably limits the applicability of post-HF methods for the computation of their photophysical properties, which remains a major challenge. In this context, our DLPNO-CCSD(T)-based protocols may represent a promising tool for the calculation of their photophysical properties.
To test the reliability of DLPNO-CCSD(T), the Silver protocol was used to compute ΔE00 of both compounds in toluene at 77 K. Solvent effects were accounted using the conductor-like polarizable continuum model (CPCM) and the Perturbation Theory Energy (PTE) approximation which is the default scheme of ORCA 5.0.1 for the treatment of the coupled-cluster Lagrangian of implicitly solvated systems. Although less crude approximations such as PTE(S) and PTES are already available in ORCA 5.0.1 (see ORCA 5.0.1 manual for further details), PTE scheme proved to be highly reliable for a wide variety of neutral organic solutes with deviations from PTE(S) and PTES energies of only few tenths of kcal mol−1.110 The results are shown in Table 5 alongside with the corresponding experimental values.
The data reported in Table 5 demonstrate that the Silver DLPNO-CCSD(T) approach returns highly accurate results also for these systems. For the 2CzPN compound, the adiabatic Silver singlet–triplet gap is 2.99 eV, while the experimental value is 2.75 eV. Thus, the deviation between theory and experiment in this case is only slightly larger than that obtained for the other aromatic compounds studied in this work. For the sake of comparison, the corresponding B3LYP value is 2.44 eV. Concerning instead the 4CzIPN compound, the Silver DLPNO-CCSD(T), the experimental and the B3LYP singlet–triplet gap are 2.94 eV, 2.67 eV and 2.28 eV, respectively. Hence, in this case, the DLPNO-CCSD(T)-based method is more accurate than B3LYP by 0.12 eV.
To further validate the reliability of Silver method, we also calculate the phosphorescence spectrum and rate constants of 2CzPN within a path integral framework, as detailed in the Section 2.4. The computed spectrum reported in Fig. 9 results from the average of spectra of the first three roots obtained from SOC-TDDFT, which approximately correspond to the three spin sub-levels of the first triplet; the experimental one instead has been recorded by Hosokai et al. in toluene at 77 K.
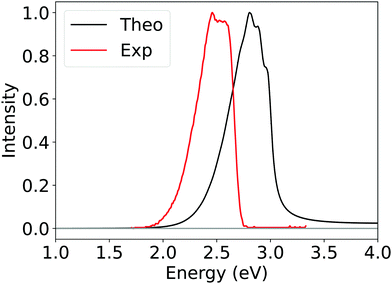 | ||
| Fig. 9 Computed phosphorescence spectrum of 2CzPN obtained by employing Silver DLPNO-CCSD(T) ΔE (black curve) and experimental phosphorescence spectrum (red curve) recorded by Hosokai et al. See text for details.113 | ||
Considering the challenging nature of this system, the qualitative agreement observed between the computed and experimental spectra is remarkable, even though the former is blue-shifted by around 0.3 eV. At least part of this effect should originate from the implicit solvation model employed. Further and deeper investigations, beyond the scope of this work, should be conducted in order to address this phenomenon.
Importantly, the theoretical average phosphorescence rate constant (3.49 s−1) is of the same order of the experimental phosphorescence rate constant (9.09 s−1)107 and well within the experimental error. The latter refers to a phosphorescence experiment in a 1,3-bis(9-carbazolyl)benzene (mCP) film at 80 K.
4 Conclusions
We assessed the accuracy and efficiency of the DLPNO-CCSD(T) method for the calculation of phosphorescence energies, spectra and rate constants of aromatics.Initially, an extensive analysis of the accuracy and computational cost of the methodology for the calculation of singlet and triplet energies of aromatic molecules was conducted, in relation to the main technical parameters of the calculation (basis set, triples correction approximation, dimension of PNOs space).
Our analysis revealed that large basis sets with cardinality N ≥ 3 are required to reduce the error below 0.09 eV with respect to the complete basis set limit. Larger basis sets and extrapolation techniques are needed to reach chemical accuracy (0.04 eV). In addition, it was found that aug-cc-pVNZ basis sets family does not provide any advantage in terms of accuracy with respect to cc-pVNZ basis sets one. In contrast, it dramatically increases the computational cost of the calculations.
Remarkably enough, the contribution of the perturbative triples correction to the gap was found to be rather small, inasmuch the deviation of the DLPNO-CCSD gap from the DLPNO-CCSD(T) one is below 0.09 eV. This suggests that methods that do not include a triples contribution may still be suitable for predicting the photophysical properties of aromatics.
The convergence of the DLPNO-CCSD(T) electronic energy for triplet and singlet states with respect to the key DLPNO parameters was also investigated in detail. It was found that standard thresholds are adequate for the description aromatic systems.
These results were used to define two DLPNO-CCSD(T) settings for the calculation of singlet–triplet gaps of aromatics, differing for their accuracy and computational cost. The “Gold” DLPNO-CSSD(T) settings provide results that are at convergence with respect to all the technical parameters of the calculation. It provides a MAE that is the same as the canonical CCSD(T) one (0.14 eV) with respect to the experimental reference data. This approach is applicable to medium-sized molecules. For larger systems, the cost-effective “Silver” DLPNO-CCSD(T) settings should be used. These settings provide MAEs with respect to the experimental phosphorescence gap that are still comparable to the “Gold” settings, enabling highly accurate simulations of large aromatic molecules.
Finally, the Silver DLPNO-CCSD(T) method was used to compute the phosphorescence gap, spectra and rate constants of prototype CDCB compounds in toluene. A very good agreement was found between theory and experiment, which suggests that our computational protocol is potentially broadly applicable. This work opens new avenues for the calculation of the photophysical properties of aromatic compounds.
Conflicts of interest
There are no conflicts to declare.References
- H.-G. Franck and J. W. Stadelhofer, Industrial Aromatic Chemistry. 1998 Search PubMed.
- P. K. Seshan, The absorption spectra of some aromatic compounds, Proc. Indian Acad. Sci., 1936, 3, 172–187 CrossRef.
- D. C. Northrop and O. Simpson, Electronic properties of aromatic hydrocarbons. iv. photo-electric effects, Proc. R. Soc. London, Ser. A, 1958, 244, 377–389 Search PubMed.
- E. Clar, The Electrical Conductivity of Aromatic Hydrocarbons, Berlin, Heidelberg: Springer Berlin Heidelberg, 1964, pp. 118–118 Search PubMed.
- A. J. Epstein, S. Etemad, A. F. Garito and A. J. Heeger, Metal–insulator transition and antiferromagnetism in a one-dimensional organic solid, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 5, 952–977 CrossRef.
- M. Weger, The Electrical Conductivity of TTF–TCNQ and Related Compounds. Boston, MA: Springer US, 1979, pp. 123–134 Search PubMed.
- J. Ferraris, D. O. Cowan, V. Walatka and J. H. Perlstein, Electron transfer in a new highly conducting donor-acceptor complex, J. Am. Chem. Soc., 1973, 95(3), 948–949 CrossRef CAS.
- B. O’Regan and M. Graetzel, A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films, Nature, 1991, 353, 737–740 CrossRef.
- A. Carella, F. Borbone and R. Centore, Research progress on photosensitizers for dssc, Front. Chem., 2018, 6, 481 CrossRef CAS PubMed.
- A. Mishra, M. Fischer and P. Bäuerle, Metal-free organic dyes for dye-sensitized solar cells: from structure: property relationships to design rules, Angew. Chem., Int. Ed., 2009, 48(14), 2474–2499 CrossRef CAS PubMed.
- J. Albero, P. Atienzar, A. Corma and H. Garcia, Efficiency records in mesoscopic dye-sensitized solar cells, Chem. Record, 2015, 15(4), 803–828 CrossRef CAS PubMed.
- T. Higashino and H. Imahori, Porphyrins as excellent dyes for dye-sensitized solar cells: recent developments and insights, Dalton Trans., 2015, 44, 448–463 RSC.
- C.-P. Lee, C.-T. Li and K.-C. Ho, Use of organic materials in dye-sensitized solar cells, Mater. Today, 2017, 20(5), 267–283 CrossRef CAS.
- T. El-Agez, S. Taya, K. Elrefi and M. Abdel latif, Dye-sensitized solar cells using some organic dyes as photosensitizers, Opt. Appl., 2014, 44, 345–351 CAS.
- D. Lee, M. J. Lee, H. M. Song, B. Song, K. Seo, M. Pastore, C. Anselmi, S. Fantacci, F. Angelis, M. Nazeeruddin and M. Graetzel, Organic dyes incorporating low-band-gap chromophores based on -extended benzothiadiazole for dye-sensitized solar cells, Dyes Pigm., 2011, 91, 192–198 CrossRef CAS.
- M. A. Filatov, Heavy-atom-free bodipy photosensitizers with intersystem crossing mediated by intramolecular photoinduced electron transfer, Org. Biomol. Chem., 2020, 18, 10–27 RSC.
- C. W. Tang and S. A. VanSlyke, Organic electroluminescent diodes, Appl. Phys. Lett., 1987, 51(12), 913–915 CrossRef CAS.
- Y. Karzaki, Organic light emitting diodes: devices and applications, J. Mater. Environ. Sci., 2014, 5, 1–12 Search PubMed.
- J. Y. Xue, T. Izumi, A. Yoshii, K. Ikemoto, T. Koretsune, R. Akashi, R. Arita, H. Taka, H. Kita, S. Sato and H. Isobe, Aromatic hydrocarbon macrocycles for highly efficient organic light-emitting devices with single-layer architectures, Chem. Sci., 2016, 7, 896–904 RSC.
- Y. Qin, G. Li, T. Qi and H. Huang, Aromatic imide/amide-based organic small-molecule emitters for organic light-emitting diodes, Mater. Chem. Front., 2020, 4, 1554–1568 RSC.
- T. Itoh, Fluorescence and Phosphorescence from Higher Excited States of Organic Molecules, Chem. Rev., 2012, 112(8), 4541–4568 CrossRef CAS PubMed.
- S. Naskar and M. Das, Singlet and triplet excited state energy ordering in cyclopenta-fused polycyclic aromatic hydrocarbons (cp-pahs) suitable for energy harvesting: an exact model and tddft study, ACS Omega, 2017, 2(5), 1795–1803 CrossRef CAS PubMed.
- E. V. Donckt, R. Dramaix, J. Nasielski and C. Vogels, Photochemistry of aromatic compounds. part 1. acid-base properties of singlet and triplet excited states of pyrene derivatives and aza-aromatic compounds, Trans. Faraday Soc., 1969, 65, 3258–3262 RSC.
- F. Masetti, U. Mazzucato and J. Birks, Photophysical behaviour of azaphenanthrenes, Chem. Phys., 1975, 9(3), 301–306 CrossRef CAS.
- H. LöfÅs, B. O. Jahn, J. Wärnå, R. Emanuelsson, R. Ahuja, A. Grigoriev and H. Ottosson, A computational study of potential molecular switches that exploit baird's rule on excited-state aromaticity and antiaromaticity, Faraday Discuss., 2014, 174, 105–124 RSC.
- Z. Tu, G. Han, T. Hu, R. Duan and Y. Yi, Nature of the lowest singlet and triplet excited states of organic thermally activated delayed fluorescence emitters: a self-consistent quantum mechanics/embedded charge study, Chem. Mater., 2019, 31(17), 6665–6671 CrossRef CAS.
- G. N. Lewis and M. Kasha, Phosphorescence and the Triplet State, J. Am. Chem. Soc., 1944, 66(12), 2100–2116 CrossRef CAS.
- R. H. Friend, R. W. Gymer, A. B. Holmes, J. H. Burroughes, R. N. Marks, C. Taliani, D. D.-C. Bradley, D. A.-D. Santos, J. L. Brédas, M. Lögdlund and W. R. Salaneck, Electroluminescence in conjugated polymers, Nature, 1999, 397(6715), 121–128 CrossRef CAS.
- D. J. Gibbons, A. Farawar, P. Mazzella, S. Leroy-Lhez and R. M. Williams, Making triplets from photo-generated charges: observations, mechanisms and theory, Photochem. Photobiol. Sci., 2020, 19, 136–158 CrossRef CAS PubMed.
- W. Paa, J.-P. Yang and S. Rentsch, Ultrafast intersystem crossing in thiophene oligomers investigated by fs-pump-probe spectroscopy, Synth. Metals, 2001, 119(1), 525–526 CrossRef CAS . Proceedings of the International Conference on Science and technology of Synthetic Metals.
- S. Hirata, Recent advances in materials with room-temperature phosphorescence: photophysics for triplet exciton stabilization, Adv. Opt. Mater., 2017, 5(17), 1700116 CrossRef.
- J. P. Zobel, J. J. Nogueira and L. González, Mechanism of ultrafast intersystem crossing in 2-nitronaphthalene, Chem. – Eur. J., 2018, 24(20), 5379–5387 CrossRef CAS PubMed.
- R. A. Vogt, C. Reichardt and C. E. Crespo-Hernández, Excited-state dynamics in nitro-naphthalene derivatives: intersystem crossing to the triplet manifold in hundreds of femtoseconds, J. Phys. Chem. A, 2013, 117(30), 6580–6588 CrossRef CAS PubMed.
- E. Collado-Fregoso, J. S. Zugazagoitia, E. F. Plaza-Medina and J. Peon, Excited-state dynamics of nitrated push–pull molecules: the importance of the relative energy of the singlet and triplet manifolds, J. Phys. Chem. A, 2009, 113(48), 13498–13508 CrossRef CAS PubMed.
- R. W. Yip, D. K. Sharma, R. Giasson and D. Gravel, Picosecond excited-state absorption of alkylnitrobenzenes in solution, J. Phys. Chem., 1984, 88, 5770–5772 CrossRef CAS.
- T. Schmierer, G. Ryseck, N. Villnow, T. Regner and P. Gilch, Kasha or state selective behavior in the photochemistry of ortho-nitrobenzaldehyde, Photochem. Photobiol. Sci., 2012, 11, 1313–1321 CrossRef CAS PubMed.
- N. J. Turro, Modern Molecular Photochemistry. Mill-Valley, California, University Science Books, 1991 Search PubMed.
- S. G. Cohen and H. M. Chao, Photoreduction of aromatic ketones by amines. studies of quantum yields and mechanism, J. Am. Chem. Soc., 1968, 90(1), 165–173 CrossRef CAS.
- S. Hirayama, Photochemical reactions of aromatic aldehydes and ketones: higher triplet state reactions and radiationless transitions, Rev. Phys. Chem. Jpn., 1972, 42(1), 49–74 CAS.
- N. C. Baird, Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3π⋯π* state of cyclic hydrocarbons, J. Am. Chem. Soc., 1972, 94, 4941–4948 CrossRef CAS.
- L. J. Karas, C.-H. Wu, H. Ottosson and J. I. Wu, Electron-driven proton transfer relieves excited-state antiaromaticity in photoexcited dna base pairs, Chem. Sci., 2020, 11, 10071–10077 RSC.
- L. J. Karas and J. I.-C. Wu, 10 – antiaromatic compounds: a brief history, applications, and the many ways they escape antiaromaticity, in Aromaticity, ed. I. Fernandez, Elsevier, 2021, pp. 319–338 Search PubMed.
- T. J. Zuehlsdorff, N. D. Hine, M. C. Payne and P. D. Haynes, Linear-scaling time-dependent density-functional theory beyond the Tamm-Dancoff approximation: obtaining efficiency and accuracy with in situ optimised local orbitals, J. Chem. Phys., 2015, 28(43(20)), 204107 CrossRef PubMed.
- M. J.-G. Peach and D. J. Tozer, Overcoming low orbital overlap and triplet instability problems in tddft, J. Phys. Chem. A, 2012, 116(39), 9783–9789 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, Single-reference ab initio methods for the calculation of excited states of large molecules, Chem. Rev., 2005, 105(11), 4009–4037 CrossRef CAS PubMed.
- C. Jamorski, M. E. Casida and D. R. Salahub, Dynamic polarizabilities and excitation spectra from a molecular implementation of time-dependent density-functional response theory: N2 as a case study, J. Chem. Phys., 1996, 104(13), 5134–5147 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory, Chem. Phys. Lett., 1996, 256(4), 454–464 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the tamm-dancoff approximation, Chem. Phys. Lett., 1999, 314(3), 291–299 CrossRef CAS.
- M. E. Casida, F. Gutierrez, J. Guan, F.-X. Gadea, D. Salahub and J.-P. Daudey, Charge-transfer correction for improved time-dependent local density approximation excited-state potential energy curves: analysis within the two-level model with illustration for h2 and lih, J. Chem. Phys., 2000, 113(17), 7062–7071 CrossRef CAS.
- F. Cordova, L. J. Doriol, A. Ipatov, M. E. Casida, C. Filippi and A. Vela, Troubleshooting time-dependent density-functional theory for photochemical applications: oxirane, J. Chem. Phys., 2007, 127(16), 164111 CrossRef PubMed.
- O. B. Lutnæs, T. Helgaker and M. Jaszuński, Spin-spin coupling constants and triplet instabilities in kohn-sham theory, Mol. Phys., 2010, 108(19–20), 2579–2590 CrossRef.
- J. S. Sears, T. Koerzdoerfer, C.-R. Zhang and J.-L. Brédas, Communication: orbital instabilities and triplet states from time-dependent density functional theory and long-range corrected functionals, J. Chem. Phys., 2011, 135(15), 151103 CrossRef PubMed.
- S. Grimme and F. Neese, Double-hybrid density functional theory for excited electronic states of molecules, J. Chem. Phys., 2007, 127(15), 154116 CrossRef PubMed.
- M. Casanova-Páez and L. Goerigk, Assessing the tamm-dancoff approximation, singlet–singlet, and singlet–triplet excitations with the latest long-range corrected double-hybrid density functionals, J. Chem. Phys., 2020, 153(6), 064106 CrossRef PubMed.
- M. Casanova-Páez and L. Goerigk, Time-dependent long-range-corrected double-hybrid density functionals with spin-component and spin-opposite scaling: a comprehensive analysis of singlet-singlet and singlet–triplet excitation energies, J. Chem. Theory Comput., 2021, 17(8), 5165–5186 CrossRef PubMed.
- L. Wilbraham, C. Adamo and I. Ciofini, Communication: evaluating non-empirical double hybrid functionals for spin-state energetics in transition-metal complexes, J. Chem. Phys., 2018, 148(4), 041103 CrossRef PubMed.
- P. M. Zimmerman, Singlet–triplet gaps through incremental full configuration interaction, J. Phys. Chem. A, 2017, 121(24), 4712–4720 CrossRef CAS PubMed.
- B. Hajgató, D. Szieberth, P. Geerlings, F. De Proft and M. S. Deleuze, A benchmark theoretical study of the electronic ground state and of the singlet–triplet split of benzene and linear acenes, J. Chem. Phys., 2009, 131(22), 224321 CrossRef PubMed.
- B. Nebgen, Dataset of singlet and triplet energies and forces for organic molecules, 2021 Search PubMed.
- J. Westermayr and P. Marquetand, Machine learning for electronically excited states of molecules, Chem. Rev., 2021, 121(16), 9873–9926 CrossRef CAS PubMed.
- A. E. Sifain, L. Lystrom, R. A. Messerly, J. S. Smith, B. Nebgen, K. Barros, S. Tretiak, N. Lubbers and B. J. Gifford, Predicting phosphorescence energies and inferring wavefunction localization with machine learning, Chem. Sci., 2021, 12, 10207–10217 RSC.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, Sparse maps—a systematic infrastructure for reduced-scaling electronic structure methods. ii. linear scaling domain based pair natural orbital coupled cluster theory, J. Chem. Phys., 2016, 144(2), 024109 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139(13), 134101 CrossRef PubMed.
- P. Pulay, S. Saebo and W. Meyer, An efficient reformulation of the closed-shell self-consistent electron pair theory, J. Chem. Phys., 1984, 81(4), 1901–1905 CrossRef CAS.
- M. Schütz and H.-J. Werner, Local perturbative triples correction (T) with linear cost scaling, Chem. Phys. Lett., 2000, 318(4), 370–378 CrossRef.
- M. Schütz and H.-J. Werner, Low-order scaling local electron correlation methods. iv. linear scaling local coupled-cluster (LCCSD), J. Chem. Phys., 2001, 114(2), 661–681 CrossRef.
- W. Siebrand, Radiationless transitions in polyatomic molecules. ii. triplet-ground-state transitions in aromatic hydrocarbons, J. Chem. Phys., 1967, 47(7), 2411–2422 CrossRef CAS.
- J. Metcalfe, M. G. Rockley and D. Phillips, Single–triplet absorption spectra of substituted benzenes, J. Chem. Soc., Faraday Trans. 2, 1974, 70, 1660–1666 RSC.
- F. Neese, The orca program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CAS.
- S. Grimme and M. Steinmetz, Effects of london dispersion correction in density functional theory on the structures of organic molecules in the gas phase, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042 RSC.
- S. Grimme, Density functional theory with london dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(2), 211–228 CAS.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Dispersion-corrected mean-field electronic structure methods, Chem. Rev., 2016, 116(9), 5105–5154 CrossRef CAS PubMed.
- M. S. Deleuze, M. G. Giuffreda and J.-P. François, Valence one-electron and shake-up ionization bands of carbon clusters. II. The Cn (n = 5, 7, 9, 11) rings, J. Phys. Chem. A, 2002, 106(23), 5626–5637 CrossRef CAS.
- J. M.-L. Martin, A. Sundermann, P. L. Fast and D. G. Truhlar, Thermochemical analysis of core correlation and scalar relativistic effects on molecular atomization energies, J. Chem. Phys., 2000, 113(4), 1348–1358 CrossRef CAS.
- F. Neese, Software update: the orca program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327 Search PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Ri-mp2: optimized auxiliary basis sets and demonstration of efficiency, Chem. Phys. Lett., 1998, 294(1), 143–152 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Auxiliary basis sets to approximate coulomb potentials, Chem. Phys. Lett., 1995, 240(4), 283–290 CrossRef CAS.
- M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, A new near-linear scaling, efficient and accurate, open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory, J. Chem. Phys., 2017, 146(16), 164105 CrossRef PubMed.
- D. G. Liakos, Y. Guo and F. Neese, Comprehensive benchmark results for the domain based local pair natural orbital coupled cluster method (DLPNO-CCSD(T)) for closed- and open-shell systems, J. Phys. Chem. A, 2020, 124(1), 90–100 CrossRef CAS PubMed.
- F. Neese, Importance of direct spin–spin coupling and spin–flip excitations for the zero-field splittings of transition metal complexes: a case study, J. Am. Chem. Soc., 2006, 128(31), 10213–10222 CrossRef CAS PubMed.
- J.-L. Heully and J.-P. Malrieu, What would be the most relevant transcription of a CCSD(T) method into a dressed sdci matrix?, J. Mol. Struct.: THEOCHEM, 2006, 768(1), 53–62 CrossRef CAS.
- M. Schütz, Low-order scaling local electron correlation methods. iii. linear scaling local perturbative triples correction (T), J. Chem. Phys., 2000, 113(22), 9986–10001 CrossRef.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148(1), 011101 CrossRef PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. i. the atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. systematic basis sets and wave functions, J. Chem. Phys., 1992, 96(9), 6796–6806 CrossRef CAS.
- A. Karton and J. M.-L. Martin, Comment on: Estimating the Hartree-Fock limit from finite basis set calculations, Theor. Chem. Acc., 2006, 115, 330–333 Search PubMed.
- S. Zhong, E. C. Barnes and G. A. Petersson, Uniformly convergent n-tuple-augmented polarized (nzap) basis sets for complete basis set extrapolations. i. self-consistent field energies, J. Chem. Phys., 2008, 129(18), 184116 CrossRef PubMed.
- D. G. Truhlar, Basis-set extrapolation, Chem. Phys. Lett., 1998, 294(1), 45–48 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106(23), 9639–9646 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Basis-set convergence in correlated calculations on Ne, N2, and H2O, Chem. Phys. Lett., 1998, 286(3), 243–252 CrossRef CAS.
- F. Neese and E. F. Valeev, Revisiting the atomic natural orbital approach for basis sets: robust systematic basis sets for explicitly correlated and conventional correlated ab initio methods?, J. Chem. Theory Comput., 2011, 7(1), 33–43 CrossRef CAS PubMed.
- A. Altun, F. Neese and G. Bistoni, Extrapolation to the limit of a complete pair natural orbital space in local coupled-cluster calculations, J. Chem. Theory Comput., 2020, 16(10), 6142–6149 CrossRef CAS PubMed.
- A. Altun, S. Ghosh, C. Riplinger, F. Neese and G. Bistoni, Addressing the system-size dependence of the local approximation error in coupled-cluster calculations, J. Phys. Chem. A, 2021, 125(45), 9932–9939 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced gmtkn55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- B. de Souza, F. Neese and R. Izsák, On the theoretical prediction of fluorescence rates from first principles using the path integral approach, J. Chem. Phys., 2018, 148(3), 034104 CrossRef PubMed.
- B. de Souza, G. Farias, F. Neese and R. Izsák, Predicting phosphorescence rates of light organic molecules using time-dependent density functional theory and the path integral approach to dynamics, J. Chem. Theory Comput., 2019, 15(3), 1896–1904 CrossRef CAS PubMed.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, An improved chain of spheres for exchange algorithm, J. Chem. Phys., 155, 10, 104109, 2021. Publisher: American Institute of Physics Search PubMed.
- R. Cammi and B. Mennucci, Linear response theory for the polarizable continuum model, J. Chem. Phys., 1999, 110(20), 9877–9886 CrossRef CAS.
- F. Neese, Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations, J. Chem. Phys., 2005, 122(3), 034107 CrossRef PubMed.
- C. U. Ibeji and D. Ghosh, Singlet–triplet gaps in polyacenes: a delicate balance between dynamic and static correlations investigated by spin-flip methods, Phys. Chem. Chem. Phys., 2015, 17, 9849–9856 RSC.
- S. Mallick, P. K. Rai and P. Kumar, Accurate estimation of singlet–triplet gap of strongly correlated systems by CCSD(T) method using improved orbitals, Comput. Theoretical Chem., 2021, 1202, 113326 CrossRef CAS.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M.-L. Martin and F. Neese, Exploring the accuracy limits of local pair natural orbital coupled-cluster theory, J. Chem. Theory Comput., 2015, 11(4), 1525–1539 CrossRef CAS PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492(7428), 234–238 CrossRef CAS PubMed . Funding Information: Acknowledgements This work was supported by the Funding Program for World-Leading Innovative R D on Science and Technology (FIRST) and the International Institute for Carbon Neutral Energy Research (WPI-I2CNER), sponsored by the Japanese Ministry of Education, Culture, Sports, Science and Technology. H.U. acknowledges a Grand-in-Aid for JSPS Fellows. We thank H. Nakanotani, J.-I. Nishide, and H. Miyazaki for their assistance with this research. We also thank K. Tokumaru, H. Sasabe, W. Potscavage and M. Gábor for their assistance with preparation of this manuscript.
- F. B. Dias, T. J. Penfold and A. P. Monkman, Photophysics of thermally activated delayed fluorescence molecules, Methods Appl. Fluoresc., 2017, 5(1), 012001 CrossRef PubMed.
- F. Rodella, S. Bagnich, E. Duda, T. Meier, J. Kahle, S. Athanasopoulos, A. Köhler and P. Strohriegl, High triplet energy host materials for blue tadf oleds—a tool box approach, Front. Chem., 2020, 8, 657 CrossRef CAS PubMed.
- B. Wex and B. R. Kaafarani, Perspective on carbazole-based organic compounds as emitters and hosts in tadf applications, J. Mater. Chem. C, 2017, 5, 8622–8653 RSC.
- E. Duda, What Controls Thermally Activated Delayed Fluorescence in Guest-Host Systems for Organic Light-Emitting Diodes?PhD thesis, Bayreuth, 2021 Search PubMed.
- E. Speckmeier, T. G. Fischer and K. Zeitler, A toolbox approach to construct broadly applicable metal-free catalysts for photoredox chemistry: deliberate tuning of redox potentials and importance of halogens in donor-acceptor cyanoarenes, J. Am. Chem. Soc., 2018, 140(45), 15353–15365 CrossRef CAS PubMed.
- M. A. Bryden and E. Zysman-Colman, Organic thermally activated delayed fluorescence (tadf) compounds used in photocatalysis, Chem. Soc. Rev., 2021, 50, 7587–7680 RSC.
- M. Garcia-Ratés, U. Becker and F. Neese, Implicit solvation in domain based pair natural orbital coupled cluster (dlpno-ccsd) theory, J. Comput. Chem., 2021, 42(27), 1959–1973 CrossRef PubMed.
- A. Rodriguez-Serrano, F. Dinkelbach and C. M. Marian, Intersystem crossing processes in the 2czpn emitter: a dft/mrci study including vibrational spin-orbit interactions, Phys. Chem. Chem. Phys., 2021, 23, 3668–3678 RSC.
- H. Noda, X. Chen, H. Nakanotani, T. Hosokai, M. Miyajima, N. Notsuka, Y. Kashima, J. Brédas and C. Adachi, Critical role of intermediate electronic states for spin-flip processes in charge-transfer-type organic molecules with multiple donors and acceptors, Nat. Mater., 2019, 18(10), 1084–1090 CrossRef CAS PubMed.
- T. Hosokai, H. Matsuzaki, H. Nakanotani, K. Tokumaru, T. Tsutsui, A. Furube, K. Nasu, H. Nomura, M. Yahiro and C. Adachi, Evidence and mechanism of efficient thermally activated delayed fluorescence promoted by delocalized excited states, Sci. Adv., 2017, 3(5), e1603282 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01623k |
| This journal is © the Owner Societies 2022 |