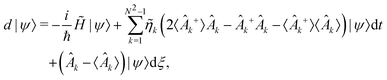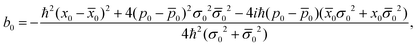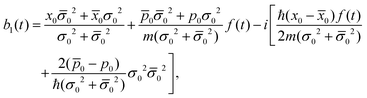Surface diffusion within the Caldeira–Leggett formalism
Received
5th April 2022
, Accepted 13th June 2022
First published on 16th June 2022
Abstract
Surface diffusion is described in terms of the intermediate scattering function in the time domain and reciprocal space. Two extreme time regimes are analyzed, ballistic (very short times) and Brownian or diffusive (very long times). This open dynamics is studied from the master equation for the reduced density matrix within the Caldeira–Leggett formalism. Several characteristic magnitudes in this decoherence process such as the coherence length, ensemble width and purity of the density matrix are analyzed. Furthermore, for flat surfaces, the surface diffusion is considered for the Schrödinger cat states and identical adsorbates or adparticles, bosons and fermions. The analytical results are compared with those issued from solving the Lindblad master equation through the stochastic wave function method. This numerical analysis is extended to be applied to corrugated surfaces.
1 Introduction
In 1954 van Hove1 showed that the scattering cross section of probe particles (low energy neutrons) by a system of interacting particles can be expressed, within the Born approximation, in terms of the so-called generalized pair-distribution function or van Hove space-time correlation function G(r, t), depending on the space vector r and time t. Under this approximation, the scattering problem is reduced essentially to a problem of statistical mechanics where the nature of the scattered particles (neutron, light, atoms, etc.) and details of the interaction potential with the interacting system are irrelevant.2 This G-function, which is a straightforward extension of the well known static pair or radial distribution function g(r) widely used in liquid theory,3 gives us the probability that given a particle at the origin and at time t = 0, any particle including the same one is to be found at the position r and at time t. A natural splitting of this G-function can be written as| | | G(r, t) = Gs(r, t) + Gd(r, t), | (1) |
where s refers to self and d to distinct, describing the correlations between positions of one and the same particle and pairs of different particles with time, respectively. The well-known properties of these distribution functions are1,2,4| | 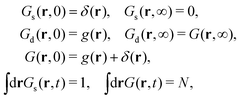 | (2) |
where N is the number of particles in the interacting system and δ(r) is Dirac's function in space.
In this type of scattering, the sample response is linear and it is given by the function S(Δk, ω) which is proportional to the scattering cross section. This response function is often called the scattering law or dynamic structure factor (DSF) depending on the momentum transfer (or scattering vector) Δk = kf − ki and energy transfer ħω = Ef − Ei. The corresponding inverse Fourier transform in time, which is also a response function, is known as the intermediate scattering function (ISF), I(Δk, t). Finally, the double inverse Fourier transform (in momentum and energy) of S(Δk, ω) gives us the G(r, t)-function. Thus, one can write
| | 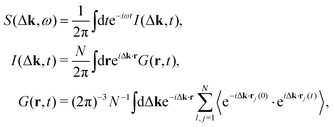 | (3) |
where 〈·〉 stands for thermal (Boltzmann) averages or quantum expectation values depending on if we are considering classical or quantum scattering and
rl,
rj are the position operators of particle
l and
j, respectively, which do not commute at different times. The functions
Gs(
r,
t) and
Gd(
r,
t) give contributions of the same (
l =
j) and distinct (
l ≠
j) particles, respectively. Due to the linearity of the Fourier transform, one can write
| | 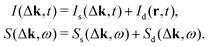 | (4) |
The so-called coherent and incoherent scattering cross sections in neutron scattering are related to
S(Δ
k,
ω) and
Ss(Δ
k,
ω) and, therefore, from
eqn (3), to
G(
r,
t) and
Gs(
r,
t), respectively. In classical mechanics, these
G-functions are real and
rl(0) and
rj(
t) represent the initial location of particle
l and the classical trajectory of particle
j, respectively.
Now, by considering that one particle is at the origin at time t = 0 and simultaneously a second particle is at r′, then the probability that, in an elapsed time t, the second particle goes from r′ to r with a net displacement given by r′ − r is denoted by P0(r, r′, t). The so-called convolution approximation due to Vineyard4 is written as
| | 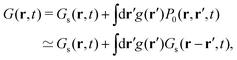 | (5) |
where it is often assumed that
P0(
r,
r′,
t) ≃
Gs(
r −
r′,
t). This approximation is expected to be better at long times and distances where the correlation between two particles is faded out. Vineyard also derived
eqn (5) from a quantum scenario. Within this approximation, one can obtain
Gd as
| | 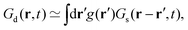 | (6) |
in order to have more or less good approximations to
G(
r,
t),
I(Δ
k,
t) and
S(Δ
k,
ω). Thus, it is then primordial to know
Gd to characterize the full scattering process.
In diffusion of adsorbates/adparticles on surfaces sampled by He atoms instead of neutrons, the scattering is fully coherent5, that is, only I(Δk, t) and S(Δk, ω) are observables; Is(Δk, t) and Ss(Δk, ω) being relevant only when the surface coverage is really very small since correlations between any of two particles are almost negligible. In this context, the momentum transfer Δk as well as adsorbate trajectories R(t) are written in capital letters meaning that they are quantities parallel to the surface. Two well established surface experimental techniques are used, the quasi-elastic He atom scattering (QHAS)6,7 and neutron scattering (QENS)8 which overlap in spatial and time resolution. The first one goes more or less from 10−13 to 10−8 seconds and from 10−11 to 10−8 m, whereas the second one goes from 10−13 to 10−6 seconds and from 10−10 to 10−6 m.9,10 QENS is, in general, more convenient for processes occurring in bulk and QHAS is essentially sensible for surfaces. More recently, these two techniques have been complemented by using spin-echo (SE), HeSE9,10 and neutron spin-echo NSE.8 In any case, the experimental results issued from any scattering technique mentioned above require an adequate theoretical framework to properly process them and extract relevant information about the physical systems of interest. For neutrons, molecular dynamics calculations are generally used where a full description of the force fields (adsorbate–adsorbate and adsorbate–substrate interactions) involved is necessary whereas, for He atoms, the Langevin formalism or its generalization to include memory effects is widely applied starting from the well-known Caldeira–Leggett Hamiltonian.11 In the second approach, the surface is usually well represented by a thermal bath consisting of an infinite number of harmonic oscillators. Friction and noise (white or color) appear after integrating over the degrees of freedom of the surface.
After eqn (3), the ISF can be calculated from the classical and quantum stochastic trajectories represented by R(t) for each adsorbate. Classical stochastic mechanics is usually sufficient except for very light adsorbates. One of the main goals is to provide simple analytical expressions to directly interpret the experimental results, shedding light on the interaction of adparticles with the surface and extracting friction and diffusion coefficients. As mentioned above, the corresponding observables or response functions are resolved in time (ISF) or energy (DSF). For such a goal, the dynamics of only one adsorbate is studied (assuming the surface coverage is small). Within the so-called Gaussian approximation, simple analytical expressions for Is and Ss are easily obtained for flat and corrugated surfaces12 or with memory friction.13 Numerical results from Langevin calculations are thus better interpreted. One way to also provide analytical expressions when the coverage is important and therefore the distinct contribution can not be neglected is through a model called interacting single adsorbate (ISA).14,15 In the ISA model, the interaction among adsorbates is replaced by a shot noise by assuming that the adsorbates are also a thermal bath (the so-called two bath model). It is clear that when we are faced to strong correlated motions due to high surface coverage, the ISA model is no longer valid. For example, this is the case for sodium atoms diffusing on a Cu(111) surface.16 However, within the range of applicability of this approximation, one is able to provide analytical expressions for I and S, overcoming the explicit knowledge of Id or Sd. Two extreme time regimes are well characterized in this open dynamics, the ballistic regime, at very short times, where the dynamics is friction and noise free and the Brownian or diffusive regime, at very long times, where the thermal equilibrium is reached with the surface. Analytical expressions for Is and Ss are given by means of very simple functions. In the first regime both response functions are Gaussian functions and, in the second regime, Is is an exponential function and Ss a Lorentzian function.
On the other hand, for very light adparticles, we have to resort to the quantum realm. The so-called quantum Brownian motion is the paradigm in this context. Here position operators do not commute at different times and some care needs to be taken into account. However, a quite straight forward extension of the methodology used for classical diffusion can be still used to provide reasonable analytical expressions.17 A second approach is to consider quantum stochastic trajectories within the Bohmian framework.18 An alternative and widely used approach to deal with open quantum systems is within the so-called system-plus-environment approach. A master equation is then derived for the evolution of this matrix which contains both frictional and thermal effects, the so-called Caldeira–Leggett (CL) master equation19 which is of Markovian type. The corresponding diagonal matrix elements give the quantum probabilities and the off-diagonal elements, the so-called coherences. Time evolution of coherences gives us an indication of how the decoherence process is gradually established leading to certain timescales of the system under study and exponential suppression of spatial interference terms.
Strictly speaking the splitting of the G-function into two parts (self and distinct) is only valid in classical statistical mechanics. Several quantum scenarios can be devised for this failure due to the presence of interference or cross terms which can drastically modify the probability density or, equivalently, the G-function: the so-called Schrödinger cat states for adsorbates which can be at both sides of two domains or shallow wells on a surface, and when several distinguishable or identical (interacting or noninteracting) adsorbates are considered in the diffusion dynamics. In this last case, the symmetry of the wave function (symmetric for bosons and anti-symmetric for fermions) adds a new ingredient to this open dynamics. In all of these example, one should only consider the G function, not anymore Gs and Gd separately. Interestingly enough, we have observed that in the ballistic regime the ISF and DSF no longer display a Gaussian function. However, in the Brownian or diffusion regime these two response functions still conserve their analytical shapes. In the interest of simplicity, this theoretical analysis is carried out for flat surfaces where an analytical expressions can be found by solving the CL master equation. On the other hand, a numerical technique has been developed to solve the stochastic Schrödinger differential equation for corrugated surfaces in order to analyze these two time regimes for low energy barriers at high temperatures. The analytical results are then compared with those issuing from solving the so-called Lindblad master equation20,21 through the stochastic wave function method.22,23 Numerical results will also be reported for model calculations on the Xe–Pt(111) system in order to check the application of this method in the surface diffusion context.
In brief, a new theoretical approach for the description of measurements of atomic diffusion by particle beams such as realized in helium atom scattering and neutron scattering is presented. This method should represent an important step on the development of quasi-elastic helium scattering and neutron spectroscopy. Due to the fact it can be applicable to a wide range of realistic systems, a high impact on a wide range of physicochemical research is expected.
This paper is organized as follows. In Section 2 the CL master equation in the coordinate representation is briefly introduced and applied in this context for the first time. Several characteristic magnitudes are then studied governing the coherence of the diffusion dynamics such as coherence length, ensemble width, purity and coherence time are presented and analyzed. In Sections 3 and 4, the Schrödinger cat state model and the diffusion of noninteracting bosons and fermions are discussed, respectively. In Sections 5 and 6, the Lindblad master equation through the stochastic wave function numerical analysis is carried out in order to compare with previous analytical results for flat and corrugated surfaces. Finally, in the last section, some conclusions and future perspective are discussed.
2 The Caldeira–Leggett formalism. The one particle problem
Many important problems in physics and chemistry are dealing with open quantum system.24–26 A complete mathematical model for the system-plus-environment dynamics can be very complicated. The environment is usually well represented by a reservoir with an infinite number of degrees of freedom.22,27 It turns out to be useful to formulate this dynamics using an appropriate equation of motion for the corresponding density matrix, known as quantum master equation, and employing some approximations.
Several techniques have been used to describe the dynamics of an exactly open quantum system in terms of the reduced density matrix. One of this techniques is the influence functional formalism used in the path integral representation where the environmental variables can be eliminated by using the Feynman–Vernon influence functional.22 This formalism is an efficient theoretical tool and has been applied for solving Langevin equation with damped harmonic oscillator,28 non-Markovian systems,29 and the spin-boson model30,31 among others.
We will focus on discussing the simplest case, the motion of a quantum Brownian particle32 in the weak-coupling and high-temperature limits. Thus, for example, by assuming short environmental correlation times, the memory effects can be safely neglected in the reduced dynamics and a Markovian quantum master equation can be easily derived which is known as the CL master equation.33 This formalism gives the evolution of the reduced density matrix in the coordinate representation by tracing out the environment degrees of freedom and contains both frictional and thermal effects due to the environment in analogy with the classical Fokker-Planck equation.22
This pioneering CL work describes the dynamics of such a particle linearly coupled to an Ohmic environment34 (linear dissipation). The CL master equation for the reduced density matrix in the position representation for one dimension ρ(x, x′, t), at the high temperature limit, takes the form33
| | 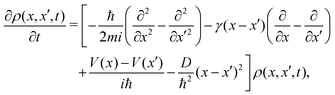 | (7) |
where
V is the external interaction potential,
m the particle mass,
γ the friction coefficient and
D the diffusion coefficient given by
with
kB being Boltzmanns constant and
T the surface temperature. This master
eqn (7) for one particle coupled to an Ohmic environment (constant friction) with a generic potential does not have an analytic solution. However, for flat surfaces (
V = 0), analytical solutions are obtained by considering, for example, a Gaussian ansatz
35 or using the Wigner representation.
36
Let us consider the initial state as a Gaussian wave packet representing a localized particle centered at the position x0, with momentum p0 and width σ0,
| | 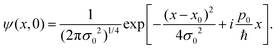 | (9) |
The initial density matrix, given by
| | | ρ(x, x′, 0) = ψ*(x′, 0)ψ(x, 0), | (10) |
can be extracted from the initial state
(9). Replacing the initial wave packet
(9) in
(10), the density matrix can be expressed as
| | 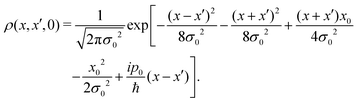 | (11) |
Using the Gaussian ansatz
| | 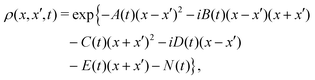 | (12) |
and inserting
eqn (12) into the master
eqn (7), a system of coupled differential equations for the time dependent coefficients
A(
t),
B(
t),
C(
t),
D(
t),
E(
t) and
N(
t) is obtained and shown in Appendix A. The diagonal elements give the probability to find the particle at position
x and time
t whereas the nondiagonal terms give the so-called coherences which provide the correlation of the particle at two different positions
x and
x′ at time
t. With time, this correlation or coherence decays obviously to zero. This solution can also be obtained by using the Wigner representation of the reduced density matrix, see Appendix B.
The generalized pair-distribution function of van Hove G(x, t) can be associated with the reduced density matrix given by eqn (12) and by imposing the condition x′ = x leading to
| | 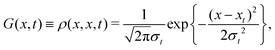 | (13) |
where
| | 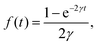 | (15) |
| | 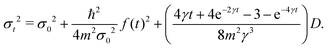 | (16) |
Thus,
G(
x,
t) is a Gaussian function with a width given by
eqn (16) and a center moving along the classical trajectory
(14). For one particle, the general properties of
G or
Gs given
eqn (2) are fulfilled. As known,
37–39 the variance of a Gaussian wave packet in general is given by
| | 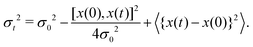 | (17) |
In correspondence with
eqn (17), the time dependent width given by
eqn (16) has three contributions: (i) the initial width, (ii) the commutator through −[
x (0),
x(
t)]
2/4
σ02 and (iii) the mean square displacement (MSD). The expression for
G(
x,
t) provides an analytical solution for the probability of finding the particle at position
x at time
t given that it was at
x0 at
t = 0.
Once G(x, t) has been identified, the corresponding ISF, I(Δk, t), and the dynamic structure factor, S(Δk, ω), can be derived from eqn (3). Thus, one has that
| | 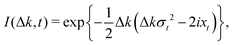 | (18) |
which is Gaussian in the momentum transfer which is represented along this work as Δ
k. In diffusion processes, two well established time regimes are characterized, ballistic and Brownian or diffusive. In the ballistic regime, at short times,
t ≪
γ−1, and by considering the linear term of the exponential,
eqn (14) and (16) reduce to
| | 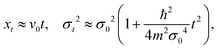 | (19) |
and the corresponding ISF is given by
| | 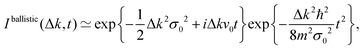 | (20) |
that is, a pure Gaussian function in time and momentum transfer is obtained for a zero initial position. The time exponential factor depends on the particle mass and the initial width. In the classical regime, this factor depends on the thermal velocity of the particle.
12 On the other hand, in the Brownian regime, we have just the opposite case,
t ≫
γ−1, and
| | 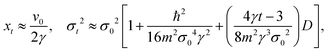 | (21) |
and the ISF is
| | 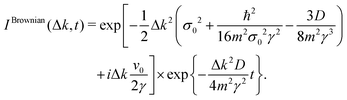 | (22) |
As expected, in the Brownian regime,
I(Δ
k,
t) is an exponential function with time and is accompanied by the diffusion coefficient
D which contains itself the surface temperature
T and the friction coefficient
γ according to
eqn (8). Thus, the ISF gradually passes from a Gaussian to an exponential function when going from the short time to the long time regime.
In Fig. 1, the real components of the intermediate scattering function, eqn (18), are plotted for Xe (blue solid curve) and Na (red dashed curve) atoms. The parameters for the initial wave packet are: x0 = 0, σ0 = 0.003 a.u. for Xe, σ0 = 0.02 a.u. for Na, p0 = 0. The friction γ = 0.25 ps−1, momentum transfer Δk = 0.12 Å−1 and surface temperature T = 105 K have been extracted from previous works with this adsorbates.40,41 For the Xe adsorbate, both the Gaussian function at short times and the exponential at long times give good fitting to the ISF. This result indicates that the adsorbate goes from a ballistic to diffusive regime. The corresponding DSF S(Δk, ω) is the time Fourier transform of eqn (18) and can not be obtained analytically due to the presence of the time dependent width. However, in both limiting regimes, analytical expressions are easily obtained. The dynamical structure factor in the ballistic regime is expressed as
| | 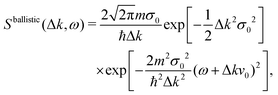 | (23) |
and in the Brownian or diffusive regime
| | 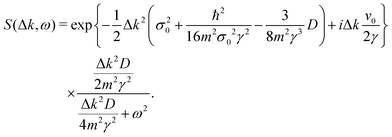 | (24) |
From
eqn (23) and (24), it can be seen that the dynamical structure factor gradually passes from a Gaussian to a Lorentzian function with the frequency when going from the ballistic to Brownian regime. This gradual transition is the so-called motional narrowing effect.
42
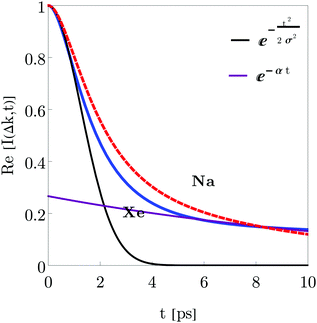 |
| | Fig. 1 The real components of the intermediate scattering function given by eqn (18) are plotted for Xe (blue solid curve) and Na (red dashed curve) atoms. The parameters for the initial wave packet are: x0 = 0, σ0 = 0.003 a.u. for Xe, σ0 = 0.02 a.u. for Na, and p0 = 0. The fitting of a Gaussian function (black line) for short times and an exponential function (purple line) for long times are shown for the Xe adsorbate. It is assumed that γ = 0.25 ps−1, Δk = 0.12 Å−1 and T = 105 K. | |
2.1 Characteristic magnitudes in decoherence dynamics
The dynamics of adsorbates on a surface seen as a thermal bath leads gradually to decoherence or, in other words, to the quantum-classical transition. Several magnitudes are used to characterize this decoherence process in the position representation of the reduced density matrix, namely: the coherence length l(t), the ensemble width Δx(t) and the so-called purity δ(t).35
One of the most important quantities in decoherence is the so-called coherence length l(t). This magnitude represents a measure of the distance over which quantum correlations are important (the width of ρ in the x–x′ direction, the nondiagonal matrix elements). In correspondence with,43 the coherence length l(t) can be obtained from the Gaussian ansatz (12) and the density matrix (11),
| | 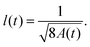 | (25) |
It also measures the characteristic distance over which the system can exhibit spatial interference effects. The explicit time dependence is found in Appendix C.
In Fig. 2, the time dependence of the coherence length for three adsorbates with different masses is plotted: mXe = 131.293, mNa = 22.989 and mLi = 6.941. These calculations are carried out for an initial Gaussian wave packet (9) with the following initial conditions: x0 = 0, σ0 = 0.003(Xe), 0.02(Na) and 0.2(Li) a.u. and momentum p0 = 0. The surface temperature is T = 105 K and the friction coefficient γ = 0.25 ps−1. The color curves are under the presence of the environment (solid lines) with Xe (blue), Na (red) and Li (purple) whereas the dashed curves give the free evolution of Xe, Na and Li. At very short times (t ≪ 4 ps), l(t) displays a very pronounced linear increase identical to the free evolution but suddenly the presence of the environment starts reducing significantly the coherence length reaching an asymptotic value around 4 ps. The decoherence process is gradual established but it is going faster for heavier adsorbates according to eqn (120) from Appendix C.
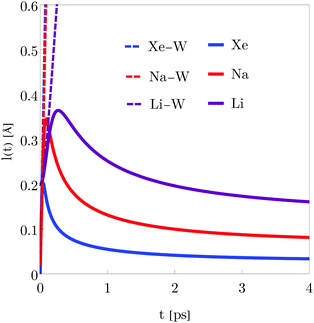 |
| | Fig. 2 Time dependence of the coherence length l(t) for three adsorbates Xe, Li and Na. The initial parameters for the Gaussian wave packet (9) are: position x0 = 0, width σ0 = 0.003(Xe), 0.02(Na) and 0.2(Li) a.u., and momentum p0 = 0, a temperature T = 105 K and a friction coefficient γ = 0.25 ps−1. With environment (solid lines) and without (dashed line): Xe (blue), Na (red) and Li (purple). | |
The second key quantity is the so-called ensemble width, Δx(t), which represents the probability distribution size P(x, t) ≡ ρ(x, x, t) and can be found from the following expression
| | 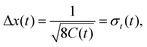 | (26) |
which coincides with the width of the probability distribution.
Fig. 3 shows the time dependence of the ensemble width, given by eqn (26), for the above three adsorbates Xe, Na and Li by assuming again the same initial conditions and environment parameters. The same color codes are used as in Fig. 2. At very short times (t ≪ 4 ps), there is no difference among the ensemble width with and without environment. This means that in the ballistic regime the adsorbates moves freely in agreement with the coherently spread out of a free Gaussian wave packet (126) from Appendix C. However, at long times (t ≫ 4 ps), the ensemble width of the three adsorbates increases more slowly and much more for heavier masses. This behavior indicates that the adsorbate can diffuse less freely as a result of the interaction with environment.
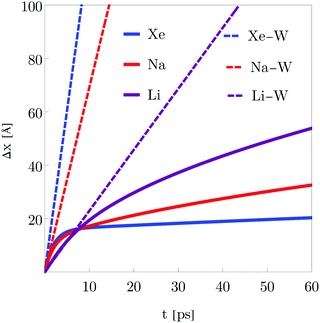 |
| | Fig. 3 Time dependence of the ensemble width Δx(t) for the three adsorbates Xe, Li and Na. The same initial conditions for the wave packet, surface temperature and friction are used as in Fig. 2 The color codes for the curves are also used in Fig. 2. | |
Finally, the third key quantity is a dimensionless measure of decoherence given by the ratio of the coherence length l(t) and the ensemble width Δx(t) called the purity of the reduced density matrix,
| | 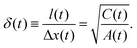 | (27) |
The purity of a normalized quantum state is also defined as
δ(
t) = Tr(
ρ2). This magnitude gives information on how much a state is mixed. If the quantum state
ρ(
x,
x′,
t) represents a pure-state density matrix,
ρ2 =
ρ and the purity is
δ(
t) = 1.
The explicit expression is again found in Appendix C.
In Fig. 4, the time dependence of the purity δ(t) is also analyzed for the same adsorbates and initial conditions. Without environment, the reduced density matrix purity remains constant equal to one since the free ensemble size eqn (126) and the free coherence length eqn (118) are equal. Under the presence of the environment, the purity decreases faster for Xe than for Na and Li. This decreasing occurs at very short times (t ≪ 4 ps). In other words, the gradual decoherence process is very fast for the initial conditions chosen in these examples.
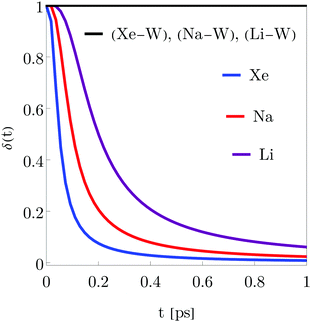 |
| | Fig. 4 Time dependence of the purity δ(t) for the three adsorbates Xe, Li and Na. The same initial conditions for the wave packet, surface temperature and friction are used as in Fig. 2 The color codes for the curves are also used in Fig. 2 and without environment for the three adsorbates (black solid curve). | |
3 The Schrödinger cat states
Sometimes the adsorbate can be at two different positions/domains at the same time; for example, if there is a barrier and the tunneling process takes place, the adsorbate has a probability different from zero to be in both side at the same time.
Let us consider now, for a single adsorbate, an initial wave function expressed as the superposition of two equal weighted Gaussian wave packets (9) centered around x = ±x0 at t = 0 and the same initial momentum p0
| | 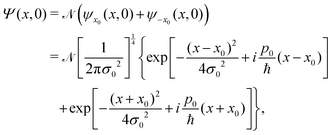 | (28) |
where
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif)
is the normalization constant. From
eqn (28), the corresponding initial reduced density matrix is given by
| | 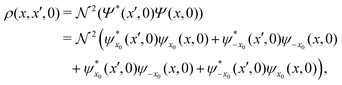 | (29) |
consisting of four contributions: two terms associated with each wave packet separately and the interference terms. Due to the linearity of the master
eqn (7), the time evolution of the reduced density matrix when
V = 0 leads to
| | 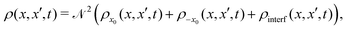 | (30) |
where the interference term is written as
| | 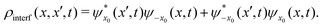 | (31) |
Using again a Gaussian ansatz
| | 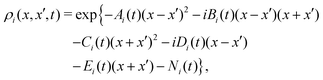 | (32) |
the explicit expression for the coefficients can be found in Appendix D. The probability of finding the adsorbate at (
x,
t) can be extracted from the reduced density matrix
eqn (30) by imposing the condition
x =
x′, that is,
| | 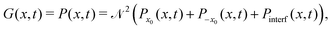 | (33) |
where
| | 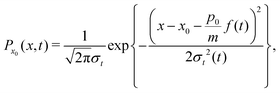 | (34) |
and analogously for
P−x0(
x,
t). Using the property of the hermiticity of the reduced density matrix, the interference term at
x and at time
t is given then by
| | 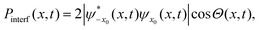 | (35) |
where
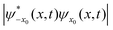
is the modulus of
ρinterf(
x,
x,
t) and
Θ(
x,
t) its phase.
Eqn (33) can be expressed as the typical interference pattern expression according to
44| | 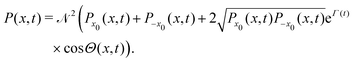 | (36) |
where
Γ(
t) is known as the decoherence function written as
| | 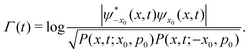 | (37) |
After some straightforward calculations, one obtains the explicit expressions for the normalization constant
| | 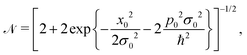 | (38) |
the phase
| | 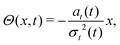 | (39) |
with
| | 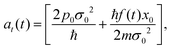 | (40) |
and the decoherence function
| | 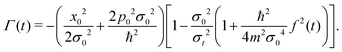 | (41) |
As can be clearly seen from
eqn (41), the decoherence function is negative since the width
σt, given by
eqn (16), is always greater than the initial width
σ0. Furthermore, when
D = 0 or
T = 0, the width
σt is
| | 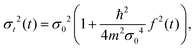 | (42) |
and the decoherence function vanishes. This is an expected behavior since the decoherence process
45 is represented by the last term of the CL master
eqn (7).
In the zero dissipation limit, γ → 0, the decoherence function is expressed as
| | 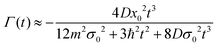 | (43) |
and when
σ0 ≪ 2
x0, the decoherence function can be written as
| | 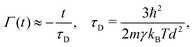 | (44) |
where
d = 2
x0 is the separation between initial wave packets and
τD is known as the decoherence time. From
eqn (44) one sees again that
τD depends on the friction coefficient, temperature and the initial wave packets separation.
46
In Fig. 5, the decoherence function is plotted for Li adsorbates with different friction coefficients (left panel) and surface temperatures (right panel). The color codes are inside each plot. As expected, the decoherence function which is a negative function decreases with friction and temperature.
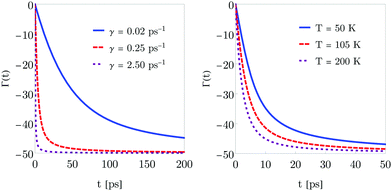 |
| | Fig. 5 Decoherence function for Li adsorbates with different friction coefficients (left panel) and surface temperatures (right panel) for an initial position x0 = ±2 a.u., width σ0 = 0.2 a.u. and momentum p0 = 0. On the left panel, the friction coefficients are 0.02 ps−1 (blue solid curve), 0.25 ps−1 (red dashed curve) and 2.50 ps−1 (purple dotted curve). On the right panel, the surface temperatures are 50 K (blue solid curve), 105 K (red dashed curve) and 200 K (purple dotted curve). | |
The ISF is then given by
| | I(Δk,t) = ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2(I(Δk,t) + Iinter(Δk,t)), 2(I(Δk,t) + Iinter(Δk,t)), | (45) |
where
| | 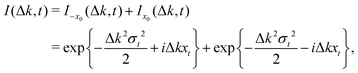 | (46) |
| | 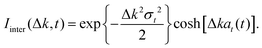 | (47) |
In the ballistic regime,
t ≪
γ−1,
eqn (40) reduces to
| | 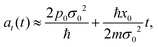 | (48) |
and the corresponding ISF is
| | 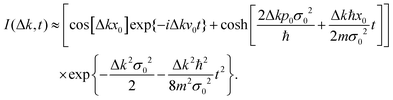 | (49) |
As can be seen, this function is not longer a Gaussian function.
However, in the Brownian regime, t ≫ γ−1, one has
| | 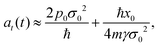 | (50) |
and the ISF is
| | 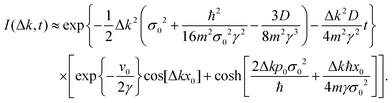 | (51) |
where the same exponential function of time is still valid.
The Schrödinger cat state or the quantum superposition states become more likely for H particles than for Na or Xe. The ratio between the decoherence time τD and relaxation time τr for a superposition of two different positions at a distance Δx is τr/τD = (Δx/λdB)2, where the thermal de Broglie wavelength is given by 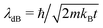 . With increasing mass, the decoherence time scale is much smaller than the relaxation time scale required to reach thermal equilibrium. It becomes more difficult to observe interference patterns for massive particles and therefore the creation of a spatial superposition.47,48
. With increasing mass, the decoherence time scale is much smaller than the relaxation time scale required to reach thermal equilibrium. It becomes more difficult to observe interference patterns for massive particles and therefore the creation of a spatial superposition.47,48
In Fig. 6, the ISF given by eqn (45) is plotted (blue solid line) for an H adsorbate with width σ0 = 0.2 a.u., positions x0 = ±0.6 a.u. and momentum ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = −p0 = 0.01 a.u., a friction coefficient γ = 0.25 ps−1, a momentum transfer Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The insets show the interference term (47) together with the ISF (46) with a (dashed red line) and a (dotted purple line), respectively. The interference term breaks the ballistic behavior of the system. As expected, when the temperature increases, the ISF decreases faster leading to the typical exponential behavior with time.
0 = −p0 = 0.01 a.u., a friction coefficient γ = 0.25 ps−1, a momentum transfer Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The insets show the interference term (47) together with the ISF (46) with a (dashed red line) and a (dotted purple line), respectively. The interference term breaks the ballistic behavior of the system. As expected, when the temperature increases, the ISF decreases faster leading to the typical exponential behavior with time.
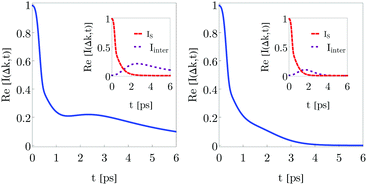 |
| | Fig. 6 Time dependency of the real part of the intermediate scattering function for a H particle with the initial wave packet (28) with width σ0 = 0.2 a.u., positions x0 = ±0.6 a.u. and momentum ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = −p0 = 0.01 a.u. for a friction coefficient γ = 0.25 ps−1, a momentum transference Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The inside panel shows the interference term (47) and the self intermediate scattering function (46) with a (dashed red line) and a (dotted purple line) respectively and the (blue solid line) the intermediate scattering function (45). 0 = −p0 = 0.01 a.u. for a friction coefficient γ = 0.25 ps−1, a momentum transference Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The inside panel shows the interference term (47) and the self intermediate scattering function (46) with a (dashed red line) and a (dotted purple line) respectively and the (blue solid line) the intermediate scattering function (45). | |
Thus, the corresponding DSF Ss(Δk, ω), in the Brownian regime, is again a Lorentzian function with the frequency.
4 Identical adsorbates
For neutral atomic adsorbates, those with an even number of neutrons are bosons whereas those with an odd number of neutrons are fermions.49 In this section, we are going to consider the diffusion of noninteracting identical adsorbates where the only interaction comes from the symmetry of the corresponding wave functions with respect to the interchange of particles, symmetric for bosons and anti-symmetric for fermions. In particular, we want to analyze how the well-known bunching and anti-bunching properties of bosons and fermions, respectively, are manifested in this open dynamics; in other words, in what extent the symmetry of the wave function is robust enough to keep it along time and how the gradual loss of being indistinguishable is established.
The initial wave function for the identical adsorbates (symmetric, +, and anti-symmetric, −) can be written as
| | Ψ±(x1,x2,0) = ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±{ψ(x1,0)ϕ(x2,0) ± ϕ(x1,0)ψ(x2,0)}, ±{ψ(x1,0)ϕ(x2,0) ± ϕ(x1,0)ψ(x2,0)}, | (52) |
where
ψ and
ϕ are one-particle Gaussian wave packets
(9) with parameters
x0,
p0,
σ0 and
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0
0,
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0
0,
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0
0, respectively. Under the Caldeira–Leggett
eqn (7), the evolution of the two-particle system is given by
| | 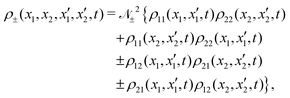 | (53) |
where
| | 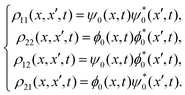 | (54) |
Note that
ρ11(
x,
x′,
t) and
ρ22(
x,
x′,
t) are the density matrix of one adsorbate. As seen before, the probabilities are given by the diagonal elements of the density matrix
eqn (53),
| | 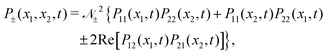 | (55) |
where
Pij(
x,
t) =
ρij(
x,
x,
t). The last or cross term of
eqn (55) is responsible for symmetry effects. For the single-particle density one has that
| | 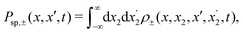 | (56) |
and the probability is written as
| | Psp,±(x, t) = ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±2{P11(x, t) + P22(x, t) ± 2Re[P12(x, t)s(t)]}, ±2{P11(x, t) + P22(x, t) ± 2Re[P12(x, t)s(t)]}, | (57) |
where
P11(
x,
t) and
P22(
x,
t) are given by
eqn (34), the overlapping integral
s(
t) being
| | 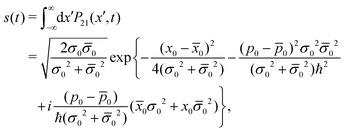 | (58) |
and the normalization factor
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±
±| | 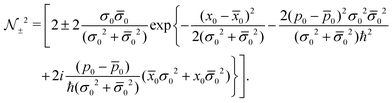 | (59) |
From
eqn (58) it can be seen that
s(
t) is time independent and does not depend on environment parameters such as
γ and
T, only depends on the initial conditions. In analogy to the cat state problem,
eqn (35), one can write
| | Psp,±(x, t) = ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±2{P11(x, t) + P22(x, t) ± 2|P12(x, t)s(t)|cos ±2{P11(x, t) + P22(x, t) ± 2|P12(x, t)s(t)|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ(x, t)}, Θ(x, t)}, | (60) |
where
| | 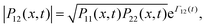 | (61) |
and
Γ12(
t) is the decoherence function for noninteracting identical adsorbate, given by
| | 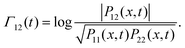 | (62) |
The probability
P12(
x,
t) is now written as
| | 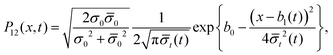 | (63) |
where
and
| | 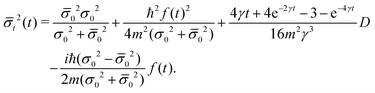 | (64) |
Note that for
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0
0 =
σ0, the width is
b2(
t) =
σt/2 and the explicit formula for the phase
Θ(
x,
t) is
| | 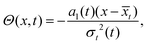 | (65) |
with
| | 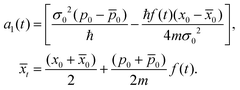 | (66) |
From
eqn (63), the interference term of the probability
(60) can be written as
| | 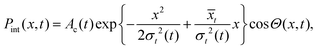 | (67) |
where
| | 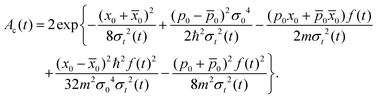 | (68) |
When
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0
0 =
x0, the probabilities
P11(
x,
t) and
P22(
x,
t) are given by
(34) for the momentum
p0 and
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0
0, respectively. In this case, from
eqn (62), one obtains the decoherence function
| | 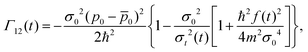 | (69) |
and the phase
| | 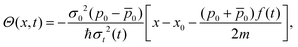 | (70) |
in correspondence with ref.
50.
Now, if we identify
| | | G(x, t) ≡ Psp,±(x, t) | (71) |
the ISF is found to be
| | Isp,±(Δk, t) = ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±2(Ix0(Δk, t) + I ±2(Ix0(Δk, t) + I![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0(Δk, t) ± Ic(Δk, t)), 0(Δk, t) ± Ic(Δk, t)), | (72) |
where
| | 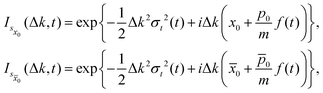 | (73) |
and the cross term
| | 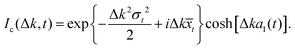 | (74) |
In contrast to distinguishable adsorbates where the intermediate scattering function is given by Ix0(Δk, t) + I![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0(Δk, t), for noninteracting identical adsorbates the cross term (74) takes into account the symmetry of the wave function. From eqn (72), we have that for the ballistic regime Isp,± is no longer a Gaussian function whereas for the Brownian regime the exponential behavior with time is still conserved.
0(Δk, t), for noninteracting identical adsorbates the cross term (74) takes into account the symmetry of the wave function. From eqn (72), we have that for the ballistic regime Isp,± is no longer a Gaussian function whereas for the Brownian regime the exponential behavior with time is still conserved.
In Fig. 7 the initial probability eqn (60) is plotted for distinguishable adsorbates (solid black curve), bosons (blue dashed curve) and fermions (red dotted curve) and for two different initial conditions of the wave packets: (i) different initial positions x0 = 0 and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 14 a.u. with the same initial momenta p0 =
0 = 14 a.u. with the same initial momenta p0 = ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 2 a.u. (left panel), and (ii) different initial momenta p0 = 0.2 a.u. and
0 = 2 a.u. (left panel), and (ii) different initial momenta p0 = 0.2 a.u. and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.3 a.u. with the same initial positions x0 =
0 = 0.3 a.u. with the same initial positions x0 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 0 a.u. (right panel). In both cases, the initial widths of the Gaussian functions are the same, σ0 =
0 = 0 a.u. (right panel). In both cases, the initial widths of the Gaussian functions are the same, σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 2 a.u. The bunching and anti-bunching property of the bosons and fermions are already seen at t = 0, respectively. The distribution is a little bit narrower for the former and the distinguishable distribution is in-between. For fermions, the bimodal character of the initial distribution is kept for both sets of initial conditions. The same behavior is reported elsewhere.51,52
0 = 2 a.u. The bunching and anti-bunching property of the bosons and fermions are already seen at t = 0, respectively. The distribution is a little bit narrower for the former and the distinguishable distribution is in-between. For fermions, the bimodal character of the initial distribution is kept for both sets of initial conditions. The same behavior is reported elsewhere.51,52
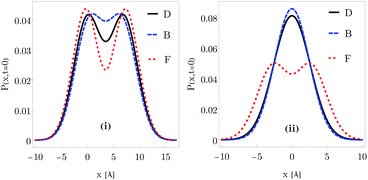 |
| | Fig. 7 Initial spatial probability for a light adsorbate considered to be distinguishable (black solid curve), boson (blue dashed curve) and fermion (red dotted curve). Two different initial conditions of the wave packets are considered: (i) different initial positions x0 = 0 and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 14 a.u. with the same initial momenta p0 = 0 = 14 a.u. with the same initial momenta p0 = ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 2 a.u. (left panel), and (ii) different initial momenta p0 = 0.2 a.u. and 0 = 2 a.u. (left panel), and (ii) different initial momenta p0 = 0.2 a.u. and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.3 a.u. with the same initial positions x0 = 0 = 0.3 a.u. with the same initial positions x0 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 0 a.u. (right panel). In both cases, the initial widths of the Gaussian functions are the same, σ0 = 0 = 0 a.u. (right panel). In both cases, the initial widths of the Gaussian functions are the same, σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u. 0 = 5.2 a.u. | |
In Fig. 8, the ISF for a light adsorbate considered to be distinguishable (black solid curves), boson (blue dashed curves) and fermion (red dotted curves) with a friction coefficient 0.25 ps−1, momentum transfer Δk = 0.12 Å−1 and surface temperature T = 105 K. In the four panels several initial conditions are considered: (a) x0 = 0, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 14 a.u., p0 =
0 = 14 a.u., p0 = ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.2 a.u., and σ0 =
0 = 0.2 a.u., and σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u.; (b) same as (a) but σ0 =
0 = 5.2 a.u.; (b) same as (a) but σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 4.8 a.u.; (c) x0 =
0 = 4.8 a.u.; (c) x0 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 0, p0 = 0.2 a.u.,
0 = 0, p0 = 0.2 a.u., ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.3 a.u. and σ0 =
0 = 0.3 a.u. and σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u. and (d) same as (c) but σ0 =
0 = 5.2 a.u. and (d) same as (c) but σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 4.8 a.u. Several interesting features are worth discussing. First, it is clear that unlike the black curve (distinguishable adsorbates), the ISF for fermions, for the ballistic regime, is no longer a Gaussian function. Second, in the Brownian or diffusion regime, the symmetry of the wave function is not robust enough to distinguish bosons and fermions since adsorbates tend to the same asymptotic exponential function. Third, the initial width makes the difference between the symmetry of the wave function more pronounced in the intermediate time region. And fourth, it should be possible to observe these differences in an experiment where the fermions decay slower than bosons in panels (c) and (d) (and bosons decay quite similar to distinguishable adsorbates); in other words, the decoherence process is much more gradual for fermions than bosons for certain initial widths.
0 = 4.8 a.u. Several interesting features are worth discussing. First, it is clear that unlike the black curve (distinguishable adsorbates), the ISF for fermions, for the ballistic regime, is no longer a Gaussian function. Second, in the Brownian or diffusion regime, the symmetry of the wave function is not robust enough to distinguish bosons and fermions since adsorbates tend to the same asymptotic exponential function. Third, the initial width makes the difference between the symmetry of the wave function more pronounced in the intermediate time region. And fourth, it should be possible to observe these differences in an experiment where the fermions decay slower than bosons in panels (c) and (d) (and bosons decay quite similar to distinguishable adsorbates); in other words, the decoherence process is much more gradual for fermions than bosons for certain initial widths.
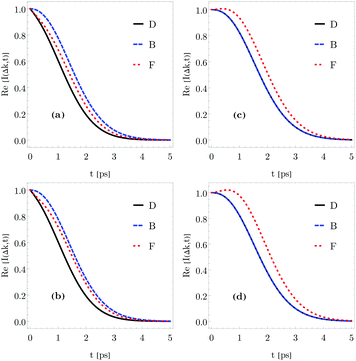 |
| | Fig. 8 Intermediate scattering function for a light adsorbate considered to be distinguishable (black solid curves), boson (blue dashed curves) and fermion (red dotted curves) with a friction coefficient 0.25 ps−1, momentum transfer Δk = 0.12 Å−1 and surface temperature T = 105 K. Panels: (a) x0 = 0, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 14 a.u., p0 = 0 = 14 a.u., p0 = ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.2 a.u., and σ0 = 0 = 0.2 a.u., and σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u.; (b) same as (a) but σ0 = 0 = 5.2 a.u.; (b) same as (a) but σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 4.8 a.u.; (c) x0 = 0 = 4.8 a.u.; (c) x0 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 0, p0 = 0.2 a.u., 0 = 0, p0 = 0.2 a.u., ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.3 a.u. and σ0 = 0 = 0.3 a.u. and σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u. and (d) same as (c) but σ0 = 0 = 5.2 a.u. and (d) same as (c) but σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 4.8 a.u. 0 = 4.8 a.u. | |
5 The Îto stochastic differential equation
The dynamics of an open quantum systems so far discussed has been based on the CL or reduced density matrix formalism which is valid for weak coupling and at high temperatures. In the density matrix formalism, the Liouville functional ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) governing the dissipative evolution of the reduced density matrix ρ
governing the dissipative evolution of the reduced density matrix ρ| | 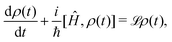 | (75) |
where Ĥ is the Hamiltonian of the system.
As demonstrated in a number of works,53,54 the Caldeira–Leggett master eqn (7) does not preserve the positivity of ρ(t). Derivation of master equations from microscopic Hamiltonians preserving the positivity of the density matrix is a fundamental problem in previous works.20,55
The Lindblad theory of quantum dynamical semigroups20 together with Kossakowski et al.21 showed that the generator for a completely positive map should be
| | 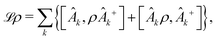 | (76) |
where
Âk are known as Lindblad dissipation operators. The structure of these operators
Âk are unknown and does not generally assure equilibrium between the system and the bath.
One might ask the question of whether the CL eqn (7) can be brought into Lindblad form. The answer is positive since it can be written in Lindblad form by just adding an additional term which is small in the high temperature limit.
Rewriting CL master eqn (7) in the operator form,
| | 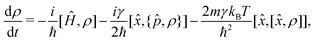 | (77) |
employing the minimal invasive modification, an additional term of the form
γ[
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif)
, [
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif)
,
ρ]]/8
mkBT can be added to the master
eqn (77)| | 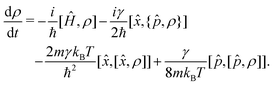 | (78) |
One can associate the CL equation with the Lindblad form if one Lindblad operator  given by a linear combination of the position ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and momentum
and momentum ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) operators is taken
operators is taken
| | Â = μ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + iν + iν![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , Â+ = μ , Â+ = μ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) − iν − iν![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , , | (79) |
where the coefficients
μ and
ν are parameters to be determined below. Replacing the generator
(76) and the Lindblad operator
(79) in the Liouville
eqn (75), a Markovian master equation is obtained
| | 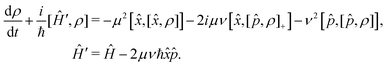 | (80) |
In the coordinate space, the master
eqn (80) takes the following form
| | 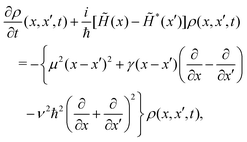 | (81) |
where
| | 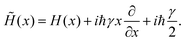 | (82) |
While the master equation can be directly solved in a double-space (two-dimensional) representation
(81), it can also be solved by using a set of stochastic wave functions {|
ψ〉}, where each function obeys the following differential equation
| | 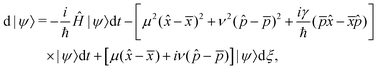 | (83) |
where
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
= 〈
ψ|
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
|
ψ〉,
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif)
= 〈
ψ|
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif)
|
ψ〉 and d
ξ are complex stochastic variables fulfilling the properties of a Wiener process:
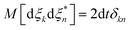
,
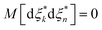
and
M[d
ξkd
ξn] = 0
56 (see Appendix E).
This formulation has been used in previous works23,55 for describing the dynamics of adsorbates on metal surfaces with some constraints.
6 Numerical results
The stochastic wave functions ψi(x, t) are obtained by solving numerically the Îto stochastic differential eqn (83). By using the variant described in ref. 57, the split operator method has been used to solve (83). The terms with only ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) or
or ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) are propagated in the coordinate or momentum space, respectively. In correspondence with previous works,22 the temperature has been incorporated in the system dynamics through the Lindblad operator coefficients
are propagated in the coordinate or momentum space, respectively. In correspondence with previous works,22 the temperature has been incorporated in the system dynamics through the Lindblad operator coefficients 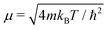 and
and 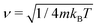 .
.
The initial wave function is a Gaussian wave packet is chosen to be
| | 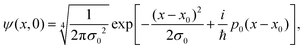 | (84) |
where the initial position is chosen to be
x0 = 0, initial width
σ0 = 0.1 a.u., momentum
p0 is distributed according to the Maxwell–Boltzmann distribution
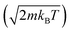
for a given temperature
T and an adsorbate with mass
m.
The numerical stochastic wave function ψ (x, t) is evaluated in equally spaced points belonging to the interval [x1, xNs], with Ns being a power of 2 in order to use the fast Fourier transform and for a number of realizations N. At each time t, the discrete wave function is represented by
| | | ψ(x, t) ≡ {ψ(x1, t);ψ(x2, t);ψ(x3, t);…;ψ(xNs, t)}. | (85) |
The discrete wave function normalization is calculated as
| | 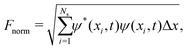 | (86) |
where Δ
x is the length between two consecutive points of the grid. The normalized stochastic wave function is then
| | 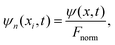 | (87) |
and the mean value of any operator
Ĉ can be expressed as
| | 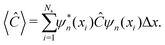 | (88) |
The numerical code was parallelized to solve N times the stochastic differential eqn (83). The number of realization is chosen in order to reach the numerical stability for the mean value of each observable. The unidimensional space x is chosen to be in the interval x ∈ [xi, xf], where xi = −120 Å and xf = 120 Å and the number of points Ns = 4096. The increment Δx can be calculated from Δx = (xf − xi)/Ns and by using these parameters, Δx = 0.05 Å.
The parameters that describe the simulation of the system were selected by taking into account the results presented elsewhere.58 For this goal, the temporal integration step is Δt = 66.1462 a.u.= 1.6 fs, γ = γ0/2m with γ0 = 5 × 10−2 ps−1 and the temperature T = 121 K.
6.1 Flat surface
It is important to analyze how the width of the wave packet σt changes with time. By fitting every 10 ps the stochastic wave function ψ(x, t) to a Gaussian wave packet, exp{−(x − xt)2/(2σt2)}, the width values σt in this time interval can be extracted as seen in Table 1. In the first column, the analytical values are reported whereas in the second and third columns the width values are listed for N = 3200 and N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. This comparison shows the importance of the statistics in this type of simulations. The temperature dependence of the coefficients μ and ν fulfill the condition reported in ref. 55. In Fig. 9–11 the time dependence of the wave packet widths up to 50 ps are displayed for different surface temperatures, frictions and adsorbate masses, respectively. The numerical (points) and analytical (solid curves) results are shown in each plot. In Fig. 9, the friction is given by γ = γ0/2m where γ0 = 5 × 10−2 ps−1 with different values of T and initial widths σ0 for Xe adsorbates: T = 170 K and σ = 0.08 a.u. (black line), T = 121 K and σ = 0.1 a.u. (red line) and T = 70 K and σ = 0.14 a.u. (blue line).
000. This comparison shows the importance of the statistics in this type of simulations. The temperature dependence of the coefficients μ and ν fulfill the condition reported in ref. 55. In Fig. 9–11 the time dependence of the wave packet widths up to 50 ps are displayed for different surface temperatures, frictions and adsorbate masses, respectively. The numerical (points) and analytical (solid curves) results are shown in each plot. In Fig. 9, the friction is given by γ = γ0/2m where γ0 = 5 × 10−2 ps−1 with different values of T and initial widths σ0 for Xe adsorbates: T = 170 K and σ = 0.08 a.u. (black line), T = 121 K and σ = 0.1 a.u. (red line) and T = 70 K and σ = 0.14 a.u. (blue line).
Table 1 Comparison between the numerical and analytic width for the dynamics of a Xe adsorbate after a time of 50 ps, a Gaussian initial wave packet with width σ0 = 0.1 a.u., friction γ = γ0/2m, where γ0 = 5 × 10−2 ps−1 and surface temperature T = 121 K
|
σ
0 = 0.049 Å |
σ
0 = 0.049 Å |
σ
0 = 0.049 Å |
| Analytic50 |
N = 3200 |
N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 0.858 |
0.858 |
0.858 |
| 0.062 |
0.061 |
0.061 |
| 0.046 |
0.045 |
0.046 |
| 0,039 |
0.039 |
0.039 |
| 0.035 |
0.034 |
0.035 |
| 0.033 |
0.031 |
0.032 |
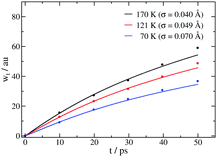 |
| | Fig. 9 Time dependence of the wave packet width for different temperatures and widths σ for Xe adsorbates up to 50 ps with friction γ = γ0/2m, where γ0 = 5 × 10−2 ps−1. The numerical and analytic results are shown by points and solid curves, respectively: T = 170 K and σ = 0.08 a.u. (black line), T = 121 K and σ = 0.1 a.u. (red line) and T = 70 K and σ = 0.14 a.u. (blue line). | |
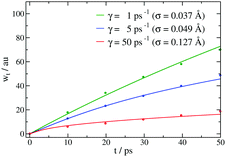 |
| | Fig. 10 Time dependence of the wave packet width for Xe adsorbates and different values of γ and σ up to 50 ps. The surface temperature is T = 121 K. The numerical and analytic results are shown by points and solid curves: γ = 1 ps−1 and σ = 0.7 a.u. (green line), γ = 5 ps−1 and σ = 0.1 a.u. (blue line) and γ = 50 ps−1 and σ = 0.25 a.u. (red line). | |
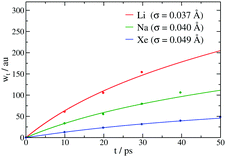 |
| | Fig. 11 Time dependence of the wave packet width for three different adsorbates Xe, Li and Na and different values of σ with the same friction coefficient γ = γ0/2m, where γ0 = 5 × 10−2 ps−1 and temperature T = 121 K after a time of 50 ps. The numerical and analytic results are shown by points and solid curves: γ = 50 ps−1 and σ = 0.07 a.u. (red line), γ = 1 ps−1 and σ = 0.08 a.u. (green line) and γ = 5 ps−1 and σ = 0.1 a.u. (blue line). | |
In Fig. 10, the analysis is carried out for Xe adsorbates and T = 121 K with different values of γ and initial widths. And in Fig. 11 different adsorbates such Xe, Na and Li and different values of σ0 with the same friction coefficient and surface temperature T = 121 K are plotted. As expected, with temperature, larger value of the wave function widths are obtained. With friction and mass, the corresponding widths reach an asymptotic value at short times. In all of cases studied, the agreement between numerical and analytical results is fairly good indicating that the number of realizations used is good enough to obtain reliable results (in fact, with 2000–4000 realizations the numerical stability is reached).
6.2 Corrugated surface
In order to know how works the stochastic wave function method (83) for more realistic systems, several numerical calculations are compared with previous Langevin simulations and experimental results from Ellis et al.41
The potential energy surface is obtained from the pairwise additive potential approximation between the Xe and a square network of Pt atoms with a distance equal to the unit cell length a = 3.93 Å.23 The metal surface is considered to be large enough so that the boundary effects do not influence the interaction potential. For this goal, the number of unit cells Nc of the surface in the XY plane is increased until the variation in the potential is as small as a given threshold, say 10−3 meV. A cosine corrugation function is assumed to represent the potential energy surface of the Xe–Pt(111) system given by 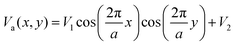 , where V1 = −13.64 meV and V2 = −12.32 meV. These values are obtained by fitting the cosine function to the numerical result of the potential energy surface. Both interaction potentials are very similar because its amplitude is around −28 meV and the periodicity match with the unit cell length of the Pt in both cases. The unidimensional corrugated potential used in the simulations is
, where V1 = −13.64 meV and V2 = −12.32 meV. These values are obtained by fitting the cosine function to the numerical result of the potential energy surface. Both interaction potentials are very similar because its amplitude is around −28 meV and the periodicity match with the unit cell length of the Pt in both cases. The unidimensional corrugated potential used in the simulations is 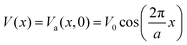 . The amplitude V0 is taken so that the energy barrier for this potential (Eb = V0) coincides with the Langevin molecular simulations.41 The diffusion of the Xe adsorbate on the metal surface of Pt is studied along the (100) direction.
. The amplitude V0 is taken so that the energy barrier for this potential (Eb = V0) coincides with the Langevin molecular simulations.41 The diffusion of the Xe adsorbate on the metal surface of Pt is studied along the (100) direction.
First, in the ballistic regime, the broadening (Γ) is analyzed in terms of the surface parallel momentum transfer Δk. In this regime, the ISF is a Gaussian function and has been fitted to exp(−t2/2σt). As we have seen previously,
| | 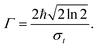 | (89) |
For an ideal gas, the width of the Gaussian function is
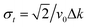
. By using
eqn (89), the quasielastic broadening is
| | 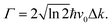 | (90) |
The unidimensional space
x is chosen to be in the interval
x ∈ [−800, 800] Å, the number of points
Ns = 8192, the position step Δ
x = 0.2 Å, the time step Δ
t = 66.1462 a.u. = 1.6 fs and the surface temperature
T = 105 K. The number of realizations is
N = 2000. This comparison is shown in
Fig. 12 for Xe adsorbates on a Pt(111) surface at two different friction coefficients,
γ = 0.25, 2.00 ps
−1. In panel (a) the following results are plotted: numerical simulations (NS) for a flat surface with 0.25 ps
−1 (blue dots) and 2.00 ps
−1 (red dots), Langevin dynamics simulations for 0.25 ps
−1 (orange star), 2.00 ps
−1 (purple star), theoretical results for an ideal gas
(90) (black line) and QHAS experimental results at two incident He beam energies
Ei = 10.15 meV (circles) and
Ei = 26.85 meV (squares). In panel (b), numerical results are plotted for two different potential energy barriers
Eb = 9.6 meV (blue dot) and
Eb = 23.6 meV (red dot) with a friction coefficient of 0.05 ps
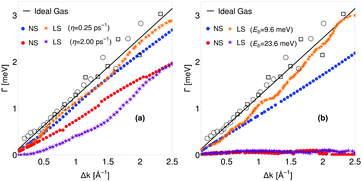
−1. The Langevin simulations are given for orange stars and purple, respectively. Experimental values are the same as before. In general, the overall agreement between our method, Langevin simulations and experimental results is fairly good.
 |
| | Fig. 12
Γ versus Δk for Xe adsorbates on a Pt(111) surface in the ballistic regime. QHAS experimental results at two incident He beam energies Ei = 10.15 meV (circles) and Ei = 26.85 meV (squares) are shown and the ideal gas (black line) given by (90). In panel (a), the following results at two different friction coefficients are plotted: numerical simulations (NS) with 0.25 ps−1 (blue dots), 2.00 ps−1 (red dots); Langevin simulations (LS) for 0.25 ps−1 (orange star) and 2.00 ps−1 (purple star). In panel (b), results for different potential energy barriers are shown: NS with 9.6 meV (blue dot), 23.6 meV (red dot); LS with 9.6 meV (orange star) and 23.6 meV (purple star). | |
Second, the next step for checking our numerical method is within the Brownian regime. For this goal, the ISF I(Δk, t) for the same system with an energy barrier Eb = 23.6 meV, surface temperature T = 105 K and initial velocity v0 = 115 m s−1 is calculated. As has previously seen, in this regime, this function is an exponential function and has been fitted to exp(−αt). In Fig. 13, the decay rate α is plotted versus Δk. The analysis has to be carried out in terms of the so-called Chudley–Elliott model59 which describes this jump diffusion by means of a rate equation according to
| | 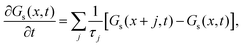 | (91) |
where
τj is the average time between successive jumps over the one-dimensional vector
j and the summation runs over all lattice vectors. In this model, it is assumed that the time for a simple jump is very short compared with the time
τ between successive jumps. Thus, the total jump rate is
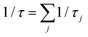
, with
τj =
τ−j. Now, due to the linearity property of the Fourier transform
| | 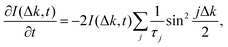 | (92) |
the solution of this first order differential equation being
| | 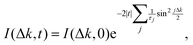 | (93) |
that is, the effect to include a simple Bravais lattice is to add an exponential factor ruling the jumps in the diffusion process. Thus,
| | 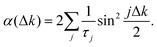 | (94) |
Numerical results are the red dots and
eqn (94) is plotted for
j = ±1 (black curve) and
j = ±6 (blue curve). As expected, at small values of Δ
k, one observes a quadratic behavior. This is well reproduced by considering
j = ±1. At higher values of Δ
k more and more values of
j are needed. This is explained because a very small friction coefficient has been considered.
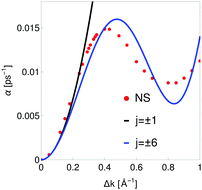 |
| | Fig. 13 The decay rate α versus Δk for the Xe–Pt(111) system is displayed for a corrugated surface with an energy barrier Eb = 23.6 meV, surface temperature T = 105 K and initial adsorbate velocity v0 = 115 m s−1. The corresponding numerical results are analyzed in terms of the so-called Chudley–Elliott model given by eqn (94). Numerical results (red dots) and Chudley–Elliott curves for j = ±1 (black curve) and six j = ±6 (blue curve) are plotted. | |
7 Conclusions
In this work, we have used the CL formalism as well as the stochastic wave function method for the first time in surface diffusion. As has been discussed along this work, the splitting of the G-function in Gs and Gd is no longer valid when considering coherent quantum surface corrugation. In particular, for such a goal, we have analyzed the cat states and identical adsorbates, bosons and fermions. The ISF function is not Gaussian in the ballistic regime but it keeps the exponential decay in the Brownian regime. This study has been carried out first for flat surfaces where analytical results are obtained. The stochastic wave function numerical method has also been used to compare with analytical results. In order to show that this numerical method can be an alternative to Langevin simulations for corrugated surfaces, model calculations have been carried out which have been analyzed in terms of the so-called Chudley–Elliott model. The agreement in all of cases studied here is fairly good. This should serve us to extend this method to different realistic systems such as for example Na–Cu(111) and Li–Cu(111) where available experimental results also exist.42,58,60 Furthermore, it should be very interesting to extend and analyze systems to light adsorbates where surface tunneling is present. The stochastic wave function method should be then modified to consider low surface temperatures. Work in this this direction is now in progress.
Author contributions
All authors have contributed equally to this work.
Conflicts of interest
There are no conflicts to declare.
Appendix A: Gaussian ansatz coefficients for one particle
From the initial wave packet (9), the initial density matrix can be extracted| | 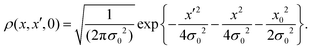 | (95) |
If one replacing the Gaussian ansatz (12) into the master eqn (7), a system of differential equations for the coefficients A(t), B(t), C(t), D(t), E(t) and N(t) we have that| | 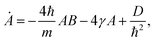 | (96) |
| | 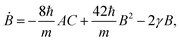 | (97) |
| | 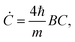 | (98) |
| | 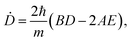 | (99) |
| | 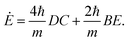 | (100) |
From the initial density matrix (95), the initial conditions for the coefficients can be extracted| | 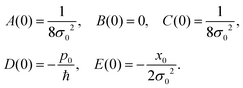 | (101) |
With the initial conditions (101), the solutions of the differential equations for the coefficients (96) are| |  | (102) |
Appendix B: Wigner representation
This representation is often used as an alternative to the density matrix for systems described by a continuous degree of freedom. This alternative way of the reduced density matrix used by Unruh and Zurek61 allows us to carry out this analysis in the (k, Δ) space. In this representation, the reduced density matrix is the characteristic function associated with the Wigner function62,63 and is defined by| | ρ(k, Δ) = Tr{ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i(kx + Δp/ħ)}, i(kx + Δp/ħ)}, | (103) |
where the Wigner function is given by| | 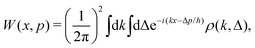 | (104) |
and both representations are connected through a Fourier transform according to| | 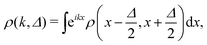 | (105) |
where Δ = x − x′ measures the distance from the diagonal in positions and 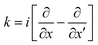 is the wave number in the direction parallel to the diagonal64. The CL master eqn (7) is then written as
is the wave number in the direction parallel to the diagonal64. The CL master eqn (7) is then written as| | 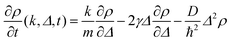 | (106) |
whose solution is| | | ρ(k, Δ, t) = exp{−c1(t)k2 − c2(t)kΔ − c3(t)Δ2 − ic4(t)k − ic5(t)Δ − c6(t)}. | (107) |
A system of linear differential equations for the coefficients ci(t) is obtained by substituting eqn (107) into eqn (106)
| | 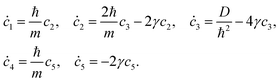 | (108) |
The initial conditions for this coefficients can be extracted from the Fourier transform of the density matrix for the initial wave packet
(9) written in the center of mass and relative coordinates
| | 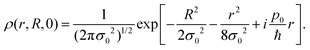 | (109) |
By carrying out the space Fourier transform of both argument
r and
R to the variables
Δ and
k| | 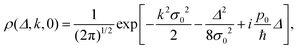 | (110) |
and comparing
(110) with the density matrix
(107) the following initial conditions for the coefficients
ci(
t) are
| | 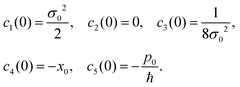 | (111) |
From
eqn (111), the solution of the differential
eqn (108) are
| | 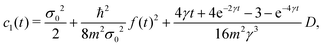 | (112) |
| | 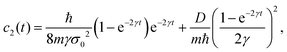 | (113) |
| | 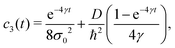 | (114) |
| | 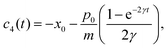 | (115) |
| | 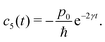 | (116) |
The coefficients
c1,
c2,
c3,
c4,
c5 and
c6 are related to the coefficients of
eqn (12) through
| | 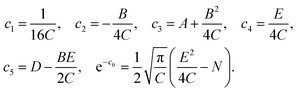 | (117) |
Appendix C: limit cases for the characteristic magnitudes in decoherence dynamics
C.1 Coherence length
In the absence of environmental interactions (D = 0 and γ = 0), the coherence length becomes| | 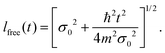 | (118) |
This expression describes the free coherent spread of the wave packet for a free particle. However, the time evolution of the coherence length (25) for times t ≪ γ−1 is| | 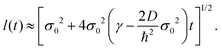 | (119) |
Due to the influence of environmental scattering, at short times, the coherence length has a constant value equal to the initial width σ0 and later on increases linearly with time. At long times t ≫ γ−1, the coherence length has an asymptomatic behavior| | 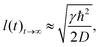 | (120) |
independently on the initial width σ0. This value is inversely proportional to the diffusion coefficient D, which includes the particle mass and temperature (8), and it is directly proportional to the friction coefficient γ.
C.2 Ensemble width
The probability distribution is given by| | 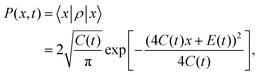 | (121) |
the first two moments being| | 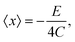 | (122) |
and| | 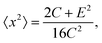 | (123) |
hence the variance in position is entirely given by the function C as| | 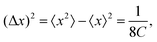 | (124) |
then| | 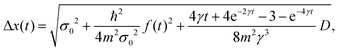 | (125) |
which quantifies the total size of the position-space ensemble. In the absence of any environmental interactions (D = 0 and γ = 0), the free ensemble width is| | 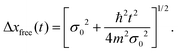 | (126) |
For short times (t ≪ γ−1), the time evolution of the ensemble width (26) is| | 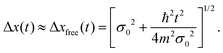 | (127) |
There is no difference between the ensemble width with or without environment. However, at long times t ≫ γ−1, the ensemble width has an asymptomatic behavior| | 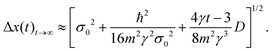 | (128) |
Appendix D: Gaussian ansatz coefficients for Schrödinger cat states
For the initial wave packet (28), the density matrix is given by (29) and can be expressed as a sum of four contributions, since the Markovian master eqn (7) is linear,| | 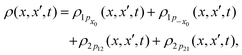 | (129) |
where each term is the solution of (7) for the corresponding initial density matrix.
Using a Gaussian ansatz (32) for each term and inserting (129) into the equation of motion eqn (7), the coupled differential equations for the coefficients Ai(t), Bi(t), Ci(t), Di(t), Ei(t) and Ni(t) with the initial conditions (29) can be solved. The coefficients of each contribution are
| | 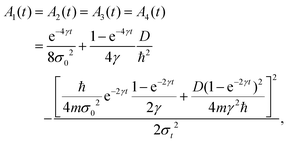 | (130) |
| | 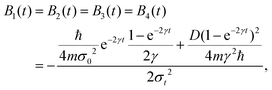 | (131) |
| | 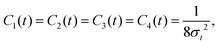 | (132) |
where
i = 1, 2, 3, 4 are the corresponding subscripts 1
px0, 1
p−x0, 2
p12, 2
p21. The coefficients
Ai(
t),
Bi(
t) and
Ci(
t) are the same in the four terms. However, the coefficients
Di(
t) are different
| | 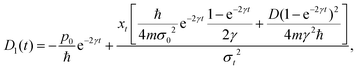 | (133) |
| | 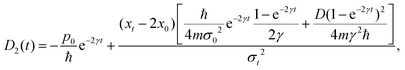 | (134) |
| | 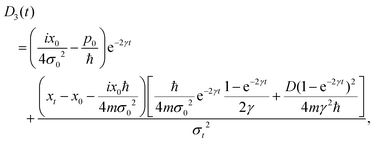 | (135) |
| |  | (136) |
The same happens for the
Ei(
t) coefficients
| | 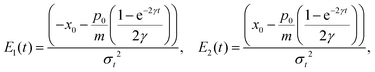 | (137) |
| | 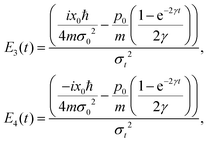 | (138) |
and
Ni(
t):
| | 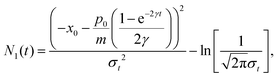 | (139) |
| | 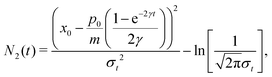 | (140) |
| | 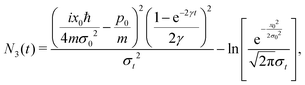 | (141) |
| | 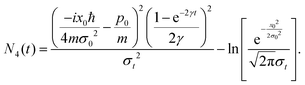 | (142) |
Appendix E: Itô stochastic differential equation
Given a specific base of wave functions, the density matrix can be expressed as a linear combination of normalized wave function |ψ〉 from the base| | 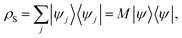 | (143) |
where M represent the average over the number of wave functions in the Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S.
S.
For an open system, the environmental interaction gives a non-deterministic evolution to the system density matrix. The probabilistic nature of the interaction turns the master equation for the density matrix into a stochastic differential equation. After a time dt, the variation of the wave function |dψ〉 is given by
| | 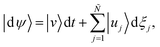 | (144) |
where |
v〉d
t is a diffusive term and |
uj〉d
ξj a stochastic term given by the Wiener independent processes
Ñ.
56 This expression is known as the Itô differential equation. In order to preserve the normalization of the state vector |
ψ〉, it should be orthogonal to the fluctuations |
uj〉
From
eqn (144) and the Wiener properties
| | 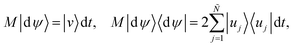 | (146) |
the diffusive and stochastic terms can be found from
(143) to be
| | | dρS = M(|ψ〉〈dψ| + |dψ〉〈ψ| + |dψ〉〈dψ|), | (147) |
and by using
eqn (146), the time evolution of the density matrix is given by
| | 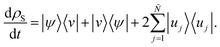 | (148) |
The vector |
uj〉 is the component of
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) S
S in the orthogonal space to |
ψ〉
| | 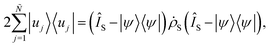 | (149) |
where
ÎS is the identity operator. Now, from
| | ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) S|ψ〉 = |ψ〉〈v|ψ〉 + |v〉, S|ψ〉 = |ψ〉〈v|ψ〉 + |v〉, | (150) |
and applying the scalar product properties
| | 〈ψ|![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) S|ψ〉 = 2 S|ψ〉 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Re〈ψ|v〉, Re〈ψ|v〉, | (151) |
the diffusive term can be written as
| | 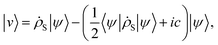 | (152) |
where
ic is an imaginary constant representing a phase change and his value is determined in such a way that, in the absence of interaction with the environment, the Schrödinger equation is recovered.
If the Lindblad master equation22
| | 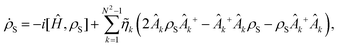 | (153) |
is replaced in
eqn (152), the diffusive term can be obtained
| | 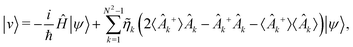 | (154) |
where 〈
Â〉 = 〈
ψ|
Â|
ψ〉 represent the operator average value
 and
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) k
k are non-negative quantities. Once the diffusive term has been found, the stochastic term |
uk〉 of the differential wave function
eqn (144) can be found by replacing
(153) in
(149) and using the scalar product properties, leading to the following expression
| | | |uk〉 = (Âk − 〈Âk〉)|ψ〉. | (155) |
Thus, one has that
| | 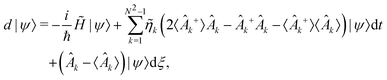 | (156) |
and replacing the Lindblad operator
(79), the time evolution of the state vector |
ψ〉 can be found by solving the stochastic differential
eqn (83), given by a deterministic part and a stochastic term.
Acknowledgements
E. E. T.-M. and S. M. A. would like to thank Fundación Humanismo y Ciencia for financial support and Spanish Project PID2021-125735NB-I00. G. R.-L. and J. R.-S. would also thank the Advanced Computational Team at Higher Institute for Technologies and Applied Sciences (Havana University) for the support provided during the realization of this work and to Project NA223LH-INSTEC-003. Finally, we would like to thank the two anonymous reviewers for very useful comments and suggestions to improve this work.
Notes and references
- L. Van Hove, Correlations in space and time and Born approximation scattering in systems of interacting particles, Phys. Rev., 1954, 95(1), 249 CrossRef CAS.
-
S. W. Lovesey, Theory of neutron scattering from condensed matter, 1984, vol. 2 Search PubMed.
-
D. A. McQuarrie, Statistical Mechanics, 1976 Search PubMed.
- G. H. Vineyard, Scattering of slow neutrons by a liquid, Phys. Rev., 1958, 110(5), 999 CrossRef CAS.
- D. J. Ward, A. Raghavan, A. Tamtögl, A. P. Jardine, E. Bahn, J. Ellis, S. Miret-Artés and W. Allison, Inter-adsorbate forces and coherent scattering in helium spin-echo experiments, Phys. Chem. Chem. Phys., 2021, 23(13), 7799–7805 RSC.
- F. Hofmann and J. P. Peter Toennies, High-resolution helium atom time-of-flight spectroscopy of low-frequency vibrations of adsorbates, Chem. Rev., 1996, 96(4), 1307–1326 CrossRef CAS PubMed , PMID: 11848791.
- A. P. Graham, The low energy dynamics of adsorbates on metal surfaces investigated with helium atom scattering, Surf. Sci. Rep., 2003, 49(4), 115–168 CrossRef CAS.
- I. Calvo-Almazán and P. Fouquet, The application of quasi-elastic neutron scattering techniques (QENS) in surface diffusion studies, Eur. Phys. J. Spec. Top., 2012, 213(4), 149–163 CrossRef.
- A. P. Jardine, G. Alexandrowicz, H. Hedgeland, W. Allison and J. Ellis, Studying the microscopic nature of diffusion with helium-3 spin-echo, Phys. Chem. Chem. Phys., 2009, 11, 3355–3374 RSC.
- A. P. Jardine, H. Hedgeland, G. Alexandrowicz, W. Allison and J. Ellis, Helium-3 spin-echo: Principles and application to dynamics at surfaces, Prog. Surf. Sci., 2009, 84(11), 323–379 CrossRef CAS.
- S. Miret-Artés and E. Pollak, The dynamics of activated surface diffusion, J. Phys.: Condens. Matter, 2005, 17(49), S4133–S4150 CrossRef.
- J. L. Vega, R. Guantes and S. Miret-Artés, Quasielastic and low vibrational lineshapes in atom–surface diffusion, J. Phys.: Condens. Matter, 2004, 16(29), S2879–S2894 CrossRef CAS.
- P. S. M. Townsend and D. J. Ward, The intermediate scattering function for quasi-elastic scattering in the presence of memory friction, J. Phys. Commun., 2018, 2(7), 075011 CrossRef.
- R. Martínez-Casado, J. L. Vega, A. S. Sanz and S. Miret-Artés, Line shape broadening in surface diffusion of interacting adsorbates with quasielastic He atom scattering, Phys. Rev. Lett., 2007, 98, 216102 CrossRef PubMed.
- R. Martínez-Casado, J. L. Vega, A. S. Sanz and S. Miret-Artés, Surface diffusion and low vibrational motion with interacting adsorbates: A shot noise description, Phys. Rev. E, 2007, 75, 051128 CrossRef PubMed.
- D. J. Ward, A. Raghavan, A. Tamtögl, A. P. Jardine, E. Bahn, J. Ellis, S. Miret-Artés and W. Allison, Inter-adsorbate forces and coherent scattering in helium spin-echo experiments, Phys. Chem. Chem. Phys., 2021, 23, 7799–7805 RSC.
- R. Martínez-Casado, A. S. Sanz, J. L. Vega, G. Rojas-Lorenzo and S. Miret-Artés, Linear response theory of activated surface diffusion with interacting adsorbates, Chem. Phys., 2010, 370(1), 180–193 CrossRef.
- S. Miret-Artés, Quantum surface diffusion in Bohmian mechanics, J. Phys. Commun., 2018, 2(9), 095020 CrossRef.
- A. O. Caldeira and A. J. Leggett, Path integral approach to quantum Brownian motion, Phys. A, 1983, 121, 374 CrossRef.
- G. Lindblad, On the generators of quantum dynamical semigroups, Commun. Math. Phys., 1976, 48(2), 119–130 CrossRef.
- A. Kossakowski, On quantum statistical mechanics of non-Hamiltonian systems, Rep. Math. Phys., 1972, 3, 247 CrossRef.
-
H. P. Breuer and F. Petruccione, The theory of open quantum systems, 2002 Search PubMed.
- E. E. Torres-Miyares, G. Rojas-Lorenzo, J. Rubayo-Soneira and S. Miret-Artés, Surface diffusion by means of stochastic wave functions. The ballistic regime, Mathematics, 2021, 9(4), 362 CrossRef.
-
C. W. Gardiner and P. Zoeller, Quantum noise, Berlin, Heidelberg, New York, 1991 Search PubMed.
- A. O. Caldeira and A. J. Leggett, Influence of dissipation on quantum tunneling in macroscopic systems, Phys. Rev. Lett., 1981, 46(4), 211 CrossRef.
-
C. Chan, Theory and application of open quantum systems, 2012 Search PubMed.
-
S. F. Huelga, et al., Open quantum systems: An introduction, 2012 Search PubMed.
- H. Grabert, P. Schramm and G. L. Ingold, Quantum Brownian motion: The functional integral approach, Phys. Rep., 1988, 168(3), 115 CrossRef CAS.
- D. Suess, A. Eisfeld and W. T. Strunz, Hierarchy of stochastic pure states for open quantum system dynamics, Phys. Rev. Lett., 2014, 113(15), 150403 CrossRef CAS PubMed.
- Y. Yan, F. Yang, Y. Liu and J. Shao, Hierarchical approach based on stochastic decoupling to dissipative systems, Chem. Phys. Lett., 2004, 395(4-6), 216–221 CrossRef CAS.
- M. A. Lane, D. Matos, I. J. Ford and L. Kantorovich, Exactly thermalized quantum dynamics of the spin-boson model coupled to a dissipative environment, Phys. Rev. B, 2020, 101(22), 224306 CrossRef CAS.
- R. Feynman, R. B. Leighton and M. Sands, The Brownian movement, Feynman Lect. Phys., 1964, 1, 41 Search PubMed.
- A. O. Caldeira and A. J. Leggett, Quantum tunneling in a dissipative system, Ann. Phys., 1983, 149(2), 374 Search PubMed.
-
U. Weiss, Quantum Dissipative Systems, World Scientific Publishing, Singapore, 2nd edn, 1999 Search PubMed.
-
M. A. Schlosshauer, Decoherence and the quantum-to-classical transition, 2007 Search PubMed.
- V. I. Tatarskiĭ, The Wigner representation of quantum mechanics, Soviet Physics Uspekhi, 1983, 26(4), 311 CrossRef.
- G. W. Ford, J. T. Lewis and R. F. O'Connell, Quantum measurement and decoherence, Phys. Rev. A, 2001, 64, 032101 CrossRef.
- G. W. Ford and R. F. O'Connell, Decoherence at zero temperature, J. Opt. B: Quantum Semiclassical Opt., 2003, 5(6), S609–S612 CrossRef.
- H. C. Peñate-Rodríguez, R. Martínez-Casado, G. Rojas-Lorenzo, A. S. Sanz and S. Miret-Artés, Quantum zeno and anti-zeno effects in surface diffusion of interacting adsorbates, J. Phys.: Condens. Matter, 2012, 24(10), 104013 CrossRef PubMed.
-
D. J. Ward, A study of spin-echo lineshapes in helium atom scattering from adsorbates, 2013 Search PubMed.
- J. Ellis, A. P. Graham and J. P. Toennies, Quasielastic helium atom scattering from a two-dimensional gas of Xe atoms on Pt(111), Phys. Rev. Lett., 1999, 82(25), 5072 CrossRef CAS.
- R. Martínez-Casado, J. L. Vega, A. S. Sanz and S. Miret-Artés, Quasielastic He atom scattering from surfaces: A stochastic description of the dynamics of interacting adsorbates, J. Phys.: Condens. Matter, 2007, 19(30), 305002 CrossRef.
- E. Joos and H. D. Zeh, The emergence of classical properties through interaction with the environment, Z. Phys. B: Condens. Matter, 1985, 59(2), 223–243 CrossRef.
- S. V. Mousavi and S. Miret-Artés, On some unexplored decoherence aspects in the Caldeira-Leggett formalism: arrival time distributions, identical particles and diffraction in time, Eur. Phys. J. Plus, 2022, 137, 1–14 CrossRef PubMed.
- W. H. Zurek, S. Habib and J. P. Paz, Coherent states via decoherence, Phys. Rev. Lett., 1993, 70(9), 1187 CrossRef PubMed.
- T. Qureshi and A. Venugopalan, Decoherence and matter wave interferometry, Int. J. Mod. Phys. B, 2008, 22(08), 981–990 CrossRef.
- W. H. Zurek, Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse?, Phys. Rev. D, 1981, 24(6), 1516 CrossRef.
- W. H. Zurek, Environment-induced superselection rules, Phys. Rev. D, 1982, 26(8), 1862 CrossRef.
-
S. Treiman, The odd quantum, in The Odd Quantum, Princeton University Press, 2002 Search PubMed.
- S. V. Mousavi and S. Miret-Artés, Dissipative quantum backflow, Eur. Phys. J. Plus, 2020, 135(3), 1–18 Search PubMed.
- S. V. Mousavi and S. Miret-Artés, Quantum-classical comparison: arrival times and statistics, Phys. Scr., 2015, 90(2), 025001 CrossRef.
- S. Miret-Artés, R. S. Dumont, T. Rivlin and E. Pollak, The influence of the symmetry of identical particles on flight times, Entropy, 2021, 23(12), 1675 CrossRef PubMed.
- V. Ambegaokar, Quantum Brownian motion and its classical limit, Ber. Bunseng. Phys. Chem., 1991, 95(3), 400–404 CrossRef CAS.
- A. Tameshtit and J. E. Sipe, Positive quantum Brownian evolution, Phys. Rev. Lett., 1996, 77(13), 2600 CrossRef CAS PubMed.
- S. Gao, Lindblad approach to quantum dynamics of open systems, Phys. Rev. B, 1998, 57(8), 4509 CrossRef CAS.
-
R. Durrett, Probability: theory and examples, 2019, vol. 49 Search PubMed.
- J. Halliwell and A. Zoupas, Quantum state diffusion, density matrix diagonalization, and decoherent histories: A model, Phys. Rev. D, 1995, 52(12), 7294 CrossRef CAS PubMed.
-
D. J. Ward, A study of spin-echo lineshapes in helium atom scattering from adsorbates, 2013 Search PubMed.
- R. J. Elliot and C. T. Chudley, Neutron scattering from a liquid on a jump diffusion model, Proc. Phys. Soc., 1961, 77(2), 353 CrossRef.
- J. G. Mantecón, S. Miret-Artés and G. Rojas-Lorenzo, Diffusion of Ar atoms on MgO(100) surfaces, Revista Cubana de Física, 2012, 29(1), 8–13 Search PubMed.
- W. G. Unruh and W. H. Zurek, Reduction of a wave packet in quantum Brownian motion, Phys. Rev. D, 1989, 40(4), 1071 CrossRef PubMed.
- M. Hillery, R. F. O'Connell, M. O. Scully and E. P. Wigner, Distribution functions in physics: Fundamentals, Phys. Rep., 1984, 106(3), 121–167 CrossRef.
- C. M. Savage and D. F. Walls, Damping of quantum coherence: the master-equation approach, Phys. Rev. A, 1985, 32(4), 2316 CrossRef PubMed.
-
E. Joos, H. D. Zeh, C. Kiefer, D. J. W. Giulini, J. Kupsch and I. O. Stamatescu, Decoherence and the appearance of a classical world in quantum theory, 2013 Search PubMed.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
G.
Rojas-Lorenzo
*a,
G.
Rojas-Lorenzo
 b,
J.
Rubayo-Soneira
b,
J.
Rubayo-Soneira
 b and
S.
Miret-Artés
b and
S.
Miret-Artés
 a
a
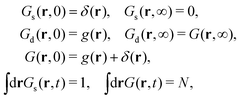
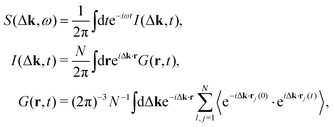
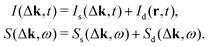
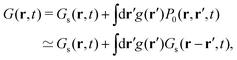
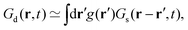
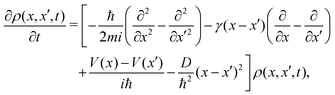
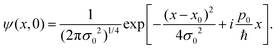
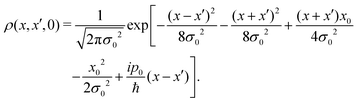
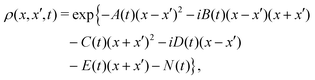
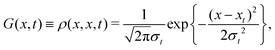
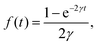
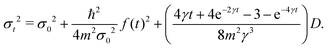
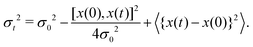
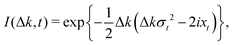
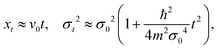
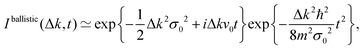
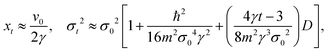
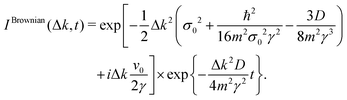
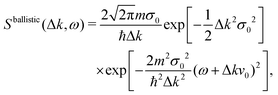
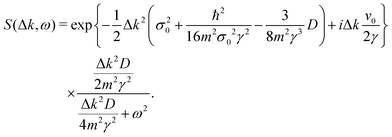

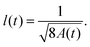

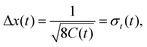

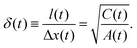

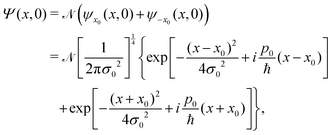
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) is the normalization constant. From eqn (28), the corresponding initial reduced density matrix is given by
is the normalization constant. From eqn (28), the corresponding initial reduced density matrix is given by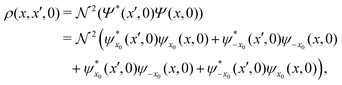
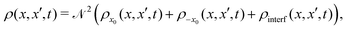
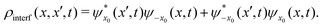
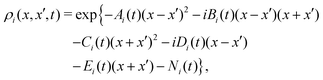
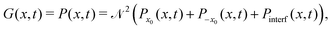
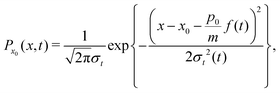
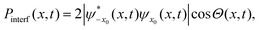
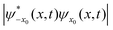 is the modulus of ρinterf(x, x, t) and Θ(x, t) its phase. Eqn (33) can be expressed as the typical interference pattern expression according to44
is the modulus of ρinterf(x, x, t) and Θ(x, t) its phase. Eqn (33) can be expressed as the typical interference pattern expression according to44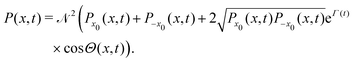
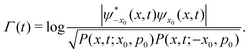
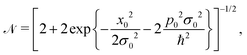
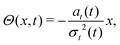
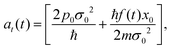
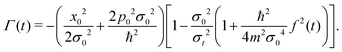
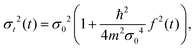
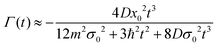
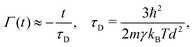
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2(I(Δk,t) + Iinter(Δk,t)),
2(I(Δk,t) + Iinter(Δk,t)),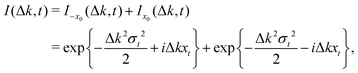
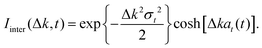
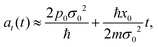
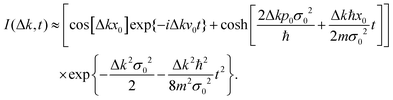
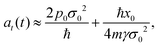
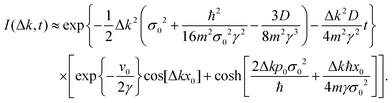
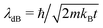 . With increasing mass, the decoherence time scale is much smaller than the relaxation time scale required to reach thermal equilibrium. It becomes more difficult to observe interference patterns for massive particles and therefore the creation of a spatial superposition.47,48
. With increasing mass, the decoherence time scale is much smaller than the relaxation time scale required to reach thermal equilibrium. It becomes more difficult to observe interference patterns for massive particles and therefore the creation of a spatial superposition.47,48![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = −p0 = 0.01 a.u., a friction coefficient γ = 0.25 ps−1, a momentum transfer Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The insets show the interference term (47) together with the ISF (46) with a (dashed red line) and a (dotted purple line), respectively. The interference term breaks the ballistic behavior of the system. As expected, when the temperature increases, the ISF decreases faster leading to the typical exponential behavior with time.
0 = −p0 = 0.01 a.u., a friction coefficient γ = 0.25 ps−1, a momentum transfer Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The insets show the interference term (47) together with the ISF (46) with a (dashed red line) and a (dotted purple line), respectively. The interference term breaks the ballistic behavior of the system. As expected, when the temperature increases, the ISF decreases faster leading to the typical exponential behavior with time.
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = −p0 = 0.01 a.u. for a friction coefficient γ = 0.25 ps−1, a momentum transference Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The inside panel shows the interference term (47) and the self intermediate scattering function (46) with a (dashed red line) and a (dotted purple line) respectively and the (blue solid line) the intermediate scattering function (45).
0 = −p0 = 0.01 a.u. for a friction coefficient γ = 0.25 ps−1, a momentum transference Δk = 0.12 Å−1 and two values of temperature: T = 10 K (left panel) and T = 100 K (right panel). The inside panel shows the interference term (47) and the self intermediate scattering function (46) with a (dashed red line) and a (dotted purple line) respectively and the (blue solid line) the intermediate scattering function (45).![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±{ψ(x1,0)ϕ(x2,0) ± ϕ(x1,0)ψ(x2,0)},
±{ψ(x1,0)ϕ(x2,0) ± ϕ(x1,0)ψ(x2,0)},![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0,
0, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0,
0, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0, respectively. Under the Caldeira–Leggett eqn (7), the evolution of the two-particle system is given by
0, respectively. Under the Caldeira–Leggett eqn (7), the evolution of the two-particle system is given by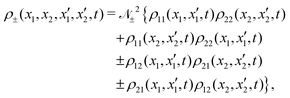
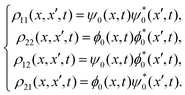
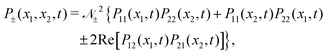
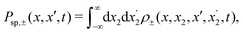
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±2{P11(x, t) + P22(x, t) ± 2Re[P12(x, t)s(t)]},
±2{P11(x, t) + P22(x, t) ± 2Re[P12(x, t)s(t)]},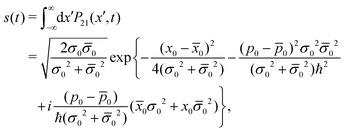
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±
±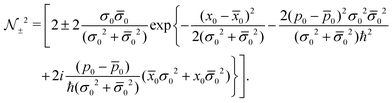
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±2{P11(x, t) + P22(x, t) ± 2|P12(x, t)s(t)|cos
±2{P11(x, t) + P22(x, t) ± 2|P12(x, t)s(t)|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ(x, t)},
Θ(x, t)},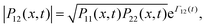
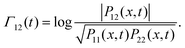
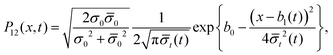
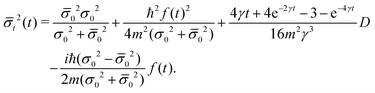
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = σ0, the width is b2(t) = σt/2 and the explicit formula for the phase Θ(x, t) is
0 = σ0, the width is b2(t) = σt/2 and the explicit formula for the phase Θ(x, t) is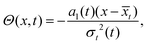
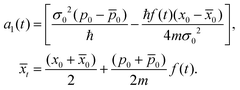
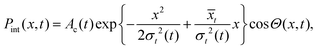
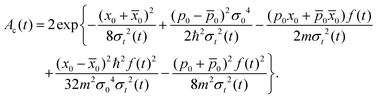
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = x0, the probabilities P11(x, t) and P22(x, t) are given by (34) for the momentum p0 and
0 = x0, the probabilities P11(x, t) and P22(x, t) are given by (34) for the momentum p0 and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0, respectively. In this case, from eqn (62), one obtains the decoherence function
0, respectively. In this case, from eqn (62), one obtains the decoherence function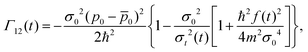
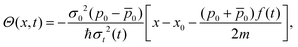
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ±2(Ix0(Δk, t) + I
±2(Ix0(Δk, t) + I![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0(Δk, t) ± Ic(Δk, t)),
0(Δk, t) ± Ic(Δk, t)),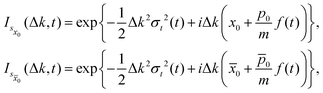
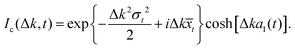
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0(Δk, t), for noninteracting identical adsorbates the cross term (74) takes into account the symmetry of the wave function. From eqn (72), we have that for the ballistic regime Isp,± is no longer a Gaussian function whereas for the Brownian regime the exponential behavior with time is still conserved.
0(Δk, t), for noninteracting identical adsorbates the cross term (74) takes into account the symmetry of the wave function. From eqn (72), we have that for the ballistic regime Isp,± is no longer a Gaussian function whereas for the Brownian regime the exponential behavior with time is still conserved.![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 14 a.u. with the same initial momenta p0 =
0 = 14 a.u. with the same initial momenta p0 = ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 2 a.u. (left panel), and (ii) different initial momenta p0 = 0.2 a.u. and
0 = 2 a.u. (left panel), and (ii) different initial momenta p0 = 0.2 a.u. and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.3 a.u. with the same initial positions x0 =
0 = 0.3 a.u. with the same initial positions x0 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 0 a.u. (right panel). In both cases, the initial widths of the Gaussian functions are the same, σ0 =
0 = 0 a.u. (right panel). In both cases, the initial widths of the Gaussian functions are the same, σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 2 a.u. The bunching and anti-bunching property of the bosons and fermions are already seen at t = 0, respectively. The distribution is a little bit narrower for the former and the distinguishable distribution is in-between. For fermions, the bimodal character of the initial distribution is kept for both sets of initial conditions. The same behavior is reported elsewhere.51,52
0 = 2 a.u. The bunching and anti-bunching property of the bosons and fermions are already seen at t = 0, respectively. The distribution is a little bit narrower for the former and the distinguishable distribution is in-between. For fermions, the bimodal character of the initial distribution is kept for both sets of initial conditions. The same behavior is reported elsewhere.51,52![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 14 a.u., p0 =
0 = 14 a.u., p0 = ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.2 a.u., and σ0 =
0 = 0.2 a.u., and σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u.; (b) same as (a) but σ0 =
0 = 5.2 a.u.; (b) same as (a) but σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 4.8 a.u.; (c) x0 =
0 = 4.8 a.u.; (c) x0 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) 0 = 0, p0 = 0.2 a.u.,
0 = 0, p0 = 0.2 a.u., ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) 0 = 0.3 a.u. and σ0 =
0 = 0.3 a.u. and σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 5.2 a.u. and (d) same as (c) but σ0 =
0 = 5.2 a.u. and (d) same as (c) but σ0 = ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0 = 4.8 a.u. Several interesting features are worth discussing. First, it is clear that unlike the black curve (distinguishable adsorbates), the ISF for fermions, for the ballistic regime, is no longer a Gaussian function. Second, in the Brownian or diffusion regime, the symmetry of the wave function is not robust enough to distinguish bosons and fermions since adsorbates tend to the same asymptotic exponential function. Third, the initial width makes the difference between the symmetry of the wave function more pronounced in the intermediate time region. And fourth, it should be possible to observe these differences in an experiment where the fermions decay slower than bosons in panels (c) and (d) (and bosons decay quite similar to distinguishable adsorbates); in other words, the decoherence process is much more gradual for fermions than bosons for certain initial widths.
0 = 4.8 a.u. Several interesting features are worth discussing. First, it is clear that unlike the black curve (distinguishable adsorbates), the ISF for fermions, for the ballistic regime, is no longer a Gaussian function. Second, in the Brownian or diffusion regime, the symmetry of the wave function is not robust enough to distinguish bosons and fermions since adsorbates tend to the same asymptotic exponential function. Third, the initial width makes the difference between the symmetry of the wave function more pronounced in the intermediate time region. And fourth, it should be possible to observe these differences in an experiment where the fermions decay slower than bosons in panels (c) and (d) (and bosons decay quite similar to distinguishable adsorbates); in other words, the decoherence process is much more gradual for fermions than bosons for certain initial widths.![[script L]](https://www.rsc.org/images/entities/char_e144.gif) governing the dissipative evolution of the reduced density matrix ρ
governing the dissipative evolution of the reduced density matrix ρ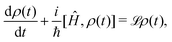
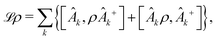
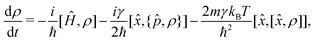
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , [
, [![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , ρ]]/8mkBT can be added to the master eqn (77)
, ρ]]/8mkBT can be added to the master eqn (77)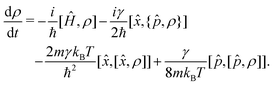
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and momentum
and momentum ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) operators is taken
operators is taken![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + iν
+ iν![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , Â+ = μ
, Â+ = μ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) − iν
− iν![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ,
,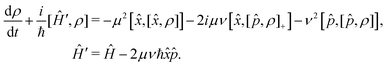
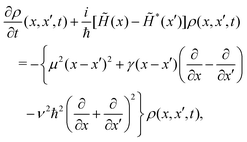
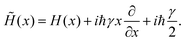
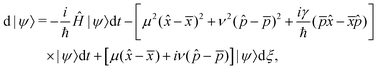
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 〈ψ|
= 〈ψ|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ψ〉,
|ψ〉, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = 〈ψ|
= 〈ψ|![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) |ψ〉 and dξ are complex stochastic variables fulfilling the properties of a Wiener process:
|ψ〉 and dξ are complex stochastic variables fulfilling the properties of a Wiener process: 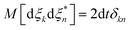 ,
, 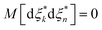 and M[dξkdξn] = 056 (see Appendix E).
and M[dξkdξn] = 056 (see Appendix E).
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) or
or ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) are propagated in the coordinate or momentum space, respectively. In correspondence with previous works,22 the temperature has been incorporated in the system dynamics through the Lindblad operator coefficients
are propagated in the coordinate or momentum space, respectively. In correspondence with previous works,22 the temperature has been incorporated in the system dynamics through the Lindblad operator coefficients 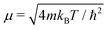 and
and 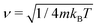 .
.
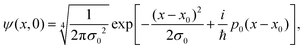
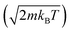 for a given temperature T and an adsorbate with mass m.
for a given temperature T and an adsorbate with mass m.
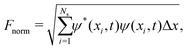
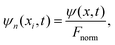
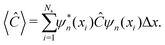
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. This comparison shows the importance of the statistics in this type of simulations. The temperature dependence of the coefficients μ and ν fulfill the condition reported in ref. 55. In Fig. 9–11 the time dependence of the wave packet widths up to 50 ps are displayed for different surface temperatures, frictions and adsorbate masses, respectively. The numerical (points) and analytical (solid curves) results are shown in each plot. In Fig. 9, the friction is given by γ = γ0/2m where γ0 = 5 × 10−2 ps−1 with different values of T and initial widths σ0 for Xe adsorbates: T = 170 K and σ = 0.08 a.u. (black line), T = 121 K and σ = 0.1 a.u. (red line) and T = 70 K and σ = 0.14 a.u. (blue line).
000. This comparison shows the importance of the statistics in this type of simulations. The temperature dependence of the coefficients μ and ν fulfill the condition reported in ref. 55. In Fig. 9–11 the time dependence of the wave packet widths up to 50 ps are displayed for different surface temperatures, frictions and adsorbate masses, respectively. The numerical (points) and analytical (solid curves) results are shown in each plot. In Fig. 9, the friction is given by γ = γ0/2m where γ0 = 5 × 10−2 ps−1 with different values of T and initial widths σ0 for Xe adsorbates: T = 170 K and σ = 0.08 a.u. (black line), T = 121 K and σ = 0.1 a.u. (red line) and T = 70 K and σ = 0.14 a.u. (blue line).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000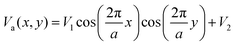 , where V1 = −13.64 meV and V2 = −12.32 meV. These values are obtained by fitting the cosine function to the numerical result of the potential energy surface. Both interaction potentials are very similar because its amplitude is around −28 meV and the periodicity match with the unit cell length of the Pt in both cases. The unidimensional corrugated potential used in the simulations is
, where V1 = −13.64 meV and V2 = −12.32 meV. These values are obtained by fitting the cosine function to the numerical result of the potential energy surface. Both interaction potentials are very similar because its amplitude is around −28 meV and the periodicity match with the unit cell length of the Pt in both cases. The unidimensional corrugated potential used in the simulations is 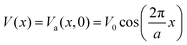 . The amplitude V0 is taken so that the energy barrier for this potential (Eb = V0) coincides with the Langevin molecular simulations.41 The diffusion of the Xe adsorbate on the metal surface of Pt is studied along the (100) direction.
. The amplitude V0 is taken so that the energy barrier for this potential (Eb = V0) coincides with the Langevin molecular simulations.41 The diffusion of the Xe adsorbate on the metal surface of Pt is studied along the (100) direction.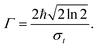
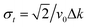 . By using eqn (89), the quasielastic broadening is
. By using eqn (89), the quasielastic broadening is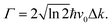

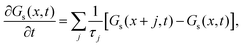
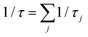 , with τj = τ−j. Now, due to the linearity property of the Fourier transform
, with τj = τ−j. Now, due to the linearity property of the Fourier transform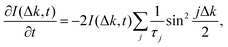
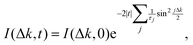
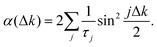

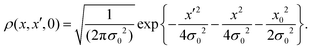
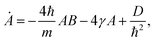
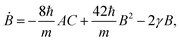
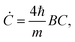
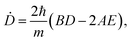
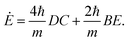
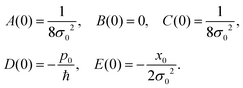

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp
exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i(kx + Δp/ħ)},
i(kx + Δp/ħ)},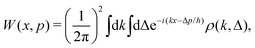
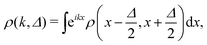
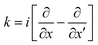 is the wave number in the direction parallel to the diagonal64. The CL master eqn (7) is then written as
is the wave number in the direction parallel to the diagonal64. The CL master eqn (7) is then written as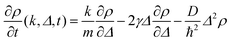
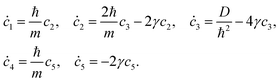
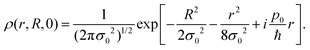
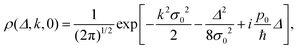
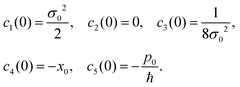
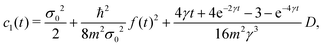
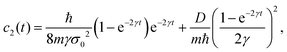
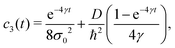
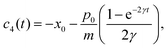
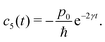
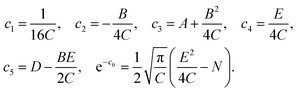
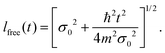
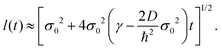
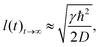
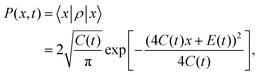
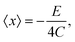
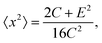
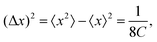
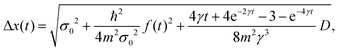
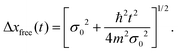
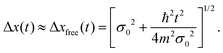
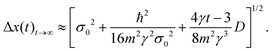
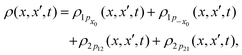
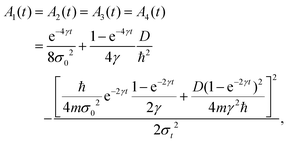
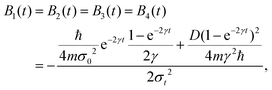
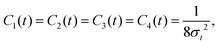
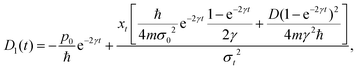
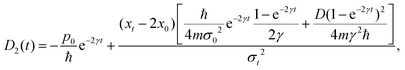


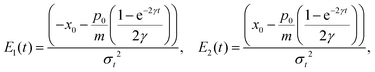
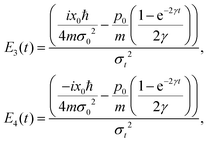
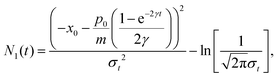
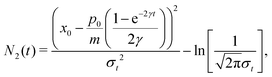
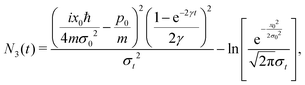
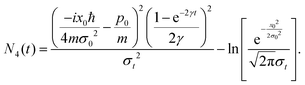
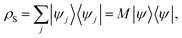
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S.
S.
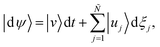
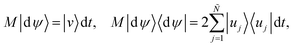
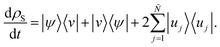
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) S in the orthogonal space to |ψ〉
S in the orthogonal space to |ψ〉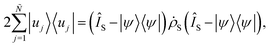
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) S|ψ〉 = |ψ〉〈v|ψ〉 + |v〉,
S|ψ〉 = |ψ〉〈v|ψ〉 + |v〉,![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) S|ψ〉 = 2
S|ψ〉 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Re〈ψ|v〉,
Re〈ψ|v〉,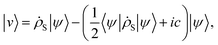
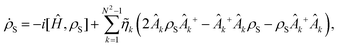
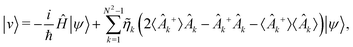
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) k are non-negative quantities. Once the diffusive term has been found, the stochastic term |uk〉 of the differential wave function eqn (144) can be found by replacing (153) in (149) and using the scalar product properties, leading to the following expression
k are non-negative quantities. Once the diffusive term has been found, the stochastic term |uk〉 of the differential wave function eqn (144) can be found by replacing (153) in (149) and using the scalar product properties, leading to the following expression