Performance of GFN1-xTB for periodic optimization of metal organic frameworks

Abstract

Tight-binding approaches bridge the gap between force field methods and Density Functional Theory (DFT). Density Functional Tight Binding (DFTB) has been employed for a wide range of systems including proteins, clays and 2D and 3D materials. DFTB is 2–3 orders of magnitude faster than DFT, allowing calculations containing up to ca. 5000 atoms. The efficiency of DFTB comes via pre-computed integrals, which are parameterized for each pair of atoms, and the requirement for this parameterization has previously prevented widespread use of DFTB for Metal–Organic Frameworks. The GFN-xTB (Geometries, Frequencies, and Non-covalent interactions Tight Binding) method provides parameters for elements up to Z ≤ 86. We have therefore employed GFN-xTB to periodic optimizations of the Computation Ready Experimental (CoRE) database of MOF structures. We find that 75% of all cell parameters remain within 5% of the reference (experimental) value and that bonds containing metal atoms are typically well conserved with a mean average deviation of 0.187 Å. Therefore GFN-xTB provides the ability to calculate MOF structures more accurately than force fields, and ca. 2 orders of magnitude faster than DFT. We therefore propose that GFN-xTB is a suitable method for screening of hypothetical MOFs (Z ≤ 86), with the advantage of accurate binding energies for adsorption applications.

---

Introduction

Interest in Metal–Organic Frameworks (MOFs) has been increasing since they were first synthesized in the 1990s. MOFs are a group of nanoporous materials made by combinations of building blocks – metal nodes and organic linkers – assembled into a specific network.¹ The modular nature of MOFs creates an effectively infinite number of possible structures, of which several tens of thousands have been synthesized. MOFs have been synthesized from all corners of the periodic table, giving rise to a wide chemical and physical diversity of MOF structures and properties. The Computation-Ready Experimental (CoRE)^2,3 database has compiled more than 12 000 crystal structures of MOFs and the Cambridge MOF subset⁴ currently stands at 88 000 structures, of which ca. 8000 are porous. While many interesting MOFs and MOF applications have been discovered serendipitously, it is normally desired to design a MOF that possesses some given property. To search for a MOF with some specific property, synthesizing every single MOF is clearly impossible, therefore computational methods have been increasingly employed to guide experiments.^5–10 One standard procedure is a combinatorial enumeration followed by molecular simulation on every hypothetical structure.^11,12 Inevitably, the important aspect determining the success of this approach is in the accuracy and efficiency of the molecular simulation methods.

Calculation methods that are used in molecular simulation can be grouped into quantum mechanics (QM) or classical simulation methods (molecular mechanics, MM). The level of theory/computational method required depends on the property of interest. For properties that require electronic structure and information about the exact binding sites, quantum mechanical methods are used. However, due to the high computational cost of quantum mechanical methods, the size of the system to model needs to be carefully chosen. Quantum mechanics based on wave function theory can only be applied to small cluster models of MOFs capturing the region of interest and limited to a few tens of atoms.¹³ Consequently, small cluster models are unable to describe long range dispersion interactions. In addition, cutting the MOF to create a feasible cluster model requires capping the cut points with e.g. hydrogen atoms or methyl groups, which introduces electronic effects not present in the parent periodic structure. For full unit cell MOF structures, periodic DFT can be used to simulate systems with as many as 100–1000 atoms.^14–19 While possible on handfuls of chosen MOFs, the expense of these quantum mechanical approaches means they cannot support screening large subsets of MOFs.

Classical mechanics such as Force Fields (FFs) can be a computationally efficient ‘shortcut’. Force fields are employed for properties that don’t need information about electronic structure and can be defined by the relevant conditions of temperature or pressure. In these cases, force fields offer a welcome reduction in cost. Existing force fields which have been routinely applied in MOF simulations are either the general force fields – such as UFF,²⁰ TraPPE²¹ and DREIDING²² – or specific force fields designed for a particular group of MOFs,^23,24 such as MOF-FF²⁵ and QuickFF.^26–29 Specific force fields are typically more accurate than general force fields, but are unsuitable for screening studies outside their parameterization. The general force field approaches are good at handling the chemical diversity of MOFs for reproducing experimental results such as crystal structures, bulk moduli, sublimation energies and fluid properties.³⁰ However, they are not ideal for explaining structural transformation over external stimuli and for explaining donor–acceptor interactions in open metal site materials.³¹ Another problem is general force fields fail to model adsorption isotherms at the lower pressure region.³²

Since the diverse inorganic fragments that comprise MOFs cannot be replicated by general force fields, a common approach is to reparametrize these force fields. The initial development of force fields for MOFs were force fields designed to accurately describe individual popular MOFs, such as extended MM3 for MOF-5,²⁶ Cu paddlewheel-based MOFs²⁷ and for the Flexible Metal–Organic Framework MIL-53(Al).²³ Subsequently, force fields have been developed to accommodate a group of MOFs, BTW-FF²³ for 6 popular MOFs associated with Cu, Zn, and Zr metal nodes; Becker et al.²⁹ optimized a polarizable force field for CO₂ and CH₄ adsorption in M-MOF-74 (M = Co, Cr, Cu, Fe, Mg, Mn, Ni, Ti, V, and Zn). QuickFF²⁸ is a program that automates the derivation of force fields for MOFs. UFF4MOF^33,34 took a different approach, aiming for universality rather than transferability and reached over 99% coverage of the 2014 CoRE database.³

Another approach frequently used is combining potentials from multiple generic force fields. Hamon et al. modelled adsorption of H₂S into MIL MOFs by combining UFF for the inorganic part of the framework and the DREIDING inter-atomic potential for the organic part.³⁵ The model matches the experimental adsorption isotherms quite well in the whole pressure range, confirming structural transitions occur in some pressure regions. Vandenbrande et al.²⁴ reviewed five different force fields, three combined generic force-field (UFF/TraPPE, Drieding- UFF/TraPPE, MM3-MBIS) and two ab initio derived force fields (SAPTFF and MEDFF), for methane adsorption in Zr-based MOFs (UiO-66, UiO-67, DUT-52, NU-1000, and MOF808),²⁴ found that UFF/TraPPE gives an acceptable agreement with the experiment in the UiO-66 framework for pressure between 30 and 80 bar. Meanwhile, other combined generic force fields do not accurately reproduce single molecule adsorption energies. The two ab initio derived force fields gave a remarkable accuracy of the individual adsorption energies.

Due to the motivation of reproducing experimental data and the requirement of having enough experimental data to parameterize and test, most force field development to date has mostly focused on fitting to a limited number of popular MOFs. The lack of transferability and the uncertain level of accuracy is the main drawback of force fields. This especially hampers screening efforts, particularly of hypothetical framework materials, and especially for MOFs using less frequently employed metals such as the lanthanides and actinides.

To achieve a compromise between high accuracy DFT or ab initio calculations and rapid, but less reliably accurate force field calculations, there are two possible strategies: One strategy is to combine Quantum Mechanical (QM) and Molecular Mechanics (MM) methods in a single QM/MM^36–38 calculation. Various forms of QM/MM have been applied to several MOFs including Fe-MOF-74,³⁹ NU-1000⁴⁰ and ZIFs.⁴¹ QM/MM is appealing for adsorption studies in MOFs because it allows for the key adsorption region to be treated accurately (QM) while the rest of the framework is treated efficiently (MM). It also allows for reaction mechanisms to be determined.⁴² However, the need to carefully specify the QM and MM regions makes it generally difficult to apply QM/MM to a wide variety of MOFs, including hypothetical structures, as might be encountered in a screening study. The second strategy to achieve a balance between QM accuracy and MM efficiency is to choose a semi-empirical method that approximates more expensive ab initio methods. One such method, Density Functional Tight Binding (DFTB) represents the desired compromise between accuracy and efficiency. DFTB approximates DFT by using pre-calculated parameters for integrals and a minimal basis. DFTB has been extensively used on large biomolecules with accuracy comparable to DFT⁴³ but is at least 2 orders of magnitude faster. DFTB has been used for some MOFs, notably those containing Zinc^44–49 and Copper.⁵⁰ However, with these few exceptions, the availability of parameters for metal atoms has been problematic. The 3ob-3-1 parameter set⁵¹ contains parameters for Mg and Zn, the matsci-0-3 set⁵² includes Cu and Al, while the pbc-0-3 set⁵³ contains parameters for Fe, but these parameters are designed to reproduce bulk Fe only and are not recommended for other systems such as MOFs. The QUASINANO parameters^54,55 include all element–element pairs, but only Z ≤ 20 + Br.

Analysis⁵⁶ of structures contained in the 2014 Computation-Ready Experimental (CoRE) MOF database,³ showed MOFs containing 42 elements with Z ≥ 20, including, second and third row transition metals, lanthanide and actinide elements. A broad application of DFTB to MOFs, especially screening studies of either real or hypothetical structures, necessarily requires parameters for all of these elements. DFTB parameters are generally for pairs of atoms (e.g. Zn–O, Zn–C, C–O), meaning that the number of parameters required scales with the square of the number of elements. Therefore, to apply DFTB to the entire periodic table, would require ∼100² parameters, and significant amounts of source data and effort in parameterisation.^54,55 Even automated methods^55,57 for deriving parameters require significant time and effort and the parameters derived are generally limited by the source data (i.e. parameters derived for metal surfaces would be expected to be only poorly applicable to MOFs). Consequently, while DFTB has been used extensively for Covalent Organic Frameworks, comprised of (C, N, O, B, F, H elements),^58–61 application of DFTB to MOFs has been largely restricted to Zn and Cu-containing MOFs.

Addressing the parametrization problem, Grimme et al. developed a semiempirical TB method, GFN-xTB,⁶² designed to produce reasonable Geometries, Frequencies, and Non-covalent interactions for diverse chemical system consisting of elements from the periodic table, Z ≤ 86. GFN-xTB is targeted to facilitate systems more than 1000 atoms; it has been successfully applied to proteins with 3000 atoms.

The GFN-xTB,⁶² method follows DFTB, approximating DFT by expanding the Kohn–Sham equation in terms of density fluctuations. The energy expression consists of terms describing electronic, (atom pairwise) repulsion, dispersion and halogen bonding.

E = E_el + E_rep + E_disp + E_XB

The electronic energy term (E_el), includes the effects of self-consistent charges and a contribution of electron smearing, which accounts for partial orbital occupations. Molecular orbitals are constructed from linear combinations of atom centred orbitals (LCAO), with the basis set consist of a minimal basis set of atom centred functions. To improve the treatment of hydrogen bonding, the 2 s function is included for hydrogen atoms.

The repulsive energy term, (E_rep) uses an atom pairwise potential, employing the effective nuclear charges of both atoms, Z^eff_A and Z^eff_B, but crucially avoiding pair related parameters. The dispersion energy, (E_disp) is computed using the D3 method⁶³ and BJ damping scheme.⁶⁴ Finally, the halogen bonding term (E_XB) employs a modified Lennard-Jones form with a correction for pairwise repulsion of halogen bond acceptor (Br, I, At) – donor (N or O) atoms.

In total, GFN-xTB has only 16 global and roughly 1000 element specific parameters, and atom pair related parameters are avoided. The parameterization is with respect to molecular structures obtained at the PBEh-3c hybrid DFT level.

The open-source release of GFN-xTB⁶⁵ only recently added the capability of undertaking periodic optimizations, and previous benchmarking of GFN-xTB for adsorption of small molecules in MOFs has employed capped cut-out structures.⁶⁶ The implementation of GFN-xTB in the AMS package⁶⁷ and DFTB+⁶⁸ does permit periodic optimizations. In this paper, we evaluated the performance of GFN-xTB as implemented in AMS to optimized geometry structures of MOF from the 2014 and 2019 CoRE Databases.

Computational details

Geometry optimization was performed for each structure in the CoRE 2014³ and 2019² database (version 1.1.0). The computation is carried out using GFN-xTB in the Amsterdam Modelling Suite (AMS) by Software for Chemistry and Materials (SCM).⁶⁷ Two separate geometry optimizations were undertaken on each structure, the first optimization only allows the atomic position to move, while the second optimization relaxed both the lattice and atomic positions.

Most of the 9895 CoRE structures are amenable to geometry optimization in this way, there are some exceptions to the simple protocol above, as follows:

1. Z ≤ 86. GFN-xTB is parameterised only for Z ≤ 86. Therefore, all structures with atoms of elements with Z > 86 were excluded. (191 structures)

2. Very large structures. Structures with total number of atoms greater than 1200 were considered too computationally expensive for a full optimization, especially given the number of “soft” deformations expected in such structures. In this case, we limit the optimization to 100 geometry optimization steps. (334 structures)

3. Partial occupancy CIF files. Structures with partial occupancies: Calculations can only be undertaken on full atoms. Structures where the total number of atoms is greater than defined by the stoichiometry are excluded from the evaluation in this work. (1407 structures)

4. Structures that collapse during geometry optimization. There are several possible causes of structural collapse: The MOF structure may be fundamentally not stable upon solvent removal – in this case, structural collapse in the calculation mirrors the structural collapse in experiment; In addition, structural collapse may be observed as an artefact of the structure curation process.^2,3 In typical MOF syntheses, metal salt and ligand solutions are mixed together in polar, high boiling point solvents. Experimentally reported metal organic frameworks may contain solvent molecules in their pores, missing charge balancing ions (CBIs) or missing hydrogen atoms and overlapping atoms. Before being imported into the CoRE database, curation is performed, however the solvent is removed with an imperfect method. As a consequence, some of the solvent still remains in the pore and/or an essential part of the MOF structure itself is accidently removed. This has been observed by other authors employing the CoRE database.⁶⁹ These structures are excluded from the analysis. (478 structures)

5. Structures that partially converged. Some structures converged (change in energy <−1 × 10⁻² Hartree), but still had residual gradients larger than the default criterion of 1 × 10⁻⁵ Hartree. These structures were manually examined to confirm convergence and extract the structure where the energy had converged. (173 structures)

Refcodes for all structures in each case above are provided in the ESI.†

The textural properties, such as gravimetric surface area and volumetric surface area, are calculated before and after optimization. They are calculated using zeo++,⁷⁰ using the high accuracy (ha) settings and using probe molecules with diameter 1.86Å representing N₂ and with a trial number of 2000.

Results and discussion

Lattice parameters

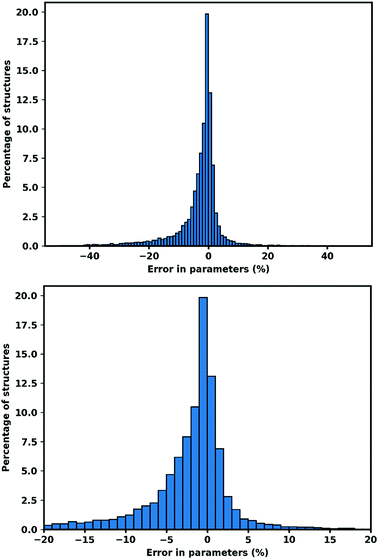Fig. 1 Error in cell parameters, calculated as (X_GFN − X_Exp) (a–c). Right hand side shows the 95.13% of cell parameters within ±20% of the experimental value.

From the successful optimizations, 74.51% of all cell parameters are within 5% of the reference value, 87.40% are within 10% and 95.13% are within 20% as shown in Fig. 1. As the lattice optimizations allowed complete relaxation of cell vectors and angles, one source of large errors in lattice parameters is breathing MOFs. Breathing in MOFs is a behaviour of reversible flexible framework occurs upon guest adsorption, temperature, pressure or other stimuli, which allows a large change in the unit cell.⁷¹ For example, Refcode FERWAC_clean⁷² begins with a = 9.97 Å, b = 15.74 Å, c = 15.74 Å, but optimized to a narrow pore structure with a = 7.80 Å b = 15.31 Å, c = 15.31 Å. Similar effects are observed in e.g. refcode GUSNEN01_SL,⁷³ QOVWOO_SL,⁷⁴ QUQGAL_clean,⁷⁵ QOSJIT_clean,⁷⁶ FOFCOU_clean,⁷⁷ QOSJOZ_clean,⁷⁶ QOVWOO01_clean,⁷⁸ CEFDAU_clean⁷⁹ and SABWAU_SL.⁸⁰ Breathing MOFs are responsible in some structures with both +20 to +30 and −20 to −40 deviations in lattice parameters (e.g. the a parameter of FERWAC_clean⁷² changes from 9.97 Å to 7.80 Å after optimization).

Another source of large negative errors is structures which were starting to collapse, when the atoms move closer to other atoms they might bind to other atoms and form a different connectivity. While breathing MOFs is indicated by a narrowing in one side of cell parameter, collapsing structures shows a large negative deviation in all cell parameters. As an example, refcode ACUBAB_clean⁸¹ which begins with a = 8.88 Å, b = 8.88 Å, c = 23.78 Å and optimized to a = 7.43 Å, b = 7.68 Å, c = 15.50 Å. This happens mostly to structures with linkers that are relatively small compared to the size of metal node (example refcode ACUBAB_clean and C6DT02320G_c6dt02320g2_clean).

The large positive deviations arise from structures with partial occupancy cif files. Automatic conversion of cif files (which permit fractional occupancy) to input files which do not permit fractional occupancy, sometimes produces erroneous output, where parts of structures are duplicated. While a lot of partial occupancy cif files could be detected and have been removed from the evaluation, some still remained. The identification of partial occupancy files is done by calculating the atom–atom distances with threshold closer than 1 Å with neither atom being a hydrogen atom. However, for some structures, multiple possible atom positions with partial occupancy are located at a distance greater than 1 Å. One example is refcode WUXYUL_clean.⁸²

Atomic position

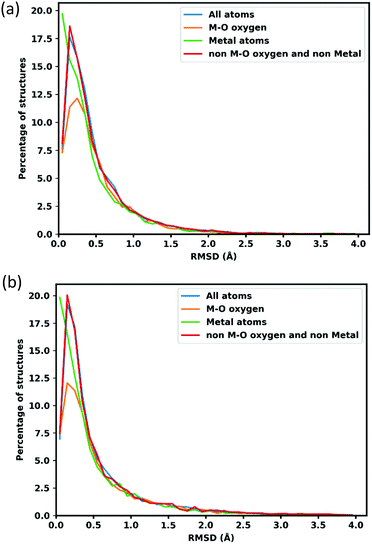
RMSD of atomic position is calculated to assess the quality of optimized structures. To calculate the RMSD atomic position of lattice optimized structures, the unit cell is scaled back to the original cell parameters. Fig. 2 shows the distribution of RMSD of GFN-xTB optimized atom positions, the blue line shows all atom positions, and the orange line shows oxygen neighbouring with metal atoms (to separate oxygens which connect the linker to metal node that might deviate more because of MOFs flexibility and errors in the metal atom positions), the green line shows the metal atoms and red for all other atoms, which represents the linkers.

Fig. 2 RMSD of GFN-xTB optimized atom positions with respect to the CoRE structures. (a) Shows optimization allowing only atom position movement. (b) Shows optimization where both the lattice and atomic positions were allowed to relax.

The average RMSD for all atoms are 0.489 Å when atom positions are optimized with the lattice fixed at its experimental value and 0.617 Å when the lattice is simultaneously optimized as shown in Table 1. Oxygens attached to metal atoms have slightly higher RMSD in both cases, but the positions of the metal atoms themselves are slightly better conserved with RMSDs of 0.439 Å and 0.560 Å for fixed and lattice-optimized structures respectively. Atoms in the organic linker have a higher deviation than the atoms in metal node since the organic linkers have more flexibility and degrees of rotational freedom around the inorganic building unit. These RMSD values compare favourably with those obtained of a set of 72 MOFs calculated with the PM7⁸³ semi-empirical method.⁸⁴

Table 1 Mean RMSD of GFN-xTB optimized atom positions with respect to the CoRE structures

	Mean RMSD with fixed lattice (Å)	Mean RMSD with lattice optimization (Å)
All atoms	0.489	0.617
M–O	0.507	0.650
Metal atoms	0.439	0.560
Non M–O and non Metal	0.490	0.619

---

Atom bonding

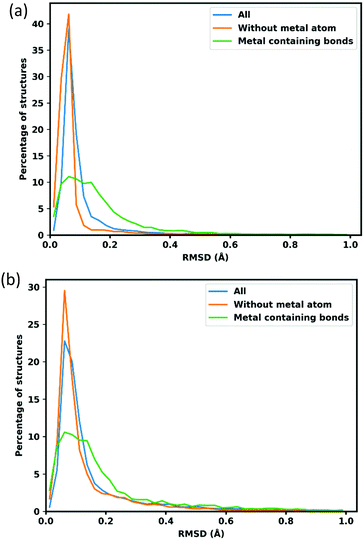
As simple consideration of atom positions fails to account for linker flexibility and rotation, a more robust consideration of error in the calculated structures employs bond lengths, the distribution and mean deviations w.r.t. the reference CoRE structures are shown in Fig. 3 and Table 2. The analysis is separated into three groups; the green line in Fig. 3 features metal containing bonds with average bond length deviation 0.120 Å with the lattice fixed and 0.175 Å with lattice optimization. The orange line represents bonds without a metal atom and have average deviation 0.093 Å and 0.150 Å respectively. Finally, all bonds altogether is shown by the blue line and exhibits an average deviation of 0.187 Å and 0.236 Å for fixed and lattice-optimized structures respectively.

Fig. 3 RMSD of GFN-xTB optimized bond lengths with respect to the CoRE structures. Blue shows all bonds, orange shows without metal atom bond, and green shows all metal containing (M−X). (a) shows optimization allowing only atom position movement. (b) shows optimization allowing lattice parameter and atom movement.

Table 2 Mean RMSD of GFN-xTB optimized bond lengths with respect to the CoRE structures

	Mean RMSD with fixed lattice(Å)	Mean RMSD with lattice optimization(Å)
All Bonds	0.120	0.175
Without metal atom	0.093	0.150
M–X	0.187	0.236

---

The sharp peaks centred around 0.063 Å in Fig. 3, show that typical organic bonds are very well replicated. Metal containing bonds are also well replicated, though to a lesser extent, with 76.63% of M–M bonds being within 0.250 Å of the reference crystal structure value. The cases where optimized M–M bonds are outside this threshold involve a change of atomic connectivity during the optimization, typically caused by the removal of structural ligands. For example, the structure AGARUW⁸⁵ is a La³⁺ containing MOF, where 1D chains of La³⁺ ions are deca-coordinated by a mixture of coordinating and chelating carbonato ligands and water. In the cleaned structure in the CoRE database (refcode AGARUW_clean⁸⁵), the water ligands are removed, resulting in a significant rearrangement of the coordination environment of each La³⁺ ion and a consequent reduction in one of the La–La distances from 4.923 Å to 2.874 Å.

Most force fields developed specially for MOFs have placed special attention on ensuring the correct geometries of common sets of inorganic building units. We checked the metal clusters used in popular MOFs such as M₂O paddlewheels found in HKUST-1, trimeric oxo-centered M₃O in MIL-100 series, M₄O octahedron in MOF-5, and finally the 12-connected M₆O cuboctahedron in UiO-66. Very good results are shown for all metal nodes, the deviation of optimized structure is presented in Fig. 4. The two key distances in building blocks that affect the lattice parameters of the optimized structure are the M–O and MM bond lengths, which in a layer-pillar MOF, affect the a, b and the c lattice dimensions respectively. Cu-based paddlewheel is highly conserved, with Cu–Cu bond length deviating only −0.030 Å from the experimental value. Other M₂O paddlewheels, Ni₂O and Zn₂O exhibit a higher deviation, contracting 0.3 Å and 0.15 Å in bond length between the two metals. For all paddlewheels, the M–O bonds are very well conserved with all deviations less than ±0.1 Å. Structures for Ni₂O and Zn₂O paddlewheels are supplied in the ESI.†

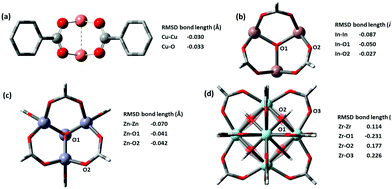Fig. 4 (a) Cu-based Paddlewheel M₂O of refcode FIQCEN⁸⁶ (b) In-based Trimeric Oxo-centred M₃O refcode FIFGIM⁸⁷ (c) Zn-based octahedron M₄O of refcode EDUSIF⁸⁸ (d) Zr-based cubohedral M₆O of recode RUBTAK03.⁸⁹ Crystal structure is represented by opaque and optimized structures are shown partly transparent.

Both M₃O and M₄O experimental structures are also reproduced very accurately shown in Fig. 4b and c respectively. We examined In, Fe, and Al-based trimeric oxo-centered metal nodes, In–In have a deviation of −0.087 Å, Fe–Fe −0.163 Å (refcode HAKSIY⁹⁰) and Al–Al −0.173 Å (refcode JALCAD⁹¹). Again, the M–O bonds are very conserved with all deviations less than ±0.1 Å. Zn-based octahedron unit found in MOF-5 (e.g. refcode EDUSIF⁸⁸) exhibits a Zn–Zn deviation of −0.0699 Å and Zn–O error of −0.04 Å.

The zirconium oxide building block, from the well-known UiO-66 MOF (e.g. refcode RUBTAK03⁸⁹) is similarly well-conserved. GFN-xTB has corrected the inner oxygen positions from being symmetric, to having two types of oxygen atoms – one capped with hydrogen and another one without hydrogen. The distinct zirconium–oxygen bonds optimized to a longer bond for Zr–OH (refer to O2 in Fig. 4d) and a shorter bond for Zr–O (refer to O1 in Fig. 4d). This correction is justified as the crystal structure represents an average of oxygen positions, where 50% of the oxygen atoms bear a hydrogen atom, but which oxygen atoms (i.e. the orientation of the building block) is not pre-defined.

Geometrical Textural properties

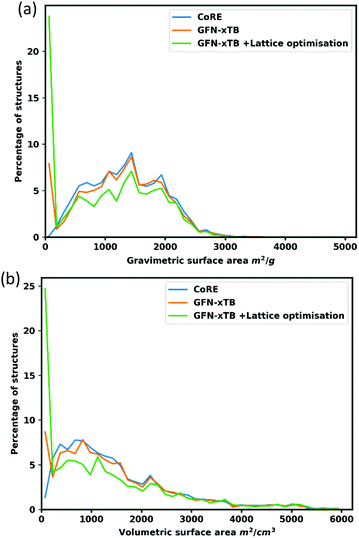
To further interrogate the quality of the optimized structures, gravimetric and volumetric surface areas were calculated and compared to the surface areas of the original CoRE structures as shown in Fig. 5. Overall, the surface areas of the optimized structures follow a similar distribution to the experimental structures. In the volumetric surface area of lattice optimized structures, there is a conspicuous dip around 800–1200 m² cm⁻³. This occurs for one of two reasons: Firstly, after optimization, structures shrink marginally, as measured by comparing initial and final unit cell volumes, which results in 20–25% of structures in this region having a pore size that is no longer adequate to fit the nitrogen probe molecule (r = 1.86 Å), or structures undergo distortion resulting in a smaller pore – e.g. a wine-rack distortion (e.g. REFCODE TURDIV_clean⁹²).

Fig. 5 (a) Gravimetric and (b) volumetric accessible surface areas of CoRE structures, as provided (blue) and after optimization using GFN-xTB in AMS with fixed lattice parameters and relaxed lattice parameters (orange and green respectively).

Conclusions

We tested GFN-xTB on MOFs for its ability to do periodic geometry optimization, we observe both the performance on fixed lattice optimization and complete relaxation of lattice optimization. The results confirm that optimized structures using GFN-xTB conserve the experimental structures very well. After optimization, 74.51% of all cell parameters are within 5% of the experimental value.

We also confirm that GFN-xTB could also reproduce the detailed atomic structures shown by the RMSD of atomic position being 0.489 Å for all atoms and 0.439 Å for metal atoms when the lattice was fixed, while for the optimized lattice, the RMSD values are 0.617 Å for all atoms and 0.560 Å for metal atoms. Bond lengths are better conserved with an RMSD of 0.120 Å for all bonds and 0.187 Å for metal containing bonds for fixed lattice optimization. While for relaxed lattice optimization 0.175 Å for all bonds and 0.236 Å for metal containing bonds.

Popular metal-containing building blocks, e.g. Cu₂O paddlewheels in HKUST-1, trimeric oxo-centered In₃O in MIL-100, Zn₄O octahedron in MOF-5, and finally the 12 connected Zr₆O cuboctahedron in UiO-66 found to be especially well replicated with M-M errors of −0.030 Å, −0.087 Å, −0.070 Å, and 0.114 Å respectively.

The accuracy of optimized structures, combined with computational efficiency and the wide coverage of the periodic table (Z ≤ 86) allow GFN-xTB to be applied for screening studies where MOFs from the entire periodic table may be encountered. The accurate non-covalent interactions in the method,⁶⁶ could allow GFN-xTB to be employed in screening for adsorption energies, an area in which force fields often have difficulty.

Author contributions

M. N. undertook all calculations and data analysis and initial draft of manuscript. M. A. A. devised the project, analysis. All authors reviewed and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

MAA acknowledges an EPSRC New Investigator Award grant no. EP/S015868/1. HPC time was provided via membership of the UK's HEC Materials Chemistry Consortium, this work used the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194). MN acknowledges a Vice Chancellor's PhD scholarship from Nottingham Trent University.

Notes and references

1. M. O’Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
2. Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998.
3. Y. G. Chung, J. Camp, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Chem. Mater., 2014, 26, 6185–6192.
4. P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625.
5. A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, Chem. Rev., 2021, 121, 10666–10741.
6. F. Zanca, L. T. Glasby, S. Chong, S. Chen, J. Kim, D. Fairen-Jimenez, B. Monserrat and P. Z. Moghadam, J. Mater. Chem. C, 2021, 9, 13584–13599.
7. J. Park, H. Kim, S. S. Han and Y. Jung, J. Chem. Phys. Lett., 2012, 3, 826–829.
8. P. Canepa, C. A. Arter, E. M. Conwill, D. H. Johnson, B. A. Shoemaker, K. Z. Soliman and T. Thonhauser, J. Mater. Chem. A, 2013, 1, 13597–13604.
9. Q. Yang, D. Liu, C. Zhong and J.-R. Li, Chem. Rev., 2013, 113, 8261–8323.
10. L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Chem. Mater., 2020, 32, 9849–9867.
11. C. E. Wilmer, O. K. Farha, Y.-S. Bae, J. T. Hupp and R. Q. Snurr, Energy Environ. Sci., 2012, 5, 9849–9856.
12. P. Z. Moghadam, D. Fairen-Jimenez and R. Q. Snurr, J. Mater. Chem. A, 2016, 4, 529–536.
13. S. O. Odoh, C. J. Cramer, D. G. Truhlar and L. Gagliardi, Chem. Rev., 2015, 115, 6051–6111.
14. D. Nazarian, J. S. Camp, Y. G. Chung, R. Q. Snurr and D. S. Sholl, Chem. Mater., 2017, 29, 2521–2528.
15. H. Q. Pham, T. Mai, N.-N. Pham-Tran, Y. Kawazoe, H. Mizuseki and D. Nguyen-Manh, J. Chem. Phys. C, 2014, 118, 4567–4577.
16. T. Mueller and G. Ceder, J. Chem. Phys. B, 2005, 109, 17974–17983.
17. E. Stavitski, E. A. Pidko, S. Couck, T. Remy, E. J. M. Hensen, B. M. Weckhuysen, J. Denayer, J. Gascon and F. Kapteijn, Langmuir, 2011, 27, 3970–3976.
18. S. Ling and B. Slater, J. Chem. Phys. C, 2015, 119, 16667–16677.
19. L. Wilbraham, F.-X. Coudert and I. Ciofini, Phys. Chem. Chem. Phys., 2016, 18, 25176–25182.
20. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
21. P. Bai, M. Tsapatsis and J. I. Siepmann, J. Chem. Phys. C, 2013, 117, 24375–24387.
22. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Chem. Phys., 1990, 94, 8897–8909.
23. L. Vanduyfhuys, T. Verstraelen, M. Vandichel, M. Waroquier and V. van Speybroeck, J. Chem. Theory Comput., 2012, 8, 3217–3231.
24. S. Vandenbrande, T. Verstraelen, J. J. Gutiérrez-Sevillano, M. Waroquier and V. van Speybroeck, J. Chem. Phys. C, 2017, 121, 25309–25322.
25. S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141.
26. M. Tafipolsky and R. Schmid, J. Chem. Phys. B, 2009, 113, 1341–1352.
27. M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Chem. Phys. C, 2010, 114, 14402–14409.
28. L. Vanduyfhuys, S. Vandenbrande, T. Verstraelen, R. Schmid, M. Waroquier and V. van Speybroeck, J. Comput. Chem., 2015, 36, 1015–1027.
29. T. M. Becker, J. Heinen, D. Dubbeldam, L.-C. Lin and T. J. H. Vlugt, J. Chem. Phys. C, 2017, 121, 4659–4673.
30. P. G. Boyd, S. M. Moosavi, M. Witman and B. Smit, J. Chem. Phys. Lett., 2017, 8, 357–363.
31. D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101.
32. Z. R. Herm, J. A. Swisher, B. Smit, R. Krishna and J. R. Long, J. Am. Chem. Soc., 2011, 133, 5664–5667.
33. M. A. Addicoat, N. Vankova, I. F. Akter and T. Heine, J. Chem. Theory Comput., 2014, 10, 880–891.
34. D. E. Coupry, M. A. Addicoat and T. Heine, J. Chem. Theory Comput., 2016, 12, 5215–5225.
35. L. Hamon, H. Leclerc, A. Ghoufi, L. Oliviero, A. Travert, J.-C. Lavalley, T. Devic, C. Serre, G. Férey, G. de Weireld, A. Vimont and G. Maurin, J. Chem. Phys. C, 2011, 115, 2047–2056.
36. T. Vreven and K. Morokuma, in Annual Reports in Computational Chemistry, ed. D. C. Spellmeyer, Elsevier, 2006, vol. 2, pp. 35–51.
37. X.-P. Wu, L. Gagliardi and D. G. Truhlar, J. Chem. Theory Comput., 2019, 15, 4208–4217.
38. X.-P. Wu, L. Gagliardi and D. G. Truhlar, Molecules, 2018, 23(6), 1309.
39. H. Hirao, W. K. H. Ng, A. M. P. Moeljadi and S. Bureekaew, ACS Catal., 2015, 5, 3287–3291.
40. X.-P. Wu, L. Gagliardi and D. G. Truhlar, Phys. Chem. Chem. Phys., 2018, 20, 1778–1786.
41. K. Cui and J. R. Schmidt, J. Chem. Phys. C, 2020, 124, 10550–10560.
42. K. Doitomi, K. Xu and H. Hirao, Dalton Trans., 2017, 46, 3470–3481.
43. M. Sugihara, V. Buss, P. Entel, M. Elstner and T. Frauenheim, Biochemistry, 2002, 41, 15259–15266.
44. A. Kuc, A. Enyashin and G. Seifert, J. Chem. Phys. B, 2007, 111, 8179–8186.
45. K. Leong, M. E. Foster, B. M. Wong, E. D. Spoerke, D. van Gough, J. C. Deaton and M. D. Allendorf, J. Mater. Chem. A, 2014, 2, 3389–3398.
46. A. D. D. Wonanke, P. Bennett, L. Caldwell and M. A. Addicoat, Front. Chem., 2021 DOI:10.3389/fchem.2021.716294.
47. G. Garberoglio and S. Taioli, Microporous Mesoporous Mater., 2012, 163, 215–220.
48. E. Eisbein, J.-O. Joswig and G. Seifert, J. Chem. Phys. C, 2014, 118, 13035–13041.
49. X. Wang, R. Guo, D. Xu, J. Chung, M. Kaviany and B. Huang, J. Chem. Phys. C, 2015, 119, 26000–26008.
50. J. Liu, B. Lukose, O. Shekhah, H. K. Arslan, P. Weidler, H. Gliemann, S. Bräse, S. Grosjean, A. Godt, X. Feng, K. Müllen, I.-B. Magdau, T. Heine and C. Wöll, Sci. Rep., 2012, 2, 921.
51. X. Lu, M. Gaus, M. Elstner and Q. Cui, J. Chem. Phys. B, 2015, 119, 1062–1082.
52. J. Frenzel, A. Oliveira, N. Jardillier, T. Heine and G. Seifert, Semi-relativistic, self-consistent charge Slater-Koster tables for density-functional based tight-binding (DFTB) for materials science simulations; TU-Dresden, Dresden, 2004–2009.
53. C. Köhler, G. Seifert and T. Frauenheim, Chem. Phys., 2005, 309, 23–31.
54. M. Wahiduzzaman, A. F. Oliveira, P. Philipsen, L. Zhechkov, E. van Lenthe, H. A. Witek and T. Heine, J. Chem. Theory Comput., 2013, 9, 4006–4017.
55. A. F. Oliveira, P. Philipsen and T. Heine, J. Chem. Theory Comput., 2015, 11, 5209–5218.
56. D. E. Coupry, M. A. Addicoat and T. Heine, J. Chem. Theory Comput., 2016, 12, 5215–5225.
57. C.-P. Chou, Y. Nishimura, C.-C. Fan, G. Mazur, S. Irle and H. A. Witek, J. Chem. Theory Comput., 2016, 12, 53–64.
58. Y. Zhang, M. Položij and T. Heine, ChemRxiv, 2022 DOI:10.33774/chemrxiv-2021-x4j63.
59. X. Chen, M. Addicoat, E. Jin, H. Xu, T. Hayashi, F. Xu, N. Huang, S. Irle and D. Jiang, Sci. Rep., 2015, 5, 14650.
60. A. M. Khayum, M. Ghosh, V. Vijayakumar, A. Halder, M. Nurhuda, S. Kumar, M. Addicoat, S. Kurungot and R. Banerjee, Chem. Sci., 2019, 10, 8889–8894.
61. S. Mondal, B. Mohanty, M. Nurhuda, S. Dalapati, R. Jana, M. Addicoat, A. Datta, B. K. Jena and A. Bhaumik, ACS Catal., 2020, 10, 5623–5630.
62. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
63. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
64. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101.
65. S. Grimme, Semiempirical Extended Tight-Binding Program Package, https://github.com/grimme-lab/xtb, 2019.
66. S. Spicher, M. Bursch and S. Grimme, J. Chem. Phys. C, 2020, 124, 27529–27541.
67. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
68. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101.
69. Y. Pramudya, S. Bonakala, D. Antypov, P. M. Bhatt, A. Shkurenko, M. Eddaoudi, M. J. Rosseinsky and M. S. Dyer, Phys. Chem. Chem. Phys., 2020, 22, 23073–23082.
70. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141.
71. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
72. Z. Arcís-Castillo, M. C. Muñoz, G. Molnár, A. Bousseksou and J. A. Real, Chem. – Eur. J., 2013, 19, 6851–6861.
73. N. Guillou, F. Millange and R. I. Walton, Chem. Commun., 2011, 47, 713–715.
74. C. Volkringer, T. Loiseau, N. Guillou, G. Férey, E. Elkaïm and A. Vimont, Dalton Trans., 2009, 2241–2249.
75. D. Banerjee, S. J. Kim, W. Li, H. Wu, J. Li, L. A. Borkowski, B. L. Philips and J. B. Parise, Cryst. Growth Des., 2010, 10, 2801–2805.
76. X.-W. Liu, R. Guo, H. Liu, Y.-Q. Yu, X.-W. Qi, J.-Y. Xu and C.-Z. Xie, RSC Adv., 2015, 5, 15059–15068.
77. J. E. Warren, C. G. Perkins, K. E. Jelfs, P. Boldrin, P. A. Chater, G. J. Miller, T. D. Manning, M. E. Briggs, K. C. Stylianou, J. B. Claridge and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2014, 53, 4592–4596.
78. G. Ortiz, G. Chaplais, J.-L. Paillaud, H. Nouali, J. Patarin, J. Raya and C. Marichal, J. Chem. Phys. C, 2014, 118, 22021–22029.
79. S. Jin, Y. Huang, S. Wei, Y. Zhou and Y. Zhou, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2012, 68, m1268–m1269.
80. T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem. – Eur. J., 2004, 10, 1373–1382.
81. J. Yu, Y. Wang, Z. Shi and R. Xu, Chem. Mater., 2001, 13, 2972–2978.
82. P. Siman, C. A. Trickett, H. Furukawa and O. M. Yaghi, Chem. Commun., 2015, 51, 17463–17466.
83. J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32.
84. C. R. A. Daniel, N. M. Rodrigues, N. B. da Costa and R. O. Freire, J. Chem. Phys. C, 2015, 119, 23398–23406.
85. J. Zhao, L.-S. Long, R.-B. Huang and L.-S. Zheng, Dalton Trans., 2008, 4714–4716.
86. S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150.
87. S.-T. Zheng, X. Zhao, S. Lau, A. Fuhr, P. Feng and X. Bu, J. Am. Chem. Soc., 2013, 135, 10270–10273.
88. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Watcher, M. O’Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472.
89. S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370–5372.
90. X. Zhao, X. Bu, E. T. Nguyen, Q.-G. Zhai, C. Mao and P. Feng, J. Am. Chem. Soc., 2016, 138, 15102–15105.
91. Y. Belmabkhout, R. S. Pillai, D. Alezi, O. Shekhah, P. M. Bhatt, Z. Chen, K. Adil, S. Vaesen, G. de Weireld, M. Pang, M. Suetin, A. J. Cairns, V. Solovyeva, A. Shkurenko, O. El Tall, G. Maurin and M. Eddaoudi, J. Mater. Chem. A, 2017, 5, 3293–3303.
92. S.-Y. Zhang, L. Wojtas and M. J. Zaworotko, J. Am. Chem. Soc., 2015, 137, 12045–12049.

---

Footnote

† Electronic supplementary information (ESI) available: Index and errors associated with all optimised CoRE structures. Complete set of GFN-xTB optimised structures. See DOI: https://doi.org/10.1039/d2cp00184e

---