Open Access Article
Open Access ArticleExploring the problem of determining human age from fingermarks using MALDI MS-machine learning combined approaches†
C. S.
Bury‡
a,
C.
Heaton§
b,
L.
Cole
b,
R.
McColm
c and
S.
Francese
 *b
*b
aMedicines Catapult Discovery, Manchester, UK
bSheffield Hallam University, Biomolecular Sciences Research Centre, Sheffield, UK. E-mail: s.francese@shu.ac.uk
cDefense, Science and Technology Laboratory, Porton Down, UK
First published on 27th January 2022
Abstract
For over a century fingerprints have been predominantly used as a means of biometric identification. Notwithstanding, the unique pattern of lines that can contribute to identifying a suspect is made up of molecules originating from touch chemistry (contaminants) as well as from within the body. It is the latter class of molecules that could provide additional information about a suspect, such as lifestyle, as well as physiological, pharmacological and pathological states. An example of the physiological state (and semi-biometric information) is the sex of an individual; recent investigations have demonstrated the opportunity to determine the sex of an individual with an 86% accuracy of prediction based on the peptidic/protein profile of their fingerprints. In the study presented here, the first of its kind, a range of supervised learning predictive methods have been evaluated to explore the depth of the issue connected to human age determination from fingermarks exploiting again the differential presence of peptides and small proteins. A number of observations could be made providing (i) an understanding of the more appropriate study design for this kind of investigation, (ii) the most promising prediction model to test within future work and (iii) the deeper issues relating to this type of determination and concerning a mismatch between chronological and biological ages. Particularly resolving point (iii) is crucial to the success in determining the age of an individual from the molecular composition of their fingermark.
1. Introduction
The type of forensic information sought from fingermarks has remained operationally unchanged for over one hundred years and refers to the recovery of biometrics. To date, no two fingermarks have been found identical, and, because of this, the ridge flow and minutiae are used for the biometric identification of perpetrators. However, since 2008, increasing attention has been paid to additional intelligence extractable from fingermarks and that can be derived from their molecular content.1 Exogenous contaminants could provide some circumstantial evidence of “activity”, as well as lifestyle information.2,3 However, endogenous molecules (normally produced in our body, excreted in sweat and transferred in a fingermark) should not be underestimated as they could contribute to significantly narrowing down the pool of suspects. Triacylglycerols have been recently tentatively proposed to have potential for providing information on diet and exercise as well as health related information.4Peptides and proteins are also endogenous sweat/fingermark components, and the sex of the offender is another type of desirable intelligence. To this end, following an initial proof of concept study,5 Heaton et al. reported comprehensive statistical modelling to determine the sex of an individual exploiting the differential peptide and small protein profiles detected by matrix assisted laser desorption ionisation mass spectrometry (MALDI MS) from natural fingermarks.6 This approach led to the best performing model/classification system yielding sex determination with 86% of accuracy of prediction. Whilst this prediction power does not permit a suspect exclusion from investigations, it does enable the adoption of this approach for triaging crime scene marks, prioritising those to investigate, as part of the forensic strategy. The lack of a higher prediction power has been partly ascribed to the additional presence of polymers, likely contaminants in fingermarks, due to their presence in toiletries and hygiene products. Whilst a more sensitive mass spectrometer would not avert polymer detection, it may be possible to increase both the relevant ion population and ion abundance and thus improving the discriminating power.
Another very interesting piece of intelligence that would contribute to narrowing down the pool of suspects is the age of an individual. Still today, age determination in living individuals is challenged by the mismatch between the chronological age (date since birth) and the biological age (related to the assessment of tissues and organs);7,8 human age determination in living individuals is an extremely complex endeavor involving an interdisciplinary approach encompassing the assessment of physicians with forensic experience and expertise in auxology, radiology, dentistry, and legal medicine,9 as well as the use of mathematical and statistical modelling,10 machine learning techniques11 and potentially modern analytical methods based on “multi-omics”12 or epigenetics.13 Most importantly, these assessments are performed either on individuals with uncertified identity or identity loss or on individuals with certified identity, for medical reasons. In both cases, these assessments are not placed in a forensic criminal investigation context, where the perpetrator is unknown.
The first study that could contribute to such forensic investigations, and the first of its kind, has been built on the knowledge that 5-hydroxymethylcytosine (5-hmC) is significantly involved in cellular differentiation and epigenetic regulation14 as well as decreasing in aging mouse brains.15 Xiong et al. applied LC-MS analysis to the blood of 238 patients aged 1–82 and demonstrated that DNA hydroxymethylation, and specifically 5-hydroxymethylcytosine (formed through conversion from 5-methylcytosine (5-mC)), was considerably decreased and negatively correlated with aging.16 The authors therefore suggested that 5-hmC could potentially be an aging phenotype. Koop et al. recently reviewed a range of epigenetic based methods for the epigenetic age estimation.13
However, to date, whilst the majority of the studies concentrate on determining the age of a fingermark left by an individual17 (time since deposition), only a few focus on determining the age of an individual from their fingermark, and only very few investigate the determination of human age exploiting the molecular content of a fingermark rather than the physical characteristics. To the best of the authors' knowledge, with the exclusion of publications encompassing age-related chemical changes from specimens other than fingermarks such as the scalp18 and forehead,19 one of the earliest papers on human age estimation was reported by Bohanan et al.20 illustrating mainly qualitative observations on the differences in the speed of the ageing process between children and adolescents. Buchanan et al.21 were the first to investigate human age from the lipid composition of a fingermark in 1996. These authors applied a destructive technique, namely GC-MS to investigate the fingermarks of 50 donors and reported a clear difference between the chemical profile of children and adults. In more recent years, Antoine et al.22 and Williams et al.23 continued to investigate children's fingermarks22,23 and their differentiation from adults'22 using some form of FT-IR and once again targeting lipids. In the former and more informative study, FT-IR microscopy was employed for investigating “artifact” fingermarks from 12 donors deposited following hand washing and fingertip sebum enrichment (groomed marks); here the authors made a qualitative assessment that lipids in children's fingermarks are not only less abundant than in adults' marks but also that they degrade faster, and as such, this degradation speed could be used as metrics to distinguish between children and adults, though no age pinpointing or more accurate age classification was attempted. Hemmila et al.24 investigated spectroscopic changes of lipid profiles in natural fingermarks and their correlation with the individual's age using a combination of FT-IR reflectance spectral analysis and partial least squares regression modelling. The authors found that, within a cohort of 78 individuals, it was possible to correlate the spectral profiles to the age of an individual within a 4 year window of error and that better models could be built if a classification “young” versus “old” was considered.
Different from previous work, and for the first time, in the present exploratory study, we have sought to make an initial assessment of the potential to retrieve the age of an individual by a combined approach encompassing the (i) exploitation of the peptide/protein content of a (natural) fingermark, (ii) the application of a non-hyphenated mass spectrometric technique instead, namely MALDI and (iii) the use of machine learning approaches. Proteins are one of the classes of biomolecules present in sweat/fingermarks and their expression and structure have been reported to change with age.25,26 On these bases, for our preliminary investigation, we have employed the same dataset acquired by Heaton et al.,6 to determine the sex of an individual to assess whether the expression profile of endogenous peptides and (small) proteins, detected by MALDI MS, can also serve as a biomarker pattern of age. As such studies are labour-, time- and resource-intensive, it was deemed sensible to capitalise on a dataset already available for this new, original and preliminary investigation.
Using this repurposed dataset, a range of supervised machine learning techniques have been evaluated for the task of chronological age prediction. The initial findings indicate that above-random donor age prediction is achievable through supervised learning methods.
2. Methods
2.1. Fingermark dataset
The collection of natural fingermarks for age determination studies has been described by Heaton et al.,6 in accordance with approved Sheffield Hallam University ethics application ER17244422. The same set of data processed to determine the sex of an individual has been used here with no further experimental laboratory work aside from reprocessing and repurposing the dataset, which was analysed using a number of statistical approaches to explore in depth the challenges and the potential of determining human age from the molecular composition of a fingermark. All data processing has been conducted in compliance with relevant laws and following the institutional guidelines following ethical approval by Sheffield Hallam University. Informed consent had already been obtained from the participants for the study published by Heaton et al.,6 which also applies to the present study according to ethics application ER17244422. Given the purpose of the Heaton et al. study,6 this dataset consisted of fingermarks from approximately 50/50 males/females deposited and kept under ambient environmental conditions until analysis which was completed within a month from deposition.2.2. Fingermark spectral processing for age determination modelling
Three spectra per individual were processed according to the Heaton et al.,6 method. In short, three marks were obtained per donor, each consisting of the summed total of three individual mass spectra acquisitions from three distinct matrix spots per fingermark. The resulting three marks per donor were then kept separate throughout the following statistical analysis.For each fingermark, peak-picking was performed in R using the MALDIquant package, including TIC normalization and spectral smoothing. Consistent with Heaton et al.,6 a range of S/N parameters (between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was used and required the peak occurrence rate across the spectra (between 1% and 90%) to be trialed, with each parameter set yielding a different count of included m/z positions to be analysed across the spectra (see Table 1 from Heaton et al.,6 for details on the number of remaining m/z positions per parameter set).
1) was used and required the peak occurrence rate across the spectra (between 1% and 90%) to be trialed, with each parameter set yielding a different count of included m/z positions to be analysed across the spectra (see Table 1 from Heaton et al.,6 for details on the number of remaining m/z positions per parameter set).
2.3. Age prediction models
Three distinct age prediction approaches have been considered (Fig. 1).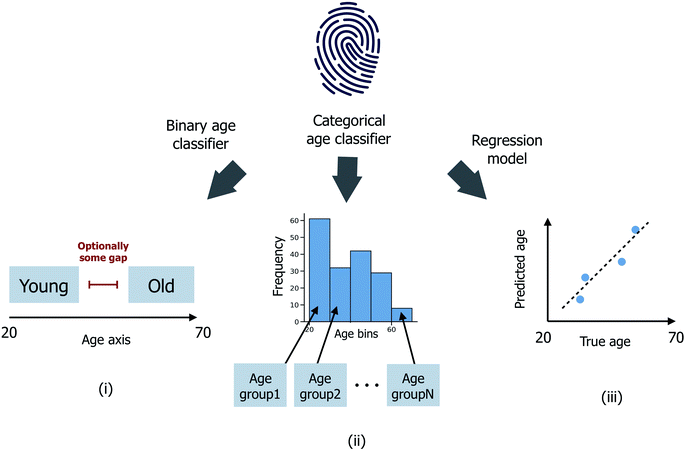 | ||
| Fig. 1 Schematic illustrating (i) binary age classification, (ii) multi-age group categorical age classification and (iii) age regression. Age is expressed in years. | ||
(i) Binary age classification: firstly, the donor ages have been divided into two distinct groups >μage + εσage (the ‘old’ class) and <μage − εσage (the ‘young’ class), where μage and σage are the mean and standard deviation of ages across all donors in the sample set, and ε ≥ 0 is a user-defined scaler, such that donors with intermediate ages in the range (μage − εσage, μage + εσage) are excluded from the model training/testing process. Classification models are then trained to predict whether each donor is ‘old’ or ‘young’;
(ii) Categorical age classification: extending from (i), donors have been split into nage ≥ 2 disjoint age groups G1, G2,…, Gnage of equal age width. Classification models are now trained to predict which age group Gi, for i ∈ {1,…,nage}, each donor is most probable to be assigned to. In the case where nage = 2, (ii) reduces directly to the binary classification problem (i) with ε = 0; (iii) age regression: models are instead trained to predict the integer age value for each donor.
In instances (i) and (ii), three classification model types have been trialed: a random forest classifier, an XGBOOST classifier, and also a dummy classifier provided by the sklearn python package, yielding a baseline for random model performance for comparison. In instance (iii), equivalent regressor models have been assessed for random forest, XGBOOST, in addition to a linear regression model (non-regularized as well as including L1 and L2 regularisations) and also a dummy baseline regressor provided by sklearn. In all cases, and identical to the training strategy presented in Heaton et al.,6k-fold cross validation (CV) was performed in the present study with k = 5. Since three separate fingerprint spectra were present per individual, and these could not be assumed to be independent, care was taken to ensure that all three spectra per individual remained within the same CV k fold throughout training, in order to preserve independence between all train and test sets. In contrast, only 1/3 randomly selected fingerprint spectra per individual was used from each test set fold to assess model performance, in order to best simulate the scenario when only one viable fingerprint sample has been extracted from a crime scene; a model which instead predicts an individual's age based on aggregated information taken from the 3 available fingerprint samples is less likely to be usable in a practical setting.
In instances (i) and (ii), the mean accuracy scored across the k = 5 hold-out test folds has been computed to assess model performances. In instance (iii), the mean squared error (MSE) and Pearson's R coefficient, again averaged over the k = 5 test CV folds, have been computed to assess model performance. A modified accuracy score has also been trialed in the case of the categorical model predictions, which has been constructed to also consider age bins that neighbor the correct age bin to also be correct, and thus mitigate unwanted boundary effects due to the artificial specification of “age bins”.
The effect of the inclusion of three distinct feature selection strategies on model performances was tested, with each strategy designed to identify the subset of m/z peaks that are most age-dependent: (a) the PLS-DA Variable Importance in Projection (VIP) score, (b) random forest feature importance derived from contributions of each feature to Gini impurity across trees, and (c) univariate feature selection via a chi-squared test. Care was taken to ensure that for the k-fold CV split, the fingerprint samples assigned to the training data subset were used for selection of features (m/z peaks), such that each test fold remained hidden during cross validation.
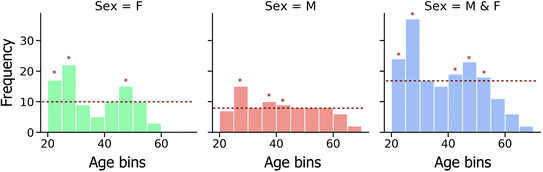
Furthermore, due to the non-uniform spread of ages within the investigated fingerprint sample set (Fig. 2), the effect of data imbalance on model performance has also been investigated. In a modified CV training strategy, training data folds are randomly down-sampled, such that the most represented age bins are identified and only a random subset of training instances from these age bins is used in model training, as illustrated in Fig. 2.
Since the underlying distribution of ages was qualitatively different between the female and male sample groups, to mitigate the risk that any downstream conclusions have been indirectly influenced by sex, age prediction models have been trained in the following analysis and evaluated separately for each sex group, in addition to being evaluated on the full sample group.
3. Results and discussion
The determination of the age of an individual could be crucial intelligence to narrow down the pool of suspects and identify a perpetrator. This is a poorly investigated topic, and fingerprints have never been taken into consideration as an analytical specimen to gather this type of information. In this study, within a strategy consistent with the sex prediction models presented in Heaton et al.,6 a series of supervised learning models have been trained, but here for the task of predicting the age of the donor associated with each mark. The same dataset previously acquired6 was used here for the purpose of gaining an initial understanding of the feasibility of such an investigation, prior to embarking on a large and time-consuming study. However, in contrast to the study by Heaton et al.,6 in which sex prediction was treated as a binary classification problem, three prediction approaches have been considered, as described in Section 2.4, namely (i) binary age classification; (ii) categorical age classification and (iii) age regression. The results from the application of these approaches are discussed in sections 3.1 to 3.3.3.1. Binary age predictions
In the most simplified treatment of the age prediction problem, a series of binary classification models were trained to classify fingerprint samples as “young” or “old”; here the sample ages are split into two disjoint groups, based on a specified interval around the mean age across all samples (calculated to be 38.1 years across both male and female samples and 40.7/35.8 for models restricted to the male/female sample subsets only). Clearly such a predictive model will have limited usefulness in a real-life practical setting; however this strategy (a) provides a baseline against which further models predicting for more informative age splits can be compared and (b) is directly analogous to the male/female sex classification models investigated previously by Heaton et al.6As illustrated in Fig. 3, 5-fold CV accuracy scores for both XGBOOST and random forest model schemes are consistently superior to random (the dummy classifier) for the task of binary age prediction. Predictive performance also appears to improve as the masked boundary region between the old and young groups, ((μage − εσage, μage + εσage)) increases above the lowest tested value of ε = 0.1, however, only for the female-sample model (Fig. 3(i)) does the median model performance (relative to random) consistently increase with increasing ε. This likely represents a tradeoff between the increasing width of the young/old boundary region and the significant reduction of available training data at high ε. As illustrated in Fig. S1,† at ε = 1.0, a significant proportion of the fingerprint samples have been discounted during model building/evaluation (with respect to the overall male & female combined median age and standard deviation), with only individuals aged <26 and >50 included.
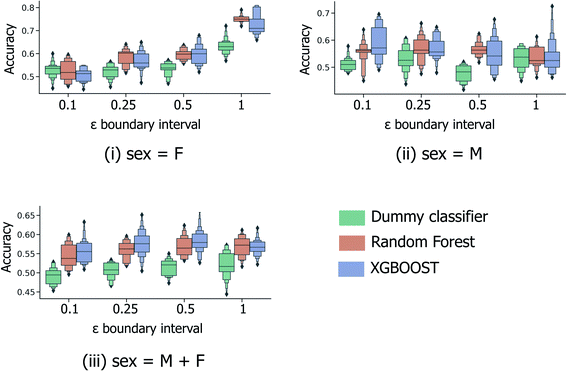 | ||
| Fig. 3 5-Fold cross validation performance results for binary classification models predicting binary old/young donor labels for XGBOOST, random forest and baseline dummy classification model types. Performance statistics are presented separately for models trained using (i) female-only and (ii) male-only data, in addition to (iii) the full sample set. Each x-axis illustrates the effect of ε, the parameter dictating the size of the masked sample region between the “young” and “old” age classes, (μage − εσage, μage + εσage). Each boxplot summarises the distribution in accuracy scores across all 4 feature selection strategies and peak picking strategies from Heaton et al.6 | ||
The performance statistics presented in Fig. 3 are comparable to the maximum/median 5-fold CV accuracy score for sex classification over the same sample set (65.6%/61.1%, Heaton et al.6), with the highest age-prediction performance over the full sample set (66.1%/57.9%, Fig. 3(iii)) being achieved by the XGBOOST model at ε = 0.5. However, in contrast to the aforementioned sex classification model, the practical usage of binary age classification is likely limited, particularly for models trained at high ε ≥ 0.5, whereby the model is trained to only distinguish between samples at the two extremities of the sample age distribution.
3.2. Categorical age predictions
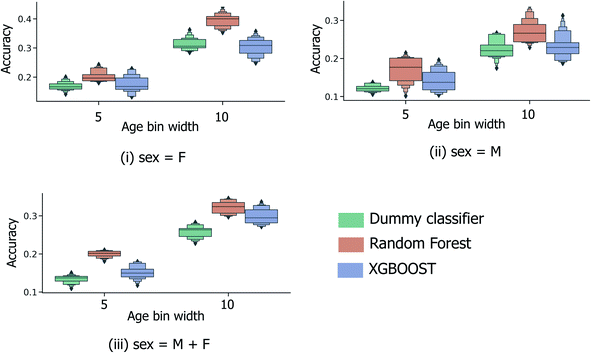
In order to be applicable in a practical setting, the development of models capable of more specific age group predictions is highly desirable. Due to the underlying mismatch between chronological and biological ages, anthropologists provide age information as an age range rather than a specific age.27 Therefore on this basis, and in consideration of the data obtained from the binary age prediction, the exploration of a categorical classification using bin widths of sizes (a) 5 years and (b) 10 years was deemed to be a reasonable approach. In Fig. 4, accuracy performances for random forest models consistently exceed the random baseline, for models trained separately on the male, female, or full sample sets. Interestingly, XGBOOST, which yields the highest performance in the binary age classification scenario (Fig. 3), did not exhibit similar superior performance in the categorical age scenario. Intuitively, accuracy scores diminish as the overall number of age bins increases (10-year vs. 5-year bins), such that the optimum age bin width becomes a tradeoff between the practical value (higher number of bins) and model performance.Fig. 5 shows the effect of counting predictions made in neighboring bins on the true age bin as also correct (through the use of the modified accuracy score presented in Section 1.2). Although the modified accuracy score is more tolerant to model errors, it can capture the potential usefulness of each model in a practical, crime scene setting, where a near miss age prediction can still be valuable. As expected, modified accuracy score values (including those for the random baseline model) are consistently higher than standard accuracy scores. However, the relative extent by which the XGBOOST and random forest models exceed baseline performance does not appear to significantly increase as the age bin width size increases, nor when neighboring age bins to the true age bin are also treated as correct. Moreover, in the case of larger age bins (Fig. 5(ii)), the modified accuracy score appears to be no better than random.
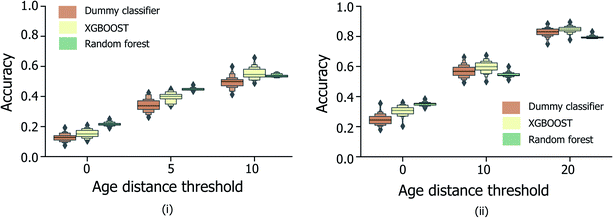 | ||
| Fig. 5 Distribution of categorical age prediction scores across XGBOOST, random forest and baseline dummy classification model types, for non-enhanced fingermark samples, and age bin widths (i) 5 and (ii) 10. For both bin widths, the effect of counting predictions made in neighboring bins within a specified age-difference of the true age (x-axis) to the true age bin are included, corresponding to the modified accuracy scores discussed in Section 1.2. The equivalent figure for the enhanced fingermark sample set in Heaton et al.,6 is presented in Fig. S3.† Age is expressed in years. | ||
To determine the influence of data imbalance on model performances shown in Fig. 4 and 5, the CV training/evaluation protocol was repeated, but with random under-sampling of highly represented age bins within each random k-fold data split. As illustrated by the data in Fig. S2i and ii,† under-sampling resulted in a reduction in model performances compared to the random baseline, consistently for different age bin sizes (5 and 10 years tested). It is suggested that any potential benefit from reducing age class imbalance was outweighed here by the low quantity of training data that remained following under-sampling, and consequent inability of each model to generalise to unseen test data.
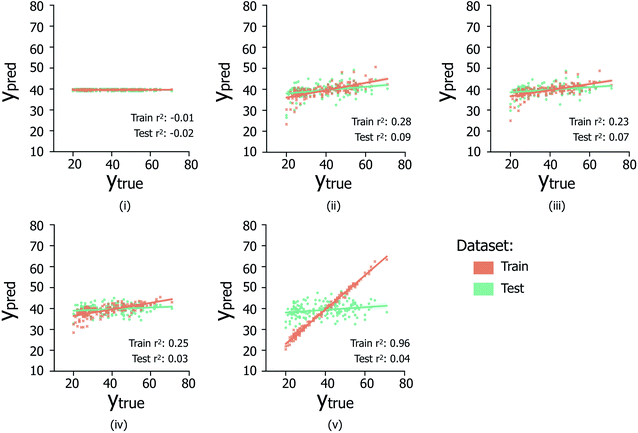
The data reported in Fig. 6 indicate the abilities of four regression model architectures to correctly generalise to unseen test data (Fig. 6(ii)–(iv)), compared to a random baseline regression model that simply predicts the mean of the training dataset (Fig. 6(i)); additional information referring to the breakdown of samples per contamination state, shown in Fig. S2iii and iv,† is illustrated in Table S1.† The presence of positive correlations between predicted and true age values for the training set data is not clearly extended to predictions made on the hidden test data (reflected by low test set Pearson's r2 values), indicating the inability of the trialed regression models to suitably generalize to unseen data. In the case of XGBOOST (Fig. 6(v)), significant overfitting to the training data is visible (train set Pearson's r2: 0.96), which is not replicated in other model types; however despite less train set overfitting, other models do not exhibit improved test set performances. Comparable poor regression performances were observed for models trained separately on the male and female sample subsets (data not shown). Overall it is suggested that the poor regression performances are likely due to the limited availability of data from which to infer age-related trends.
In conclusion, this study has investigated the potential viability of a range of supervised machine learning-based predictive methods to explore the problem of determining an individual's age based on MALDI MS spectra analysis of peptides and proteins in fingermarks. Whilst initial findings, using a binary (old/young) prediction model, yielded a predictive model that achieved competitive performance with previously reported sex-prediction models (66.1% and 65.6% maximum 5-fold CV accuracy scores for the age- and sex-classification models, respectively), this approach relied heavily on the artificial masking of a large intermediate age region of samples for such high performance (Fig. 3). In a practical crime scene setting, such a model is unlikely to be useful, since a significant number of real-life samples may fall into the masked intermediate region.
Alternatively, categorical prediction can be envisaged to provide a more informative and discriminative age prediction strategy for real-life samples. In the current initial analysis, categorical predictions are reported to consistently exceed random performance; with a 10-year age bin width, the maximum/median model performance is achieved by the random forest model type at 34.5%/32.4% (compared to the 28.3%/26.3% for the random dummy classifier). Whilst the highest attained model performance is currently inadequate for practical usage, these initial findings do indicate the existence of an underlying relationship between donor age and collected peptide/protein ions.
In this initial investigation, model performances are likely to be limited by (a) sample size and (b) the non-uniformity of the sex and age distributions across the sample set. Additionally, the exclusion of donors of age <18 years is actually creating a more difficult task for the predictive model (since the age range observed by the model is shorter). It would be very interesting to include <18 year old donors too in a further age related study, since the minor/adult age boundary (albeit a societal construct) could be used in a binary age classification set up similar to the “young/old” age boundary used in the current study.
It is also important to bear in mind for this kind of classification task, the likely impact of the unknown discrepancies between the true chronological age of each donor and the reported chronological ages. This circumstance would need to be addressed in future studies.
Finally, it is also possible, that although an average of 150 marks per week were analysed by MALDI MS, in the timeframe necessary to analyse the complete set of around 600 (1 month), some protein degradation may have occurred. As also implied by Antonine et al., the age of a mark could be impacting the human age estimation models due to the degradation of the molecules targeted as age markers, and this may be an issue for crime scenes that are not accessed promptly. Antoine et al.22 suggested that the preliminary determination of the age of the mark itself would be ideal to minimise this impact, though this intelligence remains itself a significant challenge in forensic science. Oonk et al.26 pinpointed five proteins in fingermarks that undergo chemical modifications with time, to the extent of being suggested as markers of time since deposition. However, 4/5 proteins belong to the keratin family and are not detected in the mass range explored by MALDI MS in the Heaton et al. study6 from which the data set was “borrowed” for the present study.
Notwithstanding, the observations made in this initial study justify the likely benefits of a larger-scale age determination targeted study that is designed to explicitly mitigate these aforementioned limiting factors.
4. Conclusions
Overall, this preliminary study indicates that, to appropriately address the attribution of age to an individual, a larger cohort of donors as well as a much more balanced age group distribution is needed, in order to improve the performance of the modelling approaches, particularly of the categorical approach. However, it is also possible that, even with such a cohort of donors, peptides and proteins may still not be sufficiently performing biomarkers for human age determination as they too could be affected by the underlying mismatch between the chronological age and biological age. Biological age can significantly differ from chronological age, and, as such, the approximation to the chronological age can be particularly challenging and worrying when this intelligence is to be used to narrow down the pool of suspects. In a future and more comprehensive study this issue could be mitigated by determining both biological and chronological age to develop a method allowing a relationship between chronological and biological age to be established, ultimately “adjusting” the output of the modelling strategy to align it to the true chronological age. Having access to the biological age data would also permit the design of a model that predicts biological age from mass spectral data and reports to chronological age; it would be of great interest to explore whether such a predictive method could be more/less accurate than other chronological → biological age conversion approaches. However, as already discussed, it is important to highlight that the assessment of the biological age is, in itself, complex and not an exact science; many approaches have been reported, some in combination, with some kits commercially available, mainly detecting epigenetic markers. The authors envisage a minimally invasive assessment in collaboration with a physician based on (1) conventional laboratory blood tests (cholesterol and triglyceride levels, glycaemia etc.), (2) quantification of 5-hydroxymethylcytosine using standards kits and/or using published HPLC based methods, involving collection of saliva and/or blood, and (3) physiological assessments (heart rate, blood pressure, BMI, diet, lifestyle, and exercise) including patient's anamnesis.The study illustrated here represents the first stepping stone in this specific “criminal chemical profiling” application of fingerprinting by MALDI MS, and the results have revealed the appropriate design for further experiments to assess its potential to deliver yet more personal information about an individual from their fingermarks.
Conflicts of interest
There are no conflicts of interest.References
- D. R. Ifa, N. E. Manicke, A. L. Dill and R. G. Cooks, Science, 2008, 321(5890), 805 CrossRef CAS PubMed.
- S. Francese, R. Bradshaw, L. S. Ferguson, R. Wolstenholme, S. Bleay and M. R. Clench, Analyst, 2013, 138, 4215 RSC.
- S. Francese, Aust. J. Forensic Sci., 2019, 51, 623 CrossRef.
- K. C. O'Neill, P. Hinners and Y. J. Lee, Anal. Methods, 2020, 12, 792 RSC.
- L. S. Ferguson, F. Wulfert, R. Wolstenholme, J. M. Fonville, M. R. Clench, V. A. Carolan and S. Francese, Analyst, 2012, 137, 4686 RSC.
- C. Heaton, C. Bury, E. Patel, R. Bradshaw, F. Wulfert, R. M. Heeren, L. Marchant, N. Denison, R. McColm and S. Francese, Forensic Chem., 2020, 20, 1 Search PubMed.
- W. R. Maples, The practical application of age-estimation techniques, in Age Markers in the Human Skeleton, ed. M. Y. Iscan, Charles C. Thomas Publishers, Springfield, IL, 1989, pp. 319–324 Search PubMed.
- A. Schmeling, W. Reisinger, W. Loreck, K. Vendura, W. Markus and G. Geserick, Int. J. Leg. Med., 2000, 113, 253 CrossRef CAS PubMed.
- F. Introna and C. P. Campobasso, Biological vs. legal age of living individuals, in Forensic Anthropology and Medicine: Complementary Sciences from Recovery to Cause of Death, ed. A. Schmitt, E. Cunha and J. Pinheiro, Humana Press, Inc., Totowa, NJ, 2006, pp. 57–82 Search PubMed.
- L. Jia, W. Zhang and X. Chen, Clin. Interventions Aging, 2017, 12, 759 CrossRef PubMed.
- R. S. Ashiqur, P. Giacobbi, L. Pyles, C. Mullett, G. Doretto and D. A. Adjeroh, Brief Bioinform, 2021, 22(2), 1767 CrossRef PubMed.
- I. Solovev, M. Shaposhnikov and A. Moskalev, Mech. Ageing Dev., 2020, 185, 111192 CrossRef CAS PubMed.
- B. E. Koop, A. Reckert and J. Becker, et al. , Int. J. Leg. Med., 2020, 134, 2215 CrossRef PubMed.
- M. R. Branco, G. Ficz and W. Reik, Nat. Rev. Genet., 2012, 13, 7 CrossRef CAS PubMed.
- D. L. van den Hove, L. Chouliaras and B. P. Rutten, Curr. Alzheimer Res., 2012, 9, 545 CrossRef CAS PubMed.
- J. Xiong, H. P. Jiang, C. Y. Peng, Q. Y. Deng, M. D. Lan, H. Zeng, F. Zheng, Y. Q. Feng and B. F. Yuan, Clin. Epigenet., 2015, 7, 72 CrossRef PubMed.
- Technologies for Fingermark Age Estimations: Strengthening the Reliability of Crime Evidence, ed. J. De Alcaraz-Fossoul, Springer, Cham, Switzerland, 2021 Search PubMed.
- M. E. Stewart, W. A. Steele and D. T. Downing, J. Invest. Dermatol., 1989, 92, 371 CrossRef CAS PubMed.
- E. Jacobsen, J. K. Billings, R. A. Frantz, C. K. Kinney, M. E. Stewart and D. T. Downing, J. Invest. Dermatol., 1985, 85, 483 CrossRef CAS PubMed.
- A. M. Bohanan, Journal of Forensic Identification, 1998, 48, 570 Search PubMed.
- M. V. Buchanan, K. Asano, and A. Bohanon, Chemical characterization of fingerprints from adults and children, United States: N. p., 1996, accessed at https://www.osti.gov/servlets/purl/443195on17/01/2022 Search PubMed.
- K. M. Antoine, S. Mortazavi, A. D. Miller and L. M. Miller, J. Forensic Sci., 2010, 55, 513 CrossRef CAS PubMed.
- D. K. Williams, R. L. Schwartz and E. G. Bartick, Appl. Spectrosc., 2004, 58, 313 CrossRef CAS PubMed.
- A. Hemmila, J. McGill and D. Ritter, J. Forensic Sci., 2008, 53, 369 CrossRef CAS PubMed.
- R. Chernoff, J. Am. Coll. Nutr., 2004, 23, 627S CrossRef CAS PubMed.
- S. Oonk, T. Schuurmans, M. Pabst, L. C. P. M. de Smet and M. de Puit, Sci. Rep., 2018, 8, 16425 CrossRef PubMed.
- E. Priya, Forensic Research & Criminology International Journal, 2017, 4, 41 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ay02002a |
| ‡ Present address: Exscientia Oxford, UK. |
| § Present address: Foster + Freeman, Evesham, UK. |
| This journal is © The Royal Society of Chemistry 2022 |