Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bridging the interfacial gap in mixed-matrix membranes by nature-inspired design: precise molecular sieving with polymer-grafted metal–organic frameworks†
Levente
Cseri
 a,
Rifan
Hardian
a,
Rifan
Hardian
 b,
Shizuka
Anan
b,
Shizuka
Anan
 c,
Hakkim
Vovusha
c,
Hakkim
Vovusha
 d,
Udo
Schwingenschlögl
d,
Udo
Schwingenschlögl
 d,
Peter M.
Budd
d,
Peter M.
Budd
 e,
Kazuki
Sada
e,
Kazuki
Sada
 cf,
Kenta
Kokado
cf,
Kenta
Kokado
 gh and
Gyorgy
Szekely
gh and
Gyorgy
Szekely
 *ab
*ab
aDepartment of Chemical Engineering and Analytical Science, University of Manchester, The Mill Sackville Street, Manchester, M1 3BB, UK. E-mail: gyorgy.szekely@manchester.ac.uk
bAdvanced Membranes & Porous Materials Center, Physical Science Engineering Division (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia. E-mail: gyorgy.szekely@kaust.edu.sa; Web: http://www.szekelygroup.com Web: http://www.twitter.com/SzekelyGroup Tel: +966128082769
cDepartment of Chemical Sciences and Engineering, Graduate School of Chemical Sciences and Engineering, Hokkaido University, Kita 10, Nishi 8, Kita-ku, Sapporo, 060-0810, Japan
dPhysical Science Engineering Division (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia
eDepartment of Chemistry, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
fFaculty of Science, Hokkaido University, Kita 10, Nishi 8, Kita-ku, Sapporo, 060-0810, Japan
gResearch Institute for Electronic Science, Hokkaido University, Kita 20, Nishi 10, Kita-ku, Sapporo, 001-0020, Japan
hJST, PRESTO, Honcho 4–1-8, Kawaguchi, Saitama 332-0012, Japan
First published on 2nd September 2021
Abstract
Membrane technology is a dynamically developing field of separation science that is poised to result in new and efficient processes, energy and cost savings, and sustainability benefits. A key challenge in this field is the development of highly selective membranes, which can be addressed by the development of mixed-matrix membranes (MMMs) containing fillers such as metal–organic frameworks (MOFs). However, the lack of interfacial adhesion causes nanosized gaps between the filler and the polymer matrix. In this study, we aim to elucidate the intrinsic properties of MMMs and bridge the gap between their material constituents. A series of novel membranes comprising MOF nanoparticles with similar chemical and morphological properties but increasing pore size (UiO-66–68-NH2) were prepared. The nanoparticles' surface was covalently grafted with poly(N-isopropylacrylamide) (PNIPAM) chains, which could then become entangled with the membranes' polymer matrix. Morphological characterization and organic solvent nanofiltration tests revealed that membranes with PNIPAM-grafted fillers do not suffer from the formation of pinholes at the filler–matrix interface that are detrimental to the filtration performance. For the first time, the experimental results showed an excellent match with a predictive model of nanofiltration built around the premise of liquid transport through the highly ordered pores of the MOF filler.
Introduction
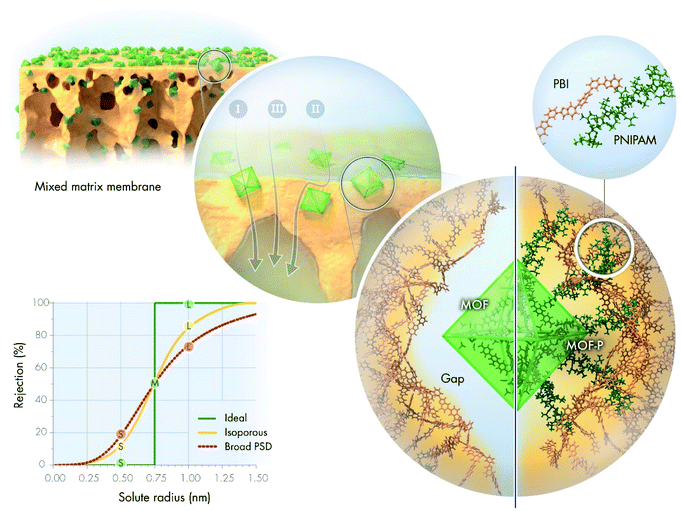
The development of sustainable and economic alternatives to conventional separation methods is a continuing challenge of the 21st century because these processes account for 40–70% of the total capital and operational cost of chemical plants.1 Membrane-based technologies are expected to consume 90% less energy than distillation.2 Organic solvent nanofiltration (OSN) is of particular importance in the petrochemical and pharmaceutical industries and is used for molecular size-dependent separation, including diluent fractionation, solvent exchange and recycling, product purification and concentration, and catalyst recovery.3The performance of OSN membranes is characterized by solvent permeance and rejection of solutes. The latter is often described by the molecular weight cut-off (MWCO) curve (Fig. 1). The shape of the MWCO curve determines the overall efficiency of separation. Solvents and low-molecular-weight solutes are collected in the permeate stream, which requires low rejection values (ideally, close to zero). On the contrary, high-molecular-weight compounds are expected to have high rejection values (close to 100%) to perfectly remain in the retentate stream. In general, the larger the difference in rejection values between the solutes, the more efficient the separation process. An ideal MWCO curve comprises distinct regions of zero and complete rejection, separated by a sharp transition region. Although the prevalently used pore flow model for membrane transport predicts that such a scenario is impossible for real separation, some researchers suggested that it can be approximated using membranes with a uniform pore size.4–6 Nonetheless, there is a general agreement, which is also supported by the pore flow model, that broader pore size distribution (PSD) results in a wider, more gradual transition region, and thus less efficient separation.7,8 Consequently, although the ideal rejection scenario is not practically achievable, isoporous membranes are the best candidates for highly selective separation.
Mixed-matrix membranes (MMMs) have become the center of scientific attention in an attempt to combine the flexibility and processability of polymer membranes with the well-defined pore structure of crystalline materials. Among crystalline materials, metal–organic frameworks (MOFs) are of particular interest owing to their intriguing properties.9,10 The endless combinations of organic linker–metal-ion pairs allow tailoring the crystal morphology, aperture size, surface area, surface chemistry, and stability to suit various applications.11 The aperture size of MOFs ranges from 0.3 to 3 nm, with a few exceptions, which places them firmly in the nanofiltration regime.12 Research into MOF-based MMMs for both aqueous and organic nanofiltration is gradually increasing (Fig. S68 and S69†). However, the role of MOF fillers is yet to be fully understood. Many researchers have argued that the improved permeance can be attributed to solvent permeation through the internal pores of MOFs, but without providing direct evidence.13,14 Some scholars have suggested that excess solvent permeation is the result of either interfacial gaps between the fillers and polymer matrix15 or the increased filtration surface area.16 Altered membrane hydrophilicity,17 surface charge and crosslinking degree have also been suggested to be important.18 The presence of simple inorganic metal salts during interfacial polymerization has a similar effect on the membrane performance as MOFs themselves.19 Sorribas et al. compared the OSN performance of composite membranes using MOFs with different pore sizes.14 Permeance proportionally improved with increasing pore volume, which indicates considerable permeation through the pores of MOFs. However, other researchers have reported comparable performance using a series of different MOFs.20 In both studies, MOFs had different crystal structures, particle sizes, metal ions, and organic linkers, which make it more difficult to draw conclusions because multiple effects other than the pore size influence the results. Currently, there is no direct evidence on how much the intrinsic pores of MOF crystals contribute to the overall permeance. Nevertheless, a systematic investigation of the pore size that eliminates other variables can provide new insights. While the prevalence of different permeation pathways in MMMs is still a subject of investigation, there is general consensus in the literature that filler aggregation results in compromised membrane performance due to the lower selectivity regions introduced by the aggregates.21 Several strategies have been attempted to overcome undesired aggregation, such as the crosslinking of MOFs,22 their hydrophobic modification,23,24 functionalization of the polymer for better interfacial adhesion,25,26 pre-deposition of MOFs in the thin-film composite sublayer,27,28 and in situ growth of MOFs in the pores or on the surface of membranes.29–31
In the present study, a series of MMMs were prepared using polybenzimidazole (PBI) and Zr-based MOFs of the UiO-series. The selected MOFs (UiO-66-NH2, UiO-67-NH2, and UiO-68-NH2) were developed to have identical crystal morphology, identical metal clusters, and analogous organic linkers of various lengths and, thus, similar surface and pore chemistries, but different pore sizes. This enabled the investigation of the effects of aperture size and porosity on the molecular sieving performance in the resulting MMMs. These MOFs also have a high degree of crystal symmetry as well as excellent mechanical and chemical stability, which makes them an ideal choice for filler materials. Similarly, PBI is commonly used for nanofiltration membranes owing to its favorable mechanical and chemical properties.
The increasing scientific and engineering interest in nature's intriguing systems prompted us towards a nature-inspired solution to bridge the gap in MMMs. The strategy to avoid filler aggregation and ensure good interfacial adhesion between the crystalline MOFs and the PBI matrix was inspired by a natural phenomenon. The calcified cementum in the tooth is connected to the surrounding tissues by collagen fibers originating from the cementoblast layer on its surface (Fig. S2†). These fibers are intermingled in the periodontal ligament with the collagen fibers stemming from the surrounding tissues to ensure excellent adhesion between the different materials. These natural polypeptide fibers help the tooth remain embedded in the jaw. Analogously, the external surface of MOFs was grafted with poly(N-isopropylacrylamide) (PNIPAM). PNIPAM is a promising candidate for polymer grafting owing to its interesting hydrogen bonding properties and its facile synthesis via reversible addition–fragmentation chain-transfer (RAFT) polymerization.32–34 Systematic investigation of interactions among the MMM constituents as well as their effect on the separation performance will facilitate the understanding of MOF composite membranes.
Results and discussion
Nanoengineering of MOF-PNIPAM fillers
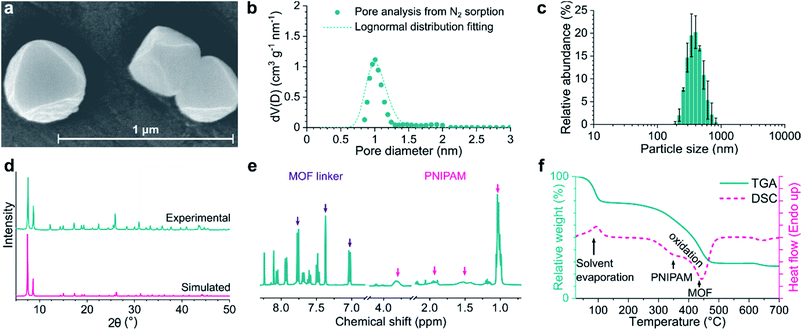
Introduction of amino groups in the organic linker of MOFs is a common strategy for functionalization. Among the organic linkers required to synthesize UiO-66-NH2, UiO-67-NH2, and UiO-68-NH2, only 2-aminoterephthalic acid was commercially purchased, while the other two were synthesized on a multigram scale. In contrast to the multistep synthesis reported in the literature,35,36 2-amino-[1,1′-biphenyl]-4,4′-dicarboxylic acid (bpdc-NH2) and 2′-amino-[1,1′:4′,1′′-terphenyl]-4,4′′-dicarboxylic acid (tpdc-NH2) were obtained via single Suzuki–Miyaura reactions with good yields of 64–90% without the need for column chromatography. The MOFs were synthesized using the solvothermal synthetic method and benzoic acid or acetic acid as a crystal growth modulator. Solvothermal synthesis enables excellent control over the crystal size and morphology at the laboratory scale and is thus the most suitable.37 The acidic modulator promoted the formation of reasonably monodisperse octahedral crystals with well-defined size and morphology. PNIPAM was synthesized using RAFT polymerization, which resulted in high monodispersity, as indicated by the size exclusion chromatography results (Mw/Mn = 1.31; see Fig. S30†). NMR spectra of the polymer confirmed the presence of N-hydroxysuccinimide (NHS) ester end groups, demonstrating their inertness during RAFT polymerization (Fig. S7 and S8†). NHS ester activation is ideal for the modification of amino-group-containing MOFs because strong acid is not formed during the reaction that can otherwise degrade the MOF crystals.Powder X-ray diffraction (PXRD) analysis of the synthesized MOFs as well as their PNIPAM-grafted counterparts revealed a highly crystalline structure (Fig. 2d and S33†). PXRD patterns confirmed the expected crystal structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group) and retained crystallinity after PNIPAM grafting. Fourier-transform infrared spectroscopy (FTIR) showed the appearance of characteristic aliphatic C–H stretching vibrations in the 2900–3000 cm−1 range in the spectra of PNIPAM-grafted MOFs (Fig. S27†). HF-digested NMR spectra showed the presence of CH peaks, which correspond to the PNIPAM polymer; however, the signal of the NHS group (2.81 ppm) was not observed, suggesting a successful reaction between the polymer chains and MOFs (Fig. 2e and S7–S20†). The PNIPAM content of the grafted MOFs and their surface coverage were calculated using NMR and elemental analysis data, as well as by taking geometric considerations into account. The PNIPAM content was in the range of 13–26 wt% with a surface density of 2.8–4.7 chain per nm2 MOF surface for all grafted MOFs. According to the thermal analysis (Fig. 2f and S45†), ungrafted MOFs degraded in a single step with an onset at approximately 350–400 °C, leaving ZrO2 as solid residue. This weight loss step can be attributed to the exothermic oxidation of the organic linker molecules. In the case of PNIPAM-grafted MOFs, an additional exothermic weight loss step was observed at approximately 250–300 °C, which is ascribed to PNIPAM oxidation.
m space group) and retained crystallinity after PNIPAM grafting. Fourier-transform infrared spectroscopy (FTIR) showed the appearance of characteristic aliphatic C–H stretching vibrations in the 2900–3000 cm−1 range in the spectra of PNIPAM-grafted MOFs (Fig. S27†). HF-digested NMR spectra showed the presence of CH peaks, which correspond to the PNIPAM polymer; however, the signal of the NHS group (2.81 ppm) was not observed, suggesting a successful reaction between the polymer chains and MOFs (Fig. 2e and S7–S20†). The PNIPAM content of the grafted MOFs and their surface coverage were calculated using NMR and elemental analysis data, as well as by taking geometric considerations into account. The PNIPAM content was in the range of 13–26 wt% with a surface density of 2.8–4.7 chain per nm2 MOF surface for all grafted MOFs. According to the thermal analysis (Fig. 2f and S45†), ungrafted MOFs degraded in a single step with an onset at approximately 350–400 °C, leaving ZrO2 as solid residue. This weight loss step can be attributed to the exothermic oxidation of the organic linker molecules. In the case of PNIPAM-grafted MOFs, an additional exothermic weight loss step was observed at approximately 250–300 °C, which is ascribed to PNIPAM oxidation.
All MOFs exhibited monodisperse particle size distributions with a mean diameter of 452–771 nm (Fig. 2c and Table S2†). While polymer grafting can increase the particle size in theory, it also increases dispersibility by mitigating aggregation and, thus, has an opposite effect on the effective size. We observed no net change in the particle size as a result of PNIPAM grafting. However, the zeta potential systematically increased after polymer grafting by 26–61% to +54.3, +24.3, and +41.6 mV for UiO-66-PNIPAM, UiO-67-PNIPAM, and UiO-68-PNIPAM, respectively. The higher absolute value of zeta potential indicates better colloidal stability and less aggregation, which is essential for the production of MMMs with good filler distribution. Scanning electron microscopy (SEM) revealed regular octahedral crystals, which is in line with the sharp PXRD peaks attesting the crystallinity of MOFs (Fig. 2a). The submicron crystal size observed via SEM was also consistent with the DLS analysis. SEM micrographs showed no significant difference in size or shape between the pristine and PNIPAM-grafted MOF crystals. While UiO-66-type MOF crystals appeared highly regular, some deformation of the octahedral structure and the presence of amorphous or polymorph phases on the surface of the crystals were observed in the case of UiO-67- and UiO-68-type MOFs. Susceptibility to more severe electron beam damage owing to the longer organic linkers, as opposed to the one in UiO-66-type MOFs, may explain this phenomenon. Alternatively, pore collapse and recrystallization may occur in the MOFs with high internal free volume upon the evaporation of the adsorbed solvent under the high vacuum required for SEM.38 Therefore, the UiO-67- and UiO-68-type MOFs were stored under solvent and used as a suspension to prevent possible pore collapse and loss of crystallinity. Nitrogen sorption experiments revealed microporosity (Fig. 2b) and high surface area, which were consistent with the fully crystalline MOF structures. The specific surface area and pore volume somewhat decreased after PNIPAM grafting. Both these quantities are calculated on a mass basis; therefore, the incorporation of a nonporous polymer was expected to result in their decrease. Furthermore, polymer chains may block some of the pores on the surface. Nonetheless, the surface areas of all MOFs remained high: 766–2045 and 533–1082 m2 g−1 for the pristine MOFs and PNIPAM-grafted counterparts, respectively.
Three pillars of molecular design
The interactions within the MOF surface–polymer membrane matrix–solvent nexus are critical to achieve efficient molecular sieving (Fig. 3). An ideal solvent possesses (i) good miscibility with water to allow membrane production via phase inversion, (ii) good solvency for both PBI and PNIPAM, and (iii) enables strong interactions between the two polymers. The latter criterion mitigates the formation of interfacial gaps in MMMs. Therefore, the membrane-forming suitability of a series of conventional and green polar aprotic solvents were assessed through solubility testing and density functional computations. Polymer interactions in N,N-dimethylformamide (DMF), dimethyl sulfoxide (DMSO), Cyrene, γ-valerolactone (GVL), N-methyl-2-pyrrolidone (NMP), propylene carbonate, PolarClean, and sulfolane solvents were studied. The calculated binding energies for the PBI–solvent, PNIPAM–solvent, PBI–PNIPAM–solvent, PBI–PBI–solvent, PNIPAM–PNIPAM–solvent, and solvent–solvent complexes along with the highest binding energy complex for each case are shown in Fig. S48–S53.† The solvent–solvent binding energy is lower than that of PBI/PNIPAM–solvent, which reveals that solvent molecules dissociate themselves, followed by complex formation with the polymers. Based on the binding energies and practical solubility limitations, DMAc was selected for the membrane fabrication process.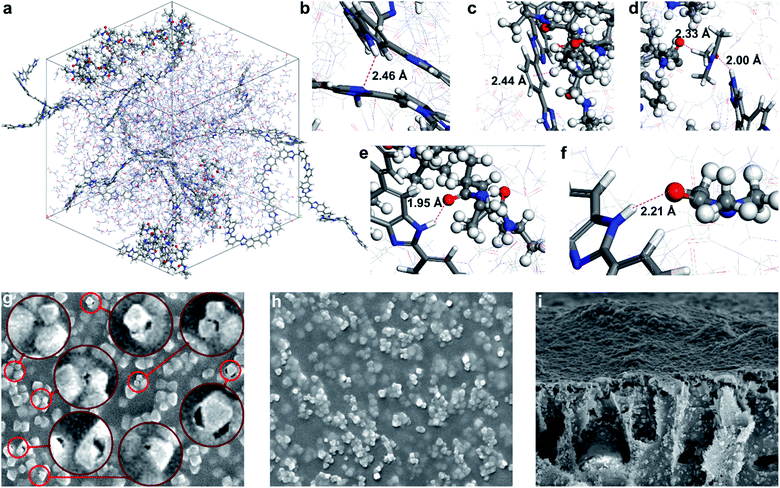 | ||
| Fig. 3 (a) Simulation cell comprising PBI and PNIPAM chains in DMAc solvent. Hydrogen bond and CH–π interactions observed in the simulation cell: (b) intramolecular hydrogen bond in PBI: NH–N, (c) CH–π interaction: Ar ring (PBI)–CH(PNIPAM). (d) Hydrogen bond: (PNIPAM)CO–H(DMAc) and (DMAc)CO–HN(PBI), (e) hydrogen bond: (PBI)NH–CO(PNIPAM), and (f) hydrogen bond: (PBI)NH–CO(DMAc). (g) Interfacial gaps between the MOF filler and PBI matrix in the absence of PNIPAM and (h) defect-free surface with a PNIPAM-grafted filler in the SEM images of M66N and M66P membranes, respectively, (both 10 μm × 8 μm; see Fig. S43† for other membranes). (i) Cross-sectional SEM image of the M66P membrane (20 μm × 16 μm). | ||
During molecular dynamics simulation, coil-like and globule-like structures were observed for PBI and PNIPAM, respectively. The intramolecular hydrogen bonding between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and NH groups of PNIPAM favors the formation of globule-like structures, whereas PBI forms coil-like structure owing to the rigidity of the fully aromatic backbone. Bonding interactions between the NH(PBI) and C
O and NH groups of PNIPAM favors the formation of globule-like structures, whereas PBI forms coil-like structure owing to the rigidity of the fully aromatic backbone. Bonding interactions between the NH(PBI) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(PNIPAM), NH(PBI) and C
O(PNIPAM), NH(PBI) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(DMAc), NH(PBI) and N(PBI) groups in the simulation cell are shown in Fig. 3b–f. In addition, the DMAc molecule favorably interacts with both PBI and PNIPAM through hydrogen bonds, and with the PBI–PNIPAM complex stabilized via CH–π interaction.
O(DMAc), NH(PBI) and N(PBI) groups in the simulation cell are shown in Fig. 3b–f. In addition, the DMAc molecule favorably interacts with both PBI and PNIPAM through hydrogen bonds, and with the PBI–PNIPAM complex stabilized via CH–π interaction.
Having selected the solvent, MMMs were fabricated by subsequent blending, solution casting, and non-solvent induced phase separation. All membranes were prepared identically using DMAc, PBI and various MOF nanoparticles to allow the membrane performance to be linked to the filler properties. High filler loading of 67 wt% (on dry-weight basis) was used to maximize its contribution during molecular sieving. Membranes were labeled using the following convention: M{sequential number of MOF in the UiO-series}{filler modification; i.e., N: MOF–NH2, P: MOF–PNIPAM}. SEM and atomic force microscopy indicated an even distribution of the filler in the polymer matrix irrespective of the PNIPAM grafting. Nevertheless, higher surface roughness (both Ra and Rq) was observed for PNIPAM-containing MMMs compared to their pristine counterparts (Fig. S47†). The higher roughness can be mostly attributed to the presence of MOF fillers bulging out of the membrane surface (Fig. 3g–h); the larger the filler, the higher the roughness. In all cases, the fillers retained their octahedral crystal structure during the membrane fabrication process. Top-section SEM images of the M66N, M67N, and M68N membranes revealed interfacial gaps in the selective layer around the MOF particles (Fig. 3g and S43†). These defects can be attributed to the poor interfacial adhesion between the ungrafted MOFs and polymer matrix. In contrast, no interfacial gaps were observed around the fillers in the M66P, M67P, and M68P membranes, which underlines the significance of PNIPAM grafting and PBI–PNIPAM entanglement.
Molecular sieving performance
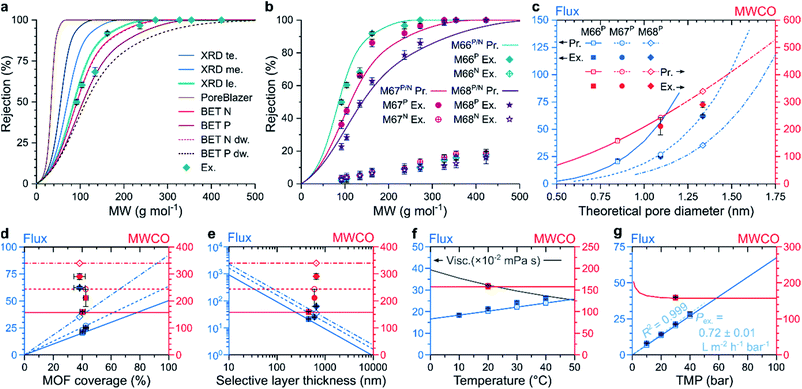
To study the effect of MOF micropores on molecular sieving, a predictive model was created to simulate nanofiltration through MMMs at different operational parameters that correlates structural properties with filtration performance. The pore flow model developed by Bowen and Welfoot was employed,39 and adjusted to describe the nanofiltration process (Section 20 in the ESI†). The agreement between the experimental rejection values and predicted MWCO curves was investigated using eight pore size estimation methods (Fig. 4a). It was found that the models based on larger pore size estimates predicted the molecular sieving performance more accurately. Overall, the solute rejections matched best with the pore size estimate obtained as the inscribed circle of the centers of the middle two carbon atoms in the linker molecules at the apertures of the MOF crystal structure. Both predictions and experimental results exhibited a downward shift in the solute rejections with increasing MOF linker lengths, following the M66P, M67P, and M68P order (Fig. 4b). Accordingly, lower rejections were coupled with higher solvent permeance (Fig. S58†). Both observed shift in rejection and increase in permeance suggest that permeation occurs through the increasingly larger pores of the MOF fillers in the studied membrane series. On the contrary, the M66N, M67N, and M68N membrane series exhibited poor rejection profiles (lower than 20%) and more than an order-of-magnitude higher permeance owing to the interfacial gaps around the MOF particles (Fig. 3g). No such interfacial gaps were observed in the membranes containing PNIPAM-grafted MOFs, which highlights the importance of interfacial adhesion in MMMs to ensure permeation through the uniform pores of the filler, as hypothesized in Fig. 1a and S1.†Owing to the good match with experimental results, the transport model can be used to computationally explore the effects of variable parameters on the filtration performance. Because the model assumes permeation through the pores of the MOF crystals, both flux and MWCO of the membranes depend on the pore size (Fig. 4c). The MWCO value is expected to change approximately linearly with the pore size. However, the flux is quasi proportional to the square of the pore size, which indicates that the quest for lower MWCO values results in quadratically diminishing flux. The flux predictions consider the filler particle size and coverage of MMMs (see Section 20 in the ESI†), which vary among the M66P, M67P, and M68P membranes. Therefore, their predicted flux–pore–diameter curves do not overlap. In contrast, the MWCO values do not depend on these parameters; thus, hypothetically adjusting the filler pore size of the M66P, M67P, and M68P membranes to the same value would result in the same MWCO irrespective of the different particle size and coverage. The prediction accuracy of the transport model was found to be exceptionally good for M66P and M67P, whereas M68P showed somewhat lower MWCO and higher flux than predicted.
The flux linearly increased with MOF coverage, as shown in Fig. 4d. Because the model assumes permeation through MOF particles, an increase in their proportion in the membrane top layer would result in larger effective filtration area per unit membrane area and, thus, increased flux. From the SEM top-section image analysis, it was found that the MOF coverage of the fabricated membranes ranged from 37.3 ± 3.6% for M66N to 42.4 ± 1.7% for M67P (Table S5†). The similar coverage values for three membranes were achieved through identical filler loading (67 wt%). The length of the pores through which permeation (described by the Hagen–Poiseuille equation) occurs is approximated from the MOF particle size. Consequently, the flux is inversely proportional to the pore length or MOF particle size (Fig. 4e). Therefore, according to the model assumptions, high loading of small MOF particles is desirable for high-permeance membranes. In practice, the ranges of attainable loadings and particle sizes are limited by membrane integrity considerations and by the control over the MOF crystal growth.
The flux increased with increasing temperature owing to lower viscosity according to the pore flow model (Fig. 4f). The experimental data for M66P in acetone followed this trend; however, the gradient of flux increase was slightly higher than that predicted by the model. Changing the solvent medium from acetone to acetonitrile or methanol is predicted to result in lower fluxes owing to higher viscosities (Fig. S64†). Although accounted for in the model, the effect of molecular size difference between three selected solvents on the flux is negligible. The MWCO value showed small variation with temperature and solvent. In line with the Hagen–Poiseuille equation, the model predicts direct proportionality between transmembrane pressure and flux. Experimental solvent flux data showed excellent linearity with an R2 of 0.999 for a linear fit through the origin. The observed permeance of 0.72 ± 0.01 L m−2 h−1 bar−1 agrees well with the 0.67 L m−2 h−1 bar−1 value predicted by the model. The MWCO value was predicted to be nearly constant in the nanofiltration pressure range with a slight increase at very low transmembrane pressures, where convection is less prevalent compared to diffusion.
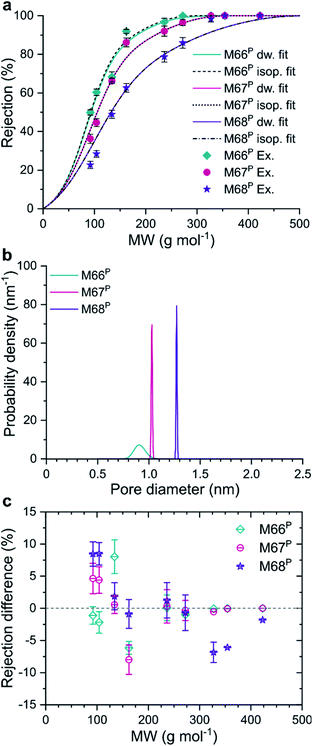
The model equations were also used to gain information on the pore size of the membranes using experimental rejection data. The fitted log-normal PSDs of the M66P, M67P, and M68P membranes were characterized by very low standard deviations (σ*), as shown in Fig. 5b. In fact, the comparison of the fitted MWCO curves with those of isoporous membranes with the same mean pore diameter reveals that these MMMs can be practically considered as isoporous membranes (Fig. 5a). The deviation of the fitted MWCO curves from the experimental values was found to be dependent on the molecular weight (Fig. 5c). The fitted pore flow model tends to overestimate and underestimate the rejection at lower and higher molecular weights, respectively. This phenomenon suggests that real membranes with narrow PSD (e.g., M66P, M67P, and M68P) can achieve even better selectivity than predicted by the pore flow model.
Regarding the question of permeation pathways, the experimental results and their comparison with the model calculation suggest that permeation occurs through the internal pores of MOF crystals; the reasonably good match between the predicted rejection and permeance trends is strong evidence. Both MWCO and permeance increased among the membranes with increasing pore size of the MOF filler; the membranes were similar in every other aspect. Furthermore, fitting an MWCO curve to the experimental data with a model that assumes log-normal PSD gave extremely narrow distributions. The obtained isoporosity indicates highly ordered internal structure or crystallinity of the filtration channels. This would not be expected if permeation occurred mostly through the polymer matrix or interfacial gaps. In pure polymer membranes, the malleability of pore walls manifests itself in the compaction phenomenon. Compaction results in (i) a decrease in permeance over the initial membrane conditioning and (ii) lower permeance with increasing pressure. Neither of these effects was observed for the M66P, M67P, and M68P membranes. The flux showed excellent linearity with the transmembrane pressure, i.e., constant permeance in the 10–40 bar nanofiltration range.
Conclusion
To realize the fabrication of selective molecular sieves as MMMs from MOFs, the contribution of the filler in the separation needs to be maximized. The MOF fillers used in this study (i.e., UiO-66-NH2, UiO-67-NH2, and UiO-68-NH2) were designed to be identical in chemical and morphological aspects and differ only in terms of the pore size. Octahedral nanocrystals of each MOF were obtained via solvothermal synthesis. Having exploited their nucleophilic amino groups, the MOFs were successfully grafted with PNIPAM chains. This nature-inspired strategy ensured good interfacial properties in MMMs. Computational chemistry unraveled the multifaceted interactions within the PNIPAM–PBI–solvent nexus, which allowed the mitigation of interfacial gaps in MMMs via PNIPAM/PBI chain entanglement. A highly accurate predictive model of nanofiltration was constructed based on the presumption of solution flow through the internal MOF pores. The model predictions for permeance and rejection profile were in good agreement with the experimental results for M66P, M67P, and M68P membranes containing PNIPAM-grafted MOF fillers. On the contrary, MMMs with ungrafted MOF fillers showed extremely high permeance and poor rejection in the nanofiltration regime owing to interfacial gaps between the fillers and polymer matrix. Transport modeling and nanofiltration experiments were used in tandem to explore the design space with regard to various structural and operational parameters. Virtual isoporosity of M66P, M67P, and M68P membranes was revealed. We deduced that the polymer grafting methodology mitigates interfacial gap formation and increases the contribution of the pores of MOFs in molecular sieving. The good acetone permeance (0.71–2.07 L m−2 h−1 bar−1) and low MWCO values (160–290 g mol−1) of the M66P, M67P, and M68P membranes are impressive on their own, but the insights gained through their study are even more important for the development of the next generation of high-selectivity molecular sieve membranes.Author contributions
LC: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft, writing —review & editing. RH: data curation, formal analysis, investigation, methodology, writing —review & editing. SA: data curation, formal analysis, investigation. HV: data curation, formal analysis, investigation, methodology, writing —review & editing. US: methodology, supervision, writing—review & editing. PMB: resources, writing – review & editing. KS: resources, supervision. KK: data curation, formal analysis, supervision, writing—review & editing. GS: conceptualization, data curation, funding acquisition, methodology, investigation, project administration, resources, supervision, writing – original draft, writing—review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research reported in this publication was supported by funding from The Royal Society (IES\R3\170080) and the King Abdullah University of Science and Technology (KAUST). Fig. 1 and ToC graphic were created by Xavier Pita, scientific illustrator at KAUST. LC is grateful to the Faculty of Science and Engineering for his PhD scholarship at the University of Manchester. The authors are thankful to Dr Hai Anh Le Phuong and Dr Kamilla Németh for the fruitful discussion.Notes and references
- S. Adler, E. Beaver, P. Bryan, S. Robinson and J. Watson, Vision 2020: 2000 Separations Roadmap, American Institute of Chemical Engineers, New York, NY, USA, 2000 Search PubMed.
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 CrossRef PubMed.
- P. Marchetti, M. F. Jimenez Solomon, G. Szekely and A. G. Livingston, Chem. Rev., 2014, 114, 10735–10806 CrossRef CAS PubMed.
- P. Marchetti, L. Peeva and A. Livingston, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 473–497 CrossRef PubMed.
- W. J. Koros and C. Zhang, Nat. Mater., 2017, 16, 289–297 CrossRef CAS PubMed.
- H. Zhang, Q. He, J. Luo, Y. Wan and S. B. Darling, ACS Appl. Mater. Interfaces, 2020, 12, 39948–39966 CrossRef CAS PubMed.
- Y. H. See-Toh, M. Silva and A. Livingston, J. Membr. Sci., 2008, 324, 220–232 CrossRef CAS.
- S. P. Nunes, P. Z. Culfaz-Emecen, G. Z. Ramon, T. Visser, G. H. Koops, W. Jin and M. Ulbricht, J. Membr. Sci., 2020, 598, 117761 CrossRef CAS.
- J. H. Huang, X. Q. Cheng, Y. Zhang, K. Wang, H. Liang, P. Wang, J. Ma and L. Shao, Cell Rep. Phys. Sci., 2020, 1, 100034 CrossRef.
- Y. Zhang, X. Cheng, X. Jiang, J. J. Urban, C. H. Lau, S. Liu and L. Shao, Mater. Today, 2020, 36, 40–47 CrossRef CAS.
- Z. Ji, H. Wang, S. Canossa, S. Wuttke and O. M. Yaghi, Adv. Funct. Mater., 2020, 30, 2000238 CrossRef CAS.
- H. Deng, S. Grunder, K. E. Cordova, C. Valente, H. Furukawa, M. Hmadeh, F. Gándara, A. C. Whalley, Z. Liu, S. Asahina, H. Kazumori, M. O'Keeffe, O. Terasaki, J. F. Stoddart and O. M. Yaghi, Science, 2012, 336, 1018–1023 CrossRef CAS PubMed.
- X. Cheng, X. Jiang, Y. Zhang, C. H. Lau, Z. Xie, D. Ng, S. J. D. Smith, M. R. Hill and L. Shao, ACS Appl. Mater. Interfaces, 2017, 9, 38877–38886 CrossRef CAS PubMed.
- S. Sorribas, P. Gorgojo, C. Téllez, J. Coronas and A. G. Livingston, J. Am. Chem. Soc., 2013, 135, 15201–15208 CrossRef CAS PubMed.
- A. Karimi, A. Khataee, M. Safarpour and V. Vatanpour, Sep. Purif. Technol., 2020, 237, 116358 CrossRef CAS.
- J. Zhu, J. Hou, S. Yuan, Y. Zhao, Y. Li, R. Zhang, M. Tian, J. Li, J. Wang and B. Van der Bruggen, J. Mater. Chem. A, 2019, 7, 16313–16322 RSC.
- L. Zhu, H. Yu, H. Zhang, J. Shen, L. Xue, C. Gao and B. van der Bruggen, RSC Adv., 2015, 5, 73068–73076 RSC.
- J. Duan, Y. Pan, F. Pacheco, E. Litwiller, Z. Lai and I. Pinnau, J. Membr. Sci., 2015, 476, 303–310 CrossRef CAS.
- C. Van Goethem, R. Verbeke, M. Pfanmöller, T. Koschine, M. Dickmann, T. Timpel-Lindner, W. Egger, S. Bals and I. F. J. Vankelecom, J. Membr. Sci., 2018, 563, 938–948 CrossRef CAS.
- S. Basu, M. Maes, A. Cano-Odena, L. Alaerts, D. E. De Vos and I. F. J. Vankelecom, J. Membr. Sci., 2009, 344, 190–198 CrossRef CAS.
- E. L. Butler, C. Petit and A. G. Livingston, J. Membr. Sci., 2020, 596, 117482 CrossRef CAS.
- C. Satheeshkumar, H. J. Yu, H. Park, M. Kim, J. S. Lee and M. Seo, J. Mater. Chem. A, 2018, 6, 21961–21968 RSC.
- H. Liu, M. Zhang, H. Zhao, Y. Jiang, G. Liu and J. Gao, RSC Adv., 2020, 10, 4045–4057 RSC.
- X. Guo, D. Liu, T. Han, H. Huang, Q. Yang and C. Zhong, AIChE J., 2017, 63, 1303–1312 CrossRef CAS.
- Z. Wang, H. Ren, S. Zhang, F. Zhang and J. Jin, J. Mater. Chem. A, 2017, 5, 10968–10977 RSC.
- M. Kalaj, K. C. Bentz, S. Ayala, J. M. Palomba, K. S. Barcus, Y. Katayama and S. M. Cohen, Chem. Rev., 2020, 120, 8267–8302 CrossRef CAS PubMed.
- M. Navarro, J. Benito, L. Paseta, I. Gascón, J. Coronas and C. Téllez, ACS Appl. Mater. Interfaces, 2018, 10, 1278–1287 CrossRef CAS PubMed.
- X. Zhang, Y. Zhang, T. Wang, Z. Fan and G. Zhang, RSC Adv., 2019, 9, 24802–24810 RSC.
- J. Campbell, J. Da Silva Burgal, G. Szekely, R. P. Davies, D. C. Braddock and A. Livingston, J. Membr. Sci., 2016, 503, 166–176 CrossRef CAS.
- D. Ma, G. Han, Z. F. Gao and S. B. Chen, ACS Appl. Mater. Interfaces, 2019, 11, 45290–45300 CrossRef CAS PubMed.
- Y. Li, L. H. Wee, A. Volodin, J. A. Martens and I. F. J. Vankelecom, Chem. Commun., 2015, 51, 918–920 RSC.
- S. Nagata, K. Kokado and K. Sada, Chem. Commun., 2015, 51, 8614–8617 RSC.
- S. Nagata, K. Kokado and K. Sada, CrystEngComm, 2020, 22, 1106–1111 RSC.
- A. Karmakar, P. G. M. Mileo, I. Bok, S. B. Peh, J. Zhang, H. Yuan, G. Maurin and D. Zhao, Angew. Chem., Int. Ed., 2020, 59, 11003–11009 CrossRef CAS PubMed.
- M. Kaposi, M. Cokoja, C. H. Hutterer, S. A. Hauser, T. Kaposi, F. Klappenberger, A. Pöthig, J. V Barth, W. A. Herrmann and F. E. Kühn, Dalton Trans., 2015, 44, 15976–15983 RSC.
- M. Carboni, Z. Lin, C. W. Abney, T. Zhang and W. Lin, Chem.–A Eur. J., 2014, 20, 14965–14970 CrossRef CAS PubMed.
- P. W. Dunne, E. Lester and R. I. Walton, React. Chem. Eng., 2016, 1, 352–360 RSC.
- M. C. Lawrence, C. Schneider and M. J. Katz, Chem. Commun., 2016, 52, 4971–4974 RSC.
- W. R. Bowen and J. S. Welfoot, Chem. Eng. Sci., 2002, 57, 1121–1137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta06205k |
| This journal is © The Royal Society of Chemistry 2021 |