Progress of low-frequency sound absorption research utilizing intelligent materials and acoustic metamaterials

Abstract

In recent years, increasing attention has been paid to the impacts of environmental noises on living creatures as well as the accuracy and stability of precise instruments. Due to inherent properties induced by large wavelength, the attenuation and manipulation of low-frequency sound waves is quite difficult to realize with traditional acoustic absorbers, yet particularly critical to modern designs. The advent of acoustic metamaterials and intelligent materials provides possibilities of energy dissipation mechanisms other than viscous dissipation and heat conduction in conventional porous sound absorbers, and therefore inspires new strategies on the design of subwavelength-scale structures. This short review aims to trace the current advancement on the low-frequency sound absorption research utilizing intelligent materials and metamaterials, including Helmholtz resonators and acoustic metamaterials based on micro-perforated plates, porous media, and decorated membrane, along with the tunable absorbing structures regulated with the function of electroactive polymers or magnetically sensitive materials. The effective principles and prospects were concluded and presented for future investigations of subwavelength-scale acoustic structures.

---

Longfei Chang

Longfei Chang is currently an Associate professor at the Hefei University of Technology. She obtained her doctorate degree in Engineering from Xi'an Jiaotong University in 2015. She visited the National Institute of Advanced Industrial Science and Technology (AIST), Japan from 2013 to 2014. Her main research interests include intelligent materials and structures, condensed matter physics, acoustic metamaterials and soft machinery.

Yucheng Wu

Yucheng Wu is now a distinguished professor and doctoral supervisor at the Hefei University of Technology. He received his PhD in Condensed Physics from the Chinese Academy of Sciences in 2000. His current research interests mainly focus on fusion materials, energy-related materials and functional nanomaterials. He has held various academic positions worldwide, including the honorary Professor at the University of St Andrews (2013-), guest Professor of RMIT University (2012-), the Council Member of Chinese Society of Micron Nanotechnology (2012-), and the director in China International S&T Cooperation Base for Advanced Energy and Environmental Materials (2017-). He has published more than 300 peer-reviewed scientific papers in journals, including Science Advances, Advanced Materials, Advanced Functional Materials, ACS Nano, with a total citation of over 12 000.

Bo Li

Bo Li is currently an Associate professor at the Xi'an Jiaotong University. He was awarded his Ph.D. degree in Instrumental science and technology from Xi'an Jiaotong University in 2012. He is the Associate Editor for IEEE Transaction on Automation Sciences and Engineering. His current research interests include acoustic and optical structures with intelligent materials, dielectric electro-active actuators as well as soft robotics.

Ying Hu

Ying Hu is currently a Professor and doctoral supervisor at the Hefei University of Technology. He obtained his Ph.D. degree from Suzhou Institute of Nano-tech and Nano-bionics (SINANO), Chinese Academy of Sciences in 2012. His research interests focus on the chemistry and physics of intelligent nanomaterials as well as their application in soft robots and acousto-optic devices. He has published more than 40 peer-reviewed scientific papers in journals, including Nature Commun., Adv. Mater., Adv. Funct. Mater., and ACS Nano, with total citation over 2000.

---

1. Introduction

With global industrialization, noise control is becoming a general challenge with increasing urgency. Due to the importance of sound absorption in noise attenuation, its practice and research have received extensive attention in the past decades.¹ Sound waves, as a kind of mechanical waves, need to be propagated through materials medium. Energy loss during sound transmission leads to continuous attenuation of sound intensity, which can be utilized to achieve sound absorption.^2,3

Low-frequency sound waves, especially in the range lower than 1000 Hz, were produced mainly by the low-order resonance of rotating machinery, power equipment, and construction vibrators, as well as the aerodynamic movements from vehicles, airplanes, and other transport equipment. They were recognized with growing evidence as quite a threat to not only the physical and psychological health of human beings but also the accuracy and stability of precise instruments and devices; however, they can penetrate powerfully and are quite difficult to dissipate through traditional sound-absorbing materials in a limited space due to the principle of causality.^4–7

The emerging concepts, acoustic metamaterials, and intelligent materials have broken through the limitation of traditional materials and opened up new paths for the design of acoustic absorbers with subwavelength-scale structures.^8–10 New physical mechanisms, other than viscous dissipation in the vicinity of the solid surface and heat conduction through solids, were introduced to achieve effective low-frequency sound absorption.^11,12 Acoustic metamaterials are artificial structural materials with periodic or non-periodic unit arrangements to obtain local resonance and special intrinsic parameters,¹³ such as negative effective mass density, negative effective modulus of elasticity, and zero refractive index.^14–18 These unconventional properties are usually difficult to find in traditional materials. Liu et al. exceeded the limits of Bragg scattering and constructed the first composite structure with negative parameters in terms of local resonance.¹⁹ Fang et al. verified the negative effective bulk modulus by an array of Helmholtz resonators.²⁰ Since then, acoustic metamaterials have initiated a reviving interest in the improvement of sound absorption performance through structural design and exploring the mechanisms.^21,22 In addition to locally resonant acoustic metamaterials, there are also acoustic metasurfaces,²³ labyrinthine or spatially coiled acoustic metamaterials that are tuned by subwavelength channel cross-sections, and porous acoustic metamaterials that use different pore sizes and arbitrarily-shaped subwavelength holes to obtain high refractive indices.^24–28 Various acoustic structures have been developed successfully to enhance the sound absorption in the low-frequency band, bringing new strategies for solving environmental noises and vibrations.²⁹

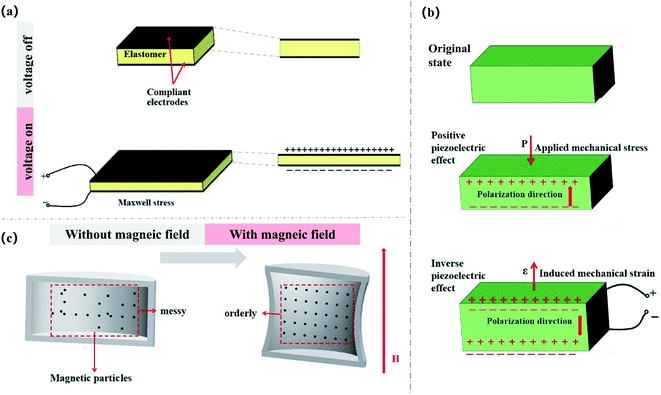
Nevertheless, in spite of those attractive attempts, most acoustic absorbers with subwavelength scales exhibited nice absorption around certain frequency bands, which are difficult to change once the structure is established. In recent years, with the rapid development of advanced materials, adopting intelligent materials to design structural units proved to be an effective and promising way to achieve broadband sound absorption or adaptable band shifting.³⁰ Intelligent materials are a class of materials that undergo changes in shape or properties when exposed to external stimuli, such as light, electric field, magnetic field, and humidity.³¹ A wide variety of intelligent materials, including electroactive polymers,³² piezoelectric materials, shape-memory materials,³³ and magnetically sensitive materials,^34,35 have been probed extensively in various applications such as soft robots, artificial muscles, actuators, sensors, and biomedicine due to their inherent advantages like high sensitivity, large displacement, and biocompatibility.^36–40 The manipulation of physical properties by adjusting external stimuli attracted increasing attention to the investigation of intelligent materials in tunable acoustic structures.² Furthermore, the application of intelligent materials can also introduce new energy dissipation mechanisms for acoustic structures, which accelerate the decay of sound energy and allow effective broadband sound absorption in the low-frequency band.^41–43

According to the above analysis and following the progressive direction, this review presents a summary of the current-status research on acoustic metamaterials and outlines recent advances in the study of acoustic structures with intelligent materials for low-frequency sound absorption. Among them, we focus on the application of intelligent materials in tunable acoustic structures and analyse the principles to achieve broadband sound absorption, including both active and passive aspects. At the end of the review, the prospects and possible future exploration of acoustic designs based on intelligent materials are proposed.

2. Acoustic metamaterials

Acoustic metamaterials are artificial composite materials, which break through the restrictions of natural laws, such as mass density and effective modulus, and exhibit unnatural acoustic properties. There are many types of acoustic metamaterials, in a broad sense, including Helmholtz resonator, micro-perforated plate (MPP), and those based on porous media, decorated membranes, coiling-up space structures, etc.

2.1 Helmholtz resonators

The Helmholtz resonator is usually composed of a neck and a cavity, characterized by a unipolar resonance type and a negative effective bulk modulus.¹⁷ Conventional Helmholtz resonators show narrow operating frequency bands and carry large-dimension structures when designed in the low-frequency range. In order to overcome these limitations, researchers have tried several ways to achieve more effective sound absorption and widen the frequency band. In a recent work by Guo et al., a thin absorber based on Helmholtz resonators was designed with an extended neck characterized with thin and compact structure, of which the thickness is only about 1/30 of the working frequency wavelength, as shown in Fig. 1(a) and (b).⁴⁴ The extended neck of the absorber ensured a shift of the resonant frequency to lower frequencies, which was dependent on the arrangements of the Helmholtz resonators. A checkerboard absorber composed of alternating resonators A and B with varying-length extended necks were then established, and the results showed that the absorbers would produce double-band absorption when the resonant frequencies of resonator A and B were widely separated, and the strong coupling between the resonators would occur, effectively extending the bandwidth, when those were adjacent. The absorption coefficient of this absorber in the band of 819.2 Hz to 919.2 Hz reached up to 0.85, achieving quasi-perfect sound absorption.⁴⁴ With the above principle, an absorber with deep subwavelength thickness was designed by assembling multiple non-uniform layers of extended-neck Helmholtz resonators with overlapping absorption peaks induced by different units, resulting in a continuous absorption band in the low frequency region.⁴⁵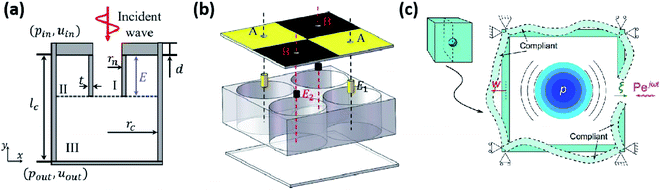

Fig. 1 Helmholtz resonance structures. (a) The cross-sectional view of a Helmholtz resonator unit with an extended neck.⁴⁴ (b) Schematic of a checkerboard absorber composed of alternating resonators A and B with varying-length extended necks.⁴⁴ (c) Schematic of the complete compliant-material resonator and a cross-section.⁴⁶

In addition to the regulation and control of structural parameters, the absorption bandwidth of Helmholtz resonators can also be broadened in the low frequency band by the design of hybrid structures with the incorporation of other acoustic structures. For example, Cui and Harne et al. created multiple low-frequency hybrid resonances through a multi-physics coupling mechanism between materials, structures, and acoustic waves.⁴⁶ By using compliant walls fabricated from a single material piece instead of the rigid wall of a traditional Helmholtz resonator, as shown in Fig. 1(c), the absorber can generate excellent sound broadband control with multiple low-frequency hybrid resonances at frequencies below 300 Hz. Liu proposed a hybrid sound-absorbing structure of a perforated composite Helmholtz-resonator, which was formed by inserting single or multiple perforated plates inside Helmholtz resonators.⁴⁷ The bandwidth of the metasurface is composed of eight perforated composite Helmholtz resonator units from 550 Hz to 910 Hz, which was widened by approximately 65% without increasing the size of the structure, which can be ascribed to the multi-stage sound absorption mechanisms.

2.2 MPP-based metamaterial absorbers

MPP is a typical acoustic metamaterial consisting of a plate surface with periodically arranged micro-perforations and a back cavity of a certain depth.^48,49 MPP absorbers are characterized by lightweight and simple structures. When the sound waves hit the panel partly through the micro-hole into the back cavity, refraction and vibration in the cavity will subsequently lead to effective dissipation of sound energy.

The sound absorption characteristics of MPP absorbers are closely related to the perforation rate, shape, cross-sectional structure, dimension, and distribution of the pores. Optimizing these parameters could regulate the operating frequency, improve the absorption performance, and broaden the effective frequency band. Qian et al. used the finite element model (FEM) analysis and found that the maximum sound absorption coefficient of the tapered hole MPP increased with the decrease of the hole entrance diameter or the increase of the hole exit diameter on the panel.⁵⁰ Ren et al. performed numerical simulations on MPPs with periodically arranged circular micropores, as shown in Fig. 2(a) and (b), and found that the sound absorption performance was significantly affected by the shape of the pores through modification of the velocity field and the viscous dissipation. Pore shapes featured as mesoscale circular pores accompanied with micro-scale bulges along the boundaries could lead to perfect sound absorption at relatively low frequencies.⁵¹ In a work by Sailesh et al., circular perforations with six different types of cross-sectional variations were realized using 3D printing based on fused filament fabrication, among which the sound absorption of perforated panels with varying cross-sections showed better performance than those with uniform cross-sectional perforation for the given frequency range.⁵²

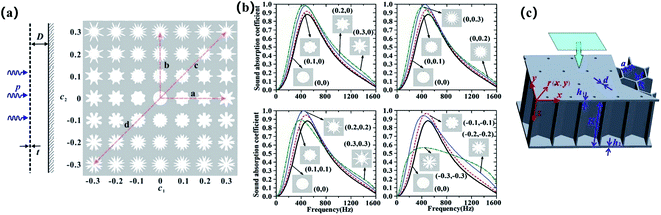Fig. 2 (a) Typical pore shapes controlled by the two shape parameters c₁ and c₂, with red dashed lines indicating the four main varying paths.⁵¹ (b) Influence of the pore shape on the sound absorption coefficient, as a function of frequency (0–1600 Hz), for MPPs with identical cross-sectional area: numbers in brackets stand for (c₁, c₂), and the label characters in the sub-figures correspond to the path characters in (a).⁵¹ (c) Schematic of surface-perforated sandwich panel with hexagonal core.⁵⁴

Furthermore, the coupling of different monomers or multiple layers can be utilized to broaden the frequency band and hybrid structures by the incorporation of the MPP structure with other structures, such as honeycomb sandwich panels and Archimedean-inspired spiral, can also be designed to achieve hybrid coupling to enhance the low-frequency acoustic absorption. For example, a three-layer MPP acoustic body designed by Cobo et al. demonstrated that an appropriate multilayer structural design could increase the absorption bandwidth significantly.⁵³ Meng et al. presented a new multifunctional structure combining honeycomb sandwich panel and perforated panel, as shown in Fig. 2(c). The analytical results showed that the panel perforation improved sound transmission loss and sound absorption coefficient at low frequencies, and the peak frequencies increased when increasing the perforation rate or decreasing the aperture size.⁵⁴ The hybrid structure sound absorber proposed by Boccaccio et al. was composed of two parallel MPPs and Archimedean-inspired spiral. By choosing different parameters of the structures, the hybrid sound absorber was designed to achieve low-frequency broadband sound absorption in the frequency range between 550–1650 Hz and 380–1250 Hz.⁵⁵

2.3 Acoustic metamaterials based on porous media

Traditional porous sound absorbers consist of a solid framework intertwined with a large number of open, semi-closed, or closed pores, which generate friction, vibration, and heat loss to dissipate energy with the propagation of sound waves, as illustrated in Fig. 3(a).^56–58 Those porous materials usually present excellent sound absorption properties in the middle and high frequencies but inherently show much weaker sound dissipation in the lower-frequency range because the thickness of the absorber is limited by the quarter working wavelength, making it difficult to achieve effective absorption of low-frequency sound waves in a limited space.⁵⁹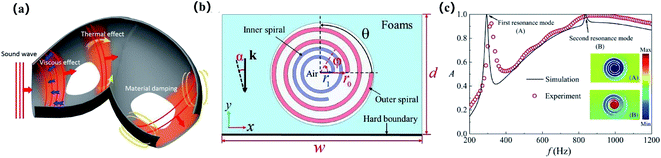

Fig. 3 Schematic of the structure of acoustic metamaterials based on porous media. (a) Schematic of common sound energy dissipation mechanisms in a porous sound-absorbing material.⁵⁸ (b) The 2D cross section of the dual-spiral structure.⁶⁸ (c) The sound absorption coefficient from the simulation and the experiment of the dual-spiral structure; the insets are the simulated acoustic field distributions.⁶⁸

In previous works, efforts have been devoted to modulating the pore size and increasing the mesh rate, which ensures the absorption peak shifts toward the lower frequency band,^59–61 but this achievement was rather limited. On the other hand, the designs of acoustic metamaterials based on porous materials exhibit prosperous results, including embedding resonators in conventional porous materials,^62–64 combining them with labyrinthine metamaterials^65–67 and special spirals.⁶⁸ For example, to improve the acoustic energy loss in the foam, Lewińska et al. chose to make changes in the fine-scale dimensions of the material and proposed the concept of acoustic metafoam. The local resonator was embedded in the porous elastic material, of which the pores were represented by cubic cells, and the micro resonator was represented by a cantilever beam with a weight attached to the tip. The FEM simulation analysis showed that a fluid–solid coupling occurred in the acoustic metafoam, which improved the low-frequency sound attenuation under the combined effects of viscous heat dissipation of the fluid and local resonance of the solid.⁶² Abbad et al. proposed a composite structured acoustic absorber composed of Helmholtz resonators with an elastic film front wall embedded in melamine foam and established a numerical model of the acoustic absorber, showing high amplitude peaks of sound absorption and transmission losses near the resonant frequency of 298 Hz.⁶³ Wang et al. also designed a local resonant structure combined with a porous material and chose Helmholtz resonators filled with aerogel to reduce the sound waves passing through it and reduce the propagation speed of the sound waves.⁶⁴ Filling aerogels with different types and thicknesses or changing the Helmholtz resonators in the composite structure can adjust the sound absorption intensity and the frequency band. As the thickness of the aerogel increases, the main absorption peak shifts toward the lower-frequency band. Compared with the composite acoustic structure of single Helmholtz resonators, the absorbers with double Helmholtz resonators showed better sound absorption performance under strong coupling.⁶⁴ Liu et al. proposed that the introduction of porous media into the channels of the single-channel labyrinth metasurface resulted in complete sound absorption at the resonance frequency. Changing the cross-sectional area of the channel results in the relative absorption bandwidth of the sound absorber up to 121%.⁶⁵ A double porosity material composed of porous materials and labyrinth channels presented a sound absorption peak of 100% at 451 Hz, which was derived from the hybrid resonance between the porous layer and the labyrinthine channel, enhancing the low-frequency sound absorption performance.⁶⁶ Besides, in a theoretical study by Yang et al., a hard-backed porous structure with periodic arrangements of rigid partitions coordinated parallel and perpendicular to the direction of incoming sound waves was proposed to ensure the first thickness resonance mode in the layer appear at much lower frequencies, and an appropriate partitioning was proved to yield multiple thickness resonances with higher absorption peaks through impedance matching.⁶⁷ As shown in Fig. 3(b) and (c), Zhou et al. constructed metaporous composites with Archimedean spirals embedded in porous materials, which were capable of achieving perfect sound absorption at low frequency resonances with frequency tunability and an insensitivity to the incident angle and conformed to the critical coupling mechanism at perfect absorption, where the balance of leakage and dissipation factors can be manipulated by the slit orientation and the parameters of porous materials.⁶⁸ Through both experimental and simulation studies, the composite material was proved to have excellent sound absorption in the low frequency region and generate a near-perfect absorption of 0.95 at the resonance frequency, with a large oblique incidence, e.g., 60°.⁶⁸

2.4 Decorated membrane-type absorbers

The membrane acoustic metamaterial based on the spring-mass system usually consists of an elastic membrane fixed in a rigid frame and a mass embedded in the membrane. The local vibration of the mass block fixed to the film can enable the increase of its energy density when operating in the low-frequency band. In 2008, Yang et al. proposed a membrane acoustic metamaterial, of which the law of mass density was broken at 100–1000 Hz, and near total acoustic reflection was achieved at 200–300 Hz.⁶⁹ The properties of the resonant mass block have a significant effect on the coefficient and bandwidth of the sound absorption. Mei et al. designed an elastic membrane decorated with asymmetric rigid platelets, and one of the specimens, sample A, was a rectangular elastic membrane with an area of 31 mm by 15 mm and a thickness of 0.2 mm. The acoustic energy dissipation of sample A at 172 Hz was as high as 70%.⁷⁰ An acoustic metasurface with hybrid resonance was then designed by adding a cavity structure to this membrane-type acoustic metamaterial. Perfect sound absorption in the low frequency band was successfully achieved through hybrid resonance with this simple structure, which showed a hybrid resonance at 147 Hz and a power conversion efficiency of 23%.⁷¹ As in Fig. 4(a), the membrane-type acoustic metamaterial designed by Liu et al. can achieve a maximum sound absorption coefficient of nearly 100% in the frequency range of 400–650 Hz, and the average sound absorption coefficient was as high as 80%, which was ascribed to the acoustic siphon effect of the structural unit that leads to greatly increased vibration of the unit.⁷²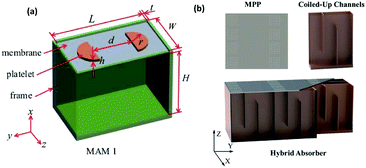

Fig. 4 (a) Schematic of a membrane-type metamaterial.⁷² (b) Schematic of the hybrid metamaterial absorber composed of a microperforated panel (MPP) as a top face sheet and coiled-up Fabry–Pérot channels with folding number n. The front wall is cut off to see the details inside.⁷⁵

2.5 Acoustic metamaterials with coiling-up space

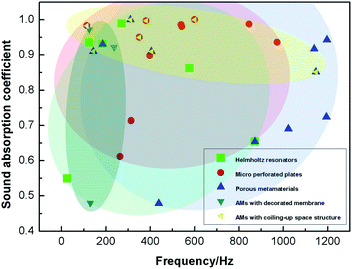
Due to space constraints, the performance of acoustic metamaterials based on cavity structures in low-frequency sound wave manipulation is greatly compromised. In order to break through the limitations, researchers have tried and successfully designed various acoustic metamaterials with coiling-up space structures, which can greatly increase the sound wave propagation path and thus increase the sound energy loss. The ultra-thin spiral metasurfaces designed by Huang et al., of which the thickness was only 1/100 of the working wavelength, achieved perfect sound absorption in the low frequency range. The embedded apertures of spiral metasurfaces could effectively adjust the impedance and introduce the tunable characteristics of perfect sound absorption frequency. The perfect absorptions of samples with different thicknesses and aperture parameters were in the frequency range of 140–170 Hz.⁷³ The resonance frequency of the deep subwavelength absorber based on the concept of coiled space can be adjusted by varying the partition in the cavity. The relative bandwidth of the sound absorber designed by adjusting the parameter combination was as high as 33.3%.⁷⁴ Wu et al. designed a hybrid sound-absorbing structure with a deep sub-wavelength thickness (5 cm) on the basis of MPP and coiled-up Fabry–Pérot channels, as shown in Fig. 4(b).⁷⁵ Increasing the folding numbers of the Fabry–Pérot channel can make the absorption peak of the sound absorber move to the low frequency direction without increasing the size of the structure. Through numerical verification, it was found that the sound absorption mechanism at low frequencies (<500 Hz) was mainly the conversion of sound energy into heat energy at the resonance frequency.

To sum up, in this section, the acoustic metamaterials, including Helmholtz resonator, MPP structures, heteromorphic porous media, decorated membranes, coiling-up space structures as well as some hybrid structures, are introduced and the mechanisms are briefly illustrated. From the numerous structures presenting effective low-frequency acoustic absorption, it can be concluded that arranging arrays of units with different resonating properties, increasing the solid surfaces by the design of coiled-up or spiral channels and micropore spaces, along with the hybrid design incorporating coupling between different structural resonances or new energy dissipation mechanisms like piezoelectric effect were verified to be efficient in broadening the low-frequency absorption band and enhancing the absorption performances. Some of the representative works and the corresponding adjusting principles of the parameters and structures are summarized and listed in Table 1. The first absorption peaks of those works are compared, as shown in Fig. 5. Those dots with overlapped marks are from hybrid absorbers incorporating more than one kind of structure. It can be seen that Helmholtz resonators showed quite a flexible capacity in designing ultra-low frequency absorbers, while the effective sound absorption frequency bands of porous metamaterials were mainly concentrated in a relatively higher frequency band. Furthermore, hybrid structures were highly effective in realizing perfect or near-perfect absorption.

Table 1 Summary of performance adjustment by controlling the parameters of the sound-absorbing structures

Basic structure forms	Adjustment	Effects	Ref.
Helmholtz resonators	Designing with an extend neck	The extended neck leads to a shift of the resonant frequency to lower frequencies and assembly of several units can result in a continuous absorption band	44 and 45
MPP structure	Optimizing the shape, dimension, and the cross-sectional morphology of the penetrated holes	Pore shapes featured as meso-scale circular pores accompanied with micro-scale bulges along the boundaries and perforated panels with varying cross-section could lead to better absorption at low frequencies	51 and 52
Decorated membrane metamaterials	Integrating with asymmetric rigid mass plate or cavity structure	The introduction of mass or cavity will allow more elastic energy dissipation during the vibration, and hence an enhanced acoustic absorption	71 and 72
Acoustic metamaterials based on porous media	Increasing the inner surfaces and combining with local resonances	Increase of inner surface will ensure more viscous dissipation, that is more effective sound absorption; while the integration of resonant structures can shift the absorption band to lower ranges	62–68
Acoustic metamaterials with coiled space	Improving the channel structures or parameters in the cavity	Coiled structure can modify the resonance frequency and move the absorption peak to lower frequency direction	46, 73, 74 and 75
Coupling units	Arrays of monomers or multi-layer arrangement	Coupling of different units can extend the absorption bandwidth	44, 45 and 53
Hybrid structures	Incorporation of different acoustic structures or resonating mechanisms	Hybrid structures, such as Helmholtz resonator with MPP, honeycomb sandwiches with perforated faceplates, MPP and Archimedean-inspired spiral, porous structure and resonant structures, can create multiple low-frequency hybrid resonances and subsequently lead to a higher sound absorption coefficient and broader frequency bands	46, 47, 54, 55 and 65–68

---

Fig. 5 Summary of sound absorption performance of Helmholtz resonators, micro-perforated plates, porous metamaterials, AMs with decorated membrane, and AMs with coiling-up space structure at the lowest resonant peak. Sound absorbers in the red circle belong to hybrid structures.

3. Intelligent materials in sound absorption

Intelligent materials are a class of rapidly-developing functional materials responding to external stimuli (electrical,^76,77 optical,⁷⁸ chemical, magnetic fields,³⁴ etc.) through inner structural evolvement or mass transport, extensively explored in interdisciplinary areas such as biomedicine, bio-nanotechnology, and drug delivery.^{31,38,79–81} According to the type of stimuli, they can be broadly classified as electro-active polymers (EAPs), magnetically sensitive materials, piezoelectric materials, light-driven/humidity-driven intelligent materials,^82,83 and shape memory materials.^34,78,84 It should be noted that those classifications are not orthometric, because various alternatives can respond to multiple stimuli and therefore belong to more than one of the above-mentioned categories. For acoustic structures, the deformation of intelligent materials and variation of physical properties inspires strategies for the regulation of structural parameters and subsequently the improvement of low-frequency sound absorption. In currently available work, electrically and magnetically tuned sound absorbers present attractive performances and promising design potential.

Four different kinds of intelligent materials, dielectric elastomers (DEs), polyvinylidene fluoride (PVDF), magnetostrictive material and carbon nanomaterials, are most frequently utilized in current acoustic absorption designs. Their function, mechanism, and energy conversion as well as their advantages and disadvantages are summarized and listed in Table 2.^{58,65–67,85–92}

Table 2 Summary of the intelligent materials utilized in current acoustic absorption designs

Material	Function	Actuation mechanism	Energy conversion	Mechanism in sound absorption	Advantages	Disadvantages
DE	Electric-induced actuation	Coulombic attraction	Electromechanical transducer	Changes of the structural parameters of the sound absorber under the electric field	Fast electromechanical response	High operating voltages
	Storing charge	Electrostatic Maxwell stress			Large areal deformations	Low relative permittivity
	Shape changing	Capacitor			High flexibility	Easy breakdown
		Dipole polarization				Low Young's moduli
Piezoelectric material	Piezo-electric	Piezoelectric effect	Electromechanical transducer	Converting sound energy into electric energy and increasing sound energy loss	Outstanding chemical resistance	Insufficient piezoelectric response
	Ferro-electric	Inverse piezoelectric effect	Mechanical energy to electric energy		High thermal stability	Low permittivity
	Pyro-electric				Dynamic flexibility;	Relatively insufficient ferroelectric activity
	Dielectrics				Wide response frequency band	High relative density
	Both actuation and sensing					High hardness
Magneto strictive material	Magnetic-induced deformation	Magneto mechanical effect	Magnetic(electric)-acoustic	Changes of the structural parameters of the sound absorber under a magnetic field	Quick response capability	Magnetorheological fluid sedimentation
	Both actuation and sensing		Magnetic(electric)-mechanical		Magnetic sensitivity	Low durability
					Remote contactless control;	Difficult to regulate microstructure
					Excellent magnetic-induced deformability
					Low energy loss
Carbon nanomaterial	Electrothermal	Energy band theory	Thermoelectric transducer;	Converting sound energy into heat energy as well as increasing the interface morphology to promote the reflection of sound waves	High electrical conductivity	High cost
	Photothermal	Infrared radiation heat transfer	Photoelectric transducer		High thermal conductivity	Inhomogeneous property
	Conductivity				Low expansion coefficient;	Structure defect
	Heat transfer				High modulus
					Thermal stability
					Adsorption properties

---

3.1 Electrically tuned sound absorbers

Electricity, of which the regulation and control technique has been maturely developed, is one of the most widely-used stimuli today. The combination of electrically-driven materials with acoustic structure provides the possibility for adjusting the resonance frequency of the absorber and increasing the absorption coefficient through the change of the structural properties. EAP, a kind of soft intelligent material, can generate dimension changes under electrical activation, appearing to be a propitious material for tunable acoustic structures.

3.1.1 Exploring DE actuators. DE is one kind of electronically active polymer (eEAPs) that undergoes extensional expansion along the horizontal direction and contraction along the vertical direction in response to an electric field.⁹³ The schematic of their working modes for the DE actuator can be seen in Fig. 6(a).^91,92 With a voltage (usually up to kV order of magnitude) applied to the compliant electrodes on both sides of the DE actuator, the generated electrostatic forces coupled with the dipole orientation polarization formed by the rotation of the dipoles, where the former is much dominating, would lead to a compression of the membrane in the thickness and a large expansion in the area. DE actuators are characterized by high strain and stress, fast response, good reliability, dynamic flexibility, and high efficiency, and are often used in devices such as biomedical, artificial muscles,⁹⁴ and micro electro-mechanical systems.⁹⁵

Fig. 6 Schematic for the working principle of some intelligent materials utilized in acoustic structures. (a) Dielectric elastomer, (b) polyvinylidene fluoride actuator, (c) magnetorheological elastomer.

In recent years, DE actuators have been explored successfully in the field of acoustics to design tunable sound absorbers and achieve effective attenuation of sound waves within low and medium frequencies. Lu et al. designed a new pipe muffler with adjustable acoustic characteristics based on DE film, consisting of a DE membrane and a back cavity mounted on the wall of the tube as a muffler, as illustrated in Fig. 7(a).⁹⁶ The first resonant frequency of this absorber can be modulated by applying a DC voltage to the DE membrane, which caused a decrease in membrane tension and a shift of the first resonant frequency and all peak frequencies to a lower band and therefore achieved tunable acoustic performance.

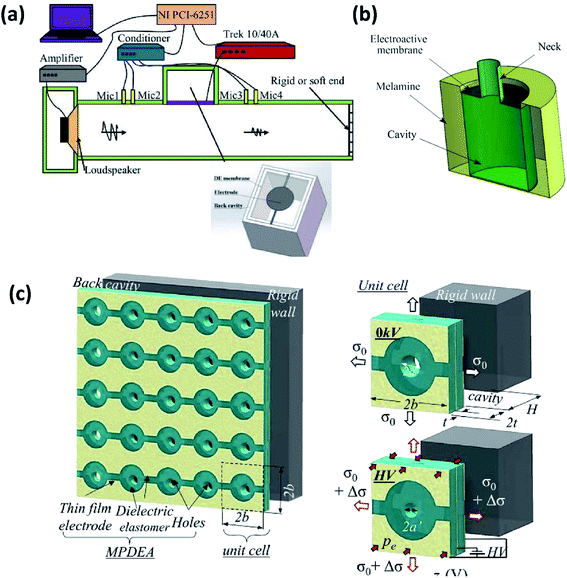Fig. 7 (a) Experimental setup for the tunable silencer based on DE actuator.⁹⁶ (b) 3D schematic of the Helmholtz resonator components with DE membrane.⁴¹ (c) A broader band acoustic absorber using DE actuators with MPP structure: an array of electrically tunable holes in DE actuators (left); its unit cell with a hole at either passive or active states (right).⁹⁷

With a DC voltage of 6 kV, the main peak moved from 348.8 Hz to 289.3 Hz, absorbing up to 90% of the acoustic energy. Abbad et al. constructed a thin-film Helmholtz resonator using a DE film as the resonator front wall, as shown in Fig. 7(b), which underwent a resonant frequency shift under voltage modulation.⁴¹ Measurements of the sound absorption performance and transmission loss of the Helmholtz resonator embedded in melamine foam at low frequency acoustic waves revealed a 59% reduction in the first absorption resonance amplitude at 65 Hz.

In addition, researchers have tried to introduce electrically responsive materials into the MPP structure to broaden the bandwidth of low-frequency sound absorption. Lu et al. constructed an acoustic absorber with pre-stretched DE actuators coated with gold electrodes and arrayed in MPP structure, as shown in Fig. 7(c).⁹⁷ The pre-stretched polyacrylate elastomer film was sandwiched between two layers of laser-perforated gold electrodes to form a micro-perforated dielectric elastomer actuator. Voltage application can regulate the diameter and depth of the holes, the depth of the back cavity as well as the membrane tension, effectively resulting in a decrease of the resonant main absorption frequency and broadening of the acoustic absorption band. Actuating with a 5 kV voltage, the peak absorbing frequency of this absorber can shift from 538.5 Hz to 467.8 Hz. Replacing the gold electrodes with transparent flexible electrodes, and preparing by inkjet printing PEDOT:PSS on the acrylate dielectric elastomer (VHB4910), the absorber presented structural transparency and a nice absorption performance in the mid-frequency range.⁹⁸

3.1.2 Exploring piezoelectric materials. PVDF, a polymer with both piezoelectric and inverse piezoelectric function, is another broadly-defined eEAP material. The basic mechanism of PVDF is illustrated as in Fig. 6(b).^87,88 When subjected to an external mechanical force, the polarization, resulting from the relative transfer of internal charges, will generate charge accumulation on the surfaces; while on the other hand, when applied with an electric field along the thickness direction, the electro-activated polarization as well as the electrostatic forces, were quite different from DE actuators, the polarization is much more dominated due to a large amount of side chains with dipoles, will lead to a mechanical strain output.

Due to its unique electrical activity, high flexibility, good processability, and long-term thermal stability, PVDF has been widely used in the field of noise and vibration reduction. In addition to the viscosity, heat dissipation, and damping effects of conventional materials, the unique mechanism for dissipating acoustic energy in open-cell PVDF foam is the piezoelectric effect that converts acoustic energy into electrical energy and increases mechanical damping, and the inverse piezoelectric effect that regulates the physical properties of the structure and therefore the absorption performance. Duan et al. has verified through experiments that active sound absorption control can significantly improve sound absorption performance. They designed a PVDF-based MPP structure, which can change the aperture size and adjust the acoustic characteristics of the MPP by applying an external voltage on the PVDF. This method also effectively reduced the size and weight of the sound absorber.⁹⁹ The piezoelectric properties of PVDF depend on the polar β-phase, which is also vital to the sound absorber design. Various methods have been proposed to increase the polar β-phase content in PVDF, such as the addition of nanofillers,^100,101 use of centrifugal spinning techniques,¹⁰² and electrostatic spinning techniques.¹⁰³ Mohamed et al. prepared open-cell PVDF foams by the sugar template method and increased the polar β-phase content by subjecting the foams to annealing heat treatment, as shown in Fig. 8(a), which leads to not only an increase in the polar β-phase but also an enhancement of the local polarization, and subsequently a significant increase of the sound absorption coefficient in the frequency range of 500–6400 Hz.¹⁰⁴ The PVDF/AgNPs nanofiber membrane developed by Wu et al. used electrostatic spinning technique and the addition of silver nanowires to promote the generation of polar β-phase, which enhanced the piezoelectric effect to improve the absorption coefficient and shift the absorption toward low frequency region.¹⁰⁵

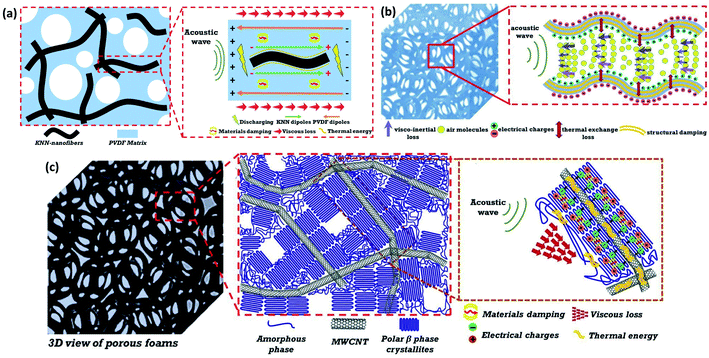Fig. 8 (a) Schematic of PVDF/KNN-nanofiber composite structure, and mechanisms for converting sound energy to electricity with local piezoelectric effect and electrical discharging to thermal energy through the opposite piezoelectric effect.⁴² (b) Schematic of an open-cell PVDF foam and mechanisms of acoustic energy absorption with polar β-phase.¹⁰⁴ (c) Schematic of 3D overview of the open-cell porous foam.¹⁰⁶

Hybrid absorbers, combining the piezoelectric effects with other energy conversion mechanisms, were proposed to further dissipate acoustic energy by consuming the generated electrical energy. For example, a hybrid functional composite foam with local piezoelectric effect and resistive losses was made by mixing single-walled carbon nanotubes (SWCNT) as a conductive element in PVDF to convert electrical energy into thermal energy to be released.⁵⁸ Mohamed et al. further added (K_0.5Na_0.5) NbO₃ (KNN) nanofibers with positive piezoelectric coefficients to the PVDF matrix to prepare a composite foam with two opposite piezoelectric responses.⁴² The sound absorption mechanism of the composite foam is shown in Fig. 8(b), where the sound waves were transmitted into the foam pores causing mechanical vibrations, and the local piezoelectric effect led to the conversion of mechanical energy into electrical energy. KNN nanofibers reflected part of the sound waves into the polymer matrix and converted electrical energy into heat, thus increasing the total mechanical energy loss, as can be seen in Fig. 8(c). The addition of multi-walled carbon nanotubes (MWCNT) to open-cell composite foams based on poly(vinylidene fluoride-trifluoroethylene) copolymer [P(VDF-TrFE)] promoted charge dissipation and enhanced the crystallinity and local piezoelectric effect of the polar β-phase. The greatly improved sound absorption performance of the composite foam in the low frequency range was attributed to the effective combination of the local piezoelectric effect and electrical conductivity that promoted sound energy dissipation.¹⁰⁶

In addition, lead zirconate titanate ceramics (PZT) and so-based composites were also explored in acoustic structures to increase the sound energy dissipation due to their excellent piezoelectric properties.^107–110 As early as 2013, the PU-based PZT composites prepared by in situ polymerization method were reported with good sound absorption performance in the low frequency range of 125–500 Hz, and the maximum sound absorption coefficient was 0.47 in 250 Hz.¹¹¹ Incorporated with the piezoelectric shunt damping technology, the piezoelectric effect was used to convert sound energy into electrical energy. Sun et al. designed a multi-layer piezoelectric film adopting PZT with a volume fraction of 30% as the coating layer, which achieved a semi-actively controlled underwater sound absorption. Through experiments and FEM simulation, they proved that the peak frequency, maximum value and bandwidth of the sound absorption coefficient can be monitored by adjusting the R–L circuit.¹¹² An adaptive acoustic metamaterial designed by Liao et al. was composed of a circular aluminium film attached with PZT-5H and a cavity containing a hybrid circuit shunt piezoelectric stack, which adjusted the effective acoustic resistance of the metamaterial based on impedance matching condition and could exhibit excellent sound absorption performance in the low frequency range, with the maximum sound absorption coefficient reaching above 0.9.¹¹³ Liu et al. studied the coupling effect of the smart MPP with surface-bonded PZT and demonstrated three energy dissipation mechanisms in sound absorption: mechanical damping, electric shunt damping, and Helmholtz resonance, in which the PZT patch enhanced the vibration of the flexible MPP at multiple frequencies.¹¹⁴ Besides, Gu et al. established a double-layer piezoelectric metamaterial with a tunable shunt circuit to achieve two-way asymmetric sound absorption, formed by attaching PZT-52 with a steel block in the center to a circular polycarbonate film. The maximum sound absorption coefficient of the metamaterial can reach 0.982 within 800–900 Hz.¹¹⁵

3.2 Magnetically tuned acoustic absorbers

Magnetic materials are popularly used in electro-mechanical systems, therefore sound absorbers with magnetically tunable properties have also received close attention. Some magnetoactive acoustic metamaterials were established by the coordination of magnetic particles or blocks. For example, a magnet was placed at the centre of a thin material layer in a spiral curl, and the force generated under the magnetic field changed the intrinsic parameters of the absorber and affected the acoustic properties.¹¹⁶ To further realize the manipulation of acoustic waves and design acoustic metamaterials that were tuned by external stimuli, Yu et al. prepared a deformable lattice structure with an octagonal truss using an elastomer containing ferromagnetic particles, as shown in Fig. 9(a). The hybrid material made of elastomer mixed ferromagnetic particles was manufactured into a lattice structure by the stereolithography-based manufacturing method. The lattice structure enabled the constitutive parameters, mass density and effective modulus of the material to switch between three states: double positive, one positive and one negative, and double negative, through remote magnetic field manipulation. This structure was further investigated in the adjustment of acoustic transmission.¹¹⁷ In a study by Montgomery et al., hard-magnetically soft active materials were chosen to design asymmetric joints. The elastomer mixture containing hard magnetic particles (15% vol) was cured in a 3D printed mold to form a unit. Asymmetric joints underwent changes in bending or folding patterns upon shifts in magnetic field direction, as shown in Fig. 9(b).¹¹⁸ The self-patching of asymmetric joints was used to form metamaterials with deformation mode branches, which showed distinct band gaps under magnetic fields of different orientations. A narrow band gap of 42–68 Hz in the low frequency region appeared under a positive magnetic field of 7 mT; the band gap widened to 47–112 Hz when the positive magnetic field increased to 20 mT.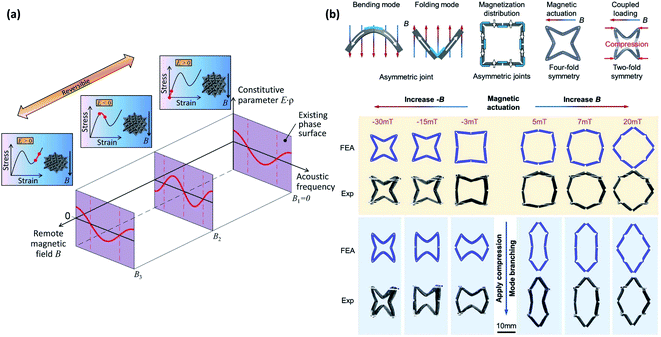

Fig. 9 (a) Conceptual schematics of study:¹¹⁷ the magnetically induced lattice buckling was harnessed to enable tunable sign of effective modulus E between positive and negative. (b) The metamaterial unit cell design and the concept of deformation mode branching.¹¹⁸

In addition, some specially designed magnetorheological materials, usually composite materials filled with magnetic particles in a soft non-magnetic matrix, are also used in low-frequency acoustic wave manipulation.^119,120 During the cross-linking process, the magnetic field activates the magnetic particles to form a columnar or chain-like structure distribution in the matrix, which can be fixed after curing. The interaction of particles in the magnetorheological material under the action of a magnetic field can trigger the magnetic deformation effect, as shown in Fig. 6(c).^85,86 In 2014, Chen et al. added materials such as FE and cross-linking agents that were close to spherical into the silicone rubber to make a magnetorheological elastomer. Magneto-acoustic metamaterials made of aluminium rings covered with magnetorheological elastomers adjusted the resonance frequency through an external magnetic field.¹²¹ Similar to electrically tuned acoustic absorbers based on DE actuator,⁹⁷ MPP structure based on magnetorheological elastomers showed tunable resonant frequencies and increased absorption bandwidth, and the deformation of the microperforated magnetorheological elastomers increased with the magnetic field magnitude, leading to a consequent change in the acoustic performance of the absorbers.⁴³

3.3 Acoustic absorbers utilizing carbon-based intelligent materials

In recent years, carbon nanomaterials have been widely explored in various applications due to their unique physical properties, multiple-level nano structures, and extensive commercial accesses. The electrical properties of some carbon nanomaterials, such as carbon nanotubes (CNT) and graphene derivatives, can be utilized as conductive fillers doped in polymers to prepare EAP actuators or sensors.^122,123 The special electrothermal properties can be exploited to design electrothermal actuators (ETA).^83,124 In addition, the hierarchical microstructures, which is manifested by a folded surface or nanopore interior,¹²⁵ ensure their integrated materials a nice mechanical tensile strength and good resistance against fracture or delamination.^126,127

Those carbon-based intelligent materials can respond to multiple stimuli, and their superior function in both actuation and sensing processes indicates a nice performance in energy conversion, which is beneficial for the design of acoustic structures. The sound absorption performance of porous materials is closely related to the opening rate, the size and structure of the pores, etc., and researchers modulated the materials in microstructure to optimize the sound absorption performance.¹²⁸ Adding fillers to polymer foams is a common method to improve the acoustic performance of foams. Liu et al. added graphene oxide (GO) and CNT into the melamine foam to form a composite with a semi-open cellular structure, where the melamine foam served as the backbone, and the self-assembled GO sheets formed a film on the surface of the foam. In the structure, CNT enhanced the connection between GO and the foam and made the GO film surface rougher, as shown in Fig. 10(a). This special innovative structure increased the airflow resistance and interface damping during the propagation of sound waves. With CNT and GO converting the mechanical energy into heat energy to increase the energy consumption, the sound absorption performance of the composite foam showed a distinguished increase in the frequency range of 250–1600 Hz, compared with pure melamine foam.¹²⁹

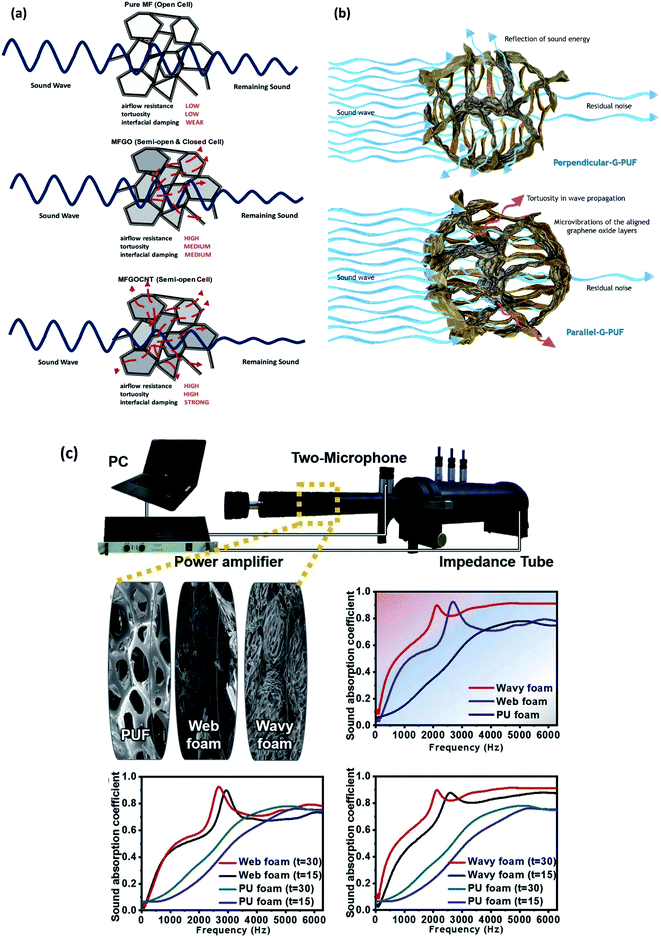Fig. 10 (a) Schematic of acoustic propagation through pure melamine foams, melamine foam with GO, melamine foam with GO and CNT.¹²⁹ (b) Schematic of the mechanism of sound absorption in a directionally antagonistic graphene sound absorber.¹³⁰ (c) Schematic of a 29 mm diameter of the polyurethane foam, the web foam, and the wavy foam. And Comparison of sound absorption performance for the three samples.¹³¹

The acoustic structures with the addition of carbon-based nanomaterials benefit not only from the electrical or mechanical activated properties, but also from the special multi-level porous nano structures. As can be seen from Fig. 10(b), a GO–polyurethane hybrid aerogel had a unique honeycomb microstructure with a polyurethane foam backbone. Two structures of GO materials with opposing orientations were prepared by the positional freezing method and can be classified into parallel and perpendicular arrangements according to the layout of GOs in them. The long channels formed in the polyurethane foam frame prolonged the propagation path of acoustic waves; and the micro vibrations of GO arrays in the channels and the multiple scattering in the pores of the composite aerogel improved the sound absorption of the material.¹³⁰ As shown in Fig. 10(c), Oh et al. fabricated spontaneous self-alignment and random assembly arrangement of graphene on polyurethane backbones with two experimental methods, forming corrugated and reticular foams, respectively.¹³¹ Compared with the original polyurethane foam, these two foams greatly improved the sound energy attenuation capability in the measurement range of 50–6400 Hz. The sound absorption performance of corrugated foam was better than that of reticulated foam due to the narrower gaps and more complex geometry of the microstructure, resulting in increased path and energy dissipation of sound waves in the internal structure.

4. Conclusions

The emergence of acoustic metamaterials and intelligent materials provides effective strategies for the attenuation of low frequency acoustic waves. To trace the latest development in this field, this review outlines the valuable research achievements on low-frequency broadband sound absorption in recent years, focusing on the design of metamaterial structures and the role of intelligent materials in widening the working frequency range of acoustic absorbers. Acoustic metamaterials with deep subwavelength scale break through the boundaries of conventional porous acoustic absorbers, and the introduction of intelligent materials further brings new properties, such as wide absorbing frequency band and tunable performances, and allows active sound absorption, resulting from the new energy dissipation mechanisms and an adaptive structural change with the external stimuli.

The current work presented outstanding advancements in low-frequency acoustic absorption, and the feasible methods and mechanisms to lower the efficient frequency and broaden the frequency band are inspired and illustrated for future references, as in Table 3.

Table 3 Summary of the methods and mechanisms of the absorption peak of the sound absorber shifting to the low frequency

Mechanisms	Methods	Ref.
Overlapping absorption peaks	Using coupling between different units to design non-uniform sound absorbers	44 and 45
Increased inner interfaces	Coiling-up or spiral inner space design	65–68, 74 and 75
Hybrid resonance	Incorporating different resonant structures or materials	46, 47 and 53–55
Adjustable structural parameters	Replacing certain acoustic partition with intelligent materials, carrying changeable dimensions or evolving physical properties under external stimuli	41, 43, 96, 99, 71 and 73
Higher sound energy dissipation or conversion	Incorporating new energy dissipation structures or energy conversion materials, such as piezoelectric materials and conductive nanomaterials	42, 62–64, 106, 111–115 and 129–131

---

Nevertheless, the acoustic absorbers in the low-frequency range, especially with tunable and adaptive performances, still leave much space for further probing. Although the large deformation or property evolvement was already emphasized in the alternative intelligent materials in acoustic design; many kinds of energy dissipation mechanisms in novel intelligent materials, such as the kinetic energy dissipation during mass transfer in multiphase materials like ionic polymer–metal composite (IPMC) and the electrochemical energy conversion during the stimulated reaction in some conductive polymers or ionic gels, are of great potential for sound absorption structures, yet have barely been explored. Besides, the application of intelligent materials such as light driven and humidity driven composites in low-frequency sound absorption may spark some innovative designs under a special occasion. We hope in the near future, this interdisciplinary research will be advanced and incorporated in intelligent device designs to promote environmental noise reduction, therefore bringing back a more harmonious planet to all living creatures.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the Natural Science Foundation of China (No. 52075140), the Fundamental Research Funds for the Central Universities of China (No. PA2020GDSK0074, JZ2020HGTB0013), and the Anhui Provincial Natural Science Foundation (2008085J22).

References

1. S. Kishore, R. Sujithra and B. Dhatreyi, Mater. Today: Proc., 2021, 47(part 14), 4700–4707.
2. S. A. Cummer, J. Christensen and A. Alu, Nat. Rev. Mater., 2016, 1, 13.
3. A. Banerjee, R. Das and E. P. Calius, Arch. Comput. Methods Eng., 2019, 26, 1029–1058.
4. N. Broner, J. Sound Vib., 1978, 58, 483–500.
5. C. T. Morrow, J. Acoust. Soc. Am., 1974, 55, 695–699.
6. W. M. Carey and R. A. Wagstaff, J. Acoust. Soc. Am., 1986, 80, 1523–1526.
7. B. Berglund, P. Hassmen and R. S. Job, J. Acoust. Soc. Am., 1996, 99, 2985–3002.
8. M. I. Hussein, M. J. Leamy and M. Ruzzene, Appl. Mech. Rev., 2014, 66(4), 040802.
9. Y. F. Wang, Y. Z. Wang, B. Wu, W. Chen and Y. S. Wang, Appl. Mech. Rev., 2020, 72, 040801.
10. M. H. Lu, L. Feng and Y. F. Chen, Mater. Today, 2009, 12, 34–42.
11. B. Assouar, B. Liang, Y. Wu, Y. Li, J. C. Cheng and Y. Jing, Nat. Rev. Mater., 2018, 3, 460–472.
12. G. Liao, C. Luan, Z. Wang, J. Liu, X. Yao and J. Fu, Adv. Mater. Technol., 2021, 6, 2000787.
13. Z. Du, E3S Web Conf., 2021, 248, 01041.
14. R. A. Shelby, Science, 2001, 292, 77–79.
15. R. Fleury, D. Sounas and A. Alù, Nat. Commun., 2015, 6, 5905.
16. G. Ma and P. Sheng, Sci. Adv., 2016, 2, e1501595.
17. H. Ge, M. Yang, C. Ma, M. H. Lu, Y. F. Chen, N. Fang and P. Sheng, Natl. Sci. Rev., 2018, 5, 159–182.
18. M. Yang, G. Ma, Z. Yang and P. Sheng, Phys. Rev. Lett., 2013, 110, 134301.
19. Z. Y. Liu, X. X. Zhang, Y. W. Mao, Y. Y. Zhu, Z. Y. Yang, C. T. Chan and P. Sheng, Science, 2000, 289, 1734–1736.
20. N. Fang, D. J. Xi, J. Y. Xu, M. Ambati, W. Srituravanich, C. Sun and X. Zhang, Nat. Mater., 2006, 5, 452–456.
21. M. Yang and P. Sheng, in Annual Review of Materials Research, ed. D. R. Clarke, Annual Reviews, Palo Alto, 2017, vol. 47, pp. 83–114.
22. Y. Y. Zhang, N. S. Gao and J. H. Wu, Appl. Acoust., 2020, 169, 107482.
23. K. Donda, Y. F. Zhu, S. W. Fan, L. Y. Cao, Y. Li and B. Assouar, Appl. Phys. Lett., 2019, 115, 5.
24. F. Zangeneh-Nejad and R. Fleury, Rev. Phys., 2019, 4, 142–158.
25. A. O. Krushynska, F. Bosia, M. Miniaci and N. M. Pugno, New J. Phys., 2017, 19, 12.
26. S. Kumar and H. P. Lee, Appl. Phys. Lett., 2020, 116, 5.
27. J. Liu, L. P. Li, B. Z. Xia and X. F. Man, Int. J. Solids Struct., 2018, 132, 20–30.
28. M. Yang, S. Chen, C. Fu and P. Sheng, Mater. Horiz., 2017, 4, 673–680.
29. M. Gulzari and C. W. Lim, Arch. Civ. Mech. Eng., 2021, 21, 1–11.
30. Z. Chen, C. Xue, L. Fan, S. Y. Zhang, X. J. Li, H. Zhang and J. Ding, Sci. Rep., 2016, 6, 11.
31. Q. Shi, H. Liu, D. Tang, Y. Li, X. Li and F. Xu, NPG Asia Mater., 2019, 11(1), 1–21.
32. R. Tiwari and E. Garcia, Smart Mater. Struct., 2011, 20(8), 083001.
33. Y. Xia, Y. He, F. Zhang, Y. Liu and J. Leng, Adv. Mater., 2020, 5, 1155–1173.
34. A. K. Bastola, M. Paudel, L. Li and W. Li, Smart Mater. Struct., 2020, 29, 123002.
35. W. Gao, L. L. Wang, X. Z. Wang and H. Z. Liu, ACS Appl. Mater. Interfaces, 2016, 8, 14182–14189.
36. J. Wang, D. Gao and P. S. Lee, Adv. Mater., 2021, 33, 2003088.
37. A. D. Valentine, T. A. Busbee, J. W. Boley, J. R. Raney, A. Chortos, A. Kotikian, J. D. Berrigan, M. F. Durstock and J. A. Lewis, Adv. Mater., 2017, 29, 8.
38. W. Mohdisa, A. Hunt and S. H. Hosseinnia, Sensors, 2019, 19, 3967.
39. M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113.
40. S. Nocentini, C. Parmeggiani, D. Martella and D. S. Wiersma, Adv. Opt. Mater., 2018, 6, 17.
41. A. Abbad, K. Rabenorosoa, M. Ouisse and N. Atalla, Smart Mater. Struct., 2018, 27, 105029.
42. A. M. Mohamed, K. Yao, Y. M. Yousry, J. Wang and S. Ramakrishna, J. Appl. Polym. Sci., 2020, 137, 49022.
43. X. F. Cao, S. H. Xuan, J. Li, Z. Y. Li, T. Hu, H. Y. Liang, L. Ding, B. S. Li and X. L. Gong, Smart Mater. Struct., 2020, 29, 11.
44. J. Guo, Y. Fang, Z. Jiang and X. Zhang, J. Phys. D: Appl. Phys., 2020, 53, 505504.
45. J. W. Guo, X. Zhang, Y. Fang and Z. Y. Jiang, Compos. Struct., 2021, 260, 12.
46. S. Cui and R. L. Harne, Phys. Rev. Appl., 2019, 12(6), 064059.
47. C. R. Liu, J. H. Wu, X. Chen and F. Y. Ma, J. Phys. D: Appl. Phys., 2019, 52, 9.
48. D. Y. Ma, Noise Control Eng. J., 1987, 29, 77–84.
49. D. Y. Ma, J. Acoust. Soc. Am., 1998, 104, 2861–2866.
50. Y. Qian, K. Cui, S. Liu, Z. Li, D. Kong and S. Sun, Noise Control Eng. J., 2014, 62, 152–159.
51. S. W. Ren, X. W. Liu, J. Q. Gong, Y. F. Tang, F. X. Xin, L. X. Huang and T. J. Lu, Europhys. Lett., 2017, 120, 6.
52. R. Sailesh, L. Yuvaraj, J. Pitchaimani, M. Doddamani and L. B. M. Chinnapandi, Appl. Acoust., 2021, 174, 107769.
53. P. Cobo, C. de la Colina, E. Roibas-Millan, M. Chimeno and F. Simon, Compos. Struct., 2019, 226, 9.
54. H. Meng, M. A. Galland, M. Ichchou, F. X. Xin and T. J. Lu, Appl. Acoust., 2019, 152, 31–40.
55. M. Boccaccio, F. Bucciarelli, G. P. M. Fierro and M. Meo, Appl. Acoust., 2021, 176, 107901.
56. J. Allard and N. Atalla, Propagation of sound in porous media: modelling sound absorbing materials 2e, John Wiley & Sons, 2009.
57. A. Abbad, K. Jaboviste, M. Ouisse and N. Dauchez, J. Cell. Plast., 2018, 54, 651–670.
58. M. Rahimabady, E. C. Statharas, K. Yao, M. Sharifzadeh Mirshekarloo, S. Chen and F. E. H. Tay, Appl. Phys. Lett., 2017, 111, 241601.
59. L. T. Cao, Q. X. Fu, Y. Si, B. Ding and J. Y. Yu, Compos. Commun., 2018, 10, 25–35.
60. O. Doutres, M. Ouisse, N. Atalla and M. Ichchou, J. Acoust. Soc. Am., 2014, 136, 1666–1681.
61. K. Gao, J. A. W. van Dommelen and M. G. D. Geers, Int. J. Solids Struct., 2016, 100, 536–546.
62. M. A. Lewińska, J. A. W. van Dommelen, V. G. Kouznetsova and M. G. D. Geers, J. Mech. Phys. Solids, 2019, 124, 189–205.
63. A. Abbad, N. Atalla, M. Ouisse and O. Doutres, J. Sound Vib., 2019, 459, 114873.
64. W. Q. Wang, Y. K. Zhou, Y. Li and T. Hao, J. Supercrit. Fluids, 2019, 150, 103–111.
65. L. Liu, H. T. Chang, C. Zhang and X. H. Hu, Appl. Phys. Lett., 2017, 111, 5.
66. H. Zhao, Y. Wang, D. Yu, H. Yang, J. Zhong, F. Wu and J. Wen, Compos. Struct., 2020, 239, 111978.
67. J. Yang, J. S. Lee and Y. Y. Kim, J. Appl. Phys., 2015, 117, 7.
68. Y. Zhou, D. Li, Y. Li and T. Hao, Appl. Phys. Lett., 2019, 115(9), 093503.
69. Z. Yang, J. Mei, M. Yang, N. Chan and P. Sheng, Phys. Rev. Lett., 2008, 101, 204301.
70. J. Mei, G. Ma, M. Yang, Z. Yang, W. Wen and P. Sheng, Nat. Commun., 2012, 3, 1–7.
71. G. C. Ma, M. Yang, S. W. Xiao, Z. Y. Yang and P. Sheng, Nat. Mater., 2014, 13, 873–878.
72. C. R. Liu, J. H. Wu, K. Lu, Z. T. Zhao and Z. Huang, Appl. Acoust., 2019, 148, 1–8.
73. S. Huang, X. Fang, X. Wang, B. Assouar, Q. Cheng and Y. Li, Appl. Phys. Lett., 2018, 113, 233501.
74. Y. Wang, H. Zhao, H. Yang, J. Zhong, D. Zhao, Z. Lu and J. Wen, J. Appl. Phys., 2018, 123, 185109.
75. F. Wu, Y. Xiao, D. L. Yu, H. G. Zhao, Y. Wang and J. H. Wen, Appl. Phys. Lett., 2019, 114, 5.
76. I. Ali, X. D. Li, X. Q. Chen, Z. W. Jiao, M. Pervaiz, W. M. Yang, H. Y. Li and M. Sain, Mater. Sci. Eng., C, 2019, 103, 17.
77. R. Pelrine, R. Kornbluh, Q. B. Pei and J. Joseph, Science, 2000, 287, 836–839.
78. H. K. Bisoyi, A. M. Urbas and Q. Li, Adv. Opt. Mater., 2018, 6, 21.
79. J. Shintake, V. Cacucciolo, D. Floreano and H. Shea, Adv. Mater., 2018, 30, 33.
80. S. Rosset and H. R. Shea, Appl. Phys. Rev., 2016, 3, 031105.
81. T. Marin, P. Montoya, O. Arnache, R. Pinal and J. Calderon, Mater. Des., 2018, 152, 78–87.
82. R. Lan, Y. Gao, C. Shen, R. Huang, J. Bao, Z. Zhang, Q. Wang, L. Zhang and H. Yang, Adv. Funct. Mater., 2021, 31, 2010578.
83. Y. Hu, J. Liu, L. Chang, L. Yang, A. Xu, K. Qi, P. Lu, G. Wu, W. Chen and Y. Wu, Adv. Funct. Mater., 2017, 27, 1704388.
84. S. Agate, M. Joyce, L. Lucia and L. Pal, Carbohydr. Polym., 2018, 198, 249–260.
85. A. K. Bastola and L. Li, Mater. Des., 2018, 157, 431–436.
86. A. K. Bastola and M. Hossain, Composites, Part B, 2020, 200, 21.
87. F. Liu, N. A. Hashim, Y. T. Liu, M. R. M. Abed and K. Li, J. Membr. Sci., 2011, 375, 1–27.
88. G. D. Kang and Y. M. Cao, J. Membr. Sci., 2014, 463, 145–165.
89. U. Gupta, L. Qin, Y. Z. Wang, H. Godaba and J. Zhu, Smart Mater. Struct., 2019, 28, 15.
90. L. J. Romasanta, M. A. Lopez-Manchado and R. Verdejo, Prog. Polym. Sci., 2015, 51, 188–211.
91. T. Q. Lu, C. Ma and T. J. Wang, Extreme Mech. Lett., 2020, 38, 37.
92. A. O'Halloran, F. O'Malley and P. McHugh, J. Appl. Phys., 2008, 104, 10.
93. D. M. Opris, M. Molberg, C. Walder, Y. S. Ko, B. Fischer and F. A. Nueesch, Adv. Funct. Mater., 2011, 21, 3531–3539.
94. Y. Qiu, E. Zhang, R. Plamthottam and Q. Pei, Acc. Chem. Res., 2019, 52, 316–325.
95. S. Rosset and H. R. Shea, Appl. Phys. Rev., 2016, 3, 031105.
96. Z. Lu, H. Godaba, Y. Cui, C. C. Foo, M. Debiasi and J. Zhu, J. Acoust. Soc. Am., 2015, 138, EL236–241.
97. Z. Lu, M. Shrestha and G.-K. Lau, Appl. Phys. Lett., 2017, 110, 182901.
98. M. Shrestha, Z. Lu and G.-K. Lau, ACS Appl. Mater. Interfaces, 2018, 10, 39942–39951.
99. X. Duan, H. Wang, Z. Li, L. Zhu, R. Chen, D. Kong and Z. Zhao, Appl. Acoust., 2015, 88, 84–89.
100. A. Sasmal, S. K. Medda, P. S. Devi and S. Sen, Nanoscale, 2020, 12, 20908–20921.
101. A. Anand, D. Meena and M. C. Bhatnagar, J. Alloys Compd., 2020, 843, 10.
102. K. Ibtehaj, M. H. H. Jumali and S. Al-Bati, Polymer, 2020, 208, 122956.
103. C. Du, Z. Wang, G. Liu, W. Wang and D. Yu, Colloids Surf., A, 2021, 624, 126790.
104. A. M. Mohamed, K. Yao, Y. M. Yousry, S. Chen, J. Wang and S. Ramakrishna, Appl. Phys. Lett., 2018, 113, 092903.
105. C. M. Wu and M. H. Chou, eXPRESS Polym. Lett., 2020, 14, 103–114.
106. A. M. Mohamed, K. Yao, Y. M. Yousry, J. Wang and S. Ramakrishna, J. Appl. Phys., 2020, 127(21), 214102.
107. P. K. Panda and B. Sahoo, Ferroelectrics, 2015, 474, 128–143.
108. H. Fan and H. E. Kim, J. Appl. Phys., 2002, 91, 317–322.
109. A. Jain, K. J. Prashanth, A. K. Sharma, A. Jain and P. N. Rashmi, Polym. Eng. Sci., 2015, 55, 1589–1616.
110. A. Presas, Y. Luo, Z. Wang, D. Valentin and M. Egusquiza, Sensors, 2018, 18, 2251.
111. C. H. Zhang, Z. Hu, G. Gao, S. Zhao and Y. D. Huang, Mater. Des., 2013, 46, 503–510.
112. Y. Sun, Z. Li, A. Huang and Q. Li, J. Sound Vib., 2015, 355, 19–38.
113. Y. Liao, X. Zhou, Y. Chen and G. Huang, Smart Mater. Struct., 2018, 28, 025005.
114. X. Liu, C. Wang, Y. Zhang and L. Huang, Int. J. Mech. Sci., 2021, 199, 106426.
115. L. Gu, C. Zhao, K. Wang, S. Li, X. Wang and Z. Huang, Appl. Phys. Lett., 2021, 119, 131903.
116. B. S. Kim, S. Kwon, S. Jeong and J. Park, J. Intell. Mater. Syst. Struct., 2019, 30, 2575–2580.
117. K. Yu, N. X. Fang, G. Huang and Q. Wang, Adv. Mater., 2018, 30, 1706348.
118. S. M. Montgomery, S. Wu, X. Kuang, C. D. Armstrong, C. Zemelka, Q. Ze, R. Zhang, R. Zhao and H. J. Qi, Adv. Funct. Mater., 2021, 31, 2005319.
119. M. Hemmatian and R. Sedaghati, Smart Mater. Struct., 2017, 26, 025006.
120. A. K. Bastola, M. Paudel, L. Li and W. H. Li, Smart Mater. Struct., 2020, 29, 27.
121. X. Chen, X. Xu, S. Ai, H. Chen, Y. Pei and X. Zhou, Appl. Phys. Lett., 2014, 105, 071913.
122. Z. Xu, S. Zheng, X. Wu, Z. Liu, R. Bao, W. Yang and M. Yang, Composites, Part A, 2019, 125, 105527.
123. J. Y. Oh, D. Lee, G. H. Jun, H. J. Ryu and S. H. Hong, J. Mater. Chem. C, 2017, 5, 8211–8218.
124. Y. Wang, K. Li, X. Li, H. Cui, G. Liu, H. Xu, X. Wu, W. Yao, B. Zhong and X. Huang, Carbon, 2019, 152, 873–881.
125. D. A. Dikin, S. Stankovich, E. J. Zimney, R. D. Piner, G. H. Dommett, G. Evmenenko, S. T. Nguyen and R. S. Ruoff, Nature, 2007, 448, 457–460.
126. W. Xu and D. H. Gracias, ACS Nano, 2019, 13, 4883–4892.
127. K. F. Mak, L. Ju, F. Wang and T. F. Heinz, Solid State Commun., 2012, 152, 1341–1349.
128. J. H. Park, K. S. Minn, H. R. Lee, S. H. Yang, C. B. Yu, S. Y. Pak, C. S. Oh, Y. S. Song, Y. J. Kang and J. R. Youn, J. Sound Vib., 2017, 406, 224–236.
129. L. Liu, Y. Chen, H. Liu, H. U. Rehman, C. Chen, H. Kang and H. Li, Soft Matter, 2019, 15, 2269–2276.
130. J.-H. Oh, J. Kim, H. Lee, Y. Kang and I.-K. Oh, ACS Appl. Mater. Interfaces, 2018, 10, 22650–22660.
131. J. H. Oh, H. R. Lee, S. Umrao, Y. J. Kang and I. K. Oh, Carbon, 2019, 147, 510–518.

---