Can the microscopic and macroscopic transport phenomena in deep eutectic solvents be reconciled?
H.
Srinivasan
 ab,
V. K.
Sharma
ab,
V. K.
Sharma
 *ab and
S.
Mitra
*ab and
S.
Mitra
 ab
ab
aSolid State Physics Division, Bhabha Atomic Research Centre, Mumbai 400085, India. E-mail: sharmavk@barc.gov.in; vksphy@gmail.com; Tel: +91-22-25594604
bHomi Bhabha National Institute, Anushaktinagar, Mumbai 400094, India
First published on 18th August 2021
Abstract
Deep eutectic solvents (DESs) have become ubiquitous in a variety of industrial and pharmaceutical applications since their discovery. However, the fundamental understanding of their physicochemical properties and their emergence from the microscopic features is still being explored fervently. Particularly, the knowledge of transport mechanisms in DESs is essential to tune their properties, which shall aid in expanding the territory of their applications. This perspective presents the current state of understanding of the bulk/macroscopic transport properties and microscopic relaxation processes in DESs. The dependence of these properties on the components and composition of the DES is explored, highlighting the role of hydrogen bonding (H-bonding) interactions. Modulation of these interactions by water and other additives, and their subsequent effect on the transport mechanisms, is also discussed. Various models (e.g. hole theory, free volume theory, etc.) have been proposed to explain the macroscopic transport phenomena from a microscopic origin. But the formation of H-bond networks and clusters in the DES reveals the insufficiency of these models, and establishes an antecedent for dynamic heterogeneity. Even significantly above the glass transition, the microscopic relaxation processes in DESs are rife with temporal and spatial heterogeneity, which causes a substantial decoupling between the viscosity and microscopic diffusion processes. However, we propose that a thorough understanding of the structural relaxation associated to the H-bond dynamics in DESs will provide the necessary framework to interpret the emergence of bulk transport properties from their microscopic counterparts.
1 Introduction
The beginning of this millennium saw the emergence of deep eutectic solvents (DESs), a novel kind of solvents synthesised using mixtures of various hydrogen bond acceptors (HBAs) and hydrogen bond donors (HBDs).1–5 DESs are among the most prominent and recent addition to the repository of sustainable non-aqueous media. In particular, they have been pursued as alternative candidates for room temperature ionic liquids (RTILs), which were perceived as “green solvents” mainly due to the low vapor pressure and high boiling points that help in their recyclization. Recently, several studies have shown the toxic effects of RTILs in various organisms including mammalian cell lines.6–9 Moreover, the synthesis of RTILs is not environmentally friendly as it requires a large amount of solvents and salts. While the physicochemical properties of DESs are akin to those of RTILs, they are not entirely composed of ions, but possess a significant molecular component. Further, as the synthesis of DESs doesn’t generate waste or require additional purification, they endorse the basic tenets of green chemistry. Cheaper and easier manufacturing protocols of DESs over RTILs give them an additional edge over the latter. The versatility of DESs is manifest in the wide range of these solvents that have been prepared with different mixtures of HBAs and HBDs at their eutectic composition.3–5 While a variety of organic/inorganic salts have been used as HBAs, DESs based on choline chloride, with different HBDs (based on amides, glycols, phenols), have been the most extensively studied, owing to their biodegradability and the availability of their raw products.2,10–14Typically DESs are synthesised by mixing the parent compounds (HBA and HBD) at their eutectic composition, at a slightly elevated temperature.3,4 However, most of these mixtures remain in the liquid phase at room temperature because of a large depression in their freezing point compared to their parent compounds. This is directly related to the interaction strength between the components in the mixture, such that stronger interaction between them leads to a larger depression in the freezing point. A schematic phase diagram of a two component eutectic mixture is shown in Fig. 1. The composition at which the lowest freezing point is achieved is called the eutectic point. The depression in the freezing point, ΔTf, which is the difference between the freezing temperature at the eutectic point and the mean freezing temperature of the mixture, is indicated in the figure. The depression in the freezing point has been rationalised by the formation of hydrogen bonds between the ionic species of the salt and the HBDs.15,16 It has also been suggested that these systems remain in a supercooled state, with the intercalation of HBDs in the salt's (HBA's) lattice, disallowing them to crystallize.15,17–19 These features allow the formation of various ion–HBD complexes16,20–23 in the DES that significantly influence their physicochemical properties. Various HBDs and HBAs which have been reported to form DESs are shown in Fig. 2.
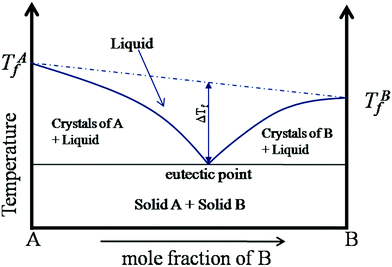 | ||
| Fig. 1 Schematic phase diagram of a two component eutectic mixture (adapted from ref. 20). | ||
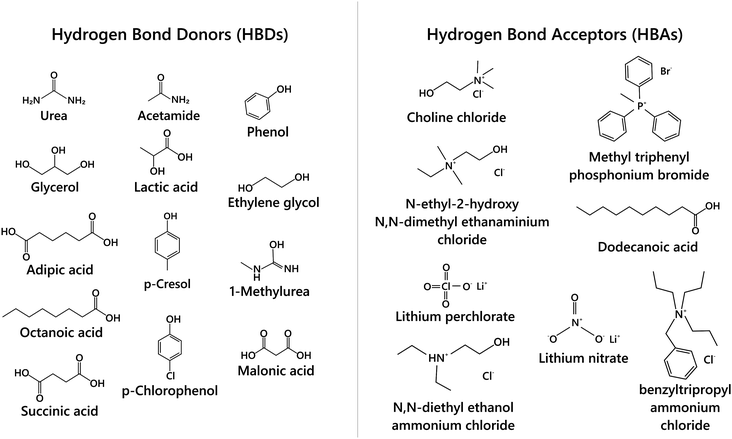 | ||
| Fig. 2 Schematic of various hydrogen bond donors (HBDs) and hydrogen bond acceptors (HBAs) used in the synthesis of DESs. | ||
DESs have found diverse applications ranging from nanoscale synthesis,24–28 electrochemical processes,29–37 catalysis,24,38–42 CO2 capture43,44 to drug solubilisation/transport.45–48 These remarkable functional aspects of DESs have sparked interest in studying their fundamental properties. The understanding of the underlying molecular mechanisms, which lead to their emergent functional properties, can be useful in the design and synthesis of various new DESs with tailored properties. In particular, the transport properties of these non-aqueous solvents are essential in exploiting their applicability in various industrial and pharmaceutical processes. For example, when DESs are used as catalysts, a lower solvent viscosity is favourable in improving the reaction rates particularly when the reaction is diffusion controlled.24,28,39 Similarly, for electrochemical processes such as electroplating/batteries, the key parameter ionic conductivity, is also significantly controlled by solvent viscosity.30,33,49,50 In contrast, it is also observed that higher viscosity of the DES is beneficial in the synthesis of gold nanofoams, which have excellent catalytic activity.28 These applications and more form a sound rationale to gain an understanding of the microscopic origin of these bulk properties.
Numerous studies have been carried out to investigate both the macroscopic and microscopic transport properties in DESs. While primary characterisation of their bulk properties has been very extensively pursued, the correlation of these parameters with the solvent's molecular structure and dynamics is also explored. In this perspective article, the current understanding of the transport properties and mechanisms in DESs, obtained through different experimental and computational studies, is discussed. Macroscopic properties like viscosity and ionic conductivity have been measured with rheology,11,13,37,39,43,44,51–61 dielectric spectroscopy,19,62–67 electrochemistry,30,33,35,36,50,64,66,68etc. Fluorescence correlation spectroscopy,64,69–72 Raman-induced Kerr effect spectroscopy,18 pulsed field gradient nuclear magnetic resonance (PFG-NMR),47,73,74 and quasielastic neutron scattering (QENS)20,21,23 are among those techniques which provide insights into microscopic transport phenomena. The various parameters that have been extracted from experimental measurements can also be corroborated with the results of computational studies, particularly through the use of time-correlation functions. Molecular dynamics (MD) simulations of these systems can provide the atomistic trajectories which can aid in calculating these time-correlation functions. Velocity autocorrelation, CV(t), is a typical example, which can be used to calculate the self-diffusivity, D, of various species in the solvent, which can be compared with experimental data on diffusivity from PFG-NMR or QENS experiments. Similarly, ionic conductivity of the solvent can also be computed by a time-correlation function from Einstein's relation, given by
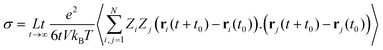 | (1) |
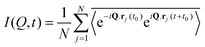 | (2) |
This perspective article is organized as follows. In the next section the results on the macroscopic/bulk properties, such as viscosity, ionic conductivity and thermal conductivity, are discussed. Various models that have been developed to describe these bulk properties, and their shortcomings and advantages are also discussed. After that, we discuss the microscopic transport phenomena in DESs, focusing on diffusion mechanisms of different species, ionic transport and hydrogen bond dynamics. We also highlight the aspects of dynamic heterogeneity in DESs due to their glassy nature. The influence of water addition on the microscopic transport mechanism and dynamic heterogeneity in DESs is also summarized. In the penultimate section, we try to establish a connection between the observed bulk transport properties and microscopic transport. A number of worthwhile investigations based on their dynamic heterogeneity are also proposed. In the last section, we explore the possibility of designing new eutectic mixtures with more efficient and improved transport properties that would be beneficial to various areas of applications.
2. Macroscopic transport properties
Macroscopic transport properties like viscosity and conductivity of DESs have been extensively studied owing to their importance in various applications like electrodeposition, battery electrolytes, catalysis, etc. It is highly desirable to develop DESs with low viscosity and/or higher conductivity for their various potential applications as green media. In this section, we discuss how the viscosity/conductivity of DESs depends on several factors including the chemical nature of the DES components (HBAs and HBDs, the molar ratio between HBAs and HBDs), temperature, and water content. In view of these factors, various models were developed to explain these dependencies which will also be discussed. In comparison to mass transport, there have been very few studies on thermal transport in DESs, which are briefly outlined at the end of this section.2.1 Viscosity – momentum transport
Choline chloride (ChCl) based DESs like reline (ChCl + urea, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), ethaline (ChCl + ethylene glycol, 1
2), ethaline (ChCl + ethylene glycol, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and glyceline (ChCl + glycerol, 1
2) and glyceline (ChCl + glycerol, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) are some of the most common DESs. Generally, in applications as alternatives to ionic liquids, the major setback of DESs is their significantly higher viscosity. For example, in the case of the most prevalent DES, reline, the viscosity at 298 K is found to be ∼1000 cP, which is a thousand times larger than that of water and 2–3 times larger than the viscosity of typical RTILs. The viscosities of different DESs obtained from various studies are listed in Table 1. A significant discrepancy is observed in the viscosity values of reline in different studies (Table 1). Similar discrepancies, although much lesser than that for reline, are also observed for ethaline and glyceline (Table 1). This has been largely attributed to the excess water content in the DES which could vary due to different preparation schemes.11,53 It has also been observed that the viscosities of DESs are significantly affected by the viscosities of the HBDs in the system, as indicated in Table 1. For example, the viscosity of the solvents follows the trend reline < glyceline < ethaline (Table 1), whereas the viscosity of the respective HBDs follows urea < glycerol < ethylene glycol. The solvent viscosity is dictated by the HBD's viscosity through the varying H-bond interaction strength in the DES, as has been observed in DESs formed between carboxylic acids and choline chloride.10 It is found that DESs synthesised from monoacids, such as levulinic/glycolic acids, show much lower viscosities than those synthesised from diacids like malonic/glutaric acids, which is due to stronger H-bonding observed in diacids. On the other hand, the salts/HBAs also play a crucial role in the viscosity of DESs. For instance, the DES formed by glycerol and ethylene glycol with N,N-diethylethanol ammonium chloride (DEEAC) shows systematically higher viscosity compared to its choline chloride counterpart.52,55 This is likely due to the larger size and asymmetry of the former's cation compared to choline. Similarly, a strong anion dependence in viscosity is observed in DESs synthesised from mixtures of lithium salts and acetamide,17,18,72 with lithium perchlorate DES being the least viscous and lithium bromide being the most viscous. Investigation of the effect of the alkyl chain of HBDs on the viscosity of DESs, using the mixtures of alkylamide and lithium perchlorate, shows an interesting trend, where propionamide as the HBD exhibits lower viscosity compared to acetamide and butyramide.72 A similar study was performed on a series of diols (ethylene glycol, 1,3-propanediol and 1,3-pentanediol) as HBDs and tetrabutylammonium bromide as the HBA.75 It was observed that the viscosity of the solvent increased as the alkyl chain length of the HBDs increased. However, when an additional OH group (when using glycerol as the HBD) was added in the form of glycerol in the HBD, the viscosity of the solvent was found to increase significantly, owing to the increased intermolecular H-bonding in the system.75
2) are some of the most common DESs. Generally, in applications as alternatives to ionic liquids, the major setback of DESs is their significantly higher viscosity. For example, in the case of the most prevalent DES, reline, the viscosity at 298 K is found to be ∼1000 cP, which is a thousand times larger than that of water and 2–3 times larger than the viscosity of typical RTILs. The viscosities of different DESs obtained from various studies are listed in Table 1. A significant discrepancy is observed in the viscosity values of reline in different studies (Table 1). Similar discrepancies, although much lesser than that for reline, are also observed for ethaline and glyceline (Table 1). This has been largely attributed to the excess water content in the DES which could vary due to different preparation schemes.11,53 It has also been observed that the viscosities of DESs are significantly affected by the viscosities of the HBDs in the system, as indicated in Table 1. For example, the viscosity of the solvents follows the trend reline < glyceline < ethaline (Table 1), whereas the viscosity of the respective HBDs follows urea < glycerol < ethylene glycol. The solvent viscosity is dictated by the HBD's viscosity through the varying H-bond interaction strength in the DES, as has been observed in DESs formed between carboxylic acids and choline chloride.10 It is found that DESs synthesised from monoacids, such as levulinic/glycolic acids, show much lower viscosities than those synthesised from diacids like malonic/glutaric acids, which is due to stronger H-bonding observed in diacids. On the other hand, the salts/HBAs also play a crucial role in the viscosity of DESs. For instance, the DES formed by glycerol and ethylene glycol with N,N-diethylethanol ammonium chloride (DEEAC) shows systematically higher viscosity compared to its choline chloride counterpart.52,55 This is likely due to the larger size and asymmetry of the former's cation compared to choline. Similarly, a strong anion dependence in viscosity is observed in DESs synthesised from mixtures of lithium salts and acetamide,17,18,72 with lithium perchlorate DES being the least viscous and lithium bromide being the most viscous. Investigation of the effect of the alkyl chain of HBDs on the viscosity of DESs, using the mixtures of alkylamide and lithium perchlorate, shows an interesting trend, where propionamide as the HBD exhibits lower viscosity compared to acetamide and butyramide.72 A similar study was performed on a series of diols (ethylene glycol, 1,3-propanediol and 1,3-pentanediol) as HBDs and tetrabutylammonium bromide as the HBA.75 It was observed that the viscosity of the solvent increased as the alkyl chain length of the HBDs increased. However, when an additional OH group (when using glycerol as the HBD) was added in the form of glycerol in the HBD, the viscosity of the solvent was found to increase significantly, owing to the increased intermolecular H-bonding in the system.75
| HBA | HBD | Molar ratio (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD) HBD) |
Viscosity (cP) |
|---|---|---|---|
| Choline chloride | Urea | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1571,76 82953 |
| Glycerol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
302,55 32911 | |
| Ethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
40,77 4457 | |
| Glycolic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
54878 | |
| Malonic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
138978 | |
| Levulinic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
22778 | |
| Glutaric acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
201578 | |
| Phenol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
10014 | |
| p-Cresol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
10214 | |
| p-Chlorophenol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
12314 | |
| N,N-Diethylethanol ammonium chloride | Glycerol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
51352 |
| Ethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
5152 | |
| Lithium bromide | Acetamide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.6 3.6 |
21117 |
| Lithium nitrate | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.6 3.6 |
131217 | |
| Lithium perchlorate | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.6 3.6 |
15872 | |
| Propionamide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.6 3.6 |
9072 | |
| Butyramide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.6 3.6 |
20572 | |
| Menthol | Phenylacetic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
3047 |
| Ibuprofen | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
8047 | |
| Benzoic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
4047 | |
| Octanoic acid | Dodecanoic acid | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
779 |
| Nonanoic acid | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
979 | |
| Decanoic acid | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1179 |
The rheology of DESs based on an aromatic salt, benzyltripropylammonium chloride, with various HBDs, such as lactic acid, glycerol, ethylene glycol and phenol, has been studied.56 In steady shear rheological measurements, all DESs show a similar constant viscosity behaviour, except the DES of lactic acid that showed shear-thinning over a shear rate of 100 s−1. This shear-thinning property has been attributed to the breakage of aggregates formed by H-bonding upon increasing the shear rate.56 Altamash et al.43 studied natural deep eutectic solvents (NADESs) prepared using mixtures of citric acid, fructose, malic acid, and lactic acid with choline chloride at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. These solvents also showed viscoelastic behaviour with a shear thinning effect at all temperatures.
1. These solvents also showed viscoelastic behaviour with a shear thinning effect at all temperatures.
While most of the DESs using choline chloride display substantially higher viscosities, relatively low viscous DESs have been synthesised using phenolic compounds (p-cresol, phenol and p-chlorophenol) as HBDs,14 which showed that the viscosity was strongly dependent on the substitution group of the HBD in the solvent. This is attributed to the functional difference between the Cl group in chlorophenol and the methyl group in p-cresol where the former exhibits strong electron-withdrawing property strengthening the H-bond structure and the latter weakens the H-bonding due to its electron-donating effect.14 Duarte et al.47 synthesised therapeutic DESs using menthol as the HBA and various active pharmaceutical ingredients (phenylacetic acid, ibuprofen, benzoic acid) as HBDs. These DESs provided excellent low viscous formulation of drugs with enhanced solubility and permeability. Fatty acids like octanoic acid, nonanoic acid, decanoic acid and dodecanoic acid can act as both HBDs and HBAs. Various binary mixtures of these acids were used to prepare different DESs, which were found to possess markedly lower viscosities in the range of 8–12 cP.79 In addition to their low viscosities they are also immiscible with water, and hence are useful as media for efficient mass transfer between two equilibrium phases, like for example extracting bisphenol from water.79 It has also been demonstrated that the viscosities of fatty acid DESs could be fine-tuned by prudent choice of the length of the alkyl chain of the fatty acids in the mixture.
The modulation of viscosity through water has been extensively studied in a variety of DESs,11,39,52–54,76,80–83 particularly with an aim to achieve a specific functionality of the DES. Moreover, the effect of water is important to study due to the inherent hygroscopic nature of DESs, which allows the presence of trace water amounts. In principle, the amount of water content in the DES also depends strongly on the preparation method.78 Water invariably decreases the density and viscosity of DESs, and the decrease in viscosity is found to be drastic in nature. For instance, the viscosity of reline at 298 K is 1571 cP, and the addition of just 0.15 mole fraction of water decreases the viscosity to 323.9 cP and subsequently at a water mole fraction of 0.46, it is as low as 21.10 cP.76 A similar behaviour is observed in other DESs too, including mixtures of DEEAC with glycerol and ethylene glycol, as indicated in Fig. 3.11,52,76,80 The plot clearly shows that the decline in viscosity is the steepest in the case of reline, indicating the strongest disruption of the H-bond network in the same. Further, it should be noted that the decrease in viscosity is rather sharp till 0.25 mole fraction of water, and then after that, it gradually tapers off. Such behaviour is also observed in the NADES made from 1,2-propanediol and glucose with choline chloride, where the drop in viscosity is sharp till 50% (w/w) of water and afterwards recedes gradually.54 NMR and FTIR measurements showed a progressive rupture of H-bonds with addition of water till 50% (w/w) and beyond it a complete rupture of H-bonds. The viscosity of the solvent was found to follow an empirical power law decay given by 0.88x−1.5, where x is the weight fraction of water. The ability of water, even in small fractions, to alleviate the large viscosities of DESs has found profound use in various catalysis and extraction processes.39,54
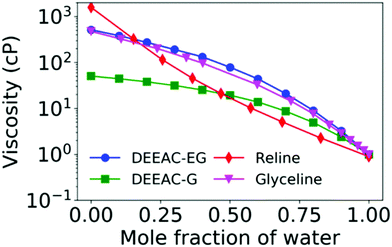 | ||
| Fig. 3 Variation of viscosity with respect to addition of water content for 4 different DESs (described in the text) from various literature studies.11,52,76 | ||
Quite similar to ionic liquids, the temperature dependence of the viscosity of DESs is generally found to obey the Vogel–Fulcher–Tammann (VFT) law, which is given by
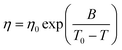 | (3) |
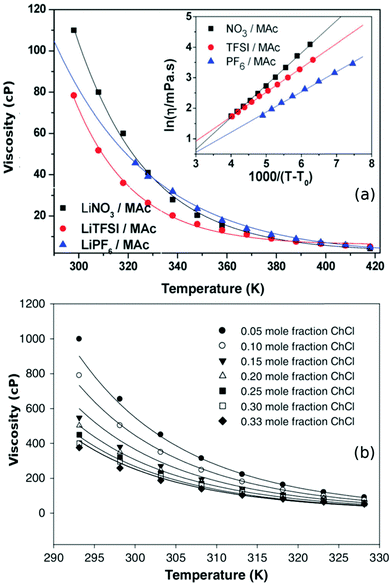 | ||
| Fig. 4 (a) The temperature dependence of DESs based on N-methylacetamide (Mac) with different lithium salts along with their VFT model fits (eqn (3)) (adapted from ref. 50). (b) Viscosity model developed by Mjalli et al.77 for choline chloride (ChCl) and glycerol based DESs at different molar compositions (adapted from ref. 77). | ||
Various models have been proposed to understand the behaviour of viscosity with respect to temperature and composition in DESs. Mjalli et al.77 developed two empirical equations to describe the viscosities of various choline chloride DESs, by inclusion of an additional dependence on molar composition in both the equations. It was concluded that solvents which were less viscous could be described well using the modified Eyring model, while the modified VFT model was found to explain their more viscous counterparts.77Fig. 4b shows the viscosity of eutectic mixtures of choline chloride and glycerol at various molar compositions. The solid lines in the plot indicate the model fits based on Mjalli et al.77 A more comprehensive model for viscosity based on equation of state (EoS) was put forward by Haghbaksh et al.85,86 They employed cubic plus association theory and perturbed chain-statistical associating fluid theory to handle the associating interactions in the EoS of DESs. Their model was able to describe the dependence of both temperature and molar composition in a wide range of DESs, including HBAs like choline chloride, 1-benzyl triphenyl phosphonium chloride, 1-acetylcholine chloride, and 1-tetraethylammonium chloride and HBDs such as glycerol, levulinic acid, urea, phenol, etc.86
Abbott et al.51,87 suggested a model based on hole theory, which had been found to be significantly useful for molecular liquids and ILs.87 In this model, the molecular transport is dictated by the formation of holes in the solvent due to density fluctuations. The size and formation of the holes in the system depend largely on the surface tension of the liquid.51,87 Based on simple calculations using kinetic theory, they derived a formula for the viscosity based on the size of HBAs and HBDs in the system, given by87
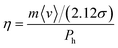 | (4) |
2.2 Electrical conductivity – charge transport
There are two main properties of DESs which govern their electrical conductivity: the first is the mobility of charge carriers that is dictated by solvent viscosity, and the second is the number of charge carriers in the solvent. In a study by Abbott et al.10 on deep eutectic mixtures of choline chloride and carboxylic acids, an almost linear correlation between molar conductivity (Λm) and inverse viscosity (1/η) was observed. This relationship between viscosity and molar conductivity is known as the Walden rule (Λmη = constant), which is satisfied in DESs where the conductivity is controlled by mobility of the charge carriers rather than their numbers.10 Employing the hole-theory in this context suggests that the density of holes in the solvent is more important than the density of charge carriers.10Table 2 lists the measured conductivity of various DESs at room temperature. However, it is observed that a majority of DESs don’t directly follow the Walden rule, as the conductivity of these solvents also strongly depends on their components (HBDs and HBAs). For instance, it is evident from Table 2 that the trend of conductivity in choline chloride based DESs follows their HBDs as, ethylene glycol > urea > glycerol > triethylene glycol > levulinic acid. It is important to note that although the viscosity of reline is significantly higher than that of glyceline (Table 1), the ionic conductivity of the former is higher than that of the latter (Table 2). This indicates that the mechanism of conduction in glyceline and reline is very different. In a study using broadband dielectric spectroscopy, Rueter et al.66 investigated the role of structural relaxations in the ionic conductivity of reline, ethaline and glyceline. They found that in ethaline and glyceline, both ionic mobility and reorientational motions were coupled with solvent viscosity and structural relaxations.88 However, in reline, it is observed that only the reorientational dynamics is coupled with viscosity, but the ionic mobility is not, and hence the conductivity of the system is enhanced even though the solvent viscosity is high.88 A multiple number of reasons have been cited to describe the non-canonical conductivity in reline, including the charge transfer from ions to HBDs and motion of complexed ions in the solvent. The effect of HBAs is manifest in the ethylene glycol based DESs, where conductivity is observed to depend on the size and geometry of the salt (HBA) being used (Table 2). In a study on NADESs by Dai et al.,54 they found that for the same HBD, the electrical conductivity was higher when HBAs were salts like choline chloride compared to HBAs like amino acids/organic acids. It was noted that this behaviour could be due to the greater availability of free ions when salts are used as HBAs.| HBA | HBD | Molar ratio (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD) HBD) |
Conductivity (mS cm−1) |
|---|---|---|---|
| Choline chloride | Urea | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2.3181 |
| Glycerol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1.7589 | |
| Ethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
7.3389 | |
| Levulinic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.8190 | |
| Triethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1.4191 | |
| Diethylethanolammonium chloride | Ethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
5.1289 |
| Glycerol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.7589 | |
| Malonic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.1335 | |
| Lithium perchlorate | Acetamide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.5 5.5 |
0.9792 |
| Lithium bis(trifluoromethane sulfone)imide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
0.8592 | |
| Lithium triflate | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
0.4892 | |
| Benzyltripropylammonium chloride | Ethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
0.8756 |
| Glycerol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
0.07956 | |
| Lithium nitrate | N-Methylacetamide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
0.7693 |
| Lithium bis(trifluoromethane sulfone)imide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
1.3593 | |
| Lithium hexafluorophosphate | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
1.4193 |
A study by Yusof et al.75 on eutectic mixtures of tetrabutylammonium bromide as the HBA and ethylene glycol and glycerol as HBDs found a peculiar relationship between viscosity and ionic conductivity. In the case of ethylene glycol, it was found that the conductivity of the DES increased with increasing molar fraction of the HBD, while in the case of glycerol the conductivity was found to decrease.75 On the other hand, it was observed that in both the cases, the viscosity of the DES was found to decrease with increasing molar fraction of the HBD. These observations were in stark contrast to the Walden rule, which applies to ions in infinitely dilute solution. However an extension of the Walden rule can be used in ionic liquids and DESs to provide a qualitative assessment of ionicity in the solvent, which is an important aspect of electrical conductivity. This is achieved by defining the Walden product, which is given by Λmηα. In ideal/good ionic solvents, which follow Walden's rule, α is 1, but when α < 1, it is known as a poor ionic liquid, and when α > 1 it is referred to as a superionic liquid. The Walden plot (log(Λm) vs. log(1/η)) succinctly captures the features of ionicity as shown in Fig. 5. Bahadori et al.35 investigated the electrochemical properties of DESs with different combinations of HBDs and HBAs. They considered the mixtures of choline chloride (HBA) with different HBDs – malonic acid (DES1), oxalic acid (DES2), triethanolamine (DES3), zinc nitrate (DES4) and trifluoroacetamide (DES5), and mixtures of N,N diethylethanol ammonium chloride with malonic acid (DES6) and zinc nitrate (DES7). In their study they illustrated using the Walden plot (Fig. 5) that only DES6 and DES7 were poor ionic liquids and the rest were either ideal or superionic.35 Such superionic characteristics are also observed in the DES of N-methylacetamide and LiTFSI.37
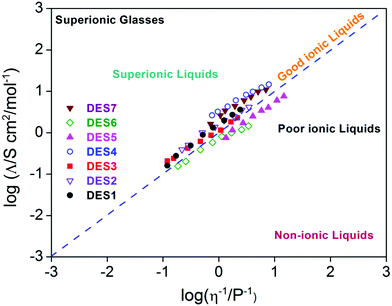 | ||
| Fig. 5 Walden plot of various DESs (as described in the text) (adapted from ref. 35). | ||
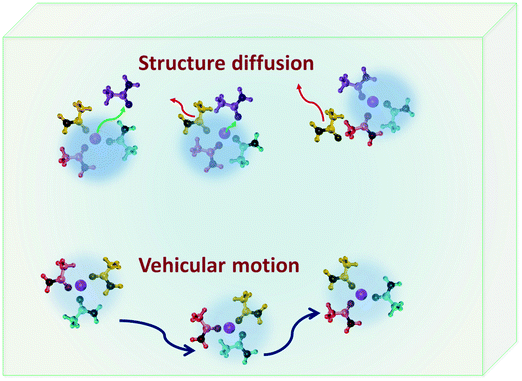
DESs have been investigated as potential candidates for electrolytes in lithium-ion batteries and supercapacitors. Anouti and co-workers have studied a series of DESs based on N-methylacetamide and lithium salts (lithium nitrate [LiNO3], lithium hexafluorophosphate [LiPF6], lithium bis(trifluoromethanesulfonyl)imide [LiTFSI]).37,49,50,93 They found that, similar to their viscosity, the temperature dependence of the ionic conductivity of these solvents also follows the VFT equation. It must be noted that the Arrhenius equation is also found to be a satisfactory and suitable model for ionic conductivity when considered in a small temperature range.10,54,78 In the case of DESs based on different lithium salts investigated by Anouti and coworkers,49,50,93 at 300 K they follow the trend LiTFSI < LiPF6 < LiNO3, but as we increase the temperature to ∼360 K, the trend is LiNO3 < LiTFSI < LiPF6, which is due to the large activation energy observed for the conductivity of the LiNO3 system.50 Choline chloride based DESs, using ethylene glycol and lactic acid as HBDs,94 were also demonstrated as favourable electrolytes for lithium-ion batteries, wherein ethaline showed better dissociation of ions and therefore was found to be a more promising candidate. In particular, 0.5 M LiPF6 in ethaline is found to have an ionic conductivity of 8 mS cm−1 at room temperature.94 The mechanism of lithium transport in DESs which is essential for their application in lithium-ion batteries was investigated by Srinivasan et al.21 Ionic conductivity as calculated using eqn (1) was found to be 16.3 mS cm−1 which compared well with experimental studies.21 They observed that there are two possible pathways for lithium transport – vehicular motion and structural diffusion. In the former, the ionic mobility is accomplished by the motion of lithium-ion complexes formed in the solvent, but in the latter the ions move by exchanging their neighbouring HBDs.21 In their study on a DES based on LiClO4 and acetamide, it was found that vehicular motion is the dominant mechanism of ionic conduction, which is associated to the long-lived nature of ion–HBD complexes formed in the system.21
Unlike in the case of viscosity, the addition of water doesn’t monotonously increase the ionic conductivity of DESs.54,95 For example, in reline, the ionic conductivity is observed to increase up to 0.9 mole fraction of water and then sharply decrease to zero.81,95 In the initial phase, up to 0.9 mole fraction, the increase in the conductivity of the DES is promoted by the decrease in its viscosity. However, a further increase in the water content in the system leads to a decrease in the ionicity of the system, causing the conductivity to decrease.54 This behaviour is also observed in ILs, where the conductivity peaks at 0.95 mole fraction of water.95 This behaviour was also found to be valid in a number of NADESs studied by Dai et al.54
2.3 Thermal conductivity
Heat transport in DESs has been a scarcely studied domain. Among the few studies existing, the thermal conductivity of the choline chloride based DESs has been the most studied.96–98 Ibrahim et al.97 studied the mixtures of choline chloride with HBDs (urea, ethylene glycol, fructose, glucose, glycerol, malonic acid and triethylene glycol), and found that the thermal conductivity was in the range of 0.21 W m−1 K−1 to 0.24 W m−1 K−1. The highest thermal conductivity was found in the case of urea as the HBD, while the lowest was in the case of malonic acid.97 It was observed that the temperature dependence of thermal conductivity was very weakly decremental, and could be modelled using a simple linear decay.97 A similar behaviour is observed in a study by Gautam et al.,98 in which they explored the effect of chain length and methyl units by considering three DESs – choline chloride and urea (DES-A), N,N-diethyl ethanolammonium chloride and urea (DES-B), and choline chloride and thiourea (DES-C). While DES-A and DES-B have very similar thermal conductivity, for DES-C it is found to be notably lower, which is likely due to the lowered hydrogen bonding density because of the sulphur group and the additional methyl units in the HBD (thiourea).The addition of water in DESs shows a marked increase in their thermal conductivity. For instance, in reline, the thermal conductivity increases from 0.241 W m−1 K−1 in its pure state to 0.377 W m−1 K−1 with 0.5 weight fraction of water.97 The increase in the thermal conductivity of aqueous mixtures of DESs is monotonous and is found to be the same for a number of different mixtures.97 The substantial increase in these aqueous mixtures has been correlated to the depletion of H-bonds between components of DESs and formation of new H-bonds between water and components of DESs. The introduction of nanoparticles like graphene oxide, Al2O3 and TiO2 is also found to significantly modulate the thermal conductivity of glyceline.99 While, in general, the thermal conductivity increases monotonically with increasing volume fraction of the nanoparticles, Al2O3 nanoparticles show a peculiar behaviour, in which the thermal conductivity peaks at a volume fraction of around ∼0.3% and then decreases. This was found to be due to the formation of H-bonds between glycerol and Al2O3 nanoparticles in the DES.
3. Microscopic transport in DESs
As DESs are a multicomponent mixture of both ions and molecules, they possess complex microscopic transport phenomena due to the several intermolecular interactions prevailing in the solvent. They also show glass-forming features suggesting a strong interplay between their structural relaxation and transport phenomena.17,66,67,100 These structural relaxations are aided by the relaxation of extensive intermolecular H-bond networks formed in DESs.20–22,62,66,88,101 A variety of experiments have been carried out to systematically characterise the microscopic transport processes in DESs. Particularly, PFG-NMR47,73,74,102–104 and QENS20,21,23,105,106 have been useful in studying the diffusion of HBDs and ionic species of the salt. Classical and ab initio MD simulations have been useful to gain molecular level insight into the transport mechanism of various species in the solvent.20–22,43,62,65,73,81,101,105,1073.1 Diffusion mechanism in DESs
The effect of constituent species of DESs on the molecular mobility is evident from a number of studies.47,62,74,101,103,104,106,108 PFG-NMR studies74,104 on a series of choline chloride based DESs showed that the diffusion of the cholinium ion was slower than that of their respective HBDs in each of these solvents, except in the case of malonic acid as the HBD. The self-diffusivities measured for all the species in these DESs74 are listed in Table 3. The strong dependence of the diffusivity on HBDs can be appreciated by observing the huge difference between the cases of ethaline (choline chloride + ethylene glycol) and maline (choline chloride + malonic acid). The anomalously slow diffusion in maline has been ascribed to the formation of dimers of malonic acid in the DES, while the large mobility in ethaline is associated to its low solvent viscosity.| HBA | HBD | Molar ratio (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD) HBD) |
D HBA (×10−12 m2 s−1) | D HBD (×10−12 m2 s−1) | |
|---|---|---|---|---|---|
| Cation | Anion | ||||
| a MD simulation. | |||||
| Choline chloride | Urea | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2.1a109 | 3.574 | 6.674 |
| Ethylene glycol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
25a12 | 26.2,74 18.1a12 | 47.7,74 37.5a12 | |
| Glycerol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
4.6a12 | 3.8,74 3.0a12 | 5.1,74 4.5a12 | |
| Malonic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.6474 | 0.60 | ||
| [BMIM]PF6 | N-Methylacetamide | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
49.3 | 50.3 | 109 |
| [HMIM]PF6 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
36.7 | 40.8 | 86.6 | |
| [BMIM] [CF3SO3] | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
64.9 | 63.8 | 115 | |
Similarly, the ionic species of HBAs also play a crucial role in the molecular diffusion in DESs. For instance, from Table 3, it is clear that the DESs formed by N-methylacetamide with different salts (1-butyl-3-methyl imidazolium hexafluorophosphate [BMIM][PF6], 1-hexyl-3-methylimidazolium hexafluorophosphate [HMIM][PF6], [BMIM]CF3SO3) show sharp differences in their diffusivities depending on the cations and anions in the solvent.103 It is found that the diffusion of all the species is slower in the DES formed by the longer chain cation, [HMIM]+, compared to that with [BMIM]+. On the other hand, replacing the anion PF6− by CF3SO3− significantly increases the molecular diffusion of all the species in the solvent.103 Biswas and coworkers19,72 have used classical MD simulation and dielectric spectroscopy on DESs formed by acetamide and various salts (LiClO4, NaClO4, LiNO3 and LiBr, NaSCN, KSCN) and has shown a strong anion/cation dependence for the molecular dynamics of acetamide in these solvents. QENS studies on DESs based on acetamide with LiClO4/LiNO3 have also illustrated the effect of HBAs.106 In their study, they found that the diffusion of acetamide is slower in the presence of LiNO3 in comparison to LiClO4,106 which is found to be consistent with recent MD simulation studies on these DESs.110 The strong dependence on the HBAs/HBDs in the molecular diffusion of different species in the solvent can be attributed to the strong role played by the H-bonding network in DESs. The formation of such networks has also been confirmed through neutron diffraction of reline111 and glyceline.112 The first liquid-phase neutron diffraction experiment on a cholinium DES was carried out by Edler and co-workers.111 They used H/D isotopically substituted samples of reline for the neutron diffraction measurements and interpreted the data using the empirical potential structure refinement model. The obtained radial distribution functions showed the presence of a strong and complex hydrogen-bonding network between the DES species. Significant ordering interactions were found not only between urea and chloride, but also between all DES components. These observations strongly vindicate the structure–dynamics relationship in such solvents, for which glassy behaviour is observed.17,66,67
As discussed earlier, hole theory was adopted to explain the viscosity and conductivity using the motion of various species through the available holes in the media,51,87 However, this theory was not successfully applicable to all the cases of DESs.51,74 A fundamental understanding of the molecular diffusion can provide deeper insights, shedding light on the validity of hole theory and unravelling the correlation between solvent viscosity and self-diffusion of species. The relationship between diffusivity (D) of a particle and viscosity (η) of the solvent is given by the famous Stokes–Einstein equation,
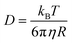 | (5) |
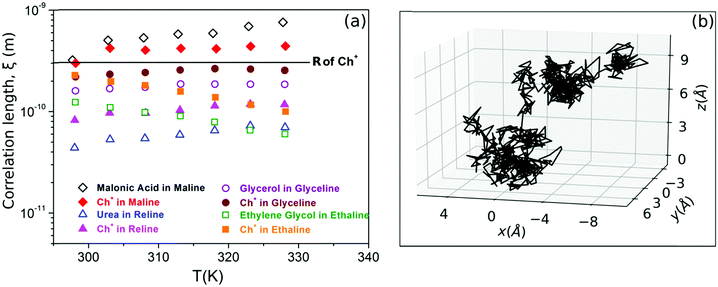 | ||
Fig. 6 (a) Correlation length of different species in maline, reline, glyceline and ethaline calculated from eqn (5) using the diffusion constant obtained from PFG-NMR (adapted from ref. 74). (b) MD simulation trajectory of acetamide molecules in DES (acetamide + lithium perchlorate, 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22), showing both long-range jumps and the localised diffusion within the cages (adapted from ref. 20). 22), showing both long-range jumps and the localised diffusion within the cages (adapted from ref. 20). | ||
The dynamic structure factor, S(Q, E), obtained from QENS experiments is useful in delineating the different dynamical processes in the solvent, through the use of an appropriate model function describing them. Apart from the long-range jump diffusion process observed from PFG-NMR, localised translational diffusion within transient cages was also observed in DESs using QENS.20,21,23 The QENS spectra of the DES were modelled using the convolution of two dynamic structure factors,20,21
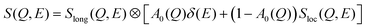 | (6) |
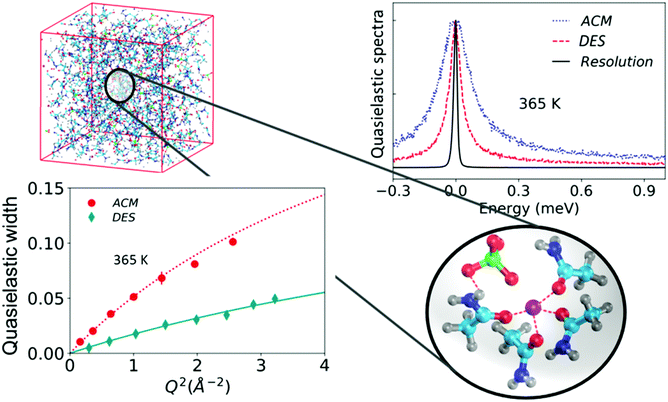 | ||
| Fig. 7 (top left) Simulation snapshot of the complete DES system. An enlarged view of the snapshot of a typical complex formed in the DES is shown. (top right) Quasielastic spectra of the DES and molten acetamide (ACM) along with the instrumental resolution, and (bottom left) quasielastic widths associated with the jump diffusion process in ACM and the DES (adapted from ref. 20). | ||
On the other hand, the localised diffusion process has been described using diffusion confined within a sphere,116 which has been associated to transient confinement in cages formed by H-bonded neighbours in the DES.20,21,23 The formation of such cages has been observed in a number of studies including classical and ab initio MD simulations.112,117–119 An interesting observation from QENS experiments on glyceline was that, despite being heavier and larger, choline ions showed a larger confinement radius in comparison to glycerol.23 This anomaly was rationalised from quantum mechanical calculations, which indicated that this was due to the strong association of glycerol and chloride ions in the DES, while choline ions were relatively free.23
In the investigation of the acetamide based DES, it was shown that the radius associated to the transient confinement of molecules in the DES followed an exponential distribution with an average radius (ravg),20 for which the EISF given in eqn (6) was given by
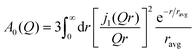 | (7) |
Complexes formed in DESs also play a vital role in the diffusion of lithium ions in DESs which forms a major scope of interest owing to their application in lithium ion batteries. In ionic liquids, lithium transport is primarily governed by vehicular and structure diffusion mechanisms.120–122 In the former, the lithium ions diffuse along with their H-bond partner, but in the latter their dynamics is propelled by the exchange of their H-bond partners.122,123Fig. 8 shows a schematic of structure and vehicular transport mechanisms in electrolytic solutions. The mechanism of lithium transport in the DES based on acetamide and lithium perchlorate has been studied in detail.21 Dynamically two distinct species of acetamide in the DES corresponding to the ones strongly bound to lithium ions and the others free were found.21 Both of them follow the diffusion model described in eqn (6).21 These two species showed markedly different long-range jump diffusivities, but comparable localised diffusivities.20,21 It was found that the motion of lithium ions is strongly correlated with the dynamics of bound acetamide molecules in the DES, indicating that lithium transport might be vehicular in nature.21 This was well validated by the long-lived H-bond complexes formed between acetamide and lithium ions. The relaxation of the H-bond autocorrelation function showed a stretched exponential behaviour, indicating a distribution of relaxation rates associated with the lifetime of these acetamide–lithium complexes. Using the distribution of relaxation rates, it was estimated that about 90% of lithium ions in the solvent were transported by vehicular motion.21 Lithium diffusion has also been studied in DESs synthesised using mixtures of LiTFSI with methanesulfonamide (MSA) and dimethylmethanesulfonamide (DMMSA), using PFG-NMR.73 The study revealed that lithium diffusion was sensitive to two main features of solvent – (a) the presence of the methyl unit in the HBD and (b) the molar ratio of LiTFSI with MSA/DMMSA. It was observed that the presence of the additional methyl unit in DMMSA decreased the association of lithium ions with the HBD and hence gave rise to faster diffusion in comparison to the case in MSA. Further, it was also found that the increase in the molar fraction also increased lithium diffusivity significantly.73 PFG-NMR studies also showed that the diffusivity of MSA/DMMSA molecules was comparable to that of lithium ions,73 indicating that vehicular motion is the more dominant transport mechanism for lithium ions in these DESs.
3.2 Dynamic heterogeneity in DESs
The complexity of relaxation processes in DESs indicates a strong relationship between structural relaxation and molecular diffusion in these systems, which has been explicitly observed in the dielectric spectroscopy of various DES systems.19,62,64–66 Temporal and spatial heterogeneities in the microscopic dynamics of these solvents are another manifestation of these complex diffusive processes.62,101 As an effect of this dynamic heterogeneity, a number of fluorescence spectroscopic studies have shown that solvent viscosity and molecular diffusion are strongly decoupled, which is an indication of the breakdown of the Stokes–Einstein relation.17,64,69–72 Generally, in solvents with temporal heterogeneity, the solvent viscosity shows a fractional dependence on average timescales (〈τ〉 ∼ ηp, p < 1), associated to the translational or rotational dynamics of the probe particle observed through fluorescence spectroscopy. The extent of heterogeneity in the system is marked by the deviation of the value of p from 1. The observed values of p for various DESs using time-resolved fluorescence techniques are shown in Fig. 9a. In their study on DESs based on alkylamides as HBDs and lithium salts as HBAs, Biswas and coworkers17,71,72 have shown that the temporal heterogeneity is strongly dependent on the chain length of the HBDs and anion identity of the HBAs. With respect to different HBDs, they found that the value of p followed the order butyramide < propionamide < acetamide, indicating that temporal heterogeneity is enhanced with increasing chain length. On the other hand, among the different anions (in the HBA), bromide is found to be the strongest promoter of heterogeneity and perchlorate the weakest. Similar studies on ChCl based DESs such as reline70 and ethaline124 have also shown the strong decoupling effect of viscosity and diffusion. It has also been observed that the addition of lithium salts in ethaline/glyceline strongly slows down the solvation response of the DES.125 Nevertheless, it is found that it doesn’t significantly alter the dynamic heterogeneity already present in the system.125 Unlike in the above mentioned ionic DESs, it is found that, in non-ionic DESs like a mixture of acetamide and urea, the molecular dynamics is found to be almost completely homogeneous.64,65,126 However the introduction of PEG in this non-ionic DES is found to make the system substantially heterogeneous.64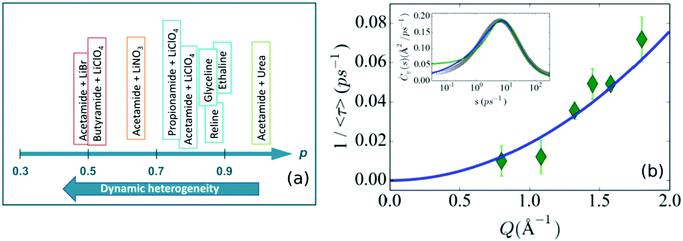 | ||
| Fig. 9 (a) The heterogeneity parameter, p, obtained for various DESs from fluorescence spectroscopic studies.70,72,124,125 The extent of dynamic heterogeneity is characterised by the deviation of p from 1. (b) The Q-dependence of the average relaxation time calculated from the stretched exponential. The lines indicate quadratic fit. Laplace transform of the simulated velocity autocorrelation function (circles) and the theoretical models based on exponential (green line) and power law memory (blue line) functions (adapted from ref. 105) are shown in the inset. | ||
MD simulations and QENS experiments have also been able to provide a direct insight into the dynamical heterogeneity of the system at a molecular level. In particular, the atomistic details obtained from MD simulations will enable us to understand the origin and nature of dynamic heterogeneity in the system. An instructive calculation of acetamide's hydrodynamic diffusivity in the DES and molten acetamide, with the use of their viscosities21 in the SE formula given in eqn (5), yields 0.8 × 10−10 m2 s−1 and 6 × 10−10 m2 s−1 respectively. The corresponding microscopic diffusivities measured by QENS experiments20 are found to be 3.0 × 10−10 m2 s−1 and 8 × 10−10 m2 s−1, which clearly reveal that the viscosity–diffusion decoupling is substantially strong in the case of the DES. Similar decoupling from the hydrodynamics has also been observed in the case of reorientational motion of acetamide in the DES.62 In congruence with this, orientational jumps of acetamide were observed in a MD simulation study on DESs based on acetamide and lithium salts.101 The waiting times between these jumps were found to have power-law decay, with the bromide anion showing the longest average waiting time between jumps.101 These features and the observations from fluorescence spectroscopy largely favour the view of temporal heterogeneity in DESs. Nevertheless, spatial heterogeneity akin to glassy systems was also observed in the translational diffusion of acetamide molecules in these DESs.110 In concurrence with the results of fluorescence studies, the extent of temporal and spatial heterogeneity observed in these systems was found to have a strong dependence on the anion identity in the DES.62,101 The origin of dynamic heterogeneity observed in these systems has been traced to the behaviour of hydrogen bond relaxation in DESs. In particular, the jump reorientation and translation of molecules has been associated to the formation and breaking of H-bonds dictated by the lifetime of H-bond complexes formed, which in turn is found to explain anion dependence of the temporal heterogeneity observed.20,22,62,101
The generalised Langevin equation (GLE) is a phenomenological approach used to describe the temporal heterogeneity in a system.127,128 In this scenario, the diffusion of particles becomes non-Markovian with a strong dependence on the structural relaxation which is mathematically governed by a memory function. These models have been effective in describing the dynamics of RTILs.129,130 The velocity autocorrelation of such a diffusion process, in the Laplace space, is given by
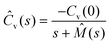 | (8) |
3.3 Influence of water on microscopic dynamics in DESs
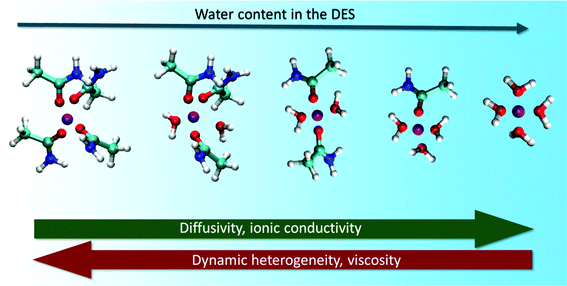
Water being a strong H-bond donor and acceptor has the ability to substantially alter the structural landscape of DESs and thereby influence their microscopic dynamics. PFG-NMR measurements used to study the effect of water on the diffusion of molecules/ions in reline, ethaline and glyceline have invariably shown an effective increase in the mobility of all the species in these solvents.104 They found that the increase in diffusion constants of choline ions and the respective HBDs showed a sharp increase beyond a water mole fraction of 0.5. It was also found that the diffusion of water molecules was slower in the solvent compared to its bulk values, suggesting the formation of local domains of water in the DES.104 These experimental observations were validated from atomistic MD simulation studies by Zhekenov et al.,109 where they showed that the diffusivity of all the species in reline, glyceline and ethaline increased with increasing water content. However, in their simulation, it was observed that the steep increase of molecular diffusivity starts from a water mole fraction of 0.3.81,109 Their investigations reveal that the increase in molecular diffusion is directly correlated to the increase in the number of H-bonds between water and HBDs in the solvent.In a recent study on the acetamide + LiClO4 DES, it has been found that addition of water not only enhances the molecular mobility, but also decreases the dynamic heterogeneity observed in the DES.131 This was attributed to the accelerated H-bond dynamics in the aqueous mixtures of the DES. It was observed that, in addition to formation of lithium–water complexes, the lifetimes of lithium–acetamide complexes systematically decreased with increasing water content in the system.131Fig. 10 shows the change in lithium complexes formed at different water content in the DES. The combined effect of these two factors was noted to be the cause of the substantial decrease in dynamic heterogeneity in the DES. Diffusion of water molecules in the system was also found to be non-Gaussian in nature and particularly slower than the bulk counterparts. The major cause of these features could be due to formation of nanodomains of water and strong H-bonding between species of the solvent.131
4 Microscopic vs. macroscopic transport: role of dynamic heterogeneity
Having surveyed the current understanding of the macroscopic and microscopic transport phenomena in DESs, we are now in a position to harmonize them. The earliest attempt to model viscosity from a microscopic perspective was based on hole theory,51 which assumed that the transport of species in the solvent was achieved through holes formed by density fluctuation. While this model was adequate for a majority of molecular liquids and some ionic liquids,87 it was not very successful for DESs.51 The investigation of molecular diffusion through PFG-NMR evinced a breakdown of the Stokes–Einstein relation and proposed a jump diffusion model with an associated correlation length. A free volume model of transport was conjectured based on the connection between the correlation length and the available molecular free volume in the DES. However, various quantum mechanical studies and MD simulations on the structure of DESs revealed the formation of H-bond networks and cage like structures,16,22,117,118 which challenged the fundamental assumption used in these theories that considered free diffusion of molecules/ions. But congruous with predictions of quantum calculations, QENS and MD simulations revealed that the diffusion of species in the DES involved multiple relaxation processes involving the rattling motion within transient cages formed through H-bonding and subsequent relaxation of these cages to execute jump-diffusion.20,21,23 In a comparative study of the acetamide based DES and molten acetamide, it was found that the jump-diffusion of acetamide was drastically slower in the DES, owing to the formation of various ion–HBD complexes.20 Further, a strong deviation from the hydrodynamic behaviour was also observed in the DES, suggesting the existence of dynamic heterogeneity.It is interesting to note that the dynamic heterogeneity in the system exists much above the glass transition temperature, as evidenced in various spectroscopic and MD simulation studies.17,67 It has been observed from dielectric spectroscopy that the fragility parameter (B/T0 in eqn (3)) obtained in the VFT temperature dependence of ionic conductivity plays an important role in the ionic conduction mechanism of the solvent.88 It has also been observed that the fragility of the DES is sensitive to the ionic species and HBDs in DESs.67 On the other hand, a strong relationship is known to exist between the dynamic heterogeneity and fragility of glass formers.132,133 Therefore, it is important to probe the dynamic heterogeneity in DESs at the molecular level using experimental techniques like QENS and neutron spin echo (NSE), to bridge the gap between the microscopic and macroscopic transport processes. For instance, a recent study on glyceline using the NSE technique showed why the viscosity of glyceline was much lower compared to that of glycerol even though the single particle diffusion was similar in both the cases.134 This behaviour was ascribed to the cooperative relaxation of H-bonds between the glycerol molecules in glyceline, which was at least 3 times faster than that observed in pure glycerol.134
MD simulations can provide additional atomistic insights into the H-bond network and dynamics, which have been shown to play a decisive role in dynamic heterogeneity in the solvents. The formation of H-bond complexes in the system and relaxation can explain the origin of structural relaxation in these glass-formers. A particular example could be the use of H-bond relaxation obtained from simulations as a driving non-Markovian noise in the GLE model to describe the diffusion process in the system. Well validated simulation models can be useful in calculating the bulk viscosity and ionic conductivity of these solvents.
Apart from being glassy, DESs have also been classified as supercooled mixtures.19,66,72 Mode coupling theory has been a useful tool to predict the transport properties in glassy systems and supercooled liquids.135–137 Therefore, the theoretical approach can be useful in predicting the bulk transport properties for different combinations of HBDs and HBAs by tuning their interaction parameters. Applying mode coupling models, in the investigation of LiPF6/propylene carbonate mixtures, the relaxation of shear stress and ionic conductivity agrees with the relaxation of the main peak and prepeak observed in their liquid structure.138 It is therefore expedient to investigate such coupling in DESs, since these structure peaks are known to be observed in them.139 Another aspect of supercooled liquids is the notable fragile-to-strong transition, which has been observed not only in water,140,141 but also in metallic glass forming liquids.132,142 The existence of such transitions in DESs should also be explored, owing to the similarity of interactions found in these systems.
5 Summary and outlook
Over the last couple of decades, deep eutectic solvents (DESs) have established themselves as a promising green alternative to room temperature ionic liquids (RTILs) and other organic solvents. While they are known to provide great solubility for a wide range of salts, their poor transport properties inhibit their widespread use. It is now understood that the aspects like high viscosity and poor conductivity are due to the glassy nature of these systems. In consideration of this fact, some of the effective approaches to improve their transport properties are (i) decreasing the glass transition temperature and (ii) increasing the fragility parameter. Apart from these fundamental aspects, it is also observed that both microscopic and macroscopic transport properties are strongly dependent on the constituent species of the DES. Therefore, a careful choice of different HBDs and HBAs might be able to alleviate these issues. It is interesting to note that non-ionic DESs (like for e.g. acetamide + urea) show very weak dynamic heterogeneity, suggesting that non-ionic DESs possess better transport ability in comparison to the usual ionic DESs. Non-ionic DESs formed from fatty acids exhibiting a significantly low viscosity are also another example.Indeed, addition of water has also been found to be a useful approach to modulate the properties of these green solvents, but it has to be done with care so as to not significantly alter the solubility and chemical nature of DESs. It has been observed from microscopic transport phenomena that water not only breaks the existing H-bond network in the DES, but also simultaneously decreases the lifetime H-bond complexes formed in these green solvents. These complexes and their long lifetimes have been found to be the major cause for the large viscosity observed in DESs. Therefore, modulation of viscosity by water is due to a three fold mechanism – (i) breaking of ion–HBD bonds in the DES, (ii) formation of ion–water or HBD–water bonds, and (iii) accelerated H-bond dynamics. A yet another consequence of these features is that water also decreases the dynamic heterogeneity in DESs quite significantly.
The role of H-bonding has been greatly investigated in DESs, but their dynamics is scarcely studied. As revealed by recent studies, H-bond dynamics plays a crucial role in the microscopic diffusion mechanism and dynamic heterogeneity in DESs. In particular, the effect of water on the microscopic transport properties can be well characterised by analysing and understanding the nature of H-bond dynamics. An extensive survey on H-bond dynamics in various ChCl based DESs and their aqueous mixture is necessary to gain a comprehensive perspective on the dynamics in these solvents.
While nanofluids based on DESs have shown some promising results with enhanced thermal conductivity and decreased viscosity, only a very few studies of these systems have been carried out so far. The incorporation of nanoparticles should also be considered an effective approach to alter the physicochemical properties, particularly the transport.
Conflicts of interest
There are no conflicts to declare.References
- A. P. Abbott, G. Capper, D. L. Davies, H. L. Munro, R. K. Rasheed and V. Tambyrajah, Preparation of novel, moisture-stable, Lewis-acidic ionic liquids containing quaternary ammonium salts with functional side chains, Chem. Commun., 2001, 2010–2011 RSC.
- A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Novel solvent properties of choline chloride/urea mixtures, Chem. Commun., 2003, 70–71 RSC.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Deep eutectic solvents (DESs) and their applications, Chem. Rev., 2014, 114(21), 11060–11082 CrossRef CAS PubMed.
- Q. Zhang, K. De Oliveira Vigier, S. Royer and F. Jérôme, Deep eutectic solvents: Syntheses, properties and applications, Chem. Soc. Rev., 2012, 41(21), 7108–7146 RSC.
- B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich, B. W. Doherty, B. Gurkan, E. J. Maginn, A. Ragauskas, M. Dadmun, T. A. Zawodzinski, G. A. Baker, M. E. Tuckerman, R. F. Savinell and J. R. Sangoro, Deep eutectic solvents: A review of fundamentals and applications, Chem. Rev., 2021, 121(3), 1232–1285 CrossRef CAS PubMed.
- T. P. Thuy Pham, C.-W. Cho and Y.-S. Yun, Environmental fate and toxicity of ionic liquids: A review, Water Res., 2010, 44(2), 352–372 CrossRef PubMed.
- M. Petkovic, K. R. Seddon, L. P. N. Rebelo and C. Silva Pereira, Ionic liquids: A pathway to environmental acceptability, Chem. Soc. Rev., 2011, 40(3), 1383–1403 RSC.
- V. K. Sharma and R. Mukhopadhyay, Deciphering interactions of ionic liquids with biomembrane, Biophys. Rev., 2018, 10(3), 721–734 CrossRef CAS PubMed.
- K. Bakshi, S. Mitra, V. K. Sharma, M. S. K. Jayadev, V. G. Sakai, R. Mukhopadhyay, A. Gupta and S. K. Ghosh, Imidazolium-based ionic liquids cause mammalian cell death due to modulated structures and dynamics of cellular membrane, Biochim. Biophys. Acta, Biomembr., 2020, 1862(2), 183103 CrossRef CAS PubMed.
- A. P. Abbott, D. Boothby, G. Capper, D. L. Davies and R. K. Rasheed, Deep eutectic solvents formed between choline chloride and carboxylic acids:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Versatile alternatives to ionic liquids, J. Am. Chem. Soc., 2004, 126(29), 9142–9147 CrossRef CAS PubMed.
Versatile alternatives to ionic liquids, J. Am. Chem. Soc., 2004, 126(29), 9142–9147 CrossRef CAS PubMed. - A. Yadav, S. Trivedi, R. Rai and S. Pandey, Densities and dynamic viscosities of (choline chloride + glycerol) deep eutectic solvent and its aqueous mixtures in the temperature range (283.15–363.15)K, Fluid Phase Equilib., 2014, 367, 135–142 CrossRef CAS.
- S. L. Perkins, P. Painter and C. M. Colina, Experimental and computational studies of choline chloride-based deep eutectic solvents, J. Chem. Eng. Data, 2014, 59(11), 3652–3662 CrossRef CAS.
- Y. Cui, C. Li, J. Yin, S. Li, Y. Jia and M. Bao, Design, synthesis and properties of acidic deep eutectic solvents based on choline chloride, J. Mol. Liq., 2017, 236, 338–343 CrossRef CAS.
- J. Zhu, K. Yu, Y. Zhu, R. Zhu, F. Ye, N. Song and Y. Xu, Physicochemical properties of deep eutectic solvents formed by choline chloride and phenolic compounds at T = (293.15 to 333.15) K: The influence of electronic effect of substitution group, J. Mol. Liq., 2017, 232, 182–187 CrossRef CAS.
- R. Stefanovic, M. Ludwig, G. B. Webber, R. Atkin and A. J. Page, Nanostructure, hydrogen bonding and rheology in choline chloride deep eutectic solvents as a function of the hydrogen bond donor, Phys. Chem. Chem. Phys., 2017, 19(4), 3297–3306 RSC.
- G. García, M. Atilhan and S. Aparicio, An approach for the rationalization of melting temperature for deep eutectic solvents from DFT, Chem. Phys. Lett., 2015, 634, 151–155 CrossRef.
- B. Guchhait, S. Daschakraborty and R. Biswas, Medium decoupling of dynamics at temperatures ∼100 K above glass-transition temperature: A case study with (acetamide + lithium bromide/nitrate) melts, J. Chem. Phys., 2012, 136(17), 174503 CrossRef PubMed.
- R. Biswas, A. Das and H. Shirota, Low-frequency collective dynamics in deep eutectic solvents of acetamide and electrolytes: A femtosecond Raman-induced Kerr effect spectroscopic study, J. Chem. Phys., 2014, 141(13), 134506 CrossRef PubMed.
- K. Mukherjee, A. Das, S. Choudhury, A. Barman and R. Biswas, Dielectric relaxations of (acetamide + electrolyte) deep eutectic solvents in the frequency window, 0.2 ≤ ν/GHz ≤ 50: Anion and cation dependence, J. Phys. Chem. B, 2015, 119(25), 8063–8071 CrossRef CAS PubMed.
- H. Srinivasan, V. K. Sharma, V. G. Sakai, J. P. Embs, R. Mukhopadhyay and S. Mitra, Transport mechanism of acetamide in deep eutectic solvents, J. Phys. Chem. B, 2020, 124(8), 1509–1520 CrossRef CAS.
- H. Srinivasan, V. K. Sharma, R. Mukhopadhyay and S. Mitra, Solvation and transport of lithium ions in deep eutectic solvents, J. Chem. Phys., 2020, 153(10), 104505 CrossRef CAS PubMed.
- S. Das, B. Mukherjee and R. Biswas, Microstructures and their lifetimes in acetamide/electrolyte deep eutectics: Anion dependence, J. Chem. Sci., 2017, 129(7), 939–951 CrossRef CAS.
- D. V. Wagle, G. A. Baker and E. Mamontov, Differential microscopic mobility of components within a deep eutectic solvent, J. Phys. Chem. Lett., 2015, 6(15), 2924–2928 CrossRef CAS PubMed.
- H.-G. Liao, Y.-X. Jiang, Z.-Y. Zhou, S.-P. Chen and S.-G. Sun, Shape-controlled synthesis of gold nanoparticles in deep eutectic solvents for studies of structure–functionality relationships in electrocatalysis, Angew. Chem., Int. Ed., 2008, 47(47), 9100–9103 CrossRef CAS PubMed.
- M. Chirea, A. Freitas, B. S. Vasile, C. Ghitulica, C. M. Pereira and F. Silva, Gold nanowire networks: Synthesis, characterization, and catalytic activity, Langmuir, 2011, 27(7), 3906–3913 CrossRef CAS PubMed.
- L. Wei, Y.-J. Fan, H.-H. Wang, N. Tian, Z.-Y. Zhou and S.-G. Sun, Electrochemically shape-controlled synthesis in deep eutectic solvents of Pt nanoflowers with enhanced activity for ethanol oxidation, Electrochim. Acta, 2012, 76, 468–474 CrossRef CAS.
- D. V. Wagle, H. Zhao and G. A. Baker, Deep eutectic solvents: Sustainable media for nanoscale and functional materials, Acc. Chem. Res., 2014, 47(8), 2299–2308 CrossRef CAS PubMed.
- H. Jia, J. An, X. Guo, C. Su, L. Zhang, H. Zhou and C. Xie, Deep eutectic solvent-assisted growth of gold nanofoams and their excellent catalytic properties, J. Mol. Liq., 2015, 212, 763–766 CrossRef CAS.
- Y.-F. Lin and I. W. Sun, Electrodeposition of zinc from a Lewis acidic zinc chloride-1-ethyl-3-methylimidazolium chloride molten salt, Electrochim. Acta, 1999, 44(16), 2771–2777 CrossRef CAS.
- C. A. Nkuku and R. J. LeSuer, Electrochemistry in deep eutectic solvents, J. Phys. Chem. B, 2007, 111(46), 13271–13277 CrossRef CAS PubMed.
- A. P. Abbott, El Ttaib, K. Ryder, K. S. Smith and E. L. Electrodeposition, of nickel using eutectic based ionic liquids, Trans. IMF, 2008, 86(4), 234–240 CrossRef CAS.
- H.-R. Jhong, D. S.-H. Wong, C.-C. Wan, Y.-Y. Wang and T.-C. Wei, A novel deep eutectic solvent-based ionic liquid used as electrolyte for dye-sensitized solar cells, Electrochem. Commun., 2009, 11(1), 209–211 CrossRef CAS.
- D. Lloyd, T. Vainikka, L. Murtomäki, K. Kontturi and E. Ahlberg, The kinetics of the Cu2+/Cu+ redox couple in deep eutectic solvents, Electrochim. Acta, 2011, 56(14), 4942–4948 CrossRef CAS.
- E. Gómez, P. Cojocaru, L. Magagnin and E. Valles, Electrodeposition of Co, Sm and SmCo from a deep eutectic solvent, J. Electroanal. Chem., 2011, 658(1), 18–24 CrossRef.
- L. Bahadori, M. H. Chakrabarti, F. S. Mjalli, I. M. AlNashef, N. S. A. Manan and M. A. Hashim, Physicochemical properties of ammonium-based deep eutectic solvents and their electrochemical evaluation using organometallic reference redox systems, Electrochim. Acta, 2013, 113, 205–211 CrossRef CAS.
- L. Bahadori, N. S. Abdul Manan, M. H. Chakrabarti, M. A. Hashim, F. S. Mjalli, I. M. AlNashef, M. A. Hussain and C. T. J. Low, The electrochemical behaviour of ferrocene in deep eutectic solvents based on quaternary ammonium and phosphonium salts, Phys. Chem. Chem. Phys., 2013, 15(5), 1707–1714 RSC.
- A. Boisset, J. Jacquemin and M. Anouti, Physical properties of a new deep eutectic solvent based on lithium bis[(trifluoromethyl)sulfonyl]imide and N-methylacetamide as superionic suitable electrolyte for lithium ion batteries and electric double layer capacitors, Electrochim. Acta, 2013, 102, 120–126 CrossRef CAS.
- P. Liu, J.-W. Hao, L.-P. Mo and Z.-H. Zhang, Recent advances in the application of deep eutectic solvents as sustainable media as well as catalysts in organic reactions, RSC Adv., 2015, 5(60), 48675–48704 RSC.
- N. Guajardo, P. Domínguez de María, K. Ahumada, R. A. Schrebler, R. Ramírez-Tagle, F. A. Crespo and C. Carlesi, Water as cosolvent: Nonviscous deep eutectic solvents for efficient lipase-catalyzed esterifications, ChemCatChem, 2017, 9(8), 1393–1396 CrossRef CAS.
- L. Cicco, N. Ríos-Lombardía, M. J. Rodríguez-Álvarez, F. Morís, F. M. Perna, V. Capriati, J. García-Álvarez and J. González-Sabín, Programming cascade reactions interfacing biocatalysis with transition-metal catalysis in deep eutectic solvents as biorenewable reaction media, Green Chem., 2018, 20(15), 3468–3475 RSC.
- P. Kalhor and K. Ghandi, Deep eutectic solvents for pretreatment, extraction, and catalysis of biomass and food waste, Molecules, 2019, 24, 22 CrossRef.
- A. E. Ünlü, A. Arıkaya and S. Takaç, Use of deep eutectic solvents as catalyst: A mini-review, Green Process. Synth., 2019, 8(1), 355–372 Search PubMed.
- T. Altamash, M. S. Nasser, Y. Elhamarnah, M. Magzoub, R. Ullah, B. Anaya, S. Aparicio and M. Atilhan, Gas solubility and rheological behavior of natural deep eutectic solvents (NADES) via combined experimental and molecular simulation techniques, ChemistrySelect, 2017, 2(24), 7278–7295 CrossRef CAS.
- T. Altamash, M. S. Nasser, Y. Elhamarnah, M. Magzoub, R. Ullah, H. Qiblawey, S. Aparicio and M. Atilhan, Gas solubility and rheological behavior study of betaine and alanine based natural deep eutectic solvents (NADES), J. Mol. Liq., 2018, 256, 286–295 CrossRef CAS.
- H. G. Morrison, C. C. Sun and S. Neervannan, Characterization of thermal behavior of deep eutectic solvents and their potential as drug solubilization vehicles, Int. J. Pharm., 2009, 378(1), 136–139 CrossRef CAS PubMed.
- Z. Li and P. I. Lee, Investigation on drug solubility enhancement using deep eutectic solvents and their derivatives, Int. J. Pharm., 2016, 505(1), 283–288 CrossRef CAS PubMed.
- A. R. C. Duarte, A. S. D. Ferreira, S. Barreiros, E. Cabrita, R. L. Reis and A. Paiva, A comparison between pure active pharmaceutical ingredients and therapeutic deep eutectic solvents: Solubility and permeability studies, Eur. J. Pharm. Biopharm., 2017, 114, 296–304 CrossRef CAS PubMed.
- S. Emami and A. Shayanfar, Deep eutectic solvents for pharmaceutical formulation and drug delivery applications, Pharm. Dev. Technol., 2020, 25(7), 779–796 CrossRef CAS.
- M. Anouti, Room-temperature molten salts: Protic ionic liquids and deep eutectic solvents as media for electrochemical application, in Electrochemistry in Ionic Liquids: Volume 1: Fundamentals, ed. A. A. J. Torriero, Springer International Publishing, Cham, 2015, pp. 217–252 Search PubMed.
- A. Boisset, S. Menne, J. Jacquemin, A. Balducci and M. Anouti, Deep eutectic solvents based on N-methylacetamide and a lithium salt as suitable electrolytes for lithium-ion batteries, Phys. Chem. Chem. Phys., 2013, 15(46), 20054–20063 RSC.
- A. P. Abbott, G. Capper and S. Gray, Design of improved deep eutectic solvents using hole theory, ChemPhysChem, 2006, 7(4), 803–806 CrossRef CAS PubMed.
- K. R. Siongco, R. B. Leron and M.-H. Li, Densities, refractive indices, and viscosities of N,N-diethylethanol ammonium chloride–glycerol or –ethylene glycol deep eutectic solvents and their aqueous solutions, J. Chem. Thermodyn., 2013, 65, 65–72 CrossRef CAS.
- Y. Xie, H. Dong, S. Zhang, X. Lu and X. Ji, Effect of water on the density, viscosity, and CO2 solubility in choline chloride/urea, J. Chem. Eng. Data, 2014, 59(11), 3344–3352 CrossRef CAS.
- Y. Dai, G.-J. Witkamp, R. Verpoorte and Y. H. Choi, Tailoring properties of natural deep eutectic solvents with water to facilitate their applications, Food Chem., 2015, 187, 14–19 CrossRef CAS PubMed.
- M. K. AlOmar, M. Hayyan, M. A. Alsaadi, S. Akib, A. Hayyan and M. A. Hashim, Glycerol-based deep eutectic solvents: Physical properties, J. Mol. Liq., 2016, 215, 98–103 CrossRef CAS.
- A. Basaiahgari, S. Panda and R. L. Gardas, Acoustic, volumetric, transport, optical and rheological properties of benzyltripropylammonium based deep eutectic solvents, Fluid Phase Equilib., 2017, 448, 41–49 CrossRef CAS.
- A. R. Harifi-Mood and R. Buchner, Density, viscosity, and conductivity of choline chloride + ethylene glycol as a deep eutectic solvent and its binary mixtures with dimethyl sulfoxide, J. Mol. Liq., 2017, 225, 689–695 CrossRef CAS.
- R. Germani, M. Orlandini, M. Tiecco and T. Del Giacco, Novel low viscous, green and amphiphilic N-oxides/phenylacetic acid based deep eutectic solvents, J. Mol. Liq., 2017, 240, 233–239 CrossRef CAS.
- S. Sarmad, Y. Xie, J.-P. Mikkola and X. Ji, Screening of deep eutectic solvents (DESs) as green CO2 sorbents: From solubility to viscosity, New J. Chem., 2017, 41(1), 290–301 RSC.
- H. Ghaedi, M. Ayoub, S. Sufian, A. M. Shariff and B. Lal, The study on temperature dependence of viscosity and surface tension of several phosphonium-based deep eutectic solvents, J. Mol. Liq., 2017, 241, 500–510 CrossRef CAS.
- I. M. Aroso, A. Paiva, R. L. Reis and A. R. C. Duarte, Natural deep eutectic solvents from choline chloride and betaine – physicochemical properties, J. Mol. Liq., 2017, 241, 654–661 CrossRef CAS.
- S. Das, R. Biswas and B. Mukherjee, Collective dynamic dipole moment and orientation fluctuations, cooperative hydrogen bond relaxations, and their connections to dielectric relaxation in ionic acetamide deep eutectics: Microscopic insight from simulations, J. Chem. Phys., 2016, 145(8), 084504 CrossRef PubMed.
- S. Daschakraborty and R. Biswas, Dielectric relaxation in ionic liquid/dipolar solvent binary mixtures: A semi-molecular theory, J. Chem. Phys., 2016, 144(10), 104505 CrossRef PubMed.
- K. Mukherjee, E. Tarif, A. Barman and R. Biswas, Dynamics of a PEG based non-ionic deep eutectic solvent: Temperature dependence, Fluid Phase Equilib., 2017, 448, 22–29 CrossRef CAS.
- K. Mukherjee, S. Das, E. Tarif, A. Barman and R. Biswas, Dielectric relaxation in acetamide + urea deep eutectics and neat molten urea: Origin of time scales via temperature dependent measurements and computer simulations, J. Chem. Phys., 2018, 149(12), 124501 CrossRef PubMed.
- D. Reuter, C. Binder, P. Lunkenheimer and A. Loidl, Ionic conductivity of deep eutectic solvents: The role of orientational dynamics and glassy freezing, Phys. Chem. Chem. Phys., 2019, 21(13), 6801–6809 RSC.
- S. N. Tripathy, Z. Wojnarowska, J. Knapik, H. Shirota, R. Biswas and M. Paluch, Glass transition dynamics and conductivity scaling in ionic deep eutectic solvents: The case of (acetamide + lithium nitrate/sodium thiocyanate) melts, J. Chem. Phys., 2015, 142(18), 184504 CrossRef PubMed.
- Q. Xu, T. S. Zhao, L. Wei, C. Zhang and X. L. Zhou, Electrochemical characteristics and transport properties of Fe(II)/Fe(III) redox couple in a non-aqueous reline deep eutectic solvent, Electrochim. Acta, 2015, 154, 462–467 CrossRef CAS.
- A. Das, S. Das and R. Biswas, Fast fluctuations in deep eutectic melts: Multi-probe fluorescence measurements and all-atom molecular dynamics simulation study, Chem. Phys. Lett., 2013, 581, 47–51 CrossRef CAS.
- A. Das and R. Biswas, Dynamic solvent control of a reaction in ionic deep eutectic solvents: Time-resolved fluorescence measurements of reactive and nonreactive dynamics in (choline chloride + urea) melts, J. Phys. Chem. B, 2015, 119(31), 10102–10113 CrossRef CAS PubMed.
- N. Subba, E. Tarif, P. Sen and R. Biswas, Subpicosecond solvation response and partial viscosity decoupling of solute diffusion in ionic acetamide deep eutectic solvents: Fluorescence up-conversion and fluorescence correlation spectroscopic measurements, J. Phys. Chem. B, 2020, 124(10), 1995–2005 CrossRef CAS PubMed.
- B. Guchhait, S. Das, S. Daschakraborty and R. Biswas, Interaction and dynamics of (alkylamide + electrolyte) deep eutectics: Dependence on alkyl chain-length, temperature, and anion identity, J. Chem. Phys., 2014, 140(10), 104514 CrossRef PubMed.
- A. D. Pauric, I. C. Halalay and G. R. Goward, Combined NMR and molecular dynamics modeling study of transport properties in sulfonamide based deep eutectic lithium electrolytes: LiTFSI based binary systems, Phys. Chem. Chem. Phys., 2016, 18(9), 6657–6667 RSC.
- C. D'Agostino, R. C. Harris, A. P. Abbott, L. F. Gladden and M. D. Mantle, Molecular motion and ion diffusion in choline chloride based deep eutectic solvents studied by 1H pulsed field gradient NMR spectroscopy, Phys. Chem. Chem. Phys., 2011, 13(48), 21383–21391 RSC.
- R. Yusof, E. Abdulmalek, K. Sirat and M. B. Rahman, Tetrabutylammonium bromide (TBABr)-based deep eutectic solvents (DESs) and their physical properties, Molecules, 2014, 19(6), 8011–8026 CrossRef PubMed.
- A. Yadav and S. Pandey, Densities and viscosities of (choline chloride + urea) deep eutectic solvent and its aqueous mixtures in the temperature range 293.15 K to 363.15 K, J. Chem. Eng. Data, 2014, 59(7), 2221–2229 CrossRef CAS.
- F. S. Mjalli and J. Naser, Viscosity model for choline chloride-based deep eutectic solvents, Asia-Pac. J. Chem. Eng., 2015, 10(2), 273–281 CrossRef CAS.
- C. Florindo, F. S. Oliveira, L. P. N. Rebelo, A. M. Fernandes and I. M. Marrucho, Insights into the synthesis and properties of deep eutectic solvents based on cholinium chloride and carboxylic acids, ACS Sustainable Chem. Eng., 2014, 2(10), 2416–2425 CrossRef CAS.
- C. Florindo, L. Romero, I. Rintoul, L. C. Branco and I. M. Marrucho, From phase change materials to green solvents: Hydrophobic low viscous fatty acid–based deep eutectic solvents, ACS Sustainable Chem. Eng., 2018, 6(3), 3888–3895 CrossRef CAS.
- H. Shekaari, M. T. Zafarani-Moattar and B. Mohammadi, Thermophysical characterization of aqueous deep eutectic solvent (choline chloride/urea) solutions in full ranges of concentration at T = (293.15–323.15) K, J. Mol. Liq., 2017, 243, 451–461 CrossRef CAS.
- D. Shah and F. S. Mjalli, Effect of water on the thermo-physical properties of Reline: An experimental and molecular simulation based approach, Phys. Chem. Chem. Phys., 2014, 16(43), 23900–23907 RSC.
- D. Lapeña, L. Lomba, M. Artal, C. Lafuente and B. Giner, Thermophysical characterization of the deep eutectic solvent choline chloride:ethylene glycol and one of its mixtures with water, Fluid Phase Equilib., 2019, 492, 1–9 CrossRef.
- A. P. Abbott, E. I. Ahmed, R. C. Harris and K. S. Ryder, Evaluating water miscible deep eutectic solvents (DESs) and ionic liquids as potential lubricants, Green Chem., 2014, 16(9), 4156–4161 RSC.
- R. Craveiro, I. Aroso, V. Flammia, T. Carvalho, M. T. Viciosa, M. Dionísio, S. Barreiros, R. L. Reis, A. R. C. Duarte and A. Paiva, Properties and thermal behavior of natural deep eutectic solvents, J. Mol. Liq., 2016, 215, 534–540 CrossRef CAS.
- R. Haghbakhsh, S. Raeissi, K. Parvaneh and A. Shariati, The friction theory for modeling the viscosities of deep eutectic solvents using the CPA and PC-SAFT equations of state, J. Mol. Liq., 2018, 249, 554–561 CrossRef CAS.
- R. Haghbakhsh, K. Parvaneh, S. Raeissi and A. Shariati, A general viscosity model for deep eutectic solvents: The free volume theory coupled with association equations of state, Fluid Phase Equilib., 2018, 470, 193–202 CrossRef CAS.
- A. P. Abbott, Application of hole theory to the viscosity of ionic and molecular liquids, ChemPhysChem, 2004, 5(8), 1242–1246 CrossRef CAS PubMed.
- D. Reuter, P. Münzner, C. Gainaru, P. Lunkenheimer, A. Loidl and R. Böhmer, Translational and reorientational dynamics in deep eutectic solvents, J. Chem. Phys., 2021, 154(15), 154501 CrossRef CAS PubMed.
- F. S. G. Bagh, K. Shahbaz, F. S. Mjalli, I. M. AlNashef and M. A. Hashim, Electrical conductivity of ammonium and phosphonium based deep eutectic solvents: Measurements and artificial intelligence-based prediction, Fluid Phase Equilib., 2013, 356, 30–37 CrossRef CAS.
- G. Li, Y. Jiang, X. Liu and D. Deng, New levulinic acid-based deep eutectic solvents: Synthesis and physicochemical property determination, J. Mol. Liq., 2016, 222, 201–207 CrossRef CAS.
- M. Hayyan, T. Aissaoui, M. A. Hashim, M. A. AlSaadi and A. Hayyan, Triethylene glycol based deep eutectic solvents and their physical properties, J. Taiwan Inst. Chem. Eng., 2015, 50, 24–30 CrossRef CAS.
- R. Chen, F. Wu, B. Xu, L. Li, X. Qiu and S. Chen, Binary complex electrolytes based on LiX [X
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(SO2CF3)2−, CF3SO3−, ClO4−]-acetamide for electric double layer capacitors, J. Electrochem. Soc., 2007, 154(7), A703–A708 CrossRef CAS.
N(SO2CF3)2−, CF3SO3−, ClO4−]-acetamide for electric double layer capacitors, J. Electrochem. Soc., 2007, 154(7), A703–A708 CrossRef CAS. - W. Zaidi, A. Boisset, J. Jacquemin, L. Timperman and M. Anouti, Deep eutectic solvents based on N-methylacetamide and a lithium salt as electrolytes at elevated temperature for activated carbon-based supercapacitors, J. Phys. Chem. C, 2014, 118(8), 4033–4042 CrossRef CAS.
- L. Millia, V. Dall'Asta, C. Ferrara, V. Berbenni, E. Quartarone, F. M. Perna, V. Capriati and P. Mustarelli, Bio-inspired choline chloride-based deep eutectic solvents as electrolytes for lithium-ion batteries, Solid State Ionics, 2018, 323, 44–48 CrossRef CAS.
- C. Ma, A. Laaksonen, C. Liu, X. Lu and X. Ji, The peculiar effect of water on ionic liquids and deep eutectic solvents, Chem. Soc. Rev., 2018, 47(23), 8685–8720 RSC.
- A. T. Celebi, T. J. H. Vlugt and O. A. Moultos, Thermal conductivity of aqueous solutions of reline, ethaline, and glyceline deep eutectic solvents; a molecular dynamics simulation study, Mol. Phys., 2021, e1876263 CrossRef.
- T. H. Ibrahim, M. A. Sabri, N. Abdel Jabbar, P. Nancarrow, F. S. Mjalli and I. AlNashef, Thermal conductivities of choline chloride-based deep eutectic solvents and their mixtures with water: Measurement and estimation, Molecules, 2020, 25(17), 3816 CrossRef CAS PubMed.
- R. K. Gautam and D. Seth, Thermal conductivity of deep eutectic solvents, J. Therm. Anal. Calorim., 2020, 140(6), 2633–2640 CrossRef CAS.
- C. Liu, H. Fang, Y. Qiao, J. Zhao and Z. Rao, Properties and heat transfer mechanistic study of glycerol/choline chloride deep eutectic solvents based nanofluids, Int. J. Heat Mass Transfer, 2019, 138, 690–698 CrossRef CAS.
- O. S. Hammond, D. T. Bowron, A. J. Jackson, T. Arnold, A. Sanchez-Fernandez, N. Tsapatsaris, V. Garcia Sakai and K. J. Edler, Resilience of malic acid natural deep eutectic solvent nanostructure to solidification and hydration, J. Phys. Chem. B, 2017, 121(31), 7473–7483 CrossRef CAS PubMed.
- S. Das, R. Biswas and B. Mukherjee, Orientational jumps in (acetamide + electrolyte) deep eutectics: Anion dependence, J. Phys. Chem. B, 2015, 119(34), 11157–11168 CrossRef CAS PubMed.
- C. J. Smith, D. V. Wagle, N. Bhawawet, S. Gehrke, O. Hollóczki, S. V. Pingali, H. O’Neill and G. A. Baker, Combined small-angle neutron scattering, diffusion NMR, and molecular dynamics study of a eutectogel: Illuminating the dynamical behavior of glyceline confined in bacterial cellulose gels, J. Phys. Chem. B, 2020, 124(35), 7647–7658 CrossRef CAS PubMed.
- Y. Wang, W. Chen, Q. Zhao, G. Jin, Z. Xue, Y. Wang and T. Mu, Ionicity of deep eutectic solvents by Walden plot and pulsed field gradient nuclear magnetic resonance (PFG-NMR), Phys. Chem. Chem. Phys., 2020, 22(44), 25760–25768 RSC.
- C. D’Agostino, L. F. Gladden, M. D. Mantle, A. P. Abbott, E. I. Ahmed, A. Y. M. Al-Murshedi and R. C. Harris, Molecular and ionic diffusion in aqueous – deep eutectic solvent mixtures: Probing inter-molecular interactions using PFG NMR, Phys. Chem. Chem. Phys., 2015, 17(23), 15297–15304 RSC.
- H. Srinivasan, V. K. Sharma, S. Mitra, R. Biswas and R. Mukhopadhyay, Dynamics in acetamide + LiNO3 deep eutectic solvents, Phys. B, 2019, 562, 13–16 CrossRef CAS.
- H. Srinivasan, P. S. Dubey, V. K. Sharma, R. Biswas, S. Mitra and R. Mukhopadhyay, Molecular dynamics of acetamide based ionic deep eutectic solvents, AIP Conf. Proc., 2018, 1942(1), 110032 CrossRef.
- J. Jeon, H. Lee, J.-H. Choi and M. Cho, Modeling and simulation of concentrated aqueous solutions of LiTFSI for battery applications, J. Phys. Chem. C, 2020, 124(22), 11790–11799 CrossRef CAS.
- I. Delso, C. Lafuente, J. Muñoz-Embid and M. Artal, NMR study of choline chloride-based deep eutectic solvents, J. Mol. Liq., 2019, 290, 111236 CrossRef CAS.
- T. Zhekenov, N. Toksanbayev, Z. Kazakbayeva, D. Shah and F. S. Mjalli, Formation of type III deep eutectic solvents and effect of water on their intermolecular interactions, Fluid Phase Equilib., 2017, 441, 43–48 CrossRef CAS.
- S. Banerjee, P. K. Ghorai, S. Das, J. Rajbangshi and R. Biswas, Heterogeneous dynamics, correlated time and length scales in ionic deep eutectics: Anion and temperature dependence, J. Chem. Phys., 2020, 153(23), 234502 CrossRef CAS PubMed.
- O. S. Hammond, D. T. Bowron and K. J. Edler, Liquid structure of the choline chloride–urea deep eutectic solvent (reline) from neutron diffraction and atomistic modelling, Green Chem., 2016, 18(9), 2736–2744 RSC.
- Y. Zhang, D. Poe, L. Heroux, H. Squire, B. W. Doherty, Z. Long, M. Dadmun, B. Gurkan, M. E. Tuckerman and E. J. Maginn, Liquid structure and transport properties of the deep eutectic solvent ethaline, J. Phys. Chem. B, 2020, 124(25), 5251–5264 CrossRef CAS PubMed.
- A. W. Taylor, P. Licence and A. P. Abbott, Non-classical diffusion in ionic liquids, Phys. Chem. Chem. Phys., 2011, 13(21), 10147–10154 RSC.
- J. Qvist, H. Schober and B. Halle, Structural dynamics of supercooled water from quasielastic neutron scattering and molecular simulations, J. Chem. Phys., 2011, 134(14), 144508 CrossRef PubMed.
- K. S. Singwi and A. Sjölander, Diffusive motions in water and cold neutron scattering, Phys. Rev., 1960, 119(3), 863–871 CrossRef CAS.
- F. Volino and A. J. Dianoux, Neutron incoherent scattering law for diffusion in a potential of spherical symmetry: General formalism and application to diffusion inside a sphere, Mol. Phys., 1980, 41(2), 271–279 CrossRef CAS.
- S. Zahn, B. Kirchner and D. Mollenhauer, Charge spreading in deep eutectic solvents, ChemPhysChem, 2016, 17(21), 3354–3358 CrossRef CAS PubMed.
- S. Zahn, Deep eutectic solvents: Similia similibus solvuntur?, Phys. Chem. Chem. Phys., 2017, 19(5), 4041–4047 RSC.
- D. V. Wagle, C. A. Deakyne and G. A. Baker, Quantum chemical insight into the interactions and thermodynamics present in choline chloride based deep eutectic solvents, J. Phys. Chem. B, 2016, 120(27), 6739–6746 CrossRef CAS PubMed.
- S. Kondou, M. L. Thomas, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, Ionic transport in highly concentrated lithium bis(fluorosulfonyl)amide electrolytes with keto ester solvents: Structural implications for ion hopping conduction in liquid electrolytes, Phys. Chem. Chem. Phys., 2019, 21(9), 5097–5105 RSC.
- Z. Li, G. D. Smith and D. Bedrov, Li+ solvation and transport properties in ionic liquid/lithium salt mixtures: A molecular dynamics simulation study, J. Phys. Chem. B, 2012, 116(42), 12801–12809 CrossRef CAS PubMed.
- Y. Saito, T. Umecky, J. Niwa, T. Sakai and S. Maeda, Existing condition and migration property of ions in lithium electrolytes with ionic liquid solvent, J. Phys. Chem. B, 2007, 111(40), 11794–11802 CrossRef CAS PubMed.
- O. Borodin, J. Self, K. A. Persson, C. Wang and K. Xu, Uncharted waters: Super-concentrated electrolytes, Joule, 2020, 4(1), 69–100 CrossRef CAS.
- S. S. Hossain and A. Samanta, Solute rotation and translation dynamics in an ionic deep eutectic solvent based on choline chloride, J. Phys. Chem. B, 2017, 121(46), 10556–10565 CrossRef CAS PubMed.
- S. Barik, M. Chakraborty and M. Sarkar, How does addition of lithium salt influence the structure and dynamics of choline chloride-based deep eutectic solvents?, J. Phys. Chem. B, 2020, 124(14), 2864–2878 CrossRef CAS PubMed.
- N. Subba, K. Polok, P. Piatkowski, B. Ratajska-Gadomska, R. Biswas, W. Gadomski and P. Sen, Temperature-dependent ultrafast solvation response and solute diffusion in acetamide–urea deep eutectic solvent, J. Phys. Chem. B, 2019, 123(43), 9212–9221 CrossRef CAS PubMed.
- G. R. Kneller, Generalized Kubo relations and conditions for anomalous diffusion: Physical insights from a mathematical theorem, J. Chem. Phys., 2011, 134(22), 224106 CrossRef PubMed.
- I. M. Sokolov, Models of anomalous diffusion in crowded environments, Soft Matter, 2012, 8(35), 9043–9052 RSC.
- M. G. Del Pópolo and G. A. Voth, On the structure and dynamics of ionic liquids, J. Phys. Chem. B, 2004, 108(5), 1744–1752 CrossRef.
- C. J. Margulis, H. A. Stern and B. J. Berne, Computer simulation of a “Green Chemistry” room-temperature ionic solvent, J. Phys. Chem. B, 2002, 106(46), 12017–12021 CrossRef CAS.
- H. Srinivasan, V. K. Sharma and S. Mitra, Water accelerates the hydrogen-bond dynamics and abates heterogeneity in deep eutectic solvent based on acetamide and lithium perchlorate, J. Chem. Phys., 2021, 155(2), 024505 CrossRef CAS PubMed.
- H. Zhang, X. Wang, H.-B. Yu and J. F. Douglas, Dynamic heterogeneity, cooperative motion, and Johari–Goldstein β-relaxation in a metallic glass-forming material exhibiting a fragile-to-strong transition, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44(4), 56 CrossRef CAS PubMed.
- L. Wang, N. Xu, W. H. Wang and P. Guan, Revealing the link between structural relaxation and dynamic heterogeneity in glass-forming liquids, Phys. Rev. Lett., 2018, 120(12), 125502 CrossRef CAS PubMed.
- A. Faraone, D. V. Wagle, G. A. Baker, E. C. Novak, M. Ohl, D. Reuter, P. Lunkenheimer, A. Loidl and E. Mamontov, Glycerol hydrogen-bonding network dominates structure and collective dynamics in a deep eutectic solvent, J. Phys. Chem. B, 2018, 122(3), 1261–1267 CrossRef CAS PubMed.
- T. Franosch and W. Götze, Mode-coupling theory for the shear viscosity in supercooled liquids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57(5), 5833–5840 CrossRef CAS.
- S. P. Das, Mode-coupling theory and the glass transition in supercooled liquids, Rev. Mod. Phys., 2004, 76(3), 785–851 CrossRef CAS.
- J. Li, I. Wang, K. Fruchey and M. D. Fayer, Dynamics in supercooled ionic organic liquids and mode coupling theory analysis, J. Phys. Chem. A, 2006, 110(35), 10384–10391 CrossRef CAS PubMed.
- T. Yamaguchi, T. Yonezawa, K. Yoshida, T. Yamaguchi, M. Nagao, A. Faraone and S. Seki, Relationship between structural relaxation, shear viscosity, and ionic conduction of LiPF6/propylene carbonate solutions, J. Phys. Chem. B, 2015, 119(51), 15675–15682 CrossRef CAS PubMed.
- S. Kaur, A. Gupta and H. K. Kashyap, Nanoscale spatial heterogeneity in deep eutectic solvents, J. Phys. Chem. B, 2016, 120(27), 6712–6720 CrossRef CAS PubMed.
- A. Faraone, L. Liu, C. Y. Mou, C. W. Yen and S. H. Chen, Fragile-to-strong liquid transition in deeply supercooled confined water, J. Chem. Phys., 2004, 121(22), 10843–10846 CrossRef CAS PubMed.
- F. Mallamace, M. Broccio, C. Corsaro, A. Faraone, U. Wanderlingh, L. Liu, C. Y. Mou and S. H. Chen, The fragile-to-strong dynamic crossover transition in confined water: Nuclear magnetic resonance results, J. Chem. Phys., 2006, 124(16), 161102 CrossRef CAS PubMed.
- K. N. Lad, N. Jakse and A. Pasturel, Signatures of fragile-to-strong transition in a binary metallic glass-forming liquid, J. Chem. Phys., 2012, 136(10), 104509 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |