Open Access Article
Open Access ArticleNucleation behaviour of racemic and enantiopure histidine†
Lina C.
Harfouche
a,
Simon
Clevers
 a,
Gérard
Coquerel
a and
Ivo B.
Rietveld
a,
Gérard
Coquerel
a and
Ivo B.
Rietveld
 *ab
*ab
aUniversité de Rouen Normandie, UFR des Sciences et Techniques, Laboratoire SMS-EA3233, Place Emile Blondel, 76821, Mont-Saint-Aignan, France. E-mail: ivo.rietveld@univ-rouen.fr
bUniversité de Paris, Faculté de Pharmacie, 4 avenue de l'observatoire, 75006, Paris, France
First published on 3rd November 2021
Abstract
Nucleation of DL- and L-histidine is examined using induction time measurements and their nucleation rates have been deduced. Results indicate a much slower nucleation for the racemic form compared to the pure enantiomer form. The effect of temperature and supersaturation on the nucleation rate is also described. Classical nucleation theory (CNT) is used to determine the interfacial energy, the nucleation energy barrier, and the nucleus size for both compounds. The large difference between the nucleation rates for the pure enantiomer and the racemic compound have so far not led to satisfactory preferential crystallization; however second harmonic generation analysis demonstrates the presence of non-centrosymmetric domains embedded within the racemic crystals implying that improving control over the nucleation conditions may lead to more efficient preferential crystallisation and symmetry breaking.
Introduction
Crystallization is an important industrial process; it is commonly used in several important industries including pharmaceuticals,1 chemicals,2 food,3 pigments,4 and microelectronics,5 in which crystallization is often used as a final separation and purification step to control the crystal size, shape, composition, and structure.6 Crystallization is used to manipulate the end-product's physical and chemical properties (polymorph, solubility, morphology, density, size, size distribution, etc.)7 especially in the pharmaceutical industry, because many pharmaceutical ingredients are manufactured in a solid, crystalline form. Ultimate control over the crystallization process requires a control of the most crucial step: ‘nucleation’.Nucleation can happen through different mechanisms that can be divided into two categories:6–8 primary nucleation and secondary nucleation. The critical nucleus may emerge either homogeneously or heterogeneously on a foreign surface such as dust particles or the wall of the container.9,10 Heterogeneous nucleation is often faster and more common than homogeneous nucleation because a surface is always present in the reaction environment.11 However, nucleation is difficult to control because several factors (e.g. nucleation rate, the number of molecules needed to form a nucleus of a critical size, the energy barrier, etc.)6 can play a major role in the nucleation onset.
In this study, racemic and enantiopure histidine (Scheme 1) have been selected as model compounds, as control over nucleation is one of the pathways to accomplish chiral resolution through crystallisation. We aim to compare the nucleation behaviour of the racemic and enantiopure materials. To the best of our knowledge, this kind of studies are rare.12
We will apply a previously developed method based on induction time measurements13,14 to determine the nucleation kinetics of the model compounds. The experimental data will be analysed against classical nucleation theory15,16 based on Arrhenius rate laws. In addition, the effect of temperature and supersaturation is studied.
Materials and methods
Materials
Racemic (DL) and enantiopure (L)-histidine (purity ≥ 99.0%) were purchased from Merck and used as received. Water used in this work is demineralized water.To check if the sample produce fluorescence, an emission spectral scan is performed. Typically, the sample is excited at a given wavelength (e.g., 1200 nm or 900 nm) while scanned through the emission wavelength (e.g., in the 385–780 nm range). The SHG and THG should appear at the half and at the third of the excitation wavelength, respectively. The spectral acquisition was performed using an internal hybrid detector. Collected photons were dispersed by a prism and a specific motorized split mirror selected the spectral detected band before the hybrid detector. Acquisitions were performed between 385 nm and 780 nm every 3 nm and a spectral bandwidth of 5 nm.
The samples are prepared by deposition of few mg on a microscope slide.
The signal generated by the sample (diffused light) was collected into an optical fiber (500 μm of core diameter) and directed onto the entrance slit of a spectrometer (Ocean Optics). A boxcar integrator allowed an average spectrum (spectral range 490–590 nm) with a resolution of 0.1 nm to be recorded over 3 s (30 pulses).
According to Kurtz and Perry SHG powder method,19 SHG signal intensities were compared to the signal of a reference compound (α-quartz powder – 45 μm average size).
Theory
P(t) = 1 − C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−JV(ti − tg)) exp(−JV(ti − tg)) | (1) |
Experimentally, the cumulative probability function, P(t), is defined as follows:
| P(t) = M+(t)/M | (2) |
According to the classical nucleation theory (CNT), the nucleation rate for a given supersaturation, β, is defined as:20,21
J = Aβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−B/ln2 exp(−B/ln2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) β) | (3) |
| B = (16πv02γ3)/(3k3T3) | (4) |
The critical Gibbs free energy (ΔG*) representing the energy barrier that the system must overcome to form a critical nucleus (kJ mol−1), and the critical number of molecules in the nucleus n* (molecules) can be calculated using these equations:7,22
ΔG* = (16πv03γ3)/3k2T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln2 ln2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = BkT/ln2 β = BkT/ln2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β | (5) |
n* = (32πv02γ3)/3k3T3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln3 ln3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β | (6) |
| Al,hom = (4π/3v0)1/3(γ/kT)1/2Ds | (7) |
The interfacial energy γ can be predicted with the aid of the Stefan–Skapski–Turnbull formula21 connecting γ to ln(1/s):
γpredicted = 0.514kT/v02/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1/NAv0s) ln(1/NAv0s) | (8) |
Using the previous equations, J for interface-transfer control can be presented as:
J = aIT/η(ln(ρc/Ms))0.5sβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bI((ln2(ρc/Ms))/(ln2 exp(−bI((ln2(ρc/Ms))/(ln2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β)) β)) | (9) |
Results and discussion
Solubility and induction time measurements
The solubility (s) curves of the two crystal forms (pure enantiomer L and racemic DL) of histidine in demineralized water are shown in Fig. 1. As seen in this figure, the solubility of L-histidine in water is higher than that of DL-histidine. Each point is the average of 4 data points. The solid lines are a fit to the experimental data, and they have been used to determine the supersaturation ratio β = C0/s, where C0 is the initial concentration of the solution at the targeted nucleation temperatures.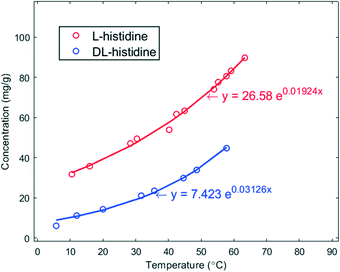 | ||
| Fig. 1 Solubility curves in mg g−1 of L- (red) and DL-histidine (blue) in water as a function of temperature in °C. The solid lines are fits of the data. | ||
The nucleation kinetics of these compounds was determined using the induction time method, as reported elsewhere.13,14 Experiments were performed with various initial concentrations at four nucleation temperatures (25, 20, 15, and 10 °C for L-histidine and 15, 10, 7, and 5 °C for DL-histidine). Each experimental run was carried out several times leading to a total number of at least 112 induction time data points per supersaturation ratio. The variation in the measured induction times at one supersaturation reflects the stochastic character of nucleation.
Using eqn (1), the nucleation rates for the different supersaturation ratios have been calculated. Its dependence on the supersaturation and on the temperature has been determined. Experimental conditions and results are shown in Table 1 and Fig. S2† for both enantiomer and racemic crystals. The high supersaturation used in the case of DL-histidine is related to the very slow nucleation rate seen in this system at low β. For instance, a sample at 15 °C with a β = 2.2 needs an average of 24 h to crystallize. Such high β could not be used in the case of L-histidine since the nucleation is too rapid. As expected, the nucleation rate J increases with increasing supersaturation and for the same supersaturation level the nucleation rate J decreases with decreasing temperature.
| Compound | T (°C) | C 0 (mg g−1) | β | J (m−3 s−1) |
|---|---|---|---|---|
| L-Histidine | 25 | 67.7 | 1.6 | 516.9 |
| 74.4 | 1.7 | 2392.0 | ||
| 77.9 | 1.8 | 2773.3 | ||
| 83.4 | 1.9 | 5914.2 | ||
| 20 | 67.7 | 1.7 | 1185.3 | |
| 74.4 | 1.9 | 3506.3 | ||
| 77.9 | 2.0 | 3658.1 | ||
| 83.4 | 2.1 | 7112.6 | ||
| 15 | 67.7 | 1.9 | 2239.9 | |
| 74.4 | 2.1 | 4939.7 | ||
| 77.9 | 2.2 | 5206.7 | ||
| 83.4 | 2.4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401.0 401.0 |
||
| 10 | 67.7 | 2.2 | 5063.0 | |
| 74.4 | 2.3 | 6232.8 | ||
| 77.9 | 2.4 | 7062.0 | ||
| 83.4 | 2.6 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070.0 070.0 |
||
| DL-Histidine | 15 | 33.0 | 2.7 | 252.7 |
| 34.5 | 2.8 | 270.2 | ||
| 36.0 | 2.9 | 863.9 | ||
| 38.0 | 3.1 | 1168.3 | ||
| 10 | 33.0 | 3.6 | 501.0 | |
| 34.5 | 3.7 | 620.8 | ||
| 36.0 | 3.9 | 1473.1 | ||
| 38.0 | 4.1 | 2244.9 | ||
| 7 | 33.0 | 4.5 | 668.3 | |
| 34.5 | 4.7 | 1201.6 | ||
| 36.0 | 4.9 | 1543.5 | ||
| 38.0 | 5.2 | 2384.0 | ||
| 5 | 33.0 | 5.7 | 848.1 | |
| 34.5 | 5.9 | 1227.2 | ||
| 36.0 | 6.2 | 2230.3 | ||
| 38.0 | 6.5 | 2572.7 |
The experimental cumulative probability distributions P(t) as a function of the measured induction times ti in seconds are given in Fig. S3 and S4 in the ESI.†
Nucleation kinetic parameters
The temperature dependence of the nucleation rate can be modelled with an Arrhenius-type equation. The natural logarithm of J/β is a linear function of ln−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β as shown in eqn (3); the data have been accordingly plotted in Fig. 2. The resulting slopes and intercepts are used to determine the experimental thermodynamic parameter Bexp and kinetic parameter Aexp respectively. The considered model does not afford an understanding of the origins of the experimentally observed not perfect linear plots and variations for L-histidine at different temperature as seen in Fig. 2. Polymorphism of L-histidine (LHISTD01, LHISTD10) might be a reason for the relatively scattered data, however, XRD measurements of the final powders did not provide any proof that a second polymorph was present.26
β as shown in eqn (3); the data have been accordingly plotted in Fig. 2. The resulting slopes and intercepts are used to determine the experimental thermodynamic parameter Bexp and kinetic parameter Aexp respectively. The considered model does not afford an understanding of the origins of the experimentally observed not perfect linear plots and variations for L-histidine at different temperature as seen in Fig. 2. Polymorphism of L-histidine (LHISTD01, LHISTD10) might be a reason for the relatively scattered data, however, XRD measurements of the final powders did not provide any proof that a second polymorph was present.26
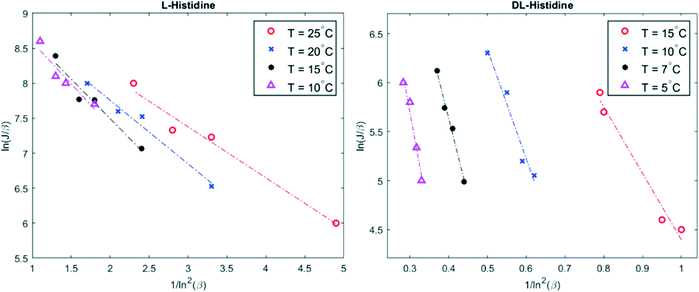 | ||
Fig. 2 Plot of ln(J/β) versus 1/ln2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β for four different temperatures. The experimental data are given by colored marker shapes and the dotted lines are the best fit to the experimental points. β for four different temperatures. The experimental data are given by colored marker shapes and the dotted lines are the best fit to the experimental points. | ||
The values of the parameters aI, bI, aD and bD are obtained from eqn (S5)–(S7)† and are reported in the ESI,† Table S1. These values are used to calculate the corresponding theoretical values of the kinetic AI(predicted) and thermodynamic BI(predicted) parameters using eqn (9).
The prediction of the kinetic parameter for homogeneous interface-transfer control AI,hom(predicted) is obtained from eqn (7). The thermodynamic parameter Bhom(predicted) is obtained theoretically by substituting γpredicted in eqn (4). The results are very similar to the one obtained by substituting aI and bI in eqn (9).
Experimental values of the interfacial energy (γexp) have been obtained from the Bexp values using eqn (4). The theoretical values of the interfacial energies (γpredicted) have been calculated using eqn (8).
All results for L and DL-histidine are presented and compared in Table 2.
| Compound | T (°C) | B exp | A exp (m−3 s−1) | γ exp (mJ m−2) | B I(predicted) | B hom(predicted) | A I(predicted) (m−3 s−1) | A I,hom(predicted) (m−3 s−1) | γ (predicted) (mJ m−2) |
|---|---|---|---|---|---|---|---|---|---|
| These parameters were calculated using. a Eqn (3). b Eqn (4). c Eqn (9) and (3). d Eqn (8) and (4). e Eqn (7). f Eqn (8). | |||||||||
| L-Histidine | 25 | 0.73 | 1.4 × 104 | 4.5 | 92 | 98 | 7.7 × 1035 | 7.8 × 1035 | 23.2 |
| 20 | 0.91 | 1.5 × 104 | 4.7 | 99 | 106 | 6.2 × 1035 | 6.3 × 1035 | 23.5 | |
| 15 | 1.13 | 1.7 × 104 | 5.0 | 108 | 115 | 4.9 × 1035 | 5.0 × 1035 | 23.7 | |
| 10 | 1.2 | 1.8 × 104 | 5.0 | 117 | 124 | 3.9 × 1035 | 3.9 × 1035 | 23.9 | |
| DL-Histidine | 15 | 6.8 | 7.1 × 104 | 9.1 | 230 | 240 | 1.9 × 1035 | 1.9 × 1035 | 30.4 |
| 10 | 11.1 | 14.8 × 104 | 10.5 | 270 | 270 | 1.3 × 1035 | 1.3 × 1035 | 31.7 | |
| 7 | 15.7 | 15.1 × 104 | 11.7 | 310 | 330 | 9.4 × 1034 | 9.5 × 1034 | 32.9 | |
| 5 | 21.8 | 20.6 × 104 | 12.9 | 350 | 380 | 7.2 × 1034 | 7.2 × 1034 | 34.1 | |
Only the results for interface-transfer control are shown here, those for volume-diffusion control obtained by linearizing the equation of J for volume-diffusion control (eqn (S4)†) by plotting ln (J/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) in terms of ln−2
β) in terms of ln−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β can be found in the ESI† (Fig. S5 and Table S2).
β can be found in the ESI† (Fig. S5 and Table S2).
As represented in Table 2, with increasing the value of the temperature, the kinetic factor A and the thermodynamic factor B decrease in both systems. Considering that with increasing the value of A (higher concentration of nucleation sites and/or higher attachment frequency) and with decreasing the value of B (low energy barrier), it is easier for the solute molecules to aggregate together and to cross the free energy barrier. Thus, in this case increasing the nucleation temperature favours the nucleation process mainly in kinetic aspect.
The experimental values of A are 30–31 orders of magnitude lower than the predicted values for homogeneous nucleation AI,hom, which can be viewed as a strong indication that the primary nucleation of histidine (L and DL) crystals is actually heterogeneous. This finding does not come as a surprise as previous papers have found a similar disagreement between experimental and theoretical values and ascribed this to heterogeneous nucleation.14,25,27 It may be related to the low concentration of nucleation sites in the solution or to the low attachment frequency of molecules to the nucleus.13 However, these explanations could not be further explored with the current experimental setup.
As is shown in Table 2, the values of the kinetic parameter, A, the thermodynamic parameters, B and the interfacial energies γ for DL-histidine are larger than those obtained for L-histidine. Although the experimental values for both compounds are lower than the predicted ones, it is in fact close to those calculated from nucleation data for other organic compounds.25,28,29
According to eqn (5) and (6), low interfacial energy is related to smaller critical nucleus size (proportional to γ). In the next part, the nucleation behaviour of the current systems will be discussed with respect to CNT in relation to the effect of γ on the critical nucleus size.
Energy barrier and cluster size
Within the CNT framework, by using Bexp values inferred from nucleation data, the thermodynamic activation barrier ΔG* and the number of molecules per nucleus n* at different temperatures have been determined in the supersaturation range of 1.7–2.4 for L-histidine and 2.6–3.6 for DL-histidine respectively (see ESI†).It is clear from the results that as supersaturation or temperature increases, ΔG* and n* values become smaller. The nucleation barrier of DL-histidine is found to be higher than the one for L-histidine also explaining the slower nucleation of the racemic form vs. the pure enantiomer form.
Such a behaviour is of interest for the chiral resolution process; however, the observed, much faster nucleation of enantiopure crystals has not yet led to the crystallization of the conglomerate. In fact, the solubility of the stable racemic form is extremely low in comparison to the conglomerate. Given the solubility curves in Fig. 1, at 20 °C, the solubility of the racemic compound is 13.9 mg g−1, whereas that of the conglomerate is two times that of the pure enantiomer 78.1 mg g−1. This difference is extreme.30 Thus, to reach at 20 °C a supersaturation of β > 1 with respect to the metastable conglomerate, where nucleation can be expected, the supersaturation with respect to the racemic form will be β ≥ 5.6. This obviously is a large impediment to nucleate the conglomerate as the high supersaturation counteracts the fast nucleation.
Microscopic behaviour observed by SHG
The Kurtz and Perry test has been performed on two racemic samples: the racemic compound as received from the manufacturer and the recrystallized solid at high supersaturation (up to β ≈ 15) under quiescent conditions. Although small, both clearly show a SHG effect (Fig. S8 and S9†).SHG microscopy on these samples (laser excitation of 900 nm) confirms the presence of domains which are non-centrosymmetric embedded in the crystals (Fig. 3 and S10†). These domains can be differentiated from the very weak SHG surface effect and must therefore be non-centrosymmetric crystallites. This is inconsistent with the centrosymmetric crystal space group P21/c of the racemic crystals. On the other hand, the PXRD patterns of the samples match the calculated one, based on P21/c. Hence, above the detection threshold for PXRD, no other polymorphic form (which could have been non-centrosymmetric) has been observed. It appears therefore likely that some deviations in the 50–50 composition is tolerated by the ‘racemic’ crystal lattice. Considering the foregoing nucleation analysis, it is possible that in the highly supersaturated racemic system, initial nucleation of enantiomerically enriched crystals occurs. However, subsequently, crystal growth is taken over by the more stable and less soluble racemic crystal. These observations are consistent with a report on limited preferential enrichment observed for histidine31 and would explain the weak SHG effect in line with symmetry breaking through crystallisation.32,33 It also explains, in the case of the racemic compound, why CNT may not work as the nucleation is clearly not a simply homogeneous process.
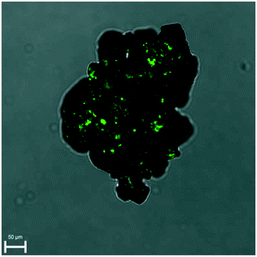 | ||
| Fig. 3 Overlay of SHG and microscope image demonstrating small non-centrosymmetric domains in the racemic crystal. | ||
Conclusions
Nucleation induction time in water has been determined for two systems: racemic histidine and pure enantiomer of histidine. The effect of the temperature and the supersaturation ratio on the nucleation rate is presented. Classic nucleation theory does not describe the data correctly and this is likely due to heterogeneous instead of homogeneous nucleation as concluded before.34 It is observed experimentally that the nucleation of DL-histidine is much slower than that of L-histidine for the same level of supersaturation and at the same temperature. This has not led to preferential crystallisation of the conglomerate due to the large differences in solubility between the conglomerate and the stable racemic compound. For the racemic compound, although the crystal structure is globally compatible with the P21/c space group, non-centrosymmetric domains are observed by SHG microscopy. As a partial reason, why CNT does not apply, the SHG signal implies that nucleation processes can in certain cases be highly complex phenomena in which the initially nucleating form loses out to the faster growing form that appears through secondary nucleation and growth, which possibly occurs on the nuclei of the initially nucleating form. Harnessing such phenomena may lead to better optimization of preferential crystallisation and separation of enantiomers by preferential enrichment.List of symbols and abbreviations
| N A | Avogadro's constant |
| k | Boltzmann constant |
| D | Diffusion coefficient |
| ΔG* | Gibbs free energy |
| t g | Growth time |
| t i | Induction time |
| C 0 | Initial concentration |
| γ | Interfacial energy |
| A | Kinetic parameter |
| ν 0 | Molecular volume |
| J | Nucleation rate |
| n* | Number of molecules in the nucleus |
| P(t) | Probability distribution |
| L | Pure enantiomer |
| DL | Racemic compound |
| SHG | Second harmonic generation |
| s | Solubility ratio |
| V | Solution volume |
| β | Supersaturation |
| B | Thermodynamic parameter |
| THG | Third harmonic generation |
| PXRD Powder | X-ray diffraction |
Author contributions
All authors contributed equally.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research received funding as part of the NACRE Project by the European Regional Development Fund (FEDER) and the Normandy region. The authors thank Jules Kachaner for help with the experimental work during his internship at the SMS laboratory.References
- J. Chen, B. Sarma, J. M. B. Evans and A. S. Myerson, Cryst. Growth Des., 2011, 11, 887–895 CrossRef CAS.
- P. A. Larsen, D. B. Patience and J. B. Rawlings, IEEE Control Syst., 2006, 26, 70–80 Search PubMed.
- A. B. N. Brito and M. Giulietti, Cryst. Res. Technol., 2007, 42, 583–588 CrossRef CAS.
- S. Suzuki and J. Mizuguchi, Dyes Pigm., 2004, 61, 69–77 CrossRef CAS.
- P. Muhammed Shafi and A. Chandra Bose, AIP Adv., 2015, 5, 057137 CrossRef.
- H.-H. Tung, E. L. Paul, M. Midler and J. A. McCauley, Crystallization of Organic Compounds: An Industrial Perspective, John Wileys & Sons, 2009 Search PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007–5019 CrossRef CAS PubMed.
- P. G. Vekilov, Nat. Mater., 2012, 11, 838–840 CrossRef CAS PubMed.
- R. P. Sear, J. Phys. Chem. B, 2006, 110, 4985–4989 CrossRef CAS PubMed.
- X. Y. Liu, J. Chem. Phys., 2000, 112, 9949–9955 CrossRef CAS.
- A. Myerson, Handbook of Industrial Crystallization, Butterworth-Heinemann, USA, 2002 Search PubMed.
- A. Robin, P. Iavicoli, K. Wurst, M. S. Dyer, S. Haq, D. B. Amabilino and R. Raval, Cryst. Growth Des., 2010, 10, 4516–4525 CrossRef CAS.
- S. A. Kulkarni, S. S. Kadam, H. Meekes, A. I. Stankiewicz and J. H. Ter Horst, Cryst. Growth Des., 2013, 13, 2435–2440 CrossRef CAS.
- S. Jiang and J. H. Ter Horst, Cryst. Growth Des., 2011, 11, 256–261 CrossRef CAS.
- M. Vollmer, Kinetik der Phasenbildung, Verlag Theodor Steinkopff, Dresden, 1939 Search PubMed.
- A. E. Nielsen, Kinetics of Precepitation, Pergamon Press, Oxford, 1964 Search PubMed.
- C. Brandel and J. H. ter Horst, Faraday Discuss., 2015, 179, 199–214 RSC.
- J. W. Mullin, Crystallization, Butterworth, London, 4th edn, 2001 Search PubMed.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- D. Kashchiev and G. M. van Rosmalen, Cryst. Res. Technol., 2003, 38, 555–574 CrossRef CAS.
- D. Kashchiev, Nucleation: Basic Theory With Applications, Butterworth-Heinemann, Oxford, first, 2000 Search PubMed.
- M. P. Anisimov, Usp. Khim., 2003, 72, 664–706 Search PubMed.
- J. T. Edward, J. Chem. Educ., 1970, 47, 261–270 CrossRef CAS.
- M. Laliberte, J. Chem. Eng. Data, 2007, 52, 1507–1508 CrossRef CAS.
- C. Lindenberg and M. Mazzotti, J. Cryst. Growth, 2009, 311, 1178–1184 CrossRef CAS.
- M. Kitamura, J. Chem. Eng. Jpn., 1993, 26, 303–307 CrossRef CAS.
- R. J. Davey, S. L. M. Schroeder and J. H. Ter Horst, Angew. Chem., Int. Ed., 2013, 52, 2166–2179 CrossRef CAS PubMed.
- L. T. Padro and A. Nenes, Atmos. Chem. Phys. Discuss., 2007, 7, 2325–2355 Search PubMed.
- L. D. Shiau and H. P. Wang, J. Cryst. Growth, 2016, 442, 47–51 CrossRef CAS.
- G. Coquerel, J. Pharm. Pharmacol., 2015, 67, 869–878 CrossRef CAS PubMed.
- S. Iwama, PhD thesis, University of Tokyo, March 2012, (thesis in Japanese) Search PubMed.
- H. Takahashi, Y. Numao, J. Motokawa, S. Clevers, G. Coquerel, H. Tsue and R. Tamura, Chem. - Eur. J., 2019, 25, 16405–16413 CrossRef CAS PubMed.
- G. Coquerel and M. Hoquante, Symmetry, 2020, 12, 1796 CrossRef CAS.
- D. Gebauer, P. Raiteri, J. D. Gale and H. Cölfen, Am. J. Sci., 2018, 318, 969–988 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ce01199e |
| This journal is © The Royal Society of Chemistry 2021 |