Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of solution chemistry on the solubility, crystallisability and nucleation behaviour of eicosane in toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) acetone mixed-solvents†
acetone mixed-solvents†
Peter L.
Kaskiewicz
 a,
Ian
Rosbottom
b,
Diana M.
Camacho Corzo
a,
Ian
Rosbottom
b,
Diana M.
Camacho Corzo
 a,
Robert B.
Hammond
a,
Robert B.
Hammond
 a,
Ruth
Downie
a,
Ruth
Downie
 c,
Peter J.
Dowding
c,
Peter J.
Dowding
 c,
Neil
George
d and
Kevin J.
Roberts
c,
Neil
George
d and
Kevin J.
Roberts
 *a
*a
aEPSRC Centre for Doctoral Training in Complex Particulate Products and Processes, School of Chemical and Process Engineering, University of Leeds, Leeds LS2 9JT, UK. E-mail: K.J.Roberts@leeds.ac.uk
bDepartment of Chemical Engineering, Imperial College London, London SW7 2AZ, UK
cInfineum UK Ltd, Milton Hill Business and Technology Centre, Abingdon OX13 6BB, UK
dSyngenta UK Ltd, Jealott's Hill International Research Centre, Berkshire RG42 6EY, UK
First published on 1st April 2021
Abstract
The interplay between the solution chemistry and crystallisability of eicosane in mixed toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone solutions is examined over the full compositional range from pure toluene to pure acetone, using a combination of polythermal crystallisation experiments and molecular modelling. Enthalpies of dissolution and mixing, as well as metastable zone widths increase with increasing acetone content, up to a mol fraction of 0.85 acetone, followed by a decrease in values to pure acetone solutions. Nucleation is found to occur via an instantaneous pathway for the pure solvent systems and also when toluene is in excess, in contrast to solutions where acetone is in excess, which are found to nucleate progressively. Rationalisation through molecular modelling highlights likely changes in the solution structure, whereby eicosane can be expected to be preferentially solvated by toluene, with this solvated cluster being surrounded by a ‘cage’ of acetone molecules. This proposed structure is consistent with a model whereby solute diffusion and hence clustering is hindered when acetone is in excess, decreasing the crystallisability of the solution and effecting a change in the mechanism of nucleation. However, above a critical acetone composition, the potential for complete toluene solvation is restricted and easier crystallisation is enabled.
acetone solutions is examined over the full compositional range from pure toluene to pure acetone, using a combination of polythermal crystallisation experiments and molecular modelling. Enthalpies of dissolution and mixing, as well as metastable zone widths increase with increasing acetone content, up to a mol fraction of 0.85 acetone, followed by a decrease in values to pure acetone solutions. Nucleation is found to occur via an instantaneous pathway for the pure solvent systems and also when toluene is in excess, in contrast to solutions where acetone is in excess, which are found to nucleate progressively. Rationalisation through molecular modelling highlights likely changes in the solution structure, whereby eicosane can be expected to be preferentially solvated by toluene, with this solvated cluster being surrounded by a ‘cage’ of acetone molecules. This proposed structure is consistent with a model whereby solute diffusion and hence clustering is hindered when acetone is in excess, decreasing the crystallisability of the solution and effecting a change in the mechanism of nucleation. However, above a critical acetone composition, the potential for complete toluene solvation is restricted and easier crystallisation is enabled.
1. Introduction
Solution phase crystallisation is an energy-efficient physical process widely utilised to isolate and/or purify solid-form ingredients. The majority of speciality chemicals are crystallised in multi-substance batch reactors, which provide limited opportunities for specialised reactor designs and for optimising crystal product properties.1 However, selection of a mixed-solvent crystallisation system, comprising two or more miscible components, provides an alternative opportunity for the control and optimisation of the crystallisation process. Mixed-solvent crystallisation systems have been intensively studied, due to their compositional variation affecting solubility,2 solid-form produced,3–5 crystal growth,6 habit,7 crystal size,8 crystallisability9–12 and nucleation.13–15Crystallisation from mixed-solvent solution systems can be directed, either through cooling of an initial solvent blend7,16 or through antisolvent crystallisation.15,17 Both routes require miscible solvents, with the latter requiring significant differences in the solubility of the solute between the solvent and antisolvent, the addition of which lowers solute solubility and hence generates supersaturated conditions. In the design of mixed-solvent crystallisation processes, it is helpful to have developed workflows for the characterisation of the solubility and solution properties over the full range of compositions used and, through this, optimise the process parameters to ensure the desired crystal product characteristics.18,19
For the design of antisolvent crystallisation processes knowledge of the solubility–temperature relationship as a function of the composition of solvent mixture is important for control of the solution supersaturation generated by the addition of the lower solubility solvent. Depending upon the magnitude and sign of the enthalpy of mixing, the addition of a second solvent can change the solution temperature15,17 and hence a detailed knowledge of a solution's mixed-solvent thermodynamics is also needed.
Changes in solution properties can, in turn, also impact upon solute mass transport within the solution phase and through this, impact upon the overall crystallisability of the material. Hence, characterisation of the metastable zone width (MSZW) as a function of solvent composition is required in order to define the operational conditions for large-scale crystallisation processes.
Variation in mixed-solvent composition can also change the nature of the intermolecular interactions associated with solute desolvation and clustering, which can directly affect the ability of the solute to nucleate, impacting, in turn, on the nucleation kinetics and associated mechanism.15,17,20 In the latter respect, polynuclear nucleation can occur either through instantaneous (IN) or progressive (PN) nucleation mechanisms,21 whereby IN describes the process in which all nuclei form instantly and subsequently undergo crystal growth, whereas in PN the nuclei continuously form in the presence of growing crystals. Such mechanistic changes can impact on the crystal product properties, e.g. IN could, in principle, result in a more uniform crystal size distribution of product. Previous studies in other organic solvents have highlighted the fact that changes in solution environment, relating to solution solvent and concentration20,22 as well as the inclusion of nucleation inhibition additives,23 can alter the mechanism of nucleation. The IN mechanism has been shown to occur when solute clustering is present in solution prior to the nucleation stage,24 in line with van't Hoff isotherms suggesting strong solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute interactions within solution.20 The relationship between solute clustering, solution structure and nucleation mechanism need to be investigated to provide insight into these cooperative effects.
solute interactions within solution.20 The relationship between solute clustering, solution structure and nucleation mechanism need to be investigated to provide insight into these cooperative effects.
In this study, the crystallisation of the long-chain hydrocarbon, eicosane (C20H42), from mixed toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone solutions is examined. Alkanes, in general, are known to be highly soluble in toluene25 but can be expected to be much less soluble in more polar solvents, such as acetone. The work presented here investigates this mixed-solvent system, examining the interplay between solvent composition and solution chemistry, in terms of the solutions solubility and crystallisability, thermodynamics and nucleation kinetics and mechanism. In this, the approach adopted encompasses experimental polythermal crystallisation/dissolution measurements26–28 to characterise the solution solubility and nucleation kinetics and mechanisms coupled with molecular-scale grid-based modelling29 of solute
acetone solutions is examined. Alkanes, in general, are known to be highly soluble in toluene25 but can be expected to be much less soluble in more polar solvents, such as acetone. The work presented here investigates this mixed-solvent system, examining the interplay between solvent composition and solution chemistry, in terms of the solutions solubility and crystallisability, thermodynamics and nucleation kinetics and mechanism. In this, the approach adopted encompasses experimental polythermal crystallisation/dissolution measurements26–28 to characterise the solution solubility and nucleation kinetics and mechanisms coupled with molecular-scale grid-based modelling29 of solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions. The latter seeks to compliment the experimental studies providing an insight into the likely molecular-scale solvation process for the mixed-solvent system and through this, produce a more complete understanding of the intermolecular interactions taking place within the solution phase, together with their concomitant impact upon the crystallisation process.
solvent interactions. The latter seeks to compliment the experimental studies providing an insight into the likely molecular-scale solvation process for the mixed-solvent system and through this, produce a more complete understanding of the intermolecular interactions taking place within the solution phase, together with their concomitant impact upon the crystallisation process.
2. Materials & methods
2.1. Workflow
The methodological workflow used in this study is given in Fig. 1, providing a standardised assessment for the characterisation of mixed-solvent solutions and their crystallisation, through an integrated approach, coupling experimental and modelling techniques.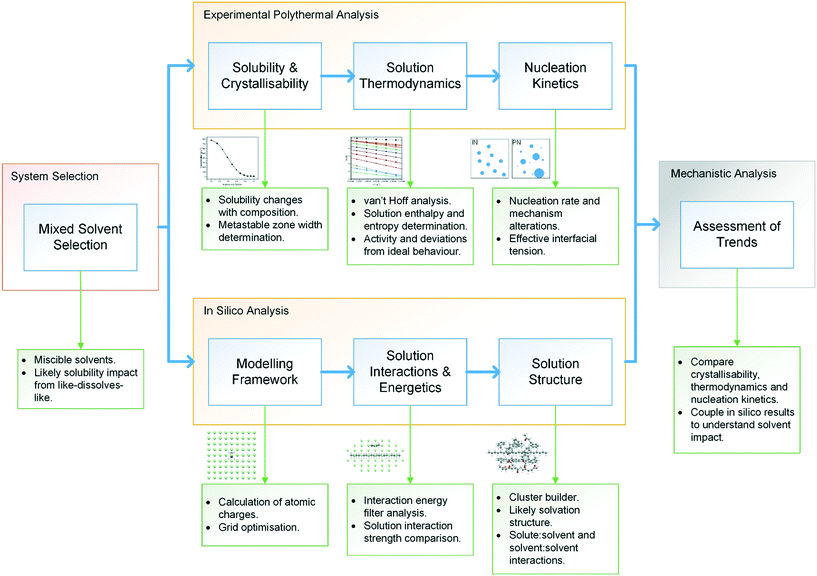 | ||
| Fig. 1 Methodological workflow incorporating crystallisation analysis with molecular modelling for enhancing process understanding. | ||
2.2. Materials
Eicosane (99% pure) was supplied by Sigma-Aldrich, toluene (≥99.3% pure) was supplied by Honeywell and acetone (99.5+% pure) was supplied by Arcos Organics. All materials were used as received without further purification.2.3. Experimental procedure
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone mixtures, e.g. 250–850 g L−1 for eicosane in pure toluene and 5–35 g L−1 for eicosane in pure acetone solutions, with concentrations varying with solvent composition to take into account changes in solubility. A total of eleven compositions of the toluene
acetone mixtures, e.g. 250–850 g L−1 for eicosane in pure toluene and 5–35 g L−1 for eicosane in pure acetone solutions, with concentrations varying with solvent composition to take into account changes in solubility. A total of eleven compositions of the toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone solvent mixtures in 10% volume increments were used.
acetone solvent mixtures in 10% volume increments were used.
Solutions were prepared by weighing eicosane into 15 ml prewashed glass vials, using a weighing scale that could measure with ±0.1 mg accuracy. A Fisherbrand 500–5000 μl micropipette was used to add the respective solvent to each concentration sample, with 5 ml total solvent volume used. A magnetic stirrer was placed into the glass vials and the mixtures were placed on a stirrer hot plate and held at 35 °C for 30 minutes under constant agitation, in order to form a homogeneous liquid solution. 1 ml of solution was added to the 1.5 ml glass vials and a standard 7 × 2 mm magnetic stirrer was added to each vial.
Crystallisation experiments were performed using the Technobis Crystal 16® system31 with crystallisation and dissolution onset points being detected by optical turbidity methods. The 1 ml solutions were subject to different cooling and heating cycles. Each temperature cycle began by heating the solutions to 35 °C, before being held at this temperature for one hour to ensure that complete homogenisation had taken place and was the solution was then subsequently cooled at a set rate to −15 °C. This temperature was then held for an hour to allow equilibration, followed by an increase in temperature back to 35 °C at the same specified rate. This temperature profile was performed for each concentration of each composition at rates (q) of 0.25, 1, 2 and 3.2 °C min−1 for both the cooling and heating segments of the temperature cycles and at a constant stirring rate of 300 rpm. Each temperature cycle was performed five times to obtain mean and standard deviation (STD) values for the rate-dependent crystallisation and dissolution temperatures determined.
A van't Hoff analysis was performed on the solubility data determined from the saturation temperatures. The solution ideality was determined with respect to the ideal solubility as obtained from DSC analysis, based upon the Hildebrand equation (eqn (1)). Activity coefficients (ϒ), enthalpy (ΔHdiss) and entropy (ΔSdiss) of dissolution were calculated based on eqn (2) and (3), respectively:25
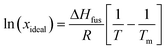 | (1) |
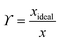 | (2) |
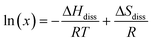 | (3) |
The calculated activity coefficients were fitted with respect to their variation in temperature, by:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϒ = aT + c ϒ = aT + c | (4) |
The enthalpy (ΔHmix) and entropy (ΔSmix) of mixing were calculated from the deviation in ΔHdiss and ΔSdiss from ideality, through the relationships:
| ΔHmix = ΔHdiss − ΔHidealdiss | (5) |
| ΔSmix = ΔSdiss − ΔSidealdiss | (6) |
Regardless of the mechanism by which nucleation occurs, the solution remains apparently unaffected until a critical level of undercooling is reached corresponding to the limit of the MSZW, at which point the amount of formed crystallites are detectable by the monitoring technique. This undercooling is dependent upon the nucleation, growth and cooling rates. The KBHR approach utilises the relationship between the relative critical solution undercooling (uc) and the cooling rate (q) to enable the determination of crystallisation parameters. uc was determined by:
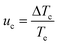 | (7) |
The mechanism of nucleation was determined through the “rule of three”, from ln–ln plots of ucvs. q, the slopes of which were fitted by linear regressions, whereby a slope >3 signifies a PN pathway and a slope <3 indicates an IN pathway.26,27
For the PN case, the final expression for uc(q) dependence, when expressed through the number of crystallites at the detection point (Ndet), can be defined as:
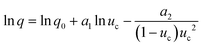 | (8) |
Plots of ucvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q fitted with eqn (8) enable the free parameters to be determined for the calculation of the nucleation parameters and the effective interfacial tension (γeff), eqn (9). This enables the calculation of the critical nucleus radius (r*), assuming spherical nuclei, and the number of molecules in the critical nucleus (i*), through eqn (10) and (11).
q fitted with eqn (8) enable the free parameters to be determined for the calculation of the nucleation parameters and the effective interfacial tension (γeff), eqn (9). This enables the calculation of the critical nucleus radius (r*), assuming spherical nuclei, and the number of molecules in the critical nucleus (i*), through eqn (10) and (11).
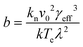 | (9) |
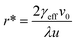 | (10) |
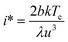 | (11) |
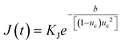 | (12) |
More detailed descriptions of the KBHR approach have been given previously.26–28
2.4. Molecular modelling
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute and solute
solute and solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
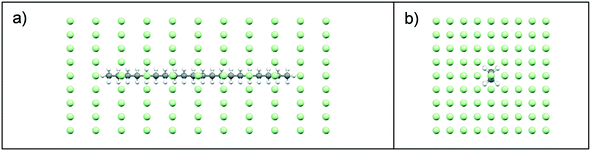
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions were examined using intermolecular grid search methods,37,38 with a spatial grid defined around a central target molecule, Fig. 3. A grid optimisation was performed and an orthogonal grid shape with size 15, 15 and 35 Å in the X, Y and Z planes, respectively was found to be optimal for energy calculations. In each plane, the number of grid points was defined with 8, 8, 10 steps of grid points on the X, Y and Z planes, respectively. This provided a grid with a total number of 891 points, Fig. 3. During the intermolecular interaction energy calculation procedure, a probe molecule was placed on each point of the grid and rotated through a set of Euler angles, which were set at 4° for the x-axis, y-axis and z-axis. This resulted in a heterogeneous six-dimensional search space, and at each point within this the interaction energy between the probe and target molecules was calculated using an atom–atom approach, with parameters from the Momany intermolecular potential.16,39 Intermolecular interactions in the form of van der Waals, hydrogen bonding and electrostatic interactions were calculated, with the summation of the repulsive and attractive components of each of these interaction types providing the total intermolecular interaction energy.
solvent interactions were examined using intermolecular grid search methods,37,38 with a spatial grid defined around a central target molecule, Fig. 3. A grid optimisation was performed and an orthogonal grid shape with size 15, 15 and 35 Å in the X, Y and Z planes, respectively was found to be optimal for energy calculations. In each plane, the number of grid points was defined with 8, 8, 10 steps of grid points on the X, Y and Z planes, respectively. This provided a grid with a total number of 891 points, Fig. 3. During the intermolecular interaction energy calculation procedure, a probe molecule was placed on each point of the grid and rotated through a set of Euler angles, which were set at 4° for the x-axis, y-axis and z-axis. This resulted in a heterogeneous six-dimensional search space, and at each point within this the interaction energy between the probe and target molecules was calculated using an atom–atom approach, with parameters from the Momany intermolecular potential.16,39 Intermolecular interactions in the form of van der Waals, hydrogen bonding and electrostatic interactions were calculated, with the summation of the repulsive and attractive components of each of these interaction types providing the total intermolecular interaction energy.
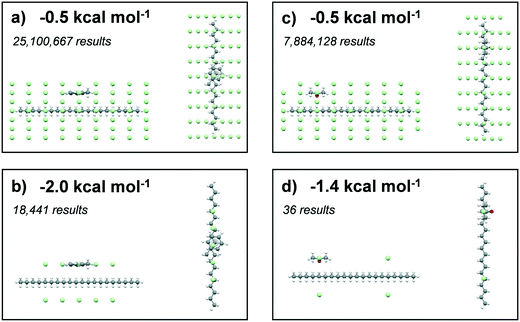
The solvating power of toluene and acetone to eicosane was assessed by comparison of the intermolecular interaction strengths of the solvents (probes) with eicosane (target). A low-pass energy filter was be applied to remove interactions below given interaction strengths, which were set at −0.5, −1.0, −1.5 and 2.0 kcal mol−1 for toluene interactions and −0.5, −1.0, −1.2 and 1.4 kcal mol−1 for acetone interactions. The more negative energy filters highlighted the most favourable interaction sites with an eicosane molecule. A total of 331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986
986![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 points (location + rotation) were searched for each simulation.
600 points (location + rotation) were searched for each simulation.
All possible solvent and solute intermolecular interactions within the solution phase (eicosane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eicosane, eicosane
eicosane, eicosane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene, eicosane
toluene, eicosane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone, toluene
acetone, toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene, acetone
toluene, acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone and toluene
acetone and toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone) were calculated using the intermolecular grid search method. A low-pass energy filter of −0.5 kcal mol−1 was used to screen out the lowest energy interactions with the screen resulting in the calculation of over 4000 possible intermolecular interaction energies for each interaction type within the solution phase.
acetone) were calculated using the intermolecular grid search method. A low-pass energy filter of −0.5 kcal mol−1 was used to screen out the lowest energy interactions with the screen resulting in the calculation of over 4000 possible intermolecular interaction energies for each interaction type within the solution phase.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone mixed solvent ratios of 0
acetone mixed solvent ratios of 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 5
20, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15, 10
15, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 15
10, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 20
5 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 molecules. Software procedures required one set of solvent
0 molecules. Software procedures required one set of solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute interactions to be calculated prior to the other. A previous study demonstrated that, in solubility mismatched mixed-solvent solutions, such as the system studied here, the local solvation environment of a nucleating solute would be likely to be dominated by the strongest solvating solvent, due to the much higher intermolecular interaction strengths.17 Therefore, for the current procedure the interactions of toluene molecules with eicosane were calculated first, followed by the acetone molecules. Whilst this molecular modelling technique provides an attractive and representative molecular-scale assessment as to likely solute
solute interactions to be calculated prior to the other. A previous study demonstrated that, in solubility mismatched mixed-solvent solutions, such as the system studied here, the local solvation environment of a nucleating solute would be likely to be dominated by the strongest solvating solvent, due to the much higher intermolecular interaction strengths.17 Therefore, for the current procedure the interactions of toluene molecules with eicosane were calculated first, followed by the acetone molecules. Whilst this molecular modelling technique provides an attractive and representative molecular-scale assessment as to likely solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent ordering within the solution, it is clearly limited by the fixed interaction procedure imposed by the chosen grid size that neither directly allows for the effects of molecular conformational flexibility nor deals with the random solute
solvent ordering within the solution, it is clearly limited by the fixed interaction procedure imposed by the chosen grid size that neither directly allows for the effects of molecular conformational flexibility nor deals with the random solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions, which might be expected within a mixed-solvent/antisolvent system, as studied here.
solvent interactions, which might be expected within a mixed-solvent/antisolvent system, as studied here.
The overall cluster structures generated were optimised using the Forcite module within Biovia Materials Studio. The SMART algorithm and a very fine tolerance was used to distinguish intra and inter-molecular interactions, ensuring solvation energies could be determined. For this, Gasteiger40,41 atom point charges were utilised. All structures were visualised using the CCDC's Mercury42 software package.
3. Results
3.1. Assessment of solubility and crystallisability
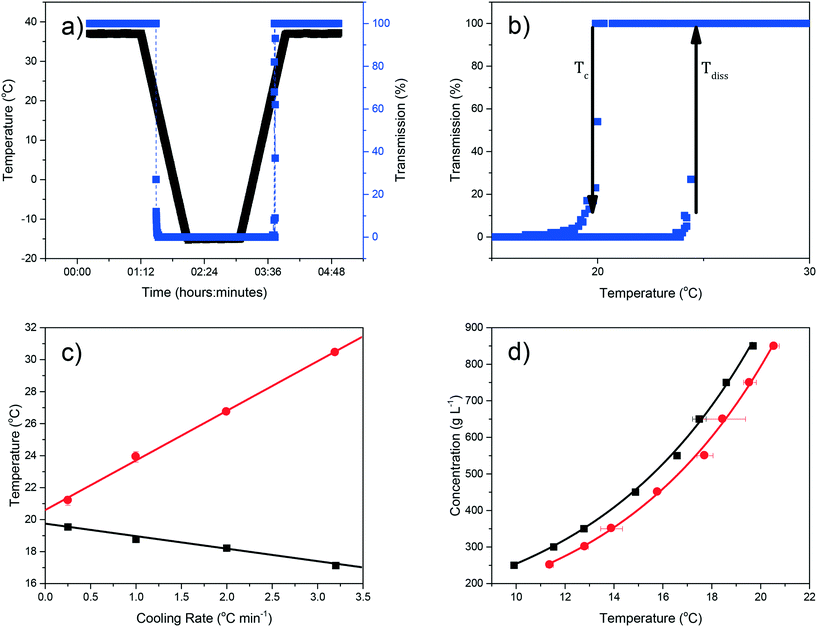
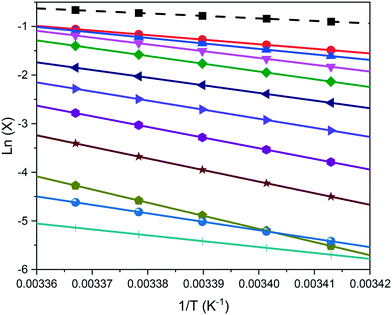
Examples of polythermal heating–cooling and turbidity profiles used for the temperature cycles are displayed in Fig. 4(a) and (b), highlighting the determination of Tdiss and Tc. The equilibrium solubility (Te) and supersolubility (Tc,l) temperatures obtained from extrapolation of Tdiss and Tc back to 0 °C min−1 are given in Table 1, together with their MSZW (ΔTc) for eicosane crystallising from toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone mixture solutions. Examples of the linear regression plots of Tdiss and Tcvs. q together with their standard deviation values from five repeats and the resulting solubility–supersolubility curves are given in Fig. 4(c) and (d), respectively. Experimental data from all of the experiments is provided in ESI† S1. To our knowledge, no current open-literature data is available on the solubility in the ternary system studied. All the solutions measured in this study showed high repeatability from five repeats of cycling experiments, with low standard deviation values.
acetone mixture solutions. Examples of the linear regression plots of Tdiss and Tcvs. q together with their standard deviation values from five repeats and the resulting solubility–supersolubility curves are given in Fig. 4(c) and (d), respectively. Experimental data from all of the experiments is provided in ESI† S1. To our knowledge, no current open-literature data is available on the solubility in the ternary system studied. All the solutions measured in this study showed high repeatability from five repeats of cycling experiments, with low standard deviation values.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone solvent mixture solutions, together with values of the slopes of the linear regressions of ln
acetone solvent mixture solutions, together with values of the slopes of the linear regressions of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ucvs. ln
ucvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q plots for the range of solvent compositions studied, with the resultant nucleation mechanism determined from the “rule of three” KBHR analysis. The ‘*’ denotes a low correlation fitting and as such the analysis has a lower confidence value and may be potentially a less reliable result
q plots for the range of solvent compositions studied, with the resultant nucleation mechanism determined from the “rule of three” KBHR analysis. The ‘*’ denotes a low correlation fitting and as such the analysis has a lower confidence value and may be potentially a less reliable result
| Conc. (g L−1) | T c,l (°C) | T e (°C) | MSZW (°C) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ucvs. ln ucvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q slope q slope |
Nucleation mechanism | Conc. (g L−1) | T c,l (°C) | T e (°C) | MSZW (°C) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ucvs. ln ucvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q slope q slope |
Nucleation mechanism |
|---|---|---|---|---|---|---|---|---|---|---|---|
| y = 0 | y = 0.14 | ||||||||||
| 250 | 9.92 | 11.37 | 1.46 | 2.87 | IN | 200 | 10.39 | 11.85 | 1.46 | 2.80 | IN |
| 350 | 12.78 | 13.90 | 1.13 | 2.51 | IN | 300 | 13.47 | 14.46 | 0.98 | 2.26 | IN |
| 450 | 14.88 | 15.79 | 0.91 | 2.25 | IN | 400 | 15.47 | 16.48 | 1.01 | 2.37 | IN |
| 550 | 16.58 | 17.72 | 1.14 | 2.45 | IN | 500 | 16.57 | 17.82 | 1.26 | 3.15 | PN* |
| y = 0.26 | y = 0.38 | ||||||||||
| 200 | 12.81 | 14.30 | 1.49 | 3.50 | PN | 200 | 15.05 | 16.51 | 1.47 | 2.87 | IN |
| 300 | 15.45 | 16.80 | 1.35 | 2.87 | IN | 300 | 17.61 | 18.36 | 0.75 | 2.05 | IN |
| 400 | 17.18 | 18.24 | 1.06 | 2.37 | IN | 400 | 18.87 | 19.74 | 0.88 | 2.41 | IN |
| 500 | 18.70 | 19.20 | 0.50 | 1.64 | IN | 500 | 20.20 | 20.94 | 0.74 | 2.01 | IN |
| y = 0.49 | y = 0.59 | ||||||||||
| 150 | 15.42 | 17.09 | 1.67 | 2.82 | IN | 150 | 18.39 | 19.88 | 1.49 | 2.70 | IN |
| 250 | 18.69 | 19.76 | 1.07 | 2.32 | IN | 250 | 20.64 | 22.37 | 1.73 | 3.08 | PN |
| 350 | 20.26 | 21.28 | 1.02 | 2.53 | IN | 350 | 21.94 | 23.67 | 1.74 | 3.41 | PN |
| 450 | 21.31 | 22.67 | 1.36 | 2.67 | IN | 450 | 22.97 | 24.58 | 1.61 | 3.32 | PN |
| y = 0.68 | y = 0.77 | ||||||||||
| 150 | 20.80 | 22.44 | 1.65 | 3.16 | PN | 100 | 21.59 | 23.23 | 1.64 | 3.18 | PN |
| 250 | 22.63 | 24.16 | 1.53 | 3.58 | PN | 200 | 24.29 | 25.84 | 1.55 | 3.27 | PN |
| 350 | 23.80 | 25.75 | 1.95 | 3.82 | PN | 300 | 25.45 | 26.92 | 1.47 | 3.04 | PN |
| 450 | 24.58 | 26.41 | 1.83 | 3.25 | PN | 400 | 26.02 | 28.22 | 2.20 | 3.91 | PN |
| y = 0.85 | y = 0.93 | ||||||||||
| 75 | 23.17 | 25.00 | 1.82 | 3.61 | PN | 20 | 18.80 | 20.60 | 1.81 | 2.84 | IN |
| 175 | 26.27 | 28.16 | 1.89 | 4.00 | PN | 60 | 25.09 | 26.85 | 1.77 | 3.74 | PN |
| 275 | 27.29 | 29.34 | 2.05 | 3.84 | PN | 100 | 27.29 | 29.00 | 1.71 | 3.70 | PN |
| 375 | 27.90 | 29.98 | 2.09 | 4.04 | PN | 140 | 28.36 | 30.18 | 1.83 | 3.92 | PN |
| y = 1 | |||||||||||
| 5 | 11.92 | 13.08 | 1.16 | 1.68 | IN | ||||||
| 15 | 20.27 | 21.53 | 1.26 | 2.28 | IN | ||||||
| 25 | 23.48 | 24.76 | 1.28 | 4.16 | PN | ||||||
| 35 | 25.81 | 26.57 | 0.76 | 1.95 | IN | ||||||
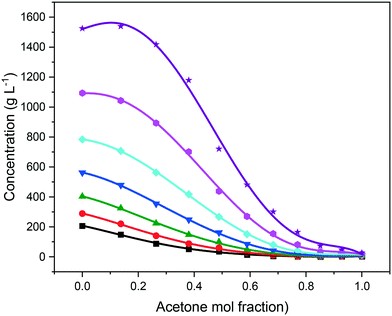
As expected, the solubility of eicosane was found to be highest in toluene, with increasing acetone composition causing a decrease in solubility over the full range of compositions studied, as shown in Fig. 5. This can be justified in terms of the adage ‘like-dissolves-like’, with eicosane being a negligibly polar molecule and as such being more likely to dissolve in a non-polar solvent. Toluene has a small dipole moment (0.36 D)43 in comparison to acetone (2.90 D),44 therefore, eicosane can be expected to have greater affinity towards toluene rather than acetone molecules in solution, consistent with a higher solubility with increased toluene composition. The limited solvation power of acetone perhaps represents an antisolvent, as opposed to a true solvent for eicosane, thus demonstrating the ability of this system to be used both as an initial solvent blend for crystallisation and/or for an antisolvent crystallisation methodology. However, at lower solution temperatures, below around 15 °C, and above an acetone mol fraction (y) of 0.85, the eicosane solubility was found to increase with small additions of acetone, perhaps suggesting alterations in solution structure that could influence solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions and hence eicosane solubility.
solvent interactions and hence eicosane solubility.
Previous studies have highlighted that in mixed-solvent solutions solute solubility can increase with small additions of lower solubility solvents,7,15 suggesting that the lower solubility solvent has the ability to solvate parts of the solute molecule that the higher solubility solvent cannot, hence contributing to and enhancing the overall solution solvation power of the mixed solvent system. This behaviour was observed for solution eicosane in toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone mixed-solvent solutions at 25 °C. However, below this temperature the addition of acetone was found to only reduce eicosane solubility, perhaps demonstrating acetone's comparatively poor ability to solvate the eicosane molecule when compared to toluene. The temperature dependence of this behaviour is interesting in that it demonstrates, perhaps, that a critical level of molecular mobility should be reached in order for the lower solubility solvent to access potential solute solvation sites that are not fully solvated by the higher solubility solvent within the mixed-solvent environment.
acetone mixed-solvent solutions at 25 °C. However, below this temperature the addition of acetone was found to only reduce eicosane solubility, perhaps demonstrating acetone's comparatively poor ability to solvate the eicosane molecule when compared to toluene. The temperature dependence of this behaviour is interesting in that it demonstrates, perhaps, that a critical level of molecular mobility should be reached in order for the lower solubility solvent to access potential solute solvation sites that are not fully solvated by the higher solubility solvent within the mixed-solvent environment.
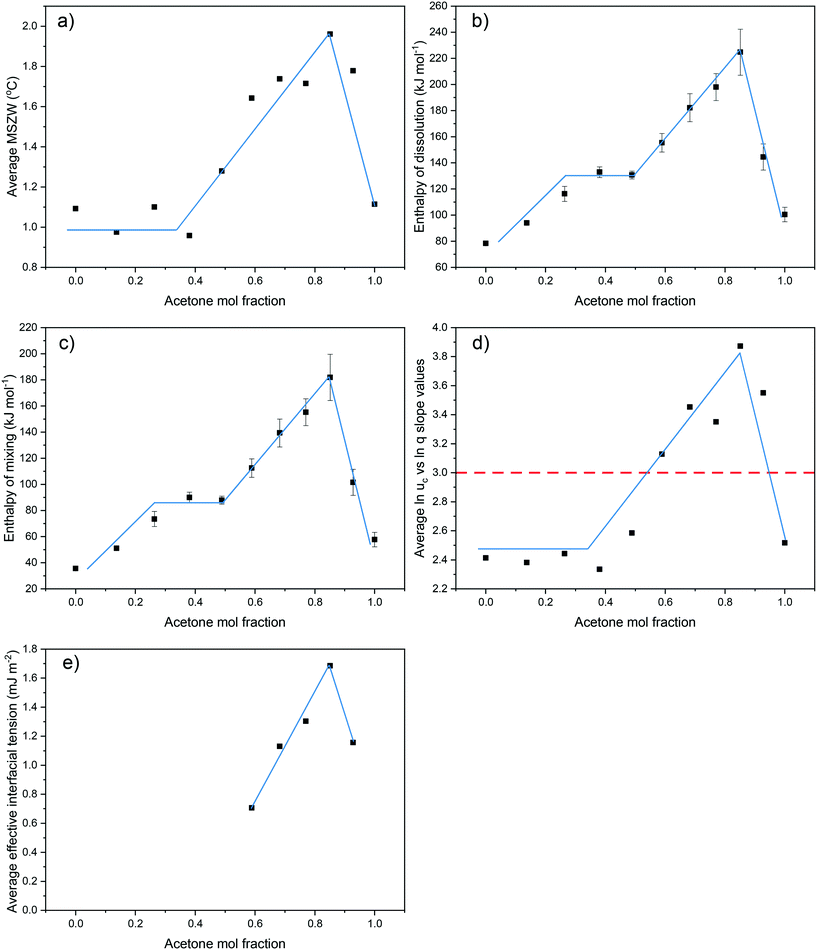
MSZW data provides an indication of the ease of which a solution overcomes its inherent nucleation barrier and crystallises, with a narrower MSZW being consistent with a tendency towards easier nucleation. For all concentrations and compositions studied, the MSZWs were found to be around 0.5–2.2 °C. These are in broad agreement with previous work,25,45–48 but quite small when compared to other typical organic solution phase systems.20,49 For solution compositions from 0 < y < 0.49 and 0.93 < y < 1 the MSZW was found, in general, to be roughly inversely proportional to the solution concentration. This would be consistent with nucleation being easier with a higher number of solute molecules within solution, which might be expected given that this would offer a greater chance for solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute interactions. In contrast, for solutions within the compositional range of 0.59 < y < 0.85, the opposite trend was observed, with, in general, an increase in MSZW with increasing concentration. This could indicate changes in solution chemistry and nucleation mechanisms over the compositional ranges studied, perhaps reflecting the changing nature of the intermolecular interactions within the solution state.
solute interactions. In contrast, for solutions within the compositional range of 0.59 < y < 0.85, the opposite trend was observed, with, in general, an increase in MSZW with increasing concentration. This could indicate changes in solution chemistry and nucleation mechanisms over the compositional ranges studied, perhaps reflecting the changing nature of the intermolecular interactions within the solution state.
3.2. Analysis of the solution thermodynamics
van't Hoff analysis provides further indication of the nature of the solution behaviour in terms of the impact of solvent and compositional effects. The van't Hoff plots, as a function of solvent composition, were found to fit well by linear regression for all the solutions studied, as shown in Fig. 6, consistent with no change in solute form. The enthalpy (ΔHdiss) and entropy (ΔSdiss) of dissolution values, enthalpy (ΔHmix) and entropy (ΔSmix) of mixing values and the activity coefficients (ϒ) calculated from van't Hoff analysis are summarised in Table 2.| Acetone mol fraction (y) | Enthalpy of dissolution (kJ mol−1) | Entropy of dissolution (kJ mol−1 K−1) | Enthalpy of mixing (kJ mol−1) | Entropy of mixing (kJ mol−1 K−1) | Concentration range (g L−1) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϒ = aT + c ϒ = aT + c |
|---|---|---|---|---|---|---|
| 0 | 78.36 | 0.255 | 35.50 | 0.116 | 250–850 | −0.05 T + 1.60 |
| 0.14 | 93.99 | 0.307 | 51.13 | 0.169 | 200–800 | −0.07 T + 2.16 |
| 0.26 | 116.28 | 0.382 | 73.42 | 0.243 | 200–500 | −0.11 T + 3.01 |
| 0.38 | 132.89 | 0.436 | 90.02 | 0.297 | 200–500 | −0.13 T + 3.76 |
| 0.49 | 130.71 | 0.425 | 87.85 | 0.286 | 150–450 | −0.12 T + 4.12 |
| 0.59 | 155.35 | 0.504 | 112.48 | 0.365 | 150–450 | −0.16 T + 5.32 |
| 0.68 | 182.22 | 0.590 | 139.36 | 0.452 | 150–450 | −0.19 T + 6.64 |
| 0.77 | 198.03 | 0.638 | 155.17 | 0.500 | 100–400 | −0.21 T + 7.73 |
| 0.85 | 224.72 | 0.721 | 181.86 | 0.582 | 75–375 | −0.24 T + 9.38 |
| 0.93 | 144.45 | 0.448 | 101.58 | 0.309 | 20–140 | −0.14 T + 7.24 |
| 1 | 100.52 | 0.296 | 57.65 | 0.157 | 5–35 | −0.08 T + 6.41 |
Less than ideal behaviour was observed for all the solutions with ϒ greater than 1 for the temperature range studied. This behaviour is consistent with a solution structure whereby homogeneous (solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute and solvent
solute and solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent) intermolecular interactions are preferred with respect to heterogeneous (solute
solvent) intermolecular interactions are preferred with respect to heterogeneous (solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent) intermolecular interactions. In line with the trend observed for the solubility studies, toluene solutions were found to show the most ideal behaviour, with larger deviations from ideal behaviour being observed with increasing acetone composition. This behaviour is consistent with toluene having much stronger intermolecular interactions with eicosane comparative to acetone, with high content acetone solutions not only having likely stronger solute
solvent) intermolecular interactions. In line with the trend observed for the solubility studies, toluene solutions were found to show the most ideal behaviour, with larger deviations from ideal behaviour being observed with increasing acetone composition. This behaviour is consistent with toluene having much stronger intermolecular interactions with eicosane comparative to acetone, with high content acetone solutions not only having likely stronger solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute interactions, but also likely stronger solvent
solute interactions, but also likely stronger solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions, making for easier eicosane desolvation and hence crystallisation from solution. This is evidenced in the calculated ΔHdiss values, in Table 2, highlighting that, in general, ΔHdiss is larger at the higher solution acetone compositions.
solvent interactions, making for easier eicosane desolvation and hence crystallisation from solution. This is evidenced in the calculated ΔHdiss values, in Table 2, highlighting that, in general, ΔHdiss is larger at the higher solution acetone compositions.
However, ΔHdiss was found to decrease with increasing acetone composition above y = 0.85, which, given the low solubility of eicosane in high acetone compositions solutions, would seem to be counter-intuitive. However, the change in van't Hoff plot slopes for these solutions suggest decreasing effects of enthalpy and entropy within solution. This is corroborated with a similar trend in the enthalpy of mixing results, suggesting that the solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions decreased in strength with increasing acetone solution content, until a critical acetone composition created a change in the ratio between solute
solvent interactions decreased in strength with increasing acetone solution content, until a critical acetone composition created a change in the ratio between solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solute/solvent
solute/solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent and solute
solvent and solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions.
solvent interactions.
Interestingly, the slopes of the van't Hoff plots were found to be relatively similar for solutions with excess toluene and for higher solution acetone content above y = 0.85. Deviations found for the mixed-solvent solutions with excess acetone content demonstrated changing temperature dependence of solution activity, and as such, solution structure, as a function of composition, as outlined by the varying values of aT in Table 2.
Values of ΔHdiss, ΔSdiss and the range of ϒ calculated for eicosane in toluene solution were close to those calculated in a previous study by Tang et al.,25 which focussed on hexadecane and octadecane mixtures crystallising from three fuel representative solvents, including toluene. Values of around 69 kJ mol−1, 0.24 kJ mol−1 K−1 and the range 1.40–1.59 were calculated in the aforementioned study, for ΔHdiss, ΔSdiss and the range of ϒ over the concentration range studied, respectively.
3.3. Analysis of the nucleation kinetics
For eicosane in mixed toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone solutions the resultant nucleation mechanisms, detailed in Table 1, were found to vary as a function of solution composition and concentration, in line with the trends observed for the solution thermodynamics and MSZW analysis. For solution compositions from 0 < y < 0.49 and y = 1, the nucleation mechanism was found to be predominantly IN, which is consistent with a previous study that focussed on the nucleation of hexandecane
acetone solutions the resultant nucleation mechanisms, detailed in Table 1, were found to vary as a function of solution composition and concentration, in line with the trends observed for the solution thermodynamics and MSZW analysis. For solution compositions from 0 < y < 0.49 and y = 1, the nucleation mechanism was found to be predominantly IN, which is consistent with a previous study that focussed on the nucleation of hexandecane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) octadecane mixtures from single solvent solutions, with both alkanes being found to predominantly nucleate via IN pathway.22 In contrast, for solution compositions ranging from 0.59 < y < 0.93, the predominant nucleation mechanism was found to be PN.
octadecane mixtures from single solvent solutions, with both alkanes being found to predominantly nucleate via IN pathway.22 In contrast, for solution compositions ranging from 0.59 < y < 0.93, the predominant nucleation mechanism was found to be PN.
For the PN cases, the calculated effective interfacial tensions, critical nuclei radius and number of molecules within the critical nuclei are given in Table 3. Comparatively, low values of effective interfacial tension, ranging from 0.38–1.94, were calculated for all PN systems studied, consistent with data on other long-chain hydrocarbons,28 and consistent with the nucleation process being predominantly heterogeneous. The latter may also explain the low calculated values for the critical nucleus size and number of molecules within the critical nucleus. Nonetheless, the overall behaviour of interfacial tension as a function of composition was found to closely mirror the variations observed for crystallisability and solution thermodynamics over the range of compositions studied.
| Conc. (g L−1) | γ eff (mJ m−2) | r* (nm) | i* |
|---|---|---|---|
| y = 0.59 | |||
| 250 | 0.38 | 0.28–0.12 | 0.18–0.01 |
| 350 | 0.86 | 0.62–0.29 | 1.95–0.20 |
| 450 | 0.87 | 0.62–0.28 | 2.20–0.19 |
| y = 0.68 | |||
| 150 | 0.89 | 0.51–0.23 | 1.10–0.10 |
| 250 | 1.19 | 0.73–0.35 | 3.26–0.37 |
| 350 | 1.41 | 0.72–0.36 | 3.14–0.40 |
| 450 | 1.02 | 0.54–0.26 | 1.33–0.14 |
| y = 0.77 | |||
| 100 | 1.15 | 0.56–0.26 | 1.44–0.14 |
| 200 | 1.16 | 0.61–0.28 | 1.92–0.19 |
| 300 | 0.96 | 0.52–0.23 | 1.20–0.10 |
| 400 | 1.94 | 0.72–0.40 | 3.06–0.53 |
| y = 0.85 | |||
| 75 | 1.54 | 0.64–0.32 | 2.23–0.28 |
| 175 | 1.72 | 0.73–0.39 | 3.19–0.50 |
| 275 | 1.62 | 0.67–0.34 | 2.48–0.32 |
| 375 | 1.86 | 0.71–0.38 | 3.03–0.46 |
| y = 0.93 | |||
| 60 | 1.19 | 0.81–0.40 | 4.46–0.55 |
| 100 | 1.00 | 0.77–0.39 | 3.82–0.50 |
| 140 | 1.28 | 0.84–0.45 | 4.89–0.77 |
3.4. Compositional trends
Examination of the results of the crystallisability, solution thermodynamics and nucleation kinetics data clearly demonstrate consistent and concurrent trends over the full compositional range for the eicosane in toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone mixed-solvent system. For all solution compositions, the average MSZWs, over the range of concentrations studied, were found to increase for compositions ranging from 0 < y < 0.85. This was subsequently followed by a decrease in average MSZW with increasing solution acetone content to a solution composition of y = 1. This same trend was observed for values of enthalpies of dissolution and mixing, the average slope values from linear regressions fitted to plots of ln
acetone mixed-solvent system. For all solution compositions, the average MSZWs, over the range of concentrations studied, were found to increase for compositions ranging from 0 < y < 0.85. This was subsequently followed by a decrease in average MSZW with increasing solution acetone content to a solution composition of y = 1. This same trend was observed for values of enthalpies of dissolution and mixing, the average slope values from linear regressions fitted to plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ucvs. ln
ucvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q, over the full compositional range studied and the values of effective interfacial tension, Fig. 7. This demonstrates a clear link between the crystallisability, solution thermodynamics and nucleation kinetics and mechanism, which are all dominated by the solution structure.
q, over the full compositional range studied and the values of effective interfacial tension, Fig. 7. This demonstrates a clear link between the crystallisability, solution thermodynamics and nucleation kinetics and mechanism, which are all dominated by the solution structure.
3.5. Intermolecular grid-search modelling
Results summarising the calculated solvation sites for a single eicosane molecule solvated with toluene and acetone, using different low-pass energy cut-off filters, are given in Fig. 8. Examination of the energy-filtered data reveals that both toluene and acetone can easily solvate the surfaces of eicosane, with the strongest binding interactions with the carbon backbone of the eicosane molecule, where the number of potential atom–atom van der Waals interactions is highest. However, higher energy cut-off filtering revealed that acetone's solvation propensity diminished quite rapidly. In contrast, toluene was found to maintain strong solvation propensity over the majority of the eicosane molecule, even at the highest energy cut-offs. The full solvation site analysis is given in ESI† S3.
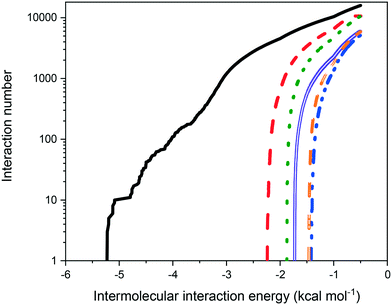
Fig. 9 shows the distribution of binding site energies as a function of the number of calculated interactions. As might be expected on the basis of molecular weight, the strength of intermolecular interaction energies of eicosane with other eicosane molecules were much higher than for other possible solution interaction types, correlating well with the less than ideal solution behaviour observed. Furthermore, in terms of solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions, toluene was found to interact more strongly with eicosane than acetone was, in line with measured relative solubilities, with acetone
solvent interactions, toluene was found to interact more strongly with eicosane than acetone was, in line with measured relative solubilities, with acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eicosane interactions found to be the weakest interaction type calculated, suggesting that in solution acetone may have been more likely to interact with either itself or toluene, instead of eicosane. This is in line with calculated atomic fractional charges for the studied molecules, provided in ESI† S2, which demonstrate increasing molecular polarisability from eicosane < toluene < acetone. Acetone, therefore, would be expected to have stronger electrostatic interactions with itself or toluene than with eicosane in the solution environment.
eicosane interactions found to be the weakest interaction type calculated, suggesting that in solution acetone may have been more likely to interact with either itself or toluene, instead of eicosane. This is in line with calculated atomic fractional charges for the studied molecules, provided in ESI† S2, which demonstrate increasing molecular polarisability from eicosane < toluene < acetone. Acetone, therefore, would be expected to have stronger electrostatic interactions with itself or toluene than with eicosane in the solution environment.
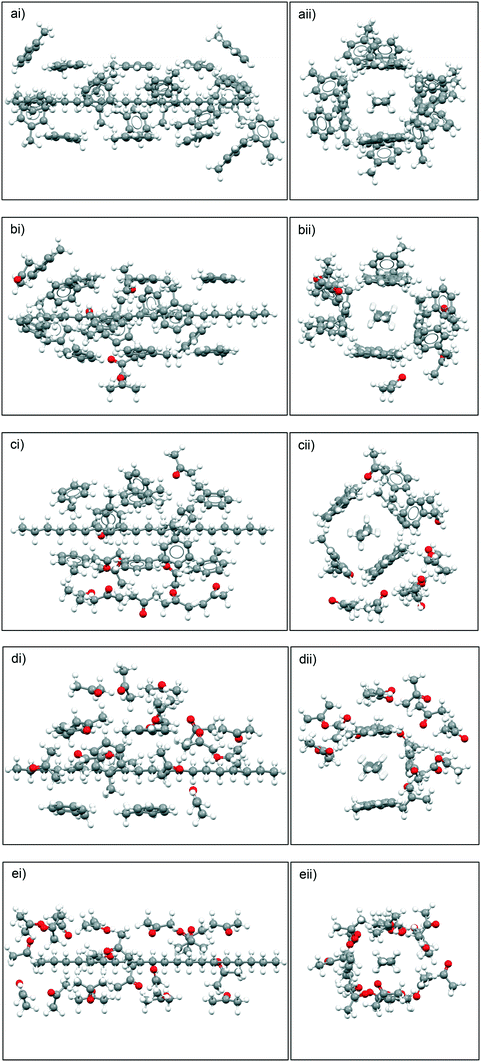
Fig. 10 summarises the results of the solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent cluster building simulations, highlighting the predicted solvation shell structures based upon different toluene
solvent cluster building simulations, highlighting the predicted solvation shell structures based upon different toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone ratios. The simulation data reveals that for the 10
acetone ratios. The simulation data reveals that for the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and 15
10 and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ratios of toluene
5 ratios of toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone, the acetone molecules preferentially bind to the toluene molecules, creating, what is effectively, a ‘second shell’ around the primary toluene solvation shell around eicosane rather than directly solvating eicosane by filling the potential empty solvation sites.
acetone, the acetone molecules preferentially bind to the toluene molecules, creating, what is effectively, a ‘second shell’ around the primary toluene solvation shell around eicosane rather than directly solvating eicosane by filling the potential empty solvation sites.
For the 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 ratio of toluene
15 ratio of toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone intermolecular grid search results the acetone molecules were still found to create a ‘second’ solvation shell around the toluene molecules that were solvating the eicosane molecule, but some free eicosane solvation sites were filled with acetone molecules. This suggests that when the ratio of acetone to toluene was high enough, the acetone molecules would more strongly solvate the eicosane molecule. Therefore, for the studied solutions, above a critical acetone composition the disruptive solvent
acetone intermolecular grid search results the acetone molecules were still found to create a ‘second’ solvation shell around the toluene molecules that were solvating the eicosane molecule, but some free eicosane solvation sites were filled with acetone molecules. This suggests that when the ratio of acetone to toluene was high enough, the acetone molecules would more strongly solvate the eicosane molecule. Therefore, for the studied solutions, above a critical acetone composition the disruptive solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interaction effect is likely to be somewhat overcome.
solvent interaction effect is likely to be somewhat overcome.
Examination of the calculated solvation energies based on these cluster structures, as well as the intermolecular solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interaction energies within the solvation shell are given in Table 4. In general, the total solvation energy was found to decrease with an increase in acetone composition, in line with the trend observed in the measured solubility over the mixed-solvent compositional range studied. However, a slight increase in solvation energy was calculated from a toluene
solvent interaction energies within the solvation shell are given in Table 4. In general, the total solvation energy was found to decrease with an increase in acetone composition, in line with the trend observed in the measured solubility over the mixed-solvent compositional range studied. However, a slight increase in solvation energy was calculated from a toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone ratio of 5
acetone ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 to 0
15 to 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20. This correlates well to the observed solubility behaviour at lower solution temperatures, whereby eicosane solubility increased from solutions with a high acetone composition to pure acetone solutions and suggests a changing nature of solvent
20. This correlates well to the observed solubility behaviour at lower solution temperatures, whereby eicosane solubility increased from solutions with a high acetone composition to pure acetone solutions and suggests a changing nature of solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions affecting solvation power.
solvent interactions affecting solvation power.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone molecular ratios
acetone molecular ratios
Toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone molecular ratio acetone molecular ratio |
Interaction energy (kcal mol−1) | |
|---|---|---|
| Total solvation | Toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone acetone |
|
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
−54.71 | — |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
−52.39 | −27.80 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
−46.54 | −41.96 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 |
−38.84 | −30.69 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
−43.72 | — |
The solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions in the solvation shell were found to be strongest for 10
solvent interactions in the solvation shell were found to be strongest for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 toluene
10 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone with decreased total intermolecular interaction energies for 5
acetone with decreased total intermolecular interaction energies for 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 and 15
15 and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 toluene
5 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone ratios. This further suggests that strong toluene
acetone ratios. This further suggests that strong toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone interactions were present in the mixed solvent solutions, with a decrease in interaction intensity when one of the solvents is in excess in solution.
acetone interactions were present in the mixed solvent solutions, with a decrease in interaction intensity when one of the solvents is in excess in solution.
4. Discussion
Intermolecular grid-search results suggest that acetone molecules could be more likely to ‘solvate’ toluene molecules and disrupt the solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions, until a critical acetone composition is reached whereby acetone molecules solvate eicosane more readily. These predictions provide insight into the increasing enthalpies of dissolution and mixing values up to a solution composition of y = 0.85, due to strong interactions between acetone and toluene in the solvation shell, decreasing the solvation power towards eicosane and, as such, decreasing solute
solvent interactions, until a critical acetone composition is reached whereby acetone molecules solvate eicosane more readily. These predictions provide insight into the increasing enthalpies of dissolution and mixing values up to a solution composition of y = 0.85, due to strong interactions between acetone and toluene in the solvation shell, decreasing the solvation power towards eicosane and, as such, decreasing solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interaction strengths, followed by a decrease in enthalpic values, due to increased acetone solvation.
solvent interaction strengths, followed by a decrease in enthalpic values, due to increased acetone solvation.
This behaviour also provides a potential insight into the similar trends in MSZW and changes in the nucleation mechanism. An IN pathway can represent solutions containing stable prenucleation clusters and at a critical level of supersaturation, there is sufficient driving force for nucleation to occur for all clusters present. Practically, this represents the case whereby all nucleation events within the solution occur at one instance, with only crystal growth occurring after this stage. In contrast, PN suggests that the prenucleation clusters could have a lower stability, therefore only certain clusters would be able to overcome the free energy barrier required for nucleation to occur at one instance of time, resulting in concomitant crystal nucleation and growth processes occurring within solution as crystallisation progresses in the system.
For the PN systems, the solution environments had an excess of acetone molecules, with respect to toluene. This change in nucleation mechanism perhaps suggests that when acetone is in excess in solution, there was a more complicated solution structure, whereby the solvation layer around eicosane molecules is more disordered and perhaps more polar, containing a high number of heterogeneous and homogeneous solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions, in line with the grid-search results. Such a structure could disrupt the diffusive transport of eicosane molecules into the prenucleation clusters, seen when toluene is in excess, given acetone's limited intermolecular interactions with eicosane. This would have the effect of lowering the attachment frequency of eicosane to a growing cluster, hence reducing the nucleation rate constant, KJ, and, as such, the rate of nucleation (eqn (12)). Thus, only some of the eicosane clusters might reach a critical cluster size and be able to nucleate, before a stable equilibrium in solution was reached. This would result in the case of nucleation events occurring over time, creating concomitant nucleation and growth processes at different locations within solution, in line with the PN mechanism.
solvent interactions, in line with the grid-search results. Such a structure could disrupt the diffusive transport of eicosane molecules into the prenucleation clusters, seen when toluene is in excess, given acetone's limited intermolecular interactions with eicosane. This would have the effect of lowering the attachment frequency of eicosane to a growing cluster, hence reducing the nucleation rate constant, KJ, and, as such, the rate of nucleation (eqn (12)). Thus, only some of the eicosane clusters might reach a critical cluster size and be able to nucleate, before a stable equilibrium in solution was reached. This would result in the case of nucleation events occurring over time, creating concomitant nucleation and growth processes at different locations within solution, in line with the PN mechanism.
In contrast, for the IN cases the solutions either had an excess toluene component with respect to acetone or a single solvent environment, with potentially less disruptive heterogeneous solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent interactions and hence a lower barrier to the formation of stable prenucleation clusters within solution. Therefore, a distribution of stable prenucleation clusters could be able to form prior to the nucleation stage, once a critical level of supersaturation corresponding to the limit of the MSZW had been reached, with all clusters nucleating at once. Although speculative, at this stage such a model could also explain the increase in MSZW with increasing acetone composition, and as such a lower ease of crystallisation, until a critical acetone composition was reached, in which this behaviour was reversed. Further support for this comes with the calculated values of effective interfacial tension, which mirror the behaviour of the MSZW with mixed-solvent composition, notably in such a case that a higher level of supersaturation would be needed to overcome the energy barrier required to create a solid nucleus surface. This suggests that strong interactions between acetone and toluene molecules might lead to weaker interactions with eicosane clusters, thereby increasing the barrier to the formation of nuclei surfaces, driving up the effective interfacial tension and lowering the crystallisability. This would be consistent with an increase in the thermodynamic parameter b associated with the nucleation rate expression (eqn (12)), which would reduce the rate of nucleation of eicosane in these solutions. This, coupled with a reduction in the nucleation rate constant, would essentially create a more thermodynamically controlled nucleation process, more consistent with the progressive nucleation pathway.
solvent interactions and hence a lower barrier to the formation of stable prenucleation clusters within solution. Therefore, a distribution of stable prenucleation clusters could be able to form prior to the nucleation stage, once a critical level of supersaturation corresponding to the limit of the MSZW had been reached, with all clusters nucleating at once. Although speculative, at this stage such a model could also explain the increase in MSZW with increasing acetone composition, and as such a lower ease of crystallisation, until a critical acetone composition was reached, in which this behaviour was reversed. Further support for this comes with the calculated values of effective interfacial tension, which mirror the behaviour of the MSZW with mixed-solvent composition, notably in such a case that a higher level of supersaturation would be needed to overcome the energy barrier required to create a solid nucleus surface. This suggests that strong interactions between acetone and toluene molecules might lead to weaker interactions with eicosane clusters, thereby increasing the barrier to the formation of nuclei surfaces, driving up the effective interfacial tension and lowering the crystallisability. This would be consistent with an increase in the thermodynamic parameter b associated with the nucleation rate expression (eqn (12)), which would reduce the rate of nucleation of eicosane in these solutions. This, coupled with a reduction in the nucleation rate constant, would essentially create a more thermodynamically controlled nucleation process, more consistent with the progressive nucleation pathway.
The resulting changes in nucleation behaviour and mechanism as a function of mixed-solvent composition, also align well with previous studies that have demonstrated that, in single solvent solutions, the IN mechanism is associated with stable prenucleation clusters in solution24 and a shift towards a PN pathway can be associated with a disruption of the ability of solutions to form stable clusters prior to nucleation.23 This demonstrates a wider applicability of the results outlined in this study towards other crystallising systems.
The changing nature of solution behaviour above a critical acetone solution content at around y = 0.85 could also represent increased solvent structuring in solution, as demonstrated by decreasing values of the entropy of dissolution and mixing. Acetone is known to structure through strong carbonyl intermolecular interactions in its crystal structure and liquid state,50 which could enable free interactions between the methyl groups and solute molecules within solutions, with a high concentration of acetone molecules. This could provide an additive solubilising effect towards eicosane in solution alongside the more strongly interacting toluene molecules, which could be responsible for the observed increases in solubility at lower solution temperatures, for solutions with a high acetone content above y = 0.85. However, further study is needed to investigate this possible behaviour.
5. Conclusions
Eicosane in mixed toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone solvent solutions was studied over a range of solution compositions from pure toluene to pure acetone, revealing comparatively small MSZWs for all solution compositions in comparison to other organic crystallising systems, highlighting their ease of crystallisability. A broadly inverse relationship between solution concentration and MSZW was found for solution compositions at acetone mol fractions (y) of 0 < y < 0.49 and 0.93 < y < 1. In contrast, the opposite relationship was observed for solution compositions of 0.53 < y < 0.85.
acetone solvent solutions was studied over a range of solution compositions from pure toluene to pure acetone, revealing comparatively small MSZWs for all solution compositions in comparison to other organic crystallising systems, highlighting their ease of crystallisability. A broadly inverse relationship between solution concentration and MSZW was found for solution compositions at acetone mol fractions (y) of 0 < y < 0.49 and 0.93 < y < 1. In contrast, the opposite relationship was observed for solution compositions of 0.53 < y < 0.85.
The solubility of eicosane was found, in general, to decrease with increasing solution acetone content. At higher solution temperatures, small additions of acetone to pure toluene solutions were found to increase solubility, whereas at lower solution temperatures this behaviour was not observed and when acetone was in excess, further additions of acetone increased solubility above a solution composition of y = 0.85. All solutions revealed less than ideal behaviour, with activity coefficient temperature dependency altering as a function of mixed-solvent composition. Both the enthalpies of dissolution and mixing were found to increase over the compositional range of 0 < y < 0.85, followed by a decrease with higher acetone content, demonstrating a change in solution chemistry above a critical solution acetone composition.
Intermolecular grid search results from energy cut-off calculations were in good agreement with the solubility findings, with toluene molecules being found to interact much more strongly with eicosane than did acetone molecules. The strongest solvation sites were found to be along the carbon backbone of the eicosane molecule, where closer atom–atom contacts and strong van der Waals interactions were readily available. Intermolecular interaction energies revealed eicosane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eicosane interactions to be the strongest, in line with the less than ideal behaviour observed for all solutions. Acetone was found to interact more strongly with itself and toluene than with eicosane, suggesting that it would have limited interaction with eicosane in a mixed-solvent solution environment.
eicosane interactions to be the strongest, in line with the less than ideal behaviour observed for all solutions. Acetone was found to interact more strongly with itself and toluene than with eicosane, suggesting that it would have limited interaction with eicosane in a mixed-solvent solution environment.
Analysis of nucleation kinetic data revealed that solution compositions in the range 0 < y < 0.49 and y = 1, nucleated via an IN mechanism, whilst in contrast, solution compositions ranging from 0.59 < y < 0.85 were found to predominantly nucleate via the PN pathway, the latter suggesting a more thermodynamically-controlled system. The kinetic and thermodynamic dependencies of the nucleation of these solutions were found to correlate to the dependency of the MSZW vs. the solution concentration behaviour observed. PN solutions crystallised with low effective interfacial tensions, in line with previous studies on alkane systems, but were found to increase with increasing acetone composition up to y = 0.85, above which, the effective interfacial was found to decrease again.
The key crystallisation process metrics were all found to follow the same consistent behaviour as a function of mixed-solvent composition, notably: MSZW, enthalpies of dissolution/mixing, interfacial tension and the balance between the thermodynamic and kinetic factors on the nucleation process, calculated by the IN/PN determination slopes. Analysis of solvation energies and cluster structures was found to provide an insight into the potential intermolecular clustering behaviour within this mixed-solvent solution, notably acetone interacts more strongly with toluene than with eicosane, with the latter not being effectively solvated by acetone molecules in the mixed-solvent solutions. A ‘cage’ of acetone molecules created due the stronger toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone interactions limited the ability of eicosane to form stable prenucleation clusters throughout solution, altering the nucleation mechanism from IN to PN when acetone was in excess. Above a critical acetone content this effect was overcome.
acetone interactions limited the ability of eicosane to form stable prenucleation clusters throughout solution, altering the nucleation mechanism from IN to PN when acetone was in excess. Above a critical acetone content this effect was overcome.
Overall, the solution chemistry and structure were found to directly relate to crystallisation behaviour and this was integrated within a methodological workflow, developed to aid future research into mixed solvent solution crystallisation processes.
5.1. Future work and current limitations
The molecular grid-search based modelling of indicative solution structure could be enhanced in future work through its integration with more atomistically detailed modelling molecular dynamic (MD) simulations, which would have the potential to provide a more complete and extended structural insight into the solution environment, associated with solvation by mixed solvent systems. Through this, the longer-range solution structure and its relationship, as well as its relationship with the solute mass transfer, could be directly related to the subsequent nucleation kinetics.Furthermore, small angle neutron scattering (SANS) of mixed-solvent systems using deuteration to confirm specific solvent species within the mixed-solvent environments, could potentially validate the solvation structural ordering proposed in this work.
Nomenclature
| a 1 | KBHR PN parameter |
| a 2 | KBHR PN parameter |
| b | Dimensionless thermodynamic parameter |
| ΔHdiss | Molar enthalpy of dissolution (kJ mol−1) |
| ΔHf | Enthalpy of fusion (kJ mol−1) |
| ΔHmix | Molar enthalpy of mixing (kJ mol−1) |
| i* | Number of molecules in the critical nucleus |
| J | Nucleation rate (nuclei m−3 s−1) |
| k | Boltzmann constant (m2 kg s−2 K−1) |
| K J | Nucleation rate constant (m−3 s−1) |
| k n | Nuclei numerical shape factor |
| λ | Molecular latent heat of crystallisation (J) |
| N det | Number of crystallites at the detection point |
| q | Cooling rate (°C min−1) |
| q 0 | KBHR PN parameter |
| R | Ideal gas constant (J K−1 mol−1) |
| r* | Critical nucleus radius (m) |
| ΔSdiss | Molar entropy of dissolution (kJ K−1 mol−1) |
| ΔSmix | Molar entropy of mixing (kJ K−1 mol−1) |
| T | Solution temperature (°C) |
| ΔTc | Undercooling (°C) |
| T c | Crystallisation temperature (°C) |
| T c,l | Crystallisation temperature at the kinetic limit/equilibrium crystallisation temperature (°C) |
| T diss | Dissolution temperature (°C) |
| T e | Equilibrium saturation temperature (°C) |
| T m | Melting point (K) |
| u c | Relative critical undercooling |
| v 0 | Volume occupied by a solute molecule in the crystal (m3) |
| x | Molar solubility |
| x ideal | Molar solubility in ideal state |
| y | Mol fraction acetone |
| ϒ | Activity coefficient |
| γ eff | Effective interfacial tension (mJ m−2) |
Abbreviations
| DSC | Differential scanning calorimetry |
| IN | Instantaneous nucleation |
| KBHR | Kashchiev–Borissova–Hammond–Roberts |
| MD | Molecular dynamics |
| MSZW | Metastable zone width |
| PN | Progressive nucleation |
| SANS | Small angle neutron scattering |
| SE | Standard error |
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research, which forms part of P. L. K. doctoral studies at University of Leeds (Accelerating, Characterising and Controlling Nucleation Processes, to be submitted 2021), was carried out at the EPSRC Centre for Doctoral Training in Complex Particulate Products and Processes (EP/L015285/1) as part of a collaborative project with Infineum Ltd. and Syngenta Ltd., who we gratefully acknowledge. We also gratefully acknowledge the support of the Advanced Manufacturing Supply Chain Initiative through the funding of the “Advanced Digital Design of Pharmaceutical Therapeutics” (Grant No. 14060) project in terms of supporting pharmaceutical crystallization and modelling research at Leeds. We would like to further acknowledge that this work also builds upon the Synthonic Engineering Program supported by the EPSRC (Grant EP/I028293/1) in collaboration with Pfizer, Boeringer-Ingellheim, Novartis and Syngenta.References
- A. S. Myerson, S. E. Decker and F. Welplng, Solvent Selection and Batch Crystallization, Ind. Eng. Chem. Process Des. Dev., 1986, 25(4), 925–929, DOI:10.1021/i200035a015.
- Y. Zhu, D. Youssef, C. Porte, A. Rannou, M. P. Delplancke-Ogletree and B. L. Mi Lung-Somarriba, Study of the Solubility and the Metastable Zone of 1,3-Dihydroxyacetone for the Drowning-out Process, J. Cryst. Growth, 2003, 257(3–4), 370–377, DOI:10.1016/S0022-0248(03)01463-5.
- C. P. M. Roelands, S. Jiang, M. Kitamura, J. H. Ter Horst, H. J. M. Kramer and P. J. Jansens, Antisolvent Crystallization of the Polymorphs of L-Histidine as a Function of Supersaturation Ratio and of Solvent Composition, Cryst. Growth Des., 2006, 6(4), 955–963, DOI:10.1021/cg050529d.
- S. Jiang, J. H. Horst and P. J. Jansens, Concomitant Polymorphism of O-Aminobenzoic Acid in Antisolvent Crystallization, Cryst. Growth Des., 2008, 8(1), 37–43, DOI:10.1021/cg070517n.
- L. Wantha, N. Punmalee, V. Sawaddiphol and A. E. Flood, Effect of Ethanol on Crystallization of the Polymorphs of L-Histidine, J. Cryst. Growth, 2018, 490, 65–70, DOI:10.1016/j.jcrysgro.2018.03.019.
- R. A. Granberg, D. G. Bloch and C. Rasmuson, Crystallization of Paracetamol in Acetone — Water Mixtures, J. Cryst. Growth, 1999, 198/199, 1287–1293, DOI:10.1016/S0022-0248(98)01013-6.
- I. Rosbottom, C. Y. Ma, T. D. Turner, R. A. O'Connell, J. Loughrey, G. Sadiq, R. J. Davey and K. J. Roberts, Influence of Solvent Composition on the Crystal Morphology and Structure of P-Aminobenzoic Acid Crystallized from Mixed Ethanol and Nitromethane Solutions, Cryst. Growth Des., 2017, 17(8), 4151–4161, DOI:10.1021/acs.cgd.7b00425.
- E. Plasari, P. H. Grisoni and J. Villermaux, Influence of Process Parameters on the Precipitation of Organic Nanoparticles by Drowning-Out, Chem. Eng. Res. Des., 1997, 75(2), 237–244, DOI:10.1205/026387697523507.
- K. Sangwal, On the Interpretation of Metastable Zone Width in Anti-Solvent Crystallization, Cryst. Res. Technol., 2010, 45(9), 909–919, DOI:10.1002/crat.201000319.
- K. Sangwal and E. Mielniczek-Brzóska, Antisolvent Crystallization of Aqueous Ammonium Dihydrogen Phosphate Solutions by Addition of Methanol, J. Cryst. Growth, 2016, 451(8), 139–149, DOI:10.1016/j.jcrysgro.2016.07.027.
- F. Zou, W. Zhuang, J. Wu, J. Zhou, P. P. Yang, Q. Liu, Y. Chen and H. Ying, Determination of Metastable Zone Widths and the Primary Nucleation and Growth Mechanisms for the Crystallization of Disodium Guanosine 5′-Monophosphate from a Water-Ethanol System, Ind. Eng. Chem. Res., 2015, 54(1), 137–145, DOI:10.1021/ie504035j.
- Y. Zhang, Y. Jiang, D. Zhang, Y. Qian and X. Z. Wang, Metastable Zone Width, Crystal Nucleation and Growth Kinetics Measurement in Anti-Solvent Crystallization of β-Artemether in the Mixture of Ethanol and Water, Chem. Eng. Res. Des., 2015, 95, 187–194, DOI:10.1016/j.cherd.2014.10.018.
- Z. Gao, Y. Wu, Y. Wu, J. Gong, Y. Bao, J. Wang and S. Rohani, Self-Induced Nucleation during the Antisolvent Crystallization Process of Candesartan Cilexetil, Cryst. Growth Des., 2018, 18(12), 7655–7662, DOI:10.1021/acs.cgd.8b01466.
- C. P. M. Roelands, J. H. Ter Horst, H. J. M. Kramer and P. J. Jansens, Analysis of Nucleation Rate Measurements in Precipitation Processes, Cryst. Growth Des., 2006, 6(6), 1380–1392, DOI:10.1021/cg050678w.
- P. L. Kaskiewicz, G. Xu, X. Lai, N. J. Warren, K. J. Roberts, C. Morton, P. Dowding and N. George, Isothermal by Design: An Accelerated Approach to the Prediction of the Crystallizability of Slowly Nucleating Systems, Org. Process Res. Dev., 2019, 23(9), 1948–1959, DOI:10.1021/acs.oprd.9b00242.
- R. B. Hammond, K. Pencheva, V. Ramachandran and K. J. Roberts, Application of Grid-Based Molecular Methods for Modeling Solvent-Dependent Crystal Growth Morphology: Aspirin Crystallized from Aqueous Ethanolic Solution, Cryst. Growth Des., 2007, 7(9), 1571–1574, DOI:10.1021/cg070310u.
- P. L. Kaskiewicz, T. D. Turner, N. J. Warren, C. Morton, P. J. Dowding, N. George and K. J. Roberts, Isothermal by Design: Comparison with an Established Isothermal Nucleation Kinetics Analysis Method, Chem. Eng. Technol., 2020, 43(10), 1971–1980, DOI:10.1002/ceat.202000113.
- F. L. Muller, M. Fielding and S. A. Black, Practical Approach for Using Solubility to Design Cooling Crystallisations, Org. Process Res. Dev., 2009, 13(6), 1315–1321, DOI:10.1021/op9001438.
- S. Black and F. Muller, On the Effect of Temperature on Aqueous Solubility of Organic Solids, Org. Process Res. Dev., 2010, 14(3), 661–665, DOI:10.1021/op100006y.
- T. D. Turner, D. M. C. Corzo, D. Toroz, A. Curtis, M. M. Dos Santos, R. B. Hammond, X. Lai and K. J. Roberts, The Influence of Solution Environment on the Nucleation Kinetics and Crystallisability of Para-Aminobenzoic Acid, Phys. Chem. Chem. Phys., 2016, 18(39), 27507–27520, 10.1039/C6CP04320H.
- D. Kashchiev, Nucleation, Butterworth-Heinemann, Oxford, 2000 Search PubMed.
- X. Tang, Crystal Structure, Phase Behaviour and Kinetics Associated with the Crystallisation of Octadecane, Hexadecane, and Mixtures Thereof Xue Tang, PhD Thesis, University of Leeds, 2017 Search PubMed.
- P. L. Kaskiewicz, I. Rosbottom, R. B. Hammond, N. J. Warren, C. Morton, P. J. Dowding, N. George and K. J. Roberts, Understanding and Designing Tailor-Made Additives for Controlling Nucleation: Case Study of P-Aminobenzoic Acid Crystallizing from Ethanolic Solutions, Cryst. Growth Des., 2021, 21(4), 1946–1958, DOI:10.1021/acs.cgd.0c01209.
- D. Toroz, I. Rosbottom, T. D. Turner, D. M. C. Corzo, R. B. Hammond, X. Lai and K. J. Roberts, Towards an Understanding of the Nucleation of Alpha-Para Amino Benzoic Acid from Ethanolic Solutions: A Multi-Scale Approach, Faraday Discuss., 2015, 179, 79–114, 10.1039/C4FD00275J.
- X. Tang, P. L. Kaskiewicz, D. M. Camacho Corzo, X. Lai, K. J. Roberts, P. Dowding and I. More, Solubility and Crystallisability of the Ternary System: Hexadecane and Octadecane Representative in Fuel Solvents, Fuel, 2018, 226, 665–674, DOI:10.1016/j.fuel.2018.04.022.
- D. Kashchiev, A. Borissova, R. B. Hammond and K. J. Roberts, Effect of Cooling Rate on the Critical Undercooling for Crystallization, J. Cryst. Growth, 2010, 312(5), 698–704, DOI:10.1016/j.jcrysgro.2009.12.031.
- D. Kashchiev, A. Borissova, R. B. Hammond and K. J. Roberts, Dependence of the Critical Undercooling for Crystallization on the Cooling Rate, J. Phys. Chem. B, 2010, 114(16), 5441–5446, DOI:10.1021/jp100202m.
- D. M. Camacho Corzo, A. Borissova, R. B. Hammond, D. Kashchiev, K. J. Roberts, K. Lewtas and I. More, Nucleation Mechanism and Kinetics from the Analysis of Polythermal Crystallisation Data: Methyl Stearate from Kerosene Solutions, CrystEngComm, 2014, 16(6), 974–991, 10.1039/C3CE41098F.
- I. Rosbottom, J. Pickering, R. B. Hammond and K. J. A. Roberts, Digital Workflow Supporting the Selection of Solvents for Optimising the Crystallisability of Para Aminobenzoic Acid, Org. Process Res. Dev., 2020, 24(4), 500–507, DOI:10.1021/acs.oprd.9b00261.
- OriginLab Corporation, Version 2014, Origin(Pro), Northampton, MA, USA Search PubMed.
- Technobis, Crystal16, https://www.crystallizationsystems.com/crystal16 Search PubMed.
- BIOVIA Dassault Systèmes, Materials Studio, https://www.3dsbiovia.com/portfolio/materials-studio.html Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- C. M. Breneman and K. B. Wiberg, Determining Atom-centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis, J. Comput. Chem., 1990, 11(3), 361–373, DOI:10.1002/jcc.540110311.
- A. D. A. Becke, New Mixing of Hartree-Fock and Local Density-Functional Theories, J. Chem. Phys., 1993, 98(2), 1372–1377, DOI:10.1063/1.464304.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789, DOI:10.1103/PhysRevB.37.785.
- R. B. Hammond, C. Ma, K. J. Roberts, P. Y. Ghi and R. K. Harris, Application of Systematic Search Methods to Studies of the Structures of Urea-Dihydroxy Benzene Cocrystals, J. Phys. Chem. B, 2003, 107(42), 11820–11826, DOI:10.1021/jp035010b.
- R. B. Hammond, R. S. Hashim, C. Ma and K. J. Roberts, Grid-Based Molecular Modeling for Pharmaceutical Salt Screening: Case Example of 3,4,6,7,8,9-Hexahydro-2H-Pyrimido (1,2-a) Pyrimidinium Acetate, J. Pharm. Sci., 2006, 95(11), 2361–2372, DOI:10.1002/jps.20657.
- F. A. Momany, L. M. Carruthers, R. F. McGuire and H. A. Scheraga, Intermolecular Potentials from Crystal Data. III. Determination of Empirical Potentials and Application to the Packing Configurations and Lattice Energies in Crystals of Hydrocarbons, Carboxylic Acids, Amines, and Amides, J. Phys. Chem., 1974, 78(16), 1595–1620, DOI:10.1021/j100609a005.
- J. Gasteiger and M. A. Marsili, New Model for Calculating Atomic Charges in Molecules, Tetrahedron Lett., 1978, 19(34), 3181–3184, DOI:10.1016/S0040-4039(01)94977-9.
- J. Gasteiger and M. Marsili, Iterative Partial Equalization of Orbital Electronegativity-a Rapid Access to Atomic Charges, Tetrahedron, 1980, 36(22), 3219–3228, DOI:10.1016/0040-4020(80)80168-2.
- The Cambridge Crystallographic Data Centre (CCDC), Mercury, https://www.ccdc.cam.ac.uk/solutions/csd-system/components/mercury/ Search PubMed.
- T. T. H. Nguyen, R. B. Hammond, K. J. Roberts, I. Marziano and G. Nichols, Precision Measurement of the Growth Rate and Mechanism of Ibuprofen {001} and {011} as a Function of Crystallization Environment, CrystEngComm, 2014, 16(21), 4568–4586, 10.1039/c4ce00097h.
- J. D. Swalen and C. C. Costain, Internal Rotation in Molecules with Two Internal Rotors: Microwave Spectrum of Acetone, J. Chem. Phys., 1959, 31, 1562, DOI:10.1063/1.1730653.
- A. R. Gerson, K. J. Roberts and J. N. Sherwood, An Instrument for the Examination of Nucleation from Solution and Its Application to the Study of Precipitation from Diesel Fuels and Solutions of N-Alkanes, Powder Technol., 1991, 65(1–3), 243–249, DOI:10.1016/0032-5910(91)80187-N.
- A. R. Gerson, K. J. Roberts, J. N. Sherwood, A. M. Taggart and G. Jackson, The Role of Growth Environment on the Crystallization of Normal Alkanes in the Homologous Series from C18H38 to C29H60, J. Cryst. Growth, 1993, 128(1–4 PART 2), 1176–1181, DOI:10.1016/S0022-0248(07)80119-9.
- A. M. Taggart, F. Voogt, G. Clydesdale and K. J. Roberts, An Examination of the Nucleation Kinetics of N-Alkanes in the Homologous Series C13H28 to C32H66, and Their Relationship to Structural Type, Associated with Crystallization from Stagnant Melts, Langmuir, 1996, 12(23), 5722–5728, DOI:10.1021/la9600816.
- K. J. Roberts, J. N. Sherwood and A. Stewart, The Nucleation of N-Eicosane Crystals from Solution in n-Dodecane in the Presence of Homologous Impurities, J. Cryst. Growth, 1990, 102(3), 419–426, DOI:10.1016/0022-0248(90)90400-F.
- D. Mealey, D. M. Croker and Å. C. Rasmuson, Crystal Nucleation of Salicylic Acid in Organic Solvents, CrystEngComm, 2015, 17(21), 3961–3973, 10.1039/c4ce01428f.
- P. Ferrer, I. Da Silva and I. Puente-Orench, Solid Acetone Structure Dependence on Pressure: A New Fibre Textured Thin Film Crystallographic Structure Studied by Grazing-Incidence X-Ray Diffraction, CrystEngComm, 2016, 18(42), 8220–8228, 10.1039/c6ce01333c.
Footnote |
| † Electronic supplementary information (ESI) available: It includes: the average crystallisation and dissolution temperatures determined for all solutions studied across the full mixed-solvent compositional range, atomic partial charges of eicosane, toluene and acetone used in grid-based molecular modelling studies and the full analysis of solvation sites of eicosane solvated by single toluene and acetone molecules. See DOI: 10.1039/d1ce00322d |
| This journal is © The Royal Society of Chemistry 2021 |