The mutual interactions of RNA, counterions and water – quantifying the electrostatics at the phosphate–water interface

Abstract

The structure and dynamics of polyanionic biomolecules, like RNA, are decisively determined by their electric interactions with the water molecules and the counterions in the environment. The solvation dynamics of the biomolecules involves a subtle balance of non-covalent and many-body interactions with structural fluctuations due to thermal motion occurring in a femto- to subnanosecond time range. This complex fluctuating many particle scenario is crucial in defining the properties of biological interfaces with far reaching significance for the folding of RNA structures and for facilitating RNA–protein interactions. Given the inherent complexity, suited model systems, carefully calibrated and benchmarked by experiments, are required to quantify the relevant interactions of RNA with the aqueous environment. In this feature article we summarize our recent progress in the understanding of the electrostatics at the biological interface of double stranded RNA (dsRNA) and transfer RNA (tRNA). Dimethyl phosphate (DMP) is introduced as a viable and rigorously accessible model system allowing the interaction strength with water molecules and counterions, their relevant fluctuation timescales and the spatial reach of interactions to be established. We find strong (up to ≈90 MV cm⁻¹) interfacial electric fields with fluctuations extending up to ≈20 THz and demonstrate how the asymmetric stretching vibration ν_AS(PO₂)⁻ of the polarizable phosphate group can serve as the most sensitive probe for interfacial interactions, establishing a rigorous link between simulations and experiment. The approach allows for the direct interfacial observation of interactions of biologically relevant Mg²⁺ counterions with phosphate groups in contact pair geometries via the rise of a new absorption band imposed by exchange repulsion interactions at short interatomic distances. The systematic extension to RNA provides microscopic insights into the changes of the hydration structure that accompany the temperature induced melting of the dsRNA double helix and quantify the ionic interactions in the folded tRNA. The results show that pairs of negatively charged phosphate groups and Mg²⁺ ions represent a key structural feature of RNA embedded in water. They highlight the importance of binding motifs made of contact pairs in the electrostatic stabilization of RNA structures that have a strong impact on the surface potential and enable the fine tuning of the local electrostatic properties which are expected to be relevant for mediating the interactions between biomolecules.

---

Benjamin Philipp Fingerhut

Benjamin Fingerhut is heading the Biomolecular Dynamics theory group at the Max-Born-Institute, Berlin, Germany. He received his doctoral degree from the Ludwig-Maximilians-Universität München (LMU) in 2011 and afterwards moved to the University of California, Irvine (UCI) as a postdoctoral fellow. He joined the Max-Born-Institute in 2014. Benjamin's research focuses on ultrafast phenomena at biological interfaces and the development of numerical methods for the description of condensed phase dissipative quantum dynamics. His research is supported by an ERC starting grant of the European Research Council and he is recipient of the Robin Hochstrasser Young Investigator Award and the Coblentz Award.

---

Introduction

DNA and RNA are charged polymers with a double helix structure that encode genetic information and act as key players in the biosynthesis of proteins.¹ The macromolecular structures of DNA and RNA are composed of a sequence of nucleic acids, linked by a sugar-phosphate backbone. The ionic phosphate groups of the sugar-phosphate backbone represent the primary hydration sites for the surrounding water molecules. Moreover, their negative charge makes them susceptible to the interaction with counter ions, establishing charge neutrality of the polyanionic biomolecule in an aqueous environment.

Hydration and charge neutralization of DNA and RNA occurs via specific hydrogen bond (HB) interactions with water molecules, contact ion pair formation and non-directed Coulomb interactions with ions that retain a complete solvation shell and are embedded in the aqueous environment. The two free oxygen atoms of the phosphate group form up to three HBs with the first solvation shell water molecules establishing a prototypical tetrahedral surrounding of each of the non-esterified oxygen atoms. Additional hydration sites are the sugar hydroxyl (OH) groups, and the polar carbonyl groups and amino (NH₂) groups of the nucleic bases.^2–5 Compared to the bulk, the biomolecule to some extent distorts the water structure in the hydration shell, with a spatial reach extending to the first few (≈5) water layers beyond which the bulk like behaviour of the liquid is approached.⁶ Mutually, the macromolecular structure, such as the particular double-helical form of DNA, is strongly affected by the interaction with the hydration shell^7,8 and the first few water layers around the biomolecules are more and more considered to be an active player in determining the structural stability and dynamics of the biological entities.⁹

The high charge density of the negatively charged phosphate groups of the sugar-phosphate backbone leads to strong repulsive electric forces that need to be compensated in the equilibrium macromolecular structures of DNA and RNA via the stabilization by positively charged ions. Compared to DNA with the preferred B-helical structures at high hydration level, double stranded RNA forms A-helical structures with shorter intra-strand (PO₂)⁻–(PO₂)⁻ distances (6.6 vs. 4.5 Å, respectively)^10,11 that render counterion stabilization particularly relevant. Moreover, the complex folded tertiary structures of RNA, such as ribosomal RNA^12,13 or the L-shaped clover leaf structure of transfer RNA (tRNA),^14–16 are characterized by the close proximity of the (PO₂)⁻ groups.

The electric interactions between the ionic molecular groups and counter ions in aqueous solution play a fundamental role in chemistry and biology.¹⁷ The interactions of the counterions with the negatively charged phosphate groups of the backbone occurs via unspecific long-range Coulomb coupling in so-called solvent separated ion pairs or in contact pairs, both leading to a net accumulation of counterions within the first few hydration layers around the biomolecule. In this context, magnesium ions (Mg²⁺) are particularly relevant, as Mg²⁺ ions not only stabilize the structure but also mediate the recognition of binding partners and act as catalytic centres. While solvent separated ion pairs are discussed prominently in the stabilization and folding of tertiary RNA structures,^18–20 the precise role of contact pairs of phosphate groups with ions, regarding their abundance in solution, molecular geometry, and their role in defining RNA structure is unknown.

Equilibrium geometries of RNA have been studied by X-ray diffraction and the positions of water oxygens and counterions have been identified.^11,12,16 X-Ray diffraction preferentially maps immobilized water molecules at dedicated interaction sites while the spatial positions and dynamics of mobile water molecules and ions have to a large extent remained elusive. Typical crystallized samples contain limited hydration levels and the identifications of ionic species can be ambiguous.^21,22 Moreover, the dynamic changes of the macromolecular structures, e.g., during the folding processes, are related to the rearrangement of the solvation shell and the ions embedded in the hydration layer, a topic that is largely unaddressed.

Electrostatic scenario at biological interfaces

The functional role of the different ion pair geometries and the mutual interactions of ionic and dipolar constituents, i.e., negatively charged phosphate groups, counter ions and the fluctuating water molecules of the first few hydration layers, are far from being understood. In particular, the different contributions of noncovalent interactions defining the ion and water dynamics of the hydration shell around RNA are only insufficiently understood. Hydration of the polar and ionic molecular entities involves the interplay of long-range electric interactions, specific short-range interactions and inductive many body interactions. At the surface of RNA, the negatively charged phosphate groups form directed hydrogen bonds with the first water shell and are polarized by the fluctuating electric fields that arise from the surrounding water molecules and the counter ions. Consequently, the biological interface of RNA constitutes a complex many-body problem for which the effective range of electric forces, their strength and the fluctuation amplitudes are barely characterized. Structural dynamics in the first water layers induces electric field fluctuations on a multitude of timescales via, e.g., librational motions and the breaking and reformation of hydrogen bonds. Similarly, the timescales of structural dynamics of the first few water layers around RNA, i.e., the timescale of breaking and reformation of hydrogen bonds, have remained controversial.^6,23,24 Insights into the spatial extent, dynamic nature and microscopic origins of the coupling of the hydration shell with the biomolecule are thus desired to establish a deeper understanding of the relevant biomolecular interactions and develop a consistent picture of the interfacial electrostatics at the molecular level.

Quantitative insights into biomolecular electrostatics

The quantification of interfacial field strength and its impact on the biomolecular properties pose persistent challenges for theory and experiment. Molecular level insights into the electrostatics of the RNA–water interface require sensitive probes that map the interfacial dynamics on the ultrafast timescale of molecular motions and allow the ion geometries to be discerned without disturbing them. In this respect, functional groups located at the interface with the water hydration shell are particularly promising for probing HB interactions, hydration dynamics and the electrostatic coupling with the environment.²⁵ The highly polarizable phosphate groups of the sugar-phosphate backbone of DNA or RNA provide sensitive, non-invasive reporters for probing the interaction with the water shell and embedded counterions.^26–28 In particular, the pronounced ≈20–40 cm⁻¹ solvatochromic shift of the asymmetric phosphate stretching vibration ν_AS(PO₂)⁻ has been established to monitor a wide range of DNA hydration levels.²⁹ Extending this approach, infrared (IR) absorption and non-linear two-dimensional infrared (2D-IR) spectroscopy³⁰ with femtosecond time resolution allowed for unprecedented insights into the coupled dynamics of biomolecules and their water shells.^28,31,32

Vice versa, simulations of the interactions that define molecular geometries, as well as transition frequencies and line shapes of the ν_AS(PO₂)⁻ vibrator, provide insights into the microscopic details of the interfacial solvation dynamics. It is thus desirable to establish quantitative models and simulation methods for accurate descriptions of the infrared spectra observed for ν_AS(PO₂)⁻. Molecular dynamics (MD) simulations have characterized the biomolecular interface³³ and the ion atmosphere around RNA by providing insights into the radial concentration profiles.^34–37 These simulations allow the different local interaction geometries of the phosphate groups, ions, and water molecules to be distinguished and accounted for directed HBs with water molecules. Nevertheless, MD simulations of interfacial hydration structures and dynamics of highly charged RNA systems pose persistent challenges, in particular for doubly charged ions, like Mg²⁺ and Ca²⁺, because of the shortcomings of the commonly employed fixed charge force fields that neglect many-body electric polarization and charge transfer among the charged and polar constituents. The use of unscreened Coulomb interaction for highly charged ions and phosphate groups typically overestimates the binding in contact pair geometries and the re-parametrization of ion (and water) force field parameters, e.g., via additional charge–dipole interaction terms or a rescaling of atomic charges, is a topic of current research.^38–41 Moreover, the required large molecular simulation boxes and long-time equilibration of the ion atmosphere extending into the microsecond (μs) timescale^36,42 require a high numerical effort, even with modern GPU-accelerated MD codes. Recent progress in polarizable force fields is promising^43–45 but, due to the increased numerical costs, large system sizes and propagation times on the μs timescale, are challenging to achieve.

Here we give an account of the recent progress in the microscopic understanding of interactions defining the molecular arrangements at the phosphate–water interface. We start by introducing dimethyl phosphate (DMP) as the model system for the hydration shell of helical double stranded RNA (dsRNA) and complex folded transfer RNA (tRNA). The hydration dynamics of native and artificial DNA strands at various hydration levels has been covered in a recent review article²⁵ and a book chapter.⁴⁶ We provide a bottom-up perspective of the relevant interactions, the fluctuations of the water environment and the molecular structures formed with counterions. We demonstrate how particular properties of the aqueous environment are reflected in the asymmetric phosphate stretching vibration ν_AS(PO₂)⁻ as a most sensitive spectroscopic observable. Changes in the hydration structure upon RNA melting and contact ion pair formation in solution between the RNA (PO₂)⁻ groups and Mg²⁺ ions are quantified via clear changes in the observed spectra where in depth-simulations allow the assigning of the underlying molecular structures. The benchmark of theoretical findings against the state-of-the-art 2D-IR experiments provides insights into the relevant spatial reach of interactions and allows access to dynamical properties like fluctuation amplitude and timescales, defining the properties of the biomolecular phosphate–water interface and allowing for unprecedented microscopic understanding of the complex electrostatics of macromolecular RNA structures.

Dimethyl phosphate (DMP) as the model for the sugar-phosphate backbone of RNA

In the following, simulations are presented for dimethyl phosphate (DMP, (CH₃)₂PO₄⁻) in a water environment. Due to its moderate molecular size, DMP is rigorously accessible and IR spectra can be simulated on a sophisticated level of theory, allowing for quantitative agreement with the experiment. DMP has repeatedly been used as a model system for the phosphodiester backbone of DNA and RNA.^47–51 The results provide a benchmark of fluctuating electric forces determining the spectral diffusion in non-linear 2D-IR spectra.³⁰

Hydration structure and fluctuating electric forces

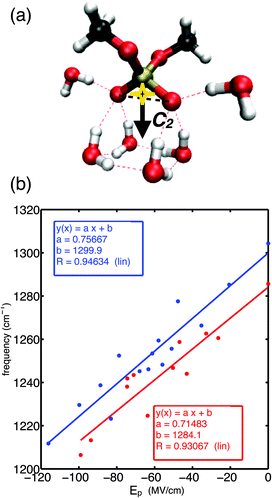
Fig. 1a shows the molecular structure of DMP with a gg methyl group conformation together with a prototypical first hydration shell of six water molecules. The gg conformer of DMP is the relevant conformation populated in the A-helical structures of RNA, while the gt conformer is also present in the B-helical structures of DNA.⁴⁷ Each of the non-esterified oxygen atoms of the phosphate group forms three HBs. Electric fields sensed at the bisector midpoint of the (PO₂)⁻ group and originating from water dipoles and charged ions embedded in the environment were found to determine the transition frequency of the asymmetric phosphate stretching vibrations ν_AS(PO₂)⁻.⁵² Because of the permanent electric dipole moment of the (PO₂)⁻ group, the relevant component of the electric field is obtained upon projection on the O1=P=O2 bisector axis giving the projected field E_p along the angle bisector of the (PO₂)⁻ group (cf.Fig. 1a). Using an empirical field-frequency correlation,^53–55 the transition frequency ω of the ν_AS(PO₂)⁻ vibration is related to the imposed electric field E_pvia the linear Stark effect

ω = ω₀ + a·E_p (1)

where the Stark tuning rate a accounts for the frequency shift of the vibration per unit electric field E_p⁵⁶ and ω₀ denotes the field-free transition frequency of the ν_AS(PO₂)⁻ vibration readily accessible from the ab initio simulations of isolated DMP. Microscopic theory of vibrational solvatochromism^57,58 was applied to investigate solvatochromic shifts of amide I and nitrile reporter modes, see ref. 59 for a recent review on intermolecular interaction based vibrational spectroscopic maps.

Fig. 1 (a) Molecular structure of dimethyl phosphate (DMP, (CH₃)₂PO₄⁻) together with an idealized first hydration shell of water molecules. The total electric field imposed by water molecules is projected on the bisector midpoint of the (PO₂)⁻ group in the direction of the angle bisector axis C₂. (b) Correlation of the projected electric field E_p and the transition frequency of the asymmetric phosphate stretching vibration ν_AS(PO₂)⁻ for DMP·xH₂O molecular clusters (x = 1–22), additionally shown are linear regressions of data points. Transition frequencies ν_AS(PO₂)⁻ were evaluated in the harmonic approximation at density functional level of theory (PBE0 functional, blue) and many body perturbation theory (MP2, red). Adapted from ref. 60, with the permission of AIP Publishing.

Fig. 1b demonstrates the correlation of eqn (1) in a large electric field range (E_p = 0–120 MV cm⁻¹) for ab initio simulated transition frequencies of the asymmetric stretching vibrations ν_AS(PO₂)⁻ of DMP·xH₂O molecular clusters (x = 1–22).⁶⁰ Because of the good linear correlation, the linear Stark effect is identified as the dominant contribution to the observed frequency shifts of the ν_as(PO₂)⁻ mode in a spectral range covering ≈90 cm⁻¹. The different theoretical methods, i.e., density functional theory (PBE0 functional) and many-body perturbation theory (MP2), provide consistent frequency shifts and predict similar Stark tuning rates a ∼ 0.71–0.75 cm⁻¹ (MV cm⁻¹)⁻¹ for the gg conformer of DMP. Slightly reduced Stark tuning rates a ∼ 0.48–0.6 cm⁻¹ (MV cm⁻¹)⁻¹ were suggested for the gt conformer.⁶⁰ The similar Stark tuning rates of the different theoretical methods lead to near-to-parallel field-frequency correlations (Fig. 1b). Notably, the analytical expressions for the field-frequency correlation allow the prediction of the field-free transition frequency ω₀ of the ν_AS(PO₂)⁻ vibration within ≈5 cm⁻¹ for the MP2 and DFT levels of theory.

Structural dynamics induced by thermal motions of the bulk solvent involves molecular librational fluctuations and HB breaking and reformation of water molecules in the hydration shell. The solvent structural dynamics thus imposes electric field fluctuations on the femto- to picosecond timescale that act on biomolecular moieties. The simulation of fluctuation properties of electric forces imposed on the (PO₂)⁻ group of DMP in a bulk water solvent is computationally expensive at the ab initio level of theory because of the large system size and the required configurational averaging over solvent degrees of freedom. The electrostatic fragment potential (EFP) model⁶¹ is a computationally efficient but accurate method to obtain insights into the relevant intermolecular interactions defining the field induced response of the asymmetric phosphate stretching vibration ν_AS(PO₂)⁻ in a water environment. By accounting for field contributions from charge, dipole and quadrupole interactions together with self-consistently converged many-body polarization contributions, near to quantitative agreement could be obtained for electric fields evaluated at the quantum mechanical MP2 level of theory.⁶⁰ The favourable agreement between electric fields evaluated at the quantum mechanical level of theory and with the EFP model allows for efficient simulations of the fluctuation properties of electric fields in a bulk water environment. The findings further demonstrate that the relevant interactions of the (PO₂)⁻ group with the solvent inducing the frequency shift of the ν_AS(PO₂)⁻ vibration are governed by electrostatic and polarization interactions at the phosphate–water interface while the contributions from exchange repulsion, charge transfer and dispersion interactions are minor.

The fluctuation properties of electric forces imposed on the (PO₂)⁻ group of DMP by water fluctuations in a bulk solvent are summarized in Fig. 2 and 3. It was found that the total electric field experienced by the (PO₂)⁻ group due to structural fluctuations of the water hydration shell has a high value of ≈90 MV cm⁻¹ and that electric field fluctuations are dominated by short-time fluctuations with large excursion amplitudes in the order of >20 MV cm⁻¹ and Gaussian statistics (Fig. 2). The magnitude of fluctuation amplitudes is in good agreement with estimates derived from the analysis of experimental 2D-IR line shapes.³¹

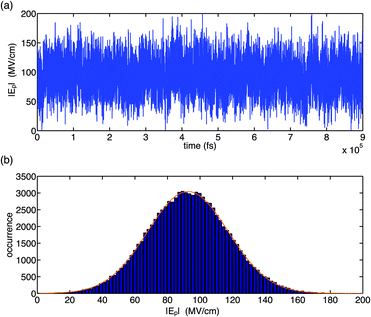Fig. 2 Temporal field fluctuation (a) and histogram distribution of field fluctuations (b) for the gg conformer of DMP in water. Electric fields were calculated using the electrostatic fragment potential (EFP) model and account for electric field contributions due to static multipoles and induced dipoles. The Gaussian fit (orange line) has a width of 24.8 MV cm⁻¹, centred at 92.6 MV cm⁻¹. Adapted from ref. 60, with the permission of AIP Publishing.

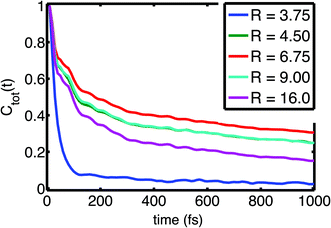Fig. 3 Field fluctuation correlation function C_tot(t) as function of size of the hydration shell R (in Å). Adapted from ref. 60, with the permission of AIP Publishing.

Time correlation functions were employed to quantify the characteristic temporal properties of electric field fluctuations imposed on the (PO₂)⁻ group by the water solvent (Fig. 3). The fluctuation timescales are characterized by a sub-100 fs, ultrafast component due to librational fluctuations of the hydration shell²⁶ and an additional 1–2 ps component leading to a residual decay of the correlation function. Librational fluctuations show a broad fluctuation spectrum from 300 cm⁻¹ extending up to 900–1000 cm⁻¹ and arise primarily from fluctuations of the static electric multipoles of the solvent. In contrast, the intermolecular HB stretch modes induce primarily the polarization of water molecules that is characterized by the fluctuations of induced dipoles with a dominant 100–200 cm⁻¹ frequency component, distinct from the fluctuations of static electric multipoles. Because the picosecond orientational relaxation of water molecules^62,63 sets a natural limit on the temporal response that underlies the high static dielectric constant of water, the local field fluctuations of the hydration shell are sensed nearly unscreened by the (PO₂)⁻ reporter mode which is reflected in the large >20 MV cm⁻¹ field excursions on short timescales set by librational motion and intermolecular HB stretch modes.

The loss of correlation on the slower, 1–2 ps timescale is microscopically associated with the breaking of the HBs in the solvation shell. The low-picosecond timescale reflects the continuous breaking and re-formation of HBs in the hydration shell while an exchange of water molecules in the first hydration shell around the (PO₂)⁻ group occurs on a slower ≈10 ps timescale. The radially-resolved field-time correlation functions presented in Fig. 3 characterize the distinct dynamics of the first few hydration shells. Water molecules of the first hydration shell (R = 3.75 Å) are essentially immobilized with a dominant sub-100 fs librational motion component. For the second and third hydration shell (R > 3.75 Å), the picosecond dynamics becomes increasingly pronounced, reflecting the structural reorganization of the HB network, the more frequent breaking of HBs and exchange of water molecules.

Of particular interest is the spatial reach of electric interactions impacting the (PO₂)⁻ group on the biomolecular surface. The analysis of the electric field dependence on the radial distance from the (PO₂)⁻ group of DMP (Fig. 4) demonstrates that strong electric forces arise locally from the first and second hydration shell, contributing ≈60 MV cm⁻¹ and ≈18 MV cm⁻¹, respectively. The EFP model further provides insights into the individual contributions of the electric field. Permanent multipoles are the dominant contribution and many-body induction arising from re-polarization of water molecules and the (PO₂)⁻ group due to hydrogen bond stretch motions are substantial (≈20%). The strong electric interactions particularly with the first hydration shell water molecules thus distort the polarizable electron density of the (PO₂)⁻ group (see the pronounced polarization contribution on the 5–6 Å length scale in Fig. 4a). The electronic degrees of freedom of the (PO₂)⁻ group are not stationary on the timescale of solvent fluctuations, and the distortion of electron density by electric interactions imposes dipole moment fluctuations of some 1–2 Debye, i.e., comparable to the permanent dipole moment of water. Many-body effects caused by high-frequency dynamics imposed by HB stretching vibrations and, to a lesser extent, librational motions are thus crucial in determining the interfacial electrostatic environment in the vicinity of the (PO₂)⁻ group. The (PO₂)⁻ group is thus a particularly sensitive reporter of the short-ranged electrostatics that converge on a length scale of ≈1 nm from the (PO₂)⁻ group. These theoretical findings are fully corroborated by the 2D-IR measurements of DNA at varying hydration levels and counter ion compositions³¹ which demonstrated that the interfacial electric field fluctuations are dominated by the water molecules in the first two layers.

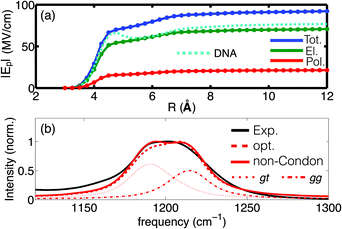Fig. 4 (a) Radial dependence of the time averaged electric field E_p as a function of the hydration shell size; the dashed cyan line shows the field derived for DNA (taken from ref. 55); (b) experimental and simulated infrared absorption spectrum of DMP in water: red dotted and dashed-dotted lines denote the respective contributions of the gt and gg conformers to the simulated spectrum. Simulations employ electrostatic field-frequency correlations with optimized slopes a^gg = 0.64 cm⁻¹ (MV cm⁻¹)⁻¹ and a^gt = 0.63 cm⁻¹ (MV cm⁻¹)⁻¹ (opt, dashed red line) and additionally account for non-Condon effects (solid red line). Adapted from ref. 60, with the permission of AIP Publishing.

Simulations of the linear absorption spectrum of DMP in water provided quantitative insights into relevance and magnitude of the underlying electrostatic interactions. Accounting for an electric field expansion up to quadrupoles and self-consistent polarization imposed by induced dipoles allowed the simulation of the solvent induced frequency shifts and line shapes of the ν_AS(PO₂)⁻ vibration in very good agreement with the experiment (Fig. 4b). The simulations reveal the contribution of the two populations of the gg and gt conformations of DMP, as reflected in the plateau like line shape of the IR spectrum, while the impact of non-Condon effects on the line shape was found to be moderate. The developed electrostatic field-frequency correlation facilitates a near-to quantitative agreement with the experiment, thus allowing the characterization of the spatio-temporal fluctuations imposed by the solvent water molecules on the (PO₂)⁻ moiety. The favourable computational scaling of the EFP model, benchmarked by high level ab initio simulations, accessed the femto- to nanosecond timescale of solvation dynamics, i.e., the natural timescale of HB dynamics around the phosphate group. The approach established that the relevant electric forces are short-ranged and arise locally, primarily from the first and second hydration shells, being characterized by a dominant sub-100 fs fluctuation timescale. The findings establish the relevant electric interactions that provide an understanding of the hydration structure and dynamics at the more complex biomolecular interface of RNA.

Counterion induced shifts of the ν_AS(PO₂)⁻ transition frequency

In aqueous solutions, positively and negatively charged ions interact in different geometries, either in the so-called site-bound or contact-pair geometries where the positive ions are in direct contact with the counterion or in the so-called solvent separated ion pairs where the ions are separated by at least one layer of water molecules. Contact pairs directly formed of oppositely charged ions are repeatedly found as a basic structural unit in electrolytes, ionic solutions and biomolecular structures. Pairs of negatively charged phosphate groups and Mg²⁺ ions represent a key structural feature of DNA and RNA embedded in water but a clear distinction between the on-site and water-solvated ions around DNA and RNA has remained difficult.¹⁹ The functional role of contact ion geometries in stabilizing folded macromolecular structures and the relevant underlying interactions are far from being understood. A deeper insight at the molecular level requires sensitive probes which allow for discerning the different ion geometries without disturbing them, and for mapping their dynamics on the ultrafast timescale of molecular motions. Establishing the vibrations of phosphate groups as selective probes of such contact pairs provides the potential for mapping of interactions and structure on the ultrafast timescales of the molecular dynamics.

By exploiting the high sensitivity of the asymmetric (PO₂)⁻ stretching vibration ν_AS(PO₂)⁻ to the local hydration environment, we could establish the ν_AS(PO₂)⁻ vibration as a sensitive and non-invasive probe for ion geometries in a water environment.^64,65 Using DMP in liquid water and prepared with an excess of Mg²⁺ ions, ions in direct contact with the (PO₂)⁻ group can be unequivocally identified via a distinct feature in the IR spectrum. It is observed that the interaction with the Mg²⁺ ion shifts the asymmetric (PO₂)⁻ stretching vibration ν_as(PO₂)⁻ to a frequency which is higher than that in the absence of Mg²⁺ ions (Fig. 5A).

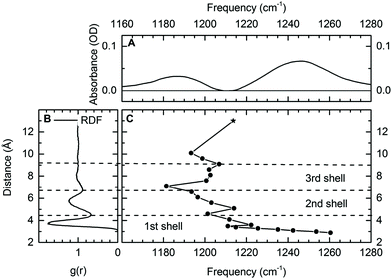Fig. 5 (A) Differential infrared absorption spectrum of 0.2 M DMP in the absence and presence of 2 M Mg(H₂O)₆Cl₂. (B) Radial distribution function (RDF) of the phosphorous P–water distance for DMP in H₂O. (C) Calculated frequency of the ν_AS(PO₂)⁻ vibration in the DMP(H₂O)₁₉Mg²⁺ cluster as function of the P–Mg²⁺ distance. Harmonic normal modes were evaluated at the DF-DFT(B3LYP)-D/aug-cc-pVDZ/aug-cc-pVTZ level of theory, the * indicates the frequency ν_AS(PO₂)⁻ of fully solvated DMP in the absence of other ions (DMP(H₂O)₆). Reprinted with permission from ref. 64. Copyright 2019 American Chemical Society.

Theoretical calculations provided a detailed analysis of the influence of the Mg²⁺ ions on the binding potential of the (PO₂)⁻ group and allowed the quantification of the relevant underlying interactions inducing a change in the ν_as(PO₂)⁻ transition frequency. Vibrational absorption spectra for varying distances of phosphorous and Mg²⁺ atoms (R(P–Mg²⁺), Fig. 5C) reveal characteristic ion induced frequency shifts. For R(P–Mg²⁺) = 10.5 Å, approximately three water layers are located between DMP and the Mg²⁺ ion. When the Mg²⁺ ion enters the second or third solvation shell (R(P–Mg²⁺) ≈ 5–9 Å), a 10–20 cm⁻¹ red-shift of the ν_AS(PO₂)⁻ transition frequency is induced, correlating with an increased absorption centred around 1180 cm⁻¹ observed in the experiment. The microscopic origin of the red-shift of the ν_AS(PO₂)⁻ vibrations is rooted in the increased electric field sensed by the (PO₂) – group (cf.Fig. 1b). The local dipolar field of DMP and Mg²⁺ ions induces the ordering and orientation of the first and second hydration shell water molecules and the associated electric field changes are reflected in a moderate red-shift of the ν_AS(PO₂)⁻ frequency. The frequency shifts of ν_AS(PO₂)⁻ are reversed, once the Mg²⁺ ion enters the first solvation shell around the (PO₂)⁻ group. The formation of contact pairs of DMP and Mg²⁺ ions induces a blue-shift of the ν_AS(PO₂)⁻ vibration (Fig. 5C), in good agreement with the increased absorption centred around 1248 cm⁻¹ observed in the experiment.

Fig. 6 depicts the potential energy for displacements along the ν_AS(PO₂)⁻ normal mode vector for a contact pair geometry (R(P–Mg²⁺) = 3.09 Å) and a solvent separated ion pair geometry (R(P–Mg²⁺) = 10.09 Å) of DMP and the Mg²⁺ ion. The symmetric shape of the ν_AS(PO₂)⁻ potential becomes severely asymmetrically distorted in the contact pair geometry, imposed by the geometric constraints at a close contact between the (PO₂)⁻ group and the Mg²⁺ ion (cf.Fig. 8c). In the contact ion pair geometry, the symmetry for displacements along the ν_AS(PO₂)⁻ normal mode coordinate is broken and the distortions of the potential induce a blue shift of the ν_as(PO₂)⁻ transition frequency. A deconstruction of the potential via absolutely localized molecular orbital energy decomposition analysis (ALMO-EDA) provides access to the characterization of intermolecular interactions in terms of underlying fundamental interactions, that is, electrostatics and exchange repulsion, induction and charge transfer. The ν_AS(PO₂)⁻ mode displacements lead to the sampling of particularly short distances of the Mg²⁺ ion and one of the oxygen atoms of the (PO₂)⁻ group. At such a short interatomic distance repulsive exchange interactions between the closed shell atoms become dominant, inducing the asymmetric distortion of the ν_AS(PO₂)⁻ mode potential. An in-depth theoretical analysis revealed that the subtle balance between the attractive electrostatic (Coulomb) forces and repulsive forces due to quantum-mechanical exchange interaction at short interatomic distances governs the ν_AS(PO₂)⁻ transition frequency in contact ion pairs. The simulations provide a strong support that the experimentally observed blue shift of the ν_AS(PO₂)⁻ vibration originates from the contact pairs made of the (PO₂)⁻ group of DMP and Mg²⁺ ions in the first solvation shell.

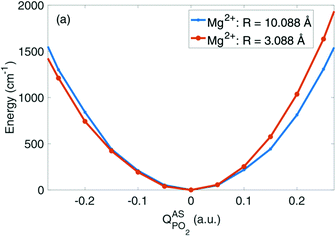Fig. 6 Potential energy surfaces in the direction of the normal mode displacement vector Q of the ν_AS(PO₂)⁻ vibration in the DMP(H₂O)₁₉Mg²⁺ cluster for selected Mg²⁺⋯P distances R. Adapted with permission from ref. 65. Copyright 2019 American Chemical Society.

The absence of crosspeaks in the 2D-IR experiments with femtosecond time resolution (Fig. 7) strongly supports the assignment of distinct contact ion pair and solvent separated pair species contributing independently at different frequency positions. The 2D-IR spectra of DMP in water (R = 0, Fig. 7a) show an elliptic shape of the ν = 0–1 peak (yellow-red contours) indicative of limited inhomogeneous broadening due to the structural heterogeneity of hydration geometries around the (PO₂)⁻ groups. With increasing Mg²⁺ content, the 2D-IR spectra develop an additional contribution that is clearly manifested in two separate peaks, M1 and M2 (R = 10, Fig. 7b). There are no cross peaks in the 2D-IR spectra demonstrating that the peaks M1 and M2 arise from different uncoupled phosphate environments, one consisting of neat water (M1) and the other representing contact pairs with the Mg²⁺ ion. The quantitative analysis of the 2D-IR spectra in density matrix simulations (Fig. 7c and d) characterizes solvent fluctuations via the frequency fluctuation correlation function with a dominant 300 fs time constant and a second slower >10 ps time constant. Lifetime weighted amplitudes of species M1 and M2 provide limits on the relative contract ion pair concentrations in the order of 20%.⁶⁵ The assignment of distinct chemical species via the absence of crosspeaks in 2D-IR spectra extends beyond the information content accessible from linear IR spectroscopy and allows to rule out alternative scenarios, e.g., relying on an excitonic coupling mechanism between the ν_AS(PO₂)⁻ modes.

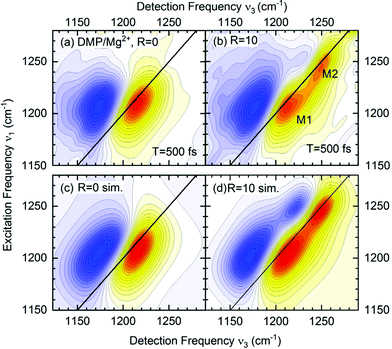Fig. 7 (a and b) 2D-IR spectra of DMP in water in the range of the ν_AS(PO₂)⁻ vibrations for a waiting time T = 500 fs. The absorptive 2D signal is shown as a function of the excitation frequency ν₁ and the detection frequency ν₃: yellow-red contours represent signals due to the fundamental (v = 0–1) transition, and blue contours the excited state v = 1–2 absorption. Signal changes between neighbouring contour lines are 7.5%. R = c(Mg²⁺)/c(DMP) is the ratio of Mg²⁺ to DMP concentration. (c and d) Simulated 2D-IR spectra for R = 0 and R = 10. Adapted with permission from ref. 75. Copyright 2021 American Chemical Society.

The close synergy of in-depth simulations and time-resolved 2D-IR experiments established a novel analytical tool to characterize the short-ranged phosphate–ion interaction in solution, complementing the currently available structural techniques. The importance of such a clear analytical tool for characterizing the phosphate–ion interaction derives from the central role counter ions have in defining the structure and dynamics of RNA polymers. While the interaction of the phosphate groups with alkali and alkaline earth ions in water has been studied via stationary infrared and Raman spectra, primarily of the symmetric phosphate stretching vibration,^66,67 our recent progress has extended such mostly qualitative studies to quantitatively assess contact ion pair formation in solution. The 2D-IR signals accentuate ion induced frequency shifts and excited state lifetimes and allow thus for higher contrast than achievable with linear IR spectroscopy. For such reasons, the 2D-IR spectra provide more meaningful information to characterize the (PO₂)⁻–ion interactions in solution. As will be discussed in subsequent sections, an extension of this approach to quantify the ionic environment and dynamics of RNA provides insights into the interactions stabilizing the equilibrium structures.

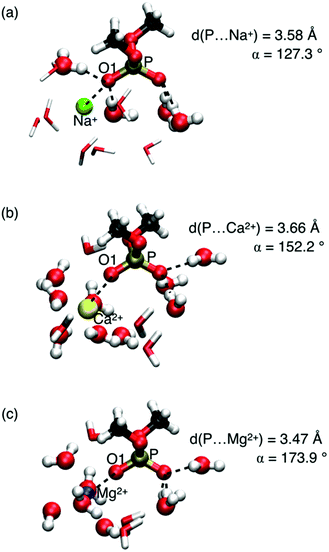
A relevant question concerns the ion identity and charge, and the selectivity of frequency shifts of the ν_AS(PO₂)⁻ vibration. Properties of contact pairs formed in water by DMP with Na⁺, Ca²⁺, and Mg²⁺ ions were addressed using a combined theoretical and experimental approach.^65,68 For the different ions, striking geometric differences were identified. Contact pairs of DMP and Mg²⁺ were found to have an approximate linear arrangement of the coordinated P=O group and the Mg²⁺ ion, characterized by the P⋯O1⋯ion angle α ≈ 174° (Fig. 8). In the contact pair geometry, one water molecule of the six-fold coordinated Mg²⁺ ion is replaced by the O1 atom of the (PO₂)⁻ group. Thus, the rigid octahedral first solvation shell of Mg²⁺ is preserved in the linear arrangement of the contact pair. The short P⋯Mg²⁺ distance ≈3.5 Å (O1⋯Mg²⁺ distance ≈2.1 Å) imposes strong repulsive exchange interactions subject to the displacement along the ν_AS(PO₂)⁻ normal mode vector inducing a pronounced blue shift of the ν_AS(PO₂)⁻ transition frequency.

Fig. 8 DMP(H₂O)_NM^x+ cluster geometries (M^x+ = Na⁺, Mg²⁺, N = 11; M^x+ = Ca²⁺, N = 13). Water molecules of the first hydration shell around the ions and hydrogen bonded water molecules with DMP in ball-and-stick representation; the O1 atom of the (PO₂)⁻ group replaces one of the water oxygen atoms in the octahedral solvation geometry around the Mg²⁺ ion. Vibrational frequencies ν_AS(PO₂)⁻ of structures shown in a, b and c are 1208, 1226, and 1248 cm⁻¹, respectively. Adapted with permission from ref. 65. Copyright 2019 American Chemical Society.

In contact pairs of DMP and Na⁺ different geometries are realized and the P⋯O1⋯Na⁺ angle α ≈ 127° is a hallmark of a tetrahedral HB geometry around the (PO₂)⁻ group. The Na⁺ ion intercalates into the preserved HB environment around the (PO₂)⁻ group by replacing a single water molecule in the first hydration shell around the O1 atom. In such contact pair geometries, spatial displacements along the displacement direction of the ν_AS(PO₂)⁻ mode are less restricted and the effect on the ν_as(PO₂)⁻ transition frequency is only modest.

Compared to Mg²⁺ ions, DMP⋯Ca²⁺ contact pairs display a larger structural variation. In contact pairs with Ca²⁺ the quasi-linear P⋯O1⋯Ca²⁺ geometry is largely preserved and one of the oxygen atoms of the (PO₂)⁻ group replaces a water oxygen in the first solvation shell of Ca²⁺. Nevertheless, because of the less rigid hydration shell around Ca²⁺, the blue shift of the ν_AS(PO₂)⁻ transition frequency is less pronounced (1226 cm⁻¹vs. 1248 cm⁻¹).

IR absorption and 2D-IR spectra of the ν_AS(PO₂)⁻ vibration confirmed the gradual behaviour for ions Na⁺, Ca²⁺, and Mg²⁺. The combined experimental and theoretical results demonstrate that in a water environment the (PO₂)⁻ group of DMP forms contact ion pairs with Na⁺, Ca²⁺, and Mg²⁺, however, with distinctly different geometric arrangements and interaction patterns. Contact pairs with Mg²⁺ ions stand out with their particularly rigid, long-lived structure and the shortest distance between one of the (PO₂)⁻ oxygens and the Mg²⁺ ions, strongly affecting the electronic structure of the phosphate group, as manifested in the pronounced changes of the vibrational potential energy surface.

The comparative experimental and theoretical investigation of contact ion pairs of DMP with Na⁺, Ca²⁺, and Mg²⁺ in water gave detailed insights into the prevailing molecular structures and revealed the characteristic structural differences between the different contact pairs. The results emphasize that the asymmetric (PO₂)⁻ stretching vibration ν_AS(PO₂)⁻ represents a most sensitive probe of the local hydration environment allowing the details on the molecular structure and dynamics to be deduced. The rigorous access to DMP and its interactions with ions in solution thus represents a valuable model and provides insights into the following aspects of phosphate–water interactions:

• Mutual interaction pattern and electric field strength induced by multipolar electrostatics, polarization and exchange repulsion at short distances;

• Effective short range spatial reach and fluctuation timescales of electric fields;

• Hydration shell induced ν_AS(PO₂)⁻ frequency shifts mediated by the linear Stark shift;

• Quantification of counter ion interactions and ion induced spectral shifts of the ν_AS(PO₂)⁻ transition frequencies.

In the macromolecular structures of RNA, the sugar-phosphate backbone of RNA imposes additional structural boundary conditions that can affect the hydration shell and fluctuation dynamics.³¹ Subsequent sections will lay out to which extent the rigorous findings of the DMP model system apply to the hydration environment and ion atmosphere of dsRNA and tRNA.

Hydration structure of A-helical dsRNA

Double-stranded RNA (dsRNA) plays an important role in a variety of biological activities, including the transport of messenger RNA (mRNA), RNA interference and editing⁶⁹ and the initiation of the immune response.⁷⁰ In folded RNA structures,¹⁶ partially helical stem domains are present that resemble A-helical dsRNA. The interactions of dsRNA and water and their particular role in the formation of the macromolecular structure are difficult to access and are only insufficiently understood.

The interaction of an alternating (AU)₂₃ dsRNA with the water shell was investigated by combining the results from MD simulations, mixed quantum mechanical – molecular mechanical (QM/MM) simulations and time-resolved 2D-IR experiments.⁷¹ By exploiting the interfacial sensitivity, the vibrations of the RNA sugar phosphate backbone serve as sensitive non-invasive probes for the influence of water molecules on the structure and dynamics of RNA. The simulations allowed for the first complete and quantitative identification of the different vibrations of the RNA backbone and showed partially ordered water arrangements around the dsRNA. Due to the A-helical structure of dsRNA, the distances between the adjacent (PO₂)⁻ groups are reduced compared to a B-helix.¹¹ In MD simulations, single water molecules were observed to bridge neighbouring (PO₂)⁻ groups. Additionally, the C2′–OH group of the ribose ring mediates ring structures made of ≈3 water molecules that connect the (PO₂)⁻ group and the OH group, leading to a partially ordered water structure in the minor groove of dsRNA (Fig. 9).

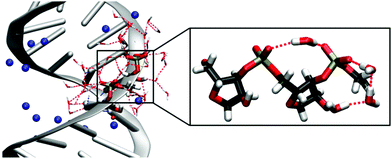Fig. 9 Solvation structure of the sugar-phosphate backbone of (AU)₂₃ dsRNA obtained from MD simulations with counterions shown in blue. The inlay magnifies a (PO₂)⁻⋯(PO₂)⁻ bridging water molecule and the hydrogen bond network ring structure mediated by the C2′–OH group. MD structures taken from Ref. 71. Adapted with permission from Ref. 46. Copyright 2020 Springer Nature.

The partially ordered hydration shell around the sugar-phosphate backbone of dsRNA observed in MD simulations is expected to reduce the heterogeneity of the first few hydration layers around the A-helix. 2D-IR spectroscopy of phosphate backbone vibrations with femtosecond time resolution allowed to resolve inhomogeneities on a few picosecond timescale.⁷¹ Such experiments corroborate a partially ordered water structure via the observation of a reduced inhomogeneous width of the 2D lineshapes of dsRNA, compared to DNA.^31,72 Diagonal peaks in 2D-spectra reveal a reduced inhomogeneity of symmetric and asymmetric phosphate stretching vibrations and cross peaks show strong couplings between the (PO₂)⁻ groups and C2′–OH stretching and the C1′–O4′–C4′ ribose stretching vibrations. Partially ordered water molecules that connect the (PO₂)⁻ group and C2′–OH group (Fig. 9) could be instrumental in inducing the pronounced inter-mode vibrational couplings between the phosphate group and the ribose unit. The ordered water arrangements around A-helical dsRNA observed in MD simulations and supported by 2D-IR spectroscopy are in agreement with the reported structures from X-ray diffraction studies^10,11 in crystallized samples with a limited hydration level.

The analysis of MD simulations and 2D-IR spectra suggests that the dynamics of water molecules at the dsRNA surface is dominated by librational tipping motions. The librating water molecules generate fluctuating electrical forces by which the water fluctuations are transferred and reflected in the vibrational lineshape. Thermal motions of the water molecules result in field fluctuations of ≈25 MV cm⁻¹ on a 300 fs timescale, in reasonable agreement to the fluctuation dynamics sensed by the (PO₂)⁻ group in DMP (Fig. 2 and 3). Compared to DMP, the slightly slower 300 fs fluctuation timescale reflects a hindrance of free water motions due to the coupling to the corrugated RNA surface and moderately deviates from that of neat water.⁷³ Heterogeneities of the macromolecular structure induce additional inhomogeneities that reflect different hydration environments with different arrangements of individual water molecules, e.g., connecting neighbouring phosphate groups. The local spatial (PO₂)⁻–water arrangements are preserved for a time range of >10 ps as reflected by the static 2D-IR lineshape within the observation time. In addition, the RNA backbone vibrations couple mutually and exchange energy among themselves and with the water shell.^32,71,74 The resulting ultrafast redistribution of excess energy is essential for avoiding a local overheating of the sensitive macromolecular structure. Combined MD simulations and 2D-IR measurements thus provide detailed insights into the hydration pattern at the RNA surface, highlighting the strong potential of non-invasive time-resolved vibrational spectroscopy in unravelling the interplay of structure and dynamics in complex biomolecular systems on molecular length and timescales.

Short-range solvent interactions define the ν_AS(PO₂)⁻ transition frequency of dsRNA

Insights into the interactions at the surface of RNA were obtained by simulations of the IR spectrum of A-helical (AU)₂₃ dsRNA. The high sensitivity of the ν_AS(PO₂)⁻ vibrations directly encodes different local hydration geometries at the helix surface. Detailed simulations of the IR spectra allow the quantification of the structures sampled in long time MD simulations. Furthermore, a benchmark of accuracy of the employed force fields can be obtained via the comparison to infrared spectra of ν_AS(PO₂)⁻ vibrations. The ab initio and QM/MM methods used for the simulation of the IR spectrum inherently account for charge transfer and many body polarization within the QM region. In this context, QM regions that accurately represent the relevant reach of interactions are important for accurate simulations of IR spectra of macromolecular RNA structures embedded in the aqueous environment.

Fig. 10 shows the IR spectrum of the ν_AS(PO₂)⁻ vibrational band simulated at the QM/MM level of theory that is compared to the experimental spectrum of the ν_AS(PO₂)⁻ vibration covering an ≈80 cm⁻¹ spectral range (1190–1270 cm⁻¹). Good agreement is obtained in the frequency position and the width of the ν_AS(PO₂)⁻ band. The favourable agreement provides insights into the underlying (PO₂)⁻ hydration structures contributing to the different ranges of the spectrum. The IR spectrum in the range of the ν_AS(PO₂)⁻ vibration shows two prominent peaks centred around 1220 and 1240 cm⁻¹. In the simulations, the frequency position of the peaks is reproduced with excellent accuracy, albeit with a slightly different intensity ratio.

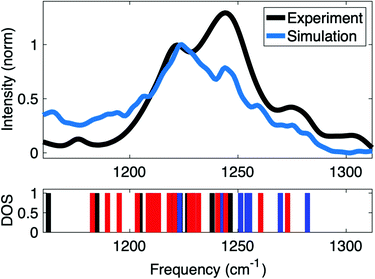Fig. 10 Comparison of experimental and simulated IR absorption spectrum of ν_AS(PO₂)⁻ vibrations and vibrational density of states (DOS) showing the frequency positions of contact pair geometries (blue), solvent separated ion pairs (red) and fully solvated (PO₂)⁻ groups (black). Simulations at QM/MM level of theory use a hybrid density functional with exact exchange and empirical dispersion corrections (B3LYP-D, basis: 6-31G* and 6-311+G** for phosphorus atoms) for the QM region and all atoms within 15 Å of the QM region were further included as point charges in the single electron Hamiltonian to account for long-range polarization of the QM region via electrostatic embedding. QM/MM vibrational frequencies were evaluated for all bi-phosphate – tri-ribose segments along the dsRNA helix in double harmonic approximation, followed by averaging over the different spatial positions. Adapted with permission from ref. 85. Copyright 2021 Elsevier.

Simulations of the vibrational frequencies of the complete sugar-phosphate backbone of (AU)₂₃ dsRNA are prohibitively expensive till date. Thus, a numerical strategy was proposed that relies on the additive construction of the macromolecular IR spectrum from smaller QM/MM models of adjacent bi-phosphate–tri-ribose segments. In this context, of particular relevance is the extent of the QM region used in simulations of the ν_AS(PO₂)⁻ vibrational band. In the QM/MM simulations, the sugar-phosphate backbone of each segment together with the water molecules in the first solvation shell of the (PO₂)⁻ groups, contact ions and water molecules in the first solvation shell of contact ion pairs were treated at the QM level of theory. Inherently such a restriction of the QM region to the adjacent phosphate groups assumes local hydration structures that span only a few phosphate-ribose segments.

Benchmarked via comparison with the experimental linear infrared absorption spectrum (Fig. 10), the QM/MM approach is fully reasoned by the hydration environment of dsRNA and builds on the findings of short-ranged electric forces arising locally from the first and second hydration shells in the DMP model system (Fig. 4). In dsRNA, the local hydration geometries are formed by water molecules in the vicinity of the sugar phosphate backbone and the interactions between neighbouring (PO₂)⁻ groups are mediated by bridging water molecules (Fig. 9 and 11a). Accordingly, the ≈90 cm⁻¹ width of the ν_AS(PO₂)⁻ band is induced by a heterogeneity of hydration environments around the (PO₂)⁻ groups. This suggests a physical picture where the frequency position of the ν_AS(PO₂)⁻ modes reflects the interaction pattern at a particular helix position via a direct impact on the (PO₂)⁻ bonding potential. Water molecules in direct contact with the (PO₂)⁻ group impose strong electric interactions and induce a mutual polarization at the interface. These many-body interactions are complemented by longer range electric interactions that further polarize the (PO₂)⁻ group on the ≈1 nm length scale.

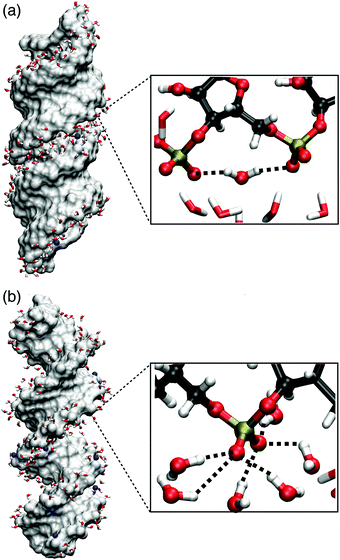Fig. 11 Molecular surface of (AU)₂₃ dsRNA (a) and (AT)₂₃ DNA (b) for structures obtained from MD simulations (ref. 75) with Na⁺ counterions shown in blue. The inlays show instantaneous hydration structures of the (PO₂)⁻ groups, highlighting a (PO₂)⁻⋯(PO₂)⁻ bridging water molecule (a) and local hydration structures of six water molecules forming HBs with one (PO₂)⁻ groups (b).

Additionally, contact pairs of Mg²⁺ ions and the (PO₂)⁻ group contribute in a range ν_AS(PO₂)⁻ = 1243–1282 cm⁻¹ to the blue edge of the ν_AS(PO₂)⁻ band while solvent separated ion pairs were found to contribute predominantly on the red side of the spectrum. Strong repulsive interactions at short distances are instrumental for establishing blue-shifted ν_AS(PO₂)⁻ vibrations in contact geometries with Mg²⁺ ions. Accordingly, the microscopic mechanism inducing the frequency shifts in DMP (cf.Fig. 5 and 6) is operational also in more complex RNA structures: ion induced ordering of the hydration shell leads to an increase of the local electric field imposed on the (PO₂)⁻ group which, via the linear Stark effect, translates into a red shift of the particular ν_AS(PO₂)⁻ vibrator. In contrast, contact pairs of (PO₂)⁻ groups with Mg²⁺ ions induce a blue-shift of the ν_AS(PO₂)⁻ vibration due to exchange repulsion induced distortions of the potential. The good agreement between theory and experiment suggests that the influence of the hydration shell on the (PO₂)⁻ binding potential is dominated by short range interactions with the first (and to a lesser extend second) hydration shell around the (PO₂)⁻ group. It was further found that the QM/MM approach is transferrable to simulations of the ν_AS(PO₂)⁻ IR band of structurally more complex tRNA^Phe (see below), stressing the universality of the short-ranged interaction pattern in defining the properties of the biomolecular phosphate–water interface.

A-Helical structural impact on the ν_AS(PO₂)⁻ absorption band

The IR spectrum of the ν_AS(PO₂)⁻ vibrations in the 1220–1240 cm⁻¹ range shows two prominent peaks. Local (PO₂)⁻ hydration geometries at particular helix positions determine the frequency position of the ν_AS(PO₂)⁻ modes which suggests a dominant inhomogeneous broadening mechanism for the ν_AS(PO₂)⁻ band. In this picture, the heterogeneity of local (PO₂)⁻ hydration environments leads to distinct peaks in the IR spectrum. The 2D-IR experiments strongly support this scenario because of negligible crosspeaks between the 1220 and 1240 cm⁻¹ peaks.^71,72 A detailed analysis of the 2D line shapes identifies a dominant inhomogeneous broadening mechanism with a residual ≈10 cm⁻¹ homogeneous broadening due to fast ≈300 fs librational fluctuations and lifetime broadening, thus suggesting a minor influence of excitonic coupling between the (PO₂)⁻ sites.

Insights into the heterogeneity of hydration geometries were obtained via the analysis of fluctuating electric fields the water environment impinges on the (PO₂)⁻ groups of dsRNA.⁷⁵ It was found that the magnitude of the total electric field imposed on the (PO₂)⁻ group reaches an average of E ≈ 80–150 MV cm⁻¹. Nevertheless, upon projection on the O1=P=O2 angle bisector axis, the projected electric field E_p is reduced at particular (PO₂)⁻ sites (mean E_p ≈ 30 MV cm⁻¹). E_p is greatly reduced because the dsRNA surface imposes steric constraints that prevent a symmetric hydration environment of the two non-esterified oxygen atoms of the (PO₂)⁻ group. Thus, the direction of the total electric field imposed on the (PO₂)⁻ group deviates substantially from the angle bisector axis (cf.Fig. 1a) and its magnitude is greatly reduced upon projection. Fig. 11 shows the instantaneous hydration geometries of dsRNA (PO₂)⁻ groups of dsRNA that rationalize the asymmetric environment of non-esterified oxygen atoms O1 and O2. In the groove region of the A-helix, the O1 oxygen atom points outward towards the solvent and is largely accessible. Thus, on average, HBs with three water molecules are formed. In contrast, the O2 oxygen atom points into the deep and spatially constrained major groove which breaks the symmetry between the O1 and O2 oxygen atoms. An economization in the number of HBs⁷ subject to the steric constraints of the deep major groove is facilitated by the short ≈4.6 Å separation of the neighbouring (PO₂)⁻ groups which allows the formation of HB bridges between the adjacent (PO₂)⁻ groups.

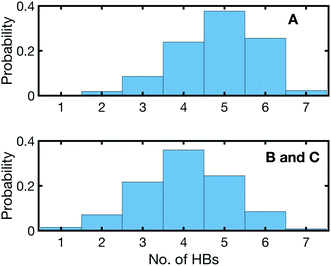
The undercoordination of the (PO₂)⁻ groups thus induces an overlap of the hydration shell of neighbouring (PO₂)⁻ groups. Additionally, coexisting DNA-like local hydration motifs are present for dsRNA in a water environment. The bimodal distribution of HBs formed by the (PO₂)⁻ groups of dsRNA reflects the different coexisting hydration motifs present in the A-helix (Fig. 12). For accessible phosphate groups, the hydration shell resembles the situation in the B-helix of DNA and on average >5 HBs are formed. For spatially constrained (PO₂)⁻ groups the number of HB is significantly reduced. Compared to the B-helix of DNA where the (PO₂)⁻ groups are fully accessible (Fig. 11b), the hydration structure of dsRNA is thus markedly different and more heterogeneous due to the constraints imposed by the macromolecular A-helical structure.

Fig. 12 Histogram of hydrogen bonds (HBs) in the first water layer around (PO₂)⁻ groups in (AU)₂₃ dsRNA. A denotes (PO₂)⁻ groups with a local hydration structure forming HBs with a single (PO₂)⁻ group and B and C denote undercoordinated (PO₂)⁻ groups with (PO₂)⁻⋯(PO₂)⁻ bridging water molecule or contact ion pair structures. Hydrogen bonds were averaged over six different 4 ns segments, equally separated in a 1.2 μs molecular dynamics trajectory. Adapted with permission from ref. 72. Copyright 2020 American Chemical Society.

The partial under-coordination of the (PO₂)⁻ groups, in particular in the major groove of dsRNA leads to an electrostatic environment where for a subset of the (PO₂)⁻ groups the projected electric field E_p is reduced by some 50 MV cm⁻¹. Note that the constraints imposed by the RNA surface lead to local heterogeneities of hydration environments and not necessarily a spatially homogeneous field distribution in the major groove. Assuming a Stark tuning rate a ≈ 0.5–0.6 cm⁻¹ (MV cm⁻¹)⁻¹,^52,60 the reduced E_p suggests a splitting of the transition frequencies of the ν_AS(PO₂)⁻ vibration by some 25–30 cm⁻¹, in excellent agreement with the 28 cm⁻¹ peak splitting observed in the IR spectrum of dsRNA (Fig. 10). It is thus suggested that the double peak structure of the ν_AS(PO₂)⁻ vibrations provides an indirect view of the different electric field interaction strength that arises from the heterogeneous hydration environments of the (PO₂)⁻ groups. The collective coordinate of the electric field interaction strength determines the spectral properties of the ν_AS(PO₂)⁻ stretching vibrations for a large variety of biomolecular systems. The Stark tuning rates of universal magnitude in the range a ≈ 0.5–0.6 cm⁻¹ (MV cm⁻¹)⁻¹ provide a consistent interaction picture for dsRNA, folded tRNA, and native DNA and DNA model systems at different hydration levels.⁷⁵

Temperature induced changes of the hydration shell

Structural changes associated with RNA folding, RNA replication or RNA melting at an elevated temperature are inevitably connected with a change in the local hydration pattern around the sugar-phosphate backbone. The exceptional sensitivity of the ν_AS(PO₂)⁻ vibration to the local hydration environment was employed to quantify the structure induced changes of hydration geometries around the (PO₂)⁻ groups at the molecular level.⁷² RNA melting at an elevated temperature was shown to be connected with a transition from the predominantly ordered chain-like hydration motifs, where the arrangements of water molecules bridge adjacent (PO₂)⁻ groups, to the local, DNA-like hydration shells of up to six water molecules that are formed around a single phosphate group (Fig. 11). Temperature induced changes in the frequency position and line shape of the ν_AS(PO₂)⁻ vibration (Fig. 13) reflect the abundance of the coexisting hydration motifs present in the RNA A-helix by mapping the local electric field that the water hydration shell exerts on the phosphate group. In the temperature range of 303–333 K, the infrared spectra show gradual changes in the double peak structure. From 338 K onwards, a qualitative change of the line shape is observed leading to a single broad absorption peak that resembles the absorption spectrum of DNA.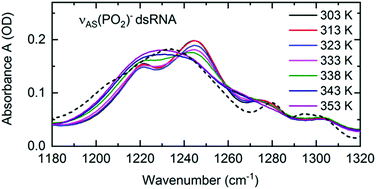

Fig. 13 Linear infrared absorption spectra of the ν_AS(PO₂)⁻ stretching vibrations of (AU)₂₃ dsRNA in water at different sample temperatures (RNA concentration c(RNA) = 2.3 mM). In the temperature range 303–333K, infrared spectra are shown in increments of 10 K. 5 K increments were employed above 333 K to highlight the major changes in the spectra around 338 K. Dashed line: infrared absorption of DNA oligomers at 303 K. The spectrum is scaled to the RNA peak absorption at 1230 cm⁻¹ (T = 353 K). Adapted with permission from ref. 72. Copyright 2020 American Chemical Society.

The thermal transition from ordered water structures to local phosphate hydration shells is accompanied by an increase in the average number of (PO₂)⁻–water HBs (Fig. 12) in the DNA-like hydration shells that are fully exposed to the solvent. At a high temperature, the RNA helix undergoes a structural transition and becomes increasingly disordered, thus exposing the buried (PO₂)⁻ groups of the major groove region to the solvent which increases their accessibility, thus favouring the formation of the DNA-like local hydration shells. The increase in the number of HBs around the (PO₂)⁻ group at an elevated temperature thus leads to an increase in the RNA hydration free energy.^76,77 Quantum chemical simulations suggest an enthalpic stabilization in the order of −(20–40) kJ mol⁻¹ per HB⁷² and a concomitant decrease of entropy. Owing to entropic compensation,^77,78 the changes in the hydration free energy are on the same order of magnitude as those due to self-association of the nucleobases. It is thus suggested that the melting induced hydration processes are a non-negligible part of the free energy balance during RNA self-association and melting that is commonly disregarded.

Contact ion interactions stabilize the tertiary structure of tRNA

Transfer RNA (tRNA) is a key biomolecule during translation that acts as an adaptor between the codon of the messenger RNA (mRNA) and the amino acids used in protein synthesis.¹ The tertiary structure of phenylalanine tRNA (tRNA^Phe) from yeast has been determined using high resolution X-ray diffraction.¹⁶ The prominent L-shaped cloverleaf structure (Fig. 14) consists of the anticodon loop, the D loop, the TΨC loop, the variable loop and the acceptor stem. An A-helical double stranded stem domain connects the anticodon loop with the D loop and the TΨC loop. The helical acceptor stem at the 3′ end serves for attaching the amino acid phenylalanine for protein synthesis.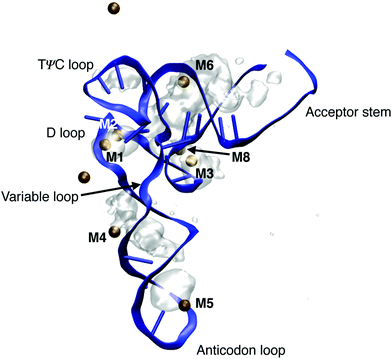

Fig. 14 Ion density around tRNA^Phe of doubly charged ions Mg²⁺ and Mn²⁺. Ion densities are averaged over a 1 μs simulation time and are shown together with the instantaneous geometry of tRNA^Phe after 1 μs and the instantaneous position of Mg²⁺ and Mn²⁺ ions (ochre spheres). Ion densities are shown for an iso-value of 0.003 Å⁻³. MD structure taken from ref. 80.

Particularly short inter-phosphate distances are found in the loop domains of the cloverleaf structure. For maintaining the folded structure, a basic prerequisite for the cellular function of tRNA, the strong repulsive electric forces between the negatively charged phosphate groups need to be compensated by positively charged ions and by water molecules in the environment. The role of the different hydration structures, ion geometries and relevant interactions for stabilizing the tertiary structure of tRNA are far from being understood at the molecular level. In particular, the local hydration geometries in the presence of ions are barely characterized and conflicting pictures of ion and water arrangements at the surface of tRNA have been suggested. The high-resolution X-ray structure¹⁶ identified dedicated binding sites of divalent metal ions Mg²⁺ and Mn²⁺ close to the positions of the (PO₂)⁻ groups in the folded backbone. Of particular interest are ion positions in the vicinity of the D loop (M1 in Fig. 14) where a strong bending of the sugar-phosphate backbone results in inter-phosphate distances of neighbouring (PO₂)⁻ oxygen atoms below 4 Å, i.e., substantially shorter than in the A-helical parts of the structure. The X-ray diffraction data suggest that such sites are preferentially populated by Mg²⁺ ions with the (PO₂)⁻ oxygens being part of the first solvation shell of the ion or separated by a single water layer. These assignments have been challenged by findings of the nonlinear Poisson–Boltzmann (PB) model that interpreted the binding of Mg²⁺ to tRNA^Phe based on a single class of Mg²⁺ ions that retain a complete water shell and stabilize the RNA structure by long-range electrostatic interactions.⁷⁹

By employing the ν_AS(PO₂)⁻ molecular vibrations of the (PO₂)⁻ groups as non-invasive probes of the coupling between tRNA^Phe, ions and the aqueous environment, contact pairs of Mg²⁺ and (PO₂)⁻ groups were identified as a decisive structural element for minimizing the electrostatic energy and, thus, the stabilization of the tertiary structure of tRNA.⁸⁰ By combining spectroscopic experiments of the Mg²⁺ ion uptake of dialyzed tRNA^Phe and in-depth theoretical calculations of molecular interactions and dynamics, detailed insights into the local hydration geometries of tRNA^Phe and the relevant ion arrangements could be obtained. Fig. 14 shows the ion density around tRNA^Phe of doubly charged ions Mg²⁺ and Mn²⁺ obtained from a 1 μs molecular dynamics simulation. In the grooves of the helical stem regions, diffuse and mobile ion populations are found where the hydration geometries of Mg²⁺ ions are determined by solvent separated ions bridging the deep and narrow groove in the stem domains of tRNA^Phe (M4 and M6). These ions show constrained mobility and exchange with ions embedded in the solvent on the μs timescale. Localized and immobilized ion populations were found in the D loop, in the contact regions of the D loop and the TΨC loop and at the tip of the anticodon loop. After 1 μs simulation time, 5 contact ion pairs with doubly charged ions are observed, in agreement with the estimates from the fluorescence and linear infrared absorption measurements (see below).

Infrared spectroscopy of contact ion pair geometries in tRNA^Phe

The existence of two distinct ion populations for tRNA in aqueous solution with different mobility properties and interaction patterns was unequivocally determined by the multi-faceted combination of fluorescence titration measurements, linear vibrational spectroscopy and two-dimensional infrared spectroscopy of dialyzed tRNA^Phe from yeast and unspecific tRNA from Escherichia coli. The frequency and infrared absorption strength of the ν_AS(PO₂)⁻ vibration again serves as the most sensitive probe for the local interactions at the tRNA surface that encode details about the interactions with ions and water molecules. Vibrational spectroscopy of the tRNA samples with different Mg²⁺ contents together with 2D-IR spectroscopy in the femtosecond time domain allowed for discerning the local geometries where the (PO₂)⁻ groups directly couple with the ions and the water shell, from unspecific long-range interactions of Mg²⁺ ions with tRNA in a mobile ion atmosphere. As demonstrated quantitatively by high level QM/MM simulations (Fig. 15a), the presence of a Mg²⁺ ion in the immediate vicinity of a (PO₂)⁻ group shifts the transition frequency of the ν_AS(PO₂)⁻ vibration to a higher frequency and generates a characteristic infrared absorption band used for detection of contact pair molecular species (cf. M2 band of the molecular model system DMP, Fig. 7). The origin of the blue shift of the ν_AS(PO₂)⁻ vibration is the incorporation of one of the (PO₂)⁻ oxygens into the rigid octahedral first hydration shell of Mg²⁺ ion. In the contact complex, the Mg²⁺⋯(PO₂)⁻ oxygen distance is particularly short (≈2.1 Å) and displacements along the normal mode induce a distortion of the potential due to repulsive interactions and an upshift of the ν_AS(PO₂)⁻ transition frequency. The mechanism of the blue-shifted transition frequency is thus fully analogous to the observed blue-shifting of the ν_AS(PO₂)⁻ transition frequency in the model system DMP (Fig. 5–8).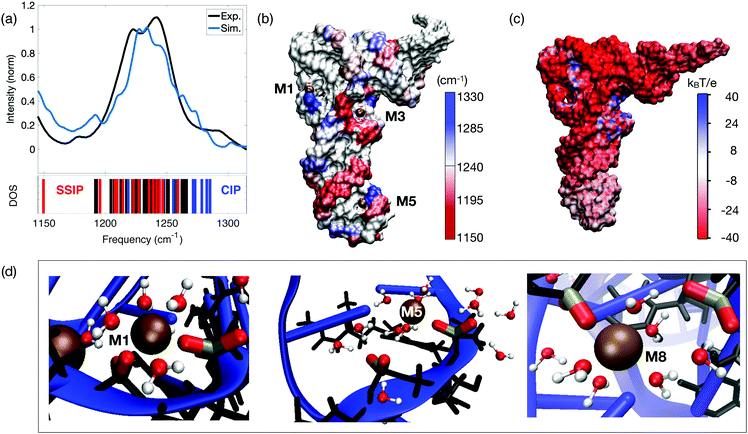

Fig. 15 (a) Simulated and experimental linear infrared absorption spectra in the frequency range of ν_AS(PO₂)⁻ stretching vibrations. Simulations are compared to the experimental infrared spectrum of undialyzed tRNA^Phe from yeast in water. The simulated vibrational DOS of the ν_AS(PO₂)⁻ band color-codes the frequency positions of contact ion pairs of the (PO₂)⁻ group with Mg²⁺ ions (CIP, blue) and of SSIPs (red). Frequency positions of the remaining (PO₂)⁻ groups are indicated in black. (b) Simulated spatial distribution of ν_AS(PO₂)⁻ vibrational frequencies. The surface color of the sugar-phosphate backbone encodes the local ν_AS(PO₂)⁻ frequency. (c) Electrostatic surface potential evaluated for 3200 snapshots at the end of a 1 μs MD trajectory. (d) Prototype solvation geometries around (PO₂)⁻ groups with the first-solvation shell water molecules around (PO₂)⁻ groups and Mg²⁺ ions shown in ball and stick representation. Solvation structure M1 (left) shows bidentate inner-sphere coordination of Mg²⁺ by two adjacent (PO₂)⁻ groups (ν_AS(PO₂)⁻ = 1285 and 1247 cm⁻¹); M5 (middle) shows contact ion pair formation of the (PO₂)⁻ group and Mg²⁺ in the anticodon loop. First-solvation shell waters are shared by Mg²⁺ and the adjacent (PO₂)⁻ group (ν_AS(PO₂)⁻ = 1278 and 1208 cm⁻¹); M8 shows a CIP within the D loop and SSIP mediated interstrand contact to the TΨC loop (ν_AS(PO₂)⁻ = 1282 and 1210 cm⁻¹). Reprinted with permission from ref. 80. Copyright 2019 American Chemical Society.

Linear and nonlinear infrared spectroscopy experiments of dialyzed tRNA^Phe, initially containing ≤1 Mg²⁺ ion per RNA molecule,^80,81 allowed the population of the Mg²⁺ sites in the vicinity of the (PO₂)⁻ groups of the ribose-phosphodiester backbone to be followed step by step for different concentrations of Mg²⁺ ions. The linear infrared absorption spectra in the range of the ν_AS(PO₂)⁻ vibrations of tRNA^Phe show two strong components with maxima at 1220 and 1241 cm⁻¹ and a shoulder around 1270 cm⁻¹ (black line in Fig. 15a). An analysis of electric field distributions indicates that steric constraints preclude the full hydration of the two non-esterified oxygen atoms at various positions of the tRNA, leading to a reduction of the electric interaction upon projection. Similar mechanisms thus appear to be operational for the formation of doublet peaks in dsRNA and tRNA.⁷⁵

Upon addition of Mg²⁺ ions, the infrared absorption undergoes systematic changes, that is, a decrease of absorption in the 1220–1241 cm⁻¹ range and an absorption increase around 1270 cm⁻¹ due to the formation of contact pairs of Mg²⁺ ions and (PO₂)⁻ groups. The increase in absorption around 1270 cm⁻¹ is initially linear for the first few (≈2) Mg²⁺ ions, followed by a more gradual increase for higher Mg²⁺ contents showing that only a fraction of all Mg²⁺ ions interacting with tRNA contribute to this particular absorption band, i.e., are accommodated as contact pairs with the (PO₂)⁻ groups. Complementary 2D-IR experiments discern the three components around 1220, 1245, and 1270 cm⁻¹. The observation of elongated line shapes along the diagonal reflects the inhomogeneous broadening due to a distribution of vibrational frequencies of the (PO₂)⁻ groups with different local hydration environments. Together the experiments show that in solution tRNA forms up to six contact ion pairs, out of the total ≈15 Mg²⁺ ions interacting with tRNA in solvent separated ion pairs and contact pairs.

The simulations show that contact pairs are formed preferentially at locations where the distance between neighbouring phosphate groups is small and the corresponding negative charge density is high. Fig. 15 provides a detailed analysis of the individual contributions of the (PO₂)⁻ groups to the linear absorption spectrum of tRNA^Phe, together with the underlying hydration geometries defining the transition frequencies. The QM/MM simulations of the tRNA^Phe backbone vibrations reveal a distribution of the ν_AS(PO₂)⁻ transition frequencies induced by differences of the local hydration geometries around the (PO₂)⁻ groups and specific ion interactions at different positions on the tRNA^Phe surface. In analogy to dsRNA (Fig. 10), accurate simulation of transition frequencies of tRNA^Phe backbone vibrations required to treat the sugar–phosphate backbone, counter ions and water molecules in the first solvation shell of the (PO₂)⁻ groups or in the first solvation shell of contact ion pairs at the QM level of theory. The frequency positions ν_AS(PO₂)⁻ of particular (PO₂)⁻ groups are determined by rather local hydration geometries that involve the water molecules of up to only a few adjacent (PO₂)⁻ groups, e.g., due to bridging water configurations (cf.Fig. 11 and 15d). With such a numerical approach, excellent agreement in the frequency position and width of the ν_AS(PO₂)⁻ band can be obtained, covering a range from ∼1180 to 1290 cm⁻¹. Some deviation in the intensity in the different frequency ranges is recognized.

Heterogeneity of the hydration geometries at the surface of tRNA^Phe

The simulated linear absorption spectrum of tRNA^Phe (blue line, Fig. 15a) was dissected to characterize the molecular hydration geometries that contribute to a particular spectral range (blue line in Fig. 15a and vibrational density of states (DOS)). The predominant contribution from the contact pairs of Mg²⁺ ions and (PO₂)⁻ groups is found in the frequency range ν_AS(PO₂)⁻ = 1247–1285 cm⁻¹, closely mimicking the experimentally observed absorption increase around 1270 cm⁻¹ for increasing Mg²⁺ content. Solvent separated ion pairs are characterized by a moderate red-shift of ν_AS(PO₂)⁻ in the frequency range 1150–1247 cm⁻¹. Characteristic hydration geometries at the surface of tRNA^Phe are illustrated in Fig. 15d. The bidentate inner-sphere complexation of Mg²⁺ ions by two (PO₂)⁻ groups of the D loop induces a pronounced blue-shift of the ν_AS(PO₂)⁻ vibration (M1 in Fig. 15d). A similar blue-shift of the ν_AS(PO₂)⁻ vibration was found for the singly coordinated contact pair in the anticodon loop (M5 in Fig. 15d). At this site, water molecules that are part of the octahedral first solvation shell of the Mg²⁺ ion form HB to the adjacent (PO₂)⁻ group. For such solvent separated ion configurations adjacent to a contact pair, a red-shift of ν_AS(PO₂)⁻ in the range 1200–1220 cm⁻¹ was found. The red-shift is induced by the ion induced ordering of the water arrangement around the (PO₂)⁻ group in the solvent separated ion pair by which the local electric field acting on the (PO₂)⁻ group is enhanced. A similar situation is realized at position M8 where the contact between the D loop and the TΨC loop is mediated via the hydration structures of the contact and solvent separated ion pairs (Fig. 15d). These observations correlate with the experimental findings of increased absorption in the range of 1180–1230 cm⁻¹ upon the addition of small amounts of Mg²⁺ ions to dialyzed tRNA^Phe.⁸⁰

The hydration motif of mixed inner- and outer-sphere coordination in adjacent contact and solvent separated ion pairs (both intra- and inter strand) results in the substantial >60 cm⁻¹ spread of asymmetric stretching frequencies ν_AS(PO₂)⁻ on a short sub-5 Å length scale. The spatial mapping of the ν_AS(PO₂)⁻ transition frequencies to the surface of tRNA^Phe exemplifies the pronounced local variations and local heterogeneities of the (PO₂)⁻ group hydration structures (Fig. 15b). Because of the high water accessibility of the helical stem connecting the anticodon loop with the D and TΨC loops, this region shows a more homogeneous frequency distribution ν_AS(PO₂)⁻ ∼ 1220 cm⁻¹.

Electrostatic surface potential of tRNA^Phe

Simulations of the electrostatic potential of DNA or RNA typically employ approaches rooted in PB theory^82–84 The interaction picture at the phosphate–water interface of dsRNA suggested by PB simulations was recently questioned.⁸⁵ Deficiencies were identified for interaction strength, the ion geometries at the RNA surface and structure–ion correlations, where predictions of PB theory were shown to be not compatible with a benchmark to experimental observations. Accounting for thermal configurational averages of the tRNA^Phe structure, the water hydration shell and counterions, the effective electrostatic potential was simulated in order to quantify the electrostatics at the tRNA surface (Fig. 15c). The expected uniform negative surface potential due to the high negative charge density of the (PO₂)⁻ groups was found to be restricted to the helical stem domains, in line with the findings for double-stranded RNA.⁸⁶ In contrast, the electrostatic potential of the anticodon loop is substantially reduced⁸⁷ due to the presence of an immobilized Mg²⁺ ion (Fig. 15c and d: position M5) that together with water molecules largely compensate the negative charges of the (PO₂)⁻ groups in the solvent accessible region of tRNA^Phe.

In the D and TΨC loop domains, the negative potential due to repulsive Coulomb interaction of the (PO₂)⁻ groups at short distance is fully compensated by the presence of a small number of immobilized (contact) Mg²⁺ ions that locally induce a net positive surface potential (cf.Fig. 14 and 15c: M1, M2, M3, M8), thus facilitating close inter-phosphate distances. The contact pairs of Mg²⁺ ions and (PO₂)⁻ groups thus make the decisive contribution to lowering the electrostatic energy and, consequently, stabilizing the tertiary structure of tRNA. Moreover, the ion pairs impose an electrical force on nearby water molecules, leading to their orientation in space, that again reduces the electrostatic energy. Such ordering and rigidifying of water molecules induced by contact pair hydration structures are reflected in the 2D-IR spectra of tRNA^Phe that reveal a smaller antidiagonal width of the 2D signal contours around 1270 cm⁻¹ than of those at lower-detection frequencies.⁸⁰ In contrast to such strongly interacting ions at the surface of tRNA, mobile ions within the first few water layers around tRNA have a minor impact on tuning the local potential and forces at the tRNA surface but are essential for the overall charge neutrality.

Conclusions and outlook

Exploiting the complementary information of detailed simulations, IR absorption and most sophisticated 2D-IR spectroscopy allowed the vibrational excitations of the RNA phosphate groups to be used as a sensitive noninvasive probe of the impact of neighbouring water molecules on the structure and dynamics of RNA and establish the contact pairs of Mg²⁺ ions and (PO₂)⁻ groups as a key structural motif in aqueous solution. The emerging picture is that the water molecules at the RNA surface differ markedly from the bulk via the existence of ordered hydration structures around dsRNA and that local hydration motifs are preserved for a time range longer than 10 ps. The contact pairs possess unique properties, i.e., a high degree of structural rigidity that imposes a pronounced impact on the local bonding potential which supports the relevance of Mg²⁺ ions in stabilizing folded biomolecular structures via their unparalleled ability to modify interaction patterns between the charged molecular units. The phosphate stretching vibrations of the RNA backbone thus represent the most sensitive approach to discern local hydration and ion geometries along the (double)-helical and folded biomolecular structures.

Contact pairs and strongly interacting solvent shared ion pair structures of Mg²⁺ ions and (PO₂)⁻ groups are relevant for various aspects in biological function. Contact pairs are an important factor in biomolecular structure stabilization where Mg²⁺ ions rigidify the RNA structure in particularly crowded regions. Exceptionally short (PO₂)⁻ distances are facilitated via the directed interaction with multi-charged ions and it is generally accepted that up to four Mg²⁺ ions are necessary to stabilise a tRNA molecule. Moreover, Mg²⁺ ions directly influence tRNA activity, e.g., in the aminoacylation reaction of tRNA^Glu where tRNA requires Mg²⁺ ions to acquire a conformation that can be aminoacylated.^88,89 As demonstrated for tRNA^Phe, the immobilization of ions at the RNA surface allows the electrostatic properties of the domains to be fine tuned thereby defining the macromolecular effective electrostatic potential of the biomolecule. Different domains of the tRNA structure, like the acceptor stem and anticodon loop, possess distinct polarity, establishing a potential gradient that is expected to be relevant for the orthogonal biological functionality of domains. A net effect of reducing the negative potential of the anticodon loop is that unfavourable interactions with mRNA get minimized upon mutual binding during translation.¹² This suggests that the interaction and binding of tRNA and mRNA are not inhibited by the overall highly negative potential of tRNA but are mediated by the locally activated anticodon domain for which access is not inhibited. Owing to the central role electrostatic interactions play in mediating the interactions between biomolecules, such ion mediated fine tuning of local electrostatic properties is expected to be relevant during translation.

An open question is how to efficiently incorporate electronic many-body polarization of the molecular constituents in simulations in order to provide a quantitative description of ion pairing and achieve predictive accuracy of numerical approaches. Most recent results on dsRNA⁸⁵ indicate that electric polarizability can be efficiently accounted for in a mean field approach via the rescaling of charges by a factor of 1/√ε_el ≈ 0.75,^39,41 thus providing a route to accurate descriptions of ion pairing of RNA with Mg²⁺ ions. Nevertheless, the strong interfacial electric fields with fluctuation components extending up to ≈20 THz call into question the assumptions for treating electronic polarization within an electronic continuum correction approach, i.e., equal polarizabilities of particles and the homogeneity of the electron density within each particle. Further investigations are required to establish optimal combinations of RNA, water and ion force field parameters within an electronic continuum correction approach and the impact on the structural properties of the biomolecules. Alternatively, explicit treatments of electronic many-body polarization benefit from recent algorithmic advances and the increase in computational capacity⁹⁰ which brings the required large simulation cells and long propagation times within reach.

Undoubtedly, Mg²⁺ ions along with the hydration shell should be considered as integral components of tRNA structures, being essential for the stabilization of active RNA folds and the mediation of RNA–RNA interactions. The tightly integrated approach of atomistic simulations and IR spectroscopy provided quantitative insights in the electric properties of key biomolecules and established the importance of contact pair structures in water. The approach appears most promising for quantifying the changes in the hydration shell and ion configurations during RNA folding and changes that come along with the formation of the RNA–protein and RNA–RNA complexes. Furthermore, the approach has the potential to provide a novel view on Mg²⁺ mediated catalytic reactivity.⁹¹ Closely related open questions involve a detailed understanding of the molecular couplings and interactions in the multi-phosphate unit of adenine di- and triphosphates and microscopic insight into the Mg²⁺ catalysed phosphate ester hydrolysis.⁹²

The presented results underscore the high relevance of the molecular probes and the strong potential of non-invasive time-resolved vibrational spectroscopy for elucidating relevant molecular interactions. Theoretical descriptions at the molecular level allow the accessing of the hydration structure and dynamics of the complex biomolecular systems with unprecedented detail and the combination with most sensitive 2D-IR spectroscopy can provide quantitative information on the local hydration motifs and the underlying interfacial interactions. Owing to the central role of electric fields in defining the properties at biological interfaces, quantitative experimental access is highly desirable. Such fields at the biomolecular surface, generated from the interaction of the electric dipoles of water molecules and the charges of the counterions are perpetually discussed in a controversial way, reflecting the structural complexity of the many-body system subject to thermal fluctuations on a multitude of timescales. The outstanding sensitivity of spectral positions and line shapes of molecular vibrators towards the locally arising electric fields allowed for a quantitative field probing that succeeded in determining the strength, range, and ultrafast dynamics at the native biomolecular surfaces.³¹ The approach is transferrable to other polarizable functional groups, like sulfonic acid head groups, and bilipid membranes where the absorption in the fingerprint IR spectral region is expected to encode rich details of the interfacial hydration structures and dynamics, as well as ion pairing geometries. This new quantitative insight is important for understanding the key role of water and its dynamics at biological interfaces, such as charged cell membranes and the surface of proteins, and for establishing rigorous benchmark to contrasting predictions of theoretical approaches.

The approach of thoroughly benchmarking the predictions of biomolecular simulations by experimental observables circumvents methodological shortcomings and uncertainties that are inherently present due to large system sizes and complexity. In particular, simulations of the highly sensitive IR absorption spectra provide insights into the relevant interactions defining the properties of the biomolecular phosphate–water interface. Apart from the provided microscopic insights into the rich electrostatics of macromolecular RNA structures, novel benchmark for force field and methodological developments is established.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank R. Costard, T. Siebert, F. Dahms, E. M. Bruening, A. Kundu, J. Schauss and T. Elsaesser for their contributions to the results discussed here. This research has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 802817).

Notes and references

1. J. D. Watson, T. A. Baker, S. P. Bell, A. Gann, M. Levine and R. Losick, Molecular Biology of the Gene, Pearson, 7th edn, 2013.
2. H. R. Drew and R. E. Dickerson, J. Mol. Biol., 1981, 151, 535–556.
3. M. L. Kopka, A. V. Fratini, H. R. Drew and R. E. Dickerson, J. Mol. Biol., 1983, 163, 129–146.
4. D. Vlieghe, J. P. Turkenburg and L. Van Meervelt, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1999, 55, 1495–1502.
5. B. Schneider, K. Patel and H. M. Berman, Biophys. J., 1998, 75, 2422–2434.
6. D. P. Zhong, S. K. Pal and A. H. Zewail, Chem. Phys. Lett., 2011, 503, 1–11.
7. W. Saenger, W. N. Hunter and O. Kennard, Nature, 1986, 324, 385–388.
8. R. E. Dickerson, H. R. Drew, B. N. Conner, R. M. Wing, A. V. Fratini and M. L. Kopka, Science, 1982, 216, 475–485.
9. M. Chaplin, Nat. Rev. Mol. Cell Biol., 2006, 7, 861–866.
10. M. Egli, S. Portmann and N. Usman, Biochemistry, 1996, 35, 8489–8494.
11. M. Egli, V. Tereshko, M. Teplova, G. Minasov, A. Joachimiak, R. Sanishvili, C. M. Weeks, R. Miller, M. A. Maier, H. Y. An, P. D. Cook and M. Manoharan, Biopolymers, 1998, 48, 234–252.
12. M. Selmer, C. M. Dunham, F. V. Murphy, A. Weixlbaumer, S. Petry, A. C. Kelley, J. R. Weir and V. Ramakrishnan, Science, 2006, 313, 1935–1942.
13. D. J. Klein, P. B. Moore and T. A. Steitz, RNA, 2004, 10, 1366–1379.
14. J. D. Robertus, J. E. Ladner, J. T. Finch, D. Rhodes, R. S. Brown, B. F. Clark and A. Klug, Nature, 1974, 250, 546–551.
15. S. H. Kim, F. L. Suddath, G. J. Quigley, A. McPherson, J. L. Sussman, A. H. Wang, N. C. Seeman and A. Rich, Science, 1974, 185, 435–440.
16. H. J. Shi and P. B. Moore, RNA, 2000, 6, 1091–1105.
17. Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621.
18. D. E. Draper, D. Grilley and A. M. Soto, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 221–243.
19. J. Lipfert, S. Doniach, R. Das and D. Herschlag, Annu. Rev. Biochem., 2014, 83, 813–841.
20. J. C. Bowman, T. K. Lenz, N. V. Hud and L. D. Williams, Curr. Opin. Struct. Biol., 2012, 22, 262–272.
21. F. Leonarski, L. D'Ascenzo and P. Auffinger, Nucleic Acids Res., 2017, 45, 987–1004.
22. P. Auffinger, E. Ennifar and L. D'Ascenzo, RNA, 2021, 27, 243–252.
23. S. K. Pal and A. H. Zewail, Chem. Rev., 2004, 104, 2099–2123.
24. D. Andreatta, J. L. P. Lustres, S. A. Kovalenko, N. P. Ernsting, C. J. Murphy, R. S. Coleman and M. A. Berg, J. Am. Chem. Soc., 2005, 127, 7270–7271.
25. D. Laage, T. Elsaesser and J. T. Hynes, Chem. Rev., 2017, 117, 10694–10725.
26. R. Costard, T. Tyborski, B. P. Fingerhut and T. Elsaesser, J. Chem. Phys., 2015, 142, 212406.
27. R. Costard, T. Tyborski and B. P. Fingerhut, Phys. Chem. Chem. Phys., 2015, 17, 29906–29917.
28. T. Siebert, B. Guchhait, Y. L. Liu, R. Costard and T. Elsaesser, J. Phys. Chem. B, 2015, 119, 9670–9677.
29. M. Falk, K. A. Hartman and R. C. Lord, J. Am. Chem. Soc., 1963, 85, 387–391.
30. P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, Cambridge, 2011.
31. T. Siebert, B. Guchhait, Y. L. Liu, B. P. Fingerhut and T. Elsaesser, J. Phys. Chem. Lett., 2016, 7, 3131–3136.
32. Y. L. Liu, B. Guchhait, T. Siebert, B. P. Fingerhut and T. Elsaesser, Struct. Dyn., 2017, 4, 044015.
33. A. A. Chen, D. E. Draper and R. V. Pappu, J. Mol. Biol., 2009, 390, 805–819.
34. A. A. Chen, M. Marucho, N. A. Baker and R. V. Pappu, Method Enzymol., 2009, 469, 411–432.
35. S. Kirmizialtin and R. Elber, J. Phys. Chem. B, 2010, 114, 8207–8220.
36. F. Pan, C. Roland and C. Sagui, Nucleic Acids Res., 2014, 42, 13981–13996.
37. K. Xi, F. H. Wang, G. Xiong, Z. L. Zhang and Z. J. Tan, Biophys. J., 2018, 114, 1776–1790.
38. P. F. Li and K. M. Merz, J. Chem. Theory Comput., 2014, 10, 289–297.
39. I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626.
40. J. J. Yoo and A. Aksimentiev, J. Phys. Chem. Lett., 2012, 3, 45–50.
41. E. Duboue-Dijon, P. E. Mason, H. E. Fischer and P. Jungwirth, J. Phys. Chem. B, 2018, 122, 3296–3306.
42. M. Pasi, J. H. Maddocks and R. Lavery, Nucleic Acids Res., 2015, 43, 2412–2423.
43. C. S. Zhang, C. Lu, Z. F. Jing, C. J. Wu, J. P. Piquemal, J. W. Ponder and P. Y. Ren, J. Chem. Theory Comput., 2018, 14, 2084–2108.
44. V. S. S. Inakollu, D. P. Geerke, C. N. Rowley and H. B. Yu, Curr. Opin. Struct. Biol., 2020, 61, 182–190.
45. Z. F. Jing, C. W. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J. P. Piquemal and P. Y. Ren, Annu. Rev. Biophys., 2019, 48, 371–394.
46. B. P. Fingerhut and T. Elsaesser, in Coherent Multidimensional Spectroscopy, ed. M. Cho, Springer Singapore, Singapore, 2019, pp. 171–195 DOI:10.1007/978-981-13-9753-0_8.
47. Y. F. Guan, G. S. C. Choy, R. Glaser and G. J. Thomas, J. Phys. Chem., 1995, 99, 12054–12062.
48. Y. Guan and G. J. Thomas, J. Mol. Struct., 1996, 379, 31–41.
49. J. Florian, V. Baumruk, M. Strajbl, L. Bednarova and J. Stepanek, J. Phys. Chem., 1996, 100, 1559–1568.
50. J. Florian, M. Strajbl and A. Warshel, J. Am. Chem. Soc., 1998, 120, 7959–7966.
51. V. Andrushchenko, L. Benda, O. Pav, M. Dracinsky and P. Bour, J. Phys. Chem. B, 2015, 119, 10682–10692.
52. N. M. Levinson, E. E. Bolte, C. S. Miller, S. A. Corcelli and S. G. Boxer, J. Am. Chem. Soc., 2011, 133, 13236–13239.
53. S. A. Corcelli, C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2004, 120, 8107–8117.
54. T. Hayashi, T. L. Jansen, W. Zhuang and S. Mukamel, J. Phys. Chem. A, 2005, 109, 64–82.
55. D. J. Floisand and S. A. Corcelli, J. Phys. Chem. Lett., 2015, 6, 4012–4017.
56. S. D. Fried and S. G. Boxer, Acc. Chem. Res., 2015, 48, 998–1006.
57. M. Cho, J. Chem. Phys., 2009, 130, 094505.
58. B. Blasiak and M. Cho, J. Chem. Phys., 2014, 140, 164107.
59. C. R. Baiz, B. Blasiak, J. Bredenbeck, M. Cho, J. H. Choi, S. A. Corcelli, A. G. Dijkstra, C. J. Feng, S. Garrett-Roe, N. H. Ge, M. W. D. Hanson-Heine, J. D. Hirst, T. L. C. Jansen, K. Kwac, K. J. Kubarych, C. H. Londergan, H. Maekawa, M. Reppert, S. Saito, S. Roy, J. L. Skinner, G. Stock, J. E. Straub, M. C. Thielges, K. Tominaga, A. Tokmakoff, H. Torii, L. Wang, L. J. Webb and M. T. Zanni, Chem. Rev., 2020, 120, 7152–7218.
60. B. P. Fingerhut, R. Costard and T. Elsaesser, J. Chem. Phys., 2016, 145, 115101.
61. M. S. Gordon, M. A. Freitag, P. Bandyopadhyay, J. H. Jensen, V. Kairys and W. J. Stevens, J. Phys. Chem. A, 2001, 105, 293–307.
62. D. Laage and J. T. Hynes, Science, 2006, 311, 832–835.
63. M. B. Ji, M. Odelius and K. J. Gaffney, Science, 2010, 328, 1003–1005.
64. J. Schauss, F. Dahms, B. P. Fingerhut and T. Elsaesser, J. Phys. Chem. Lett., 2019, 10, 238–243.
65. J. Schauss, A. Kundu, B. P. Fingerhut and T. Elsaesser, J. Phys. Chem. Lett., 2019, 10, 6281–6286.
66. J. Stangret and R. Savoie, Can. J. Chem., 1992, 70, 2875–2883.
67. E. L. Christian, V. E. Anderson, P. R. Carey and M. E. Harris, Biochemistry, 2010, 49, 2869–2879.
68. B. P. Fingerhut, J. Schauss, A. Kundu and T. Elsaesser, Z. Phys. Chem., 2020, 234, 1453–1474.
69. P. A. Sharp, Genes Dev., 1999, 13, 139–141.
70. S. J. Poynter and S. J. DeWitte-Orr, Front. Immunol., 2018, 9, 829.
71. E. M. Bruening, J. Schauss, T. Siebert, B. P. Fingerhut and T. Elsaesser, J. Phys. Chem. Lett., 2018, 9, 583–587.
72. A. Kundu, J. Schauss, B. P. Fingerhut and T. Elsaesser, J. Phys. Chem. B, 2020, 124, 2132–2138.
73. T. L. C. Jansen, B. M. Auer, M. Yang and J. L. Skinner, J. Chem. Phys., 2010, 132, 224503.
74. G. Hithell, D. J. Shaw, P. M. Donaldson, G. M. Greetham, M. Towrie, G. A. Burley, A. W. Parker and N. T. Hunt, J. Phys. Chem. B, 2016, 120, 4009–4018.
75. T. Elsaesser, J. Schauss, A. Kundu and B. P. Fingerhut, J. Phys. Chem. B, 2021, 125, 3899–3908.
76. R. Lumry and S. Rajender, Biopolymers, 1970, 9, 1125–1227.
77. A. I. Dragan, C. M. Read and C. Crane-Robinson, Eur. Biophys. J. Biophys., 2017, 46, 301–308.
78. M. S. Searle and D. H. Williams, Nucleic Acids Res., 1993, 21, 2051–2056.
79. V. K. Misra and D. E. Draper, J. Mol. Biol., 2000, 299, 813–825.
80. J. Schauss, A. Kundu, B. P. Fingerhut and T. Elsaesser, J. Phys. Chem. B, 2021, 125, 740–747.
81. R. Romer and R. Hach, Eur. J. Biochem., 1975, 55, 271–284.
82. F. Fogolari, A. Brigo and H. Molinari, J. Mol. Recognit., 2002, 15, 377–392.
83. I. Borukhov, D. Andelman and H. Orland, Phys. Rev. Lett., 1997, 79, 435–438.
84. V. B. Chu, Y. Bai, J. Lipfert, D. Herschlag and S. Doniach, Biophys. J., 2007, 93, 3202–3209.
85. B. P. Fingerhut, J. Schauss, A. Kundu and T. Elsaesser, Biophys. J., 2021, 120 DOI:10.1016/j.bpj.2021.1010.1029.
86. M. Gebala and D. Herschlag, Biophys. J., 2019, 117, 1116–1124.
87. K. A. Sharp, B. Honig and S. C. Harvey, Biochemistry, 1990, 29, 340–346.
88. E. Westhof and P. Auffinger, Transfer RNA Structure, eLS, John Wiley & Sons, Ltd., Chichester, 2012 DOI:10.1002/9780470015902.a0000527.pub2.
89. E. Madore, C. Florentz, R. Giege and J. Lapointe, Nucleic Acids Res., 1999, 27, 3583–3588.
90. J. Melcr and J. P. Piquemal, Front. Mol. Biosci., 2019, 6, 143.
91. M. Teplova, C. Falschlunger, O. Krasheninina, M. Egger, A. M. Ren, D. J. Patel and R. Micura, Angew. Chem., Int. Ed., 2020, 59, 2837–2843.
92. S. J. Admiraal and D. Herschlag, Chem. Biol., 1995, 2, 729–739.

---