Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the factors influencing the chiroptical response of conjugated polymer thin films†
Beth
Laidlaw
a,
Julien
Eng
 a,
Jessica
Wade
bc,
Xingyuan
Shi
a,
Jessica
Wade
bc,
Xingyuan
Shi
 cd,
Francesco
Salerno
cd,
Matthew J.
Fuchter
cd,
Francesco
Salerno
cd,
Matthew J.
Fuchter
 cd and
Thomas J.
Penfold
cd and
Thomas J.
Penfold
 *a
*a
aChemistry – School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK. E-mail: tom.penfold@ncl.ac.uk
bDepartment of Materials, Imperial College London, South Kensington Campus, London, SW7 2AZ, UK
cCentre for Processable Electronics, Imperial College London, South Kensington Campus, London, SW7 2AZ, UK
dDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, 82 Wood Lane, London W12 0BZ, UK
First published on 2nd September 2021
Abstract
We study the influence of the physical and chemical structure on the chiroptical response of fluorene-based polymeric systems, namely poly(9,9-dioctylfluorene) (PFO) and the donor–acceptor type copolymer poly(9,9-dioctylfluorene-alt-benzothiadiazole) (F8BT). We reveal the significance of electric-magnetic coupling, at both short (molecular-level) and intermediate (delocalised over multiple polymer chains) length scales, on the magnitude of the dissymmetry. These findings provide a framework for the design of new materials with an enhanced chiroptical response.
Chirality is a fundamental symmetry property, which can play a defining role in a broad range of areas. Recently, it has gained significant interest in optoelectronic applications, such as organic light-emitting diodes (OLEDs) and organic photodetectors, where the use of a chiral material in the active layer enables the emission or detection of circularly polarised (CP) light, respectively.1 Interest in the development of chiral organic materials for CP-OLEDs2 has led to a variety of approaches being pursued. These can be broadly grouped into two classes; small-molecule emitters3–7 and polymer-based emitters.8–12 The dissymmetry of the emitted light (g-factor) can determined by the coupling between the electric (μ) and magnetic (m) transition dipole moments,13 and can be expressed as:
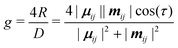 | (1) |
When considering transitions allowed within the electric dipole approximation, eqn (1) indicates that g-factors are limited to values of ∼10−3.15 Larger dissymmetric responses can be achieved for molecules that make use of electric-dipole forbidden transitions, including chiral lanthanide complexes (g ∼ 1.4).16 However, owing to their small μ, they typically demonstrate low emission cross sections, which results in luminescence quantum yields too low for display applications. While efforts continue to address the trade-off between luminescence quantum yield and dissymmetry,15 it remains a challenge to identify highly emissive organic molecules with excellent CP characteristics.
An alternative approach to sizeable CP response is based upon non-intrinsic light-matter interactions observed in systems with long-range structural chirality, such as in chiral nematic (cholesteric) liquid crystals (LC).17 Here dissymmetry is determined by Bragg-type circular selective reflections off the thin film and not the intrinsic polarisation of light at the site of emission. The magnitude of this phenomenon is therefore sensitive to the pitch and thickness of cholesteric LC films.18
Currently, organic systems generating the largest dissymmetric response in the solid state (g-factors up to ∼1) are conjugated polymers, especially amongst the polyfluorene class.11 It has been proposed that this strong CP luminescence occurs due to structural chirality.8,12,19 However, recent works9,20 have indicated that long-range structural chirality only dominates the chiroptical response when an alignment layer is used to template molecular packing of polymer chains at or beyond the mesoscale. Highly dissymmetric emission from non-aligned thin polymer films (i.e., those where the film thickness is considerably less than those at which this structural chiroptical phenomena manifest) suggests that intrinsic CP emission may play a significant role.20,21
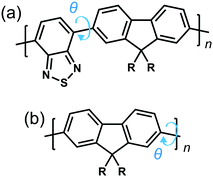
To explore the origins of the strong chiroptical response of polymer-based systems, we turn to time-dependent density functional theory (TDDFT), within the approximation of the CAM-B3LYP exchange and correlation functional22 (see ESI†). We consider the influence of four variables on the g-factor; chemical composition, the intramolecular twist angle (θ) between adjacent repeat units, the number of monomers (n) a single oligomer chain is made of and the role of interchain (intermolecular) coupling. Two model fluorene-based systems were studied (Fig. 1), namely PFO and F8BT. To reduce computational expense, we focus on low numbers of monomer repeat units (often n = 2) and the C8H17 side chains were replaced with methyl groups, noting that it has been shown that the side chains can play an important role in controlling chiral induction in thin films.23 The lowest excited state of PFO corresponds to the π → π* transition. The calculated S1 state of an isolated oligomer (θ = 40°, n > 4) is 318 nm (see Fig. S1, ESI†). For F8BT (θ = 40°, n > 3), the lowest transition exhibits a charge-transfer character between the F8 and BT units and the calculated S1 state of the isolated oligomer is 427 nm (see Fig. S1, ESI†). These are in reasonable agreement with the lowest absorption bands, 375 nm and 475 nm, measured for PFO and F8BT, respectively.20
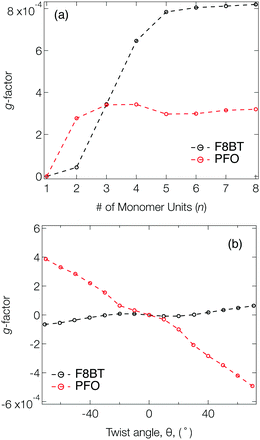
Fig. 2a shows the g-factor (calculated using eqn (1)) of the S1 state of isolated PFO and F8BT oligomers as a function of n with a fixed θ = 40°, close to the optimised twist angle for F8BT9 and the glassy-phase PFO.24 In both cases, the g-factor initially increases before a plateau is reached at n = 3 and n = 5 for PFO and F8BT, respectively. This behaviour bears some resemblance to the work of Greenfield et al.,25 who reported a plateau associated maximum length over which the exciton can delocalise for a given configuration. Here the plateau is reached earlier for PFO (n = 3) than F8BT owing to a larger exciton binding energy of PFO compared to F8BT (F8BT = 0.2 eV,9 PFO = 0.3 eV26). For the non-planar polymers studied in the present work, the enhanced delocalisation of F8BT9 means that kr for F8BT will be larger than that of PFO. This results in an increase of m relative to μ, which can be seen in the decreasing μ2/m2 ratio (Fig. S2, ESI†) and the larger predicted g-factors.
Fig. 2b shows the g-factor as a function of θ for PFO and F8BT 2-mers (i.e., n = 2). In both cases the g-factor increases with the magnitude of θ, and its sign is determined by direction, which indicates that the handedness/sign of the CP response can be controlled by the direction of the cumulative twist along the polymer backbone. The impact of θ is more pronounced for PFO because (i) the ratio μ2/m2 is considerably smaller in PFO for θ >30° (Fig. S3a, ESI†) and (ii) the angle τ between μ and m (Fig. S3b, ESI†) deviates more from 90°. In general, μ and m decreases as θ increases and this reduction is greater for F8BT as the coupling strength between the (intrachain) donor and acceptor decreases as θ approaches orthogonality. This leads to a larger relative decrease in m compared to μ and therefore an increase in the ratio μ2/m2 (Fig. S3a, ESI†). Whilst this is unfavourable for achieving high g-factors, it is offset by the increase in cos(τ). The same is not observed for PFO as we are considering the π–π* transition of the homopolymer. As θ increases, the delocalised exciton exhibits an increased m compared to μ, reflected in the ratio μ2/m2 (Fig. S3a, ESI†). The angle τ between m and μ increases, which supports the enhancement of the g-factor.
The above examples have shown how, for isolated oligomers, the g-factor depends on the extent of exciton delocalisation, which is ultimately related to the validity of the dipole approximation eqn (2). Despite increasing kr and a larger contribution from the magnetic transition dipole moment, the calculated g-factors still do not exceed 10−3, i.e. values that are consistent with molecular-level mechanisms and considerably smaller than dissymmetry factors reported for chiral polyfluorene thin films.9,20 Instead of isolated oligomers, we next consider the impact of inter-chain coupling on the g-factors.
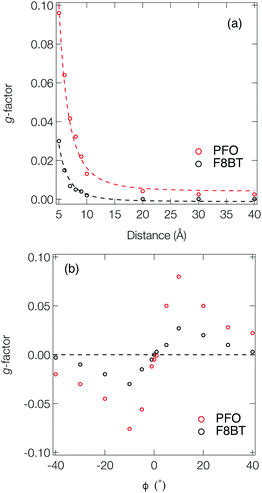
Fig. 3a shows the dissymmetry of coupled F8BT and PFO dimers, where the geometry is determined by the centre-of-mass separation (d) and mutual orientation (ϕ) of the two oligomers (Fig. 4a). Initially, we fixed both the mutual orientation of the oligomers (ϕ = 10°) and the intrachain twist angle (θ = 40°). The method for calculating the g-factor for these systems is described in the ESI.† It is immediately evident that exciton delocalisation over two polymer chains, illustrated in Fig. 4b, leads to an increase in the calculated dissymmetry. At short distances (d < 7 Å) g-factors of ∼0.1 and ∼0.03 are observed for PFO and F8BT, respectively. The g-factor decreases as a function of d−3 (dashed line in Fig. 3a) reflecting the decrease in exciton coupling (V) with distance. Fig. 3b shows the dissymmetry of the F8BT or PFO 2-mers as a function of ϕ, the angle between the oblique chains (Fig. 4b). This shows that for ϕ = 0°, the dissymmetry is similar to that of the isolated oligomers. However, as the angle increases, a large increase in the dissymmetry is observed as the coupling between the oligomers reaches a maximum at ϕ = 10°. After this the dissymmetry decreases as μ increases and m decreases. These calculations demonstrate that like θ for the isolate polymers, the direction of ϕ can control the sign of the g-factor and overall only small angles are preferred to maximise the g-factor.
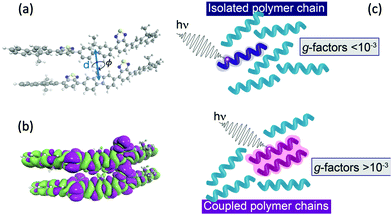 | ||
| Fig. 4 (a) Schematic of two polymer chains and the coordinates (d and ϕ) manipulated in Fig. 3. (b) Density difference of the lowest exciton of a F8BT dimer model illustrating the electron density delocalised over the two chains. (c) Schematic of the effect of interacting polymer chains on the electric and magnetic transition dipole moments. | ||
To understand the origin of the increase in dissymmetry shown in Fig. 3 we turn to the well-established exciton chirality model (ECM),27,28 where the rotatory strength (R) for a dimer of coupled excitonic states can be defined as:
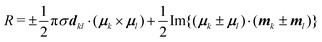 | (2) |
Understanding the relative contributions of local short-range electric-magnetic coupling and longer-range structural chirality is crucial for the rational design of new materials that exhibit an intense chiroptical response. Here we demonstrate that the extension of the exciton over nearby polymer chains is critically important for enhancing the dissymmetry. By exploiting the intrinsic magnetic transition dipole moment (and therefore invoking μ–m coupling) arising from the helically configured polymer backbones it is possible to significantly increase the dissymmetry of dimer systems. This model may not hold in polymers which adopt a planar structure in the aggregate state as they are more likely to have negligible transition magnetic dipoles,30 however when strong interchain excitonic coupling dominated, as recently shown in thin films of PFO21 exceptional chiroptical response can still be achieved, but in this case it would be dominated by the μ–μ coupling, as the electric-magnetic coupling negligible.
Finally, we note that the present work does not consider further exciton delocalisation over a larger stack (e.g. trimers, tetramers), nor how the delocalisation would be impacted by conformational and environmental disorder, which are likely to play a role for longer polymer chains and excitonically coupled systems comprising a larger number of chains. In addition, it is important to recognise that the polymer thin files optimised for CP-OLEDs31 are only weakly ordered and therefore the dissymmetry will be an average over multiple orientations and configurations which emit in the film. Given that reducing the inter-chain coupling signifcnatly quenches the dissymmetry, it is possible that the overall chiroptical response would be reduced if all sites were equally likely to interact with the CP light. However, this inter-chain coupling modulates both the energy and oscillator strengths of the states involved meaning that not all sites are equally likely to absorb/emit light. To understand this, further investigations using molecular dynamics is essential and will be the focus of future work.
This research made use of the Rocket High Performance Computing service at Newcastle University. M. J. F. would like to thank the EPSRC for an Established Career Fellowship (EP/R00188X/1). Data supporting this publication is openly available under an “Open Data Commons Open Database License” and available at: 10.25405/data.ncl.14872287.
Conflicts of interest
There are no conflicts to declare.References
- J. R. Brandt, F. Salerno and M. J. Fuchter, Nat. Rev. Chem., 2017, 1, 0045 CrossRef CAS.
- D.-W. Zhang, M. Li and C.-F. Chen, Chem. Soc. Rev., 2020, 49, 1331–1343 RSC.
- F. Zinna, U. Giovanella and L. D. Bari, Adv. Mater., 2015, 27, 1791–1795 CrossRef CAS PubMed.
- F. Zinna, M. Pasini, F. Galeotti, C. Botta, L. Di Bari and U. Giovanella, Adv. Funct. Mater., 2017, 27, 1603719 CrossRef.
- J. R. Brandt, X. Wang, Y. Yang, A. J. Campbell and M. J. Fuchter, J. Am. Chem. Soc., 2016, 138, 9743–9746 CrossRef CAS PubMed.
- F. Song, Z. Xu, Q. Zhang, Z. Zhao, H. Zhang, W. Zhao, Z. Qiu, C. Qi, H. Zhang and H. H. Sung, et al. , Adv. Funct. Mater., 2018, 28, 1800051 CrossRef.
- Z.-P. Yan, X.-F. Luo, W.-Q. Liu, Z.-G. Wu, X. Liang, K. Liao, Y. Wang, Y.-X. Zheng, L. Zhou and J.-L. Zuo, et al. , Chem. – Eur. J., 2019, 25, 5672–5676 CrossRef CAS PubMed.
- D. Di Nuzzo, C. Kulkarni, B. Zhao, E. Smolinsky, F. Tassinari, S. C. Meskers, R. Naaman, E. Meijer and R. H. Friend, ACS Nano, 2017, 11, 12713–12722 CrossRef CAS PubMed.
- L. Wan, J. Wade, F. Salerno, O. Arteaga, B. Laidlaw, X. Wang, T. Penfold, M. J. Fuchter and A. J. Campbell, ACS Nano, 2019, 13, 8099–8105 CrossRef CAS PubMed.
- Y. Yang, R. C. da Costa, D.-M. Smilgies, A. J. Campbell and M. J. Fuchter, Adv. Mater., 2013, 25, 2624–2628 CrossRef CAS PubMed.
- L. Wan, J. Wade, X. Shi, S. Xu, M. J. Fuchter and A. J. Campbell, ACS Appl. Mater. Interfaces, 2020, 12, 39471–39478 CrossRef CAS PubMed.
- D.-M. Lee, J.-W. Song, Y.-J. Lee, C.-J. Yu and J.-H. Kim, Adv. Mater., 2017, 29, 1700907 CrossRef PubMed.
- H. Tanaka, Y. Inoue and T. Mori, ChemPhotoChem, 2018, 2, 386–402 CrossRef CAS.
- S. Bernadotte, A. J. Atkins and C. R. Jacob, J. Chem. Phys., 2012, 137, 204106 CrossRef PubMed.
- J. Greenfield, J. Wade, J. Brandt, X. Shi, T. Penfold and M. Fuchter, Chem. Sci., 2021, 12, 8589–8602 RSC.
- J. L. Lunkley, D. Shirotani, K. Yamanari, S. Kaizaki and G. Muller, J. Am. Chem. Soc., 2008, 130, 13814–13815 CrossRef CAS PubMed.
- N. Tamaoki, Adv. Mater., 2001, 13, 1135–1147 CrossRef CAS.
- X. Yang, X. Jin, T. Zhao and P. Duan, Mater. Chem. Front., 2021, 5, 4821–4832 RSC.
- Y. Geng, A. Trajkovska, D. Katsis, J. J. Ou, S. W. Culligan and S. H. Chen, J. Am. Chem. Soc., 2002, 124, 8337–8347 CrossRef CAS PubMed.
- J. Wade, J. N. Hilfiker, J. R. Brandt, L. Liirò-Peluso, L. Wan, X. Shi, F. Salerno, S. T. Ryan, S. Schöche and O. Arteaga, et al. , Nat. Commun., 2020, 11, 1–11 Search PubMed.
- L. Wan, X. Shi, J. Wade, A. J. Campbell and M. J. Fuchter, Adv. Opt. Mater., 2021, 2100066 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao, H. Chen, L. Yin, X. Cheng, W. Zhang and X. Zhu, Polym. Chem., 2018, 9, 2295–2301 RSC.
- X. Shi, V. Nádaždy, A. Perevedentsev, J. M. Frost, X. Wang, E. von Hauff, R. C. MacKenzie and J. Nelson, Phys. Rev. X, 2019, 9, 021038 CAS.
- J. L. Greenfield, E. W. Evans, D. Di Nuzzo, M. Di Antonio, R. H. Friend and J. R. Nitschke, J. Am. Chem. Soc., 2018, 140, 10344–10353 CrossRef PubMed.
- M. A. Stevens, C. Silva, D. M. Russell and R. H. Friend, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 165213 CrossRef.
- N. Harada, S.-M. L. Chen and K. Nakanishi, J. Am. Chem. Soc., 1975, 97, 5345–5352 CrossRef CAS.
- T. Bruhn, G. Pescitelli, S. Jurinovich, A. Schaumlöffel, F. Witterauf, J. Ahrens, M. Bröring and G. Bringmann, Angew. Chem., Int. Ed., 2014, 53, 14592–14595 CrossRef CAS PubMed.
- B. Langeveld-Voss, R. Janssen and E. Meijer, J. Mol. Struct., 2000, 521, 285–301 CrossRef CAS.
- G. Albano, G. Pescitelli and L. Di Bari, Chem. Rev., 2020, 120, 10145–10243 CrossRef CAS PubMed.
- W. Barford and M. Marcus, J. Chem. Phys., 2017, 146, 130902 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cc02918e |
| This journal is © The Royal Society of Chemistry 2021 |