Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Successes, challenges, and opportunities for quantum chemistry in understanding metalloenzymes for solar fuels research
Maylis
Orio
 *a and
Dimitrios A.
Pantazis
*a and
Dimitrios A.
Pantazis
 *b
*b
aAix-Marseille Université, CNRS, iSm2, Marseille, France. E-mail: maylis.orio@univ-amu.fr
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: dimitrios.pantazis@kofo.mpg.de
First published on 19th March 2021
Abstract
Quantum chemical approaches today are a powerful tool to study the properties and reactivity of metalloenzymes. In the field of solar fuels research these involve predominantly photosystem II and hydrogenases, which catalyze water oxidation and hydrogen evolution, as well as related biomimetic and bio-inspired models. Theoretical methods are extensively used to better comprehend the nature of catalytic intermediates, establish important structure–function and structure–property correlations, elucidate functional principles, and uncover the catalytic activity of these complex systems by unravelling the key steps of their reaction mechanism. Computations in the field of water oxidation and hydrogen evolution are used as predictive tools to elucidate structures, explain and synthesize complex experimental observations from advanced spectroscopic techniques, rationalize reactivity on the basis of atomistic models and electronic structure, and guide the design of new synthetic targets. This feature article covers recent advances in the application of quantum chemical methods for understanding the nature of catalytic intermediates and the mechanism by which photosystem II and hydrogenases achieve their function, and points at essential questions that remain only partly answered and at challenges that will have to be met by future advances and applications of quantum and computational chemistry.
1. Introduction
The pressing need to develop energy sources and alternative fuels that are based on renewable, environmentally friendly, and affordable approaches is critical for successfully facing the mounting energy and climate challenges.1,2 Molecular solar fuels, such as hydrogen,3 that can in principle be obtained by mimicking biological processes, represent the most promising way of meeting this need. In the hydrogen evolution reaction (HER), electrons and protons are combined to generate molecular H2, which stores energy in its chemical bond. Hydrogen production through water splitting is one of the preferred solutions in the long run for the storage of renewable energy. Today hydrogen is principally used for industrial processes. However, it has the potential to play a major role as energy carrier in transportation, the gas industry, as well as in the generation of electricity and heat. In addition to other technical challenges, for the expansion of H2 usage in these directions it would be necessary to increase the global production of H2 considerably and sustainably.4Nature can provide useful guidelines in this quest, because metalloenzymes involved in water oxidation and hydrogen evolution serve as archetypes for these reactions and for the development of artificial catalysts for solar fuels.2,5–14 Nature offers a unique example of a water-oxidizing enzyme, photosystem II (PSII).15,16 This harbours the oxygen-evolving complex (OEC) with its manganese–calcium cluster (Scheme 1a) that catalyses the oxidation of water into dioxygen, protons, and electrons, powered by light-driven charge separation. Several aspects of the function of PSII remain unclear,17 while the development of molecular manganese-based structural mimics of the OEC18–25 has not been accompanied by comparable catalytic water oxidizing activity.26–28
In terms of H2 evolution, biology provides good examples in hydrogenases (HG). These enzymes contain nickel and iron active sites (Scheme 1b) and achieve catalytic performances that rival synthetic platinum-based catalysts for hydrogen production.29–32 Therefore, in analogy to the manganese-based water oxidizing PSII, hydrogenases serve to inspire the design of artificial hydrogen evolution catalysts based on Earth-abundant metals.33 Several studies have reported homo-34–37 and hetero-polynuclear38–41 metal complexes as electrocatalysts for HER reproducing the structure of the active site of hydrogenases. In addition to biomimetic approaches, a variety of molecular electrocatalysts have been developed to facilitate hydrogen production by making it occur faster with a lower energy input. Up to now, platinum-based catalysts provide the best performance in hydrogen evolution.42 However, due to its scarcity and cost, intense research efforts have been devoted in developing non-noble transition metal catalysts.43 In this connection, diverse ligand skeletons with cobalt, iron, and nickel complexes44–51 were shown to evolve hydrogen both in organic and aqueous media (Scheme 2).
 | ||
| Scheme 2 Selected biomimetic and bioinspired models of the hydrogenases.39,40,44,45,58–63 | ||
Research in the PSII and HG fields has benefited greatly from the contributions of quantum chemistry. During the last two decades of the 20th century the density functional theory (DFT) revolution extended the applicability of quantum chemistry to realistic transition metal systems in general and metalloenzymes in particular.52–56 Particularly after the advent of hybrid functionals it was possible to predict molecular structures and reaction profiles with sufficient accuracy to make meaningful analysis of geometric and mechanistic aspects of bioinorganic systems. The further combination of DFT with classical force-field methods within QM/MM approaches57 has become a considerably powerful component of modern computational chemistry.
The first two decades of the 21st century broadened even more the realm of applicability of quantum chemistry to metalloenzymes. One major development is that “quantum chemistry” in this field is no longer synonymous with “DFT”, but relentless advances in methodology, implementation, and infrastructure have made single and multireference wave function theory a practical and accessible option. Moreover, quantum chemistry today reaches much further than mere geometry optimizations and simple reaction energetics. Theoretical advances mean that much deeper insights into the electronic structure and properties can be obtained, and hence much deeper and more insightful connections with experiment can be established.
The two title systems of the present feature article, photosystem II and hydrogenases, have served as application platforms on which quantum chemistry has reached new heights in terms of what can be computed, and how it advances the broader research fields. In the following we will describe selected examples of specific challenges that have been met for each system using quantum chemistry, focusing on properties and questions that require more than a trivial application of standard computational approaches. Furthermore, we will point to challenges that remain to be satisfactorily addressed, and to opportunities for future theoretical advances and demanding applications. Thus, we hope to offer a broad overview of where we stand and to provide motivation towards expanding the frontiers of quantum chemistry as applied to these metalloenzymes.
2. Photosystem II
Photosynthesis involves light harvesting, excitation energy transfer, and creation of charge separated states that drive subsequent redox transformations.15,16 In oxygenic photosynthesis the pigment–protein complex PSII utilizes this charge separation, likely initiated at the primary donor ChlD1,64–67 to create the most oxidizing agent in biology, a radical cation (P680˙+) delocalized among a pair of chlorophylls (PD1/PD2). This oxidizes the Mn4CaOx cluster of the OEC in successive one-electron abstraction steps via an intermediary redox-active tyrosine (YZ), until the OEC becomes able to complete the four-electron oxidation of water to dioxygen. The intermediate “charging” or “storage” states of the OEC are known as Si states, where the subscript denotes the number of stored oxidizing equivalents (i = 0–4). S1 is the resting (dark-stable) state with commonly accepted Mn oxidation states of Mn(III)2Mn(IV)2, while S4 is an unobserved transient state that evolves dioxygen (Fig. 1). Electron and proton transfers take place alternately,68 maintaining a narrow potential range for the OEC for all Si → Si+1 state transitions. On the electron acceptor side of PSII a plastoquinone is doubly reduced and released from the complex to transfer reducing equivalents further along the photosynthetic chain, eventually to be used in CO2 fixation.Our primary focus here is on the site of water oxidation and the contributions of quantum chemistry in understanding its nature, its properties, and its function. We will cover selected developments and applications in recent years, mostly from our group, that had significant impact on discovering specific correlations between structural features and spectroscopic properties of the OEC, and which contributed to interpreting experimental results and directing further investigations. We will also identify outstanding challenges that will require more than simple extensions of present quantum chemical approaches to be successfully met in the future.
2.1. Correlating molecular structure with spin states
For a long time geometric information on the OEC was confined to metal–metal distances derived from EXAFS.69 This allowed discussion of plausible structural features but could not lead to well-defined atomistic model that are required for quantum chemical investigations. Even the first crystallographic models70–72 were not of sufficient resolution to allow definition of a unique structure. Therefore, early computational studies73,74 explored a range of geometric and mechanistic possibilities but incorporated numerous structural assumptions that later proved inaccurate. Crystallographic models of sufficiently high resolution that appeared in the last decade and that more recently utilize pulses from X-ray free electron lasers changed this situation by accurately defining the spatial arrangement of metal ions and oxygen bridges as well as the type and mode of coordination of first and second sphere ligands.75–81 As shown in Scheme 1a the core of the OEC consists of four Mn and one Ca ions connected by oxo bridges and additionally bridged mostly by carboxylate residues, while there are also two terminal water-derived ligands (H2O or OH) on each of Mn4 and Ca. The redox-active tyrosine residue (Tyr161, or YZ) is in close proximity and interacts with Ca and the rest of the inorganic cluster via hydrogen bonding. Ambiguities remained,82 and they still do,17 for example regarding the protonation states of oxo bridges and the extent of radiation-induced reduction of metal ions,83–85 but these advances nevertheless enabled quantum chemical studies to be performed on a much safer basis than ever before.86 One important consequence was that the spatial arrangement was sufficiently well defined to allow theoretical studies of electronic structure, spin states, and spectroscopic properties beyond superficial energy comparisons, thus enabling for the first time direct connections between quantum chemical studies and the vast repository of spectroscopic observations on various catalytic intermediates.The most obvious target property to begin with is the spin state of specific catalytic intermediates, which in many cases had been identified, or at least constrained, by EPR spectroscopy. Advances in this direction were tied to the investigation of magnetostructural correlations and began with the spectroscopically well-studied S2 state of the OEC and synthetic analogues. The S2 state was long known to exhibit two types of EPR signal that correspond either to a low-spin (S = 1/2, g ≈ 2) multiline state or to a higher-spin state (S ≥ 5/2, g ≥ 4.1).87–92 A landmark study in 2012 established a correspondence between two structural forms of the OEC core and these two spin states.93 The structural forms were derived from refinement of the 2011 crystallographic model.75 They were almost isoenergetic and featured different distribution of Mn valences (III–IV–IV–IV versus IV–IV–IV–III) and slightly different connectivity of an oxo bridge that led to their description as open-cubane (S2A) and closed-cubane (S2B).93 As will be explained below, quantum chemical investigations of the spin-dependent properties of these models supported their association with the two observed EPR signals.
The quantum chemical approach used for determining the spin states is based on a generalization of the two-centre broken symmetry (BS) DFT methodology94–97 to the tetranuclear case. The low-lying states of a cluster representing the OEC can be described using the effective Heisenberg–Dirac–van Vleck Hamiltonian (HDvV), which describes magnetic levels in terms of fictitious interactions between local spin magnetic moments:
This lengthy procedure obviously involves significantly increased computational and human effort compared to studies that simply ignore the spin state problem. For each structural model to be considered one has to complete a series of calculations that often exhibit challenging convergence behaviour, and then perform additional analysis to extract exchange coupling constants and magnetic spin states. Yet, despite the considerable overhead, the results have been richly rewarding and have pushed research in natural water oxidation in new and fruitful directions. It is crucial to stress that no discussion of spin states can be made by comparing energies of different broken-symmetry determinant, simply because these do not correspond to observable states. It is an unfortunate fact that several papers erroneously discuss spin states by direct reference to broken-symmetry solutions.
The application of the approach to the two valence isomers found for the S2 state of the OEC showed that they differ in their exchange coupling scheme (Fig. 3).93 The isomer labelled as S2A (III–IV–IV–IV) has antiferromagnetic interaction between Mn1–Mn2 and Mn3–Mn4 resulting in a spin S = 1/2 ground state, whereas S2B features strong ferromagnetic interactions within the cuboidal Mn1–Mn2–Mn3 unit (effective spin of the cube S = 9/2) resulting in a total ground state spin of S = 5/2 for this isomer. This suggests already a potential correspondence between the two structural models and the observed spin states. This was further supported by explicit simulations of EPR spectra, which associated the S2A with the g = 2 EPR signal and the S2B model with the g = 4.1 signal.93
Importantly, the results on the magnetic properties of the S2 state isomers are aligned with experimental and theoretical results on synthetic trinuclear and tetranuclear analogues.101,102 For example, synthetic Mn(IV)3Ca cubane complexes22,103 that mimic this structural unit of the S2B model similarly have dominant ferromagnetic coupling among their Mn ions and display high-spin (S = 9/2) ground states.102 This can be explained at the orbital level by elimination of superexchange interactions between the Mn ions due to the angles of the oxo bridges.102 The broken-symmetry approach can be equally well applied to spin-frustrated systems with antiferromagnetic ground states, as exemplified by a combined experimental and theoretical study of a low-spin trinuclear terpyridine cluster with a Mn(IV)3O4 core.101
Consideration of spin state alone may be insufficient to establish a firm one-to-one correspondence between a computational model and a true catalytic intermediate. For example, other structural models or protonation patterns can be shown to have the same spin state as that observed experimentally.104,105 It is only the combined evaluation of geometries, spin states, energetics, and spectroscopic parameters that can lead to safe assignments. In any case, spin states are strong constraints and essential for discussing the relevance of any computational model to an experimentally observable state of the physical system. Thus, they have been central in many studies that examined the nature of specific intermediates, by showing connections between structural features and magnetic properties. For example, BS-DFT analysis of spin states for various isomeric forms of the S3 state established that the S = 3 states observed by magnetic resonance spectroscopies106–108 must be attributed to structural forms that have one additional water-derived ligand compared to the preceding S2 state, and hence forms where all four Mn ions are six-coordinated.104,106 By contrast, a form of the S3 state that has no additional ligand and contains a five-coordinated Mn(IV) ion is characterized by the highest possible spin for a Mn(IV)4 cluster, of S = 6 (Fig. 4).108,109
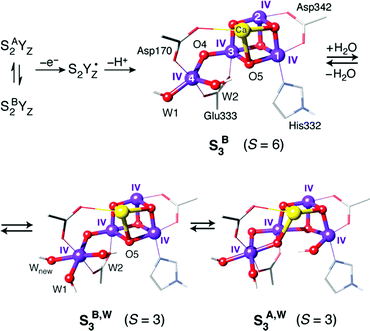 | ||
| Fig. 4 Possible structural components of the S3 state of the OEC with their corresponding spin states. | ||
Similar structure–magnetism correlations have been used to examine the effect of protonation of oxo bridges on specific exchange coupling pathways. It is known that in general an oxo bridge enables stronger superexchange and thus enhances antiferromagnetic coupling between two Mn ions compared to a hydroxo bridge.110–112 Applied to the OEC, study of the effects of protonation or hydrogen bonding to specific oxygen bridges contributed, among others, to screening of structural models for the S0 state104,113 and to evaluation of possibilities for the interaction of small molecules such as methanol and ammonia with the manganese cluster.114–117 It is also important to note that since different oxidation states of the Mn ions lead to different exchange interactions, analysis of magnetic properties in terms of exchange couplings and spin ladders is essential for evaluating redox-isomeric forms of specific S-state intermediates104 and for evaluating competing oxidation state paradigms.104,118,119
These successful applications should not obscure the fact that the spin-projected broken-symmetry DFT methodology, even if applied correctly, depends considerably on the nature of the functional, on the nature of the system under study, and on the validity of the effective spin Hamiltonian assumed to describe the system. High-valent/high-spin manganese systems are among the most favourable systems for this approach. Indeed, according to a study by Krewald et al.,104 the broken-symmetry approach using the TPSSh functional and the complete methodology for calculation of exchange coupling constants and spin states predicts with absolute accuracy the correct ground spin state of all known oligonuclear manganese complexes with oxidation states relevant to the OEC. Exceptions may be associated with limitations of the isotropic exchange model rather than with failures at the DFT level. Of course, even if the energetics obtained by the above procedure are useful, it is always desirable to have direct access to the spin states themselves, which can only be achieved by using multireference methods. For multi-electron systems such as those containing high-valent Mn ions, multireference approaches have found limited application so far.120,121 Notable studies that are directly relevant for the OEC include the use of density matrix renormalization group (DMRG) based complete active space self-consistent field (CASSCF) and N-electron valence state perturbation theory (NEVPT2) calculations on dinuclear Mn and Cr complexes.112,122,123 Such calculations are far from trivial. They require careful study of convergence with respect to the active space and other technical parameters, and they present a series of requirements that must be satisfied for the results to be meaningful and reliable. As defined by Roemelt et al.,122 these requirements include the necessity for state-averaged orbital optimization over all spin multiplets that are part of the exchange coupling problem and the necessity to include dynamic correlation. Results obtained without state averaging, without complete orbital optimization, and without additional treatment of dynamic correlation are numerically inadequate and may show substantial deviations from the correct order and spacing of spin states. In cases where such deviations have been reported for non-manganese systems,124,125 it is not always clear whether the correct application of the methodology as defined above would suppress or eliminate them.126 Systems with more than two Mn ions present profoundly greater difficulties for such methods. This is not strictly because of the larger active space but because of how the calculations should be performed in order to enable us to derive and discuss magnetic properties. Although state-specific DMRG-based CASSCF calculations have been demonstrated for tetramanganese models,127,128 these calculations have not dealt with, and cannot address, the questions of exchange coupling and spin state energetics; it cannot even be verified in principle that the correct ground state is computed. The above stated requirements derived from application of DMRG-CASSCF/NEVPT2 on a dinuclear Mn complex,122 particularly the need for state-averaged orbital optimization over all magnetic spin levels, imply a steep increase of computational complexity and cost for exchange coupling analysis of a trimanganese system, which is an open challenge for multireference treatments, and probably render the tetranuclear case intractable with standard algorithms on conventional computers.
2.2. Spectroscopic parameters
In addition to spin states, an important point of contact between quantum chemistry and experiment are the various forms of spectroscopy used to study catalytic intermediates of the OEC. Here we focus only on parameters relevant to magnetic resonance spectroscopies. Spectroscopy-oriented quantum chemistry is more than a powerful tool for analysing experimental results and more than a way of maximizing the extraction of information from experimental spectroscopic data. It allows access to information that lies beyond the limitations of specific experimental approaches and can achieve unification of disparate sources of information into a common interpretation that connects experimental observations with the electronic structure of computational structural models.Hyperfine coupling constants of Mn ions contain rich information on the local and global electronic structure of the OEC. Here the great challenge for quantum chemistry has been how to properly compute Mn HFCs for an oligonuclear exchange coupled system with DFT. This was addressed with the development of a generally applicable theoretical methodology that allows the use of the standard broken-symmetry DFT approach and makes connections between the various levels of Hamiltonian approximations involved in the fitting of HFC parameters from experimental spectra and in the calculation of HFCs from approximate DFT.98 The interested reader is referred to the original publication for methodological details.98 It is noted that for comparisons to experimental values a scaling factor has to be used for the final spin projected HFCs because of the systematic underestimation of core spin polarization by DFT.129,130 This factor is not universal and may differ depending on details of the methodology such as the type of functional and the treatment of relativity, as well as on the reference set of compounds used to derive the required scaling.98,99,110,131–133 New theoretical developments in this area will be important for making the calculations of HFCs by DFT more robust.134,135 Recent advances in the calculation of HFCs by correlated wave function methods such as coupled cluster theory136 are also very promising but their applicability and reliability remain incompletely explored.137
Following a pilot application98 on a synthetic tetramanganese complex that is a Mn(III)Mn(IV)3 analogue138 of the S2 state, broken-symmetry DFT was used in combination with the above method to compute spin states and hyperfine coupling constants of a wide variety of structural models that were considered at the time as geometric possibilities for the OEC.99 This study showed that many ideas derived from EXAFS studies139 as well as practically all models reported in computational studies until that time140–143 were not consistent with the spectroscopic data on the S2 state. These methods were essential in establishing that model S2A described in Fig. 3 corresponds very well with the 55Mn HFCs determined experimentally by ENDOR spectroscopy,144–150 with one large, two medium, and one smaller hyperfine coupling constant.93 These results demonstrated the importance of spectroscopy-oriented quantum chemistry in discriminating between structural possibilities and encouraged numerous subsequent applications to the OEC and other exchange-coupled oligonuclear systems, including refinements and extensions of the method.131,151–154
An obvious use of quantum chemistry in the study of 55Mn HFCs is in the evaluation of different oxidation state possibilities, both in terms of absolute oxidation levels for the whole cluster and in terms of internal distribution of local oxidation states (valence isomeric forms) for a given total oxidation level or S-state intermediate. This approach has been adopted for evaluating various isomers of the half-integer-spin S0 and S2 states that have been studied extensively by ENDOR spectroscopy.144–148 In particular for the S0 state the situation arises where in principle the total number of unpaired electrons can be distributed among the four Mn ions with a formal Mn(III)3Mn(IV) or Mn(II)Mn(III)Mn(IV)2 configuration. In combination with analysis of exchange coupling and spin states, computed 55Mn HFCs have helped in evaluating various possible structure models.104,113 Another important use of computed 55Mn HFCs has been in the evaluation of possible models for the S3 state. ENDOR-detected NMR studies on one of the components of this state showed that all Mn ions were electronic similar and isotropic.106 Quantum chemical calculations helped to show that all-Mn(IV) cluster models where all Mn ions are octahedrally coordinated due to coordination of an additional water-derived ligand compared to the S2 state are most consistent with the data.104,106 This carries significant weight for the persistent question of whether the S2 → S3 transition involves metal-centred or ligand-centred oxidation.155–157 The calculations firmly support the Mn-centred option because they demonstrate that the experimentally determined 55Mn HFCs for the S3 state are not reproduced with a Mn(III)Mn(IV)3 cluster such as in the preceding S2 state. Owing in part to its heterogeneous nature, as clearly revealed by various magnetic resonance spectroscopic studies106–108,158–160 – though not resolved by currently available structural methods which can only provide spatially or temporally averaged representations – the composition of the S3 state remains under investigation.161–164
55Mn HFCs have also been used in evaluating possible protonation states of oxo bridges and Mn-bound water-derived terminal ligands, and hence determine the most likely overall protonation level and pattern of the active site.100,104 This analysis eliminated the possibility of bridge protonation in the S2 state and led to the conclusion that the terminal Mn in the S2 state is most likely ligated by one water and one hydroxo ligand.100 The focus on spectroscopic properties enables direct screening of computational models against experimental constraints and therefore guides the study of the catalytic mechanism in ways that are otherwise impossible.
Although emphasis in the above was placed on metal ions, ligand HFCs provide significant additional information. It is possible to use ligand HFCs (e.g. of Mn-coordinating oxygen or nitrogen nuclei) to assign metal oxidation states,165 to study the identity and kinetics of exchangeable atoms, and to discover the mechanisms by which small molecules access the active site and interact with the Mn ions.114,115,166–171 An example that will be highlighted here concerns the interaction of the substrate analogue methanol with the OEC cluster. The importance of these studies is that they point to likely pathways for substrate delivery to the OEC. It has long been known that methanol modifies the magnetic energy levels and EPR signals of the manganese cluster of the OEC, but the access pathway(s) and mode of interaction remained unknown.167,172–178 Based on the experimental determination of the 13C hyperfine parameters of isotopically labelled methanol interacting with the S2 state of the OEC,167 an extensive computational screening of structural models was carried out that involved calculation of spin state energetics and 13C isotropic and dipolar HFCs for each one.116 This led to rejection of several possibilities such as direct binding of methanol to Ca2+ or one of the Mn ions, supporting instead a second-sphere interaction that resulted in reorganization of the hydrogen bonding network affecting the O4 bridge and the Mn3–Mn4 exchange coupling interaction (Fig. 5).116 This is in contrast to the case of ammonia, which binds directly to Mn4,115,170,171,179 at least in one of its interaction modes. The identification of a crucial difference between cyanobacteria and higher plants in a residue close to the proposed site of methanol binding (D1-N87A)117 is consistent with the different response of plant versus cyanobacterial OEC to methanol, which can be explained by the restricted accessibility in the case of cyanobacterial OEC due to the more constrained channel architecture.117
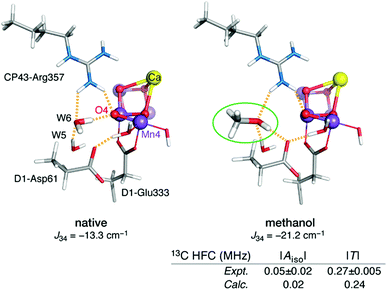 | ||
| Fig. 5 Proposed model for interaction of methanol with the OEC.116 The increase in Mn3–Mn4 antiferromagnetic exchange coupling explains the stabilization of the low-spin S = 1/2 state of the cluster. The model is the only one of those examined that simultaneously agrees with the experimental 13C hyperfine coupling parameters of Oyala et al.167 Figure adapted from ref. 116 – Published by The Royal Society of Chemistry. | ||
An important methodological advance in terms of studying and understanding the local anisotropy of the Mn ions was been the development of the local complete active space configuration interaction (L-CASCI) approach.180 This enables the use of multireference methods for the calculation of local zero field splitting tensors and consists in conducting a multireference (CASCI) calculation with an active space specifically constructed to contain local orbitals for any given metal ion. Successive application of the method for each centre of interest eventually yields all on-site parameters for further analysis. Application of the L-CASCI approach to the S2 state models of Fig. 3 allowed the explicit calculation of site ZFS tensors (specifically the spin–orbit coupling contribution DSOC) for the Mn(III) ions in each valence isomer (Fig. 6).180 The orientation of the DSOC principal axes correlate directly with the orientation of the pseudo-Jahn–Teller axes of the Mn(III) ions, which are oriented along the formally open coordination site of Mn(III) in each isomer. Importantly, the valence distribution, geometric parameters, and computed local ZFS for the Mn4(III) ion in the valence isomer S2B agree perfectly with analogous experimental studies of the g ≈ 4.1 component of the OEC,181 With Dz oriented along the W2–Mn4–O5 axis. This strongly supports the assignment of S2B to the high-spin g ≈ 4.1 signal, in contrast to other hypotheses that do not place the Mn(III) ion at the Mn4 site. The L-CASCI approach will certainly see increased use in the future as more in-depth analysis of catalytic intermediates is undertaken, not only for other intermediates of the OEC but also for other biological or synthetic clusters with multiple open-shell transition metal ions.
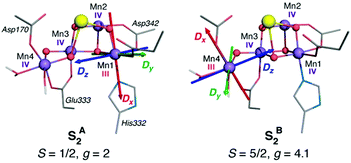 | ||
| Fig. 6 Orientation of principal axes of the DSOC for the five-coordinate Mn(III) ion in each isomer of the S2 state of the OEC, computed with the L-CASCI approach. Adapted with permission from Retegan et al.180 Copyright 2014 American Chemical Society. | ||
Quantum chemical studies that focus on spectroscopic properties have also helped to elucidate critical aspects of the redox-active tyrosine YZ and YD residues.182,183 Here it is the g-tensor of the tyrosyl radical that is the central spectroscopic parameter. This can be calculated with standard DFT approaches, although particular care has to be taken to ensure that the calculations correctly represent the electronic structure of both the YZ radical and the Mn cluster. Most relevant for the OEC are studies that focus on the nature of tyrosyl radical intermediates formed during the S2 → S2YZ˙ → S3 transition.109,182 Detailed investigations of the initial stages of the S2 → S3 transition showed that formation of the tyrosyl radical is accompanied by reorientation of the dipole moment of the OEC in the S2B state,182 which likely triggers proton release from the terminal water ligand W1 of the Mn4 ion to the second-sphere Asp61 residue that acts as proton acceptor.184–186 This deprotonation is necessary for subsequent oxidation of the Mn ion by the tyrosyl radical.109 YZ oxidation is accompanied by shifting of the phenolic proton to His190. The ultimate fate of this proton is still under investigation.187–189 In terms of the spectroscopic properties of the formed tyrosyl radical, Retegan et al.182 established a clear correlation between the hydrogen bonding environment and the g values of the tyrosyl radical. The gx component is oriented along the C–O bond and its correlates almost linearly with the change in the spin population of the phenolic oxygen, the atom with the largest spin–orbit coupling contribution. The spin population is in turn correlated with the number of hydrogen bonds and the electron affinity of the tyrosyl radical. This makes the gx value a direct probe of the hydrogen bonding environment and of the redox potential of YZ˙. In the native system the gx value was relatively low compared to analogous literature precedents, which was attributed to the presence of three hydrogen-bonding interactions, two from adjacent water molecules and one from the His190 proton (Fig. 7).182
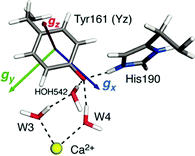 | ||
| Fig. 7 Orientation and components of the g-matrix for the S2BYZ˙ state according to Retegan et al.182 with DFT-computed values gx = 2.0054 > gy = 2.0042 > gz = 2.0022. The immediate hydrogen bonding environment of the radical is also depicted. | ||
Similar correlations derived from quantum chemical studies have been essential for probing the hydration and uncovering the structural basis of spectroscopic observations for the other redox-active tyrosine of PSII, YD.183 Intriguingly, the above observations suggest a direct role for Ca in structuring the hydrogen-bonding environment of YZ and hence directly modulating its redox properties,182 which is crucial for ensuring efficient coupling between the manganese cluster of the OEC and the charge-separation site (reaction centre) of PSII. Complementing this hypothesis, explicit calculations of the effect of calcium substitution by various redox-inactive cations showed that the redox potential of the OEC responds only to the total charge of the cation while remaining insensitive to its Lewis acidity,190 in contrast to correlations established for synthetic complexes.190–192
2.3. Challenges in computational setup and modelling
The preceding sections highlighted contributions of quantum chemistry to understanding Nature's water oxidizing catalyst from the perspective of predicting magnetic and spectroscopic properties. However, it should be stressed that the use of an appropriate theoretical method or procedure to calculate geometries, energies, or other properties, in no way ensures attainment of reliable results that can be meaningfully correlated with experiment and used to evaluate computational models. This is because there are often practical aspects relating to the definition and treatment of the atomistic model itself that may introduce weaknesses which undermine the overall reliability of quantum chemical studies regardless of the “intrinsic” ability of any given theoretical method to deliver high quality numbers. Unfortunately such weaknesses may remain unnoticed because the results obtained by calculations on inappropriate models are rarely, if ever, noticeably wrong in an absolute numerical sense. Here we single out a few issues in model setup that may compromise the relevance of computational results for understanding the real system. Although the examples are taken from OEC studies, the broader lessons are universally valid.When dealing with large and complex active sites such as the OEC, a principal concern is to build a quantum mechanics (QM) cluster model large enough to incorporate the effects of the immediate environment directly or indirectly. The QM model needs to be large enough to explicitly include the complete first coordination sphere and all elements of the second coordination sphere that interact via hydrogen bonding. Information about the structure of the protein matrix that is not explicitly included in the QM cluster model is included indirectly by constraining specific atoms. Constraints are typically applied to backbone atoms such as α-carbons and groups used to terminate peptide chains. When the QM cluster model omits hydrogens bonds that are present in the crystal structure, then additional geometric constraints may be considered, e.g. of specific dihedral angles, or at least optimized models should be examined very carefully for structural compliance with the absent protein matrix. A specific example of this is offered by His332, ligand to Mn1. Inspection of the complete environment of the OEC shows that the orientation of the His332 imidazole ring is restrained by a hydrogen bonding interaction with the peptide carbonyl of Glu329 (Fig. 8), which normally would not be included in QM cluster models of the OEC. The absence of this interaction may result in rotation of the His332 ring by ca. 90° during geometry optimization. Retegan et al. showed that such rotation directly affects the 55Mn hyperfine parameters for Mn1 by modifying the nature of the Mn–N bonding.193 Moreover, the incorrect rotation of His332 artificially increases the accessibility to Mn1, for example by water molecules. Therefore, the orientation of this residue affects considerably the computed relative energetics for water or hydroxy binding and the relevant models reported in the computational literature should always be scrutinized for structural correctness.
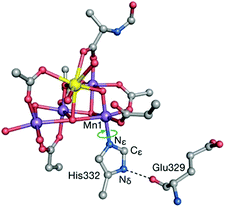 | ||
| Fig. 8 The His332–Glu329 hydrogen bonding interaction constrains the imidazole plane of the histidine residue. Computational models that do not take this into account lead to incorrect description of the coordination sphere of Mn1 and all processes and properties associated with it. Adapted with permission from ref. 193. Copyright 2013 American Chemical Society. | ||
The combination of quantum mechanics with a force-field (molecular mechanics) treatment of the environment, i.e. the QM/MM approach, has a strong tradition in the OEC140,186,193–195 and it is expected to offer a better treatment of the environment when applied correctly. Here we would stress that the use of the QM/MM approach rarely allows for appreciable reduction in the size of the QM region compared to a standard QM cluster approach and does not negate the need to incorporate all important hydrogen bonding groups (including essential crystallographic waters) in the QM region. In fact, the use of a very small QM region leads with certainty to artefacts, which include spurious redox activity arising at the periphery of the QM region that results from redox imbalance (see below) or overpolarization from force-field charges.
Related to the above is the inclusion of the redox-active Tyr161 residue (YZ) in QM cluster models, or in the QM region of QM/MM models. YZ is both structurally coupled to the rest of the OEC via a tight network of hydrogen bonds, and redox-coupled as amply evident by the catalytic cycle depicted in Fig. 1 and by preceding discussions. Thus, omission of the Tyr161–His190 pair from computational models can lead to two critical artefacts: (a) removal of the hydrogen bonding network and drastic reorganization of the water molecules that are situated between YZ and the Mn ions, and (b) absence of redox balance in the computational model, or inability to evaluate it. The first issue means that in the absence of the Tyr161–His190 pair and of the physiological associated hydrogen bonding network, calculations of hypothetical processes implicating these waters have unnaturally low barriers and little physical connection to the real system. The second issue means that without the tyrosine and without explicitly studying the relative energies of SiYZ˙ versus Si+1YZ states, no credible discussion of S-state transition energetics can be made. Explicit consideration of YZ and of its redox role is not only essential when S-state transitions are examined or when YZ participates directly in the mechanism.109,182,196–198 The redox properties of any computational model should be examined as standard practice to ensure that intrinsic redox balance is achieved and that no unphysical properties are inadvertently introduced. For example, a recent study showed that a set of assumptions regarding Mn oxidation states and protonation states of specific ligands results in the unphysical shifting of the site of subsequent oxidation from YZ to the second-sphere histidine His337.199
2.4. Catalytic progression and O–O bond formation
The precise details of the water oxidation mechanism during the later stages of the catalytic cycle remain a constantly evolving discussion.17,200–202 Open questions revolve around the steps of the S2 → S3 transition, the composition of the heterogeneous S3 state and the “active” population of S3 state that progresses further to form the O–O bond. Very little, and often indirect, experimental data exist on the S3YZ˙ intermediate and the most critical part of the cycle that involves dioxygen evolution and reconstitution of the S0 state.203–205The two valence isomeric forms of the S2 state of the OEC depicted in Fig. 3 were shown to behave differently upon oxidation. Independent computational studies confirmed that after formation of the tyrosyl radical intermediate, the valence isomer with the Mn(III) ion at the Mn4 site, S2BYZ˙, is the one where the tyrosyl radical can be reduced by manganese so that the cluster advances to a Mn(IV)4 S3 state109,197 (see above for comments regarding the irrelevance of computational models that do not explicitly incorporate the YZ–His190 pair and hence neglect the central question of redox balance between the manganese cluster and the redox-active tyrosine). Although various other possibilities may be envisioned, at this time the above S2 → S3 sequence appears to be the best attempt so far to accommodate most experimental observations on S2, S2YZ˙ and S3 states, particularly from EPR spectroscopy.
In the above scenario a key species is the S3 component with a five-coordinate Mn(IV) ion (S3B in Fig. 4), which must have a high spin state (S = 6) as predicted by the quantum chemical analysis of Retegan et al.109 This has received very strong experimental support by a recent multifrequency EPR experimental study of the S3 state in spinach PSII, which directly identified an S = 6 population with high effective anisotropy deriving from anisotropic exchange coupling between the coordinatively unsaturated Mn4(IV) ion and the Mn(IV)3Ca cubane subunit.108 Importantly, the S = 6 component was found to be the exclusive species in methanol-treated spinach PSII and to form a major part of S3 even in the native system.108 Although the water bound intermediate-spin (S = 3) isomers of Fig. 4 have been experimentally confirmed as distinct populations of the S3 state, Krewald et al. showed that water binding is not required to oxidize the cluster to the S4 state.206 Assuming the water-unbound form is catalytically active, this would allow Mn-based oxidation, leading to an S4 state of the OEC with a five-coordinate Mn4(V) ion bearing a terminal oxo group at the formally “W2” position of earlier states.206 This can then couple nucleophilically in an acid–base with the internal oxo bridge to form the O–O bond (Fig. 9a).206 The above mechanism is the only currently discussed possibility that allows for complete separation of the charging phase (four Mn-cantered oxidations) from the actual catalytic phase, which can be achieved by even-electron O–O bond formation even in a single concerted step.206
On the other hand, if a water-bound S3 species is the active population of S3, then it is expected that the more stable S3A,W isomer will be involved. The reactivity in this case has been investigated by extensive computational studies and it is expected that the final S3 → S4 step involves ligand-cantered oxidation to create an oxyl radical.143,207 This would subsequently couple in a radical oxyl–oxo coupling mechanism (Fig. 9b), which can itself be realized in multiple alternatives.185,208,209
Note that both of the above scenarios involve homovalent Mn(IV)4 S3 isomers and assume a regular sequence of Mn-centered oxidations at least up to the S3 state (for a radical oxyl–oxo coupling mechanism) or all the way to an S4 state (for a nucleophilic oxo coupling mechanism). Several similar or distinct possibilities are being discussed,81,161,162,164,210–213 including alternatives avoiding alternative valence isomeric forms for the S2 state, invoking early water binding before advancement to the S3 state, assuming formation of an oxyl radical in the S3 state or even “early onset” O–O bond formation already in the S3 state, and others. Some of these alternatives may be in explicit or implicit disagreement with the most obvious interpretations of experimental data up to the S3 state,161 but in view of the absence of meaningful constraints past the S3 state, they need to be carefully evaluated and for this reason further and more ambitious experimental and theoretical studies will be required.
A specific challenge for quantum chemistry in this case is to accurately distinguish energetically between different redox isomeric forms. Isobe et al. have already shown the sensitivity and precariousness of DFT when dealing with this problem.163,211 The question of accurate energetics in this context is closely related to the general problem of spin-state energetics for transition metal systems,214 though magnified in complexity by the presence of the four interacting open-shell Mn ions and the potential for oxygen-based radicals and O–O bonded intermediates. Achieving systematically accurate energetics in this case might be possible by a new generation of linear scaling coupled cluster approaches. A prominent example is the domain-based local pair natural orbital approach to the popular coupled cluster theory with single, double, and perturbative triple excitations, i.e. DLPNO-CCSD(T).215–217 The method has already been applied with success in smaller transition metal systems,218–221 but the OEC presents much greater challenges. Pilot applications on minimal structural models have been reported but it remains to be seen whether successful applications are possible on realistic models of the OEC.
In the context of electronic structure challenges it should also be noted that the remarks made above regarding the nature of broken symmetry solutions also hold for any other aspect of the system, including DFT-derived mechanistic schemes. The use of a single spin configuration to follow a reaction pathway, particularly a reaction that involves multiple spin states of an exchange-coupled system, is an approximation whose crudeness is impossible to determine beforehand. Without negating the value of straightforward DFT studies in guiding our thinking on the mechanism of water oxidation, it is highly desirable to eventually approach the question of O–O bond formation in the OEC with proper consideration and formally correct treatment of the multireference nature of the process.
3. Hydrogenases
3.1. Background
Evolution led some organisms to develop enzymes with the ability to catalyse the reversible heterolytic splitting/formation of H2. In contrast to the OEC of PSII, which is unique and identical in all oxygenic photosynthetic organisms, hydrogenases show a wider variability. They are typically divided into three families depending on the transition metal composition of their active site: [Fe], [FeFe] and [NiFe] types.29 Hydrogenases produce H2 with turnover frequencies reaching (3 × 104 s−1 at 30 °C) at marginal potential beyond equilibrium (−400 mV vs. NHE, pH = 7).222 This catalytic activity can only be matched by platinum.223 Their catalytic efficiency, thermostability, and low overpotentials, make hydrogenases ideal models for the bioinspired synthesis of new organometallic catalysts. However, their complex protein structure and the nature of the reaction they perform have posed obstacles in obtaining a clear and precise view on the details of how they function. The size and composition of the active sites make hydrogenases challenging systems to study also from the theoretical point of view.224The structural elucidation of the [NiFe] hydrogenase revealed an organometallic Ni–Fe complex with CO and CN-ligands bound to Fe,225 while four cysteine residues ligate the Ni site. Two of the cysteines bridge the two metal ions as shown in Scheme 1b. The nickel center has been suggested to play a critical role in hydrogen binding/proton activation and in the redox chemistry of the catalytic cycle. It is postulated that three different active states are involved during catalysis: Ni–SIa, Ni–R, and Ni–C.34 Although broad agreement exists on the presence of Ni–C and Ni–R, uncertainties remain about the completion of the cycle and about how each state converts to the other.
Consequently, there is still lack of consensus on the catalytic cycle of [NiFe]-hydrogenases even if distinct mechanisms have been proposed on the basis of combined experimental and theoretical evidence (Fig. 10). In the proposed cycle, H2 is activated through binding to the diamagnetic Ni–SIa state, where the metals are present as NiII and FeII and have a low spin state. This activation leads to heterolytic cleavage of the H–H bond and the formation of the Ni–R state, which contains a bridging hydrido ligand. The two-electron oxidation of Ni–R regenerates the Ni–SIa while the second proton is released. The intermediate Ni–C species corresponds to the one-electron oxidized form of Ni–R and is assigned to a NiIIIFeII-hydrido complex, which has been experimentally characterized.226
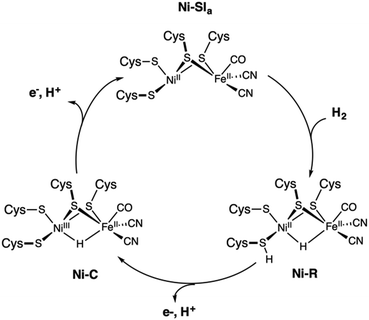 | ||
| Fig. 10 Proposed catalytic cycle of the [NiFe] hydrogenase involving the Ni–SIa, Ni–R, and Ni–C states. | ||
The [FeFe] hydrogenase shares some features with the [NiFe] type. Its catalytic center, the so-called H-cluster, is a di-iron center [2Fe] composed of a proximal Fe covalently attached via a cysteine thiol bridge to a cubane-like [4Fe4S] cluster, and a distal Fe, which has an open coordination site for H2 binding (Scheme 1). Similarly to the [NiFe]-hydrogenase, each iron site binds two CO and CN ligands, with one CO shared between the two metal ions.227 The ligand sphere leads to FeII metal centers in the low-spin state. A key structural difference to the [NiFe]-hydrogenase is the presence of a dithiomethylamine (dtma) ligand that bridges the Fe ions.228
The catalytic cycle of [FeFe] HG (Fig. 11) remains controversial despite extensive research efforts. According to recent reports, binding of H2 to the oxidized active ready state, Hox, results in the heterolytic cleavage of H2, and in the formation of Hhyd. The latter species is a mixed-valence FeIIFeI intermediate featuring a protonated dtma and a terminal hydride ligand. On deprotonation, Hhyd is converted into the rather stable Hsred state with both metals being at the (+I) oxidation state. The one electron oxidation of Hsred yields Hred before a proton-coupled electron transfer recycle Hox. Overall, the mechanism of the [FeFe] HG remains debated particularly with respect to the one- and two-electron reduced intermediates.33
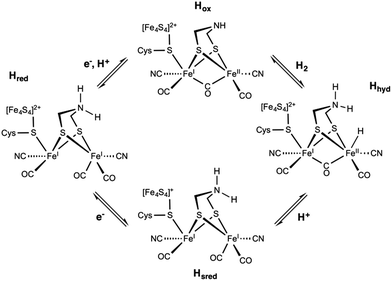 | ||
| Fig. 11 Postulated reaction mechanism of the [FeFe] hydrogenase involving the Hox, Hhyd, Hred, and Hsred states. | ||
The absence of consensus regarding the complete catalytic cycle of hydrogenases has driven developments towards proficient catalysts for HER. Studying smaller catalysts is insightful for the proper design of new molecular electrocatalysts even if they lack the functionally important protein matrix. Many biomimetic and bio-inspired complexes have been developed and investigated with the purpose to understand and mimic the proficiency of hydrogenases. In this respect, computational approaches combined with experiment can play a key role in the development of efficient synthetic catalysts.229–231 Contributions of quantum chemistry are not limited to rationalizing experimental observations; the correlation between theory and experiment drives conceptual and methodological developments toward new experimentally accessible systems. As in the case of the OEC, studies combining experiment and theory contribute to understanding the properties and reactivity of the enzymes, but they have also assisted more directly in the design of more effective HER catalysts.
In the following, we report on the extensive use of the theoretical methods to better apprehend and get insight into the geometric structures, electronic structures, and properties of hydrogenases as well as related biomimetic and bio-inspired models. We will show that quantum chemical studies are crucial to identify the electronic and thermodynamic parameters that govern the reactivity of catalytic centers, to determine the crucial structural determinants of catalytic activity, and to unravel the key steps of their reaction mechanism. Such investigations in the fields of hydrogen evolution nowadays offer ample proof of the use of quantum chemistry as a predictive tool and as an essential component in the understanding of the natural system and in the design of novel synthetic catalysts.
3.2. Geometric structures
The complexity of hydrogenases and the various limitations pertaining to their experimental characterization have fuelled great interest in applying theoretical methods to investigate the structures of models of the different redox states of HG. Looking at the structural aspect of the hydrogenases, theoretical tools have been successfully employed to model both the models and the enzymes. It is now accepted that geometries can be reliably predicted by DFT methods and converge quickly with basis set size, making such prediction rather economical. Long experience has established that the cluster approach using relatively small models (for example, up to ca. 200 atoms) of the protein active sites can provide meaningful mechanistic insights like hydrogen evolution by HG (Fig. 12).53,54 On the other hand, realistic modelling of the protein environment is achieved by quantum mechanics/molecular mechanics (QM/MM) and “Big QM” approaches. In the case of the hydrogenases, many studies employing these approaches have been reported over the years and contributed to understanding the enzymatic environment and the reaction channels of hydrogenases.226,232 In the case of the [NiFe] HG, QM/MM geometry optimizations have contributed to the interpretation of data from crystallography by identifying likely positions of transient H atoms.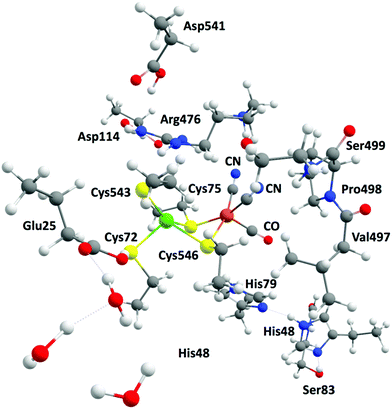 | ||
| Fig. 12 Example of a large model system including relevant amino acids and mimicking the active site of the [NiFe] hydrogenase. | ||
Computational studies have identified the heterolytic cleavage of H2 as the initial step of the reaction and determined that one hydrogen becomes a bridging hydride whereas the other is accommodated as a proton on one of the cysteine residues.233,234 For [FeFe] hydrogenase, QM/MM studies have been extensive and multifaceted. For example, it was shown that the inclusion of two [4Fe4S] clusters in the QM part in addition to the H-cluster provided useful insights into the oxidation states of the active site and the interplay between the two cubanes.235–237 We can also cite alternative approaches such as the quantum refinement approach based on accurate DFT calculations that was applied to the [FeFe] enzyme to elucidate the nature of the dithiolate ligand.238
Molecular dynamics studies have offered support for a proton transport channel to facilitate substrate and product delivery in both hydrogenases.239 A specific pathway was recently suggested for the second proton, whereby reduction of the active site triggers a structural change, opening a water channel with favourable energetics for the second proton transfer in the [FeFe] HG.240 In addition, a glutamic residue near the active site was shown to be important for proton transport as its mutation results in loss of activity of [NiFe] hydrogenase.241 Molecular dynamics can be also combined to other approaches like the coarse-grained (CG) analysis in order to probe important catalytic steps of [FeFe]-hydrogenase, including the transport of electrons to the active site via the iron–sulfur clusters.242
Population analysis schemes are simple yet valuable tools, as recently proven by a study using conceptual DFT and Natural Bond Order (NBO) to get new insight regarding the transformation of a proton into a hydride during the catalytic cycle of the [NiFe] HG. Their results indicated that such a transformation is driven by spontaneous rearrangements of the electron density at room temperature.243 Such analysis can be very informative about the ligand binding mode and strength to the metal centers of the [FeFe] active site. For instance, a recent report showed that, upon reduction, the distal iron is favoured by the bridging carbonyl which suggests that electrostatic stabilization would influence the charge accumulation occurring prior to H2 release.244 Topological analyses based on NBO were also used to revisit the nature and strength of the hydride and dihydrogen interaction with the iron center in the [Ni–Fe] enzyme.245
3.3. Electronic structures
Deciphering the spin states of the species that are involved in the catalytic cycle of hydrogenases has reached a whole new level with recent studies showing that it is now possible to conduct calculations with accurate wave function quantum chemical methods, such as the coupled cluster method with single, double and perturbative triple excitations, CCSD(T), and multireference approaches (CASSCF, DMRG). These new advances are very important as energies for reactions involving two-electron transfers to the metal centers like in hydrogenases can be sensitive to the nature of the DFT functional and higher-level methods are thus necessary to obtain more reliable energies and reaction pathways. For example, multi-reference Møller–Plesset246 and CAS-PT2 calculations247 were conducted on the active site of the [NiFe] hydrogenase and helped to assign the ground spin state as a singlet through the evaluation of singlet–triplet energy splitting. Wave function methods including CCSD(T) and DMRG have been employed to investigate the interaction of dihydrogen with the [NiFe] active site. These calculations showed that H2 binds more favourably the Ni site in the singlet state and provided additional understanding about how the active site behaves in the presence of H2.248 A similar work based on multiconfigurational short-range DFT calculations supported this conclusion.249 DMRG has also been applied to study the electronic structure of [4Fe-4S] clusters relevant to the description of the hydrogenase active sites125 and demonstrated the importance of developing sophisticated methods for electronic structure calculations for an accurate evaluation of the low-lying states that have implications for the reactivity of most bioinorganic systems.A different aspect of spin-state energetics is found with magnetically interacting (exchange-coupled) transition metal ions as in the case of the [FeFe] hydrogenase whose active site, the H-cluster, corresponds to a [2Fe] subunit coupled to a [4Fe4S] cluster. Such systems can be handled within the DFT framework using the broken-symmetry (BS) approach, which gives access to exchange coupling constants and hence magnetic spin states and energies. Several studies have been reported using this approach showing its capability to provide useful insight on the electronic configuration of the complicated [FeFe] active site by revealing the distribution of metal valences and spin-coupling schemes for the iron–sulfur clusters.250–252 Similar studies were conducted in the case of the O2-tolerant [NiFe] hydrogenases that contain a proximal [4Fe–3S] cluster whose redox states and magnetic couplings were elucidated and discussed using BS-DFT calculations.253–255
3.4. Spectroscopic properties
In conjunction with experimental methods, theoretical calculations appear as an invaluable tool for the interpretation of spectroscopic results. Spectroscopic data for a sufficiently complex system rarely have a unique interpretation in terms of electronic structure. On the other hand, it can be difficult or impossible to identify the most appropriate electronic structure description using only total energies as criterion in quantum chemical studies. Therefore, the explicit calculation of spectroscopic properties is the way toward a better understanding and more reliable verification of the geometric and electronic structures of a complex system that is being modeled. Spectroscopic techniques including FT-IR, Nuclear resonance vibrational spectroscopy (NRVS), Electron Paramagnetic Resonance (EPR) or Mössbauer have been widely employed to investigate [NiFe] and [FeFe] enzymes and models, and often combined with theoretical methods (Fig. 13).29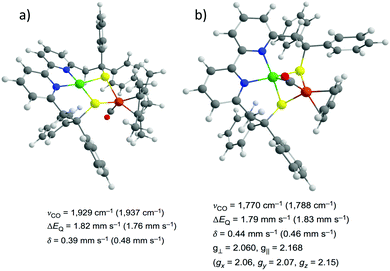 | ||
| Fig. 13 Structures of the biomimetic models for the Ni–SIa (a) and Ni–L (b) states of the [NiFe] hydrogenase identified by combining spectroscopic measurements and DFT computations. Adapted with permission from ref. 40. Copyright 2016 Nature Publishing Group. | ||
Following the development of a computational methodology for an accurate prediction of the IR spectra of the active site of [FeFe]-hydrogenase,256 many studies have been conducted using DFT calculations and helped in the unambiguous assignment of the structure and redox states of intermediates like for the H-cluster.257–260 While the calculated absolute vibrational frequencies are often not quantitatively accurate, shifts in frequencies due to protonation and/or reduction events are reliable. Due to the peculiar vibrational frequencies of the CN and CO groups, it is possible to distinguish the redox states of the [NiFe] active site. Indeed, the stretching frequencies of these ligands are spectroscopic fingerprints that can probe the electronic structure of the metal core and the structural composition of the active site.261 Comparison between computed and experimental vibrational frequencies can provide even more subtle information like the influence of the second coordination sphere on the electronic structure of the [NiFe] active site.262 A review article recently highlighted that the correlation between experimental and DFT-calculated IR spectra is a powerful tool to identify some key features of the active site cofactor of HG and to unravel the structure of transient intermediates with great precision.227
NRVS is emerging as spectroscopic technique to study hydrogenases. The vibrational density of states spectra that are obtained when using NRVS can be reliably predicted using density functional theory (DFT) and assists in spectral assignments. A striking example comes from a recent study that combined IR and NRVS spectroscopic techniques to DFT calculations to elucidate the structures and the local coordination spheres of the one and two-electron reduced intermediates of the [FeFe] HG. Their results showed no evidence for a bridging hydride which may have important consequences for the mechanism of H2 conversion by this enzyme.263 In a similar manner, the NRVS spectroscopy was employed together with DFT calculations to identify one catalytic state of the [FeFe] hydrogenase, providing decisive information regarding H2 bond formation by the enzyme. This study was conducted on an [FeFe] HG using NRVS experiments in conjunction with DFT calculations and showed that Hhyd is the catalytic state one step prior H2 formation264 while another report studying an [FeFe] variant elucidated the bending modes of the terminal Fe–H species,265 both providing mechanistic insight into the reaction coordinate for H2 bond formation by [FeFe]-hydrogenases. Similar studies were also conducted on [NiFe] enzymes and enabled the distinct observation of Fe–CN and Fe–CO bending and stretching modes for the active sites in [NiFe] HG266,267 while a recent report showed the direct evidence for a hydride bridge in the active site of the fully reduced Ni–R form whose electronic structure could be assigned as a low-spin Ni‖(μ-H)Fe‖ core.268
EPR spectroscopic techniques have been demonstrated as extremely useful to investigate paramagnetic intermediate states during hydrogen conversion catalytic cycle.228 Understanding the hydrogenase mechanism implies being able to determine the exact structure of the active site and its surrounding for all states. In addition to this information, EPR spectroscopy can also give access to the oxidation and spin states of the metal ions involved and their interaction with each other or with the ligand sphere. One known example of the use of theoretical EPR spectroscopy to study HG deals with the Ni–L state, detected when the Ni–C state is put under illumination. DFT calculations were conducted on all possible structures of Ni–L state and g tensors together with hyperfine coupling constants were computed as indicators to compare with EPR data. From the calculated spectroscopic parameters, it was proposed that the proton most likely binds to the terminal cysteines rather than the bridging ones and that a metal–metal bond between nickel and iron was present.269 Another example lies in the study of an artificial [FeFe] hydrogenase for which DFT calculations helped to determine the structure of the active site. Specially, computation of the hyperfine coupling constants reproduced experimental data and highlighted the presence of a CN ligand with the cyanide C atom bridging one mixed-valent iron of the [4Fe4S] cluster and the N atom bound to one iron of the binuclear unit.270 Several experimental and theoretical investigations of the H-cluster using advanced pulsed EPR techniques and DFT calculations have been carried out. They showed that spin polarization in the dtma ligand can be linked to the asymmetric coordination of the distal iron site with its terminal CN− and CO ligands which would have implication on stabilizing the iron-hydride intermediate in the catalytic cycle.271 More recently, EPR data together with DFT calculations clearly showed that a specific conformation of the external CO ligand is favoured so that it binds in an apical position on the iron center. These combined studies highlighted the rigid configuration of the CO and CN ligands which is stabilized by H-bonds and has implication on the reactivity of the enzyme as it ensures minimal reorganization energy during catalysis.272
As an indispensable analytical tool in iron coordination chemistry, Mössbauer spectroscopy is a valuable spectroscopic technique to study hydrogenases. It can probe the spin state of the metal centers in the active sites as well as their local environment like the coordination geometry. For instance, theoretical Mössbauer spectroscopy has been used to investigate the [4Fe3S] cluster proximal to the active site of the O2 tolerant [NiFe] HG. The calculated isomer shifts and quadrupole splitting helped in discriminating between different interpretation of the data and a clear assignment of both the spin coupling scheme and the redox states within the iron–sulphur cluster was made possible.273 Combined with theoretical calculations, this spectroscopic technique has been also employed to study diverse [FeFe] hydrogenase intermediates. The putative structures of these intermediates were obtained from QM/MM calculations and the comparison between calculated and experimental isomer shifts could be used to discriminate between different intermediates following a proper calibration based on iron-based model systems.274 The same approach was also used for studying the coordination environment of an active site model complex. Based on the calculated isomer shifts and quadrupole splitting, they could determine the protonation states, the presence of a bound water and the redox state of the iron center providing meaningful insight regarding the proton transfer mechanism.275 A more recent study made use of several techniques including Mössbauer spectroscopy and DFT calculations to set-up structure–property relationships and to show how that the reactivity of all HG enzymes could be mimicked using isomers of a [NiFe] bio-inspired model.276
With the recent development of dedicated quantum chemistry program packages277–280 the use of theoretical spectroscopy has been democratized with the aim to connect the results of computations to experimental observables since spectroscopic properties remain a precise and sensitive fingerprint of the electronic structure for a given system. Consequently, combining spectroscopic characterizations with theoretical calculations has been successfully employed by many research groups to identify the geometric and electronic structures of biomimetic40,60,265,268,281–283 and bio-inspired284–290 models of hydrogenases and appears as a prerequisite to any further computational investigation of their reactivity towards H2 evolution.
3.5. Thermodynamics
Studying the reactivity of hydrogenases and related model systems implies the initial determination of thermodynamic properties like redox potentials and pKa values. Indeed, the hydrogen evolution reaction proceeds via the transfer of two electrons and two protons to form H2. For a given catalyst, six sequences can be formally considered: ECEC, ECCE, EECC, CCEE, CEEC and CECE with E being the electrochemical event i.e. the electron transfer step and C being the chemical event i.e. the proton transfer step (Fig. 14). Through the computational evaluation of the free energies of the species associated to these chemical and electrochemical steps, it is possible to get access to the thermodynamic quantities with a reasonably high level of accuracy. The theoretical prediction of these parameters is usually conducted using Born–Haber cycle and the calculated Gibbs free energy change associated with the reduction and protonation event in solution, respectively. To calculate experimentally relevant electrochemical quantities, reference systems have to be considered. To do so, the absolute reduction potential of the reference electrode and the pKa of the acid serving as the proton source have to be computed and further subtracted from the Gibbs free energy change in solution for reduction and protonation.229,291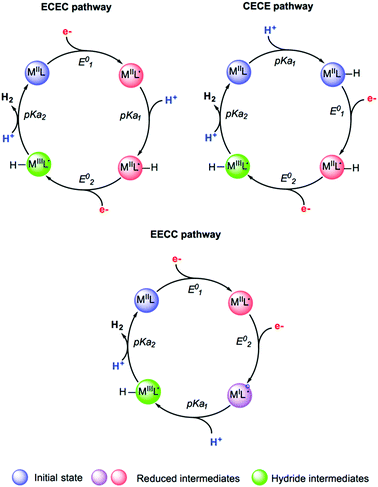 | ||
| Fig. 14 Selected examples of sequences and putative intermediates considered during hydrogen evolution reaction. Adapted with permission from ref. 291. Copyright 2019 Chem Pub Soc. | ||
Electronic structure methods have extensively used to predict relative redox potentials and pKa values of molecular electrocatalysts and hydrogenases models as a first step for further mechanistic investigations.33,226,231,287,292,293
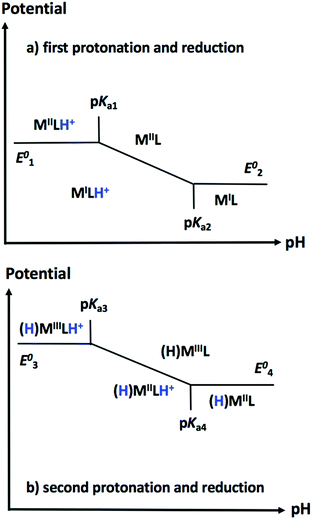
One useful tool for envisioning the relationship between E and C steps during hydrogen evolution finally lies in the construction of Pourbaix diagrams. These diagrams depict the thermodynamically most stable species for a given reduction potential and pH value (Fig. 15). For a given catalyst, constructing a theoretical Pourbaix diagram allows to evaluate the stability of all possible intermediate species on a broad pH range. Linear correlations using Pourbaix diagrams, redox potentials and pKa values have been established for cobalt and nickel electrocatalysts as powerful tools in catalyst design, enabling the computational prediction of properties for electrocatalysts that have not yet been synthesized.292,294–296
3.6. Reaction mechanisms
Computational approaches have been widely used to elucidate various mechanistic aspects of catalytic hydrogen evolution, including possible protonation sites, energetics of distinct pathways, order of steps, and stepwise versus concerted processes. The reliable calculation of relative stabilities of various isomeric forms and the detailed insight into plausible pathways for their interconversion are crucial to address reactivity problems in hydrogenase chemistry. Using DFT methods, free energy profiles of possible mechanistic routes can be evaluated along with the corresponding intermediates and transition states resulting from reduction and/or protonation events. The theoretical determination of the quantities associated to the electrochemical and chemical steps was shown to help to determine which pathway is favoured among all possible sequences. Many studies made use of detailed DFT calculations to inspect free energy landscapes and to identify the predominant pathway for proton reduction among all possible sequences in the case of molecular electrocatalysts61,62,292,294,297–309 and hydrogenase models (Fig. 16).39,59,281,282,287,288,310–316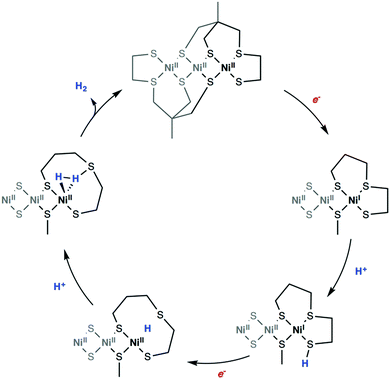 | ||
| Fig. 16 DFT computed reaction mechanism for hydrogen evolution mediated by a bio-inspired mimic for the [Ni–Fe] hydrogenase. Adapted with permission from ref. 299. Published by The Royal Society of Chemistry. | ||
Environmental effects play an important role in modulating the energetics of every intermediate state in the reaction pathway of HER catalysts. Specially, the presence of solvent molecules or anions from the acid serving as the proton source can play a crucial role in modulating the kinetic and thermodynamic aspects of the reaction.317 For instance, the proton source can affect the thermodynamics of catalytic event and a theoretical description of these effects on the pKa value, metal redox states or protonation states are necessary to inspect the feasibility of different pathways for the catalytic cycle of cobalt catalysts.293,318 The DFT investigation of a nickel catalyst reported the effect of the solvent on redox properties and how it can affect the stability of the metal oxidation state by changing its coordination. In this study, accurate estimates of redox potentials could be estimated by accounting for a possible ligand release.296 The importance of the anation was demonstrated in a recent DFT study on a cobalt catalyst which showed that substitution of a bound acetonitrile with acetate alters the proton reduction energetics (Fig. 17).317 Thus, accounting for these effects and the possible direct involvement of the solvent are critical considerations in computational studies.
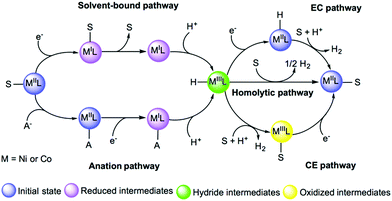 | ||
| Fig. 17 Examples of solvent-bound and anation reaction pathways to form hydride intermediates. Adapted with permission from ref. 291. Copyright 2019 Chem Pub Soc. | ||
For a complete rationalization of the reactivity towards hydrogen evolution, it is often sufficient to evaluate the activation barrier for thermally activated processes. For other cases, free energies of reactions have to be combined with kinetic rates (Fig. 18). To do so, the rate constants for proton transfer, electron transfer, and concerted events have to be calculated as the kinetics of these various steps can play an important role in the reaction pathways. Such an estimate requires further analysis, involving accurate evaluation of reorganization energies, adiabatic couplings for electron transfer, and methods that can properly sample the quantum dynamics of proton-coupled electron transfer. Several studies on molecular electrocatalysts have reported the theoretical evaluation of electrochemical non-adiabatic rate constants for electron and proton transfer within the Marcus theory framework.229,319–321 In the case of hydrogenases, kinetic rates have proven hard to extract.322 However, combining MD data with phenomenological rate equations, hydrogen diffusion constants in HG were recently calculated and found to be in agreement with experiments.323,324
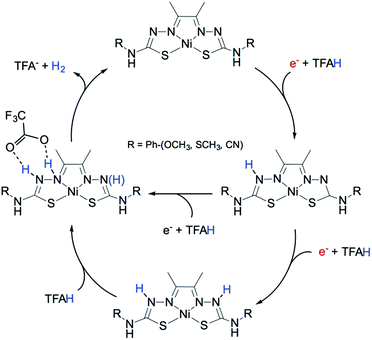 | ||
| Fig. 18 DFT computed reaction mechanism for hydrogen evolution mediated by a molecular catalyst highlighting the influence of the proton source on the preferable pathway. Adapted with permission from ref. 309. Published by The Royal Society of Chemistry. | ||
Computational studies on the mechanistic aspects of hydrogen evolution by hydrogenases have been an active topic of research in many groups.224,291,325,326 For instance, various computational works have been performed to study the reaction cycle of the [NiFe] HG with a special emphasis on H2 binding site and proton binding position.233,234,327,328 While there has not being a complete consensus on the catalytic cycle (Fig. 10), the mechanism presumably starts with the Ni–SIa state binding H2 on the NiII site. H2 is heterolytically cleaved yielding the Ni–R state displaying a hydride bound to both two metals and a proton binding the Cys546. The next step involves two possibilities, depending on whether a proton or an electron is removed first. Both scenario lead to the formation of the Ni–C intermediate featuring a NiIII center. Subsequently, the formed hydride is oxidized, the metal reaches its NiI state, and the resulting proton is transferred to Cys546. The cycle is then completed with the formation of the Ni–SIa resting state. The reaction mechanism of H2 oxidation by [NiFe] hydrogenase was recently revised using DFT methods and focused on the energetics of the entire catalytic cycle. Here two different mechanisms were investigated: the heterolytic cleavage of H2 and the homolytic one that occur with different redox states of the [NiFe] core. Their main finding is that reaching the homolytic mechanism implies one cycle of the heterolytic mechanism. They also correlated the design of the [NiFe] active site complex to the criteria of energy minimization upon proton and electron release, and thus observed an endergonic binding of H2 which has direct implications on the development of efficient HG mimics.329,330 Another study using DFT calculations recently reported new mechanistic insights on the reactivation process involving oxidized forms of the [NiFe] HG. While [FeFe]-hydrogenases are irreversibly inactivated by O2, [NiFe] are more resistant to oxidation. However, oxygen exposure creates a mixture of two inactive, oxidized forms, the Ni–B and Ni–A states. Importantly, these are not permanently inactivated but can be reactivated by reduction. The results of this study showed that the bridging hydroxide ligand found in the two states is lost upon reduction and protonation steps at the active site. Structures for the species obtained upon reduction of Ni–A and Ni–B were proposed and specific structural features were shown to impact the reactivation kinetics of the oxidized and inactive states.331
Similarly, with [NiFe] hydrogenases, distinct mechanisms were proposed for the [FeFe] ones and differ mainly in the protonation sites and H2 binding. Lately, computational studies together with experimental investigations seem consistent with one scenario. When considering the catalytic cycle in the direction of H2 production (Fig. 11), the [FeFe]-hydrogenase state directly involved in hydrogen binding is Hox. In this state, the redox of the H-cluster can formally be described as FeIIFeI. One electron reduction and protonation of Hox yields a transient FeIFeI species featuring a protonated dtma ligand and referred as Hred. Further proton-electron transfer takes place resulting in the formation of Hhyd, a mixed-valence FeIFeII species featuring a terminal hydride ligand and a protonated amine. H2 detachment from this intermediate brings the H-cluster back to the initial FeIIFeI redox state.332–335 The catalytic activation of H2 by [FeFe] HG has been recently revised by means of DFT methods to elucidate the specific details underlying the different performances of the enzymes when compared to biomimetic models. Their results highlighted that the enzyme performs better which can be correlated with two requisites: (i) the presence of an electron-poor iron center which favors H2 binding and (ii) a electron-rich cofactor which ensures oxidation of the metal–H2 adduct. Disclosure of these differences will guide the development of novel biomimetic models and lead to reconsider the utility of CN ligand in the catalyst design.336
In addition to the extensive use of DFT methods, QM/MM thermodynamic cycle perturbation (QTCP) computations were recently shown as a valuable approach to obtain accurate free energies to model the catalytic cycle for hydrogen evolution by hydrogenases. In these calculations, the QM/MM method is used to compute the energy differences on configurations generated by MD simulations. QTCP currently gives access to reaction energies with an accuracy of 20 kJ mol−1. Reaching higher degree of precision will require, among other things, to take into account other factors like polarization or short-range electrostatics and the development of high-level methods, both being the topic of intense research efforts.233,234,337,338
4. Conclusions
Impressive advances have been made in recent years in understanding the structure and function of the photosynthetic oxygen-evolving complex and of hydrogenases. Quantum chemistry has played a key role in most of these efforts, especially when it has been fruitfully combined with experiment. Nevertheless, photosystem II and the hydrogenases continue to pose great challenges, both in terms of fundamental understanding and in terms of the technical difficulties involved in studying them. In the field of water oxidation an incredible amount of insight has been gained on the geometric and electronic structure of the oxygen-evolving complex, yet serious questions remain open regarding the precise nature of several catalytic intermediates and nothing is known with certainty about the critical dioxygen formation and evolution steps. In the field of hydrogen evolution, despite the recent advances made in the understanding of the mechanism by which hydrogenases exert their function, especially the formation of hydride species or the key role of the metal site involved in catalysis, many essential aspects of the catalytic process including CO/O2 inhibition or activation/deactivation processes are incompletely understood. From the point of view of quantum chemistry both more accurate methods and more reliable models will be needed to retain the pace of theory-led discovery in the field of metalloenzyme solar fuel research. Among the points highlighted in this article is the development of first principles electronic structure methods that overcome deficiencies associated with existing DFT implementations and deliver accurate predictions of spin-state and reaction energetics for systems containing several interacting open-shell metal ions. Coupled to that will be the more extensive and more reliable use of quantum chemical approaches for the prediction of spectroscopic properties, which is a major point of contact between electronic structure theory and experiment. In terms of model definition, the conventional QM-cluster approach will be increasingly disfavoured over a more complete treatment of the protein environment. This is not a luxury but a necessity: the active site is not a catalyst, the whole enzyme is. The protein matrix is exclusively responsible for critical elements of enzyme function such as electron transfer, regulation of substrate delivery, proton access/egress, product release, etc., therefore our understanding of enzyme function will keep expanding to encompass the functional role of the protein beyond the immediate vicinity of the active sites. A multitude of different methods are emerging to achieve this type of treatment, many of which will in addition be able to offer access to a dynamical view of the system. Computational simulations will increasingly influence our understanding of kinetics related both to the transport of substrates to active sites that are buried within the protein and only accessible via specific channels, and to the release of products. With the broader goal in mind of overcoming the efficiency gap between the biological systems and biomimetic/bio-inspired compounds, the most successful strategy remains to combine insights from both systems to uncover differences as well as common principles that can be put to use in the design of water oxidation and hydrogen evolution catalysts. Computational methods have made tremendous advances to reach the level of utility they have today in this effort, and their contribution in the future is certain to increase.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support of this work by the French National Research Agency and the Deutsche Forschungsgemeinschaft (CODEC, ANR-19-CE05_0030_01; NiFemim, ANR-DFG-2016-NLE), from the France–Germany Hubert Curien Program – German Academic Exchange Service (DAAD) (Procope 2019-2020 project 42525PB/DAAD project 57445526), and from the Max Planck Society.References
- A. Borgschulte, Front. Energy Res., 2016, 4, 11 CrossRef.
- J. Barber, Chem. Soc. Rev., 2009, 38, 185–196 RSC.
- T. R. Cook, D. K. Dogutan, S. Y. Reece, Y. Surendranath, T. S. Teets and D. G. Nocera, Chem. Rev., 2010, 110, 6474–6502 CrossRef CAS PubMed.
- W. Lubitz and W. Tumas, Chem. Rev., 2007, 107, 3900–3903 CrossRef CAS PubMed.
- N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Interface Focus, 2015, 5, 20150009 CrossRef PubMed.
- J. Barber and P. D. Tran, J. R. Soc., Interface, 2013, 10, 20120984 CrossRef PubMed.
- W. Lubitz, E. J. Reijerse and J. Messinger, Energy Environ. Sci., 2008, 1, 15–31 RSC.
- J. Messinger, W. Lubitz and J.-R. Shen, Phys. Chem. Chem. Phys., 2014, 16, 11810–11811 RSC.
- D. Kim, K. K. Sakimoto, D. Hong and P. Yang, Angew. Chem., Int. Ed., 2015, 54, 3259–3266 CrossRef CAS PubMed.
- M. E. El-Khouly, E. El-Mohsnawy and S. Fukuzumi, J. Photochem. Photobiol., C, 2017, 31, 36–83 CrossRef CAS.
- B. Zhang and L. Sun, Chem. Soc. Rev., 2019, 48, 2216–2264 RSC.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890–1898 CrossRef CAS PubMed.
- D. G. Nocera, Acc. Chem. Res., 2012, 45, 767–776 CrossRef CAS PubMed.
- Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511–518 CrossRef CAS.
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley, Chichester, 2nd edn, 2014 Search PubMed.
- V. Krewald, M. Retegan and D. A. Pantazis, Top. Curr. Chem., 2016, 371, 23–48 CrossRef CAS PubMed.
- D. A. Pantazis, ACS Catal., 2018, 8, 9477–9507 CrossRef CAS.
- S. Paul, F. Neese and D. A. Pantazis, Green Chem., 2017, 19, 2309–2325 RSC.
- C. Zhang, C. Chen, H. Dong, J.-R. Shen, H. Dau and J. Zhao, Science, 2015, 348, 690–693 CrossRef CAS PubMed.
- C. Chen, Y. Li, G. Zhao, R. Yao and C. Zhang, ChemSusChem, 2017, 10, 4403–4408 CrossRef CAS PubMed.
- Y. Li, R. Yao, Y. Chen, B. Xu, C. Chen and C. Zhang, Catalysts, 2020, 10, 185 CrossRef CAS.
- J. S. Kanady, E. Y. Tsui, M. W. Day and T. Agapie, Science, 2011, 333, 733–736 CrossRef CAS PubMed.
- Z. Han, K. T. Horak, H. B. Lee and T. Agapie, J. Am. Chem. Soc., 2017, 139, 9108–9111 CrossRef CAS PubMed.
- H. B. Lee, A. A. Shiau, P. H. Oyala, D. A. Marchiori, S. Gul, R. Chatterjee, J. Yano, R. D. Britt and T. Agapie, J. Am. Chem. Soc., 2018, 140, 17175–17187 CrossRef CAS PubMed.
- H. B. Lee, D. A. Marchiori, R. Chatterjee, P. H. Oyala, J. Yano, R. D. Britt and T. Agapie, J. Am. Chem. Soc., 2020, 142, 3753–3761 CrossRef CAS PubMed.
- P. Kurz, Top. Curr. Chem., 2016, 371, 49–72 CrossRef CAS PubMed.
- M. M. Najafpour, G. Renger, M. Hołyńska, A. N. Moghaddam, E.-M. Aro, R. Carpentier, H. Nishihara, J. J. Eaton-Rye, J.-R. Shen and S. I. Allakhverdiev, Chem. Rev., 2016, 116, 2886–2936 CrossRef CAS PubMed.
- J. D. Blakemore, R. H. Crabtree and G. W. Brudvig, Chem. Rev., 2015, 115, 12974–13005 CrossRef CAS PubMed.
- W. Lubitz, H. Ogata, O. Rudiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148 CrossRef CAS PubMed.
- M. Y. Darensbourg and W. Weigand, Eur. J. Inorg. Chem., 2011, 917–918 CrossRef.
- R. K. Thauer, Eur. J. Inorg. Chem., 2011, 919–921 CrossRef CAS.
- P. Vashi, Eur. J. Inorg. Chem., 2011, 915–916 CrossRef.
- D. Schilter, J. M. Camara, M. T. Huynh, S. Hammes-Schiffer and T. B. Rauchfuss, Chem. Rev., 2016, 116, 8693–8749 CrossRef CAS PubMed.
- T. R. Simmons, G. Berggren, M. Bacchi, M. Fontecave and V. Artero, Coord. Chem. Rev., 2014, 270-271, 127–150 CrossRef CAS.
- T. B. Rauchfuss, Acc. Chem. Res., 2015, 48, 2107–2116 CrossRef CAS PubMed.
- M. Y. Darensbourg, E. J. Lyon and J. J. Smee, Coord. Chem. Rev., 2000, 206-207, 533–561 CrossRef CAS.
- M. E. Carroll, B. E. Barton, T. B. Rauchfuss and P. J. Carroll, J. Am. Chem. Soc., 2012, 134, 18843–18852 CrossRef CAS PubMed.
- Z. Li, Y. Ohki and K. Tatsumi, J. Am. Chem. Soc., 2005, 127, 8950–8951 CrossRef CAS PubMed.
- S. Canaguier, M. Field, Y. Oudart, J. Pécaut, M. Fontecave and V. Artero, Chem. Commun., 2010, 46, 5876–5878 RSC.
- D. Brazzolotto, M. Gennari, N. Queyriaux, T. R. Simmons, J. Pécaut, S. Demeshko, F. Meyer, M. Orio, V. Artero and C. Duboc, Nat. Chem., 2016, 8, 1054–1060 CrossRef CAS PubMed.
- Y. Ohki, K. Yasumura, M. Ando, S. Shimokata and K. Tatsumi, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 3994–3997 CrossRef CAS PubMed.
- O. T. Holton and J. W. Stevenson, Platinum Met. Rev., 2013, 57, 259–271 CrossRef.
- J. R. McKone, S. C. Marinescu, B. S. Brunschwig, J. R. Winkler and H. B. Gray, Chem. Sci., 2014, 5, 865–878 RSC.
- M. L. Helm, M. P. Stewart, R. M. Bullock, M. R. DuBois and D. L. DuBois, Science, 2011, 333, 863–866 CrossRef CAS PubMed.
- M. Razavet, V. Artero and M. Fontecave, Inorg. Chem., 2005, 44, 4786–4795 CrossRef CAS PubMed.
- V. Artero and J.-M. Saveant, Energy Environ. Sci., 2014, 7, 3808–3814 RSC.
- S. Cherdo, S. E. Ghachtouli, M. Sircoglou, F. Brisset, M. Orio and A. Aukauloo, Chem. Commun., 2014, 50, 13514–13516 RSC.
- M. Beyler, S. Ezzaher, M. Karnahl, M.-P. Santoni, R. Lomoth and S. Ott, Chem. Commun., 2011, 47, 11662–11664 RSC.
- J. L. Dempsey, B. S. Brunschwig, J. R. Winkler and H. B. Gray, Acc. Chem. Res., 2009, 42, 1995–2004 CrossRef CAS PubMed.
- N. Kaeffer, M. Chavarot-Kerlidou and V. Artero, Acc. Chem. Res., 2015, 48, 1286–1295 CrossRef CAS PubMed.
- X. Hu, B. S. Brunschwig and J. C. Peters, J. Am. Chem. Soc., 2007, 129, 8988–8998 CrossRef CAS PubMed.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- M. R. A. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Chem. Rev., 2014, 114, 3601–3658 CrossRef CAS PubMed.
- F. Himo, J. Am. Chem. Soc., 2017, 139, 6780–6786 CrossRef CAS PubMed.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, Chem. Soc. Rev., 2012, 41, 3025–3038 RSC.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- K. Weber, T. Krämer, H. S. Shafaat, T. Weyhermüller, E. Bill, M. van Gastel, F. Neese and W. Lubitz, J. Am. Chem. Soc., 2012, 134, 20745–20755 CrossRef CAS PubMed.
- S. Ding, P. Ghosh, A. M. Lunsford, N. Wang, N. Bhuvanesh, M. B. Hall and M. Y. Darensbourg, J. Am. Chem. Soc., 2016, 138, 12920–12927 CrossRef CAS PubMed.
- L. Wang, M. Gennari, A. Barrozo, J. Fize, C. Philouze, S. Demeshko, F. Meyer, M. Orio, V. Artero and C. Duboc, ACS Catal., 2019, 10, 177–186 CrossRef.
- T. Straistari, J. Fize, S. Shova, M. Réglier, V. Artero and M. Orio, ChemCatChem, 2017, 9, 2262–2268 CrossRef CAS.
- T. Straistari, R. Hardré, J. Fize, S. Shova, M. Giorgi, M. Réglier, V. Artero and M. Orio, Chem. – Eur. J., 2018, 24, 8779–8786 CrossRef CAS PubMed.
- C. Greco, G. Zampella, L. Bertini, M. Bruschi, P. Fantucci and L. De Gioia, Inorg. Chem., 2007, 46, 108–116 CrossRef CAS PubMed.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2020, 142, 18174–18190 CrossRef CAS PubMed.
- T. Cardona, A. Sedoud, N. Cox and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 26–43 CrossRef CAS PubMed.
- A. W. Rutherford, A. Osyczka and F. Rappaport, FEBS Lett., 2012, 586, 603–616 CrossRef CAS PubMed.
- R. Croce and H. van Amerongen, Nat. Chem. Biol., 2014, 10, 492–501 CrossRef CAS PubMed.
- A. Klauss, M. Haumann and H. Dau, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16035–16040 CrossRef CAS PubMed.
- V. K. Yachandra, K. Sauer and M. P. Klein, Chem. Rev., 1996, 96, 2927–2950 CrossRef CAS PubMed.
- A. Zouni, H. T. Witt, J. Kern, P. Fromme, N. Krauss, W. Saenger and P. Orth, Nature, 2001, 409, 739–743 CrossRef CAS PubMed.
- K. N. Ferreira, T. M. Iverson, K. Maghlaoui, J. Barber and S. Iwata, Science, 2004, 303, 1831–1838 CrossRef CAS PubMed.
- B. Loll, J. Kern, W. Saenger, A. Zouni and J. Biesiadka, Nature, 2005, 438, 1040–1044 CrossRef CAS.
- M. Lundberg and P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2004, 6, 4772–4780 RSC.
- E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, J. Chem. Theory Comput., 2006, 2, 1119–1134 CrossRef CAS PubMed.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS PubMed.
- M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2015, 517, 99–103 CrossRef CAS PubMed.
- I. D. Young, M. Ibrahim, R. Chatterjee, S. Gul, F. D. Fuller, S. Koroidov, A. S. Brewster, R. Tran, R. Alonso-Mori, T. Kroll, T. Michels-Clark, H. Laksmono, R. G. Sierra, C. A. Stan, R. Hussein, M. Zhang, L. Douthit, M. Kubin, C. de Lichtenberg, L. Vo Pham, H. Nilsson, M. H. Cheah, D. Shevela, C. Saracini, M. A. Bean, I. Seuffert, D. Sokaras, T.-C. Weng, E. Pastor, C. Weninger, T. Fransson, L. Lassalle, P. Bräuer, P. Aller, P. T. Docker, B. Andi, A. M. Orville, J. M. Glownia, S. Nelson, M. Sikorski, D. Zhu, M. S. Hunter, T. J. Lane, A. Aquila, J. E. Koglin, J. Robinson, M. Liang, S. Boutet, A. Y. Lyubimov, M. Uervirojnangkoorn, N. W. Moriarty, D. Liebschner, P. V. Afonine, D. G. Waterman, G. Evans, P. Wernet, H. Dobbek, W. I. Weis, A. T. Brunger, P. H. Zwart, P. D. Adams, A. Zouni, J. Messinger, U. Bergmann, N. K. Sauter, J. Kern, V. K. Yachandra and J. Yano, Nature, 2016, 540, 453–457 CrossRef CAS PubMed.
- M. Suga, F. Akita, M. Sugahara, M. Kubo, Y. Nakajima, T. Nakane, K. Yamashita, Y. Umena, M. Nakabayashi, T. Yamane, T. Nakano, M. Suzuki, T. Masuda, S. Inoue, T. Kimura, T. Nomura, S. Yonekura, L.-J. Yu, T. Sakamoto, T. Motomura, J.-H. Chen, Y. Kato, T. Noguchi, K. Tono, Y. Joti, T. Kameshima, T. Hatsui, E. Nango, R. Tanaka, H. Naitow, Y. Matsuura, A. Yamashita, M. Yamamoto, O. Nureki, M. Yabashi, T. Ishikawa, S. Iwata and J.-R. Shen, Nature, 2017, 543, 131–135 CrossRef CAS PubMed.
- A. Tanaka, Y. Fukushima and N. Kamiya, J. Am. Chem. Soc., 2017, 139, 1718–1721 CrossRef CAS PubMed.
- J. Kern, R. Chatterjee, I. D. Young, F. D. Fuller, L. Lassalle, M. Ibrahim, S. Gul, T. Fransson, A. S. Brewster, R. Alonso-Mori, R. Hussein, M. Zhang, L. Douthit, C. de Lichtenberg, M. H. Cheah, D. Shevela, J. Wersig, I. Seuffert, D. Sokaras, E. Pastor, C. Weninger, T. Kroll, R. G. Sierra, P. Aller, A. Butryn, A. M. Orville, M. Liang, A. Batyuk, J. E. Koglin, S. Carbajo, S. Boutet, N. W. Moriarty, J. M. Holton, H. Dobbek, P. D. Adams, U. Bergmann, N. K. Sauter, A. Zouni, J. Messinger, J. Yano and V. K. Yachandra, Nature, 2018, 563, 421–425 CrossRef CAS PubMed.
- M. Suga, F. Akita, K. Yamashita, Y. Nakajima, G. Ueno, H. Li, T. Yamane, K. Hirata, Y. Umena, S. Yonekura, L.-J. Yu, H. Murakami, T. Nomura, T. Kimura, M. Kubo, S. Baba, T. Kumasaka, K. Tono, M. Yabashi, H. Isobe, K. Yamaguchi, M. Yamamoto, H. Ago and J.-R. Shen, Science, 2019, 366, 334 CrossRef CAS PubMed.
- A. Grundmeier and H. Dau, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 88–105 CrossRef CAS PubMed.
- J. Yano, J. Kern, K.-D. Irrgang, M. J. Latimer, U. Bergmann, P. Glatzel, Y. Pushkar, J. Biesiadka, B. Loll, K. Sauer, J. Messinger, A. Zouni and V. K. Yachandra, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12047–12052 CrossRef CAS PubMed.
- M. Grabolle, M. Haumann, C. Müller, P. Liebisch and H. Dau, J. Biol. Chem., 2006, 281, 4580–4588 CrossRef CAS PubMed.
- A. Galstyan, A. Robertazzi and E. W. Knapp, J. Am. Chem. Soc., 2012, 134, 7442–7449 CrossRef CAS PubMed.
- P. Chernev, I. Zaharieva, E. Rossini, A. Galstyan, H. Dau and E.-W. Knapp, J. Phys. Chem. B, 2016, 120, 10899–10922 CrossRef CAS PubMed.
- A. Haddy, Photosynth. Res., 2007, 92, 357–368 CrossRef CAS PubMed.
- A. Haddy, K. V. Lakshmi, G. W. Brudvig and H. A. Frank, Biophys. J., 2004, 87, 2885–2896 CrossRef CAS PubMed.
- G. C. Dismukes and Y. Siderer, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 274–278 CrossRef CAS PubMed.
- J. C. de Paula, W. F. Beck, A.-F. Miller, R. B. Wilson and G. W. Brudvig, J. Chem. Soc., Faraday Trans., 1987, 3635–3651 RSC.
- A. Boussac, S. Un, O. Horner and A. W. Rutherford, Biochemistry, 1998, 37, 4001–4007 CrossRef CAS PubMed.
- A. Boussac and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 2000, 1457, 145–156 CrossRef CAS.
- D. A. Pantazis, W. Ames, N. Cox, W. Lubitz and F. Neese, Angew. Chem., Int. Ed., 2012, 51, 9935–9940 CrossRef CAS PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- K. Yamaguchi, Chem. Phys. Lett., 1975, 33, 330–335 CrossRef CAS.
- K. Yamaguchi, T. Tsunekawa, Y. Toyoda and T. Fueno, Chem. Phys. Lett., 1988, 143, 371–376 CrossRef CAS.
- M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Chem. Phys. Lett., 2006, 432, 343–347 CrossRef CAS.
- D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, E. Bill, W. Lubitz, J. Messinger and F. Neese, Chem. – Eur. J., 2009, 15, 5108–5123 CrossRef CAS PubMed.
- D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, W. Lubitz, J. Messinger and F. Neese, Phys. Chem. Chem. Phys., 2009, 11, 6788–6798 RSC.
- W. Ames, D. A. Pantazis, V. Krewald, N. Cox, J. Messinger, W. Lubitz and F. Neese, J. Am. Chem. Soc., 2011, 133, 19743–19757 CrossRef CAS PubMed.
- C. Baffert, M. Orio, D. A. Pantazis, C. Duboc, A. G. Blackman, G. Blondin, F. Neese, A. Deronzier and M.-N. Collomb, Inorg. Chem., 2009, 48, 10281–10288 CrossRef CAS PubMed.
- V. Krewald, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2013, 135, 5726–5739 CrossRef CAS PubMed.
- S. Mukherjee, J. A. Stull, J. Yano, T. C. Stamatatos, K. Pringouri, T. A. Stich, K. A. Abboud, R. D. Britt, V. K. Yachandra and G. Christou, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2257–2262 CrossRef CAS PubMed.
- V. Krewald, M. Retegan, N. Cox, J. Messinger, W. Lubitz, S. DeBeer, F. Neese and D. A. Pantazis, Chem. Sci., 2015, 6, 1676–1695 RSC.
- T. A. Corry and P. J. O’Malley, J. Phys. Chem. Lett., 2019, 10, 5226–5230 CrossRef CAS PubMed.
- N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808 CrossRef CAS PubMed.
- A. Boussac, A. W. Rutherford and M. Sugiura, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 576–586 CrossRef CAS PubMed.
- G. Zahariou, N. Ioannidis, Y. Sanakis and D. A. Pantazis, Angew. Chem., Int. Ed., 2021, 60, 3156–3162 CrossRef CAS PubMed.
- M. Retegan, V. Krewald, F. Mamedov, F. Neese, W. Lubitz, N. Cox and D. A. Pantazis, Chem. Sci., 2016, 7, 72–84 RSC.
- D. A. Pantazis, V. Krewald, M. Orio and F. Neese, Dalton Trans., 2010, 39, 4959–4967 RSC.
- V. Krewald, B. Lassalle-Kaiser, T. T. Boron, C. J. Pollock, J. Kern, M. A. Beckwith, V. K. Yachandra, V. L. Pecoraro, J. Yano, F. Neese and S. DeBeer, Inorg. Chem., 2013, 52, 12904–12914 CrossRef CAS PubMed.
- C. J. Stein, D. A. Pantazis and V. Krewald, J. Phys. Chem. Lett., 2019, 10, 6762–6770 CrossRef CAS PubMed.
- T. Lohmiller, V. Krewald, A. Sedoud, A. W. Rutherford, F. Neese, W. Lubitz, D. A. Pantazis and N. Cox, J. Am. Chem. Soc., 2017, 139, 14412–14424 CrossRef CAS PubMed.
- M. Pérez Navarro, W. M. Ames, H. Nilsson, T. Lohmiller, D. A. Pantazis, L. Rapatskiy, M. M. Nowaczyk, F. Neese, A. Boussac, J. Messinger, W. Lubitz and N. Cox, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15561–15566 CrossRef PubMed.
- T. Lohmiller, V. Krewald, M. Pérez Navarro, M. Retegan, L. Rapatskiy, M. M. Nowaczyk, A. Boussac, F. Neese, W. Lubitz, D. A. Pantazis and N. Cox, Phys. Chem. Chem. Phys., 2014, 16, 11877–11892 RSC.
- M. Retegan and D. A. Pantazis, Chem. Sci., 2016, 7, 6463–6476 RSC.
- M. Retegan and D. A. Pantazis, J. Am. Chem. Soc., 2017, 139, 14340–14343 CrossRef CAS PubMed.
- V. Krewald, F. Neese and D. A. Pantazis, Isr. J. Chem., 2015, 55, 1219–1232 CrossRef CAS.
- V. Krewald, M. Retegan, F. Neese, W. Lubitz, D. A. Pantazis and N. Cox, Inorg. Chem., 2016, 55, 488–501 CrossRef CAS PubMed.
- M. Roemelt and D. A. Pantazis, Adv. Theor. Simul., 2019, 1800201, DOI:10.1002/adts.201800201.
- V. Krewald and D. A. Pantazis, in Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints, ed. E. Broclawik, T. Borowski and M. Radoń, Springer International Publishing, Cham, 2019, pp. 91–120 DOI:10.1007/978-3-030-11714-6_4.
- M. Roemelt, V. Krewald and D. A. Pantazis, J. Chem. Theory Comput., 2018, 14, 166–179 CrossRef CAS PubMed.
- D. A. Pantazis, J. Chem. Theory Comput., 2019, 15, 938–948 CrossRef CAS PubMed.
- T. V. Harris, Y. Kurashige, T. Yanai and K. Morokuma, J. Chem. Phys., 2014, 140, 054303 CrossRef PubMed.
- S. Sharma, K. Sivalingam, F. Neese and G. K.-L. Chan, Nat. Chem., 2014, 6, 927–933 CrossRef CAS PubMed.
- M. Spivak, C. Angeli, C. J. Calzado and C. de Graaf, J. Comput. Chem., 2014, 35, 1665–1671 CrossRef CAS PubMed.
- Y. Kurashige, G. K.-L. Chan and T. Yanai, Nat. Chem., 2013, 5, 660–666 CrossRef CAS PubMed.
- S. Paul, N. Cox and D. A. Pantazis, Inorg. Chem., 2017, 56, 3875–3888 CrossRef CAS PubMed.
- M. Munzarová and M. Kaupp, J. Phys. Chem. A, 1999, 103, 9966–9983 CrossRef.
- M. L. Munzarová, P. Kubáček and M. Kaupp, J. Am. Chem. Soc., 2000, 122, 11900–11913 CrossRef.
- S. Schinzel, J. Schraut, A. V. Arbuznikov, P. E. M. Siegbahn and M. Kaupp, Chem. – Eur. J., 2010, 16, 10424–10438 CrossRef CAS PubMed.
- J. Schraut, A. V. Arbuznikov, S. Schinzel and M. Kaupp, ChemPhysChem, 2011, 12, 3170–3179 CrossRef CAS PubMed.
- M. Orio, D. A. Pantazis, T. Petrenko and F. Neese, Inorg. Chem., 2009, 48, 7251–7260 CrossRef CAS PubMed.
- C. J. Schattenberg, T. M. Maier and M. Kaupp, J. Chem. Theory Comput., 2018, 14, 5653–5672 CrossRef CAS PubMed.
- A. Wodyński and M. Kaupp, J. Chem. Theory Comput., 2020, 16, 314–325 CrossRef.
- M. Saitow and F. Neese, J. Chem. Phys., 2018, 149, 034104 CrossRef PubMed.
- R. J. Gómez-Piñeiro, D. A. Pantazis and M. Orio, ChemPhysChem, 2020, 21, 2667–2679 CrossRef PubMed.
- G. Blondin, R. Davydov, C. Philouze, M.-F. Charlot, S. Styring, B. Åkermark, J.-J. Girerd and A. Boussac, J. Chem. Soc., Dalton Trans., 1997, 4069–4074, 10.1039/A703381H.
- J. Yano, J. Kern, K. Sauer, M. J. Latimer, Y. Pushkar, J. Biesiadka, B. Loll, W. Saenger, J. Messinger, A. Zouni and V. K. Yachandra, Science, 2006, 314, 821–825 CrossRef CAS PubMed.
- E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, Coord. Chem. Rev., 2008, 252, 395–415 CrossRef CAS.
- P. E. M. Siegbahn, Inorg. Chem., 2008, 47, 1779–1786 CrossRef CAS PubMed.
- E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, J. Am. Chem. Soc., 2008, 130, 6728–6730 CrossRef CAS PubMed.
- P. E. M. Siegbahn, Acc. Chem. Res., 2009, 42, 1871–1880 CrossRef CAS PubMed.
- J. M. Peloquin, K. A. Campbell and R. D. Britt, J. Am. Chem. Soc., 1998, 120, 6840–6841 CrossRef CAS.
- J. M. Peloquin, K. A. Campbell, D. W. Randall, M. A. Evanchik, V. L. Pecoraro, W. H. Armstrong and R. D. Britt, J. Am. Chem. Soc., 2000, 122, 10926–10942 CrossRef CAS.
- R. D. Britt, K. A. Campbell, J. M. Peloquin, M. L. Gilchrist, C. P. Aznar, M. M. Dicus, J. Robblee and J. Messinger, Biochim. Biophys. Acta, 2004, 1655, 158–171 CrossRef CAS PubMed.
- L. V. Kulik, B. Epel, W. Lubitz and J. Messinger, J. Am. Chem. Soc., 2005, 127, 2392–2393 CrossRef CAS PubMed.
- L. V. Kulik, B. Epel, W. Lubitz and J. Messinger, J. Am. Chem. Soc., 2007, 129, 13421–13435 CrossRef CAS PubMed.
- N. Cox, L. Rapatskiy, J.-H. Su, D. A. Pantazis, M. Sugiura, L. Kulik, P. Dorlet, A. W. Rutherford, F. Neese, A. Boussac, W. Lubitz and J. Messinger, J. Am. Chem. Soc., 2011, 133, 3635–3648 CrossRef CAS PubMed.
- N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Acc. Chem. Res., 2013, 46, 1588–1596 CrossRef CAS PubMed.
- C. Mehlich and C. van Wüllen, J. Phys. Chem. C, 2018, 123, 7717–7730 CrossRef.
- C. Mehlich and C. van Wüllen, Phys. Chem. Chem. Phys., 2019, 21, 22902–22909 RSC.
- N. J. Beal, T. A. Corry and P. J. O’Malley, J. Phys. Chem. B, 2017, 121, 11273–11283 CrossRef CAS PubMed.
- N. J. Beal, T. A. Corry and P. J. O’Malley, J. Phys. Chem. B, 2018, 122, 1394–1407 CrossRef CAS PubMed.
- J. Messinger, J. H. Robblee, U. Bergmann, C. Fernandez, P. Glatzel, H. Visser, R. M. Cinco, K. L. McFarlane, E. Bellacchio, S. A. Pizarro, S. P. Cramer, K. Sauer, M. P. Klein and V. K. Yachandra, J. Am. Chem. Soc., 2001, 123, 7804–7820 CrossRef CAS PubMed.
- H. Dau, P. Liebisch and M. Haumann, Phys. Scr., 2005, 2005, 844 CrossRef.
- H. Dau and M. Haumann, Biochim. Biophys. Acta, Bioenerg., 2007, 1767, 472–483 CrossRef CAS PubMed.
- A. Boussac, Biochim. Biophys. Acta, Bioenerg., 2019, 1860, 508–518 CrossRef CAS PubMed.
- D. A. Marchiori, R. J. Debus and R. D. Britt, Biochemistry, 2020, 59, 4864–4872 CrossRef CAS PubMed.
- M. Chrysina, E. Heyno, Y. Kutin, M. Reus, H. Nilsson, M. M. Nowaczyk, S. DeBeer, F. Neese, J. Messinger, W. Lubitz and N. Cox, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16841 CrossRef CAS PubMed.
- D. A. Pantazis, Inorganics, 2019, 7, 55 CrossRef CAS.
- T. A. Corry and P. J. O’Malley, J. Phys. Chem. Lett., 2018, 9, 6269–6274 CrossRef CAS PubMed.
- H. Isobe, M. Shoji, T. Suzuki, J.-R. Shen and K. Yamaguchi, J. Chem. Theory Comput., 2019, 15, 2375–2391 CrossRef CAS PubMed.
- Y. Pushkar, K. M. Davis and M. C. Palenik, J. Phys. Chem. Lett., 2018, 9, 3525–3531 CrossRef CAS PubMed.
- P. H. Oyala, T. A. Stich and R. D. Britt, Photosynth. Res., 2015, 124, 7–18 CrossRef CAS PubMed.
- L. Rapatskiy, N. Cox, A. Savitsky, W. M. Ames, J. Sander, M. M. Nowaczyk, M. Rögner, A. Boussac, F. Neese, J. Messinger and W. Lubitz, J. Am. Chem. Soc., 2012, 134, 16619–16634 CrossRef CAS.
- P. H. Oyala, T. A. Stich, J. A. Stull, F. Yu, V. L. Pecoraro and R. D. Britt, Biochemistry, 2014, 53, 7914–7928 CrossRef CAS PubMed.
- P. H. Oyala, T. A. Stich, R. J. Debus and R. D. Britt, J. Am. Chem. Soc., 2015, 137, 8829–8837 CrossRef CAS PubMed.
- D. A. Marchiori, P. H. Oyala, R. J. Debus, T. A. Stich and R. D. Britt, J. Phys. Chem. B, 2018, 122, 1588–1599 CrossRef CAS PubMed.
- J. Schraut and M. Kaupp, Chem. – Eur. J., 2014, 20, 7300–7308 CrossRef CAS PubMed.
- Y. Guo, L.-L. He, D.-X. Zhao, L.-D. Gong, C. Liu and Z.-Z. Yang, Phys. Chem. Chem. Phys., 2016, 18, 31551–31565 RSC.
- A. Boussac, Y. Deligiannakis and A. W. Rutherford, in Photosynthesis: Mechanisms and Effects, vol. II, ed. G. Garab, Kluwer Academic Publishers, Dordrecht, 1998, pp. 1233–1240 Search PubMed.
- Z. Deák, S. Peterson, P. Geijer, K. A. Åhrling and S. Styring, Biochim. Biophys. Acta, Bioenerg., 1999, 1412, 240–249 CrossRef.
- K. A. Åhrling, M. C. W. Evans, J. H. A. Nugent and R. J. Pace, Biochim. Biophys. Acta, Bioenerg., 2004, 1656, 66–77 CrossRef PubMed.
- J.-H. Su, K. G. V. Havelius, F. Mamedov, F. M. Ho and S. Styring, Biochemistry, 2006, 45, 7617–7627 CrossRef CAS.
- F. M. Ho and S. Styring, Biochim. Biophys. Acta, Bioenerg., 2008, 1777, 140–153 CrossRef CAS PubMed.
- B. Nöring, D. Shevela, G. Renger and J. Messinger, Photosynth. Res., 2008, 98, 251–260 CrossRef PubMed.
- J.-H. Su, N. Cox, W. Ames, D. A. Pantazis, L. Rapatskiy, T. Lohmiller, L. V. Kulik, P. Dorlet, A. W. Rutherford, F. Neese, A. Boussac, W. Lubitz and J. Messinger, Biochim. Biophys. Acta, Bioenerg., 2011, 1807, 829–840 CrossRef CAS PubMed.
- M. Askerka, D. J. Vinyard, G. W. Brudvig and V. S. Batista, Biochemistry, 2015, 54, 5783–5786 CrossRef CAS PubMed.
- M. Retegan, N. Cox, D. A. Pantazis and F. Neese, Inorg. Chem., 2014, 53, 11785–11793 CrossRef CAS PubMed.
- H. Mino and H. Nagashima, J. Phys. Chem. B, 2019, 124, 128–133 CrossRef PubMed.
- M. Retegan, N. Cox, W. Lubitz, F. Neese and D. A. Pantazis, Phys. Chem. Chem. Phys., 2014, 16, 11901–11910 RSC.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2019, 141, 3217–3231 CrossRef CAS PubMed.
- P. E. M. Siegbahn, J. Am. Chem. Soc., 2013, 135, 9442–9449 CrossRef CAS PubMed.
- P. E. M. Siegbahn, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1003–1019 CrossRef CAS PubMed.
- D. Bovi, D. Narzi and L. Guidoni, Angew. Chem., Int. Ed., 2013, 52, 11744–11749 CrossRef CAS PubMed.
- M. Chrysina, J. C. de Mendonça Silva, G. Zahariou, D. A. Pantazis and N. Ioannidis, J. Phys. Chem. B, 2019, 123, 3068–3078 CrossRef CAS PubMed.
- H. Sakamoto, T. Shimizu, R. Nagao and T. Noguchi, J. Am. Chem. Soc., 2017, 139, 2022–2029 CrossRef CAS PubMed.
- K. Kawashima, K. Saito and H. Ishikita, Biochemistry, 2018, 57, 4997–5004 CrossRef CAS PubMed.
- V. Krewald, F. Neese and D. A. Pantazis, Phys. Chem. Chem. Phys., 2016, 18, 10739–10750 RSC.
- E. Y. Tsui and T. Agapie, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10084–10088 CrossRef CAS PubMed.
- E. Y. Tsui, R. Tran, J. Yano and T. Agapie, Nat. Chem., 2013, 5, 293–299 CrossRef CAS PubMed.
- M. Retegan, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2013, 9, 3832–3842 CrossRef CAS PubMed.
- M. Shoji, H. Isobe, S. Yamanaka, Y. Umena, K. Kawakami, N. Kamiya, J.-R. Shen, T. Nakajima and K. Yamaguchi, Mol. Phys., 2015, 113, 359–384 CrossRef CAS.
- M. Askerka, G. W. Brudvig and V. S. Batista, Acc. Chem. Res., 2017, 50, 41–48 CrossRef CAS PubMed.
- S. Nakamura, M. Capone, D. Narzi and L. Guidoni, Phys. Chem. Chem. Phys., 2020, 22(1), 273–285 RSC.
- D. Narzi, D. Bovi and L. Guidoni, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8723–8728 CrossRef CAS PubMed.
- M. Shoji, H. Isobe, Y. Shigeta, T. Nakajima and K. Yamaguchi, Chem. Phys. Lett., 2018, 698, 138–146 CrossRef CAS.
- D. A. Pantazis, Chem. Phys. Lett., 2020, 753, 137629 CrossRef CAS.
- N. Cox, D. A. Pantazis and W. Lubitz, Annu. Rev. Biochem., 2020, 89, 795–820 CrossRef CAS PubMed.
- J.-R. Shen, Annu. Rev. Plant Biol., 2015, 66, 23–48 CrossRef CAS PubMed.
- K. Yamaguchi, M. Shoji, H. Isobe, S. Yamanaka, T. Kawakami, S. Yamada, M. Katouda and T. Nakajima, Mol. Phys., 2018, 116, 717–745 CrossRef CAS.
- G. Zahariou and N. Ioannidis, Photosynth. Res., 2016, 130, 417–426 CrossRef CAS PubMed.
- H. Nilsson, F. Rappaport, A. Boussac and J. Messinger, Nat. Commun., 2014, 5, 4305 CrossRef CAS PubMed.
- M. Haumann, P. Liebisch, C. Müller, M. Barra, M. Grabolle and H. Dau, Science, 2005, 310, 1019–1021 CrossRef CAS PubMed.
- V. Krewald, F. Neese and D. A. Pantazis, J. Inorg. Biochem., 2019, 199, 110797 CrossRef CAS PubMed.
- P. E. M. Siegbahn, Chem. – Eur. J., 2008, 14, 8290–8302 CrossRef CAS PubMed.
- X. Li and P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2015, 17, 12168–12174 RSC.
- Y. Guo, H. Li, L.-L. He, D.-X. Zhao, L.-D. Gong and Z.-Z. Yang, Phys. Chem. Chem. Phys., 2017, 19, 13909–13923 RSC.
- M. Ibrahim, T. Fransson, R. Chatterjee, M. H. Cheah, R. Hussein, L. Lassalle, K. D. Sutherlin, I. D. Young, F. D. Fuller, S. Gul, I.-S. Kim, P. S. Simon, C. de Lichtenberg, P. Chernev, I. Bogacz, C. C. Pham, A. M. Orville, N. Saichek, T. Northen, A. Batyuk, S. Carbajo, R. Alonso-Mori, K. Tono, S. Owada, A. Bhowmick, R. Bolotovsky, D. Mendez, N. W. Moriarty, J. M. Holton, H. Dobbek, A. S. Brewster, P. D. Adams, N. K. Sauter, U. Bergmann, A. Zouni, J. Messinger, J. Kern, V. K. Yachandra and J. Yano, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12624–12635 CrossRef CAS PubMed.
- H. Isobe, M. Shoji, J.-R. Shen and K. Yamaguchi, Inorg. Chem., 2016, 55, 502–511 CrossRef CAS PubMed.
- Y. Pushkar, A. K. Ravari, S. C. Jensen and M. Palenik, J. Phys. Chem. Lett., 2019, 10, 5284–5291 CrossRef CAS PubMed.
- D. Narzi, M. Capone, D. Bovi and L. Guidoni, Chem. – Eur. J., 2018, 24, 10820–10828 CrossRef CAS PubMed.
- M. Swart and M. Costas, Spin States in Biochemistry and Inorganic Chemistry, John Wiley & Sons, Chichester, 2016 Search PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2017, 146, 164105 CrossRef PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- P. Paiva, M. J. Ramos and P. A. Fernandes, J. Comput. Chem., 2020, 41, 2459–2468 CrossRef CAS PubMed.
- D. G. Liakos, Y. Guo and F. Neese, J. Phys. Chem. A, 2019, 124, 90–100 CrossRef PubMed.
- S. E. Neale, D. A. Pantazis and S. A. Macgregor, Dalton Trans., 2020, 49, 6478–6487 RSC.
- B. M. Flöser, Y. Guo, C. Riplinger, F. Tuczek and F. Neese, J. Chem. Theory Comput., 2020, 16, 2224–2235 CrossRef PubMed.
- K. A. Vincent, A. Parkin and F. A. Armstrong, Chem. Rev., 2007, 107, 4366–4413 CrossRef CAS PubMed.
- A. L. De Lacey, V. M. Fernández, M. Rousset and R. Cammack, Chem. Rev., 2007, 107, 4304–4330 CrossRef CAS PubMed.
- P. E. M. Siegbahn, J. W. Tye and M. B. Hall, Chem. Rev., 2007, 107, 4414–4435 CrossRef CAS PubMed.
- A. Volbeda, M.-H. Charon, C. Piras, E. C. Hatchikian, M. Frey and J. C. Fontecilla-Camps, Nature, 1995, 373, 580–587 CrossRef CAS PubMed.
- V. Vaissier and T. Van Voorhis, Essays Biochem., 2017, 61, 293–303 CrossRef.
- F. Wittkamp, M. Senger, S. T. Stripp and U. P. Apfel, Chem. Commun., 2018, 54, 5934–5942 RSC.
- H. Land, M. Senger, G. Berggren and S. T. Stripp, ACS Catal., 2020, 10, 7069–7086 CrossRef CAS.
- B. H. Solis and S. Hammes-Schiffer, Inorg. Chem., 2014, 53, 6427–6443 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Acc. Chem. Res., 2018, 51, 1975–1983 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Acc. Chem. Res., 2017, 50, 561–566 CrossRef CAS.
- A. Petrenko and M. Stein, Spin States in Biochemistry and Inorganic Chemistry, 2015, ch. 14, pp. 327–367 DOI:10.1002/9781118898277.
- G. Dong, Q. M. Phung, K. Pierloot and U. Ryde, Inorg. Chem., 2018, 57, 15289–15298 CrossRef CAS PubMed.
- G. Dong and U. Ryde, J. Biol. Inorg. Chem., 2016, 21, 383–394 CrossRef CAS PubMed.
- A. R. Finkelmann, M. T. Stiebritz and M. Reiher, Chem. Commun., 2013, 49, 8099–8101 RSC.
- E. D. Hedegård, J. Kongsted and U. Ryde, Angew. Chem., Int. Ed., 2015, 54, 6246–6250 CrossRef PubMed.
- C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, J. Am. Chem. Soc., 2011, 133, 18742–18749 CrossRef CAS PubMed.
- U. Ryde, C. Greco and L. De Gioia, J. Am. Chem. Soc., 2010, 132, 4512–4513 CrossRef CAS PubMed.
- B. Ginovska, S. Raugei and W. J. Shaw, Methods Enzymol., 2016, 578, 73–101 CAS.
- O. Sode and G. A. Voth, J. Chem. Phys., 2014, 141, 22D527 CrossRef PubMed.
- V. H. Teixeira, C. M. Soares and A. M. Baptista, Proteins: Struct., Funct., Bioinf., 2008, 70, 1010–1022 CrossRef CAS PubMed.
- M. McCullagh and G. A. Voth, J. Phys. Chem. B, 2013, 117, 4062–4071 CrossRef CAS PubMed.
- S. Qiu, L. M. Azofra, D. R. MacFarlane and C. Sun, Phys. Chem. Chem. Phys., 2016, 18, 15369–15374 RSC.
- C. H. Chang, J. Phys. Chem. A, 2011, 115, 8691–8704 CrossRef CAS PubMed.
- M. Z. Makoś, M. Freindorf, D. Sethio and E. Kraka, Theor. Chem. Acc., 2019, 138, 76 Search PubMed.
- P. Jayapal, D. Robinson, M. Sundararajan, I. H. Hillier and J. J. W. McDouall, Phys. Chem. Chem. Phys., 2008, 10, 1734–1738 RSC.
- M. G. Delcey, K. Pierloot, Q. M. Phung, S. Vancoillie, R. Lindh and U. Ryde, Phys. Chem. Chem. Phys., 2014, 16, 7927–7938 RSC.
- G. Dong, Q. M. Phung, S. D. Hallaert, K. Pierloot and U. Ryde, Phys. Chem. Chem. Phys., 2017, 19, 10590–10601 RSC.
- G. Dong, U. Ryde, H. J. Aa Jensen and E. D. Hedegard, Phys. Chem. Chem. Phys., 2018, 20, 794–801 RSC.
- C. Greco, P. Fantucci, U. Ryde and L. D. Gioia, Int. J. Quantum Chem., 2011, 111, 3949–3960 CAS.
- C. Greco, A. Silakov, M. Bruschi, U. Ryde, L. De Gioia and W. Lubitz, Eur. J. Inorg. Chem., 2011, 1043–1049 CrossRef CAS.
- L. Bertini, M. Bruschi, U. Cosentino, C. Greco, G. Moro, G. Zampella and L. De Gioia, in Metalloproteins: Methods and Protocols, ed. J. C. Fontecilla-Camps and Y. Nicolet, Humana Press, Totowa, NJ, 2014, pp. 207–268 DOI:10.1007/978-1-62703-794-5_14.
- J.-M. Mouesca, J. C. Fontecilla-Camps and P. Amara, Angew. Chem., Int. Ed., 2013, 52, 2002–2006 CrossRef CAS PubMed.
- M.-E. Pandelia, D. Bykov, R. Izsak, P. Infossi, M.-T. Giudici-Orticoni, E. Bill, F. Neese and W. Lubitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 483–488 CrossRef CAS PubMed.
- V. Pelmenschikov and M. Kaupp, J. Am. Chem. Soc., 2013, 135, 11809–11823 CrossRef CAS.
- L. Yu, C. Greco, M. Bruschi, U. Ryde, L. De Gioia and M. Reiher, Inorg. Chem., 2011, 50, 3888–3900 CrossRef CAS PubMed.
- D. W. Mulder, M. W. Ratzloff, M. Bruschi, C. Greco, E. Koonce, J. W. Peters and P. W. King, J. Am. Chem. Soc., 2014, 136, 15394–15402 CrossRef CAS PubMed.
- P. S. Corrigan, J. L. Tirsch and A. Silakov, J. Am. Chem. Soc., 2020, 142, 12409–12419 CrossRef CAS PubMed.
- S. Mebs, M. Senger, J. Duan, F. Wittkamp, U.-P. Apfel, T. Happe, M. Winkler, S. T. Stripp and M. Haumann, J. Am. Chem. Soc., 2017, 139, 12157–12160 CrossRef CAS PubMed.
- C. C. Pham, D. W. Mulder, V. Pelmenschikov, P. W. King, M. W. Ratzloff, H. Wang, N. Mishra, E. E. Alp, J. Zhao, M. Y. Hu, K. Tamasaku, Y. Yoda and S. P. Cramer, Angew. Chem., Int. Ed., 2018, 57, 10605–10609 CrossRef CAS PubMed.
- T. Krämer, M. Kampa, W. Lubitz, M. van Gastel and F. Neese, ChemBioChem, 2013, 14, 1898–1905 CrossRef PubMed.
- M. Kampa, W. Lubitz, M. van Gastel and F. Neese, J. Biol. Inorg. Chem., 2012, 17, 1269–1281 CrossRef CAS PubMed.
- J. A. Birrell, V. Pelmenschikov, N. Mishra, H. Wang, Y. Yoda, K. Tamasaku, T. B. Rauchfuss, S. P. Cramer, W. Lubitz and S. DeBeer, J. Am. Chem. Soc., 2020, 142, 222–232 CrossRef CAS PubMed.
- V. Pelmenschikov, J. A. Birrell, C. C. Pham, N. Mishra, H. Wang, C. Sommer, E. Reijerse, C. P. Richers, K. Tamasaku, Y. Yoda, T. B. Rauchfuss, W. Lubitz and S. P. Cramer, J. Am. Chem. Soc., 2017, 139, 16894–16902 CrossRef CAS PubMed.
- E. J. Reijerse, C. C. Pham, V. Pelmenschikov, R. Gilbert-Wilson, A. Adamska-Venkatesh, J. F. Siebel, L. B. Gee, Y. Yoda, K. Tamasaku, W. Lubitz, T. B. Rauchfuss and S. P. Cramer, J. Am. Chem. Soc., 2017, 139, 4306–4309 CrossRef CAS PubMed.
- S. Kamali, H. Wang, D. Mitra, H. Ogata, W. Lubitz, B. C. Manor, T. B. Rauchfuss, D. Byrne, V. Bonnefoy, F. E. Jenney Jr., M. W. W. Adams, Y. Yoda, E. Alp, J. Zhao and S. P. Cramer, Angew. Chem., Int. Ed., 2013, 52, 724–728 CrossRef CAS PubMed.
- L. Lauterbach, H. Wang, M. Horch, L. B. Gee, Y. Yoda, Y. Tanaka, I. Zebger, O. Lenz and S. P. Cramer, Chem. Sci., 2015, 6, 1055–1060 RSC.
- H. Ogata, T. Krämer, H. Wang, D. Schilter, V. Pelmenschikov, M. van Gastel, F. Neese, T. B. Rauchfuss, L. B. Gee, A. D. Scott, Y. Yoda, Y. Tanaka, W. Lubitz and S. P. Cramer, Nat. Commun., 2015, 6, 7890 CrossRef CAS.
- M. Kampa, M.-E. Pandelia, W. Lubitz, M. van Gastel and F. Neese, J. Am. Chem. Soc., 2013, 135, 3915–3925 CrossRef CAS.
- G. Berggren, A. Adamska, C. Lambertz, T. R. Simmons, J. Esselborn, M. Atta, S. Gambarelli, J. M. Mouesca, E. Reijerse, W. Lubitz, T. Happe, V. Artero and M. Fontecave, Nature, 2013, 499, 66–69 CrossRef CAS PubMed.
- E. J. Reijerse, V. Pelmenschikov, J. A. Birrell, C. P. Richers, M. Kaupp, T. B. Rauchfuss, S. P. Cramer and W. Lubitz, J. Phys. Chem. Lett., 2019, 10, 6794–6799 CrossRef CAS PubMed.
- E. Reijerse, J. A. Birrell and W. Lubitz, J. Phys. Chem. Lett., 2020, 11, 4597–4602 CrossRef CAS PubMed.
- S. G. Tabrizi, V. Pelmenschikov, L. Noodleman and M. Kaupp, J. Chem. Theory Comput., 2016, 12, 174–187 CrossRef CAS PubMed.
- E. D. Hedegård, S. Knecht, U. Ryde, J. Kongsted and T. Saue, Phys. Chem. Chem. Phys., 2014, 16, 4853–4863 RSC.
- J. Gubler, A. R. Finkelmann and M. Reiher, Inorg. Chem., 2013, 52, 14205–14215 CrossRef CAS.
- S. Ogo, T. Kishima, T. Yatabe, K. Miyazawa, R. Yamasaki, T. Matsumoto, T. Ando, M. Kikkawa, M. Isegawa, K.-S. Yoon and S. Hayami, Sci. Adv., 2020, 6, eaaz8181 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. D. Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. M. Khah, S. K. Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. V. Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS.
- E. Aprà, E. J. Bylaska, W. A. D. Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. V. Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning Jr., M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. M. D. Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. V. Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- H. Tang and M. B. Hall, J. Am. Chem. Soc., 2017, 139, 18065–18070 CrossRef CAS PubMed.
- D. Brazzolotto, L. Wang, H. Tang, M. Gennari, N. Queyriaux, C. Philouze, S. Demeshko, F. Meyer, M. Orio, V. Artero, M. B. Hall and C. Duboc, ACS Catal., 2018, 8, 10658–10667 CrossRef CAS.
- J. L. Barilone, H. Ogata, W. Lubitz and M. van Gastel, Phys. Chem. Chem. Phys., 2015, 17, 16204–16212 RSC.
- C. V. Popescu, S. Ding, P. Ghosh, M. B. Hall and M. Cohara, Inorg. Chem., 2019, 58, 7069–7077 CrossRef CAS PubMed.
- S. Niu, A. E. Nelson, P. De La Torre, H. Li, C. F. Works and M. B. Hall, Inorg. Chem., 2019, 58, 13737–13741 CrossRef CAS PubMed.
- A. Kochem, E. Bill, F. Neese and M. van Gastel, Chem. Commun., 2015, 51, 2099–2102 RSC.
- M. T. Huynh, W. Wang, T. B. Rauchfuss and S. Hammes-Schiffer, Inorg. Chem., 2014, 53, 10301–10311 CrossRef CAS.
- G. M. Chambers, M. T. Huynh, Y. Li, S. Hammes-Schiffer, T. B. Rauchfuss, E. Reijerse and W. Lubitz, Inorg. Chem., 2016, 55, 419–431 CrossRef CAS PubMed.
- A. Kochem, T. Weyhermüller, F. Neese and M. van Gastel, Organometallics, 2015, 34, 995–1000 CrossRef CAS.
- A. Kochem, F. Neese and M. van Gastel, J. Phys. Chem. C, 2014, 118, 2350–2360 CrossRef CAS.
- A. Barrozo and M. Orio, ChemSusChem, 2019, 12, 4905–4915 CrossRef CAS PubMed.
- B. H. Solis and S. Hammes-Schiffer, J. Am. Chem. Soc., 2011, 133, 19036–19039 CrossRef CAS PubMed.
- A. Bhattacharjee, E. S. Andreiadis, M. Chavarot-Kerlidou, M. Fontecave, M. J. Field and V. Artero, Chemistry, 2013, 19, 15166–15174 CrossRef CAS PubMed.
- B. H. Solis and S. Hammes-Schiffer, Inorg. Chem., 2011, 50, 11252–11262 CrossRef CAS PubMed.
- Y. A. Small, D. L. DuBois, E. Fujita and J. T. Muckerman, Energy Environ. Sci., 2011, 4, 3008–3020 RSC.
- S. Horvath, L. E. Fernandez, A. M. Appel and S. Hammes-Schiffer, Inorg. Chem., 2013, 52, 3643–3652 CrossRef CAS PubMed.
- M. RakowskinDuBois and D. L. DuBois, Chem. Soc. Rev., 2009, 38, 62–72 RSC.
- W. J. Shaw, M. L. Helm and D. L. DuBois, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1123–1139 CrossRef CAS PubMed.
- C. Pieri, A. Bhattacharjee, A. Barrozo, B. Faure, M. Giorgi, J. Fize, M. Réglier, M. Field, M. Orio, V. Artero and R. Hardré, Chem. Commun., 2020, 56, 11106–11109 RSC.
- J. T. Muckerman and E. Fujita, Chem. Commun., 2011, 47, 12456–12458 RSC.
- R. Jain, A. A. Mamun, R. M. Buchanan, P. M. Kozlowski and C. A. Grapperhaus, Inorg. Chem., 2018, 57, 13486–13493 CrossRef CAS PubMed.
- A. Z. Haddad, B. D. Garabato, P. M. Kozlowski, R. M. Buchanan and C. A. Grapperhaus, J. Am. Chem. Soc., 2016, 138, 7844–7847 CrossRef CAS PubMed.
- H. Tang, E. N. Brothers, C. A. Grapperhaus and M. B. Hall, ACS Catal., 2020, 10, 3778–3789 CrossRef CAS.
- B. H. Solis, A. G. Maher, D. K. Dogutan, D. G. Nocera and S. Hammes-Schiffer, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 485–492 CrossRef CAS PubMed.
- R.-Z. Liao, M. Wang, L. Sun and P. E. M. Siegbahn, Dalton Trans., 2015, 44, 9736–9739 RSC.
- K. Ye, Y.-Y. Li and R.-Z. Liao, RSC Adv., 2016, 6, 90035–90045 RSC.
- M. Papadakis, A. Barrozo, T. Straistari, N. Queyriaux, A. Putri, J. Fize, M. Giorgi, M. Réglier, J. Massin, R. Hardré and M. Orio, Dalton Trans., 2020, 49, 5064–5073 RSC.
- T. Straistari, R. Hardré, J. Massin, M. Attolini, B. Faure, M. Giorgi, M. Réglier and M. Orio, Eur. J. Inorg. Chem., 2018, 2259–2266 CrossRef CAS.
- A. Barrozo and M. Orio, RSC Adv., 2021, 11, 5232–5238 RSC.
- G. M. Chambers, J. Mitra, T. B. Rauchfuss and M. Stein, Inorg. Chem., 2014, 53, 4243–4249 CrossRef CAS PubMed.
- L. Vaccaro, V. Artero, S. Canaguier, M. Fontecave and M. J. Field, Dalton Trans., 2010, 39, 3043–3049 RSC.
- R. Das, F. Neese and M. van Gastel, Phys. Chem. Chem. Phys., 2016, 18, 24681–24692 RSC.
- S. Kaur-Ghumaan and M. Stein, Dalton Trans., 2014, 43, 9392–9405 RSC.
- M. T. Huynh, D. Schilter, S. Hammes-Schiffer and T. B. Rauchfuss, J. Am. Chem. Soc., 2014, 136, 12385–12395 CrossRef CAS PubMed.
- D. Schilter, M. J. Nilges, M. Chakrabarti, P. A. Lindahl, T. B. Rauchfuss and M. Stein, Inorg. Chem., 2012, 51, 2338–2348 CrossRef CAS PubMed.
- J. M. Keith and M. B. Hall, Inorg. Chem., 2010, 49, 6378–6380 CrossRef CAS PubMed.
- M. Panneerselvam and M. Jaccob, Inorg. Chem., 2018, 57, 8116–8127 CrossRef CAS PubMed.
- B. H. Solis, Y. Yu and S. Hammes-Schiffer, Inorg. Chem., 2013, 52, 6994–6999 CrossRef CAS PubMed.
- S. Horvath, L. E. Fernandez, A. V. Soudackov and S. Hammes-Schiffer, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15663–15668 CrossRef CAS PubMed.
- L. E. Fernandez, S. Horvath and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2013, 4, 542–546 CrossRef CAS PubMed.
- J. P. Layfield and S. Hammes-Schiffer, Chem. Rev., 2014, 114, 3466–3494 CrossRef CAS PubMed.
- D. M. A. Smith, Y. Xiong, T. P. Straatsma, K. M. Rosso and T. C. Squier, J. Chem. Theory Comput., 2012, 8, 2103–2114 CrossRef CAS PubMed.
- P.-h. Wang, R. B. Best and J. Blumberger, J. Am. Chem. Soc., 2011, 133, 3548–3556 CrossRef CAS PubMed.
- P. H. Wang, D. De Sancho, R. B. Best and J. Blumberger, in Methods Enzymology, ed. G. A. Voth, Academic Press, 2016, vol. 578, pp. 299–326 Search PubMed.
- L. Bertini, M. Bruschi, L. D. Gioia, P. Fantucci, C. Greco and G. Zampella, Top. Curr. Chem., 2007, 268, 1–46 CAS.
- S. Qiu, Q. Li, Y. Xu, S. Shen and C. Sun, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1422 CAS.
- S. Qiu, L. M. Azofra, D. R. MacFarlane and C. Sun, ACS Catal., 2016, 6, 5541–5548 CrossRef CAS.
- S. Qiu, L. M. Azofra, D. R. MacFarlane and C. Sun, Phys. Chem. Chem. Phys., 2018, 20, 6735–6743 RSC.
- P. E. M. Siegbahn and R.-Z. Liao, ACS Catal., 2020, 10, 5603–5613 CrossRef CAS.
- P. E. M. Siegbahn, RSC Adv., 2021, 11, 3495–3508 RSC.
- R. Breglia, C. Greco, P. Fantucci, L. De Gioia and M. Bruschi, Inorg. Chem., 2019, 58, 279–293 CrossRef CAS PubMed.
- S. Sicolo, M. Bruschi, L. Bertini, G. Zampella, G. Filippi, F. Arrigoni, L. De Gioia and C. Greco, Int. J. Hydrogen Energy, 2014, 39, 18565–18573 CrossRef CAS.
- M. Bruschi, C. Greco, M. Kaukonen, P. Fantucci, U. Ryde and L. De Gioia, Angew. Chem., Int. Ed., 2009, 48, 3503–3506 CrossRef CAS PubMed.
- C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, Chem. – Eur. J., 2011, 17, 1954–1965 CrossRef CAS PubMed.
- C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, ChemPhysChem, 2011, 12, 3376–3382 CrossRef CAS PubMed.
- F. Arrigoni, L. Bertini, M. Bruschi, C. Greco, L. De Gioia and G. Zampella, Chem. – Eur. J., 2019, 25, 1227–1241 CrossRef CAS PubMed.
- S. Sumner, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 4205–4214 CrossRef CAS PubMed.
- L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2011, 7, 761–777 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |



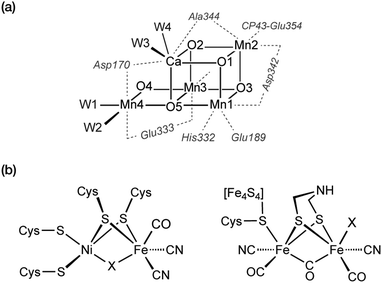
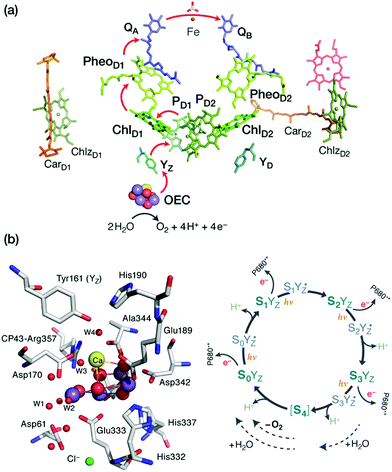
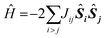
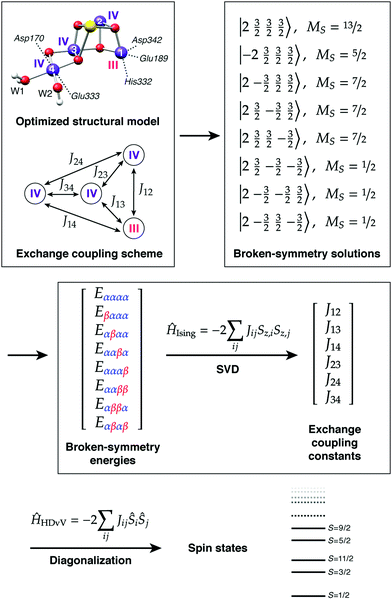
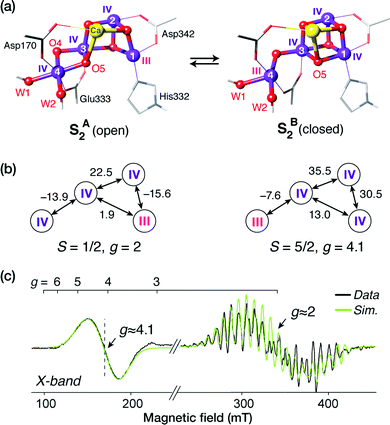
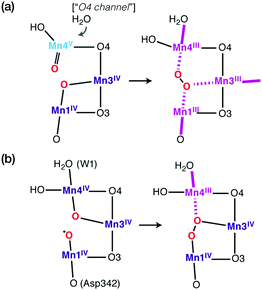
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) oxo species from a preceding water-unbound conformation of the S3 state enables even-electron intramolecular nucleophilic coupling that resets the cluster to the S0 oxidation state level. (b) Creation of a Mn(
oxo species from a preceding water-unbound conformation of the S3 state enables even-electron intramolecular nucleophilic coupling that resets the cluster to the S0 oxidation state level. (b) Creation of a Mn(