Open Access Article
Open Access ArticleCation recognition on a fullerene-based macrocycle†
Yoshifumi
Hashikawa
 and
Yasujiro
Murata
and
Yasujiro
Murata
 *
*
Institute for Chemical Research, Kyoto University, Uji, Kyoto 611-0011, Japan. E-mail: yasujiro@scl.kyoto-u.ac.jp
First published on 22nd October 2020
Abstract
Heterocyclic orifices in cage-opened fullerene derivatives are regarded as potential ligands toward metals or ions, being reminiscent of truncated fullerenes as a hypothetical class of macrocycles with spherical π-conjugation. Among a number of cage-opened examples reported thus far, the coordination ability and dynamic behavior in solution still remained unclear due to difficulties in structural determination with multiple coordination sites on the macrocycles. Herein, we present the detailed solution dynamics of a cage-opened C60 derivative bearing a diketo bis(hemiketal) moiety in the presence of alkali metal ions. The NMR spectroscopy disclosed the coordination behavior which is identified as a two-step process with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry. Upon coordination to the Li+ ion, the macrocycle largely varies its properties, i.e., increased absorption coefficients in the visible region due to weakly-allowed charge transfer transitions as well as the inner potential field from neutral to positive by the charge delocalization along with the spherical π-surface. The Li+-complexes formed in situ underwent unprecedented selective dehydroxyhydrogenation under high-pressure conditions. These findings would facilitate further studies on fullerene-based macrocycles as metal sensors, bulky ligands in organic reactions, and ion carriers in batteries and biosystems.
2 stoichiometry. Upon coordination to the Li+ ion, the macrocycle largely varies its properties, i.e., increased absorption coefficients in the visible region due to weakly-allowed charge transfer transitions as well as the inner potential field from neutral to positive by the charge delocalization along with the spherical π-surface. The Li+-complexes formed in situ underwent unprecedented selective dehydroxyhydrogenation under high-pressure conditions. These findings would facilitate further studies on fullerene-based macrocycles as metal sensors, bulky ligands in organic reactions, and ion carriers in batteries and biosystems.
Introduction
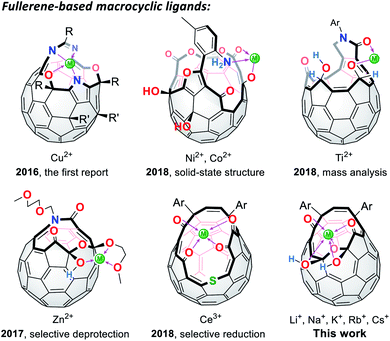
Since the successful synthesis of cyclic polyethers by Pedersen in 1967,1 a number of macrocyclic ligands have been produced in pursuit of their potential utilities in organic syntheses, metal sensors, ion carriers, and so forth.2 Among macrocycles developed thus far, fully-conjugated planar systems are of particular importance to introduce additional features. Porphyrins and phthalocyanines are representative examples in which a variety of metal ions can be incorporated at the central rings, showing characteristic aromaticity and SMM (single-molecule magnet) properties.3 As curved ligands with spherical π-conjugation, truncated heterofullerenes were proposed by Karfunkel and coworkers in 1992.4 This hypothetical class of macrocycles can be described as pseudo-fullerenes in which two carbon atoms are at least removed from the C60 cage and heteroatoms are further replaced with the carbon atoms remaining on the thus-formed orifices. Currently, synthesis of truncated heterofullerenes still remains a formidable challenge while they potentially lead to the construction of spherical metal–organic frameworks as well as an isolation of a single metal atom or ion by passing through the macrocyclic orifice.5
In lieu of truncated heterofullerenes, open-cage C60 derivatives6 can be alternatively utilized for this purpose since they in general possess Lewis basic functional groups (Fig. 1). Nevertheless, the studies on fullerene-based macrocycles are quite limited7 because of the difficulty in structural characterization with multiple coordination sites on their rims of orifices, being in stark contrast to pristine C60 and its exohedral derivatives.8,9 In 2016, the first cage-opened C60 ligand toward Cu(II) was reported by Gan and co-workers.10 In 2018, they synthesized another types of ligand systems which coordinate with Ni(II),11 Co(II),11 and Ti(II).12 Around the same time, we also reported the Zn(II)13 and Ce(III)14 coordination on fullerene-based macrocycles, which resulted in selective deprotection and reduction, respectively. With these unique macrocycles exemplified above, however, the structures in solution accompanied by the association/dissociation dynamics have not yet been elucidated so far even though this is crucially informative for surveying properties of long-sought truncated heterofullerenes as well as for chemically synthesizing endohedral metallofullerenes. In this paper, we discuss the orifice flexibility on a cage-opened C60 derivative having a diketo bis(hemiketal) moiety (Fig. 1), which enables coordination to alkali metal ions including Li+, Na+, K+, Rb+, and Cs+. By employing 7Li NMR titration, the coordination mode was examined in a solution, showing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexation with a Li+ ion. We also report the effect of the Li+-coordination on the rotational dynamics of the encapsulated H2O molecule as well as the unprecedented Li+[B(C6F5)4]−-mediated selective dehydroxyhydrogenation under high-pressure conditions.
2 complexation with a Li+ ion. We also report the effect of the Li+-coordination on the rotational dynamics of the encapsulated H2O molecule as well as the unprecedented Li+[B(C6F5)4]−-mediated selective dehydroxyhydrogenation under high-pressure conditions.
Results and discussion
A cage-opened C60 ligand
We have previously reported the synthesis of 1 (Fig. 2a) as a precursor for the quantitative encapsulation of a water molecule inside its cage under high-pressure conditions.15 This compound has several coordination sites on its orifice, which are considered to work as ligands toward metals or ions. Different from common macrocyclic ligands in which unshared electron pairs involved in coordination are projected to the inner cavity, open-cage C60 derivatives possess functional groups protruded unidirectionally, reflecting the orifice topology. In the case of diketo bis(hemiketal) 1, the electrostatically negative potential field therefore emerges on its orifice as colored with red in Fig. 2b. Since the binding in complexes with alkali metal ions is in principle predominantly electrostatic,16 we examined the alkali-metal-ion affinity for 1 by NMR and absorption spectroscopies together with mass spectrometry.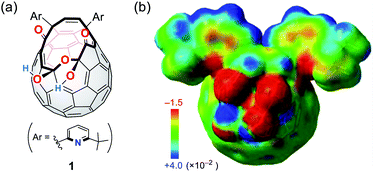 | ||
| Fig. 2 (a) Structure of a cage-opened C60 ligand 1 and (b) its electrostatic potential map around the orifice (MP2/6-31G(d,p)//M06-2X/6-31G(d,p)). | ||
Li+-coordination studied by NMR and absorption spectroscopies
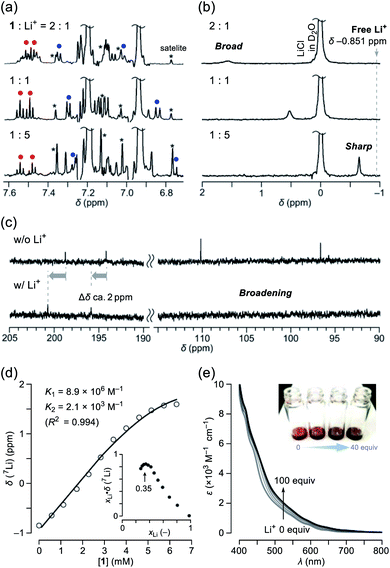
Among alkali metals, lithium has an NMR active isotope with a natural abundance of 92.58% as 7Li (I = 3/2),17 which is suitable for unveiling the solution dynamics of its complex with 1. As a Li+-source, we selected lithium tetrakis(pentafluorophenyl)borate ethyl etherate (Li+[B(C6F5)4]−·2.5Et2O) showing a high solubility in common organic solvents. The NMR titration was conducted by adding a portion of 1 to a solution containing the lithium salt in o-dichlorobenzene-d4 (ODCB-d4). Fig. 3a represents the spectral change at the aromatic region in 1H NMR. Upon increasing the ratio of Li+, the signals assignable to the pyridyl protons (shown as red and blue circles) became simple pairs of triplet and doublet ones, respectively, from a complicated signal pattern. This change was accompanied by the signal sharpening of 7Li with higher-field shift, getting closer to the free Li+ in ODCB-d4 (Fig. 3b). These phenomena are suggestive of coordination/dissociation dynamics of the Li+ ion with 1. To clarify where the Li+ ion locates, 13C NMR spectra were recorded using solutions of 1 with and without 20 equiv. of Li+ (Fig. 3c). Despite negligible change in aliphatic and aromatic regions, the lower field shifts (Δδ ca. +2 ppm) of the two carbonyl carbon signals were observed together with significant broadening of the two hemiketal carbon signals, presumably due to depleted electron densities caused by Li+-coordination and quadrupole effect of 7Li, respectively. The Job's plot based on the 7Li chemical shifts showed a maximum value at a mole fraction of 0.35, conclusively indicating the formation of a complex with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry, i.e., Li+⊂1 and Li+⊂(1)2 (Fig. 3d). Since only a slight change in 1H NMR spectra was observed at the Li+-content exceeding 1 equivalent (Fig. 3a), 1
2 stoichiometry, i.e., Li+⊂1 and Li+⊂(1)2 (Fig. 3d). Since only a slight change in 1H NMR spectra was observed at the Li+-content exceeding 1 equivalent (Fig. 3a), 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexation is considered to be less favored than 1
2 complexation is considered to be less favored than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation (K1 > K2). By employing a 1
1 complexation (K1 > K2). By employing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexation model,18 we obtained association constants of K1 = 8.9 × 106 M−1 and K2 = 2.1 × 103 M−1, appearing negative cooperativity of α = K1/4K2 = 10−3 < 1, while complexes Li+⊂1 and Li+⊂(1)2 were found to be considerably stable relative to Li+ + 1 by ΔG −9.5 and −4.6 kcal mol−1, respectively. This biding event caused significant change even in absorption spectra (Fig. 3e). Upon addition of Li+ into the ODCB solution of 1, absorption coefficients in the visible region at 400–800 nm were obviously increased, concomitantly varying the solution color from reddish brown to dark black.
2 complexation model,18 we obtained association constants of K1 = 8.9 × 106 M−1 and K2 = 2.1 × 103 M−1, appearing negative cooperativity of α = K1/4K2 = 10−3 < 1, while complexes Li+⊂1 and Li+⊂(1)2 were found to be considerably stable relative to Li+ + 1 by ΔG −9.5 and −4.6 kcal mol−1, respectively. This biding event caused significant change even in absorption spectra (Fig. 3e). Upon addition of Li+ into the ODCB solution of 1, absorption coefficients in the visible region at 400–800 nm were obviously increased, concomitantly varying the solution color from reddish brown to dark black.
Alkali-metal-ion recognition
According to Pearson's HSAB (hard and soft acids and bases) principle,19 diketo bis(hemiketal) 1 possesses hard (OH groups) and soft (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups) Lewis bases on its macrocyclic orifice. Hence, 1 is considered to have affinity toward a variety of metal ions from hard (Li+) to soft (Cs+) Lewis acids. Using a benzonitrile solution of 1 mixed with 1 equiv. of M+BPh4− (M = Li, Na, K, Rb, and Cs), mass spectra were measured by applying the ESI (electrospray ionization) method. As confirmed by the NMR studies, a molecular ion peak of Li+⊂1 was clearly observed at m/z 1127.2192 which is matched well with the calculated value (m/z 1127.2154) (Fig. 4a). Likewise, other alkali metal ions were also found to coordinate with 1. Notably, dimeric host–guest complexes M+⊂(1)2 were suggested to be formed for all alkali metal ions despite lower magnitude of the peak intensities by a tenth compared with M+⊂1 (Fig. 4b). In general, common macrocyclic ligands such as crown ethers and cryptands show the size-selectivity.20 These results, however, indicate anomalous feature for 1 to capture alkali metal ions regardless of their ionic sizes even under mass spectrometric conditions at 200 °C, likely arising from a self-tunable coordination mode with a high degree of flexibility on the orifice. Conversely, the fact that the addition of alkali metal ions resulted in facile detection with high resolution also means that it would be helpful to characterize unstable and/or large molecular cage-opened C60 derivatives as we have previously observed.21
O groups) Lewis bases on its macrocyclic orifice. Hence, 1 is considered to have affinity toward a variety of metal ions from hard (Li+) to soft (Cs+) Lewis acids. Using a benzonitrile solution of 1 mixed with 1 equiv. of M+BPh4− (M = Li, Na, K, Rb, and Cs), mass spectra were measured by applying the ESI (electrospray ionization) method. As confirmed by the NMR studies, a molecular ion peak of Li+⊂1 was clearly observed at m/z 1127.2192 which is matched well with the calculated value (m/z 1127.2154) (Fig. 4a). Likewise, other alkali metal ions were also found to coordinate with 1. Notably, dimeric host–guest complexes M+⊂(1)2 were suggested to be formed for all alkali metal ions despite lower magnitude of the peak intensities by a tenth compared with M+⊂1 (Fig. 4b). In general, common macrocyclic ligands such as crown ethers and cryptands show the size-selectivity.20 These results, however, indicate anomalous feature for 1 to capture alkali metal ions regardless of their ionic sizes even under mass spectrometric conditions at 200 °C, likely arising from a self-tunable coordination mode with a high degree of flexibility on the orifice. Conversely, the fact that the addition of alkali metal ions resulted in facile detection with high resolution also means that it would be helpful to characterize unstable and/or large molecular cage-opened C60 derivatives as we have previously observed.21
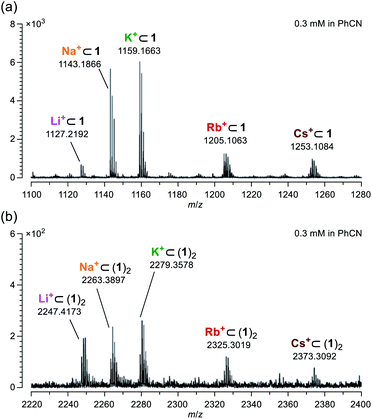 | ||
| Fig. 4 Mass spectra of (a) M+⊂1 and (b) M+⊂(1)2 measured using a benzonitrile solution on ESI method. | ||
Theoretical models of coordination
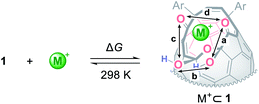
To get insights into coordination modes of Li+⊂1, theoretical calculations were performed at the M06-2X/6-31G(d,p) level of theory. Among three possible configurations, C was suggested to have the priority over A and B in terms of thermodynamic stability (Fig. 5, S8 and S15†). In the global minimum structure of C, the Li+ ion locates on the center of the diketo bis(hemiketal) moiety which forms five dative bonds with distances of 1.89–2.34 Å, seemingly being the same as those in typical Li+-complexes (1.9–2.4 Å).16 This coordination mode is in excellent accordance with the structure determined experimentally as described above. The similar configurations were suggested for M+⊂1 by the calculations at the M06-2X level of theory with the basis sets of LanL2DZ for alkali metals and 6-31G(d,p) for the rest. As listed in Table 1, all alkali metal ions would form thermodynamically stable complexes M+⊂1 in which the stabilization energies decrease with increasing atomic number whereas the distances between oxygen atoms (a–d) on 1 get longer in a concentric fashion, further supporting a great flexibility of the fullerene-based macrocyclic ligand. Considering the changes in Gibbs energies, 1 could be regarded as a hard Lewis basic ligand rather than soft one.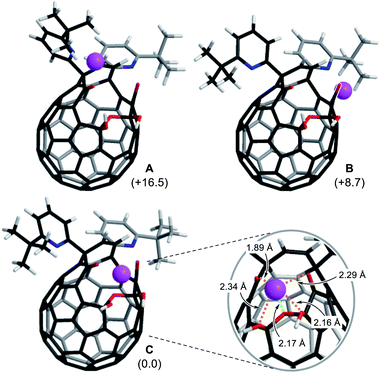 | ||
| Fig. 5 Three possible coordination modes of 1 toward Li+ (M06-2X/6-31G(d,p)). The values in parentheses represent the differences in Gibbs energies at 298 K. | ||
| M+ | ΔG (kcal mol−1) | a (Å) | b (Å) | c (Å) | d (Å) |
|---|---|---|---|---|---|
| a Calculated at the M06-2X level of theory with basis sets of LanL2DZ for alkali metal ions and 6-31G(d,p) for the rest. | |||||
| Li+ | −53.2 | 3.14 | 3.70 | 3.13 | 3.17 |
| K+ | −30.0 | 3.26 | 3.77 | 3.16 | 3.40 |
| Na+ | −17.3 | 3.34 | 3.81 | 3.18 | 3.56 |
| Rb+ | −9.2 | 3.37 | 3.83 | 3.18 | 3.65 |
| Cs+ | −4.1 | 3.36 | 3.84 | 3.17 | 3.69 |
To get more details on the observed absorption behavior of 1 in the presence of Li+, TD DFT calculations were conducted at the CAM-B3LYP/6-31G(d)//B3LYP/6-31G(d) level of theory. The Li+-coordination on 1 causes lowering of the LUMO level from −3.13 to −3.74 eV as well as a considerable drop of energy levels of the HOMO (−5.80 eV) and HOMO−1 (−5.83 eV) for 1 into those of the HOMO−3 (−6.40 eV) and HOMO−4 (−6.43 eV) for (Li+⊂1)[B(C6F5)4]− in which the HOMO and HOMO−1 are now localized on a part of the counter anion (Fig. S14†). The oscillator strengths at optical transitions over 400 nm were plotted in Fig. 6a and b. Whereas the two plots of 1 and (Li+⊂1)[B(C6F5)4]− showed close resemblance with each other, the number of weakly-allowed transitions are definitely increased (34 to 49), rationally explaining the intense solution color of 1 by the addition of Li+. Upon seeing the two of newly-appeared transitions at the longest wavelengths of λ = 531 and 519 nm (marked with a circle in Fig. 6b), these absorption bands in the visible region are attributed to intra- and intermolecular charge transfer (CT) transitions corresponding to the HOMO−2 → LUMO+3 (contribution: 27%) and HOMO−5 → LUMO+2 (15%) with a oscillator strength of f = 0.0066 (λ = 531) as well as the HOMO−3 → LUMO+3 (30%) and HOMO−2 → LUMO+3 (18%) with f = 0.0065 (λ = 519) (Fig. 6c). To verify the role of the counter anion, we also calculated the transition energies for Li+⊂1, showing the increased number of weakly-allowed transitions, relative to 1 (34 to 42), with an intramolecular CT character such as the HOMO−1 → LUMO+2 transition (27%) with f = 0.013 at λ = 555 nm (Fig. S13†). The observed intense absorption in 1 upon addition of Li+ is therefore triggered by the Li+-coordination which promotes intra- and intermolecular CT transitions with larger oscillator strengths compared with pristine 1.
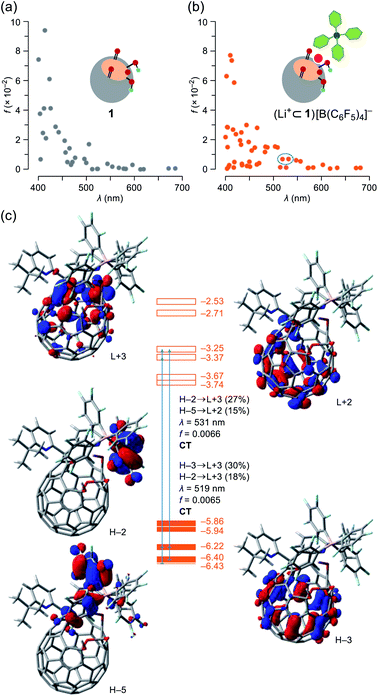 | ||
| Fig. 6 Plots of oscillator strengths for (a) 1 and (b) (Li+⊂1)[B(C6F5)4]– with (c) pictorial representation of the HOMOs and LUMOs, abbreviated as H and L, respectively. The transition energies were calibrated with a factor of 0.7222 (TD-CAM-B3LYP/6-31G(d)//B3LYP/6-31G(d)). | ||
Effect of Li+-coordination on rotational dynamics of entrapped H2O molecules
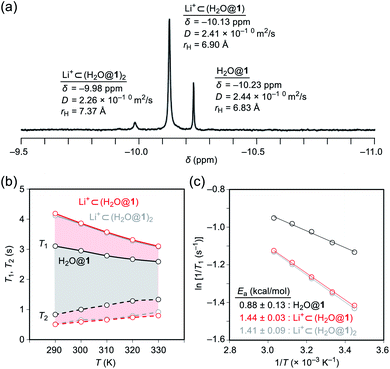
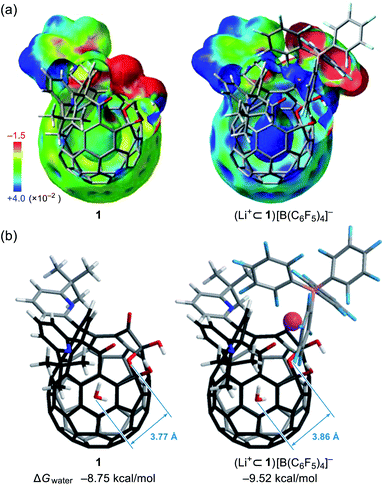
To probe the physical picture inside 1, the incarcerated H2O molecule could be utilized as a magnetic measure in NMR which tells the rotational dynamics inside the spherical electrostatic potential field.23 According to the reported method, H2O@1 was prepared.15 Curiously enough, the high-field region in the NMR spectrum of H2O@1 with Li+[B(C6F5)3]−·2.5Et2O exhibited three singlet signals at δ −9.98, −10.13, and −10.23 ppm, indicative of the H2O molecules existing in different chemical environment (Fig. 7a). The two signals at δ −9.98 and −10.13 ppm were observed only in the presence of the lithium salt whereas their signal intensities diminished substantially at the elevated temperature. The PFG (pulsed field-gradient) NMR spectroscopy24 revealed the different diffusion coefficients D and effective hydrodynamic radii rH for these three chemical species assignable to H2O@1 (δ −10.23 ppm), Li+⊂(H2O@1) (δ −10.13 ppm), and Li+⊂(H2O@1)2 (δ −9.98 ppm) whilst the molecular size of the last one was underestimated presumably due to the deviation from the hypothetical Brownian motion, caused by its dimeric structure largely different from a shape of a particle.Importantly, full widths at half maximum of the 1H signals were found to be increased by the Li+-coordination, implying the change in relaxation mechanism or dynamic behavior (Fig. 7a). Thus, the longitudinal and transverse relaxation times (T1 and T2) were measured in degassed ODCB-d4 within a temperature range of 290–330 K under a field strength of 800 MHz. As depicted in Fig. 7b, the T1 values were increased by lowering the temperature, demonstrative of the dominant relaxation via spin-rotation mechanism,25 irrespective of the existence of Li+. This indicates that the distance between (1H)2O and 7Li+ is far enough to interact magnetically each other. The shortened T2 values by the Li+-coordination are consistent with the observed signal broadening. The large T1–T2 gaps in Li+⊂(H2O@1)n (n = 1, 2) indicate the restricted motion of the H2O molecules.14,26 Upon assuming the spin-rotation mechanism as the sole contribution to the 1H relaxation,27 angular momentum correlation times τJ (330 K) were obtained to be less than 1 ps, showing close resemblance to the dynamic behavior of supercritical water.28 Considering the Arrhenius-type thermal activation process,29 the rotational barriers of the H2O molecules were experimentally determined to be 0.88 ± 0.13 for H2O@1, 1.44 ± 0.03 for Li+⊂(H2O@1), and 1.41 ± 0.09 kcal mol−1 for Li+⊂(H2O@1)2, respectively (Fig. 3c).
Since the dynamic behavior of water inside hydrophobic subnanospace is explainable by the different interaction strength between water and the wall,30 electrostatic potential fields inside 1 and (Li+⊂1)[B(C6F5)4]− were computed at the MP2/6-31G(d,p)//M06-2X/6-31G(d,p) level of theory. As drawn in Fig. 8a, the inner potential surface of 1 seems to be neutral. A partial negative charge nearby the orifice has negligible perturbation toward the rotational motion of H2O since the H-bonded conformation (O⋯O distance: 3.33 Å)14,31 is suggested to be thermodynamically unfavorable by ΔG +1.07 kcal mol−1 relative to non-bonded one (3.77 Å) (Fig. 8 and S10†). The Li+-coordination causes a significant change in the potential field: delocalization of the cationic charge both inside and outside the π-framework, rendering the water orientation at the center of the cage to maximize enthalpy gain via the electrostatic interaction. Considering the stabilization energies ΔGwater given by the H2O-encapsulation, (Li+⊂1)[B(C6F5)4]− has a larger energetic gain by ΔΔGwater 0.77 kcal mol−1 compared with 1. This is comparable to the observed difference in rotational barriers (ΔEa 0.56 kcal mol−1). Thus, the rotational motion of the H2O molecules in 1 and Li+⊂1 is regarded to be governed by the van der Waals and electrostatic interactions, respectively.
Li+[B(C6F5)4]−-mediated dehydroxyhydrogenation under high pressure
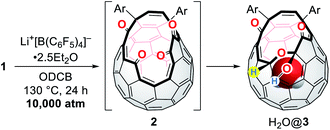
Subsequently, we turned our focus to high-pressure effect on the complexation of 1 with Li+. Initially, we expected either precipitation of (Li+⊂(1)2)[B(C6F5)4]− by lowering its solubility under high pressure conditions or formation of (Li+@1)[B(C6F5)4]− as stable salts. Hence, the solution of 1 and Li+[B(C6F5)4]−·2.5Et2O in ODCB was subjected to a pressure of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm at 130 °C for 24 h (Table 2). After the treatment, the crude mixture still maintained homogeneity without precipitation, suggestive of negligible pressure effect on the solubility of the lithium salt sandwiched with two cage-opened C60 ligands. The 7Li NMR measurement of the crude mixture confirmed no encapsulation of a Li+ ion inside 1. Theoretical calculations suggested that the Li+-encapsulation is thermodynamically unfavored (ΔG = +26.0 kcal mol−1). Instead, we found the formation of H2O@3 in which one of the hydroxy groups in 1 was replaced with a hydrogen atom.13,32 Under these conditions, a water molecule released from the bis(hemiketal) moiety of 1 was trapped inside the cavity of 2 which was formed in situ,15,33 thus affording H2O@1 and H2O@3 after chromatographic purification. Importantly, H2O@3 was not formed in the absence of Li+[B(C6F5)4]− (entry 1). By employing 0.2 equiv. of Li+[B(C6F5)4]−, H2O@3 was obtained in 6% isolated yield with an occupation level of H2O being 96%. This indicates that the conversion of 1 into 3 is kinetically less preferred relative to the insertion of H2O into 2. By increasing the amount of Li+[B(C6F5)4]−, the yield of H2O@3 was improved up to 34% with a significantly decreased occupation level of H2O from 96 to 75% probably due to (i) the formation of lithium hydrates Li+(H2O)n, (ii) prevented dehydration from 1 by the Li+-coordination onto 1, or (iii) prevented H2O-insertion by the Li+-coordination onto 2 (entries 2–4). Contrastingly, the addition of the excessive amount of water resulted in lowering yield of H2O@3 (17%) with an elevated occupation level of H2O (88%) (entry 5). It should be noted that this reaction did not proceed well under ambient pressure (entry 6).
000 atm at 130 °C for 24 h (Table 2). After the treatment, the crude mixture still maintained homogeneity without precipitation, suggestive of negligible pressure effect on the solubility of the lithium salt sandwiched with two cage-opened C60 ligands. The 7Li NMR measurement of the crude mixture confirmed no encapsulation of a Li+ ion inside 1. Theoretical calculations suggested that the Li+-encapsulation is thermodynamically unfavored (ΔG = +26.0 kcal mol−1). Instead, we found the formation of H2O@3 in which one of the hydroxy groups in 1 was replaced with a hydrogen atom.13,32 Under these conditions, a water molecule released from the bis(hemiketal) moiety of 1 was trapped inside the cavity of 2 which was formed in situ,15,33 thus affording H2O@1 and H2O@3 after chromatographic purification. Importantly, H2O@3 was not formed in the absence of Li+[B(C6F5)4]− (entry 1). By employing 0.2 equiv. of Li+[B(C6F5)4]−, H2O@3 was obtained in 6% isolated yield with an occupation level of H2O being 96%. This indicates that the conversion of 1 into 3 is kinetically less preferred relative to the insertion of H2O into 2. By increasing the amount of Li+[B(C6F5)4]−, the yield of H2O@3 was improved up to 34% with a significantly decreased occupation level of H2O from 96 to 75% probably due to (i) the formation of lithium hydrates Li+(H2O)n, (ii) prevented dehydration from 1 by the Li+-coordination onto 1, or (iii) prevented H2O-insertion by the Li+-coordination onto 2 (entries 2–4). Contrastingly, the addition of the excessive amount of water resulted in lowering yield of H2O@3 (17%) with an elevated occupation level of H2O (88%) (entry 5). It should be noted that this reaction did not proceed well under ambient pressure (entry 6).
| Entry | Li+[B(C6F5)4]− | H2O | H2O@3a |
|---|---|---|---|
| a Isolated yields. Values in parentheses are encapsulation ratio of H2O determined by 1H NMR. b Conducted under ambient pressure. | |||
| 1 | — | Excess | Not formed |
| 2 | 0.2 equiv. | — | 6% (96%) |
| 3 | 1.0 equiv. | — | 23% (94%) |
| 4 | 10 equiv. | — | 34% (75%) |
| 5 | 10 equiv. | Excess | 17% (88%) |
| 6b | 10 equiv. | — | Trace |
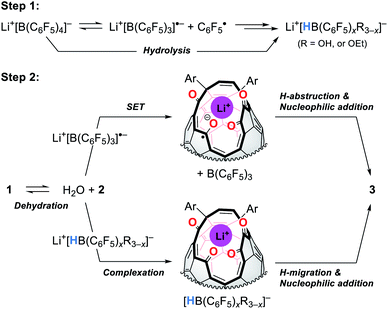
Fig. 9 shows the proposed mechanism consisting of two steps. Under high-pressure conditions, this reaction is considered to be initiated with the homolytic cleavage of the C–B bond in Li+[B(C6F5)4]−,34 giving a radical anion of triarylborane, i.e., B(C6F5)3˙− which is a stable organic radical species owing to its structure isoelectronic to triarylmethyl radicals.35 In solution, however, B(C6F5)3˙− is known to decompose to furnish four-coordinate borate species bearing a B–H bond such as HB(C6F5)3−via solvolytic radical reactions.36 The similar borate species could be generated from Li+[B(C6F5)4]− which is transformed into B(C6F5)xR3−xvia aryl migration followed by hydrolysis.37 The further hydride abstraction from solvents provides [HB(C6F5)xR3−x]−.38 The mass spectrometric analysis of the crude mixture showed molecular ion peaks possibly assignable to B(C6F5)3, B(C6F5)2OH, and B(C6F5)2OEt, supporting the partial decomposition of Li+[B(C6F5)4]−. In the second step, 1 will lose a water molecule from its orifice to afford 2. During this equilibrium, the water molecule is encapsulated inside 2 which works as a desiccant to prevent the decomposition of active borane and borate species generated in the first step. Tetraketo derivative 2 then undergoes single-electron transfer (SET) to provide a ketyl radical complex (Li+⊂2˙−) which is eventually converted into 3via H-abstraction with an intramolecular nucleophilic addition. Another possible route is commenced with the complexation of Li+[HB(C6F5)xR3−x]− on 2, followed by H-migration with an SN2′-type cyclization. In both these two pathways, Li+-coordination would facilitate the bond polarization of the carbonyl group. This reaction is, as a consequence, accompanied by the formation/regeneration of three-coordinate boron compounds, i.e., B(C6F5)3 or B(C6F5)xR3−x, as observed experimentally.
Conclusions
In summary, we disclosed the solution dynamics of a fullerene-based macrocyclic ligand 1 in the presence of a Li+ ion. The NMR spectroscopy demonstrated the coordination of the Li+ ion to the diketo bis(hemiketal) moiety in 1 with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometries which were identified with the association constants of K1 = 8.9 × 106 M−1 (Li+⊂1) and K2 = 2.1 × 103 M−1 (Li+⊂(1)2). The mass spectrometric analyses further suggested the formation of the 1
2 stoichiometries which were identified with the association constants of K1 = 8.9 × 106 M−1 (Li+⊂1) and K2 = 2.1 × 103 M−1 (Li+⊂(1)2). The mass spectrometric analyses further suggested the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes even for other alkali metal ions including Na+, K+, Rb+, and Cs+, indicative of the flexibility of 1 as the Lewis basic ligand. Upon complexation of 1 with Li+, intense absorption was induced in the visible region by intra- and intermolecular CT transitions. Intriguingly, the Li+-coordination caused major perturbations to the electrostatic potential field inside 1 from neutral to positive, which was confirmed by the use of incarcerated H2O molecules as magnetic probes, demonstrating the considerable restriction on its rotational dynamics particularly at lower temperatures accompanied by the increase of the T1 values. By exposure to high-pressure conditions, complexes Li+⊂(1)n (n = 1, 2) that formed in situ underwent unprecedented dehydroxyhydrogenation to furnish 3 in a moderate yield. This reaction occurred only under high pressure conditions in the presence of Li+[B(C6F5)4]−, in which B(C6F5)3˙− and [HB(C6F5)xR3−x]− would be actual active species. The characteristic association behavior and reactivity of the fullerene-based macrocycles would potentially provide utilities as metal sensors with tunable electronic configurations, batteries with modifiable ionic conductivities, and polydentate bulky ligands in organic reactions, as well as a guidepost for the long-awaited chemical synthesis of metallofullerenes.
2 complexes even for other alkali metal ions including Na+, K+, Rb+, and Cs+, indicative of the flexibility of 1 as the Lewis basic ligand. Upon complexation of 1 with Li+, intense absorption was induced in the visible region by intra- and intermolecular CT transitions. Intriguingly, the Li+-coordination caused major perturbations to the electrostatic potential field inside 1 from neutral to positive, which was confirmed by the use of incarcerated H2O molecules as magnetic probes, demonstrating the considerable restriction on its rotational dynamics particularly at lower temperatures accompanied by the increase of the T1 values. By exposure to high-pressure conditions, complexes Li+⊂(1)n (n = 1, 2) that formed in situ underwent unprecedented dehydroxyhydrogenation to furnish 3 in a moderate yield. This reaction occurred only under high pressure conditions in the presence of Li+[B(C6F5)4]−, in which B(C6F5)3˙− and [HB(C6F5)xR3−x]− would be actual active species. The characteristic association behavior and reactivity of the fullerene-based macrocycles would potentially provide utilities as metal sensors with tunable electronic configurations, batteries with modifiable ionic conductivities, and polydentate bulky ligands in organic reactions, as well as a guidepost for the long-awaited chemical synthesis of metallofullerenes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support was partially provided by the JSPS KAKENHI Grant Number JP17H06119, JP20K15260, and JP20H05218. The NMR measurements were partly supported by the Joint Usage/Research Center (JURC) at the ICR, Kyoto University.Notes and references
- C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 7017–7036 CrossRef CAS.
- (a) G. W. Gokel, W. M. Leevy and M. E. Weber, Chem. Rev., 2004, 104, 2723–2750 CrossRef CAS; (b) Z. Liu, S. K. M. Nalluri and J. F. Stoddart, Chem. Soc. Rev., 2017, 46, 2459–2478 RSC.
- (a) S. Saito and A. Osuka, Angew. Chem., Int. Ed., 2011, 50, 4342–4373 CrossRef CAS; (b) H. Lu and N. Kobayashi, Chem. Rev., 2016, 116, 6184–6261 CrossRef CAS; (c) E. A. Kuzmina, T. V. Dubinina and L. G. Tomilova, New J. Chem., 2019, 43, 9314–9327 RSC.
- H. R. Karfunkel, T. Dressler and A. Hirsch, J. Comput.-Aided Mol. Des., 1992, 6, 521–535 CrossRef CAS.
- A. Hirsch, Fullerenes: Chemistry and Reactions, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2005 Search PubMed.
- (a) Y. Rubin, Chem.–Eur. J., 1997, 3, 1009–1016 CrossRef CAS; (b) M. Murata, Y. Murata and K. Komatsu, Chem. Commun., 2008, 6083–6094 RSC; (c) G. C. Vougioukala-Kis, M. M. Roubelakis and M. Orfanopoulos, Chem. Soc. Rev., 2010, 39, 817–844 RSC; (d) L. Shi and L. Gan, J. Phys. Org. Chem., 2013, 26, 766–772 CrossRef CAS.
- Y. Li and L. Gan, Chem.–Eur. J., 2017, 23, 10485–10490 CrossRef CAS.
- (a) P. J. Fagan, J. C. Calabrese and B. Malone, Acc. Chem. Res., 1992, 25, 134–142 CrossRef CAS; (b) A. L. Balch and M. M. Olmstead, Chem. Rev., 1998, 98, 2123–2165 CrossRef CAS; (c) W.-Y. Yeh, J. Organomet. Chem., 2015, 784, 13–23 CrossRef CAS.
- (a) Y. Hashikawa, M. Murata, A. Wakamiya and Y. Murata, Org. Lett., 2016, 18, 6348–6351 CrossRef CAS; (b) H. Zhang, Z. Zhou, L. Yang, J. Su, P. Jin and L. Gan, Organometallics, 2019, 38, 3139–3143 CrossRef CAS.
- Y. Li, G. Zhang, D. Wang, B. Xu, D. Xu, N. Lou and L. Gan, Angew. Chem., Int. Ed., 2016, 55, 14590–14594 CrossRef CAS.
- Z. Zhou, N. Xin and L. Gan, Chem.–Eur. J., 2018, 24, 451–457 CrossRef CAS.
- H. Zhang, C. Pan, X. Lu and L. Gan, Org. Chem. Front., 2019, 6, 1397–1402 RSC.
- Y. Hashikawa, M. Murata, A. Wakamiya and Y. Murata, Can. J. Chem., 2017, 95, 320–328 CrossRef CAS.
- Y. Hashikawa, S. Hasegawa and Y. Murata, Chem. Commun., 2018, 54, 13686–13689 RSC.
- K. Kurotobi and Y. Murata, Science, 2011, 33, 613–616 CrossRef.
- U. Olsher, Chem. Rev., 1991, 91, 137–164 CrossRef CAS.
- H. Günther, Lithium NMR, in Encyclopedia of Magnetic Resonance, John Wiley & Sons, Ltd, Chichester, UK, 2007 Search PubMed.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- J. J. Christensen, D. J. Eatough and R. M. Izatt, Chem. Rev., 1974, 74, 351–384 CrossRef.
- Y. Hashikawa and Y. Murata, Chem.–Eur. J., 2019, 25, 2482–2485 CrossRef CAS.
- (a) Y. Hashikawa, H. Yasui, K. Kurotobi and Y. Murata, Mater. Chem. Front., 2018, 2, 206–213 RSC; (b) Y. Hashikawa, S. Okamoto and Y. Murata, Commun. Chem., 2020, 3, 90 CrossRef CAS.
- Y. Li, J. Y.-C. Chen, X. Lei, R. G. Lawler, Y. Murata, K. Komatsu and N. J. Turro, J. Phys. Chem. Lett., 2012, 3, 1165–1168 CrossRef CAS.
- Y. Cohen, L. Avram and L. Frish, Angew. Chem., Int. Ed., 2005, 44, 520–554 CrossRef CAS.
- E. Sartori, M. Ruzzi, N. J. Turro, J. D. Decatur, D. C. Doetsch-Man, R. G. Lawler, A. L. Buchachenko, Y. Murata and K. Komatsu, J. Am. Chem. Soc., 2006, 128, 14752–14753 CrossRef CAS.
- Y. Hashikawa, M. Murata, A. Wakamiya and Y. Murata, J. Am. Chem. Soc., 2016, 138, 4096–4104 CrossRef CAS.
- P. S. Hubbard, Phys. Rev., 1963, 131, 1155–1165 CrossRef CAS.
- W. J. Lamb and J. Jonas, J. Chem. Phys., 1981, 74, 913–921 CrossRef CAS.
- (a) J. Jonas, T. DeFries and W. J. Lamb, J. Chem. Phys., 1978, 68, 2988–2989 CrossRef CAS; (b) Y. Hashikawa and Y. Murata, J. Am. Chem. Soc., 2019, 141, 12928–12938 CrossRef CAS; (c) Y. Hashikawa and Y. Murata, Chem. Lett., 2020, 49, 244–247 CrossRef CAS.
- (a) H. Kyakuno, K. Matsuda, Y. Nakai, R. Ichimura, T. Saito, Y. Miyata, K. Hata and Y. Maniwa, Sci. Rep., 2017, 7, 14834 CrossRef; (b) Y. Hashikawa, M. Murata, A. Wakamiya and Y. Murata, Angew. Chem., Int. Ed., 2016, 55, 13109–13113 CrossRef CAS; (c) Y. Hashikawa and Y. Murata, J. Am. Chem. Soc., 2017, 139, 18468–18471 CrossRef CAS.
- M. D. Battistel, H. F. Azurmendi, M. Frank and D. I. Freedberg, J. Am. Chem. Soc., 2015, 137, 13444–13447 CrossRef CAS.
- A. Krachmalnicoff, M. H. Levitt and R. J. Whitby, Chem. Commun., 2014, 50, 13037–13040 RSC.
- Y. Hashikawa, M. Murata, A. Wakamiya and Y. Murata, Org. Lett., 2014, 16, 2970–2973 CrossRef CAS.
- (a) T. Onak, Organoborane Chemistry, Academic Press, Inc., New York, 1975 Search PubMed; (b) S. N. Mlondo, P. O'Brien, P. J. Thomas, M. Helliwell, J. Raftery and D. J. Procter, Chem. Commun., 2008, 2456–2458 RSC.
- T. Kushida and S. Yamaguchi, Organometallics, 2013, 32, 6654–6657 CrossRef CAS.
- E. J. Lawrence, V. S. Oganesyan, G. G. Wildgoose and A. E. Ashley, Dalton Trans., 2013, 42, 782–789 RSC.
- P. J. Grisdale, J. L. R. Williams, M. E. Glogowski and B. E. Babb, J. Org. Chem., 1971, 36, 544–549 CrossRef CAS.
- M. Shang, J. Z. Chan, M. Cao, Y. Chang, Q. Wang, B. Cook, S. Torker and M. Wasa, J. Am. Chem. Soc., 2018, 140, 10593–10601 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed synthetic procedures, spectra, and optimized geometries. See DOI: 10.1039/d0sc05280a |
| This journal is © The Royal Society of Chemistry 2020 |