Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic exchange interactions in symmetric lanthanide dimetallics†
Marcus J.
Giansiracusa‡
 a,
Susan
Al-Badran‡
ab,
Andreas K.
Kostopoulos
a,
Susan
Al-Badran‡
ab,
Andreas K.
Kostopoulos
 a,
George F. S.
Whitehead
a,
George F. S.
Whitehead
 a,
Eric J. L.
McInnes
a,
David
Collison
*a,
Richard E. P.
Winpenny
a,
Eric J. L.
McInnes
a,
David
Collison
*a,
Richard E. P.
Winpenny
 a and
Nicholas F.
Chilton
a and
Nicholas F.
Chilton
 *a
*a
aDepartment of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: david.collison@manchester.ac.uk; nicholas.chilton@manchester.ac.uk
bChemistry Department, College of Science, Basrah University, Basrah, Iraq
First published on 4th September 2020
Abstract
We report the synthesis and characterization of two symmetric homo-dimetallic lanthanide complexes based on methyl-substituted 8-hydroxyquinoline (HMeQ). The aryloxo-bridged core gives rise to weak magnetic coupling between pairs of ErIII and YbIII ions, as revealed by magnetic and EPR spectroscopy studies. EPR measurements of magnetically dilute species, coupled with CASSCF-SO calculations, allows modelling of the EPR spectra of the exchange coupled species and the magnetic data simultaneously. This work adds to the database of exchange coupled {Ln}2 molecules which have been thoroughly characterised by EPR spectroscopy and modelled using an Seff = 1/2 approach to describe the interaction of ground Kramers states, and highlights the differences between centro-symmetric and asymmetric dimetallics.
Introduction
The unique chemistry of the trivalent lanthanides (LnIII) stems from their electronic configuration with the 4f orbitals shielded by filled 5s25p6 subshells.1 This makes LnIII ions extremely stable, hard Lewis acids with a tendency towards high coordination numbers.2 The optical and magnetic properties of lanthanide complexes have attracted much attention over the past two decades,3–7 for applications in medical imaging, molecular magnetism and quantum information processing (QIP).5–10 Dimetallic LnIII complexes, where the ions are close enough to allow a magnetic interaction, can open new avenues for QIP,4,11–14 and also provide a simple model to study the fundamental magnetic interactions between 4f electronic manifolds.15The 8-hydroxyquinoline pro-ligand and its derivatives are employed primarily in gravimetric analysis and as extraction reagents due to their excellent chelating properties that are applicable to many metals including lanthanides.16,17 Furthermore, they have attracted interest in use for preparing coordination complexes since the report of tris-8-oxoquinolinato aluminium in 1987,18,19 and more recently for generating polymetallic lanthanide complexes.20–26 We have recently used this pro-ligand to assemble a series of asymmetric lanthanide dimetallics to study the magnetic interactions by magnetometry, electron paramagnetic resonance (EPR) and inelastic neutron scattering (INS) spectroscopies.27,28 We found that the exchange interactions for the asymmetric Dy2 and Er2 species are reasonably well described by the point-dipole model, however, there is a non-negligible superexchange component.27,28 For the Yb2 asymmetric species, the point-dipole calculation underestimates the interaction, which is clearly dominated by superexchange.27
Here, we study a related series of centro-symmetric molecular dimetallics (Ci point group symmetry), prepared using 2-methyl-8-hydroxyquinoline (HMeQ) with formula [Ln2(HMeQ*)4(NO3)6] where LnIII = ErIII (1), YbIII (2) and YIII (3), in which the pro-ligand is deprotonated at O and protonated at N. The structures of the YIII, LaIII, GdIII, DyIII and YbIII analogues have been reported previously,29,30 and here we report the novel ErIII analogue. Herein, we study 1 and 2 with multi-frequency EPR spectroscopy, following our previous work,27,28 in order to add to the database of exchange coupled species that have been comprehensively studied experimentally. We employ a pseudospin S = 1/2 approach to fit the EPR spectra to extract the nature of the low-lying exchange coupled states to allow benchmarking of theoretical models.31
Results
Synthesis
A family of three lanthanide complexes with the formula [Ln2(HMeQ*)2(NO3)6] (HMeQ* is the zwitterion deprotonated at O and protonated at N; Ln = Er (1), Yb (2) and Y (3)) were synthesised by reacting hydrated lanthanide nitrate Ln(NO3)3·xH2O and HMeQ in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in methanol. After heating to reflux for 3 hours, the solution was filtered and slowly evaporated yielding yellow block-shape crystals suitable for single crystal X-ray diffraction, which revealed the symmetric LnIII dimetallics. The doped samples (Ln@3), where Ln = Er (1a) or Yb (2a), were synthesised using the same procedure but employing a mixture of Ln(NO3)3·xH2O and Y(NO3)3·xH2O in a 1
2 in methanol. After heating to reflux for 3 hours, the solution was filtered and slowly evaporated yielding yellow block-shape crystals suitable for single crystal X-ray diffraction, which revealed the symmetric LnIII dimetallics. The doped samples (Ln@3), where Ln = Er (1a) or Yb (2a), were synthesised using the same procedure but employing a mixture of Ln(NO3)3·xH2O and Y(NO3)3·xH2O in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 molar ratio with HMeQ in methanol (1
19 molar ratio with HMeQ in methanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 ratio for the 2a EPR spectroscopy sample).
49 ratio for the 2a EPR spectroscopy sample).
Structural description
The complexes [Ln2(HMeQ*)2(NO3)6] 1–3 crystallise in the monoclinic space group P21/n, Fig. 1, S1, and Table S1/2.† The structure lies about a crystallographic inversion centre. Here, the structure of 1 is described as representative of the isostructural series.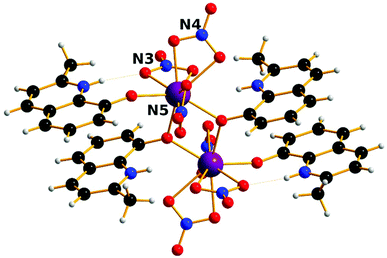 | ||
| Fig. 1 Solid state molecular structure of 1; Scheme: Er, purple; N, blue; O, red; C, grey; H, light grey. | ||
The ErIII site is bonded to three chelating nitrate anions, two μ-O-atoms from bridging HMeQ* ligands and an O-atom from a third terminal HMeQ* unit. The Er-Er distance is 3.8725(7) Å and the Er–O–Er angle is 112.3(2)°, compared to the shorter 3.4456(8) Å distance between the two ErIII ions in the asymmetric dimetallic [H2Q][Ln2(Q)4(NO3)3]·MeOH, which contains an unsubstituted oxoquinolinate (HQ) molecule.28 The smaller separation in the asymmetric molecule is likely a result of the reduced steric bulk which allowed three bridging ligands forcing a wider Er–O–Er angle 96.6(7)°.
The coordination of the ErIII site consists of nine oxygen atoms: the shortest Er–O distance, 2.189(8) Å, is to the oxygen from the terminal HMeQ*. The two bonds to the μ-O from HMeQ* have 2.328(7) and 2.334(5) Å distances. The six oxygen atoms from three chelating nitrate ligands have longer bonds with an average distance of 2.46(4) Å. Two of the nitrate ligands at Er, defined by N3 and N5, are approximately trans to each other. Selected angles and distances are reported in the ESI† for comparison across the series. The coordination environment of the metal can be described as a spherical capped square antiprism, Fig. S2,† and is confirmed by the program SHAPE, Table S3.†32,33 Despite the coordination environment being well-distributed on a sphere (i.e. arrangement of donor atoms lacking significant anisotropy), the presence of a short terminal bond to monodentate HMeQ* will contribute to the magnetic anisotropy, as was previously found for the DyIII analogue, which behaves as a single-molecule magnet.29
Magnetometry
The solid-state magnetic properties of 1 and 2 were studied with magnetic susceptibility measurements between 1.8–300 K. For both samples the values of χMT at room temperature are close to the expected value for two non-interacting LnIII ions (Table S4†) and decline smoothly on cooling due to depopulation of the crystal field levels, Fig. S3.† Magnetisation data do not reveal any additional information with the YbIII analogue approaching saturation at 3.8 NAμB at 7 T and 2 K, while the ErIII system does not saturate reaching 10.1 NAμB at 7 T and 2 K, Fig. S4.†Investigation of [Er2(HMeQ*)2(NO3)6] (1)
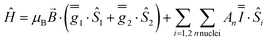 | (1) |
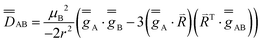 | (2) |
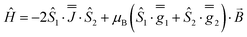 | (3) |
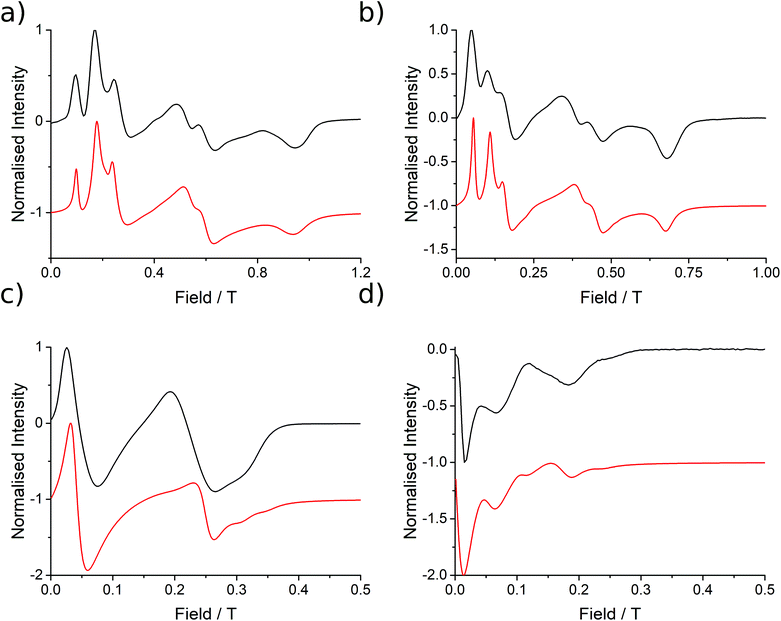 | ||
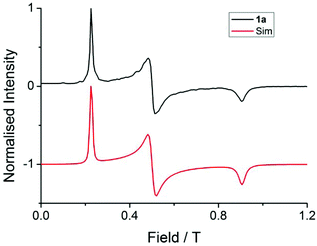
| Fig. 3 EPR spectra (black lines) collected at 5 K for 1 at (a) Q-band (33.970818 GHz), (b) K-band (23.791 GHz), (c) X-band (9.37198 GHz) and (d) S-band (3.87285 GHz), with simulations in red from the parameters presented in Table 1. | ||
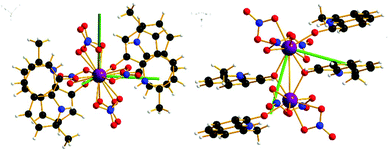 | ||
| Fig. 4 Orientation of the principal g-axes (g1 = dark green) for the ground doublet from CASSCF-SO single site calculations of 1, with view down Er–Er bond (left) and down g1 axis (right). | ||
These simulations (Fig. S5†) clearly show that dipolar coupling alone is not sufficient to explain the exchange interactions in 1, and hence there must be a non-zero superexchange component. Thus, following our previous work, we fit the data of the pure species with an explicit exchange coupling Hamiltonian. In this case the principal g-values for the two ErIII ions are identical and their orientations are rigorously co-parallel (due to the centre of symmetry), and we define the diagonal anisotropic exchange matrix such that the Jz component lies along the Er–Er vector. Note that here we perform simulations in the g-matrix reference frame where the principal g-values are associated with the Cartesian axes, and due to the centre of symmetry, the only rotations required to define the orientation of the principal g-values with respect to the molecular geometry are the α and β angles that fix Jz along the Er–Er vector. The orientation of the Jx and Jy directions are left as a fitting parameter via the angle γ (Fig. S21;† corresponding to clockwise rotation around Jz); when γ = 0, the angle between Jy and the terminal Er–hq oxide is ca. 8° (eqn (S1)–(S3) and Fig. S15†). As a result of the centre of symmetry, neither the Zeeman term (magnetic field) nor the anisotropic exchange coupling can mix the Seff = 0 and Seff = 1 states, and due to the ΔS = 0 and Δms = ±1 EPR selection rules, the spectra are insensitive to the isotropic component of the exchange interaction. Therefore, we enforce a traceless exchange matrix for the modelling of 1 and 2. Surveying values of the anisotropic exchange parameters in the range −1 < Ja < +1 cm−1 allows us to find parameters that give excellent simulations of the experimental data (Fig. 3 and Table 1). The exchange frame is shown in Fig. S15,† depicting the initial and the final fitted orientations.
| Parameter | Value(s) | ||
|---|---|---|---|
| a Rotation matrices use PHI convention, eqn (S1)–(S3).† | |||
| J x (cm−1) | J y (cm−1) | J z (cm−1) | |
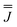
|
0.31 | −0.25 | −0.07 |
| g 1 | g 2 | g 3 | |
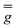
|
10.72 (fixed) | 4.85 (fixed) | 2.68 (fixed) |
| α (°) | β (°) | γ (°) | |
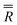
|
16.7 (fixed) | 261.0 (fixed) | 35.0 |
| Linewidths (Lorentzian) | lwx (GHz) | lwy (GHz) | lwz (GHz) |
| Q-band | 4.0 | 5.0 | 5.0 |
| K-band | 2.0 | 4.0 | 3.0 |
| X-band | 2.0 | 2.0 | 3.5 |
| S-band | 2.0 | 2.0 | 3.0 |
We present the simulation using the traceless anisotropic interaction matrix 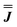 , Fig. 3 and Table 1, which are in excellent agreement across all frequencies. A similar quality simulation, with slight variations in the peak intensities, is obtained using the opposite sign (
, Fig. 3 and Table 1, which are in excellent agreement across all frequencies. A similar quality simulation, with slight variations in the peak intensities, is obtained using the opposite sign (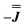 ) interaction matrix, Fig. S6.† As the reported best-fit parameters are independent of the isotropic part, there is an infinite number of solutions of the form
) interaction matrix, Fig. S6.† As the reported best-fit parameters are independent of the isotropic part, there is an infinite number of solutions of the form 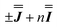 , where n is any real number and
, where n is any real number and 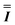 is the identity matrix. To estimate the isotropic component, we simulate the low temperature magnetic data using our exchange models (
is the identity matrix. To estimate the isotropic component, we simulate the low temperature magnetic data using our exchange models (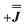 or
or 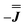 ) from EPR simulations along with a variable n, where we find good agreement for n between −0.5 and +1.0 cm−1 (Fig. S12†). It is worth noting that both
) from EPR simulations along with a variable n, where we find good agreement for n between −0.5 and +1.0 cm−1 (Fig. S12†). It is worth noting that both 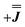 and
and 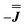 predict lower values for magnetic data at low temperature compared with experiment, which likely indicates a positive isotropic component is needed. Despite the excellent reproduction of the experimental EPR spectra, literature has shown that while CASSCF-SO calculations are a powerful tool for approximating the electronic structure of Ln(III)-based molecules,35 the principal magnetic axes of highly-anisotropic ions are not always predicted accurately enough compared to experiment. While there tends to be good agreement for Dy(III) complexes,36–41 a landmark study found that the calculated axes for isostructural Er(III) and Yb(III) molecules can have significant deviations compared to experimental axes from single-crystal measurements,42 although there are counter-examples where theory is supported by experiment for Er(III).43 However, due to the lack of single-crystal magnetometry/EPR data here, it is necessary to assess the validity of fixing the orientations of the principal g-values from CASSCF-SO calculations. Therefore, we have altered the rotation of the exchange matrix α and β angles (see above) for combinations of ±5° and ±10°, and re-optimised the exchange coupling parameters; here we are relying on the highly-featured nature of the multi-frequency EPR spectra to validate our orientation model. Variations of ±5° show no visual changes to the best-fit spectra and there is no change to the fitted exchange couplings (Table S10 and Fig. S18†); at ±10 degrees the fits are less good in all cases, but the refined parameters are nearly identical across all fits (Table S10 and Fig. S17†). Therefore, we believe that the CASSCF-SO-calculated orientations are reliable for the purposes of extracting information on the low-lying exchange coupling.
predict lower values for magnetic data at low temperature compared with experiment, which likely indicates a positive isotropic component is needed. Despite the excellent reproduction of the experimental EPR spectra, literature has shown that while CASSCF-SO calculations are a powerful tool for approximating the electronic structure of Ln(III)-based molecules,35 the principal magnetic axes of highly-anisotropic ions are not always predicted accurately enough compared to experiment. While there tends to be good agreement for Dy(III) complexes,36–41 a landmark study found that the calculated axes for isostructural Er(III) and Yb(III) molecules can have significant deviations compared to experimental axes from single-crystal measurements,42 although there are counter-examples where theory is supported by experiment for Er(III).43 However, due to the lack of single-crystal magnetometry/EPR data here, it is necessary to assess the validity of fixing the orientations of the principal g-values from CASSCF-SO calculations. Therefore, we have altered the rotation of the exchange matrix α and β angles (see above) for combinations of ±5° and ±10°, and re-optimised the exchange coupling parameters; here we are relying on the highly-featured nature of the multi-frequency EPR spectra to validate our orientation model. Variations of ±5° show no visual changes to the best-fit spectra and there is no change to the fitted exchange couplings (Table S10 and Fig. S18†); at ±10 degrees the fits are less good in all cases, but the refined parameters are nearly identical across all fits (Table S10 and Fig. S17†). Therefore, we believe that the CASSCF-SO-calculated orientations are reliable for the purposes of extracting information on the low-lying exchange coupling.
Investigation of [Yb2(HMeQ*)2(NO3)6] (2)
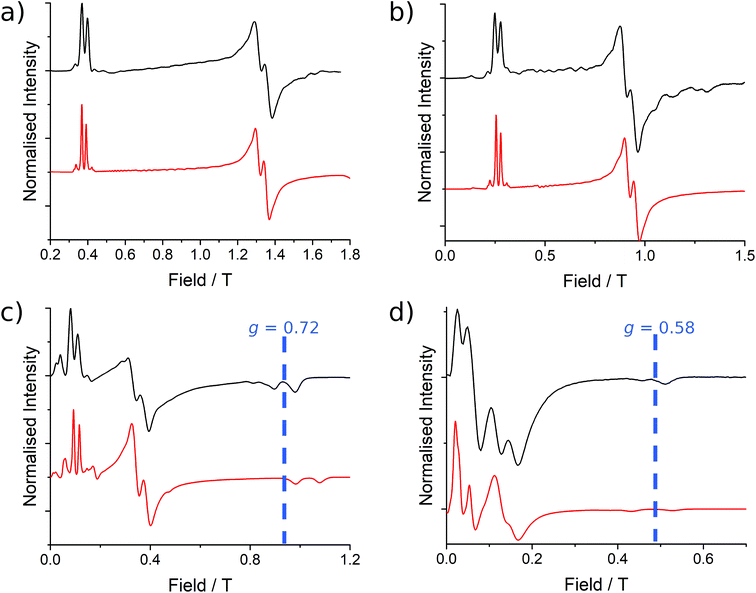 | ||
| Fig. 6 EPR spectra collected at 5 K for 2 at (a) Q-band (34.092351 GHz), (b) K-band (23.870 GHz), (c) X-band (9.374342 GHz) and (d) S-band (3.875789 GHz) frequencies with simulations in red from the parameters presented in Table 2. The variation in the mean g3 position is indicated at X- and S-band. | ||
As before, the experimental g-values from 2a are used as the starting point for the model, with CASSCF-SO defining the orientation of the g-frames and the diagonal exchange matrix defined with Jz along the interatomic Yb–Yb vector. Comparing the spectra of 2 and 2a, there is a clear shift in the position of the g1 feature, which is centred at a lower field in the pure Yb2 sample, Fig. S8.† This observation is consistent with our previous work showing that doping into diamagnetic lattices can give slight changes in the local CF environment compared to the pure sample, which manifests as shifts in the g-values.27 We therefore allowed g1 as a variable parameter in the modelling process, which gives g1 = 6.4, Table 2. As the CASSCF-SO calculated g3 value (0.68) lies between the mean observed g3-features (0.72 and 0.58), it is fixed for the simulations. Simulating the spectra with Easyspin44 using eqn (4), we obtain good agreement with the observed spectra using an axially-symmetric exchange Hamiltonian, Fig. 6 and Table 2. As with the analysis of 1, the trace of the exchange matrix is fixed to zero. As axial symmetry is adequate for the simulation (where Jx = Jy) rotation of the exchange reference frame around Jz is irrelevant and γ is arbitrary. Again, the isotropic component does not influence the EPR spectrum, and inverting the sign of the reported exchange matrix (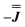 ) gives a similar splitting with opposite relative intensities of the g1 peaks evident in the Q- and K-band simulations, Fig. S10.† Here, both
) gives a similar splitting with opposite relative intensities of the g1 peaks evident in the Q- and K-band simulations, Fig. S10.† Here, both 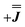 and
and 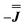 are in good agreement with low temperature magnetic data, Fig. S13.† Using the magnetic data as a probe of the isotropic component, in the form
are in good agreement with low temperature magnetic data, Fig. S13.† Using the magnetic data as a probe of the isotropic component, in the form 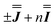 , we find n in the range −0.5 to +0.5 cm−1, Fig. S14.†
, we find n in the range −0.5 to +0.5 cm−1, Fig. S14.†
| Parameter | Value(s) | ||
|---|---|---|---|
| a Rotation matrices use EasySpin convention, eqn (S4)–(S6).† | |||
| J x (cm−1) | J y (cm−1) | J z (cm−1) | |
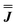
|
0.023 | 0.023 | −0.047 |
| A 1 (MHz) | A 2 (MHz) | A 3 (MHz) | |
| A (171Yb) | 5051 | 1406 | 498 |
| A (173Yb) | 1467 | 404 | 140 |
| g 1 | g 2 | g 3 | |
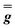
|
6.4 | 1.8 (fixed) | 0.68 (fixed) |
| α (°) | β (°) | γ (°) | |
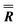
|
46.24 (fixed) | 84.26 (fixed) | 0 (fixed) |
| Linewidths (FWHM) | lwx | lwy | lwz |
| H strain (X-, K-, Q-band) | 300 MHz | 700 MHz | 100 MHz |
| H strain (S-band) | 300 MHz | 600 MHz | 100 MHz |
| Field-space (all bands) | 8 mT | ||
To assess the accuracy of the CASSCF-SO-calculated g-matrix orientations, we have again altered the rotation of the exchange matrix α and β angles for combinations of ±5° and ±10°, and re-optimised the exchange coupling parameter. Two out of four variations of ±5° show good best-fit spectra while the other two are poor, but in all cases the fitted exchange coupling parameter changes by <8% (Fig. S19 and Table S10†) At ±10 degrees the fits are significantly worse in all cases, but even here the exchange coupling only changes <26% (Fig. S20 and Table S10†). Thus we believe the CASSCF-SO-calculated orientations are reliable.
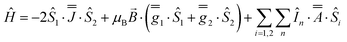 | (4) |
Discussion
With these simulations in hand, we can compare the fitted exchange matrices to the point-dipolar ones. It is worth comparing both the magnitude of the overall exchange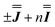 , as well as the observed anisotropy between the largest and smallest parameters. We find that the point dipole matrix for 1 predicts only a single significant term as a result of the large co-parallel principal g1 values (eqn (S7),† left). Representing this dipolar interaction in the same reference frame as the final simulation (eqn (S7),† right) shows major negative contributions (−0.15 to −0.32 cm−1) in the Jxx, Jxy and Jyx positions. The magnitudes of these terms are comparable with those obtained simulating the EPR spectra for 1, while the negative sign of the Jxx component in the dipolar matrix could indicate that the true parameters are the
, as well as the observed anisotropy between the largest and smallest parameters. We find that the point dipole matrix for 1 predicts only a single significant term as a result of the large co-parallel principal g1 values (eqn (S7),† left). Representing this dipolar interaction in the same reference frame as the final simulation (eqn (S7),† right) shows major negative contributions (−0.15 to −0.32 cm−1) in the Jxx, Jxy and Jyx positions. The magnitudes of these terms are comparable with those obtained simulating the EPR spectra for 1, while the negative sign of the Jxx component in the dipolar matrix could indicate that the true parameters are the 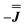 variant, Fig. S6.†
variant, Fig. S6.†
The dipolar exchange matrix for 2 also has a single major component in the Jzz position for the same reason as for 1. The magnitude of this term, 0.14 cm−1 (eqn (S8)†), is approximately double the anisotropy in the axially-symmetric parameters required to simulate the spectrum (|J⊥ − J∥| = 0.07 cm−1), explaining the overly-large splitting observed in the dipolar simulation (Fig. S9†).
The interaction of two Seff = 1/2 doublets results in four states arising from the coupled spin states Seff = 1 and Seff = 0, Tables S7 and S8.† As discussed above with respect to EPR transitions, the energy of the Seff = 0 state is determined by the isotropic component of the interaction matrix, so has an arbitrary value in these simulations.
Exchange interactions of the magnitudes determined by the presented 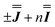 models are consistent with previous studies of the asymmetric dimetallic compounds [H2Q][Ln2(Q)4(NO3)3]·MeOH with similar oxo bridges (on the order of ca. 1 cm−1).27 In these compounds, the asymmetry allowed determination of both the isotropic and anisotropic components uniquely.
models are consistent with previous studies of the asymmetric dimetallic compounds [H2Q][Ln2(Q)4(NO3)3]·MeOH with similar oxo bridges (on the order of ca. 1 cm−1).27 In these compounds, the asymmetry allowed determination of both the isotropic and anisotropic components uniquely.
Initially focussing on the {Er2} compounds, the difference between the largest and smallest anisotropic exchange parameters is similar for 1 and [H2Q][Er2(Q)4(NO3)3]·MeOH (0.56 and 0.78 cm−1, respectively) and there are some similarities between the two sets of multi-frequency EPR spectra. All spectra have the major spectral feature occurring at low field, likely still having a strong relationship to the g1 feature of the individual ions. In 1, the exchange-free g-features from 1a are still discernible as multiplet peaks, while for [H2Q][Er2(Q)4(NO3)3]·MeOH it is impossible to assign the spectra in such a way. It is important to recall that [H2Q][Er2(Q)4(NO3)3]·MeOH has six unique g-values corresponding to the two distinct and non-collinear ErIII environments,27 and this is likely the origin of the increased complexity.
The biggest contrast is seen between 2 and [H2Q][Yb2(Q)4(NO3)3]·MeOH, where 2 is very weakly coupled and all features are clearly assignable to the g-features of the exchange-free ions; this is drastically different to the highly detailed spectra observed for [H2Q][Yb2(Q)4(NO3)3]·MeOH. Correspondingly, there is a large change in the difference between the largest and smallest anisotropic exchange parameters for 2 and [H2Q][Yb2(Q)4(NO3)3]·MeOH (0.07 vs. 0.55 cm−1, respectively). We found that dipolar coupling alone was insufficient to describe the spectra for [H2Q][Yb2(Q)4(NO3)3]·MeOH, and for 2 the predicted dipolar coupling produces larger splitting in the spectra than what is observed experimentally, thus suggesting that there is a superexchange component working in opposition to the dipolar interaction in 2. These differences are all consistent with the larger Yb–Yb separation observed in 2 compared to [H2Q][Yb2(Q)4(NO3)3]·MeOH.
Conclusions
Multi-frequency EPR spectroscopy has been performed on magnetically dilute and pure samples of [Ln2(HMeQ*)4(NO3)6] where LnIII = ErIII (1) and YbIII (2). The EPR spectra for the dilute samples show simple rhombic signals of the ground Kramers doublets, while the EPR spectra for the pure samples are highly-featured, providing direct evidence of the exchange interactions between the lowest lying doublets. By modelling the EPR spectra of pure samples of 1 and 2 using a combined experimental and theoretical approach, we have been able to effectively measure the exchange coupling. We find that dipolar coupling alone is not sufficient to explain the coupled spectra for 1, allowing us to infer a significant superexchange component. For 2, we find that dipolar exchange coupling is approximately twice as large as the observed exchange anisotropy, again suggesting an important, yet small, superexchange component. Compared to the asymmetric relatives of 1 and 2, [H2Q][Ln2(Q)4(NO3)3]·MeOH LnIII = DyIII, ErIII and YbIII that we have studied previously,27,28 the magnitude of the anisotropic exchange is comparable for the {Er2} dimetallics, while the symmetric {Yb2} species 2 exhibits far weaker exchange coupling than [H2Q][Yb2(Q)4(NO3)3]·MeOH, leading to much simpler EPR spectra.Experimental section
Reagents and general procedures
All metal salts, pro-ligands and solvent were used without further purification. Lanthanides salts Ln(NO3)3·xH2O, where Ln = Er, Yb and Y and 2-methyl-8-hydroxyquinoline were purchased from Sigma Aldrich.Infrared spectroscopy, SQUID and elemental analysis
IR spectra of pure powders were recorded using a Thermo Scientific Nicolet iS5 IR Spectrometer equipped with an iD5 ATR. All magnetic measurements were performed using a Quantum Design MPMS-XL7 SQUID magnetometer equipped with a 7 T magnet. Elemental analysis of the complexes was obtained by The University of Manchester microanalytical service.X-ray crystallography
The crystal data for compound 1 were collected on an Agilent Technologies SuperNova 4-circle diffractometer with a MoKα microfocus source and an EOS CCD detector at a temperature of 150 K. The crystal data for compounds 2 and 3 were collected on a Bruker X8 Prospector 3-circle diffractometer with a CuKα mircofocus source and an APEX II detector at a temperature of 100 K.Structure solution and refinement was performed with the Shelx package47 using the program Olex2.48
The structures were solved by direct methods and completed by iterative cycles full-matrix least-squares refinement against F2. All nonhydrogen atoms were refined anisotropically. Hydrogen atoms were calculated geometrically and refined in riding mode on their respective atoms.
Synthesis
The general procedure requires 1 mmol of 2-methyl-8-hydroxyquinoline (HMeQ) added to a solution of Ln(NO3)3·xH2O (0.5 mmol) in methanol (20 mL), where Ln = Er, Yb and Y. Then the resultant solution was heated to reflux for 3 hours.29 The solution was filtered and left for slow evaporation for 1 to 3 days, resulting in yellow block-shaped crystals suitable for X-ray crystallography.The doped samples (Ln@Y2) where Ln = ErIII (1a), YbIII (2a) were prepared by mixing Ln(NO3)3·nH2O and Y(NO3)3·nH2O in a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95 or 2
95 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98 molar ratio with HMeQ in methanol according to the synthesis method above.
98 molar ratio with HMeQ in methanol according to the synthesis method above.
Electron paramagnetic resonance
EPR spectra were collected at S-, X-, K- and Q-band frequencies using Bruker EMX300 and Elexsys E580 spectrometers. Measurements were performed on lightly ground polycrystalline samples restrained in eicosane as a means of avoiding magnetic torque alignment during measurements. The spectra were collected at 5 K cooled using either a closed cycle cooling system or liquid helium cooling.Ab initio calculations
Complete active space self-consistent field spin-orbit (CASSCF-SO) calculations were performed using Molcas 8.049 on the isolated molecules using the structural solutions reported from XRD measurements. Due to the inversion symmetry of the dimetallic, only a single calculation on one of the ion sites is necessary to determine the exchange-free properties. The central ion is described using VTZP quality from the ANO-RCC library and the ion not in focus was replaced by the diamagnetic LuIII ion.50,51 The first coordination sphere atoms use VDZP quality and all other atoms use VDZ quality. The active space comprises the 4f orbitals with 11 and 13 active electrons for ErIII and YbIII, respectively. State averaged CASSCF calculations are performed for ErIII with 35 quartets and 112 doublets, with all states incorporated for SO coupling, while for YbIII only 7 doublet states are required for CASSCF and SO coupling.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank The University of Manchester and EPSRC EPR National Research Facility (NS/A000055/1) for access to the EPR spectrometers and SQUID magnetometer, and the EPSRC for funding an X-ray diffractometer (grant number EP/K039547/1). We thank Dr Jim Raftery for assistance with X-ray crystallography. M. J. G. thanks The University of Manchester for a President's Doctoral Scholarship. S. A.-B. thanks the Higher Committee for Education Development in Iraq (HCED) for the award of a research scholarship. N. F. C. thanks The University of Manchester for a Presidential Fellowship, The Royal Society for a University Research Fellowship, and the European Research Council for a Starting Grant (ERC-2019-STG-851504). R. E. P. W. thanks the EPSRC for an Established Career Fellowship (EP/R011079/1) and the European Research Council for an Advanced Grant (ERC-2017-ADG-786734). This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreements no. 786734 and 851504).Notes and references
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Magnetic Relaxation Pathways in Lanthanide Single-Molecule Magnets, Nat. Chem., 2013, 5, 673–678 CrossRef CAS.
- K. A. Thiakou, V. Nastopoulos, A. Terzis, C. P. Raptopoulou and S. P. Perlepes, Di-2-Pyridyl Ketone in Lanthanide(III) Chemistry: Mononuclear and Dinuclear Erbium(III) Complexes, Polyhedron, 2006, 25, 539–549 CrossRef CAS.
- J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, Single-Molecule Magnet Behavior for an Antiferromagnetically Superexchange-Coupled Dinuclear Dysprosium(III) Complex, J. Am. Chem. Soc., 2011, 133, 5319–5328 CrossRef CAS.
- D. Aguilà, L. A. Barrios, V. Velasco, L. Arnedo, N. Aliaga-Alcalde, M. Menelaou, S. J. Teat, O. Roubeau, F. Luis and G. Aromí, Lanthanide Contraction within a Series of Asymmetric Dinuclear [Ln2] Complexes, Chem. – Eur. J., 2013, 19, 5881–5891 CrossRef.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Y. Koshihara and Y. Kaizu, Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular Magnetic Hysteresis at 60 Kelvin in Dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS.
- F. Guo, B. M. Day, Y. Chen, M. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic Hysteresis up to 80 Kelvin in a Dysprosium Metallocene Single-Molecule Magnet, Science, 2018, 362, 1400–1403 CrossRef CAS.
- K. S. Pedersen, A.-M. Ariciu, S. G. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, Toward Molecular 4f Single-Ion Magnet Qubits, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Enhancing Coherence in Molecular Spin Qubits via Atomic Clock Transitions, Nature, 2016, 531, 348–351 CrossRef CAS.
- P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Gadolinium(III) Chelates as MRI Contrast Agents: Structure, Dynamics, and Applications, Chem. Rev., 1999, 99, 2293–2352 CrossRef CAS.
- D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, Heterodimetallic [LnLn′] Lanthanide Complexes: Toward a Chemical Design of Two-Qubit Molecular Spin Quantum Gates, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef.
- D. Aguilà, V. Velasco, L. A. Barrios, J. González-Fabra, C. Bo, S. J. Teat, O. Roubeau and G. Aromí, Selective Lanthanide Distribution within a Comprehensive Series of Heterometallic [LnPr] Complexes, Inorg. Chem., 2018, 57, 8429–8439 CrossRef.
- J. Gónzalez-Fabra, N. A. G. Bandeira, V. Velasco, L. A. Barrios, D. Aguilà, S. J. Teat, O. Roubeau, C. Bo and G. Aromí, Thermodynamic Stability of Heterodimetallic [LnLn′] Complexes: Synthesis and DFT Studies, Chem. – Eur. J., 2017, 23, 5117–5125 CrossRef.
- D. Aguilà, L. A. Barrios, F. Luis, A. Repollés, O. Roubeau, S. J. Teat and G. Aromí, Synthesis and Properties of a Family of Unsymmetric Dinuclear Complexes of Ln III (Ln = Eu, Gd, Tb), Inorg. Chem., 2010, 49, 6784–6786 CrossRef.
- X. Yi, G. Calvez, C. Daiguebonne, O. Guillou and K. Bernot, Rational Organization of Lanthanide-Based SMM Dimers into Three-Dimensional Networks, Inorg. Chem., 2015, 54, 5213–5219 CrossRef CAS.
- H.-B. Xu, J. Li, L.-X. Shi and Z.-N. Chen, Sensitized Luminescence in Dinuclear Lanthanide(III) Complexes of Bridging 8-Hydroxyquinoline Derivatives with Different Electronic Properties, Dalton Trans., 2011, 40, 5549 RSC.
- R. Van Deun, P. Fias, P. Nockemann, A. Schepers, T. N. Parac-Vogt, K. Van Hecke, L. Van Meervelt and K. Binnemans, Rare-Earth Quinolinates: Infrared-Emitting Molecular Materials with a Rich Structural Chemistry, Inorg. Chem., 2004, 43, 8461–8469 CrossRef CAS.
- C. H. Chen and J. Shi, Metal Chelates as Emitting Materials for Organic Electroluminescence, Coord. Chem. Rev., 1998, 171, 161–174 CrossRef CAS.
- C. W. Tang and S. A. Vanslyke, Organic Electroluminescent Diodes, Appl. Phys. Lett., 1987, 51, 913–915 CrossRef CAS.
- M. J. Giansiracusa, S. Al-Badran, A. K. Kostopoulos, G. F. S. Whitehead, D. Collison, F. Tuna, R. E. P. Winpenny and N. F. Chilton, A Large Barrier Single-Molecule Magnet without Magnetic Memory, Dalton Trans., 2019, 48, 10795–10798 RSC.
- G. B. Deacon, C. M. Forsyth, P. C. Junk and A. Urbatsch, Syntheses at Elevated Temperature and Structures of Lanthanoid/Alkaline Earth Heterobimetallic Derivatives of 2-Methyl-8-Hydroxyquinoline, Eur. J. Inorg. Chem., 2010, 3, 2787–2797 CrossRef.
- G. B. Deacon, C. M. Forsyth, O. Gazukin, P. C. Junk, G. Meyer, J. Sierau and D. R. Turner, An Unexpected Coupling Reaction of 8-Quinolinolate at Elevated Temperature, Aust. J. Chem., 2014, 67, 1251–1256 CrossRef CAS.
- G. B. Deacon, C. M. Forsyth, P. C. Junk and S. G. Leary, A Rare Earth Alloy as a Synthetic Reagent: Contrasting Homometallic Rare Earth and Heterobimetallic Outcomes, New J. Chem., 2006, 30, 592–596 RSC.
- G. B. Deacon, P. C. Junk, S. G. Leary and A. Urbatsch, Expanding the Series of [RE2Ca(OQ)8] Structures: New Heterobimetallic Rare Earth/Alkaline Earth 8-Quinolinolate Complexes, Z. Anorg. Allg. Chem., 2012, 638, 2001–2007 CrossRef CAS.
- S. G. Leary, G. B. Deacon and P. C. Junk, The Synthesis of a Homoleptic Lanthanoid Complex of the 8-Quinolinolate Ion Directly from the Metal, Z. Anorg. Allg. Chem., 2005, 631, 2647–2650 CrossRef CAS.
- G. B. Deacon, T. Dierkes, M. Hübner, P. C. Junk, Y. Lorenz and A. Urbatsch, Alkali Metal/Lanthanoid Heterobimetallic Complexes of 8-Hydroxyquinolines Accessed by Pseudo-Solid-State Reactions, Eur. J. Inorg. Chem., 2011, 4338–4348 CrossRef CAS.
- M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren, S. Carretta, T. Guidi, E. J. L. McInnes, R. E. P. Winpenny and N. F. Chilton, Measurement of Magnetic Exchange in Asymmetric Lanthanide Dimetallics: Toward a Transferable Theoretical Framework, J. Am. Chem. Soc., 2018, 140, 2504–2513 CrossRef CAS.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Direct Measurement of Dysprosium(III)⋯dysprosium(III) Interactions in a Single-Molecule Magnet, Nat. Commun., 2014, 5, 5243 CrossRef CAS.
- F. Yang, Q. Zhou, G. Zeng, G. Li, L. Gao, Z. Shi and S. Feng, Anion Effects on the Structures and Magnetic Properties of Binuclear Lanthanide Single-Molecule Magnets, Dalton Trans., 2014, 43, 1238–1245 RSC.
- L. Mandal, S. Biswas, G. Cosquer, Y. Shen and M. Yamashita, Anion-Driven Structures and SMM Behavior of Dinuclear Terbium and Ytterbium Complexes, Dalton Trans., 2018, 47, 17493–17499 RSC.
- P. P. Hallmen, H. J. Werner, D. Kats, S. Lenz, G. Rauhut, H. Stoll and J. Van Slageren, Toward Fast and Accurate: Ab Initio Calculation of Magnetic Exchange in Polynuclear Lanthanide Complexes, Phys. Chem. Chem. Phys., 2019, 21, 9769–9778 RSC.
- A. Ruiz-Martínez, D. Casanova and S. Alvarez, Polyhedral Structures with an Odd Number of Vertices: Nine-Coordinate Metal Compounds, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef.
- P. Llunell, M. Casanova, D. Cirera, J. Bofill, J. M. Alemany and D. Alvarez, S. Pinsky and M. Avnir, SHAPE 2.1, Universitat de Barcelona and The Hebrew University of Jerusalem, Barcelona and Jerusalem, 2003 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A Powerful New Program for the Analysis of Anisotropic Monomeric and Exchange-Coupled Polynuclear d- and f-Block Complexes, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS.
- J. Luzon and R. Sessoli, Lanthanides in Molecular Magnetism: So Fascinating, so Challenging, Dalton Trans., 2012, 41, 13556–13567 RSC.
- Y. Fang, M. X. Xu, Y. C. Hui, H. L. Sun, X. Yan and S. Da Jiang, Determination of the Magnetic Principal Axes of a Dysprosium Complex with Slow Relaxation on a Single Crystal, J. Magn. Magn. Mater., 2019, 490, 165475 CrossRef CAS.
- T. T. da Cunha, J. Jung, M. E. Boulon, G. Campo, F. Pointillart, C. L. M. Pereira, B. Le Guennic, O. Cador, K. Bernot, F. Pineider, S. Golhen and L. Ouahab, Magnetic Poles Determinations and Robustness of Memory Effect upon Solubilization in a DyIII-Based Single Ion Magnet, J. Am. Chem. Soc., 2013, 135, 16332–16335 CrossRef CAS.
- K. Qian, J. J. Baldoví, S. Da Jiang, A. Gaita-Ariño, Y. Q. Zhang, J. Overgaard, B. W. Wang, E. Coronado and S. Gao, Does the Thermal Evolution of Molecular Structures Critically Affect the Magnetic Anisotropy?, Chem. Sci., 2015, 6, 4587–4593 RSC.
- K. Bernot, J. Luzon, L. Bogani, M. Etienne, C. Sangregorio, M. Shanmugam, A. Caneschi, R. Sessoli and D. Gatteschi, Magnetic Anisotropy of Dysprosium(III) in a Low-Symmetry Environment: A Theoretical and Experimental Investigation, J. Am. Chem. Soc., 2009, 131, 5573–5579 CrossRef CAS.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Magnetic Anisotropy in a Dysprosium/DOTA Single-Molecule Magnet: Beyond Simple Magneto-Structural Correlations, Angew. Chem., 2012, 124, 1638–1642 CrossRef.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, An Electrostatic Model for the Determination of Magnetic Anisotropy in Dysprosium Complexes, Nat. Commun., 2013, 4, 2551 CrossRef.
- M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Magnetic Anisotropy and Spin-Parity Effect Along the Series of Lanthanide Complexes with DOTA, Angew. Chem., Int. Ed., 2013, 52, 350–354 CrossRef CAS.
- M. Perfetti, G. Cucinotta, M. E. Boulon, F. ElHallak, S. Gao and R. Sessoli, Angular-Resolved Magnetometry beyond Triclinic Crystals Part II: Torque Magnetometry of Cp*ErCOT Single-Molecule Magnets, Chem. – Eur. J., 2014, 20, 14051–14056 CrossRef CAS.
- S. Stoll and A. Schweiger, EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS.
- R. G. Denning, J. Harmer, J. C. Green and M. Irwin, Covalency in the 4f Shell of Tris-Cyclopentadienyl Ytterbium (YbCp3)-A Spectroscopic Evaluation, J. Am. Chem. Soc., 2011, 133, 20644–20660 CrossRef CAS.
- J. Sievers, Asphericity of 4f-Shells in Their Hund's Rule Ground States, Z. Phys. B: Condens. Matter, 1982, 45, 289–296 CrossRef CAS.
- G. M. Sheldrick, A Short History of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: A Complete Structure Solution, Refinement and Analysis Program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations across the Periodic Table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS.
- B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P. O. Widmark, Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Characterisation, EPR, CASSCF and SQUID data. CCDC 2015503–2015505. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0qi00854k |
| ‡ These two authors contributed equally. |
| This journal is © the Partner Organisations 2020 |