Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental signature of a topological quantum dot
Marie S.
Rider
*a,
Maria
Sokolikova
 b,
Stephen M.
Hanham
b,
Stephen M.
Hanham
 bc,
Miguel
Navarro-Cía
bc,
Miguel
Navarro-Cía
 d,
Peter D.
Haynes
d,
Peter D.
Haynes
 b,
Derek K. K.
Lee
a,
Maddalena
Daniele
e,
Mariangela
Cestelli Guidi
f,
Cecilia
Mattevi
b,
Derek K. K.
Lee
a,
Maddalena
Daniele
e,
Mariangela
Cestelli Guidi
f,
Cecilia
Mattevi
 b,
Stefano
Lupi
e and
Vincenzo
Giannini
b,
Stefano
Lupi
e and
Vincenzo
Giannini
 g
g
aThe Blackett Laboratory, Imperial College London, London SW7 2AZ, UK. E-mail: marie.rider@ic.ac.uk
bDepartment of Materials, Imperial College London, London SW7 2AZ, UK
cDepartment of Electronic, Electrical and Systems Engineering, University of Birmingham, Birmingham B15 2TT, UK
dSchool of Physics and Astronomy, University of Birmingham, Birmingham B15 2TT, UK
eINFN and Department of Physics, Sapienza University of Rome, Piazzale A. Moro 2, 00185 Rome, Italy
fINFN-LNF, Via Enrico Fermi 40, 00444 Frascati (Roma), Italy
gInstituto de Estructura de la Materia (IEM-CSIC), Consejo Superior de Investigaciones Científicas, Serrano 121, 28006 Madrid, Spain Web: http://www.GianniniLab.com
First published on 4th November 2020
Abstract
Topological insulator nanoparticles (TINPs) host topologically protected Dirac surface states, just like their bulk counterparts. For TINPs of radius <100 nm, quantum confinement on the surface results in the discretization of the Dirac cone. This system of discrete energy levels is referred to as a topological quantum dot (TQD) with energy level spacing on the order of Terahertz (THz), which is tunable with material-type and particle size. The presence of these discretized energy levels in turn leads to a new electron-mediated phonon-light coupling in the THz range, and the resulting mode can be observed in the absorption cross-section of the TINPs. We present the first experimental evidence of this new quantum phenomenon in Bi2Te3 topological quantum dots, remarkably observed at room temperature.
Topological nanophotonics is an emerging discipline that aims to control light at the nanoscale using topological states.1 Topological insulator nanoparticles (TINPs) provide an excellent route towards this goal, and so understanding and experimentally demonstrating how they interact with light is of paramount importance.
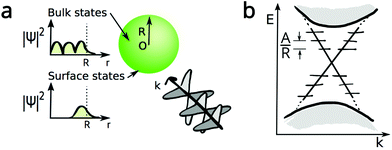
Topological insulators (TIs) are 3D materials which are insulating in the bulk but host topologically protected, conducting surface states.2–5 These surface states display a linear dispersion relation, seen as a Dirac cone which bridges the bulk band gap. The Dirac cone can only be opened by breaking time-reversal symmetry, making these states remarkably robust to perturbations such as material defects and stray (non-magnetic) fields. These surface states also do not exhibit back scattering.
In a bulk sample, only a small number of atoms in the material contribute to surface state behaviour and so topological effects are notoriously weak. Nanoscale structures have an enhanced surface area to bulk ratio, and a larger proportion of atoms participate in the surface physics. This results in a pronounced topological contribution to the electronic and optical properties of the system. Pioneering theoretical work6,7 has studied spherical topological insulator particles. Spherical TINPs have a maximal surface to volume ratio whilst still maintaining a true 3D ‘bulk’. These finite systems exhibit the same level of topological protection as their continuous counterparts,8 but quantum confinement results in the discretization of the surface state energies, with energy spacing on the order of Terahertz (THz). This has exciting implications for both the electronic and optical properties of the nanostructures9–14 and recent theoretical work has also studied the optical properties of hybrid systems coupling the energy levels of TINPs with quantum dots and emitters.15,16 The THz regime (∼0.1–10 THz) is notoriously difficult to access with plasmonic or purely photonic technologies, so investigation of TINPs and their hybrid systems could lead to important advancements in the development of THz sensors, lasers and waveguides.1,17,18
Some nanostructures (such as nanoribbons and thin films19) can already be reliably produced, but equiaxed (e.g. spherical or rhombohedral) TINPs have so far proved technically challenging.20,21 This means that their optical properties have received relatively little experimental attention. The identification and classification of modes in the optical spectra of other TI nanostructure samples (such as nanosheets and nanoplates) has been a lively endeavour, oftentimes leading to contradictory conclusions.22–28 Unexpected peaks observed with Raman and optical spectroscopy have been attributed to multiple different origins, such as surface oxidation, phonon confinement effects, unverified topological effects or simply left unclassified. The presence of discretized energy levels in TINPs leads to a new electron-mediated phonon–light coupling in the Terahertz (THz) range. This work presents evidence of a new, purely topological contribution to the spectra of TINPs.
In the case of small (5 < R/nm < 100) TINPs the continuous Dirac cone becomes discretized due to finite size effects, giving a set of discrete energy levels much like those in a quantum dot.12,13 A schematic of a spherical TINP and its bulk and surface states is given in Fig. 1a. These energy levels are equally spaced, with energies increasing away from the Γ-point in integer values of A/R (as illustrated schematically in Fig. 1b). A = 2.0 eV Å is a material-dependent quantity, given by the matrix element of momentum calculated for a four band model Hamiltonian of Bi2Te3 and averaged over three axes, calculated by a density functional theory approach and taken from Liu et al.,29 discussed in more detail in Appendix A. When irradiated with THz (1 THz = 33 cm−1 = 4 meV) light, a transition between two of these topological, delocalised surface states occurs within the same frequency range as a bulk phonon excitation, resulting in a strong Fano resonance, referred to as the surface topological particle (SToP) mode.12 This is a purely quantum mechanical feature of the system, and the asymmetric profile of this resonance creates a point of zero-absorption when the energy spacing of the surface states is matched by the incident light. This means that the excitation of a single electron occupying a topological surface state can shield the bulk from the absorption of incoming light. This mode has been theoretically predicted but had not been experimentally observed until the present work. Light–matter interactions in nanoparticles requiring a quantum mechanical approach have attracted much attention in quantum plasmonics in recent years,30 and TINPs made of materials such as Bi2Te3 present a promising extension of this field.
Bismuth telluride nanoparticle synthesis
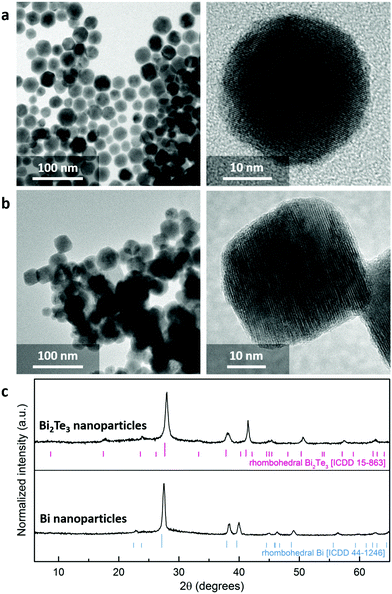
Bi2Te3 has a layered crystal structure with quintuple covalently-bonded Te–Bi–Te–Bi–Te layers stacked along the c-axis and therefore can be easily produced in the form of two-dimensional sheets via physical31 or wet-chemical methods.32 In order to suppress preferential formation of anisotropic two-dimensional structures unavoidable in the direct solution-phase synthesis due to the high reactivity of Bi salts, spherical Bi2Te3 nanoparticles were synthesised using a two-stage reaction analogously to ref. 20. Briefly, the growth involved the reduction of Bi ions by organic primary amine in an inert atmosphere leading to the formation of spherical Bi nanoparticles and followed by tellurisation of the produced Bi nanospheres in trioctylphosphine telluride solution. Transmission electron microscopy (TEM) images shown in Fig. 2a and b are representative images of the ensembles of Bi and Bi2Te3 nanoparticles respectively. The Bi nanoparticles are nearly spherical with radius of 14.4 ± 2.3 nm, while upon tellurisation the shape of Bi2Te3 nanoparticles changes to slightly rhombohedral with a larger average radius of 17.5 nm (standard deviation 1.8 nm) due to the inclusion of tellurium species. Powder X-ray diffraction (XRD) patterns of both intermediate Bi and final Bi2Te3 nanoparticles clearly demonstrate a phase change accompanied by a significant shift of the diffraction peaks to the higher angles corresponding to smaller interplanar distances of the rhombohedral Bi2Te3 lattice (Fig. 2c). A more detailed experimental method is provided in Appendix B.Theoretical framework
In the theoretical treatment of a TINP irradiated with THz light of frequency ν, we treat the bulk behaviour classically with a bulk dielectric function and the surface states are treated quantum mechanically. We focus on Bi2Te3 but the following analytic results are valid for other materials within the Bi2Te3 family given the correct parameter substitutions. We follow the theory method given in ref. 12. We work in the limit in which the particle radius R is much smaller than the wavelength of incoming light, R ≪ λ. The bulk dielectric function of Bi2Te3 is a rank 2 tensor and to treat the system analytically we take ε(ν) as a diagonal matrix with principal components [ε⊥(ν), ε⊥(ν), ε∥(ν)] and all other components equal to 0. ε∥(ν) gives the dielectric function along the c-axis of the material, while ε⊥(ν) is the dielectric function in both axes perpendicular to the c-axis. Here, we assume that each component can be described through a Lorentzian shape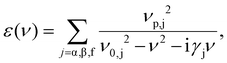 | (1) |
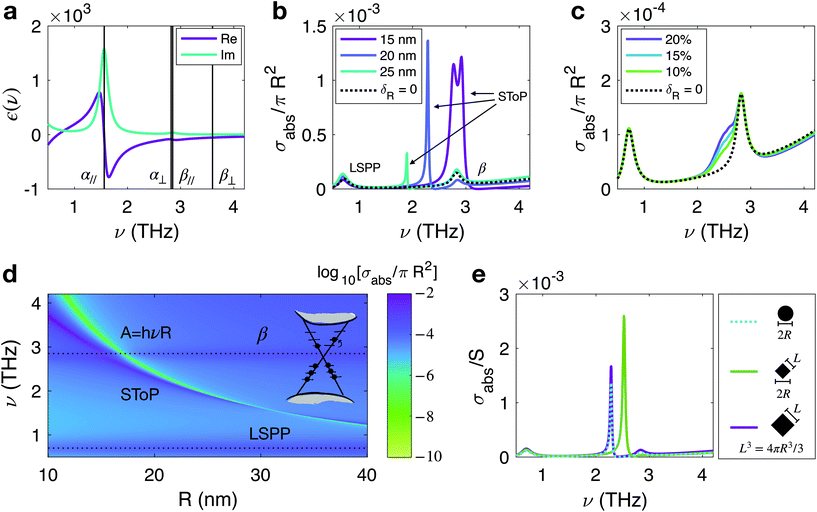 | ||
Fig. 3 Theoretical SToP results: (a) The real (purple) and imaginary (green) components of Bi2Te3 bulk dielectric function ε∥(v), for incident light parallel to the c-axis using parameters fitted to data in ref. 33, presented in Table 1. The positions of the α and β phonon frequencies are annotated for both k∥c-axis and k⊥c-axis incoming light (denoted α∥, β∥, α⊥, and β⊥ respectively). (b) Absorption cross-section of a TINP with EF = A/R, R = (15, 20, 25) nm and a TINP of radius 15 nm for which δR = 0. The LSPP and β mode are visible and labelled, whilst the α mode is over-damped and thus not seen in the theoretically calculated absorption cross-section. Increased TINP radius results in a lower frequency SToP mode peak (also labelled). For R = 15 nm, the SToP mode and β modes overlap and a split peak is seen. For each SToP mode there is a point of zero absorption which occurs to the right of the peak. (c) For an ensemble of particles with a Gaussian distribution of radii (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) = 17.5 nm and standard deviation 1.8 nm) and in which only (10, 15, 20)% of TINPs show a SToP mode, the peak height is reduced and no longer displays a point of zero absorption. (d) Absorption cross-section varying with R and v. The bulk LSPP and β phonon positions remain constant for varying radius size, and the line of zero-absorption is annotated (A = hvR). (e) Comparison of absorption cross-section for nanoparticles of varying geometry and size. Absorption cross-section of sphere (dotted blue) with R = 20 nm, projection S = πR2. Absorption cross-section for a cube with diagonal length 2R = 40 nm (green), such that L = 28.2 nm, and projection S = L2. Absorption cross-section of cube of length L = 32.2 nm (purple) and S = L2, with volume V = L = 4πReff3/3 such that effective radius Reff = 20 nm. = 17.5 nm and standard deviation 1.8 nm) and in which only (10, 15, 20)% of TINPs show a SToP mode, the peak height is reduced and no longer displays a point of zero absorption. (d) Absorption cross-section varying with R and v. The bulk LSPP and β phonon positions remain constant for varying radius size, and the line of zero-absorption is annotated (A = hvR). (e) Comparison of absorption cross-section for nanoparticles of varying geometry and size. Absorption cross-section of sphere (dotted blue) with R = 20 nm, projection S = πR2. Absorption cross-section for a cube with diagonal length 2R = 40 nm (green), such that L = 28.2 nm, and projection S = L2. Absorption cross-section of cube of length L = 32.2 nm (purple) and S = L2, with volume V = L = 4πReff3/3 such that effective radius Reff = 20 nm. | ||
| ν p,j (THZ) | ν 0,j (THZ) | γ j (THZ) | |
|---|---|---|---|
| α | 21 | 1.56 | 0.18 |
| β | 4 | 2.85 | 0.2 |
| f | 11 | 0 | 0.24 |
The absorption cross-section for a spherical particle suspended in a transparent material (in our case, mineral oil in order to preserve the quality of the particles, for which noil = 1.47 and εoil = noil2 = 2.16, (ref. 35) is calculated from the imaginary component of the particle polarizability α0, such that 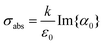 and is given by
and is given by
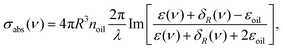 | (2) |
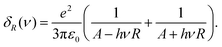 | (3) |
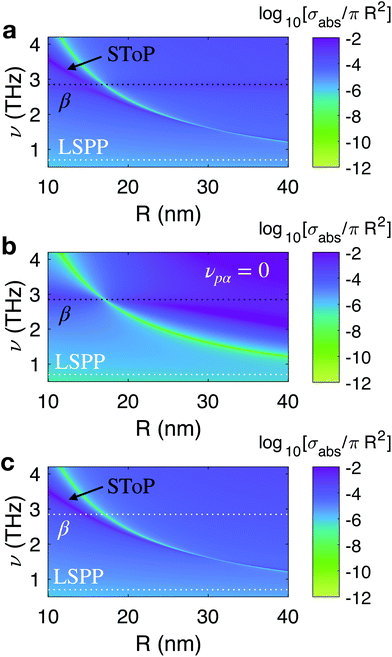
For a given Fermi level, δR varies only with R and ν. In Fig. 3b, we plot the theoretically expected absorption cross-sections of TINPs with EF = A/R and radii 15, 20 and 25 nm respectively, and the topologically trivial case where δR = 0. Each cross-section with a topological contribution has a characteristic shape of three peaks, corresponding to the β phonon mode, a localised surface plasmon-polariton (LSPP) mode, and the SToP mode. A point of zero absorption can be seen for each SToP mode, at which a single electron in a Dirac state shields the bulk from absorbing incoming light. The LSPP and β modes are bulk contributions and as such, their positions do not change with particle size. The SToP peak position and point of zero-absorption do vary with R. As the particle size varies, the spacing between discretized surface state energies varies as ∼1/R. This in turn changes the frequency at which the particle polarizability is modified when a surface state is excited, as described by δR(ν) in eqn (3). This in turn leads to a R-dependence of the absorption cross-section of the nanoparticle. As particle size is reduced, the frequency of surface state excitations increases, and thus the SToP mode peak and point of zero-absorption both shift to higher frequencies. For particles of approximately R = 15 nm, the SToP mode appears on top of the β phonon mode, resulting in a double peak structure of broader linewidth. The R and ν dependence of the absorption cross-section is illustrated in Fig. 3d. A study of how the absorption cross-section is modified by isolating the various phonon contributions in the dielectric function is given in the Appendix D.
The synthesised Bi2Te3 nanoparticles discussed in this work are rhombohedral, however their topological properties are well-approximated by those of spherical particles, due to the robustness of topological states against surface deformation. This is demonstrated in ref. 6 and 12 in which it is shown that the discrete energy levels of TI spheres and cubes of equal volume converge for particles of radius R > 10 nm. This means that the topological contribution to the absorption cross-section is also the same for particles of equal volume. If a cube of volume V were to be deformed to a sphere, it would have an effective radius Reff, such that V = 4πReff3/3. This value of Reff can then be used in eqn (3) to calculate the topological contribution to the absorption cross-section, δR. The absorption cross-section of a cube can be calculated analytically,36 with the topological contribution described as above. In Fig. 3e we plot the absorption cross-sections of a sphere with R = 20 nm (dotted blue), a cube with diagonal length 2R (green), such that L = 28.3 nm and cube with Reff = 20 nm (purple), such that it has the same volume as the sphere. The cross-sections are normalised by the projection of each nanostructure, i.e. S = πR2 for the sphere and S = L2 for the cubes. The qualitative results for each nanostructure are very similar, with the sphere and cube of equal volume demonstrating a SToP peak and point of zero-absorption at the same position. The cube with diagonal length equal to the diameter of the sphere has a slightly smaller effective radius, and thus presents a SToP mode and point of zero-absorption shifted to a slightly higher frequency. As the rhombohedral nanoparticles in our experiment fall between the two limits of a sphere and a cube, we conclude that approximating the rhombohedral nanoparticles as spherical should give a qualitatively good result.
So far we have discussed the optical properties of a single TINP, which is representative of an ensemble of non-interacting particles of equal radius, normalised to the number of TINPs. However in our experimental sample, we have a partial agglomerate of nanoparticles, and the nanoparticles have a range of radii. Before measurements were taken, the sample was agitated to separate the nanoparticles. It is however inevitable that some particles will remain as an agglomerate. We would expect this agglomerate to contribute to the bulk properties of the absorption-cross section, but lose the quantum confinement effects expected from small, separate nanoparticles. Any topological peak from such a large mass of material would occur at such a low frequency as to not be measured in our experiment. For example, a particle of R = 100 nm would be expected to exhibit a SToP mode peak at approximately 0.45 THz with a greatly suppressed amplitude. This is outside of the frequency range of our measured data. Due to uncertainty in the Fermi level and orientation of each TINP in relation to the incoming light, it can be assumed that while all TINPs contribute to the bulk properties of the absorption cross-section, only a small percentage will give a topological contribution. Fig. 3c illustrates the theoretically calculated absorption cross-section of an ensemble of TINPs of mean radius 17.5 nm and standard deviation 1.8 nm (values taken from analysis of TEM images of the experimental sample), with a varying percentage contributing to the topological property. The peak height is greatly suppressed and a point of zero-absorption is no longer observed.
Results
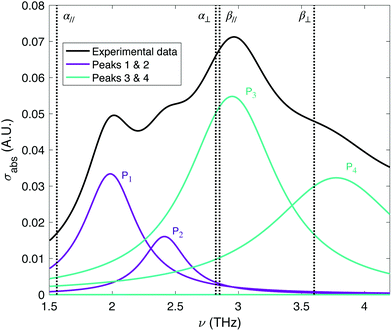
In Fig. 4, we show the experimental absorption cross-section (solid black line) of Bi2Te3 TINPs suspended in mineral oil, measured at 300 K. The vertical dotted lines denote the four phonon frequencies (α∥, β∥, α⊥, β⊥) corresponding to the two bulk dielectric functions ε∥ and ε⊥ respectively. We have performed a Lorentzian decomposition using four Lorentz peaks, with fit values given in Table 2. Using four peaks (which we label P1–P4) yields a fitting error of 0.23%, whereas using three or five peaks results in an error of 2.3% or 3.4% respectively. We assign P3 and P4 to the β∥ and β⊥ phonons respectively. α phonons are typically under-damped in bulk samples and so not observed in the theoretical calculations of the absorption cross-section using the bulk dielectric function (as demonstrated in Fig. 3b and c). This can be understood by studying the bulk dielectric function for Bi2Te3 depicted in Fig. 3a, where the very large value of Im[ε(ν)] at the α phonon frequency will result in a very small contribution to σabs (given in eqn (2)) at this frequency. However, finite size effects may reduce damping of transverse modes, resulting in an increased amplitude which may be visible in the absorption cross-section. So, it is possible that the α⊥ phonon also slightly contributes to the amplitude of P3.| P1 | P2 | P3 | P4 | |
|---|---|---|---|---|
| Peak position (THz) | 1.98 | 2.41 | 2.95 | 3.77 |
| Peak width (THz) | 0.51 | 0.42 | 0.86 | 1.26 |
P1 and P2 do not appear to relate to any expected bulk modes. We rule out oxidation effects as the sample was kept in chloroform, and exchanged for mineral oil for THz measurements. Samples typically show oxidation effects on the time-scale of days,25 which is not the case for our sample. We note that P2 appears at a frequency commensurate with the SToP mode peak predicted for an ensemble of varying radius as demonstrated in Fig. 3c. While the short height of the SToP mode peak is partially explained by the assumption that very few particles contribute to the topological properties of the sample, we also note that our theory is modelled at zero temperature, whereas the experiment operates at room temperature (∼6 THz), where the probability of finding a level empty in our system is low. Temperature smearing will result in the modes seen experimentally being less visible than those seen in theory. This could be remedied by studying a TI with a bigger band gap and/or smaller particles. It is possible that the presence of two new non-bulk modes (P1 and P2) is due to SToP modes resulting from both the α∥ and α⊥ phonons.
The observation of two unexpected peaks at frequencies which do not relate to expected bulk modes allows us to conclude that at least one of the peaks is likely topological in origin. We conclude from this experimental comparison with the theory model that we have observed the SToP mode in Bi2Te3 nanoparticles, which was theoretically predicted in ref. 12.
Author contributions
V.G. and M.S.R. proposed the initial idea. M.S. and C.M. synthesized the nanoparticles and performed the X-ray characterization. S.L., M.C.G., and M.D performed the THz measurements. S.M.H. and M.N.-C. together with M.S. and C.M. worked on how to stabilize the nanoparticles in oil. S.M.H. and M.N.-C. also performed some initial THz measurement. P.D.H., D.L., V.G., and M.S.R. discussed the theoretical model as well as the numerical implementation. M.S.R. performed the simulations and wrote the first draft. All authors discussed the results and contributed to the manuscript. V.G. supervised the project.Appendix A: Four band model Hamiltonian
The important topological physics occurs near the Γ-point, allowing us to use k·p perturbation theory to expand about the Γ-point and write down a low-energy, 4-band effective Hamiltonian,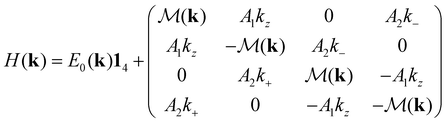 | (4) |
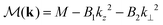 . The parameters (A1, A2, B1, B2, C, D1, D2, M) in this effective model can be determined by fitting the energy spectrum of the Hamiltonian to that of ab initio calculations,37 with the results for Bi2(SexTe1−x)3 presented by Liu et al.29 In the theory model used in this work, the crystal structure is taken to be isotropic, such that
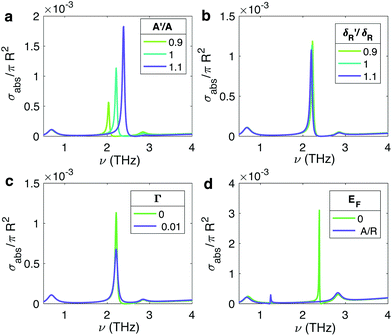
. The parameters (A1, A2, B1, B2, C, D1, D2, M) in this effective model can be determined by fitting the energy spectrum of the Hamiltonian to that of ab initio calculations,37 with the results for Bi2(SexTe1−x)3 presented by Liu et al.29 In the theory model used in this work, the crystal structure is taken to be isotropic, such that 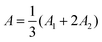 . Fig. 5a shows how the theoretically calculated absorption cross-section varies with uncertainty in A. Shifting A → A′ by 10% shifts the position of the SToP peak by <10%. Fig. 5b illustrates that modifying the magnitude of the topological contribution to the particle polarizability δR(ν) (by multiplying by a constant coefficient δcoeff), has little effect on the position of the SToP peak. Fig. 5c shows that when a finite lifetime of excited surface states is considered (by detracting a small, complex component iΓA from the denominator of all δR(ν) terms), the height of the SToP mode peak becomes smaller (for a particle of R = 20 nm and Γ = 0.01, the height of the SToP mode peak reduces by ∼45%) and the position remains the same.
. Fig. 5a shows how the theoretically calculated absorption cross-section varies with uncertainty in A. Shifting A → A′ by 10% shifts the position of the SToP peak by <10%. Fig. 5b illustrates that modifying the magnitude of the topological contribution to the particle polarizability δR(ν) (by multiplying by a constant coefficient δcoeff), has little effect on the position of the SToP peak. Fig. 5c shows that when a finite lifetime of excited surface states is considered (by detracting a small, complex component iΓA from the denominator of all δR(ν) terms), the height of the SToP mode peak becomes smaller (for a particle of R = 20 nm and Γ = 0.01, the height of the SToP mode peak reduces by ∼45%) and the position remains the same.
Appendix B: Experimental method – further details of synthesis and THz measurements
In a standard synthesis, 114 mg of bismuth acetate (Bi(CH3COO)3, 99% Aldrich) and 3.5 mL of 1-dodecanethiol (DDT, 98% Aldrich) were mixed in a three-neck flask and heated to 45 °C under vacuum and kept at this temperature until a transparent pale-yellow solution is formed. Then the flask was flashed with nitrogen and heated to 60 °C and 6.5 mL of oleylamine (OlAm, 70%, Aldrich) was quickly added. After 24 hours the as-prepared bismuth nanoparticles were used without any further purification. For tellurisation 0.45 mL of 1 M trioctylphosphine telluride (TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te) was injected at 60 °C into the solution containing bismuth nanoparticles. The reaction mixture was kept at this temperature for 48 hours until complete tellurisation and then annealed at 110 °C for 8 hours in order to restore crystallinity. Thus produced Bi2Te3 nanoparticles were washed three times with ethanol and then redispersed in chloroform. For THz measurements solvent was exchanged to mineral oil. THz measurements were been performed in transmission through a Vertex 70 V Bruker interferometer equipped with a Hg THz source, a Pyroelectric detector and a broad band high resistivity Si beamsplitter.
Te) was injected at 60 °C into the solution containing bismuth nanoparticles. The reaction mixture was kept at this temperature for 48 hours until complete tellurisation and then annealed at 110 °C for 8 hours in order to restore crystallinity. Thus produced Bi2Te3 nanoparticles were washed three times with ethanol and then redispersed in chloroform. For THz measurements solvent was exchanged to mineral oil. THz measurements were been performed in transmission through a Vertex 70 V Bruker interferometer equipped with a Hg THz source, a Pyroelectric detector and a broad band high resistivity Si beamsplitter.
Appendix C: Modifying the Fermi level
For −A/R < EF < A/R, the dominant transition is between energy levels directly below and above the Fermi-level, of energy 2A/R.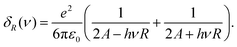 | (5) |
Fig. 5d shows σabs/πR2 for a particle R = 40 nm, at the two Fermi levels EF = A/R and EF = 0. While the bulk modes remain in the same positions, we see a shift in the SToP mode peaks. The behaviour of the SToP mode and zero absorption trough can be seen in Fig. 3e. Although we do not know the precise Fermi level of each TINP in the sample, for particles whose Fermi level resides in the band gap (and thus contribute to the SToP mode peak in the absorption cross-section) it is most likely that transitions are occurring between energy levels separated by A/R rather than 2A/R.
Appendix D: Modifying theory parameters
The δR term in eqn (3) has no dependence on the dielectric function of either the topological material or the mineral oil, but is affected by the A value. The peak in absorption due to the topological term will experience a shift dependent on which material is being used. For example, the SToP peak for a R = 20 nm TINP made of Bi2Te3 and Fermi level EF = A/R will occur at 2.21 THz, whereas for a Bi2Se3 TINP of the same radius (with A = 3.0 eV Å,29 as studied in the original work by Siroki et al.12) the peak will occur at 3.1 THz.In order to demonstrate how the various contributions to the dielectric function manifest in the absorption cross-section, we perform a study in which we artificially remove first the α phonon and then the β phonon contribution from the theoretical calculation. For clarity, Fig. 6a gives the absorption cross-section as a function of ν and R with the LSPP contribution artifically removed (such that νp,f = 0). The position of the removed mode is given in white, while the β phonon peak, SToP mode and trough of zero absorption can be clearly seen. In Fig. 6b, the α phonon contribution is also removed, (such that νp,f = νp,α = 0. The trough of zero absorption can still be seen, but the SToP mode peak is no longer present. This confirms that the SToP mode is mediated by the α phonon. This is further confirmed in Fig. 6c, in which both the LSPP and β phonon contributions are removed (νp,f = νp,β = 0) and the SToP mode is still present.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. S. would like to acknowledge the President's PhD Scholarship programme at Imperial College London for financial support. C. M. would like to acknowledge the EPSRC award EP/M022250/1, and the award of a Royal Society University Research Fellowship by the UK Royal Society. M. S. R. is supported through a studentship in the Centre for Doctoral Training on Theory and Simulation of Materials at Imperial College London funded by EPSRC Grant No. EP/L015579/1. M. N.-C. acknowledges support from the University of Birmingham (Birmingham Fellowship) and the EPSRC (grant no. EP/S018395/1). V. G. acknowledges the Spanish Ministerio de Economia y Competitividad for financial support through the grant NANOTOPO (FIS2017-91413-EXP), and also the Ministerio de Ciencia, Innovación y Universidades through the grant MELODIA (PGC2018-095777-B-C21).References
- M. S. Rider, S. J. Palmer, S. R. Pocock, X. Xiao, P. Arroyo Huidobro and V. Giannini, A perspective on topological nanophotonics: Current status and future challenges, J. Appl. Phys., 2019, 125(12), 120901 CrossRef.
- L. Fu, C. L. Kane and E. J. Mele, Topological insulators in three dimensions, Phys. Rev. Lett., 2007, 98(10), 106803 CrossRef.
- Y. L. Chen, J. G. Analytis, J.-H. Chu, Z. Liu, S.-K. Mo, X.-L. Qi, H. J. Zhang, D. H. Lu, Xi Dai and Z. Fang, et al., Experimental realization of a three-dimensional topological insulator, Bi2Te3, Science, 2009, 325(5937), 178–181 CrossRef CAS.
- J. E. Moore, The birth of topological insulators, Nature, 2010, 464(7286), 194 CrossRef CAS.
- T. Stauber, G. Gómez-Santos and L. Brey, Plasmonics in topological insulators: Spin-charge separation, the influence of the inversion layer, and phonon-plasmon coupling, ACS Photonics, 2017, 4(12), 2978–2988 CrossRef CAS.
- K.-I. Imura, Y. Yoshimura, Y. Takane and T. Fukui, Spherical topological insulator, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(23), 235119 CrossRef.
- F. Zhang, C. L. Kane and E. J. Mele, Surface states of topological insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(8), 081303 CrossRef.
- G. Siroki, P. D. Haynes, D. K. K. Lee and V. Giannini, Protection of surface states in topological nanoparticles, Phys. Rev. Mater., 2017, 1, 024201 CrossRef.
- H.-Z. Lu, W.-Y. Shan, W. Yao, Q. Niu and S.-Q. Shen, Massive Dirac fermions and spin physics in an ultrathin film of topological insulator, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(11), 115407 CrossRef.
- H. P. Paudel and M. N. Leuenberger, Three-dimensional topological insulator quantum dot for optically controlled quantum memory and quantum computing, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(8), 085316 CrossRef.
- P. Di Pietro, M. Ortolani, O. Limaj, A. Di Gaspare, V. Giliberti, F. Giorgianni, M. Brahlek, N. Bansal, N. Koirala and S. Oh, et al., Observation of Dirac plasmons in a topological insulator, Nat. Nanotechnol., 2013, 8(8), 556–560 CrossRef CAS.
- G. Siroki, D. K. K. Lee, P. D. Haynes and V. Giannini, Single-electron induced surface plasmons on a topological nanoparticle, Nat. Commun., 2016, 7, 12375 CrossRef CAS.
- L. Gioia, M. Christie, U. Zülicke, M. Governale and A. Sneyd, Spherical topological insulator nanoparticles: Quantum size effects and optical transitions, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100(20), 205417 CrossRef CAS.
- P. Di Pietro, N. Adhlakha, F. Piccirilli, A. Di Gaspare, J. Moon, S. Oh, S. Di Mitri, S. Spampinati, A. Perucchi and S. Lupi, Terahertz Tuning of Dirac Plasmons in Bi2Se3 Topological Insulator, Phys. Rev. Lett., 2020, 124(22), 226403 CrossRef CAS.
- G. D. Chatzidakis and V. Yannopapas, Strong electromagnetic coupling in dimers of topological-insulator nanoparticles and quantum emitters, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 165410 CrossRef CAS.
- L. A. Castro-Enriquez, L. F. Quezada and A. Martín-Ruiz, Optical response of a topological-insulator–quantum-dot hybrid interacting with a probe electric field, Phys. Rev. A, 2020, 102, 013720 CrossRef CAS.
- S. Atakaramians, S. Afshar, T. M. Monro and D. Abbott, Terahertz dielectric waveguides, Adv. Opt. Photonics, 2013, 5(2), 169–215 CrossRef.
- B. Ferguson and X.-C. Zhang, Materials for terahertz science and technology, Nat. Mater., 2002, 1(1), 26–33 CrossRef CAS.
- J. J. Cha, K. J. Koski and Y. Cui, Topological insulator nanostructures, Phys. Status Solidi RRL, 2013, 7(1–2), 15–25 CrossRef CAS.
- M. Scheele, N. Oeschler, K. Meier, A. Kornowski, C. Klinke and H. Weller, Synthesis and thermoelectric characterization of Bi2Te3 nanoparticles, Adv. Funct. Mater., 2009, 19(21), 3476–3483 CrossRef CAS.
- M. R. Dirmyer, J. Martin, G. S. Nolas, A. Sen and J. V. Badding, Thermal and electrical conductivity of size-tuned bismuth telluride nanoparticles, Small, 2009, 5(8), 933–937 CrossRef CAS.
- K. M. F. Shahil, M. Z. Hossain, V. Goyal and A. A. Balandin, Micro-Raman spectroscopy of mechanically exfoliated few-quintuple layers of Bi2Te3, Bi2Se3, and Sb2Te3 materials, J. Appl. Phys., 2012, 111(5), 054305 CrossRef.
- O. Caha, A. Dubroka, J. Humlicek, V. Holy, H. Steiner, M. Ul-Hassan, J. Sánchez-Barriga, O. Rader, T. Stanislavchuk and A. Sirenko, et al., Growth, structure, and electronic properties of epitaxial Bismuth Telluride topological insulator films on BaF2 (111) substrates, Cryst. Growth Des., 2013, 13(8), 3365–3373 CrossRef CAS.
- C. Wang, X. Zhu, L. Nilsson, J. Wen, G. Wang, X. Shan, Q. Zhang, S. Zhang, J. Jia and Q. Xue, In situ Raman spectroscopy of topological insulator Bi2Te3 films with varying thickness, Nano Res., 2013, 6(9), 688–692 CrossRef CAS.
- G. Jian-Hua, Q. Feng, Z. Yun, D. Hui-Yong, H. Gu-Jin, L. Xiao-Nan, Y. Guo-Lin and D. Ning, Surface oxidation properties in a topological insulator Bi2Te3 film, Chin. Phys. Lett., 2013, 30(10), 106801 CrossRef.
- H. Xu, Y. Song, Q. Gong, W. Pan, X. Wu and S. Wang, Raman spectroscopy of epitaxial topological insulator Bi2Te3 thin films on GaN substrates, Mod. Phys. Lett. B, 2015, 29(15), 1550075 CrossRef.
- X. Qi, W. Ma, X. Zhang and C. Zhang, Raman characterization and transport properties of morphology-dependent two-dimensional Bi2Te3 nanofilms, Appl. Surf. Sci., 2018, 457, 41–48 CrossRef CAS.
- I. Boulares, G. Shi, E. Kioupakis, P. Lošt’ák, C. Uher and R. Merlin, Surface phonons in the topological insulators Bi2Se3 and Bi2Te3, Solid State Commun., 2018, 271, 1–5 CrossRef CAS.
- C.-X. Liu, X.-L. Qi, H. Zhang, Xi Dai, Z. Fang and S.-C. Zhang, Model Hamiltonian for topological insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(4), 045122 CrossRef.
- J. M. Fitzgerald, P. Narang, R. V. Craster, S. A. Maier and V. Giannini, Quantum plasmonics, Proc. IEEE, 2016, 104(12), 2307–2322 CAS.
- D. Teweldebrhan, V. Goyal and A. A. Balandin, Exfoliation and characterization of Bismuth Telluride atomic quintuples and quasi-two-dimensional crystals, Nano Lett., 2010, 10(4), 1209–1218 CrossRef CAS.
- M. S. Sokolikova, P. C. Sherrell, P. Palczynski, V. L. Bemmer and C. Mattevi, Room-temperature growth of colloidal Bi2Te3 nanosheets, Chem. Commun., 2017, 53(57), 8026–8029 RSC.
- A. Dubroka, O. Caha, M. Hronček, P. Friš, M. Orlita, V. Holý, H. Steiner, G. Bauer, G. Springholz and J. Humlíček, Interband absorption edge in the topological insulators Bi2(Te1−xSex)3, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 235202 CrossRef.
- W. Richter and C. R. Becker, A Raman and far-infrared investigation of phonons in the rhombohedral V2−VI3 compounds Bi2Te3, Bi2Se3, Sb2Te3 and Bi2(Te1−xSex)3 (0 < x < 1), (Bi1−ySby)2Te3 (0 < y < 1), Phys. Status Solidi B, 1977, 84(2), 619–628 CrossRef CAS.
- M. Naftaly, Terahertz metrology, Artech House, 2015 Search PubMed.
- E. Massa, S. A. Maier and V. Giannini, An analytical approach to light scattering from small cubic and rectangular cuboidal nanoantennas, New J. Phys., 2013, 15(6), 063013 CrossRef.
- H. Zhang, C.-X. Liu, X.-L. Qi, Xi Dai, Z. Fang and S.-C. Zhang, Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface, Nat. Phys., 2009, 5(6), 438 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |