Open Access Article
Open Access ArticleEnhanced nanoparticle rejection in aligned boron nitride nanotube membranes†
Serena
Casanova
a,
Sritay
Mistry
b,
Saeed
Mazinani
a,
Matthew K.
Borg
b,
Y. M. John
Chew
a and
Davide
Mattia
 *a
*a
aDepartment of Chemical Engineering and Centre for Advanced Separations Engineering, University of Bath, BA27AY, UK. E-mail: d.mattia@bath.ac.uk
bSchool of Engineering, University of Edinburgh, EH9 3FB, UK
First published on 9th July 2020
Abstract
The rejection of particles with different charges and sizes, ranging from a few Ångstroms to tens of nanometers, is key to a wide range of industrial applications, from wastewater treatment to product purification in biotech processes. Carbon nanotubes (CNTs) have long held the promise to revolutionize filtration, with orders of magnitude higher fluxes compared to commercial membranes. CNTs, however, can only reject particles and ions wider than their internal diameter. In this work, the fabrication of aligned boron nitride nanotube (BNNT) membranes capable of rejecting nanoparticles smaller than their internal diameter is reported for the first time. This is due to a mechanism of charge-based rejection in addition to the size-based one, enabled by the BNNTs surface structure and chemistry and elucidated here using high fidelity molecular dynamics and Brownian dynamics simulations. This results in ∼40% higher rejection of the same particles by BNNT membranes than CNT ones with comparable nanotube diameter. Furthermore, since permeance is proportional to the square of the nanotubes’ diameter, using BNNT membranes with ∼30% larger nanotube diameter than a CNT membrane with comparable rejection would result in up to 70% higher permeance. These results open the way to the design of more effective nanotube membranes, capable of high particle rejection and, at the same time, high water permeance.
Introduction
Membrane filters capable of rejecting charged particles between 0.5–50 nm are crucial to a broad number of industrial applications, ranging from ion and bacteria removal in wastewater treatment,1 to catalyst retrieval in heterogeneous reactions,2 to product recovery in biotech processes.3 In commercial membranes, however, higher rejection is often associated with reduced water permeation,4 stimulating research in novel materials that could provide both. Carbon nanotubes (CNTs) showed promise, with high particle rejection5 and high pure water flux,6,7 leading to significant efforts towards developing membranes made of carbon nanotubes.8 However, in CNTs, rejection is solely based on the relative size of a particle compared to the nanotubes’ diameter,9 due to the neutral surface charge of the tubes. This necessitates the use of very narrow tubes to reject small ions, dyes and particles.10 As a result, the amount of water that can flow through these nanotubes is limited, as flux scales with the square of a tube's diameter. Attempts to functionalize the tubes’ entrance to improve rejection have been successful,5 but at the cost of reducing water transport by 20–30%.11 Molecular dynamics (MD) simulations have shown that depending on the functional groups used, the decrease in flux could be as high as up to 80%,10 thereby negating the main advantage of CNTs, i.e. their high flux. Boron nitride nanotubes (BNNTs), on the other hand, have the potential to address this limitation. Although they are iso-structural to graphitic carbon with a similar water contact angle,12,13 they have surface charges given by the different electronegativity of the constituent boron and nitrogen atoms.14,15 There is still limited literature on the flow of water through BNNTs, although molecular dynamics (MD) simulations of sub-nanometre BNNTs and CNTs have showed larger flow enhancement for the former compared to the latter.16,17 However, this superior performance was not observed in experiments through an individual tube, which reported significantly slower water flow in larger BNNTs (diameters ranging from 14 to 46 nm), compared to CNTs,18 and in mixed matrix membranes containing randomly aligned BNNTs.19 as well in MD simulations of nanotube with diameters >1 nm.20 A potential explanation for this discrepancy is that in sub-nanometre tubes alone, the energy barriers for water transport at the entrance of and through the tubes are lower for BNNTs than CNTs,16 hence, the overall transport of water through the BN tubes is faster than CNTs, as a result of different water–nanotube wall interactions. In terms of rejection, there is yet no molecular dynamics nor experimental evidence of BNNTs performance.16Here we report the fabrication of novel membranes of aligned BNNTs and provide the first experimental evidence that BNNTs reject charged particles smaller than their internal diameter, whereas CNTs do not. In addition, we also show that BNNT membranes with comparable rejection as CNT ones, have higher permeance due to the use of larger BNNTs, enabled by the charge-rejection mechanism with no requirement for surface functionalization. We anticipate our results will facilitate the design of more effective nanotube membranes, capable of high rejection and high water permeance. Furthermore, our results are of direct relevance to the emerging area of 2D membranes, where both graphene and boron nitride nanosheets have been tested for ion and particle rejection for water purification.15,21
Materials and methods
Nanotube membrane synthesis
Boron nitride and carbon nanotubes were deposited via chemical vapour deposition (CVD) inside symmetric anodic alumina membranes (AAMs) in a custom-made quartz holder inside a quartz tube (ID 20 mm, OD 22 mm) to be inserted in the centre of a horizontal 3-zone furnace (Fig. S1†). The AAMs (InRedox) were 13 mm in diameter, thermally treated, with pore diameters ranging from ∼10 nm to ∼30 nm.For BNNT–AAM membranes, the temperature was first ramped up to 1000 °C under 150 sccm Ar flow. Borazane (≥97% purity, Sigma Aldrich) was sublimated at 80–100 °C and the synthesis was carried out for 40 min under a 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 sccm H2
135 sccm H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar flow. For the synthesis of CNTs membranes,13 AAMs were pre-annealed with a 1 °C min−1 ramp, up to 900 °C and then brought to 670 °C, when the feed was changed to ethylene and argon (CH4
Ar flow. For the synthesis of CNTs membranes,13 AAMs were pre-annealed with a 1 °C min−1 ramp, up to 900 °C and then brought to 670 °C, when the feed was changed to ethylene and argon (CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar 36
Ar 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 v/v%) for 4 hours (Fig. S2†). The membranes were then cured at 800 °C for 2 hours under a 50 sccm flow of H2.22
84 v/v%) for 4 hours (Fig. S2†). The membranes were then cured at 800 °C for 2 hours under a 50 sccm flow of H2.22
Nanoparticle probes
Silica nanoparticles were labelled S1, S2, S3 and S4 and hematite nanoparticles H1, H2 and H3 in order of increasing size. Silica nanoparticles were sourced from Sigma Aldrich (S1: Ludox SM, S2: Ludox HS and S4: Ludox TM-50) and from Fisher Scientific (S3: Alfa Aesar). Iron oxide H3 nanoparticle was purchased from Sigma Aldrich, while the hematite Sicotrans series (H1 = Sicotrans L2915, H2 = Sicotrans 2715D) were sourced from BASF. Silica suspensions were received in stable form. Hematite particles were stabilised with 1% reagent grade acetyl acetone (Sigma Aldrich). The ionic strength of each suspension was calculated using eqn (1) as a function of the molar concentration of each ionic species ci, and their charge number zi. Na+ was used to stabilise silica suspensions (total number of ionic species, n = 3) leading to notably higher ionic strengths than for the hematite suspensions were the only ionic species identified were H+ and OH− (n = 2).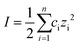 | (1) |
Characterisation methods
FESEM micrographs of the produced membranes were taken with a Zeiss Sigma HD Field Emission Gun Analytical SEM (ASEM) at 5 kV with an aperture size of 10 μm. Samples were either coated with 5 nm AuPd or imaged as is, based on the degree of charging. EDX scans on the same machine were performed with 30 seconds livetime, 16 μs process time, all elements measured, normalised to 100% using 5 kV and 60 μm aperture. The nanotube diameters (Dp) were calculated via statistical image analysis of FESEM micrographs using ImageJ.13,23 A JEOL JSM-2100Plus TEM was used to assess the size of the nanoparticles used for rejection tests (Table S1 and Fig. S3, S4†).Before EELS analysis, the samples were finely grinded with mortar and pestle and then diluted in 5 ml of DI water. A JEM – ARM 200F was used, with 8C spot size 30 μm aperture, CL2 – 20 cm CL (JEOL ADF1) for imaging. The Gatan Spectrum Imaging Toolbox was used for data acquisition and processing. EELS settings were 6C; 40 μm CL2; 2.5 cm CL and 5 mm entrance aperture.
X-ray photoelectron spectroscopy (XPS) was performed on a Thermo Fisher Scientific K-alpha+ spectrometer. The membrane samples were analysed using a micro-focused monochromatic Al X-ray source (72 W) over an area of approximately 400 μm2. Data was recorded at pass energies of 150 eV for survey scans and 40 eV for high resolution scan with 1 eV and 0.1 eV step sizes respectively. Charge neutralisation of the sample was achieved using a combination of both low energy electrons and argon ions. Data analysis was performed in CasaXPS using a Shirley type background and Scofield cross sections, with an energy dependence of −0.6. Raman spectroscopy (Renishaw Raman Microscope series 1000, wavelength 244 cm−1 (5.08 eV), spectral resolution of 5–10 cm−1 and spatial resolution of about 5 μm), and FTIR-ATR (PerkinElmer Frontier FTIR spectrometer) were used on clean samples.
Malvern Zetasizer NS was used to measure the membranes’ surface and the particles’ zeta potential. The tracer solution for surface zeta membrane potential measurements was prepared by adding a low concentration of 0.48 μm polystyrene microbeads (Polysciences, Inc.) in an aqueous solution of pH 6. Membranes were glued to a silicone sheet, left to dry overnight, and then cut into the size of the sample holder prior to measurement, to avoid breaking the membrane and accidentally covering the electrodes with glue. The membranes’ zeta potential (ζm) was calculated by subtracting the measured zeta potential at zero displacement from the tracer potential.24 The linear relationship between displacement and reported zeta potential was obtained from three repeats at four displacement locations and the zeta potential at zero displacement was obtained from this relationship. Hanna standard buffer solutions from Sigma Aldrich at pH 10.01 and 4.01 were used to adjust the tracer solutions pH. For the colloidal suspensions, fixed concentrations of 0.08 g L−1 were sonicated for 5 minutes prior to zeta potential tests (Table S1†). Boron nitride was also deposited on 13 mm diameter non-porous α alumina (Pi-kem Ltd) discs with the aim of measuring BN's contact angle. DI water was used as the solvent for the sessile droplet method in air at 20 °C with 2.5 μl droplets. Images of the drop on dense alumina and BN-coated alumina discs were obtained using a Dataphysics Optical Contact Angle (OCA) goniometer each minute for 10 minutes per measurement. The accuracy of the machine is ±2°. The Young contact angle (θY) on a flat smooth surface is related to the measured contact angle (θW) using the Wenzel model:25
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θW = r θW = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY θY | (2) |
Permeance and rejection methods
The nanotube membranes were tested for pure water permeance in a custom-made dead-end filtration setup with effective diameters of 4, 5 or 10 mm. The membrane holder was connected to a fluid flow measurement apparatus acquiring data via a Labview program. The transmembrane pressure was recorded using pressure transducers (Swagelok) with resolution of ±5 kPa. The temperature of the water during the experiment was measured by using a type-T thermocouple (Omega). Ultrapure water (18.2 ΩM at 25 °C) was supplied by a syringe pump (Nexus 6000) with controllable flow rate. Each nanotube membrane was tested at a stable transmembrane pressure (values are reported in Table S2†) and the water permeate was collected in a beaker pre-filled with a thin layer of silicone oil on a scale (Mettler Toledo, MS304S/01, 0.1 mg sensitivity).For each membrane, the permeance K in m3 m−2 s−1 Pa−1 was calculated as an average of two to four measurements at different water flow rates as follows:
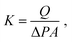 | (3) |
Rejection performance was tested in a crossflow setup, based on a bored-through tee in a dead-end flow cell (Fig. 1). The feed approached the membrane normally at 0.01 ml min−1 and flowed radially outwards once it touched the membrane. The retentate was directed to the cell outlet by the side junction of the bored-through tee. The feed line was thoroughly cleaned and dried after each experiment. Filling with the nanoparticle suspension was followed by degassing before each run.
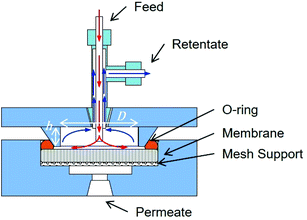 | ||
| Fig. 1 Cross flow filtration cell. The dimensions for the water tangential flow in the feed side are 20 mm × 2 mm D × h. Image courtesy of InRedox. | ||
The first permeating drops of permeate, collected after discarding a volume equal to the membrane's dead volume, were analysed with UV-vis (details and calibration data in Fig. S6†) to minimise evaporation. Then the membranes were slowly backflushed after each rejection test for each particle (Fig. S5†). Silica nanoparticles rejection tests were performed prior to the hematite nanoparticle tests for all membranes. Smaller nanoparticles were tested first. Rejection R(%) is calculated as:
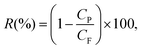 | (4) |
Molecular dynamics
The LAMMPS27 MD software was used to simulate pressure-driven flows of water containing a negative-charged particle through BNNT and CNT membranes. The MD setups consisted of solvent and permeate reservoirs filled with water, with a piston applied to each reservoir to control local pressure and pressure drop across the membrane (Fig. 2).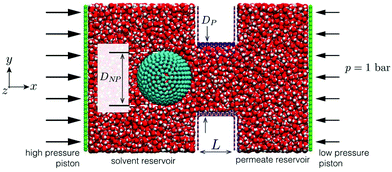 | ||
| Fig. 2 MD snapshot of case setup for BNNT membrane with particle placed in the solvent reservoir (left); a slice is taken at the xy plane of the domain for a better visual of the system. | ||
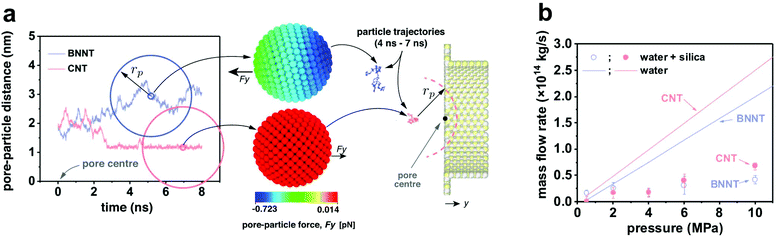
To obtain MD results as close to the experiments as possible, calibration studies of intermolecular potentials between water–BNNT and water–CNT were performed to match experimental contact angles.23 Partial charges on BN atoms were calibrated using the ReaxFF force field,28 setting an experimental surface charge density of −1.28 × 10−20 C nm−2 for BNNT and −6.99 × 10−21 C nm−2 for the silica particles. No charge was set on the carbon atoms in the CNT case. The effective hydrated diameter DNP of the particles was chosen to be smaller than the nanotube diameter DP, such that 0.7 < DNP/DP < 1, in analogy to experimental data, and pressure drops varying between 5 and 1000 bar. Measurements were conducted for particle trajectories, particle-water force, particle–surface force and membrane mass flow rates. Full details on the MD set-up can be found in the ESI.†
Computational fluid dynamics
A system of differential equations describing the forces acting on a single particle was solved via Brownian Dynamics (BD) using COMSOL Multiphysics™ v5.4 in a two-dimensional domain in proximity to the entrance of a single pore for BNNTs and CNTs. In all the numerical models presented in this study, the flowing fluid was assumed to be Newtonian and incompressible. The overall domain size was 40 nm × 84 nm (height × length) (Fig. S7†).The fluid flow was modelled by solving the continuity and Navier Stokes equations (eqn (S3) and (S4)†) for Newtonian and incompressible fluids and the flow regimes was assumed laminar throughout. Sieving and fouling are governed by the interplay of forces acting on feed particles:29 Drag (FD), electrostatic (FE) and Brownian (FB) force are reputed as the primary non negligible forces that should be analysed when pollutants size is comparable to membrane pore size.30 The combined effect of such forces on particle trajectories in dead end filtration can be modelled by numerically integrating the Langevin equation:31
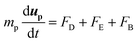 | (5) |
The electrostatic force FE can be described by the DLVO (Derjaguin, Landau, Verwey, and Overbeek)32 which is a function of the surface zeta potential of the particle and membrane, the distance between the particle centre and the membrane and the Debye length (eqn (S7)†). Values of the surface zeta potential of the particle and membrane were obtained from experimental values at pH 6. Finally, the Brownian force FB is modelled on the basis of the Gaussian white noise method (eqn (S8)†).33
Particle tracing simulations were conducted to track single particles (DNP/DP = 0.85) subjected to the combined drag, electrostatic and Brownian forces30 for 0.0001 s. The predetermined time-step in all simulations was set to 10−7 s to ensure convergence. Further simulations that omitted Brownian forces with four particles were conducted for the same time step, to determine the isoforce FEL = FD lines.
Results and discussion
Membrane characterisation
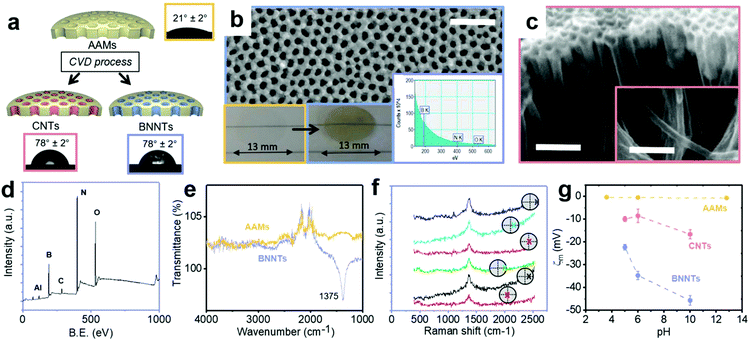
BNNTs and CNTs were deposited in the pores of anodic alumina membranes (AAMs) by non-catalytic chemical vapor deposition (CVD), resulting in all the nanotubes being aligned perpendicularly to the membrane surface (Fig. 3a and S8†). While this process is well-known for CNTs,13 it has been demonstrated here for the first time for BNNTs via the decomposition of borazane at high temperature, previously used for deposition of planar BN on Cu34 and Pt foils.35 BNNT and CNT deposition due to the different synthesis conditions, resulting in marginally different internal average diameters (Table 1). Contact angle data for both BNNTs and CNTs is in line with literature values.15 Contact angle data for AAMs can be found in Fig. S9.†| θ | r | R a | ζ m | A | φ | D P | K | R | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ° ± 2° | — | nm | mV | % | — | nm | LMH per bar | % | |||
| W | Y | Silica | Hematite | ||||||||
| AAMs | 41 | 21 | 1.23 | 392 | −0.6 ± 0.2 | 0–7 | 0–5 | 0.16 | 18 ± 3 | 7.5 | 35.6 |
| CNTs | 80 | 78 | −8.55 ± 2.9 | 0 | 0–4 | 0.13 | 22.6 ± 4.4 | 19.6 | 27.5 | ||
| BNNTs | 80 | 78 | −34.7 ± 1.8 | 0–6 | 0–22 | 0.14 | 21.2 ± 3.7 | 9.0 | 71.0 | ||
High resolution XPS spectra revealed a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N stoichiometry of 1.2 with the characteristic BN peak at 398.3 eV for N and 190.7 eV for B (Fig. 3d).36 This value is close to the theoretical B
N stoichiometry of 1.2 with the characteristic BN peak at 398.3 eV for N and 190.7 eV for B (Fig. 3d).36 This value is close to the theoretical B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N value of 1, with similar deviations observed in the literature for different synthesis methods, due to the presence of defects in the nanotubes produced experimentally.37 BN was also directly observed on the AAMs via electron energy loss spectroscopy (EELS) (Fig. 3b inset), with the boron and nitrogen K edges appearing near 200 and 400 eV, respectively.38 The FTIR peak (Fig. 3e) for the BN in-plane bond was identified on the produced BNNT membranes at 1375 cm−1.39 Additional peaks around 2000–2500 cm−1 in these spectra are associated to the background (Fig. S11†).
N value of 1, with similar deviations observed in the literature for different synthesis methods, due to the presence of defects in the nanotubes produced experimentally.37 BN was also directly observed on the AAMs via electron energy loss spectroscopy (EELS) (Fig. 3b inset), with the boron and nitrogen K edges appearing near 200 and 400 eV, respectively.38 The FTIR peak (Fig. 3e) for the BN in-plane bond was identified on the produced BNNT membranes at 1375 cm−1.39 Additional peaks around 2000–2500 cm−1 in these spectra are associated to the background (Fig. S11†).
Raman spectra were recorded on both sides of the support membranes after deposition showed the characteristic BN peaks at 1369 cm−1 in all the locations investigated (Fig. 3f).
The surface zeta potential was close to zero for the bare AAMs across a wide pH range (Fig. 3g). Literature values for the zeta potential value of AAMs vary, with some reporting a decreasing linear dependence with pH, with an isoelectric point around pH 8,40 while others reporting an isoelectric point closer to pH 6 and dependent on pore size.41 The present behaviour is tentatively attributed to the thermal annealing process, in analogy to what observed previously for CNTs.22 The as-synthesized CNT membranes had a zeta potential of −20.8 mV, indicating the presence of defects and functional groups on their surface, a well-known consequence of the non-catalytic CVD synthesis method used here.13 Post-synthesis annealing in hydrogen was used to improve the quality of the CNTs,22 closer to CNT membranes produced via infiltration of polymers in a aligned CNT forest grown via catalytic CVD.6 This resulted in a zeta potential value of −8.5 mV. For the BNNT membranes, the surface zeta potential was −34.7 mV at pH 6, in excellent agreement with literature values (−34 ± 4 mV) on few layered BN.39 The surface zeta potential as a function of pH for the 3 nanotube materials is reported in Fig. 3g.
Before performing permeance and rejection tests, the amount of silica and hematite adsorbed on the AAMs, CNTs–AAMs and BNNT–AAMs was determined. Silica presents low adsorption i.e. below 7% on all three membranes. For hematite, however, adsorption on BNNTs was as high as 22%, implying that some of the apparent rejection observed is to be ascribed to adsorption. The size, pH and surface zeta potential of the particle dispersions used in this work are reported in Table S1.† Each particle dispersion was tested at the same pH and ionic strength for all three materials.
Permeance and rejection tests
Pure water permeance tests (Fig. 4a and b) show that the CNTs modestly outperform (∼1.8×) BNNTs, with the difference between the CNTs and BNNTs membranes being comparable to what was previously observed for flow in single carbon and boron nitride nanotubes.18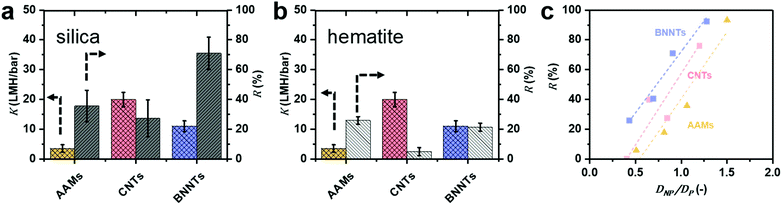 | ||
| Fig. 4 Experimental permeance K and rejection R for (a) negatively charged silica (pH = 5.5) and (b) positively charged hematite (pH = 5.3) nanoparticles are reported for particles S3, which is smaller than the average CNT and BNNT and comparable with the AAM (DNP ≤ DP). Full information on the particles and nanotubes, including sizes, can be found in Table 1. (c) Calculated silica NP rejection of AAMs, CNTs and BNNTs membranes as a function of DNP/DP. | ||
This difference is smaller than what we computed via MD, where the permeance of pristine CNTs is 3.8 times bigger than that in pristine BNNTs. The discrepancy is attributed to the synthesis method used here, non-catalytic CVD in the pores of AAMs, which results in nanotubes with a certain amount of defects,13 which, in turn, depresses permeance.42 The presence of defects in the BNNTs was confirmed by the oxidised BN species in the XPS spectrum (Fig. S8e†), which generate a large charge on the surface when in contact with water.43 All experimental data can be found in Table S3 and Fig. S13.†
BNNTs have consistently higher rejection of negatively charged silica nanoparticles than bare AAMs and CNTs (Fig. 4a) for average diameters of the nanoparticle (DNP) smaller than or equal to the pore diameter (DP) of all 3 nanotube materials (Fig. 4c). In fact, AAMs and CNTs show appreciable rejections only when the particle diameter DNP is larger than tube diameter DP (Fig. 4a). For example, BNNT membranes with DP = 21.2 ± 3.7 could reject 71% of S3 silica nanoparticles (DNP = 19.2 ± 2.6 nm), with a permeance of 8.65 ± 0.06 LMH per bar. A CNT membrane with DP = 22.6 ± 4.4 nm, par contra, could only reject 27% of the same particles with comparable permeance. For the AAM, with DP = 18 ± 3 nm, the rejection is higher (38%) than for the CNT. However, in this case, the silica nanoparticle is slightly larger than the AAMs average pore size. If one considers particle S2 (DNP = 14.7 ± 1.8 nm), which is significantly smaller than both AAM and CNT, the latter has a rejection which is double than the former, 40% vs. 18%, respectively. Conversely, since permeance is proportional to the square of the nanotubes’ diameter, using BNNT membranes with ∼30% larger diameters that a CNT membrane with comparable rejection would result in up to 70% higher permeance (Fig. 4c and S14d†). This advantage is retained across a wide DNP/DP ratios (Fig. 4c). All rejection and permeance data are reported in Tables S4–S6.† This difference is not as marked for the positively charged hematite particles in Fig. 4b (H2 particles only), though rejection is still higher for BNNTs. In this case, the difference could also be due to adsorption as previously discussed.
Molecular dynamics and computational fluid dynamics simulations were employed to model the experimental phenomena with a theoretical model accounting for the main forces acting on the particle.30 Details of both simulations are provided in the ESI.† In the MD simulations, negative-charged nanoparticles were released near the entrance of pores of BNNT and CNT membranes. Fig. 5a shows that the dynamics of the nanoparticle for DNP/DP ∼ 0.9 at 20 bar pressure drop are very different between BNNT and CNT membranes. In the CNT, the particle approaches the pore and remains trapped at the centre of the pore entrance under the same applied pressure, whereas in the BNNT, the negative partial charges between pore and particle repels the nanoparticle away from the pore. The pressure loss at the entrance of the membrane increases when the particle is partially blocking the entrance of the pore, which can be elucidated from the response of the mass flow rate in the MD simulations. At low applied pressures, there is a lower impact by the particle on the flow rate through the BNNT (e.g. −13% mass flow rate at 20 bar) than there is through the CNT (−40%), as seen in Fig. 5b. At higher pressure drops (≳40 bar), however, the pressure force is large enough to also trap the particle near the BNNT pore, although with higher constrained dynamics. As such, the impact on flow rate becomes the same for both nanotube membrane materials for larger pressures. Further evidence of differences in particle mobility are also measured using the Mean Squared Displacement,44 as shown in Fig. S18.†
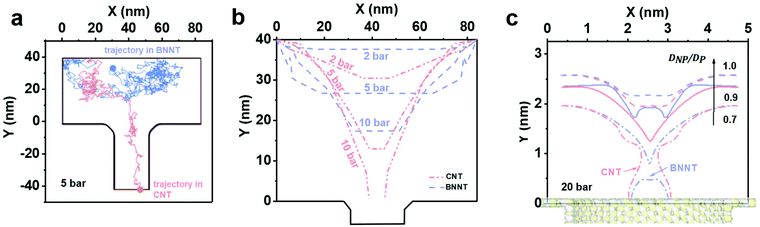
For Brownian Dynamics (BD), particles were introduced from the top of the domain and particle tracing equations were solved via a time dependent solver using small time steps of 10−7 s, resulting in very small particle displacement but very high computational expense. Consequently, only one particle was introduced at the inlet. Fig. 6a shows the trajectory of a negatively charged silica nanoparticle on the feed side of a BNNT (blue line) and of a CNT (red line) in presence of the forces (Brownian, drag and electrostatic) found in a cross-flow filtration apparatus such as the one used here, with an external pressure of 5 bar. The silica particle quickly reaches the CNT pore entrance and enters the tube, while it remained in the bulk of the feed for the BNNTs membrane, as observed in both MD simulations (Fig. 5) and experiments (Fig. 4a). The Brownian force was modelled as a Gaussian white noise process,30 with its direction constantly changing.
By taking out the randomness of Brownian force, whether a particle enters a tube or not, is the result of a balance between drag and electrostatic forces: ΔF = FD − FEL.
Fig. 6b shows isoforce lines in a 2D geometry for which ΔF = 0, where the particle effectively halts in the simulation in absence of Brownian forces. The pressure domain can be divided in three zones based on the particle behaviour when it reaches the pore entrance, in the absence of Brownian forces: one below 6.6 bar, where both CNTs and BNNTs are able to reject the silica particle. A second zone between 6.6 bar and 29 bar, where only BNNTs allow for the rejection of the particle due to their higher electrostatic repulsion, and a final zone where no rejection occurs. In both experiments and in the BD simulation in Fig. 6b, improved rejection for pressures below 6.6 bar for the BNNTs was observed. This is due to the presence of Brownian forces, which, as suggested by both MD and BD, tend to draw the nanoparticles back in the bulk.
In the MD, the iso-force lines are measured directly from surface-particle and water-particle intermolecular forces. Fig. 6c shows that when the nanoparticle/pore ratio DNP/DP is reduced below 1.0 at a fixed pressure of 20 bar, the particle always prefers being closer to the CNT entrance than to the BNNT, indicating the BNNT is more likely to reject particles than the CNT. At around DNP/DP ∼ 0.6–0.7 there is evidence of full particle passage through both membranes, which agrees well with experimental observations.
Conclusions
We have shown that the choice of boron nitride nanotubes over carbon nanotubes for the filtration of negatively charged nanoparticles results in the ability to reject nanoparticles smaller than the tubes’ diameters and in up to 70% higher permeance for the same rejection, due to the larger nanotube diameters that can be used. Computational studies showed that this is due to charge-based rejection, enabled by the charged structured of the BNNTs as opposed to the neutrally charged CNTs. Both experiments and simulation show that BNNTs can reject nanoparticles down to 0.7 times smaller than their internal diameter and up to an external pressure of 6.6 bar. Thus, boron nitride nanotubes with larger diameters and, hence, higher permeance, can be chosen to achieve comparable rejection to carbon nanotubes, opening the way to significantly increasing the performance of commercial membranes in a variety of applications, from water treatment to bioprocessing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the UK EPSRC (grants EP/M01486X/1, EP/N016602/1 and EP/R007438/1). The MD simulation results were obtained using ARCHER, the UK's national supercomputer. We acknowledge Diamond Light Source for time on Instrument E01 under Proposal EM21253 and Dr Mohsen Danaie for support. XPS data collection was performed at the EPSRC National Facility for XPS (‘HarwellXPS’), operated by Cardiff University and UCL, under contract no. PR16195. We deeply thank Dr Daniel Wolverson for allowing us the use of his Raman spectroscopy setup. SC thanks Dr Salvador Eslava for providing hematite nanoparticles and Dr Jing Ji for her helpful remarks. All raw data produced in the manuscript can be found in the ESI.†References
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- P. Marchetti, M. F. Jimenez Solomon, G. Szekely and A. G. Livingston, Chem. Rev., 2014, 114, 10735–10806 CrossRef CAS PubMed.
- J. A. Howell, V. Sanchez and R. W. Field, Membranes in bioprocessing: theory and applications, Springer Science & Business Media, 2012 Search PubMed.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, eaab0530 CrossRef PubMed.
- F. Fornasiero, H. G. Park, J. K. Holt, M. Stadermann, C. P. Grigoropoulos, A. Noy and O. Bakajin, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17250–17255 CrossRef CAS PubMed.
- M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Nature, 2005, 438, 44 CrossRef CAS.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- D. Mattia, K. P. Lee and F. Calabrò, Curr. Opin. Chem. Eng., 2014, 4, 32–37 CrossRef.
- S.-M. Park, J. Jung, S. Lee, Y. Baek, J. Yoon, D. K. Seo and Y. H. Kim, Desalination, 2014, 343, 180–186 CrossRef CAS.
- B. Corry, Energy Environ. Sci., 2011, 4, 751–759 RSC.
- M. Majumder and B. Corry, Chem. Commun., 2011, 47, 7683–7685 RSC.
- H. Li and X. C. Zeng, ACS Nano, 2012, 6, 2401–2409 CrossRef CAS PubMed.
- D. Mattia, H. Leese and K. P. Lee, J. Membr. Sci., 2015, 475, 266–272 CrossRef CAS.
- D. Golberg, Y. Bando, C. Tang and C. Zhi, Adv. Mater., 2007, 19, 2413–2432 CrossRef CAS.
- K. Ritos, D. Mattia, F. Calabrò and J. M. Reese, J. Chem. Phys., 2014, 140, 014702 CrossRef PubMed.
- M. Suk, A. Raghunathan and N. Aluru, Appl. Phys. Lett., 2008, 92, 133120 CrossRef.
- T. A. Hilder, D. Gordon and S. H. Chung, Small, 2009, 5, 2183–2190 CrossRef CAS PubMed.
- E. Secchi, S. Marbach, A. Niguès, D. Stein, A. Siria and L. Bocquet, Nature, 2016, 537, 210–213 CrossRef CAS PubMed.
- S. Casanova, T.-Y. Liu, Y.-M. J. Chew, A. Livingston and D. Mattia, J. Membr. Sci., 2020, 597, 117749 CrossRef CAS.
- X. Wei and T. Luo, J. Phys. Chem. C, 2018, 122, 5131–5140 CrossRef CAS.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335, 442–444 CrossRef CAS PubMed.
- D. Mattia, M. P. Rossi, B. M. Kim, G. Korneva, H. H. Bau and Y. Gogotsi, J. Phys. Chem. B, 2006, 110, 9850–9855 CrossRef CAS PubMed.
- S. Casanova, M. K. Borg, Y. M. J. Chew and D. Mattia, ACS Appl. Mater. Interfaces, 2019, 11, 1689–1698 CrossRef CAS PubMed.
- Z.-X. Low, J. Ji, D. Blumenstock, Y.-M. Chew, D. Wolverson and D. Mattia, J. Membr. Sci., 2018, 563, 949–956 CrossRef CAS.
- R. N. Wenzel, J. Phys. Chem., 1949, 53, 1466–1467 CrossRef CAS.
- J. Mulder, Basic principles of membrane technology, Springer Science & Business Media, 2012 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. S. Han, J. K. Kang, H. M. Lee, A. C. Van Duin and W. A. Goddard III, J. Chem. Phys., 2005, 123, 114703 CrossRef PubMed.
- T. Lin, J. Zhang and W. Chen, J. Membr. Sci., 2017, 544, 174–185 CrossRef CAS.
- M.-M. Kim and A. L. Zydney, J. Colloid Interface Sci., 2004, 269, 425–431 CrossRef CAS PubMed.
- D. L. Ermak and H. Buckholz, J. Comput. Phys., 1980, 35, 169–182 CrossRef.
- W. R. Bowen, A. N. Filippov, A. O. Sharif and V. M. Starov, Adv. Colloid Interface Sci., 1999, 81, 35–72 CrossRef.
- A. Li and G. Ahmadi, Aerosol Sci. Technol., 1992, 16, 209–226 CrossRef CAS.
- K. K. Kim, A. Hsu, X. Jia, S. M. Kim, Y. Shi, M. Hofmann, D. Nezich, J. F. Rodriguez-Nieva, M. Dresselhaus and T. Palacios, Nano Lett., 2011, 12, 161–166 CrossRef PubMed.
- G. Kim, A.-R. Jang, H. Y. Jeong, Z. Lee, D. J. Kang and H. S. Shin, Nano Lett., 2013, 13, 1834–1839 CrossRef CAS PubMed.
- G. N. B. Baroña, J. Lim, M. Choi and B. Jung, Desalination, 2013, 325, 138–147 CrossRef.
- X. J. Dai, Y. Chen, Z. Chen, P. R. Lamb, L. H. Li, J. du Plessis, D. G. McCulloch and X. Wang, Nanotechnology, 2011, 22, 245301 CrossRef PubMed.
- A. Pakdel, C. Zhi, Y. Bando, T. Nakayama and D. Golberg, Nanotechnology, 2012, 23, 215601 CrossRef PubMed.
- W. Lei, V. N. Mochalin, D. Liu, S. Qin, Y. Gogotsi and Y. Chen, Nat. Commun., 2015, 6, 8849 CrossRef CAS PubMed.
- B. H. Winkler and R. E. Baltus, J. Membr. Sci., 2003, 226, 75–84 CrossRef CAS.
- B. J. Pedimonte, T. Moest, T. Luxbacher, C. von Wilmowsky, T. Fey, K. A. Schlegel and P. Greil, Acta Biomater., 2014, 10, 968–974 CrossRef CAS PubMed.
- W. Nicholls, M. K. Borg, D. A. Lockerby and J. Reese, Mol. Simul., 2012, 38, 781–785 CrossRef CAS.
- M. Crimp, D. Oppermann and K. Krehbiel, J. Mater. Sci., 1999, 34, 2621–2625 CrossRef CAS.
- N. Tarantino, J.-Y. Tinevez, E. F. Crowell, B. Boisson, R. Henriques, M. Mhlanga, F. Agou, A. Israël and E. Laplantine, J. Cell Biol., 2014, 204, 231–245 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr04058d |
| This journal is © The Royal Society of Chemistry 2020 |