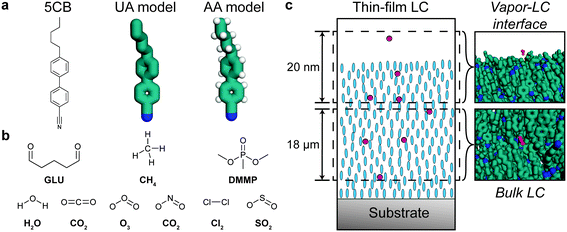
Molecular simulations of analyte partitioning and diffusion in liquid crystal sensors†
Jonathan K.
Sheavly
 ,
Jake I.
Gold
,
Jake I.
Gold
 ,
Manos
Mavrikakis
,
Manos
Mavrikakis
 and
Reid C.
Van Lehn
and
Reid C.
Van Lehn
 *
*
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, Madison, WI 53706, USA. E-mail: vanlehn@wisc.edu
First published on 25th October 2019
Abstract
Chemoresponsive liquid crystal (LC) sensors are promising platforms for the detection of vapor-phase analytes. Understanding the transport of analyte molecules within LC films could guide the design of LC sensors with improved selectivity. In this work, we use molecular dynamics simulations to quantify the partitioning and diffusion of nine small-molecule analytes, including four common atmospheric pollutants, in model systems representative of LC sensors. We first parameterize all-atom models for 4-cyano-4′-pentylbiphenyl (5CB), a mesogen typically used for LC sensors, and all analytes. We validate these models by reproducing experimentally determined 5CB structural parameters, 5CB diffusivity, and analyte Henry's law constants in 5CB. Using the all-atom models, we calculate analyte solvation free energies and diffusivities in bulk 5CB. These simulation-derived quantities are then used to parameterize an analytical mass-transport model to predict sensor activation times. These results demonstrate that differences in analyte–LC interactions can translate into distinct activation times to distinguish activation by different analytes. Finally, we quantify the effect of LC composition by calculating analyte solvation free energies in TL205, a proprietary LC mixture. These calculations indicate that varying the LC composition can modulate activation times to further improve sensor selectivity. These results thus provide a computational framework for guiding LC sensor design by using molecular simulations to predict analyte transport as a function of LC composition.
Design, System, ApplicationChemoresponsive liquid crystal (LC) sensors can detect the presence of atmospheric pollutants, chemical warfare agents, and other vapor-phase toxins at concentrations in the low ppm range. For LC sensors to be useful, they must rapidly, selectively activate in the presence of target analytes. LC sensors are composed of a thin LC film that is deposited on a reactive substrate, and thus sensor design requires the selection of both the LC and substrate material. Previous studies have primarily focused on tuning the substrate properties as a means of changing the sensor activation time and selectivity. However, analyte transport through the LC film, which depends on molecular-scale analyte–LC interactions, can also influence the activation time. In this work, we use molecular simulations to quantify the influence of LC sensor material properties on sensor activation times for common atmospheric pollutants. Based on calculations of analyte permeances and corresponding transport timescales, we suggest that tuning the composition of the LC film can modulate activation times to distinguish activation by different analytes. These findings indicate that molecular simulations can be used to select LC materials for improved sensor selectivity by predicting the effect of LC composition on analyte transport. |
Introduction
Human exposure to high concentrations of air contaminants is a significant problem associated with adverse health effects.1–3 For example, the U.S. Environmental Protection Agency and Occupational Safety and Health Administration recommend limiting personal exposure to common atmospheric pollutants such as ozone, sulfur dioxide, and nitrogen dioxide.4–6 Minimizing the risk of contaminant exposure requires the development of mobile chemical sensing platforms capable of monitoring the local concentration of environmental contaminants in real time.3 Such sensors must be sufficiently simple and small to facilitate mobile monitoring and must differentiate between pollutants and ambient species that do not pose a risk to human health (e.g., water and carbon dioxide).Recently, chemoresponsive liquid crystal (LC) sensors have been used to sense toxic analytes, such as hydrogen sulfide, chemical warfare agents, Cl2, and NO2 at concentrations in the low ppm range.7–14 These examples of chemoresponsive LC sensors are composed of a nematic LC film that is deposited on a substrate and undergoes a detectable change in its adsorption, orientation, and optical properties when exposed to a vapor stream containing the analyte.7,8 For example, previously developed sensors that detect the chemical warfare agent simulant dimethyl methylphosphonate (DMMP) consist of an 18 μm thick film of 4-cyano-4′-pentylbiphenyl (5CB) deposited on a substrate containing metal salts.13,16,17 In the initial state of the sensor, 5CB molecules bind to the substrate due to interactions between their nitrile groups and the metal salts. Binding causes the LC director vector to align perpendicular to the substrate. Non-covalent interactions between 5CB molecules also cause the LC director vector to align perpendicular to the vapor–LC interface,18 leading to a mostly uniform director vector throughout the film. The sensor is then exposed to vapor-phase DMMP molecules that partition into the LC film and diffuse to the substrate. Interactions between the substrate and DMMP molecules outcompete interactions between the substrate and 5CB molecules, causing the displacement and reorientation of previously bound 5CB molecules.8,17 Displacing a sufficient number of surface-bound 5CB molecules leads to spatial variations in the LC director vector throughout the film that can be observed optically.19 This transition, driven by the presence of an analyte, is the response of the sensor that can be easily transduced optically. Similar chemoresponsive LC sensors that rely on the competition between mesogen–substrate and analyte–substrate interactions have also been developed to detect different analytes.12,20
Recent sensor development has focused on improving sensor selectivity to different analytes.12,21 One mechanism for increasing selectivity is by modulating analyte binding to the substrate. In particular, density functional theory (DFT) calculations have shown that the difference between the binding energy of DMMP and the binding energy of 5CB, which quantifies competitive binding at the substrate, correlates with the sensor activation time (i.e., the time required for an optical response to be measured).16,17 In addition, DFT calculations have been used to guide the development of water tolerant DMMP LC sensors by the use of a stronger binding mesogen, a pyrimidine containing mesogen, which can be displaced by DMMP but not water. However, these stronger binding mesogens still have the drawback of increasing response time.22 Alternatively, the time required for analyte transport through the LC film could also be used to distinguish sensor activation by specific analytes, particularly if the timescale for analyte transport is slower than the timescale for changes to mesogen reorientation at the substrate. For example, one study showed that the sensor activation time for DMMP depends on the timescale for analyte transport across the vapor–LC interface.23 Since analyte transport through the LC film does not depend on interactions with the substrate, it may be possible to tune the timescale for analyte transport independently from substrate properties to improve sensor selectivity.
Characterizing analyte transport across the LC film requires knowledge of both the thermodynamics of analyte partitioning into the film and the dynamics of analyte diffusion. Previous experimental measurements of analyte partitioning have used vapor pressure measurements to determine the Henry's law constant for high pressures of carbon dioxide (CO2) and methane (CH4) in 5CB.24,25 Another study determined the partition coefficient of glutaraldehyde (GLU) in 5CB using chemically specific absorbance measurements.26 However, in general quantifying analyte partitioning in LCs is challenging, particularly for toxic species with the associated experimental hazards. Measuring analyte diffusivity is also challenging and has been limited to the study of larger species using fluorescent recovery after photo bleaching.27
Alternatively, molecular dynamics (MD) simulations can model the molecular-scale interactions needed to quantify analyte partitioning and diffusion. Significant work has characterized the structural and elastic properties of LCs using MD simulations that accurately reproduce experimental measurements, such as the 5CB nematic–isotropic transition temperature (TNI) and the structure near a vapor–LC interface.28–33 Fewer studies have considered the transport of small molecules through LC films. One recent example investigated the transport of water through LC films to determine the influence of water flux on the LC director vector.34 However, studies of interactions between alternative small-molecule analytes and bulk LC are largely lacking. Moreover, simulation models have largely focused on 5CB due to the availability of an accurate united-atom (UA) force field for this material,30–32,35 but extending this model to other possible mesogens is challenging. Utilizing MD simulations to guide the design of new LC sensors for selective analyte detection thus requires new simulation models and techniques.
Herein, we use atomistic MD simulations to quantify analyte partitioning and diffusion in LC films. We model nine analytes: GLU, DMMP, CH4, CO2, chlorine (Cl2), nitrogen dioxide (NO2), water (H2O), ozone (O3), and sulfur dioxide (SO2). GLU, DMMP, and CH4 are selected to validate the computational models against experiments, H2O and CO2 are ambient species in the atmosphere, and Cl2, NO2, O3, and SO2 are atmospheric pollutants. These latter six analytes are thus of particular interest for pollutant sensing applications. We assume that analyte–substrate interactions can be tuned to obtain chemoresponsive LC sensors that can detect these analytes and focus on the impact of analyte transport through the LC film on sensor activation times. We first develop atomistic models for 5CB–analyte interactions and show that the models reproduce 5CB diffusivity measurements and Henry's law constants in good agreement with experiments. We then calculate analyte solvation free energies and diffusivities and use this information to parameterize a mass transport model to predict sensor activation times. Finally, we show that changing the composition of the LC film to contain TL205, another commonly studied mesogen, leads to changes in analyte transport properties that can be used to tailor sensor selectivity. These results demonstrate the potential of MD simulations to guide the design of chemoresponsive LC sensors with improved selectivity by tuning analyte partitioning and diffusion.
Methods
Classical MD simulations were performed to quantify the partitioning and transport of analytes in simulation systems designed to model a chemoresponsive LC sensor. The mesogen 5CB was simulated using both a united atom (UA) model and all-atom (AA) model with explicit hydrogen atoms (Fig. 1a). The UA model used the force field developed by Tiberio et al.32 The AA model was based on a reparameterization of the generalized AMBER force field (GAFF)36 based on prior literature recommendations.37 We developed the 5CB model using GAFF LJ parameters and followed the parameterization strategy used by Cheung et al. to fit partial charges and dihedral potentials to DFT calculations.37–39 These DFT calculations were performed in Gaussian16 using the B3LYP40 functional with a 6-31g* basis set. Atomic partial charges were fit using CHELPG (charges from electrostatic potentials using a grid-based method)41 with a constraint on the dipole. This approach ensures that the point charges used in the MD simulation reproduce the electrostatic potential calculated by DFT beyond the molecular surface.41 To determine dihedral potentials for the biphenyl dihedral and the first alkyl tail dihedral in 5CB, we performed a relaxed scan and fit the classical potentials to reproduce the DFT calculations (ESI† Fig. S1). Additional details on this parameterization strategy and corresponding results are shown in the ESI.†AA models were developed for the nine analytes shown in Fig. 1b: GLU, DMMP, CH4, CO2, Cl2, NO2, H2O, O3, and SO2. All analytes, other than water, were parameterized using the same GAFF parameter assignment scheme and charge-fitting procedure that was used for 5CB. The SPC/E (simple point charge/extended)42 model was used for water, although parameterizing water using the same methods as the other analytes yielded similar results (ESI† Fig. S2c). Complete details on all AA parameters are included in the ESI.†
The bulk of the LC sensor and the vapor–LC interface were separately modeled to determine contributions of both regions of the system to analyte transport (Fig. 1c). The bulk system consisted of 1020 molecules that were initially arranged in an evenly spaced grid using gmx genconf, a tool implemented in GROMACS 2016.43 The system was equilibrated using a simulated annealing protocol in which the temperature was initially set to 400 K and then reduced to the temperature of interest at a rate of 1 K ns−1 while maintaining a pressure of 1 bar. After annealing, the system was simulated at constant temperature and pressure for 50 ns. The first 25 ns were disregarded as further equilibration and the final 25 ns were used to measure the equilibrium bulk properties of the system. The final box size after equilibration at 1 bar and 300 K was 6.400 × 8.597 × 7.488 nm3.
Using the bulk system, we performed alchemical free energy calculations to calculate the solvation free energy of each analyte. A single analyte molecule was inserted into the system using gmx insert-molecule, a tool implemented in GROMACS 2016.43 The coupling parameters λLJ and λelec were used to modify the magnitude of the Lennard-Jones (LJ) and electrostatic interactions, respectively, between the analyte and mesogen molecules. Coupling parameters were varied between 1, corresponding to normal interactions between the analyte and mesogens, to 0, corresponding to no interactions between the analyte and mesogens, in 16 independent simulation windows: 6 in which λLJ = 1.0 and λelec = 0.000, 0.167, 0.333, 0.500, 0.667, or 0.833, and 10 in which λelec = 0 and λLJ = 0.000, 0.100, 0.200, 0.300, 0.400, 0.500, 0.600, 0.700, 0.800, or 0.900. The multistate Bennett acceptance ratio (MBAR) method44 was used to compute the solvation free energy as the free energy difference between the solvated analyte state (λLJ = λelec = 1.0) and an ideal gas reference state (λLJ = λelec = 0). Each window consisted of 3 ns of equilibration at 300 K and 1 bar followed by 7 ns of production at 300 K and constant volume. This simulation time was sufficient to obtain convergence (ESI† Fig. S5). The solvation free energy was calculated 3 times for each analyte using different initial insertion positions. All solvation free energy results report the average and standard error between these trials.
The interfacial system consisted of a slab of 2500 molecules initially arranged within a 7.5 × 7.5 × 24.0 nm3 volume using the PACKMOL program.45 The simulation box was then extended in the z-direction by 16.615 nm to create a vacuum layer between the two interfaces. This z-dimension is large enough to allow the formation of smectic layers near the vapor–LC interface while achieving bulk nematic properties near the center of the LC slab.33 The system was equilibrated using a simulated annealing protocol in which the temperature was set to 420 K and decreased at a rate of 1 K ns−1 for 120 ns. The system was then equilibrated for a further 100 ns at 300 K. All simulations of the interfacial system were performed at constant volume to maintain the vacuum layer. The thickness of the LC slab after equilibration was 19.495 nm.
Using the interfacial system, we performed umbrella sampling to measure the potential of mean force (PMF) for the transport of an analyte molecule across the vapor–LC interface. We used the z-component of the distance between the center-of-mass (COM) of the analyte and the COM of the LC slab as the reaction coordinate. Umbrella sampling was performed using 70 windows spaced by 0.1 nm along the reaction coordinate. The analyte was restrained to the desired value of the reaction coordinate using a harmonic potential with a spring constant of 500 kJ mol−1 nm−2. Each window consisted of 10 ns of equilibration followed by 45 ns of production at 300 K. This simulation time was sufficient to obtain convergence (ESI† Fig. S5). The weighted histogram analysis method (WHAM) was used to compute the PMF.46
All simulations used a 2 fs timestep. Verlet lists were generated every 20 timesteps using a 1.2 nm cutoff. Electrostatic interactions were computed using the smooth particle mesh Ewald (PME) method with a 1.2 nm short-range cutoff, Fourier spacing of 0.14 nm, and PME order of 4. LJ interactions were smoothly shifted to zero between 1.0 nm and 1.2 nm with no dispersion correction. Temperature coupling was performed using a Nóse–Hoover thermostat with a time constant of 2 ps and isotropic Parrinello–Rahman barostat with a compressibility of 3 × 10−5 bar−1. All simulations were performed using Gromacs 2016.43
Finally, we also calculated the binding of water to benzonitrile (a surrogate molecule for 5CB) with DFT in the gas phase. For these calculations, we used Gaussian 09 version D.01 (ref. 47) with M06-2X-D3/def2-TZVP48–50 level of theory. The value reported is corrected for calculated zero-point energies of the respective terms.
Results and discussion
Validation of force field parameters
Investigating analyte partitioning and transport through a nematic LC film using MD simulations requires analyte and mesogen force field parameters that can capture experimentally relevant structural and dynamic parameters. Extensive previous simulations have studied the behavior of 5CB, a mesogen utilized experimentally in sensor operation,30,31,51,52 using a UA force field that has been parameterized to reproduce the temperature at which the nematic–isotropic phase transition occurs (TNI).32 These past simulations have largely focused on LC phase behavior and structural properties.30–32 However, the removal of explicit hydrogen atoms in UA models can lead to unphysically large diffusivities,53,54 and moreover the UA model for 5CB cannot be easily generalized to other mesogens. Due to these considerations, we instead parameterized 5CB using the AA GAFF force field (as described in the Methods) to facilitate the modeling of new mesogens and analytes without extensive parameterization.The 5CB model was validated by comparing the temperature variation in structural and dynamical properties calculated using the AA and UA models to experimental measurements (Fig. 2). Each property was computed from a 50 ns simulation performed at the indicated temperature after annealing as described in the Methods. Fig. 2a shows the P2 order parameter, which is related to the average angle between a mesogen molecular axis and the LC director vector, θ, by eqn (1):
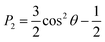 | (1) |
 | ||
| Fig. 2 Comparison of 5CB model predictions to experimental measurements. All plots compare the temperature dependence of a bulk 5CB property calculated using either the UA (blue) or AA (yellow) model to experimental measurements (red). Squares indicate the temperatures at which simulations/experiments were performed. A dashed line is drawn at 300 K as a guide to the eye. Properties include: (a) the P2 order parameter, with experimental data from ref. 56; (b) the bulk density, with experimental data from ref. 57; and (c) 5CB diffusion coefficients, with experimental data from ref. 58. The component of the diffusion coefficient parallel to the director vector (D∥), the component perpendicular to the director vector (D⊥), and the average diffusion coefficient (<D>) are separately reported. | ||
The P2 order parameter varies from a value near 1 in the nematic phase and a value near 0 in the isotropic phase at the TNI.55 Details on the calculation of this parameter are presented in the ESI.† The experimental data indicate that TNI is near 308.2 K,56–58 which is reasonably reproduced by the UA model as expected. The AA model instead produces a nematic phase at temperatures higher than the experimentally determined TNI. However, the value of the P2 order parameter calculated in the nematic phase using the AA model is in good agreement with the UA model and only slightly exceeds the experimental value, suggesting that structural properties of the nematic phase are reasonable even if the thermodynamics of the phase transition are inaccurate. Fig. 2b shows the LC density as a function of temperature. The AA model is in much better agreement with the experimental data than the UA model, again indicating that the model reproduces LC structure accurately. Finally, Fig. 2c shows the average mesogen diffusion coefficient and components of the diffusion coefficient parallel and perpendicular to the LC director vector. These data show that the AA model is in excellent agreement with experimental measurements while the UA model overestimates mesogen diffusivity by nearly two orders of magnitude. We attribute the increased diffusivity in the UA model to the absence of explicit hydrogen atoms as previously noted for other UA models.53,54 Together, these data indicate that the structural and dynamic properties of nematic-phase 5CB predicted by the AA model are in good agreement with experimental values, permitting further evaluation of LC–analyte interactions.
Analyte partitioning into bulk 5CB
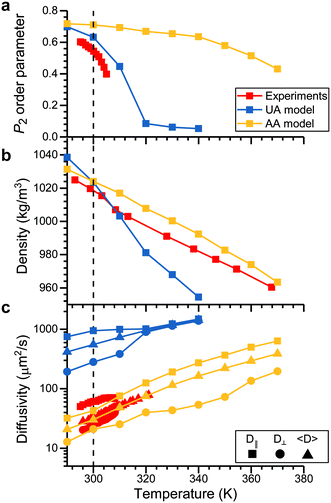
Sensor activation requires the partitioning of analytes from the vapor phase into the LC followed by analyte diffusion to the substrate. We thus sought to quantify the thermodynamics of analyte partitioning into the LC as a first step toward characterizing analyte transport. Analyte partitioning was quantified by computing the solvation free energy, ΔGsolv, which is the free energy change for transferring the analyte from an ideal gas vapor phase to bulk LC (schematically illustrated in Fig. 3a). ΔGsolv can be related to the Henry's law constant, KH, the LC molar density, ρLC, the pressure, p, the temperature, T, and the ideal gas constant, R, by eqn (2):59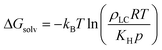 | (2) |
 | ||
| Fig. 3 Validation of solvation free energy calculations. a) Simulation snapshots illustrating the two states used to calculate the solvation free energy (ΔGsolv). The analyte is shown in red. b) ΔGsolv calculated using the UA and AA 5CB models. Values are compared to experimental estimates based on Henry's law constants using eqn (2). | ||
Negative values of ΔGsolv correspond to smaller values of KH, indicating more favorable partitioning into the LC film. To validate the computational approach, we calculated ΔGsolv for analytes with experimentally reported Henry's law constants in 5CB. Fig. 3b shows the solvation free energies using both the UA and AA 5CB models for methane (CH4), carbon dioxide (CO2), glutaraldehyde (GLU), and DMMP. Simulation values are compared to solvation free energies calculated using eqn (2) with experimentally determined Henry's law constants. The CH4 and CO2 Henry's law constants were computed by de Groen et al. by measuring the bubble point of the gas in a closed system with the LC.24,25 The GLU Henry's law constant was measured using the Purpald method60 in which aldehydes react with a dye to allow their concentration to be inferred from absorbance measurements.26 The DMMP Henry's law constant is an order-of-magnitude estimate based on experimental measurements using a mass-transfer model of chemoresponsive LC sensor activation.15,23 Values of ΔGsolv calculated using both the AA and UA 5CB models reproduce the experimental values within ∼1–2 kBT for each analyte. The agreement between these values indicates that the AA 5CB and analyte models can reproduce experimental measurements of analyte partitioning and that the AA and UA models are of comparable accuracy.
In addition, we compared the values calculated with the AA model to polarizable continuum (PC) model using benzonitrile as a solvent (details of the DFT calculations and comparisons are presented in Fig. S8†), which has been used previously as a DFT alternative for calculating solvation energies for benzonitrile-containing LCs.61 We found that errors between the AA and PC models are within the DFT mean squared error of 0.2 eV.62 We note that while this justifies the use of the PC model for comparison with DFT-calculated values for small molecules in 5CB, the AA model error is smaller than DFT errors compared to experiments as shown in Fig. 3b. Because the results in Fig. 2c indicate that the AA 5CB model provides more accurate calculations of 5CB diffusion than the UA model and diffusivities cannot be obtained from the PC model, we will only present results using the AA model for the remainder of this study.
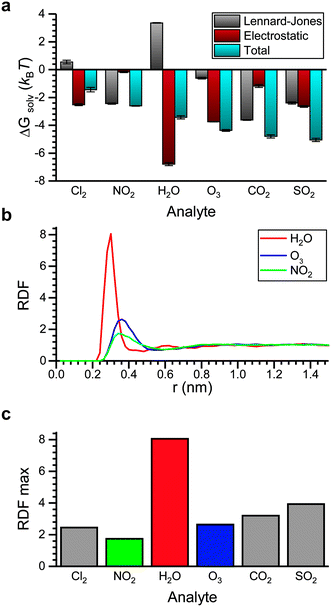
We next computed ΔGsolv for the six atmospheric analytes of interest (Fig. 4a). ΔGsolv is negative for each analyte, indicating that partitioning into the LC from the vapor phase is thermodynamically favorable. The magnitude of ΔGsolv varies between −1.44 kBT for Cl2, which partitions least favorably into the LC, and −5.05 kBT for SO2, which partitions most favorably. These differences indicate that corresponding Henry's law constants and thus dissolved analyte concentrations should vary by an order of magnitude according to eqn (2). We note that the free energies predicted by these simulations neglect any possible analyte dissociation or reactions between analytes such as O3 or Cl2 and 5CB that could affect partitioning.63,64
Fig. 4a further decomposes ΔGsolv into contributions related to electrostatic interactions and LJ interactions. The electrostatic contribution accounts for hydrogen bonding and dipole–dipole interactions and is largest for the analytes with the largest dipole moments (H2O, SO2, and O3; see ESI† Fig. S2). The significant contribution of the electrostatic interactions to ΔGsolv for these analytes suggests that their partitioning would be sensitive to the dielectric constant of the bulk LC. The largest electrostatic contribution is obtained for H2O, which we attribute to hydrogen bond formation as further discussed below. The LJ contribution accounts for van der Waals interactions between the analyte and surrounding LC as well as the perturbation to LC structure due to excluded volume interactions. Because multiple energetic interactions contribute to the LJ contribution, trends are more difficult to discern. However, we do note that the magnitude of the LJ contribution to ΔGsolv is similar for NO2, CO2, and SO2 due to the similar chemical structures and molecular geometries of these analytes. H2O is the only analyte with a significant positive LJ contribution.
To investigate interactions with the polar nitrile group on 5CB, Fig. 4b shows radial distribution functions (RDFs) that report the density of analyte molecules at a distance r from the COM of the nitrile group with values normalized by the bulk density of analyte. RDFs are computed for H2O, O3, and NO2 because these analytes span a range of electrostatic contributions to ΔGsolv (Fig. 4a). The RDF for H2O shows a significantly larger peak than the other two analytes, indicating the preferential coordination of water molecules with the nitrile group. This result is consistent with the formation of hydrogen bonds. We also calculated a significant hydrogen bond strength of −0.27 eV between the water molecule and the benzonitrile in gas phase with DFT. Fig. 4c compares the maximum value of the RDF for all six analytes. H2O exhibits the strongest coordination to the nitrile group, followed by SO2 which also has a large dipole moment. These results suggest that in addition to tuning the bulk electrostatic properties of the LC to mediate partitioning, tuning the specific chemistry of polar groups can affect analyte interactions with the mesogen.
Interfacial partitioning and dynamics
Values of ΔGsolv report the thermodynamics of analyte partitioning between the vapor phase and bulk LC. However, the structure of a LC can differ from its bulk structure near the vapor–LC interface. Fig. 5a shows the normalized density of the LC as a function of the z-component of the distance from the vapor–LC interface (dz). The interface was defined as the position at which the 5CB density was half that of the bulk density. We note that the density approaches zero on the vapor side of the interface because mesogens do not enter the vapor phase within the simulation timescale. The oscillations in the density near the interface (−3 < dz < 0 nm) indicate smectic-like ordering, whereas the density plateaus to a bulk value far from the interface (dz < −3 nm). This result, which is consistent with prior simulation and experimental findings,18 suggests that the smectic-like region near the interface could lead to interfacial barriers to analyte partitioning that are not captured by ΔGsolv.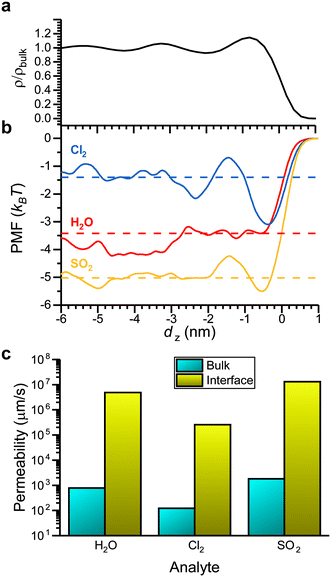 | ||
| Fig. 5 Comparison of bulk and interfacial partitioning. a) 5CB density as a function of the z-component of the distance from the vapor–LC interface (dz). The density is normalized by the density of bulk 5CB in the nematic phase. b) Potentials of mean force (PMFs) as a function of dz for Cl2, H2O, and SO2. PMF values are set to zero at dz= 1 nm. c) Permeabilities computed for the bulk LC and the interfacial region using eqn (4). | ||
To investigate this possibility, we performed umbrella sampling to compute the potential of mean force (PMF) for transferring an analyte across the vapor–LC interface. The PMF reports the free energy change associated with moving an analyte from a reference position in the vapor phase as a function of dz. Umbrella sampling was performed for H2O, Cl2, and SO2 because they span the range of ΔGsolv values according to Fig. 4a. Fig. 5b shows PMFs for each analyte. For reference, the corresponding value of ΔGsolv computed for partitioning between the vapor phase and bulk LC is shown as a dashed line. The PMFs exhibit similar features, including a plateau at a value similar to ΔGsolv for dz < −3 nm, oscillations for −3 < dz < 0 nm, and a local minimum near dz = 0 nm (i.e., at the vapor–liquid interface), although the local minimum is not observed for H2O. The agreement between values of ΔGsolv and the PMF values far from the interface confirms that the system size is sufficient to model interfacial behavior without finite size effects. The oscillations in the PMFs correspond to oscillations in the LC density, indicating that PMF features mirror the smectic layering of the LC. The local minima at the interface for Cl2, and SO2 suggest that these analytes could potentially accumulate at the interface, affecting transport into the bulk LC film. However, the magnitude of the PMF variations are small (<3 kBT).
To determine if variations in the PMF are significant enough to affect analyte transport across the LC film, we computed analyte permeabilities in the bulk LC and at the vapor–LC interface. The permeability, P, relates the analyte flux across an interface, J, to the concentration difference, ΔC, as shown in eqn (3):
| J = PΔC | (3) |
The permeability can be calculated using the inhomogeneous solubility-diffusion model (eqn (4)) which accounts for spatial variations in analyte diffusivity and solubility. D(dz) is the analyte diffusion coefficient as a function of dz and the PMF accounts for spatial variations in solubility:65
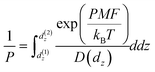 | (4) |
We applied eqn (4) to compute analyte permeability at the vapor–LC interface using the PMFs shown in Fig. 5a and by calculating D(dz) from the umbrella sampling trajectories as described in the ESI† (ESI Fig. S4). We defined the limits of integration as d(1)z = − 6 nm and d(2)z = 1 nm to capture only interfacial behavior. We similarly applied eqn (4) to compute the permeability of the bulk LC by equating the PMF to ΔGsolv and D(dz) to the component of the bulk analyte diffusion coefficient parallel to the LC director vector. Since these values are constant in bulk LC, the integrand can be factored out of the integral in eqn (4) and the remaining integral evaluates to the LC film thickness, δ, which we set to 18 μm based on experimental systems.8,15–17Fig. 5c compares the interfacial and bulk permeabilities for O3, H2O, and Cl2. For all three analytes, the bulk permeability is four orders of magnitude lower than the interfacial permeability. This suggests that transport across the LC region near the vapor–LC interface is fast in comparison to the transport through the bulk LC film and the oscillations in the PMFs do not significantly influence analyte transport.
Estimated times for sensor activation using transport model
We next sought to predict the sensor activation time using the simulation results to determine if this timescale could be used to distinguish between activation by different analytes. Since Fig. 5c indicates that analyte transport is dominated by the bulk properties of the LC, we modified a mass-transport model originally derived by Hunter and Abbott to relate the analyte solvation free energies and diffusivities in bulk LC to the sensor activation time, tact.15,23 We assume that analyte transport to the substrate is slow compared to the timescale for the displacement of substrate-bound mesogens (i.e., sensor activation is transport-limited). This assumption is justified by prior experimental measurements for the activation of LC sensors by DMMP that showed that the sensor activation time is limited by mass transfer across the vapor–LC interface.23 Prior computational and experimental studies have also shown that mesogen displacement timescales can be varied by modifying the chemical composition of the substrate independently of the bulk LC composition.16,17 Therefore, we assume that the transport-limited regime is achievable experimentally and investigate the ability of tact to distinguish activation by different analytes.To relate tact to simulation quantities, we assume that analyte transport within the LC is at pseudo steady-state and analyte accumulates within the LC film. tact is then the time necessary for the average concentration of analyte in the LC film to reach a threshold concentration, Cact, for which there is a sufficient thermodynamic driving force to displace the mesogens at the substrate's surface and trigger sensor activation. Cact is a quantity that depends on the elastic properties of the LC and the analyte–substrate chemistry. Therefore, Cact will likely be different for each analyte and may vary by orders of magnitude. However, we can still identify trends relating analyte diffusivity and partition coefficients to tact by assuming that Cact is constant for all studied analytes. The ESI† includes further discussion of these assumptions, a derivation of the mass-transfer model presented below, and a derivation of an alternate mass-transport model which assumes that Cact approaches zero.
Using these assumptions, eqn (5) relates tact to the film thickness, δ, the overall mass transfer coefficient, Kov, the concentration of analyte in the vapor stream, Cvap, and Cact:
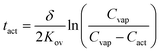 | (5) |
Eqn (5) indicates that the activation time will decrease as a function of the overall mass transfer coefficient. Kov is related to the diffusion coefficient, D, partition coefficient, Kp, and the vapor–LC interface mass transfer coefficient, kcviaeqn (6):
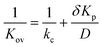 | (6) |
The overall mass transfer coefficient can exist in two regimes: either mass transfer at the interface dominates or analyte partitioning and diffusion dominates. Kp is related to the Henry's law constant, and correspondingly, the solvation free energy of an analyte viaeqn (7):
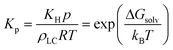 | (7) |
Since the diffusivities of vapor-phase small molecules typically vary by less than a factor of two,66 we assume kc = 312.5 μm s−1 for all analytes based on the value obtained by Hunter and Abbott.23Kov then depends on two experimentally determined, analyte independent quantities (kc and δ) and two simulation-derived, analyte specific quantities (Kp and D). For simplicity, eqn (8) defines the permeance, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) , in terms of the two simulation-derived quantities:
, in terms of the two simulation-derived quantities:
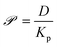 | (8) |
Calculating the permeance thus allows Kov to be compared between different analytes. Computing tact, however, requires knowledge of Cact, which is dependent on the thermodynamic driving force. Eqn (9) eliminates Cact by normalizing the sensor activation time by the sensor activation time previously reported for DMMP transport across 5CB, tDMMP, which is between 10–100 s depending on the substrate properties, and assuming Cact is constant between different analytes and detection schemes.23
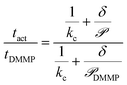 | (9) |
The only unknown quantity in eqn (9) is the permeance, which is computed from the simulations for each analyte. We note that an alternative mass-transport model, which instead assumes that analyte molecules rapidly, irreversibly adsorb to the substrate without accumulating in the film, also leads to the same dependence of tact on ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) as in eqn (9) without assuming similar Cact. Further details on this model are presented in the ESI.†
as in eqn (9) without assuming similar Cact. Further details on this model are presented in the ESI.†
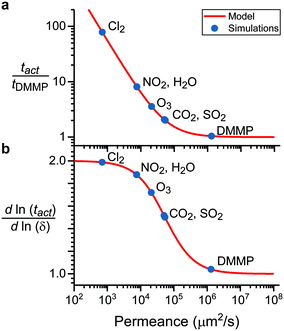
Fig. 6a shows the relative sensor activation times in 5CB determined by eqn (9) for the six atmospheric analytes of interest and for DMMP as a reference. Points are labeled based on values of the permeance computed using ΔGsolv and the bulk-phase analyte diffusivity while eqn (9) is plotted as a red line. Different analytes exhibit different sensor activation times, supporting the hypothesis that this timescale could be used to distinguish sensor activation by different analytes. DMMP, which has the highest permeance due to its highly favorable partitioning into 5CB (Fig. 3b), lies in a regime where the activation time plateaus because 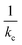 is significantly larger than
is significantly larger than 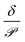 in eqn (9), indicating that overall mass transport is limited by mass transfer across the vapor–LC interface. This result agrees with previous experimental conclusions for DMMP transport.23 However, the other six analytes all have permeances lower than that of DMMP, and as a result their sensor activation times are limited by analyte transport through the LC film.
in eqn (9), indicating that overall mass transport is limited by mass transfer across the vapor–LC interface. This result agrees with previous experimental conclusions for DMMP transport.23 However, the other six analytes all have permeances lower than that of DMMP, and as a result their sensor activation times are limited by analyte transport through the LC film.
To facilitate experimental validation of the transport model, eqn (10) quantifies the dependence of the activation time on the film thickness as a function of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) :
:
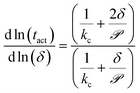 | (10) |
Fig. 6b shows the dependence of the activation time on the film thickness for the same seven analytes as Fig. 6a. Most of the analytes lie between the two regimes of linear and quadratic dependence, with the extremes being Cl2, which is closer to the quadratic regime, and DMMP, which is closer to the linear regime. This model of the dependence on film thickness allows for experimental verification of the transport model and predicted permeance values by determining the change in activation time associated with a change in film thickness.
Comparison of transport in TL205 analog to 5CB
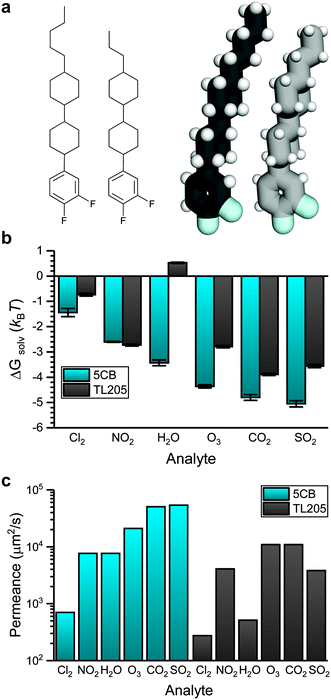
Fig. 6 shows how the sensor activation time in the transport-limited regime depends on analyte permeance in the bulk LC. This analysis suggests that the activation times for NO2 and H2O are similar, as are the activation times for CO2 and SO2, which suggests that sensor activation times in 5CB may not distinguish these analytes due to their similar permeances (within the assumptions of the mass-transport model). Instead, alternative LC materials may lead to distinct permeances for these pairs of analytes. Differences in analyte permeance in 5CB are primarily related to differences in analyte solvation free energies. For example, the partition coefficients for the seven analytes studied in Fig. 6 varies from 0.24 to 0.0064 whereas the diffusivity varies from 243 μm2 s−1 to 637 μm2 s−1. This comparison indicates that tuning the solvation free energy is the more important factor when considering sensor design. Fig. 3 further suggests that solvation free energies depend on electrostatic interactions and hydrogen bonding interactions with the LC to different degrees for different analytes, suggesting that tuning mesogen chemical properties can affect activation times to further improve sensor selectivity.To evaluate the effect of mesogen chemical properties on transport, we computed ΔGsolv and determined corresponding analyte permeances in TL205. TL205 is a proprietary mixture of fluorinated, nonpolar mesogens that is in the nematic phase at room temperature.20 We approximated TL205 as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of the two components shown in Fig. 7a. AA models for both components were parameterized using the same strategy used for 5CB. The mixture was similarly annealed to obtain a well-mixed nematic phase that was then used to perform analyte solvation free energy calculations. While both TL205 components lack the nitrile groups needed to bind to metal salt substrates, mixtures of mesogens with additives containing nitrile groups can act as chemoresponsive sensors.8 We assume that bulk TL205 is thus a suitable model for a chemoresponsive mixture of TL205 with a nitrile-containing additive (e.g., 5CB).
1 mixture of the two components shown in Fig. 7a. AA models for both components were parameterized using the same strategy used for 5CB. The mixture was similarly annealed to obtain a well-mixed nematic phase that was then used to perform analyte solvation free energy calculations. While both TL205 components lack the nitrile groups needed to bind to metal salt substrates, mixtures of mesogens with additives containing nitrile groups can act as chemoresponsive sensors.8 We assume that bulk TL205 is thus a suitable model for a chemoresponsive mixture of TL205 with a nitrile-containing additive (e.g., 5CB).
Fig. 7b compares ΔGsolv for the six atmospheric analytes in bulk 5CB and TL205. ΔGsolv is less favorable in TL205 than in 5CB for all analytes except NO2, with H2O, O3, and SO2 exhibiting the largest increases in ΔGsolv. These three analytes had the largest contribution from electrostatic interactions for partitioning in 5CB (Fig. 4a), and as expected the electrostatic contribution to the solvation free energy in TL205 also dictates the change in the total solvation free energy (ESI† Fig. S7). The dielectric constant of TL205 is approximately half of the dielectric constant of 5CB,67,68 explaining the less favorable partitioning of these three analytes. H2O is the only analyte for which the value of ΔGsolv is positive, indicating unfavorable partitioning. This result can be explained by the importance of hydrogen bonds to the nitrile group in 5CB (Fig. 4c), which are absent in TL205.
We next translated the results of Fig. 7b and analyte diffusion coefficient measurements (ESI† Fig. S3) into permeances using eqn (8). Fig. 7c compares analyte permeances in both 5CB and TL205. In general, the less favorable partitioning of more polar analytes into TL205 translates into lower permeances in TL205 than in 5CB. In particular, the permeances of H2O and SO2 are significantly reduced. Importantly, the permeances of NO2 and H2O differ significantly in TL205, as do the permeances of CO2 and SO2. Thus, while sensor activation times for these analytes were indistinguishable in 5CB, constructing a sensor from TL205 instead would facilitate selectivity between these analytes, potentially enabling the construction of sensor arrays comprised of both 5CB- and TL205-based sensors to distinguish between all six atmospheric analytes.
Conclusions
In this work, we performed classical molecular dynamics simulations to study the partitioning and diffusion of small-molecule analytes in chemoresponsive liquid crystal sensors. We developed an all-atom model of a common mesogen, 5CB, and nine analytes, including four atmospheric pollutants and two ambient atmospheric species. We validated the simulation models by showing that the all-atom 5CB model reproduces experimental measurements of LC structure and more closely matches experimental diffusivity measurements than a widely used united-atom model. Simulated solvation free energies for a subset of analytes also compared favorably to solvation free energies obtained from experimentally determined Henry's law constants. Using these models, we calculated the solvation free energies of the six atmospheric analytes in the bulk LC to quantify analyte partitioning. These results showed that electrostatic interactions, and particularly interactions between polar analytes and the nitrile group on 5CB, significantly impact partitioning. We also determined that variations in the LC density near the vapor–LC interface have minimal impact on analyte transport across LC films. Using the simulation-derived estimates of analyte partitioning and diffusivity in the bulk LC, we predicted sensor activation times by modifying a previously developed mass-transfer model. Our results indicate that differences in transport across the film translate to order-of-magnitude differences in activation times, suggesting that transport properties can be used to identify what analyte causes sensor activation. We further predict that replacing 5CB with TL205, another experimentally accessible LC, can lead to variations in relative sensor activation times to improve sensor selectivity. These results suggest that the computational screening of analyte interactions with mesogens or LC additives can be used to increase sensor selectivity to different analytes by tuning analyte transport and corresponding sensor activation times.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
J. K. S., J. I. G., M. M., and R. C. V.'s work is supported by the National Science Foundation under Grant No. 1837812. J. K. S. and R. C. V. used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1549562. J. K. S. and R. C. V. also used the computing resources and assistance of the UW-Madison Center for High Throughput Computing (CHTC) in the Department of Computer Sciences. The CHTC is supported by UW-Madison, the Advanced Computing Initiative, the Wisconsin Alumni Research Foundation, the Wisconsin Institutes for Discovery, and the National Science Foundation, and is an active member of the Open Science Grid, which is supported by the National Science Foundation and the U.S. Department of Energy's Office of Science. Part of the computational work conducted by J. I. G. and M. M. in this study was carried out through external computational resource facilities at the DoD High Performance Computing Modernization Program (US Air Force Research Laboratory DoD Supercomputing Resource Center (AFRL DSRC), the US Army Engineer Research and Development Center (ERDC), and the Navy DoD Supercomputing Resource Center (Navy DSRC), grant number: ARONC43623362), supported by the Department of Defense; and the National Energy Research Scientific Computing Center (NERSC) through the U.S. DOE, Office of Science under Contract No. DE-AC02-05CH11231. The authors would also like to acknowledge helpful discussions with N. L. Abbott, N. Bao, S. Jiang, J. Schauer, A. Smith, T. Szilvási, H. Yu, and V. M. Zavala.References
- M. Kampa and E. Castanas, Human health effects of air pollution, Environ. Pollut., 2008, 151(2), 362–367 CrossRef CAS PubMed.
- J. A. Bernstein, N. Alexis, C. Barnes, I. L. Bernstein, A. Nel, D. Peden, D. Diaz-Sanchez, S. M. Tarlo and P. B. Williams, Health effects of air pollution, J. Allergy Clin. Immunol., 2004, 114(5), 1116–1123 CrossRef.
- D. J. Nowak, S. Hirabayashi, M. Doyle, M. McGovern and J. Pasher, Air pollution removal by urban forests in Canada and its effect on air quality and human health, Urban Forestry & Urban Greening, 2018, 29, 40–48 Search PubMed.
- N. A. Ashford and C. C. Caldart, Environmental Protection Laws, Oxford Academic Press, 2015 Search PubMed.
- N. Greenberg, R. S. Carel, E. Derazne, H. Bibi, M. Shpriz, D. Tzur and B. A. Portnov, Different effects of long-term exposures to SO2 and NO2 air pollutants on asthma severity in young adults, J. Toxicol. Environ. Health, Part A, 2016, 79(8), 342–351 CrossRef CAS.
- T. Godish, Indoor air pollution control, CRC Press, 2019 Search PubMed.
- R. R. Shah and N. L. Abbott, Principles for measurement of chemical exposure based on recognition-driven anchoring transitions in liquid crystals, Science, 2001, 293(5533), 1296–1299 CrossRef CAS.
- T. Szilvasi, N. Bao, K. Nayani, H. Yu, P. Rai, R. J. Twieg, M. Mavrikakis and N. L. Abbott, Redox-Triggered Orientational Responses of Liquid Crystals to Chlorine Gas, Angew. Chem., Int. Ed., 2018, 57(31), 9665–9669 CrossRef CAS PubMed.
- K. J. Kek, J. J. Z. Lee, Y. Otono and S. Ishihara, Chemical gas sensors using chiral nematic liquid crystals and its applications, J. Soc. Inf. Disp., 2017, 25(6), 366–373 CrossRef CAS.
- R. Nandi and S. K. Pal, Liquid crystal based sensing device using a smartphone, Analyst, 2018, 143(5), 1046–1052 RSC.
- X. Ding and K.-L. Yang, Liquid crystal based optical sensor for detection of vaporous butylamine in air, Sens. Actuators, B, 2012, 173, 607–613 CrossRef CAS.
- A. Sen, K. A. Kupcho, B. A. Grinwald, H. J. VanTreeck and B. R. Acharya, Liquid crystal-based sensors for selective and quantitative detection of nitrogen dioxide, Sens. Actuators, B, 2013, 178, 222–227 CrossRef CAS PubMed.
- K. D. Cadwell, N. A. Lockwood, B. A. Nellis, M. E. Alf, C. R. Willis and N. L. Abbott, Detection of organophosphorous nerve agents using liquid crystals supported on chemically functionalized surfaces, Sens. Actuators, B, 2007, 128(1), 91–98 CrossRef CAS.
- H. Yu, T. Szilvási, K. Wang, J. I. Gold, N. Bao, R. J. Twieg, M. Mavrikakis and N. L. Abbott, Amplification of Elementary Surface Reaction Steps on Transition Metal Surfaces using Liquid Crystals: Dissociative Adsorption and Dehydrogenation, J. Am. Chem. Soc., 2019, 141(40), 16003–16013 CrossRef CAS PubMed.
- J. T. Hunter and N. L. Abbott, Adsorbate-induced anchoring transitions of liquid crystals on surfaces presenting metal salts with mixed anions, ACS Appl. Mater. Interfaces, 2014, 6(4), 2362–2369 CrossRef CAS.
- T. Szilvási, L. T. Roling, H. Yu, P. Rai, S. Choi, R. J. Twieg, M. Mavrikakis and N. L. Abbott, Design of chemoresponsive liquid crystals through integration of computational chemistry and experimental studies, Chem. Mater., 2017, 29(8), 3563–3571 CrossRef.
- T. Szilvasi, N. Bao, H. Yu, R. J. Twieg, M. Mavrikakis and N. L. Abbott, The role of anions in adsorbate-induced anchoring transitions of liquid crystals on surfaces with discrete cation binding sites, Soft Matter, 2018, 14(5), 797–805 RSC.
- M. Sadati, H. Ramezani-Dakhel, W. Bu, E. Sevgen, Z. Liang, C. Erol, M. Rahimi, N. Taheri Qazvini, B. Lin and N. L. Abbott, Molecular Structure of Canonical Liquid Crystal Interfaces, J. Am. Chem. Soc., 2017, 139(10), 3841–3850 CrossRef CAS.
- V. K. Gupta, J. J. Skaife, T. B. Dubrovsky and N. L. Abbott, Optical amplification of ligand-receptor binding using liquid crystals, Science, 1998, 279(5359), 2077–2080 CrossRef CAS PubMed.
- Z. Hussain, F. Qazi, M. I. Ahmed, A. Usman, A. Riaz and A. D. Abbasi, Liquid crystals based sensing platform-technological aspects, Biosens. Bioelectron., 2016, 85, 110–127 CrossRef CAS.
- Y. Cao, H. Yu, N. L. Abbott and V. M. Zavala, Machine Learning Algorithms for Liquid Crystal-Based Sensors, ACS Sens., 2018, 3(11), 2237–2245 CrossRef CAS.
- H. Yu, T. Szilvási, P. Rai, R. J. Twieg, M. Mavrikakis and N. L. Abbott, Computational chemistry-guided design of selective chemoresponsive liquid crystals using pyridine and pyrimidine functional groups, Adv. Funct. Mater., 2018, 28(13), 1703581 CrossRef.
- J. T. Hunter and N. L. Abbott, Dynamics of the chemo-optical response of supported films of nematic liquid crystals, Sens. Actuators, B, 2013, 183, 71–80 CrossRef CAS.
- M. de Groen, O. M. Molet, T. J. H. Vlugt and T. W. de Loos, Phase Behavior of Binary Mixtures of a Liquid Crystal and Methane, J. Chem. Eng. Data, 2015, 60(7), 2167–2171 CrossRef CAS.
- M. de Groen, B. C. Ramaker, T. J. H. Vlugt and T. W. de Loos, Phase Behavior of Liquid Crystal + CO2 Mixtures, J. Chem. Eng. Data, 2014, 59(5), 1667–1672 CrossRef CAS.
- X. Y. Bi and K. L. Yang, Real-time liquid crystal-based glutaraldehyde sensor, Sens. Actuators, B, 2008, 134(2), 432–437 CrossRef CAS.
- D. Tauber and C. von Borczyskowski, Single molecule studies on dynamics in liquid crystals, Int. J. Mol. Sci., 2013, 14(10), 19506–19525 CrossRef PubMed.
- A. Pizzirusso, R. Berardi, L. Muccioli, M. Ricci and C. Zannoni, Predicting surface anchoring: molecular organization across a thin film of 5CB liquid crystal on silicon, Chem. Sci., 2012, 3(2), 573–579 RSC.
- M. Ilk Capar, A. Nar, A. Ferrarini, E. Frezza, C. Greco, A. V. Zakharov and A. A. Vakulenko, Molecular structure and elastic properties of thermotropic liquid crystals: integrated molecular dynamics–statistical mechanical theory vs molecular field approach, J. Chem. Phys., 2013, 138(11), 114902 CrossRef CAS PubMed.
- A. A. Joshi, J. K. Whitmer, O. Guzmán, N. L. Abbott and J. J. de Pablo, Measuring liquid crystal elastic constants with free energy perturbations, Soft Matter, 2014, 10(6), 882–893 RSC.
- H. Sidky, J. J. de Pablo and J. K. Whitmer, In Silico Measurement of Elastic Moduli of Nematic Liquid Crystals, Phys. Rev. Lett., 2018, 120(10), 107801 CrossRef CAS PubMed.
- G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, Towards in silico liquid crystals. Realistic transition temperatures and physical properties for n-cyanobiphenyls via molecular dynamics simulations, ChemPhysChem, 2009, 10(1), 125–136 CrossRef CAS PubMed.
- M. Sadati, H. Ramezani-Dakhel, W. Bu, E. Sevgen, Z. Liang, C. Erol, M. Rahimi, N. Taheri Qazvini, B. Lin, N. L. Abbott, B. T. Roux, M. L. Schlossman and J. J. de Pablo, Molecular Structure of Canonical Liquid Crystal Interfaces, J. Am. Chem. Soc., 2017, 139(10), 3841–3850 CrossRef CAS PubMed.
- H. Ramezani-Dakhel, M. Sadati, R. Zhang, M. Rahimi, K. Kurtenbach, B. Roux and J. J. de Pablo, Water Flux Induced Reorientation of Liquid Crystals, ACS Cent. Sci., 2017, 3(12), 1345–1349 CrossRef CAS PubMed.
- H. Ramezani-Dakhel, M. Sadati, M. Rahimi, A. Ramirez-Hernandez, B. Roux and J. J. de Pablo, Understanding Atomic-Scale Behavior of Liquid Crystals at Aqueous Interfaces, J. Chem. Theory Comput., 2017, 13(1), 237–244 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef CAS PubMed.
- N. J. Boyd and M. R. Wilson, Optimization of the GAFF force field to describe liquid crystal molecules: the path to a dramatic improvement in transition temperature predictions, Phys. Chem. Chem. Phys., 2015, 17(38), 24851–24865 RSC.
- D. L. Cheung, S. J. Clark and M. R. Wilson, Parametrization and validation of a force field for liquid-crystal forming molecules, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(5 Pt 1), 051709 CrossRef CAS.
- X. Wei, J. B. Hooper and D. Bedrov, Influence of electrostatic interactions on the properties of cyanobiphenyl liquid crystals predicted from atomistic molecular dynamics simulations, Liq. Cryst., 2017, 44(2), 332–347 CAS.
- P. J. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98(45), 11623–11627 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis, J. Comput. Chem., 1990, 11(3), 361–373 CrossRef CAS.
- H. Berendsen, J. Grigera and T. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91(24), 6269–6271 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25 CrossRef.
- S. Bruckner and S. Boresch, Efficiency of alchemical free energy simulations. I. A practical comparison of the exponential formula, thermodynamic integration, and Bennett's acceptance ratio method, J. Comput. Chem., 2011, 32(7), 1303–1319 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30(13), 2157–2164 CrossRef.
- J. S. Hub, B. L. de Groot and D. van der Spoel, g_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates, J. Chem. Theory Comput., 2010, 6(12), 3713–3720 CrossRef CAS.
- M. J. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision D. 01, Gaussian. Inc., Wallingford, CT, 2009 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120(1–3), 215–241 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- H. Ramezani-Dakhel, M. Sadati, M. Rahimi, A. Ramirez-Hernandez, B. Roux and J. J. de Pablo, Understanding Atomic-Scale Behavior of Liquid Crystals at Aqueous Interfaces, J. Chem. Theory Comput., 2017, 13(1), 237–244 CrossRef CAS.
- M. R. Wilson, Molecular simulation of liquid crystals: progress towards a better understanding of bulk structure and the prediction of material properties, Chem. Soc. Rev., 2007, 36(12), 1881–1888 RSC.
- G. Gyawali, S. Sternfield, R. Kumar and S. W. Rick, Coarse-grained models of aqueous and pure liquid alkanes, J. Chem. Theory Comput., 2017, 13(8), 3846–3853 CrossRef CAS.
- N. D. Kondratyuk, G. E. Norman and V. V. Stegailov, Self-consistent molecular dynamics calculation of diffusion in higher n-alkanes, J. Chem. Phys., 2016, 145(20), 204504 CrossRef.
- D. Andrienko, Introduction to liquid crystals, J. Mol. Liq., 2018, 267, 520–541 CrossRef CAS.
- L. G. P. Dalmolen, S. J. Picken, A. F. de Jong and W. H. de Jeu, The order parameters < P2 > and < P4 > in nematic p-alkyl-p' -cyano-biphenyls : polarized Raman measurements and the influence of molecular association, J. Phys., 1985, 46(8), 1443–1449 CrossRef CAS.
- J. Deschamps, J. M. Trusler and G. Jackson, Vapor pressure and density of thermotropic liquid crystals: MBBA, 5CB, and novel fluorinated mesogens, J. Phys. Chem. B, 2008, 112(13), 3918–3926 CrossRef CAS PubMed.
- S. V. Dvinskikh, I. Furo, H. Zimmermann and A. Maliniak, Anisotropic self-diffusion in thermotropic liquid crystals studied by 1H and 2H pulse-field-gradient spin-echo NMR, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(6 Pt 1), 061701 CrossRef CAS PubMed.
- R. Olsen, B. Kvamme and T. Kuznetsova, Free energy of solvation and Henry's law solubility constants for mono-, di-and tri-ethylene glycol in water and methane, Fluid Phase Equilib., 2016, 418, 152–159 CrossRef CAS.
- J. J. Cournoyer, T. Kshirsagar, P. P. Fantauzzi, G. M. Figliozzi, T. Makdessian and B. Yan, Color test for the detection of resin-bound aldehyde in solid-phase combinatorial synthesis, J. Comb. Chem., 2002, 4(2), 120–124 CrossRef CAS PubMed.
- K. Wang, M. Jirka, P. Rai, R. J. Twieg, T. Szilvási, H. Yu, N. L. Abbott and M. Mavrikakis, Synthesis and properties of hydroxy tail-terminated cyanobiphenyl liquid crystals, Liq. Cryst., 2019, 46(3), 397–407 CrossRef CAS.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, A benchmark database for adsorption bond energies to transition metal surfaces and comparison to selected DFT functionals, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- H. F. Ridgway, B. Mohan, X. Cui, K. J. Chua and M. R. Islam, Molecular dynamics simulation of gas-phase ozone reactions with sabinene and benzene, J. Mol. Graphics Modell., 2017, 74, 241–250 CrossRef CAS PubMed.
- W. Dorrepaal and R. Louw, The mechanism of the vapor-phase chlorination of benzene derivatives, Int. J. Chem. Kinet., 1978, 10(3), 249–275 CrossRef CAS.
- C. T. Lee, J. Comer, C. Herndon, N. Leung, A. Pavlova, R. V. Swift, C. Tung, C. N. Rowley, R. E. Amaro, C. Chipot, Y. Wang and J. C. Gumbart, Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds, J. Chem. Inf. Model., 2016, 56(4), 721–733 CrossRef CAS PubMed.
- E. N. Fuller, P. D. Schettler and J. C. Giddings, New method for prediction of binary gas-phase diffusion coefficients, Ind. Eng. Chem., 1966, 58(5), 18–27 CrossRef CAS.
- N. Podoliak, O. Buchnev, M. Herrington, E. Mavrona, M. Kaczmarek, A. G. Kanaras, E. Stratakis, J.-F. Blach, J.-F. Henninot and M. Warenghem, Elastic constants, viscosity and response time in nematic liquid crystals doped with ferroelectric nanoparticles, RSC Adv., 2014, 4(86), 46068–46074 RSC.
- A. Bogi and S. Faetti, Elastic, dielectric and optical constants of 4'-pentyl-4-cyanobiphenyl, Liq. Cryst., 2001, 28(5), 729–739 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00126c |
| This journal is © The Royal Society of Chemistry 2020 |