Open Access Article
Open Access ArticleThe impact of reaction rate on the formation of flow-driven confined precipitate patterns†
Edina
Balog‡
a,
Paszkál
Papp‡
a,
Ágota
Tóth
 a,
Dezső
Horváth
a,
Dezső
Horváth
 b and
Gábor
Schuszter
b and
Gábor
Schuszter
 *a
*a
aDepartment of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1, Szeged, H-6720, Hungary. E-mail: schuszti@chem.u-szeged.hu
bDepartment of Applied and Environmental Chemistry, University of Szeged, Hungary
First published on 1st May 2020
Abstract
The production of solid materials via chemical reactions is abundant both in nature and in industrial processes. Precipitation reactions coupled with transport phenomena lead to enhanced product properties not observed in the traditional well-stirred systems. Herein, we present a flow-driven pattern formation upon radial injection in a confined geometry for various chemical systems to show how reaction kinetics modifies the emerging precipitation patterns. It is found that chemically similar elements, such as alkaline earth or transition metals react on very different time scales under the same experimental conditions. The patterns are quantified and compared both with literature results obtained in unconfined solution layers and with hydrodynamic simulations.
1 Introduction
Precipitation reactions play an important role in nature, science, and industry. Examples related to living organisms are the hexagonal aragonite (a polymorph of CaCO3) platelets building up the nacre covering some molluscs' interior shell1 and the antigen–antibody precipitation used to identify certain diseases.2 Synthetic grafts, i.e., artificial bone, are made of hydroxyapatite and collagen via bone tissue engineering by applying diammonium phosphate and calcium chloride precursors.3,4 The synthesis of superparamagnetic materials5 and layered double hydroxides6 is also often performed through one-pot precipitation reactions. Industrially relevant products (e.g., pharmaceuticals, pigments, metal oxides, etc.) are also synthesised in such a way.7In recent years, it has been shown that the properties of precipitate particles, e.g., their size and shape, can be highly controlled if the reaction is not performed with the traditional one-pot method. Processes involving transport phenomena, like diffusion or flow, inherently provide various spatial gradients (e.g., pH, concentration, etc.), which lead to modified crystallisation. In addition, avoiding vigorous mixing results in complex precipitation pattern formation. In this way, size controlled metal–organic frameworks,8 thermodynamically unstable polymorphs,9 one-dimensional membranes,10 and chemical gardens exhibiting a potential difference11 can be produced, to name a few. Some studies attempted to understand the possible consequences of underground carbon dioxide sequestration12 and the bioenergetics of membranes.13 The versatility of precipitation reactions was also shown by the observation of periodic calcium phosphate formation and pH change through the general enzymatic hydrolysis of urea.14 The stretching history of elastic materials can be retrieved via Liesegang-type precipitation reactions as well.15
All the examples listed above highlight how diverse precipitation studies are in either applied or fundamental research areas. As a next step to improve the control over product properties, an appropriate coupling, i.e., time scale matching of the chemical reaction with the transport phenomenon, is essential. Although crystallisation processes are thoroughly studied from this perspective, much less work has been done on precipitation, i.e., reactive crystallisation systems.7
An extensive precipitation kinetics study is not the focus of the present work. It is rather the investigation of how the reaction rate affects precipitation pattern formation under flow conditions in a confined geometry. Therefore, various reactants with equal concentrations are brought into contact with a common reactant (aqueous solution of oxalate ions) to ensure a large variety of reaction rates. Although sparingly soluble salts are produced in each case, some reactions can be considered instantaneous (e.g., the reactions of Ca(II), Sr(II), and Ba(II) ions) with respect to the flow while others take significantly longer times to yield a precipitate (Mg(II), Co(II), Ni(II), Cu(II), and Zn(II) ions). The patterns obtained with different chemical systems under the same experimental conditions are compared and the effect of a varying flow rate together with direct and reverse injection procedures is addressed. Hydrodynamic simulations are used to support experimental observations.
2 Experimental
The experimental setup was a horizontally oriented Plexiglas Hele-Shaw cell with a 21 × 21 cm2 practical reactor area, as frequently applied in the literature (see ESI† for a sketch).16–19 The lower and upper lids of the cell were separated by four tiny spacers (gap height h = 0.5 mm) at the corners. In the beginning of the direct injection experiments, an aqueous solution of either an alkaline earth or a transition metal chloride salt was filled into the cell gap as a host solution into which the other reactant solution was pumped (KDS-210 P-CE syringe pump) from below through a tiny hole (id = 1.15 mm) in the middle of the lower lid. In this way, the injected solution radially invaded the gap and displaced the host solution. The host solution was prepared in 0.25 M concentration by dissolving an appropriate amount of chloride salt of one alkaline earth or transition metal (i.e., either MgCl2·6H2O, CaCl2·2H2O, SrCl2·6H2O, BaCl2·2H2O, CoCl2·6H2O, NiCl2·6H2O, CuCl2·2H2O or ZnCl2). The injected solution (5 mL in each case) was 0.25 M sodium oxalate (Na2(COO)2) in the direct injection experiments. The volumetric flow rate changed from one experiment to another (Q = 1, 5, 10, 20, and 90 mL min−1). In the reverse injection experiments, the sodium oxalate solution served as a host solution, while the alkaline earth or transition metal solution invaded upon pumping.The Hele-Shaw cell was illuminated from above by two light sources and a dark metal sheet was placed below the reactor to provide a homogeneous background for recording the precipitate patterns. Top-view images (20.5 × 15.2 cm2 field of view with 1024 × 768 px2 spatial resolution) were obtained using a monochrome digital camera (Unibrain Compact Firewire-400) equipped with a wide angle Vivitar lens (28 mm, f 2.8).
The density, viscosity, and pH of each solution was measured using an Anton Paar DMA 500 density meter, ViscoQC 300-L rotational viscometer, and Thermo Orion 420A+ pH meter, respectively. The data set is presented in the ESI,† together with the solubility product of the corresponding sparingly soluble oxalate salts. Based on the experimental parameters, one can estimate a laminar flow in the cell gap characterised by the Reynolds number 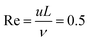 , where u, L, and ν are linear flow rate (10−3 m s−1), characteristic linear dimension (5 × 10−4 m), and kinematic viscosity (10−6 m2 s−1), respectively.
, where u, L, and ν are linear flow rate (10−3 m s−1), characteristic linear dimension (5 × 10−4 m), and kinematic viscosity (10−6 m2 s−1), respectively.
3 Modelling
In parallel with experiments, 3D hydrodynamic simulations were performed with an in-house modified version of the BoussinesqPimpleFoam solver of the OpenFOAM program to investigate the flow evolving in the confined geometry and leading to distinct patterns. Since the targeted experimental patterns exhibit radial symmetry, only a segment of the reactor (50 × 5 × 0.5 mm3 physical dimensions with 100 × 50 × 25 volume element discretisation) is modelled during the calculations. The mixing of the two miscible liquids with different densities is described by solving the Navier–Stokes equation applying the Boussinesq approximation, i.e.,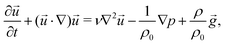 | (1) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , t, ν, ρ0, ρ, and g are linear flow velocity vector, time, kinematic viscosity, density of solvent (water), density of medium, and gravitational acceleration, respectively. The density of the medium is defined as
, t, ν, ρ0, ρ, and g are linear flow velocity vector, time, kinematic viscosity, density of solvent (water), density of medium, and gravitational acceleration, respectively. The density of the medium is defined as| ρ = ρ0 + ∑ρici, | (2) |
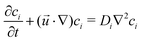 | (3) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , Dirichlet boundaries are defined for the inlet and outlet sides of the rectangular mesh with respect to the flow; a Neumann zero gradient is maintained on the upper and lower sides corresponding to the liquid–reactor wall interface; periodic boundaries are applied on the sides of the liquid perpendicular to the main stream to ensure continuity in the horizontal plane. The same conditions are used for ci as well with the exception of the outlet, where a Neumann zero gradient is set to avoid the generation of a reactant sink. To compare experiments and simulations, patterns emerging at similar linear flow velocities are obtained for which the volumetric flow rate set in experiments is converted into a linear one (see ESI†).
, Dirichlet boundaries are defined for the inlet and outlet sides of the rectangular mesh with respect to the flow; a Neumann zero gradient is maintained on the upper and lower sides corresponding to the liquid–reactor wall interface; periodic boundaries are applied on the sides of the liquid perpendicular to the main stream to ensure continuity in the horizontal plane. The same conditions are used for ci as well with the exception of the outlet, where a Neumann zero gradient is set to avoid the generation of a reactant sink. To compare experiments and simulations, patterns emerging at similar linear flow velocities are obtained for which the volumetric flow rate set in experiments is converted into a linear one (see ESI†).
4 Results and discussion
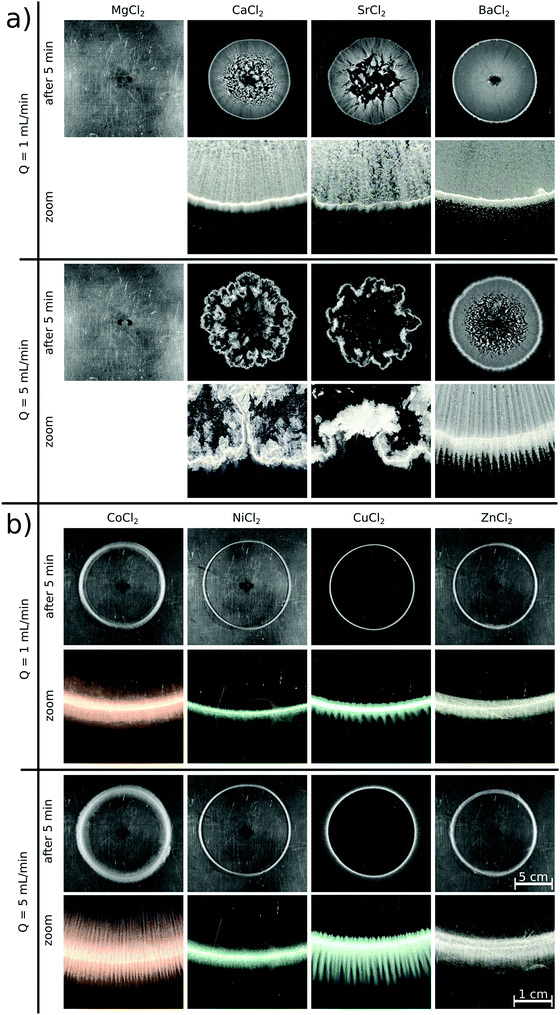
Upon radially injecting the oxalate solution into the appropriate host solution, convective mixing takes place within the confinement across the gap height because of the density difference between the solutions (see ESI† for concentration profile). The estimated Péclet number (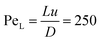 , where D = 2 × 10−9 m2 s−1 is the mass diffusion coefficient) shows that diffusive mixing is negligible in the main flow direction. Supersaturation (S) of the reactants is reached in the mixing zone and precipitation will commence. The characteristics of the emerging pattern depend on the coupling of hydrodynamics and chemical reaction; representative images are shown in Fig. 1.
, where D = 2 × 10−9 m2 s−1 is the mass diffusion coefficient) shows that diffusive mixing is negligible in the main flow direction. Supersaturation (S) of the reactants is reached in the mixing zone and precipitation will commence. The characteristics of the emerging pattern depend on the coupling of hydrodynamics and chemical reaction; representative images are shown in Fig. 1.
Although supersaturation is maintained in the case of the MgCl2 host solution as well, a precipitate is not seen either at the end of the injection or after waiting 5 minutes independent of the flow rate (Fig. 1a). A rough estimate for the supersaturation is S > 102 supposing that 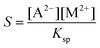 is applicable, where [A2−] and [M2+] stand for the concentration of oxalate and magnesium ions in the mixing zone, respectively, and Ksp is the solubility product of the Mg(COO)2(s) precipitate (pKsp = 4.07).20 Mixing the two reactants in a beaker leads to precipitation after approximately 7 min. Therefore, the absence of the precipitate within the time frame of the injection experiment suggests that the reaction is slow compared to the time scale of the convective transport.
is applicable, where [A2−] and [M2+] stand for the concentration of oxalate and magnesium ions in the mixing zone, respectively, and Ksp is the solubility product of the Mg(COO)2(s) precipitate (pKsp = 4.07).20 Mixing the two reactants in a beaker leads to precipitation after approximately 7 min. Therefore, the absence of the precipitate within the time frame of the injection experiment suggests that the reaction is slow compared to the time scale of the convective transport.
By changing the host solution to another alkaline earth metal ion (i.e., Ca(II), Sr(II), or Ba(II)) solution, a precipitate immediately appears upon injection, proving that those reactions are significantly faster than the previous chemical system. Patterns evolve with a radial symmetry in each case at Q = 1 mL min−1 flow rate (Fig. 1a). The major difference between them is seen in the interior part, which becomes more homogeneously covered as the molar weight of the product increases, i.e., towards the Ba(II) system. In addition, the shapes of the Ca(II), Sr(II), and Ba(II) oxalate patterns presented here are in good agreement with the literature where likewise fast reactions and the formation of carbonates are investigated.19,21 In those studies, significantly larger crystals are found in the case of the barium ion, which thus sediment faster resulting in a homogeneous interior pattern at a sufficiently low flow rate. Increasing the injection rate to Q = 5 mL min−1 leads to symmetry breaking because of the emergence of hydrodynamic instabilities when the aggregated precipitate particles are flushed away and sediment.22 This effect is more pronounced in the Ca(II) and Sr(II) systems than in the Ba(II) one due to the weight of the crystals. Focusing on the pattern peripheries (close-ups in Fig. 1a), some patterns exhibit a stripy structure, which depends on the flow rate as well. The buoyancy-driven Rayleigh–Taylor hydrodynamic instability leading to such pattern formation is well-known in the literature.23,24 At Q = 1 mL min−1, the stripes become less visible from the Ca(II) to the Ba(II) system, and they are more and more suppressed outside of the pattern. Further increasing the flow rate leads to different Ca(II) and Sr(II) patterns with radial symmetry breaking, since the particles start forming aggregates. In the Ba(II) system, however, the greater flow rate results in clearly visible precipitate stripes both in the interior and exterior parts of the pattern.
If the host solution is changed from an alkaline earth metal to a transition metal solution, significantly different patterns are formed even if the experimental conditions maintained are identical with the previous systems (Fig. 1b). Right at the end of injection, a precipitate is only seen in the Cu(II) system. Five minutes later, however, an annular precipitate region is visible in each case. This suggests that – under the given experimental conditions - the Co(II), Ni(II), and Zn(II) systems are faster than the Mg(II) system, but slower than the Cu(II) one where the precipitate appears shortly after the start of injection. The observations are valid for both flow rates. These reactions being relatively slow compared to the flow lead to different patterns than that seen for the alkaline earth metal solutions, i.e., no precipitate appears within the pattern perimeter. Although supersaturation is reached in the mixing zone of the reactants, neither a colloidal solution nor macroscopic crystals form within the time scale of the injection because of slow nucleation and/or crystal growth. Therefore, the mixing is only determined by the density distribution of the invading and host solutions and not modified by the sedimentation of particles. A precipitate is present only in the region where the leading edge of the invading solution stops at the end of injection. Although the Cu(II) system is significantly faster than the other transition metal systems used, very similar patterns are obtained.
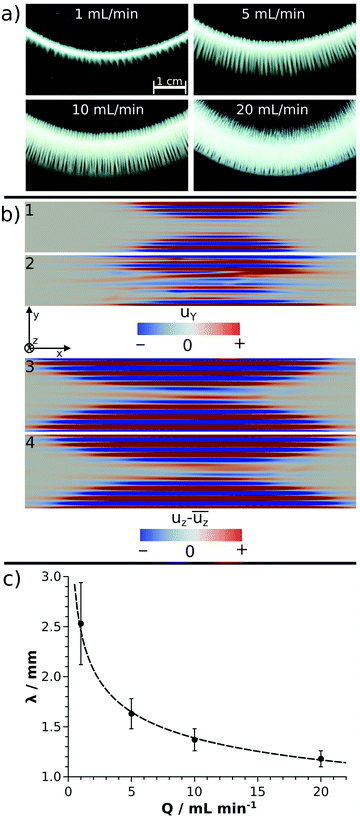
In a closer view, each annular pattern seen in Fig. 1b exhibits a stripy, saw-like structure; only the number and the length of the saw teeth change (Fig. 2a). Similar patterns have been observed if the host solution is not confined between two sheets or if the gap height is sufficiently large, which therefore gives rise to the formation of a gravity current at the tip of the invading solution.23 Three distinct regimes of such a flow field can be identified: (i) convection rolls in the flow direction at the tip of the injected liquid; (ii) transverse convection rolls slightly behind the tip; and (iii) diffusive mixing above the body of the injected liquid. Precipitate stripes appear if the precipitation and sedimentation are prominent in the transverse mixing zone. In those systems, according to the literature,25 the distance between the middle of two stripes (λ/mm) scales as λ ∝ Δρ−1/3, where Δρ is the density difference (g cm−3) of the invading and host solutions. Since the gap height is small (0.5 mm) in our confined experiments, the invading liquid fills the entire gap and displacement takes place instead of the evolution of gravity current. In this context, Δρ is expected to play a less dominant role in pattern formation, since buoyancy-driven mixing is hindered behind the tip. On the other hand, the injection rate influencing the expansion of the flow profile can contribute significantly. The λ values determined in our confined experiments for various chemical systems (Ba(II), Co(II), Ni(II), Cu(II), and Zn(II)) at Q = 5 mL min−1 have been plotted as a function of Δρ (see ESI†). As expected for sufficiently fast reactions (Ba(II) and Cu(II)), λ decreases with increasing Δρ. The scaling mentioned could not be tested because of the low Δρ range available in our experiments, and also, only a few fast reactions produced a saw-like pattern at a given flow rate. On the other hand, we observed that λ strongly depends on the ratio of the chemical and hydrodynamic time scales at a given Δρ. The smaller the reaction rate, the more densely populated the stripes; e.g., the Cu(II)-oxalate formation being significantly faster than that of Zn(II)-oxalate exhibits λ ≈ 1.6 mm while λ ≈ 0.5 mm in the latter case. The Co(II) and Ni(II) systems being in between the two previous systems in terms of reaction rate show intermediate spacing values (λ ≈ 1.1–1.2 mm). One may speculate that such an effect either originates in the different precipitate particle size influencing sedimentation or it is related to the time elapsed between the end of injection and the appearance of precipitate due to the diminishing flow field.
The hydrodynamic simulations performed with different flow rates for the Cu(II) model system show undulating flow profiles in both directions (y and z) perpendicular to the main stream (x), as presented in Fig. 2b. Since the time scale of the chemical reaction is comparable to the flow in the modelled systems, the evolution of the precipitate stripes can be understood on the basis of the flow profiles. The precipitate particles start forming in the vicinity of the supersaturated tip of the invading liquid and settle down in the regions where the flow becomes sufficiently weak. The blue stream lines in Fig. 2b3 and 4 are the zones with downward convective flow, which are therefore responsible for sedimentation. These results obtained in a confined geometry agree well with the literature25 where similar buoyancy stripes were observed in sufficiently thick solution layers. The crossing red stream lines in Fig. 2b2 are comparable with the crossing of precipitate stripes found in experiments at Q = 10 mL min−1 flow rate (Fig. 2a). Although it is qualitatively seen both in experiments and simulations that the stripes become longer and more crowded with an increasing flow rate (Fig. 2a and b), a quantitative agreement is not achieved. In experiments, λ ≈ 1.4 mm is found at Q = 10 mL min−1 and it scales with flow rate as λ/mm = (2.5 ± 0.1)(Q/mL min−1)−0.25±0.01, as depicted by the fitted curve in Fig. 2c. In contrast, λ = 0.7 mm is determined for Q = 9.4 mL min−1 and changes only slightly with increasing flow rate, i.e., λ = 0.6 mm at Q = 94 mL min−1. This discrepancy might be attributed to the fact that our model does not take precipitation into account, only the mixing of the two miscible liquids is considered. In the experiments, however, the appearance of a solid phase and thus the change of reactant concentration via chemical reaction lead to a local density change in addition to the original Δρ. To achieve quantitative agreement between experiments and simulations in future works, these effects must be considered together with the effect of particle sedimentation on the local flow field. Besides the changes observed for the precipitate stripes, no further pattern type is seen in the transition metal systems upon increasing the flow rate. Since no (Co(II), Ni(II), and Zn(II) systems) or only a few (Cu(II) system) precipitates are present during injection, radial symmetry does not break even at higher flow rates (Fig. 1b, Q = 5 mL min−1).
As mentioned previously, although Cu(COO)2(s) forms during injection unlike the other presented transition metal oxalates, a rather similar macroscopic pattern is obtained by the end of the injection. The reason for this is that the precipitate particles start dissolving shortly after the reaction front passes by. Images taken during and after injection showing the evolution and dissolution of the pattern are presented in the ESI,† together with the grayscale based light intensity (I) and precipitate area (A) measurements over time (t). The maxima seen on the curves also highlight that the amount of precipitate and the area it covers significantly decrease once the injection stops. The dissolution of Cu(COO)2(s) is attributed to the formation of the dioxalatocuprate(II) complex in large oxalate ion excess provided by the invading oxalate solution around the sedimented particles. After the dissolution of the initially formed crystals, a few larger crystals grow within the pattern perimeter (see ESI;† a real time movie is also available). Optical microscopy revealed that the tiny and separated crystals formed during injection exhibit a prism shape, while the recrystallised and significantly larger needle-shaped particles form aggregates. Although the characterisation of such crystals does not fall into the scope of this study, we note that those were identified as Na2Cu(C2O4)2·2H2O in a similar system.26
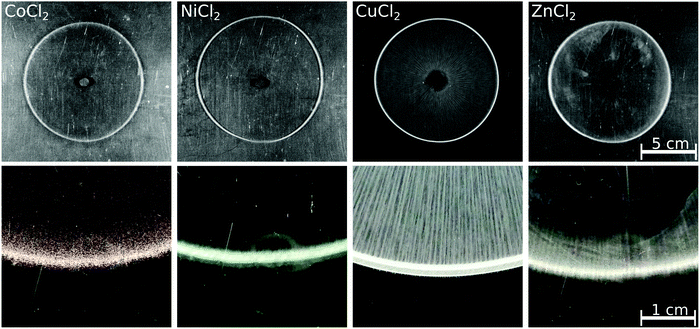
To see whether a pattern different from the annular one can be achieved in the case of the chosen transition metals when dissolution is excluded, reverse injection experiments were also performed. In these situations, the solution of the transition metal ions was pumped into the host oxalate solution; the patterns observed at Q = 1 mL min−1 flow rate are presented in Fig. 3. Similar to the direct injections, no precipitate was present at the end of the injection for the Co(II), Ni(II), and Zn(II) cases. After 5 minutes, however, precipitate rings became easy to see. Since the obtained patterns were not disks but annuli, one can conclude that dissolution did not play a role in pattern formation in these cases even during direct injection. As expected for the faster reaction, the Cu(COO)2(s) precipitate is formed from the beginning of the injection. The dissolution is successfully avoided by the reverse injection, as indicated by the numerous precipitate stripes drawn from the inlet to the pattern perimeter; thus, a disk-like pattern is yielded rather than an annulus. An obvious difference between the direct and reverse injection patterns is that the outer perimeter does not show a saw-like structure in the latter case.
It is important to note that significantly less Cu(COO)2(s) precipitate is produced during injection than in the Ca(II), Sr(II), and Ba(II) systems, even though their solubility products fall in the same order of magnitude (pKsp,Ca(COO)2 = 7.9, pKsp,Sr(COO)2 = 6.4, pKsp,Ba(COO)2 = 6.0, pKsp,Cu(COO)2 = 7.5).20 The grayscale based estimations for the amount of precipitate are presented in the ESI,† for comparison. This suggests that the kinetics of the reaction, i.e., the characteristics of crystallisation determines the coupling strength of hydrodynamics and precipitation in flow-driven systems. Comparing only thermodynamic properties, e.g., solubility products and complexation equilibria, does not provide sufficient insight in order to control product properties under flow conditions.
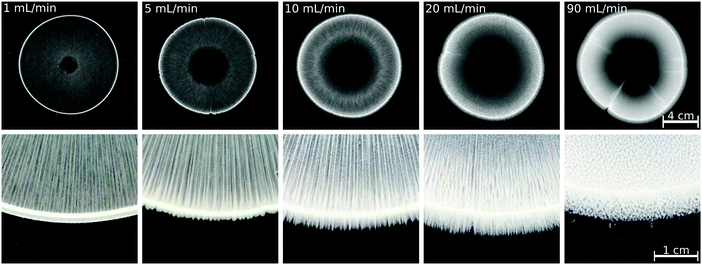
To achieve a more complex coupling between hydrodynamics and precipitation and thus more complex patterns in a confined geometry, there are several possibilities, e.g., applying a smaller gap height, increased reactant concentration, or increased injection rate.22 Considering the practical reactor area used here (21 × 21 cm2), uniformly decreasing the gap height is technically challenging. The reactant concentration cannot be further increased without changing the stoichiometric ratio of the reactants because of the solubility of Na2(COO)2 salt. Therefore, we increased the injection rate to see whether a pattern similar to that obtained with, e.g., Ca(II) or Sr(II) ions, at Q = 5 mL min−1 can be grown; the results are presented in Fig. 4 for the Cu(II) system, which was the one yielding the largest amount of precipitate among the transition metals tested at Q = 1 mL min−1 (Fig. 3). The increasing flow rate results in a growing precipitate-less region in the vicinity of the inlet because the particles are flushed away to a higher extent. Although symmetry breaking and precipitate finger formation could not be reached with the present reactant concentrations, the number of precipitate stripes within the pattern perimeter increases with the flow rate. Also, the saw-like structure becomes visible at the pattern periphery if a sufficiently high flow rate is provided. At the highest injection rate applied (Q = 90 mL min−1), no stripes are found; the pattern is composed of homogeneously distributed and separated precipitate aggregates (Fig. 4), which could be attributed to two different effects. On one hand, the injection is over within a short period of time, thus hydrodynamic instability exhibiting an undulating flow field may not have sufficiently long time to set in. A second scenario could be that λ decreases significantly with the increasing flow rate thus distinct stripes cannot emerge above the flow rate threshold. Although the experimental results presented here are not appropriate to determine the exact reason, it can be concluded that a complex pattern different from the annular one could not be achieved maybe because the amount of precipitate is significantly lower than in the Ca(II), Sr(II), and Ba(II) systems.
5 Conclusion
Flow-driven precipitation experiments applying radial injection were performed with numerous chemical systems in a confined geometry in order to investigate the effect of reaction rate on pattern formation. It was found that even if the experimental conditions, such as injection rate, gap height, reactant concentration, and the host solution, are kept constant, significantly different patterns can be obtained upon changing the chemical character of the injected solution. In good agreement with the literature,25 if such reactants are brought together such that the time scale of the reaction is long compared to the injection, the characteristics of the evolving pattern only rely on the hydrodynamic instability present in the system according to the apparent solution properties (herein the density difference was addressed). The validity of this conclusion based on sufficiently thick liquid layers is presented here for the example of the Co(II), Ni(II), and Zn(II) systems. It is also seen that the time elapsed between the end of injection and the appearance of a precipitate can alter the evolving pattern. If the time scale of the reaction and the flow is comparable, a radially expanding pattern grows, which conserves the flow field present during precipitation. A good example of this behaviour is the formation of Cu(COO)2(s). Lastly and in contrast with that observed in thicker liquid layers, when the reaction is significantly faster than the flow and provides a large amount of precipitate, the coupling of precipitation and hydrodynamics becomes strong, leading to complex pattern formation (e.g., Ca(II), Sr(II), and Ba(II) systems). By comparing the experimental results with hydrodynamic simulations, we found that a simple model is already able to qualitatively describe the system. However, it is also seen that a quantitative agreement can only be expected if the precipitation reaction modifying the flow field via density change and the appearance of a solid phase are taken into account.Our results emphasise the need for elaborate precipitation kinetics studies before being able to achieve controlled pattern growth. In this context, Damköhler numbers characterising the ratio of the chemical time scale and the rate of transport phenomena could be determined provided that the appropriate rate coefficients are available. However, those rate coefficients and a suitable kinetic description are still missing for macroscopic precipitation processes. Our experiments prove that although a high supersaturation was maintained in each and every case, the reactions took place on a significantly different time scale. What determines the kinetics of the precipitation reactions and why do similar elements (i.e., Mg, Ca, Sr, and Ba; Co, Ni, Cu, and Zn) react on significantly different time scales with the same oxalate ion? These interesting questions are to be addressed in further studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research, Development and Innovation Office (K119795, PD121010) and UNKP-19-2-SZTE-7 project.References
- F. Nudelman, B. A. Gotliv, L. Addadi and S. Weiner, Mollusk Shell Formation: Mapping the Distribution of Organic Matrix Components Underlying a Single Aragonitic Tablet in Nacre, J. Struct. Biol., 2006, 153(2), 176–187 CrossRef CAS PubMed.
- F. Aladjem, R. W. Jaross, R. L. Paldino and J. A. Lackner, The antigen-antibody reaction. III. Theoretical Considerations Concerning the Formation, Location, and Curvature of the Antigen-Antibody Precipitation Zone in Agar Diffusion Plates, and a Method for the Determination of Diffusion Coefficients of Antigens and Antibodies, J. Immunol., 1959, 83(3), 221–231 CAS.
- C. Fan, J. Li, G. Xu, H. He, X. Ye, Y. Chen, X. Sheng, J. Fu and D. He, Facile Fabrication of Nano-hydroxyapatite/silk Fibroin Composite via a Simplified Coprecipitation Route, J. Mater. Sci., 2010, 45(21), 5814–5819 CrossRef CAS.
- E. Hughes, R. Williams, M. Jenkins and L. Grover, Formulation of a Covalently Bonded Hydroxyapatite and Poly(Ether Ether Ketone) Composite, J. Tissue Eng., 2018, 9, 1–13 CAS.
- M. C. Mascolo, Y. Pei and T. A. Ring, Room Temperature Co-Precipitation Synthesis of Magnetite Nanoparticles in a Large pH Window with Different Bases, Materials, 2013, 6, 5549–5567 CrossRef CAS PubMed.
- A. I. Khan and D. O'hare, Intercalation Chemistry of Layered Double Hydroxides: Recent Developments and Applications, J. Mater. Chem., 2002, 12, 3191–3198 RSC.
- A. S. Myerson, D. Erdemir and A. Y. Lee, Handbook of Industrial Crystallization, Cambridge University Press, 3rd edn, 2019 Search PubMed.
- R. Z. Douaihy, M. Al-Ghoul and M. Hmadeh, Liesegang Banding for Controlled Size and Growth of Zeolitic-Imidazolate Frameworks, Small, 2019, 1901605 CrossRef PubMed.
- B. Bohner, G. Schuszter, O. Berkesi, D. Horváth and Á. Tóth, Self-organization of Calcium Oxalate by Flow-driven Precipitation, Chem. Commun., 2014, 50, 4289 RSC.
- Q. Wang, M. R. Bentley and O. Steinbock, Self-Organization of Layered Inorganic Membranes in Microfluidic Devices, J. Phys. Chem. C, 2017, 121(26), 14120–14127 CrossRef CAS.
- F. Glaab, M. Kellermeier, W. Kunz, E. Morallon and J. M. García-Ruiz, Formation and Evolution of Chemical Gradients and Potential Differences Across Self-assembling Inorganic Membranes, Angew. Chem., 2012, 124, 4393–4397 CrossRef.
- S. S. S. Cardoso and J. T. H. Andres, Geochemistry of Silicate-rich Rocks Can Curtail Spreading of Carbon Dioxide in Subsurface Aquifers, Nat. Commun., 2014, 5, 5743 CrossRef CAS PubMed.
- Y. Ding, B. Batista, O. Steinbock, J. H. E. Cartwright and S. S. S. Cardoso, Wavy Membranes and the Growth Rate of a Planar Chemical Garden: Enhanced Diffusion and Bioenergetics, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(33), 9182 CrossRef CAS.
- B. Bohner, T. Bánsági, Á. Tóth, D. Horváth and A. Taylor, Periodic Nucleation of Calcium Phosphate in a Stirred Bio-catalytic Reaction, Angew. Chem., Int. Ed., 2020, 59, 2–8 CrossRef.
- M. Morsali, M. T. A. Khan, R. Ashirov, G. Holló, H. T. Baytekin, I. Lagzi and B. Baytekin, Mechanical Control of Periodic Precipitation in Stretchable Gels to Retrieve Information on Elastic Deformation and for the Complex Patterning of Matter, Adv. Mater., 2020, 1905779 CrossRef CAS PubMed.
- F. Haudin, J. H. E. Cartwright, F. Brau and A. De Wit, Spiral Precipitation Patterns in Confined Chemical Gardens, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(49), 17363–17367 CrossRef CAS PubMed.
- F. Haudin, J. H. E. Cartwright and A. De Wit, Direct and Reverse Chemical Garden Patterns Grown upon Injection in Confined Geometries, J. Phys. Chem. C, 2015, 119, 15067–15076 CrossRef CAS.
- F. Haudin, V. Brasiliense, J. H. E. Cartwright, F. Brau and A. De Wit, Genericity of Confined Chemical Garden Patterns with Regard to Changes in the Reactants, Phys. Chem. Chem. Phys., 2015, 17, 12804 RSC.
- G. Schuszter, F. Brau and A. De Wit, Flow-Driven Control of Calcium Carbonate Precipitation Patterns in Confined Geometry, Phys. Chem. Chem. Phys., 2016, 18, 25592 RSC.
- S. Kotrlý and L. Šucha, Handbook of Chemical Equilibria in Analytical Chemistry, Ellis Horwood Limited, England, 1985 Search PubMed.
- G. Schuszter and A. De Wit, Comparison of Flow-controlled Calcium and Barium Carbonate Precipitation Patterns, J. Chem. Phys., 2016, 145, 224201 CrossRef CAS PubMed.
- E. Balog, K. Bittmann, K. Schwarzenberger, K. Eckert, A. De Wit and G. Schuszter, Influence of Microscopic Precipitate Structures on Macroscopic Pattern Formation in Reactive Flows in a Confined Geometry, Phys. Chem. Chem. Phys., 2019, 21, 2910 RSC.
- A. Baker, Á. Tóth, D. Horváth, J. Walkush, A. S. Ali, W. Kukovecz, J. J. Pantaleone and J. Maselko, Precipitation Pattern Formation in the Copper(ii) Oxalate System with Gravity Flow and Axial Symmetry, J. Phys. Chem. A, 2009, 113(29), 8243–8248 CrossRef CAS PubMed.
- F. Haudin, L. A. Riolfo, B. Knaepen, G. M. Homsy and A. De Wit, Experimental Study of Buoyancy-driven Instability of Miscible Horizontal Displacement in a Hele-Shaw Cell, Phys. Fluids, 2014, 26, 044102 CrossRef.
- G. Pótári, Á. Tóth and D. Horváth, Precipitation Patterns Driven by Gravity Current, Chaos, 2019, 29, 073117 CrossRef PubMed.
- Á. Tóth, D. Horváth, Á. Kukovecz, M. Maselko, A. Baker, S. Ali and J. Maselko, Pathway Control in the Self-construction of Complex Precipitation Forms in a Cu(II)-oxalate System, J. Syst. Chem., 2012, 3, 4 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01036g |
| ‡ Authors contributed equally to the work. |
| This journal is © the Owner Societies 2020 |