Open Access Article
Open Access ArticleCrystallographic characterization of Y2C2n (2n = 82, 88–94): direct Y–Y bonding and cage-dependent cluster evolution†
Changwang
Pan‡
a,
Wangqiang
Shen‡
a,
Le
Yang‡
b,
Lipiao
Bao
a,
Zhan
Wei
b,
Peng
Jin
 *b,
Hongyun
Fang
*a,
Yunpeng
Xie
*b,
Hongyun
Fang
*a,
Yunpeng
Xie
 *a,
Takeshi
Akasaka
a and
Xing
Lu
*a,
Takeshi
Akasaka
a and
Xing
Lu
 *a
*a
aState Key Laboratory of Materials Processing and Die & Mould Technology, School of Materials Science and Engineering, Huazhong University of Science and Technology, 1037 Luoyu Road, Wuhan, 430074 China. E-mail: lux@hust.edu.cn
bSchool of Materials Science and Engineering, Hebei University of Technology, Tianjin, 300130 China. E-mail: china.peng.jin@gmail.com
First published on 26th March 2019
Abstract
Direct yttrium–yttrium bonding has been a long-sought puzzle in organometallic chemistry to understand the catalytic processes that involve yttrium. Herein, we report the first crystallographic authentication of direct Y–Y bonding inside the hollow cavity of fullerene cages by forming endohedral metallofullerenes (EMFs). Based on an efficient separation/purification process, which involves Lewis-acid treatment and HPLC separation, we have obtained sufficient amounts of a series of Y2C2n (2n = 82, 88–94) isomers for systematic studies. The unambiguous single-crystal X-ray diffraction (XRD) crystallographic results show that two of them are di-EMFs, namely Y2@Cs(6)-C82 and Y2@C3v(8)-C82, in which the long-sought Y–Y single bond between the two divalent yttrium ions is experimentally confirmed for the first time. In contrast, all the other EMFs with relatively large cages are carbide cluster metallofullerenes (CCMFs), namely, Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90 and Y2C2@C2(61)-C92. Consistently, our computational results prove that these experimentally obtained EMFs are all abundant at the high temperatures for fullerene formation (∼1500–3000 K) due to the strong coordination ability of yttrium ions, which enables the formation of either direct Y–Y bonds (for Y2@Cs(6)-C82 and Y2@C3v(8)-C82) or the inclusion of a C2-unit (in Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90 and Y2C2@C2(61)-C92). Our results suggest that metal atoms such as yttrium tend to adopt a low valence state during the arc-discharge process because of the presence of the highly reductive carbon plasma in the chamber, enabling the formation of an Y2 dimer with direct Y–Y bonding in small cages like C82.
Introduction
The pursuit of novel metal–metal bonds, either supported or unsupported, is of fundamental importance for the in-depth understanding of industrial catalysis, surface chemistry and even bio-inorganic processes.1 Unsupported bonds are more attractive because ligand bridging may alter the nature of metal–metal bonding.2 Metal–metal bonds involving elements in the f-block, especially rare-earth metals including scandium and yttrium, have attracted much attention to advance new bonding theory or novel chemical transformations.3 Most of the studies have focused on the synthesis and characterization of such complexes containing metal–metal bonds between a rare-earth metal and a main group or a transition metal. To the best of our knowledge, confirmed direct metal–metal bonding between pure rare-earth elements is very rare.2The advent of fullerenes whose hollow cavity can host a variety of metallic elements to form endohedral metallofullerenes (EMFs) presents a huge possibility for the investigation of metal–metal interactions by using single crystal X-ray diffraction (XRD) studies.4–6 Traditional EMFs are those encapsulating one or two metal atoms, which transfer a certain number of electrons to the cage.7,8 When multiple metal ions are introduced into the cages, a non-metal element is generally required to stabilize the whole cluster to form species such as a metal carbide,9–11 nitride,12,13 sulphide,14 oxide15–17 and even cyanide.18,19
In principle, the positively charged metal ions suffer from strong Coulomb repulsion inside fullerene cages. For example, the estimated repulsion energy between the two La ions in La2@C80 is as high as 10 eV, which is comparable to the dissociation energy of the strongest covalent bonds like the N–N triple bond (9.8 eV).20 Accordingly, direct (unsupported) metal–metal bonding has not been realized in EMFs until the theoretical analysis of Y2@C79N revealing a single-electron bond between the two repulsive metal ions.21 In the following studies, single-electron bonds between two metal ions have also been observed for functionalized or reduced M2@C80 compounds (M = La, Y and Dy).22–24 These results are explained theoretically by Popov and co-workers by considering metal-localized HOMOs which exhibit pronounced metal–metal bonding character.20 In addition, theoretical calculations of Lu2@C76 (ref. 25) predicted the presence of a normal metal–metal bond between the two Lu2+ ions, and crystallographic evidence for direct Lu–Lu bonding has been reported recently by our group in a series of Lu-containing EMFs, such as Lu2@C2n.26,27 These results suggest that the confined inner space of fullerene cages can restrict the separation of the repulsive metal ions so as to facilitate the formation of metal–metal bonds, which stimulates us to seek for other unsupported metal–metal bonds between rare earth metals.
Herein, we report the isolation and systematic characterization of a series of di-yttrium EMFs, namely Y2@Cs(6)-C82, Y2@C3v(8)-C82, Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90 and Y2C2@C2(61)-C92. Importantly, this is the first crystallographic identification of di-yttrium EMFs, Y2@Cs(6)-C82 and Y2@C3v(8)-C82, featuring unsupported Y–Y bonds. Prior to our work, direct yttrium–yttrium contacts have only been observed in the interstitial compounds Y4I5C and Y6I7C2 (ref. 28) but never in any organometallic complexes. Interestingly, our results show that the cluster configuration changes from Y2 to Y2C2 as the cage enlarges accompanied by the donation of the valence electrons forming a Y–Y bond with the inserted C2-unit, and Y2C2@C2n (2n = 86–92) are finally formed.
Results and discussion
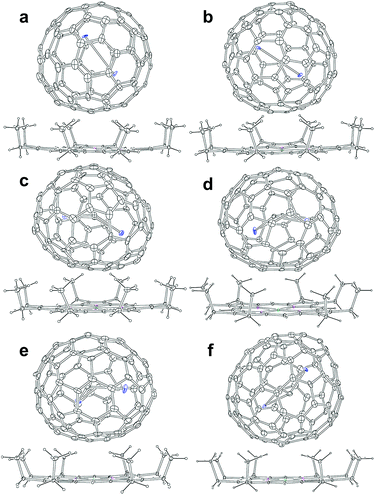
Soot containing Y2C2n (2n = 82, 88–94) isomers was synthesized by a direct-current arc discharge method and Y2C2n isomers were isolated via a combinational process involving Lewis-acid treatment and high performance liquid chromatography (HPLC) separation (Fig. S1–S5†). Experimental details are provided in the ESI.† The analytical HPLC chromatograms (Fig. S6†) and the laser-desorption/ionization time-of-flight (LDI-TOF) mass spectra (Fig. S7†) of Y2C2n (2n = 82, 88–94) reveal their high purity which guarantee the following characterization.Co-crystals of Y2C2n (2n = 82, 88–94) with NiII(OEP) (OEP = 2,3,7,8,12,13,17,18-octaethylporphyrin dianion) were obtained by layering a benzene solution of NiII(OEP) over the CS2 solution of each Y2C2n isomer, and were used to unambiguously determine their molecular structures by single-crystal X-ray diffraction (XRD) crystallography. Details of the crystallographic data are listed in Table S1.† The results unambiguously confirm that two of them are di-EMFs with relatively small cages, namely Y2@Cs(6)-C82 and Y2@C3v(8)-C82, whereas the others are all carbide cluster metallofullerenes (CCMFs), i.e., Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92, respectively. Although the Cs(6)-C82, C3v(8)-C82 and C2(41)-C90 cages have been observed for other EMFs, such as Lu2@Cs(6)-C82, Lu2@C3v(8)-C82 and La2C2@C2(41)-C90,26,29 the Cs(15)-C86, C1(26)-C88 and C2(61)-C92 cages are unprecedented.
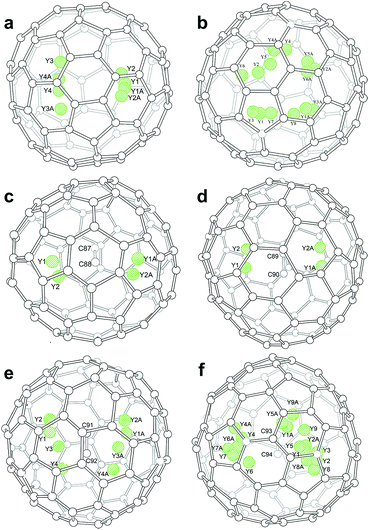
Inside the fullerene cages, the yttrium atoms show some degree of disorder. Details of the disorder are illustrated in Fig. 1 and the occupancy values are summarized in Table S2.† In the two di-EMFs, 8 and 14 yttrium sites were found for the two Y atoms in Cs(6)-C82 and C3v(8)-C82, respectively, indicating a motional behavior of the Y atom to pursue strong yttrium–cage interactions. As for the CCMFs, i.e., Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92, the number of the disordered yttrium sites increases along with cage expansion (Fig. 1). In detail, the Y2C2 unit displays 4, 4, 8 and 17 sites in Cs(15)-C86,C1(26)-C88, C2(41)-C90 and C2(61)-C92, respectively. It appears that the motional behavior of the metal atoms inside fullerene cages is an effective way to ensure sufficient metal–cage/metal–C2 unit interactions.
Moreover, the representative structural data of Y2C2n (2n = 82, 88–94) isomers, such as the structural parameters of the internal species, and Ni–cage and Y–cage distances, are summarized in Table S3.† In detail, the shortest Y–cage distances are 2.321 Å, 2.357 Å, 2.203 Å, 2.041 Å, 2.010 Å and 2.042 Å for Y2@Cs(6)-C82, Y2@C3v(8)-C82, Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90 and Y2C2@C2(61)-C92, respectively. These values are comparable to those observed for the derivatives of Y2C2@Cs(6)-C82,30 suggesting strong Y–cage interactions. Moreover, the distances between the Y ions and the internal C2 units for these CCMFs range from 2.034 Å to 2.711 Å (Table S3†), which are similar to that observed for Y2C2@C1(1660)-C108, representing typical coordination bonds.31
Fig. 2 presents the molecular structures of these EMFs showing the major components together with the co-crystallized NiII(OEP) molecule. The shortest Ni–cage distances range from 2.725 Å to 3.027 Å, suggesting substantial π–π interactions between the fullerene cage and NiII(OEP). For M2@C2n-type EMFs, Popov et al. have suggested theoretically that the internal metals may not adopt their highest oxidation states, thus yielding a possibility of covalent metal–metal bonding in such EMFs as Lu2@C76 and M2@C82 (M = Sc, Y, Er, Lu, etc.).20,25,32 Indeed, our concrete crystallographic results reveal that Lu2@C2n (2n = 82–86) are all di-EMFs with a Lu–Lu single bond formed between the two internal lutetium ions.26 Consistently, formation of the Y–Y bond is also confirmed by our crystallographic results of the two di-EMFs. The Y–Y distances between the major Y sites are 3.635 Å and 3.596 Å for Y2@C3v(6)-C82 and Y2@Cs(8)-C82, respectively, which are comparable to the calculated Y–Y single bond length (3.695 Å) for Y2@C82 isomers,20,32 confirming that each Y atom adopts a low divalent state of +2 and the third valence electron is donated to form the metal–metal bond.
As for the CCMFs, the Y–Y distances between the two major Y sites are 4.121 Å, 4.271 Å, 4.024 Å, and 4.349 Å, for Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92, respectively (Table S3†), which are all much longer than the theoretical value of an Y–Y single bond (3.695 Å),20,32 thus enabling the insertion of a C2-unit to coordinate with the two Y atoms. In addition, the C–C distances of the C2 unit in Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92 are 1.075 Å, 1.131 Å, 1.052 Å, and 1.046 Å, respectively, indicative of typical C–C triple bonds (Fig. S8 and Table S3†).33–36
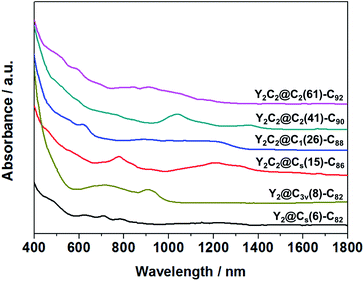
Fig. 3 shows the visible-near-infrared (Vis-NIR) absorption spectra of the EMFs dissolved in carbon disulfide (CS2) under study, all showing characteristic bands in the range of 400–1400 nm, as summarized in Table S4.† Specifically, the absorption onsets result in a large optical bandgap for Y2@C3v(8)-C82 (1.13 eV), small bandgaps for Y2C2@Cs(15)-C86 (0.72 eV) and Y2C2@C2(41)-C90 (0.86 eV), and moderate bandgaps for Y2@Cs(6)-C82 (0.90 eV), Y2C2@C1(26)-C88 (0.91 eV) and Y2C2@C2(61)-C92 (0.98 eV).
The two di-EMFs, namely Y2@C3v(8)-C82 and Y2@Cs(6)-C82, and the largest CCMF, Y2C2@C2(61)-C92, are chosen as representatives for the study of their electrochemical properties by cyclic voltammetry (Fig. S9†), whereas the redox behaviors of the other EMFs under study have not been obtained due to their limited amounts. In general, these three EMFs exhibit one reversible oxidation step and four reversible reduction processes (Fig. S9†). The detailed redox potentials are given in Table 1 along with the values of related EMFs for comparison. It is noteworthy that the first oxidation potentials for the two di-EMFs, i.e., Y2@Cs(6)-C82 and Y2@C3v(8)-C82, are identical (−0.16 V), which are much lower than that of Y2C2@C2(61)-C92 (0.28 V) as well as those of the other di-EMFs reported previously,22,26,37,38 such as Sc2@C3v(8)-C82 (0.05 V), Lu2@Cs(6)-C82 (0.34 V) and La2@Ih(7)-C80 (0.56 V), revealing their high electron affinity. These results are in good agreement with the speculation by Popov et al. and show the metal dependence of the first oxidation potential for di-EMFs with the same cages, which is rationalized through analysis of the energy of M–M bonding molecular orbitals because the electron should be removed from M–M bonding orbitals in the first oxidation process.32 Hence the lowest first oxidation potential of Y2@C82 (e.g., C3v(8)- or Cs(6)-C82) among M2@C82 (M = Sc, Y, Lu and Er) is probably ascribed to the high energy of the Y–Y bonding orbital.20 In addition, the redox potentials of Y2@C3v(8)-C82 are cathodically shifted as compared to the corresponding values of M2@C3v(8)-C82 (M = Sc, Er and Lu),32 indicating that the electrochemical properties of EMFs can be readily manipulated by adjusting the encapsulated species inside the cages.
| EMFs | ox E 1 | red E 1 | red E 2 | red E 3 | red E 3 | E gap | Ref. |
|---|---|---|---|---|---|---|---|
| a Half-cell potentials are given unless otherwise stated. b E gap = (oxE1 − redE1). | |||||||
| Y2@C3v(8)-C82 | −0.16 | −1.23 | −1.61 | −2.18 | −2.46 | 1.07 | This work |
| Sc2@C3v(8)-C82 | 0.02 | −1.16 | −1.53 | −1.73 | −2.02 | 1.18 | 32 |
| Er2@C3v(8)-C82 | 0.13 | −1.14 | −1.41 | −1.83 | — | 1.27 | 32 |
| Lu2@C3v(8)-C82 | 0.50 | −1.16 | −1.46 | −1.77 | — | 1.66 | 32 |
| Y2@Cs(6)-C82 | −0.16 | −1.06 | −1.39 | −1.85 | −2.15 | 0.90 | This work |
| Er2@Cs(6)-C82 | 0.02 | −1.01 | −1.31 | — | — | 1.03 | 32 |
| Lu2@Cs(6)-C82 | 0.34 | −1.02 | −1.35 | −1.77 | — | 1.36 | 26 |
| Y2C2@C2(61)-C92 | 0.28 | −1.00 | −1.49 | −1.73 | −1.98 | 1.28 | This work |
Density functional theory (DFT) calculations at the M06-2X/6-31G*∼SDD level were conducted to rationalize the formation of these stable Y2C2n (2n = 82, 88–94) isomers. Fig. S10† depicts their optimized geometries, which agree well with the X-ray structures. For the two di-EMFs, the optimized Y–Y distances are 3.60 Å and 3.54 Å for Y2@Cs(6)-C82 and Y2@C3v(8)-C82, respectively, which are consistent with our crystallographic results, clearly indicating a direct Y–Y bond between the two yttrium ions. Moreover, it was proposed that both the Cs(6)-C82 and C3v(8)-C82 cages have a low-lying LUMO and LUMO+1, but a high-lying LUMO+2, whose energies are higher than that of the Y–Y bonding MO.20 Therefore, the two Y atoms ([Kr]4d15s2) tend to adopt the divalent state with the remaining two electrons paring to generate an Y–Y single bond. Indeed, our calculations for Y2, Cs(6)-C82, C3v(8)-C82, Y2@Cs(6)-C82 and Y2@C3v(8)-C82 confirm that there are large energy gaps between the LUMO+2 of the two hollow cages and the HOMOs of the Y2 dimer, implying unfavorable electron transfer from the latter to the former (Fig. S11†). Further natural bond orbital (NBO) analysis demonstrates that the two Y atoms in the two Y2@C82 isomers form an Y–Y single bond with an electron occupancy of 1.97 e, which is supported by the calculated Wiberg bond orders (WBOs) for Y2@Cs(6)-C82 and Y2@C3v(8)-C82 ranging from 1.11 to 1.12 (Table S5†). The Y–Y bonds have spd-hybrid character with the Y-5s orbitals contributing the most to the metal bonding MOs, and each Y atom donates one 4d electron and one 5s electron to the cage.
As for the CCMFs, however, the calculated Y–Y distances in Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92 are as long as 4.53 Å, 4.25 Å, 4.40 Å and 4.56 Å, respectively, which are consistent with the X-ray diffraction values, indicating the absence of direct Y–Y bonding. Consistently, the calculated WBO values for these CCMFs range from 0.29 to 0.41 (Table S5†), revealing clearly that the valence electrons forming the Y–Y bond in di-EMFs are donated to the C2-unit to form the CCMFs.
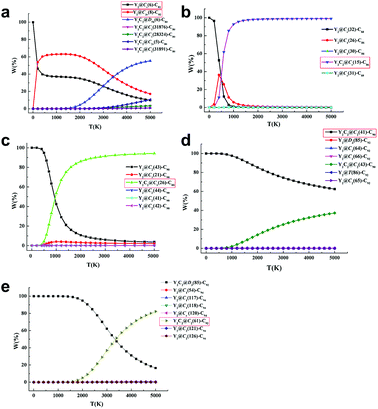
Further computational studies were done on different low-lying Y2C2n (2n = 82, 88–94) isomers in either the Y2@C2n or Y2C2@C2n−2 form to rationalize the existence of the experimentally obtained Y2C2n isomers. Fig. S12† to S16 show their optimized structures and relative energies as well as HOMO–LUMO gap energies. Since fullerenes and EMFs are formed at very high temperatures (1500–3000 K) under arc discharge conditions,39 we have also analyzed the relative stability of the most favorable EMFs in terms of their relative Gibbs free energies.40 As clearly shown in Fig. S12,†Y2@Cs(6)-C82 and Y2@C3v(8)-C82 are the lowest-energy ones among all the considered isomers, and Fig. 4a clearly shows that they are the most abundant isomers in the temperature range for EMF formation. In comparison, when the number of carbon atoms increases from C88 to C90, our calculations reveal that the experimentally obtained CCMF isomers, Y2C2@Cs(15)-C86 and Y2C2@C1(26)-C88, are more than 8.2 kcal mol−1 higher in energy than the corresponding lowest-lying di-EMFs isomers (Fig. S13 and S14†). However, when the Gibbs energy is taken into account, they become the most abundant isomers above 1500 K, with the molar fractions of the corresponding di-EMFs being almost negligible (Fig. 4b and c).
As for Y2C92−94, Y2C2@C2(41)-C90, Y2C2@C2(61)-C92 and their corresponding di-EMF isomers are mixed in terms of their potential energy, and the most stable Y2C92 and Y2C94 are both CCMFs, namely, Y2C2@C2(41)-C90 and Y2C2@D3(85)-C92, respectively (Fig. S15 and S16†). From Fig. 4d, we can see that Y2C2@C2(41)-C90 is the dominant species in the whole range of temperatures up to 5000 K. Moreover, as for Y2C94, although Y2C2@D3(85)-C92 is the dominant species at low temperatures, the concentration of the experimentally obtained Y2C2@C2(61)-C92 rapidly increases when the temperature rises, finally surpassing that of Y2C2@D3(85)-C92 after 3400 K (Fig. 4e).
Overall, our experimental and theoretical results have unambiguously confirmed that the Y2 dimer chose to form a Y–Y single bond in relatively small cages like C82, but the cluster configuration changes from Y2 to Y2C2 when the cage expands, thus forming the CCMFs in large cages C86–92. It is inferred that larger metals such as erbium and lanthanum may prefer a larger cage to form the corresponding CCMFs. For example, Stevenson et al. reported the isolation and crystallographic characterization of an erbium-based CCMF with a giant C92 cage, namely Er2C2@D3(85)-C92.41 Moreover, our group found that the even larger La3+ ions tend to form CCMFs with some giant cages such as C90–104.29,35,36 In addition, the cluster configuration is another critical factor that may affect the cage size. For instance, a linear Y2C2 cluster can be encapsulated into the giant C108 cage to template the formation of Y2C2@C1(1660)-C108.31 There is still a long way to finally clarify the mysteries in the metal–metal interactions in EMFs and new theories of coordination chemistry are expected.
Conclusions
A series of di-yttrium EMFs Y2C2n (2n = 82, 88–94) have been successfully isolated and fully characterized by mass spectrometry, UV-vis-NIR and single-crystal X-ray crystallography. The crystallographic results unambiguously confirm that two of them are di-EMFs, namely Y2@Cs(6)-C82 and Y2@C3v(8)-C82, whereas the others are all CCMFs, i.e., Y2C2@Cs(15)-C86, Y2C2@C1(26)-C88, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92, respectively. It is noteworthy that our experimental and theoretical studies clearly reveal that the Y2 dimer preferentially forms a Y–Y single bond in the di-EMFs with small cages, and further cage expansion alters its configuration to Y2C2 because the valence electrons forming the Y–Y bond are donated to the inserted C2-unit, thus resulting in the formation of the corresponding CCMFs in larger cages. In addition, our computational results demonstrate that the high thermodynamic stability of all these EMFs originates from a four-electron transfer and the bonding nature between the internal metallic species and cages. Accordingly, this work has confirmed for the first time the existence of the Y–Y bond inside fullerene cages and the transformation from di-EMFs to CCMFs along with the cage expansion, presenting an in-depth understanding and new sights into the metal–metal/metal–carbon interactions in such rarely explored metal–carbon hybrid molecules.Experimental section
Synthesis of Y2C2n (2n = 82, 88–94) isomers
Soot containing yttrium-EMFs was synthesized using a direct-current arc discharge method. Briefly, a core-drilled graphite rod filled with graphite/Y2O3 (molar ratio: Y/C = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) was burned under a 225 Torr helium atmosphere with a power of 100 A × 20 V. The soot was then extracted with CS2. After removal of CS2, the residue was dissolved in toluene and the solution was subjected to high performance liquid chromatography (HPLC) for the subsequent separation. After a combinational process involving Lewis-acid treatment and multi-stage HPLC separation, six pure isomers of yttrium-EMFs are finally obtained. Experimental details are described in the ESI.†
50) was burned under a 225 Torr helium atmosphere with a power of 100 A × 20 V. The soot was then extracted with CS2. After removal of CS2, the residue was dissolved in toluene and the solution was subjected to high performance liquid chromatography (HPLC) for the subsequent separation. After a combinational process involving Lewis-acid treatment and multi-stage HPLC separation, six pure isomers of yttrium-EMFs are finally obtained. Experimental details are described in the ESI.†
Co-crystallization and crystallographic solutions of Y2C2n (2n = 82, 88–94) cocrystals
Crystalline blocks of Y2C2@C2n·Ni(OEP) were obtained by layering a benzene solution of Ni(OEP) over a CS2 solution of the corresponding metallofullerene at room temperature for two weeks. Single-crystal XRD measurements of Y2C2@C1(26)-C88 and Y2@C3v(8)-C82 were performed at 173 K on a Bruker D8 QUEST machine equipped with a CMOS camera (Bruker AXS Inc., Germany), and X-ray data of Y2@Cs(6)-C82 were obtained at 100 K at the BL17U station of the Shanghai Synchrotron Radiation Facility. Crystallographic characterization of the other three EMFs, i.e., Y2C2@Cs(15)-C86, Y2C2@C2(41)-C90, and Y2C2@C2(61)-C92, was performed at 100 K at the BL17B station of the Shanghai Synchrotron Radiation Facility. The multi-scan method was used for absorption corrections. The structures were solved by the direct method and were refined with SHELXL-2014/7.42 Co-crystals of Y2@C3v(8)-C82·NiII(OEP) and Y2C2@C2(61)-C92·NiII(OEP) contain a severely disordered lattice of C6H6 and CS2 molecules that could not be modeled properly. Therefore, the SQUEEZE program, a part of the PLATON package of crystallographic software,43,44 was used to calculate the solvent disorder area and remove its contribution from the intensity data. CCDC-1811906 (Y2@Cs(6)-C82), CCDC-1812333 (Y2@C3v(8)-C82), CCDC-1528591 (Y2C2@Cs(15)-C86), CCDC-1528590 (Y2C2@C1(26)-C88), CCDC-1528691 (Y2C2@C2(41)-C90), and CCDC-1812135 (Y2C2@C2(61)-C92) contain the supplementary crystallographic data for this paper.†Computational details
Density functional theory calculations were carried out by using the M06-2X45 functional in conjunction with the 6-31G* basis set for C46,47 and SDD basis set and the corresponding effective core potential for Y48 (denoted as 6-31G*∼SDD), as implemented in the Gaussian 09 software package.49 More details are given in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the NSFC (No. 51672093, 51602112, 51602097 and 21103224) is gratefully acknowledged. We thank the staff of the BL17B & BL17U beamline of National Facility for Protein Science Shanghai (NFPS) at the Shanghai Synchrotron Radiation Facility for assistance during data collection. Also, we are grateful to the Analytical and Testing Center in Huazhong University of Science and Technology for all related measurements.Notes and references
- M. S. Hill, P. B. Hitchcock and R. Pongtavornpinyo, Science, 2006, 311, 1904–1907 CrossRef CAS PubMed.
- M. V. Butovskii and R. Kempe, New J. Chem., 2015, 39, 7544–7558 RSC.
- S. T. Liddle and D. P. Mills, Dalton Trans., 2009, 5592–5605 RSC.
- L. Bao, P. Peng and X. Lu, Acc. Chem. Res., 2018, 51, 810–815 CrossRef CAS PubMed.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723 RSC.
- X. Zhang, Y. Wang, R. Morales-Martínez, J. Zhong, C. de Graaf, A. Rodríguez-Fortea, J. M. Poblet, L. Echegoyen, L. Feng and N. Chen, J. Am. Chem. Soc., 2018, 140, 3907–3915 CrossRef CAS PubMed.
- W. Cai, R. Morales-Martínez, X. Zhang, D. Najera, E. L. Romero, A. Metta-Magaña, A. Rodríguez-Fortea, S. Fortier, N. Chen, J. M. Poblet and L. Echegoyen, Chem. Sci., 2017, 8, 5282–5290 RSC.
- T.-S. Wang, N. Chen, J.-F. Xiang, B. Li, J.-Y. Wu, W. Xu, L. Jiang, K. Tan, C.-Y. Shu, X. Lu and C.-R. Wang, J. Am. Chem. Soc., 2009, 131, 16646–16647 CrossRef CAS PubMed.
- H. Fang, H. Cong, M. Suzuki, L. Bao, B. Yu, Y. Xie, N. Mizorogi, M. M. Olmstead, A. L. Balch, S. Nagase, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2014, 136, 10534–10540 CrossRef CAS PubMed.
- C.-H. Chen, K. B. Ghiassi, M. R. Cerón, M. A. Guerrero-Ayala, L. Echegoyen, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2015, 137, 10116–10119 CrossRef CAS PubMed.
- T. Cai, L. Xu, M. R. Anderson, Z. Ge, T. Zuo, X. Wang, M. M. Olmstead, A. L. Balch, H. W. Gibson and H. C. Dorn, J. Am. Chem. Soc., 2006, 128, 8581–8589 CrossRef CAS PubMed.
- S. Stevenson, H. M. Lee, M. M. Olmstead, C. Kozikowski, P. Stevenson and A. L. Balch, Chem.–Eur. J., 2002, 8, 4528–4535 CrossRef CAS.
- N. Chen, M. N. Chaur, C. Moore, J. R. Pinzón, R. Valencia, A. Rodríguez-Fortea, J. M. Poblet and L. Echegoyen, Chem. Commun., 2010, 46, 4818–4820 RSC.
- S. Stevenson, M. A. Mackey, M. A. Stuart, J. P. Phillips, M. L. Easterling, C. J. Chancellor, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 11844–11845 CrossRef CAS PubMed.
- B. Q. Mercado, M. M. Olmstead, C. M. Beavers, M. L. Easterling, S. Stevenson, M. A. Mackey, C. E. Coumbe, J. D. Phillips, J. Paige Phillips, J. M. Poblet and A. L. Balch, Chem. Commun., 2010, 46, 279–281 RSC.
- Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Inorg. Chem., 2015, 54, 9845–9852 CrossRef CAS PubMed.
- T.-S. Wang, L. Feng, J.-Y. Wu, W. Xu, J.-F. Xiang, K. Tan, Y.-H. Ma, J.-P. Zheng, L. Jiang, X. Lu, C.-Y. Shu and C.-R. Wang, J. Am. Chem. Soc., 2010, 132, 16362–16364 CrossRef CAS PubMed.
- F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, J. Am. Chem. Soc., 2016, 138, 14764–14771 CrossRef CAS PubMed.
- A. A. Popov, S. M. Avdoshenko, A. M. Pendás and L. Dunsch, Chem. Commun., 2012, 48, 8031 RSC.
- T. Zuo, L. Xu, C. M. Beavers, M. M. Olmstead, W. Fu, T. D. Crawford, A. L. Balch and H. C. Dorn, J. Am. Chem. Soc., 2008, 130, 12992–12997 CrossRef CAS PubMed.
- L. Bao, M. Chen, C. Pan, T. Yamaguchi, T. Kato, M. M. Olmstead, A. L. Balch, T. Akasaka and X. Lu, Angew. Chem., Int. Ed., 2016, 55, 4242–4246 CrossRef CAS PubMed.
- M. Yamada, H. Kurihara, M. Suzuki, M. Saito, Z. Slanina, F. Uhlik, T. Aizawa, T. Kato, M. M. Olmstead, A. L. Balch, Y. Maeda, S. Nagase, X. Lu and T. Akasaka, J. Am. Chem. Soc., 2015, 137, 232–238 CrossRef CAS PubMed.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
- T. Yang, X. Zhao and E. Osawa, Chem.–Eur. J., 2011, 17, 10230–10234 CrossRef CAS PubMed.
- W. Shen, L. Bao, Y. Wu, C. Pan, S. Zhao, H. Fang, Y. Xie, P. Jin, P. Peng, F.-F. Li and X. Lu, J. Am. Chem. Soc., 2017, 139, 9979–9984 CrossRef CAS PubMed.
- W. Shen, L. Bao, S. Hu, L. Yang, P. Jin, Y. Xie, T. Akasaka and X. Lu, Chem. Sci., 2019, 10, 829–836 RSC.
- S. M. Kauzlarich, T. Hughbanks, J. D. Corbett, P. Klavins and R. N. Shelton, Inorg. Chem., 1988, 27, 1791–1797 CrossRef CAS.
- S. Zhao, P. Zhao, W. Cai, L. Bao, M. Chen, Y. Xie, X. Zhao and X. Lu, J. Am. Chem. Soc., 2017, 139, 4724–4728 CrossRef CAS PubMed.
- F. Jin, N. B. Tamm, S. I. Troyanov and S. Yang, J. Am. Chem. Soc., 2018, 140, 3496–3499 CrossRef CAS PubMed.
- C. Pan, L. Bao, X. Yu, H. Fang, Y. Xie, T. Akasaka and X. Lu, ACS Nano, 2018, 12, 2065–2069 CrossRef CAS PubMed.
- N. A. Samoylova, S. M. Avdoshenko, D. S. Krylov, H. R. Thompson, A. C. Kirkhorn, M. Rosenkranz, S. Schiemenz, F. Ziegs, A. U. B. Wolter, S. Yang, S. Stevenson and A. A. Popov, Nanoscale, 2017, 23, 7977–7990 RSC.
- C.-H. Chen, L. Abella, M. R. Cerón, M. A. Guerrero-Ayala, A. Rodríguez-Fortea, M. M. Olmstead, X. B. Powers, A. L. Balch, J. M. Poblet and L. Echegoyen, J. Am. Chem. Soc., 2016, 138, 13030–13037 CrossRef CAS PubMed.
- H. Yang, C. Lu, Z. Liu, H. Jin, Y. Che, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 17296–17300 CrossRef CAS PubMed.
- W. Cai, F.-F. Li, L. Bao, Y. Xie and X. Lu, J. Am. Chem. Soc., 2016, 138, 6670–6675 CrossRef CAS PubMed.
- W. Cai, L. Bao, S. Zhao, Y. Xie, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2015, 137, 10292–10296 CrossRef CAS PubMed.
- M. Yamada, M. Minowa, S. Sato, Z. Slanina, T. Tsuchiya, Y. Maeda, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2011, 133, 3796–3799 CrossRef CAS PubMed.
- H. Kurihara, X. Lu, Y. Iiduka, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, Chem. Commun., 2012, 48, 1290–1292 RSC.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354–358 CrossRef.
- Z. Slanina, S.-L. Lee, F. Uhlík, L. Adamowicz and S. Nagase, Theor. Chem. Acc., 2007, 117, 315–322 Search PubMed.
- A. L. Balch, M. M. Olmstead, X. Powers, C. M. Davison, S. Stevenson and K. R. Tepper, Chem.–Eur. J., 2018, 24, 13479–13484 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- P. van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 194–201 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1528590, 1528591, 1528691, 1811906, 1812135 and 1812333. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc00941h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |