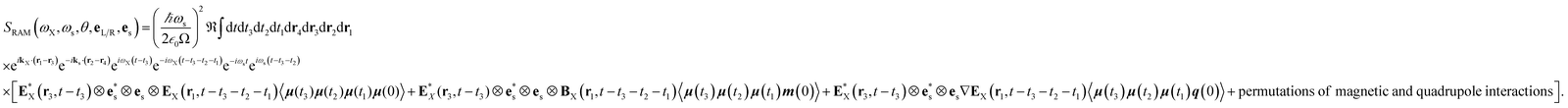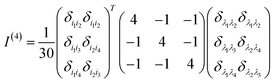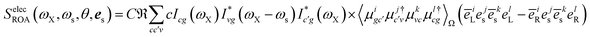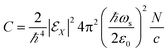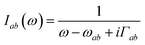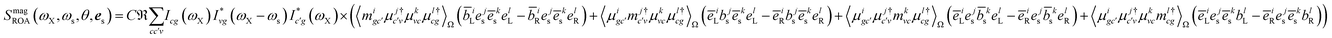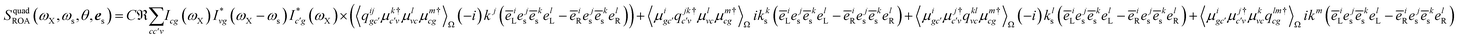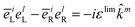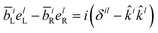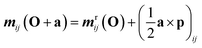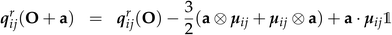DOI:
10.1039/C8SC04120B
(Edge Article)
Chem. Sci., 2019,
10, 898-908
X-ray Raman optical activity of chiral molecules†
Received
16th September 2018
, Accepted 30th October 2018
First published on 2nd November 2018
Abstract
Resonant and off-resonant Raman Optical Activity signals in the X-ray regime (XROA) are predicted. XROA is a chiral-sensitive variant of the spontaneous Resonant Inelastic Scattering (RIXS) signal. Thanks to the highly localized nature of core excitations, these signals provide a direct probe of local chirality with high sensitivity to the molecular structure. We derive sum-over-states expressions for frequency domain XROA signals and apply them to tyrosine at the nitrogen and oxygen K-edges. Time-resolved extensions of ROA made possible by using additional pulses are briefly outlined.
1 Introduction
The recent development of intense X-ray light from synchrotron or X-ray free electron lasers (XFELs)1,2 makes it possible to extend well established infrared and optical nonlinear spectroscopic techniques3–6 to the X-ray regime. One notable advantage is that the light–matter interaction of X-ray light resonant with core excitations in molecules is highly spatially localized and element specific. Signals specifically targeting molecular chirality thus offer important structural information.7 Chirality is crucial for the biological activity of biomolecules and has been extensively studied using visible and IR techniques such as circular dichroism (CD), optical rotation8 and Raman Optical Activity (ROA).9,10 Chiral signals are intrinsically weak and considerable effort has been made to increase their magnitude11,12 which is vital, e.g. for sensor applications.13,14
ROA employs circularly polarized light to measure the vibrational or electronic optical activity and is routinely used in the infrared15 and the visible16 regimes to obtain information on the absolute configuration of small chiral molecules and on the secondary and tertiary structure of proteins. This is particularly important for drug design since many important drugs are chiral. The X-ray extension of ROA should also provide favorable scaling since it increases as ω5 compared to the conventional Raman background that scales as ω4.17 Expressions for XROA signals are derived in Section 2 and simulation results of the amino acid tyrosine are presented and analyzed in Section 3. Our findings are summarized in Section 4.
2 The X-ray Raman optical activity signal
ROA has its origin in the pioneering work of Barron16,18,19 who demonstrated that the spontaneous Raman scattering intensity induced by circularly polarized light from chiral enantiomers is different. The ROA signal is usually measured by taking the difference between spontaneous Raman spectra induced by left and right polarized light at different scattering angles. The detector then measures all polarizations of the scattered light. This configuration is shown in Fig. 1. ROA signals can also be acquired in other ways by detecting, for example, the difference between the left and right polarized components of the scattered light when the incident light is linearly polarized or unpolarized.16 Mixed schemes in which both the polarization of the incoming light and the scattered light are varied have been used as well. By varying the polarization and detecting the signal at different scattering angles, it is possible to isolate different tensor components of the rotationally averaged chiral signal.16
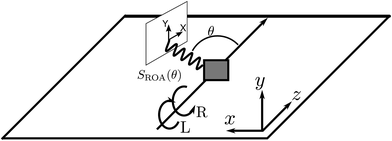 |
| | Fig. 1 The ROA measurement scheme. Left and right circularly polarized X-ray pulses propagating along the z direction generate two Raman signals which are recorded as a function of the scattering angle. Their small difference constitutes the ROA signal, eqn (9). The detector polarization basis by X and Y provides an extra degree of freedom for the measurement. | |
ROA with visible light is by now a well established experimental technique for probing the optical activity of the vibrational manifold.9 The electronic chirality is most commonly observed by visible or UV CD.20,21 XROA measures the optical activity of the valence electronic excited manifold accessible through intermediate core electronic excitations. For the setup shown in Fig. 1, the relevant matter correlation function is a pseudo-tensor involving a magnetic dipole or an electric quadrupole interaction. The sum of these scattering intensities depends only on true tensor quantities (electric dipole–electric dipole interactions). The ROA signals can be directly deduced from the loop diagrams shown in Fig. 2 and are usually normalized by the sum of the spectra (eqn (9)).
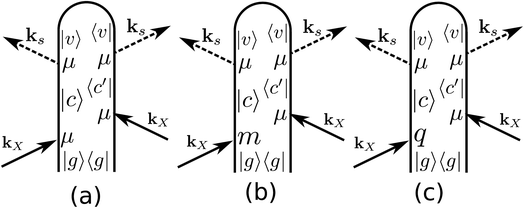 |
| | Fig. 2 Loop diagrams for the electric dipole (a), magnetic dipole (b) and electric quadrupole (c) contributions to the ROA signal. We only plot one of the four diagrams involving the magnetic dipole contribution to the signal. The other three can be obtained for (b) by permuting the magnetic dipole interaction with the electric dipole ones. Similarly, there are four diagrams for the electric quadrupole interaction (c). | |
In this paper, we study the difference in the Raman signal induced by the incoming left and right polarizations. The radiation/matter coupling is given by the multipolar Hamiltonian22 truncated at the electric quadrupole
| | | Hint(t) = −μ·Es − m·Bs − q·∇Es | (1) |
Fig. 2(a), (b) and (c) represent the non-chiral electric dipole contribution, the magnetic dipole and the electric quadrupole, respectively. We shall denote the detected spontaneous Raman intensity by SRAM(ωX,ωs,θ,eL/R,es), where ωX is the incident pulse frequency, ωs is the detected frequency, θ is the angle between the incident pulse and the detected light, and eL/R and es are the incident and diffracted pulse polarizations.
The XROA signal is given by the difference between left and right incoming polarizations:
| | | SXROA(ωX,ωs,θ,es) = SRAM(ωX,ωs,θ,eL,es) − SRAM(ωX,ωs,θ,eR,es) | (2) |
Without loss of generality, in an isotropic sample, we assume that the incident pulse propagates along the z axis (this implies that kX = ez) and that the scattered Raman signal is measured in the xz plane (see Fig. 1).
The spontaneous Raman signal is defined as the change of photon number emitted in the detected direction
| | 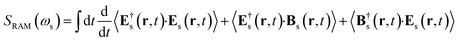 | (3) |
We shall neglect the magnetic field contribution because it is orders of magnitude smaller.23 The time derivative can be calculated by using the expectation value of the Heisenberg equation of motion of the number operator.
| | 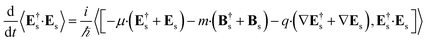 | (4) |
The commutator can be calculated in a straightforward manner using the definition of the Es and Bs operators
| | 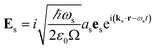 | (5) |
| | 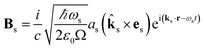 | (6) |
where
ks is the wavevector of the emitted photon,
Ω is the quantization volume and we have the boson commutation
Upon evaluating the commutator, the Raman signal (eqn (3)) becomes
| | 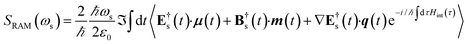 | (8) |
where
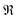
and
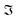
denote the real and imaginary parts respectively. To obtain the ROA signal, we expand the exponent to second order in the incident field. Three terms then contribute to the signals. The leading term is given by the interaction with the electric dipoles only (diagram (a)) and does not contribute to the ROA signal since it vanishes upon rotational averaging. Diagram (b) contains one magnetic dipole and diagram (c) has one electric quadrupole interaction.
| | 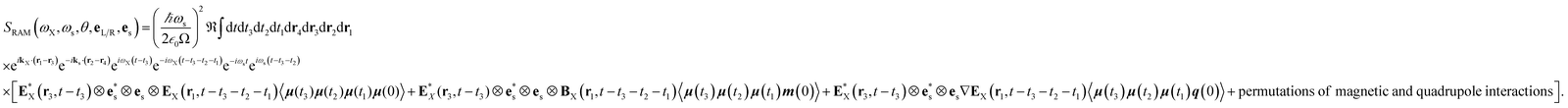 | (9) |
where the
eL/R dependence of the signal is contained in the vector components of E
X and B
X.The three terms in brackets correspond to diagrams (a), (b) and (c), respectively in
Fig. 2 and all operators evolve with the free molecular Hamiltonian in the interaction picture.
Eqn (9) allows us to calculate time-resolved signals induced by broadband pulses. In that case, the spatial and temporal integrals can be then expressed as a Fourier transform. In this paper, we focus on ROA signals in the frequency domain measured with monochromatic light excitation. The total XROA signal is given by the sum of the magnetic and the quadrupole contributions:
| | | SXROA(ωX,ωs;θ,es) = SmagXROA(ωX,ωs;θ,es) + SquadXROA(ωX,ωs;θ,es) | (10) |
Sum-over-states expressions for eqn (9) are given in Appendix B.
3 XROA signals of tyrosine
We have calculated the XROA signal, eqn (9), for a randomly oriented ensemble of L-tyrosine (Fig. 3(a)) with an X-ray incident pulse tuned at the N (ωX ∼ 389–397 eV) and O (ωX ∼ 519–526 eV) K-edges. The incoming X-rays are thus resonant with the excited transitions. The signals on D-tyrosine are identical but with an opposite sign and thus are not displayed. We focus on the zwitterionic structure (see Fig. 3(a)) of the molecule in water since this is its dominant form at physiological pH. The geometry was optimized at the B3LYP24,25/aug-cc-pVTZ26,27 level of theory using the Gaussian program package.28 The water solvent effect was considered with the PCM model.29–31 All quantities needed for XROA signal calculations were calculated using the CD spectrum32–34 and the restricted excitation window time-dependent density functional (REW-TDDFT)35–40 implementations in the quantum chemistry package NWChem41 under the Tamm–Dancoff approximation (TDA).42–44 The computational protocol for the relevant transition moments (electric and magnetic dipoles, electric quadrupoles) has been presented in ref. 40. The B3LYP hybrid functional and the cc-pVTZ basis set26 were used for all NWChem calculations. The water solvent effect was included using the COSMO model.45 It is a common practice to apply constant shifts to the calculated core excitation energies from TDDFT to match the experimental results. Since in this study only the relative positions of spectroscopic features matter, we retain all original core excitation energies from the TDDFT calculations. We adopted a tight SCF convergence criterion (energy change of SCF cycles <10−8 a.u.) and an ultrafine grid in all NWChem calculations.
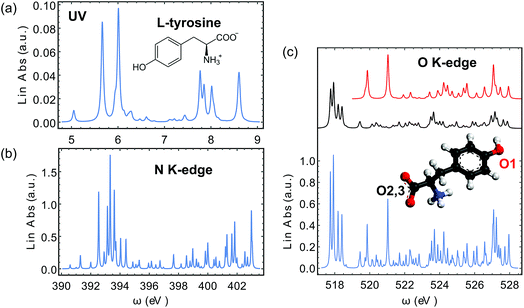 |
| | Fig. 3 Calculated spectra of L-tyrosine in its zwitterionic form. (a) UV-vis spectrum. (b) N K-edge X-ray absorption spectrum. (c) O K-edge X-ray absorption spectrum. The 3D molecular model is also shown and the x, y, z axes are marked in red, green and blue, respectively. The oxygen atom in the phenol group is labelled O1 and the other two in the carbonyl group are labelled O2,3. The separate contributions of these two types of O atoms to the total signal (in light blue) are plotted in red and black, respectively. The signal contributions are normalized to different scales. | |
It is well known that TDDFT–TDA in general produces excitation energies of identical or even better quality of full TDDFT, but possibly worse oscillator strengths because of violation of the sum rule.46,47 However, previous TDDFT–TDA studies on core spectroscopy, which is the major topic of this manuscript, showed that TDDFT–TDA and full TDDFT gave almost indistinguishable results.39,48 TDDFT–TDA is computationally much cheaper than full TDDFT, which facilitates its use in large systems. Moreover, it handles triplet instabilities much better than full TDDFT.49 In addition, it also gives better nonadiabatic couplings by reducing the local-density-approximation (LDA) error.50 With all the considerations above, we use TDDFT–TDA in this study.
Under the multipolar expansion, only the first non-vanishing multipole is origin invariant. Thus, in the present work, the electric quadrupoles and the magnetic dipoles are origin dependent.51 Indeed, the spectroscopic observables calculated from exact wave functions must be independent of the origin.52 However, numerical truncation of the basis set can induce origin-dependence of the spectroscopic observables. A possible solution is to use Gauge Invariant Atomic Orbitals (GIAOs) or London orbitals.34,53–55 Alternatively, as shown by Reiher et al.,52 by evaluating multipoles in the velocity gauge, the corresponding spectroscopic tensors are origin-independent even with a truncated basis. The behavior of the spectroscopic tensors upon changing the coordinates is given in Appendix C for completeness. To obtain origin-independent XROA signals, in this study we employed electric transition dipoles in the velocity gauge and kept the electric transition quadrupoles in the length gauge as their relevant spectroscopic tensors are origin-independent in both gauges.52
The calculated absorption spectra from TDDFT are displayed in the near UV range (Fig. 3(a)), at the N K-edge (Fig. 3(b)) and the O K-edge (Fig. 3(c)). Tyrosine has three O atoms, one in the phenol group and the other two in the carbonyl group. The carbonyl O atoms are chemically indistinguishable. Thus we separate the three O atoms into two groups, in which the phenol O atom is labelled O1 and the carbonyl O atoms are labelled O2,3 (Fig. 3). In our analysis, we have also decomposed the O K-edge spectrum into the contributions from O1 and O2,3, and plotted them in red and black in Fig. 3(c).
The XROA signal at the N K-edge vs. the incoming plane wave frequency and of the Raman shift ωX − ωs is displayed in Fig. 4 for various scattering angles. The corresponding 2D Raman signal at the scattering angle of π/2 is given in the ESI.† The ratio of the chiral contribution to the nonchiral one is 1.7% at the main peak of the spectrum (392.2 eV excitation and 8.4 eV Raman shift). The former provides spectroscopic information on the core-excited manifold while the latter covers the valence excited state manifold. The signals are given for both polarizations of detection ex and ey (see Fig. 1). Each panel depicts the signal acquired at various scattering angles between the incoming and emitted light. At θ = 0 (forward scattering), the signal is independent of the polarization. Due to the tight localization of the X-ray excitations in the vicinity of the core excited atom, strong peaks appear when the wave function overlap between the core-excited state and the valence excited state is high. Fig. 5 shows several slices of the N K-edge XROA at π/2 scattering. The spectrum varies with θ while retaining the same structural information.
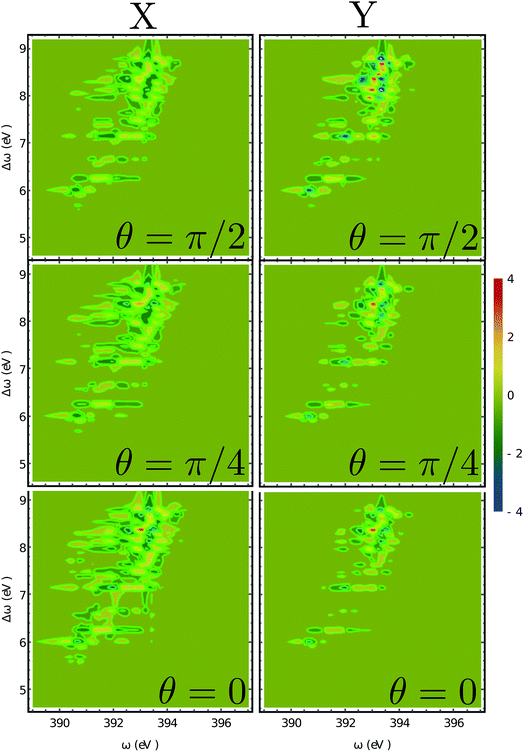 |
| | Fig. 4 2D XROA signals (eqn (9)) displayed vs. the incoming frequency ωX and the Raman frequency shift Δω = ωX − ωs at the N K-edge for various scattering angles. The left and right columns represent X and Y polarizations of the detected photons in the detector frame. | |
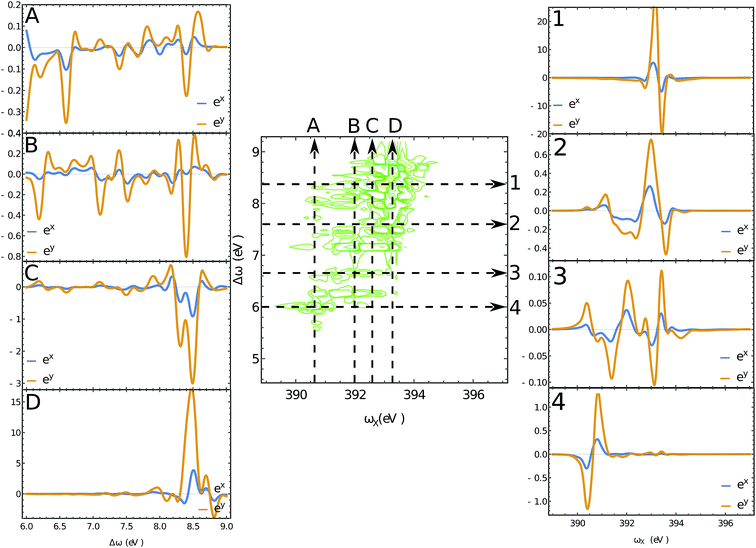 |
| | Fig. 5 Slices of the 2D XROA signals at the N K-edge, Fig. 4 for the scattering angle θ = π/2. The polarizations of the detected photons are shown in blue (eX) and orange (eY). | |
Fig. 6 depicts the total XROA signals calculated at various K-edges, nitrogen and two groups of oxygen atoms for both X- and Y-polarization detection at a scattering angle of π/2. The X- and Y-polarization detected signals show similar patterns. As can be seen in Section B-eqn (16), the ROA signal depends on multiple transitions and their orientations, hence there is no simple relationship between a single transition momentum and the signal. However, as a general rule, strong ROA signals require that the relevant core and valence excitations involve the same particle orbitals (since the corresponding transition moment is a single-electron operator), and the involved particle or hole orbital should be close to the chiral centers if they exist. We can take the strong N 1s ROA features as an example. Important molecular orbitals (MOs) (S1) and an analysis on relevant excitations (Table S1†) are provided in the ESI.† The strong feature around the point (390.6, 6.0) eV involves the weak N 1s core excitation at 390.6 eV and the strong valence excitation at 6.0 eV. The two excitations couple through the LUMO, which is distributed on the benzene ring (see S1). Since the LUMO (L) is not close to the N atom, the corresponding X-ray absorption is weak (Fig. 3). However, the relevant valence hole orbital HOMO-3 (H-3) lies on the N atom as well as the chiral center, and the benzene ring, so the corresponding valence excitation and the chiral ROA signal is strong. Another strong ROA feature around the point (393.4, 8.4) eV can be explained similarly. The core excitation around 393.4 eV couples with the valence excitation around 8.4 eV through the L + 7 particle orbital. This orbital is delocalized over all atoms, and the corresponding valence hole orbital H-1 carries the information regarding the chiral center.
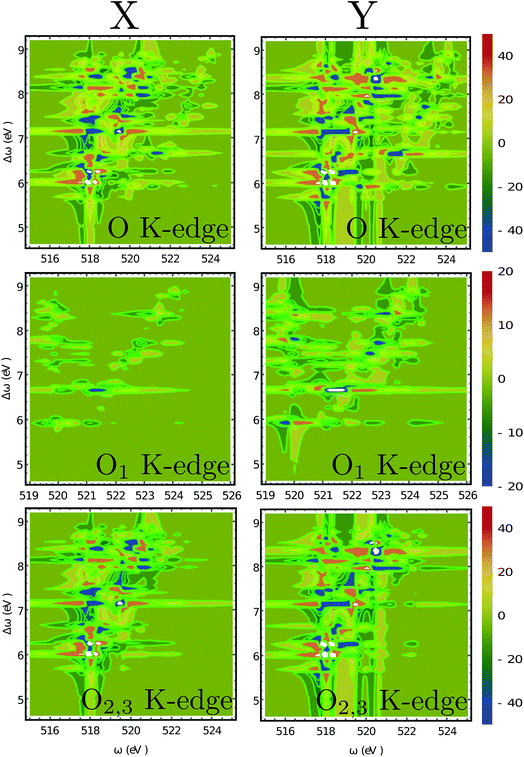 |
| | Fig. 6 2D XROA signals (eqn (9)) displayed vs. the incoming frequency ωX and the frequency shift Δω = ωX − ωs at various edges. O1 refers to the oxygen atom in the OH group near the benzene ring while O2,3 are the two equivalent oxygen atoms at the carbonyl group. These two atoms are spectroscopically equivalent since the hydrogen atom can easily migrate between them. The scattering angle is π/2. | |
The O 1s ROA signals are more complicated since there are two inequivalent O atoms in the molecule. The total O 1s ROA signals and the contributions from the O1 and O2,3 atoms are displayed in Fig. 6. As discussed in our previous work on X-ray CD,56 the chiral X-ray signal intensity depends on the distance between the X-ray chromophore and the molecular chiral center. This propensity is also clearly observed here by comparing the XROA signals of O1 and O2,3. One can see from Fig. 6 that the signals of O2,3 are much stronger than O1 signals since the carbonyl oxygens are closer to the chiral center. Taking the x-polarized detection as an example, O1 only shows a strong feature around the (521.5, 6.6) eV point. The involved core excitation couples with the valence excitation through the orbital L + 2. We see that L + 2 almost covers the entire chiral center (S1) and is involved in many important core and valence transitions (Table S1†), thus it is the key orbital responsible for strong ROA signals. The strong O2,3 features around the points (518.2, 6.2) eV and (519.4, 7.2) eV all involve L + 2. Alternatively, the O2,3 core excitations near 518 eV also couple with the 6.0 eV valence excitation through the L orbital. The other significant features can be analyzed in a similar manner.
Moreover, even though one can see the chemical shifts of O1 and O2,3 in the calculated linear X-ray absorption signals (Fig. 3(c), O1 has strong features near 520 and 521 eV, and O2,3 have strong features around 518 eV), the two spectra overlap around 520 eV (note that the two spectra are plotted in different scales and the O2,3 signals are actually stronger than they appear in Fig. 3(c) compared to the O1 signals). The large core hole lifetime broadening could produce a broad peak around 520 eV which will complicate the assignment of the O peaks. However, the situation is different for the XROA signals. As shown in Fig. 6, the cross-peaks of O1 and O2,3 now have chemical shifts in both the core excitation and Raman shift energy dimensions. The various features of O1 and O2,3 can be better resolved in the valence excitation manifold, thanks to the much smaller lifetime broadening of the final valence excited states. Therefore, XROA signals have advantages over XCD signals by better separating the contributions from different atoms to the chiral signal and resolving the local chirality information at a new level.
Fig. 7 depicts the magnetic and quadrupole contributions to the XROA signal at the N K-edge (ωX = 393.25 eV, θ = π/2), eqn (16), for x and y polarization of the signal. The total signal measured at the N K-edge is given by the sum of the magnetic and the electric contributions. For x-polarized detection, the total signal (blue curve) is a mixture of magnetic dipole and electric quadrupole contributions of similar weight. The y-polarized signal under the same conditions is dominated by the magnetic interaction. The polarization direction of detection along which the quadrupole contribution is important is determined by the geometric and electronic structure of the system, but the fact that this contribution varies significantly for different polarizations of detection is general. The sensitivity of XROA signals to the electric quadrupole interaction opens a new window to molecular chirality compared to XCD signals which do not depend on the electric quadrupole because of cancellation caused by rotational averaging.
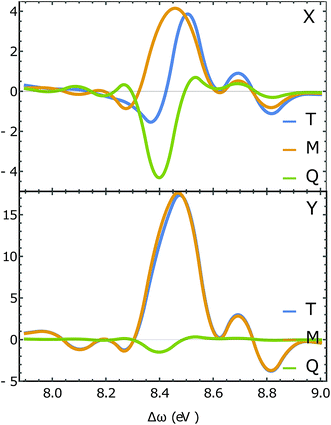 |
| | Fig. 7 Slices of the XROA signal at the N K-edge (ωX = 393.25 eV, θ = π/2 for x-polarized detection (top) and y-polarized detection (bottom). The total XROA signal measured (T, blue) is the sum of magnetic dipole (M, orange) and electric quadrupole (Q, green) contributions. | |
4 Conclusions
The most common technique to study chirality with circularly polarized X-ray light is CD.56–58 We have recently shown how X-ray CD may be used to locally probe chiral structures. In the present study we have simulated the XROA signals of L-tyrosine at the N and O K-edges. ROA is routinely used in the IR and visible regimes, but has not been reported yet for X-rays. The technique has been made feasible by the use of advanced X-ray sources.
One advantage of ROA spectroscopy is that the signals can be detected in a non-collinear geometry thus avoiding the strong background of an intense incoming X-ray beam. Moreover, like optical Raman signals, ROA signals may detect dark states in the corresponding absorption spectra because of different selection rules, and usually have better spectral resolution than their absorption counterparts. Unlike XCD, ROA also depends on the electric quadrupole interactions for randomly oriented molecules and can thus probe molecular chirality even when magnetic dipoles are weak, as has been demonstrated for tris(ethylenediamine) cobalt(III) ion (Co(en)33+).59
The signal in eqn (9) was calculated for a monochromatic excitation. It will be interesting to extend this technique to the time-domain by using ultrashort X-ray pulses. Time-resolved extension can be achieved by adding an actinic pulse with a controlled delay in an optical pump/X-ray probe scheme. This can be done by starting with eqn (9) and expanding the exponent to higher orders in the incoming pulses in order to trigger some chiral dynamics. XROA can then be used as a novel detection mode on top of a nonlinear process that would be sensitive to local change of the chiral structure in the vicinity of an X-ray chromophore. Time-domain XROA should be a powerful spectroscopy tool to track chiral molecules in chemical reactions.
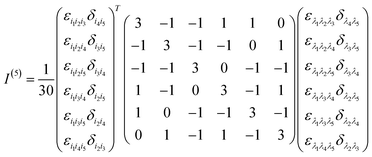
Appendix A rotationally averaged tensors
A n-th rank tensor T is rotationally averaged using the averaging tensor I(n).60 The correlation tensor involving electric and magnetic dipoles are only fourth rank tensors for ROA and the ones involving electric quadrupole are of rank 5.| | 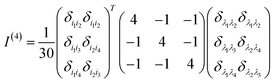 | (11) |
| |  | (12) |
where δ and ε are the Kronecker and Levi-Civita symbols respectively.
The I(4) tensor is used to rotationally average the magnetic correlation functions (e.g. 〈μμμm〉) and I(5) for the electric quadrupole ones (e.g. 〈μμμq〉). For example, we have
| | | (〈μμμm〉Ω)ijkl = (I(4))i′j′k′l′ijkl〈μμμm〉i′j′k′l′ | (13) |
where we used Einstein summation convention for the Cartesian indices
i,
j,
k, and
l, and 〈…〉
Ω stands for rotational averaging.
Appendix B sum-over-states expressions of the XROA signals
Here, we provide the sum-over-states expressions of the three diagrams shown in Fig. 2. Assuming the the incoming pulses are plane waves, the electric contribution (Fig. 2(a)) is given by| | 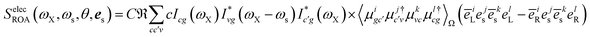 | (14) |
where| | 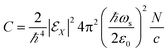 | (15) |
| | 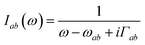 | (16) |
The magnetic contribution given in Fig. 2(b) is summed over the permutations of the magnetic interaction
| | 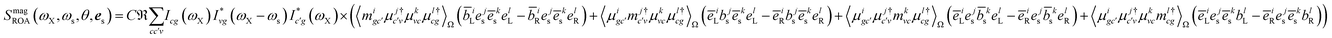 | (17) |
Finally, the quadrupole contribution is given in the diagram in Fig. 2(c)
| | 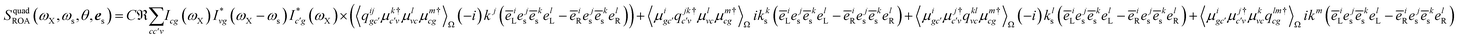 | (18) |
Note that the variable k and ks are the wavevectors of the incoming and outgoing photons respectively while the superscripts k refer to the dummy summation index over cartesian components. The four-point correlation function of matter can be expanded in eigenstates. Chiral signals are measured in ensembles of randomly oriented chiral molecules. Thus, the four-point matter correlation function, eqn (17) and (18), must be rotationally averaged (see Appendix A). We use the following identities to simplify the polarization vector differences:
| | 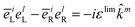 | (19) |
| | 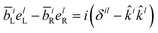 | (20) |
Appendix C origin dependence upon coordinate change
The transition matrix elements can be computed either in the length or in the velocity gauge, denoted as r and p respectively. Their transformations under a coordinate translation a from the origin O are given by| | 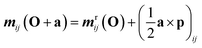 | (22) |
| | 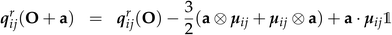 | (23) |
| | | μpij(O + a) = μpij(O) | (24) |
| | | qpij(O + a) = qpij(O) − (a ⊗ μij + μij ⊗ a) | (25) |
The magnetic dipole remains unchanged in the length and velocity gauge.51 The ROA spectroscopic signal is origin independent with truncated basis sets only in the velocity gauge. Thus the velocity gauge has been used to compute the signals.52
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The support of the Chemical Sciences, Geosciences, and Biosciences division, Office of Basic Energy Sciences, Office of Science, U.S. Deparment of Energy through Award No. DE-FG02-04ER15571 and of the National Science Foundation (Grant No CHE-1663822) is gratefully acknowledged. J. R was supported by the DOE grant. Y. Z. would like to thank Prof. Jochen Autschbach for helpful discussions.
References
- Y. Ding, Z. Huang, D. Ratner, P. Bucksbaum and H. Merdji, Generation of attosecond X-ray pulses with a multicycle two-color enhanced self-amplified spontaneous emission scheme, Phys. Rev. Spec. Top.--Accel. Beams, 2009, 12, 060703 CrossRef.
- M. Chini, K. Zhao and Z. Chang, The generation, characterization and applications of broadband isolated attosecond pulses, Nat. Photonics, 2014, 8, 178 CrossRef CAS.
- J. D. Biggs, Y. Zhang, D. Healion and S. Mukamel, Two-dimensional stimulated resonance Raman spectroscopy of molecules with broadband X-ray pulses, J. Chem. Phys., 2012, 136(17), 174117 CrossRef PubMed.
- Y. Zhang, J. D. Biggs and S. Mukamel, Understanding excitation energy transfer in metalloporphyrin heterodimers with different linkers, bonding structures, and geometries through stimulated X-ray Raman spectroscopy, J. Mod. Opt., 2014, 61, 558–567 CrossRef CAS PubMed.
- S.-K. Son, H. N. Chapman and R. Santra, Determination of multiwavelength anomalous diffraction coefficients at high x-ray intensity, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 164015 CrossRef.
- K. Tamasaku, E. Shigemasa, Y. Inubushi, T. Katayama, K. Sawada, H. Yumoto, H. Ohashi, H. Mimura, M. Yabashi and K. Yamauchi,
et al., X-ray two-photon absorption competing against single and sequential multiphoton processes, Nat. Photonics, 2014, 8, 313 CrossRef CAS.
-
N. Berova, K. Nakanashi and R. W. Woody, in Circular Dichroism, Principles and Applications, Wiley, 2000 Search PubMed.
- A. Lázár, J. G. Ángyán, M. Hollósi, P. Huszthy and P. R. Surján, Theoretical CD spectrum calculations of the crown-ether aralkyl-ammonium salt complex, Chirality, 2002, 14, 377–385 CrossRef PubMed.
- L. Ashton, P. Pudney, E. Blanch and G. Yakubov, Understanding glycoprotein behaviours using Raman and Raman optical activity spectroscopies: Characterising the entanglement induced conformational changes in oligosaccharide chains of mucin, Adv. Colloid Interface Sci., 2013, 199, 66–77 CrossRef PubMed.
- L. D. Barron, The development of biomolecular Raman optical activity spectroscopy, Biomed. Spectrosc. Imaging, 2015, 4, 223–253 CAS.
- Y. Tang and A. E. Cohen, Optical chirality and its interaction with matter, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed.
- J. R. Rouxel, V. Y. Chernyak and S. Mukamel, Non-local real-space analysis of chiral optical signals, Chem. Sci., 2016, 7, 6824–6831 RSC.
- H. Zhang and A. Govorov, Giant circular dichroism of a molecule in a region of strong plasmon resonances between two neighboring gold nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075410 CrossRef.
- M. Schäferling, D. Dregely, M. Hentschel and H. Giessen, Tailoring enhanced optical chirality: design principles for chiral plasmonic nanostructures, Phys. Rev. X, 2012, 2, 031010 Search PubMed.
- L. A. Nafie, Infrared and Raman vibrational optical activity: theoretical and experimental aspects, Annu. Rev. Phys. Chem., 1997, 48, 357–386 CrossRef CAS PubMed.
-
L. Barron, in Molecular light scattering and optical activity, Cambridge, 2004 Search PubMed.
- J. Kapitán, L. D. Barron and L. Hecht, A novel Raman optical activity instrument operating in the deep ultraviolet spectral region, J. Raman Spectrosc., 2015, 46, 392–399 CrossRef.
- L. Barron and A. Buckingham, Rayleigh and Raman scattering from optically active molecules, Mol. Phys., 1971, 20, 1111–1119 CrossRef CAS.
- L. Barron, M. Bogaard and A. Buckingham, Raman scattering of circularly polarized light by optically active molecules, J. Am. Chem. Soc., 1973, 95, 603–605 CrossRef CAS.
- T. Dartigalongue and F. Hache, Time-resolved circular dichroism in carbonmonoxy-myoglobin: The central role of the proximal histidine, Chirality, 2006, 18, 273–278 CrossRef CAS PubMed.
- F. Hache, M.-C. Schanne-Klein, H. Mesnil, M. Alexandre, G. Lemercier and C. Andraud, Nonlinear optical activity in chiral molecules: surface second harmonic generation and nonlinear circular dichroism, C. R. Phys., 2002, 3, 429–437 CrossRef CAS.
-
A. Salam, Molecular quantum electrodynamics: long-range intermolecular interactions, John Wiley & Sons, 2010 Search PubMed.
- D. Abramavicius, B. Palmieri, D. V. Voronine, F. Sanda and S. Mukamel, Coherent multidimensional optical spectroscopy of excitons in molecular aggregates; quasiparticle versus supermolecule perspectives, Chem. Rev., 2009, 109, 2350–2408 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch,
Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the firstâĂŘrow atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96(9), 6796–6806 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- S. Miertus, E. Scrocco and J. Tomasi, Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of ab initio Molecular Potentials for the Prevision of Solvent Effects, Chem. Phys., 1981, 55(1), 117–129 CrossRef CAS.
- S. Miertus and J. Tomasi, Approximate Evaluations of the Electrostatic Free Energy and Internal Energy Changes in Solution Processes, Chem. Phys., 1982, 65, 239 CrossRef CAS.
- J. L. Pascual-Ahuir, E. Silla and I. Tuñón, GEPOL: An improved description of molecular-surfaces. 3. A new algorithm for the computation of a solvent-excluding surface, J. Comput. Chem., 1994, 15(10), 1127–1138 CrossRef CAS.
- J. Autschbach, T. Ziegler, S. J. A. van Gisbergen and E. J. Baerends, Chiroptical Properties from Time-dependent
Density Functional Theory. I. Circular Dichroism Spectra of Organic Molecules, J. Chem. Phys., 2002, 116, 6930–6940 CrossRef CAS.
- J. Autschbach and T. Ziegler, Calculating Molecular Electric and Magnetic Properties from Time-dependent Density Functional Response Theory, J. Chem. Phys., 2002, 116, 891–896 CrossRef CAS.
- J. Autschbach, Time-Dependent Density Functional Theory for Calculating Origin-Independent Optical Rotation and Rotatory Strength Tensors, ChemPhysChem, 2011, 12, 3224–3235 CrossRef CAS PubMed.
- M. Stener, G. Fronzoni and M. de Simone, Time Dependent Density Functional Theory of Core Electrons Excitations, Chem. Phys. Lett., 2003, 373, 115–123 CrossRef CAS.
- N. A. Besley and A. Noble, Time-Dependent Density Functional Theory Study of the X-ray Absorption Spectroscopy of Acetylene, Ethylene, and Benzene on Si(100), J. Phys. Chem. C, 2007, 111, 3333–3340 CrossRef CAS.
- S. DeBeer-George, T. Petrenko and F. Neese, Time-dependent Density Functional Calculations of Ligand K-edge X-ray Absorption Spectra, Inorg. Chim. Acta, 2008, 361, 965–972 CrossRef CAS.
- W. Liang, S. A. Fischer, M. J. Frisch and X. Li, Energy-Specific Linear Response TDHF/TDDFT for Calculating High-Energy Excited States, J. Chem. Theory Comput., 2011, 7, 3540–3547 CrossRef CAS PubMed.
- K. Lopata, B. E. V. Kuiken, M. Khalil and N. Govind, Linear-Response and Real-Time Time-Dependent Density Functional Theory Studies of Core-Level Near-Edge X-Ray Absorption, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- Y. Zhang, J. D. Biggs, D. Healion, N. Govind and S. Mukamel, Core and Valence Excitations in Resonant X-ray Spectroscopy Using Restricted Excitation Window Time-dependent Density Functional Theory, J. Chem. Phys., 2012, 137, 194306 CrossRef PubMed.
- M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. V. Dam, D. Wang, J. Nieplocha, E. Apra and T. Windus,
et al., NWChem: A Comprehensive and Scalable Open-source Solution for Large Scale Molecular Simulations, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- I. Tamm, Relativistic interaction of elementary particles, J. Phys., 1945, 9, 449 Search PubMed.
- S. M. Dancoff, Non-Adiabatic Meson Theory of Nuclear Forces, Phys. Rev., 1950, 78, 382–385 CrossRef.
- S. Hirata and M. Head-Gordon, Time-dependent Density Functional Theory within the Tamm–Dancoff Approximation, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- M. E. Casida and M. Huix-Rotllant, Progress in time-dependent density-functional theory, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, Is the Tamm-Dancoff approximation reliable for the calculation of absorption and fluorescence band shapes?, J. Chem. Theory Comput., 2013, 9, 4517–4525 CrossRef CAS PubMed.
- S. DeBeer George and F. Neese, Calibration of scalar relativistic density functional theory for the calculation of sulfur K-edge X-ray absorption spectra, Inorg. Chem., 2010, 49, 1849–1853 CrossRef CAS PubMed.
- M. J. Peach, M. J. Williamson and D. J. Tozer, Influence of triplet instabilities in TDDFT, J. Chem. Theory Comput., 2011, 7, 3578–3585 CrossRef CAS PubMed.
- C. Hu, O. Sugino and K. Watanabe, Performance of Tamm-Dancoff approximation on nonadiabatic couplings by time-dependent density functional theory, J. Chem. Phys., 2014, 140, 054106 CrossRef PubMed.
-
L. K. Sørensen, R. Lindh and M. Lundberg, What do we approximate and what are the consequences in perturbation theory?, arXiv preprint arXiv:1608.02399 2016.
- S. Luber and M. Reiher, Raman optical activity spectra of chiral transition metal complexes, Chem. Phys., 2008, 346, 212–223 CrossRef CAS.
- F. London, Théorie quantique des courants interatomiques dans les combinaisons aromatiques, J. Phys. Radium, 1937, 8, 397 CrossRef CAS.
- T. Helgaker, K. Ruud, K. L. Bak, P. Jørgensen and J. Olsen, Vibrational Raman optical activity calculations using London atomic orbitals, Faraday Discuss., 1994, 99, 165–180 RSC.
- M. Krykunov and J. Autschbach, Calculation of origin-independent optical rotation tensor components in approximate time-dependent density functional theory, J. Chem. Phys., 2006, 125(3), 034102 CrossRef PubMed.
- Y. Zhang, J. R. Rouxel, J. Autschbach, N. Govind and S. Mukamel, X-ray circular dichroism signals: a unique probe of local molecular chirality, Chem. Sci., 2017, 8, 5969–5978 RSC.
- J. Goulon, A. Rogalev, F. Wilhelm, N. Jaouen, C. Goulon-Ginet and C. Brouder, Optical activity probed with x-rays, J. Phys.: Condens. Matter, 2003, 15, S633 CrossRef CAS.
- L. Alagna, T. Prosperi, S. Turchini, J. Goulon, A. Rogalev, C. Goulon-Ginet, C. R. Natoli, R. D. Peacock and B. Stewart, X-ray natural circular dichroism, Phys. Rev. Lett., 1998, 80, 4799 CrossRef CAS.
- B. Stewart, R. D. Peacock, L. Alagna, T. Prosperi, S. Turchini, J. Goulon, A. Rogalev and C. Goulon-Ginet, Circular Dichroism at the Edge: Large X-ray Natural CD in the 1s -> 3d Pre-Edge Feature of 2 [Co (en) 3Cl3].NaCl·6H2O, J. Am. Chem. Soc., 1999, 121, 10233–10234 CrossRef CAS.
-
D. P. Craig and T. Thirunamachandran, Molecular quantum electrodynamics: an introduction to radiation-molecule interactions, Courier Corporation, 1984 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc04120b |
| ‡ J. R. Rouxel and Y. Zhang have equal contributions. |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Yu
Zhang‡
*a,
Yu
Zhang‡
 *b and
Shaul
Mukamel
*cd
*b and
Shaul
Mukamel
*cd

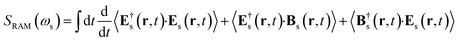
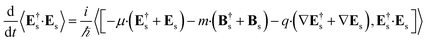
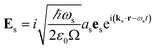
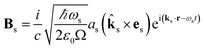
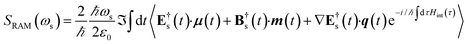
 and
and  denote the real and imaginary parts respectively. To obtain the ROA signal, we expand the exponent to second order in the incident field. Three terms then contribute to the signals. The leading term is given by the interaction with the electric dipoles only (diagram (a)) and does not contribute to the ROA signal since it vanishes upon rotational averaging. Diagram (b) contains one magnetic dipole and diagram (c) has one electric quadrupole interaction.
denote the real and imaginary parts respectively. To obtain the ROA signal, we expand the exponent to second order in the incident field. Three terms then contribute to the signals. The leading term is given by the interaction with the electric dipoles only (diagram (a)) and does not contribute to the ROA signal since it vanishes upon rotational averaging. Diagram (b) contains one magnetic dipole and diagram (c) has one electric quadrupole interaction.