Open Access Article
Open Access ArticleA topological model for predicting adsorption energies of polycyclic aromatic hydrocarbons on late-transition metal surfaces†
Zhao-Bin
Ding
 a,
Matteo
Tommasini
a,
Matteo
Tommasini
 b and
Matteo
Maestri
b and
Matteo
Maestri
 *a
*a
aLaboratory of Catalysis and Catalytic Processes, Dipartimento di Energia, Politecnico di Milano, Via La Masa 34, 20156, Milano, Italy. E-mail: matteo.maestri@polimi.it
bDipartimento di Chimica, Materiali e Ingegneria Chimica “G. Natta”, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133, Milano, Italy
First published on 20th December 2018
Abstract
We introduce and validate by first-principles calculations an analogy between metal coordination chemistry and the adsorption of polycyclic aromatic hydrocarbons (PAHs) at metal surfaces for the derivation of a model for predicting the PAH adsorption energies. We correlate the binding of PAH on the metal surface with the coordination between metal atom and the ligands in the metal complex, where the formation enthalpy of metal complexes is mainly determined by the strength of a single metal–ligand (M–L) bond and by the number of the M–L bonds. This analogy allows estimation of the adsorption energies only on the basis of the structure of the PAHs and of their adsorption configurations. The adsorption energies of PAHs are found to depend on simple geometric parameters, such as the number of metal–carbon bonds. Moreover, when the lattice of the metal surface is commensurate with the size of benzene rings, the contribution to the adsorption energy from η2-coordination is about twice that from η1-coordination. These results show that the principles of coordination chemistry can facilitate the modeling of processes at metal surfaces, and pave the way to systematically model reactions involving complex adsorbates at surfaces.
Introduction
The formation of polycyclic aromatic hydrocarbons (PAH) on metal surfaces is involved in critical processes such as catalyst coking1,2 and graphene formation reactions.3–5 In particular, understanding the kinetics of PAH formation on metal surfaces is of utmost importance for improving, for instance, either the coke-resistance of catalysts or to optimise operating conditions for the synthesis of graphene. In this respect, the first key-point to model the PAH formation under arbitrary reaction conditions is to describe in detail the general adsorption mechanism of PAHs on metal surfaces.6 This task is significantly hindered by both the broad variety of PAH structures and by their different adsorption configurations. For instance, even for benzene, which is the simplest aromatic molecule, theoretical studies have identified at least six adsorption configurations.7–9 Moreover, the mismatch between the size of the aromatic rings and the lattice of metal surfaces leads to the deformation of the PAH molecules upon adsorption and to the variation of the binding sites of each ring of the PAH, as reported, for instance, for the graphene adsorption on Rh(111) surface.10 As the size of the PAH increases, so do the number of adsorption configurations and the required surface models. Thus, a systematic first-principles investigation of PAH adsorption may quickly become impractical for large PAH molecules of interest. This calls for the development of models able to predict the PAH adsorption energies on the basis of a limited number of descriptors, thus overcoming the intrinsic complexity of the problem.11–15A first attempt to model the adsorption of PAH was provided by Sautet and co-workers.16 Their model is based on the consideration that the adsorption of a PAH can be regarded as the summation of the adsorption of multiple benzene rings. Therefore, the overall adsorption energy of PAH can be calculated by the adsorption energy of benzene on the bridge site multiplied by a factor that is proportional to the number of metal atoms which bind to the PAH. Such approach, however, limits the applicability of this model to the adsorption configurations that are derived from the bridge adsorption of benzene. Therefore, it cannot give an a priori estimation of the relative stability of all the adsorption configurations especially for the large PAHs on the surfaces with large lattice, where not all the aromatic rings can be adsorbed on the bridge site.10 Moreover, this model cannot provide a conceptual explanation on why different configurations (e.g., naphthalene binding on bridge site of Ni(111) surfaces17) can exhibit the same adsorption energy.
To overcome these limitations, here we propose an approach to systematically model the adsorption of PAH on metal surfaces by introducing an analogy between the case of PAH coordination and metal–organic complexes. This analogy between the coordination of PAH to the metal atoms complexes and its adsorption on a metal surface is inferred by previous investigations where the same bonding mechanism was found both with the metal–organic complexes and at the metal surfaces. For instance, the same π-back-bonding mechanism, where metal d-orbitals donates electrons to the π antibonding orbitals of the molecules, has been found in CO adsorption,18 M–C2H4 (where M is the transition metal) complex formation,19,20 and, in particular, in the coordination of cyclopentadienyl both in ferrocene and on Pt(111).21 More specifically, in this work we successfully correlate the binding of PAH on the metal surface with the coordination between metal atom and the ligands in the metal complex, where the formation enthalpy of metal complexes is mainly determined by the strength of a single metal–ligand (M–L) bond and by the number of the M–L bonds.22 The validity of this analogy allows for describing the PAH adsorption only on the basis of the topological features of PAHs. The origin of the analogy is discussed by analyzing the binding mechanism of PAHs at the surface on the basis of density functional theory (DFT) calculations – at the level of dispersion-corrected PBE functional – of representative PAHs on four close-packed late-transition-metal surfaces, namely Ni(111), Rh(111), Pd(111) and Pt(111). On a more general basis, these results, by quantitatively connecting the trends in surface chemistry to the principles of coordination chemistry, may dramatically facilitate the developing of detailed microkinetic models that involve complex adsorbates at surfaces.
Models and theoretical methods
Density functional theory (DFT) calculations were carried out with the Quantum-Espresso code.23 We adopted a plane-wave basis set with an energy cutoff of 680 eV. The ultrasoft-pseudopotential24 approximation was used for describing the interactions between core electrons and valence electrons. We used the Perdew–Burke–Ernzerhof (PBE) functionals25 to describe the exchange–correlation potentials. Grimme D2 correction26 scheme was applied to include the van der Waals interactions between the PAHs and the metal surfaces, which are relevant for molecules of this size.8 We selected benzene, naphthalene, phenanthrene, pyrene, and tetracene to represent PAHs of different size and structure. The metal surface was described by a 4-layer slab model with only the topmost layer allowed to relax. The size of the unit cell varied according to the size of the adsorbed PAH to sufficiently separate the PAHs in different unit cells (details are reported in Tables S1 and S2 of the ESI†). To eliminate spurious interactions between the periodic replicas of the slabs, a vacuum layer of 12 Å between the slabs was considered. We sampled the reciprocal space of this slab model with a k-point mesh equivalent to the 12 × 12 × 1 Monkhorst–Pack grid27 of the 1 × 1 unit cell of the metal slab. All the parameters above have been tested to ensure the convergence of the adsorption energies within 0.01 eV. The geometry optimization of the models was carried out until the forces were converged within a threshold of 2.57 × 10−3 eV Å−1. This value was needed to guarantee that the computed adsorption configurations are true local minima, even in the situation where the potential energy surface is relatively flat vs. the degrees of freedom describing the relative position of the PAHs with respect to the metal surface.Results and discussion
Fig. 1 shows the adsorption configurations of the PAHs investigated in this work. These structures have been selected by considering the previous studies reported in the literature about the most stable adsorption configurations of naphthalene28 (di-bridge[6] and di-bridge[7], where the number indicates the metal atoms that bind with naphthalene). Both configurations of the adsorbed naphthalene are derived from the bri30 adsorbed benzene where two metal–carbon bonds (M–C bonds in η1 coordination) and two C–M–C bonds (η2 coordination, equivalent to two effective M–C bonds) are formed. Also, to evaluate the applicability of our model on a less stable adsorption configuration, we considered the hollow[8] adsorbed pyrene, which is derived from the hcp0 adsorbed benzene where no η1 coordination is involved. Here we focus on the flat adsorption configuration, which has been reported to be the most favoured configuration for the linear PAHs with less than 5 aromatic rings.29,30 Geometric optimisation results show that only the outermost carbon atoms are bent up on all the PAHs, except for the buckled tetracene-bridge[10] structure on Pt(111) surface. The largest bending measured by the vertical distance between carbon atoms and the lowermost plane are 0.21 Å on Ni, 0.24 Å on Rh, 0.27 Å on Pd and 0.27 Å on Pt. The only structure that severely deviates from the planar configuration is the buckled tetracene-bridge[10] structure on Pt(111) surface as shown in Fig. 1. In this configuration, the central ring of the molecule, which is above the hcp site, is bent up by 0.61 Å with respect to the plane formed by the rings at both ends. Such buckling pattern corresponds to the unstable adsorption of benzene in the hcp30 configuration (where three C atoms stand above 3f-hollow sites) on Pt(111) surface,7,31 and is also observed on graphene on Rh(111) surfaces.10 The C–C bonds of all the PAHs are all stretched upon adsorption. In particular, the η2-coordinated C–C bonds elongate to 1.41–1.46 Å, and the others elongate to 1.44–1.49 Å. We observe that the values of the C–C bond elongation upon adsorption are not correlated to the values of the corresponding C–C bonds in the gas phase structures. The comparison of the C–C bond lengths both on adsorbed naphthalene and on adsorbed phenanthrene (which are listed in Tables S6 and S7 of the ESI†) reveals that such expansion occurs for all the PAHs herein considered and indicates that the PAHs tend to adapt to the pattern of the metal atoms at the surface upon adsorption. This evidence is also consistent with the fact that upon adsorption the PAHs tend to maximize the number of C atoms bound by metal atoms, as also observed for benzene and naphthalene.9,28,32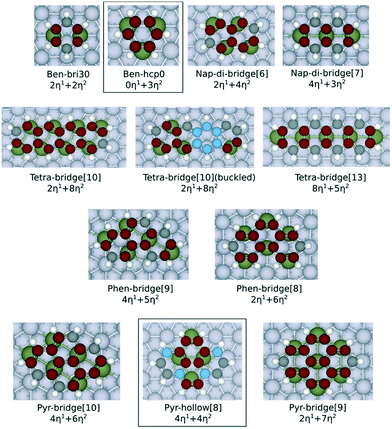 | ||
| Fig. 1 Ball and stick models of the adsorption configurations investigated in this work. All the C atoms involved with η2 coordination are displayed in red colour. The C atoms involved with η1 coordination are displayed in black colour. Non-bonded C atoms are displayed in blue colour. The η2-coordinated metal atom is labelled in dark green. The ben-hcp0 derived configurations are contained in a box, and the other ones are all ben-bri30 derived structures. The naming scheme chosen for benzene follows Morin et al.7 The adsorption configurations of the other PAHs follow the naming scheme from Santarossa et al.:28 (compound name)-(dominate adsorption site)[(number of metal atoms bonded)]. The compound names are abbreviated here as: ben = benzene, nap = naphthalene, tetra = tetracene, phen = phenanthrene, pyr = pyrene. The tetracene-bridge[10] and buckled tetracene-bridge[10] configurations have the same symmetric structure on the surface, but they differ by the fact that the central aromatic ring of the molecule is lifted from the metal surface in buckled tetracene-bridge[10], while it is flat for the tetracene-bridge[10]. | ||
The adsorption energies of all the PAHs considered in this work are listed in Fig. 2. On all the metals, we find that the order of adsorption energies of the bri30 derived structures (where each C atom binds with only one metal atom and have at least two η1 coordinated carbon atoms) is always tetracene > pyrene > phenanthrene > naphthalene > benzene. This sequence indicates that the adsorption energy increases with the number of carbon atoms and consequently with the number of C atoms bound at the surface. This observation agrees with previous findings on the adsorption of linear PAHs on Pt(111) surface.16 Besides the case of tetracene on Pt(111), for the other PAHs, the adsorption energies of the bri30 derived structures of the same PAH differ by less than 0.30 eV. The hcp0 derived pyr-hollow[8], however, binds at least 0.50 eV weaker than all the bri30 derived pyrenes on Rh(111), Pd(111) and Pt(111). This is even weaker than the binding energies for phenanthrenes. This trend is correlated with the reduction of the number of C atoms bound at the surface, which is 16 for pyr-bridge[8] and pyr-bridge[9], 12 in pyr-hollow[8], and 14 for phenanthrenes. All these observations reveal a direct correlation between the adsorption energy and the number of C atoms bound at the surface.
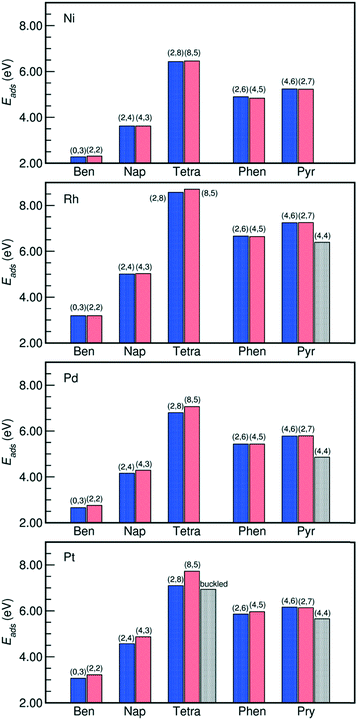 | ||
| Fig. 2 Adsorption energies of PAHs binding on M(111) surfaces in the configurations listed in Fig. 1. The number of η1-coordinated M atoms and the number of η2-coordinated M atoms of each PAH is reported on the histograms as (n1, n2). The “buckled” tetracene corresponds to the buckled tetra-bridge[10] structure. The adsorption energies are calculated by Ebinding = −(Etotal − Eslab − EPAH), where “total” denotes the PAH adsorbed on the slab, “slab” is the bare slab, and the “PAH” denotes the free PAH molecule. A more positive value indicates a stronger PAH–M binding. Detailed values are listed in Table S3 in the ESI.† | ||
To gain insights into the physical origin of the correlation between the adsorption energy and the number of C atoms that are bound at the surface, we compute the charge density difference upon adsorption as follows:
| Δρ = ρ(PAH:M) − ρ(PAH0) − ρ(M0) | (1) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in metal-alkene complexes.19,20 This picture is further confirmed by an analysis of the partial density of states of two naphthalene adsorption configurations provided in Fig. S1 of the ESI.† Because of the wider variety of the PAH species and the configurations herein considered in this work, such d–π hybridization mechanism of metal–PAH bonding can be extended to all the PAHs. Therefore, the formation of more M–C bonds induces a larger charge transfer between the PAH and the metal surface, and, thus strengthens the bond.
C bond in metal-alkene complexes.19,20 This picture is further confirmed by an analysis of the partial density of states of two naphthalene adsorption configurations provided in Fig. S1 of the ESI.† Because of the wider variety of the PAH species and the configurations herein considered in this work, such d–π hybridization mechanism of metal–PAH bonding can be extended to all the PAHs. Therefore, the formation of more M–C bonds induces a larger charge transfer between the PAH and the metal surface, and, thus strengthens the bond.
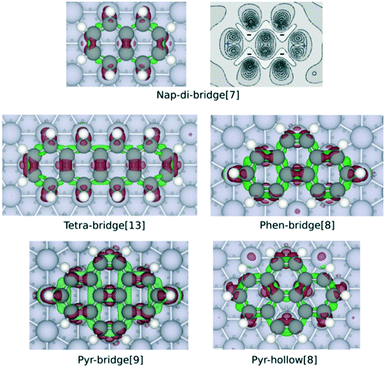 | ||
| Fig. 3 Charge density difference maps of nap-di-bridge[7], tetra-bridge[13], phen-bridge[8], pyr-bridge[9] and pyr-hollow[8] on Rh(111) surface. The maps are obtained by calculating Δρ by eqn (1), with the structure of the isolated PAH and slab both rigidly taken from the optimised structure of adsorbed PAH. The red isosurface (0.05 Å−3) show electron gain while the green isosurface (−0.03 Å−3) indicate electron loss. The contour plot of the charge difference of nap-di-bridge[7] on Rh(111) displays the electron density change between −0.03 Å−3 and 0.13 Å−3 with ten isolines. The dark region shows electron gaining, and the light region indicates electron depletion. | ||
Hence, on the basis of the strong correlation between the adsorption energy and the number of C atoms that bind to the surface in both forms of M–C bonds, we now propose a model to relate the adsorption energy of PAHs to the topology of the PAH–metal bond (namely the number of η1 coordinations (n1) and the number of η2 coordinations (n2)). We also take nph as a variable of the model to account for the non-local interactions between metal and PAHs. These interactions include the Pauli repulsion and the van der Waals forces that were previously reported to be proportional to the number of rings in contact with the metal surface (nph).33 Therefore, the model can be written as:
| Ebind = Ephnph + EM–Cn1 + gEM–Cn2 | (2) |
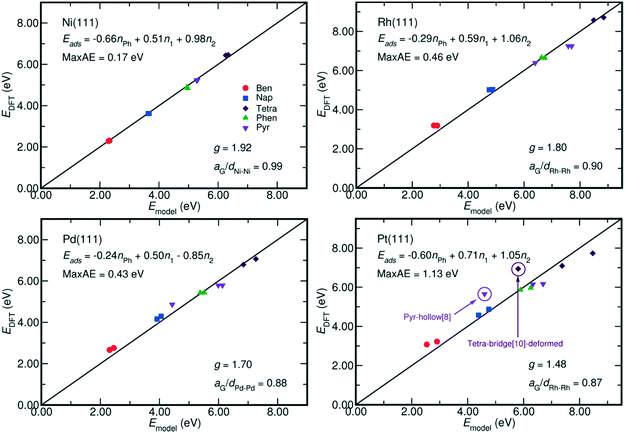 | ||
| Fig. 4 Comparison between the adsorption energy estimated by eqn (2) and that calculated by DFT. The fitted models and their maximum absolute error (MaxAE) are written on each plot. The lattice mismatch is measured by aG/dM–M, where aG is the lattice constant of graphene and dM–M denotes the M–M bond length on M(111) surface. In our calculation, the aG equals to 2.47 Å, which is close to the experimental value of 2.46 Å;35 and the dM–M of Ni, Rh, Pd, and Pt are respectively 2.49 Å, 2.73 Å, 2.79 Å and 2.82 Å. A smaller aG/dM–M value indicates a larger mismatch. The MaxAE on Pt surface becomes 0.53 eV by excluding the weaker bound benzene-hcp-0, deformed tetracene-bridge[10] and pyrene-hollow[8]. | ||
The coefficients of each term in eqn (2) also reveal the different contribution of metal–PAH interactions to the adsorption energy. First, the contribution from the non-bonding interactions between aromatic rings and the metal surface, Eph, is always negative. It indicates an overall repulsive non-bonding interaction between the electrons on the C–C bonds and the electrons on the metal surfaces. Such repulsive interaction is due to the short distances between the PAH plane and the surface, around 1.97 Å on Ni and 2.05 Å on Pt. Both of them are shorter than the sum of the Van der Waals radii, which amounts to 3.40 Å (Ni–C) and 3.49 Å (Pt–C).34 Second, the contributions from the M–C bonds (EM–C, gEM–C) are always positive, and this is in line with the fact that the most stable adsorption configurations of the PAHs are the ones with the highest number of C atoms bound at the surface.9,28,32 Furthermore, the g factor, the ratio between the contributions from each η2 coordination and that from each η1 coordination to the adsorption energy, is close to 2 especially on Ni(111) where the Ni–Ni bond length, 2.49 Å, is close to the lattice constant of graphene, 2.47 Å. This indicates an equal energetic contribution from the interactions between M and every C in the η2-coordination and from the M–C bond of each η1 coordination when the lattice of metal surface perfectly matches the lattice of graphene. This is in analogy with the energetics of chelate metal complexes, for which the formation enthalpy is mainly determined by the number of M–L bonds, and by the characteristic bond strength of a single M–L bond.22
Moreover, Fig. 4 reveals that the g factor in eqn (2) monotonically decreases as the lattice mismatch increases (the relationship is illustrated in Fig. S2 of the ESI†). For instance, the g factor reduces from 2 on the ideal surfaces, which do not induce strain on PAH upon adsorption, to 1.48 on Pt(111) surfaces, which have the largest difference between M–M bond (2.82 Å) length and the size of each aromatic ring (2.47 Å). Such decrease of the g factor implies a relative reduction of the contribution from each η2-coordinated bond. This is also suggested by the adsorption energy shown in Fig. 2, where on Rh(111), Pd(111) and Pt(111) the adsorption of the benzene-bridge-30 derived configurations with more η2-coordinated atoms are always weaker than those with more η1-coordinated atoms, even though the number of carbon atoms that are bound on the surface does not change. Such energy difference increases from 0.14 eV on Rh(111) to 0.60 eV on Pt(111) along with the increase of the difference between the dimension of the aromatic rings and the lattice of the metal surface. This confirms that the contributions from η2 coordinations are sensitive to the lattice mismatch. Also, Fig. 2 indicates that among all the PAHs on a single metal, the order of the difference between the adsorption energies of the two benzene-bri30 derived configurations is tetracene > naphthalene > benzene > phenanthrene > pyrene. This sequence reveals that when the lattice mismatch exists, the binding strength of an angular or a clustered PAH is less sensitive to the adsorption configuration than a linear PAH.
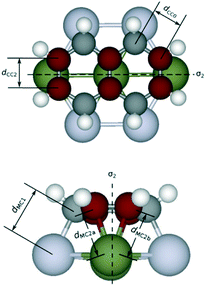
To gain insights into the effects of the lattice mismatch on the energy contributions from η2 coordination, which is reflected by the variation of the bond lengths, we analyze in detail the geometry upon adsorption. As reported in Fig. 5, we use the notation CC2 (MC2a, MC2b) to denote C–C (M–C) bonds involved with η2-coordinations, CC0 to denote all the other C–C bonds, and MC1 to denote the M–C bonds involved with η1-coordinations; the mirror planes bisecting the CC2 bonds are labelled by σ2. We take naphthalene as an example of linear PAH. The structural analysis shows that the average dCC2 ranges from 1.43 to 1.44 Å, regardless of the adsorption configurations and of the metal. In contrast, the average dCC0 varies from 1.45 Å (Ni) to 1.48 Å (Pt), which follows the increasing lattice constant of the metal (and consequently the increasing lattice mismatch). This observation suggests that the PAH fits the lattice of different metal surfaces upon adsorption mainly by varying the lengths of CC0 bonds while CC2 bonds are more rigid and do not change for the different metal surfaces. On nap-di-bridge[7], all the CC2 bonds share the same σ2 mirror plane as shown in Fig. 1. This adsorption geometry facilitates stretching the rings perpendicularly to σ2 to accommodate the η1 coordinations, and therefore strengthens the binding of PAH especially on metal surfaces where the lattice constant largely differs from the lattice of graphene. In contrast, as shown in Fig. 1, on nap-di-bridge[6] the CC2 bonds belong to two parallel σ2 local symmetry planes, which leads to conflicts when both rings are expanding perpendicular to their own σ2 local symmetry planes. As a result, the rings become more rigid. This hinders the possibility of adapting the PAH bonds upon adsorption and it leads to a weaker PAH binding. In fact, on Pt(111) surface, on one hand, the average dMC1 value is 2.18 Å on di-bridge[7], while it increases to 2.23 Å on di-bridge[6]. On the other hand, the average dMC2 values are all around 2.22 Å for both configurations (within a variation of less than 0.01 Å), which indicates the same energy contribution from each η2 coordination to the adsorption energies of both configurations. Therefore, we can correlate the larger adsorption energy of the di-bridge[7] configuration (by 0.30 eV) with the shorter dMC1. As a consequence, for non-ideal surfaces, the higher is the number of CC2 bonds in the adsorption configuration of the linear PAH, the lower is the adsorption energy, thus leading to values of g-factor lower than 2.
We have also extended our analysis to the case of phenanthrene, as an example of angular PAHs and clustered PAHs. Fig. 1 shows that the CC2 bonds belong to two parallel σ2 planes in bridge[9] configuration, and to three σ2 planes in bridge[8] configuration. Thus, in both structures, similar to the case of naphthalene-di-bridge[6], the expansion of the aromatic rings are all confined by symmetry which results in a small energy difference. This is confirmed by the same average dMC2, and by the slight difference in the average dMC1 of both structures, which is 0.02 Å on Pt(111) surface. Therefore, the adsorption energy becomes less configuration-sensitive for the PAHs containing more than two local symmetry σ2 planes.
Besides the sensitivity of the length of MC1 bond (dMC1) to the adsorption configuration, we also observed that the number of η2-coordinated C–C bonds which have significantly different MC2a and MC2b bonds increases with the mismatch between the metal surface and the PAH rings. We find that on Pt(111) surface 11 pairs (out of 46) have such difference larger than 0.10 Å, while on Ni(111) this number reduces to 3. This is because the maximum C–C bond extension (1.49 Å, corresponding to the lattice constant of 2.58 Å of graphene) is not enough to match the characteristic M–M bond length on Rh(111) (2.74 Å), Pd(111) (2.80 Å) and Pt(111) (2.82 Å) surfaces. Consequently, the C–M–C structure of η2 coordination deviates from the reflectional symmetric arrangement. This fact reduces the adsorption energy contribution of an MC2 bond and therefore reduces the g ratio. However, we also find that the adsorption energies of both pyrene-bridge[9] and pyrene-bridge[10] on Pt(111) surface, as reported in Fig. 2, are similar, even though the average deviation, |dMC2a–dMC2b|, on bridge[10] structure, 0.07 Å, is appreciably longer than that on bridge[9], 0.03 Å. We thus conclude that the effect of the deviation from ideal η2-coordination where dMC2a = dMC2b become significant only when one of the two M–C bonds becomes as long as to neglect the interaction between metal atom and the C atom. This indicates that the stiffness of the molecule upon adsorption is the dominant reason for the deviation of the g factor from 2 (i.e. the g factor for the metal surfaces that will not introduce the strain of PAH upon adsorption) and further confirms that the adsorption of the PAH at the metal surface is determined only by the topological nature of the PAH and the strength of the M–C bonds in analogy with the mechanism of metal organic complex coordination.
On a more general perspective, the analogy between the binding mechanisms for the PAH adsorption and the metal–organic complex paves the way to systematically investigate the thermodynamic properties upon adsorption of PAHs by exploiting the principles of coordination chemistry such as the chelate effect. In particular, the model herein developed on the basis of such analogy lays the foundation for studying the adsorption of more complex aromatic systems on different metal surfaces. For instance, the model can be used to obtain the binding energy of PAHs with substituted functional groups by incorporating the correction derived from the hard and soft acids and bases theory.36 Also, by making use of the d-band center theory, the model can be employed to predict the adsorption energy of different PAHs on different metal surfaces.37
Conclusions
We have found that PAH adsorption at metal surfaces mainly depends on the number and strength of the formed M–C bonds by means of Grimme D2 DFT-PBE calculations of the adsorption of benzene, naphthalene, tetracene, phenanthrene and pyrene on Ni(111), Rh(111), Pd(111) and Pt(111) surfaces. This dependency is found to be analogous to the coordination between metal atom and the ligands in a metal complex, where the formation enthalpy is only determined by the number of metal–carbon bonds. On the basis of this analogy, we proposed a model for the adsorption energy which applies to PAHs of different size and shape. The model is linear vs. the number of η1- and η2-coordinated metal atoms, and vs. the number of aromatic rings. This model can describe the adsorption energies of the examined PAHs on all the metal surfaces considered, and predicts the relative stability of all the adsorption configurations. We have also investigated the effects of the mismatch between the metal surface lattice and the size of benzene rings. This lattice mismatch mainly affects the adsorption energy by changing the ratio between the energy contribution of η2- and η1-coordination from the ideal value of g = 2. The effect is more evident in linear PAHs, i.e., naphthalene, and tetracene. It results from both the rigidness of the η2-coordinated C–C bonds and from symmetry constraints as the PAHs expand upon adsorption on the metal surface.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The projects leading to this work have received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Project SHAPE – grant agreement No. 677423) and from MIUR, (Rome, Italy) under the action SIR 2014 (Scientific Independence of Young Researchers) 2014 (Project THEOREMA Grant No. RBSI14TG3E). Computational time at CINECA, Bologna (Italy) is gratefully acknowledged.References
- M. D. Argyle and C. H. Bartholomew, Catalysts, 2015, 5, 145–269 CrossRef CAS.
- C. H. Bartholomew, Catal. Rev.: Sci. Eng., 1982, 24, 67–112 CrossRef CAS.
- X. Wan, K. Chen, D. Liu, J. Chen, Q. Miao and J. Xu, Chem. Mater., 2012, 24, 3906–3915 CrossRef CAS.
- B. Wang, X. Ma, M. Caffio, R. Schaub and W.-X. Li, Nano Lett., 2011, 11, 424–430 CrossRef CAS PubMed.
- B. Wang, M. König, C. J. Bromley, B. Yoon, M.-J. Treanor, J. A. Garrido Torres, M. Caffio, F. Grillo, H. Früchtl, N. V. Richardson, F. Esch, U. Heiz, U. Landman and R. Schaub, J. Phys. Chem. C, 2017, 121, 9413–9423 CrossRef CAS.
- R. J. Maurer, V. G. Ruiz, J. Camarillo-Cisneros, W. Liu, N. Ferri, K. Reuter and A. Tkatchenko, Prog. Surf. Sci., 2016, 91, 72–100 CrossRef CAS.
- C. Morin, D. Simon and P. Sautet, J. Phys. Chem. B, 2003, 107, 2995–3002 CrossRef CAS.
- W. Liu, J. Carrasco, B. Santra, A. Michaelides, M. Scheffler and A. Tkatchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245405 CrossRef.
- F. Mittendorfer and J. Hafner, Surf. Sci., 2001, 472, 133–153 CrossRef CAS.
- B. Wang, M. Caffio, C. Bromley, H. Früchtl and R. Schaub, ACS Nano, 2010, 4, 5773–5782 CrossRef CAS PubMed.
- M. Maestri, Chem. Commun., 2017, 53, 10244–10254 RSC.
- Z.-B. Ding, E. Di Marco, M. Pelucchi, T. Faravelli and M. Maestri, Chem. Eng. J. DOI:10.1016/J.CEJ.2018.08.077.
- G. H. Gu and D. G. Vlachos, J. Phys. Chem. C, 2016, 120, 19234–19241 CrossRef CAS.
- M. Salciccioli, Y. Chen and D. G. Vlachos, J. Phys. Chem. C, 2010, 114, 20155–20166 CrossRef CAS.
- D. C. Tranca and F. J. Keil, J. Chem. Phys., 2011, 134, 104708 CrossRef CAS PubMed.
- C. Morin, D. Simon and P. Sautet, J. Phys. Chem. B, 2004, 108, 12084–12091 CrossRef CAS.
- M. Ghadami Yazdi, P. H. Moud, K. Marks, W. Piskorz, H. Öström, T. Hansson, A. Kotarba, K. Engvall and M. Göthelid, J. Phys. Chem. C, 2017, 121, 22199–22207 CrossRef CAS.
- G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2777 CrossRef CAS.
- M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C71 Search PubMed.
- B. J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939 RSC.
- N. R. Avery, Surf. Sci., 1984, 146, 363–381 CrossRef CAS.
- C. G. Spike and R. W. Parry, J. Am. Chem. Soc., 1982, 75, 2726–2729 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, http://www.quantum-espresso.org/pseudopotentials/.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Santarossa, M. Iannuzzi, A. Vargas and A. Baiker, ChemPhysChem, 2008, 9, 401–413 CrossRef CAS PubMed.
- W. Liu, V. G. Ruiz, G.-X. Zhang, B. Santra, X. Ren, M. Scheffler and A. Tkatchenko, New J. Phys., 2013, 15, 053046 CrossRef.
- S. J. Jenkins, Proc. R. Soc. A, 2009, 465, 2949–2976 CrossRef CAS.
- P. K. Ayishabi, K. G. Lakshmikanth and R. Chatanathodi, Chem. Phys. Lett., 2015, 637, 182–188 CrossRef CAS.
- C. Morin, D. Simon and P. Sautet, J. Phys. Chem. B, 2004, 108, 5653–5665 CrossRef CAS.
- Y. Jiang, S. Yang, S. Li and W. Liu, Sci. Rep., 2016, 6, 39529 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- D. Reddy, L. F. Register, G. D. Carpenter and S. K. Banerjee, J. Phys. D: Appl. Phys., 2012, 45, 019501 CrossRef.
- R. Réocreux, M. Huynh, C. Michel and P. Sautet, J. Phys. Chem. Lett., 2016, 7, 2074–2079 CrossRef PubMed.
- X. Jia and W. An, J. Phys. Chem. C, 2018, 122, 21897–21909 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Adsorption energies of PAHs, analysis of interactions between the bands on metal surfaces and the orbitals on PAHs, coefficients of the adsorption energy model, geometries of the free and the adsorbed naphthalene and phenanthrene molecules. See DOI: 10.1039/c8re00229k |
| This journal is © The Royal Society of Chemistry 2019 |