Carbon fragments as highly active metal-free catalysts for the oxygen reduction reaction: a mechanistic study†
Keke
Mao‡
ab,
Wei
Zhang‡
bc,
Jun
Dai
 b and
Xiao Cheng
Zeng
b and
Xiao Cheng
Zeng
 *b
*b
aSchool of Energy and Environment Science, Anhui University of Technology, Maanshan, Anhui 243032, China
bDepartment of Chemistry, University of Nebraska, Lincoln, NE 68588, USA. E-mail: xzeng1@unl.edu
cBeijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, China
First published on 29th July 2019
Abstract
In metal-free carbon-fullerene-based or defective graphene-based electrocatalysts, pentagon rings are known to play a key role in boosting catalytic activities for the oxygen reduction reaction (ORR). However, the fundamental chemical mechanism underlying the remarkable catalytic effect of the pentagon rings towards the ORR is still not fully understood. Herein, we perform a comprehensive computational study of the catalytic activities of various carbon fullerenes and fullerene fragment species, all containing pentagon rings, by using the density functional theory (DFT) and computational hydrogen electrode (CHE) methods. We find that more active sites on carbon are associated with more neighbouring pentagon rings and stronger adsorption of the key intermediates of O*, OH* and OOH* for the ORR. Importantly, two C60-based fragments, namely, C60-frag1 and C60-frag2l, show a very high activity towards the ORR, as both yield overpotentials as low as 0.389 and 0.407 V, and entail suitable adsorption free energy of OH* and OOH* species. These desirable chemical properties of fullerene fragments can be attributed to the high-energy HOMO orbitals, induced by the low-symmetry fullerene-fragment structures. Both the number of neighbouring pentagon rings and the degree of overall symmetry of the fragment appear to be the two important factors that can be adjusted for the design of optimal metal-free carbon electrocatalysts towards high ORR activities.
Introduction
The oxygen reduction reaction (ORR) is a key and rate-limiting process in many applications associated with renewable energy conversion, for example, rechargeable metal–air batteries and proton-exchange membrane fuel cells. The state-of-the-art ORR catalysts include precious-group metal (PGM) platinum (Pt) and Pt-based catalysts, while their large-scale commercial applications are still hindered by the high cost and scarcity and by Pt's sensitivity to deactivation in the presence of CO. Intense studies have been devoted to improve the efficiency of utilization of platinum1,2 or to search for alternative more cost-effective Non-precious-group-metal (N-PGM) based electrocatalysts. For example, carbon or metal oxide material supported nanoparticles or single atom electrocatalysts can significantly reduce the dosage of precious Pt while maintaining a good ORR activity.1,2 One particular class of Pt replacement electrocatalysts, many belong to the N-PGM catalysts,3 are atomically dispersed M–N–C catalysts4–6 which show a comparable ORR performance as Pt.Another class of promising and alternative electrocatalysts for the ORR is the metal-free heteroatom-doped carbon materials (carbon nanotubes,7 graphene,8–10 graphite11,12 and mesoporous carbon13–15). This class of catalysts has been extensively investigated since Dai et al.7 first discovered that nitrogen-doped carbon nanotubes (N-C) can exhibit a high electrocatalytic activity, long-term operation stability, and high tolerance to crossover effect in alkaline fuel cells. Heteroatom-doping can effectively tune the carbon materials’ local electronic properties and induce charge/spin redistribution on the sp2-conjugated carbon matrix, thereby promoting the ORR on the doped C electrode.7,16,17 Moreover, co-doping of N and another heteroatom such as B, S, and P can further modulate the catalysts’ electronic properties and polarization,18–20 thereby enhancing the overall catalytic activity.
Recently, it was demonstrated that bare carbon materials containing appropriate defects21 or a large number of edge sites18,22 can also exhibit outstanding ORR activity. Indeed, a perfect graphene sheet is known as a poor ORR catalyst, whereas a defective graphene catalyst exhibits a much higher ORR performance.23,24 For example, Yao et al.23 indicated that a defective graphene catalyst for a Zn–air battery presents very stable charge and discharge voltages, high current and power density, all comparable to those of Pt. Dai et al.22 predicated that dopant-free and edge-rich graphene is a highly efficient ORR catalyst. Intrinsic pentagon carbon rings can also play a critical role in enhancing the carbon materials’ ORR activity.25,26 This is because pentagons and other defects or edges can markedly strengthen the adsorption of O species, compared with the graphene basal plane, leading to desirable intermediate chemisorption. Note that 0-dimensional carbon fullerenes also contain intrinsic pentagon rings.27
Although previous work indicated that pentagon rings can effectively enhance the carbon materials’ ORR activity,25 and carbon nanocatalysts with adjacent pentagon and hexagon rings yield the lowest overpotential for the ORR,24,26,28 a detailed chemical mechanism on how pentagon rings affect the ORR's activity is still not fully understood. Is the most active site solely dependent on the number of neighbouring pentagon rings? Would the carbon site with adjacent pentagon and hexagon rings show good ORR activities? In this study, we address these questions by performing a systematic investigation on the ORR activities of various carbon fullerene species, including C60,29 C36,30 C24,31 and C20,32 as well as fullerene-based carbon fragments with H saturated edges. Interestingly, we find that fullerene fragments contain both intrinsic pentagon rings and numerous edge sites entail an outstanding ORR performance comparable to that of Pt.
Results and discussion
Results of the catalytic activities of small- and mid-sized fullerenes
Fullerenes are 0-dimensional carbon materials. Here, four kinds of small- and mid-sized fullerenes (C20, C24, C36 and C60), all containing pentagon carbon rings, are considered as possible metal-free electrocatalysts for the ORR. The structures of C60,29 C36,30 C24,31 and C20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 are taken from the literature. Fig. 1 shows the geometrical structures of C20, C24, C36 and C60. It can be seen that C20 possesses pentagon rings only, while C24, C36 and C60 possess both pentagon and hexagon rings. For C20, each C atom has three adjacent pentagon rings. We denote the active site in C20 as the “C20-3p” site. Meanwhile, for C60, each C atom has two adjacent hexagon and one adjacent pentagon rings. We denote the active site as the “C60-1p2h” site. For either C60 or C20, all the C atoms have the same neighbouring polygons and thus all are the same active sites. For C24, two types of active sites can be seen: one (denoted as C24-2p1h site) has two adjacent pentagon and one adjacent hexagon rings, and another (denoted as C24-3p) has three adjacent pentagon rings. For C36, there are three types of active sites: one (denoted as C36-1p2h site) has one adjacent pentagon and two adjacent hexagon rings. The other two sites have two adjacent pentagon and one adjacent hexagon rings, denoted as “C36-2p1h-1” and “C36-2p1h-2” sites.
32 are taken from the literature. Fig. 1 shows the geometrical structures of C20, C24, C36 and C60. It can be seen that C20 possesses pentagon rings only, while C24, C36 and C60 possess both pentagon and hexagon rings. For C20, each C atom has three adjacent pentagon rings. We denote the active site in C20 as the “C20-3p” site. Meanwhile, for C60, each C atom has two adjacent hexagon and one adjacent pentagon rings. We denote the active site as the “C60-1p2h” site. For either C60 or C20, all the C atoms have the same neighbouring polygons and thus all are the same active sites. For C24, two types of active sites can be seen: one (denoted as C24-2p1h site) has two adjacent pentagon and one adjacent hexagon rings, and another (denoted as C24-3p) has three adjacent pentagon rings. For C36, there are three types of active sites: one (denoted as C36-1p2h site) has one adjacent pentagon and two adjacent hexagon rings. The other two sites have two adjacent pentagon and one adjacent hexagon rings, denoted as “C36-2p1h-1” and “C36-2p1h-2” sites.
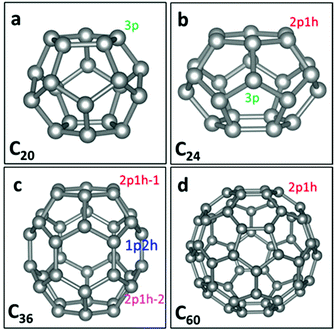 | ||
| Fig. 1 Graphs of C20, C24, C36, and C60 fullerene structures. The grey balls represent carbon atoms. 3p, 2p1h and 1p2h denote different active sites on four types of fullerenes. | ||
Next, we examine the adsorption properties of the key intermediates (O*, OH*, and OOH*) at various sites of C20, C24, C36, and C60 fullerenes. Table 1 presents the computed Gibbs adsorption free energies (ΔG(O*), ΔG(OH*), and ΔG(OOH*)) of O*, OH* and OOH* species at all distinctly different sites. In ESI Fig. S1,† the lowest-energy adsorption structures are displayed, where it can be seen that the O atom favors being adsorbed on the bridge site between two adjacent C atoms by forming two O–C bonds, but OH* and OOH* species are more likely to be adsorbed on the top site of a C atom by forming one O–C bond. As shown in ESI Fig. S1d† and Table 1, O* adsorbed on the bridge sites of C24-3p and C24-2p1h on C24 exhibits the same Gibbs adsorption free energy. Similarly, the C36-2p1h-2 site entails the same ΔG(O*) as C36-1p2h as both sites are bridge sites. For OH*, its adsorption free energies follow the trend ΔG(OH*)C60-1p2h > ΔG(OH*)C36-1p2h > ΔG(OH*)C36-2p1h-1 > ΔG(OH*)C36-2p1h-2 > ΔG(OH*)C24-2p1h > ΔG(OH*)C24-3p > ΔG(OH*)C20-3p. So the C60-1p2h site is the weakest adsorption site whereas the C20-3p site is the strongest site for OH*. It seems that the site with more adjacent pentagon rings exhibits a stronger adsorption of OH* species.
| Sites | ΔG(O*) | ΔG(OH*) | ΔG(OOH*) | ΔG1 | ΔG2 | ΔG3 | ΔG4 | U over |
|---|---|---|---|---|---|---|---|---|
| C20-3p | 0.111 | −0.687 | 2.566 | −2.354 | −2.455 | −0.798 | 0.687 | 1.917 |
| C24-3p | 0.068 | −0.532 | 2.770 | −2.150 | −2.703 | −0.600 | 0.532 | 1.762 |
| C24-2p1h | 0.068 | −0.251 | 3.022 | −1.898 | −2.954 | −0.319 | 0.251 | 1.481 |
| C36-2p1h-1 | 1.481 | 0.342 | 3.608 | −1.312 | −2.128 | −1.139 | −0.342 | 0.888 |
| C36-2p1h-2 | 1.594 | −0.240 | 3.039 | −1.881 | −1.445 | −1.834 | 0.240 | 1.470 |
| C36-1p2h | 1.594 | 1.090 | 4.354 | −0.566 | −2.760 | −0.504 | −1.090 | 0.726 |
| C60-1p2h | 1.836 | 1.367 | 4.627 | −0.293 | −2.790 | −0.470 | −1.367 | 0.937 |
For the site with the same number of adjacent pentagon and hexagon rings, the adsorption strength depends on the size of fullerenes: the larger the size of the fullerene, the weaker the adsorption of the OH* species. Note that O* and OOH* species also follow this generic trend for their adsorption.
Based on the adsorption of key O species on fullerenes, the ORR activities are evaluated (see Table 1). All of the four fullerenes are not good ORR catalysts since the overpotentials of various active sites on four fullerenes are all higher than 0.7 V, as shown in Table 1. On the sites with more than two adjacent pentagon rings of C20, C24, and C36, the step involving the last electron transfer and OH* reduction to water is the rate-limiting step, and the corresponding ORR activities are very poor due to very strong OH* adsorption (i.e., ΔG(OH*) is much smaller than 1.23 eV). In addition, on the sites with only one adjacent pentagon ring of C36 or C60, the third electron transfer step to form OH* or the first electron transfer step to form OOH* is the rate limiting step, respectively, and the ORR activities are still not high due to very strong O* adsorption (i.e., ΔG(O*) is much smaller than 2.46 eV) and very weak OH* and OOH* adsorption.
Results of the catalytic activities of C60 fragments
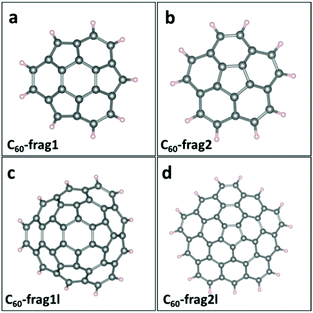
Since perfect small- and mid-sized fullerenes exhibit poor ORR activities, edge modulation is introduced as a promising strategy to tune the catalytic activities of fullerene-based materials. Here, we divide C60 fullerene into smaller fragments and passivate the edge with H atoms. Fig. 2a–d presents the structures of four distinct C60-based fragments, namely, C60-frag1, C60-frag2, C60-frag1l and C60-frag2l, respectively. C60-frag1 is composed of one central hexagon ring, and three peripheral pentagon and three peripheral hexagon rings. C60-frag2 is composed of one central pentagon ring and five peripheral hexagon rings. Compared with C60-frag1 and C60-frag2, C60-frag1l and C60-frag21 exhibit one more layer of hexagon rings surrounding the central C60-frag1 and C60-frag2, respectively. The thermal stabilities of the four fragments are examined by computing the formation energy of the four fragments with respect to gaseous hydrogen molecules and C60 fullerene. As shown in ESI Table S1,† the formation energies are all negative, indicating that the formation reactions of C60-frag1 and C60-frag2, C60-frag1l and C60-frag21 from C60 would all be exothermic.Next, adsorption of the key ORR intermediates of O species, O*, OH* and OOH*, on the four C60 fragments is evaluated. For all the four fragments, the most favorable active sites are those C atoms associated with the central hexagonal or pentagon ring. ESI Table S2† presents the computed Gibbs adsorption free energies of the intermediate species on the most favorable adsorption sites, while ESI Fig. S2† displays the corresponding adsorption structures. Again, the O atoms favor to be adsorbed on the bridge site between the active C atom and one adjacent C atom, forming two C–O bonds. The ΔG(O*) associated with C60-frag1, C60-frag2, C60-frag1l and C60-frag2l fragments are 2.625, 2.505, 2.276 and 2.309 eV, respectively, all notably greater than 1.836 eV on a perfect C60. This result indicates that the adsorption of O* on C60 fragments is much weaker than that on C60, which can facilitate the ORR on fragments since the adsorption of O* on C60 fragments is not too strong. The adsorption free energies of OH* and OOH* species differ appreciably on different fragments. As shown in ESI Table S2,† ΔG(OH*) on C60-frag1, C60-frag2, C60-frag1l and C60-frag2l fragments are 0.850, 1.826, 1.439, and 0.848 eV respectively. So the adsorption of OH* on C60-frag1 and C60-frag2l is much stronger than that on C60-frag1l and C60-frag2; even these four fragments exhibit similar active sites but different edges. The adsorption free energy of OOH on four fragments exhibits a similar trend, i.e., ΔG(OOH*)C60-frag1 < ΔG(OOH*)C60-frag2l < ΔG(OOH*)C60-frag1l < ΔG(OOH*)C60-frag2. Thus, both OH* and OOH* species are adsorbed more strongly on C60-frag1 and C60-frag2l than on C60-frag2 and C60-frag1l, as well as than on C60. It is understood that OH* and OOH* show the same adsorption trend on different fragments, since there is a widely accepted scaling relationship between OH* and OOH* on their adsorption free energies.33 On adsorption structures, both OH* and OOH* are adsorbed on the active sites of fragments, forming one O–C bond as on fullerenes. Bader charge analysis (see ESI Table S3†) suggests that all the adsorbed O*/OH*/OOH* species gain electrons during the adsorption, while the active C atoms lose electrons.
Note that the four-electron reaction pathways are commonly associated with metal-free carbon catalysts. Here, we focus on the four-electron reaction pathways. Fig. 3 shows the obtained four-electron ORR free-energy diagram at U0 = 0 V for the four model fragments, based on the CHE model. ESI Table S2† gives the corresponding ORR free-energy changes in the four-electron transfer steps. Both ESI Fig. 3 and Table S2† show that the rate-limiting steps for the ORR are the first step of electron transfer and O2 reduction to OOH*: O2* + H2O(l) + e− → OOH* + OH−. Except for the first step for C60-frag2, all other 15 steps for the four fragments are exothermic with ΔG < 0. Notably, C60-frag1 yields the lowest overpotential of 0.389 V, suggesting that the C60-frag1 is the most active ORR catalyst among the four fragments. Meanwhile, the overpotential of C60-frag2l (0.407 V) is only slightly higher than that of C60-frag1, consistent with the previous results.26,28 Both C60-frag1's and C60-frag2l's ORR activities are comparable to those of Pt catalysts, as the onset potential of Pt catalysts is about 0.8 V. So, the overpotential of Pt catalysts would be about 0.43 V.34–37 In contrast, the computed overpotentials of C60-frag1l and C60-frag2 are 0.986 and 1.377 V, respectively, much higher than those of C60-frag1 and C60-frag2l, indicating that both C60-frag1l and C60-frag2 are poor ORR catalysts. Overall, the weakened O* adsorption and enhanced OH*, OOH* species adsorption both boost the ORR catalytic performance of C60-frag1 and C60-frag2l, thereby rendering both as highly active ORR catalysts.
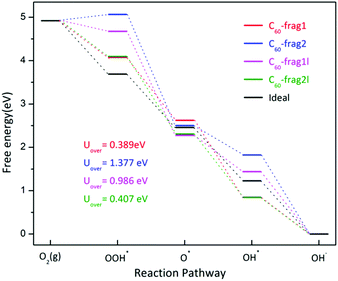 | ||
| Fig. 3 Four-electron ORR free-energy diagram on C60-frag1, C60-frag2, C60-frag1l and C60-frag2l fragments. Uover is the corresponding ORR overpotential. | ||
Discussions
From the aforementioned calculation results, we can see that similar active sites of C atoms with one adjacent pentagon and two adjacent hexagon rings can exhibit markedly different ORR activities. To gain insights into this puzzling behaviour, we focus on the effect of the edges of fullerene fragments on their overall ORR activities. The active sites of C60-frag1 and C60-frag1l are all associated with the central hexagon ring, and possess the same first-nearest-neighbours. Moreover, C60-frag2 and C60-frag2l have similar active sites, but show very different activities. The apparent differences in ORR activities on similar active sites are likely due to the different adsorption behaviours of the key O species, especially OH* and OOH* species. So our attention is placed on understanding the edge dependent adsorption behaviour of OH* and OOH* species.The OH* and OOH* species are adsorbed on the C60 fragments by forming one O–C bond. As mentioned above, the adsorption free energies follow the trend ΔGOH*/OOH* (C60-frag1) < ΔGOH*/OOH* (C60-frag2l) < ΔGOH*/OOH* (C60-frag1l) < ΔGOH*/OOH* (C60-frag2), indicating that C60-frag1 and C60-frag2l exhibit much stronger adsorption towards the OH*/OOH* species. To understand this trend, we performed Bader charge analysis. ESI Table S3† shows the charge variation during the adsorption and Fig. 4 shows the calculated HOMO and LUMO energy levels. Clearly, C60-frag1 and C60-frag2l exhibit a much higher HOMO level than C60-frag2 and C60-frag1l, suggesting that C60-frag1 and C60-frag2l are more likely to lose electrons compared to C60-frag2 and C60-frag1l. This frontier orbital behaviour explains why C60-frag1 and C60-frag2l fragments can adsorb OH*/OOH* species much more strongly. In general, OH*/OOH* species tend to gain electrons during the adsorption while the fragments lose electrons. The higher HOMO level of the fragments can lead to the stronger adsorption of OH*/OOH* species.
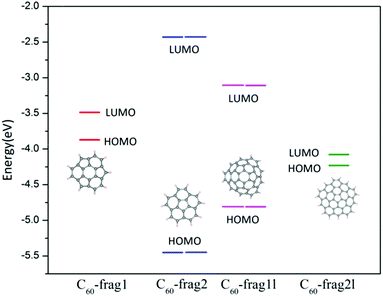 | ||
| Fig. 4 Frontier orbital energy level diagram of C60-frag1, C60-frag2, C60-frag1l and C60-frag2l fragments. | ||
Moreover, we note that the geometry structures of C60-frag1, C60-frag2, C60-frag1l and C60-frag2l exhibit Cs, C5v, C3v and C1 symmetry, respectively. As shown in Fig. 4, C60-frag2 and C60-frag1l exhibit relatively lower HOMO levels. So it seems that the trend in HOMO levels and the trend in the degree of the overall point-group may be correlated, since the lowered symmetry results in higher HOMO levels, thereby facilitating the adsorption. Indeed, we notice that among the four fragments, C60-frag2 possesses the highest symmetry C5v and the lowest HOMO level, and the latter leads to the weakest adsorption of OH* and OOH* species. Compared with C60-frag2 and C60-frag1l, C60-frag1 and C60-frag2l exhibit a lower symmetry and higher HOMO levels, thereby leading to a stronger adsorption of OH*/OOH* species. So even though C60-frag1 and C60-frag1l possess similar active sites, they have different edges and point-group symmetry. The same reasoning is applicable to C60-frag2 and C60-frag2l. In sum, the rings at the edges dictate the point-group symmetry of C60-frag1 and C60-frag2l fragments and the HOMO level, thereby affecting the strength of adsorption of OH*/OOH* species and the ORR activities.
To further confirm the correlation between the overall structural symmetry and the ORR activities, we modulate the structure of C60-frag2 by substituting half of the passivation hydrogen atoms by fluorine atoms (denoted as C60frag2-HF); or by changing one peripheral hexagon ring to one heptagon ring (denoted as C60frag2-hep). Both modifications lower the overall symmetry of C60-frag2 to C1, one is due to change of the passivation atom and another is due to change of the carbon framework. ESI Fig. S3† presents the structures, and ESI Table S4† gives the corresponding adsorption free energies of the key O species and the reaction free energy for each electron transfer step in the ORR. For the most active site on C60frag2-HF, the OH*/OOH* adsorption free energy (ΔG(OH*) = 1.786 eV, ΔG(OOH*) = 5.040 eV) decreases slightly and the ORR activity (Uover = 1.350 V) improves a little, compared with C60-frag2 ((ΔG(OH*) = 1.826 eV, ΔG(OOH*) = 5.067 eV, Uover = 1.377 V). For C60frag2-hep, the OH*/OOH* adsorption free energies increase more substantially while the ORR activity exhibits marked improvement at the most favorable active sites, i.e., the two central C atoms in the heptagon ring. ΔGOH* and ΔGOOH* are reduced to 0.955 and 4.212 eV, respectively, while the overpotential is only 0.522 V, much lower than that on C60-frag2 (1.377 V). These additional results confirm that by lowering the point-group symmetry, especially through changing the carbon framework, the ORR activities can be significantly improved.
In addition to the central active sites, we investigated the ORR activities on other sites of the four fragments and various sites on three other fragments (C60frag2l, C24frag1, and C36frag1). ESI Fig. S4† displays all the active sites on the seven fragments and ESI Table S5† presents all the adsorption free energies, reaction free energies and overpotentials of various active sites. Generally, fullerene-based fragments exhibit better ORR activities than the corresponding full fullerenes. ESI Fig. S5† shows a plot of overpotentials versus ΔG(OH*). It is noted that ΔG(OH*) between 0.8 and 0.9 eV exhibits the lowest overpotential of about 0.4 V. As discussed, the central active sites of C60-frag1 and C60-frag2l (C60frag1C3 and C60frag2lC3) yield overpotentials as low as 0.389 and 0.407 V, respectively. Moreover, C60-frag1C2, C60-frag1C4, and C60-frag1l2C1 also exhibit quite low overpotentials of 0.415, 0.453 and 0.394 V. All the five active sites considered exhibit relatively high ORR activities.
Computational details
The spin-polarized density functional theory (DFT) method implemented in the Vienna Ab initio Simulation Package (VASP 5.4)33–35 was employed to perform the calculations. The ionic cores were described by using the projector augmented wave (PAW) method.36 The generalized gradient approximation (GGA)37 in the formalism of the Perdew–Burke–Ernzerhof (PBE) functional was used to describe the electronic exchange–correlation energy in the energy calculations and the PBEsol38 exchange–correlation functional was used in the optimization calculations. 1 × 1 × 1 Gamma centered grid k-points were used for non-periodic calculations. The convergence criterion of the electronic calculations was set to 10−5 eV and the force was set to be 10−2 eV Å−1. The energy cutoff of the plane-wave basis set was 500 eV. The thickness of the vacuum layer between two neighbouring fullerenes or fullerene fragments was set to be more than 20 Å so that the interaction between two neighbouring species can be neglected.The ORR intermediates’ adsorption free energies were calculated based on the computational hydrogen electrode (CHE) model proposed by Nørskov et al.38 relative to H2O (g) and H2 (g) according to the following equation: ΔG = Δ(E) + Δ(ZPE) − TΔS, where Δ(E) is the calculated adsorption energy, Δ(ZPE) is the change of zero-point energy and ΔS is the change of entropy between the adsorbed state and the gas phase. The adsorption energies were calculated based on the following formulas: ΔE(O*) = E(O*) − E(*) − [E(H2O) − E(H2)], ΔE(OH*) = E(OH*) − E(*) − [E(H2O) − 1/2E(H2)], and ΔE(OOH*) = E(OOH*) − E(*) − [2E(H2O) − 3/2E(H2)]. The temperature is 298.15 K. The gaseous entropies of H2O (g) and H2 (g) were taken from the NIST database.39 The ZPE was derived from the calculated vibrational frequencies. Moreover, solvent corrections40 were added to the adsorption free energies, in which the adsorption energies of OH* and OOH* were amended by ∼0.3 eV. Note that the adsorption free energy is relative to H2O (g) and H2 (g), which can be a positive value. A larger positive value represents weaker adsorption.
The ORR reaction was assumed to proceed through the 4-electron pathway in alkaline conditions, as shown in the following equations: (1) O2* + H2O(l) + e− → OOH* + OH−, (2) OOH* + e− → O* + OH−, (3) O* + H2O(l) + e− → OH* + OH−, and (4) OH* + e− → OH− + *, where * denotes the possible active sites on the catalysts; O*, OH* and OOH* are the adsorbed intermediates. The difference in free-energy change between the initial and final states in each step is defined as the reaction free energy ΔG. The reaction free energies in the four steps are directly related to the adsorption free energies of the intermediates: (1) ΔG1 = ΔG(OOH*) − 4.92 eV + ΔG(pH) + eU, (2) ΔG2 = ΔG(O*) − ΔG(OOH*) + ΔG(pH) + eU, (3) ΔG3 = ΔG(OH*) − ΔG(O*) + ΔG(pH) + eU, and (4) ΔG4 = −ΔG(OH*) + ΔG(pH) + eU. U is the applied electrode potential. The theoretical onset potential is Uonset = max{ΔG1, ΔG2, ΔG3, ΔG4}/e, and the theoretical overpotential is defined as Uover = max{ΔG1, ΔG2, ΔG3, ΔG4}/e + 1.23 [V].
Conclusions
The ORR activities of four kinds of C20, C24, C36 and C60 fullerenes and fullerene-based fragments are theoretically investigated by using DFT and computational hydrogen electrode (CHE) methods. Compared with perfect fullerenes, fullerene-based fragments exhibit much higher ORR activities. In general, the active sites associated with more pentagon rings show a stronger adsorption toward OH* and OOH* species. For the four C60-based fragments, C60-frag1, C60-frag2, C60-frag1l and C60-frag2l, they possess similar active sites with one adjacent pentagon and two adjacent hexagon rings, but their adsorption behaviours and ORR activities are markedly different. C60-frag1 and C60-frag2l exhibit excellent ORR activities, with the theoretical overpotentials as low as 0.389 and 0.407 V, respectively. In contrast, the overpotentials of C60-frag1l and C60-frag2 are much higher (0.986, 1.377 V), suggesting poor ORR activities. In addition to the location of active sites, the overall degree of point-group symmetry of the fragment seems to correlate closely with the ORR activities. The two C60-frag1 and C60-frag2l fragments with a lower point-group symmetry exhibit a higher HOMO level, and are more likely to lose electrons, thereby resulting in a stronger adsorption of OH*/OOH* species and higher ORR activities. In contrast, C60-frag2 exhibits the highest symmetry of C5v, but the weakest adsorption of OH*/OOH* species and the lowest ORR activities among the four fragment models considered. Insights into the molecular mechanisms of ORR activities can provide theoretical guidance towards the rational design of metal-free carbon-based electrocatalysts for the ORR.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr. Haoxiang Xu for valuable discussions. KKM was supported by the National Natural Science Foundation of China (21803002) and a scholarship from the China Scholarship Council (CSC). XCZ was supported by the University of Nebraska Holland Computing Center.References
- W. Gao, Z. Zhang, M. Dou and F. Wang, ACS Catal., 2019, 3278–3288 CrossRef CAS.
- J. Liu, M. Jiao, B. Mei, Y. Tong, Y. Li, M. Ruan, P. Song, G. Sun, L. Jiang, Y. Wang, Z. Jiang, L. Gu, Z. Zhou and W. Xu, Angew. Chem., Int. Ed., 2019, 58, 1163–1167 CrossRef CAS PubMed.
- D. Zhou, S. Wang, Y. Jia, X. Xiong, H. Yang, S. Liu, J. Tang, J. Zhang, D. Liu, L. Zheng, Y. Kuang, X. Sun and B. Liu, Angew. Chem., Int. Ed., 2019, 58, 736–740 CrossRef CAS PubMed.
- Y. Zhu, B. Zhang, X. Liu, D.-W. Wang and D. S. Su, Angew. Chem., Int. Ed., 2014, 53, 10673–10677 CrossRef CAS PubMed.
- C. Bezerra, L. Zhang, K. Lee, H. Liu, A. Marques, M. Pereira, H. Wang and J. Zhang, Electrochim. Acta, 2008, 53, 4937–4951 CrossRef CAS.
- T. Palaniselvam, V. Kashyap, S. N. Bhange, J.-B. Baek and S. Kurungot, Adv. Funct. Mater., 2016, 26, 2150–2162 CrossRef CAS.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed.
- C. Zhang, N. Mahmood, H. Yin, F. Liu and Y. Hou, Adv. Mater., 2013, 25, 4932–4937 CrossRef CAS PubMed.
- X. Wang, G. Sun, P. Routh, D.-H. Kim, W. Huang and P. Chen, Chem. Soc. Rev., 2014, 43, 7067–7098 RSC.
- I.-Y. Jeon, H.-J. Choi, S.-M. Jung, J.-M. Seo, M.-J. Kim, L. Dai and J.-B. Baek, J. Am. Chem. Soc., 2013, 135, 1386–1393 CrossRef CAS PubMed.
- S. Chen, J. Bi, Y. Zhao, L. Yang, C. Zhang, Y. Ma, Q. Wu, X. Wang and Z. Hu, Adv. Mater., 2012, 24, 5593–5597 CrossRef CAS PubMed.
- Z.-W. Liu, F. Peng, H.-J. Wang, H. Yu, W.-X. Zheng and J. Yang, Angew. Chem., Int. Ed., 2011, 50, 3257–3261 CrossRef PubMed.
- R. Liu, D. Wu, X. Feng and K. Müllen, Angew. Chem., 2010, 122, 2619–2623 CrossRef.
- J. Wang, H. Jin, Y. He, D. Lin, A. Liu, S. Wang and J. Wang, Nanoscale, 2014, 6, 7204–7208 RSC.
- A. Aijaz, N. Fujiwara and Q. Xu, J. Am. Chem. Soc., 2014, 136, 6790–6793 CrossRef CAS PubMed.
- J. Y. Cheon, J. H. Kim, J. H. Kim, K. C. Goddeti, J. Y. Park and S. H. Joo, J. Am. Chem. Soc., 2014, 136, 8875–8878 CrossRef CAS PubMed.
- D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365 CrossRef CAS PubMed.
- J. Zhang, Z. Zhao, Z. Xia and L. Dai, Nat. Nanotechnol., 2015, 10, 444 CrossRef CAS PubMed.
- K. Gao, B. Wang, L. Tao, B. V. Cunning, Z. Zhang, S. Wang, R. S. Ruoff and L. Qu, Adv. Mater., 2019, 31, 1805121 CrossRef PubMed.
- X. Zou, L. Wang and B. I. Yakobson, Nanoscale, 2018, 10, 1129–1134 RSC.
- D. Yan, Y. Li, J. Huo, R. Chen, L. Dai and S. Wang, Adv. Mater., 2017, 29, 1606459 CrossRef PubMed.
- L. Tao, Q. Wang, S. Dou, Z. Ma, J. Huo, S. Wang and L. Dai, Chem. Commun., 2016, 52, 2764–2767 RSC.
- Y. Jia, L. Zhang, A. Du, G. Gao, J. Chen, X. Yan, C. L. Brown and X. Yao, Adv. Mater., 2016, 28, 9532–9538 CrossRef CAS PubMed.
- L. Zhang, Q. Xu, J. Niu and Z. Xia, Phys. Chem. Chem. Phys., 2015, 17, 16733–16743 RSC.
- C. Tang, H.-F. Wang, X. Chen, B.-Q. Li, T.-Z. Hou, B. Zhang, Q. Zhang, M.-M. Titirici and F. Wei, Adv. Mater., 2016, 28, 6845–6851 CrossRef CAS PubMed.
- J. Zhu, Y. Huang, W. Mei, C. Zhao, C. Zhang, J. Zhang, I. S. Amiinu and S. Mu, Angew. Chem., Int. Ed., 2019, 58, 3859–3864 CrossRef CAS PubMed.
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- Y. Jiang, L. Yang, T. Sun, J. Zhao, Z. Lyu, O. Zhuo, X. Wang, Q. Wu, J. Ma and Z. Hu, ACS Catal., 2015, 5, 6707–6712 CrossRef CAS.
- F. Diederich and C. Thilgen, Science, 1996, 271, 317–324 CrossRef CAS.
- Z. Chen, H. Jiao, M. Bühl, A. Hirsch and W. Thiel, Theor. Chem. Acc., 2001, 106, 352–363 Search PubMed.
- W. An, N. Shao, S. Bulusu and X. C. Zeng, J. Chem. Phys., 2008, 128, 084301 CrossRef PubMed.
- W. An, Y. Gao, S. Bulusu and X. C. Zeng, J. Chem. Phys., 2005, 122, 204109 CrossRef PubMed.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS.
- J. Wang, Z. Huang, W. Liu, C. Chang, H. Tang, Z. Li, W. Chen, C. Jia, T. Yao, S. Wei, Y. Wu and Y. Li, J. Am. Chem. Soc., 2017, 139, 17281–17284 CrossRef CAS PubMed.
- M. Xiao, H. Zhang, Y. Chen, J. Zhu, L. Gao, Z. Jin, J. Ge, Z. Jiang, S. Chen, C. Liu and W. Xing, Nano Energy, 2018, 46, 396–403 CrossRef CAS.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS.
- K. Yuan, S. Sfaelou, M. Qiu, D. Lützenkirchen-Hecht, X. Zhuang, Y. Chen, C. Yuan, X. Feng and U. Scherf, ACS Energy Lett., 2018, 3, 252–260 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- https://webbook.nist.gov/chemistry/ .
- F. Calle-Vallejo, J. I. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr05338g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |