Open Access Article
Open Access ArticleInertial focusing with sub-micron resolution for separation of bacteria†
Javier
Cruz
 *a,
Tiscar
Graells
*a,
Tiscar
Graells
 b,
Mats
Walldén
b,
Mats
Walldén
 a and
Klas
Hjort
a and
Klas
Hjort
 a
a
aEngineering Sciences, Uppsala University, Ångström Laboratoriet, Uppsala, Sweden. E-mail: javier.cruz@angstrom.uu.se
bDepartment of Medical Biochemistry and Microbiology, Uppsala University, Uppsala, Sweden
First published on 19th February 2019
Abstract
In this paper, we study inertial focusing in curved channels and demonstrate the alignment of particles with diameters between 0.5 and 2.0 μm, a range of biological relevance since it comprises a multitude of bacteria and organelles of eukaryotic cells. The devices offer very sensitive control over the equilibrium positions and allow two modes of operation. In the first, particles having a large variation in size are focused and concentrated together. In the second, the distribution spreads in a range of sizes achieving separation with sub-micron resolution. These systems were validated with three bacteria species (Escherichia coli, Salmonella typhimurium and Klebsiella pneumoniae) showing good alignment while maintaining the viability in all cases. The experiments also revealed that the particles follow a helicoidal trajectory to reach the equilibrium positions, similar to the fluid streamlines simulated in COMSOL, implying that these positions occupy different heights in the cross section. When the equilibrium positions move to the inner wall as the flow rate increases, they are at a similar distance from the centre than in straight channels (∼0.6R), but when the equilibrium positions move to the outer wall as the flow rate increases, they are closer to the centre and the particles pass close to the inner wall to elevate their position before reaching them. These observations were used along with COMSOL simulations to explain the mechanism behind the local force balance and the migration of particles, which we believe contributes to further understanding of the phenomenon. Hopefully, this will make designing more intuitive and reduce the high pressure demands, enabling manipulation of particles much smaller than a micrometer.
Introduction
Inertial focusing is a passive technique for high-resolution particle manipulation (only pressure is needed to run the system) where the velocity profile of the fluid induces migration of particles to size-dependent equilibrium positions along the cross section of a microchannel. It is label-free (the separation of particles is based on size and geometry), its throughput is very high compared to most other approaches and it is less prone to clogging since particles do not contact the walls of the channel. This technique has been used for manipulation of biological samples, such as label-free separation of erythrocytes and leukocytes from a blood sample,1 acquisition of circulating tumour cells2,3 or cell synchronization.4 For smaller particles, like prokaryotic cells, less work has been done since the forces causing the migration are strongly related to the size of the particles.In addition, for particles in the micron range and smaller, the high throughput comes with high shear forces that could be harmful to the particles.5 There are also high pressure demands, which is not common in the microfluidics community (although high-pressure capillary systems are often used in clinical laboratories, with high performance liquid chromatography (HPLC) equipments being one of the most common analytical instruments). Still, the few groups that have been pursuing this have made good demonstration of the potential in working at high pressures.6–10
In inertial focusing, it is generally accepted that in a straight channel, the migration and equilibrium of particles are mainly due to two forces; the shear gradient lift force, directed towards the walls of the channel and originated from the non-zero curvature of the flow profile, and the wall force, repelling particles from the walls and originated from the interaction of the stresslet around the particle and the wall. Reviews on the phenomenon can be found elsewhere,11–14 but an introduction with key points is included in the following paragraphs to ease the understanding of the results and discussion.
In 1974, Ho and Leal combined both forces aforementioned and calculated the net lift force (FL) on a particle much smaller than the channel (a/DH ≪ 1) in a two-dimensional Poiseuille flow for very low Reynolds numbers (Re = ρUmDH/μ ≪ 1), concluding that FL = CLρUm2a4/DH2, where ρ and μ are the density and the dynamic viscosity of the fluid, Um is the maximum flow velocity, a is the particle diameter, DH is the hydraulic diameter of the channel and CL is a coefficient that adjusts the value of the force according to Re and the lateral position of the particle in the channel.15 Since then, the theory has been expanded for moderate16 and high17 Re numbers, for particle sizes in the order of magnitude of the channel and for 3D flows.18–20 Under such conditions and based on numerical results, Di Carlo et al. introduced some corrections to the estimation of FL, stating that FL ∼ ρUm2a3/DH close to the channel centre and FL ∼ ρUm2a6/DH4 close to the wall.18 Recently, Hood et al. and Chao Liu et al. proposed mathematical models for FL based on Ho and Leal's work.19,20 In particular, to provide a notion on what is nowadays taken into account in the prediction of the lift forces, Chao Liu's formula was reached by fitting numerical results with an equation composed of four terms. The first two, dominating the radial migration, come from Ho and Leal's work: the shear gradient lift and the wall-induced forces. The third is a Saffman force induced by the lag of the particles in the proximity to the wall that, although much weaker than the previous, is responsible for the migration of particles along the perimeter where the first two forces are cancelled, bringing them to four stable equilibrium positions. The last term is a correction to the shear gradient lift that couples to the aspect ratio of the channel.
Even though it is a complex phenomenon still in debate, there are facts that are generally accepted for inertial focusing of particles in straight channels:
- The dominant forces are the shear gradient lift force and the wall force. The first pushes the particles towards the walls; the second repels them away from them. These two forces cancel each other at an equilibrium perimeter.21–23
- In channels with circular cross sections and for particles that are small (a/H ≪ 1), the perimeter is at ∼0.6 of the radius from the center. As Re increases, it comes closer to the walls, and for larger particles, it is slightly closer to the centre.18 Such a perimeter exists for different cross sections adapted to the geometry.21–23
- In channels with rectangular cross sections, the interaction with the walls not only repels the particles but also makes them move laterally to four equilibrium points (two under certain conditions). The movement to the perimeter happens faster than the lateral migration, making the latter the limiting factor in the alignment.18–23
- FL is strongly dependent on the size of the particle; large particles will migrate faster than smaller ones under the same conditions (FL ∼ a3−4).13,15,18–20,22
Fig. 1(a) shows the typical paraboloid-like shape of the flow profile in a rectangular microchannel with aspect ratio W/H = 2, where W and H are the width and the depth of the channel, respectively, and its representation in 2D with the four equilibrium positions for a particle with a/H = 0.1. In Fig. 1(b), the net lift force is represented for such particles under Re = 100, based on Chao Liu's simulations.24
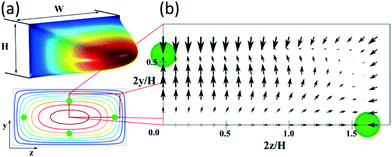 | ||
| Fig. 1 (a) 3D flow profile in a straight microchannel (aspect ratio W/H = 2) and its representation in 2D with isovelocity curves showing the equilibrium positions for particles with a/H = 0.1. (b) Map of the net force acting on such particles at Re = 100, based on the results of Chao Liu et al.24 | ||
Straight channels have the limitation of a slow lateral migration and multiple equilibrium positions. To overcome these, secondary flows (perpendicular to the main flow) can be generated. Common techniques are addition of curvature,25,26 expansion–contraction of the channel,27 addition of obstacles,28etc. For instance, Russom showed how the secondary flow in a curved channel (Dean flow) makes particles focus only close to the inner wall in two equilibrium positions (mirrored to the horizontal centre line and appearing as one from the top view).29 Martel and Toner observed that these positions depend on the curvature of the channel, Re and size of the particle for a given cross section, and that, under certain conditions, the mirrored positions become only one situated very close to the inner wall. In the same work, they suggested that the location of the equilibrium positions migrates not only in the lateral position but also vertically,30 which we confirm in this paper. Another benefit of introducing a secondary flow is the high sensitivity for particle separation based on size, which has been exploited by several groups.1,31,32
It is assumed that the main force originated by the secondary flow is Stokes' drag (named Dean drag; FD) parallel to its stream lines; 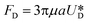 , where
, where 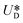 is the relative velocity of the secondary flow compared to that of the particle in the direction of the secondary streamlines. When the particle is at the equilibrium position,
is the relative velocity of the secondary flow compared to that of the particle in the direction of the secondary streamlines. When the particle is at the equilibrium position, 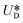 reaches its maximum and coincides with the velocity of the secondary flow;
reaches its maximum and coincides with the velocity of the secondary flow; 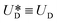 and, as an indicator of the magnitude,
and, as an indicator of the magnitude, 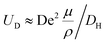 can be used, where
can be used, where 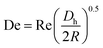 is the Dean number,
is the Dean number, 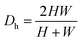 is the hydraulic diameter of a rectangular channel and R is the radius of curvature.33 Although many applications have been shown for curved channels, there is a lack of understanding of how particles actually reach the equilibrium positions, where they lay and how the forces are balanced; there is discrepancy in the force balance in the publications aforementioned. Understanding how and where particles equilibrate needs further local analysis rather than generalizing over the cross section with parameters like Re or De. Indeed, in this study, we present evidence that, under certain conditions, the equilibrium in curved channels is due to the vertical component of the secondary flow, which is generally overlooked.
is the hydraulic diameter of a rectangular channel and R is the radius of curvature.33 Although many applications have been shown for curved channels, there is a lack of understanding of how particles actually reach the equilibrium positions, where they lay and how the forces are balanced; there is discrepancy in the force balance in the publications aforementioned. Understanding how and where particles equilibrate needs further local analysis rather than generalizing over the cross section with parameters like Re or De. Indeed, in this study, we present evidence that, under certain conditions, the equilibrium in curved channels is due to the vertical component of the secondary flow, which is generally overlooked.
Also, the manipulation and balance of forces become challenging when small particles (∼1 μm and smaller) are targeted. This is due to the strong dependency of the net lift force to the size of the particle (FL ∼ a3−4).15,18 Nevertheless, Cruz et al.9 and Wang et al.34 showed alignment of ∼1 μm particles by single phase inertial focusing. For that, the channels were 10 × 20 μm (H × W)9 and 5 × 10 μm (H × W).34 Microchannels with such dimensions have a high hydraulic resistance and the pressures needed to run the system amount to tens of bars despite the length of the channel being only a few millimetres. Also, if a system that works for a certain size is simply scaled down to target a smaller one, the pressure needed to run the system increases quadratically with the reduction in size of the particle,9 which is nowadays the main limitation for the technology to be used for particles much smaller than 1 μm.
Recently, Mutlu et al. introduced the novel concept of oscillatory inertial microfluidics, where a sample is moved forth and back in a straight channel to achieve an “infinite channel” and by so they showed manipulation of very small particles (down to 0.5 μm) at low Re numbers.35 While the concept is attractive, it comes with some limitations compared to the traditional, passive inertial microfluidics; it needs external control equipment to tune the performance and it does not have a high throughput. In addition, inertial focusing in straight channels gives multiple equilibrium positions and cannot perform high-resolution separation.
To sum up, successful manipulation of small particles has been recently demonstrated but it is on the edge of the technology; there is little work and further characterization is needed. The main limitation is the need of high pressures, which is unavoidable with the current theoretical knowledge. Further understanding of the phenomenon may help to minimize the demands of the system, to enable separation of even smaller particles and open up new applications.
In this paper, we study and characterize inertial focusing in curved channels for small particles (∼1 μm), achieving focus of as small as 0.5 μm particles. Moreover, in the range of 1 to 2 μm, we distinguished two modes of operation for the same device: as a concentrator or as a separator with sub-micron resolution. These systems also focused three clinically relevant bacteria of the Enterobacteriaceae family while successfully maintaining their viability. These bacteria were Escherichia coli, known as a model in microbiology that can cause opportunistic infections, Salmonella typhimurium, a pathogen that causes gastroenteritis in humans and other mammals, and Klebsiella pneumoniae, that causes human infections in immunodeficient patients. We believe that this novel, versatile, simple and robust high-pressure inertial microfluidic system is ready to be integrated in real applications.
Apart from the outstanding performance, the experiments combined with COMSOL simulations contributed to novel understanding of the mechanisms behind the force balance and the migration of particles.
Experimental
Design and fabrication of the channels
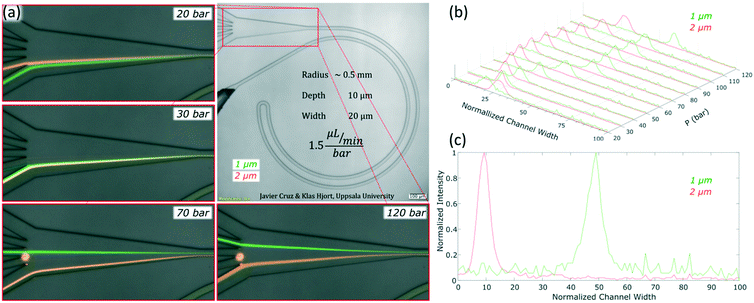
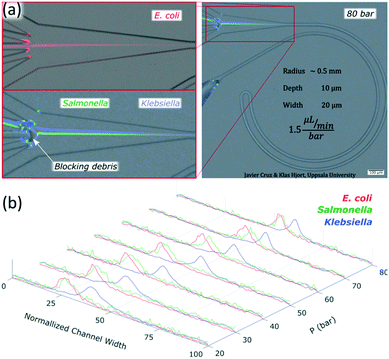
The channels were designed based on our experience from recent results, where we presented a theoretical study on how to scale the microchannels to target different particle sizes and demonstrated the concept by focusing 3 and 1 μm particles as well as Escherichia coli.9 Most of the results were obtained with the microchannels consisting of two curves with a radius (R) of 0.5 mm, 10 μm in depth (H) and 20 μm in width (W) connected by a small turn (R of 30 μm), Fig. 2(a). This cross section and radius provided the specific conditions to match FD and FL within the range of feasible flow rates (below the threshold set by the pressure threshold that compromises the devices (∼200 bar); see section “Formation of equilibrium positions” under “Results and discussion”).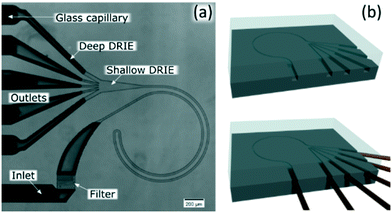 | ||
| Fig. 2 (a) Microfluidic chip consisting of two curves with 0.5 mm in radius (R); 10 μm in depth (H) and 20 μm in width (W) connected by a small turn (30 μm in R). (b) Sketch of the fabrication. | ||
We included a pillar section that acted like a filter at the inlet and 400 μm of a straight channel before the curves to allow particles to initiate their migration to the perimeter by the lift force prior to being swept by the secondary flow. An expansion in the end of the channels facilitated the optical evaluation, which was preceded with 100 μm of a straight channel to stop the rotation of the fluid. Finally, the inlets and outlets were ∼180 μm in H and W, which compared to the functional part, offered negligible hydraulic resistance.
The channels were dry etched in silicon (DRIE), sealed with glass (anodically bonded) and glass capillaries were glued with epoxy as connections, Fig. 2(b). Further details can be found in the ESI.† Microchannels fabricated with these materials can stand at least 200 bar.9
Experiments
The samples were prepared by suspending fluorescent polystyrene particles (Thermoscientific Fluoro-Max) or bacteria in deionized water (∼106–8 particles per mL). With the particles, 0.1% of Triton X was added to reduce agglomeration.Three rod-shaped species of the family Enterobacteriaceae, carrying fluorescent proteins, were used to make suspensions to test the microchannel. The strains were seeded from a frozen stock to LB agar plates. These agar plates were incubated for 36 hours under aerobic conditions at 37 °C (Escherichia coli and Klebsiella pneumoniae) or at 42 °C (Salmonella typhimurium). Bacteria from the middle of the colonies were suspended in deionized water using a loop. Vortex for 30 s and mixing by inversion were done until the suspension was homogeneous. Optical density at wavelength 600 nm was adjusted between 0.15 and 0.25 to reach a concentration of ∼108 cells per mL (UV-mini 1240 spectrophotometer, Shimadzu). The suspensions were observed using a fluorescence microscope (Leica DFC3000G, Leica Microsystems) to see the size range of bacteria.
Escherichia coli carried an orange fluorescent protein (dTomato: excitation wavelength 554 nm, emission 581 nm) and was ∼0.5 μm in width by ∼1 μm in length (as observed in Fig. S8†).
Salmonella typhimurium carried a super-yellow fluorescent protein (SYFP2: excitation wavelength 515 nm, emission 527 nm) and was ∼0.4 μm in width by ∼1–1.5 μm in length (Fig. S8†).
Klebsiella pneumoniae carried a red fluorescent protein (mScarlet: excitation wavelength 569 nm, emission 594 nm) and was ∼0.6 μm in width by ∼0.9 μm in length (Fig. S8†). This last species is covered naturally by a capsule; i.e. a gel structure outside the cell that gives them protection.
An HPLC pump (Waters, model 515) was used to pump the samples at the desired flow rates with a read out of the pressure. To avoid particles passing through the pump, the samples were loaded in a metallic tube with ∼5 mL capacity in-between the chip and the pump.
The evaluation of the microchannels was done optically with a microscope with fluorescence filters/light source. Since the main limitation to run these systems is the need for high pressure, this was the variable controlled in the experiments; images were taken while increasing the pressure in steps of 10 bar. The analysis of the intensity profiles was done with ImageJ at the expansion of the outlet where the width of the channel was 108 pixels at 10× magnification (corresponding to 70 μm).
To measure flow rates and particle concentration from each outlet individually, we collected samples in vials during a fixed time. The collected samples were weighed to know the flow rate and, after mixing with a vortex, 1 μL was pipetted and allowed to dry on a glass slide for particle counting, which was done with ImageJ.
The viability evaluation was done by counting the colony forming units in cultures in LB agar plates after 24 hours from samples before (control) and after passing through a microchannel with a single outlet. Samples were collected when the pressure was increased to 50, 100 and 150 bar consecutively, and decreased to 50 bar again to distinguish the effect of high static pressure and the shear forces in the microchannels.
Results and discussion
In this section, we first show the results obtained with microchannels with a R of 0.5 mm and 10 × 20 μm (H × W), which performed excellent alignment for 1 and 2 μm particles and revealed some information about the equilibrium positions. We compared the results from the microchannels with the same cross section but different radii (increased FD), or with reduced depth to 7.3 μm (increased FL/FD). From the experimental results and COMSOL simulations, we propose a migration mechanism in agreement with that of Martel and Toner.30 To finalize, we validate the performance with bacteria.Microchannels with R of 0.5 mm and 10 × 20 μm (H × W)
For microfluidic channels with R of 0.5 mm and cross section 10 × 20 μm (H × W), the pressures recorded ranged from 20 bar (30 μL min−1; Re = 22) to 120 bar (180 μL min−1; Re = 133). We observed that 1 and 2 μm particles were successfully aligned and that the equilibrium positions were strongly dependent on the size of the particle and the flow rate. 2 μm particles (H/5) aligned initially close to the middle and as the flow rate increased, they moved towards the inner wall but eventually changed direction towards the outer wall. On the other hand, 1 μm particles (H/10) started to show good alignment close to the inner wall and migrated towards the outer wall as the flow rate increased. The evolution of the equilibrium positions with the flow rate is shown in Fig. 3 and more detailed information with steps of 10 bar is provided as a video in the ESI.† Such channels could almost align 0.7 μm particles well but only at the lowest flow rates, Fig. S1.† Thanks to the strong dependency of the equilibrium positions on the particle size and flow rate, these microchannels offered two different modes of operation for the particle size range of 1 to 2 μm. In the first, all particles are focused and can be extracted together, Fig. 3, at 30 bar (45 μL min−1). In the second mode, the range of sizes spreads and smaller particles get closer to the outer wall, Fig. 3, above 30 bar. In particular, the optimum separation was achieved at 70 bar (∼100 μL min−1), where the lateral position was z = 0.1 for 2 μm and z = 0.5 for 1 μm particles, respectively (with z = 0 corresponding to the inner wall and z = 1 to the outer wall). Note that the 2 μm particles were initiating their migration to the outer wall at that moment and therefore any intermediate size should be ahead forming a rainbow of sizes between them and the 1 μm particles, achieving sub-micron resolution in the separation. Separation by size also occurred for pressures below 30 bar, although with opposite order; the smaller the particle, the closer to the inner wall its equilibrium position was. This scenario offers lower throughput and less resolution since 2 and 1 μm particles are closer, but demands less pressure and the shear forces are lower.To measure the quality of the separation, we collected each outlet simultaneously for several minutes and measured the volume and particle concentration through them while running the device at 70 bar (∼100 μL min−1). The factor of concentration was 6.7 and 3.4 with recoveries of 96.8% and 98.1% for 1 and 2 μm particles respectively, cf. Table S1.†
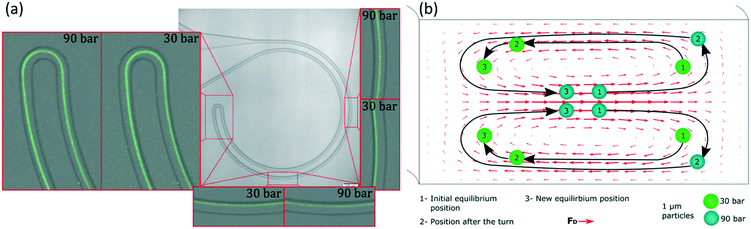
Apart from the excellent performance in the particle size range of 1 to 2 μm, these experiments revealed an interesting insight into the phenomenon of inertial focusing in curved channels. Focusing on the small turn connecting the two loops and on what happened after it, information about the location of the equilibrium position and how particles reached it could be inferred. In such channels, the two curves with R of 0.5 mm had opposite curvature; their equilibrium positions were mirrored in the cross section. Particles that had already reached the first equilibrium position had to migrate again towards the new one and, since the majority were almost well focused already in the first loop, a line revealing the migration could be seen. Also, the connecting turn had an extremely small radius (30 μm) compared to the rest of the system and the Dean drag dominated in that section. The data in Fig. 4 come from the same data as in Fig. 3 but zooming in at the turn and other relevant parts. Let us start by analysing the turn when the sample was 1 μm particles and the equilibrium position was close to the inner wall; for instance at 30 bar (45 μL min−1), Fig. 4(a). From their position at the inner wall, particles entered the turn, which had opposite curvature and thus opposite Dean flow; they were suddenly at the outer wall, far away from the equilibrium position (position 1 in Fig. 4(b)). With no force opposing the secondary flow, they followed its streamlines and migrated towards the new inner wall. By the end of the turn, they were close to their new equilibrium position (position 2 in Fig. 4(b)). This connection of the two loops was efficient at such flow rate, i.e., particles did not waste much channel length traveling towards the new equilibrium position (position 3 in Fig. 4(b)) and kept improving the alignment.
Let us now analyse the case when the equilibrium position had moved towards the outer wall; for instance at 90 bar (135 μL min−1), Fig. 4(a). At that position, particles were in equilibrium close to the middle (position 1 in Fig. 4(b)). As they entered the turn, they quickly moved to the outer wall, likely following the strong Dean flow. This means they were in the middle region of such flow, in contrast to the previous case where they were pushed towards the new inner wall (indicating that they were in the lower/top region of the Dean flow or in its vertical part). This was a first indication of that, depending on the flow rate, the equilibrium position belonged to different sections of the secondary flow and thus to different heights in the channel. Now, after the turn, particles were very close to the outer wall (position 2 in Fig. 4(b)) and they started migrating towards their new equilibrium position (position 3 in Fig. 4(b)). However, from the top view, Fig. 4(a), it could be seen how the particles passed by the new equilibrium position and left it behind as they approached the inner wall, changed direction towards the outer wall and finally stopped at the equilibrium position. This sinusoidal trajectory matches the top view of the 3D helicoidal trajectory of the fluid streamlines in a curved channel (simulated with COMSOL, Fig. S2†). This was the second indication of the equilibrium positions belonging to different heights. Regarding the connection of the two loops, it was inefficient at these higher flow rates. After the turn, particles needed to travel around half loop of the microchannel to reach the new equilibrium position and, while particles migrate, the quality of the focus is likely not improving. Therefore, the half loop of the channel that followed the turn only contributed with pressure drop. Fig. 4(b) shows an intuitive interpretation of the 3D trajectory of the particles migrating right after entering the turn at both flow rates (shown from the top view in Fig. 4(a)). The actual position of the particles in the microchannel is discussed in the following paragraphs.
A similar trend could be observed for other flow rates and particle sizes. The reader can study them in the full pictures provided in the ESI.† With these pieces of evidence, it was clear that the changes in the equilibrium positions were both in the lateral position and vertically. The positions started at the bottom/top of the channel, they evolved towards the inner wall and eventually they reached a height that allowed them to move towards the outer wall. The smaller the particle, the more advanced its position; i.e. while 2 μm particles started to move towards the outer wall, 1 μm particles were already halfway.
Microchannels with other radii and depths
To expand the understanding, we evaluated a device that had consecutive channels with the same cross section but different radii (1, 0.5, 0.25 and 0.125 mm) and observed how a smaller radius forwarded the equilibrium position ahead in the transition towards the outer wall (a similar trend as to increasing the flow rate) for both 1 and 2 μm particles, Fig. S3.† Note that a smaller radius translates into larger FD while maintaining FL; thus lower FL/FD.We also tested the design shown in Fig. 3 with a reduced depth of 7.3 μm. The reduction of depth induced an increase of the ratio FL/FD and for 1 and 2 μm particles, the lift force dominated over the secondary drag. The alignment was successful, Fig. 5, but, in contrast to the previous scenario, the lateral position was not very sensitive to the flow rate; 2 μm particles focused close to the centre and moved slowly towards the inner wall as the flow rate increased (from z = 0.35 to z = 0.25) while 1 μm particles aligned very close to the inner wall (z = 0.1) with very small migration towards the outer wall as the flow rate increased, Fig. S4.† Nevertheless, this shallower channel was suited for the alignment of smaller particles since, as explained in the introduction, FL ∼ a3−4 and FD ∼ a, meaning that the same conditions lead to different FL/FD ratios depending on the particle size. 0.7 μm particles aligned well after 60 bar (45 μL min−1) at the inner wall and migrated slowly towards the centre keeping the good alignment. Also 0.5 μm particles showed good alignment, although only at 60 bar (at the inner wall, closer to the centre than 0.7 μm particles), Fig. 5 and S4.† Including an extra turn in the system improved the quality of the alignment for 0.5 μm particles but the range of flow rates that made good focusing was the same, ∼40–50 μL min−1, and the pressure drop for 45 μL min−1 was 90 bar in this triple loop instead of 60 bar in the double loop, Fig. S5.†
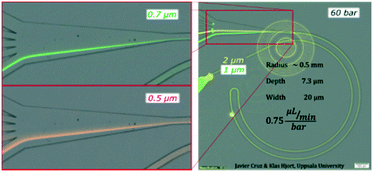 | ||
| Fig. 5 Test on a microchannel with dimensions 7.3 × 20 μm (H × W), R 0.5 mm and 60 bar (45 μL min−1) with 0.5, 0.7, 1 and 2 μm particles. | ||
Formation of equilibrium positions
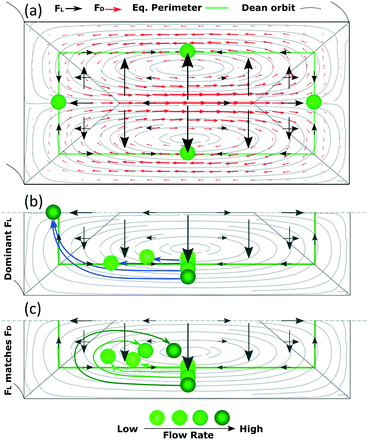
In this section, we aim at complementing the current understanding about inertial focusing in curved microchannels with the experimental results and simulations in COMSOL. As a simplification to build some intuitive understanding, the phenomenon can be considered similar to that in a straight channel to which a secondary flow is imposed. This simplification is reasonable as long as the main flow is not deformed much by the curvature, which according to our COMSOL simulations was the case for the microchannel in Fig. 3 up to ∼100 μL min−1. Flow profiles of such a microchannel and of a straight one with the same cross section are and presented in Fig. S6† at 50–150 μL min−1.Since the main flow is very similar to that of a straight channel, the same forces are likely to be present and, although they vary with Re and particle size, the general characteristics are like those shown in Fig. 1. A conceptual version of the lift force map at 50 μL min−1 with an overimposed secondary flow is shown in Fig. 6(a) (omitting the strong wall force that repels particles towards the equilibrium perimeter).
Following this lift force map, particles will migrate radially towards the equilibrium perimeter and eventually towards the four equilibrium positions. However, as we impose, the secondary flow, particles easily migrate along most of the perimeter since FL is very weak there; FD dominates and drags the particles until they approach the inner wall, where the orbit turns and opposes FL. Under this scenario, the equilibrium position close to the outer wall is not stable. The position close to the inner wall also vanishes in most cases, likely due to that the horizontal component of FD (FDH) exceeds the weak, horizontal FL (FLH) in that region in channels with a low aspect ratio. However, this position has been reported to be stable under certain circumstances,30 as will be discussed in the following paragraphs. The analysis is more complex for the remaining two mirrored positions, where particles coming from the horizontal lines of the perimeter focus in straight channels. Particles in these horizontal lines are initially dragged by FD, which is orthogonal to the main, vertical component of FL (FLV). As the Dean orbit approaches the inner wall it turns, diminishing the previously strong FDH while the vertical component of FD (FDV) starts to grow and pushes particles outwards from the perimeter, Fig. 6. From here on, we distinguish three possible scenarios:
Based on this, particles that occupy a more external Dean orbit travel closer to the inner wall before the orbit turns vertical. This is why smaller particles align closer to the inner wall when FL dominates (since their perimeter is naturally closer to the walls), Fig. 7(a), and why a fixed size particle comes closer to the inner wall with an increase in the flow rate (since their equilibrium perimeter is pushed closer to the wall), Fig. 6(b). An extreme situation occurs when particles follow the most external orbits, which coincide with the perimeter, and enter the region close to the inner wall where the perimeter turns vertical. Here FLH is relatively strong (symbolized by a triangular region in Fig. 6) and the particles keep following the secondary flow along the perimeter until H/2, where the two mirrored positions converge into one. These situations are depicted in Fig. 6(b) and correspond to our experimental section for 1 and 2 μm particles in the microchannels of 7.3 × 20 μm (H × W) and R of 0.5 mm.
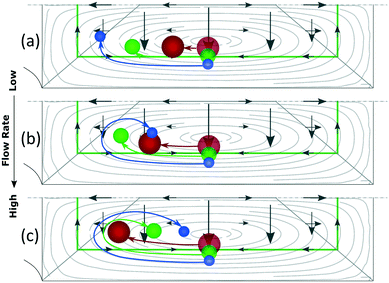
Note the strong dependency of the lift force on the size of the particle compared to the dependency of the Dean drag; FL ∼ a3−4 and FD ∼ a. It implies that for the same microchannel, the three scenarios can be present simultaneously: large particles will not be able to move vertically, small particles will be mixed and a range of sizes in-between will be in the last scenario, which offers three possibilities to align particles by size, Fig. 7. At the lowest flow rates and between the center and the inner walls, particles are ordered from large to small, Fig. 7(a) corresponding to Fig. 3 at 20 bar. The opposite ordering is achieved at the highest flow rates, Fig. 7(c) corresponding to Fig. 3 at 40–120 bar, while middle flow rates allow overlapping of several sizes, Fig. 7(b) corresponding to Fig. 3 at 30 bar. Scenarios I and III spread the range of sizes in a rainbow allowing high definition separation while scenario II overlaps the range of sizes allowing its extraction in a single outlet.
Another fact that contributes to the migration of the equilibrium position as the flow increases is that, although both FD and FL are proportional to Um2, FD scales faster since CL decays as Re increases,23,36 and a relative increase in FD makes particles follow the Dean orbits further. This trend is evident in Fig. S3,† where consecutive reductions in R moved the equilibrium positions closer to the outer wall for a given cross section and flow rate.
To finalize this discussion, the change in shape of the main flow as the flow rate increases must be included since, according to the previous statements, particles find force balance in-between the center of the Dean vortexes and the inner wall, which limits the lateral position to the center of the channel (W/2). As it was shown experimentally (Fig. 3), it can go beyond W/2. This is due to the inertia playing a bigger and bigger role as the flow rate increases, which makes the paraboloid of the main flow deform; its tip moves towards the outer wall (and so do the centers of the Dean vortexes), Fig. S6 and S7.† This translation of the paraboloid allows particles to align past z = W/2 and likely contributes to the migration of the equilibrium positions to the outer wall.
Demonstration with bacteria
Chips with R of 0.5 mm and a cross section 10 × 20 μm (H × W) were tested with three different species of bacteria: Escherichia coli, Salmonella typhimurium and Klebsiella pneumoniae. Images of the bacteria a few minutes after the dilution in sterile deionized water can be found in the ESI,† Fig. S8. The three species were focused successfully. Escherichia coli and Salmonella typhimurium behaved as particles slightly smaller than 1 μm while Klebsiella pneumoniae showed a different behavior not comparable to any observed rigid spherical particle; its first equilibrium position was close to the middle and moved towards the outer wall as the flow rate increased, Fig. 8 and S9.† Our results with Escherichia coli (∼1 μm long) were in agreement with previous studies, where elongated particles have been reported to focus as spherical particles with an equivalent diameter approximately similar to the largest dimension.37,38Salmonella typhimurium (∼1–1.5 μm long) was thus expected to behave as larger particles than Escherichia coli since they were observed to be a bit longer. However, they behaved as particles slightly smaller than the equivalent for Escherichia coli; Fig. 8 and S9.† These deviations in the predictions were most likely because the bacteria were imaged minutes after being moved from the agar plate to sterile deionized water and the experiments were carried out some hours after. A slight change of shape and homogenization in size of the bacteria in time is expected when bacteria are moved to a medium with fewer nutrients.39 Regarding Klebsiella pneumoniae, the fact that they started the alignment in the middle and moved towards the outer wall with an increase of flow rate without migrating first to the inner wall suggests that they were following the tip of the flow paraboloid (where the velocity is the highest. See how such tip moves towards the outer wall as the flow rate increases as shown in Fig. S6†). Such behavior has been reported for deformable particles.40,41 Indeed, Klebsiella pneumoniae produces a shell of mucous called capsule (or K antigen) around its body that likely turns it into a deformable particle.To confirm the alignment, we ran a test with Escherichia coli and collected each outlet simultaneously for several minutes and measured the volumes through them and the bacteria concentration while running the chip at 80 bar (120 μL min−1), Fig. 8(a). The factor of concentration was 6.5 with a recovery of 99.3%, Table S2,† showing good potential for separation and concentration of bacteria.
The viability tests indicated that all the species survived the process for all the pressures tested (up to 150 bar), Table S3.†
Finally, although the functional part is clog-free thanks to the wall force, it was not the case for our outlet region. In particular, when the sample contained bacteria, matter was accumulated at the sharp corners that split the channel into the multiple outlets. Future work is needed to further reduce aggregation of particles in this region.
Conclusion
In this paper, we demonstrate single phase inertial focusing in curved microchannels for as small as 0.5 μm spherical particles. We also demonstrate two modes of operation in the range of 1 to 2 μm particles. In the first, particles in the whole range are focused together. In the second, particles spread out in a range of sizes providing sub-micron resolution. These systems were validated with three bacteria species (Escherichia coli, Salmonella typhimurium and Klebsiella pneumoniae), showing good alignment and maintaining the viability in all cases. These simple, versatile and robust systems offer excellent performances and could be integrated for separation and concentration of bacteria prior to further analysis.Apart from the versatile performance of the microchannels, it was shown that particles follow a helicoidal trajectory similar to the fluid streamlines to reach the equilibrium positions, implying that these positions occupy different heights in the cross section. When the equilibrium positions move to the inner wall as the flow rate increases, they are at a similar distance from the centre as in straight channels (∼0.6R), but when the equilibrium positions move to the outer wall as the flow rate increases, they are closer to the centre and particles pass close to the inner wall to elevate their position before reaching them.
We also made progress in decreasing the pressure demanded by the systems to achieve good focus of 1 μm particles (as low as 20 bar at 30 μL min−1). However, to reach good focusing and separation for much smaller particles, improved designs are needed. A first step was taken in this work by revealing the helicoidal trajectories of particles towards the equilibrium positions, which brings light to the phenomenon, making it more intuitive and easy to design and optimize.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project received funding from the European Union's Horizon 2020 research and innovation program under grant agreement no. 644669. The authors would like to acknowledge the Dan Andersson lab members who provided the fluorescent strains: Erik Wistrand-Yuen, and Greta Zaborskyte.References
- N. Nivedita and I. Papautsky, Biomicrofluidics, 2013, 7, 054101 CrossRef PubMed.
- E. Ozkumur, A. M. Shah, J. C. Ciciliano, B. L. Emmink, D. T. Miyamoto, E. Brachtel, M. Yu, P. Chen, B. Morgan, J. Trautwein, A. Kimura, S. Sengupta, S. L. Stott, N. M. Karabacak, T. A. Barber, J. R. Walsh, K. Smith, P. S. Spuhler, J. P. Sullivan, R. J. Lee, D. T. Ting, X. Luo, A. T. Shaw, A. Bardia, L. V. Sequist, D. N. Louis, S. Maheswaran, R. Kapur, D. A. Haber and M. Toner, Sci. Transl. Med., 2013, 5, 179ra47 Search PubMed.
- Y. Zhang, J. Zhang, F. Tang, W. Li and X. Wang, Anal. Chem., 2018, 90, 1786–1794 CrossRef CAS PubMed.
- W. C. Lee, A. A. S. Bhagat, S. Huang, K. J. Van Vliet, J. Han and C. T. Lim, Lab Chip, 2011, 11, 1359 RSC.
- L. Nan, Z. Jiang and X. Wei, Lab Chip, 2014, 14, 1060–1073 RSC.
- K. B. Lynch, A. Chen and S. Liu, Talanta, 2018, 177, 94–103 CrossRef CAS PubMed.
- S. Ogden, L. Klintberg, G. Thornell, K. Hjort and R. Bodén, Microfluid. Nanofluid., 2014, 17, 53–71 CrossRef CAS.
- H. S. Cao, H. J. Holland, C. H. Vermeer, S. Vanapalli, P. P. P. M. Lerou, M. Blom and H. J. M. ter Brake, J. Micromech. Microeng., 2013, 23, 025014 CrossRef.
- J. Cruz, S. Hooshmand Zadeh, T. Graells, M. Andersson, J. Malmström, Z. G. Wu and K. Hjort, J. Micromech. Microeng., 2017, 27, 084001 CrossRef.
- M. Andersson, K. Svensson, L. Klintberg and K. Hjort, Anal. Chem., 2018, 90, 12601–12608 CrossRef CAS PubMed.
- J. Zhang, S. Yan, D. Yuan, G. Alici, N. T. Nguyen, M. Ebrahimi Warkiani and W. Li, Lab Chip, 2016, 16, 10–34 RSC.
- J. M. Martel and M. Toner, Annu. Rev. Biomed. Eng., 2014, 16, 371–396 CrossRef CAS PubMed.
- H. Amini, W. Lee and D. Di Carlo, Lab Chip, 2014, 14, 2739–2761 RSC.
- Y. Gou, Y. Jia, P. Wang and C. Sun, Sensors, 2018, 18, 1762 CrossRef PubMed.
- B. P. Ho and L. G. Leal, J. Fluid Mech., 1974, 65, 365 CrossRef.
- J. A. Schonberg and E. J. Hinch, J. Fluid Mech., 1989, 203, 517 CrossRef CAS.
- E. S. Asmolov, J. Fluid Mech., 1999, 381, 63–87 CrossRef CAS.
- D. Di Carlo, J. F. Edd, K. J. Humphry, H. A. Stone and M. Toner, Phys. Rev. Lett., 2009, 102, 094503 CrossRef PubMed.
- K. Hood, S. Lee and M. Roper, J. Fluid Mech., 2015, 765, 452–479 CrossRef CAS.
- C. Liu, C. Xue, J. Sun and G. Hu, Lab Chip, 2016, 16, 884–892 RSC.
- B. Chun and A. J. C. Ladd, Phys. Fluids, 2006, 18, 031704 CrossRef.
- Y. S. Choi, K. W. Seo and S. J. Lee, Lab Chip, 2011, 11, 460–465 RSC.
- J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132 RSC.
- C. Liu, G. Hu, X. Jiang and J. Sun, Lab Chip, 2015, 15, 1168–1177 RSC.
- S. A. Berger, L. Talbot and L. S. Yao, Annu. Rev. Fluid Mech., 1983, 15, 461–512 CrossRef.
- D. Di Carlo, Lab Chip, 2009, 9, 3038–3046 RSC.
- L. L. Fan, Q. Yan, J. Guo, H. Zhao, L. Zhao and J. Zhe, J. Micromech. Microeng., 2017, 27, 015027 CrossRef.
- H. Amini, E. Sollier, M. Masaeli, Y. Xie, B. Ganapathysubramanian, H. A. Stone and D. Di Carlo, Nat. Commun., 2013, 4, 1826 CrossRef PubMed.
- A. Russom, A. K. Gupta, S. Nagrath, D. Di Carlo, J. F. Edd and M. Toner, New J. Phys., 2009, 11, 075025 CrossRef PubMed.
- J. M. Martel and M. Toner, Sci. Rep., 2013, 3, 1–8 Search PubMed.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Lab Chip, 2008, 8, 1906–1914 RSC.
- H. M. Tay, S. Kharel, R. Dalan, Z. J. Chen, K. K. Tan, B. O. Boehm, S. C. J. Loo and H. W. Hou, NPG Asia Mater., 2017, 9, e434 CrossRef.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977 CrossRef CAS.
- L. Wang and D. S. Dandy, Adv. Sci., 2017, 4, 1700153 CrossRef PubMed.
- B. R. Mutlu, J. F. Edd and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7682–7687 CrossRef CAS PubMed.
- D. Di Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897 CrossRef CAS PubMed.
- S. C. Hur, S. E. Choi, S. Kwon and D. Di Carlo, Appl. Phys. Lett., 2011, 99, 1–4 CrossRef.
- J. Su, X. Chen and G. Hu, Phys. Fluids, 2018, 30, 032007 CrossRef.
- M. Wallden, D. Fange, E. G. Lundius, Ö. Baltekin and J. Elf, Cell, 2016, 166, 729–739 CrossRef CAS PubMed.
- S. C. Hur, N. K. Henderson-Maclennan, E. R. B. McCabe and D. Di Carlo, Lab Chip, 2011, 11, 912–920 RSC.
- C. K. W. Tam and W. A. Hyman, J. Fluid Mech., 1973, 59, 177 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9lc00080a |
| This journal is © The Royal Society of Chemistry 2019 |