Magnetic order and enhanced exchange in the quasi-one-dimensional molecule-based antiferromagnet Cu(NO₃)₂(pyz)₃

Abstract

The quasi-one-dimensional molecule-based Heisenberg antiferromagnet Cu(NO₃)₂(pyz)₃ has an intrachain coupling J = 13.7(1) K (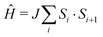) and exhibits a state of long-range magnetic order below T_N = 0.105(1) K. The ratio of interchain to intrachain coupling is estimated to be |J′/J| = 3.3 × 10⁻³, demonstrating a high degree of isolation for the Cu chains.

---

Recent progress in the field of molecular magnetism has shown the clear potential for gaining control over the structural building blocks of molecular materials in order to engineer low-dimensional magnetic properties. In some notable cases, large intermolecular spacing and pseudo Jahn–Teller (JT) distortions result in exchange interactions between transition metal ions being facilitated by bridging ligands such as pyrazine (=pyz=C₄H₄N₂). This allows for the construction of polymeric networks whose primary exchange occurs along one, two or three dimensions.¹ The manipulation of these building blocks, combined with further ingredients such as counterions² and additional ligands,³ enables the synthesis of materials with a wide range of magnetic properties. Furthermore, such systems act as experimental realizations of simple and well-studied model systems, such as the one-dimensional⁴ and two-dimensional⁵S = 1/2 quantum Heisenberg antiferromagnets.

The molecule-based antiferromagnet Cu(NO₃)₂(pyz) (1) represents a highly-ideal experimental realization of the one-dimensional quantum Heisenberg antiferromagnet (1DQHAFM),⁶ described by the Hamiltonian 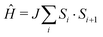. Exchange coupling between Cu²⁺ ions is facilitated by pyz ligands [see Fig. 1(a)] with an exchange constant J = 10.3(1) K determined from magnetic susceptibility.⁶ Weak interchain coupling J′ results in a state of 3D long range magnetic order at T_N = 0.107 K, which was detected using muon-spin relaxation.⁷ These measurements give an estimate |J′/J| = 4.4 × 10⁻³ for the ratio of interchain to intrachain coupling.⁷

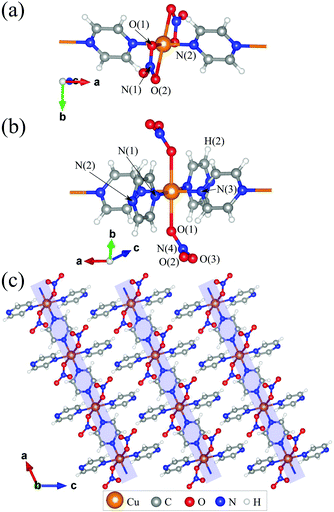Fig. 1 Local environments of the Cu²⁺ ions in (a) 1 and (b) 2. (c) Structure of 2 demonstrating the packing of chains.

In this paper, we report the magnetic properties of the Heisenberg antiferromagnetic chain system Cu(NO₃)₂(pyz)₃ (2). Like 1, 2 comprises Heisenberg S = 1/2 Cu²⁺ ions connected via pyz ligands to form a chain along the a-axis [Fig. 1(b)].⁸ Different from 1, each metal centre has two further trans-coordinated non-bridging pyz ligands extending perpendicular to the chains, keeping them well separated [Fig. 1(b)]. This results in regular octahedral coordination of the Cu²⁺ ions in 2, which has a much higher degree of symmetry than the distorted octahedral environment for Cu²⁺ in 1 [Fig. 1(a)]. For 2, we obtain an intrachain coupling of J = 13.7(1) K (30% larger than in 1) from measurements of magnetic susceptibility and pulsed-field magnetization and we argue that different local environments for the Cu²⁺ ions is the main factor responsible for this higher intrachain coupling. Muon-spin spectroscopy reveals a state of long range magnetic order below T_N = 0.105(1) K. The ratio of intrachain to interchain coupling is lower than that obtained for 1, suggesting that this system is an even more successful realization of a 1DQHAFM.

We prepared deep blue rods of 2 following the procedure previously described by Parkin et al.‡⁸ We re-determined the X-ray crystal structure of 2 as it is relevant to our interpretation of its magnetic properties (see ESI†). Different to 1, which contains four oxygen donor atoms (from chelated nitrate ligands) and two N-donor atoms from pyz, 2 contains two oxygen donor atoms from coordinated NO₃⁻ ligands and four N-donor atoms belonging to pyz [Cu–N(1) = 2.0719(14) and Cu–N(3) = 2.0149(16) Å]. The local coordination geometry of the Cu²⁺ ion in 2 is elongated due to a JT distortion along the O–Cu–O axis [Cu–O(1) = 2.3808(11) Å]. Importantly, this places the magnetic d_x²–y² orbital in the CuN₄ plane such that it can interact with two other Cu²⁺ ions along the chain through the pyz molecules. The resulting structure is that of a polymeric linear chain [Fig. 1(c)] which propagates along the crystallographic a-axis. Successive chains stagger along the c-direction and pack to form pseudo two-dimensional sheets in the ab-plane [Fig. 1(c)]. Supramolecular interactions within these sheets are weak whereas H(2) forms a bifurcated interaction with the two non-coordinated oxygen atoms from NO₃⁻ on an adjacent chain, O(2) and O(3), at distances of 2.5959(15) Å and 2.5548(14) Å, respectively. As a result of these weak interchain interactions we anticipate small magnetic coupling between chains as well.

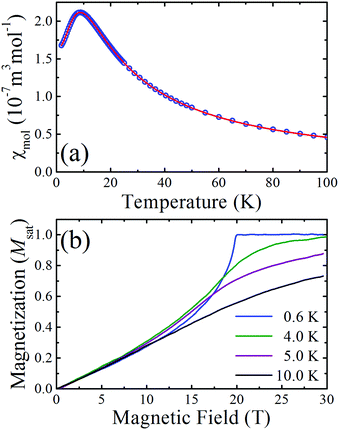
The measured molar susceptibility, χ_mol, of 2 [Fig. 2(a)] shows a broad maximum at 9 K indicative of the individual copper moments becoming correlated along the chains and the onset of low-dimensional behaviour below this temperature. Motivated by the structural analysis, the data are fitted to a model of S = 1/2 Heisenberg spins connected in a 1D chain with a single nearest-neighbour interaction J.†¹⁰ The resultant fitted parameters are g = 2.04(1) and J = 13.7(1) K. A Curie–Weiss analysis of the inverse susceptibility data for temperatures above 100 K returned fitted values g = 2.03(1) and an antiferromagnetic Curie–Weiss temperature |θ_cw| = 5.4(5) K, which is consistent with the energy scale and nature of the intrachain Heisenberg exchange constant.

Fig. 2 (a) Molar susceptibility (χ_mol) vs. temperature for 2 shows a broad maximum at 9 K. (b) Magnetization in units of the saturation magnetization (M_sat) vs. magnetic field provided by a short-pulse magnet. Down sweeps of the magnetic field at various temperatures are shown. Data at 0.6 K are typical of well-isolated S = 1/2 antiferromagnetic chains.

Pulsed-field magnetization² measurements up to 60 T (rise time to full field ∼10 ms) were carried out at the National High Magnetic Field Laboratory in Los Alamos. The magnetization measured at several temperatures is shown in Fig. 2(b) as a fraction of the saturated value. The concave rise observed at the lowest temperature and the sharp change in gradient at saturation is characteristic of highly isolated S = 1/2 antiferromagnetic chains, where, for the ideal system, dM/dB is known to diverge at the saturation field.¹¹ As the temperature increases the magnetization exhibits a more gradual approach to saturation.

The structural, susceptibility and magnetization data all imply that the interchain interactions are orders of magnitude smaller than the intrachain exchange (J). In this case, the low-temperature value of J can be estimated from the saturation field B_c²via the expression gμ_bB_c = 2J. From the T = 0.6 K magnetization data it is found that B_c = 19.9(1) T and so, using the g-factor determined from the Curie–Weiss fit, J is found to be 13.6(1) K, in agreement with the fits of the magnetic susceptibility.

Implanted muons are very sensitive to small magnetic fields and were therefore used to probe the low-temperature magnetic behaviour. Zero-field muon-spin relaxation (ZF μ⁺SR) measurements were made on a polycrystalline sample using the low temperature facility (LTF) spectrometer at the Swiss Muon Source. Example μ⁺SR spectra are shown in Fig. 3 (inset). For T < 0.105 K we resolve oscillations at a single frequency in the asymmetry, A(t), characteristic of quasistatic long range magnetic order (LRO) at one magnetically distinct muon site. We note that, in an earlier work on 1, oscillations in the μ⁺SR spectra were observed at two distinct frequencies;⁷ the additional pyz branches in 2 may block muons from occupying one of the candidate muon sites. We fit the spectra to the functional form A(t) = A₁e^−λ₁t + A₂e^−λ₂t cos(2πνt + ϕ) + A_bg, where the components with amplitudes A₁ and A₂, due to muons stopping in the sample, have relaxation rates λ₁ and λ₂ respectively and the component with amplitude A₂ oscillates with a frequency ν. A_bg is the constant background asymmetry due to muons in the sample holder or those with their spins aligned parallel to the internal field. Above T = 0.105 K the spectra change shape and we instead fit the data to the sum of a Gaussian and an exponential relaxation. The oscillation frequency ν (Fig. 3) is related to the magnitude of the magnetic field at the muon site through ν = γ_μB/2π where γ_μ is the muon gyromagnetic ratio (=2π × 135.5 MHz T⁻¹) and serves as an effective order parameter for the system. A fit to the phenomenological function ν(T) = ν(0)[1 − (T/T_N)^α]^β with α = 3 (fixed) yields ν(0) = 1.59(1) MHz, β = 0.12(2) and T_N = 0.105(1) K. A precipitous drop in ν on approaching T_N and an accompanying small value for the critical exponent β is also observed in 1, for which β = 0.18(5),⁷ and likely reflects the reduced dimensionality of these systems.

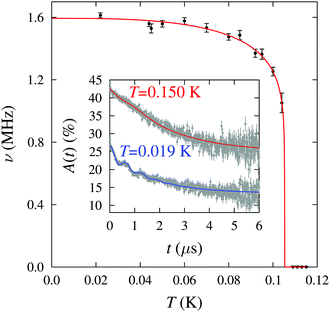Fig. 3 Temperature dependence of the muon precession frequency ν for the fits described in the text. Inset: Example μ⁺SR spectra for 2 measured above and below the magnetic ordering temperature.

An empirical formula based on Monte Carlo simulations¹² allows us to estimate the interchain coupling J′ from our measurements of J and T_N. Substituting |J|/k_B = 13.7 K and T_N = 0.105(1) K we obtain |J′|/k_B = 0.045 K and |J′/J| = 3.3 × 10⁻³. These values are very similar to those obtained for 1.⁷ Furthermore, we can obtain an estimate of the magnetic moment of Cu²⁺ in this system through¹³m ≈ 1.017|J′/J|^1/2 and obtain m ≈ 0.059 μ_B. The moment is very small, highlighting the effect of quantum fluctuations in suppressing the ordered moment in this low-dimensional system. It is worth noting that the ratio of larger muon precession frequency observed for 1 and the corresponding frequency for 2 is similar to the ratio of the Cu²⁺ magnetic moments in these two systems. This suggests that the muon site in 2 is similar to the higher frequency site in 1, but with a smaller local field as a result of the slightly smaller Cu²⁺ moment.

Periodic DFT Calculations were carried out using the CRYSTAL14 software.¹⁴ The functional B3LYP was used with basis set 86-411G(41d)¹⁵ for the Cu and pob-TZVP¹⁶ for all the other atoms. Gas-phase DFT calculations on a dimeric unit were carried out with Gaussian09¹⁷ using again the B3LYP functional and the basis set 6-311G(2d,2p). We have calculated the exchange couplings J using both periodic DFT and gas phase DFT on a single dimer and find J = 14.88 K and J = 11.49 K respectively. Our calculations indicate antiferromagnetic coupling between Cu spins and show reasonable agreement with the values of J obtained experimentally. These values are larger than the coupling constants J = 10.70 K and J = 11.02 K obtained for 1 using periodic DFT and a dimer fragment approach repectively,⁹ supporting the experimentally observed trend. The calculated spin density distribution through the pyz ligand is shown in Fig. 4. The largest part of the spin density is located at the Cu atoms, with some delocalization to the adjacent N atoms.

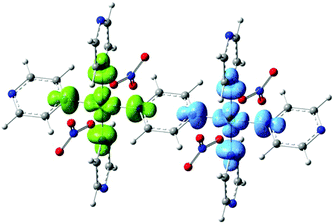Fig. 4 Spin density distribution through the pyrazine ligand in 2 calculated using density functional theory.

Considering the DFT results, we can rationalize the computed J in terms of symmetry, orbital overlap and structural comparisons. In both 1 and 2, a JT distortion places lobes of the magnetic Cu d_x²−y² orbitals along the Cu–N bonds. The primary exchange pathway between Cu²⁺ ions is through the bridging pyz ligands along the 1D chain resulting in similar magnetic properties for 1 and 2. However, the enhanced magnetic exchange observed in 2 requires careful analyses of the local environment surrounding the Cu²⁺ ions. Aside from the shared inversion symmetry of the Cu²⁺ ion in 1 and 2, the enhanced spin exchange in 2 results from the particular bonds and angles making up the coordination sphere. In 1 the d_x²−y² orbital lies in the plane containing the Cu–N bonds (=1.976 Å) and the two shorter Cu–O(1) bonds (=2.002 Å). Nitrate coordination in 1 is quite different wherein it chelates to the Cu²⁺ ion resulting in a O(1)–Cu–O(2) bite angle of 56.3°, far from the ideal 90° observed for purely octahedral symmetry [see Fig. 1(a)]. For 2, the d_x²−y² orbital lies in the plane containing four Cu–N bonds with the Cu–O bonds lying perpendicular to this plane [see Fig. 1(b)]. The net result is a higher symmetry environment for the Cu²⁺ in 2 relative to 1. In terms of the electronic structure, the lower symmetry environment of Cu in 1 can be expected to result in splittings of the d orbitals, altering the energy differences between the various Cu d orbitals and the sp²-hybridized orbital at N responsible for superexchange. For example, we expect the repulsion between O(2) and the magnetic Cu d_x²−y² orbital (which would be smaller if O(2) was occupying the ideal octahedral position) to raise the energy of electrons in the d_x²−y² orbital, thus reducing the contribution of this superexchange pathway to J.

In 1 and 2 the angles between pyz and the plane containing the d_x²−y² orbitals are similar (51° and 55° respectively) and we find that J in 1 is smaller despite the tilt angle being closer to the theoetically ideal value of 45° which would be expected to maximize π-overlap.¹⁸ This is consistent with an X-ray charge-density study on 1 and the 3D coordination polymer [Cu(NO₃)(pyz)₂]NO₃·H₂O (3).⁹ Bond ellipticity profiles ruled out π-type exchange between the Cu d_yz and d_xy orbitals and the pyz π orbitals, favouring a σ-only exchange mechanism. This places emphasis on the Cu–N interactions and these are most important factor in driving the topology of the spin density.

Finally, 3 is structurally similar to 1 and 2, with pyz ligands providing the primary exchange pathway between Cu²⁺ ions.⁹ The intrachain Cu–N bonds and the Cu–N bonds of the terminal pyz ligands in 2 are both shorter than the Cu–N bonds in 3.⁹ The shorter intrachain Cu–N bonds in 2 concentrate electron density along these bonds, enhancing exchange along the chain. By analogy, the shorter apical Cu–O bond in 3 (2.337 Å) than in 2 (2.381 Å) results in a greater depletion of the spin density in the CuN₄ plane, reducing the effectiveness of the magnetic exchange through pyz. The magnitude of J in 1 is intermediate between 2 and 3 owing to ligand variation in the Cu equatorial plane. Oxygen is more electronegative than N and this likely plays a role in depleting spin density away from the intrachain Cu–N bond axis in 1.

In conclusion, the spin-1/2 chain compound Cu(NO₃)₂(pyz)₃ exhibits a larger intrachain coupling J = 13.7 K and a lower magnetic ordering temperature T_N = 0.105 K than Cu(NO₃)₂(pyz), making it a more successful realization of a 1DQHAFM. The slightly enhanced J is likely due to the details of the local Cu²⁺ environment, while effective chain isolation is maintained by non-bridging pyz branches.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the Swiss Muon Source and thank Chris Baines for experimental assistance. We thank EPSRC for financial support under grants EP/N024028/1, EP/N024486/1 and EP/N023803/1. BMH thanks STFC for support via a studentship. The work at EWU was supported by the U.S. National Science Foundation (NSF) under grant no. DMR-1703003. PAG acknowledges that this project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant Agreement No. 681260). Part of this work was carried out at the National High Magnetic Field Laboratory, which is funded by NSF Cooperative Agreement DMR-1157490, the State of Florida and U.S. DoE. It was also supported by the US DoE Basic Energy Science Field Work Project Science in 100 T. JS thanks the University of Oxford for the provision of a Visiting Professorship. PM and RS acknowledge funding from the Swiss National Science Foundation under grant no. 160157. Data presented in this paper will be made available via DOI: 10.15128/r23b5918582.

Notes and references

1. J. L. Manson, J. A. Schlueter, K. A. Funk, H. I. Southerland, B. Twamley, T. Lancaster, S. J. Blundell, P. J. Baker, F. L. Pratt, J. Singleton, R. D. McDonald, P. A. Goddard, P. Sengupta, C. D. Batista, L. Ding, C. Lee, M.-H. Whangbo, I. Franke, S. Cox, C. Baines and D. Trial, J. Am. Chem. Soc., 2009, 131, 6733–6747.
2. P. A. Goddard, J. Singleton, P. Sengupta, R. D. McDonald, T. Lancaster, S. J. Blundell, F. L. Pratt, S. Cox, N. Harrison, J. L. Manson, H. I. Southerland and J. A. Schlueter, New J. Phys., 2008, 10, 083025.
3. P. A. Goddard, J. Singleton, I. Franke, J. S. Möller, T. Lancaster, A. J. Steele, C. V. Topping, S. J. Blundell, F. L. Pratt, C. Baines, J. Bendix, R. D. McDonald, J. Brambleby, M. R. Lees, S. H. Lapidus, P. W. Stephens, B. W. Twamley, M. M. Conner, K. Funk, J. F. Corbey, H. E. Tran, J. A. Schlueter and J. L. Manson, Phys. Rev. B, 2016, 93, 094430.
4. G. Müller, H. Thomas, H. Beck and J. C. Bonner, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 1429–1467.
5. E. Manousakis, Rev. Mod. Phys., 1991, 63, 1–62.
6. P. R. Hammar, M. B. Stone, D. H. Reich, C. Broholm, P. J. Gibson, M. M. Turnbull, C. P. Landee and M. Oshikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1008–1015.
7. T. Lancaster, S. J. Blundell, M. L. Brooks, P. J. Baker, F. L. Pratt, J. L. Manson, C. P. Landee and C. Baines, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 020410.
8. T. Otieno, A. M. Gipson and S. Parkin, J. Chem. Crystallogr., 2002, 32, 81–85.
9. L. H. R. Dos Santos, A. Lanza, A. M. Barton, J. Brambleby, W. J. A. Blackmore, P. A. Goddard, F. Xiao, R. C. Williams, T. Lancaster, F. L. Pratt, S. J. Blundell, J. Singleton, J. L. Manson and P. Macchi, J. Am. Chem. Soc., 2016, 138, 2280–2291.
10. D. C. Johnston, R. K. Kremer, M. Troyer, X. Wang, A. Klümper, S. L. Bud'ko, A. F. Panchula and P. C. Canfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9558–9606.
11. J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640–A658.
12. C. Yasuda, S. Todo, K. Hukushima, F. Alet, M. Keller, M. Troyer and H. Takayama, Phys. Rev. Lett., 2005, 94, 217201.
13. H. J. Schulz, Phys. Rev. Lett., 1996, 77, 2790–2793.
14. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
15. K. Doll and N. Harrison, Chem. Phys. Lett., 2000, 317, 282–289.
16. M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford CT, 2009.
18. H. W. Richardson and W. E. Hatfield, J. Am. Chem. Soc., 1976, 98, 835–839.

---

Footnotes

† Electronic supplementary information (ESI) available: CIF for Cu(NO₃)₂(pyz)₃ at 173 K. Experimental details for magnetic susceptibility, pulsed-field magnetization and muon-spin spectroscopy measurements. Additional information about density functional theory calculations. CCDC 1879250. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8cp07160h

‡ Further increasing the amount of pyrazine in the chemical reaction yields square plates of [Cu(NO₃)(pyz)₂]NO₃·H₂O recently reported by some of us.⁹

---