Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rationalising crystal nucleation of organic molecules in solution using artificial neural networks
Timothy Hjorth a,
Michael Svärd
a,
Michael Svärd *ab and
Åke C. Rasmuson
*ab and
Åke C. Rasmuson ab
ab
aDepartment of Chemical Engineering, KTH Royal Institute of Technology, Stockholm, Sweden. E-mail: micsva@kth.se
bSynthesis and Solid State Pharmaceutical Centre, Department of Chemical and Environmental Science, Bernal Institute, University of Limerick, Castletroy, Ireland
First published on 19th November 2018
Abstract
In this study, the method of artificial neural networks (ANNs) is applied to analyse the effect of various solute, solvent, and solution properties on the difficulty of primary nucleation, without bias towards any particular nucleation theory. Sets of ANN models are developed and fitted to data for 36 binary systems of 9 organic solutes in 11 solvents, using Bayesian regularisation without early stopping and 6-fold cross validation. An initial model set with 21 input parameters is developed and analysed. A refined model set with 10 input parameters is then evaluated, with an overall improvement in accuracy. The results indicate partial qualitative consistency between the ANN models and the classical nucleation theory (CNT), with the nucleation difficulty increasing with an increase in mass transport resistance and a reduction in solubility. Notably, some parameters not included in CNT, including solute molecule bond rotational flexibility, the entropy of melting of the solute, and intermolecular interactions, also exhibit explanatory importance and significant qualitative effect relationships. A high entropy of melting and solute bond rotational flexibility increase the nucleation difficulty. Stronger solute–solute or solvent–solvent interactions are correlated with a facilitated nucleation, which is reasonable in the context of desolvation. A dissimilarity between solute and solvent hydrophobicities is connected with an easier nucleation.
Introduction
Nucleation is an important first step of many crystallisation processes, both natural and industrial, with a direct impact on several properties of the final crystal products. There is a long history of research in the field of crystal nucleation, primary nucleation in particular. Nevertheless, the present understanding is limited as regards the governing mechanisms and the predictability of nucleation from solute and solvent properties. As a consequence, industrial crystallisation processes including a nucleation step are often designed on an empirical basis, with limited control of important governing variables. The product quality may suffer, resulting in e.g. inconsistent bioavailability of pharmaceutical drugs and variable properties of specialised materials.1,2The use of artificial neural networks (ANNs) is a relatively novel method for data pattern analysis, using machine learning. Its inspiration stems from the mechanism of biological neural networks, such as in mammalian brains. Because of their ability to find accurate, complex, non-linear prediction models, ANNs have great potential for various research areas and engineering disciplines.3,4 In fact, it has been demonstrated that with certain minor design constraints an ANN is able to accurately approximate any continuous function.5
Crystal nucleation is a complex and stochastic process, particularly sensitive to minor changes in key conditions.1,2 Accurate prediction of nucleation behaviour is difficult through ordinary regression analysis and related methods, and ANNs could provide a new path towards analysing this complex process and provide important predictive capability. Moreover, ANN modelling does not explicitly require assumptions regarding the functional relationships of the modelled process: the functional mapping between the input and output is produced during calibration to a supplied training dataset.6
There have been a number of studies on the use of ANNs in the design and control of industrial crystallisers.7–13 However, little has been reported on using this method for gaining understanding about the fundamental underlying mechanisms of crystal nucleation. In a study by Kumar,14 ANNs were used to predict the solution–solid interfacial energy for 57 different inorganic systems. The produced ANN model outperformed the classical expression derived by Mersmann.
To the knowledge of the authors, to date no successful attempt has been made to rationalise the nucleation behaviour of organic solutes in solution, especially not without filtering results through the classical nucleation theory (CNT). The twin aims of the present study are to evaluate if ANN modelling can provide accurate analysis of nucleation behaviour and if the obtained functional relationships can enhance the fundamental understanding of crystal nucleation. Specifically, for a selected set of organic solutes and solvents, sets of ANN models are developed for analysis and prediction of the difficulty of nucleation, using properties of the solute, solvent and solution as the input. The functional dependence between the input parameters and the nucleation difficulty is derived, and the corresponding sensitivities are investigated and discussed.
Method
Nucleation difficulty – the target parameter
The selected target parameter is a representation of the nucleation difficulty: the chemical potential driving force required to obtain a distribution of primary nucleation events with a certain predefined median value of the induction time. This is an empirical parameter, completely independent of the choice of any particular nucleation theory. The crystallisation driving force in this work is estimated using the expression commonly found in the literature,15–19 given in eqn (1):
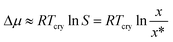 | (1) |
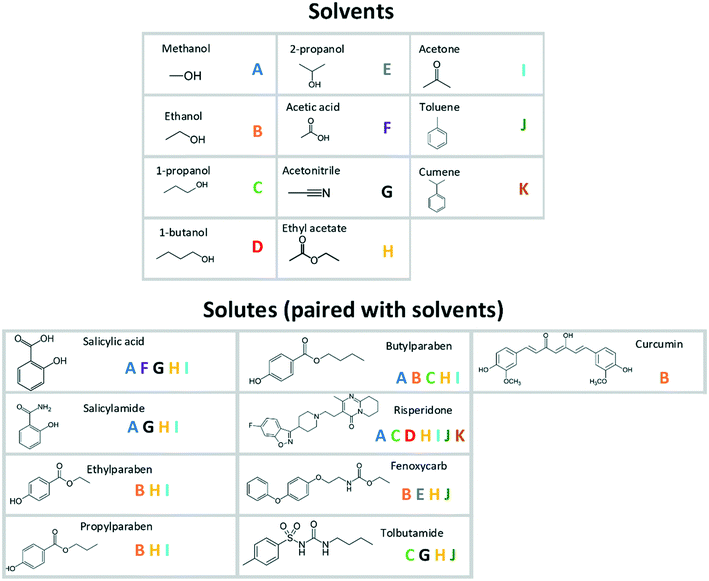
Primary nucleation data have been compiled from a number of studies with strong similarities in experimental conditions and setups: the selected studies all report time-dependent cumulative distributions of nucleation events in small, magnetically stirred, capped vials, with 30–100 replicates under each condition and with ocular detection of the onset of nucleation. The experiments were all carried out under isothermal conditions in binary systems consisting of one solute and one solvent. The included studies comprise 9 different organic solutes with molar masses in the range of 137–410 g mol−1, in different industrially common organic solvents, resulting in a total of 36 unique systems, shown in Fig. 1.16–19,21–24 The solvents include polar protic, polar aprotic, and non-polar molecules, although the majority of the systems feature fairly polar solvents. The solutes differ significantly with regard to properties such as molar mass, the number of rotatable bonds, intermolecular interactions, and melting properties.
Since most of the reported experimental median induction times were in the range from around 10 minutes up to a few hours, the driving force, Δμ, required to reach a median induction time tind,50% = 3000 s was selected as the measure of nucleation difficulty. Although the value 3000 s was representative of the experimental data set, extrapolation was still necessary for 12 of the 36 systems. For interpolation and extrapolation, a simple empirical power law expression: Δμ = A tind,50%B was fitted to experimental data over driving force vs. median induction time for each solute–solvent system. A similar approach has been previously used for comparing the nucleation difficulty of solutes in different solvents.16,17,19 The power law functional form overall provides a very good fit to the data. Over all the systems, the average coefficient of determination is 0.96; for one system the value is 0.83, and for the remaining 35 systems the value is in the range of 0.89–1.00.
The target value, the nucleation difficulty of a pure solute in solution, is conceptually related to the nucleation rate and as such, is affected by both thermodynamic and kinetic factors. In the present study, a large selection of input parameters related to the molecular structure and the thermodynamic and kinetic aspects of crystallisation is initially evaluated. The parameters include pure solute, pure solvent, and solute–solvent combination parameters. They are selected without specific regard to any particular nucleation theory.
Experimental isothermal induction time data are not abundantly available in the literature. In order to focus the analysis on the chemical and physical properties of the molecules, data where the experimental process conditions (most importantly vessel geometry, solution volume and agitation) are overall very similar have been selected. On that basis, process conditions have not been included as parameters in the ANN analysis. All experimental data have been collected from small vial experiments (5–20 mL), with agitation supplied through PTFE-coated stir bars (200–400 rpm) and at normal temperatures. Although the temperature range is limited, it would have been possible to include temperature specifically as an ANN parameter. However, a more physically rigorous way to account for temperature would entail the use of various physical property values at the experimental temperature, which would make the data collection much more complex. It should be noted that the effect of temperature is partly accounted for through the definition of the driving force as a chemical potential difference, and in terms of the classical nucleation theory this accounts for a major portion of the temperature dependence of the nucleation work.
The importance of each included input parameter, and how it affects the output parameter, is evaluated in a sensitivity analysis, and the results of this are used to refine the input parameter set, through removing and/or combining parameters, in an attempt to reduce the model complexity. These measures are applied to improve the physicochemical analysability of the models by refinement of the input set and a reduction of possible overparameterisation.
Multi-level perceptron-type artificial neural networks
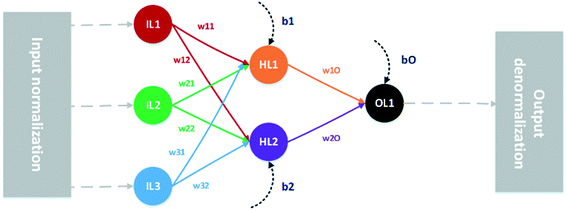
Regression multi-layer perceptron-type ANNs3,4 are nodal networks of interconnected mathematical processing nodes; artificial neurons. Each neuron, receiving an input from the preceding neuron layer, generates a new output by means of a mathematical function and transmits it to the next layer. The importance of each input value to a given neuron is determined by the weight of that particular connection, and the output is further modified by the bias value given to that particular neuron. The weights and biases define the information flow through the network and are parameters determined by regression during the training step. In this work, evaluated networks consist of one input layer, with one neuron per input parameter, one hidden layer with 10 neurons, and one output neuron. Such a network, for reasons of clarity shown with only three input parameters and two hidden neurons, is depicted schematically in Fig. 2.The ANN models used in this work have been designed and evaluated using MATLAB functions developed in-house. The mathematical activation function for each hidden neuron is the tan-sigmoid function: g(u) = tanh(u) = (1 + exp(u))/(1 − exp(u)). 00The models are optimised using the Levenberg–Marquardt algorithm, without early stopping.25 For each model, the dataset is divided into a training set used to parameterise, or calibrate, the network and a test set used to validate the generalisability of the trained model.
It is important to mention that ANN models by nature are flexible and can be overfitted to the supplied data if there are a large number of model parameters, i.e. the number of neurons with connected weights and biases.26 In the present study, this effect is limited by means of three techniques; by Bayesian regularisation, by k-fold cross-validation, and by a manual process of input parameter refinement based on a sensitivity analysis of an initial parameter set.
In Bayesian regularisation,25–27 the objective function, the mean square error, is summed with the mean square weights and biases. Upon minimisation of the objective function during fitting of the model parameters to the experimental data, an optimum simultaneously with regard to the size of weights and biases and the overall error is located. This way it is possible to design an ANN model without knowing the optimal number of model parameters, by initially setting a large number of parameters and then reducing the effective number of model parameters during training. Model parameters that do not contribute to a reduction in the overall error are effectively turned off, and input parameters with low importance are in essence removed from the model. This method is suitable for analysis of data sets of limited size and where there is limited a priori knowledge of the effect of input parameters, and should thus be suitable for the present case.
In order to maximise the use of the limited data set and to improve the analysis of the parameter dependencies by reducing potential bias from a random subset division, k-fold cross validation is used, with k = 6.28 In this method the entire dataset of 36 systems is randomly divided into 6 equally sized parts. Each part is used once as a test set, and k − 1 = 5 times as part of training sets. The prediction and sensitivity results of all 6 parts are pooled and averaged with 10 repeated trainings and evaluations per fold. Thus all data points are used for both training and testing, thereby reducing overfitting to effects within specific data sets, and instead generating more general results. A set consisting of 60 trained ANN models is produced for each set of input parameters. In the evaluation, the entire set of ANN models is used, and consequently this study does not report any final optimised parameter values.
Sensitivity analysis of the generated ANN models is performed using a method inspired by the partial derivative method of Dimopoulos et al.29–31 In contrast to the original formulation of this method, the present study uses training and testing data points in the sensitivity analysis. This is conducted to reduce the possible bias from the randomly divided training and testing subsets: all systems are used in the sensitivity analysis. A disadvantage of this approach is, however, that the testing errors are normally larger than the training errors, which in turn introduces possibly larger, albeit less biased, errors in the resulting sensitivities. The implemented method uses analytical partial derivatives chained between one input parameter and the output and evaluates their numerical value at each model output. The sums of squares of normalised partial derivatives belonging to every input parameter are then compared to obtain a relative importance rating for each input parameter within the studied dataset. The separate sums of positive and negative partial derivatives for each input parameter are also calculated, to obtain a qualitative comparison of the nature of the input–output relationship: their signed sensitivity.
The applied method of combining k-fold cross validation with sensitivity analysis allows for an analysis and ranking of the importance of each input parameter for prediction of nucleation difficulty, as well as the nature of observed input–output relationships for all included solute–solvent systems.
The remaining overfitting could possibly be further reduced by a combination of Bayesian regularisation and the more commonly applied method of early stopping. In early stopping the model training is halted when an additional validation dataset produces a minimum in the error vs. training epoch space.3 However, such a method would require an additional subset of data for the early stopping, resulting in a total of 3 subsets compared to the current 2 subsets. Given the already limited dataset, this approach could possibly worsen the accuracy, since less data would be used for training the model. Consequently, this method has not been applied or evaluated in the present study.
Results and discussion
In a first step, a set of parameters characterising the solute and the solvent molecules from a more general chemical and physical point of view has been evaluated. In a second step, based on the outcome of the first step, a revision of the parameters is made and justified as discussed below.Initial parameter set – 21 parameters
The initial set of input parameters comprises 8 solute properties, 11 solvent properties, and 2 solution properties. The solute parameters are: molar mass (1); melting point (2); enthalpy of melting (3); the number of rotatable bonds (4), defined as the number of non-ring single bonds connected to non-terminal non-hydrogen atoms; topological polar surface area (5), which is a measure of the surface area of the molecules occupied by polar elements such as oxygen, nitrogen, and fluorine; XLogP3 (6), which is a measure of the solute molecular hydrophobicity estimated as the octanol partition coefficient by the XLogP3 prediction method;32 molecular complexity (7) determined using the Bertz–Hendrickson–Ihlenfeldt equation,33 which is a function of the molecular size, symmetry, number of distinct atoms, aromaticity, and bond connectivity; and the number of solute–solute hydrogen bonds (8), taken as the number of hydrogen bond donor and acceptor pairs between two solute molecules. The solvent parameters are: molar mass (9); Reichardt polarity (10), which is an empirical polarity value;34 dynamic viscosity (11); density (12); boiling point (13); enthalpy of vaporisation (14); topological polar surface area (15); XLogP3 (16); molecular complexity (17); melting point (18); and refractive index (19). The solution parameters are: the number of solute–solvent hydrogen bonds (20) and the solid–liquid solubility (21).The results of the training and testing of the ANN models using the initial set of 21 input parameters are shown in Fig. 3 and 4. The average unsigned training and testing errors are 13.4 J mol−1 and 387.7 J mol−1, respectively. The median unsigned errors are 6.4 J mol−1 and 342.4 J mol−1, signifying that some larger residuals produce a small offset to the average. The residuals are distributed seemingly randomly across the output space, without notable systematicity. It should also be noted that there is an unpopulated span in the target space, between approximately 2500 J mol−1 and 4500 J mol−1. However, the average errors before and after this span are similar.
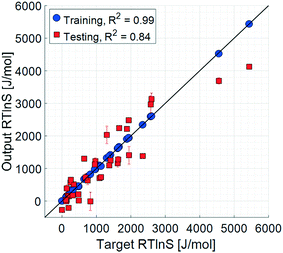 | ||
| Fig. 3 Parity plots, 21 input parameters. Error bars show the 95% confidence limits from k-fold cross validation. | ||
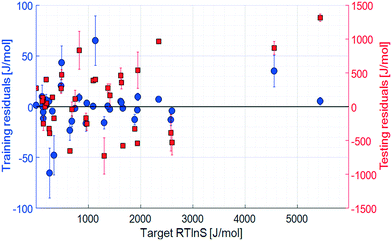 | ||
| Fig. 4 Residuals, 21 input parameters. Error bars show the 95% confidence limits from k-fold cross validation. | ||
The complete set of training results has very small errors, with a coefficient of determination close to unity. This means that all trainings successfully captured a pattern between the supplied input set and the targets. Moreover, the testing results show that the models to a certain extent are generalizable3 and able to predict the unknown target values. The testing prediction errors are larger compared to those of the training set, which to a certain degree is expected; perfect prediction results could only be obtained for a perfect model applied using error-free parameters. Even then, the prediction accuracy will always be limited by the uncertainty in the target data values. In this case, as mentioned earlier, the target parameter as calculated with eqn (1) is associated with an unavoidable error. Nevertheless, the discrepancy between training and testing accuracies, with average errors differing by more than an order of magnitude, indicates a noticeable degree of overfitting to the training sets. The use of Bayesian regularisation was not sufficient to entirely eliminate overfitting, given the limited size of data for the training sets. However, for the purpose of a qualitative analysis of the sensitivity of the model to the different input parameters and as a basis for a manual parameter refinement, the results are sufficiently accurate.
The results of the sensitivity analysis are shown in Fig. 5, both as signed sensitivities and relative importance. In the top graph, for every input parameter the positive partial derivatives are summed to produce a blue bar, and the negative ones are summed to produce a red bar. This figure thus summarises the overall sign tendency of each input–output relationship, analogous to the coefficients of a normal regression model.
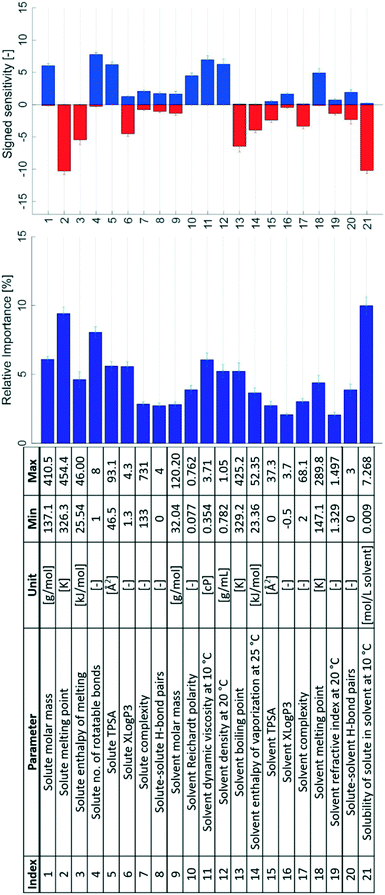 | ||
| Fig. 5 The 21 initial input parameters together with their signed sensitivities and relative importance values. Error bars show the 95% confidence limits from k-fold cross validation. | ||
It is apparent that all input parameters exhibit some importance for prediction of the output parameter. Some parameters show significantly larger importance ratings compared to the others. The five parameters with the largest relative importance ratings are, in descending order: solubility (index 21 in Fig. 5), solute melting point (2), the number of rotatable bonds in the solute (4), solute molar mass (1), and solvent viscosity (11). Thus, these solute, solvent, and solution parameters are all important descriptors for nucleation difficulty in the evaluated ANN models.
Some parameters either result in mostly negatively or positively signed sensitivities – especially the ones with the largest relative importance ratings. An exclusively positive sensitivity implies a positive input–output relationship, i.e. increasing the input parameter value causes an increase in the nucleation difficulty. The solute molar mass (1) has an exclusively positive effect on the nucleation difficulty; increasing the molar mass of the solute results in a more difficult nucleation. Conversely, the molar mass of the solvent (9) does not show a clear effect and a comparably low relative importance rating.
Increasing the solute melting point (2) and solute enthalpy of melting (3) had negative effects on the nucleation difficulty. The number of rotatable bonds of the solute molecule (4) shows an overall positive effect, with only a small sum of negative partial derivatives. Increasing the topological polar surface area of the solute (5) generally increases the nucleation difficulty, whereas the effect of the octanol partition coefficient (6) is mostly but not exclusively negative. As expected the topological polar surface area, which generally increases with increasing hydrophilicity, has the opposite effect on the nucleation difficulty compared to the octanol partition coefficient, which increases with decreasing hydrophilicity.
The solute complexity (7) and the number of possible solute–solute hydrogen bonds (8) are among the solute parameters with the lowest importance ratings in Fig. 5. Both parameters produce small sensitivities in both directions. Distributions between both positive and negative sensitivities suggest parameters that affect the nucleation difficulty differently depending on which system is investigated. The solvent complexity (17) also exhibits a low relative importance rating, but with an exclusively negative effect: an increased solvent complexity is associated with a facilitated nucleation.
The results with respect to the solute parameters (1–8) point to the fact that large molecules and molecules with many rotatable bonds nucleate with more difficulty compared to small molecules with fewer rotatable bonds. Large molecules entail larger mass transport resistance, in accordance with the Stokes–Einstein equation, shown in a simplified form in eqn (2), where η is the dynamic viscosity of the solvent and r is the solvodynamic radius of the solute. A high conformational flexibility, on the other hand, results in a reduced availability of suitable conformers for incorporation into the crystal lattice and thus in increased energy barriers, and is known to reduce the tendency towards crystallisation for small molecules35 as well as proteins.36 Notably, this phenomenon is not captured by the CNT, but it is treated within the two-step theory.37 The solute enthalpy of melting (3) and the solute melting point38 (2) are both found to be negatively correlated with the nucleation difficulty. These parameters describe the interactions in the crystal structure with respect to the pure melt, where the combination of the two translates to the entropy of melting.
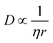 | (2) |
The boiling point of the solvent (13) is a solvent parameter with a large relative importance rating and an overall negative contribution to the nucleation difficulty: over all the included systems, an increased boiling point of the solvent decreases the nucleation difficulty. A similar effect with a large importance rating is found for the enthalpy of vaporisation of the solvent (14). Both parameters are to different extents descriptors of the strength of solvent–solvent interactions, including hydrogen bonding: stronger attractive forces between solvent molecules result in a higher enthalpy of vaporisation and to some extent a higher boiling point.38 A likely rate-contributing step in the nucleation process is the desolvation of dissolved solute molecules, i.e. breaking of solute–solvent bonds in favour of forming solvent–solvent and solute–solute bonds.39 A system with stronger attractive solvent–solvent interactions is thus likely to exhibit a facilitated nucleation. The opposite sensitivity behaviour is seen for the solvent melting point (18), which can be explained by the fact that this property does not sufficiently quantify the interactions in the liquid state.
Similarly, the possible hydrogen bond pairs between the solute and solvent (20) could be expected to positively correlate with a more difficult desolvation: solutes and solvents that are able to form many solute–solvent hydrogen bonds in the solution will likely have to overcome a larger desolvation energy barrier during nucleation. The effect of this parameter is distributed between positive and negative sensitivities, and this could be explained by the fact that nucleation entails desolvation of solute molecules as well as the formation of a solid–solution interface. The formation of the interface is energetically favoured by a larger number of solute–solvent hydrogen bonds at the interface. Together these mechanisms contribute to both positive and negative effects of this parameter on the nucleation difficulty. What is perhaps even more important, however, is that the parameter itself is a simplification of the complex nature of hydrogen bonds; a simple integer value cannot account for varying bond strength or steric effects.
The solubility (21) is found to have the largest relative importance for prediction of nucleation difficulty out of all the input parameters. Its effect is found to be exclusively negative: a higher solubility reduces the nucleation difficulty. A lower number of molecules per unit volume leads to a lower collision frequency between solute molecules, which will have a negative impact on nucleation. As regards the CNT, this effect is captured in the pre-exponential factor of the rate expression. Moreover, a higher solubility is connected with a lower interfacial energy, as given by the Mersmann equation,40 shown in a simplified form in eqn (3) with the interfacial energy σ in units of J m−2. At least in the CNT, a lower interfacial energy is connected with a higher nucleation rate, through both the pre-exponential and exponential terms of the rate expression.41
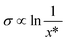 | (3) |
High viscosity (11) and high solvent density (12) are expected to lead to reduced mass diffusivity of the solute, and both parameters are indeed found to have positive effects on the nucleation difficulty. The refractive index of the solvent (19) shows a distribution between positive and negative effects, despite being correlated with density through e.g. the Lorentz–Lorenz equation.42,43 It has the lowest relative importance rating of all the included parameters and is possibly not a good descriptor for this effect, compared to the density itself.
Regarding the different polarity and hydrophilicity parameters, the analysis overall suggests that polar (5), less hydrophobic (6) solutes are comparatively more difficult to nucleate. Analysing similar parameters for the solvent, it is shown that an increased Reichardt polarity (10) leads to an increased nucleation difficulty. Conversely, the topological polar surface area of the solvent (15) exhibits a negative effect on nucleation difficulty, while the XLogP3 of the solvent (16) shows a distribution between positive and negative sensitivities, although with among the lowest relative importance rating of all solvent parameters. These results seem somewhat contradictory: different measures of the solvent polarity show opposite or unclear effects on the nucleation difficulty. The reason for these results could be that the polarity of individual molecules will affect the nucleation difficulty differently in different systems. Increasing polarity increases the number of possible bonds between molecules in the solution, whereas a lowered polarity reduces the number of possible bonds. Most solvents used in the analysis are fairly polar, which could specifically explain the pronounced polarity effect for the solute: if most solvents are polar, less polar solutes will in general be easier to nucleate due to less energetically favourable solute–solvent interactions. The analysis of the effect of polarity could thus be improved by using parameters that compare the polarity of the solute to that of the solvent.
Parameter refinement
It is possible for input parameters to exhibit covariance and for particular input–output effects to be accurately described with fewer parameters. The individually low relative importance of covariant parameters could present a larger combined importance, describing the same physicochemical input–output effect. Although this has not been systematically quantified and analysed in the present study, the refinement of the model addresses many such aspects.The solute enthalpy of melting (3) and to some extent the solute melting point38 (2) are descriptors of the strength of solute–solute interactions, specifically governing the stability of the final crystalline phase. They both show exclusively negative effects in the sensitivity analysis. Therefore, in the refined model only the solute enthalpy of melting (3) is retained as a descriptor of the effect of the strength of solute–solute interactions in the final crystal. The solute entropy of melting is introduced as a new parameter combining the enthalpy of melting (3) with the melting point (2). Together, these parameters encompass various interactions between solute molecules, including hydrogen bonds, π–π interactions44 and van der Waals forces. As the number of solute–solute hydrogen-bond pairs (8) shows a small and inconclusive effect, and as it contains no information about the strength of each bond or about steric effects, it is omitted in the refined model. The solute enthalpy of melting (3) should overall be a better descriptor of this effect.
The complexity ratings of the solute (7) and the solvent (17) are approximate estimates of the synthetic accessibility of the compounds, not direct measures of any physicochemical properties that could correlate with nucleation behaviour. Rather, they are functions of constituent parameters that could themselves serve as descriptors. In addition, both of these parameters show low relative importance ratings in the sensitivity analysis. Both parameters are omitted in the refined model.
The solute molar mass (1) is likely to be not directly connected with the nucleation behaviour. Rather, it is an indirect measure of the molecular size. In an attempt to improve this descriptor, it is replaced by an estimate of the molar volume of the solute, using the molar mass combined with crystal cell volumes obtained from the Cambridge Structural Database.
The solvent refractive index (19) shows a low relative importance rating, and as previously mentioned it is correlated with other included parameters, such as the solvent density (12). The density is combined with the solvent molar mass (9), to obtain a descriptor for the molar volume of the solvent molecule, and the refractive index and molar mass are removed. It has been discussed that the solvent viscosity plays an important role in nucleation kinetics, as it quantifies part of the mass transport resistance in the solution as given by the Stokes–Einstein equation, eqn (2), and in the CNT, the pre-exponential factor is proportional to the diffusion coefficient.41 A new input parameter is constructed by approximating the diffusion coefficient at 10 °C.
Although the number of rotatable bonds of the solute molecule (4) is a rather crude, integral measure of the molecular flexibility, it is kept in the refined model for two reasons: i) it produces a large and almost exclusively positive effect on the nucleation difficulty, and ii) it is a descriptor of an effect that is not captured by any other parameter, except partly by the solute entropy of melting.
Individual polarity ((5), (10), and (15)) and hydrophobicity ((6) and (16)) parameters for the solute and solvent separately yield inconclusive results in the sensitivity analysis. A potential improvement would be to construct parameters that describe these properties in a relative manner between the solvent and solute. Relative parameters are expected to give better descriptions of these effects, since the polarity or hydrophobicity of the solvent compared to those of the solute quantify possible solute–solvent interactions in the solution. In the refined model, these five parameters are reduced to two combination parameters, one for polarity and one for hydrophobicity. Because of the lack of Reichardt polarity data for the solutes, TPSA is used to estimate a relative polarity, and the solvent Reichardt polarity (10) is omitted. The refined model thus contains the ratio in TPSA of the solvent to the solute, shown in eqn (4) and the logarithmic ratio in XLogP3 of the solute to the solvent, shown in eqn (5). These parameters to some extent cover possible interactions between solute and solvent molecules, such as hydrogen bonding and π–π interactions.
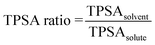 | (4) |
| ΔXLogP3 = XLogP3solvent − XLogP3solute | (5) |
The boiling point of the solvent (13), the solvent enthalpy of vaporisation (14), and the solvent melting point (18) are all to different degrees descriptors of the strength of solvent–solvent interactions, and as such are mainly connected with the desolvation step. All three are replaced by the square of the Hildebrand solubility parameter, δ2 as given in eqn (6), being a quantification of the cohesive energy density of the solvent, with the enthalpy of vaporisation 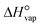 at T = 298 K, and the molar volume υ.45 The solvent melting point is thus completely omitted from the input data set.
at T = 298 K, and the molar volume υ.45 The solvent melting point is thus completely omitted from the input data set.
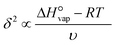 | (6) |
The number of solvent–solute hydrogen-bond pairs (20) does not seem to capture the complex effect of the hydrogen bonding between solute and solvent molecules in solution and is therefore removed from the refined model. Finally, the solubility (21) is kept unaltered in the refined model due to its large relative importance rating as well as high expected relevance.
Refined parameter set – 10 input parameters
The final refined parameter set contains 10 input parameters: solute molar volume, solute enthalpy of melting, solute entropy of melting, the number of rotatable bonds in the solute, solvent molar volume, solvent cohesive energy density, the diffusion coefficient of the solute in the solvent, the relative polarity as the solvent TPSA divided by the solute TPSA, the relative hydrophobicity as the solvent XLogP3 subtracted from the solute XLogP3, and the solubility of the solute in the solvent.The model set is analysed using the same methods as for the unrefined set. The averaged training and testing accuracies are shown in Fig. 6 and 7.
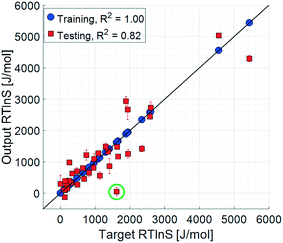 | ||
| Fig. 6 Parity plots, 10 input parameters. Error bars show the 95% confidence limits from k-fold cross validation. | ||
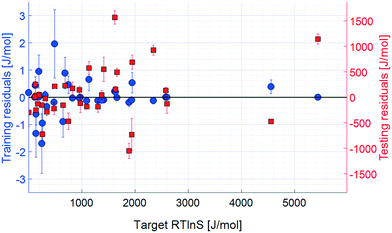 | ||
| Fig. 7 Residuals, 10 input parameters. Error bars show the 95% confidence limits from k-fold cross validation. | ||
The coefficient of determination for the training set of the refined model set is close to unity, and the test set coefficient is slightly below, but very close to, that of the unrefined set. The average unsigned training and testing errors are 0.4 J mol−1 and 361.3 J mol−1, respectively, which are comparable to those of the unrefined model set. The residuals spread randomly across the target space, with no notable systematicity. The median unsigned training and testing errors are 0.2 J mol−1 and 218.7 J mol−1, respectively. The refined model set thus shows a clear overall improvement in accuracy, both in training and testing results. The average errors are, however, offset by a few larger residuals, which also results in the lower testing coefficient of determination. This offset for the test set is significantly larger compared to the that of unrefined model set, indicating that there are some data points in the test set that are more difficult to predict with the refined model set, even though the overall accuracy is comparable: the residual distribution of this set has a higher kurtosis than that of the unrefined one.
One data point with a noticeably large error is salicylic acid in acetic acid, highlighted with a green circle in Fig. 6, which has a target value of 1618.4 J mol−1 and an average test output of 51.1 J mol−1; i.e. the model set underestimates the nucleation difficulty of this system. This is the only system where the solvent is an acid, which in combination with the acidic solute makes this system notably different compared to the other systems included in the study. It is possible that the effects of interactions between these acids, such as stronger hydrogen bonds, are more pronounced than in the other included systems. As such, when the models are trained to the remaining systems, this effect is not well captured.
Moreover, because of the randomised division between the training and test datasets during the k-fold cross validation, it is possible that some effects are not accurately captured during training, resulting in large testing errors. The precise extent of this possible error source has not been systematically assessed in the present study, but it is a likely partial explanation for the large testing errors, which highlights the sensitivity of this model approach to the limited dataset of 36 data points where only 30 points are used for each training. To produce more accurate prediction models, larger training datasets would be required to ascertain that they are trained with all effects of the input parameters and allow for generalisation to systems not included in the trainings. It should be noted that the large testing errors affect the estimated sensitivities and contribute to their uncertainty and errors.
A sensitivity analysis of the refined model set is presented in Fig. 8. The analysis shows that the parameters of the refined set exhibit a more even distribution of the relative importance. Significantly, the parameters that show a high relative importance in the unrefined model set also do so in the refined one. The size of the solute molecule, in the refined set included as its molar volume (index 1 in Fig. 8), the number of rotatable bonds in the solute (4), and solubility (10) all show high importance ratings also in the refined model set. The hydrophobicity ratio between the solvent and solute (9) exhibits a high importance rating, whereas the solute entropy of melting (3), solvent cohesive energy density (6), diffusion coefficient (7), and polarity ratio of the solvent and solute (8) all exhibit moderate to high importance ratings. The size of the solvent molecule, in the form of the solvent molar volume (5), shows an increased relative importance in this model set compared to the molar mass in the unrefined set. The solute enthalpy of melting (2) has a moderate rating in the unrefined model set but shows a large rating in the refined set.
 | ||
| Fig. 8 The 10 refined input parameters together with their signed sensitivities and relative importance values. Error bars show the 95% confidence limits from k-fold cross validation. | ||
The solvent to solute polarity ratio (8) has the lowest relative importance of the included parameters. To some extent this is possibly compensated by the high relative importance of the hydrophobicity ratio (9): these two parameters to some extent describe the same effect. However, the topological polar surface area is only an estimate of the polarity from the area of polar elements in the molecule and does not account for the size of non-polar parts, in contrast to the approximated octanol partition coefficient, XLogP3, which accounts for both non-polar and polar parts of the molecule. The hydrophobicity ratio should thus be a better quantification of the possible solute–solvent interactions in the solution, such as hydrogen bonding and van der Waals interactions, which influence desolvation.
Many descriptors capturing approximately the same properties in the unrefined and refined model sets show similar signed sensitivities. The solute molar volume (1), like the solute molar mass in the unrefined model set, shows an almost exclusively positive effect on the nucleation difficulty: a solute molecule that occupies a larger volume in the solution will be more difficult to nucleate compared to a smaller one. This is consistent with the Stokes–Einstein equation, eqn (2), and the pre-exponential factor of the CNT rate expression is proportional to the diffusion coefficient. Moreover, a larger solute molar volume implies fewer solute molecules per crystal volume and thus a greater Gibbs free energy barrier to forming a critical nucleus according to CNT, as is shown with ΔGcrit in eqn (7) for a spherical geometry.2
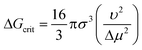 | (7) |
In the refined model set, the diffusion coefficient is also a separate input parameter (7), which shows an almost exclusively negative effect on the nucleation difficulty: a higher diffusion coefficient results in an easier nucleation. This further illustrates that the mass transport resistance is an important effect in nucleation, and that a higher resistance results in a more difficult nucleation.
The solute enthalpy of melting (2) exhibits a similar signed sensitivity to that in the unrefined model set, indicating consistency in the obtained input–output relationship. This parameter describes the enthalpy change between the pure solute phases; lacking the enthalpy of mixing with the solvent, it captures only the ideal component of the enthalpy of solution. This highlights the importance of a descriptor for the strength of solute–solute bonds in predicting the nucleation difficulty.
The entropy of melting (3) produces an overall positively signed sensitivity. During nucleation the solute transforms from a state of higher entropy in the dissolved liquid state to one of lower entropy in the solid state. Although this parameter only describes the entropy change between the solid and liquid states of the pure solute, this entropy change is a component of the transition from the dissolved solute to a nucleated solid in solution. A larger entropy of melting is thus expected to be associated with a larger entropic barrier to nucleation, which explains that an increase in the entropy of melting is connected with a more difficult nucleation.
The number of rotatable bonds in the solute (4) shows an overall positive sensitivity, still together with a smaller negative component, as for the unrefined model set. The reason for this distribution in sensitivities is likely that it is a simplified parameter which only considers the number of rotatable bonds as an integer, but not their relative ability to rotate nor the size or flexibility of the rotating segment. A possible improvement to this parameter would be to estimate the rotational energy barriers of the solute molecule, but this has not been done in the present study. It is notable that the rotatable bonds and the entropy of melting show the same sign tendency for nucleation difficulty in the sensitivity analysis. A solute with more rotatable bonds has more available conformational states, which is generally expected to lead to a higher entropic change associated with conformation to the crystal lattice. It would be possible to analyse more systematically the effect of the conformational freedom and entropy on the nucleation behaviour, using more thoroughly defined energetics for rotational barriers and conformational states of the solute molecule.
The cohesive energy density of the solvent (6) exhibits an overall negative effect on the nucleation difficulty. These results are similar to the results for the solvent boiling point and solvent enthalpy of vaporisation in the unrefined model set, and all of these parameters are to different extents measures of the strength of solvent–solvent interactions. Relatively strong solvent–solvent interactions likely lead to a reduced energy barrier for desolvation and hence a facilitated nucleation.
The solvent to solute polarity ratio (7) shows the lowest relative importance in the refined model set. Expectedly, the effect is also shown to have a small signed sensitivity, almost equally distributed between positive and negative, and the influence of this parameter is therefore somewhat inconclusive. This can in part be explained by the fact that the TPSA is a relatively crude estimate of the polarity. In the unrefined model set the solute TPSA has an exclusively positive effect, whereas the solvent TPSA shows an almost exclusively negative effect: a solute with a larger polar area resulted in a more difficult nucleation, while a larger polar area in the solvent led to an easier nucleation. This is in part explained by the fact that most of the systems contain polar solvents, and a larger polar surface area of the solute thus in general implies a higher degree of similarity between the solute and solvent molecules. It is also possible that the spread between positive and negative effects reflects that the effect of polarity is different in different systems. An improvement to this parameter could be to use a ratio of Reichardt polarity, which is an experimental parameter that captures the effect of the structure of the entire molecule, but there is presently insufficient data available for such an analysis. Alternatively, a combination parameter between the solute TPSA and the solvent Reichardt polarity could be constructed, but this was not attempted in the present study.
For cases where the solute and solvent molecules show similar interactions both with octanol and water, the hydrophobicity ratio (9) will tend towards zero. Negative values indicate that the solute is more hydrophobic than the solvent, and vice versa. Notably, all systems included in the present study lead to negative values, except for two systems with positive values at or below 1, and one system at zero. The signed average value of all input hydrophobicity ratios is −2.3, and the median is −2.4. The separate sums of negative and positive input hydrophobicity ratios are −84.9 and 1.4, respectively. Almost all solutes are appreciably more hydrophobic than the solvents. The uneven distribution of hydrophobicity ratios indicates that the captured model behaviour has an input range between negative values and close to zero, and thus that increasing the input ratio corresponds to a situation where the solute and solvent have more similar hydrophobicities. In Fig. 8 the hydrophobicity ratio has a mostly positive effect; increasing the ratio increases the nucleation difficulty. These results are consistent with those of the solute XLogP3 in the unrefined model set. Increasing the solute hydrophobicity in the unrefined set is connected with the decrease in nucleation difficulty. Because majority of the solvents have relatively low hydrophobicities, an increase in the solute hydrophobicity generally leads to an increased dissimilarity between the solute and solvent in terms of possible interactions. This is expected to lead to weaker interactions in solution, and in turn to a more facilitated desolvation step, consequently resulting in a reduced nucleation difficulty.
The unrefined model set shows a small and unclear effect of solvent molar mass and an exclusively positive effect of solvent density. In the refined model set these parameters are combined to obtain the solvent molar volume (5). This combined parameter exhibits an exclusively negative effect on the nucleation difficulty: a larger solvent molar volume results in an easier nucleation, as seen in Fig. 8. A solvent molecule with a larger molar volume will occupy more space in the solvation shell around the solute molecule, resulting in the solvation shell containing fewer solvent molecules, with overall fewer solute–solvent interactions such as hydrogen bonds, due to steric effects.
Finally, the solubility (10) exhibits a large and almost exclusively negatively signed sensitivity in the refined model set. This is consistent with the results from the unrefined set, clearly indicating the relevance of this parameter in nucleation models.
The results of the present work are to a large extent qualitatively consistent within the context of the CNT as well as other nucleation theories, both for the unrefined and the refined model sets. As regards the CNT, this includes the results with respect to the effect of the size of the solute molecule, where within the CNT framework a larger solute molecule has a greater Gibbs free energy nucleation barrier. Furthermore, the solubility is related to the interfacial energy, as shown by e.g. the Mersmann equation. This effect is consistent with the qualitative effect on the nucleation difficulty given by the CNT rate expression. Constituent parameters of the pre-exponential factor show the expected behaviour in the prediction of nucleation difficulty. Essentially, parameters that are connected with an increase in mass transport resistance correlate with an increase in nucleation difficulty.
Alternative nucleation theories, including the two-step theory, also contain mass transport steps. However, in the first step of the nucleation mechanism the solute molecules concentrate into clusters or solute-rich droplets, wherein crystalline nuclei form in the second step.37,46–53 The rate of the process can be either mass transport or nucleation controlled, but the second step is generally assumed to be rate-determining39 and governed by e.g. entropic and conformational barriers as well as intermolecular interactions: parameters whose importance to the nucleation process are clearly indicated by both the unrefined and the refined models.
As a final remark, the results of the present work indicate that further analysis, especially of how the nucleation behaviour is affected by intermolecular interactions, the conformational energy landscape, and entropic contributions, is warranted. It is clear that this analysis would be improved if additional systems could be included, increasing not only the number of systems but also the diversity of solvent–solute combinations and with data spanning more nonpolar solvents. In particular, inclusion of larger, more flexible solute molecules and contrasting these against smaller, rigid as well as flexible molecules would be an interesting avenue to pursue. Given the availability of a larger data set, it would be possible to further refine the ANN model approach and obtain even more generalizable results. Thus, the present study should be regarded as a promising first step towards elucidating the complex process of crystal nucleation in solution, to derive nucleation models that can qualitatively and quantitatively capture the behaviour of real systems.
Conclusions
A set of ANN models for prediction of nucleation difficulty, with 21 input parameters, exhibits training and testing coefficients of determination of 0.99 and 0.84, respectively. A refined model set with 10 input parameters exhibits the corresponding coefficients of determination of 1.00 and 0.82, with an overall improvement in accuracy. There is no obvious systematicity in the produced residuals, but the lower testing coefficients suggest a certain degree of overfitting.The model analysis shows that large, flexible solute molecules are more difficult to nucleate compared to smaller more rigid ones. An increased entropy of melting of the solute molecule is connected with a more difficult nucleation. Moreover, stronger solute–solute bonds and stronger solvent–solvent bonds reduce the nucleation difficulty, and these results are reasonable within the context of desolvation. Increased values of parameters connected with an increase in the mass transport resistance lead to increased nucleation difficulty. A low similarity between solute and solvent molecules in terms of the hydrophobicity ratio, which describes possible intermolecular interactions, is connected with an easier nucleation.
Parameters included in the CNT, specifically those connected to the critical nucleation work, attachment frequency, and solubility, give results qualitatively consistent with the theory. Some parameters not included in the CNT, specifically parameters related to the rotational and entropic barriers of the solute and intermolecular interactions, also show appreciable explanatory importance and reasonable effects. These parameters could therefore be important descriptors for prediction of nucleation behaviour and could be used to improve nucleation models.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication has emanated from research conducted with the financial support of the Swedish Research Council VR (grant no. 2015-5240). The authors would like to acknowledge networking support by the EU COST Action CM1402 Crystallize.Notes and references
- D. Kashchiev, Nucleation: basic theory with applications, Butterworth Heinemann, Oxford, UK, Boston, MA, USA, 2000 Search PubMed.
- J. W. Mullin, Crystallization, Butterworth-Heinemann, Ipswitch, 4th edn 2001.
- S. Samarasinghe, Neural networks for applied sciences and engineering: from fundamentals to complex pattern recognition, Auerbach, Boca Raton, FL, USA, 2007 Search PubMed.
- C. M. Bishop, Neural networks for pattern recognition, Clarendon Press, Oxford University Press, Oxford, UK, New York, NY, USA, 1995 Search PubMed.
- G. Cybenko, Math. Control Signals Syst., 1989, 2, 303 CrossRef.
- J. C. Hoskins and D. M. Himmelblau, Comput. Chem. Eng., 1988, 12, 881 CrossRef CAS.
- Z. Sha, M. Louhi-Kultanen and S. Palosaari, Chem. Eng. J., 2001, 81, 101 CrossRef CAS.
- M. Yang and H. Wei, Ind. Eng. Chem. Res., 2006, 45, 70 CrossRef CAS.
- S. Y. Wong, R. K. Bund, R. K. Connelly and R. W. Hartel, Cryst. Growth Des., 2010, 10, 2620 CrossRef CAS.
- A. Velásco-Mejía, V. Vallejo-Becerra, A. U. Chávez-Ramírez, J. Torres-González, Y. Reyes-Vidal and F. Castañeda-Zaldivar, Powder Technol., 2016, 292, 122 CrossRef.
- C. Damour, M. Benne, B. Grondin-Perez and J.-P. Chabriat, J. Food Eng., 2010, 99, 225 CrossRef.
- W. Daosud, J. Thampasato and P. Kittisupakorn, Eng. J., 2017, 21, 127 CrossRef CAS.
- K. V. Kumar, P. Martins and F. Rocha, Ind. Eng. Chem. Res., 2008, 47, 4917 CrossRef.
- K. V. Kumar, Ind. Eng. Chem. Res., 2009, 48, 4160 CrossRef CAS.
- J. Liu, M. Svärd and Å. C. Rasmuson, Cryst. Growth Des., 2014, 14, 5521 CrossRef CAS.
- D. Mealey, D. M. Croker and Å. C. Rasmuson, CrystEngComm, 2015, 17, 3961 RSC.
- D. Mealey, J. Zeglinski, D. Khamar and Å. C. Rasmuson, Faraday Discuss., 2015, 179, 309 RSC.
- H. Yang and Å. C. Rasmuson, Cryst. Growth Des., 2013, 13, 4226 CrossRef CAS.
- H. Yang, M. Svärd, J. Zeglinski and Å. C. Rasmuson, Cryst. Growth Des., 2014, 14, 3890 CrossRef CAS.
- M. Valavi, M. Svärd and Å. C. Rasmuson, Cryst. Growth Des., 2016, 16, 6951 CrossRef CAS.
- J. Liu, M. Svärd, P. Hippen and Å. C. Rasmuson, J. Pharm. Sci., 2015, 104, 2183 CrossRef CAS PubMed.
- S. Kakkar, R. K. Devi, M. Svärd and Å. C. Rasmuson, Unpublished manuscripts.
- J. Zeglinski, M. Kuhs, R. K. Devi, D. Khamar, A. C. Hegarty, D. Thompson and Å. C. Rasmuson, Unpublished manuscripts.
- J. Zeglinski, M. Kuhs, D. Khamar, A. C. Hegarty, R. K. Devi and Å. C. Rasmuson, Chem. – Eur. J., 2018, 24, 4916 CrossRef CAS PubMed.
- F. D. Foresee and M. T. Hagan. Gauss-Newton approximation to Bayesian learning, in IEEE International Conference on Neural Networks, Houston, TX, USA 1997 Search PubMed.
- F. Burden and D. Winkler, in Artificial Neural Networks: Methods and Applications, ed. D. J. Livingstone, Humana Press, 2008, p. 23 Search PubMed.
- D. J. C. MacKay, Neural Comput., 1992, 4, 415 CrossRef.
- G. Dougherty, Pattern Recognition and Classification An Introduction, SpringerNew York, NY, USA, London, UK, 2012 Search PubMed.
- Y. Dimopoulos, P. Bourret and S. Lek, Neural Process. Lett., 1995, 2, 1 CrossRef.
- I. Dimopoulos, J. Chronopoulos, A. Chronopoulou-Sereli and S. Lek, Ecol. Model., 1999, 120, 157 CrossRef CAS.
- G. B. Humphrey, H. R. Maier, W. Wu, N. J. Mount, G. C. Dandy, R. J. Abrahart and C. W. Dawson, Environ. Model. Softw., 2017, 92, 82 CrossRef.
- T. Cheng, Y. Zhao, X. Li, F. Lin, Y. Xu, X. Zhang, Y. Li, R. Wang and L. Lai, J. Chem. Inf. Model., 2007, 47, 2140 CrossRef CAS PubMed.
- W. D. Ihlenfeld, Computergestützte Syntheseplanung durch Erkennung synthetisch nutzbarer Ähnlichkeit von Molekülen, Technical University of Munich, Munich, Germany, 1991 Search PubMed.
- C. Reichardt, Chem. Rev., 1994, 94, 2319 CrossRef CAS.
- L. Yu, S. M. Reutzel-Edens and C. A. Mitchell, Org. Process Res. Dev., 2000, 4, 396 CrossRef CAS.
- P. G. Vekilov, Prog. Cryst. Growth Charact. Mater., 2016, 62, 136 CrossRef CAS.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621 CrossRef CAS PubMed.
- F. Trouton, Philos. Mag., 1884, 18, 54 Search PubMed.
- D. Zahn, ChemPhysChem, 2015, 16, 2069 CrossRef CAS PubMed.
- A. Mersmann, J. Cryst. Growth, 1990, 102, 841 CrossRef CAS.
- M. Svärd and Å. C. Rasmuson, Cryst. Growth Des., 2013, 13, 1140 CrossRef.
- C. M. Knobler, C. P. Abbiss and C. J. Pings, J. Chem. Phys., 1964, 41, 2200 CrossRef CAS.
- D. Beysens and P. Calmettes, J. Chem. Phys., 1977, 66, 766 CrossRef CAS.
- A. J. Cruz-Cabeza, R. J. Davey, S. S. Sachithananthan, R. Smith, S. K. Tang, T. Vetter and Y. Xiao, Chem. Commun., 2017, 53, 7905 RSC.
- W. Zeng, Y. Du, Y. Xue and H. L. Frisch, in Physical Properties of Polymers Handbook, ed. J. E. Mark, Springer, New York, NY, USA, 2007, p. 289 Search PubMed.
- R. J. Davey, S. L. Schroeder and J. H. ter Horst, Angew. Chem., Int. Ed., 2013, 52, 2166 CrossRef CAS PubMed.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348 RSC.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819 CrossRef CAS PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007 CrossRef CAS PubMed.
- W. Pan, A. B. Kolomeisky and P. G. Vekilov, J. Chem. Phys., 2005, 122, 174905 CrossRef PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2004, 4, 671 CrossRef CAS.
- H. Cölfen and M. Antonietti, Mesocrystals and Nonclassical Crystallization, John Wiley & Sons, Ltd, Chichester, UK, 2008 Search PubMed.
- T. J. Sorensen, P. C. Sontum, J. Samseth, G. Thorsen and D. Malthe-Sorenssen, Chem. Eng. Technol., 2003, 26, 307 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |