Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Negative thermal expansion in high pressure layered perovskite Ca2GeO4†
Wei-Tin
Chen
 ab,
Chris
Ablitt
ab,
Chris
Ablitt
 c,
Nicholas C.
Bristowe
c,
Nicholas C.
Bristowe
 d,
Arash A.
Mostofi
d,
Arash A.
Mostofi
 ce,
Takashi
Saito
fg,
Yuichi
Shimakawa
ce,
Takashi
Saito
fg,
Yuichi
Shimakawa
 fg and
Mark S.
Senn
fg and
Mark S.
Senn
 *h
*h
aCenter for Condensed Matter Sciences, National Taiwan University, Taipei 10617, Taiwan
bTaiwan Consortium of Emergent Crystalline Materials, Ministry of Science and Technology, Taipei 10622, Taiwan
cDepartment of Materials and the Thomas Young Centre, Imperial College London, London SW7 2AZ, UK
dSchool of Physical Sciences, University of Kent, Canterbury CT2 7NH, UK
eDepartment of Physics, Imperial College London, London SW7 2AZ, UK
fInstitute for Chemical Research, Kyoto University, Uji, Kyoto 611-0011, Japan
gIntegrated Research Consortium on Chemical Sciences, Uji, Kyoto 611-0011, Japan
hDepartment of Chemistry, University of Warwick, Gibbet Hill, Coventry, CV4 7AL, UK. E-mail: m.senn@warwick.ac.uk
First published on 20th February 2019
Abstract
We report the high pressure synthesis of a layered perovskite Ca2GeO4 which is found to have the Ruddlesden–Popper structure with I41/acd symmetry. Consonant with our recent predictions [Ablitt et al., npj Comput. Mater., 2017, 3, 44], the phase displays pronounced uniaxial negative thermal expansion over a large temperature range. Negative thermal expansion that persists over a large temperature range is very unusual in the perovskite structure, and its occurrence in this instance can be understood to arise due to both soft lattice vibrations associated with a phase competition and the unusually compliant nature of this structure, which effectively couples thermal expansion in the layer plane to lattice contractions perpendicular to the layering direction via a “corkscrew” mechanism.
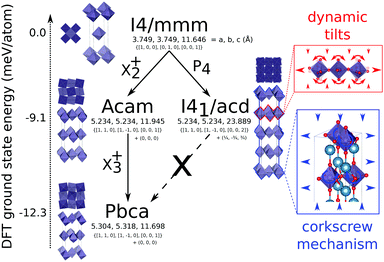
Recently there has been renewed interest in layered perovskite Ruddlesden–Popper systems due to the improper ferroelectricity discovered in the n = 2 family member.1–5 In this structure, octahedral rotation and out-of-phase octahedral tilt modes couple to drive polar distortions leading to a ferroelectric ground state.6 A phase that competes thermodynamically with the improper ferroelectric phase is one with a single out-of-phase rotation of the BO6 octahedra about the layering axis, c. While this phase is not ferroelectric it does exhibit pronounced uniaxial negative thermal expansion (NTE)7 that may be tuned systematically through chemical control.8 We have recently shown that this thermal expansion arises precisely due to this phase competition and the high compliance of the octahedrally rotated phase. Dynamic, low frequency tilts of octahedra about in-plane axes provide the thermodynamic driving force for large in-plane thermal expansion and slight uniaxial contraction at low temperatures. However, thanks to a corkscrew mechanism strongly coupling ab plane, the frozen rotation angle, θ, and c9 (Fig. 1 inset), these modes drive substantial NTE along c over a wide temperature range.10 By studying the nature of the compliance matrix in the Ruddlesden–Popper series Can+1GenO3n+1 as a function of n we recently predicted that the magnitude of NTE should be maximised for n = 111 in which an analogous phase competition to that observed in the n = 2 structure occurs (see Fig. 1). With this in mind, we have synthesised Ca2GeO4 using high pressure techniques and show that it has the most pronounced NTE over the largest temperature range recorded to date in these systems.
Olivine Ca2GeO4 precursor was prepared with stoichiometric amounts of CaCO3 (99.9965%, Alfa) and GeO2 (99.999%, Alfa). The starting materials were mixed well and heated at 1200 °C for 12 hours, and after intermediate grinding, the mixture was then sintered at 1500 °C for a further 24 hours. The obtained precursor was sealed into a platinum capsule, and heated at 1000 °C at 15 GPa for 30 minutes in a Kawai type 2-stage high pressure apparatus. After the heating treatment the sample was quenched to room temperature over 5 minutes and the pressure slowly released. The sample was studied by temperature dependent synchrotron X-ray powder diffraction on beamline 09A of the Taiwan Photon Source, National Synchrotron Radiation Research Center (TPS, NSRRC) with a 15 keV incident beam and MYTHEN detector. The obtained Ca2GeO4 powder sample was sealed in a 0.3 mm diameter borosilicate capillary and 0.3 mm quartz capillary for high temperature experiment which was kept spinning during data collection for better averaging. A DynaFlow cryostat (designed and manufactured by ESRF) with dynamic cooling flow of exchange gas was utilised to provide low temperature diffraction data, for which the sample was cooled first to base temperature (10 K) and collect every 2 K on warming to 150 K. A Cryostream 800 Plus (Oxford Cryosystems) was utilised for data collection from 90 K to 480 K, at intervals of every 5 K to 150 K, every 10 K to 300 K, every 20 K to 480 K. A hot air gas blower (FMB Oxford) was utilised for data collection from 400 K to 800 K, at intervals of every 20 K to 600 K and every 50 K to 850 K. A broadening of diffraction peaks was observed around 800 K and the sample was fully decomposed to the olivine ambient pressure phase by 850 K. The collected patterns were analysed with the Rietveld method using TOPAS.12 First-principles calculations were performed using plane-wave density functional theory (DFT) as implemented in CASTEP v7.0.313 using the PBEsol functional to describe exchange and correlation.14 A 1400 eV plane wave cutoff energy was employed for representing the wavefunctions in all calculations, and a 7 × 7 × 2 grid of k-points were used for the I4/mmm unit cell. This grid was scaled appropriately for larger unit cells to approximately maintain the density of grid points in k-space. Norm conserving pseudopotentials were generated using CASTEP v16.0 and the details may be found in the supplementary output files. In all geometry optimisation calculations, forces were relaxed to below 0.1 meV Å−1 and stresses to below 10 MPa.
The preliminary X-ray powder diffraction analysis revealed that the Ca2GeO4 precursor has the olivine type structure in which Ge are tetrahedrally coordinated, with space group Pnma. A temperature induced phase transition of olivine phase into glaserite type structure with transition temperature 1453 °C has previously been reported as the only other ambient pressure phase of this system.15 The desired meta-stable high pressure phase with K2MgF4 (Ruddlesden–Popper n = 1) type structure has previously been reported under the conditions 900–1000 °C at 10–12 GPa for 3–5 min,16,17 and crystallising in the space group I4/mmm. Our initial high pressure synthesis attempts using the olivine Ca2GeO4 as precursor with 1000 °C at 6 GPa for 30 min and 1200 °C at 9.5 GPa for 30 min conditions with DIA-type cubic anvil high pressure apparatus proved unsuccessful. In the present study we found that we had to use a much higher pressure of 15 GPa, afforded to us by the Kawai type 2-stage high pressure apparatus, to achieve the desired phase transformation to the K2MgF4 type structure.
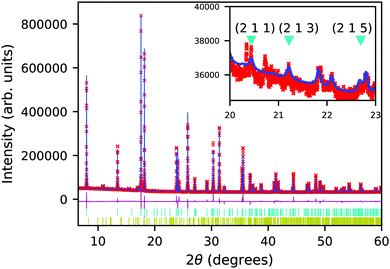
The synchrotron PXRD data was refined in TOPAS using the Rietveld method. The main-phase corresponds to Ruddlesden–Popper n = 1 phase of Ca2GeO4 with aristotypical symmetry I4/mmm. Closer inspection of the room temperature diffraction pattern reveals very weak and broad superstructure peaks (Fig. 2) (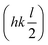 with respect to the aristotype unit cell) indicating that a structure with an out-of-phase octahedral rotation about the c-axis is adopted (I41/acd, a = 5.236339(5) Å, c = 23.81675(3) Å – see Fig. 1). These peaks are significantly broadened on account of the short coherence length of the octahedral rotations along the layering axis. The presence of an impurity with 10% phase fraction by weight corresponding to the ambient pressure phase of Ca2GeO4 (Pnma, a = 11.404194 Å, b = 6.794365 Å, c = 5.242485 Å), significantly convolutes the region of the diffraction pattern 20–23° (see inset of Fig. 2), meaning that these peaks cannot be used to unambiguously assign the symmetry. However, a comparison of the fitting statistics for I4/mmm (Rwp = 2.07, for two internal degrees of freedom) and I41/acd (Rwp = 2.00, for three internal degrees of freedom), along with physically unrealistic atomic displacement parameters in the prior refinement, and DFT lattice parameters (see Table 1) and a ground state energy of I41/acd which we find to be 9.1 meV per atom more stable than the I4/mmm phase (see Fig. 1), all support this assignment.
with respect to the aristotype unit cell) indicating that a structure with an out-of-phase octahedral rotation about the c-axis is adopted (I41/acd, a = 5.236339(5) Å, c = 23.81675(3) Å – see Fig. 1). These peaks are significantly broadened on account of the short coherence length of the octahedral rotations along the layering axis. The presence of an impurity with 10% phase fraction by weight corresponding to the ambient pressure phase of Ca2GeO4 (Pnma, a = 11.404194 Å, b = 6.794365 Å, c = 5.242485 Å), significantly convolutes the region of the diffraction pattern 20–23° (see inset of Fig. 2), meaning that these peaks cannot be used to unambiguously assign the symmetry. However, a comparison of the fitting statistics for I4/mmm (Rwp = 2.07, for two internal degrees of freedom) and I41/acd (Rwp = 2.00, for three internal degrees of freedom), along with physically unrealistic atomic displacement parameters in the prior refinement, and DFT lattice parameters (see Table 1) and a ground state energy of I41/acd which we find to be 9.1 meV per atom more stable than the I4/mmm phase (see Fig. 1), all support this assignment.
| Method | T (K) | a (Å) | c (Å) | Ca(z) | O1(y) | O2(z) | θ (°) |
|---|---|---|---|---|---|---|---|
| X-ray (Rietveld) | 24 | 5.217182(7) | 23.85752(4) | 0.050876(19) | 0.0393(3) | −0.04491(7) | 8.93(17) |
| X-ray (Rietveld) | 300 | 5.236339(4) | 23.81675(3) | 0.051094(14) | 0.0270(4) | −0.04454(5) | 6.16(23) |
| DFT | 0 | 5.234 | 23.89 | 0.0503 | 0.0466 | −0.0446 | 10.6 |
I41/acd (with a frozen rotation about c) is one of several known phases of A2BO4 Ruddlesden–Popper oxides18 that include the aristotype I4/mmm (no rotations or tilts) and competing Pbca phase (rotation about c and in-plane tilts) shown in Fig. 1. It is an interesting question why Ca2GeO4 crystallises as I41/acd and not alternative phases, despite DFT showing Pbca to be lower in energy. The answer likely relates to vibrational entropy favouring I41/acd over the energetic ground state, however, this discussion is beyond the scope of the current study. It is noteworthy that there is no direct transition between I41/acd and Pbca without unravelling the anti-phase P4 rotations to transform them to in-phase X2+ rotations. It is this so-called symmetry trapping that we have previously argued prevents the transition to the energetic ground state7 thus allowing octahedral tilts that have been shown to drive NTE8,10 to remain low in frequency without condensing.
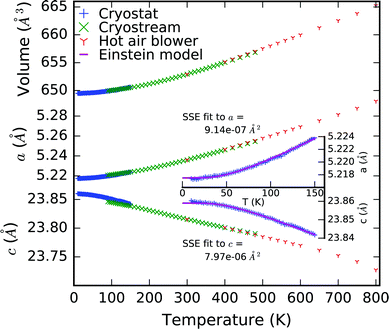
Lattice parameters were extracted from the temperature dependent powder X-ray diffraction data by performing sequential Pawley refinement and are shown in Fig. 3. No discontinuities or anomalies in the lattice parameters were observed. Data collected on warming using the cryostat in the region 10–140 K shows a slight discontinuity with the data collected on cooling (despite normalisation using the volumes at 120 K) evidencing some hysteresis in the thermal expansion behaviour of the sample. This likely arises as a result of individual domains and grains expanding and contracting at vastly different rates along different directions, resulting in substantial macroscopic strain and hysteresis in the sample. Indeed, asymmetric peak broadening and shifts are observed at lower temperature. Fitting a Scherrer particle size Gaussian peak broadening model to the (hkl) l = odd reflections gives an estimate of the domain size of 16.7 (1.4) nm.
Fitting the low temperature a and c lattice parameter data with a single Einstein mode model of the form
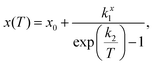 | (1) |
We have previously shown that the character of the low energy vibrations giving rise to NTE along c are the same as those giving rise to PTE along a.10 Therefore a and c were fitted in tandem using least squares optimisation where the optimisation function was the sum of the errors normalised by lattice parameter for both a and c. This meant that a single characteristic frequency could be applied to both models. The characteristic phonon frequency, k2, is found to be 155 K (13.4 meV, 108 cm−1). Fitting the same single Einstein mode model to a and c from our previous measurements of the isosymmetric system Ca2MnO410 over an equivalent temperature range gives a k2 of 261 K (22.5 meV, 182 cm−1) which is substantially higher than in Ca2GeO4 (see Table 2 for full model parameters for both compounds). This is evident both in that the flattening of the NTE occurs at much lower temperatures in Ca2GeO4, and that it is more pronounced compared to that observed in Ca2MnO4. The average thermal expansion coefficient along the c direction, αc, in Ca2GeO4 (100–400 K) is −6.3 ppm K−1, which is substantially larger than for Ca2MnO4 measured over the same temperature range (αc = −4.4 ppm K−1).10
| Compound | a 0 (Å) | c 0 (Å) | k 1 a (Å) | k 1 c (Å) | k 2 (K) |
|---|---|---|---|---|---|
| Ca2GeO4 | 5.2175 | 23.859 | 0.01119 | −0.03101 | 154.9 |
| Ca2MnO410 | 5.1684 | 24.153 | 0.02907 | −0.06214 | 261.2 |
It is worth noting that in our previous computational studies of NTE in these systems,10 we used Ca2GeO4 as a substitute for Ca2MnO4 by applying a 4.3 GPa biaxial pressure to account for the in-plane exchange striction associated with Mn sites. The effect of this was to harden the soft phonon modes in our calculations with respect to the unstrained Ca2GeO4 phase. It is hence to be expected that in the experiment Ca2GeO4 shows more pronounced NTE than Ca2MnO4, and the resulting trend is consistent with this picture. Ca2GeO4 and Ca2MnO410,19 are not the only n = 1 family compounds exhibiting uniaxial NTE. Other examples found in the literature include Sr2IrO420–22 and Sr2RhO4,23,24 both of which crystallise in the I41/acd phase. However, in this instance the magnitudes of αc are much smaller with an average of −2.4 ppm K−1 for Sr2RhO4 (calculated for 10–300 K from ref. 23) and −2.1 ppm K−1 in Sr2IrO4 (calculated for 13–295 K from ref. 20). It should be noted that Ca2RuO425 and related materials, which crystallise in an orthorhombic space group, exhibit NTE as a result of electronic instabilities and Jahn–Teller ordering, which can be very pronounced effects but which tend to be confined to a relatively narrow temperature range.
Recently, it has been proposed that the quantity χαV, given by the product of the average volume thermal expansion coefficient αV and the temperature range over which NTE is observed, can be used as a metric for classifying different regimes of volume NTE26 and to help identify systems that exhibit remarkable NTE properties. Within this picture, Ca2GeO4 exhibits linear NTE with χα = 0.55% measured across the full 10–800 K window of stability of the I41/acd phase. This compares to χαV = 2.74% (χα = 0.913%) in the prototypical NTE material ZrW2O827 (note the factor of 3 between linear α and volume αV). It is, however, as yet unclear whether this metric may be used to meaningfully compare systems exhibiting volume (bulk) NTE and those exhibiting only uniaxial NTE. A recent report of pronounced uniaxial negative linear thermal expansion as large as α = −40 ppm K−1 for the orthorhombic (Cmc21) phase in the (110)-cut perovskite LaTaO4 represents possibly one of the largest linear CTEs in hard ceramic materials to date.28 This phase, which we have recently shown to be very compliant with respect to coupling expansion along the PTE axis to contraction along NTE axes,10 has a χα = 0.68%, which is larger yet comparable to Ca2GeO4, except here NTE persists over a much narrower temperature range (<300 K). By tuning the chemistry, it should be possible to synthesise an A2BO4 layered perovskite with I41/acd symmetry which is stable to higher temperatures thus extending the temperature range of NTE. Even down to cryogenic temperatures we find that Ca2GeO4 does not transform into the competing Pbca phase. Therefore it should be possible to tune the tolerance factor to bring the system closer to this transition – thus increasing the thermodynamic driving force for NTE. If either (or both) of these enhancements could be achieved by chemical substitution, it may be possible to engineer a Ruddlesden–Popper possessing a significantly greater magnitude of NTE than LaTaO4 by this χα metric.
In summary, we have successfully synthesised the layered perovskite Ca2GeO4 showing that it crystallises in the I41/acd rather than I4/mmm space group. In accordance with our predictions this structure shows pronounced uniaxial NTE over a large temperature range. This phenomenon can be understood to be driven by low energy lattice vibrations related to a thermodynamically competing Pbca phase (shown in Fig. 1) in which these octahedral tilts condense, and the unusually compliant nature of the I41/acd structure. Single Einstein mode fits of the a and c lattice parameters as a function of temperature provide an upper estimate for the phonon frequency of 155 K (108 cm−1) for the characteristic modes driving NTE. The unusually wide temperature range over which these soft phonon modes persist may make them useful in controlling properties associated with thermal expansion, dielectric response and other phonon-mediated properties such as thermal transport, and the thermoelectric effect.
This work was partly supported by Ministry of Science and Technology (Taiwan) (MOST-106-2112-M-002-021-MY3), the Collaborative Research Program of Institute for Chemical Research, Kyoto University (grant 2017-88) and the Japan Society for the Promotion of Science (JSPS) Core-to-Core Program (A) Advanced Research Networks. The synchrotron experiment was supported by National Synchrotron Radiation Research Center (NSRRC, Taiwan) with proposal no. 2017-3-298. M. S. S. is supported by a Royal Society University Research Fellowship (UF160265), and C. A. is supported by a studentship in the Centre for Doctoral Training in Theory and Simulation of Materials at Imperial College London funded by the EPSRC (EP/L015579/1). We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1).
Conflicts of interest
There are no conflicts to declare.Notes and references
- M. J. Pitcher, P. Mandal, M. S. Dyer, J. Alaria, P. Borisov, H. Niu, J. B. Claridge and M. J. Rosseinsky, Science, 2015, 347, 420–424 CrossRef CAS PubMed.
- R. Zhang, M. S. Senn and M. A. Hayward, Chem. Mater., 2016, 28, 8399–8406 CrossRef CAS.
- S. Yoshida, H. Akamatsu, R. Tsuji, O. Hernandez, A. S. Gupta, A. S. Gibbs, K. Mibu, S. Murai, J. M. Rondinelli, V. Gopalan, K. Tanaka and K. Fujita, J. Am. Chem. Soc., 2018, 140, 15690–15700 CrossRef CAS PubMed.
- H. Zhang, S. Gao, Q. Zhang, J. Wu, J. Liang, C. Dong, L. Gu, S. Dong, J. Sun, F. Liao, J. Lin, R. Zou and G. Li, Chem. Mater., 2017, 29, 9840–9850 CrossRef CAS.
- T. Zhu, T. Cohen, A. S. Gibbs, W. Zhang, P. S. Halasyamani, M. A. Hayward and N. A. Benedek, Chem. Mater., 2017, 29, 9489–9497 CrossRef CAS.
- N. A. Benedek and C. J. Fennie, Phys. Rev. Lett., 2011, 106, 107204 CrossRef PubMed.
- M. S. Senn, A. Bombardi, C. A. Murray, C. Vecchini, A. Scherillo, X. Luo and S. W. Cheong, Phys. Rev. Lett., 2015, 114, 035701 CrossRef CAS PubMed.
- M. S. Senn, C. A. Murray, X. Luo, L. Wang, F.-T. Huang, S.-W. Cheong, A. Bombardi, C. Ablitt, A. A. Mostofi and N. C. Bristowe, J. Am. Chem. Soc., 2016, 138, 5479–5482 CrossRef CAS PubMed.
- C. Ablitt, M. S. Senn, N. C. Bristowe and A. A. Mostofi, arXiv, 2018, arxiv:1810.02697.
- C. Ablitt, S. Craddock, M. S. Senn, A. A. Mostofi and N. C. Bristowe, npj Comput. Mater., 2017, 3, 44 CrossRef.
- C. Ablitt, A. A. Mostofi, N. C. Bristowe and M. S. Senn, Front. Chem., 2018, 6, 455 CrossRef PubMed.
- A. A. Coelho, Topas v4.2: General Profile and Structure Analysis Software for Powder, 2009 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- W. Eysel and T. Hahn, Z. Kristallogr., 1970, 131, 322–341 CrossRef CAS.
- A. E. Ringwood and A. F. Reid, Earth Planet. Sci. Lett., 1968, 5, 67–70 CrossRef CAS.
- A. F. Reid and A. E. Ringwood, J. Solid State Chem., 1970, 1, 557–565 CrossRef.
- P. V. Balachandran, D. Puggioni and J. M. Rondinelli, Inorg. Chem., 2014, 53, 336–348 CrossRef CAS PubMed.
- J. Takahashi and N. Kamegashira, Mater. Res. Bull., 1993, 28, 565–573 CrossRef CAS.
- Q. Huang, J. L. Soubeyroux, O. Chmaissem, I. Natali Sora, A. Santoro, R. J. Cava, J. J. Krajewski and W. F. Peck, J. Solid State Chem., 1994, 112, 335–361 CrossRef.
- M. K. Crawford, M. A. Subramanian, R. L. Harlow, J. A. Fernandez-Baca, Z. R. Wang and D. C. Johnston, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 9198 CrossRef.
- B. Ranjbar and B. J. Kennedy, J. Solid State Chem., 2015, 232, 178–181 CrossRef CAS.
- T. Vogt and D. J. Buttrey, J. Solid State Chem., 1996, 189, 186–189 CrossRef.
- B. Ranjbar and B. J. Kennedy, Solid State Sci., 2015, 49, 43–46 CrossRef CAS.
- M. Braden, G. Andre, S. Nakatsugi and Y. Maeno, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 847–861 CrossRef CAS.
- C. S. Coates and A. L. Goodwin, Mater. Horiz., 2018 10.1039/C8MH01065J.
- T. a. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92 CrossRef CAS.
- K. J. Cordrey, M. Stanczyk, C. A. L. Dixon, K. S. Knight, J. Gardner, F. D. Morrison and P. Lightfoot, Dalton Trans., 2015, 44, 10673–10680 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cc09614g |
| This journal is © The Royal Society of Chemistry 2019 |