Open Access Article
Open Access ArticleA two-qubit molecular architecture for electron-mediated nuclear quantum simulation†
Matteo
Atzori
 *a,
Alessandro
Chiesa
*a,
Alessandro
Chiesa
 bc,
Elena
Morra
bc,
Elena
Morra
 d,
Mario
Chiesa
d,
Mario
Chiesa
 d,
Lorenzo
Sorace
d,
Lorenzo
Sorace
 a,
Stefano
Carretta
a,
Stefano
Carretta
 *b and
Roberta
Sessoli
*b and
Roberta
Sessoli
 *a
*a
aDipartimento di Chimica “Ugo Schiff” & INSTM, Università Degli Studi di Firenze, I-50019 Sesto Fiorentino, Italy. E-mail: matteo.atzori@unifi.it; roberta.sessoli@unifi.it
bDipartimento di Scienze Matematiche, Fisiche e Informatiche, Università di Parma, I-43124 Parma, Italy. E-mail: stefano.carretta@unipr.it
cInstitute for Advanced Simulation, Forschungszentrum Jülich, D-52425 Jülich, Germany
dDipartimento di Chimica & NIS Centre, Università di Torino, Via P. Giuria 7, I-10125 Torino, Italy
First published on 15th June 2018
Abstract
A switchable interaction between pairs of highly coherent qubits is a crucial ingredient for the physical realization of quantum information processing. One promising route to enable quantum logic operations involves the use of nuclear spins as protected elementary units of information, qubits. Here we propose a simple way to use fast electronic spin excitations to switch the effective interaction between nuclear spin qubits and the realization of a two-qubit molecular architecture based on highly coherent vanadyl moieties to implement quantum logic operations. Controlled generation of entanglement between qubits is possible here through chemically tuned magnetic coupling between electronic spins, which is clearly evidenced by the splitting of the vanadium(IV) hyperfine lines in the continuous-wave electron paramagnetic resonance spectrum. The system has been further characterized by pulsed electron paramagnetic resonance spectroscopy, evidencing remarkably long coherence times. The experimentally derived spin Hamiltonian parameters have been used to simulate the system dynamics under the sequence of pulses required to implement quantum gates in a realistic description that includes also the harmful effect of decoherence. This demonstrates the possibility of using this molecular complex to implement a control-Z (CZ) gate and simple quantum simulations. Indeed, we also propose a proof-of-principle experiment based on the simulation of the quantum tunneling of the magnetization in a S = 1 spin system.
Introduction
Quantum Information Processing (QIP) has the promise to shift the current computational paradigm based on classical bits to a more performing computational protocol that exploits the quantum properties of matter to perform quantum logic operations, i.e. quantum gates.1 The physical realization of quantum computers2,3 can be in principle achieved by using a variety of quantum systems, such as superconducting circuits,4 photons,5–7 or electronic defects in inorganic solids.8,9Molecular spin qubits have recently emerged as an alternative platform with great promise in terms of long coherence times and fine-tuning of their magnetic/electronic properties.10–17 The current challenge is the realization of molecular quantum gates based on two or more interacting qubits with a long coherence time that can be efficiently manipulated by electromagnetic radiation pulses. Supramolecular assemblies of heterometallic Cr7Ni rings18–21 and dinuclear lanthanide complexes22,23 are currently the most investigated systems for this purpose. Although they represent elegant realizations of coupled molecular qubits, further improvements such as narrow Electron Paramagnetic Resonance (EPR) spectral lines are necessary to allow precise qubit control. Also, long coherence times retained at high temperatures would be important for practical applications.
These features have been partially achieved through a fine engineering of the Landé g factor in organic multi-radical systems to address different qubits individually.24,25 However, they present permanent qubit–qubit interactions that lead to an unwanted continuous many body evolution that has to be corrected during gating through complex pulse sequences.
An alternative possibility to the use of electronic spins is the use of nuclear spins to encode qubits that are more weakly coupled to the environment and hence substantially protected from decoherence.26 Indeed, Grover's quantum search algorithm has been recently implemented on a multi-level system consisting of a TbIII nuclear spin sitting on a molecular transistor and controlled by electric fields.27,28 However, purely nuclear spin platforms have the drawback of showing very weak and permanent direct couplings, yielding very slow two-qubit gates and unwanted two-qubit evolutions.26
Hybrid electron-nuclear approaches,8,29–33 exploiting electronic transitions to achieve a universal control of nuclear qubits via sophisticated sequences of pulses, have been proposed.24,34–38 In particular, electrons allow one to obtain high nuclear polarization, thus enabling the initialization of the nuclear register,37 while nuclei provide long coherence times, as shown in Electron-Nuclear Double Resonance (ENDOR) based QIP.31
Here we propose a novel scheme for electron-mediated nuclear quantum simulation. In contrast to recently reported NMR quantum computation approaches,25 we do not rely on the free evolution induced by the internal Hamiltonian to drive two-qubit gates. Furthermore, the qubit–qubit coupling is not permanent. Indeed, in our approach the interaction between nuclear qubits is effectively and rapidly switched on and off by exciting the coupled electronic spins via simple microwave (EPR-like) pulses, while single-qubit rotations between decoupled nuclear spins are obtained by means of radio-frequency (NMR-like) pulses. This leads to simple pulse sequences, thus requiring few operations, for the implementation of quantum simulations. In addition, individual spin addressing and the related g-engineering are not needed to simulate symmetric quantum mechanical problems.
A prototypical realization of this idea is a molecular architecture composed of two paramagnetic metal ions with magnetic nuclei (I ≠ 0) and sizeable hyperfine couplings. Indeed, a small but measurable interaction between the two electronic spins can be used to effectively couple nuclear qubits and controllably generate entangled two-qubit states. Long electronic spin coherence times are also a key ingredient to ensure the robustness of such a system during the implementation of electron-mediated two-qubit gates.
To this aim, we have synthesised a dinuclear molecular architecture consisting of two weakly interacting vanadyl moieties. They are the ideal building blocks for this scheme thanks to their magnetic nuclei (I = 7/2), large hyperfine splitting, and long coherence times.15 We have fully characterized the system by continuous-wave and pulsed EPR measurements, thus extracting all the parameters of the spin Hamiltonian, as well as the phase memory time. This was found to be remarkably long (ca. 1 μs) and of the same order of magnitude as that of a representative mononuclear derivative.39 We have used the set of parameters determined from EPR spectroscopy to numerically simulate the dynamics of the system subject to the microwave (mw) and radiofrequency (rf) pulses necessary to implement single and two-qubit gates. Our realistic simulations also include the detrimental effect of decoherence in a Lindblad master-equation formalism.40 Finally, we have designed a proof-of-principle experiment of quantum simulation that could be implemented with the present system.
Results and discussion
Electron-mediated nuclear-spin QIP: conception, design and synthesis
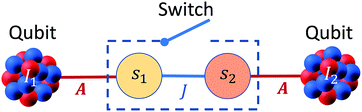
A sketch of the proposed scheme is shown in Fig. 1. It consists of a dinuclear molecular architecture of transition metal ions with both electronic (s1,2) and nuclear spins (I1,2). The electronic spins are coupled by an interaction (described by J) and each nuclear spin is coupled to its electronic spin via the hyperfine interaction (described by A).In significant magnetic fields, the electronic and nuclear spin states are practically factorized because of the large difference in their Zeeman energies. Hence, if electrons stay in their ground state, the effect of the hyperfine interaction 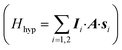 is simply equivalent to a renormalization of the magnetic field felt by the nuclear spins. Therefore, the energy to rotate one of the nuclear spins does not depend on the state of the other. By using a pair of nuclear spin states to encode the qubits, single-qubit rotations can then be implemented by means of rf pulses resonant with the nuclear Zeeman energy gap. Conversely, the energy to rotate the coupled electron spins depends on the state of both nuclei, because of the hyperfine coupling. Thus, the effect of a resonant mw pulse depends on the states of the nuclear qubits and this can be directly exploited to implement a conditional two-qubit gate. Hence, the two coupled electron spins act as a sort of fast switch of the effective interaction between nuclear qubits.
is simply equivalent to a renormalization of the magnetic field felt by the nuclear spins. Therefore, the energy to rotate one of the nuclear spins does not depend on the state of the other. By using a pair of nuclear spin states to encode the qubits, single-qubit rotations can then be implemented by means of rf pulses resonant with the nuclear Zeeman energy gap. Conversely, the energy to rotate the coupled electron spins depends on the state of both nuclei, because of the hyperfine coupling. Thus, the effect of a resonant mw pulse depends on the states of the nuclear qubits and this can be directly exploited to implement a conditional two-qubit gate. Hence, the two coupled electron spins act as a sort of fast switch of the effective interaction between nuclear qubits.
Potential building blocks for a molecular realization of such a two-qubit architecture are coordination compounds of vanadium(IV) ions. Indeed, recent promising results in terms of long coherence times related to a manifold of narrow resonance lines have been reported for a variety of vanadium(IV) molecular single-qubit systems,12–16 in particular those where the vanadium(IV) is embedded in a vanadyl moiety.12–15 Several efforts have been devoted to establishing chemical design strategies to increase both the coherence time Tm12,41 and the spin-lattice relaxation time T1,12,39 but the realization of a molecular system containing two weakly interacting single d-metal ions for the purpose of quantum gate implementation is still missing.
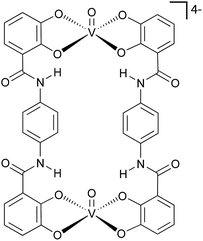
To address this challenge, we have selected ditopic-catecholate ligands as suitable qubit-linking systems. These ligands allow the modulation of the qubit–qubit distance by changing the central spacer, providing a fine-tuning of the magnetic interaction (Fig. 2). Moreover, catecholates have been recently identified as ideal ligands to prepare single-qubit vanadium(IV)-complexes with long spin-lattice relaxation and long spin coherence times.39 By following this approach, we targeted and succeeded in the preparation of a molecular system of the formula [PPh4]4[(VO)2(L1)2] (1) (L1 = tetraanion of C6H3(OH)2–CONH–C6H4–CONH–C6H3(OH)2) (Fig. 2), which can be used to implement our QIP scheme. The properties of 1 are herein compared to that of a recently reported mononuclear compound of the formula [PPh4]2[VO(catecholate)2] (2)39 that has been taken as a reference.
Compound 1 shows low solubility in most of the common organic solvents, being soluble only in the most polar ones such as dimethylformamide (DMF) and dimethylsulfoxide (DMSO). This precluded a crystallographic analysis through single crystal X-ray diffraction. To provide structural insights into the molecular structure of 1 we have supported the classical analytical characterization (see the Experimental section) with hyperfine sublevel correlation (HYSCORE) spectroscopy experiments at the Q-band frequency. HYSCORE data for 1 show a diagonal peak at the 51V Larmor frequency (Fig. S1†). From the presence of a diagonal peak, a lower limit of 5 Å for the V⋯V distance can be estimated based on a pure dipole–dipole interaction. This diagonal peak is not observed for monomeric vanadyl complexes at comparable concentrations, strongly supporting the existence of a dinuclear structure with a well-defined V⋯V distance compatible with the ligands used.42,43 Cross peaks due to the hyperfine coupling with a 14N (I = 1) nucleus (ca. 4.5 MHz) are also observed when dissolving the complex in DMF but not in DMSO (Fig. S1†). This excludes an interaction originating from the amidic nitrogen atom of the ligand and suggests the presence of an interaction with a DMF solvent molecule in the equatorial plane, as already reported for other vanadyl complexes.44,45 The comparison of the X-band EPR spectra of 1 recorded in DMF and DMSO, which are completely superimposable (Fig. S2†), confirms that interaction with the solvent does not significantly affect the molecular structure in solution.
Magnetic characterization and spectroscopic studies by CW- and pulsed-EPR
The VIV spin centres in compound 1 are not directly connected through a bridging ligand. Therefore, the most relevant magnetic interaction is expected to be through-space, that is, a dipolar interaction. On the basis of the estimated V⋯V distance, this should be of the order of 3 × 10−3 cm−1 and accordingly its magnetic behaviour follows a Curie–Weiss law (Fig. S3†).Frozen solution continuous wave EPR spectra of 1 were recorded to get insights into its electronic properties and to determine with reasonable accuracy the magnitude of the dipolar qubit–qubit interaction. The spectrum shows an eight-fold hyperfine splitting due to the coupling between the s = 1/2 electronic spin of VIV and the I = 7/2 nuclear spin of 51V (natural abundance 99.76%). The signal is further split by the anisotropic components of the Landé factor and the hyperfine coupling. Furthermore, each hyperfine resonance line appears additionally split into two components (Fig. 3a), a phenomenon which can be attributed to the weak dipolar coupling between the VIV spins. Importantly, such a splitting is not observed in the spectrum of the reference compound 2.39
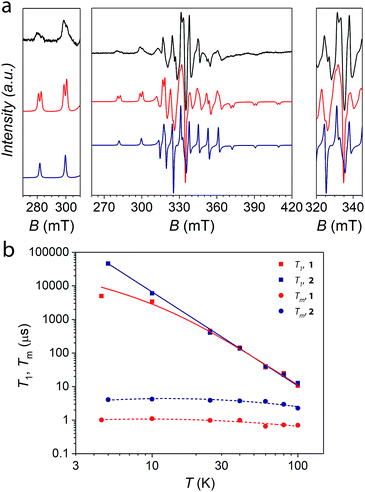 | ||
| Fig. 3 (a) Experimental frozen solution (0.75 mM in DMF) spectrum of 1 at T = 10 K and the X-band frequency (9.39 GHz) (black line). Spectral simulation assuming a dipolar magnetic interaction (red line) and comparison with the non-interacting case (blue line). Lateral panels are zooms over the regions of allowed parallel and perpendicular transitions from states characterized by |mI1, mI2〉 = |7/2, 7/2〉 and |5/2, 5/2〉. They are the relevant ones for our computational basis. (b) Temperature dependence of T1 and Tm for 1 and 2 at the X-band frequency in a frozen solution of DMSO and DMF, respectively. Solid lines are the best-fit of the model (see the ESI†). Dashed lines represent a guide for the eyes. Error bars are within the size of the symbols. | ||
Spectral simulations46 were performed on the basis of the following spin Hamiltonian‡ (for an easier discussion of quantum gates, vide infra, z has been chosen along the V⋯V direction and y as the principal axis of the single spin g and A anisotropy, i.e. along the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond):
O bond):
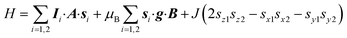 | (1) |
This allowed us to satisfactorily simulate the spectrum of 1 at both X-(Fig. 3a) and Q-band (Fig. S4†) frequencies by considering the two VIV ions as axially symmetric and equivalent and using the following parameters: gz = 1.982 ± 0.002, gx = 1.982 ± 0.002, gy = 1.941 ± 0.001, Az = 186 ± 2 MHz, Ax = 186 ± 2 MHz, Ay = 498 ± 4 MHz, and J = −(1.65 ± 0.10) × 10−3 cm−1. This gives the energy pattern reported in Fig. S5†, where the two MS = 0 states are largely overlapping. The principal values of Zeeman and hyperfine tensors are in the expected range for vanadyl paramagnetic centers.12–14 The value of the spin–spin interaction is consistent with a purely dipolar interaction for an interatomic V⋯V distance of 10.1 ± 0.2 Å, which is in agreement with expectations based on HYSCORE results and ligand connectivity. We also note that the through-space isotropic contribution arising from the anisotropy of the g tensors is calculated to be negligible and has no effect on the simulated spectrum.
Inversion recovery and echo decay experiments were performed at the X-band frequency to investigate the temperature dependence (4.5–100 K T range) of the spin-lattice relaxation time T1, and the coherence time Tm, respectively. The extracted values of T1 and Tm obtained from the fit of the inversion recovery and echo decay traces (Fig. S6†) are reported in Fig. 3b. T1 and Tm values for the single-qubit reference compound 2 are also reported for comparison. The coherence times of the order of 1 μs are detected for 1 up to 100 K. Although these values are reduced by a factor of ca. 4 with respect to the reference single-qubit system 2, they are comparable or slightly higher than those reported for molecular dimers based on either Cr7Ni rings21 or lanthanide complexes.23 The coherence time decrease from 4 μs to 1 μs in the two-qubit quantum gate 1 is not surprising given the presence of a proximal vanadium(IV) electronic magnetic moment and the nuclear-spin active (1H and 14N) richer molecular structure needed to link two spin centres. We note that observing such long coherence times for two electronic spins placed in close proximity is not commonplace. This result indicates that the molecular design of the qubits (the vanadyl moieties) and the qubit-linking system (the catecholate-based ligand) have played a crucial role here in preserving the long spin coherence. It should be also highlighted that coherence times are retained almost unchanged up to 100 K, a temperature which is an order of magnitude larger than that at which Tms are reported for state-of-the-art molecular quantum gate systems.21,23 The possibility to perform coherent spin manipulations in this system is also demonstrated by nutation experiments, performed at different microwave powers, up to 80 K at both X- and Q-bands (Fig. S7 and S8†).
The temperature dependence of T1 for 1 shows values that perfectly match those of the single-vanadyl-qubit reference system 2 for T > 30 K, thus suggesting that T1 in that temperature regime is mainly determined by structural parameters that are in common for the two systems, i.e. the first coordination sphere. For T < 30 K, the values of T1 for the two complexes show a divergence, being shorter for 1 than for 2. This behaviour can be related to a prevalent direct mechanism of relaxation for 1, rather than a Raman one that seems instead dominating for 2. Longer T1 at low temperatures for molecules with a smaller mass but the same magnetic core has been already observed in a recent comparative study of vanadyl catecholate derivatives and tentatively attributed to the higher energy of low frequency vibrational modes admixed to rigid rotations.39
Frequency dependent AC susceptibility measurements were performed on a concentrated sample of 1 as a function of both temperature and applied static magnetic field (Fig. S9 and S10†). As expected for S = 1/2 spin systems, slow relaxation is detected only under applied magnetic fields. The extracted relaxation times (τ) show a behaviour that is qualitatively similar to that of 2 (see Fig. S11† for a comparison). Faster relaxation at low temperature is observed for 1, in agreement with pulsed EPR findings.
Quantum gates
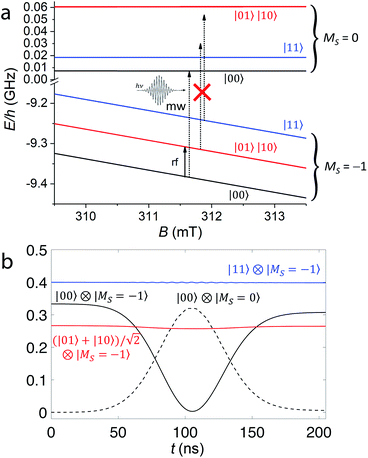
In the following, we illustrate how compound 1 can be used as an elementary unit for quantum information processing. Fig. 4a shows the lower part of the level diagram for 1 as a function of the external static magnetic field applied along the V⋯V axis z, while the full Zeeman diagram is available in Fig. S3.† For typical X or Q band EPR static fields, the electronic Zeeman interaction is the leading term in the Hamiltonian, while all the other terms act as perturbations. Indeed, the electronic Zeeman splitting separates the states into three groups, according to their total spin component along the direction of the field (MS). Qubits can be encoded into 4 of the (2I + 1)2 nuclear spin levels of the MS = −1 subspace, in which both electrons are in their ms = −1/2 state, i.e. |↓↓〉 (Fig. 4a). More specifically, the mI = 7/2 and 5/2 states of each V nucleus are used to encode the logical |0〉 and |1〉 states of the qubits. The gaps between the nuclear states of the computational basis (|00〉, |01〉, |10〉 and |11〉) are mainly induced by the hyperfine interaction and fall in the radiofrequency range. As long as the switch (the coupled electronic spins) is frozen into its MS = −1 subspace, the hyperfine interaction I·A·s is equivalent to a renormalization of the nuclear Zeeman term. Hence, the energy needed to rotate one of the nuclear spins does not depend on the state of the other, and the nuclear qubits can be considered effectively decoupled. Single-qubit gates can then be directly performed by means of rf pulses resonant with the |0〉 → |1〉 (|mI = 7/2〉 → |mI = 5/2〉) gap (Fig. 4a).§ In addition, Rz rotations can be directly implemented by exploiting 2π pulses semi-resonant with the |mI = 5/2〉 →|mI = 3/2〉 gap (see the ESI†).Conversely, entanglement between qubits can be generated with the controlled-phase shift (Cφ) two-qubit gate. The effect of this gate is to add a φ phase to the |00〉 component of the two-qubit wave-function and leave the other three components unaffected. In the following we will consider a particularly important Cφ gate obtained when φ = π, the CZ gate. This gate is able to generate maximally entangled states starting from a factorized wave-function. For instance, considering |ψ0〉 the initial factorized wave-function with both nuclear qubits in a superposition of |0〉 and |1〉 obtained by single-qubit rotations:
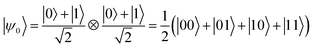 | (2) |
The effect of a CZ gate is to implement the transformation |ψ0〉 → |ψ1〉, with
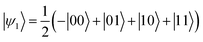 | (3) |
Clearly, |ψ1〉 cannot be written as the direct product of the separate states of the two qubits and it is a maximally entangled two-qubit state.
In the present molecular architecture, this gate can be implemented by targeting a specific EPR transition of the coupled electronic spins from the MS = −1 to the corresponding MS = 0 state. The hyperfine couplings make the energy required for such excitation dependent on the nuclear qubit state. Hence, applying a mw pulse resonant with the transition |00〉|MS = −1〉 → |00〉|MS = 0〉 and performing a full Rabi oscillation of the electronic spin, a π phase will be added only to the |00〉 component of the wave-function, thus implementing the CZ gate. Other components are unaffected because the corresponding transitions would occur at different frequencies, as schematically shown in Fig. 4a.
Numerical simulation
We have numerically simulated single- and two-qubit quantum gate operation through mw and rf Gaussian pulses, using the parameters determined from EPR measurements, with the same gz and Az for the two ions.¶ To gain more insight into the real feasibility of the gates, the effect of decoherence on the electron spin dynamics has been included by solving the master equation for the system density matrix in a Lindblad formalism40 (see the ESI†). We have used Tm = 1 μs, as determined by the pulsed-EPR measurements, and neglected nuclear dephasing and relaxation, which are expected to occur on a much longer timescale. Fig. 4b shows the resulting time evolution of the components of the wave-function on the computational basis states under the 2π mw pulse required to implement the CZ gate. In order to demonstrate the possible implementation of the gate independently from the initial state, we assumed to initialize the system in a superposition α|00〉 + β|01〉 + β|10〉 + γ|11〉. Fig. 4b shows that only the |00〉 component of the system wave-function is subject to a Rabi-flop with the corresponding excited MS = 0 state. The other components are practically unaffected by the pulse because they are off-resonance. This is exactly what is expected for the CZ gate. It is worth noting that the gate fidelity, i.e. the overlap between the ideal wave-function obtained with a perfect unitary gate and the actual result of the simulation, is high (97%) even with the inclusion of decoherence. In the present regime of parameters (with |Az| > |J|), the spectral resolution needed to implement a CZ gate results from the combined effect of hyperfine and spin–spin interactions (see the ESI† for details). In particular, the closest unwanted excitation is found at about 20 MHz, thus requiring the use of a rather long pulse (about 150 ns) to ensure spectral selectivity. This means that a slightly larger spin–spin interaction, i.e. a shorter distance, would enable a faster processing. However, the presented results do not rely critically on the actual Az and J values and on the precise form of the spin–spin interaction.Quantum simulation
These promising results allow us to devise sequences of gates in order to implement quantum simulation of interesting physical models. A quantum simulator is a device that, thanks to its intrinsically quantum nature, can efficiently mimic the time evolution of other quantum systems.47 In the present implementation, this device would consist of the two-nuclear-qubit vanadyl-based molecular architecture, i.e. the physical hardware, manipulated by mw and rf pulses. Since the hardware consists of effective spin-1/2 units (the |mI = 7/2〉, |mI = 5/2〉 states of the two nuclear qubits in our architecture), the target Hamiltonian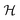 (whose dynamics we want to simulate) needs to be encoded into a spin-1/2 model
(whose dynamics we want to simulate) needs to be encoded into a spin-1/2 model 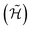 , expressed in the following in terms of Pauli matrices, σα. Then, the time evolution operator induced by
, expressed in the following in terms of Pauli matrices, σα. Then, the time evolution operator induced by 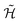 ,
,  , is divided into small time-steps, each implemented via a sequence of elementary gates (see ref. 48 and the ESI†). As a result, the physical hardware mimics the time evolution of the target, whose properties can then be extracted by the experimenter.48–50
, is divided into small time-steps, each implemented via a sequence of elementary gates (see ref. 48 and the ESI†). As a result, the physical hardware mimics the time evolution of the target, whose properties can then be extracted by the experimenter.48–50
As a possible proof-of-principle experiment with 1, we propose the quantum simulation of the time evolution of the magnetization of a spin S = 1 experiencing quantum tunneling. The target Hamiltonian reads
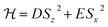 | (4) |
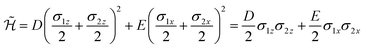 | (5) |
The corresponding time evolution operator  is the product of two unitary evolutions (e−iDσ1zσ2zt/2ℏ and e−iEσ1xσ2xt/2ℏ), each one corresponding to a sequence of single-qubit rotations and two-qubit Cφ gates, whose implementation is described in details in the ESI.†
is the product of two unitary evolutions (e−iDσ1zσ2zt/2ℏ and e−iEσ1xσ2xt/2ℏ), each one corresponding to a sequence of single-qubit rotations and two-qubit Cφ gates, whose implementation is described in details in the ESI.†
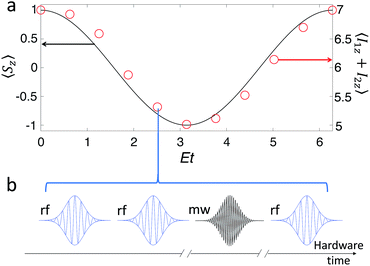
Fig. 5a reports the comparison between the time evolution of the S = 1 magnetization calculated exactly (line) and the one simulated assuming 1 as hardware (circles), for a state initialized in |00〉. As schematically depicted in Fig. 5b, at each simulation time t three single-qubit rotations on the nuclear qubits (obtained with rf pulses) and a two-qubit Cφ gate (implemented by a 2π mw pulse) are needed to simulate the evolution.|| For each point (red circle), corresponding to a different simulation time t, a Cφ gate with φ = Et is implemented. Finally, the total nuclear magnetization along the static field I1z + I2z is measured. Oscillations are reported as a function of the dimensionless parameter Et, since they occur on a timescale 2π/E. In our encoding there is a direct relationship between the magnetization Sz of the simulated system and the nuclear magnetization of our hardware that corresponds to Sz = I1z + I2z − 6. The output of the quantum simulation, i.e. the nuclear magnetization of our hardware (red circles referring to the right axis of Fig. 5a) as a function of the rescaled variable Et, well compares with the exact one (continuous line), obtained by computing the time evolution of Sz induced by (4).
The simulation was performed assuming a static field of 3.5 T, corresponding to an electronic resonance frequency of ca. 98 GHz (i.e. W-band EPR), since this improves the gate fidelity. The latter is important when several gates are concatenated. It must also be noted that at experimentally achievable temperatures for standard spectrometers (a few K) all the computational basis states are nearly equally populated, but initialization in a pure state (|00〉) could be achieved by electron-nuclear polarization transfer53 or heat-bath cooling techniques36 as explained with more details in the ESI.†
It is worth noting that our scheme is intrinsically robust against the electronic Tm. Indeed, the final average fidelity is very high (98%), even if the total time required for the simulation is 10–20 μs, much longer than Tm. In fact, the dephasing induced by the finite value of Tm affects the dynamics only during the implementation of fast (≤150 ns) two-qubit gates. Conversely, during slow single-qubit rotations (each lasting a few μs) the electronic part of the wave-function is factorized from the computational (nuclear) subspace, and hence does not affect its dynamics.
Comparing our prototypical simulator with a recent proposal also based on nuclear qubits and electronic spins,25 we note that a much simpler gate sequence, consisting of a fast two-qubit Cφ gate and a single-qubit rotation of the nuclei, is herein required in the simulation of the elementary using interaction (first term in eqn (5)) between nuclear qubits.
Conclusions
In conclusion, through a rational design that has started from the selection of single-qubit building blocks with long coherence times we have here realized a molecular platform to implement a new quantum simulation scheme. The proposal presented herein has several remarkable advantages to be highlighted: (i) at variance with purely electron spin-based schemes, qubits are isolated from environmental decoherence for most of the computational time; (ii) as opposite to typical NMR schemes, the interaction between pairs of qubits is not permanent, but can be rapidly switched on and off by uniform EPR pulses. This avoids unwanted two-qubit evolutions and simplifies sequences of pulses needed for quantum simulation; (iii) additional nuclear levels, that are not used to encode the qubits, can be exploited as additional resources for complex gate operations.54,55The necessary experimental set-up to implement such a computational scheme requires both mw and rf excitations, although it differs from ENDOR spectrometers in the detection mode, based here on the nuclear spins.
The operation of the platform as a quantum simulator would also benefit from some chemical improvements that appear within reach. First, the dilution in a solid diamagnetic matrix would allow an efficient addressing of the individual transitions. We have previously employed low-spin MoIV = O complexes as diamagnetic analogues of VIV = O systems whose stabilization will require a chemical modification of the catecholate ligands to dithiolene ones. An increase in the interaction between spin centers, reducing the length of the spacer, will also allow a better resolution of the individual electronic resonances exploitable in the computational scheme.
The present results highlight the great potential of molecular/coordination chemistry to provide a valuable contribution to quantum information technologies based on electronic and nuclear spins thanks to the intrinsic scalability of molecular architectures. We can indeed foresee further extensions of this approach to build more complex platforms, e.g. trimers or polynuclear assemblies, or even organize the molecular units in extended networks.
It is also clear from this study that synthetic efforts need to be accompanied by a theoretical modelling of the most promising computation platforms. This needs to be realized keeping under control key parameters, such as decoherence and magnetic interactions between metal centers, through a rational choice of the single-qubit building blocks and a careful design of the resulting polynuclear molecular architectures.
Experimental
General remarks
H4L (N,N′-bis(2,3-hydroxybenzoyl)-1,4-phenylenediamine) was synthesized by a slightly modified literature method.41 All other reagents were purchased from Sigma-Aldrich and used as received.Synthesis
![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) max/cm−1, KBr pellet): 3077vw, 3055w, 3023vw, 2994vw, 1644s, 1604w, 1585m, 1548w, 1513vs, 1483w, 1463m, 1456vs, 1405w, 1340w, 1309m, 1287w, 1251s, 1207s, 1164w, 1108s, 1058w, 995w, 960m, 930m, 839w, 787vw, 748m, 722s, 670s, 641m, 526vs, 472w. ESI-MS, m/z found (calcd): (negative ion mode) 521.21 (521.24) [Na4[(VO)2(L)2]·CH3OH]2−; 955.51 (955.52) [Na3[(VO)2(L)2]]−; (positive ion mode) 339.40 (339.39) [Ph4P+].
max/cm−1, KBr pellet): 3077vw, 3055w, 3023vw, 2994vw, 1644s, 1604w, 1585m, 1548w, 1513vs, 1483w, 1463m, 1456vs, 1405w, 1340w, 1309m, 1287w, 1251s, 1207s, 1164w, 1108s, 1058w, 995w, 960m, 930m, 839w, 787vw, 748m, 722s, 670s, 641m, 526vs, 472w. ESI-MS, m/z found (calcd): (negative ion mode) 521.21 (521.24) [Na4[(VO)2(L)2]·CH3OH]2−; 955.51 (955.52) [Na3[(VO)2(L)2]]−; (positive ion mode) 339.40 (339.39) [Ph4P+].
Characterization
1H NMR spectra were measured at 298 K on a Bruker Ultrashield Plus 400 MHz spectrometer. C, H, and N analyses were performed with a CHN–S Flash E1112 Thermo Finnigan analyzer. FT-IR spectra were obtained on KBr pellets and collected with a Shimadzu-8400S spectrophotometer. Electrospray Ionization Mass Spectrometry (ESI-MS) data were acquired on HPLC grade methanol by using a Thermo Scientific LCQ-Fleet mass spectrometer under electrospray ionization (Thermo Scientific, Austin TX, USA) by direct infusion with a 500 KL Hamilton microsyringe. Data were acquired over hundred scans after the stabilization of the ionic current for 5 min at a sample flow of 10 μl min−1. The mass spectrometer parameters used were: sheet gas flow = 10, auxiliary gas flow = 0, sweep gas flow = 0, spray voltage = 5.00 kV, capillary tube temperature = 220 °C, and capillary voltage = 12.0 V.Electron paramagnetic resonance
CW X-Band EPR spectra were recorded on a Bruker Elexsys E500 spectrometer equipped with a SHQ cavity (ν = 9.39 GHz). Low temperature measurements were obtained using an Oxford Instruments ESR900 continuous flow helium cryostat. Pulsed EPR measurements were carried out with a Bruker Elexsys E580 at X-band (ν ≅ 9.70 GHz) equipped with a flexline dielectric ring ENDOR resonator (Bruker EN 4118X-MD4). Temperatures between 4.5 and 100 K were obtained with an Oxford Instruments CF935 continuous flow helium cryostat. Echo detected field swept EPR spectra were recorded by using the Hahn Echo pulse sequence (π/2 − τ − π − τ − echo) with a fixed interpulse delay time τ = 200 ns, tπ/2 = 16 ns and tπ = 32 ns. Both phase memory times were measured by using the Hahn Echo sequence upon increasing the interpulse delay τ starting from τ = 98 ns. Spin-lattice relaxation times were measured using the standard inversion recovery sequence (π − td − π/2 − τ − π − τ − echo), with π/2 = 16 ns. The uncertainty in T1 estimated from replicate measurements was 5–10% depending upon the signal-to-noise ratio at a given temperature-field combination.HYSCORE spectroscopy
Six-pulse Hyperfine Sublevel Correlation experiments56,57 were carried out with the extended pulse sequence (π/2)x − τ1 − (π)x − τ1 − (π/2)y − t1 − (π)y − t2 − (π/2)y − τ2 − (π)y − τ2 − echo. An eight-step phase cycle was adopted in order to eliminate unwanted echoes. The t1 and t2 time intervals were incremented in steps of 16 ns, starting from 100 ns to 3300 ns. Pulse lengths tπ/2 = 16 ns and tπ = 32 ns, a 0.5 kHz shot repetition rate, and τ1 = τ2 = 110 ns were used. The time traces of the HYSCORE spectra were baseline corrected with a third-order polynomial, apodized with a Hamming window, and zero-filled. After two-dimensional Fourier transformation, the absolute-value spectra were calculated.DC and AC magnetic characterization
The DC (direct current) magnetic susceptibility measurements were performed with a Quantum Design Magnetic Property Measurement System (MPMS) SQUID magnetometer. The measurements were performed on a polycrystalline sample of 1 (4.3 mg) in the 2.0–300 K T range by applying a static magnetic field of 1.0 T for T > 20 K and 0.1 T for T < 20 K. AC susceptibility measurements were performed at T = 5 K with applied magnetic fields up to 8.5 T on a polycrystalline sample of compound 1 (49.4 mg) by using a Quantum Design Physical Property Measurement System (PPMS) equipped with a AC susceptometer operating in the 10 Hz to 10 kHz frequency range. Data were corrected for the sample holder previously measured using the same conditions and for the diamagnetic contributions as deduced by using Pascal's constant tables.58Conflicts of interest
There are no conflicts to declare.Acknowledgements
Italian MIUR, through the PRIN project QCNaMoS (2015-HYFSRT), and Fondazione Ente Cassa di Risparmio di Firenze are acknowledged for financial support. European COST Action CA15128 MOLSPIN is also acknowledged. We are indebted to Dr Marie-Emmanuelle Boulon (University of Florence) for her assistance in CW-EPR data collection and to Mr Lorenzo Tesi (University of Florence) for stimulating discussions.Notes and references
- M. Nielsen and I. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2004 Search PubMed.
- D. P. DiVincenzo, Science, 1995, 270, 255–261 CrossRef.
- T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O'Brien, Nature, 2010, 464, 45–53 CrossRef PubMed.
- J. Clarke and F. K. Wilhelm, Nature, 2008, 453, 1031–1042 CrossRef PubMed.
- S. Carretta, A. Chiesa, F. Troiani, D. Gerace, G. Amoretti and P. Santini, Phys. Rev. Lett., 2013, 111, 110501 CrossRef PubMed.
- E. Knill, R. Laflamme and G. J. A. Milburn, Nature, 2001, 409, 46–52 CrossRef PubMed.
- B. Hacker, S. Welte, G. Rempe and S. A. Ritter, Nature, 2016, 536, 193–196 CrossRef PubMed.
- G. Tosi, F. A. Mohiyaddin, V. Schmitt, S. Tenberg, R. Rahman, G. Klimeck and A. Morello, Nat. Commun., 2017, 8, 450 CrossRef PubMed.
- B. Pingault, J. N. Becker, C. H. H. Schulte, C. Arend, C. Hepp, T. Godde, A. I. Tartakovskii, M. Markham, C. Becher and M. Atatüre, Phys. Rev. Lett., 2014, 113, 263601 CrossRef PubMed.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef PubMed.
- K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626 RSC.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef PubMed.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2015, 7, 2074–2083 RSC.
- C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492 CrossRef PubMed.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef PubMed.
- G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Chem. Soc. Rev., 2013, 42, 1796–1806 RSC.
- A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, Npj Quantum Inf., 2015, 1, 15012 CrossRef.
- J. Ferrando-Soria, E. Moreno Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef PubMed.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, A. J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef PubMed.
- D. Aguila, L. A. Barrios, V. Velasco, O. Roubeau, A. Repolles, P. J. Alonso, J. Sese, S. J. Teat, F. Luis and G. Aromi, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef PubMed.
- S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. D. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, Angew. Chem., Int. Ed., 2012, 51, 9860–9864 CrossRef PubMed.
- S. Yamamoto, S. Nakazawa, K. Sugisaki, K. Sato, K. Toyota, D. Shiomi and T. Takui, Phys. Chem. Chem. Phys., 2015, 17, 2742–2749 RSC.
- J. A. Jones, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 59, 91–120 CrossRef PubMed.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef PubMed.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501 RSC.
- J. J. L. Morton, A. M. Tyryshkin, A. Ardavan, S. C. Benjamin, K. Porfyrakis, S. A. Lyon and G. A. D. Briggs, Nat. Phys., 2005, 2, 40 Search PubMed.
- Y. Zhang, C. A. Ryan, R. Laflamme and J. Baugh, Phys. Rev. Lett., 2011, 107, 170503 CrossRef PubMed.
- K. Sato, S. Nakazawa, R. Rahimi, T. Ise, S. Nishida, T. Yoshino, N. Mori, K. Toyota, D. Shiomi, Y. Yakiyama, Y. Morita, M. Kitagawa, K. Nakasuji, M. Nakahara, H. Hara, P. Carl, P. Hofer and T. Takui, J. Mater. Chem., 2009, 19, 3739–3754 RSC.
- R. R. Darabad, K. Sato, P. Carl, P. Höfer, R. Laflamme and T. Takui in Electron Spin Resonance (Esr) Based Quantum Computing, ed. T. Takui, L. Berliner and G. Hanson, Springer New York, New York, NY, 2016, pp. 25–50 Search PubMed.
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, F. A. Zwanenburg, D. N. Jamieson, A. S. Dzurak and A. Morello, Nature, 2013, 496, 334 CrossRef PubMed.
- M. Mehring and J. Mende, Phys. Rev. A, 2006, 73, 052303 CrossRef.
- J. S. Hodges, J. C. Yang, C. Ramanathan and D. G. Cory, Phys. Rev. A, 2008, 78, 010303 CrossRef.
- M. Mehring, J. Mende and W. Scherer, Phys. Rev. Lett., 2003, 90, 153001 CrossRef PubMed.
- D. K. Park, G. Feng, R. Rahimi, S. Labruyère, T. Shibata, S. Nakazawa, K. Sato, T. Takui, R. Laflamme and J. Baugh, Quantum Inf. Process., 2015, 14, 2435–2461 CrossRef.
- J. Zhang, D. Burgarth, R. Laflamme and D. Suter, Phys. Rev. A, 2015, 91, 012330 CrossRef.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731 CrossRef PubMed.
- H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, 2002 Search PubMed.
- M. J. Graham, C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 3196–3201 CrossRef PubMed.
- B. Kersting, M. Meyer, R. E. Powers and K. N. Raymond, J. Am. Chem. Soc., 1996, 118, 7221–7222 CrossRef.
- M. Meyer, B. Kersting, R. E. Powers and K. N. Raymond, Inorg. Chem., 1997, 36, 5179–5191 CrossRef.
- C. V. Grant, J. A. Ball, B. J. Hamstra, V. L. Pecoraro and R. D. Britt, J. Phys. Chem. B, 1998, 102, 8145–8150 CrossRef.
- B. Kirste and H. Van Willigen, J. Phys. Chem., 1982, 86, 2743–2749 CrossRef.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef PubMed.
- R. P. Feynman, Int. J. Theor. Phys., 1982, 21, 467–488 CrossRef.
- S. Lloyd, Science, 1996, 273, 1073–1078 CrossRef PubMed.
- I. Buluta and F. Nori, Science, 2009, 326, 108–111 CrossRef PubMed.
- I. M. Georgescu, S. Ashhab and F. Nori, Rev. Mod. Phys., 2014, 86, 153–185 CrossRef.
- P. Santini, S. Carretta, F. Troiani and G. Amoretti, Phys. Rev. Lett., 2011, 107, 230502 CrossRef PubMed.
- A. Chiesa, P. Santini, D. Gerace, J. Raftery, A. A. Houck and S. Carretta, Sci. Rep., 2015, 5, 16036 CrossRef PubMed.
- C. Tanmoy, Z. Jingfu and S. Dieter, New J. Phys., 2017, 19, 073030 CrossRef.
- M. D. Jenkins, Y. Duan, B. Diosdado, J. J. García-Ripoll, A. Gaita-Arino, A. C. Giménez-Saiz, P. J. Alonso, E. Coronado and F. Luis, Phys. Rev. B, 2017, 95, 064423 CrossRef.
- B. P. Lanyon, M. Barbieri, M. P. Almeida, T. Jennewein, T. C. Ralph, K. J. Resch, G. J. Pryde, J. L. O'Brien, A. Gilchrist and A. G. White, Nat. Phys., 2008, 5, 134–140 Search PubMed.
- R. Song, Y. C. Zhong, C. J. Noble, J. R. Pilbrow and D. R. Hutton, Chem. Phys. Lett., 1995, 237, 86–90 CrossRef.
- B. Kasumaj and S. Stoll, J. Magn. Reson., 2008, 190, 233–247 CrossRef PubMed.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional figures, tables, equations and computational details as mentioned in the text. See DOI: 10.1039/c8sc01695j |
‡ We neglected here the isotropic part of the dipolar interactions, since this is calculated to be negligible in the point dipole approximation when considering the estimated distance between the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O centers and the measured anisotropy of g. O centers and the measured anisotropy of g. |
| § Notice that the |0〉 → |1〉 (|mI = 7/2〉 → |mI = 5/2〉) transition is made distinguishable from other |mI〉 → |mI ± 1〉 transitions by second order shifts due to virtual hyperfine-induced excitations, as well as by nuclear quadrupole coupling PI2z typical of penta-coordinated vanadyl ions (ca. −0.9 MHz).33 It is worth stressing that the precise value of P does not affect the feasibility of the proposed quantum gates. |
| ¶ We need J ≫ ΔgzμBB, ΔAzmI to induce a collective excitation of the two electronic spins. |
| || For the system initialized in |00〉, gates corresponding to the evolution e−iDσ1zσ2zt/2ℏ do not affect the dynamics. |
| This journal is © The Royal Society of Chemistry 2018 |