Open Access Article
Open Access ArticleNew strategy for designing promising mid-infrared nonlinear optical materials: narrowing the band gap for large nonlinear optical efficiencies and reducing the thermal effect for a high laser-induced damage threshold†
Shu-Fang
Li
a,
Xiao-Ming
Jiang
*a,
Yu-Hang
Fan
b,
Bin-Wen
Liu
a,
Hui-Yi
Zeng
a and
Guo-Cong
Guo
 *a
*a
aState Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, P. R. China. E-mail: gcguo@fjirsm.ac.cn; xmjiang@fjirsm.ac.cn
bSchool of Chemistry and Chemical Engineering, Yangtze Normal University, P. R. China
First published on 16th May 2018
Abstract
To circumvent the incompatibility between large nonlinear optical (NLO) efficiencies and high laser-induced damage thresholds (LIDTs) in mid-infrared NLO materials, a new strategy for designing materials with both excellent properties is proposed. This strategy involves narrowing the band gap for large NLO efficiencies and reducing the thermal effect for a high LIDT. To support these proposals, a series of isostructural chalcogenides with various tetrahedral center cations, Na2Ga2MQ6 (M = Ge, Sn; Q = S, Se), were synthesized and studied in detail. Compared with the benchmark AGS, these chalcogenides exhibit significantly narrower band gaps (1.56–1.73 eV, AGS: 2.62 eV) and high NLO efficiencies (1.6–3.9 times that of AGS at 1910 nm), and also outstanding LIDTs of 8.5–13.3 × those of AGS for potential high-power applications, which are contrary to the conventional band gap view but can be attributed to their small thermal expansion anisotropy, surmounting the NLO–LIDT incompatibility. These results shed light on the search for practical IR NLO materials with excellent performance not restricted by NLO–LIDT incompatibility.
Introduction
Nonlinear optical (NLO) materials are at the front-line of research in laser science and technology because of their ability to produce coherent and tunable light from solid-state lasers in the medical, military and communication network fields.1–4 For decades, various NLO materials such as β-BaB2O4 (BBO),5 LiB3O5 (LBO),6 KH2PO4 (KDP),7 KBe2B2O6F2 (KBBF),8 and KTiOPO4 (KTP)9 have been discovered and used commercially. Although these materials are applicable to generating coherent light in the ultraviolet region to the near-infrared (IR) region, direct generation of mid-IR (2–20 μm) coherent light by second harmonic generation (SHG) remains particularly challenging, but is crucial to various communication and optoelectronic devices.10 For decades, numerous mid-IR NLO materials with obvious SHG responses, mainly including pnictides, chalcogenides, and halogenides, have been reported.11,12 However, only a few of them, namely, AgGaS2 (AGS),13,14 AgGaSe2 (AGSe),15,16 and ZnGeP2 (ZGP),17 can be used. Unfortunately, these materials suffer from drawbacks such as low laser-induced damage thresholds (LIDTs) that hinder their high-power applications.11 Therefore, developing new mid-IR NLO materials with excellent comprehensive performance (large NLO efficiencies, high LIDT, a wide transparency window, and sufficient birefringence to achieve phase matchability)18 is technologically and scientifically important.Among all the requirements for high-power applications, large NLO efficiencies and high LIDTs are the most challenging to achieve concurrently. Previous theoretical and experimental studies on IR NLO materials show that a wider band gap is beneficial for a high LIDT,1,19,20 while also resulting in a small NLO efficiency, which implies an incompatibility between large NLO efficiencies and high LIDTs. Two main methods have been adopted to balance this conflict. One is increasing the band gap by replacing Ag+ in the classical IA–IIIA–VIA2 type of IR NLO material with a strongly electropositive alkali or alkaline-earth metal. Thus, the LiBQ2 (B = Ga, In; Q = S, Se, Te) family and BaGa4S7 were discovered,21–25 with their band gaps of up to 4 eV leading to LIDTs exceeding those of the Ag analogs, while their NLO efficiencies were slightly lower. For example, the band gap of LiGaS2 is 3.65 eV, which is significantly larger than that of AGS (2.62 eV);26 nevertheless, the SHG coefficient of LiGaS2 is approximately a quarter of that of AGS.27 The other method involves combining two or more NLO-active motifs such as GaQ4, InQ4, GeQ4, or SiQ4 (Q = S, Se) tetrahedra in a single IR NLO chalcogenide compound to modulate the LIDT and NLO efficiency.28–44 The combination of different NLO-active motifs can optimize the NLO efficiency and LIDT effectively. For example, by incorporating GeS2 into AgGaS2, quaternary AgGaGeS4 was developed with an improved LIDT, which makes it a promising alternative to the widely used AGS.45–47 Additionally, a series of Li-containing quaternary compounds have been reported, including Li2Ga2GeS6, LiGaGe2Se6, Li2In2GeSe6, and Li2In2SiSe6; the combination of different microscopic NLO-active units, namely, GaQ4, InQ4, GeQ4 and SiQ4, in these compounds strengthens their nonlinear susceptibilities compared with those of the corresponding ternary compounds.21,48,49 Although there have been many attempts using these two main methods, excellent IR NLO materials with both a high LIDT and high NLO efficiency are rare.
Theoretically, SHG is a two-photon process, and the value for NLO efficiency is determined by the optical transition matrix elements, which strongly depend on the band gap of an IR NLO material.50 Normally, a small band gap can easily result in a strong optical transition and is therefore beneficial for a large NLO efficiency. Compared with SHG, laser damage on NLO crystals is a highly complicated process that involves pitting, erosion, melting, delamination, fracture, and discoloration.51 The mechanisms of the laser damage process can be mainly categorized into thermal processes and dielectric processes. For NLO crystals with high laser transparency and few defects for optical absorption, the dielectric process mechanism is applied, and the dielectric LIDT is proportional to the atomic density/(n2 − 1), where n is refractivity and has large values for materials with narrow band gaps. Therefore, narrow band gaps simultaneously lead to large NLO efficiencies and low LIDTs. This result is also the reason for the so-called incompatibility between a large NLO efficiency and a high LIDT in some NLO compound systems, such as the well-known oxides and the IA–IIIA–VIA2 type of IR NLO material.7
However, for many practical mid-IR NLO materials, intrinsic and defect-induced optical absorptions are non-negligible, which may lead to a temperature increase when the laser beam is incident on the surface of an NLO crystal, thereby resulting in thermal expansion, strain, distortion, cracking, catastrophic shattering and so on. Under these conditions, the thermal process mechanism can be applied;51 the corresponding thermal LIDTs scale proportionally to CκS/αβ, where C is the heat capacity of the material, for which values can seem close together for any solids with similar atomic densities above room temperature, κ is the thermal conductivity, S is the damaging stress and is positively correlated with the Young’s modulus and shear modulus of the material, β is the expansion coefficient and α is the absorption coefficient. These results show that the LIDT can be enhanced by reducing the thermal effects, i.e., by increasing the thermal conductivity and damaging stress, and decreasing the expansion and absorption coefficients of IR NLO materials.
The intrinsic physical parameters of NLO crystals, the thermal conductivity, damaging stress, and absorption coefficients, strongly depend on the microscopic structural features of crystals, such as the number and size of localized absorbing defects and impurities.52–54 Nevertheless, the expansion coefficient of a particular type of NLO crystal does not change significantly under different crystal growing conditions. Therefore, from the perspective of the crystal structure design of mid-IR NLO materials, the parameter of expansion coefficient may be modulated in a relatively easy manner to enhance the LIDT. The expansion coefficient of a compound depends on the expansion coefficients (dR/dT) of all its chemical bonds, which can be evaluated through dR/dT = 1.35 k/G based on the bond-valence theory,55 where k is the Boltzmann constant and G is the force constant of the chemical bonds. Normally, for the same type of chemical bond, G is larger for shorter bond lengths. However, for the same types of center and coordinated ion, according to the bond-valence-sum rule, center ions that have fewer coordinated atoms are likely to have shorter bond lengths and larger force constants. In such circumstances, relatively smaller thermal expansion coefficients and higher LIDT values can be predicted.
For the case in which a thermal LIDT dominates the laser-induced damage process in the practical application of mid-IR NLO materials, the NLO efficiency and LIDT are relatively independent of each other, and almost no incompatibility exists between them. We propose a new strategy for designing IR NLO materials by narrowing the band gap for a large NLO efficiency and reducing the thermal effect for a high laser-induced damage threshold. This approach is effective in achieving high NLO efficiency and a high LIDT concurrently.
Recently, metal chalcogenides have been found to be highly attractive for the exploration of new mid-IR NLO materials. Some alkali-metal-containing quaternary chalcogenides were reported to exhibit large NLO efficiencies, such as K4GeP4Se12,56 Na2Ge2Se5,57 K3TaAsS11,10 and CsZrPSe6,58 which possess NLO coefficients of 14.02, 12.01, 9.91, and 9.92 times that of AGS, respectively. Highly electropositive alkali metals in these chalcogenides usually play the role of dimensional reduction agents to reduce the coordinated atoms of the host chalcogenide frameworks. Based on the preceding analysis, besides having high NLO efficiencies, alkali-metal-containing chalcogenides may exhibit high LIDTs due to the strengthening of their force constants and the reduction in the thermal expansion coefficients of the metal–chalcogen bonds.
To verify our new strategy, we synthesized four new compounds in the alkali metal sodium-containing chalcogenides, namely, Na2Ga2GeSSe5 (1), Na2Ga2GeSe6 (2), Na2Ga2SnSSe5 (3), and Na2Ga2SnSe6 (4). All these materials exhibit phase-matching behavior with a large NLO efficiency of 1.6–3.9 × that of AGS. Their band gaps are obviously narrower than those of AGS, which should result in relatively smaller LIDTs based on the conventional view. However, the four compounds exhibit extremely large LIDTs of 8.5–13.3 × that of AGS, which can be attributed to their small thermal expansion anisotropy compared to that of AGS. In the following section, we report the synthesis and characterization and the optical and thermal properties of these compounds. Theoretical calculation of the electronic band structures and NLO efficiencies was also conducted for these compounds.
Experimental section
Synthesis
The following chemicals were used in this study: Na (99.7%), Ga (99.99%), Ge (99.99%), Sn (99.9%), S (99.5%), and Se (99.9%). All of these chemicals were from Aladdin Chemistry Co. Ltd. and were used as received without further purification. The Na2S and Na2Se starting materials were prepared through stoichiometric reaction of Na and S or Se in liquid ammonia.30 For the synthesis of the target compounds, a stoichiometric mixture of the starting materials Na2S, Ga, Ge (Sn), and Se in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 for 1 and 3, and Na2Se, Ga, Ge (Sn), and Se in a molar ratio of 1
5 for 1 and 3, and Na2Se, Ga, Ge (Sn), and Se in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 for 2 and 4, were loaded into a graphite crucible and placed in quartz tubes. The tubes were flame-sealed under vacuum (∼10−4 Torr) and then placed in a temperature-controlled muffle furnace, heated from room temperature to 800 °C in 40 h, kept at that temperature for 96 h, and then cooled to room temperature at 4 °C per hour. The products were washed with degassed DMF and dried with ethanol. Yellow crystals of 1 and 2, orange crystals of 3, and red crystals of 4, with the respective yields of 60%, 60%, 70%, and 50% based on Ga for 1–4, were obtained. All the compounds were stable in air and water.
6 for 2 and 4, were loaded into a graphite crucible and placed in quartz tubes. The tubes were flame-sealed under vacuum (∼10−4 Torr) and then placed in a temperature-controlled muffle furnace, heated from room temperature to 800 °C in 40 h, kept at that temperature for 96 h, and then cooled to room temperature at 4 °C per hour. The products were washed with degassed DMF and dried with ethanol. Yellow crystals of 1 and 2, orange crystals of 3, and red crystals of 4, with the respective yields of 60%, 60%, 70%, and 50% based on Ga for 1–4, were obtained. All the compounds were stable in air and water.
Single-crystal structure determination
Block single crystals of 1–4 were selected for single-crystal diffraction. Diffraction data were collected using graphite monochromated Mo Kα radiation (λ = 0.71073 Å) on a Rigaku Pilatus CCD diffractometer at 293 K. The intensity data sets were collected with a ω-scan technique and reduced using CrystalClear software.59The structures of 1–4 were solved by direct methods and refined using the full-matrix least-squares method on F2 with anisotropic thermal parameters for all the atoms. All the calculations were performed with a SHELXL package of crystallographic software.60 The formulas collectively consider the crystallographically refined compositions and requirements of charge neutrality. The Addsym/Platon program was used to check the final structures for additional symmetry, and no other missed or higher symmetry element was found.61 The crystal data and structural refinement information for 1–4 are summarized in Table 1. The atomic coordinates and equivalent isotropic displacement parameters are listed in Table S1.† Selected bond distances are reported in Table S2.†
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| Chemical formula | Na2Ga2GeSSe5 | Na2Ga2GeSe6 | Na2Ga2SnSSe5 | Na2Ga2SnSe6 |
| Formula weight | 684.87 | 731.77 | 730.97 | 777.87 |
| Crystal size (mm3) | 0.117 × 0.115 × 0.106 | 0.110 × 0.105 × 0.102 | 0.117 × 0.083 × 0.066 | 0.071 × 0.063 × 0.046 |
| Crystal system | Orthorhombic | |||
| Space group | Fdd2 | |||
| a (Å) | 12.987(10) | 12.985(4) | 13.264(4) | 13.329(3) |
| b (Å) | 23.653(17) | 23.880(8) | 23.936(7) | 24.291(7) |
| c (Å) | 7.519(5) | 7.585(3) | 7.514(2) | 7.621(2) |
| V (Å3) | 2310(3) | 2352.0(14) | 2385.6(12) | 2467.5(11) |
| Z | 8 | 8 | 8 | 8 |
| D calcd (g cm−3) | 3.939 | 4.133 | 4.070 | 4.188 |
| μ (mm−1) | 23.170 | 25.671 | 22.007 | 24.058 |
| θ Range (°) | 3.25–25.46 | 3.23–25.46 | 3.40–25.46 | 3.19–25.47 |
| GOF on F2 | 1.049 | 0.977 | 1.114 | 1.101 |
| R 1 a [I > 2σ (I)] | 0.0375 | 0.0238 | 0.0257 | 0.0209 |
| wR2b [I > 2σ (I)] | 0.0990 | 0.0486 | 0.0661 | 0.0549 |
| R 1 a (all data) | 0.0389 | 0.0285 | 0.0270 | 0.0218 |
| wR2b (all data) | 0.1009 | 0.0496 | 0.0668 | 0.0551 |
| Flack parameter x | 0.00 | 0.00 | 0.00 | 0.00 |
| Δρmax/Δρmin (e Å−3) | 1.288/−0.991 | 0.538/−0.986 | 0.662/−0.768 | 0.852/−0.528 |
Powder X-ray diffraction
Powder X-ray diffraction (PXRD) measurements were performed on a Rigaku MiniFlex II diffractometer using Cu Kα radiation in reflection mode at room temperature with a step size of 0.02° in the range 2θ = 5–65°. The experimental and simulated PXRD patterns of 1–4 are shown in Fig. S2,† indicating the purity of the as-synthesized samples, despite the possible existence of a tiny amount of NaGa3Se5 in phase 2.Energy-dispersive X-ray spectroscopy analysis
Semiquantitative microprobe element analyses of crystals of the four compounds were performed with a field emission scanning electron microscope (FESEM, JSM6700F) equipped with an energy-dispersive X-ray spectroscopy instrument (EDX, Oxford INCA). The empirical formulas Na2.3Ga2.1Ge1.0S0.8Se5.1 for 1, Na1.9Ga2.3Ge1.0Se5.8 for 2, Na2.2Ga2.3Sn1.0S1.0Se5.1 for 3, and Na1.8Ga2.0Sn1.0Se6.1 for 4 were obtained, and no other element was detected (Fig. S1†), which was consistent with the results determined from single-crystal XRD.SHG measurements
The SHG measurements of 1–4 were taken using a modified Kurtz–Perry powder technique with 1910 nm laser radiation.62 Microcrystalline powder samples were ground and sieved into several distinct particle size ranges (30–50, 50–75, 75–100, 100–125, 125–150, and 150–200 μm) for the SHG phase-matching measurements. AGS crystals with similar particle sizes were used as references. During measurement, all of the samples were pressed between two glass microscope cover slides and secured in the 1 mm-thick plastic holders. After the mixed signals passed through the monochromator, the doubled frequency signals (955 nm) were detected by an Andor DU420A-BR-DD CCD.Powder LIDT measurements
The powder LIDTs of 1–4 and the reference AGS were evaluated using the single-pulse measurement method using a focused high-power 1064 nm laser beam with a pulse width (τp) of 10 ns and a repetition rate of 1 Hz.63 The measurements were conducted by gradually increasing the laser power until a damaged spot on the samples was observed under the microscope after irradiation. The Nova II sensor with a PE50-DIF-C energy sensor and a vernier caliper were respectively used to measure the power of the laser beam and to identify the damaged spots.Thermal analyses
The thermal properties of 1–4 were investigated using differential scanning calorimetry (DSC) analysis using a Netzsch STA 449C thermal analyzer under a nitrogen atmosphere. Each sample of approximately 10 mg was placed in a sealed silica tube evacuated to 10−4 Torr, heated to 900 °C at 10 °C min−1 and cooled to 30 °C at 10 °C min−1.Electronic structure calculations
Electronic band structures and densities of states (DOS) of 1–4 were calculated using the structure models obtained directly from single-crystal XRD analysis, which were calculated based on density functional theory (DFT) with CASTEP code provided by a Materials Studio package.64,65 The electrons in Na: 2s22p63s1, Ga: 3d104s24p1, Ge: 4s24p2, Sn: 5s25p2, S: 3s23p4 and Se: 4s24p4 were treated as valence electrons. The plane-wave cutoff energy was set to 800 eV for 1–4. Moreover, the numerical integration of the Brillouin zone was performed using 2 × 1 × 3 Monkhorst–Pack k-point meshes for all the compounds. The Fermi level (Ef = 0 eV) was selected as a reference.Theoretical calculations on the optical properties regarding the complex dielectric function ε(ω) = ε1(ω) + iε2(ω) were carried out as follows:66,67
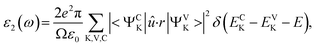 | (1) |
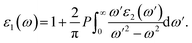 | (2) |
The P before the integral indicates the principal value. The first-order nonresonant susceptibility at the low-frequency region is given by χ(1)(ω) = ε1(ω) − 1, and the second-order susceptibilities were calculated using the anharmonic oscillator model.50
Results and discussion
Crystal structure
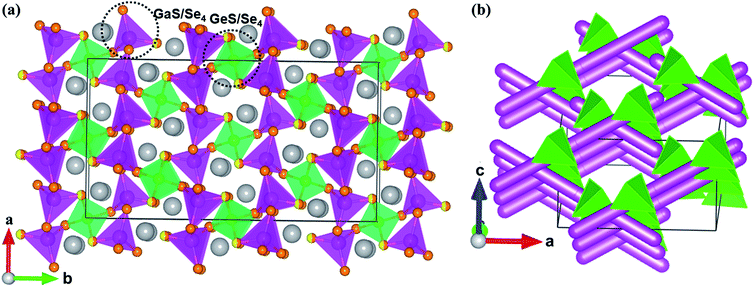
Compounds 1–4 are isostructural and crystallize in the NCS space group Fdd2 in the orthorhombic system with the unit cell parameters a = 12.432(4)–13.329(3) Å, b = 22.584(7)–24.291(7) Å, c = 7.239(2)–7.261(2) Å, and Z = 8. In the asymmetric unit, two crystallographically independent positions are observed for Ga, Ge, or mixed Ga/Sn atoms; three positions for fully occupied S, Se, or mixed S/Se atoms; and one position for Na.In compound 1, the 3D framework consists of two different building blocks, namely, 1D infinite ∞1[Ga(S/Se)Se2)]3− chains (pink tetrahedral chains in Fig. 1a) and isolated [Ge(S/Se)2Se2]4− tetrahedra (green tetrahedra in Fig. 1a). Each Ga atom is coordinated by one mixed S/Se and three Se atoms forming the [Ga(S/Se)Se3)]5− tetrahedra with Ga–S/Se distances ranging from 2.359 Å to 2.406 Å, which then connect with each other by sharing common S/Se atoms to form infinite linear ∞1[Ga(S/Se)Se2)]3− chains. Similar to the Ga atoms, each Ge atom is tetrahedrally coordinated by two mixed S/Se and two Se atoms to form the [Ge(S/Se)2Se2]4− tetrahedra with Ge–S/Se distances ranging from 2.352 Å to 2.374 Å. These two different building blocks, namely, the infinite ∞1[Ga(S/Se)Se2)]3− chains and the isolated [Ge(S/Se)2Se2]4− tetrahedra, are assembled to form the 3D anionic (Ga2GeSSe5)2− framework of 1 (Fig. 1b). Two groups of ∞1[Ga(S/Se)Se2)]3− chains along the a + c and a − c directions intersect each other with [Ge(S/Se)2Se2]4− tetrahedra acting as the connections between them and forming tunnels along the c direction, which are embedded with the Na+ counter cations.
All positions in 2 are fully occupied. In compound 3, besides the S/Se mixing, the Ga and Sn positions are mixed with the molar ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The Sn positions in 4, similar to the Ge positions in 1, are mixed with Ga with half occupancy. The mixed occupancy of the S/Se and Ga/Sn positions is determined by the structural refinements that consider charge balance. The Ga–S(Se), Ge–S(Se), (Ga/Sn)–S, and Na–S(Se) bond lengths in 1–4 (Table S2†) are close to those in BaGa4S7,25 BaGa2GeS6,36 Ba2Ga8GeS16,41 PbGa2GeSe6,18 Na4MgGeSe6,68 Ba5Ga2Se8,69 KCd4Ga5Se12,70 Na3Mo15Se19,71 and Na4Sn3S8.72
1. The Sn positions in 4, similar to the Ge positions in 1, are mixed with Ga with half occupancy. The mixed occupancy of the S/Se and Ga/Sn positions is determined by the structural refinements that consider charge balance. The Ga–S(Se), Ge–S(Se), (Ga/Sn)–S, and Na–S(Se) bond lengths in 1–4 (Table S2†) are close to those in BaGa4S7,25 BaGa2GeS6,36 Ba2Ga8GeS16,41 PbGa2GeSe6,18 Na4MgGeSe6,68 Ba5Ga2Se8,69 KCd4Ga5Se12,70 Na3Mo15Se19,71 and Na4Sn3S8.72
Interestingly, modifying the chalcogen ratio and mutual replacement of Ga, Ge, and Sn atoms does not lead to structural changes in the Na2Ga2MQ6 (M = Ge, Sn; Q = S, Se) system. Structure retention such as this is important when conducting chalcogen or metal doping to optimize the physical performance of these materials, similar to the case with nonlinear optical materials.73
NLO properties
The SHG of 1–4 was investigated using a 1910 nm laser and AGS as the reference. The SHG signals of 1–4 as a function of particle size are shown in Fig. 2. Their SHG intensities increase with the growth in particle size. These results are consistent with type-I phase-matching behavior, which is important in practical applications. Remarkably, the SHG intensities of 1–4 are about 2.3, 1.6, 3.9, and 2.1 times that of commercial AGS with the particle size from 75–100 μm (Fig. 2b). Generally, the SHG signal intensity measured by the Kurtz–Perry powder method is proportional to the square of the second-order NLO coefficient deff, and the reported deff of AGS is 12.5 pm V−1.26 Thus, the derived deff values for 1–4 are 18.95, 15.81, 24.68, and 18.11 pm V−1.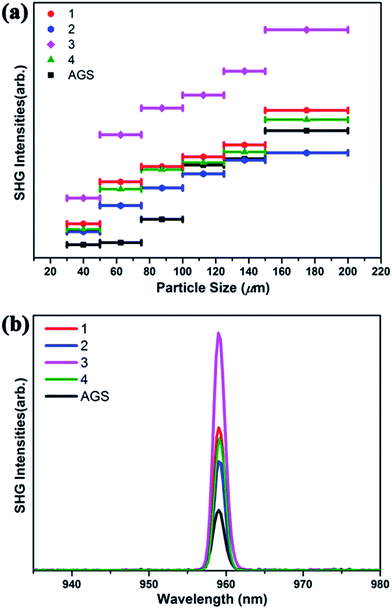 | ||
| Fig. 2 (a) Phase-matching curves of 1–4 and the reference AGS. (b) SHG intensities of 1–4 with AGS as the reference in the particle size range 75–100 μm. | ||
Interestingly, compound 3 Na2Ga2SnSSe5 has the highest SHG intensity among these compounds, whereas compound 2 has the lowest. This result is reasonable according to the structural analysis. Both S/Se and Ga/Sn occupancy disorders are observed in 3, which can lead to structural distortion and the enhancement of noncentrality and SHG intensity, compared to that in the corresponding perfect structure. Moreover, the cation size effect may also have an effect on the formation of these compounds and ultimately their NLO properties.74,75
In contrast, no mixing position can be observed in 2, and no additional SHG enhancement from the structural distortion is present. In the case of 1 and 4, either S/Se (1) or Ga/Sn (4) is present in their structures, and their SHG intensities are between those of 2 and 3. Given the structure retention of the Na2Ga2MQ6 (M = Ge, Sn; Q = S, Se) system under chalcogen and metal variation, new compounds with SHG intensity even higher than that of 3 could be obtained by chalcogen and metal variation.
The IR transmission spectra show that compounds 1–4 have no obvious intrinsic absorption from chemical bonds in a broad spectral range from 0.25 to 25 μm (Fig. S3†), indicating that compounds 1–4 may be good candidates for a variety of NLO applications in the mid- and far-IR regions. The optical diffuse reflectance spectra indicate optical band gaps (Eg) of 1.56, 1.61, 1.63 and 1.73 eV for 1–4 (Fig. S4†), which are significantly smaller than that of AGS (2.65 eV).1 The NLO efficiency is positively associated with the band gap, and the band gaps of 1–4 being narrower than that of AGS is consistent with their NLO efficiencies being larger than that of AGS. The band-gap order Eg(1) < Eg(2) < Eg(3) < Eg(4) is not in accordance with the opposite of the NLO efficiency order deff(2) < deff(4) < deff(1) < deff(3), which can be attributed to the role of structure distortion induced by atom mixing. Overall, narrowing the band gap of an NLO material is an effective way to achieve a large NLO efficiency.
Powder LIDTs
The powder LIDTs of 1–4 and the benchmark AGS measured by the single pulse method are summarized in Table 2. For measurement, small spot areas with the sizes 0.1590, 0.1662, 0.2463 and 0.1963 cm2 were selected for 1–4, respectively. The measured damage energies of 1–4 (20.07–27.99 mJ) were much higher than that of AGS (11.02 mJ). The derived powder LIDTs of 1–4 were 9.9, 13.3, 8.5, and 10.1 times that of AGS, supporting their potential for high-power applications. In this study, the experimental LIDT of the benchmark AGS was 1.27 MW per cm−2, which is close to reported values.18 According to the conventional view of the incompatibility between a large NLO efficiency and a high LIDT for NLO materials, compounds 1–4 with band gaps significantly narrower than that of AGS should have a smaller LIDT.| Compound | Damage energy (mJ) | Spot area (cm2) | Damage threshold [MW cm−2] |
|---|---|---|---|
| 1 | 20.07 | 0.1590 | 12.62 |
| 2 | 27.99 | 0.1662 | 16.84 |
| 3 | 26.59 | 0.2463 | 10.79 |
| 4 | 25.19 | 0.1963 | 12.82 |
| AGS | 11.02 | 0.8659 | 1.27 |
However, the experimental LIDT values for 1–4 are much higher than that of AGS, and there should be other factors that dominate the LIDT of 1–4, rather than the band gap, although the LIDT order LIDT (3) < LIDT (1) < LIDT (4) < LIDT (2) is in accordance with the opposite of the NLO efficiency order deff(2) < deff(4) < deff(1) < deff(3). This issue is discussed in the following section.
Thermal properties
Thermal effects are non-negligible in the practical application of mid-IR NLO materials; the large temperature increase caused by optical absorptions leads to thermal expansion, strain, distortion, cracking, catastrophic shattering, and damage of crystals.51 The thermal expansion anisotropy (TEA, δ) of NLO materials is identified as one of the most important intrinsic parameters to influence the ultimate experimentally derived LIDTs. NLO materials with smaller TEAs tend to sustain a larger thermal shock under laser irradiation and exhibit higher LIDTs. To study the TEA of 1–4 and the reference AGS, the temperature dependence of the lattice parameters was measured using an X-ray diffractometer from 300 K to 500 K with a step of ∼20 K (Fig. S6†). The thermal expansion coefficients (TECs, αL = R0−1[dR(T)/dT], where R0 is the value at T = 0 K) of the lattice parameters (a, b and c are the axis lengths) of 1–4 were derived. The TEA (δ) values, defined as the ratio of the maximum and minimum of the TEC, are 1.59, 1.49, 2.01 and 1.51 for 1–4 (Table 3). The TEC and TEA of AGS have been measured in our previous work76 and are close to other reported values.77| 1 | 2 | 3 | 4 | AGS | |
|---|---|---|---|---|---|
| a | 5.58 | 5.86 | −5.46 | 3.68 | 3.08 |
| b | −5.54 | 6.85 | −2.71 | −4.09 | 3.08 |
| c | −8.81 | −8.75 | 2.99 | 5.52 | −9.158 |
| δ | 1.59 | 1.49 | 2.01 | 1.51 | 2.97 |
The measured TEA order δ(AGS) > δ(3) > δ(1) > δ(4) > δ(2) is in accordance with the experimental LIDTs, which have the opposite order. According to the structural analysis of the four compounds, atom mixing occurs in all the structures except 2, where the structural defects are indispensable, as are the defect-induced optical absorptions during measurement. The TEA is proposed to be the dominant factor in the LIDTs of the Na2Ga2MQ6 (M = Ge, Sn; Q = S, Se) system, as supported by the experimental results. Reducing the thermal effect, especially by decreasing the thermal expansion anisotropy of an NLO material, is reasonable for achieving a high LIDT. The TEA and LIDT values of some typical IR NLO crystals, LiInS2, ZnGeP2, GaSe and AgGaSe2 have been listed in Table S3.† The TEAs of ZnGeP2 and GaSe are close to each other, resulting in them having similar LIDTs. The TEA of LiInS2 is much larger than that of AGS. However, its LIDT is also much larger than that of AGS, which can be ascribed to the shorter pulse width used for the LIDT measurement of LiInS2.
The DSC results in Fig. S5† show that compounds 1–4 undergo congruent melting upon heating and crystallization upon cooling with relatively low melting temperatures (606, 571, 659, and 689 °C for 1–4). In comparison, the melting points of the known IR NLO materials, such as AGS (998 °C), LiGaS2 (1050 °C), LiGaSe2 (915 °C), BaGa4S7 (1090 °C), and BaGa4Se7 (968 °C)40 are significantly higher. These results reveal that large crystals of 1–4 can be grown using the Bridgman method at lower temperatures.
Theoretical calculations
The theoretical band gaps of 1–4 were calculated to be 2.01, 2.02, 2.00, and 1.95 eV, (Fig. S7†). Compared with the experimental results, the calculated band gaps of 1–4 have certain deviations due to the limitations of the DFT method in semiconductors and insulators.78,79 As observed from the partial DOS presented in Fig. S8,† for all four compounds, the valence band close to the Fermi level originates predominantly from Se-4p and S-3p states for 1 and 3 and Se-4p for 2 and 4. The conduction bands (CB) of 1–4 close to the bottom of the CB are mostly composed of Ga-4p, Ge-4p and Se-4p states in 1, Ge-4p and Se-4s states in 2, and Sn-5p and Se-4s states in 3 and 4. Therefore, their optical absorptions can be mainly attributed to charge transfer from the Se-4p (S-3p) states to the Sn-5p (Ga-4p, Ge-4p) and Se-4p (Se-4s) states, and the electronic structure around the band edges is mainly derived from the (Sn/Ga/Ge)(S/Se)4 tetrahedra units, which provide the dominant states in the optical matrix elements describing the virtual excitations of the SHG effect in 1–4. The strongly isolated s and p orbitals of the Na+ cations are localized far from the band gaps and have a negligible influence on the SHG effect.To obtain a profound understanding of the NLO properties of 1–4, theoretical calculations of the SHG coefficients were performed. The real (ε1) and imaginary (ε2) parts of the optical dielectric constants along the x, y and z directions are shown in Fig. S9 and S10.† The curves of ε2ave, defined as (εx + εy + εz)/3, reveal that the strongest absorptions of 1 are at 5.72, of 2 are at 5.54, of 3 are at 8.54, and of 4 are at 8.74 eV, which can be mainly assigned to the electronic interband transitions according to the DOS analysis. Owing to the NCS point group of mm2, compounds 1–4 have three independent non-zero SHG tensors d113, d223, and d333 under the restriction of Kleinman symmetry. The calculated energy dependence of the SHG tensors of 1–4 is shown in Fig. 3, at the wavelength 1910 nm (0.6492 eV). The d113, d223, and d333 values are 18.72, 19.22 and 19.09 pm V−1 for 1; 13.89, 13.39 and 13.84 pm V−1 for 2; 23.69, 22.10 and 22.28 pm V−1 for 3; and 17.06, 16.83 and 16.21 pm V−1 for 4. The calculated average SHG coefficients dcal defined as the arithmetic mean of all the SHG tensors which in descending order are dcal(3, 22.69 pm V−1) > dcal(1, 19.01 pm V−1) > dcal(4, 16.70 pm V−1) > dcal(2, 13.71 pm V−1) are consistent with the experimental results.
Conclusions
A new strategy to circumvent the incompatibility between large NLO efficiencies and high LIDTs in mid-infrared NLO materials, namely, narrowing the band gap for a large NLO efficiency and reducing the thermal effect for a high LIDT, is proposed in this study. To support this proposal, a series of isostructural chalcogenides with different tetrahedral center cations, Na2Ga2MQ6 (M = Ge, Sn; Q = S, Se), were successfully synthesized using the solid-state method. The 3D structures of these chalcogenides were assembled in 1D infinite ∞1[Ga(Sn)Q3)]3− tetrahedral chains and [MQ4]4− tetrahedral connections. All of them exhibit large SHG responses of approximately 1.6–3.9 × that of AGS with phase-matching ability, which result from their relatively small band gaps (1.56–1.73 eV) compared with that of AGS (2.65 eV). They also exhibit outstanding LIDTs of 8.5–13.3 × that of AGS for potential high-power applications, which is contrary to the conventional view on band gaps. However, the measured thermal expansion anisotropy order of these compounds is in agreement with their experimental LIDTs, which have the opposite order, indicating that the thermal expansion anisotropy is one of the main thermal parameters to influence the LIDTs of IR NLO materials and a high LIDT can be achieved by reducing the thermal effect. The results of this study shed light on the search for practical IR NLO materials with excellent performance which are not restricted by the NLO–LIDT incompatibility.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the NSF of China (21701176), the National Postdoctoral Program for Innovative Talents (BX201600163), the China Postdoctoral Science Foundation (2016M600510), the National Key Laboratory Development Fund (20180026) and the NSF of Fujian Province (2018J05034).Notes and references
- L. Kang, M. Zhou, J. Yao, Z. Lin, Y. Wu and C. Chen, J. Am. Chem. Soc., 2015, 137, 13049 CrossRef PubMed.
- H. Zhang, M. Zhang, S. Pan, X. Dong, Z. Yang, X. Hou, Z. Wang, K. B. Chang and K. R. Poeppelmeier, J. Am. Chem. Soc., 2015, 137, 8360 CrossRef PubMed.
- H. Yu, J. Young, H. Wu, W. Zhang, J. M. Rondinelli and P. S. Halasyamani, J. Am. Chem. Soc., 2016, 138, 4984 CrossRef PubMed.
- I. Chung and M. G. Kanatzidis, Chem. Mater., 2014, 26, 849 CrossRef.
- C. Chen, Sci. Sin., Ser. B, 1985, 28, 235 Search PubMed.
- C. Chen, Y. Wu, A. Jiang, B. Wu, G. You, R. Li and S. Lin, J. Opt. Soc. Am. B, 1989, 6, 616 CrossRef.
- V. G. Dmitriev, G. G. Gurzadyan and D. N. Nikogosyan, Handbook of nonlinear optical crystals, Springer-Verlag, New York, 1999 Search PubMed.
- C. Chen, Y. Wang, B. Wu, K. Wu, W. Zeng and L. Yu, Nature, 1995, 373, 322 CrossRef.
- T. A. Driscoll, P. E. Perkins, H. J. Hoffman and R. E. Stone, J. Opt. Soc. Am. B, 1986, 3, 683 CrossRef.
- T. K. Bera, J. I. Jang, J. B. Ketterson and M. G. Kanatzidis, J. Am. Chem. Soc., 2008, 131, 75 CrossRef PubMed.
- I. Chung and M. G. Kanatzidis, Chem. Mater., 2013, 26, 849 CrossRef.
- F. Liang, L. Kang, Z. Lin and Y. Wu, Cryst. Growth Des., 2017, 17, 2254 Search PubMed.
- A. Harasaki and K. Kato, Jpn. J. Appl. Phys., 1997, 36, 700 CrossRef.
- A. Jayaraman, V. Narayanamurti, H. Kasper, M. Chin and R. Maines, Phys. Rev. B: Solid State, 1976, 14, 3516 CrossRef.
- G. Catella, L. Shiozawa, J. Hietanen, R. Eckardt, R. Route, R. Feigelson, D. Cooper and C. Marquardt, Appl. Opt., 1993, 32, 3948 CrossRef PubMed.
- M. C. Ohmer and R. Pandey, MRS Bull., 1998, 23, 16–22 CrossRef.
- G. Boyd, E. Buehler and F. Storz, Appl. Phys. Lett., 1971, 18, 301 CrossRef.
- Z. Z. Luo, C. S. Lin, H. H. Cui, W. L. Zhang, H. Zhang, H. Chen, Z. Z. He and W. D. Cheng, Chem. Mater., 2015, 27, 914 CrossRef.
- G. Li, K. Wu, Q. Liu, Z. Yang and S. Pan, J. Am. Chem. Soc., 2016, 138, 7422 CrossRef PubMed.
- K. Wu, Z. Yang and S. Pan, Chem. Mater., 2016, 28, 2795 CrossRef.
- A. P. Yelisseyev, L. I. Isaenko, P. Krinitsin, F. Liang, A. A. Goloshumova, D. Y. Naumov and Z. Lin, Inorg. Chem., 2016, 55, 8672 CrossRef PubMed.
- S. Fossier, S. Salaün, J. Mangin, O. Bidault, I. Thénot, J.-J. Zondy, W. Chen, F. Rotermund, V. Petrov, P. Petrov, J. Henningsen, A. Yelisseyev, L. Isaenko, S. Lobanov, O. Balachninaite, G. Slekys and V. Sirutkaitis, J. Opt. Soc. Am. B, 2004, 21, 1981 CrossRef.
- V. Petrov, J. J. Zondy, O. Bidault, L. Isaenko, V. Vedenyapin, A. Yelisseyev, W. Chen, A. Tyazhev, S. Lobanov and G. Marchev, J. Opt. Soc. Am. B, 2010, 27, 1902 CrossRef.
- L. Isaenko, A. Yelisseyev, S. Lobanov, P. Krinitsin, V. Petrov and J. J. Zondy, J. Non-Cryst. Solids, 2006, 352, 2439 CrossRef.
- X. Lin, G. Zhang and N. Ye, Cryst. Growth Des., 2008, 9, 1186 Search PubMed.
- J. J. Zondy, D. Touahri and O. Acef, J. Opt. Soc. Am. B, 1997, 14, 2481 CrossRef.
- V. Petrov, A. Yelisseyev, L. Isaenko, S. Lobanov, A. Titov and J. J. Zondy, Appl. Phys. B: Lasers Opt., 2004, 78, 543 CrossRef.
- G. A. Marking, J. A. Hanko and M. G. Kanatzidis, Chem. Mater., 1998, 10, 1191 CrossRef.
- T. V. Misuryaev, T. V. Murzina, O. A. Aktsipetrov, N. E. Sherstyuk, V. B. Cajipe and X. Bourdon, Solid State Commun., 2000, 115, 605 CrossRef.
- J. H. Liao, G. Marking, K. Hsu, Y. Matsushita, M. Ewbank, R. Borwick, P. Cunningham, M. Rosker and M. Kanatzidis, J. Am. Chem. Soc., 2003, 125, 9484 CrossRef PubMed.
- J. W. Lekse, M. A. Moreau, K. L. McNerny, J. Yeon, P. S. Halasyamani and J. A. Aitken, Inorg. Chem., 2009, 48, 7516 CrossRef PubMed.
- L. Geng, W. D. Cheng, C. S. Lin, W. L. Zhang, H. Zhang and Z. Z. He, Inorg. Chem., 2011, 50, 5679 CrossRef PubMed.
- D. Mei, W. Yin, K. Feng, Z. Lin, L. Bai, J. Yao and Y. Wu, Inorg. Chem., 2011, 51, 1035 CrossRef PubMed.
- H. Lin, L. J. Zhou and L. Chen, Chem. Mater., 2012, 24, 3406 CrossRef.
- D. Mei, W. Yin, K. Feng, Z. Lin, L. Bai, J. Yao and Y. Wu, Inorg. Chem., 2012, 51, 1035 CrossRef PubMed.
- W. Yin, K. Feng, R. He, D. Mei, Z. Lin, J. Yao and Y. Wu, Dalton Trans., 2012, 41, 5653 RSC.
- J. I. Jang, S. Park, C. M. Harrison, D. J. Clark, C. D. Morris, I. Chung and M. G. Kanatzidis, Opt. Lett., 2013, 38, 1316 CrossRef PubMed.
- S. M. Kuo, Y. M. Chang, I. Chung, J. I. Jang, B. H. Her, S. H. Yang, J. B. Ketterson, M. G. Kanatzidis and K. F. Hsu, Chem. Mater., 2013, 25, 2427 CrossRef.
- J. A. Brant, D. J. Clark, Y. S. Kim, J. I. Jang, J.-H. Zhang and J. A. Aitken, Chem. Mater., 2014, 26, 3045 CrossRef.
- X. Li, C. Li, P. Gong, Z. Lin, J. Yao and Y. Wu, J. Mater. Chem. C, 2015, 3, 10998 RSC.
- B.-W. Liu, H.-Y. Zeng, M.-J. Zhang, Y.-H. Fan, G.-C. Guo, J.-S. Huang and Z.-C. Dong, Inorg. Chem., 2015, 54, 976 CrossRef PubMed.
- B.-W. Liu, H.-Y. Zeng, X.-M. Jiang, G.-E. Wang, S.-F. Li, L. Xu and G.-C. Guo, Chem. Sci., 2016, 7, 6273 RSC.
- K. Wu, Z. Yang and S. Pan, Angew. Chem., Int. Ed., 2016, 55, 6713 CrossRef PubMed.
- K. Wu, Z. Yang and S. Pan, Chem. Commun., 2017, 53, 3010 RSC.
- S. Das, C. Ghosh, S. Gangopadhyay, Y. M. Andreev and V. V. Badikov, Jpn. J. Appl. Phys., 2006, 45, 5795 CrossRef.
- O. M. Yurchenko, I. D. Olekseyuk and O. V. Parasyuk, J. Cryst. Growth, 2005, 275, e1983 CrossRef.
- V. Petrov, V. Badikov, G. Shevyrdyaeva, V. Panyutin and V. Chizhikov, Opt. Mater., 2004, 26, 217 CrossRef.
- W. Yin, K. Feng, W. Hao, J. Yao and Y. Wu, Inorg. Chem., 2012, 51, 5839 CrossRef PubMed.
- Y. Kim, I. S. Seo, S. W. Martin and J. Baek, Chem. Mater., 2008, 20, 6048 CrossRef.
- R. W. Boyd, Nonlinear optics, Academic press, 2003 Search PubMed.
- D. Ristau, Laser-induced damage in optical materials, CRC Press, 2014 Search PubMed.
- G.-C. Guo, Y. Yao, K. Wu, L. Wu and J. Huang, Prog. Chem., 2001, 13, 151 CrossRef.
- S.-P. Guo, Y. Chi and G.-C. Guo, Coord. Chem. Rev., 2017, 335, 44 CrossRef.
- B.-W. Liu, M.-Y. Zhang, X.-M. Jiang, S.-F. Li, H.-Y. Zeng, G.-Q. Wang, Y.-H. Fan, Y.-F. Su, C. Li, G.-C. Guo and J.-S. Huang, Chem. Mater., 2017, 29, 9200 CrossRef.
- I. D. Brown, Struct. Bonding, 2014, 158, 11 CrossRef.
- C. D. Morris, I. Chung, S. Park, C. M. Harrison, D. J. Clark, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 20733 CrossRef PubMed.
- I. Chung, J.-H. Song, J. I. Jang, A. J. Freeman and M. G. Kanatzidis, J. Solid State Chem., 2012, 195, 161 CrossRef.
- A. S. Haynes, F. O. Saouma, C. O. Otieno, D. J. Clark, D. P. Shoemaker, J. I. Jang and M. G. Kanatzidis, Chem. Mater., 2015, 27, 1837 CrossRef.
- Rigaku CrystalClear, 1.3.5, Rigaku Corp., Tokyo, 2002 Search PubMed.
- G. Sheldrick, SHELXS-97, program for X-ray crystal structure solution, University of Göttingen, Germany, 1997 Search PubMed.
- A. Spek, Single-crystal structure validation with the program PLATON, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef.
- S. Kurtz and T. J. Perry, Appl. Phys., 1968, 39, 3798 Search PubMed.
- M.-J. Zhang, X.-M. Jiang, L.-J. Zhou and G.-C. Guo, J. Mater. Chem. C, 2013, 1, 4754 RSC.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 Search PubMed.
- F. P. Bassani and G. P. Parravicini, Electronic States and Optical Transitions in Solids, Pergamon Press Ltd., Oxford, 1975, pp. 149–154 Search PubMed.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B, 2006, 73, 045112 CrossRef.
- K. Wu, Z. Yang and S. Pan, Inorg. Chem., 2015, 54, 10108 CrossRef PubMed.
- D. Mei, W. Yin, Z. Lin, R. He, J. Yao, P. Fu and Y. Wu, J. Alloys Compd., 2011, 509, 2981 CrossRef.
- H. Lin, L. Chen, L. J. Zhou and L. M. Wu, J. Am. Chem. Soc., 2013, 135, 12914 CrossRef PubMed.
- J. Tarascon, G. Hull and J. Waszczak, Mater. Res. Bull., 1985, 20, 935 CrossRef.
- J. C. Jumas, E. Philippot and M. Maurin, J. Solid State Chem., 1975, 14, 152 CrossRef.
- A. Rothenberger, H. H. Wang, D. Chung and M. G. Kanatzidis, Inorg. Chem., 2010, 49, 1144 CrossRef PubMed.
- K. M. Ok, Acc. Chem. Res., 2016, 49, 2774 CrossRef PubMed.
- H. Jo, S.-J. Oh and K. M. Ok, Dalton Trans., 2017, 46, 15628 RSC.
- S.-F. Li, X.-M. Jiang, B.-W. Liu, D. Yan, C.-S. Lin, H.-Y. Zeng and G.-C. Guo, Chem. Mater., 2017, 29, 1796 CrossRef.
- I. Bodnar and N. Orlova, Phys. Status Solidi A, 1985, 91, 50 CrossRef.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1842640, 1842642, 1842643 and 1842644. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc01210e |
| This journal is © The Royal Society of Chemistry 2018 |