Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio kinetic Monte Carlo simulation of seeded emulsion polymerizations of styrene
Marco
Drache
 *,
Katrin
Brandl
,
Rebecca
Reinhardt
and
Sabine
Beuermann
*,
Katrin
Brandl
,
Rebecca
Reinhardt
and
Sabine
Beuermann
 *
*
Institute of Technical Chemistry, Clausthal University of Technology, Arnold-Sommerfeld-Straße 4, 38678 Clausthal-Zellerfeld, Germany. E-mail: marco.drache@tu-clausthal.de; sabine.beuermann@tu-clausthal.de
First published on 31st January 2018
Abstract
Seeded emulsion polymerizations of styrene are modeled on the basis of a detailed kinetic scheme accounting for the chain length and conversion dependence of termination rate coefficients. A holistic kinetic Monte Carlo approach was developed, which simulates the elemental reactions in the aqueous phase, the transfer of radicals into individual particles, and the radical polymerization in each particle based on a complete kinetic model. Experimentally-derived particle size distributions are used as input for the simulations. The required rate coefficients were taken from literature. Without any adjustment of this data a very good agreement between simulation results and experimental data is found. The validation of the model is performed based on monomer conversion – time data and full molar mass distributions.
Introduction
Emulsion polymerization processes are associated with a number of advantages, such as excellent heat dissipation, low viscosity of the emulsion, and a high weight fraction of polymer in the latex. Since water is used as the continuous phase in most cases the processes are considered to be environmentally friendly. Due to the compartmentalization of radicals into particles, higher polymerization rates and molar masses are achieved compared to polymerizations in bulk or solution.1 The latex produced has many applications. For example it may be used directly as surface coating or after processing as bulk polymer.2,3The kinetics of emulsion polymerizations are complex. In addition to the common elemental reaction steps in radical polymerization (initiation, propagation, transfer and termination), it is necessary to consider radical phase-transfer processes.4 The reaction starts in the aqueous phase. Then, the radical formed passes through a few propagation steps in the continuous phase before it enters a particle. Apart from this so-called radical entry process, a radical can also leave a particle (radical exit). Polymerization takes exclusively place in the particles. Each particle can be considered as a nanoreactor. In addition to radical entry and exit, the key mechanistic aspects include particle formation and growth, as well as termination processes and secondary nucleation.2 Reliable modelling of emulsion polymerizations has to consider all these processes.
For a typical batch emulsion polymerization three distinct intervals are operative.5 In interval I particle formation takes place. Monomer droplets, surfactant molecules, micelles in cases of surfactant concentrations being above the critical micelle concentration, and precursor particles are present. Interval II is characterized by a constant particle number. The particles grow by propagation in the presences of monomer droplets, which serve as a reservoir for monomer ensuring that the monomer concentration in the particles is constant. In interval III no monomer droplets are present and particle growth can be neglected. The remaining monomer in the particles is polymerized.2,3
To gain a deeper understanding of mechanistic aspects related to emulsion polymerizations experimental data was modeled. Frequently, the emulsion polymerization of styrene6 was considered. Thus, this system often serves as a reference. For radical entry the most widely accepted model is the propagation-controlled mechanism.7 This model, introduced by Maxwell et al.,8 assumes that a radical grows in the aqueous phase up to a critical chain length until it becomes surface active and then enters a particle. Another important aspect of the emulsion polymerization is reduced termination due to compartmentalization of radicals. Therefore, two approaches were put forward, the zero-one and the pseudo-bulk model.9 In the zero-one model particles with two or more radicals are neglected. It is assumed, that termination is pseudo instantaneous. Typically, this approach is applied to simulate the polymerization in small particles at low conversion. It also allows for checking, if a system obeys zero-one kinetics. The group of Gilbert applied this model to interpret the mechanism of particle formation.1,10 The pseudo-bulk approach assumes that all particles of the same size have the same average number of radicals. Systems with a high number of radicals per particle or high radical entry rates are described well by this model. Compared to the zero-one approach, it allows for the simulation of the emulsion polymerization over the entire conversions range.2,9 In addition to these approaches, extensions (e.g. 0-1-2 model11) and combinations (e.g. hybrid model) were reported to reduce the limits of the models. Coen et al.12 first proposed a hybrid model for simulation of the emulsion polymerization of butyl acrylate. For styrene, Gomes and Jung13 introduced a model, where in the pseudo bulk region chain-length-dependent termination is considered by using an average termination rate coefficient. A review by Sheibat-Othman et al.9 provides an overview on simulations using these approaches with the goal to model particle size distributions (PSD). One further aspect is the radical exit. During polymerization in a particle also chain-transfer to monomer takes place. The resulting radical with chain length one can desorb from the particle. In the next step, it can grow or undergo a termination reaction in the aqueous phase, as well as re-enter into a particle.2,9,14,15 It was noted that radical exit may take place up to a monomer conversion of 0.6.16–18 At higher conversions the probability of a radical exit is negligible due to the increased viscosity. In addition to monomer conversion, other factors influence whether radical exit is operative, namely particle size, initiator concentration, the monomer used, the emulsifier and the related nature of stabilization.
The kinetic Monte Carlo (kMC) simulation offers the advantage that discrete polymer molecules with specific properties may be analyzed and detailed information is accessible.19 MC simulations are particularly well suited for the determination of copolymer compositions20–23 and sequence length distributions of gradient copolymers,24 for quantifying defect structures,25 and for studying the polymer network formation during cross-linking copolymerizations.26,27 In the context of emulsion polymerizations kMC approaches are used in combination with mass transport between the aqueous and particle phase, is used.28–30 For kMC modeling of emulsion polymerizations it is feasible to simulate the development of all macromolecules in one particle, because the particle diameter is in the nanometer range. Therefore, the number of molecules inside a particle is easy to handle in kMC simulations.
In the present work a new holistic approach for modeling the reactions in aqueous phase and in isolated particles using the kinetic Monte Carlo simulation is introduced. To perform the Monte Carlo modeling, an extension of the mcPolymer simulator31–33 based on the Gillespie algorithm34 is applied. The seeded emulsion polymerization of styrene was chosen as an example. The processes occurring during this special kind of emulsion polymerization are illustrated in Fig. 1. The seeded emulsion polymerization is characterized by the fact that all particles are already existing at the beginning of the reaction. The term “seed” refers to the presence of pre-synthesized polymer particles. Upon addition of monomer the polymer particles are swollen with monomer molecules.2 If the concentration of added monomer is below the saturation concentration in the particles, further particle generation does not occur, and consequently, does not need to be considered in the simulations. It should be noted that in contrast to conventional emulsion polymerizations, there are no monomer droplets present in the system. Decomposition of the water-soluble initiator starts the reaction in aqueous phase. After passing through a few propagation steps the macroradical may either enter into a particle or undergo a termination reaction in the aqueous phase. Inside the particle the radical adds monomer molecules and chain growth occurs. Further, a radical inside a particle may also undergo chain transfer to monomer. A termination reaction may only happen, if a second radical is present in the particle. The experiments were designed in a way that particle nucleation and particle growth do not have to be taken into account. The seeded emulsion polymerization carried out in this work essentially corresponds to interval III of the emulsion polymerization. Due to the initial seed, the polymer weight fraction in the particles is always around 50 percent. Thus, as discussed above radical exit can be neglected due to the high viscosity inside the particles. Because of the simplifications associated with the selected polymerization conditions, the method of seeding is of particular interest to study the mechanism of emulsion polymerization and to establish new holistic modeling approaches.3
The polymerization in the particles is assumed to be well treated as a bulk polymerization. Due to the excellent knowledge of styrene bulk polymerization kinetics, this system provides a reliable basis to verify the current modeling approach. In addition to the propagation rate coefficient, kp,35 and the transfer rate coefficient to monomer, ktrM,36 the termination rate coefficients, kt, have been extensively studied. Buback and Kattner introduced a composite model accounting for the chain-length dependence of kt37 and an extension for polymerizations up to high conversions.38
The modeling approach presented for the seeded emulsion polymerization of styrene aims to demonstrate the feasibility of simulating experimental data without the need of adjusting any coefficients. The polymerization is performed in a large ensemble of discrete pre-synthesized polymer particles with different sizes, thus, the compartmentalization of radicals is naturally taken into account. Therefore, it is possible to model the process without further assumptions with respect to the termination kinetics in contrast to approaches published, where termination rate coefficients were manipulated to simulate the separation of radicals inside the particles. The aqueous phase is also simulated by the kMC approach to generate the radicals, which will be transferred into the particles. The combination of the simulation of aqueous phase and the simulation in the particles results in a holistic model that describes the experimental reality as accurately as possible.
Experimental
Materials
The surfactant Aerosol MA 80 (technical grade ∼80% in H2O, Sigma-Aldrich), the initiator potassium persulfate (KPS, >98%, MERCK) and sodium hydrogen carbonate (≥99%, Roth) were used as received. The inhibitor was removed from styrene (99.5%, Sigma-Aldrich) by distillation under reduced pressure. Tetrahydrofuran (THF, 99%, VWR Prolab) was distilled prior to use as eluent for size-exclusion chromatography.Preparation of the polystyrene seed
Typically, 3.2 g (0.04 mol L−1) of the surfactant Aerosol MA80 and 0.2 g (0.012 mol L−1) of sodium hydrogen carbonate, which was used as buffer, were dissolved in 165 g Milli-Q (Millipore) deionized water. The solution was heated up to 70 °C in a 250 mL double-jacketed stainless steel reactor under stirring with an impeller agitator at 500 rpm. During the heat-up phase the reactor was purged with nitrogen. After the reaction temperature was reached, 32 g of styrene and 0.16 g (3 × 10−3 mol L−1) of potassium persulfate were added. After a polymerization time of two hours the reaction mixture was heated to 85 °C to remove residual KPS. The recipe was adapted from the work of Winschel.39 For one reaction the stirrer speed was reduced to 345 rpm.Seeded emulsion polymerization
The seeded emulsion polymerization was usually carried out as follows. 70 g of polystyrene seed produced in the first step was mixed with 60 g of deionized water and 0.06 g (5 × 10−3 mol L−1) of sodium hydrogen carbonate. After the reaction mixture was heated to 70 °C 11.2 g of styrene was added. In one case 7.3 g of styrene were used at otherwise identical conditions. To achieve an almost complete swelling of the particles with the monomer, the solution was stirred at 550 rpm for five hours under nitrogen and subsequently 0.07 g (1.8 × 10−3 mol L−1) of KPS was added. The reaction was terminated after two hours. The conversion was measured gravimetrically by weighing the dry content of the samples.Size-exclusion chromatography
Molar mass distributions were determined by size-exclusion chromatography using a Waters 515 HPLC pump, a Knauer Marathon autosampler, a Knauer Smartline refractive index Detector 2300, and four PSS SDV columns (guard, 100 Å, 1000 Å and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å). The system is operated at 25 °C and THF is used as eluent with a flow rate of 1 mL min−1. Calibration was established with narrow polystyrene standards (PSS) with number average molar masses, Mn, ranging from 700 to 2.57 × 106 g mol−1.
000 Å). The system is operated at 25 °C and THF is used as eluent with a flow rate of 1 mL min−1. Calibration was established with narrow polystyrene standards (PSS) with number average molar masses, Mn, ranging from 700 to 2.57 × 106 g mol−1.
Dynamic light scattering
Dynamic light scattering (DLS) measurements were carried out using an instrument from ALV (Langen, Germany) at 25 °C. For the discussion of the experimental results mass-weighted radii were considered.Computing resources
The simulations were executed on application servers (transtec CALLEO, 2xIntel Xeon E5-2670 CPU 16 cores, 2.6 GHz, 256 GB RAM) running a virtualized CentOS 7.3 Linux operating system. Compilation of the simulation program written in C++ was executed with gcc 4.8.5. In addition, the Open MPI v2.1.1 software environment40 was integrated for the parallelization of the simulation.Modeling strategy
The model introduced for the seeded emulsion polymerization of styrene links the kinetic Monte Carlo simulation of a radical polymerization with the special requirements for an emulsion polymerization: radical generation and propagation in the aqueous phase, transfer of radicals into the particles and polymerization in isolated particles. Contrary to other modeling approaches, in this work the particles are of realistic size. Thus, each particle contains a discrete number of monomer molecules that correlates with the particle size. During polymerization each particle constitutes a polymerization reactor with a real volume, which is associated with the complete kinetic polymerization model consisting of chain propagation, transfer to monomer, and bimolecular termination. The modeling is performed with a statistically sound number of discrete particles, here 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 512
000 to 512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The processes in the aqueous phase are represented by the kMC simulation, too. The reaction volume of the aqueous phase is between 2.2 × 10−13 and 4.1 × 10−13 L, related to the number and volume of the particles. In aqueous phase initiator decomposition, addition of the initiator fragments to monomer forming the so-called primary macroradicals as well as propagation and termination of the macroradicals takes place. After reaching a certain chain length z the macroradical is transferred from the aqueous phase into a particular particle and subsequently becomes a part of the kMC model of the particle. In order to properly simulate the reactions in aqueous phase, it is necessary to select a sufficiently large number of particles to obtain a representative sample of discrete molecules in this phase. The modeling strategy introduced in this contribution represents an ab initio kinetic Monte Carlo simulation of a seeded emulsion polymerization.
000. The processes in the aqueous phase are represented by the kMC simulation, too. The reaction volume of the aqueous phase is between 2.2 × 10−13 and 4.1 × 10−13 L, related to the number and volume of the particles. In aqueous phase initiator decomposition, addition of the initiator fragments to monomer forming the so-called primary macroradicals as well as propagation and termination of the macroradicals takes place. After reaching a certain chain length z the macroradical is transferred from the aqueous phase into a particular particle and subsequently becomes a part of the kMC model of the particle. In order to properly simulate the reactions in aqueous phase, it is necessary to select a sufficiently large number of particles to obtain a representative sample of discrete molecules in this phase. The modeling strategy introduced in this contribution represents an ab initio kinetic Monte Carlo simulation of a seeded emulsion polymerization.
The kinetic model for a seeded styrene emulsion polymerization comprises the following reactions in the aqueous phase. The scheme in Fig. 2 is based on the Maxwell–Morrison mechanism8 for the macroradical generation and entry into the particle. The initiator fragment (I) obtained from the thermal decomposition of the initiator instantaneously adds to a monomer molecule (M) to form a macroradical of chain length one (R1). R1 may terminate with another R1 radical or add a second monomer molecule to form a radical of chain length two (R2). According to the Maxwell–Morrison model chain growth proceeds in the aqueous phase up to a characteristic chain length z. Once z is reached the radical becomes surface active and entry into a particle occurs immediately. For seeded emulsion polymerizations of styrene with potassium persulfate as initiator in conjunction with the surfactant Aerosol MA-80 a value of z = 2 was reported caused by the low water solubility of the styrene monomer and macroradicals.7,8 Therefore, in the kMC model introduced here a macroradical of chain length 2 (R2) is removed from the water phase and transferred into a specific particle.
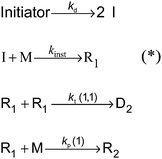 | ||
| Fig. 2 Reaction scheme representing the processes in the aqueous phase of a seeded emulsion polymerization of styrene using z = 2;7,8 (*) with the chosen high value for kinst = 2 × 108 L mol−1 s−1 an instantaneous execution of these reactions is enforced. | ||
Following the mechanism in Fig. 2 primary initiator derived radicals are lost due to termination of R1 radicals, and consequently, the rate at which radicals R2 enter particles is lower than the rate of radical generation in the aqueous phase. This effect is more pronounced for higher initiator concentrations in the water phase. The termination and propagation reactions in the aqueous phase are characterized by the termination and propagation rate coefficients for radicals of chain length 1 (kp(1)41 and kt(1,1)37) taken from literature. The values are summarized in Table 1.
Due to the very low solubility of styrene in water the styrene saturation concentration at 70 °C is reported to be 6.5 × 10−3 mol L−1,42 which is several orders of magnitude lower than the styrene concentration inside the swollen particles. The latter value is in the range of 5.5 to 6.2 mol L−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 depending on the recipe. A dynamic equilibrium of monomer distribution in both phases being in direct contact is assumed to occur. Consequently, the styrene concentration in the aqueous phase is set to be constant throughout the reaction in the model.
6 depending on the recipe. A dynamic equilibrium of monomer distribution in both phases being in direct contact is assumed to occur. Consequently, the styrene concentration in the aqueous phase is set to be constant throughout the reaction in the model.
Each particle constitutes an isolated reaction volume, in which the polymerization proceeds. At the reaction conditions chosen (initiator concentration, temperature and particle size) it is anticipated that up to at most 5 radicals may be found within an individual particle. Therefore, within the kinetic model for each particle five radicals are defined, which may undergo propagation, termination or transfer to monomer. Once a radical R2 from the water phase is transferred into a specific particle it will be allocated to an unoccupied radical R#1 to R#5. For example, if the macroradical R#1j with chain length j is already existing inside the particle, R2 originating from radical entry is assigned to an additional macroradical R#2k with chain length k = 2. All reactions occurring in a single particle are summarized in Fig. 3. With the exception of the termination rate coefficient for the polymerization inside the particles the rate coefficients are listed in Table 1.
The reaction scheme indicates that the chain length dependence of the termination rate coefficients is considered. Generally, in deterministic12,38 and in kMC simulations31 a chain length averaged termination rate coefficient 〈kt〉 is used for all macroradicals of different chain length, because a large number of radicals is present in the reaction volume in the case of polymerizations in bulk or in solution. Consideration of the chain length dependence of each individual termination rate coefficient would result in a combinatorial explosion and kinetic modeling of such a system would not be feasible with the current computing resources. On the contrary, the approach followed here considers individual particles of real size as reaction volumes. As pointed out above the number of radicals per particle is limited to a maximum of five. Mostly, one or two radicals are contained in a particle. Due to compartmentalization of the radicals termination reactions between two radicals of an individual chain length occur. For these reactions between a radical of length i and a radical of length j the individual termination rate coefficient kt(i,j) may be used. For the monomer system under investigation the correlation of kt with the chain lengths i and j is provided by Kattner and Buback.37 The approach allows for appropriate accounting of the termination reaction between two radicals with chain length(s) below the crossover chain length of ic = 30 in eqn (1). This point is particularly important for the time interval after entry of a short radical into the particles, and the monomer conversion as a function of time as well as the molar mass distributions are directly affected. If radicals with chain lengths above the critical chain length are involved, the termination rate coefficient is calculated by eqn (2).
Since termination is a diffusion controlled reaction in addition to the chain length dependence of kt the impact of monomer conversion or more generally the viscosity is important to be considered.45,46 For styrene both impact factors on kt are combined in eqn (1)–(5).38Eqn (3) and (4) were adjusted to the special requirements of the seeded emulsion polymerization compared to the original form.
| kt(i,i) = kt(1,1)·i−αs i ≤ ic | (1) |
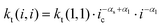 | (2) |
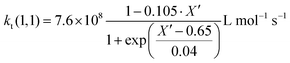 | (3) |
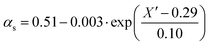 | (4) |
| kt(i,j) = 0.5·(kt(i,i) + kt(j,j)) | (5) |
In the special case of a seeded emulsion polymerization each particle resembles a bulk polymerization system. Thus, the monomer conversion inside the particle during polymerization should be considered. In contrast to monomer conversion in bulk systems, here the content of polymer inside the particle needs to be considered. Already the monomer swollen particles contain the seed polymer prior to the onset of the polymerization. Thus, already at the very beginning of the reaction the situation with respect to the ratio of polymer to monomer may be similar to bulk polymerizations at intermediate conversion. Thus, eqn (3) and (4) originally derived for bulk styrene polymerizations were adapted for the styrene seeded emulsion polymerization. Knowing the amount of polymer in the entire system and assuming that all the monomer added is contained in the swollen seed particles the polymer to monomer content prior to polymerization may be calculated. The apparent conversion X′ of the seeded emulsion polymerization described in analogy to a bulk system with corresponding conversion. X′ is calculated from the current conversion and applied in eqn (3) and (4). During the polymerization after each Monte Carlo step this ratio needs to be updated to account for consumption of one monomer molecule in each propagation reaction, and subsequently a new kt(i,j) needs to be calculated within the Gillespie-algorithm.34
Software architecture
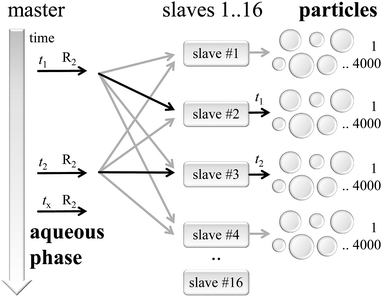
As shown in Fig. 4 the simulation is organized following the master-slave principle in which a single master instance carries out most of the administrative parts, while several slave knots simulate numerous particle instances.48The master is responsible for the initialization of all kinetic models corresponding to the reaction conditions and the recipe of the seeded emulsion polymerization. Additionally, the master controls the global timeline and synchronizes the kMC simulations inside the particles at defined time stamps. Furthermore, the master process takes care of the aqueous phase model, in particular with respect to the generation of macroradicals triggering the polymerization in the particles.
On the right hand side of Fig. 4 the slaves handle simulation instances of individual particles. Here, typically 4000 to 8000 particles were assigned to each slave with 16 slave processes in total. During the initialization phase the master process prepared parameters for each particle, which serve as input in the kMC simulation set-up. Particles are assumed to be discrete reactors simulated by an instance of the mcPolymer simulation program.33 After the initialization all particles remain non-reactive due to the lack of macroradicals inside.
At a distinct point in time t1, t2,… macroradicals of type R2 will be generated in the aqueous phase. The master process recognizes the presence of such a macroradical at time = tx and will select one of the slaves as target for the radical entry in a particle. Per definition all slave processes have an equal probability for radical transfer. This is a valid approach due to the large number of stored particles in each slave representing the particle size distribution of the entire model. A second selection step takes place inside the slave process picking a distinct particle from its pool of particles according to a probability, which correlates with the surface area of a single particle.
The communication between the master and its slave processes is realized with the Message Passing Interface (MPI).49 Each message contains a time stamp for the radical transfer and the chain length of the macroradical. Message transfer is a non-blocking operation; the master will not wait for an acknowledgement of the slave and will continue its simulation process (fire & forget policy).
Particle simulations run on their own timeline and will advance to the point in time tx of every related macroradical entry. The kMC calculations in the particles are provided by the slave processes, which determine the calculation speed of the whole simulation. Those slave knots and their local simulation processes are only loosely coupled to the master and totally independent of each other, thus, allowing to scale efficiently the simulation on many parallel processor cores making use of the resources of multi-processor systems. Thus, the architectural layout of the simulation approach is very close to the experimental reality.
Results and discussion
Experimental validation
Three styrene swollen seeds (SwS1, SwS2 and SwS3) differing in particle size and molar mass distribution were selected for experimental validation of the modeling approach described above. The seeds are characterized in Table 2. SwS1 and SwS2 are associated with the same mean radius, whereas the particles of SwS3 are slightly larger. Fig. 5 shows the same behavior for the corresponding DLS-derived particle size distributions. In addition, it is seen that the PSD for latex SP3 obtained after polymerization is shifted to larger values compared to the PSD of the initial seed SwS3. The mean radius is increased from 52 to 57 nm. The shape of the PSD is not varied significantly after polymerization. Since the probability of radical entry is calculated based on relative particle sizes the shift of the entire PSD does not affect modeling of the radical entry throughout the entire polymerization.| Sample | Mean radius, nm | M n, kg mol−1 | M w, kg mol−1 | Đ |
|---|---|---|---|---|
| SwS1 | 43 | 84.0 | 633 | 7.5 |
| SwS2 | 44 | 229 | 865 | 3.9 |
| SwS3 | 52 | 58.3 | 225 | 3.9 |
| SwS4 | 45 | 235 | 866 | 3.7 |
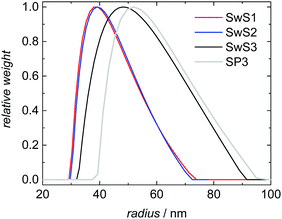 | ||
| Fig. 5 DLS-derived particle size distributions for monomer swollen seeds SwS1 to SwS3 and for SP3 after polymerization starting with SwS3. | ||
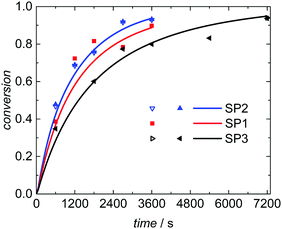
Seeded emulsion polymerization SP1 to SP3 were carried out with the same KPS concentration. In addition, reactions with increased (SP4) or reduced (SP5) initiator concentration were performed. The seeds used, the reaction time, and the styrene concentration inside the particle, cS(particle) are listed in Table 3. The experimental results may be used for analyzing the selectivity of the kMC model with respect to monomer concentration (SP1 and SP2), to initiator concentration (SP4 and SP5) as well as the PSD (SP1 and SP3). cS(particle) used for SP1 and SP3 represents the saturation concentration of the monomer styrene in its polymer.2 The simulated conversion vs. time data given in Fig. 6 demonstrates that both, cS(particle) and the PSD have a significant impact on the polymerization rate. Similarly, for a given PSD a smaller monomer concentration (SP2) leads to a faster conversion of monomer. As the mass ratio of monomer to polymer is lower for SP2, the apparent conversion X′ in the termination model (eqn (3) and (4)) is increased. Therefore, the conversion dependence of the termination reaction results in a lower value for kt than in SP1. At a given monomer concentration a seed with smaller particles (SP1) leads to a faster polymerization. This finding is due to radical separation.1,2 A larger number of particles is associated with a reduced probability of radical entry, thus, termination is reduced and higher monomer conversions are accessible. The experimental data in Fig. 6 is represented very well by the simulation results indicated by the full lines. Thus, further information from the modeling will be used to explain the findings below.
| Sample | Seed sample | Reaction time, s | c KPS, mol L−1 | c S(particle), mol L−1 |
|---|---|---|---|---|
| SP1 | SwS1 | 3600 | 1.8 × 10−3 | 6.2 |
| SP2 | SwS2 | 3600 | 1.8 × 10−3 | 5.5 |
| SP3 | SwS3 | 7200 | 1.8 × 10−3 | 6.2 |
| SP4 | SwS4 | 3600 | 3.5 × 10−3 | 6.2 |
| SP5 | SwS4 | 3600 | 0.8 × 10−3 | 6.2 |
Due to identical KPS concentration in experiments SP1 to SP3 the radical balance in the aqueous phase is expected to be identical with respect to the ratio of the macroradicals entering the particles (R2) and the initially formed primary radicals I. Within the kMC simulation all radicals are represented by discrete molecules and the number of each species is accessible. Modeling of experiment SP1 based on a sample of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles leads to the production of 10
000 particles leads to the production of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 primary radicals I per second. This number is associated with a radical flux of 7 × 10−8 mol L−1 s−1 with respect to the volume of the aqueous phase of 2.2 × 10−13 L−1 used in the kMC simulation. Since only a small fraction of KPS, namely 7%, is decomposed at 70 °C in one hour it may be assumed that a stationary concentration of the radicals that may terminate in aqueous phase is established. In the simulation, the concentration of these radicals is cR1 = 5 × 10−8 mol L−1. At the modeling conditions chosen this concentration refers to around 700 radicals of type R1. Once the chain length two is reached (R2) a radical flux of 2.7 × 10−8 mol L−1 s−1 is transferred into the particle. Together with the initially produced radical flux of 7 × 10−8 mol L−1 s−1 an initiation efficiency of fentry = 0.38 is derived from the simulation. This value is higher than the value of 0.20 reported by van Berkel et al.7 for styrene polymerizations carried out at 50 °C using the same initiator and surfactant. A radical flux of 1 × 10−8 mol L−1 s−1 was reported. Most probably the differences are due to the difference in polymerization temperatures. Since the activation energy of kp is significantly higher than for kt, 32.5 kJ mol−1 compared to 9.3 kJ mol−1,35,37 an increase in temperature favors chain propagation over chain termination. Thus, the critical chain length of 2 for radical entry into a particle is reached by a higher number of radicals. Additionally, the saturation concentration of styrene in water is increased from 4.3 × 10−3 at 50 °C to 6.5 × 10−3 mol L−1 at 70 °C,2 which leads to a faster propagation, too. However, this effect is expected to be less important than the above mentioned impact of the different activation energies.
000 primary radicals I per second. This number is associated with a radical flux of 7 × 10−8 mol L−1 s−1 with respect to the volume of the aqueous phase of 2.2 × 10−13 L−1 used in the kMC simulation. Since only a small fraction of KPS, namely 7%, is decomposed at 70 °C in one hour it may be assumed that a stationary concentration of the radicals that may terminate in aqueous phase is established. In the simulation, the concentration of these radicals is cR1 = 5 × 10−8 mol L−1. At the modeling conditions chosen this concentration refers to around 700 radicals of type R1. Once the chain length two is reached (R2) a radical flux of 2.7 × 10−8 mol L−1 s−1 is transferred into the particle. Together with the initially produced radical flux of 7 × 10−8 mol L−1 s−1 an initiation efficiency of fentry = 0.38 is derived from the simulation. This value is higher than the value of 0.20 reported by van Berkel et al.7 for styrene polymerizations carried out at 50 °C using the same initiator and surfactant. A radical flux of 1 × 10−8 mol L−1 s−1 was reported. Most probably the differences are due to the difference in polymerization temperatures. Since the activation energy of kp is significantly higher than for kt, 32.5 kJ mol−1 compared to 9.3 kJ mol−1,35,37 an increase in temperature favors chain propagation over chain termination. Thus, the critical chain length of 2 for radical entry into a particle is reached by a higher number of radicals. Additionally, the saturation concentration of styrene in water is increased from 4.3 × 10−3 at 50 °C to 6.5 × 10−3 mol L−1 at 70 °C,2 which leads to a faster propagation, too. However, this effect is expected to be less important than the above mentioned impact of the different activation energies.
To understand the impact of the PSD on the conversion vs. time data in Fig. 6 the number of particles in the emulsion is considered. In the case of SwS1 with the smaller mean radius 2.65 × 1017 L−1 particles occur, whereas for seed SwS3 with the higher mean radius 1.45 × 1017 L−1 particles are calculated based on experimentally determined solid content and mean radius. Considering the same radical flux into the particles for modeling experiment SP3 radical entry happens more frequently with respect to a given particle than for SP1. Consequently, the termination probability is enhanced for SP3 and the polymerization rate depicted in Fig. 6 is lower for SP3 compared to SP1. A decrease in polymerization rate due to increasing particle is in good agreement with literature reports.6,50,51
Moreover, the number average degree of polymerization, Pn, is lowered in the simulations: Pn(SP1) = 4535 and Pn(SP3) = 3190. The comparison between SP1 and SP2 indicates, that a lower average degree of polymerization Pn(SP2) = 3910 was achieved in SP2, which is due to the lower monomer concentration in the particles.
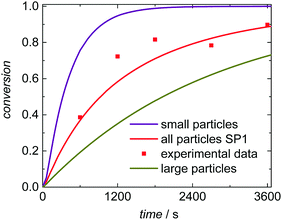
Further, the simulations allow for a deeper understanding of the polymerization and the product distribution in fractions of the PSD. Here SP1 is analyzed. Since radical entry into the particles scales with the surface of the particles within the model radical entry is weighted according to the particle surface. Thus, within a given time interval a smaller number of radicals enters particles of smaller size than of larger size, which is associated with a slightly lower termination rate inside the smaller particles compared to the larger particles. To elucidate this aspect simulation SP1 was evaluated for (i) the entire ensemble of particles, (ii) the fraction of small particles with radii between 64.0 and 68.5 nm, (iii) and for the fraction of large particles with radii ranging from 118 to 141 nm. The absolute numbers of radicals inside a particle are expected to be rather close. Thus, for this special aspect a rather large ensemble consisting of 512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles was simulated simultaneously to identify statistically sound contributions of the fractions of small and large particles on conversion and molar mass distributions. Within the first 600 s of polymerization time the number of radicals per small particles was 1.46 and 1.50 in case of the large particles. This argument may explain the differences in the conversion vs. time data in Fig. 7. The smaller the particles the faster the monomer conversion in a given time interval. These differences are paralleled with variations in the molar mass distributions due to differing termination rates. For comparison a monomer conversion of 0.50 is chosen. If the entire ensemble of particles is considered, Mn is 716 kg mol−1. The fraction of small particles leads to polymer with Mn of 805 kg mol−1 and for the larger particles Mn is 657 kg mol−1.
000 particles was simulated simultaneously to identify statistically sound contributions of the fractions of small and large particles on conversion and molar mass distributions. Within the first 600 s of polymerization time the number of radicals per small particles was 1.46 and 1.50 in case of the large particles. This argument may explain the differences in the conversion vs. time data in Fig. 7. The smaller the particles the faster the monomer conversion in a given time interval. These differences are paralleled with variations in the molar mass distributions due to differing termination rates. For comparison a monomer conversion of 0.50 is chosen. If the entire ensemble of particles is considered, Mn is 716 kg mol−1. The fraction of small particles leads to polymer with Mn of 805 kg mol−1 and for the larger particles Mn is 657 kg mol−1.
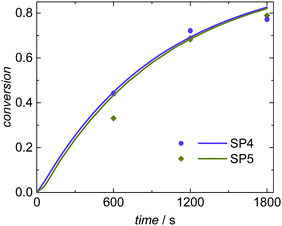
The simulated and experimentally determined conversion vs. time data for SP4 and SP5 given in Fig. 8 show a good agreement as well. Both experiments and simulations show very similar conversion vs. time data at high (3.5 × 10−3 mol L−1; SP4) and low (0.8 × 10−3 mol L−1; SP5) KPS concentrations. The evaluation of the radical balance in aqueous phase indicates an increase of the initiation efficiency fentry with reduced KPS concentration. This trend is also described by Hawkett et al.6 For SP4 (high initiator concentration) an initiation efficiency of fentry = 0.29 is derived from the simulation. In comparison, for SP5 with decreased KPS concentration an initiation efficiency of fentry = 0.46 is determined. As discussed above, for a mean initiator concentration under otherwise similar conditions (SP1; cKPS = 1.8 × 10−3 mol L−1) an intermediate value of 0.38 was obtained for fentry. Due to these opposing variations in cKPS and fentry the radical flux is rather similar for SP1, SP4 and SP5. Consequently, there are just minor differences in the conversion vs. time data.
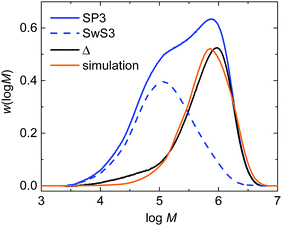
The experimental validation of the simulated molar mass distributions is depicted in Fig. 9 for experiment SP3. The figure shows the experimental distribution of the seed (SwS3) and the latex after the seeded emulsion polymerization (SP3). In addition, the simulated distribution is given. Since the seed was associated with a rather low Mn of 53.8 kg mol−1 and the product obtained during the seeded emulsion polymerization is of rather high Mn the molar mass distributions is bimodal, being indicative of both fractions of polymer. After the seeded emulsion polymerization is finalized the weight fraction of the seed inside the particle is 0.5. To obtain an estimate of the molar mass distribution (MMD) for the polymer of the seeded emulsion polymerization the MMD of the seed is multiplied with 0.5 and then subtracted from the MMD of SP3 resulting in the curve labeled with “Δ” in Fig. 9. The simulated MMD originates from modeling with an ensemble of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles and a total number of 4.519 × 107 discrete polymer chains. The comparison of the simulated MMD with the distribution labelled “Δ” shows a very good agreement. This result strongly supports the model approach chosen. It should be noted that all kinetic data is taken from literature. There are no adjustable parameters in the model.
000 particles and a total number of 4.519 × 107 discrete polymer chains. The comparison of the simulated MMD with the distribution labelled “Δ” shows a very good agreement. This result strongly supports the model approach chosen. It should be noted that all kinetic data is taken from literature. There are no adjustable parameters in the model.
Simulation design
It goes without saying that the time required for computing increases with the number of particles. The data given in Fig. 6–9 was obtained with an ensemble size of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles. This number is feasible, since a polymerization time of 60 min required a computing time of 124 min. Moreover, the resulting data set was sufficiently large to analyze subsets of the data, as shown in Fig. 7.
000 particles. This number is feasible, since a polymerization time of 60 min required a computing time of 124 min. Moreover, the resulting data set was sufficiently large to analyze subsets of the data, as shown in Fig. 7.
In the kMC simulation concentrations are expressed by discrete molecules. Due to the particle size, it is possible to simulate the particles with realistic molecule numbers. The continuous aqueous phase is coupled with a given number of discrete particles in this simulation approach. The particle number determines the dimension of the kMC model in the aqueous phase. The initiation and termination processes in the aqueous phase result in an initiation efficiency fentry of less than 1. This influences the radical balance of the seeded emulsion polymerization. The initiation efficiency is calculated from the balance of all propagation and termination reactions in the aqueous phase shown in Fig. 2. It is particularly important that the bimolecular termination in the kMC simulation is calculated with a statistically sound number of species R1. Using 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles, a quasi-stationary molecule number R1 of about 1000 is observed, which corresponds to a concentration of about 5 × 10−8 mol L−1. As a result, at least 10
000 particles, a quasi-stationary molecule number R1 of about 1000 is observed, which corresponds to a concentration of about 5 × 10−8 mol L−1. As a result, at least 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles should be used in the simulation.
000 particles should be used in the simulation.
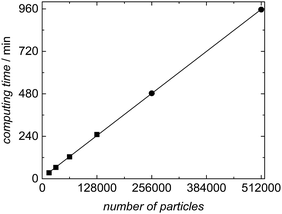
The variation of computing time with the number of particles was evaluated systematically for experiment SP1 to show which sample sizes are feasible. The results are listed in Table 4 and plotted in Fig. 10. As already detailed in the section on software architecture the calculation of the kinetic model in aqueous phase and the distribution of the macroradicals is administered in the master process, while the associated slave processes perform the kMC simulations in the particles. The product of the number of slave processes and the number of particles per slave results in the total number of particles accounted for in the simulation. Table 4 lists the details for simulations of experiment SP1 for a polymerization of 60 min with the number of particles and slaves as well as the time required for computing. The ensemble size varied from 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 512
000 to 512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles with 16 or 64 slaves. The compute server used consists of a total of 16 hardware cores, which were used to full capacity exclusively for the simulations introduced here.
000 particles with 16 or 64 slaves. The compute server used consists of a total of 16 hardware cores, which were used to full capacity exclusively for the simulations introduced here.
| Particles | Slaves | Particles per slave | Computing time, min |
|---|---|---|---|
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 | 1000 | 34 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 | 2000 | 64 |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 | 4000 | 124 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 | 8000 | 250 |
256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
64 | 4000 | 483 |
512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
64 | 8000 | 956 |
 | ||
| Fig. 10 Correlation between computing time and number of particles for the simulation of experiment SP1 with a reaction time of 60 min. Further details are contained in Table 4. | ||
Fig. 10 demonstrates a linear increase in computing time with the number of particles. This finding reveals that the master-slave concept chosen is perfectly suited for parallelization of the simulation. The memory required for each particle in the kMC simulation increases with monomer conversion to around 125 kB, which depends on the particle size and the number of polymer chains inside the particle. Thus, the memory requirement of 8 GB for an ensemble size of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles may be considered as moderate.
000 particles may be considered as moderate.
Summary
The holistic modeling approach introduced for an ab initio kMC simulation of seeded emulsion polymerization enables to model a large ensemble of particles due to parallelization. The number of particles involved, and thus, the sample size can be selected freely depending on the requested result. Typically ensembles of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 were used for modeling. Additionally, simulations were performed up to 512
000 were used for modeling. Additionally, simulations were performed up to 512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles.
000 particles.
The simulation was successfully applied to the seeded emulsion polymerization of styrene. A termination model was used, which allows for the calculation of an individual termination rate coefficient in each MC step for every macroradical in a particle. The termination model considers the individual chain-length dependence of each radical and accounts for the variation of the termination rate coefficient with the polymer content in the particle. Each particle is simulated as a nanoreactor of realistic size. Therefore, it is possible to apply current kinetic models for kt derived for bulk polymerizations37,38 to emulsion polymerizations. The simulation results were validated on the basis of experimental data. Very good agreement with respect to conversion vs. time data and molar mass distributions was observed using kinetic parameters published without any adjustments of these parameters. It is shown that the simulation is sensitive to particle size distribution and styrene concentration in the particles. This new kMC modeling approach allows for deep insight into the molar mass distribution in individual particles. The simulations allow to establish correlations between particle size, conversion and molar mass distribution. This information may be derived for individual particles or pre-defined subsets of particles. In future, the validated model will be used for more complex polymerization systems.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Computing Centre of the Technical University of Clausthal for the provision of computing resources and especially Frank Ebeling for the administration of the compute servers.References
- R. G. Gilbert, Emulsion Polymerization: A Mechanistic Approach, Academic Press, London, UK, 1995 Search PubMed.
- S. C. Thickett and R. G. Gilbert, Polymer, 2007, 48, 6965–6991 CrossRef CAS.
- P. Bataille, E. T. Van and Q. B. Pham, J. Polym. Sci., Part A: Polym. Chem., 1982, 20, 795–810 CrossRef CAS.
- S. W. Prescott, M. J. Ballard and R. G. Gilbert, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 1076–1089 CrossRef CAS.
- W. D. Harkins, J. Am. Chem. Soc., 1947, 69, 1428–1444 CrossRef CAS PubMed.
- B. S. Hawkett, D. H. Napper and R. G. Gilbert, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 1323–1343 RSC.
- K. Y. van Berkel, G. T. Russell and R. G. Gilbert, Macromolecules, 2003, 36, 3921–3931 CrossRef CAS.
- I. A. Maxwell, B. R. Morrison, D. H. Napper and R. G. Gilbert, Macromolecules, 1991, 24, 1629–1640 CrossRef CAS.
- N. Sheibat-Othman, H. M. Vale, J. M. Pohn and T. F. L. McKenna, Macromol. React. Eng., 2017, 11, 1600059 CrossRef.
- E. M. Coen, R. G. Gilbert, B. R. Morrison, H. Leube and S. Peach, Polymer, 1998, 39, 7099–7112 CrossRef CAS.
- H. M. Vale and T. F. McKenna, Ind. Eng. Chem. Res., 2009, 48, 5193–5210 CrossRef CAS.
- E. M. Coen, S. Peach, B. R. Morrison and R. G. Gilbert, Polymer, 2004, 45, 3595–3608 CrossRef CAS.
- S. M. Jung and V. G. Gomes, Chem. Eng. Sci., 2011, 66, 4251–4260 CrossRef CAS.
- B. R. Morrison, B. S. Casey, I. Lacik, G. L. Leslie, D. F. Sangster, R. G. Gilbert and D. H. Napper, J. Polym. Sci., Part A: Polym. Chem., 1994, 32, 631–649 CrossRef CAS.
- H. A. S. Schoonbrood, A. L. German and R. G. Gilbert, Macromolecules, 1995, 38, 34–49 CrossRef.
- C. M. Fellows, R. D. Murison and G. T. Russel, Macromol. Theory Simul., 2011, 20, 425–432 CrossRef CAS.
- N. Friis and A. E. Hamielec, ACS Symp. Ser., 1976, 24, 82–91 CrossRef CAS.
- B. S. Casey, B. R. Morrison, I. A. Maxwell, R. G. Gilbert and D. H. Napper, J. Polym. Sci., Part A: Polym. Chem., 1994, 32, 605–630 CrossRef CAS.
- A. L. T. Brandão, J. B. P. Soares, J. C. Pinto and A. L. Alberton, Macromol. React. Eng., 2015, 9, 141–185 CrossRef.
- P. H. M. van Steeneberge, D. R. D’hooge, Y. Wang, M. Zhong, M.-F. Reyniers, D. Konkolewicz, K. Matyjaszewski and G. B. Marin, Macromolecules, 2012, 45, 8519–8531 CrossRef.
- L. Wang and L. J. Broadbelt, Macromol. Theory Simul., 2011, 20, 191–204 CrossRef CAS.
- P. H. M. van Steeneberge, D. R. D’hooge, M.-F. Reyniers and G. B. Marin, Chem. Eng. Sci., 2014, 110, 185–199 CrossRef.
- H. Gao, I. A. Konstantinov, S. G. Arturo and L. J. Broadbelt, Chem. Eng. J., 2017, 327, 906–913 CrossRef CAS.
- L. Wang and L. J. Broadbelt, Macromol. Theory Simul., 2011, 20, 54–64 CrossRef CAS.
- P. H. M. van Steeneberge, J. Vandenbergh, D. R. D’hooge, M.-F. Reyniers, P. J. Adriaensens, L. Lutsen, D. J. M. Vanderzande and G. B. Marin, Macromolecules, 2011, 44, 8716–8726 CrossRef.
- S. Hamzehlou, Y. Reyes and J. R. Leiza, Macromolecules, 2013, 46, 9064–9073 CrossRef CAS.
- S. Lazzari, S. Hamzehlou, Y. Reyes, J. R. Leiza, M. R. P. F. N. Costa, R. C. S. Dias and G. Storti, Macromol. React. Eng., 2014, 8, 678–695 CrossRef CAS.
- G. Arzamendi and J. R. Leiza, Ind. Eng. Chem. Res., 2008, 47, 5934–5947 CrossRef CAS.
- S. Hamzehlou, N. Ballard, P. Carretero, M. Paulis, J. M. Asua, Y. Reyes and J. R. Leiza, Polymer, 2014, 19, 4801–4811 CrossRef.
- J. Strubbs, R. Carrier and D. C. Sundberg, Macromol. Theory Simul., 2008, 17, 147–162 CrossRef.
- M. Drache, B. Hosemann, T. Laba and S. Beuermann, Macromol. Theory Simul., 2015, 24, 301–310 CrossRef CAS.
- B. Hosemann, M. Drache and S. Beuermann, Macromol. Symp., 2016, 360, 17–25 CrossRef.
- M. Drache and G. Drache, Polymers, 2012, 4, 1416–1442 CrossRef.
- D. T. Gillespie, J. Phys. Chem., 1977, 81, 2340–2361 CrossRef CAS.
- M. Buback, R. G. Gilbert, R. A. Hutchinson, B. Klumperman, F.-D. Kuchta, B. G. Manders, K. F. O’Driscoll, G. T. Russell and J. Schweer, Macromol. Chem. Phys., 1995, 196, 3267–3280 CrossRef CAS.
- H. Kapfenstein-Doak, C. Barner-Kowollik, T. P. Davis and J. Schweer, Macromolecules, 2001, 34, 2822–2829 CrossRef CAS.
- H. Kattner and M. Buback, Macromolecules, 2015, 48, 309–315 CrossRef CAS.
- H. Kattner and M. Buback, Macromolecules, 2017, 50, 5308–5314 CrossRef CAS.
- R. Winschel, PhD thesis, Universität Hamburg, 2004.
- Open MPI: Open Source High Performance Computing, http://https://www.open-mpi.org/, accessed November 2017.
- S. Beuermann, Macromolecules, 2002, 35, 9300–9305 CrossRef CAS.
- W. H. Lane, Ind. Eng. Chem., Anal. Ed., 1946, 18, 295–296 CrossRef CAS.
- A. Bovey and I. M. Kolthoff, J. Polym. Sci., Part A: Polym. Chem., 1950, 5, 487–504 Search PubMed.
- K. Tauer, R. Deckwer, I. Kühn and C. Schellenberg, Colloid Polym. Sci., 1999, 277, 607–626 CAS.
- G. V. Schultz, Z. Phys. Chem., 1956, 8, 290–317 CrossRef.
- M. Buback, M. Egorov, R. G. Gilbert, V. Kaminsky, O. F. Olaj, G. T. Russell, P. Vana and G. Zifferer, Macromol. Chem. Phys., 2002, 203, 2570–2582 CrossRef CAS.
- B. Friedman and B. O’Shaughnessy, Macromolecules, 1993, 26, 5726–5739 CrossRef CAS.
- F. Buschmann, Pattern-Oriented Software Architecture, Wiley, Chichester, UK, 2001 Search PubMed.
- W. Gropp, E. Lusk and A. Skjellum, Using MPI. Portable parallel programming with the message-passing interface, MIT Press, Cambridge, Massachusetts, 1999 Search PubMed.
- E. D. Sudol, M. S. El-Aasser and J. W. Vanderhoff, J. Polym. Sci., Part A: Polym. Chem., 1986, 24, 3499–3513 CrossRef CAS.
- M. Slawinski, M. A. J. Schellekens, J. Meuldijk, A. M. van Herk and A. L. German, J. Appl. Polym. Sci., 2000, 76, 1186–1196 CrossRef CAS.
| This journal is © the Owner Societies 2018 |