Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Near-room-temperature Chern insulator and Dirac spin-gapless semiconductor: nickel chloride monolayer
Junjie
He
 a,
Xiao
Li
a,
Xiao
Li
 *b,
Pengbo
Lyu
*b,
Pengbo
Lyu
 a and
Petr
Nachtigall
a and
Petr
Nachtigall
 *a
*a
aDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University in Prague, 128 43 Prague 2, Czech Republic. E-mail: lixiao150@gmail.com; petr.nachtigall@natur.cuni.cz
bDepartment of Physics, University of Texas at Austin, Austin, TX, USA
First published on 9th January 2017
Abstract
A great obstacle for practical applications of the quantum anomalous Hall (QAH) effect is the lack of suitable QAH materials (Chern insulators) with a large non-trivial band gap, room-temperature magnetic order and high carrier mobility. Based on first-principles calculations it is shown here that a nickel chloride (NiCl3) monolayer has all these characteristics. Thus, the NiCl3 monolayer represents a new class of Dirac materials with Dirac spin-gapless semiconducting properties and high-temperature ferromagnetism (∼400 K). Taking into account the spin–orbit coupling, the NiCl3 monolayer becomes an intrinsic Chern insulator with a large non-trivial band gap of ∼24 meV, corresponding to an operating temperature as high as ∼280 K at which the quantum anomalous Hall effect could be observed. The calculated large non-trivial gap, high Curie temperature and single-spin Dirac states reported herein for the NiCl3 monolayer led us to propose that this material gives a great promise for potential realization of a near-room temperature QAH effect and potential applications in spintronics. Last but not least the calculated Fermi velocities of Dirac fermions of about 4 × 105 m s−1 indicate very high mobility in NiCl3 monolayers.
1. Introduction
A Chern insulator or quantum anomalous Hall insulator is a novel topological phase of matter characterized by a finite Chern number and helical edge electron states within the bulk band gap.1 Without an external magnetic field, the internal magnetic exchange interaction (ferromagnetic or antiferromagnetic order) can break time-reversal symmetry (TRS) while opening a non-trivial spin–orbital coupling induced gap, giving rise to a quantized anomalous Hall conductivity.2 The helical edge states are robust against defects and impurities and, thus, such materials are attractive for applications in low power consumption electronic and spintronic devices.2 Introducing magnetic order to break the TRS in topological insulators (TIs), such as chromium-doped Bi2Te3,3 manganese doped HgTe quantum wells (QWs)4etc., is expected to be a promising route for realizing the quantum anomalous Hall (QAH) effect. Very recently, the QAH effect has been observed experimentally in the topological insulator Cr doped (Bi,Sb)2Te3 film5 at an extremely low temperature (below 30 mK) due to only a weak magnetic coupling and a corresponding small band gap. For practical applications it is crucial to search for QAH materials with a sizeable band gap, high Curie temperature (Tc), as well as a high carrier mobility.6 Recently, a variety of QAH materials have been predicted based on impurities,3,4,7 adatoms,8,9 or chemical decorations10 of graphene-like and Bi-based materials, and also in metal–organic-frameworks,11,12 interface structures13,14 and heterostructure materials (i.e. CrO2/TiO2, (Bi,Sb)2Te3/GdI2, and double perovskites).15–17 Most of these theoretically proposed materials show the QAH effect below the room-temperature Tc due to a weak magnetic order or a small spin–orbit coupling (SOC) gap.Spin-gapless semiconductors (SGSs), exhibiting a band gap in one of the spin channels and a zero band gap in the other, have received considerable attention lately due to their unique electronic properties and potential applications in novel spintronic devices.18 The Dirac spin-gapless semiconductors with half semi-Dirac states are based on a combination of single-spin massless Dirac fermions and half-semimetal with broken TRS. Such materials are particularly suitable for utilization of their electronic spin degrees in electronic devices.19–22 Accounting for SOC, the gap opening may trigger QAH insulator transition in one spin channel only, which has been predicted for a few systems, such as transition-metal intercalated epitaxial graphene on SiC(0001),17 and CrO2/TiO2 heterostructures.14 The search for a new member of the Dirac SGS family with the QAH effect is of great importance for both fundamental interest and practical applications.
Transition metal trichlorides (TMCl3), a family of layered materials with the general formula TMCl3 have unique electronic and magnetic properties.23–28 Among them, relatively weakly interacting layers of a 3D RuCl3 (dominated by van der Waals interactions) have been exfoliated into 2D materials from the bulk phase recently29 and the first-principles calculations demonstrate that the RuCl3 monolayer is metallic. Zhou et al.30 have recently indicated that the mixed metal chlorides (NiRuCl6) are intrinsic half-metal antiferromagnets, which can lead towards the QAH effect with an antiferromagnetic order. Based on the first principles calculations we found that the 2D NiCl3 monolayer, as another member of the TMH family, is an intrinsic Dirac spin-gapless semiconductor with a high temperature ferromagnetism. When SOC is taken into account, a large gap opening is found (24 meV at the HSE06 level), giving rise to the quantum anomalous Hall states. We further confirm that the NiCl3 monolayer has nontrivial topological Dirac-gap states characterized by a Chern number of C = −1 and chiral edge states. The physical origin of this QAH effect is due to both the intrinsic SOC and ferromagnetism of the NiCl3 monolayer.
2. Results and discussion
The structure of the NiCl3 monolayer is shown in Fig. 1a. Ni atoms form a 2D honeycomb lattice and each Ni atom is bonded to six Cl atoms in an octahedral environment. Geometry optimization carried out at the PBE level gives a lattice constant of 5.966 Å (Fig. 1b) and the dNi–Cl bond length is 2.60 Å. The vertical distance between the two halide planes is calculated to be 2.93 Å. The 2D Young's modulus for the NiCl3 monolayer is calculated as: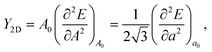 | (1) |
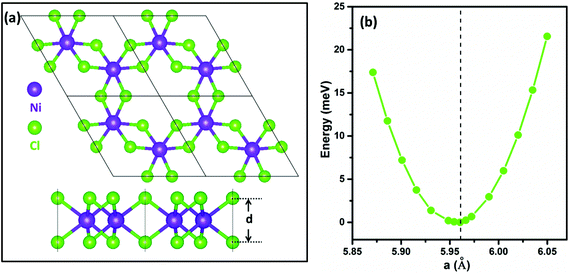 | ||
| Fig. 1 (a) The top and the side views of the optimized NiCl3 monolayer. (b) Variation of total energy with the lattice constant. | ||
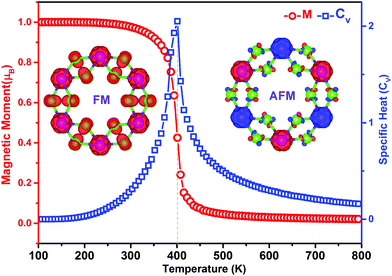
The spin-polarized FM ground state with a total magnetic moment of 2μB per unit cell was found for NiCl3 at 0 K. It corresponds to the d4↑3↓ spin configuration of Ni3+, which can be verified by the Bader charge analysis.34 To determine the preferred magnetic ground state structures of NiCl3 systems at T > 0, the collinear FM and AFM states were considered. The nearest-neighbor exchange-coupling parameter J (the second and the third neighbor exchange-coupling are found to be a magnitude smaller than the nearest-neighbor) can be extracted by mapping the total energies of the systems with different magnetic structures to the Ising model:
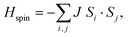 | (2) |
The Curie temperature TC is a key parameter for realization of the high temperature QAH effect and for spintronic applications. Based on the Weiss molecular-field theory (MFT), TC can be simply estimated as:
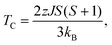 | (3) |
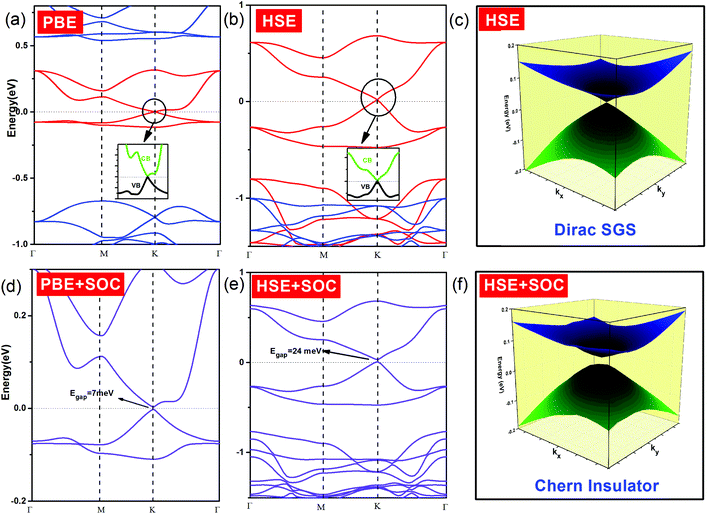
The band structure of the NiCl3 FM ground state is shown in Fig. 4. The spin-down channels of NiCl3 possess a 1.22 eV and 4.09 eV band gap at PBE and HSE06 levels, respectively, whereas the spin-up channel shows a gapless semiconductor feature with a linear dispersion relation around the Fermi level. The spin-polarized massless Dirac fermions are found in the spin up channels of NiCl3 at the high-symmetry K point of the Brillouin zone. The electronic structure of NiCl3 shows rather rare Dirac spin-gapless semiconductor characteristics that are essential for potential high-speed spin filter devices. To further investigate the distribution of the linear dispersion relation in the Brillouin zone, the corresponding three dimensional band structures are also presented (Fig. 4c). The calculated Fermi velocities (υF) of Dirac fermions are about 4 × 105 m s−1 for NiCl3 monolayers at the HSE06 level, a value that is approximately half of that found for graphene (8 × 105 m s−1).36
Dirac materials, such as graphene, silicene, germanene, etc. are characterized by Dirac states composed of p-orbitals with weak spin–orbital couplings. Thus, SOC opens just a small gap, making these materials the Z2 topological insulators with TRS protected edged states. However, the Dirac states of NiCl3 are mainly derived from the Ni-d orbitals. The larger SOC gap of Ni-d orbitals with the broken TRS may lead to the Chern insulator and QAH effect. The SOC gap was calculated by relativistic PBE + SOC calculations to be 7 meV (Fig. 4). However, SOC gaps calculated at the HSE06 level are considered more reliable and they are often comparable with experimental values. The HSE06 + SOC calculations show the 24 meV gap which is sufficiently large for the QAH effect to be operative at the temperature as high as 280 K. The Chern insulator states of the NiCl3 monolayer can be confirmed by the non-zero Chern numbers (C) calculated from the k-space integral of the Berry curvature (Ω(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )) of all the states below the Fermi level using the formula of Kubo:35–37
)) of all the states below the Fermi level using the formula of Kubo:35–37
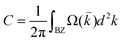 | (4) |
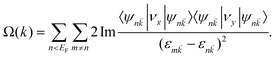 | (5) |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) is the spinor Bloch wave function of band n with the corresponding eigenenergy εn
is the spinor Bloch wave function of band n with the corresponding eigenenergy εn![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) . νx and νy are the i-th Cartesian components of the velocity operator.
. νx and νy are the i-th Cartesian components of the velocity operator.
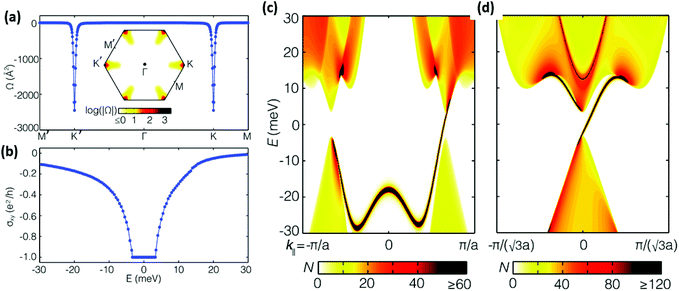
The Berry curvature Ω(![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ) along the high-symmetry direction (M′–K′–Γ–K–M) has two sharp spikes of the same sign located at the K and K′ points as shown in Fig. 5a. By integrating the Berry curvature in the entire Brillouin zone, the calculated Chern number C is −1 with a non-trivial topological state. As expected from the non-zero Chern number, the anomalous Hall conductivity shows a quantized charge Hall plateau of σxy = Ce2/h when the Fermi level is located in the insulating gap of the spin-up Dirac cone.
) along the high-symmetry direction (M′–K′–Γ–K–M) has two sharp spikes of the same sign located at the K and K′ points as shown in Fig. 5a. By integrating the Berry curvature in the entire Brillouin zone, the calculated Chern number C is −1 with a non-trivial topological state. As expected from the non-zero Chern number, the anomalous Hall conductivity shows a quantized charge Hall plateau of σxy = Ce2/h when the Fermi level is located in the insulating gap of the spin-up Dirac cone.
The existence of topologically protected chiral edge states is one of the most important consequences of the QAH state. To further reveal the nontrivial topological nature of the NiCl3 monolayer, we calculate the edge states of the NiCl3 monolayer with zigzag and armchair insulators using Green's functions based on Wannier functions obtained from PBE calculations, which reduces the cost of calculations while it does not change the topology of the electronic structure, besides a smaller band of 7 meV. As shown in Fig. 5, the nontrivial edge states (dark line) connecting the valence and conduction bands cross the insulating gap of the Dirac cone. The appearance of only one chiral edge state is consistent with the calculated Chern number C = −1, confirming the nontrivial topological nature of the NiCl3 monolayer. The calculated gap of 24 meV corresponds roughly to 280 K, leading us to conclude that the QAH effect in NiCl3 is expected to be robust up to 280 K. This is three orders of magnitude higher than the experimental temperature (<100 mK) at which QAH was observed for a Cr doped Bi2Se3 film.5 Furthermore, the FM ordering temperature as high as 400 K for NiCl3 is large enough to retain the QAH phase in the above-mentioned temperature range. The single spin Dirac fermion mediated topological properties of the NiCl3 monolayer show a great potential to generate the QAH effect. Moreover, manipulation of valley degrees of freedom for electrons may result in potential applications in nanoelectronic devices. The valley polarized edge states can be used as a valley filter analogous to a “spin filter”.38,39 The 2D mirror symmetry breaking in TMCl3 materials leads to Rashba SOC, which may lead to the valley-polarized edge state.40 However, Fig. 5a shows that Berry phases of two valleys are nearly identical with π contribution in each valley. The edge states in Fig. 5c connect the VB of the left valley and the CB of the right valley. Therefore, there is no observable valley-polarized edge state in NiCl3. The valley-polarized edge states based on considerable Rashba SOC may be found in other TMCl3 layered materials.
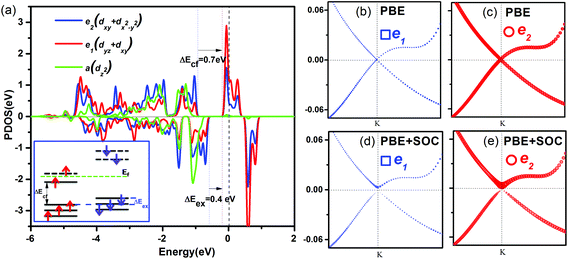
Finally, the PDOS and orbital-projected band structures around the Fermi level were calculated for the NiCl3 monolayer to gain insight into the origin of electronic, magnetic and topological properties (Fig. 6). Under the distorted octahedral crystal field of Cl atoms, the d orbital of Ni would be split into e1 (dxz, dyz), e2 (dxy, dx2−y2) and a1 (dz2) states. Based on Griffith's crystal field theory, the spin states of TM ions can be determined by the relative strength between crystal field splitting (ΔEcf) and Hund exchange splitting (ΔEex) of d orbitals. The exchange splitting (0.4 eV) is smaller than the crystal field splitting (0.7 eV) for the NiCl3 monolayer resulting in a low spin (1μB) state which is in agreement with the Ni(d↑4↓3) spin configuration. The states near the Fermi level have main contributions from the e1 and e2 states in [−0.2, 0.44 eV] windows, while the a1 state does not contribute significantly. The partially occupied e1 and e2 orbitals around the Fermi level form a Dirac point in the NiCl3 monolayer. PDOS for e1 and e2 orbitals are shown in Fig. 6 together with orbital-projected band structures. The states near the Fermi level are dominated by e2 orbitals with only a small contribution from e1 orbitals. Without SOC, both VB and CB show an equivalent weight for e1 and e2 states. Calculations with SOC show significantly increased contributions of both e1 and e2 in CB while the e1 and e2 contributions to VB decrease. As a result, the degeneracy of e1 levels (and similarly the degeneracy of e2 levels) around the Dirac point is lifted, opening thus a global energy gap between CB and VB bands (Fig. 6b). The SOC results in the significant changes of e1 and e2 orbital energies and their contributions to CB and VB and consequently it plays a crucial role in the topological properties of the NiCl3 monolayer.
3. Conclusions
DFT calculations were used in a systematic investigation of the stability, and electronic and magnetic structures of NiCl3 monolayers. The thermal and dynamical stabilities have been confirmed by phonon calculations and ab initio molecular dynamics simulations. The NiCl3 monolayers show the Dirac spin-gapless semiconducting characteristics and high-temperature ferromagnetism. The Monte Carlo simulations based on the Ising model demonstrate that the Curie temperature of the NiCl3 monolayer is estimated to be as high as 400 K. In addition, a Fermi velocity (vF) in the NiCl3 monolayer is calculated to be 4 × 105 m s−1, which is comparable to graphene (8 × 105 m s−1). Taking the spin–orbit coupling into account, the NiCl3 monolayer becomes an intrinsic Chern insulator with a large non-trivial band gap of about 24 meV, corresponding to an operating temperature of 280 K. The large non-trivial gap, high Curie temperature and single-spin Dirac states for NiCl3 monolayers give rise to great expectations for both the realization of near room temperature QAH effect and potential applications in spintronics.4. Methods and computational details
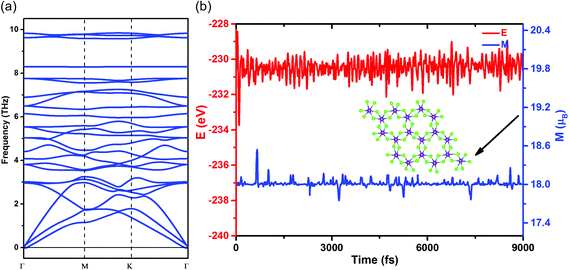
All calculations were performed using the Vienna ab initio simulation package (VASP)41,42 within the generalized gradient approximation, using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.43 Electronic properties (SOC in particular) were also calculated with the hybrid HSE06 functional. Interactions between electrons and nuclei were described by the projector-augmented wave (PAW) method. The criteria of energy and atom force convergence were set to 10−6 eV and 0.001 eV Å−1, respectively. A plane-wave kinetic energy cutoff of 500 eV was employed. The vacuum space of 15 Å along the NiCl3 normal was adopted for calculations on monolayers. The Brillouin zone (BZ) was sampled using 15 × 15 × 1 gamma-centered Monkhorst–Pack grids for the calculations of relaxation and electronic structures. Furthermore, to examine the thermal stability of NiCl3, the ab initio molecular dynamics (AIMD) simulations at 300 K were performed using the Nosé heat bath approach in a canonical ensemble. A 3 × 3 × 1 supercell of the NiCl3 monolayer was used in MD simulations. The phonon frequencies were calculated using a finite displacement approach as implemented in the PHONOPY code, in which a 2 × 2 × 1 supercell and a displacement of 0.01 Å from the equilibrium atomic positions were employed.44,45 The electronic properties of the NiCl3 monolayer obtained by VASP have been further reproduced by the QUANTUM ESPRESSO package,46 with the norm-conserving pseudopotentials from the PS library47 and a 120 Ry plane wave cutoff. Based on the Wannier functions obtained from the first-principles calculations in QUANTUM ESPRESSO,48–50 we construct the edge Green's function of the semi-infinite NiCl3 monolayer. The edge spectral density of states, computed by the edge Green's function, shows the energy dispersion of edge states.51 The Berry curvature and the anomalous Hall conductivity are also calculated by the Wannier interpolation.49Acknowledgements
This work was funded by the Czech Science Foundation Grant No. P106/12/G015 and by OP VVV “Excellent Research Teams”, project No. CZ.02.1.01/0.0/0.0/15_003/0000417 – CUCAM. Support by the 973 Program (Projects 2013CB921900), DOE (DE-FG03-02ER45958, Division of Materials Science and Engineering) and Welch Foundation (F-1255) is also acknowledged (XL).References
- F. D. M. Haldane, Phys. Rev. Lett., 1988, 61, 2015 CrossRef CAS PubMed.
- B. I. Halperin, Phys. Rev. B: Condens. Matter, 1982, 25, 2185 CrossRef.
- R. Yu, W. Zhang, H. J. Zhang, S. C. Zhang, X. Dai and Z. Fang, Science, 2010, 329, 61–64 CrossRef CAS PubMed.
- C. X. Liu, X. L. Qi, X. Dai, Z. Fang and S. C. Zhang, Phys. Rev. Lett., 2008, 101, 146802 CrossRef PubMed.
- C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo and Z. Q. Ji, Science, 2013, 340, 167–170 CrossRef CAS PubMed.
- H. Weng, R. Yu, X. Hu, X. Dai and Z. Fang, Adv. Phys., 2015, 64, 227–282 CrossRef.
- H. Jiang, Z. Qiao, H. Liu and Q. Niu, Phys. Rev. B: Condens. Matter, 2012, 85, 045445 CrossRef.
- H. Zhang, C. Lazo, S. Blügel, S. Heinze and Y. Mokrousov, Phys. Rev. Lett., 2012, 108, 056802 CrossRef PubMed.
- J. Liu, S. Y. Park, K. F. Garrity and D. Vanderbilt, Phys. Rev. Lett., 2016, 117, 257201 CrossRef PubMed.
- S. C. Wu, G. Shan and B. Yan, Phys. Rev. Lett., 2014, 113, 256401 CrossRef PubMed.
- L. Dong, Y. Kim, D. Er, A. M. Rappe and V. B. Shenoy, Phys. Rev. Lett., 2016, 116, 096601 CrossRef PubMed.
- Z. F. Wang, Z. Liu and F. Liu, Phys. Rev. Lett., 2013, 110, 196801 CrossRef CAS PubMed.
- H. Fu, Z. Liu, C. Lian, J. Zhang, H. Li, J. T. Sun and S. Meng, Phys. Rev. B: Condens. Matter, 2016, 94, 035427 CrossRef.
- K. F. Garrity and D. Vanderbilt, Phys. Rev. B: Condens. Matter, 2014, 90, 121103 CrossRef.
- A. M. Cook and A. Paramekanti, Phys. Rev. Lett., 2014, 113, 077203 CrossRef PubMed.
- T. Cai, X. Li, F. Wang, S. Ju, J. Feng and C. D. Gong, Nano Lett., 2015, 15, 6434–6439 CrossRef CAS PubMed.
- G. Xu, J. Wang, C. Felser, X. L. Qi and S. C. Zhang, Nano Lett., 2015, 15, 2019–2023 CrossRef CAS PubMed.
- X. L. Wang, Phys. Rev. Lett., 2008, 100, 156404 CrossRef CAS PubMed.
- V. Pardo and W. E. Pickett, Phys. Rev. Lett., 2009, 102, 166803 CrossRef PubMed.
- H. Ishizuka and Y. Motome, Phys. Rev. Lett., 2012, 109, 237207 CrossRef PubMed.
- Y. Li, D. West, H. Huang, J. Li, S. B. Zhang and W. Duan, Phys. Rev. B: Condens. Matter, 2015, 92, 201403 CrossRef.
- X. L. Wang, 2016, arXiv:1607.06057.
- M. A. McGuire, H. Dixit, V. R. Cooper and B. C. Sales, Chem. Mater., 2015, 27, 612–620 CrossRef CAS.
- H. Hillebrecht, P. J. Schmidt, H. W. Rotter, G. Thiele, P. Zönnchen, H. Bengel and M. H. Whangbo, J. Alloys Compd., 1997, 246, 70–79 CrossRef CAS.
- F. Hulliger, Structural chemistry of layer-type phases, Springer Science & Business Media, 2012 Search PubMed.
- J. He, S. Ma, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 2518–2526 RSC.
- W. B. Zhang, Q. Qu, P. Zhu and C. H. Lam, J. Mater. Chem. C, 2015, 3, 12457–12468 RSC.
- J. Liu, Q. Sun, Y. Kawazoe and P. Jena, Phys. Chem. Chem. Phys., 2016, 18, 8777–8784 RSC.
- P. Miró, M. Audiffred and T. Heine, Chem. Soc. Rev., 2014, 43, 6537–6554 RSC.
- P. Zhou, C. Q. Sun and L. Z. Sun, Nano Lett., 2016, 16(10), 6325–6330 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Phys. Rev. Lett., 2009, 102(23), 236804 CrossRef CAS PubMed.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter, 2009, 80(15), 155453 CrossRef.
- G. Henkelman, A. Arnaldsson and H. J́lonsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- D. J. Thouless, M. Kohmoto, M. P. Nightingale and M. Den Nijs, Phys. Rev. Lett., 1982, 49, 405 CrossRef CAS.
- Y. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D. S. Wang and Q. Niu, Phys. Rev. Lett., 2004, 92, 037204 CrossRef PubMed.
- D. Xiao, M. C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959 CrossRef CAS.
- A. Rycerz, J. Tworzydło and C. W. J. Beenakker, Nat. Phys., 2007, 3, 172–175 CrossRef CAS.
- S. G. Cheng, J. Zhou, H. Jiang and Q. F. Sun, New J. Phys., 2016, 18(10), 103024 CrossRef.
- T. Zhou, J. Zhang, Y. Xue, B. Zhao, H. Zhang, H. Jiang and Z. Yang, 2016, arXiv preprint arXiv:1611.04715.
- G. Kresse and H. Jürgen, Phys. Rev. B: Condens. Matter, 1993, 47, 558 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter, 2008, 78, 134106 CrossRef.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed http://www.quantum-espresso.org .
- Pseudopotentials are available at http://qe-forge.org/gf/project/pslibrary.
- N. Marzari and D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1997, 56, 12847 CrossRef CAS.
- A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS.
- M. L. Sancho, J. L. Sancho and J. Rubio, J. Phys. F: Met. Phys., 1984, 14, 1205 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |