Active sites engineering leads to exceptional ORR and OER bifunctionality in P,N Co-doped graphene frameworks

Abstract

Bifunctional catalysts for the oxygen reduction reaction (ORR) and the oxygen evolution reaction (OER) are highly desirable for rechargeable metal–air batteries and regenerative fuel cells. However, the commercial oxygen electrocatalysts (mainly noble metal based) can only exhibit either ORR or OER activity and also suffer from inherent cost and stability issues. It remains challenging to achieve efficient ORR and OER bifunctionality on a single catalyst. Metal-free structures offer relatively large scope for this bifunctionality to be engineered within one catalyst, together with improved cost-effectiveness and durability. Herein, by closely coupled computational design and experimental development, highly effective bifunctionality was achieved in a phosphorus and nitrogen co-doped graphene framework (PNGF) – with both ORR and OER activities reaching the theoretical limits of metal-free catalysts, superior to their noble metal counterparts in both (bi)functionality and durability. In particular, with the identification of active P–N sites for OER and N-doped sites for ORR, we successfully intensified these sites by one-pot synthesis to tailor the PNGF. The resulting catalyst achieved an ORR potential of 0.845 V vs. RHE at 3 mA cm⁻² and an OER potential of 1.55 V vs. RHE at 10 mA cm⁻². Its combined ORR and OER overpotential of 705 mV is much lower than those previously reported for metal-free bifunctional catalysts.

---

Broader context

Rechargeable metal–air batteries and regenerative fuel cells are very promising technologies for energy storage in portable devices, electric vehicles and the grid. However, such practical applications are hindered by expensive air electrode catalysts and overall efficiency, particularly at a large scale. Moreover, the commercial noble metal catalysts such as Pt/C and Ir/C only exhibit mono-functional activity for either the oxygen reduction or evolution reaction (ORR or OER). Metal-free materials are increasingly considered as cost-effective alternatives, but their catalytic activities, especially OER performance, are yet to match their metallic counterparts. Here, by closely coupling theory and experiment, we have identified the most effective catalytic sites in phosphorus-nitrogen co-doped graphene frameworks (PNGF), and then engineered the synthetic formulations to enrich such sites. The developed electrocatalysts show highly efficient bifunctionality for both ORR and OER. The ORR/OER potential gap is reduced successively from the initial 1.252 mV, to 1.037 mV with P,N co-doping, then to 795 mV after PNGF optimisation, and finally to 705 mV after purposeful enrichment of the active P–N sites. This design strategy, synthesis approach and the efficient catalysts offer great opportunities for the development of highly cost-effective energy storage technologies on a large scale.

Introduction

The oxygen reduction reaction (ORR) and oxygen evolution reaction (OER) are crucial for energy conversion and storage.^1–4 The development of efficient bifunctional ORR/OER catalysts has attracted significant interest as a result of the increasing demand for rechargeable metal–air batteries and regenerative fuel cells of further improved performance.^5–10 However, to date, the commercial noble metals catalysts, such as platinum or iridium/ruthenium based materials, can only exhibit either ORR or OER activity rather than both, in addition to their cost and stability issues, which greatly hinder their large-scale applications.^11–13

Fundamentally, an effective bifunctional catalyst is achieved when both OER and ORR overpotentials are minimised. For these multi-electron transfer reactions, the overpotentials are constrained by the scaling relationships among the binding energies of reaction intermediates such as *O, *OH and *OOH (* stands for adsorbed state of the respective species).^14–17 For instance, it was shown in our previous study that the optimum ORR limiting potential of 0.8 V for nitrogen-doped carbon is determined by a ‘constant’ gap of 3.33 eV between the adsorption of *O and *OOH.¹⁸ More importantly, the scaling relationship implies that it is very challenging to achieve effective ORR/OER bifunctionality in a single catalyst. Hence, an ideal bifunctional catalyst needs to contain a substantial amount of effective ORR and OER active sites simultaneously. Heteroatom-doped metal-free carbon or graphene based materials are likely candidates for such a purpose.^18–20 Heteroatom co-doping remains the most robust approach to tuning the catalytic activities of metal-free materials. The synergy between co-dopants and the corresponding catalytic sites has never been fully understood, and is still one of the key challenges impeding the rational design of high-performing metal-free catalysts.^21–24

Recently, phosphorus and nitrogen co-doped carbons were reported to show bifunctional ORR and OER activities,^8,25 but the specific active sites have yet to be resolved. Note that the N-doping has been determined to promote the electron donation from the catalyst to the O₂ molecule, facilitating ORR;^18,26 while the role of P-doping is unclear, though its relatively low electronegativity may promote OER.

To tackle such challenges, we firstly used the density functional theory (DFT) simulations to identify the P-doped and P,N co-doped structures with the highest ORR/OER activity, and then formulated and experimentally populated the active sites into metal-free catalysts via one-pot synthesis. Since the ORR/OER activity depends on the binding of reaction intermediates, the lifetime of which is too short to be detected experimentally, first-principles simulations are powerful for understanding the reaction mechanisms and guiding the design and synthesis of the targeted bifunctional catalysts.¹⁴ Herein, we further demonstrated that the simulated binding energies of the proposed catalytic structures are comparable to the experimentally measured values of corresponding binding configurations from X-ray photoelectron spectroscopy (XPS), thus confirming another robust link between simulation and experiment.

Our closely coupled first-principles simulations and experiments successfully elucidated that the OER activity of P,N co-doped carbon catalysts originates from the P–N bonds, while the ORR activity is due to different local structures that only contain the N dopant. In addition, the performance of either site is shown to be very close to the theoretical limit of metal-free catalysts for ORR or OER. Accordingly, the optimised bifunctional sample with a substantial amount of targeted catalytic sites shows superior ORR and OER activity for the respective performance of commercial noble metal catalysts; the potential gap of 705 mV between the OER current density of 10 mA cm⁻² and ORR of 3 mA cm⁻² is significantly smaller than the previously reported metal-free bifunctional catalysts as well.^8,9,27–36 Such improvement in the performance directly results from active site engineering by well-coupled computational design and experimental development in the present report. Moreover, the durability of the optimal catalysts outperforms that of their noble metal counterparts.

Methods

Theoretical simulations

Edges and bulk surfaces of P,N doped graphenes were investigated for carbon material catalysts as shown in Fig. 1 and Fig. S1 (ESI†). The curvature effect was also studied to control the ratio between sp² and sp³ hybridization of different types of local carbon frameworks. The Car–Parrinello molecular dynamics (CPMD) simulations were performed to calculate the free energy barriers for activation of the O₂ molecule.^37,38 The simulation box contains about 200 atoms, including a bi-layer graphene, an O₂ molecule and water solution. The Blue Moon ensemble was employed at 300 K with a time step of 4.0 a.u.³⁹ The total MD time for each free energy profile was about 30 ps. The sampling of the Brillouin zone was restricted to the Γ point. The Troullier–Martins pseudopotentials (PP) were used for C, N, O and P.⁴⁰ The von Barth–Car PP was used for H.⁴¹ The GGA-HCTH exchange–correlation functional was adopted in a spin-polarized scheme.⁴² The multiplicity of the systems with odd numbers of electrons were set to two. For the systems with even numbers of electrons, one more N was doped in the bottom layer of bi-layer graphene to make it odd.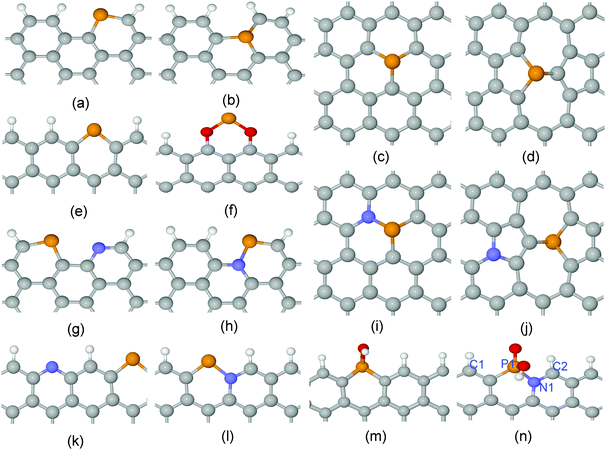

Fig. 1 Local atomic structures for (a) A-P-1, (b) A-P-3, (c) G-P-1, (d) SW-P-1, (e) Z-P-1, (f) Z-P-3, (g) A-PN-4, (h) A-PN-5, (i) G-PN-1, (j) SW-PN-3, (k) Z-PN-4, (l) Z-PN-5, (m) Z-P-1-OX1, and (n) Z-PN-5-OX2. The unit cells are shown in Fig. S1 (ESI†). “A” and “Z” stand for armchair and zigzag edges, respectively; “P” and “N” stand for phosphorus and nitrogen; “G” and “SW” denote perfect and Stone–Wales defected graphenes; “OX” stands for oxidized structure. The white, grey, blue, red and brown spheres denote H, C, N, O and P atoms, respectively.

Total energies were calculated by employing static DFT with Quantum ESPRESSO code.⁴³ The supercell contains about 60 atoms, as in our previous paper.^18,44 The generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE) was adopted for the exchange correlation functional in the DFT.⁴⁵ Spin polarization was considered for all the cases. The kinetic energy cutoffs for the wavefunction and the charge were set to 40 Ry and 400 Ry, respectively. The calculated total energies were converted to Gibbs free energies to obtain the ORR/OER limiting potentials as described in ESI.†

The theoretical X-ray photoelectron spectroscopy (XPS) was simulated by using the CP2K code.⁴⁶ The total energy difference (ΔSCF) method was employed.⁴⁷ The Gaussian and augmented plane wave (GAPW) all-electron formalism were used.⁴⁸ The 6-311G** basis set was used for C, N, O, P and H atomic orbitals. Exchange and correlation functionals were described by GGA-PBE. The cutoff energy for charge density for solving the Poisson equation was 280 Ry.

Experiments

All the chemicals such as graphite, Nafion, hydrogen peroxide, diammonium phosphate (DAP), ammonium dihydrogen phosphate (ADP) and cyanamide (CA) were used as received. Graphene oxide was synthesized by a modified Hummers’ method as in our previous papers.⁴⁹ The phosphorus and nitrogen co-doped graphene frameworks (PNGF) were prepared via a one-pot hydrothermal reaction using graphene oxide as the carbon source, DAP or ADP as the single phosphorus and nitrogen precursors, and/or CA as an extra nitrogen precursor, followed by freeze-drying with/without the high-temperature calcinations. The achieved samples were named PNGF_DAP, PNGF_ADP, PNGF_ADP(op), and PNGF(op), according to the corresponding synthesis conditions. DAP/ADP was chosen as the sole source of P/N dopants since they were supposed to be more likely to form P–N bonds. The extra CA as nitrogen precursor was chosen to further enhance the catalytic nitrogen doping. Details on the synthesis the P,N codoped carbon catalysts are described in Supporting Information. The chemical compositions of the catalysts were analyzed by X-ray photon spectroscopy (Thermo Scientific K-Alpha).

For electrochemical ORR/OER performance, rotating disk electrode (RDE) measurements were conducted in O₂-saturated 0.1 M KOH. RDE (glassy carbon tip, Metrohm) was used as the working electrode, Ag/AgCl (sat. KCl, Metrohm) was the reference electrode, and a platinum sheet (Metrohm) was used as the counter electrode. The electrolyte was saturated with pure oxygen. The scan rate for rotating voltammetry was 10 mV s⁻¹. The potentials obtained in this work were converted to the reversible hydrogen electrode (RHE) scale by a shift value of 0.965 V. For RDE, the electron transfer number (ETN) was calculated based on the Koutecky–Levich (K–L) equation. The potential cycling was conducted between 0.2 and 1.2 V vs. RHE for ORR, or between 1.2 and 2.0 V vs. RHE for OER, using a scan rate of 100 mV s⁻¹ for 5000 cycles. The chronoamperometry measurements were conducted at the potentials under which the current density reached 3 or 10 mA cm⁻² at 1600 rpm for ORR and OER, respectively, and lasted for 20 hours in total.

Results and discussion

Selective screening of P containing catalytic sites: structural stability, electronic properties and O₂ adsorption barriers

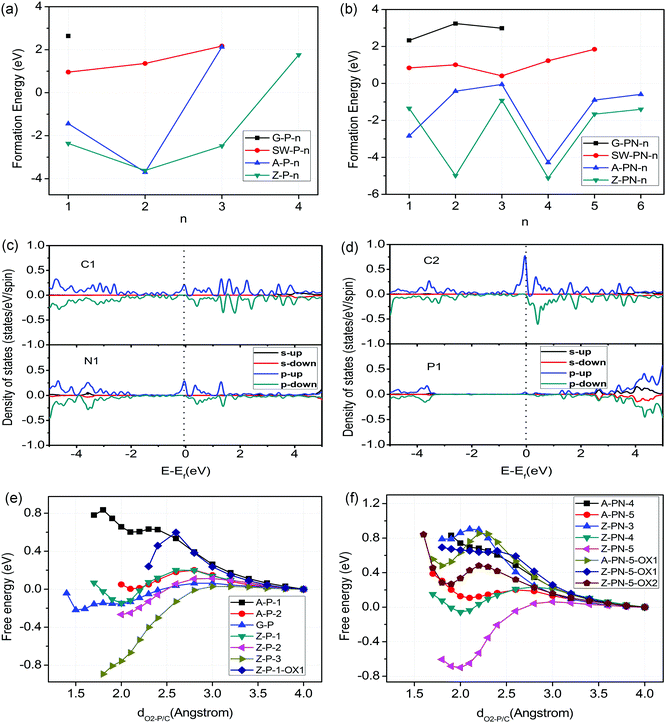
For heteroatom doped carbon based catalysts, different types of local microstructures may exist within the same material. The stability of these different structures was calculated first to shortlist the possible active sites before further study of their ORR/OER performance. The stability of N-doped carbon catalysts has been investigated systemically in one of our previous papers.¹⁸ However, the P atom is very different from the N atom, with a relatively large atomic radius and high electron donating properties as mentioned above. Here, we calculated the formation energies for four different cases of P doped and P,N co-doped graphene as shown in Fig. 1 and Fig. S1 (ESI†), which include the perfect surface, Stone–Wales defect, armchair edge, and zigzag edge of graphene. The details of formation energy calculations are described in the Supporting Information. The results related to the formation energies are shown in Fig. 2(a) and (b). Negative (or positive) formation energy denotes the exothermic (or endothermic) process. When the P atom is doped in the interior surface sites of graphene, such as the perfect surface and Stone–Wales defect surface mentioned above, it is endothermic for all the cases. The doped P atom always moves out of the planar surface when doped in such surfaces, due to its large atomic radius compared to the N atom. On the other hand, for most cases of armchair and zigzag edges, it is exothermic as shown in Fig. 2(a) and (b). Therefore, the P doped or P,N co-doped structures are mainly populated at the edges.

Fig. 2 Formation energy of (a) P doped structures and (b) P,N co-doped structures. (c) and (d) are the PDOS for the Z-PN-5-OX2 structure. (e) and (f) are O₂ adsorption/desorption barriers for P doped structures and P,N co-doped structures, respectively.

The densities of states (DOSs) of the shortlisted structures were calculated and are shown in Fig. 2(c) and (d) and Fig. S4 to S9 in the ESI.† The DOS at valence band maximum (VBM) and the conduction band minimum (CBM) are associated with electron donating and accepting mechanisms, which are employed for the selection of potential active sites for ORR/OER. For all the un-oxidized structures, the P site shows the highest DOSs just below the Fermi level, which makes it the most active to donate electrons to O₂, as shown in the Supporting Information. The O₂ adsorption/desorption free energy barriers for different structures are shown in Fig. 2(e) and (f). Here, the O₂ adsorption and desorption are involved in the ORR and OER processes, respectively, and control the kinetics for most of the cases. The results indicate that the P site is readily oxidized by an approaching O₂ molecule with a very low kinetic barrier. However, for further ORR electron transfer steps, the OH or O groups bound to P are rather difficult to remove as the P site is far too active, compared to N. Details of the oxidization states of P sites are discussed by free energy variation in Fig. 3. In this regard, the oxidized edge P sites are the most popular local structures.

Fig. 3 (a) Free energy variations of ORR/OER elementary steps for different P containing structures. (b) ORR/OER limiting potentials for Z-NP-5-OX2 and Stone–Wales defect structures. (c) Bifunctional ORR/OER activities of PNGA_DAP and PNGF_DAP_800 (inset: the electron transfer number and kinetic current density for ORR at 0.6 V vs. RHE). XPS (d) P2p and (e) N1s spectra for PNGF_DAP and PNGF_DAP_800.

For the P-doped oxidized structures, we consider the case of the “Z-P-1-OX1” structure, Fig. 3(m): a zigzag edge with a pyridine-like P attached with one OH group (oxidized Z-P-1 structure). The O₂ adsorption barrier for the P site of this structure is about 0.6 eV, while the edge C site is more difficult to activate according to the DOS in Fig. S8 of the ESI.† We will not consider the structure oxidized by two oxygen-related groups because no more active sites are available after two oxygen-related groups fully occupy the P site. However, the situation is different for the P,N co-doped oxidized structure, Z-PN-5-OX2 (oxidized Z-PN-5 structure) as shown in Fig. 1(n), where the P site can be fully occupied by one OH and one O group. For this structure, the C2 atomic site shows the highest DOS at both VBM and CBM, as shown in Fig. 2(c) and (d), which is selected as a possible active site for ORR/OER. The O₂ adsorption and desorption barriers for the Z-PN-5-OX2 structure are only 0.48 and 0.21 eV, respectively, as shown in Fig. 2(d), which implies that the kinetics for ORR/OER should be fast for this site. More details for ORR/OER thermodynamic potentials of these structures will be discussed in the following section.

Correlations between ORR/OER potentials and structures: linking simulations with experiments

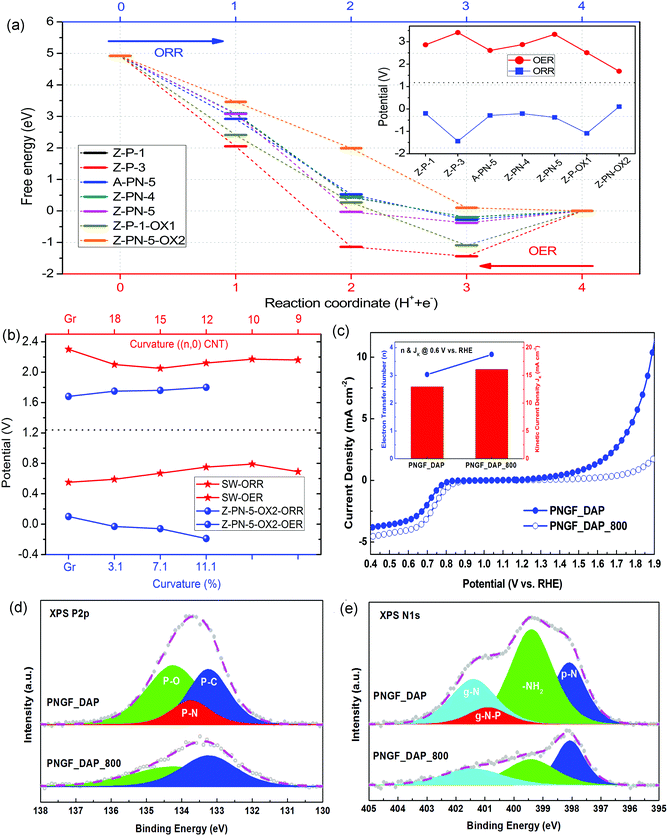
Theoretical limiting potentials can be calculated by DFT simulations, and then compared with the experimentally measured values, i.e., half-wave potentials for ORR. Here, the limiting potential for ORR/OER is defined as the maximum/minimum potential, respectively, under which all of the relevant elementary steps in each case are downhill in free energy. More details about the calculation methods are in the ESI.†

Fig. 3(a) shows the free energy variation for ORR/OER of the investigated structures for the four-electron process. The forward process is for ORR, and the backward process for OER. Note that the solvation energies for ORR and OER are a little different and that the free energy variation for OER in Fig. 3(a) will be modified accordingly for the calculation of limiting potentials as described in the ESI.†

For P-doped Z-P-1 and Z-P-3 structures, Fig. 3(a), the ORR cannot proceed to completion because the *OH intermediate cannot be removed under a positive potential. The corresponding OER potentials are as high as 2.64 and 3.19 V, respectively. These potentials are too high and far from the equilibrium of 1.23 V. If we consider the oxidized structure as the initial structure, Z-P-1-OX1, the last step of ORR is still endothermic. In short, there is no suitable P doped structure for either ORR or OER, which probably explains the poor catalytic activity of the metal-free catalysts only with P-doping.^50,51 For the P,N co-doped structures, we considered an armchair edge (A-PN-5), a zigzag edge with pyridine-like P and N (Z-PN-4), a zigzag edge with pyridine-like P and graphite-like N (Z-PN-5). The ORR/OER free energy variations for these structures are similar to that of Z-P-1, which makes it impossible for ORR to occur and OER occurs with high overpotentials.

However, if we consider an oxidized structure of Z-PN-5 as an initial structure (Z-PN-5-OX2), the P site is deactivated by oxidization but the edge C atom bonded to the graphite-like N is still active as indicated by the DOS in Fig. 2(c) and (d). Note that the doped pyridine-like P and graphite-like N tend to bond together, compared to the separated case as indicated by the formation energies shown in Fig. 2(b) and the structures in Fig. S1 (ESI†). For the Z-PN-5-OX2 structure, the ORR potential is also low at about 0.13 V, while the OER potential is significantly decreased to 1.68 V as shown in Fig. 3(b).

Therefore, we find that the P–N bond in the Z-PN-5-OX2 structure is a key factor that may control the OER performance. Our previous study indicates that curvature in carbon-based catalysts can tune the ratio of sp² and sp³ carbons, and thus the performance of ORR as well.¹⁸ Herein, the curvature effect is investigated for the most promising structures of Z-PN-5-OX2 to tune the ORR/OER limiting potential as shown in Fig. 3(b). Details on the curvature control are described in Fig. S10 of the ESI.† The results show that the curvature effect can tune the ORR/OER activity of Z-PN-5-OX2, but does not contribute much to the reduction of its limiting potentials. Hence, the best OER limiting potential for Z-PN-5-OX2 is still 1.68 V and it is not favourable for ORR even under curvature. We also put the ORR/OER performance of the N doped Stone–Wales (SW) structure for comparison, Fig. 3(b), which is suggested in our previous work to be the best metal-free active site for ORR.¹⁸ It is seen that the N doped SW defect structure can show an ORR limiting potential of about 0.8 V under curvature, while the corresponding OER limiting potential is always high and in the range of 2.0–2.5 V. Given that the scaling relation between *OH and *OOH for most sites in heteroatom doped carbon is ca. 3.33 eV,¹⁸ the overpotential of 0.43–0.45 V for Z-PN-5-OX2 in OER or SW in ORR is indeed very close to the theoretical limit of metal-free catalysts. Note that the simulated limiting potential is achieved under the assumption that reaction is completely thermodynamically favourable; the experimentally measured overpotentials for ORR and OER at a certain current density could be ca. 0.1 V smaller than the computationally predicted values. No matter what, it is clear from the simulation results that for a P,N co-doped carbon, the P–N bonds are favourable for OER and the local structures with solely N dopant contribute to ORR.

It is shown in our density of states (DOS) calculations, Fig. 2(c) and (d), that the ‘real’ active sites in the P/N co-doped structures (Z-PN-5-OX2) are the edge carbon atoms next to the nitrogen dopants, highlighted as ‘C2’ in Fig. 1(n). Hence, the P,N co-doping and N-doping employed in this work were considered to modify the electronic structure and the binding energy of reaction intermediates on carbon. Note that an effective catalytic site should bind intermediates neither too weakly nor too strongly, according to the Sabatier principle. The 1st and 4th elementary steps of proton-electron transfer are most likely to be the rate determining step (RDS) for ORR, while the 2nd and the 3rd steps are the RDS for OER, as shown in Fig. (3), due to the restriction of a scaling relationship. In our case, the P,N co-doping and N-doping clearly show the respective desirable bond strength for the relevant intermediates and steps (Fig. 3(a)), which are almost identical to the ideal bond strength of carbon based OER/ORR catalysts for the smallest thermodynamic barriers. Moreover, the corresponding O₂ desorption (Fig. 2(f)) and adsorption barriers of the above structures are also reasonably small, indicating good kinetics as well.

We then experimentally formed the P,N co-doped graphene framework (PNGF) containing the aforementioned P–N bonds to validate the computational predictions. Herein, we used diammonium phosphate (DAP, (NH₄)₂HPO₄) or ammonium dihydrogen phosphate (ADP, NH₄H₂PO₄) as the single P/N precursor, which facilitates the formation of P–N bonds at intermediate temperatures. We also demonstrated that a more balanced P/N ratio in ADP further enhances the concentration of P–N bonds in the final product.

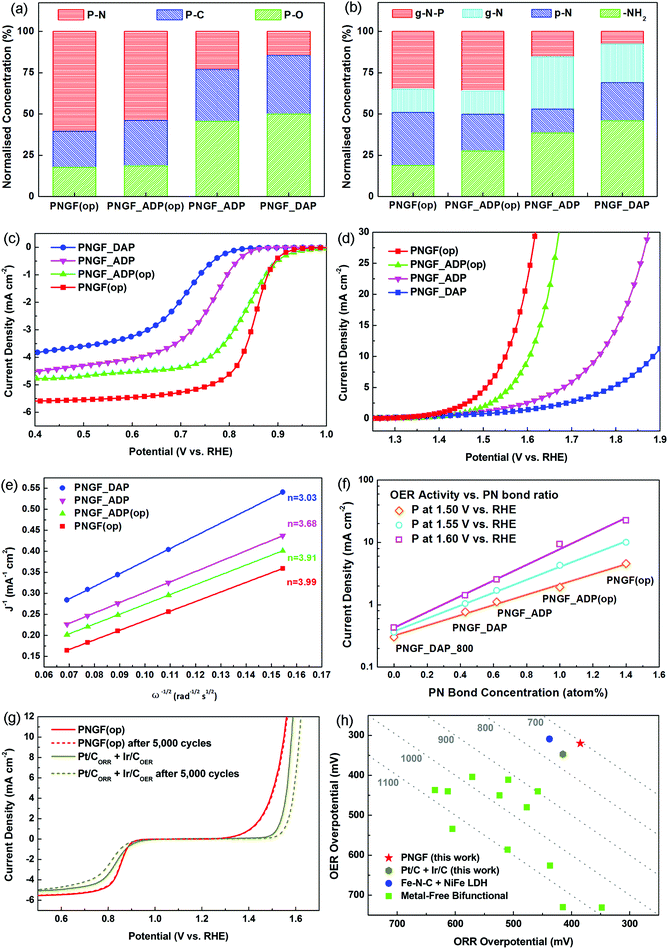
Firstly, the samples were prepared via a one-pot hydrothermal reaction using graphene oxide as the carbon source, and diammonium phosphate (DAP) as the phosphorus and nitrogen precursor, followed by freeze-drying and without the high-temperature calcinations, as detailed in the Methods section. The achieved samples have been named PNGF with the suffix of ‘_DAP’ and without the suffix of ‘_800’, according to the specific synthesis conditions. The X-ray photoelectron spectroscopy (XPS) P2p spectrum of the synthesized P,N co-doped sample PNGF_DAP, Fig. 3(d), demonstrates the existence of the P–N bond (ca. 133.7 eV) apart from the P–O (ca. 134.2 eV) and P–C (ca. 133.2 eV) bonds; however, the PN structure has been completely removed in the PNGF_DAP_800 sample after the high temperature calcination. At the same time, the XPS N1s spectrum of PNGF_DAP, Fig. 3(e) further confirms the existence of the proposed PN structure (g-N–P, ca. 400.9 eV) in PNGF_DAP but not in PNGF_DAP_800, of which the peak position is close to, but slightly more negative (e.g. 0.5 eV) than that of graphitic nitrogen (g-N, ca. 401.4 eV). The peak position of both the P–N bond in the XPS P2p spectrum and the g-N–P structure in XPS N1s spectrum are in good agreement with our computational predictions, Fig. S11 (ESI†). The levels of PN structures (atom%) calculated from elemental concentrations of phosphorus (atom%) and the normalised concentrations of P–N bond in P2p binding configurations (%) are almost identical to the values calculated from the elemental concentrations of nitrogen and the normalised concentrations of g-N–P bonds, Table 1. In addition, the normalised concentrations of dangling amine groups on the edge of P,N co-doped graphene (–NH₂, ca. 399.4 eV) decreased after thermal treatment, while that of pyridinic nitrogen (P–N, ca. 398.1 eV) increased.

Table 1 XPS elemental concentrations (C1s, N1s, O1s, and P2p, in atom%), normalised concentrations of N1s (–NH₂, p-N, g-N, and g-N–P) and P2p (P–O, P–C, and P–N) binding configurations (in %), and levels of PN structures and –NH₂ groups (in atom%) in PNGF. The ‘–NH₂’ refers to the amine structures in the XPS N1s spectra, ‘p-N’ to pyridinic N, ‘g-N’ to normal graphitic N, and ‘g-N–P’ to the proposed PN structures, Fig. 3(d); the ‘P–O’, ‘P–C’ and ‘P–N’ refer to the corresponding P–O, P–C and P–N bonds in XPS P2p spectra, Fig. 3(e). [Note: the levels of PN structures (atom%) were calculated based on the normalised concentrations of the P–N bonds in the P2p binding configurations (%) and the elemental concentrations of P sites (in atom%); while the values in brackets were calculated based on the normalised concentrations of the g-N–P structures in the N1s binding configurations (%) and the elemental concentrations of N sites (atom%). The levels of the –NH₂ group (atom%) were calculated based on the normalised concentrations of the –NH₂ in the N1s binding configurations (%) and the elemental concentrations of N sites (in atom%)]

Catalysts	Elemental (atom%)				N1s (%)				P2p (%)			PN (atom%)	–NH2 (atom%)
	C1s	N1s	O1s	P2p	–NH2	p-N	g-N	g-N–P	P–O	P–C	P–N
PNGF_DAP_800	86.98	3.50	8.06	1.46	35.70	36.20	28.10	0.00	50.00	50.00	0.00	0.00 (0.00)	1.25
PNGF_DAP	69.13	7.05	20.33	3.49	46.05	23.02	24.43	7.50	50.00	35.47	14.53	0.51 (0.53)	3.24
PNGF_ADP	78.86	4.15	14.24	2.75	38.52	14.39	31.89	15.20	45.63	31.34	23.03	0.63 (0.63)	1.59
PNGF_ADP(op)	88.97	2.86	6.31	1.86	27.65	22.12	14.35	35.88	18.69	27.51	53.80	1.00 (1.03)	0.79
PNGF(op)	88.13	4.00	5.55	2.32	18.84	32.18	14.00	34.98	17.72	21.91	60.37	1.40 (1.39)	0.75

---

The comparison between the catalytic ORR/OER activities of PNGF_DAP and PNGF_DAP_800 are given in Fig. 3(c). The former shows a better OER activity than the latter, and its ORR and OER potential gap at any given current is also significantly smaller (i.e. >200 mV at 2 mA cm⁻²), although the high-temperature calcined counterpart shows slightly better ORR reduction potential and current. Note that the number of electrons transferred (n) during ORR at 0.6 V vs. RHE increases from 3.03 for the PNGF_DAP to 3.75 for the PNGF_DAP_800, insert in Fig. 3(c), indicating an enhanced selectivity on ORR via the 4e-transfer pathway after thermal treatment. This is mainly attributed to the fact that the –NH₂ group is more favourable for a 2e⁻ pathway, which can be easily formed when using DAP as the precursor; thus, the PNGF_DAP_800 after high temperature calcination should lead to better selectivity in the 4e⁻ pathway. Through such analysis, it is reasonable to state that the PN structure in PNGF is favourable for OER but not ORR, which is in accordance with its calculated catalytic performance. The ORR activity of P,N co-doped metal-free catalysts is however still dominated by the nitrogen doping. In this case, it is imperative to deliberately tune the phosphorous and nitrogen binding configurations of PNGF so as to achieve an optimal bifunctionality.

Smart tuning the bifunctional ORR/OER performance of PNGF: intensification of the identified active sites

Based on the above findings on the correlation between the ORR/OER activities and P/N binding configurations, the key principle for improving bifunctionality is to increase the levels of PN structures, while reducing the amount of –NH₂. To further validate this notion, the previous P/N precursor (DAP) was first replaced by ammonium dihydrogen phosphate (ADP), which possesses a more balanced P/N ratio of 1 : 1 and may promote the formation of PN structures and prevent the formation of –NH₂. In addition, the concentration of ADP precursor was further optimized to intensify the P–N bonds. Lastly, in order to promote the ORR activity of PNGF, cyanamide (CA) was added as an extra N precursor in the hydrothermal reaction of the sample with an optimal ADP concentration. The obtained samples were named PNGF_ADP, PNGF_ADP(op), and PNGF(op), accordingly.

It was first confirmed by XPS (Fig. 4(a)–(b)) that both the targeted ORR and OER active sites were substantially enhanced in PNGF. For instance, the level of PN structures was almost tripled from 0.51 atom% in PNGF_DAP to 1.40 atom% in PNGF(op) (the normalised concentrations of P–N bonds in XPS P2p binding configurations also increased from less than 15% to more than 60%), while the normalised concentrations of the non-reactive –NH₂ were reduced from roughly 50% in PNGF_DAP to less than 20% in PNGF(op).

Fig. 4 Relative ratio of XPS (a) P2p and (b) N1s binding configurations for PNGF_DAP, PNGF_ADP, PNGF_ADP(op) and PNGF(op). (c) ORR and (d) OER activities of PNGF_DAP, PNGF_ADP, PNGF_ADP(op), and PNGF(op), measured by rotating disk electrode at 1600 RPM. (e) Koutecky–Levich plots of PNGF_DAP, PNGF_ADP, PNGF_ADP(op) and PNGF(op) at 0.6 V vs. RHE, derived from the corresponding linear sweep voltammograms, Fig. S2(a)–(e). (f) Correlation between the OER current densities of PNGF at 1.5, 1.55 and 1.6 V vs. RHE, and the respective concentrations of P–N bonds. (g) Durability of PNGF(op) and Pt/C + Ir/C before and after potential cycling 5000 times. (h) Comparison of ORR/OER overpotentials for PNGF(op), Pt/C + Ir/C, Fe–N–C + NiFe LDF, and other metal-free bifunctional catalysts.

It is clearly demonstrated in Fig. 4(c) and (d) that the ORR/OER overpotentials of PNGF decreased and their current densities increased as the PN structure was intensified and the –NH₂ group was reduced. The ORR potential of the optimal bifunctional catalysts, PNGF(op), can reach 0.845 V vs. RHE at 3 mA cm⁻² (measured by rotating disk electrode under 1600 RPM), while its OER potential at 10 mA cm⁻² is 1.55 V vs. RHE. The combined overpotentials between 3 or 10 mA cm⁻² for ORR or OER, respectively, are reduced from 1252 mV of PNGF_DAP, to 1037 mV of PNGF_ADP, further to 795 mV of PNGF_ADP(op), and finally to 705 mV of PNGF(op).

Moreover, it is shown in Fig. 4(e) that the ORR electron transfer number increases from 3.03 for PNGF_DAP, to 3.68 for PNGF_ADP, to 3.91 for PNGF_ADP(op), and finally to 3.99 for PNGF(op), as the respective amount (%atom) of –NH₂ sites are reduced from 3.24% in PNGF_DAP to 0.75% in PNGF(op), Table 1. The respective normalised concentrations (%) of –NH₂ are reduced from roughly 50% in PNGF_DAP to less than 20% in PNGF(op), Fig. 4(b). This further supports our previous argument on how to improve the ORR activity. Meanwhile, it is also shown in Fig. 4(f) that the OER current density of PNGF at 1.50, 1.55 and 1.60 V vs. RHE increases significantly as the concentration of the PN structure in PNGF is enhanced, clearly demonstrating the contribution of PN structures to OER activity.

The catalytic activities of PNGF(op) are superior to the commercial noble metal catalysts, e.g. Pt/C for ORR and Ir/C for OER, Fig. 4(g). Additionally, the durability of PNGF(op) (performance loss during potential cycling) and its stability (performance loss during chronoamperometry) are also considerably superior to their respective noble metal counterparts. As shown in Fig. 4(g), the combined ORR/OER overpotential of Pt/C + Ir/C increases by 61 mV after 5000 cycles from 769 to 830 mV, while almost zero change in overpotential was observed for PNGF_(OP). The ORR or OER current density of PNGF(op) decreased by only 7.6 or 5%, after being continuously measured for 20 hours, while the respective ORR or OER current density decreased by 25.2 or 35.8% for Pt/C or Ir/C, Fig. S2(e) and (f) (ESI†).

Finally, the combined ORR/OER overpotential of 705 mV exhibited by PNGF(op) is not only superior to that of Pt/C for OR+ Ir/C (769 mV) or the state-of-the-art two component non-precious metal catalysts (747 mV),⁵²Fig. 4(e), but also outperforms all the previously reported metal-free catalysts.^8,9,27–36

Conclusions

Successfully coupled first-principles simulations and one-pot synthesis have clearly identified and intensified the effective ORR and OER active sites for P,N co-doped metal-free materials. The simulations show that the P atom is too large to be doped in the graphitic surface of carbon catalysts, and can only be effectively populated at edge sites. The DOSs of the structures indicate that the P sites are always the most active in the un-oxidized catalysts. However, such P sites are far too active and can be readily oxidized by oxygen groups and become non-reactive for sustainable ORR/OER in practice. On the other hand, when a P site is oxidized and bound to an N co-dopant (e.g. in a Z-PN-5-OX2 structure), it stabilizes the graphitic N and activates a neighbouring C site for effective OER.

Such findings agree well with the experimental XPS spectra and electrochemical outcome of P,N co-doped graphene frameworks, PNGF_DAP, which confirms that its high OER performance indeed originates from the P–N bonds in the catalysts. Consequently, the high-temperature calcined sample, PNGF_DAP_800, shows a much reduced OER activity since the thermally unstable P–N bonds were completely removed. However, the ORR performance of PNGF_DAP_800 was improved, mainly because the 2e⁻ pathway related groups (−NH₂) were removed simultaneously during thermal annealing while the 4e⁻ components (pyridinic/graphitic N) were largely preserved.

According to these observations, the ORR/OER bifunctionality of the P,N co-doped graphene framework was further tuned through the promotion of the level of the P–N bonds and the reduction of the amount of −NH₂, by means of selective P/N precursors. The potential gap of our P,N co-doped graphene framework has been significantly reduced from 1252 mV of PNGF_DAP, to 1037 mV of PNGF_ADP, further to 795 mV of PNGF_ADP(op), and finally to 705 mV of PNGF(op) after active site engineering. The optimized catalyst, PNGF(op), shows an ORR potential of 0.845 V vs. RHE at 3 mA cm⁻² and OER potential of 1.55 V vs. RHE at 10 mA cm⁻². Such catalytic activities outperform all the previous metal-free bifunctional catalysts, to the best of our knowledge, and are even superior to Pt/C for ORR and Ir/C for OER. Moreover, the durability and stability of PNGF(op) are much better than the respective commercial noble metal counterparts. Clearly, this work is an example of simulation-facilitated experimental development of (metal-free) ORR/OER bifunctional catalysts by active site engineering. This approach is not only indispensable for the development of ORR/OER catalysts, but should also be widely applicable in (electro)catalysis research. The approach and the findings not only provide great insight into the mechanisms of P,N co-doped metal free catalysts, but also promote controlled engineering and scale-up activities for practical development of multifunctional nanostructures for metal–air batteries and fuel cells.

Acknowledgements

This work is supported by the Engineering and Physical Sciences Research Council (EPSRC) grants (Ref: EP/L018330/1; EP/K021192/1 and EP/K002252/1). The authors would also acknowledge the use of the UCL Legion and Grace High Performance Computing Facility, the UK National Supercomputing Service ARCHER, and the supercomputing facilities (Cray XC30 and Fujitsu CX250 Cluster) at Japan Advanced Institute of Science and Technology (JAIST).

Notes and references

1. M. Lefevre, E. Proietti, F. Jaouen and J. P. Dodelet, Science, 2009, 324, 71–74.
2. J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550.
3. L. Liao, Q. Zhang, Z. Su, Z. Zhao, Y. Wang, Y. Li, X. Lu, D. Wei, G. Feng, Q. Yu, X. Cai, J. Zhao, Z. Ren, H. Fang, F. Robles-Hernandez, S. Baldelli and J. Bao, Nat. Nanotechol., 2014, 9, 69–73.
4. K. Qiu, G. Chai, C. Jiang, M. Ling, J. Tang and Z. Guo, ACS Catal., 2016, 6, 3558–3568.
5. B. Y. Xia, Y. Yan, N. Li, H. B. Wu, X. W. Lou and X. Wang, Nat. Energy, 2016, 1, 15006.
6. A. Zitolo, V. Goellner, V. Armel, M. T. Sougrati, T. Mineva, L. Stievano, E. Fonda and F. Jaouen, Nat. Mater., 2015, 14, 937–942.
7. J. Snyder, T. Fujita, M. W. Chen and J. Erlebacher, Nat. Mater., 2010, 9, 904–907.
8. J. Zhang, Z. Zhao, Z. Xia and L. Dai, Nat. Nanotechol., 2015, 10, 444–452.
9. C. Tang, H. F. Wang, X. Chen, B. Q. Li, T. Z. Hou, B. Zhang, Q. Zhang, M. M. Titirici and F. Wei, Adv. Mater., 2016, 28, 6845–6851.
10. G. L. Tian, Q. Zhang, B. Zhang, Y. G. Jin, J. Q. Huang, D. S. Su and F. Wei, Adv. Funct. Mater., 2014, 24, 5956–5961.
11. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
12. B. C. H. Steele and A. Heinzel, Nature, 2011, 414, 345–352.
13. X. Huang, Z. Zhao, L. Cao, Y. Chen, E. Zhu, Z. Lin, M. Li, A. Yan, A. Zettl, Y. M. Wang, X. Duan, T. Mueller and Y. Huang, Science, 2015, 348, 1230–1234.
14. J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556.
15. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46.
16. F. Calle-Vallejo, J. I. Martínezac and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643.
17. Y. Lee, J. Suntivich, K. J. May, E. E. Perry and Y. Shao-Hong, J. Phys. Chem. Lett., 2012, 3, 399–404.
18. G. L. Chai, Z. F. Hou, D. J. Shu, T. Ikeda and K. Terakura, J. Am. Chem. Soc., 2014, 136, 13629–13640.
19. K. P. Gong, F. Du, Z. H. Xia, M. Durstock and L. M. Dai, Science, 2009, 323, 760–764.
20. T. Lin, I. W. Chen, F. Liu, C. Yang, H. Bi, F. Xu and F. Huang, Science, 2015, 350, 1508–1513.
21. Y. Jiao, Y. Zheng, K. Davey and S. Z. Qiao, Nat. Energy, 2016, 1, 16130.
22. J. Zhang and L. Dai, Angew. Chem., Int. Ed., 2016, 55, 13296–13300.
23. K. Qu, Y. Zheng, Y. Jiao, X. Zhang, S. Dai and S. Z. Qiao, Adv. Energy Mater., 2017 DOI:10.1002/aenm.201602068.
24. X. Liu and L. Dai, Nat. Rev. Mater., 2016, 1, 16064.
25. R. Li, Z. Wei and X. Gou, ACS Catal., 2015, 5, 4133–4142.
26. M. Qiao, C. Tang, G. He, K. Qiu, R. Binions, I. P. Parkin, Q. Zhang, Z. Guo and M. M. Titirici, J. Mater. Chem. A, 2016, 4, 12658–12666.
27. R. M. Yadav, J. Wu, R. Kochandra, L. Ma, C. S. Tiwar, L. Ge, G. Ye, R. Vajtai, J. Lou and P. M. Ajayan, ACS Appl. Mater. Interfaces, 2015, 7, 11991–12000.
28. G. L. Tian, M. Q. Zhao, D. Yu, X. Y. Kong, J. Q. Huang, Q. Zhang and F. Wei, Small, 2014, 10, 2251–2259.
29. Z. Shao, W. Zhang, D. An, G. Zhang and Y. Wang, RSC Adv., 2015, 5, 97508–97511.
30. G. L. Tian, Q. Zhang, B. Zhang, Y. G. Jin, J. Q. Huang, D. S. Su and F. Wei, Adv. Funct. Mater., 2014, 24, 5956–5961.
31. Q. Liu, Y. Wang, L. Dai and J. Yao, Adv. Mater., 2016, 28, 3000–3006.
32. Z. Lina, G. H. Waller, Y. Liu, M. Liu and C. Wong, Carbon, 2013, 53, 130–136.
33. J. Zhang and L. Dai, Angew. Chem., Int. Ed., 2016, 55, 13296–13300.
34. X. Li, Y. Fang, S. Zhao, J. Wu, F. Li, M. Tian, X. Long, J. Jin and J. Ma, J. Mater. Chem. A, 2016, 4, 13133–13141.
35. H. Yuan, L. Deng, X. Cai, S. Zhou, Y. Chen and Y. Yuan, RSC Adv., 2015, 5, 56121–56129.
36. T. Pan, Y. Li, H. Liu, X. Lu, G. Ren and Y. Zhu, Sci. Bull., 2016, 61, 889–896.
37. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471.
38. CPMD. MPI fur Festkorperforshung Stuttgart, 1997–2001. IBMCorp, 1990–2008, http://www.cpmd.org, 1990–2008.
39. M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744.
40. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993.
41. M. Sprik, J. Hutter and M. Parrinello, J. Chem. Phys., 1996, 105, 1142–1152.
42. F. A. Hamprecht, A. J. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 6264–6271.
43. P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
44. G. L. Chai and Z. X. Guo, Chem. Sci., 2016, 7, 1268–1275.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
46. The CP2K developers group, http://cp2k.berlios.de/, 2004.
47. X. Wang, Z. Hou, T. Ikeda, M. Oshima, M. Kakimoto and K. Terakura, J. Phys. Chem. A, 2012, 117, 579–589.
48. G. Lippert, J. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140.
49. K. Qiu and Z. X. Guo, J. Mater. Chem. A, 2014, 2, 3209–3215.
50. D. Yang, D. Bhattacharjya, S. Inamdar, J. Park and J. S. Yu, J. Am. Chem. Soc., 2012, 134, 16127–16130.
51. C. Zhang, N. Mahmood, H. Yin, F. Liu and Y. Hou, Adv. Mater., 2013, 25, 4932–4937.
52. S. Dresp, F. Luo, R. Schmack, S. Kühl, M. Gliech and P. Strasser, Energy Environ. Sci., 2016, 9, 2020–2024.

---

Footnotes

† Electronic supplementary information (ESI) available: Calculations of formation energy calculation, limiting potentials, experimental details, LSV, K–L plots, chronoamperometry, XPS, DOS, and curvature effect. See DOI: 10.1039/c6ee03446b

‡ These authors contributed equally to this work.

---