Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How amino and nitro substituents direct electrophilic aromatic substitution in benzene: an explanation with Kohn–Sham molecular orbital theory and Voronoi deformation density analysis†
O. A.
Stasyuk
a,
H.
Szatylowicz
a,
T. M.
Krygowski
b and
C.
Fonseca Guerra
*c
aFaculty of Chemistry, Warsaw University of Technology, Noakowskiego 3, Warsaw 00-664, Poland
bDepartment of Chemistry, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland
cDepartment of Theoretical Chemistry and Amsterdam Center for Multiscale Modeling, Vrije Universiteit Amsterdam, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands. E-mail: c.fonsecaguerra@vu.nl
First published on 15th January 2016
Abstract
The substituent effect of the amino and nitro groups on the electronic system of benzene has been investigated quantum chemically using quantitative Kohn–Sham molecular orbital theory and a corresponding energy decomposition analysis (EDA). The directionality of electrophilic substitution in aniline can accurately be explained with the amount of contribution of the 2pz orbitals on the unsubstituted carbon atoms to the highest occupied π orbital. For nitrobenzene, the molecular π orbitals cannot explain the regioselectivity of electrophilic substitution as there are two almost degenerate π orbitals with nearly the same 2pz contributions on the unsubstituted carbon atoms. The Voronoi deformation density analysis has been applied to aniline and nitrobenzene to obtain an insight into the charge rearrangements due to the substituent. This analysis method identified the orbitals involved in the C–N bond formation of the π system as the cause for the π charge accumulation at the ortho and para positions in the case of the NH2 group and the largest charge depletion at these same positions for the NO2 substituent. Furthermore, we showed that it is the repulsive interaction between the πHOMO of the phenyl radical and the πHOMO of the NH2 radical that is responsible for pushing up the πHOMO of aniline and therefore activating this π orbital of the phenyl ring towards electrophilic substitution.
Introduction
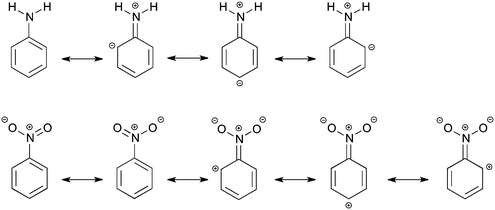
In modern organic chemistry textbooks an explanation of the chemical reactivity of the benzene ring in electrophilic aromatic substitution is directly connected with electron-donating or electron-withdrawing influence of substituents on the electronic system. The explanation is not relying on modern quantitative computational techniques, but quite often on the concepts of Lewis from 1916,1e where the electrons are thought to be at an intermediate state between different resonance structures (see Scheme 1).1 This, however, does not describe what happens quantum chemically in the electronic system. The effect of the substituent on the reactivity of the benzene ring can be divided into the field/inductive effect and the resonance (or mesomeric) effect.1 The main problem is to determine individual contributions of each effect for a particular substituent.2 When the resonance and field effects act in the same direction, their separation becomes even more difficult. Undoubtedly, the classical Hammett approach3 (proposed in 1937) expressed by the σ substituent constants has been the first attempt of a quantitative description of the substituent effects. Also this approach, based on experimental data on benzoic acid derivatives, is still widely used in chemistry. To date, different quantitative characteristics are also used to estimate contributions of inductive and resonance effects but they are not general and usually depend on the kind of studied systems.4 It is known that the inductive effect operates through σ-bonds, while the resonance effect is transmitted through π-electrons. Lewis structures, which can be seen as a qualitative application of the valence bond theory, are used to explain activating or deactivating substituent properties and also to predict a favored product of the electrophilic attack. A more rigorous way to describe a relationship between molecular structure and electron density is the analysis using qualitative molecular orbitals.1a,d,5In this work, we would like to study the substituent effects of NH2 and NO2 groups on benzene using Kohn–Sham density functional theory. As is known, these two substituents have completely opposite electronic properties and therefore, opposite effects on the electrophilic substitution reactions of benzene.1 The amino group is activating and ortho- and para-directing, whereas the nitro substituent is known to be deactivating and meta-directing. This difference in reactivity can be made plausible by the Lewis structures of aniline and nitrobenzene (Scheme 1), but it does not give an explanation of the influence of the substituent on the molecular σ and π orbitals located on the phenyl ring. The resonance structures suggest that the amino group increases the electron density only at ortho- and para-positions of the ring, making them more preferred to the electrophilic attack. In turn, the nitro group, according to the resonance structures, promotes the formation of a meta-product by decreasing the π-electron density at the ortho and para positions (Scheme 1). The field effect was deduced to be also important for the nitro substituent and to explain its deactivating properties.1a,6a In previous studies,6b–d some attempts were done to separate the total substituent effect of the nitro group into σ- and π-contributions. However, the outcome was not conclusive, in particular about an importance of the resonance effect, that is the directing effect, in nitrobenzene.
In this study, the resonance and inductive effects of the substituents on the benzene ring are analyzed and separated using Kohn–Sham Molecular Orbital (KS-MO) theory and the accompanying Energy Decomposition Analysis7 (EDA). The quantitative KS-MO model together with the EDA have proven to be able to elucidate the nature of different types of bonds: the nature of resonance-assisted hydrogen bonding8 and halogen bonding9 has been defined. Moreover, the KS-MO model was successfully used for explaining the organic reaction mechanism,10 the concept of aromaticity and other properties of chemical compounds.11 This method uses symmetry which allows separating the interactions into σ- and π-electronic systems of the benzene ring and the substituents. Previously, Fernandez et al.11d found a correlation between the Hammett constants and the π electronic energy term. We will also use the Voronoi Deformation Density (VDD) charge analysis, which enables us to track the reorganization in the σ and π electron densities of the phenyl ring due to the substituent and to determine the resonance and inductive effects on the ring. Based on frontier molecular orbital theory to explain chemical reactivity, our quantitative KS-MO results together with the VDD charges clarify the orientation of the electrophilic aromatic substitution and the change in reactivity of the benzene ring caused by the NH2 or NO2 substituents.
Methodology
General procedure
All calculations were carried out using the Amsterdam Density Functional (ADF) program.12 Geometries and energies were calculated using the generalized gradient approximation (GGA) with the BLYP functional.12c,d The MOs were expanded in uncontracted sets of Slater type orbitals (STOs) containing diffuse functions with two sets of polarization functions (TZ2P).12e The 1s core shells of carbon, nitrogen and oxygen were treated by the frozen-core approximation. Geometries were optimized in the gas phase assuming C2v symmetry (the difference in energy of the amino group between planar and pyramidal geometries is only 0.3 kcal mol−1, see also ref. 13).Energy decomposition analysis
To analyze the effect of the substituent on the benzene ring, we defined two fragments consisting of two radicals with opposite spins, which are combined into aniline or nitrobenzene (see Scheme 2). The fragments are treated in the KS open-shell restricted formalism as proposed in ref. 7a.The interaction energy is examined in the substituted benzene in the framework of the KS-MO model using a quantitative energy decomposition analysis (EDA)7a into electrostatic interactions, Pauli repulsive orbital interactions and attractive orbital interactions:
| ΔEint = ΔVelstat + ΔEPauli + ΔEoi | (1) |
The orbital interaction energy can be further decomposed into the contributions from each irreducible representation Γ of the interacting system (eqn (2)):7
| ΔEoi = ΔEσ + ΔEπ | (2) |
Analysis of the charge distribution
The Voronoi Deformation Density14 (VDD) atomic charges for aniline and nitrobenzene have also been computed. The VDD charge QA is computed as the (numerical) integral of the deformation density Δρ(r) associated with the formation of the molecule from its atoms in the volume of the Voronoi cell of atom A (eqn (3)). The Voronoi cell of an atom A is defined as the compartment of space bound by the bond midplanes on and perpendicular to all bond axes between the nucleus A and its neighboring nuclei.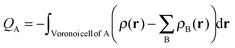 | (3) |
The VDD method also allows us to analyze the electronic redistributions within two polyatomic fragments when a chemical bond is formed between these two molecular fragments. Previously, we have shown that this method is most informative to analyze resonance-assisted hydrogen bonding appropriately as it allows decomposition of the total changes into σ and π electronic rearangements.8a,b The change in VDD atomic charges ΔQA is defined by eqn (4), which relates this quantity directly to the deformation density ρPh–NX2(r) − ρPh˙(r) − ρ˙NX2(r) associated with the formation of the overall molecule from the two fragments Ph˙ and ˙NX2 (with X = H or O).8a,b,14
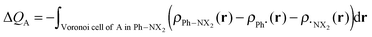 | (4) |
This functionality is extended by the decomposition into σ and π components (for the planar, Cs symmetric molecules):
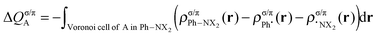 | (5) |
For the π system, this functionality is additionally extended by the decomposition of the electronic redistribution per atom ΔQA into a component associated with the Pauli repulsion ΔEPauli and a component associated with the bonding orbital interactions ΔEoi.
| ΔQπA = ΔQπA,Pauli + ΔQπA,oi | (6) |
| Δρπ(r) = ΔρπPauli(r) + Δρπoi(r) | (7) |
The change in π atomic charge caused by Pauli repulsion between the monomers in the complex is defined by eqn (8), and the corresponding change caused by charge transfer and polarization is given by eqn (9).
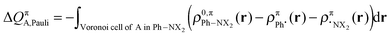 | (8) |
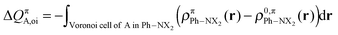 | (9) |
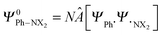 through explicit anti-symmetrization (Â operator) and renormalization (N constant) of the product of monomer wave functions when the unperturbed monomer densities ρPh˙ + ρ˙NX2 are superimposed. The π density ρπ is obtained as the sum of orbital densities of the occupied molecular orbitals belonging to the A′′ irreducible representation (in Cs symmetry). As the molecular symmetry of aniline and nitrobenzene is C2v, thus of higher symmetry than Cs, the changes in the atomic charge can be split further into A2 and B1.
through explicit anti-symmetrization (Â operator) and renormalization (N constant) of the product of monomer wave functions when the unperturbed monomer densities ρPh˙ + ρ˙NX2 are superimposed. The π density ρπ is obtained as the sum of orbital densities of the occupied molecular orbitals belonging to the A′′ irreducible representation (in Cs symmetry). As the molecular symmetry of aniline and nitrobenzene is C2v, thus of higher symmetry than Cs, the changes in the atomic charge can be split further into A2 and B1.| ΔQπA,Pauli = ΔQA2A,Pauli + ΔQB1A,Pauli | (10) |
| ΔQπA,oi = ΔQA2A,oi + ΔQB1A,oi | (11) |
Results and discussion
Energy decomposition analysis and bonding mechanism
The energy decomposition analysis and the molecular orbital diagrams of the bonding mechanism in nitrobenzene and aniline between Ph˙ and ˙NX2, obtained at the KS-DFT BLYP/TZ2P level of theory, are displayed in Table 1 and Fig. 1 and 2 (only the most important interactions are represented).| NX2 | d(CN)/Å | ΔVelstat | ΔEPauli | ΔEσ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ΔEA1 | ΔEB2 | ΔEπ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ΔEA2 | ΔEB1 | ΔEoi | ΔEint | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a ΔEσ = ΔEA1 + ΔEB2 and ΔEπ = ΔEA2 + ΔEB1. | ||||||||||||
| ˙NH2 | 0 | 1.389 | −160.0 | 288.5 | −247.0 | −239.5 | −7.5 | −25.1 | −0.2 | −24.9 | −272.1 | −143.6 |
| ˙NH2 | 90 | 1.389 | −165.5 | 292.3 | −249.5 | −238.0 | −11.5 | −11.0 | −0.1 | −9.2 | −260.5 | −133.7 |
| ˙NH2 | 0 | 1.492 | −124.2 | 211.0 | −208.9 | −204.1 | −4.8 | −17.3 | −0.1 | −17.2 | −226.2 | −139.4 |
| ˙NO2 | 0 | 1.492 | −161.2 | 330.0 | −224.4 | −217.7 | −6.7 | −18.5 | −0.7 | −17.8 | −242.9 | −74.1 |
| ˙NO2 | 90 | 1.492 | −159.5 | 330.3 | −229.6 | −219.9 | −9.7 | −11.0 | −0.7 | −9.1 | −239.6 | −68.8 |
| ˙NO2 | 0 | 1.389 | −211.6 | 445.0 | −276.0 | −265.9 | −10.1 | −27.9 | −1.0 | −26.9 | −303.9 | −70.5 |
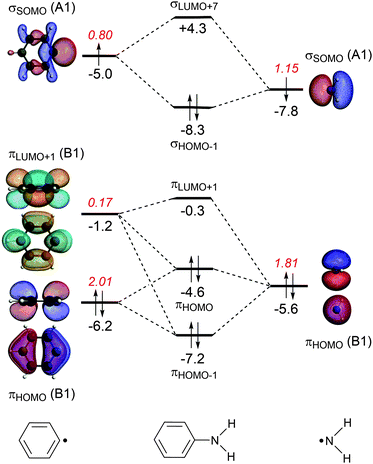
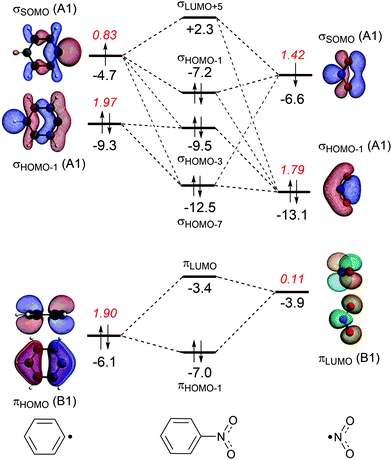
The energy decomposition analysis of the electron-pair bond formation between Ph˙ and the substituent ˙NX2 shows that interaction energy for the formation of nitrobenzene is about half of the formation of aniline (−74.1 kcal mol−1 and −143.6 kcal mol−1, respectively) and the C–N bond is also shorter in aniline than in nitrobenzene (1.389 Å and 1.492 Å, respectively). The longer C–N distance in nitrobenzene is caused by the larger Pauli repulsion (330.0 kcal mol−1 for Ph–NO2 and 288.5 for Ph–NH2). Compression of the C–N distance in nitrobenzene to the distance in aniline makes the Pauli repulsion go up from 330.0 kcal mol−1 to 445.0 kcal mol−1, whereas in aniline the Pauli repulsion is only 288.5 kcal mol−1 at 1.389 Å. The shortening of the C–N distance in nitrobenzene results in an increase of 115.0 kcal of the Pauli repulsion and only in an extra attraction of −111.4 kcal mol−1 of the bonding components (electrostatic and orbital interaction). The σ MO diagram shows the repulsive interaction between the occupied σHOMO−1 of Ph˙ and σHOMO−1 of ˙NO2, which is absent in the σ MO diagram of aniline (see Fig. 1 and 2). The largest bonding contribution to the interaction energy is the A1 component of the orbital interaction (that is the formation of the electron-pair bond), which amounts to −239.5 kcal mol−1 for aniline and −217.7 kcal mol−1 for nitrobenzene. The electrostatic interaction is of similar strength for both systems: −160.0 kcal mol−1 for aniline and −161.2 kcal mol−1 for nitrobenzene. Note that the ΔEA2 and ΔEB2 only account for polarization within each fragment as the A2 and B2 orbitals have no amplitude on the atoms located on the C2 rotation axis and therefore do not overlap.
The stabilization caused by the donor–acceptor interactions in the B1 irreducible representation (that is in the π electronic system) is larger for aniline (−24.9 kcal mol−1) than for nitrobenzene (−17.8 kcal mol−1). Compression of the C–N bond in Ph–NO2 to the distance of Ph–NH2 enlarges the ΔEB1 to −26.9 kcal mol−1.
For both substituents, NH2 and NO2, the formation of the electron-pair bond in the σ electronic system causes the singly occupied molecular orbital (SOMO) of the phenyl radical to donate 0.2 electrons to the SOMO of the substituent accounting for the inductive effect of the substituent. In the case of nitrobenzene, the bond formation is accompanied by the Pauli repulsive interaction between occupied orbitals on the Ph˙ and ˙NO2 fragments (see Fig. 2).
The donor–acceptor interactions in the π electronic system of aniline and nitrobenzene have an opposite effect on the phenyl radical: NH2 is electron donating and NO2 is electron-withdrawing. The MO diagrams illustrate this clearly. For aniline, the π-orbital of the NH2 group donates 0.17 electrons to the πLUMO+1 orbital of the benzene ring (see Fig. 1). This counteracts the charge-flow in the σ system. There is also Pauli repulsion between the πHOMO on Ph˙ and ˙NH2, which pushes up the energy of the πHOMO of aniline to −4.6 eV and accounts for the activation towards electrophilic substitution and not the donor–acceptor interactions. This mechanism has also been encountered in the study of the substituent effects on the optical properties of naphthalene diimides.11c
In the case of nitrobenzene, the electron transfer goes in the opposite direction. The πLUMO of the NO2 group accepts 0.11 electrons from the π-system of the benzene ring increasing the deactivation for electrophilic substitution (see Fig. 2). The πHOMO of nitrobenzene lies at −7.0 eV, which is 2.4 eV lower than the same orbital in aniline and explains the lower reactivity of nitrobenzene.
Another way to investigate the effect of the substituents is to rotate the substituents by 90 degrees, that is, perpendicular to the plane of the benzene ring and analyze the capability of the substituents to participate in the π-electron delocalization of the ring. The donor–acceptor interactions are either lost as in the nitrobenzene or become negligible as in aniline (the amino group donates only 0.03 electrons, see Fig. S1 and S2, ESI†). Rotation of the substituent NX2 (the rotation barriers are given in Table S1, ESI†) switches off the donor–acceptor interactions in the π electronic system, however the energetic loss is quite small in both cases. For nitrobenzene, ΔEπ goes from −18.5 kcal mol−1 to −11.0 kcal mol−1 and for aniline from −25.1 kcal mol−1 to −11.0 kcal mol−1. Clearly, the π orbitals of the phenyl ring can also interact with the perpendicular substituent and the π delocalization is therefore not switched off completely (see Fig. S1 and S2 in the ESI,† for the MO diagrams for the perpendicular conformation).
After this explanation of the activating and deactivating effects of the NH2 and NO2 substituents on the benzene ring based on the MO diagrams, we would also like to understand the directionality of the electrophilic attack. Recently, Fievez et al.10c showed that the orbital interaction is the driving force towards selectivity in electrophilic aromatic substitution for activating substituents, but it is not the main factor for the NO2 substituent. They studied the interaction energy and its components (eqn (1)) between monosubstituted benzene derivatives and a model electrophile at the onset of the reaction in a plane parallel to the molecular plane.
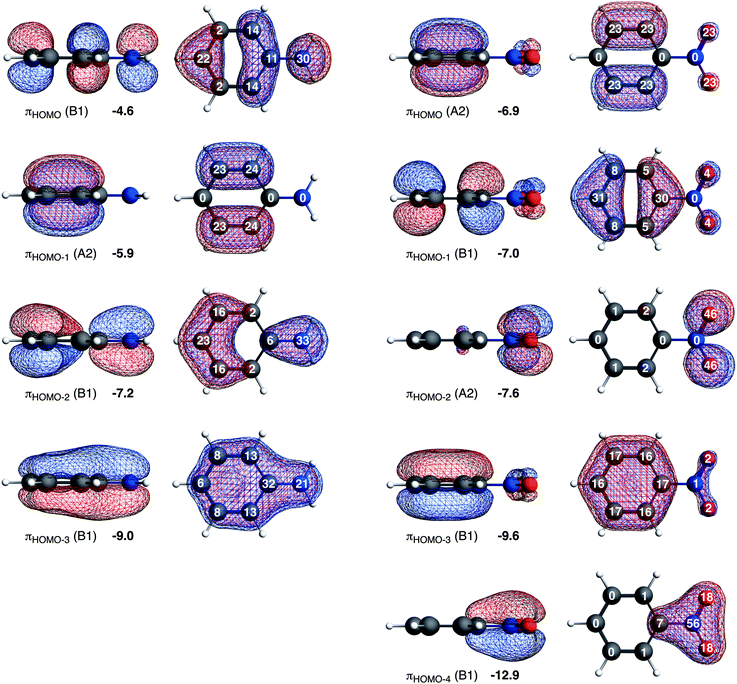
Here, we would like to analyze the molecular orbitals of the substituted benzenes in terms of the contribution of the 2pz orbitals on the carbon, nitrogen and oxygen atoms to the molecular π orbitals, allowing us to explain the directionality from the molecular orbital perspective (see Fig. 3). The high contribution of a 2pz orbital on a certain carbon atom to the πHOMO of the substituted benzene will direct the electrophilic attack towards that atom because of the larger overlap between the accepting orbital of the electrophile and the πHOMO of the substituted benzene. The most favorable interaction occurs at the atom with the highest 2pz contribution to the πHOMO.
Aniline has only one highest occupied π orbital at −4.6 eV with the largest gross Mulliken contributions on the meta (14%) and the para (22%) positions. The electrophilic attack will therefore occur at these positions. Nitrobenzene has two almost degenerate highest occupied π orbitals at −6.9 eV and −7.0 eV. The πHOMO directs the electrophilic attack towards ortho and meta positions with 2pz contributions of 23% on these two positions, and the πHOMO−1 towards the para position with a 2pz contribution of 31% on the para (contributions on the ortho and meta positions are small, 5% and 8% respectively). Thus, the π orbitals of nitrobenzene are deactivated (because they are low-lying) and the experimentally observed meta directing effect of the nitro substituent for electrophilic aromatic substitution cannot be explained from the character of the πHOMO and πHOMO−1.
VDD charge analysis
Complementary to the KS-MO analysis and the EDA, we have also investigated the VDD atomic charges (eqn (3)) and charge rearrangements (eqn (4)) on the phenyl ring due to the substituent effects to predict the regioselectivity of electrophilic substitution and explain the reactivity of the aromatic ring. Fig. 4 displays the VDD atomic charges (eqn (3)) for benzene, nitrobenzene and aniline, which are the differences between the final density and the density of the promolecule (the sum over spherical atomic densities). The comparison of the VDD atomic charges shows that aniline has a more negative charge than benzene at the ortho and para positions, −78 and −74 milli-electrons, respectively, compared to only −48 milli-electrons in benzene. This is in line with the large amplitudes of the πHOMO on the ortho and para carbon atoms. Nitrobenzene has at all positions a less negative charge than benzene, which is in line with the deactivating properties of the nitro group. The meta position in nitrobenzene is slightly more negative (−41 milli-electrons) than the ortho and para positions (−34 and −28 milli-electrons). Note that the differences in aniline are larger than in nitrobenzene. | ||
| Fig. 4 VDD atomic charges (milli-electrons) of benzene, aniline and nitrobenzene (eqn (3)). | ||
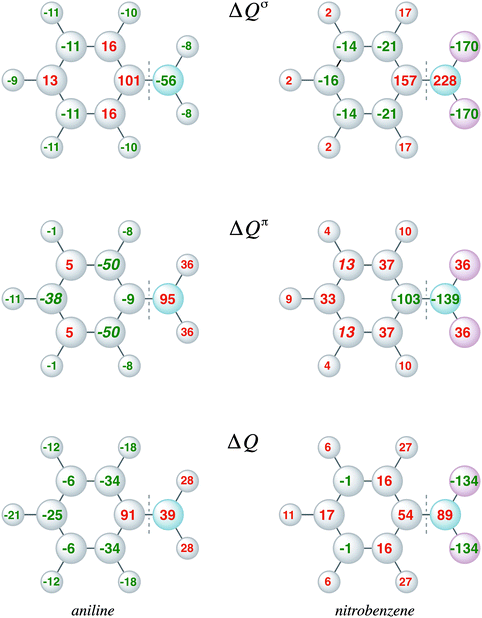
The VDD charge rearrangements, as defined in eqn (4), allows analysis of the charge redistributions within two polyatomic fragments when a chemical bond is formed between these two molecular fragments. Furthermore, it allows decomposition of the total changes into the components of different irreducible representations. In Fig. 5, the VDD charge rearrangements (ΔQ) due to the formation of the C–N bond in aniline and nitrobenzene are given. The bond formation causes the phenyl ring of aniline to be activated with the largest electronic charge accumulations on the ortho and para positions, and the phenyl ring of nitrobenzene to be deactivated with the smallest electronic charge depletions at the meta positions. Decomposition into σ and π charge rearrangements, shown in Fig. 5, reveals that the π electronic system, and thus the π bond formation, is responsible for the regioselectivity of electrophilic substitution, which is in line with previous research.6c Negative numbers on the atoms mean an accumulation of π-electron density on those atoms and positive numbers mean a depletion of π-electron density at atoms. The π C–N bond formation in aniline causes ΔQπ to become more negative at the ortho and para positions (−50 and −38 milli-electrons) experimentally leading to a mixture of ortho and para products, and in nitrobenzene to become more positive at all positions, but less positive at the meta position (only 13 millielectrons are lost at the meta position), thus the nitro group is a deactivating meta-directing substituent.15,16 The VDD electronic rearrangements are in line with the experimentally observed regioselectivity of electrophilic aromatic substitution. To determine which factor is more important, orbital interactions or charge redistribution, an additional investigation of the transition state of an electrophile with the substituted benzene is necessary.
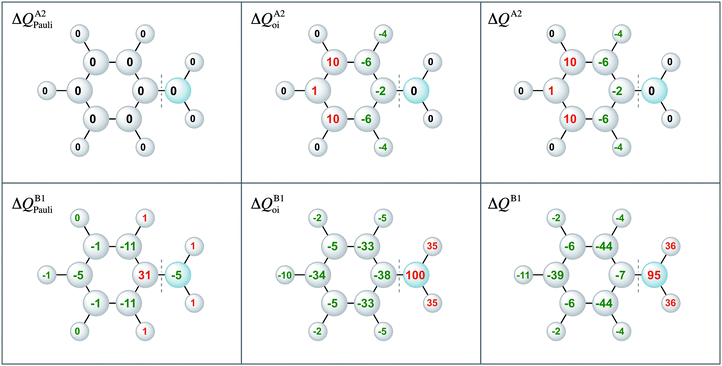
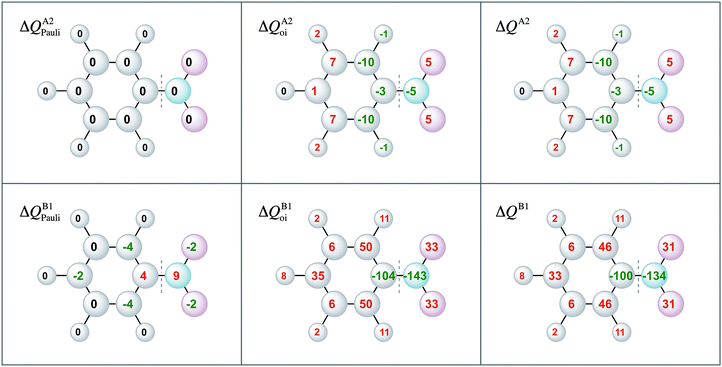
Moreover, the VDD charge rearrangements allow for decomposition into the charge rearrangements caused by the Pauli repulsion and orbital interactions. As aniline and nitrobenzene are C2v symmetric molecules, we decomposed the π charge rearrangements into the A2 and B1 contributions. Only the B1 charge rearrangements are caused by the C–N bond formation, whereas the A2 charge rearrangements are only due to polarization (no A2 orbital has amplitude on the atoms lying on the C2 symmetry axis). Fig. 6 and 7 clearly show that the directionality of the electrophilic substitution is caused by the B1 charge rearrangements in the orbital interactions, ΔQB1oi. The largest charge accumulations of ΔQB1oi are at the ortho and para positions for aniline and the largest charge depletions of ΔQB1oi are at the ortho and para positions for nitrobenzene. For aniline, this finding confirms our results from the molecular orbital analysis, whereas for nitrobenzene the VDD charge rearrangements are essential to pinpoint the orbitals responsible for the directionality, namely the B1 orbitals are responsible for the C–N bond formation.
Conclusions
In this paper, we studied using density functional theory the substituent effect of NH2 and NO2 groups on the electronic system of benzene caused by the formation of the C–N bond. The computations revealed that the C–N bond in aniline is stronger and shorter than in nitrobenzene. With our quantitative Kohn–Sham molecular orbital (KS-MO) model and the corresponding energy decomposition analysis (EDA) we explained that the NH2 group can approach the phenyl ring closer than the NO2 group because there is less Pauli repulsion between the hydrogen atoms of NH2 and the hydrogen atoms of the phenyl radical at the ortho positions, whereas these hydrogen atoms experience Pauli repulsion with the lone pairs of the oxygen atoms of NO2. We separated the inductive and resonance effects. The σ component of the C–N bond formation shows for both substituents the inductive effect whereby the phenyl ring donates electronic density to the substituent. In the π electronic system, the effects of the substituents are opposite: NH2 donates the electronic charge, whereas NO2 accepts the electronic charge from the π system of the phenyl radical.The donor–acceptor interactions from the πHOMO of ˙NH2 to the πLUMO of the phenyl radical for the C–N bond formation in aniline are accompanied by the repulsive interaction between the two π HOMOs on the two fragments. It is this repulsive interaction between the occupied orbitals, which pushes up the πHOMO on the phenyl ring of aniline and activates it to electrophilic substitution. The directionality of aniline can be understood from the 2pz contributions (located on the unsubstituted carbon atoms) to the πHOMO of aniline, which have the largest amplitude at the ortho and para positions.
In the case of nitrobenzene, the donor–acceptor interactions lead to a lowering of the πHOMO on the phenyl ring, which deactivates this orbital. Further inspection of the πHOMO and πHOMO−1 orbitals does not explain the directionality of nitrobenzene clearly. It is the VDD charge analysis which shows that the π electronic rearrangements due to C–N bond formation in nitrobenzene are responsible for the largest deactivation at the ortho and para positions of nitrobenzene, making the nitro group meta directing for electrophilic aromatic substitution.
Acknowledgements
O. A. S., H. S. and T. M. K. gratefully acknowledge the Foundation for Polish Science for supporting this work under the MPD/2010/4 project “Towards Advanced Functional Materials and Novel Devices – Joint UW and WUT International PhD Programme”. H. S. and T. M. K. thank the National Science Centre and the Ministry of Science and Higher Education of Poland for supporting this work under grant no. UMO-2013/11/B/ST4/00531. C. F. G. acknowledges the financial support from the Netherlands Organization for Scientific Research NWO.References
- (a) M. B. Smith, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, Wiley, New Jersey, 7th edn, 2013 Search PubMed; (b) F. A. Carey, Organic Chemistry, McGraw-Hill Higher Education, 2008 Search PubMed; (c) P. Y. Bruice, Organic Chemistry, Pearson/Prentice Hall, 2004 Search PubMed; (d) F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Part A: Structure and Mechanisms, Springer, New York, 2007 Search PubMed; (e) G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- (a) F. Bernardi, M. Guerra and G. F. Pedulli, Tetrahedron, 1978, 34, 2141–2146 CrossRef; (b) R. F. Johnston and J. C. Cooper, THEOCHEM, 1991, 82, 297–307 CrossRef CAS; (c) R. R. Monaco and W. C. Gardiner, J. Phys. Org. Chem., 1995, 8, 629–636 CrossRef CAS.
- (a) L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS; (b) L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 1st edn, 1940, 2nd edn, 1970 Search PubMed.
- (a) C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS; (b) T. M. Krygowski and B. T. Stpień, Chem. Rev., 2005, 105, 3482–3512 CrossRef CAS PubMed; (c) O. Exner and S. Bohm, Curr. Org. Chem., 2006, 10, 763–778 CrossRef CAS.
- (a) K. Fukui and H. Fujimoto, Frontier Orbitals and Reactions Paths, World Scientific, Singapore, 1997 Search PubMed; (b) M. J. S. Dewar, THEOCHEM, 1989, 200, 301–323 CrossRef; (c) H. Hirao and T. Ohwada, J. Phys. Chem. A, 2003, 107, 2875–2881 CrossRef CAS.
- (a) O. Exner and T. M. Krygowski, Chem. Soc. Rev., 1996, 25, 71–75 RSC; (b) P. Politzer, L. Abrahmsen and P. Sjoberg, J. Am. Chem. Soc., 1984, 106, 855–860 CrossRef CAS; (c) J. P. Ritchie, Tetrahedron, 1988, 44, 7465–7478 CrossRef CAS; (d) S. Irle, T. M. Krygowski, J. E. Niu and W. H. E. Schwarz, J. Org. Chem., 1995, 60, 6744–6755 CrossRef CAS.
- (a) F. M. Bickelhaupt and E. J. Baerends, Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, in Rev. Comput. Chem., ed. K. B. Lipkowitz and D. B. Boyd, Wiley, New York, 2000, vol. 15, pp. 1–86 Search PubMed; (b) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS; (c) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef CAS; (d) K. Morokuma, J. Chem. Phys., 1971, 55, 1236 CrossRef CAS.
- (a) L. Guillaumes, S. Simon and C. Fonseca Guerra, ChemistryOpen, 2015, 4, 318–327 CrossRef CAS PubMed; (b) C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Chem. – Eur. J., 1999, 5, 3581–3594 CrossRef; (c) C. Fonseca Guerra and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2002, 41, 2092–2095 CrossRef; (d) C. Fonseca Guerra, H. Zijlstra, G. Paragi and F. M. Bickelhaupt, Chem. – Eur. J., 2011, 17, 12612–12622 CrossRef CAS PubMed.
- (a) L. P. Wolters and F. M. Bickelhaupt, ChemistryOpen, 2012, 1, 96–105 CrossRef CAS PubMed; (b) L. P. Wolters, N. W. G. Smits and C. Fonseca Guerra, Phys. Chem. Chem. Phys., 2015, 17, 1585–1592 RSC.
- (a) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS; (b) F. M. Bickelhaupt, E. J. Baerends and N. M. M. Nibbering, Chem. – Eur. J., 1996, 2, 196 CrossRef CAS; (c) T. Fievez, B. Pinter, P. Geerlings, F. M. Bickelhaupt and F. De Proft, Eur. J. Org. Chem., 2011, 2958 CrossRef CAS; (d) G. T. de Jong and F. M. Bickelhaupt, ChemPhysChem, 2007, 8, 1170–1181 CrossRef CAS PubMed.
- (a) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, J. Phys. Chem. A, 2008, 112, 12816–12822 CrossRef CAS PubMed; (b) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, Aust. J. Chem., 2008, 61, 209–215 CrossRef CAS; (c) J. R. Mulder, C. Fonseca Guerra, J. C. Slootweg, K. Lammertsma and F. M. Bickelhaupt, J. Comput. Chem., 2016, 37, 304–313 CrossRef CAS PubMed; (d) I. Fernandez and G. Frenking, J. Org. Chem., 2006, 71, 2251–2256 CrossRef CAS PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS; (b) E. J. Baerends, et al., ADF 2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com; (c) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS; (d) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS; (e) J. G. Snijders, E. J. Baerends and P. Vernooijs, At. Data Nucl. Data Tables 26, 1981, 483 CrossRef CAS.
- H. Szatyłowicz, T. M. Krygowski and P. Hobza, J. Phys. Chem. A, 2007, 111, 170–175 CrossRef PubMed.
- (a) F. M. Bickelhaupt, N. J. R. van Eikema Hommes, C. Fonseca Guerra and E. J. Baerends, Organometallics, 1996, 15, 2923–2931 CrossRef CAS; (b) C. Fonseca Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef PubMed.
- (a) P. V. Vyas, A. K. Bhatt, G. Ramachandraiah and A. V. Bedekar, Tetrahedron Lett., 2003, 44, 4085–4088 CrossRef CAS; (b) S. Patai, The Chemistry of the Amino Group, Wiley, New York, 1968, pp. 250–265 Search PubMed.
- S. Rozen and O. Lerman, J. Org. Chem., 1993, 58, 239–240 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: MO diagrams for nitrobenzene and aniline in a perpendicular orientation; interaction energies and rotational barriers for substituted benzenes; and Cartesian coordinates of nitrobenzene and aniline at the BLYP/TZ2P level. See DOI: 10.1039/c5cp07483e |
| This journal is © the Owner Societies 2016 |