Mechanistic studies on C–C reductive coupling of five-coordinate Rh(III) complexes†
Shanshan
Chen
ac,
Yan
Su
b,
Keli
Han
b and
Xingwei
Li
*ab
aDivision of Chemistry and Biological Chemistry, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore 637371
bDalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China. E-mail: xwli@dicp.ac.cn
cDepartment of Applied Chemistry, School of Sciences, Anhui Agricultural University, Hefei 230036, China
First published on 29th April 2015
Abstract
A series of five-coordinate Rh(III) vinyl complexes [Rh(N^C)(PAr3)2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR]PF6 have been isolated as an intermediate in the coupling of a Rh(III) hydride with terminal alkynes. These Rh(III) vinyl complexes underwent aryl–vinyl reductive coupling to afford the Rh(I) chelating complex [Rh(N^C–CH
CHR]PF6 have been isolated as an intermediate in the coupling of a Rh(III) hydride with terminal alkynes. These Rh(III) vinyl complexes underwent aryl–vinyl reductive coupling to afford the Rh(I) chelating complex [Rh(N^C–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR)–(PAr3)2]PF6 in high yields. Kinetic studies on the C–C reductive elimination revealed that the reaction kinetics is first order for a Rh(III)(4-trifluoromethyl)styryl complex with activation parameters of ΔH≠ = 20.9 kcal mol−1 and ΔS≠ = −6.1 eu. The electronic effects of the styryl group and the phosphine ligands on the rate of C–C reductive elimination were studied, and the rate constant decreases for a more electron-poor styryl group but increases for a less donating phosphine. The inhibitive effect of the added phosphine indicates that the dissociation of phosphine to afford a four-coordinate intermediate is involved, which was further supported by DFT calculations. Although intermediacy of a 4-coordinate species has been suggested, the active intermediate that directly undergoes C–C coupling was pinpointed to a five-coordinate cis phosphine complex on the basis of DFT studies. Significant accelerating effects were observed for oxygen donor solvents (THF-d8 and acetone-d6), possibly via efficient stabilization of the four-coordinate intermediate. However coordination of CO forms an inert six-coordinate Rh(III) complex. Thus an overall detailed mechanism of alkyne insertion and subsequent aryl–vinyl reductive elimination from the Rh(III) center has been proposed based on the experimental and theoretical data.
CHR)–(PAr3)2]PF6 in high yields. Kinetic studies on the C–C reductive elimination revealed that the reaction kinetics is first order for a Rh(III)(4-trifluoromethyl)styryl complex with activation parameters of ΔH≠ = 20.9 kcal mol−1 and ΔS≠ = −6.1 eu. The electronic effects of the styryl group and the phosphine ligands on the rate of C–C reductive elimination were studied, and the rate constant decreases for a more electron-poor styryl group but increases for a less donating phosphine. The inhibitive effect of the added phosphine indicates that the dissociation of phosphine to afford a four-coordinate intermediate is involved, which was further supported by DFT calculations. Although intermediacy of a 4-coordinate species has been suggested, the active intermediate that directly undergoes C–C coupling was pinpointed to a five-coordinate cis phosphine complex on the basis of DFT studies. Significant accelerating effects were observed for oxygen donor solvents (THF-d8 and acetone-d6), possibly via efficient stabilization of the four-coordinate intermediate. However coordination of CO forms an inert six-coordinate Rh(III) complex. Thus an overall detailed mechanism of alkyne insertion and subsequent aryl–vinyl reductive elimination from the Rh(III) center has been proposed based on the experimental and theoretical data.
Introduction
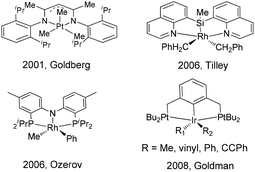
Transition-metal catalyzed C–C bond formation reactions via direct C–H bond activation have been increasingly developed in organic synthesis during the past several decades.1–14 Among these reactions, the reductive elimination of a C–C bond is one of the most important elementary steps because in many catalytic systems this is the product-forming step. Experimental and computational studies of C(sp3)–C(sp3), C(sp3)–C(sp2), C(sp2)–C(sp2) reductive elimination from palladium and platinum complexes have been extensively explored.15–24 However, the mechanism and controlling factors in C–C reductive elimination from other transition-metal complexes (Rh, Ir, Ru, Os, Co) are relatively less studied.25–35According to the reported mechanistic studies, C–C reductive elimination from d6 transition-metal complexes often proceeds via a five-coordinate intermediate,36–39 which is generated by ligand dissociation. In many cases, the five-coordinate intermediate is relatively unstable and is hardly isolable, which defies subsequent detailed mechanistic studies. As far as we know, only a few stoichiometric C–C coupling systems with authenticated five-coordinate intermediates have been documented. For example, a series of five-coordinate Pt(IV) alkyl intermediates bearing nitrogen pincers have been isolated and characterized by Goldberg,40 Tilley,41 Wang,42 and Song.43 Goldman reported a series of five-coordinate iridium(III) pincer complexes (PCP)Ir(R)(R)′ (R = alkyl, vinyl, aryl, alkynyl), which were synthesized from the corresponding RX and R′Li reactants. However, these intermediates were not stable for isolation, and they were only characterized by 1H and 31P NMR spectroscopy and by X-ray crystallography in their six-coordinate derivatives.44 Five-coordinate (PNP)Rh(R)(R)′ pincer intermediates that can reductively eliminate have been reported by Ozerov, but their structures were only proposed on the basis of spectroscopic characterization (Scheme 1).45
On the other hand, very recently, rhodium(III)-catalyzed C–H activation/C–C coupling reactions have been increasingly explored and a vast majority of efficient synthetic methods have been developed.8,11,13 These methods also offered important synthetic complements to palladium- and ruthenium-catalyzed C–H activation/C–C coupling reactions. The C–C reductive elimination of a Rh(III) complex is particularly important because it is proposed as a key product-forming step in many catalytic systems with a Rh(III)/Rh(I) cycle. Despite the significance, only a few reports detailed the stoichiometric C–C reductive elimination of Rh(III) complexes,27,35,41b,45 which stands in sharp contrast to the majority of reports on stoichiometric C–C and C–N coupling of palladium complexes. Inspired by the above reports, we aim to synthesize a range of rhodium(III) complexes to delve into the mechanism of subsequent C–C reductive coupling using a combination of experimental and theoretical methods.
Results and discussion
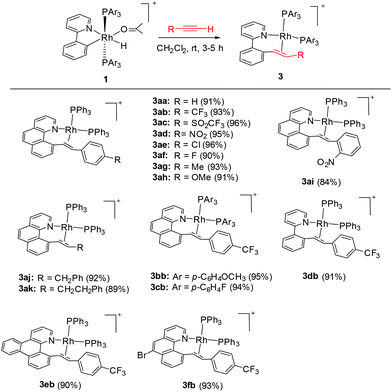
In 2003, Crabtree and coworkers reported the double insertion of a terminal alkyne into a cyclometalated iridium(III) hydride to afford a butadienyl complex, with the cylometalated ligand being a spectator.27a In contrast to iridium, rhodium generally forms a weaker M–C bond. Therefore, the interactions of Rh(III) hydrides with alkynes may follow a different reaction pattern. Thus the cyclometalated ligand might act as a participating group in subsequent C–C coupling.Synthesis of [Rh(N^C)(PAr3)2(CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) CHR)]PF6 intermediate 2
CHR)]PF6 intermediate 2
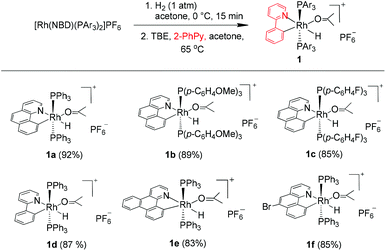
We reasoned that the insertion of a terminal alkyne into a stable rhodium aryl hydride may afford an isolable alkenyl complex that can be a suitable candidate for subsequent C(aryl)–C(alkenyl) coupling studies. This is based on the rationale that a Rh–C(aryl) bond is usually kinetically more labile than the iridium counterpart. To achieve this goal, a series of cyclometalated rhodium(III) hydride complexes 1 have been prepared via cyclometalation according to our previously reported procedure in the presence of tert-butylethylene (TBE) (Scheme 2).46 All these hydride complexes were fully characterized and, in particular, the hydride signal resonates as a doublet of triplets in a narrow range of δ −12.13 to −12.49 in the 1H NMR spectroscopy and the Rh–C resonates as a doublet of triplets (δ 153.08 to 163.83) in 13C NMR spectroscopy (acetone-d6).
Isolation of five-coordinate Rh(III) alkenyl complexes
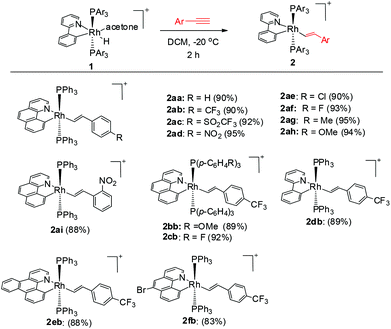
To our delight, stirring a mixture of hydride 1a and an excess of (4-trifluoromethyl)phenylacetylene in DCM at −20 °C led to a red solution with the clean formation of a Rh(III) trans-styryl complex 2ab, although the reaction at rt afforded a Rh(I) C–C coupled product (vide infra). Rapid removal of the solvent followed by washing with diethyl ether afforded 2ab in analytical purity in 90% yield. Complex 2ab was fully characterized at −20 °C. On the basis of 1H NMR spectroscopy, only one equiv. of alkyne was incorporated and a characteristic doublet of triplets signal at δ 8.36 (dt, 3JHH = 17.0 Hz, 3JPH = 5.5 Hz) was observed and was assigned to the β proton of the trans-styryl unit (Rh–CH = CH(C6H4)CF3). The other olefinic CH was detected at δ 5.13 (d, 3JHH = 17.0 Hz). Furthermore, no ligated acetone could be detected by 1H NMR spectroscopy, indicating that complex 2a might be five-coordinate. In the 13C NMR spectrum, two Rh–C signals were detected each as a triplet of doublets at δ 145.08 (dt, 2JRhC = 42.9 Hz, 3JPC = 9.2 Hz, Rh-aryl) and δ 153.65 (dt, 2JRhC = 32.2 Hz, 3JPC = 10.7 Hz, Rh-styryl). In the 31P NMR spectrum, a doublet signal (δ 23.4, 1JRhP = 112.1 Hz) was observed for the two equivalent phosphorus atoms, indicative of their trans orientation.By following this procedure, a series of terminal alkynes bearing various electron-donating and -withdrawing substituents underwent smooth insertion into the Rh–H bond to afford the corresponding Rh(III) alkenyl complexes in high yields (Scheme 3). These results stand in contrast to the facile double insertion of alkyne into the iridium congener of rhodium hydrides 1, where the insertion of the 2nd equiv. of alkyne into the Ir–vinyl bond readily proceeded so that no iridium(III) vinyl intermediate could be isolated in a less coordinating solvent such as DCM.27a
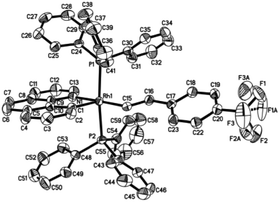
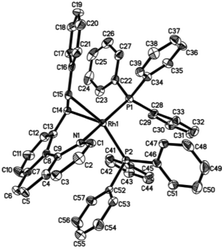
Crystal structure
Single crystals of 2ab suitable for X-ray crystallographic studies were obtained by slow diffusion of diethyl ether to a dichloromethane solution at −20 °C. X-ray crystallographic studies unambiguously confirmed the identity of 2ab (Fig. 1). As depicted in Fig. 1, the two PPh3 ligands are mutually trans and the coordination sphere involves five regular bonds, while the sixth coordination site is unoccupied and is trans to the high trans-effect aryl ligand. No secondary interaction between the rhodium center and the styryl group could be detected. Therefore this Rh(III) styryl complex represents a rare example of a five-coordinate d6 complex generated from the insertion of an alkyne into a metal hydride.C–C reductive elimination of the vinyl complexes
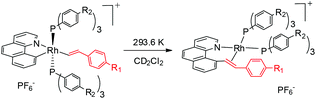
It has been well studied that metal complexes with coordinative unsaturation tend to undergo facile reductive elimination.36–39 Thus, we reasoned that our coordinatively unsaturated and fluxional complexes 2 might be labile toward reductive coupling, and consequently they may be a suitable subject for stoichiometric studies. Indeed, dissolution of the five-coordinate vinyl complex 2ab in CD2Cl2 at room temperature led to clean and quantitative formation of the C–C coupled product 3ab within hours. Alternatively, this product could be isolated in a similar yield directly from the room temperature reaction of rhodium hydride 1a and (4-trifluoromethyl)phenylacetylene. The reductively coupled product was fully characterized by NMR spectroscopy and X-ray crystallography. In the 1H NMR spectrum of 3ab (CD2Cl2), two doublets of doublets resonate at δ 6.48 ppm and δ 5.50 ppm and were assigned to the α and the β protons in the styryl unit, respectively, on the basis of HMBC and HMQC spectroscopy. The observed coupling constant (13.8 Hz) between these two protons is slightly less than 16 Hz as a result of the change in the hybridization to a more sp3 character, suggestive of a metal-bound olefin group. In the 13C NMR spectrum (CD2Cl2), the two olefinic carbon signals were detected at δ 78.6 (dd, 2JRhC = 19.9 Hz, 3JPC = 6.2 Hz) and δ 85.0 (d, 2JRhC = 12.1 Hz). The ipso carbons of the phenyl groups in PPh3 appear as a doublet at δ 130.6 (1JPC = 45.8 Hz) and 130.9 (1JPC = 41.1 Hz) with no virtual coupling, indicative of the cis orientation of the PPh3 ligands. In line with the 13C NMR data, the 31P NMR spectrum gave two mutually coupled signals at δ 30.95 (dd, 1JRhP = 169.4 Hz, 2JPP = 44.5 Hz) and 36.21 (dd, 1JRhP = 155.6 Hz, 2JPP = 44.0 Hz), the latter signal being assigned to the PPh3trans to the olefin ligand, where the smaller JRh–P is caused by the high trans, labilizing effect of the olefin.By following this generic procedure, C–C reductively coupled products were conveniently prepared in a broad scope from the room temperature reaction between the Rh(III) hydride complex and a terminal alkyne (Scheme 4). Since this process involved the insertion of alkyne into a rhodium(III) hydride, deuterium labeling studies have been performed using 1a and phenylacetylene-d (eqn (1)). 1H NMR analysis of the isolated Rh(I) olefin complex revealed that the deuterium was located exclusively at the carbon adjacent to the benzo[h]quinoline unit. This suggests no cleavage of the alkynyl C–H bond during the insertion of the alkyne, hence ruling out the intermediacy of a vinylidiene species.
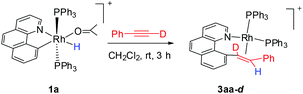 | (1) |
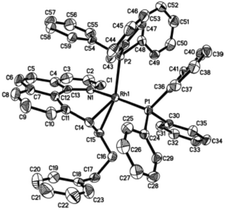
Crystal structure of Rh(I) products
Single crystals of 3aa and 3ak suitable for X-ray crystallographic studies were obtained by the slow diffusion of diethyl ether to their dichloromethane solutions at room temperature (Fig. 2 and 3). As shown in Fig. 2, 3aa is best described as a square planar complex and the coordination sphere includes a chelating pyridine-olefine ligand and two cis PPh3 ligands. The benzo[h]quinoline ring is slightly twisted to accommodate this chelation mode in a rather sterically congested setting. Detailed crystallographic data on complexes 3aa and 3ak are provided in the ESI.†Although the five-coordinate vinyl complexes readily coupled at room temperature, bubbling CO through a solution of 2ab led to the formation of a six-coordinate carbonyl complex 4 which was isolated in quantitative yield (eqn (2)). The CO occupies the sixth site to give a stable Rh(III) complex so that no C–C reductive elimination was observed. This observation further indicates that C–C reductive elimination tends to occur preferentially for coordinatively unsaturated species.
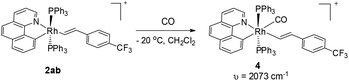 | (2) |
Kinetic studies
Kinetic parameters for the conversion of 2ab to 3ab were experimentally assessed by monitoring the decay of 2ab by 19F NMR spectroscopy in CD2Cl2 to reveal k = 2.28(1) × 10−3 min−1 at 287.7 K. The reaction was found to obey first-order kinetics. The rate constants measured at different temperatures are displayed in Table 1. Temperature dependence studies of the 2ab to 3ab conversion allowed for the extraction of the activation parameters ΔH≠ = 20.9(3) kcal mol−1 and ΔS≠ = −6.1(3) cal (mol K)−1 from the Eyring plot. This negative value of ΔS≠ suggests that the transition state is slightly more ordered than the ground state. However, the ΔS≠ value is not significant enough to warrant conclusive discussion of the mechanism.| Entry | T (K) | k (min−1) |
|---|---|---|
| 1 | 287.7 | 0.00228(1) |
| 2 | 293.6 | 0.00471(7) |
| 3 | 297.0 | 0.00704(4) |
| 4 | 305.3 | 0.0197(1) |
To gain further insight into the mechanism of this reductive elimination, the electronic effect of the reactive styryl group has been perturbed. It was found that the introduction of a more electron-donating substituent into the para position of the phenyl ring in the styryl group resulted in a more rapid decay (Table 2, entries 1–5), and the most electron-withdrawing substituent –SO2CF3 gave the lowest rate. The linear free energy correlation between the rate constant and the σp of the para substituent gave a straight line (R2 = 0.955). An alternative plot using the resonance substituent constant σp+ also gave a straight line with R2 = 0.954, indicating that the resonance effects probably have a dominant influence on the rate of the coupling reaction (Chart 1). On the other hand, the reaction occurred faster for more electron-poor ancillary phosphine ligands (entries 1, 6, and 7). These observations are typical and are consistent with those in most kinetic studies on the (concerted) reductive elimination of Pd(II) complexes,20 where these two baseline electronic effects are attributed to the electronic effects of the ground state.
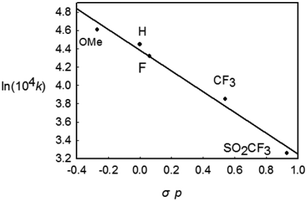 | ||
| Chart 1 The Hammett plot for the decay of Rh(III) complexes bearing different p-substituents in the styryl group. | ||
Effects of cyclometalated ligands
We next investigated the effects of the reactive cyclometalated aryl ligand, and the data are given in Scheme 5. It was found that an aryl group with extended conjugation gives a higher rate, although this effect is not significant. This observation seems counterintuitive in terms of the ground state electronic effects because an extended conjugated aryl group tends to facilitate π-back donation to give a stronger Rh–Aryl bond. However, this observation may be ascribable to transition state stabilization or stabilization of the ligated olefin product, where a more rigid chelating N^C group gives a better stabilized π-olefin complex. Clearly, pre-decoordination of the pyridyl group is unlikely because in this case the 2-phenylpyridyl ligand is most flexible among all the three and the decay of 2db to 3db would have been fastest.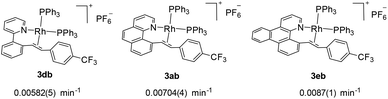 | ||
| Scheme 5 Effects of the cyclometalated aryl ligands on the rate of C–C reductive coupling (297.0 K, CD2Cl2). | ||
The solvent effects
The effect of solvents on the reductive elimination has also been investigated (Table 3). Reactions conducted at 281 K in a weakly coordinating, oxygen-containing solvent such as acetone-d6 and THF-d8 occurred significantly faster than in CD2Cl2, but there is no correlation between the dielectric constant of the solvent and the reaction rate. Instead, the donating capacity of the solvent seems to play an important role, possibly by stabilization of a cationic, unsaturated four- or five-coordinate intermediate.| Entry | Solvent | Dielectric constant | k (min−1) |
|---|---|---|---|
| 1 | CD2Cl2 | 9.1 | 0.000958 (extrapolated) |
| 2 | THF-d8 | 7.5 | 0.0214(2) |
| 3 | Acetone-d6 | 21 | 0.0231(2) |
The fact that the reductive coupling occurred at a higher rate in a more coordinating solvent simply suggests that the reaction proceeds either via a four coordinate or a five coordinate intermediate such as a five coordinate diphosphine or a PPh3/solvent complex. Furthermore, the PPh3/solvent intermediate is quite unlikely when CH2Cl2 was used as a solvent. To gain further insight, the effect of added phosphine has been examined.
Effects of added phosphine ligands
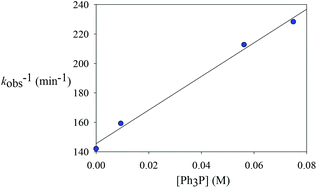
To explore whether the reductive elimination occurs via a four-coordinate Rh(III) intermediate via phosphine dissociation, phosphine concentration-dependent kinetic studies have been performed at 297 K (Table 4). It was found that the decay of 2ab was slightly inhibited with the introduction of various amounts of PPh3. On the other hand, 31P and 19F NMR spectroscopy revealed that no new phosphine-containing species was generated and the only detectable species are 2ab and PPh3. This indicates that the initial concentration of 2ab was not affected upon addition of PPh3 and the starting five-coordinate rhodium species is not a directly reactive species. Instead, reversible phosphine dissociation to afford a reactive four-coordinate monophosphine intermediate was suggested and is kinetically important, and the formation of such a four-coordinate species was inhibited by the introduction of phosphine. Indeed, this proposal of four-coordinate species seems to correlate well with the solvent effect. This reactive four-coordinate species was stabilized by weakly coordinating solvents such as acetone and THF by oxygen binding, leading to a more rapid decay.| Entry | [PPh3] (M) | k obs (M−1 min−1) |
|---|---|---|
| 1 | 0 | 0.00704(4) |
| 2 | 0.00936 (1 equiv.) | 0.00628(13) |
| 3 | 0.0562 (6 equiv.) | 0.0047(1) |
| 4 | 0.0749 (8 equiv.) | 0.00438(4) |
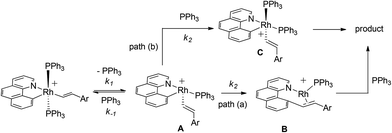
Postulated elementary steps for the decay of 2ab to 3ab are depicted in Scheme 6. In path (a), phosphine dissociation generates a four-coordinate intermediate, which undergoes reorganization (A) and reductive elimination to afford a three-coordinate olefin intermediate (B). The final product was produced with the rapid recoordination of the PPh3. Alternatively (path (b)), the four-coordinate intermediate A may be trapped by PPh3 to give a cis phosphine intermediate C, C–C coupling of which furnishes the final product. These two pathways are kinetically undistinguishable by experimental methods if the steps after the formation of the four-coordinate intermediate are not rate-determining.
 | (3) |
The DFT method
For the calculation of the free energy associated with the elementary process which involves adduct formation between the Rhodium complex and phosphine and the process which involves dissociation of the phosphine from the Rhodium complex, entropy effects should be taken into consideration.We evaluate free energy change at 298 K by two ways. In one way, translation, rotation, and vibration movements are taken into consideration to estimate the thermal entropy and free energy, where all substrates are treated as the ideal gas. In the other way, only the vibration movements are considered in the estimation of the thermal energy and free energy, but translation and rotation movements are neglected, because in the solution the translation and rotation movements are highly suppressed. In the former method, entropy significantly decreases upon the formation of adduct from two molecules, as expected. In the latter method, on the other hand, formation of adduct induces a very small entropy change, as will be discussed below. The former method apparently overestimates the entropy effects and the thermal energy of the solution reaction, because translation and rotation movements are highly suppressed in solution. On the other hand, the latter method underestimates the entropy effects and the thermal energy, because translation and rotation movements are not completely suppressed in solution. The true value would be intermediate between the value (ΔG°) obtained by the former method and that (ΔGv°) by the latter one, and more or less close to the free energy change estimated by the latter method, when the reaction is carried out in solution.
Because this ambiguity remains in the estimation of the entropy and thermal energy, we will discuss each elementary step based on the usual total energy changes with zero-point energy correction (ΔE). Of course, the free energy change does not differ so much from the total energy change in the elementary steps that involve neither the formation of adduct nor the release of product. Also, the free energy change that is evaluated by considering only vibration movements does not differ so much from the total energy change. The significant difference between the free energy change and the total energy change is observed in the elementary process that involves either the formation of adduct or the release of product, when translation, rotation, and vibration movements are considered in the estimation of free energy.
All the DFT calculations were carried out using the GAUSSIAN 09 series of programs. Density functional theory and B3LYP with a standard 6-31+G(d) basis set (SDD basis set for Rh) were used for geometry optimizations. The solvent effects were considered by single point calculations on the gas-phase stationary points with a SMD continuum solvation model.
DFT studies
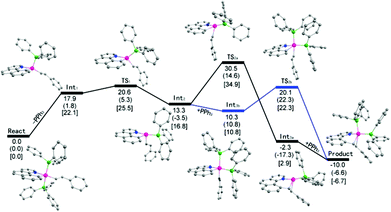
Theoretical studies at the DFT level have been performed (Scheme 7). It was found that the initial phosphine dissociation occurs with ΔG = 22.1 kcal mol−1 because this process is unfavorable in both entropy and enthalpy. Int1 readily isomerizes by Berry pseudorotation to produce a slightly more stable four coordinate Int2 with a minimal barrier, where the styryl group is oriented to the epical position. DFT studies suggest that path (a) is unlikely because a rather high free energy of 34.9 kcal mol−1 (18.1 kcal mol−1 for this step) was located for the TS2a when Int2 directly reductively eliminates to give Int3a. In contrast, by following path (b), PPh3 binding to Int2 gives Int3b with slight exergonicity. Thus the conversion of the starting complex to Int3b represents a facile stepwise trans to cis isomerization of phosphine complexes. Reductive elimination of Int3b can readily occur at a barrier of 11.5 kcal mol−1, and this barrier is rather low partially because of the steric assistance: the repulsion between the two cis phosphine ligands is partially released when the final product is formed. In addition, the ligands experience minimal reorganization during the reductive elimination. The overall reaction is slightly exergonic by 6.7 kcal mol−1. It should be noted that although DFT studies seemingly suggest a positive ΔS≠ with the dissociation of a phosphine ligand, the entropy change was overlooked. Solvent reorganization or polarization by a cationic metal center may contribute to a slightly negative ΔS≠. Clearly, path (b) is preferred. The calculated energy profile is in both qualitative and quantitative agreement with the experimental data in terms of the activation energy and the rate law of the phosphine. The calculated highest barrier of ΔG≠ = 25.5 kcal mol−1 represents the barriers of the dissociation of the phosphine ligand. This theoretical value stays in line with the experimental value of ΔG≠ = 23.6 kcal mol−1 derived from the rate constant of 8.6 × 10−3 min−1 at 293 K (Table 2, entry 2). In addition to these two possible pathways, direct reductive elimination of the starting complex has been attempted, and indeed a significantly higher kinetic barrier was located.While the fact that the C–C reductive coupling occurred at a higher rate in oxygen-containing solvents may not lead to any solid conclusion on the intermediacy of the kinetically important species (both four and five coordinate species remain possible), our DFT studies provided further evidence. Our solvent-dependent kinetics is at least consistent with the DFT studies. The starting trans phosphine complex is kinetically inert and cannot undergo direct C–C reductive coupling. In a more coordinating solvent, the dissociation of one of the phosphine ligands is facilitated because the resulting four coordinate intermediate Int1 is coordinatively unsaturated and can be better stabilized. This extra stabilization does not exist in a poorly coordinating solvent such as CH2Cl2.
Conclusions
A series of rare five-coordinate [Rh(C^N)(PAr3)2(CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR)]–PF6 complexes have been isolated from the insertion of alkyne into stable Rh(III) hydrides. These five-coordinate complexes are kinetically labile at room temperature and undergo clean reductive coupling to afford stable Rh(I) alkene complexes [Rh(N^C–CH
CHR)]–PF6 complexes have been isolated from the insertion of alkyne into stable Rh(III) hydrides. These five-coordinate complexes are kinetically labile at room temperature and undergo clean reductive coupling to afford stable Rh(I) alkene complexes [Rh(N^C–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR)(PAr3)2]PF6. Thus direct observation of C–C reductive coupling from five-coordinate d6 transition metals has been made, and mechanistic details of this process have been studied by a combination of experimental and theoretical approaches.
CHR)(PAr3)2]PF6. Thus direct observation of C–C reductive coupling from five-coordinate d6 transition metals has been made, and mechanistic details of this process have been studied by a combination of experimental and theoretical approaches.
Activation parameters were obtained from temperature-dependent kinetic studies. The solvent effect and the electronic effects of the reactive and ancillary ligands have been established, where the electronic effects pointed to typical ground state electronic influences. Introduction of phosphine has an inhibitive effect on the rate of decay and the phosphine concentration-dependent studies suggest that dissociation of a phosphine is involved. Thus the intermediacy of a four-coordinate intermediate plays an important role. Weakly coordinating oxygen-containing solvents tend to favor the reductive elimination possibly by ligation and stabilization of a lower-coordinate intermediate. The phosphine concentration-dependent studies suggest reversible phosphine dissociation and a four-coordinate intermediate is involved. Two mechanistically distinct pathways have been suggested based on experimental studies.
DFT studies have been applied to distinguish between these two possible pathways. It turned out that although a four-coordinate intermediate is involved, it does not undergo direct C–C reductive elimination to give a three coordinate olefin complex intermediate. Instead, recoordination of the departed phosphine ligands yields an isomerized cis phosphine intermediate that is the active species toward C–C reductive elimination. The DFT studies revealed that phosphine dissociation is rate-limiting and the activation free energy is in good agreement with the experimental result. The five-coordinate Rh(III) and the coupled Rh(I) complexes obtained in our system offered direct experimental data for related catalytic C–H activation and C–C coupling reactions since C–C reductive elimination studies are particularly rare for cationic complexes. Insights gained in this work may provide useful information for the design of new catalysts for C–C coupling.
Acknowledgements
We thank the Dalian Institute of Chemical Physics, Chinese Academy of Sciences and School of Physical and Mathematical Sciences, Nanyang Technological University, for financial support. Financial support from the NSFC is also gratefully acknowledged (no. 21272231). We thank Dr Yongxin Li for crystallographic analyses.Notes and references
- S. Murai, F. Kakiuchi, S. Sekine, Y. Tanaka, A. Kamatani, M. Sonoda and N. Chatani, Nature, 1993, 366, 529 CrossRef CAS PubMed.
- B. M. Trost, Angew. Chem., Int. Ed., 1995, 34, 259 CrossRef CAS PubMed.
- W. D. Jones, Topics in Organometallic Chemistry, ed. S. Murai, Spring-Verlag, New York, 1999, vol. 3, p. 9 Search PubMed.
- F. Kaikiuchi and S. Murai, Topics in Organometallic Chemistry, ed. S. Murai, Spring-Verlag, New York, 1999, vol. 3, p. 47 Search PubMed.
- V. Ritleng, C. Sirlin and M. Preffer, Chem. Rev., 2002, 102, 1731 CrossRef CAS PubMed.
- K. Fagnou and M. Lautens, Chem. Rev., 2003, 103, 169 CrossRef CAS PubMed.
- F. Kakiuchi, Top. Organomet. Chem., 2007, 24, 1 CrossRef CAS.
- D. A. Colby, R. G. Bergman and J. A. Ellman, Chem. Rev., 2010, 110, 624 CrossRef CAS PubMed.
- X. Wang, L. Zhou and W. Lu, Curr. Org. Chem., 2010, 14, 289 CrossRef CAS.
- D. J. Schipper, M. Hutchinson and K. Fagnou, J. Am. Chem. Soc., 2010, 132, 6910 CrossRef CAS PubMed.
- D. A. Colby, A. S. Tsai, R. G. Bergman and J. A. Ellman, Acc. Chem. Res., 2012, 45, 814 CrossRef CAS PubMed.
- P. B. Arockiam, C. Bruneau and P. H. Dixneuf, Chem. Rev., 2012, 112, 5879 CrossRef CAS PubMed.
- (a) G. Y. Song, F. Wang and X. Li, Chem. Soc. Rev., 2012, 41, 3651 RSC; (b) T. Satoh and M. Miura, Chem. – Eur. J., 2010, 16, 11212 CrossRef CAS PubMed; (c) F. W. Patureau, J. Wencel-Delord and F. Glorius, Aldrichimica Acta, 2012, 45, 31 CAS; (d) N. Kuhl, N. Schroder and F. Glorius, Adv. Synth. Catal., 2014, 356, 1443 CrossRef CAS PubMed; (e) G. Song and X. Li, Acc. Chem. Res., 2015, 48, 1007 CrossRef CAS PubMed. For a report on rhodium-catalyzed C–H activation that generated olefinated arenes bearing a heteroarene directing group (related to the chelating ligand in products 3 in this work), see: (f) N. Schroder, T. Besset and F. Glorius, Adv. Synth. Catal., 2012, 354, 579 CrossRef PubMed.
- K. Gao and N. Yoshikai, Acc. Chem. Res., 2014, 47, 1208 CrossRef CAS PubMed.
- (a) D. M. Crumpton and K. I. Goldberg, J. Am. Chem. Soc., 2000, 122, 962 CrossRef CAS; (b) D. M. Crumpton-Bregel and K. I. Goldberg, J. Am. Chem. Soc., 2003, 125, 9442 CrossRef CAS PubMed; (c) K. L. Arthur, Q. L. Wang, D. M. Bregel, N. A. Smythe, B. A. O'Neill, K. I. Goldberg and K. G. Moloy, Organometallics, 2005, 24, 4624 CrossRef CAS; (d) J. Procelewska, A. Zahl, G. Liehr, R. V. Eldik, N. A. Smythe, B. Scott Williams and K. I. Goldberg, Inorg. Chem., 2005, 44, 7732 CrossRef CAS PubMed; (e) A. T. Luedtke and K. I. Goldberg, Inorg. Chem., 2007, 46, 8496 CrossRef CAS PubMed.
- T. Korenaga, K. Abe, A. Ko, R. Maenishi and T. Sakai, Organometallics, 2010, 29, 4025 CrossRef CAS.
- M. P. Lanci, M. S. Remy, D. B. Lao, M. S. Sanford and J. M. Mayer, Organometallics, 2011, 30, 3704 CrossRef CAS.
- (a) A. Ariafard and B. F. Yates, J. Organomet. Chem., 2009, 694, 2075 CrossRef CAS PubMed; (b) A. Ariafard, Z. Ejehi, H. Sadrara, T. Mehrabi, S. Etaati, A. Moradzadeh, M. Moshtaghi, H. Nosrati, N. J. Brookes and B. F. Yates, Organometallics, 2011, 30, 422 CrossRef CAS.
- (a) A. J. Canty, in Comprehensive Organometallic Chemistry, ed. R. J. Puddephatt, Pergamon, New York, 2nd edn, 1995, vol. 9, Chapter 5 Search PubMed; (b) D. Kruis, M. A. Markies, A. J. Canty, J. Boersma and G. van Koten, J. Organomet. Chem., 1997, 532, 235 CrossRef CAS; (c) A. J. Canty, J. L. Hoare, N. W. Davies and P. R. Traill, Organometallics, 1998, 17, 2046 CrossRef CAS; (d) A. J. Canty, J. L. Hoare, J. Patel, P. M. Feffer, B. W. Skelton and A. H. White, Organometallics, 1999, 18, 2660 CrossRef CAS; (e) A. Bayler, A. J. Canty, P. G. Edwards, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 2000, 3325 RSC.
- J. F. Hartwig, Inorg. Chem., 2007, 46, 1936 CrossRef CAS PubMed.
- B. L. Madison, S. B. Thyme, S. Keene and B. S. Williams, J. Am. Chem. Soc., 2007, 129, 9538 CrossRef CAS PubMed.
- (a) V. P. Ananikov, D. G. Musaev and K. Morokuma, J. Am. Chem. Soc., 2002, 124, 2839 CrossRef CAS PubMed; (b) V. P. Ananikov, D. G. Musaev and K. Morokuma, Organometallics, 2005, 24, 715 CrossRef CAS; (c) V. P. Ananikov, D. G. Musaev and K. Morokuma, Eur. J. Inorg. Chem., 2007, 5390 CrossRef CAS PubMed; (d) V. P. Ananikov and I. P. Beletskaya, Chem. – Asian J., 2011, 6, 1423 CrossRef CAS PubMed.
- (a) R. A. Widenhoefer and S. L. Buchwald, J. Am. Chem. Soc., 1998, 120, 6504 CrossRef CAS; (b) M. R. Biscoe, T. E. Barder and S. L. Buchwald, Angew. Chem., Int. Ed., 2007, 46, 7232 CrossRef CAS PubMed.
- (a) J. M. Racowski, A. R. Dick and M. S. Sanford, J. Am. Chem. Soc., 2009, 131, 10974 CrossRef CAS PubMed; (b) N. D. Ball, J. B. Gary, Y. Ye and M. S. Sanford, J. Am. Chem. Soc., 2011, 133, 7577 CrossRef CAS PubMed; (c) A. M. Wagner, A. J. Hickman and M. S. Sanford, J. Am. Chem. Soc., 2013, 135, 15710 CrossRef CAS PubMed.
- C. Hahn, M. Spiegler, E. Herdtweck and R. Taube, Eur. J. Inorg. Chem., 1999, 435 CrossRef CAS.
- J. Navarro, E. Sola, M. Martín, I. T. Dobrinovitch, F. J. Lahoz and L. A. Oro, Organometallics, 2004, 23, 1908 CrossRef CAS.
- (a) X. Li, C. D. Incarvito and R. H. Crabtree, J. Am. Chem. Soc., 2003, 125, 3698 CrossRef CAS PubMed; (b) X. Li, L. N. Appelhans, J. W. Faller and R. H. Crabtree, Organometallics, 2004, 23, 3378 CrossRef CAS.
- M. A. Esteruelas, F. J. Fernández-Alvarez, M. Oliván and E. Oñate, J. Am. Chem. Soc., 2006, 128, 4596 CrossRef CAS PubMed.
- S. H. Wiedemann, J. C. Lewis, J. A. Ellman and R. G. Bergman, J. Am. Chem. Soc., 2006, 128, 2452 CrossRef CAS PubMed.
- L. Benhamou, V. César, N. Lugan and G. Lavigne, Organometallics, 2007, 26, 4673 CrossRef CAS.
- K. J. Hawkes, K. J. Cavell and B. F. Yates, Organometallics, 2008, 27, 4758 CrossRef CAS.
- R. Ghosh, T. J. Emge, K. Krogh-Jespersen and A. S. Goldman, J. Am. Chem. Soc., 2008, 130, 11317 CrossRef CAS PubMed.
- H. Xu and W. H. Bernskoetter, J. Am. Chem. Soc., 2011, 133, 14956 CrossRef CAS PubMed.
- R. J. Pawley, M. A. Huertos, G. C. Lloyd-Jones, A. S. Weller and M. C. Willis, Organometallics, 2012, 31, 5650 CrossRef CAS.
- (a) N. Wang, B. Li, H. Song, S. Xu and B. Wang, Chem. – Eur. J., 2013, 19, 358 CrossRef CAS PubMed; (b) G. Zhang, L. Yang, Y. Wang, Y. Xie and H. Huang, J. Am. Chem. Soc., 2013, 135, 8850 CrossRef CAS PubMed; (c) M. Brasse, J. Campora, J. A. Ellman and R. G. Bergman, J. Am. Chem. Soc., 2013, 135, 6427 CrossRef CAS PubMed.
- B. Rybtchinski and D. Milstein, in Activation and Functionalization of C-H Bonds, ACS Symposium Series, American Chemical Society, Washington, DC, 2004, vol. 885, pp. 70–85 Search PubMed.
- (a) M. P. Brown, R. J. Puddephatt and C. E. E. Upton, J. Organomet. Chem., 1973, 49, C61 CrossRef CAS; (b) M. P. Brown, R. J. Puddephatt and C. E. E. Upton, J. Chem. Soc., Dalton Trans., 1974, 2457 RSC.
- G. S. Hill, G. P. A. Yap and R. J. Puddephatt, Organometallics, 1999, 18, 1408 CrossRef CAS and references therein.
- R. Cohen, M. E. Van der Boom, L. J. W. Shimon, H. Rozenberg and D. Milstein, J. Am. Chem. Soc., 2000, 122, 7723 CrossRef CAS.
- (a) U. Fekl, W. Kaminsky and K. I. Goldberg, J. Am. Chem. Soc., 2001, 123, 6423 CrossRef CAS; (b) U. Fekl and K. I. Goldberg, J. Am. Chem. Soc., 2002, 124, 6804 CrossRef CAS PubMed; (c) U. Fekl, W. Kaminsky and K. I. Goldberg, J. Am. Chem. Soc., 2003, 125, 15286 CrossRef CAS PubMed; (d) S. M. Kloek and K. I. Goldberg, J. Am. Chem. Soc., 2007, 129, 3460 CrossRef CAS PubMed; (e) A. T. Luedtke and K. I. Goldberg, Inorg. Chem., 2007, 46, 8496 CrossRef CAS PubMed; (f) M. L. Scheuermann, A. T. Luedtke, S. K. Hanson, U. Fekl, W. Kaminsky and K. I. Goldberg, Organometallics, 2013, 32, 4752 CrossRef CAS.
- (a) D. Karshtedt, J. L. McBee, A. T. Bell and T. D. Tilley, Organometallics, 2006, 25, 1801 CrossRef CAS; (b) P. Sangtrirutnugul, M. Stradiotto and T. D. Tilley, Organometallics, 2006, 25, 1607 Search PubMed; (c) P. Sangtrirutnugul and T. D. Tilley, Organometallics, 2008, 27, 2223 CrossRef CAS.
- (a) S. B. Zhao, G. Wu and S. Wang, Organometallics, 2008, 27, 1030 CrossRef CAS; (b) S. B. Zhao, Q. Cui and S. Wang, Organometallics, 2010, 29, 998 CrossRef CAS.
- R. Tan and D. Song, Inorg. Chem., 2011, 50, 10614 CrossRef CAS PubMed.
- (a) R. Ghosh, X. Zhang, P. Achord, T. J. Emge, K. Krogh-Jespersen and A. S. Goldman, J. Am. Chem. Soc., 2007, 129, 853 CrossRef CAS PubMed; (b) R. Ghosh, T. J. Emge, K. Krogh-Jespersen and A. S. Goldman, J. Am. Chem. Soc., 2008, 130, 11317 CrossRef CAS PubMed.
- S. Gatard, R. Çelenligil-Çetin, C. Y. Guo, B. M. Foxman and O. V. Ozerov, J. Am. Chem. Soc., 2006, 128, 2808 CrossRef CAS PubMed.
- (a) S. S. Chen, G. Y. Song and X. Li, Tetrahedron Lett., 2008, 49, 6929 CrossRef CAS PubMed; (b) S. S. Chen, Y. Li, J. Zhao and X. Li, Inorg. Chem., 2009, 48, 1198 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information on the syntheses, characterization data of all rhodium complexes, X-Ray crystal data (2ab, 3aa and 3ak), and the kinetic results. CCDC 1008419–1008421. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qo00049a |
| This journal is © the Partner Organisations 2015 |